The Sensitivity of Subsurface Microbes to Ocean Warming Accentuates Future Declines in Particulate Carbon Export

Introduction

The biological pump exports large amounts of carbon from the surface ocean to the deep, where it can be stored on climatically-relevant timescales helping to regulate atmospheric carbon dioxide levels (Volk and Hoffert, 1985; Falkowski et al., 1998). However future ocean warming threatens to decrease the amount of particulate organic carbon (POC) reaching the deep ocean (Laufkötter et al., 2016). The magnitude of deep ocean carbon storage by the biological pump is largely dependent on 3 factors; (1) the magnitude and size-partitioning of primary production taking place in the surface mixed layer, (2) the sinking rate of the particles formed initially from particle production, and (3) the organic remineralisation rate by organisms such as zooplankton and microbes that degrade POC (Buesseler and Boyd, 2009; Turner, 2015). Each of these parameters is a function of temperature, with warming increasing all three rates if other factors, such as nutrient supply, remain unchanged (López-Urrutia et al., 2006; Taucher and Oschlies, 2011; Iversen and Ploug, 2013).

Warming is projected to increase metabolic rates (Brown et al., 2004), which will increase both primary production (more carbon available to sink to deep ocean) and the metabolic rates of heterotrophs that consume phytoplankton and sinking POC (decreasing the carbon sink) (López-Urrutia et al., 2006; Taucher and Oschlies, 2011; Cavan and Boyd, 2018). In parallel warming-induced stratification and shoaling of the mixed layer will reduce nutrient inputs to the sunlit upper ocean (Bopp et al., 2001), expanding oligotrophic waters thus likely favoring smaller phytoplankton species and ultimately reducing primary production (Bopp et al., 2005). The decrease in nutrient supply to surface waters is typically considered to have the greatest effect on the magnitude of future primary production (Marañón et al., 2014) and thus overall primary production is expected to decline, although there is some disagreement amongst models (Laufkötter et al., 2015). One feedback from warming that will increase the carbon sink is the reduction in water viscosity, allowing particles to sink through the water column faster, escaping the upper ocean where remineralisation is most intense (Bach et al., 2012).

Export production is projected to decline by 1–12% depending on the Earth System Model (ESM) model used, due to declines in the magnitude and changes in the size-partitioning of primary production, and increased remineralisation of POC due to warming (Laufkötter et al., 2016). Remineralisation occurs throughout the water column and affects both the amount of POC exported and POC attenuation through the mesopelagic zone. Export or formation of detritus can either be parameterised by simple empirical algorithms, which may include primary production and temperature terms (Dunne et al., 2005; Henson et al., 2011; Britten et al., 2017) or in ESMs by phytoplankton aggregation and remineralisation parameterisations (Aumont et al., 2015).

Currently, there are a range of approaches to parameterise temperature-dependent terms in models. For example, in the biogeochemical model REcoM2, one theoretical exponential (Arrhenius type) relationship is used to describe all temperature-dependent terms; remineralisation of particulate and dissolved organic matter, silicon uptake, zooplankton respiration, and zooplankton grazing (Schourup-Kristensen et al., 2014). However, in the PISCES-v2 model, a constant Q₁₀ of 1.9 from Eppley (1972), which correlated phytoplankton growth rates with temperature, is used to describe both phytoplankton growth rates and POC degradation (Aumont et al., 2015). A Q₁₀ of 1.9 implies an increase in 10°C will result in metabolic rates that are 1.9 times higher. None of the marine biogeochemical components of the ESMs account for adaptation, which may be an important response to ocean warming with knock-on effects for POC export. For example, a laboratory study has shown that after 100 generations (freshwater) phytoplankton can adapt to warming by down-regulating respiration relative to photosynthesis to maintain the carbon allocation efficiency needed for growth (Padfield et al., 2016). Although phytoplankton in nutrient-poor regions may exhibit a different adaptation response as nutrient limitation can supress the temperature dependence of phytoplankton (Marañón et al., 2014).

In some ESMs temperature dependence varies between different metabolic rates (e.g., heterotrophic processes have a higher rate of change to temperature than autotrophic processes) (López-Urrutia et al., 2006; Dunne, 2013) thus incorporating differences in temperature sensitivity are only captured at a coarse scale. At present these biogeochemical models do not acknowledge temperature sensitivity within rates i.e., differences in the response to temperature between species or between the same species living in a different biogeochemical province. However, there is unlikely to be one uniform metabolic response to warming globally.

Sensitivity to temperature can be quantified as the activation energy (E_a) of a metabolic reaction—the amount of energy needed for a chemical reaction to occur (Schoolfield et al., 1981; Clarke and Johnston, 1999; Yvon-Durocher et al., 2012). E_a can be estimated via the Metabolic Theory of Ecology (MTE), which describes how metabolic processes vary as a function of organismal mass and temperature (Brown et al., 2004):

$\begin{array}{cc}\ln \left(I{M}^{-0.75}\right)=-E_a\left(\frac{1}{cT}\right)+\text{ln}(i_0)& (1)\end{array}$

Where I is the metabolic rate normalized by mass (M), E_a is the activation energy, c is Boltzmann's constant (8.62 × 10⁻⁵ eV K⁻¹), T is the temperature in Kelvin and finally i₀ is a normalization constant. The latter can be used to describe how organisms or communities are adapted to living at different temperatures (Clarke, 2006). When computed in the context of MTE using Equation 1, the E_a is the slope between mass-normalized metabolism and temperature. MTE states all organisms have an activation energy of 0.6–0.7 eV (Gillooly et al., 2001; Brown et al., 2004), thus there is little natural variation in temperature sensitivity. Activation energies higher than this range suggest organisms are more sensitive to changes in temperature, as shown in Arctic, and Antarctic zooplankton [E_a = 1.29 eV, (Alcaraz, 2016)], mesopelagic heterotrophs [E_a = 0.9 eV, (Brewer and Peltzer, 2016)] and a mixed heterotrophic microbial community from the sub-Antarctic [E_a = 0.9 eV, (Cavan and Boyd, 2018)]. As primary production and respiration (remineralisation) are both metabolic rates, MTE can be used to describe how they might change with future warming in the global oceans, and thus their influence on POC export. Model experiments have confirmed that temperature sensitivities of metabolic rates have an important role in ecosystem function, by regulating the magnitude of primary production and respiration (Taucher and Oschlies, 2011).

If organisms do respond differently to warming based on the environmental conditions they currently encounter, then biogeochemical models are likely to be inaccurately projecting carbon sequestration under future warming scenarios. Therefore, the objective of this study is to use empirical algorithms, including MTE, satellite data, and ESM outputs to determine the effect of temperature sensitivity on future POC export projections by 2100. We varied the activation energy in line with observations to investigate how temperature sensitivity influences POC export. MTE only accounts for changes in metabolic rates due to temperature, and thus using this framework implies that nutrients, phytoplankton community composition, and ocean physical changes, such as stratification, are unaltered in the year 2100.

Methods

Data

Annual satellite sea surface temperature (SST) and output from the Vertically Generalized Production Model (VGPM) for primary production for 2003–2016 (Oregon State University, 2017) were used as the baseline data for the beginning of this century. Coupled-Model Intercomparison Project-Phase 5 (CMIP5) ESM outputs over 1986–2005 (historical run) and under the IPCC Representative Concentration Pathway (RCP) 8.5 (business-as-usual run) for 2081–2100 were used to estimate the change in temperature at the sea surface and at 100 m depth and the change in export and primary production by the end of this century. See Table 1 for a list of frequently used acronyms. The 8 models used were GFDL-ESM2G and GFDL-ESM2M (Dunne et al., 2013), HadGEM2-CC and HadGEM2-ES (Bellouin et al., 2011; Collins et al., 2011), IPSL-LR and IPSL-MR (Séférian et al., 2013), MPI-LR and MPI-MR (Jungclaus et al., 2013) (see Supplementary Table 1 and Bopp et al. (2013) for a summary of model set-ups). These models were selected as they were the ones available in the CMIP5 (at the time of our analysis) that simulated export, primary production, and temperature.

TABLE 1

Table 1. Frequently used acronyms.

Satellite-Derived Climatologies

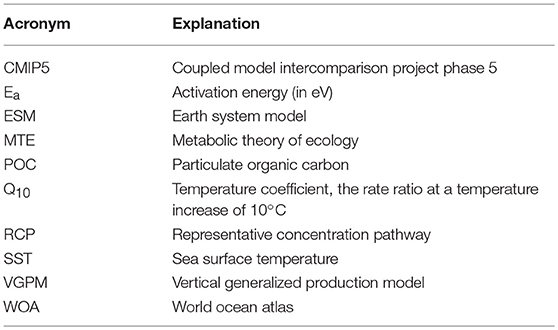
Global, 9 km resolution, mean SST data for the years 2003–2016 inclusive were downloaded from the NASA ocean color database (https://oceancolor.gsfc.nasa.gov) in annual composites. The data were then averaged (mean) over the 14 years and re-gridded onto a 1 × 1° grid (Figure 1A). The temperature at our chosen export depth of 100 m was extracted from World Ocean Atlas (WOA) climatology (Figure 1B). We chose 100 m as this is typically below the sunlit mixed layer and conventionally defines the upper mesopelagic zone. Global, mean monthly primary production data (9 km resolution) for the same years (2003–2016) were downloaded from the Ocean Productivity site (Oregon State University, 2017, https://www.science.oregonstate.edu/ocean.productivity/), using the standard product of the VGPM (Behrenfeld and Falkowski, 1997). Monthly means were summed to produce a total primary production (mg C m⁻² yr⁻¹) per year for all years, which were then converted to g C m⁻² yr⁻¹ and finally the mean over the 14 years was computed. These data were also re-gridded onto a 1 × 1° grid.

FIGURE 1

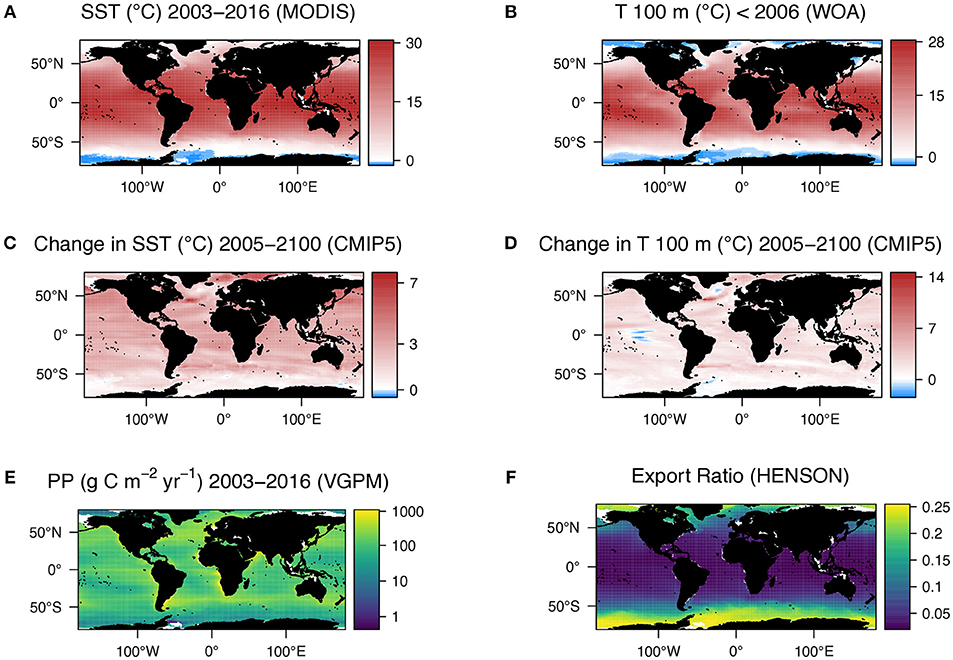
Figure 1. (A) Global mean sea surface temperature climatology for 2003–2016 derived from AQUA MODIS satellite data. (B) Global temperature at 100 m (our chosen export depth) from WOA data collected over 1955–2012, heavily weighted toward the latter years. (C) Multi-model median change in sea surface temperature from 1986–2005 to 2081–2100 predicted from CMIP5 models with representative concentration pathway 8.5 applied. (D) Multi-model median change in sea temperature at 100 m from 1986–2005 to 2081–2100 predicted from CMIP5 models with representative concentration pathway 8.5 applied. (E) Mean annual primary production climatology for 2003–2016 (VGPM) and (F) Export ratio calculated from VGPM using algorithm of Henson et al. (2011).

The exported POC at 100 m was calculated using the export ratio (e-ratio; export/primary production) from (Henson et al., 2011) (Equation 2):

$\begin{array}{rc}e-ratio=0.23^{*}{e}^{(-0.08{}^{*}SST)}& (2)\end{array}$

where SST is the mean annual satellite-derived SST for 2003–2016. The e-ratio was then multiplied by primary production to give a global POC export at 100 m as in Henson et al. (2011). Primary production and exported POC were then summed globally (accounting for variability in the areal extent of the grid cells with latitude) to give production and export estimates as Gt C yr⁻¹. The input parameters (primary production and export algorithms) were varied to run a sensitivity analysis (see Supplementary Methods) to calculate the change in export by the year 2100 and sequentially compare the effects of each parameter on export.

ESM Projected Future Changes

Output from eight different ESMs were downloaded from the CMIP5 archive (https://esgf-node.llnl.gov/projects/esgf-llnl/) to compute the projected increase in sea temperature by 2100 (Supplementary Table 1). Most of the models include two phytoplankton functional groups (diatom and non-diatom) and at least one zooplankton group. The ensemble member for each model dataset was r1i1p1. Monthly historical and RCP 8.5 runs [business-as-usual (Moss et al., 2010)] were downloaded and the last 20 years of each run (1986–2005 and 2081–2100, respectively) were extracted. An annual mean, and then the mean across all years was computed for each model and time period. The desired depth levels (0 and 100 m) were extracted, temperatures converted from Kelvin to Celsius and the data re-gridded onto a 1 × 1° longitude-latitude grid. Finally, a multi-model median was computed over all 8 model outputs resulting in two datasets for SST and temperature at 100 m, one for each run (historical, 1986–2005, and RCP8.5, 2081–2100). The change in temperature by the end of the century for each depth was calculated by subtracting the historical period from the end-of-century period.

The parameter “epc100” was downloaded for the same model runs and years. epc100 is the sinking mole flux of particulate organic matter expressed as carbon in seawater at 100 m. For primary production the integrated primary production “intpp” was downloaded. To make the model output comparable with the satellite-derived export estimates, the mean monthly export was summed for each year and then the mean taken for all years per model. The data were converted to a 1 × 1° longitude-latitude grid and a multi-model median taken over the 8 model outputs. This was done for both the historical and RCP8.5 runs and the change in export by 2100 computed as the difference between the two datasets. The same processing steps were applied to the modeled primary production.

Applying Metabolic Theory of Ecology

To determine the change in POC export due solely to the effects of rising temperatures on microbial metabolism, the metabolic theory of ecology (MTE) was applied (Brown et al., 2004). MTE is partly based on the biomass of metabolizing organisms (Equation 1). Microbial biomass scales in the ocean with POC, such that as POC decreases with depth so does microbial biomass (Boyd et al., 1999). Bacterial biomass contributes between 20 to >100% of exported POC mass, depending on the region (Steinberg et al., 2001; Stewart et al., 2010; Collins et al., 2015), with most estimates close to 50% of POC (Ducklow et al., 1993; Boyd et al., 1999). Therefore, we normalized our estimated POC mass at 100 m to 50% to estimate heterotrophic microbial biomass, as also applied in Cavan et al. (2018). As we are computing the relative change in respiration, and the mass term is the same in all model simulations (only the temperature changes), the magnitude of the mass term has little effect on the change in respiration (see sensitivity analysis in Supplementary Materials).

The respiration of microbes (R_micro) can therefore be calculated following Equation 3:

$\begin{array}{rc}{R}_{micro}=I*{M_{HB}}^{0.75}*e^{\frac{-Ea}{k*T}}& (3)\end{array}$

where I and E_a are the normalization constant and activation energy, respectively, M_HB is the mass of heterotrophic bacteria at 100 m, k is the Boltzmann constant (8.62 × 10⁻⁵ eV K⁻¹) and T is the temperature in Kelvin. For this global analysis I was determined as the mean of constants given for unicells (I = 19.21) and inverts (I = 19.75) in Brown et al. (2004), which was 19.48. The E_a (0.7 eV) used was also from Brown et al. (2004), which was consistent in their study over all groups of organisms tested (unicells to fish). Although deviations away from this value do exist with published E_a's ranging from 0.29 eV for primary production (López-Urrutia et al., 2006) to 1.3 eV for zooplankton respiration (Gleiber et al., 2015). For the beginning of the century, R_micro was calculated using the WOA temperature data at 100 m. For the end of the century we altered only the temperature term by adding the temperature change between the beginning (1986–2005) and end of the century (2081–2100) projected by the CMIP5 models at 100 m onto the WOA temperature climatology at 100 m (mean temperature 1955–2012). The change in respiration (Figure 2A) was computed by subtracting the beginning of the century R_micro from the end of the century R_micro.

FIGURE 2

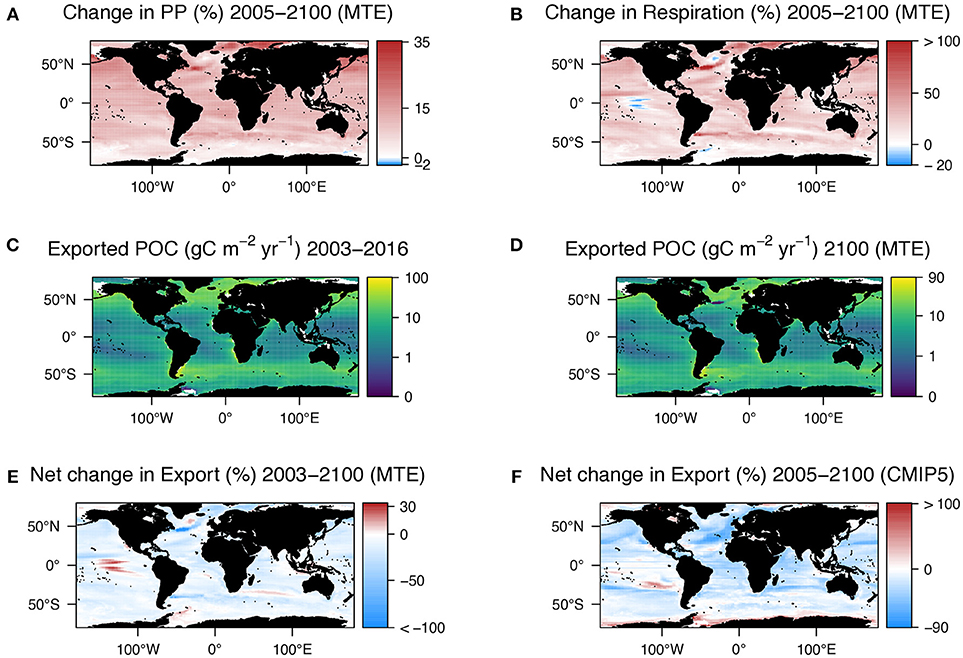
Figure 2. (A) Change in primary production from current (2003–2016) data in Figure 1E and that estimated using the metabolic theory of ecology (MTE) and SST changes shown in Figure 1C. (B) Difference in microbial respiration of exported POC between present day (2003–2016) and 2100 estimated using MTE and the temperature changes at 100 m shown in Figure 1D. Notice how the patterns in both a and b match those in Figures 1C,D, respectively. (C) POC export at 100 m calculated by multiplying primary production (Figure 1E) by export ratio (Figure 1F). (D) POC export at 100 m in 2100 calculated by multiplying the current export (C) by the net change in export [E = change in respiration (B)—change in primary production (A)]. (E) Net change in export used to calculated export by 2100 in D. (F) Net change in export as determined by a suite of CMIP5 models. For both plots positive change (red) indicates an increase in export.

The change in the rate of primary production (Figure 2B) due to increasing temperature alone was also calculated to determine the overall net decrease in POC at 100 m. For primary production the MTE constants from López-Urrutia et al. (2006) were used where in Equation (1) I = −11.28 and the E_a = 0.29 eV with M (mass) being the satellite-derived primary production (Figure 1E). Here though the change in SST by 2100 predicted by the difference in the beginning and end of the century runs of the CMIP5 models was used rather than the change in T at 100 m. The net change in export was calculated by subtracting the change in autotrophic primary production from the change in heterotrophic microbial respiration.

Results

Using the business-as-usual representative concentration pathway (RCP8.5) the global mean projected SST increases from the beginning to the end of the century according to 8 CMIP5 ESMs (ESMs) is 2.5 ± 1.1°C (Figure 1C), with temperature at 100 m only increasing by 2.0 ± 1.1°C (Figure 1D). SST is projected to increase globally, apart from a small area in the Pacific Southern Ocean. However, whilst the temperature at 100 m is mostly predicted to increase, there are large regions where the temperature is predicted to decrease, namely in some Atlantic polar regions and the equatorial Pacific. The largest change of temperature at 100 m is in the North Atlantic. Immediately north of this warming is a region of projected cooling.

As MTE is principally based on temperature, the change in respiration, and primary production spatially reflect the change in temperature at 100 m. Using the VGPM (Figure 1E), Henson e-ratio (Figure 1F), and the change in temperature according to the CMIP5 models (Figure 1D), the MTE model projects an increase in the rate of microbial respiration by 2100 of 22.5% and an increase in the rate of primary production of 10.5%, resulting in a net decline in export of 12% (Figure 2E, Supplementary Table 2). Deviations from classical MTE occurred where the decline in export was large (>50%), as shown in the Arrhenius plot (Figure 3A, < 0.5% of data points). Globally, export is projected to decrease from 3 Gt C yr⁻¹ (2003–2016 climatology) to 2.6 Gt C yr⁻¹ by the end of this century according to MTE, with the maximum decreasing from 100 g C m⁻² yr⁻¹ (Figure 2C) to 90 g C m⁻² yr⁻¹ (Figure 2D), found off the west coast of the US. The global total current (2003–2016 climatology) primary production is 51 Gt C yr⁻¹ according to the VGPM, suggesting 6% of primary production is exported each year when applying the Henson e-ratio in present day. Under future warming, MTE projects increased primary production to 59 Gt C yr⁻¹ and decreasing POC export, reducing the global mean e-ratio to 4%.

FIGURE 3

Figure 3. (A) Arrhenius plot of temperature (1/kT), where k is Boltzmann's constant, and T is temperature in Kelvin against the natural log of mass-corrected (M-0.75) respiration (R). Color is the net change in export by 2100 as predicted by MTE. Black line is regression with a slope of −0.7, which is the activation energy. Where decrease in export is > ~30% the points deviate from the line. (B) Change in metabolic rate. The red solid line is the change with an E_a of 0.7 eV according to metabolic theory and the red dashed line is with an E_a of 1 eV as determined by previous experimental warming studies and applied in this study. (C) Change in Q₁₀ using Equation 4. The contours and colors are activation energies (0.1–2 eV). The orange lines show the temperature (in Kelvin) and E_a at which Q₁₀ = 2, a commonly used parameterisation in ESMs.

We also explored the effect of varying E_a, both globally and regionally, on projected POC export. First we increased the E_a from 0.7 to 1 eV globally resulting in 2.2 Gt C yr⁻¹ of POC export in 2100, due to of an increase in respiration. Thus, the total projected reduction in POC export globally was 30%. We then explored the effect of varying E_a by latitude and temperature. Following results from a recent study in the Southern Ocean (Cavan and Boyd, 2018) we set all microbes residing below 40°S (30% of global ocean by area) to have an activation energy of 1 eV and all those northwards an E_a of 0.7 eV. This resulted in a 17% decline in POC export by 2100. Second, we imposed an E_a of 1 eV on just those regions where the temperature at 100 m is <13°C (46% of global ocean), in accordance with observational studies by Alcaraz et al. (2013, 2014) and (Cavan and Boyd, 2018), resulting in a decline in POC export of 23% by 2100.

The CMIP5 multi-model median historical (1986–2005) export was 7.6 Gt C yr⁻¹ and the future (2081–2100) export is projected to be 6.4 Gt C yr⁻¹. Both these estimates are higher than our estimates made using the Henson algorithm and the MTE model. However, the net global change in POC export from our analysis of the CMIP5 model output was 16% (Figure 2F), the same direction of change (a decline) in export as predicted our MTE model (Figure 2E). The greatest effect on the change in export in the MTE model was the temperature term, which is to be expected given it forms the exponential part of the algorithm. Changing the temperature by even just a small amount (median temperature difference +0.5°C) increased the decline in export from 12 to 18% (Supplementary Table 2). A large temperature change (median temperature difference +3.5°C) resulted in a greater decline in export of 61%. Changing the mass term using different primary production or export algorithms did not change the total decline in export as the only change imposed between the beginning and end of the century was temperature. See Supplementary Table 2 and supplementary text for results of the sensitivity analyses.

Discussion

Satellite data can be combined with empirical algorithms and MTE to investigate the effect of future warming on the rates effecting the oceans biological pump and carbon storage. Here, we investigated the theoretical effect of warming by 2100 globally, focusing solely on temperature-driven metabolic changes to microbial respiration and primary production, and thus POC export flux. We compared our results with an analysis of CMIP5 model output projections for export production by the end of this century to put our results into context.

Our MTE model predicted a similar decline in export (12%) as our CMIP5 model analysis (16%), which was unexpected given that our MTE model is based on a simple physiologically-based exponential equation (Equation 1) and does not include changes in physics or plankton community structure. The MTE model only accounts for two possible changes due to increasing temperature that can affect POC export (energetics of respiration and primary production), whereas the 3D CMIP5 models include future physical and chemical changes such as water circulation, stratification and nutrient availability. We expected our MTE model to potentially overestimate changes in export given it is based on an exponential relationship between temperature and metabolism and does not consider optimum temperatures for metabolism.

The lack of an optimal temperature in our MTE approach is a limitation of our model, although Cavan and Boyd (2018) found that in the Southern Ocean an optimal temperature for microbial respiration was never reached (maximum experimental temperature was 8°C above the annual maximum). In our model, metabolic rates will continue to increase exponentially with temperature, potentially over-estimating the future declines in POC export. In addition our MTE model does not account for any adaptation of microbial respiration to rising temperatures (Listmann et al., 2016), which would act to decrease the reduction in export by 2100. Nevertheless, we expect the inclusion of an adaptation term would still result in larger declines in future export when temperature sensitivity is high, which is the main aim and result of this study.

Previous studies have observed higher activation energies (E_a, 1 eV) in organisms residing at cool (polar and deeper waters) temperatures (Alcaraz, 2016; Brewer and Peltzer, 2016), suggesting these organisms are more sensitive to temperature changes when adaptation is not considered. A recent study on the effect of warming on POC export showed sub-Antarctic microbial respiration on sinking particles presents a higher E_a (0.9 eV) than predicted by typical MTE (0.7 eV and I = 19) (Cavan and Boyd, 2018). In our first model experiment in this study we originally set the E_a to 0.7 eV (Figure 3A) globally for heterotrophic respiration (Brown et al., 2004, Equation 1). Increasing the E_a from 0.7 to 1 eV (Figure 3B) resulted in a 30% decline in POC export globally. This is more than double our original MTE estimate of 12% when E_a = 0.7 eV and higher than our CMIP5 model output analysis (16%) and other ESM analyses and empirical models (Cael and Follows, 2016; Laufkötter et al., 2016).

Varying E_a by latitude and water temperature produced an intermediate response of POC export by 2100, with a 17% decline in POC export by 2100 in the Southern Ocean and 23% decline in regions where the water temperature at 100 m is < 13°C. Our estimates of the spatial patters of microbial temperature sensitivity, based on a few empirical data, are likely to be over-simplifications the global sensitivity to E_a. This is because of the limited empirical data available to make more advanced simulations of the spatial variability on marine microbial E_a. As well as spatial heterogeneity in the response to temperature, there may also be variability in the organismal adaptation to warming, potentially damping the effects of variable E_a. To be able to confirm with any certainty the change in POC export associated with temperature change, observational studies need to be conducted on the response of organisms to future warming in different ocean ecosystems.

It is important to note that our MTE analysis assumes that neither the physical environment nutrient availability nor community structure change with ocean warming. Biogeochemical models do however predict shifts in phytoplankton composition, nutrient availability, magnitude of primary production, and increases in particle sinking rates (Richardson, 2008; Bach et al., 2012; Thomas et al., 2012; Dutkiewicz et al., 2013). We consider our results in the context of these predicted changes. Reduced primary production and smaller phytoplankton will produce fewer smaller, slow-sinking particles (Baker et al., 2017) where small phytoplankton dominate the community (Richardson and Jackson, 2007; Cavan et al., 2018). The reduced sinking rate due to smaller particles may be offset if viscosity decreases (due to increasing temperature) allowing particles to sink through the water column faster (Bach et al., 2012), potentially resulting in negligible changes to particle sinking rates.

Incorporating reduced primary production in our MTE model would only influence the mass term, which we have shown does not significantly influence our results (Supplementary Table 2). Conversely, as microbial turnover on small particles is faster than on large particles at the same temperature, likely due to the larger surface area for microbes to attach to Cavan et al. (2017), it is possible that the response of microbes to temperature will differ depending on particle size, i.e., microbes on smaller particles may exhibit a faster response to temperature change (higher E_a) than those on larger particles, but this hypothesis needs testing. Any difference in temperature sensitivity driven by the particle type/composition or size will be set principally by the mixed layer plankton composition, which could be a useful descriptor in parameterising E_a, along with biogeochemical province and/or latitude.

Accounting for the additional temperature sensitivity outlined above may alter our projections on the direction and magnitude of future carbon export, but data is currently lacking on the response of particle-attached microbes in different regions and the response of microbes residing on particles of different size and composition. Spatial variance in temperature sensitivity has been frequently observed over the past few decades, in different biomes and with different organisms, including coastal mussel populations (Gilman et al., 2006), insects (Deutsch et al., 2008), and soil microbes (Lloyd and Taylor, 1994). However, similar observations are scarce in the marine realm, hence the lack of temperature sensitivity parameterisations in marine models. The potential for a non-uniform microbial response to ocean warming across the globe has important implications for biogeochemical models, and thus ESMs. We recommend that to more accurately project the effects of climate change on carbon sequestration we need to consider that heterotrophic organisms will not necessarily respond to warming in a straightforward manner. Their response will be dependent on their ability to adapt (Visser, 2008; Thomas et al., 2012; Sal et al., 2015; Padfield et al., 2016), the species composition, and the biogeographical province and latitude they inhabit. ESMs do not currently account for a varying metabolic response such that, for example, if organisms at the Equator are exposed to a 2°C increase in temperature, current parameterizations in ESMs will elicit the same metabolic response as those at the poles exposed to the same temperature increase.

Ocean biogeochemical models that parameterize metabolic processes as a function of temperature typically use a Q₁₀ approach, with some using the same value of Q₁₀ = ~2 globally (Bopp et al., 2013). A Q₁₀ of 2 suggests that if the temperature increases by 10°C, the rate of the reaction will double. The value of 2 is from the seminal work of Eppley (1972). There are two limitations to using the Eppley (1972) study for heterotrophic processes in biogeochemical models: (1) the study solely assessed the response of phytoplankton growth to temperature, an autotrophic process, and (2) the data were only from laboratory cultures. It is well known that autotrophic and heterotrophic processes respond differently to temperature change (López-Urrutia et al., 2006), and that organisms in laboratory conditions react differently to those in their natural environment. The Eppley Q₁₀ should only be applied to phytoplankton growth and with caution given only laboratory cultures were used. Whilst the PISCES model does use higher Q₁₀ for zooplankton processes, temperature dependency of POC degradation is still based on phytoplankton production rates (Buitenhuis et al., 2006) and the TOPAZ2 model uses a combination of the Eppley (1972) temperature and stoichiometry to parameterise grazing (Dunne, 2013). In the TOPAZ2 model though, export is parameterised using a temperature-dependent empirical algorithm (Dunne et al., 2005).

In the natural world, deviations away from a Q₁₀ of 2 occur because Q₁₀ varies depending on (1) the initial temperature, and (2) the activation energy of the reaction (which in itself varies, depending on the type of reaction being measured, Figure 3C). This has been highlighted in an ocean study where the bacterial degradation of dissolved organic carbon (DOC) varied (Q₁₀ = 2–8) as different compounds of different labilities within the DOC degraded at different rates (Lønborg et al., 2018). Q₁₀ can be related to activation energy using the following equation (Li and Dickie, 1987):

$\begin{array}{cc}{Q}_{10}=e^{\left[\frac{E_a\ast (T_2-T_1)}{R\ast T_1\ast T_2}\right]}& (4)\end{array}$

Where E_a is the activation energy here expressed as J mol⁻¹ (1 eV = 96 kJ mol⁻¹), T¹ is the initial temperature in Kelvin and T² = T¹ + 10, and R is the gas constant of 8.31 J mol⁻¹ K⁻¹. For example, a Q₁₀ of 2 is obtained with an activation energy of 0.5 eV and at a temperature of 285 K (12°C, Figure 3C). If E_a within the range found experimentally in the oceans is applied to Equation 4, then at E_a = 0.7 eV, T must be 338 K (65°C) to give a Q₁₀ of 2. If E_a = 1 eV, T will be 405 K (132°C, Figure 3C). Only the first example here is within the normal temperature range found in the ocean (excluding proximity to deep ocean vents). At most ocean temperatures (<30°C) Q₁₀ is higher (>2.5) if a typical activation energy, according to MTE, of 0.6–0.7 eV is used (Figure 3C). Many studies, particularly in terrestrial ecology, have shown that using a constant Q₁₀ is not appropriate and variable Q₁₀, where the rate of increase is dependent on the baseline temperature, should be imposed in models (Lloyd and Taylor, 1994; Wang et al., 2014; Jian et al., 2018).

A final point to acknowledge is whether incorporating varying Q₁₀ (suggested by other studies e.g., Jian et al. 2018) or E_a (suggested in our study) into ocean biogeochemical models will result in more accurate estimates of export, as these theoretical models are often deemed over-simplified. The Arrhenius equation has been continuously developed since its origins in the nineteenth Century to more closely reflect a biological system (Johnson et al., 1942), including more recently the addition of temperature-induced enzyme denaturation (Ratkowsky et al., 2005; Corkrey et al., 2012, 2016). However, these improved theoretical models have escaped the attention of many oceanographers. Whilst incorporating these more sophisticated thermodynamic models into biogeochemical models might be a step too far at present, with too many unknown parameters and certainly beyond the scope of this study, we as an oceanographic community should consider moving away from Q₁₀ and the data from Eppley (1972) and start to apply process-based parameterizations founded on empirical data from natural ocean communities.

In conclusion, POC export is projected to decline by 12% by the end of the century according to fundamental metabolic theory and ESMs. The inclusion of spatially variable temperature sensitivity terms that deviate from classical MTE resulted in more pronounced projected declines in POC export; applying high sensitivity globally resulted in a decline in export of 30% and applying it just to cold regions resulted in a global decline of up to 23%. This is an important finding. Current biogeochemical models that do not account for variable temperature sensitivity are likely underestimating the change in future POC export decline, because metabolic reactions degrading POC will occur faster than currently parameterized in some regions. Where possible, metabolic functions such as respiration should be parameterized as a function of temperature as standard in models, and in turn the temperature dependence term should vary spatially. Incorporating an activation energy that varies with latitude and/or biogeochemical province would be a simple first step to assess the response of organisms to temperature change. However, we should also consider incorporating more complex thermodynamic models that can biologically explain the temperature-dependence of metabolic reactions. Future research that generates empirical data on the differing response of the same functional groups adapted to different temperature conditions is needed to elucidate these processes further and more accurately understand how carbon sequestration will change with future warming.

Author Contributions

EC designed the study, collated the data with SH and did the analysis. All authors interpreted the results and EC wrote the manuscript with contributions from SH and PB.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was funded by the Australian Research Council by a Laureate awarded to PB (FL160100131) and a European Research Council Consolidator grant to SH (GOCART, agreement number 724416). We would like to thank Joan Llort and Mike Sumner for their help in some of the early code development. We are also greatly indebted to David Ratkowsky, Ross Corkrey, and Tom Ross for discussions on thermodynamic theory and the appropriateness of using different models. The input data and the code used to build the initial MTE model is available at www.github.com/e-cavan. This study is dedicated to the memory of Dr Chris Daniels.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2018.00230/full#supplementary-material

References

Alcaraz, M. (2016). Marine zooplankton and the metabolic theory of ecology: is it a predictive tool? J. Plankton Res. 38, 762–770. doi: 10.1093/plankt/fbw012

CrossRef Full Text | Google Scholar

Alcaraz, M., Almeda, R., Duarte, C. M., Horstkotte, B., Lasternas, S., and Agust, Ã- S. (2014). Changes in the C, N, and P cycles by the predicted salps-krill shift in the southern ocean. Front Mar. Sci. 1:45. doi: 10.3389/fmars.2014.00045

CrossRef Full Text | Google Scholar

Alcaraz, M., Almeda, R., Saiz, E., Calbet, A., Duarte, C. M., Agustí, S., et al. (2013). Effects of temperature on the metabolic stoichiometry of Arctic zooplankton. Biogeosciences 10, 689–697. doi: 10.5194/bg-10-689-2013

CrossRef Full Text | Google Scholar

Aumont, O., Ethé, C., Tagliabue, A., Bopp, L., and Gehlen, M. (2015). PISCES-v2: an ocean biogeochemical model for carbon and ecosystem studies. Geosci. Model Dev. 8, 2465–2513. doi: 10.5194/gmd-8-2465-2015

CrossRef Full Text | Google Scholar

Bach, L. T., Riebesell, U., Sett, S., Febiri, S., Rzepka, P., and Schulz, K. G. (2012). An approach for particle sinking velocity measurements in the 3-400 μm size range and considerations on the effect of temperature on sinking rates. Mar. Biol. 159, 1853–1864. doi: 10.1007/s00227-012-1945-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Baker, C. A., Henson, S. A., Cavan, E. L., Giering, S. L. C., Yool, A., Gehlen, M., et al. (2017). Slow-sinking particulate organic carbon in the Atlantic Ocean: magnitude, flux, and potential controls. Glob. Biogeochem. Cycles 31, 1051–65. doi: 10.1002/2017GB005638

CrossRef Full Text | Google Scholar

Behrenfeld, M. J., and Falkowski, P. G. (1997). Photosynthetic rates derived from satellite-based chlorophyll concentration. Limnol. Oceanogr. 42, 1–20. doi: 10.4319/lo.1997.42.1.0001

CrossRef Full Text | Google Scholar

Bellouin, N., Collins, W. J., Culverwell, I. D., Halloran, P. R., Hardiman, S. C., Hinton, T. J., et al. (2011). The HadGEM2 family of met office unified model climate configurations. Geosci. Model Dev. 4, 723–757. doi: 10.5194/gmd-4-723-2011

CrossRef Full Text | Google Scholar

Bopp, L., Aumont, O., Cadule, P., Alvain, S., and Gehlen, M. (2005). Response of diatoms distribution to global warning and potential implications: a global model study. Geophys. Res. Lett. 32:L19606. doi: 10.1029/2005GL023653

CrossRef Full Text | Google Scholar

Bopp, L., Monfray, P., Aumont, O., Dufresne, J. L., Treut, H., Le, M. G., et al. (2001). Potential impact of climate change on marine export production. Glob. Biogeochem. Cycles 15, 81–99. doi: 10.1029/1999GB001256

CrossRef Full Text | Google Scholar

Bopp, L., Resplandy, L., Orr, J. C., Doney, S. C., Dunne, J. P., Gehlen, M., et al. (2013). Multiple stressors of ocean ecosystems in the 21st century: projections with CMIP5 models. Biogeosciences 10, 6225–6245. doi: 10.5194/bg-10-6225-2013

CrossRef Full Text | Google Scholar

Boyd, P. W., Sherry, N. D., Berges, J. A., Bishop, J. K. B., Calvert, S. E., Charette, M. A., et al. (1999). Transformations of biogenic particulates from the pelagic to the deep ocean realm. Deep Res. II 46, 2761–2792. doi: 10.1016/S0967-0645(99)00083-1

CrossRef Full Text | Google Scholar

Brewer, P. G., and Peltzer, E. T. (2016). Ocean chemistry, ocean warming and emerging hypoxia: commentary. J. Geophys. Res. Ocean 121, 3659–3667. doi: 10.1002/2016JC011651

CrossRef Full Text | Google Scholar

Britten, G. L., Wakamatsu, L., and Primeau, F. W. (2017). The temperature-ballast hypothesis explains carbon export efficiency observations in the Southern Ocean. Geophys. Res. Lett. 44, 1831–1838. doi: 10.1002/2016GL072378

CrossRef Full Text | Google Scholar

Brown, J. H., Gillooly, J. F., Allen, A. P., Savage, V. M., and West, G. B. (2004). Toward a metbolic theory of ecology. Ecology 85, 1771–1789. doi: 10.1890/03-9000

CrossRef Full Text | Google Scholar

Buesseler, K., and Boyd, P. (2009). Shedding light on processes that control particle export and flux attenuation in the twilight zone of the open ocean. Limnol. Oceanogr. 54, 1210–1232. doi: 10.4319/lo.2009.54.4.1210

CrossRef Full Text | Google Scholar

Buitenhuis, E., Quéré, C., Le, A. O., Beaugrand, G., Bunker, A., Hirst, A., et al. (2006). Biogeochemical fluxes through mesozooplankton. Glob. Biogeochem. Cycles 20:GB2003. doi: 10.1029/2005GB002511

CrossRef Full Text | Google Scholar

Cael, B. B., and Follows, M. J. (2016). On the temperature dependence of oceanic export efficiency. Geophys. Res. Lett. 43, 5170–5175. doi: 10.1002/2016GL068877

CrossRef Full Text | Google Scholar

Cavan, E. L., and Boyd, P. W. (2018). The effect of anthropogenic warming on microbial respiration and particulate organic carbon export rates in the sub-Antarctic Southern Ocean. Aquat. Microb. Ecol. 82, 111–127. doi: 10.3354/ame01889

CrossRef Full Text | Google Scholar

Cavan, E. L., Giering, S. L. C., Wolff, G. A., Trimmer, M., and Sanders, R. (2018). Alternative particle formation pathways in the eastern tropical north pacific's biological carbon pump. J. Geophys. Res. Biogeosci. 123, 2198–2211. doi: 10.1029/2018JG004392

CrossRef Full Text | Google Scholar

Cavan, E. L., Trimmer, M., Shelley, F., and Sanders, R. (2017). Remineralization of particulate organic carbon in an ocean oxygen minimum zone. Nat. Commun. 8:14847. doi: 10.1038/ncomms14847

PubMed Abstract | CrossRef Full Text | Google Scholar

Clarke, A. (2006). Temperature and the metabolic theory of ecology. Funct. Ecol. 20, 405–412. doi: 10.1111/j.1365-2435.2006.01109.x

CrossRef Full Text | Google Scholar

Clarke, A., and Johnston, N. M. (1999). Scaling of metabolic rate with body mass and temperature in teleost fish. J. Anim. Ecol. 68, 893–905. doi: 10.1046/j.1365-2656.1999.00337.x

CrossRef Full Text | Google Scholar

Collins, J. R., Edwards, B. R., Thamatrakoln, K., Ossolinski, J. E., Ditullio, G. R., Bidle, K. D., et al. (2015). The multiple fates of sinking particles in the North Atlantic Ocean. Glob. Biogeochem. Cycles 29, 1471–1494. doi: 10.1002/2014GB005037

CrossRef Full Text | Google Scholar

Collins, W. J., Bellouin, N., Doutriaux-Boucher, M., Gedney, N., Halloran, P., Hinton, T., et al. (2011). Development and evaluation of an Earth-System model – HadGEM2. Geosci. Model Dev. 4, 1051–1075. doi: 10.5194/gmd-4-1051-2011

CrossRef Full Text | Google Scholar

Corkrey, R., McMeekin, T. A., Bowman, J. P., Ratkowsky, D. A., Olley, J., and Ross, T. (2016). The biokinetic spectrum for temperature. PLoS ONE 11:e0153343. doi: 10.1371/journal.pone.0153343

CrossRef Full Text | Google Scholar

Corkrey, R., Olley, J., Ratkowsky, D., McMeekin, T., and Ross, T. (2012). Universality of thermodynamic constants governing biological growth rates. PLoS ONE 7:e32003. doi: 10.1371/journal.pone.0032003

PubMed Abstract | CrossRef Full Text | Google Scholar

Deutsch, C. A., Tewksbury, J. J., Huey, R. B., Sheldon, K. S., Ghalambor, C. K., Haak, D. C., et al. (2008). Impacts of climate warming on terrestrial ectotherms across latitude. Proc. Natl. Acad. Sci. U.S.A. 105, 6668–6672. doi: 10.1073/pnas.0709472105

PubMed Abstract | CrossRef Full Text | Google Scholar

Ducklow, H. W., Kirchman, D. L., Quinby, H. L., Carlson, C. A., and Dam, H. G. (1993). Stocks and dynamics of bacterioplankton carbon during the spring bloom in the eastern North Atlantic Ocean. Deep Sea Res. Part II Top. Stud. Oceanogr. 40, 245–263. doi: 10.1016/0967-0645(93)90016-G

CrossRef Full Text | Google Scholar

Dunne, J. P. (2013). Technical Description of Tracers of Ocean Phytoplankton with Allometric Zooplankton Version 2 (TOPAZ2) Used in GFDL's ESM2M and ESM2G Submitted as Part of the Coupled Model Intercomparison Project phase 5. doi: 10.1175/JCLI-D-12-00150.s1

CrossRef Full Text

Dunne, J. P., Armstrong, R. A., Gnanadesikan, A., and Sarmiento, J. L. (2005). Empirical and mechanistic models for the particle export ratio. Glob. Biogeochem. Cycles 19:GB4026. doi: 10.1029/2004GB002390

CrossRef Full Text | Google Scholar

Dunne, J. P., John, J. G., Shevliakova, E., Stouffer, R. J., Krasting, J. P., Malyshev, S. L., et al. (2013). GFDL's ESM2 global coupled climate–carbon earth system models. Part II: carbon system formulation and baseline simulation characteristics. J. Clim. 26, 2247–2267. doi: 10.1175/JCLI-D-12-00150.1

CrossRef Full Text | Google Scholar

Dutkiewicz, S., Scott, J. R., and Follows, M. J. (2013). Winners and losers: ecological and biogeochemical changes in a warming ocean. Glob. Biogeochem. Cycles 27, 463–477. doi: 10.1002/gbc.20042

CrossRef Full Text | Google Scholar

Eppley, R. W (1972). Temperature and phytoplankton growth in the sea. Fish Bull. 70, 1063–1085.

Google Scholar

Falkowski, P. G., Barber, R. T., and Smetacek, V. (1998). Biogeochemical controls and feedbacks on ocean primary production. Science 281, 200–206. doi: 10.1126/science.281.5374.200

PubMed Abstract | CrossRef Full Text | Google Scholar

Gillooly, J. F., Brown, J. H., West, G. B., Savage, V. M., and Charnov, E. L. (2001). Effects of size and temperature on metabolic rate. Adv. Sci. 293, 2248–2251. doi: 10.1126/science.1061967

PubMed Abstract | CrossRef Full Text | Google Scholar

Gilman, S. E., Wethey, D. S., and Helmuth, B. (2006). Variation in the sensitivity of organismal body temperature to climate change over local and geographic scales. Proc. Natl. Acad. Sci. U.S.A. 103, 9560–9565. doi: 10.1073/pnas.0510992103

PubMed Abstract | CrossRef Full Text | Google Scholar

Gleiber, M. R., Steinberg, D. K., and Schofield, O. M. E. (2015). Copepod summer grazing and fecal pellet production along the Western Antarctic Peninsula. J. Plankton Res. 38, 732–750. doi: 10.1093/plankt/fbv070

CrossRef Full Text | Google Scholar

Henson, S., Sanders, R., Madsen, E., Morris, P., Moigne, F., and Le, Q. G. (2011). A reduced estimate of the strength of the ocean's bioloical carbon pump. Geophys. Res. Lett. 38:L04606. doi: 10.1029/2011GL046735

CrossRef Full Text | Google Scholar

Iversen, M. H., and Ploug, H. (2013). Temperature effects on carbon-specific respiration rate and sinking velocity of diatom aggregates — potential implications for deep ocean export processes. Biogeosciences 10, 4073–4085. doi: 10.5194/bg-10-4073-2013

CrossRef Full Text | Google Scholar

Jian, J., Steele, M. K., Thomas, R. Q., Day, S. D., and Hodges, S. C. (2018). Constraining estimates of global soil respiration by quantifying sources of variability. Glob. Chang. Biol. 24, 4143–4159. doi: 10.1111/gcb.14301

CrossRef Full Text | Google Scholar

Johnson, F. H., Eyring, H., and Williams, R. W. (1942). The nature of enzyme inhibitions in bacterial luminescence: sulfanilamide, urethane, temperature and pressure. J. Cell. Comp. Physiol. 20, 247–268. doi: 10.1002/jcp.1030200302

CrossRef Full Text | Google Scholar

Jungclaus, H. J., Fischer, N., Haak, H., and Lohmann, K. J. M. (2013). Characteristics of the ocean simulations in the Max Planck Institute Ocean Model (MPIOM) the ocean component of the MPI-Earth system model. J. Adv. Model Earth Syst. 5, 422–446. doi: 10.1002/jame.20023

CrossRef Full Text | Google Scholar

Laufkötter, C., Vogt, M., Gruber, N., Aita-Noguchi, M., Aumont, O., Bopp, L., et al. (2015). Drivers and uncertainties of future global marine primary production in marine ecosystem models. Biogeosciences 12, 6955–6984. doi: 10.5194/bg-12-6955-2015

CrossRef Full Text | Google Scholar

Laufkötter, C., Vogt, M., Gruber, N., Aumont, O., Bopp, L., Doney, S. C., et al. (2016). Projected decreases in future marine export production: the role of the carbon flux through the upper ocean ecosystem. Biogeosciences 13, 4023–4047. doi: 10.5194/bg-13-4023-2016

CrossRef Full Text | Google Scholar

Li, W. K., and Dickie, P. M. (1987). Temperature characteristics of photosynthetic and heterotrophic activities: seasonal variations in temperate microbial plankton. Appl. Environ. Microbiol. 53, 2282–2295.

PubMed Abstract | Google Scholar

Listmann, L., LeRoch, M., Schlüter, L., Thomas, M. K., and Reusch, T. B. H. (2016). Swift thermal reaction norm evolution in a key marine phytoplankton species. Evol. Appl. 9, 1156–1164. doi: 10.1111/eva.12362

PubMed Abstract | CrossRef Full Text | Google Scholar

Lloyd, J., and Taylor, J. A. (1994). On the temperature dependence of soil respiration. Funct. Ecol. 8, 315–323. doi: 10.2307/2389824

CrossRef Full Text | Google Scholar

Lønborg, C., Álvarez–Salgado, X. A., Letscher, R. T., and Hansell, D. A. (2018). Large stimulation of recalcitrant dissolved organic carbon degradation by increasing ocean temperatures. Front. Mar. Sci. 4:436. doi: 10.3389/fmars.2017.00436

CrossRef Full Text | Google Scholar

López-Urrutia, A., San Martin, E., Harris, R. P., and Irigoien, X. (2006). Scaling the metabolic balance of the oceans. Proc. Natl. Acad. Sci. U.S.A. 103, 8739–8744. doi: 10.1073/pnas.0601137103

PubMed Abstract | CrossRef Full Text | Google Scholar

Marañón, E., Cermeño, P., Huete-Ortega, M., López-Sandoval, D. C., Mouriño-Carballido, B., and Rodríguez-Ramos, T. (2014). Resource supply overrides temperature as a controlling factor of marine phytoplankton growth. PLoS ONE 9:e99312 doi: 10.1371/journal.pone.0099312

PubMed Abstract | CrossRef Full Text | Google Scholar

Moss, R. H., Edmonds, J. A., Hibbard, K. A., Manning, M. R., Rose, S. K., Vuuren, D. P., et al. (2010). The next generation of scenarios for climate change research and assessment. Nature 463, 747–756. doi: 10.1038/nature08823

PubMed Abstract | CrossRef Full Text | Google Scholar

Oregon State University (2017). Ocean Productivity. Oregon State Univ. Available online at: http://www.science.oregonstate.edu/ocean.productivity/index.php (Accessed June 5, 2017).

Padfield, D., Yvon-Durocher, G., Buckling, A., Jennings, S., and Yvon-Durocher, G. (2016). Rapid evolution of metabolic traits explains thermal adaptation in phytoplankton. Ecol. Lett. 19, 133–142. doi: 10.1111/ele.12545

PubMed Abstract | CrossRef Full Text | Google Scholar

Ratkowsky, D. A., Olley, J., and Ross, T. (2005). Unifying temperature effects on the growth rate of bacteria and the stability of globular proteins. J. Theor. Biol. 233, 351–362. doi: 10.1016/j.jtbi.2004.10.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Richardson, A. J. (2008). In hot water: zooplankton and climate change. ICES J. Mar. Sci. 65, 279–295. doi: 10.1093/icesjms/fsn028

CrossRef Full Text | Google Scholar

Richardson, T. L., and Jackson, G. A. (2007). Small phytoplankton and carbon export from the surface ocean. Science 315, 838–840. doi: 10.1126/science.1133471

PubMed Abstract | CrossRef Full Text | Google Scholar

Sal, S., Alonso-Sáez, L., Bueno, J., García, F. C., and López-Urrutia, Á. (2015). Thermal adaptation, phylogeny, and the unimodal size scaling of marine phytoplankton growth. Limnol. Oceanogr. 60, 1212–1221. doi: 10.1002/lno.10094

CrossRef Full Text | Google Scholar

Schoolfield, R. M., Sharpe, P. J. H., and Magnuson, C. E. (1981). Non-linear regression of biological temperature-dependent rate models based on absolute reaction-rate theory. J. Theor. Biol. 88, 719–731. doi: 10.1016/0022-5193(81)90246-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Schourup-Kristensen, V., Sidorenko, D., Wolf-Gladrow, D. A., and Völker, C. (2014). A skill assessment of the biogeochemical model REcoM2 coupled to the Finite Element Sea Ice–Ocean Model (FESOM 1.3). Geosci. Model Dev. 7, 2769–2802. doi: 10.5194/gmd-7-2769-2014

CrossRef Full Text | Google Scholar

Séférian, R., Bopp, L., Gehlen, M., Orr, J. C., Ethé, C., Cadule, P., et al. (2013). Skill assessment of three earth system models with common marine biogeochemistry. Clim. Dyn. 40, 2549–2573. doi: 10.1007/s00382-012-1362-8

CrossRef Full Text | Google Scholar

Steinberg, D. K., Carlson, C. A., Bates, N. R., Johnson, R. J., Michaels, A. F., and Knap, A. H. (2001). Overview of the US JGOFS Bermuda Atlantic Time-series Study (BATS): a decade-scale look at ocean biology and biogeochemistry. Deep Sea Res. Part II Top. Stud. Oceanogr. 48, 1405–1447. doi: 10.1016/S0967-0645(00)00148-X

CrossRef Full Text | Google Scholar

Stewart, G., Moran, S. B., Lomas, M. W., and Kelly, R. P. (2010). Direct comparison of 210Po, 234Th and POC particle-size distributions ans export fluxes at the Bermuda Atlantic Study (BATS) site. J. Environ. Radioact. 102, 479–489. doi: 10.1016/j.jenvrad.2010.09.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Taucher, J., and Oschlies, A. (2011). Can we predict the direction of marine primary production change under global warming? Geophys. Res. Lett. 38:L02603. doi: 10.1029/2010GL045934

CrossRef Full Text | Google Scholar

Thomas, M. K., Kremer, C. T., Klausmeier, C. A., and Litchman, E. (2012). A global pattern of thermal adaptation in marine phytoplankton. Science 338, 1085–1088. doi: 10.1126/science.1224836

PubMed Abstract | CrossRef Full Text | Google Scholar

Turner, J. T. (2015). Zooplankton fecal pellets, marine snow, phytodetritus and the ocean's biological pump. Prog. Oceanogr. 130, 205–248. doi: 10.1016/j.pocean.2014.08.005

CrossRef Full Text | Google Scholar

Visser, M. E. (2008). Keeping up with a warming world; assessing the rate of adaptation to climate change. Proc. R Soc. B Biol. Sci. 275, 649–659. doi: 10.1098/rspb.2007.0997

PubMed Abstract | CrossRef Full Text | Google Scholar

Volk, T., and Hoffert, M. I. (2013). “Ocean carbon pumps: analysis of relative strengths and efficiencies in ocean-driven atmospheric CO₂ changes,” in The Carbon Cycle and Atmospheric CO₂: Natural Variations Archean to Present, eds E. Sundquist and W. Broecker, (American Geophysical Union), 99–110. doi: 10.1029/GM032p0099

CrossRef Full Text | Google Scholar

Wang, X., Liu, L., Piao, S., Janssens, I. A., Tang, J., Liu, W., et al. (2014). Soil respiration under climate warming: differential response of heterotrophic and autotrophic respiration. Glob. Chang. Biol. 20, 3229–3237. doi: 10.1111/gcb.12620

PubMed Abstract | CrossRef Full Text | Google Scholar

Yvon-Durocher, G., Caffrey, J. M., Cescatti, A., Dossena, M., Giorgio, P., del Gasol, J. M., et al. (2012). Reconciling the temperature dependence of respiration across timescales and ecosystem types. Nature 487, 472–476. doi: 10.1038/nature11205

PubMed Abstract | CrossRef Full Text | Google Scholar