Interaction Dimensionality Scales Up to Generate Bimodal Consumer-Resource Size-Ratio Distributions in Ecological Communities

Introduction

For at least a century, biologists have wondered why “Spiders do not catch elephants in their webs, nor do water scorpions prey on geese” (Elton, 1927; Riede et al., 2011). That is, why does only a subset of all possible resource-consumer body size ratios exist in nature? Answering this question is important because it could reveal general principles underlying the ecological and evolutionary dynamics of communities (Yodzis and Innes, 1992; Cohen et al., 1993; Brose et al., 2006a,b; Tang et al., 2014; Pawar et al., 2015). Indeed, a prominent hypothesis for why size-ratio distributions show strong central tendencies within and across communities is that only certain size combinations permit species coexistence (Emmerson et al., 2005; Brose et al., 2006a; Otto et al., 2007; Tang et al., 2014). Also, size-ratio distributions exhibit multiple peaks within and across communities; for example, predators tend to be much larger than their prey in water than on land, invertebrate predators tend to be closer in relative size to their prey than vertebrate predators, filter feeders may be a million times larger than their resources, and parasitoids and ectoparasites can be 10 or down to 1 million times smaller than their hosts (Peters, 1986; Cohen et al., 1993; Brose et al., 2005, 2006a). These different peaks likely reflect different regions of feasible coexistence, population stability, or fitness, influenced by both abiotic (e.g., spatial habitat complexity) and biotic (e.g., foraging strategy) factors (Brose et al., 2006a; Cohen, 2008).

Several studies have developed mathematical models to understand how body size determines the feasibility of consumer-resource size-ratios in specific taxa and trophic interaction types (e.g., McArdle and Lawton, 1979; Persson et al., 1998; Aljetlawi et al., 2004). Others have generalized such models by incorporating metabolic scaling (Schmidt-Nielsen, 1984; Peters, 1986; Brown et al., 2004; Savage et al., 2004) into consumer-resource interaction and life history models (Brose et al., 2005; Weitz and Levin, 2006; Williams et al., 2007; Riede et al., 2011; Kalinkat et al., 2013; Carbone et al., 2014). However, studies thus far have failed to yield systematic predictions about central tendencies or the shapes of community-level size-ratio distributions (Brose et al., 2006a).

Arguably, the key to a more nuanced understanding of variation in community size-ratios is to incorporate community- and environment-specific biomechanical constraints into models of consumer-resource interactions (Vucic-Pestic et al., 2010; Dell et al., 2011; Pawar et al., 2012, 2015; Portalier et al., 2019). In this paper, we investigate this possibility by including biomechanical and physiological constraints on the components of consumption rate—search, detection, and handling (attack, pursuit, subjugation, and ingestion) (Figure 1). In particular, we focus on whether interaction dimensionality combined with other biomechanical (velocity, handling) and physiological (metabolic rate) constraints affect consumer-resource size-ratios in local ecological communities. Recent work suggests that the dimensionality of trophic interactions—Euclidean dimension of the space in which the consumer searches for resources (2D vs. 3D)—is a ubiquitous and important factor that strongly affects consumer-resource interactions via encounter rates (McGill and Mittelbach, 2006; Pawar et al., 2012; Carbone et al., 2014). Specifically, if the chance of finding a resource is roughly the same in all directions, then increasing either the dimensionality of resource dispersion (Ritchie, 2009) or the consumer's detection region will increase encounter rates (McGill and Mittelbach, 2006; Pawar et al., 2012, 2015). This leads us to hypothesize that the size-ratio distributions of interacting species in communities should vary systematically with spatial complexity of the habitat. This would be driven by variation in conditions for energetically-feasible stable coexistence of consumer-resource species pairs within different sub-habitats (e.g., pelagic vs. benthic zones in aquatic ecosystems). We first derive theoretical predictions for differences in limits to feasible size-ratios in 2D vs. 3D interactions. We then use an extensive dataset of 4,685 consumer-resource interactions from nine aquatic and terrestrial communities to test our predictions.

FIGURE 1

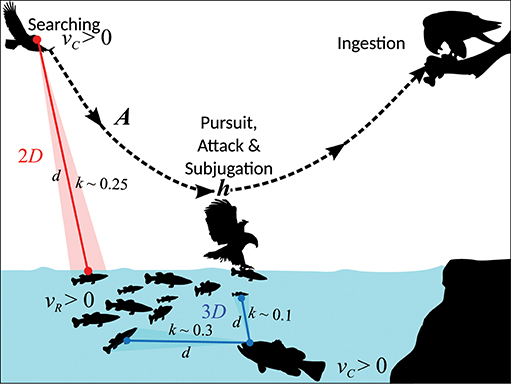
Figure 1. An illustration of components of consumption rate and environmental constraints on them. The parameters shown belong to our model for size-mediated consumer-resource dynamics. Feasible body size-ratios depend on consumer and resource body velocities (v_R and v_C), reaction distance (d), attack success probability (A) following attack and pursuit, handling time h (sum of pursuit, attack, subjugation, and ingestion times), and interaction dimensionality (D). Our theory predicts that 3D interactions, by allowing an additional dimension for detection (depicted here by the largemouth bass' search space), can allow 3D consumers to subsist on a wider range of resource sizes (k denotes consumer-resource size ratio; see text after Equation 3). Thus, feasible size-ratios for the fishing eagle searching in 2D (water surface) are expected to be more strongly constrained than the largemouth bass searching in 3D (water column), although they are both feeding on the same resource.

Methods

Theory

We develop a mathematical model to predict the feasibility of community-wide resource to consumer size-ratios. To this end, we first incorporate body size constraints on components of consumer-resource interactions—relative velocity, detection distance, attack success, and handling time (Figure 1)—which altogether determine per-capita biomass consumption rate. Consumption is a fundamental rate controlling the energy budget of an individual (net energy gain or loss) and population dynamics (coupled changes in consumer and resource population biomasses or numbers) (DeLong and Vasseur, 2012; Pawar et al., 2012, 2015; Carbone et al., 2014). We then derive feasible size-ratios from both energetic and population dynamical perspectives.

We begin with a general equation for consumption rate c (mass × time⁻¹) (Pawar et al., 2012, 2015; Carbone et al., 2014):

$\begin{array}{ll}c=aA{x_{R}m}_{R}f& (1)\end{array}$

Here, x_R is resource number density (individuals × m⁻² or m⁻³), m_R is resource body mass, a is per-capita area or volume search rate (m² or m³ × s⁻¹), A is probability of attack success (conditional on an attack occurring), and f is a dimensionless prey risk function that determines the shape of the consumer's functional response (Pawar et al., 2012; Dell et al., 2014). In principle, f can be of any form, but we focus on the commonly observed Type II form

$\begin{array}{ll}f=\frac{1}{1+aAh{x}_R}& (2)\end{array}$

where h is consumer's handling time (s). If h is instantaneous (→ 0), Equation (2) reduces to the linear Type I functional response (f = 1). Our subsequent results about feasible size-ratios from both energetic and population dynamical perspectives remain qualitatively unchanged if we use a Type III functional response (Appendix 3; Figure S2).

We now define size-dependence of the components of c. In Appendix 3 we show that our results are robust to considerable variation in parameterizations of the following scaling equations. The parameterizations are listed in Table S3. First, for search rate we use an empirically well-supported scaling model (Pawar et al., 2012; Dell et al., 2014; Rizzuto et al., 2018):

$\begin{array}{ll}a=a_0{m}_C^{p_v+2p_d(D-1)}{k}^{p_d(D-1)}.& (3)\end{array}$

Here, a₀ is a constant that includes effects of temperature and dimensionality, p_v is the scaling exponent for consumer body velocity, p_d is the scaling exponent for reaction distance between consumer and resource, D is interaction dimensionality defined by the space in which the consumer can search for and detect a resource (2D or 3D; Figure 1), and k = m_R/m_C is body size-ratio. We emphasize that this simple definition of interaction dimensionality arises because resource detection typically occurs in Euclidean space, regardless of which sensory modality is used. Later, we discuss how our model can be extended to more complex definitions of dimensionality by considering non-sensory components (such as relative velocity) of consumer-resource interactions. As such, Equation (3) is a scaling model for grazing (i.e., consumer searching for sessile resources) but also well-approximates the scaling of search rate in active-capture interactions (i.e., both consumer and resource moving actively across the landscape) when m_C > m_R (Appendix 3) (Pawar et al., 2012; Dell et al., 2014). We use just the grazing model because our dataset is dominated by grazing and active-capture interactions with m_C > m_R (Appendix 1, Table S2; see also Table S5). Furthermore, in Appendix 3 we show that relative to dimensionality, foraging strategy is expected to have minor effects on feasible size-ratios.

Next, for attack success probability A, we use an empirically supported function (Appendix 1; Figure S1),

$\begin{array}{ll}A={\left(1+k^{\gamma }\right)}^{-1},& (4)\end{array}$

where γ is a constant that governs the decrease in attack success as resources get very large relative to consumer size (m_R ≫ m_C). The exponent γ in Equation (4) captures biomechanical constraints that appear at upper size-ratios (McArdle and Lawton, 1979; Persson et al., 1998; Aljetlawi et al., 2004; Weitz and Levin, 2006). In particular, increasing γ can emulate increasing consumer gape-limitation, which was previously suggested to be a bigger constraint on size-ratios in aquatic interactions relative to terrestrial ones (Hairston and Hairston, 1993). Hairston and Hairston (1993) argue that gape limitation is stronger in aquatic interactions because the bodies and appendages of aquatic organisms are modified for efficient locomotion in water, and thus are of limited use for handling resources. As a result, aquatic consumers cannot be too close to or smaller in size than resources (relative to terrestrial consumers). By increasing γ, we can explore the importance of gape-limitation relative to detection dimensionality in constraining feasible size-ratios. Similarly, by relaxing γ we can consider interactions where attack success and therefore consumption rate is relatively insensitive to size-ratio, such as in the case of ecto-parasites, which are largely limited by encounter (therefore, search) rate, and can successfully feed on wide range of resource sizes once they are encountered.

Substituting Equations (3, 4) into (1) and rearranging to gives the scaling of per-capita (biomass) consumption rate:

$\begin{array}{ll}c=a_0{m}_C^{p_v+2p_d(D-1)+1}{k}^{p_d(D-1)+1}{\left(1+k^{\gamma }\right)}^{-1}{x}_{R}f.& (5)\end{array}$

Note that here the resource mass term m_R from Equation (1) has been absorbed into the size-ratio term. This equation captures four essential features of consumption rate:

(i) For a given resource size and therefore size-ratio k, consumption rate c increases with consumer mass m_C because larger consumers have greater body velocity,

(ii) Consumption rate c increases with size-ratio k because when m_R < m_C (i.e., k < 1) search rate increases with resource mass m_R due to increasing reaction distance (and for active-capture, also increasing relative velocity; Appendix 3, Equation S14),

(iii) When resource mass far exceeds consumer mass (k ≫ 1), c declines because resources become difficult for the consumer to attack and handle due to the (1 + k^γ)⁻¹ term. That is, the product of per-capita search rate (a monotonically increasing function with respect to size and size-ratio; Equation 3) and attack success probability A (monotonically decreasing function), aA, yields an empirically realistic unimodal (hump-shaped) function (McArdle and Lawton, 1979; Persson et al., 1998; Aljetlawi et al., 2004; Brose et al., 2008) (Appendix 1; Figure S5).

(iv) Consumption rate c increases faster with consumer mass m_C and size-ratio k when consumers forage in 3D (D = 3; e.g., pelagic zones in lakes and oceans) than 2D (D = 2; e.g., benthic zones) because above a threshold consumer size, 3D search space (m⁻³) allows higher detection probability than 2D search space (m⁻²) (Pawar et al., 2012, 2015).

Finally, for handling time we use another empirically well-supported model (Pawar et al., 2012):

$\begin{array}{ll}h=h_0{m}_C^{-{\beta }_h}{m}_R& (6)\end{array}$

where h₀ is a constant and β_h is the scaling of the metabolic rate of a consumer during pursuit, subjugation, and ingestion of resources.

Energetically Feasible Size-Ratios

We first derive feasible ranges of size-ratios that meet consumer energy requirements for somatic maintenance, by setting a lower bound on energy gain from resource consumption (Carbone et al., 2014; Rizzuto et al., 2018):

$\begin{array}{ll}ec>B_C& (7)\end{array}$

Here, B_C is the rate of the consumer's energy use converted to mass units (kg/s) while resting (resting metabolic rate, RMR), e the efficiency of conversion of resource biomass into consumer biomass (a proportion). All other parameters are as defined in Equations (1)–(6). Conversion efficiency e is approximately independent of body size (Peters, 1986; DeLong et al., 2010; Lang et al., 2017), and between 0.5 and 0.85, with carnivores having higher values than herbivores (Yodzis and Innes, 1992; Lang et al., 2017). Our results remain qualitatively robust to a even wider variation in e than this (Appendix 3). Convert B_c to mass units (like the quantity ec on the left hand size) we assume 1 kg = 7 × 10⁶ J (the combustion energy content per unit of wet biomass) (Peters, 1986). Note that the Inequality (7) sets a lower bound on consumption rate because B_C is RMR, which is an underestimate of maintenance energy needs because it typically does not include the energy required for somatic growth, producing offspring, storage, and bursts of activity (such as during foraging). These may cause significant additions to the energy needs of adult animals in certain periods of their lifetime (Rizzuto et al., 2018). Therefore, we expect the coexistence bounds to be somewhat narrower than those we predict below; but this does not change our conclusions about the differences in coexistence due to dimensionality. Also, assuming there are no systematic differences in conversion efficiency in 2D vs. 3D interactions, variation in e will have negligible effect on our subsequent results.

We already have the size scaling of a and A, but require the scaling of B_C and biomass abundance x_R m_R. For B_C, we use the scaling of basal or resting metabolic rate (Peters, 1986; Nagy, 1987; Brown et al., 2004; DeLong et al., 2010):

$\begin{array}{ll}{B}_C=B_0{m}_C^{\beta }& (8)\end{array}$

where B₀ is a constant that includes the effect of temperature and converts metabolic rate units (J/s) to mass use rate units, and β is the scaling exponent of metabolic rate. For biomass abundance we use (Peters, 1986; Brown et al., 2004):

$\begin{array}{ll}{x}_R{m}_R=x_0{m}_R^{1-{\beta }_x}& (9)\end{array}$

Where x₀ is a normalization constant that includes the effect of temperature, and β_x is the scaling exponent of numerical abundance. Substituting the scaling (Equations 5, 6, 8, 9) into (7) and solving for m_R gives the bounds on resource mass m_R and therefore size-ratios that guarantee a balanced energy budget. To obtain an exact solution for this we set h = 0 [Type I f (R)] and solve for m_R, which gives:

$\begin{array}{ll}{m}_R>{c\left(m_C^{\beta -p_d(D-1)-p_v}{\left(1+k^{\gamma }\right)}^{-1}\right)}^{\frac{1}{1+p_d(D-1)-{\beta }_x}}& (10)\end{array}$

Where $c={(B_0/e{a}_0{x}_0)}^{\frac{1}{1-p_d(D+1)-{\beta }_x}}$. In Appendix 3 we show that our subsequent results are qualitatively unchanged if h > 0. Substituting the values of scaling exponents (Table S3) into Inequality (10) gives

$\begin{array}{ll}\begin{array}{c}{m}_R>m_0{m}_C^{0.64}{\left(1+k^{\gamma }\right)}^{-2.22}in2D\\ m_R>m_0{m}_C^{0.14}{\left(1+k^{\gamma }\right)}^{-1.54}in3D\end{array}& (11)\end{array}$

where m₀ = (B₀/ea₀x₀)^2.22 in 2D and (B₀/ea₀x₀)^1.54 in 3D. Inequalities (10) and (11) yield three important theoretical insights and predictions (illustrated in Figure 2):

(i) The smaller m_C and k exponents for 3D compared with 2D in Equation (11) imply that size constraints weaken as dimensionality increases. Therefore, relative to 2D, a wider range of resource sizes become feasible for larger 3D consumers. Conversely, 3D foraging allows an increased range of consumer sizes on a given sized resource because for a given size-ratio, larger consumers enjoy a greater mass-specific search rate in 3D than in 2D [$a/m_C\propto m_C^{0.04}$in 3D but $m_C^{-0.34}$ in 2D, from parameterized Equation (3)].

(ii) Within either 2D or 3D, feasible size-ratios for coexistence are predicted to be constrained by baseline resource density (x₀) through the term m₀. In particular, following empirical data (Peters, 1986; Pawar et al., 2012), if we assume baseline abundance (x₀) is about two orders of magnitude higher in 3D than 2D, the widening of energetically feasible size ratios is magnified because then the advantage of 3D detection dimensionality is enhanced. In this context, note that although biomass density is expressed in per-volume units in 3D and per-area units in 2D (Table S3), what matters is that a greater amount of resource biomass can be packed into a 3D space, which boosts consumption rate due to increased detection dimensionality.

(iii) The upper bound on size ratios (where m_R > m_C so k > 1) is set by the scaling of A through the exponent γ. Therefore, all these results are qualitatively robust as long as decline in attack success at high size-ratios is strong enough to render consumption rate (Equation 5) unimodal with respect to k. Values of the exponents in Equation (5) dictate that consumption rate will be unimodal with respect to size-ratio as long as γ > 0.2 in 2D and >0.4 in 3D (also see Figure S4). Our meta-analysis (Appendix 1) shows this condition generally holds for real interactions and is in agreement with previous studies (Aljetlawi et al., 2004; Brose et al., 2008).

FIGURE 2

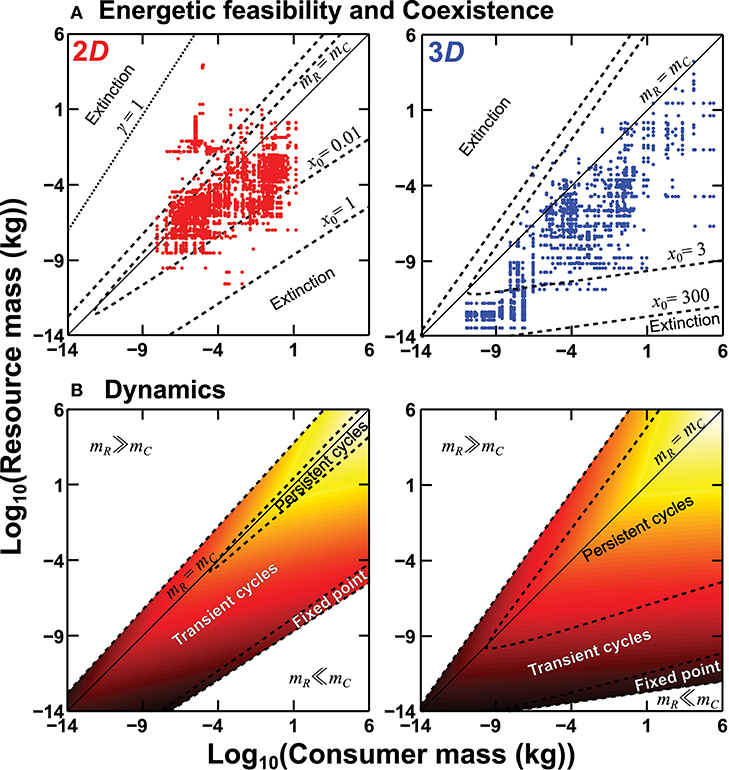
Figure 2. Predicted effects of interaction dimensionality on consumer energetic feasibility and consumer-resource coexistence (A) and population dynamics (B). In (A) real consumer-resource pairs (dots) from nine communities have been overlaid (n = 3,055 in 2D and 1,630 in 3D; Table 1), with dashed lines delineating predicted coexistence regions for different baseline carrying capacities x₀ (because baseline abundances tend to be higher by orders of magnitude in 3D than 2D; see main text). In (B) dashed lines delineate population stability regimes and equilibrium abundance is represented by a heat-map of log₁₀ number density (darker means more abundant). These results are for h₀ = 10⁴ s (Equation 6) and γ = 2 (Equation 4; cf. Table S3). When attack success declines more weakly (γ decreases) at size-ratios m_R ≫ m_C, possibly due to decrease in gape-limitation, coexistence becomes possible at those extreme ratios, illustrated by the dotted γ = 1 line (at x₀ = 1, with other parameter values remaining the same) in the 2D plot in (A).

Population-Dynamically Feasible Size-Ratios

The above theory based upon the consumer's energetic considerations does not account for consumer-resource population dynamics. Therefore, we consider whether accounting for population dynamics changes our predictions about the effect of dimensionality on feasible size-ratios. Using a general consumer-resource model, in Appendix 2 we show that both consumer-resource coexistence and mutual population stability yield similar predictions as above. Specifically, coexistence is possible only if

$\begin{array}{ll}{m}_R>m_0{\left(m_C^{\beta -p_d(D-1)-p_v}{\left(1+k^{\gamma }\right)}^{-1}\right)}^{\frac{1}{1+p_d(D-1)-\beta }}& (12)\end{array}$

where $m_0={\left(\frac{B_0}{e{a}_0{x}_0}\right)}^{\frac{1}{1+p_d(D-1)-\beta }}$. This is same as inequality (10), except that β (consumer's RMR scaling exponent) replaces resource carrying capacity scaling exponent β_x. That is, the above predictions (i)–(iv) from the energetic model also hold for the population dynamics model. We also show that local asymptotic stability to small perturbations around equilibrium abundances of consumer and resource (Equations S8–S9) differs between 2D and 3D. Figure 2 shows that regions of cycles over the size-combination plane coincide with regions of low abundance (along the k = 1 line). Consistent with consumer-resource theory, as h → 0 and the functional response becomes Type I, regions of persistent cycles are replaced by transient cycles (Appendix 3). Furthermore, in Appendix 3, we show that the scaling of coexistence in Equation (11) is qualitatively similar for Type II and III functional responses. These results and those from the energetic model above are robust even if decline in attack success (Equation 4) is not strictly a power-law (Figure S6).

Theoretical Predictions

Next, we calculated community-specific predictions about the magnitude of difference in central tendency of 2D and 3D size-ratio distributions to compare with the empirical data (next section) on size ratios. For this, for each community, and for a given K and γ (which set the lower and upper bound of the coexistence region, respectively; Figure 2), we generated 10,000 random interactions by first generating model consumer and resource size distributions within that community's observed size limits. The size distributions were generated using the beta distribution, using the method used by Pawar (2015). This approach allows realistic, right-skewed size distributions of different shapes to be generated. As long as the size distribution is right-skewed, the following results remain qualitatively robust. We then determined what subset of size-ratios in these random interactions allowed stable population coexistence (criteria i–ii in Appendix 2). This is equivalent to “carving out” the general predicted coexistence region (Figure 2) into its stable community-specific sub-regions. Differences in the median of these feasible and stable log₁₀-transformed 2D and 3D size-ratios were then the predicted difference for that community. This difference was compared with the empirically observed difference (see data analysis below). We use the median (log₁₀-transformed) size ratio of each local community as a measure of central tendency because most communities exhibit skewed and multimodal size-ratio distributions (Figure 3). Also, we focus on predicted differences in medians and not the absolute values of medians themselves, because feasible size-ratios are expected to depend on carrying capacity [Figure 2; also see text following Inequality (11)], which is an unknown parameter in all our community datasets.

FIGURE 3

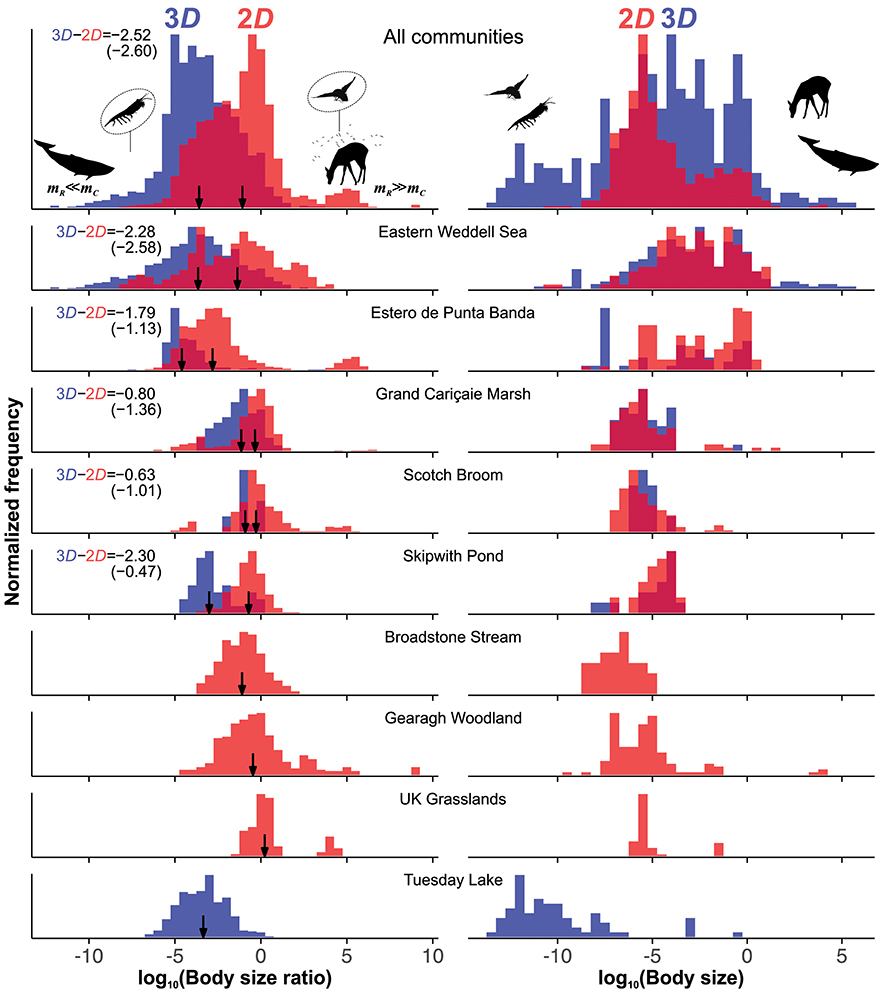
Figure 3. Effect of interaction dimensionality on species' log₁₀ size-ratio and size (mass, kg) distributions across communities. All pairs of 2D (red) and 3D (blue) distributions have been normalized by respective peak frequency to allow comparison within and between communities. In all sub-plots a darker shade of red represents the overlap between the 2D and 3D distributions. Black vertical arrows mark locations of observed median 2D and 3D interaction size-ratios, along with their observed and predicted (in parentheses) differences. In all communities, the range and median of log₁₀ size in 2D and 3D are similar while median 3D size-ratios are significantly lower than 2D as predicted by our theory (Table 1). Note that there are three pure 2D and one pure 3D community. Two real interactions are shown to illustrate extreme size-ratios: Blue Whale eating Krill (m_R≪m_C; k ~ 10⁻¹⁰) in the Eastern Weddell Sea, and Deer Flies on Roe Deer (m_R≫m_C; k ~ 10^6.5) in Grand Cariçaie Marsh.

Empirical Data

To study size-ratio distributions and test our theoretical predictions we compiled published data on interacting consumer-resource pairs for nine communities (four terrestrial, five aquatic; Table S5). If average body mass for a particular taxon was not reported in the original study, it was estimated using methods previously described (Dell et al., 2011, 2013, 2014). Each consumer-resource interaction was assigned a 2D or 3D search-space dimensionality by combining information on the consumer's movement space and foraging strategy—sit-and-wait, active foraging, or grazing—and the resource's movement space (Table S1). Classification of interactions by dimensionality in this way requires knowing the taxonomy, feeding behavior, body size, and foraging strategy of individual taxa (see Table S1). Although there are many communities with data on trophic links, few have the adequate body size and taxonomic information required for this level of classification. These nine communities are the available datasets for which all these pieces of information are available or could be obtained from the literature. The final dataset comprised 4,685 interactions between 964 taxa, comprising 3,055 2D and 1,630 3D consumer-resource interactions (Table S5).

Data Analysis

We tested whether, as predicted by our theory, 2D and 3D size-ratio distributions had significantly different central tendencies, both within each of the nine communities as well as the overall dataset. A parametric approach to testing this statistically is not appropriate because size-ratios within communities are often not independent (multiple resources may be fed upon by the same consumer and multiple consumers often feed on the same resource). Furthermore, the (log₁₀) size-ratio distributions are often right-skewed with long tails and/or multi-modal (Figure 2). Therefore, we developed the following bootstrap-like test for significance of differences in size-ratios. For each community we separately generated 10⁵ lists of random 2D and 3D consumer-resource interaction pairs by independently sampling (with replacement) the observed pairs of consumers and resources. Each randomly generated 2D and 3D “sub-community” was constrained to have the same number of interaction pairs as observed in the original 2D or 3D sub-community. We then calculated differences in median log₁₀-transformed size-ratios (3D or 2D) across the 10⁵ random lists. The distribution of these 10⁵ differences is an approximation of the sampling distribution of differences assuming random partitioning of the community into 2D and 3D sub-communities. Thus, the proportion of times the observed difference between median values of log-transformed 2D and 3D size-ratios matches or exceeds a value in the sampling distribution can be used as an estimate of the one-tailed p-value of the observed difference. We also compared each community's predicted difference in median 2D vs. 3D size ratios (see “Theoretical predictions” above) with its sampling distribution of random differences in medians to test whether these also significantly matched the observed differences in median size-ratios.

As an even more stringent test in the face of non-independent size-ratios, we also re-analyzed the data for differences between 2D and 3D size-ratios as described above after collapsing all the links of a single consumer to a single size ratio by taking the geometric average of the sizes of all its resources. After doing so, our results about significant differences in central tendencies of 2D vs. 3D size-ratio distributions remain qualitatively the same (Appendix 3; Table S4).

Finally, to determine whether size ranges [m_{C, min}, m_{C, max}] and [m_{R, min}, m_{R, max}] are influenced by factors independent of dimensionality, such as oxygen limitation, physical medium for locomotion, and phylogenetic history (Allen et al., 2006), we also tested for differences in median sizes of all 2D an 3D species using the Wilcox test after removing consumers and resources that were in both the sets, and also tested for differences in variances around the median values using the Brown–Forsythe test.

Results

We find strong and statistically significant empirical evidence that median 3D size-ratios are consistently lower than 2D size-ratios across all nine communities (Figure 3), with observed differences in median size-ratios closely matching our theoretical predictions (Table 1). The magnitude of difference between 2D and 3D size-ratios varies with community, ranging from the median 3D size-ratio being about four times smaller than 2D for the Scotch Broom community to 2.29 orders of magnitude smaller for the Eastern Weddell Sea community. Even in the case of pure 2D communities, size-ratios tend to be higher than 3D ratios observed in other communities. Similarly, in the single pure 3D community (Tuesday lake), size-ratios are generally lower than the 2D ratios from the other communities (Figure 3; Table 1).

TABLE 1

Table 1. Differences between 2D and 3D size-ratio distributions.

We also found multimodalities in 2D size-ratio distributions (Figure 3), one at extremely small size-ratios (m_R ≪ m_C) and another at extremely large ratios (m_C ≪ m_R). The lower 2D peak (where m_R ≪ m_C) found in several communities corresponds to grazing. Scotch Broom, UK Grasslands, and Estero de Punta Banda also each have a peak at very high 2D size-ratios (m_R ≫ m_C), corresponding to macroparasites, parasitoids, herbivores, and micropredators. Indeed, these types of interactions are why only 87.8% of 2D interactions lie within the predicted 2D coexistence region (the γ = 2 and high x₀ case in Figure 2), while 99.9% of 3D interactions fall within the predicted 3D coexistence region. This is not surprising because macroparasitism, parasitoidism, herbivory, and micropredation are likely to be more limited by search and detection than attack success. We can account for this by decreasing the value of γ in Equation (4) and recalculating coexistence bounds. Doing so relaxes constraints on coexistence at high size-ratios (k ≫ 1 or m_R ≫ m_C) (Figure 2, Figure S4), and helps explain deviation of these interactions from predicted coexistence bounds. Note that, as γ → 0, the upper coexistence bound (Figure 2) will vanish because attack success probability A becomes independent of size-ratio. We chose γ = 1 to illustrate that a weaker decline in attack success with size-ratio can explain feasibility and coexistence of interactions at those size-ratios. The value of γ = 1—where A declines weakly with decreasing size-ratio (resources get very large relative to consumers)—is necessarily arbitrary because we have practically no information about A at those extreme size-ratios, which future work needs to address.

Eastern Weddell Sea, Grand Cariçaie Marsh, and Scotch Broom also show a secondary 2D peak at very small size-ratios (m_R ≪ m_C) (Figure 3), mostly corresponding to large endothermic vertebrates feeding on arthropods—effectively grazing interactions because of the large size difference between consumer and resource, and therefore in their body velocities Appendix 3; (Pawar et al., 2012; Dell et al., 2014). This is also qualitatively consistent with our theory, which predicts a relaxation of coexistence constraints in grazing interactions where m_R ≪ m_C (Figure S3).

In communities that have both interaction dimensionalities, median body size distributions of species in 2D and 3D interactions are statistically indistinguishable (Figure 3; Table 1). Body size ranges of species involved in 2D and 3D interactions also tend to be similar, with only Eastern Weddell Sea and Estero de Punta Banda showing significant differences in variance of sizes (p < 0.001, Brown-Forsythe test of unequal variances). Thus, bimodality in size-ratios is not driven simply by different 2D and 3D size distributions. Indeed, the high overlap between 2D and 3D size distributions supports an assumption implicit in our theory: that size ranges of consumers or resources are set by factors extrinsic to dimensionality. The similarity in size distributions partly stems from the fact that although consumers forage on completely different resources (and therefore potentially different habitat zones) in 2D and 3D in certain communities (i.e., Eastern Weddell Sea, Skipwith pond, and Estero de Punta Banda), a relatively constant proportion of resources are fed upon by both 2D and 3D consumers in all communities (compare consumer and resource 2D/3D overlap in Table 1). An example of how the same resource can be exploited in both 2D and 3D is shown in Figure 1. Thus, 2D and 3D components of each community are consistently coupled through shared resources.

Discussion

By combining theory with extensive empirical data, we have shown that interaction dimensionality strongly constrains resource-to-consumer size ratios in ecological communities. Specifically, 3D interactions allow a lower median size-ratio as well as a wider range of size-ratios than 2D, with the magnitude of observed difference in most communities similar to the difference predicted by our theory (Table 1). This emergent difference between 3D and 2D size-ratios arises because in 3D, the additional dimension for resource detection usually elevates baseline encounter rates and steepens the scaling of consumption rate with body size (Pawar et al., 2012). As a result, communities from spatially complex environments that can support both 2D and 3D interactions show distinct size-ratio distributions (Figure 3). For example, bimodal size-ratio distributions exist in the Eastern Weddell Sea, which has pelagic (mostly 3D) and benthic (mostly 2D) zones, and in the Grand Cariçaie Marsh, which has shallow-water (mostly 2D), grassland (mostly 2D), and tree-dominated zones (mixture of 2D and 3D). We emphasize that the difference in median 2D and 3D size-ratios is repeatedly observed across communities, despite considerable variation in habitat (e.g., aquatic vs. terrestrial), consumer foraging behaviors (e.g., 2D benthic vs. 2D water surface foraging), and organismal types (e.g., vertebrates vs. invertebrates).

Our results provide an explanation for three important empirical patterns in the body size structure of communities. First, our theory predicts that wider ranges of size-ratios become feasible as consumer size increases in both 2D and 3D (Figure 2). This explains why smaller consumers tend to be restricted to a narrower range of resource sizes (Cohen et al., 1993), and therefore why invertebrate predators tend to be closer in size to their prey than vertebrate predators (Peters, 1986; Brose et al., 2006a). Second, our theory predicts that the widening of coexistence bounds with consumer size is much more pronounced in 3D than 2D, and that this widening occurs in the direction of lower size-ratios. That is, consumers are able to coexist with resources much smaller than themselves in 3D in comparison to 2D. This helps explain why pelagic predators (3D) tend to be so much larger than their prey in comparison to terrestrial (2D) predators (Cohen and Fenchel, 1994; Brose et al., 2006a). Similarly, we would also expect size-ratios in other 3D interactions, such as those for aerial predators, to be more extreme than in terrestrial 2D interactions. Indeed, the mean size-ratio of terrestrial 3D interactions from real communities—all from Grand Cariçaie Marsh, Gearagh Woodland, Scotch Broom, or UK Grasslands—is about an order of magnitude lower than 2D interactions (0.07 in 3D vs. 0.51 in 2D). Third, if coexistence bounds widen with body size, it follows that if consumer size increases systematically with trophic level then so will size-ratios. This can explain why the traditional Eltonian paradigm (Elton, 1927) of invariance of size-ratios with trophic level does not always, or even typically, hold (Cohen and Fenchel, 1994; Brose, 2010; Riede et al., 2011).

Our theory also predicts that irrespective of dimensionality, size-ratios will be smaller in magnitude (closer to k = 1) and show less variance (i.e., be more constrained) in resource-poor environments (with low carrying capacity; Figure 2). Although we could not test this directly, carrying capacity may account for additional variation in size-ratio distributions across communities. Furthermore, abundance of resources is particularly important to consumer-resource coexistence in 3D because the potential advantage of stronger scaling of search rate from the additional dimension is not realized if resources are not sufficiently abundant. For example, the higher encounter of resources in 3D would not be realized if resources have the same numbers (but not densities) in 2D and 3D habitats (e.g., 1 kg/m² and 1 kg/m³), irrespective of whether abundance was high or low.

Hairston and Hairston (1993) suggest that size-ratios in aquatic interactions are more constrained than in terrestrial environments because of gape-limitation. That is, they argue that gape-limitation is stronger in aquatic interactions because bodies and appendages of aquatic organisms are modified for efficient locomotion in water, and thus are of limited use for handling resources. As a result, aquatic consumers may be larger, but not too close to or smaller in size compared to resources. However, we find that size-ratios exhibit 2D-3D bimodality even within aquatic environments, suggesting that gape-limitation may not be the primary constraint on size-ratios.

Our theory can partly explain multimodalities found in 2D size-ratio distributions (Figure 3) in terms of foraging strategies. The 2D peak in several communities where m_R ≪ m_C corresponds to grazing. Our theory predicts that grazing allows a wider range of size-ratios (Figure S3), although observed size-ratios peak at even more extreme values than predicted. Similarly, by decreasing γ, which determines the strength in decline of attack success (A) as resources become much larger than consumers (m_R ≫ m_C), we are able to explain the 2D peak in size-ratios at m_R ≫ m_C (corresponding to macroparasitism, parasitoidism, herbivory and micropredation) seen in several communities. This is also consistent with the fact that the empirical data on consumption rates we used to obtain estimates of γ are only from predator-prey interactions, not macroparasitism, parasitoidism, herbivory or micropredation. At the same time, we did not find multimodalities in 3D size-ratio distributions. This could occur because strategies, such as macroparasitism and micropredation are less feasible in 3D environments than in 2D (which is possible if γ itself increases with dimensionality), or because such interactions are simply under-sampled in 3D. In either case, further research is needed. This is particularly important given the important role of parasitism in food webs (Hechinger et al., 2011). For example, the addition of parameters that account for the biomechanics of attack and escape (which must differ with foraging strategy) will likely help explain some of this additional variation and multi-modalities.

Empirical biases also need to be considered while interpreting our results. For example, the fact that no observed species pairs lie in the predicted feasible regions at smallest and largest consumer sizes in 2D likely reflects a lack of sampling of interactions for the smallest (e.g., microorganisms and microinvertebrates) and largest (e.g., large carnivores) consumers (Brose et al., 2006a). More importantly, sampling biases are also likely to skew the estimate of the proportion of 2D and 3D interactions in each community—the “pure” 2D and 3D communities likely contain interactions with both dimensionalities and only more accurate trophic and foraging data will resolve this issue.

Our theoretical analysis assumes that the criteria for energy balance and stable coexistence of two-species systems approximately hold even when these pairwise interactions are embedded in food webs. We are encouraged by the fact that we are able to correctly predict the differences between median 2D and 3D size ratios, even without incorporating higher-order or indirect effects. This is consistent with the result that community stability is most strongly determined by the strengths of the direct coupling between consumer-resource interactions (Pawar, 2009; Tang et al., 2014). Thus, we have shown for the first time, that a combination of environmental, behavioral, and biomechanical constraints on species interactions scale up to an emergent property (the community-wide size-ratio distribution) through a combination of natural selection (the energetics constraint; inequality 10) and species sorting (the coexistence constraint; inequality 12). This scaling up and emergence effectively results in the reorganization of communities from more spatially complex environments into distinct compartments (in terms of food web topology), as evidenced by the typically low overlap in 2D and 3D consumer and resource species and interaction identities (last two columns of Table 1). This stems from localization or specialization of consumers as well as resources to a specific, preferred sub-environment (2D or 3D). Nevertheless, future extensions of our work to multispecies interactions should account for the stability consequences of indirect interactions and polyphagy, and these modifications may lead to more accurate predictions about the effect of dimensionality on size-ratio distributions in real communities. Given the apparently ubiquitous difference in 2D and 3D size-ratios within communities, food web models with coupled 2D and 3D sub-communities should be especially enlightening for these questions and might explain some of the differences between predicted and observed features of size-ratio distributions reported here. In this respect, we were intrigued to find that 2D and 3D sub-communities are coupled, as must be the population dynamics, through shared resources in all the communities we analyzed.

Our classification of interactions according to dimensionality of the search and interaction space is appealingly simple, and necessarily so because detection typically occurs in Euclidean space (McGill and Mittelbach, 2006; Pawar et al., 2012). An extension of our model would be to include more complex habitats with non-integer dimensionality by relaxing the assumption of random movement of the consumer and/or resource. For example, non-random searching by consumers for resources that are dispersed or moving in fractal dimensions (Ritchie, 2009)—a more continuous measure of dimensionality—could alter how spatial complexity influences size-ratios. Testing these additional factors would require more detailed knowledge of foraging behavior for specific taxa and of habitat complexity in local communities.

In conclusion, our study helps explain a number of empirical observations in which community size structure varies with habitat, type of consumer-resource interaction, and foraging strategy (Elton, 1927; Cohen et al., 1993; Brose et al., 2006a,b; Riede et al., 2011). Our theory generalizes previous models that incorporate body size into components of consumer-resource interactions (McArdle and Lawton, 1979; Persson et al., 1998; Aljetlawi et al., 2004; Weitz and Levin, 2006) to multiple foraging strategies—active-capture, sit-and-wait, or grazing—and interaction dimensionalities. Thus, our framework can be used to develop models for specific organisms and habitats by relying on estimates of body sizes, foraging strategies, and interaction dimensionalities. Ultimately, models that explicitly incorporate biomechanical and environmental constraints on the components of consumer-resource interactions should form the foundation of a general theory that can explain variation in the structure and function of ecological communities across environments.

Author Contributions

SP and VS developed the theory. SP and TL conducted the theoretical and numerical analyses. SP and AD collected empirical data for the main analysis and meta-analysis. SP, AD, and DW analyzed the empirical data. SP, AD, TL, DW, and VS wrote the manuscript.

Funding

SP, AD, and VS were supported by UCLA Biomathematics start-up funds and by NSF DEB Award 1021010. SP was supported by UK NERC Grant NE/M003205/1. TL, DW, and VS were supported by a McDonnell Complex Systems Scholar Award.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank P. Amarasekare, C. Johnson, and the reviewers for helpful discussions and comments.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2019.00202/full#supplementary-material

References

Aljetlawi, A. A., Sparrevik, E., and Leonardsson, K. (2004). Prey-predator size-dependent functional response: derivation and rescaling to the real world. J. Anim. Ecol. 73, 239–252. doi: 10.1111/j.0021-8790.2004.00800.x

CrossRef Full Text | Google Scholar

Allen, C. R., Garmestani, A. S., Havlicek, T. D., Marquet, P. A., Peterson, G. D., Restrepo, C., et al. (2006). Patterns in body mass distributions: sifting among alternative hypotheses. Ecol. Lett. 9, 630–643. doi: 10.1111/j.1461-0248.2006.00902.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Brose, U. (2010). Body-mass constraints on foraging behaviour determine population and food-web dynamics. Funct. Ecol. 24, 28–34. doi: 10.1111/j.1365-2435.2009.01618.x

CrossRef Full Text | Google Scholar

Brose, U., Cushing, L., Berlow, E. L., Jonsson, T., Banasek-Richter, C., Bersier, L. -F., et al. (2005). Body sizes of consumers and their resources. Ecology 86:2545. doi: 10.1890/05-0379

CrossRef Full Text | Google Scholar

Brose, U., Ehnes, R. B., Rall, B. C., Vucic-Pestic, O., Berlow, E. L., and Scheu, S. (2008). Foraging theory predicts predator-prey energy fluxes. J. Anim. Ecol. 77, 1072–1078. doi: 10.1111/j.1365-2656.2008.01408.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Brose, U., Jonsson, T., Berlow, E. L., Warren, P., Banasek-Richter, C., Bersier, L.-F., et al. (2006a). Consumer-resource body-size relationships in natural food webs. Ecology 87, 2411–2417. doi: 10.1890/0012-9658(2006)87[2411:CBRINF]2.0.CO;2

PubMed Abstract | CrossRef Full Text | Google Scholar

Brose, U., Williams, R. J., and Martinez, N. D. (2006b). Allometric scaling enhances stability in complex food webs. Ecol. Lett. 9, 1228–1236. doi: 10.1111/j.1461-0248.2006.00978.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Brown, J. H., Gillooly, J. F., Allen, A. P., Savage, V. M., and West, G. B. (2004). Toward a metabolic theory of ecology. Ecology 85, 1771–1789. doi: 10.1890/03-9000

CrossRef Full Text | Google Scholar

Carbone, C., Codron, D., Scofield, C., Clauss, M., and Bielby, J. (2014). Geometric factors influencing the diet of vertebrate predators in marine and terrestrial environments. Ecol. Lett. 17, 1553–1559. doi: 10.1111/ele.12375

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohen, J. E. (2008). “Body sizes in food chains of animal predators and parasites,” in Body Size: The Structure and Function of Aquatic Ecosystems, eds A. G. Hildrew, D. G. Raffaelli, and R. Edmonds-Brown (Cambridge: Cambridge University Press, 306–325.

Google Scholar

Cohen, J. E., and Fenchel, T. (1994). Marine and continental food webs: three paradoxes? Proc. R. Soc. B Biol. Sci. 343, 57–69. doi: 10.1098/rstb.1994.0008

CrossRef Full Text | Google Scholar

Cohen, J. E., Pimm, S. L., Yodzis, P., Saldaña, J., and Saldana, J. (1993). Body sizes of animal predators and animal prey in food webs. J. Anim. Ecol. 62, 67–78. doi: 10.2307/5483

CrossRef Full Text | Google Scholar

Dell, A. I., Pawar, S., and Savage, V. M. (2011). Systematic variation in the temperature dependence of physiological and ecological traits. Proc. Natl. Acad. Sci. U.S.A. 108, 10591–10596. doi: 10.1073/pnas.1015178108

PubMed Abstract | CrossRef Full Text | Google Scholar

Dell, A. I., Pawar, S., and Savage, V. M. (2013). The thermal dependence of biological traits. Ecology 94:1205. doi: 10.1890/12-2060.1

CrossRef Full Text | Google Scholar

Dell, A. I., Pawar, S., and Savage, V. M. (2014). Temperature dependence of trophic interactions are driven by asymmetry of species responses and foraging strategy. J. Anim. Ecol. 83, 70–84. doi: 10.1111/1365-2656.12081

PubMed Abstract | CrossRef Full Text | Google Scholar

DeLong, J., and Vasseur, D. (2012). A dynamic explanation of size-density scaling in carnivores. Ecology 93, 470–476. doi: 10.1890/11-1138.1

PubMed Abstract | CrossRef Full Text | Google Scholar

DeLong, J. P., Okie, J. G., Moses, M. E., Sibly, R. M., and Brown, J. H. (2010). Shifts in metabolic scaling, production, and efficiency across major evolutionary transitions of life. Proc. Natl. Acad. Sci. U.S.A. 107, 12941–12945. doi: 10.1073/pnas.1007783107

PubMed Abstract | CrossRef Full Text | Google Scholar

Elton, C. S. (1927). Animal Ecology. New York, NY: Macmillan.

Google Scholar

Emmerson, M. E., Montoya, J. M., and Woodward, G. (2005). “Body size, interaction strength and food web dynamics,” in Dynamic Food Webs: Multispecies Assemblages, Ecosystem Development, and Environmental Change, eds P. C. de Ruiter, V. Wolters, and J. C. Moore (San Diego, CA: Academic Press, 167–178.

Google Scholar

Hairston, N. G. Jr., and Hairston, N. G. Sr. (1993). Cause-effect relationships in energy flow, trophic structure, and interspecific interactions. Am. Nat. 142, 379–411. doi: 10.1086/285546

CrossRef Full Text | Google Scholar

Hechinger, R. F., Lafferty, K. D., Dobson, A. P., Brown, J. H., and Kuris, A. M. (2011). A common scaling rule for abundance, energetics, and production of parasitic and free-living species. Science 333, 445–448. doi: 10.1126/science.1204337

PubMed Abstract | CrossRef Full Text | Google Scholar

Kalinkat, G., Schneider, F. D., Digel, C., Guill, C., Rall, B. C., and Brose, U. (2013). Body masses, functional responses and predator-prey stability. Ecol. Lett. 16, 1126–1134. doi: 10.1111/ele.12147

PubMed Abstract | CrossRef Full Text | Google Scholar

Lang, B., Ehnes, R. B., Brose, U., and Rall, B. C. (2017). Temperature and consumer type dependencies of energy flows in natural communities. Oikos 126, 1717–1725. doi: 10.1111/oik.04419

CrossRef Full Text | Google Scholar

McArdle, B. H., and Lawton, J. H. (1979). Effects of prey-size and predator-instar on the predation of Daphnia by Notonecta. Ecol. Entomol. 4, 267–275. doi: 10.1111/j.1365-2311.1979.tb00584.x

CrossRef Full Text | Google Scholar

McGill, B. J., and Mittelbach, G. G. (2006). An allometric vision and motion model to predict prey encounter rates. Evol. Ecol. Res. 8, 691–701.

Google Scholar

Nagy, K. (1987). Field metabolic rate and food requirement scaling in mammals and birds. Ecol. Monogr. 57, 111–128. doi: 10.2307/1942620

CrossRef Full Text | Google Scholar

Otto, S. B., Rall, B. C., and Brose, U. (2007). Allometric degree distributions facilitate food-web stability. Nature 450, 1226–1229. doi: 10.1038/nature06359

PubMed Abstract | CrossRef Full Text | Google Scholar

Pawar, S. (2009). Community assembly, stability and signatures of dynamical constraints on food web structure. J. Theor. Biol. 259, 601–612. doi: 10.1016/j.jtbi.2009.04.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Pawar, S. (2015). The role of body size variation in community assembly. Adv. Ecol. Res. 52, 201–248. doi: 10.1016/bs.aecr.2015.02.003

CrossRef Full Text | Google Scholar

Pawar, S., Dell, A. I., and Savage, V. M. (2015). “From metabolic constraints on individuals to the dynamics of ecosystems,” in Aquatic Functional Biodiversity, eds A. Belgrano, G. Woodward, and U. Jacob (San Diego, CA: Academic Press), 3–36.

Google Scholar

Pawar, S., Dell, A. I. A., and Savage, V. M. V. (2012). Dimensionality of consumer search space drives trophic interaction strengths. Nature 486, 485–489. doi: 10.1038/nature11131

PubMed Abstract | CrossRef Full Text | Google Scholar

Persson, L., Leonardsson, K., de Roos, A. M., Gyllenberg, M., and Christensen, B. (1998). Ontogenetic scaling of foraging rates and the dynamics of a size-structured consumer-resource model. Theor. Popul. Biol. 54, 270–293. doi: 10.1006/tpbi.1998.1380

PubMed Abstract | CrossRef Full Text | Google Scholar

Peters, R. (1986). The Ecological Implications of Body Size. Cambridge: Cambridge University Press.

Google Scholar

Portalier, S. M. J., Fussmann, G. F., Loreau, M., and Cherif, M. (2019). The mechanics of predator–prey interactions: first principles of physics predict predator–prey size ratios. Funct. Ecol. 33, 323–334. doi: 10.1111/1365-2435.13254

CrossRef Full Text | Google Scholar

Riede, J. O., Brose, U., Ebenman, B., Jacob, U., Thompson, R., Townsend, C. R., et al. (2011). Stepping in Elton's footprints: a general scaling model for body masses and trophic levels across ecosystems. Ecol. Lett. 14, 169–178. doi: 10.1111/j.1461-0248.2010.01568.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Ritchie, M. E. (2009). Scale, Heterogeneity, and The Structure and Diversity of Ecological Communities. Princeton, NJ: Princeton University Press.

Google Scholar

Rizzuto, M., Carbone, C., and Pawar, S. (2018). Foraging constraints reverse the scaling of activity time in carnivores. Nature Ecol. Evol. 2, 247–253. doi: 10.1038/s41559-017-0386-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Savage, V. M., Gilloly, J. F., Brown, J. H., Charnov, E. L., Gillooly, J. F., and West, G. B. (2004). Effects of body size and temperature on population growth. Am. Nat. 163, 429–441. doi: 10.1086/381872

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmidt-Nielsen, K. (1984). Scaling, Why is Animal Size so Important? Cambridge; New York, NY: Cambridge University Press.

Google Scholar

Tang, S., Pawar, S., and Allesina, S. (2014). Correlation between interaction strengths drives stability in large ecological networks. Ecol. Lett. 17, 1094–1100. doi: 10.1111/ele.12312

PubMed Abstract | CrossRef Full Text | Google Scholar

Vucic-Pestic, O., Rall, B. C., Kalinkat, G., and Brose, U. (2010). Allometric functional response model: body masses constrain interaction strengths. J. Anim. Ecol. 79, 249–256. doi: 10.1111/j.1365-2656.2009.01622.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Weitz, J. S., and Levin, S. A. (2006). Size and scaling of predator-prey dynamics. Ecol. Lett. 9, 548–557. doi: 10.1111/j.1461-0248.2006.00900.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, R. J. R., Brose, U., and Martinez, N. D. N. (2007). “Homage to Yodzis and Innes 1992: scaling up feeding-based population dynamics to complex ecological networks,” in From Energetics to Ecosystems: The Dynamics and Structure of Ecological Systems, eds N. Rooney, K. S. McCann, and D. L. G. Noakes (Dordrecht: Springer Netherlands, 37–51.

Google Scholar

Yodzis, P., and Innes, S. (1992). Body size and consumer-resource dynamics. Am. Nat. 139, 1151–1175. doi: 10.1086/285380

CrossRef Full Text | Google Scholar