- 1Yale School of Forestry & Environmental Studies, New Haven, CT, United States
- 2Department of Ecosystem and Conservation Sciences, W.A. Franke College of Forestry & Conservation, University of Montana, Missoula, MT, United States
- 3Environmental Sciences Division and Climate Change Science Institute, Oak Ridge National Laboratory, Oak Ridge, TN, United States
- 4Department of Biology, School of Humanities and Sciences, Stanford University, Stanford, CA, United States
- 5Stockbridge School of Agriculture, University of Massachusetts Amherst, Amherst, MA, United States
- 6Department of Ecology, Evolution and Behavior, University of Minnesota, St. Paul, MN, United States
Soil organic matter (SOM) is central to soil carbon (C) storage and terrestrial nutrient cycling. New data have upended the traditional model of stabilization, which held that stable SOM was mostly made of undecomposed plant molecules. We now know that microbial by-products and dead cells comprise unexpectedly large amounts of stable SOM because they can become attached to mineral surfaces or physically protected within soil aggregates. SOM models have been built to incorporate the microbial to mineral stabilization of organic matter, but now face a new challenge of accurately capturing microbial productivity and metabolism. Explicitly representing stoichiometry, the relative nutrient requirements for growth and maintenance of organisms, could provide a way forward. Stoichiometry limits SOM formation and turnover in nature, but important nutrients like nitrogen (N), phosphorus (P), and sulfur (S) are often missing from the new generation of SOM models. In this synthesis, we seek to facilitate the addition of these nutrients to SOM models by (1) reviewing the stoichiometric bias—the tendency to favor one element over another—of four key processes in the new framework of SOM cycling and (2) applying this knowledge to build a stoichiometrically explicit budget of C, N, P, and S flow through the major SOM pools. By quantifying the role of stoichiometry in SOM cycling, we discover that constraining the C:N:P:S ratio of microorganisms and SOM to specific values reduces uncertainty in C and nutrient flow as effectively as using microbial C use efficiency (CUE) parameters. We find that the value of additional constraints on stoichiometry vs. CUE varies across ecosystems, depending on how precise the available data are for that ecosystem and which biogeochemical pathways are present. Moreover, because CUE summarizes many different processes, stoichiometric measurements of key soil pools are likely to be more robust when extrapolated from soil incubations to plot or biome scale estimates. Our results suggest that measuring SOM stoichiometry should be a priority for future empirical work and that the inclusion of new nutrients in SOM models may be an effective way to improve precision.
Introduction
Why does some soil organic matter (SOM) persist for hundreds of years while other SOM turns over quickly, rapidly losing its carbon (C), and nutrients? Throughout the twentieth century, most scientists believed that stable SOM was composed primarily of plant compounds that persisted in soil because their complex chemical structures resisted microbial degradation (Brady and Weil, 2007). Now, new evidence indicates that more than 50% of stable SOM may instead be made of chemically simple compounds incorporated into microbial residue and dead microbial cells (i.e., necromass; Simpson et al., 2007; Ludwig et al., 2015). Microbial residues and necromass can become attached to mineral surfaces or trapped within soil aggregates, rendering them inaccessible to decomposition (Prescott, 2010; Bradford et al., 2013; Cotrufo et al., 2013; Kallenbach et al., 2015; Lehmann and Kleber, 2015; Jilling et al., 2018). These new findings represent a major shift in our understanding of SOM formation, and have spurred the development of a new generation of SOM models. These models outperform those without microbial and mineral pathways (Wieder et al., 2013; Robertson et al., 2019).
However, to represent the influence of microbial productivity and mineral sorption accurately, models need to include not only a new set of pathways, but also the factors that control those pathways. One of the most important determinants of microbial productivity is the degree to which the relative elemental composition, or stoichiometry, of microbial biomass matches the substrate on which it grows (Sterner and Elser, 2002; Schimel and Weintraub, 2003; Cleveland and Liptzin, 2007; Buchkowski et al., 2015). A closer match enables greater thermodynamic efficiency and reduces the potential for nutrient limitation (Sterner and Elser, 2002; Schimel and Weintraub, 2003). The stoichiometries of plant inputs, SOM, and microbial biomass are known to affect C and nutrient flows in soil (Griffiths et al., 2012; Tipping et al., 2016) but remain absent from many SOM models (Allison et al., 2010; Wieder et al., 2014).
SOM models developed in the past decade often contain no more than two elements (Moorhead et al., 2012; Abramoff et al., 2017; Sulman et al., 2019) because analytical tractability decreases sharply with the inclusion of each additional elemental cycle. Instead, new models designed to assess the microbial components of SOM often rely on substrate use efficiency parameters, which succinctly represent the proportion of nutrient uptake that can be converted into organism biomass (Allison et al., 2010; Manzoni et al., 2012). In fact, substrate use efficiency is a summary of a number of factors such as resource chemical quality, stoichiometry, and climatic conditions. Modeling work has repeatedly demonstrated that adding the underlying mechanisms behind substrate use efficiency can improve our predictions about SOM cycling (Schimel and Weintraub, 2003; Wieder et al., 2013; Abramoff et al., 2017; Sulman et al., 2019).
To facilitate the development of stoichiometrically comprehensive SOM models capable of better prediction and accuracy, we (1) qualitatively review any changes in stoichiometry that occur during the flow of organic matter into soil, and (2) use this information to build a stoichiometrically explicit SOM budget, which we refer to as the Linear SOM Description (LSD). The LSD is a static representation of the SOM cycle, including microbial and mineral pathways as well as flows of C, nitrogen (N), phosphorus (P), and sulfur (S). Rather than assessing changes in flow rates over time, as in dynamic SOM models like CENTURY (Parton et al., 1987), LSD allows us to calculate the possible range of possible flow rates in the system (van Oevelen et al., 2010). Just as a set of pool measurements can be used to build a whole-ecosystem C and nutrient budget, LSD shows us how data on substrate use efficiency and the stoichiometry of different pools changes the range of flows that mass balance can allow. Using this approach, we can quantify how effectively new information reduces uncertainty (i.e., the range between minimum and maximum possible flows) in the system.
The LSD can be used to efficiently analyze many model structures and parameter sets. When selecting model structures, we considered recent conceptual advances about SOM in the context of stoichiometry, so we could determine when stoichiometry can be an effective tool for incorporating field data into numerical models (sensu Blankinship et al., 2018). We hypothesized that the specific stoichiometric constraints on microbes and mineral-associated organic matter (MAOM) would reduce model uncertainty as effectively as carbon use efficiency (CUE), especially when we included the stoichiometry of many elements (i.e., C, N, P, and S).
We also parameterized versions of the LSD for 27 terrestrial ecosystem × biome combinations with open-source data (Bond-Lamberty and Thomson, 2014; Iversen et al., 2017; Qiao et al., 2019). Our goal was to ground the analysis of model structures and parameters by using case studies from real ecosystems. We hypothesized that the difference in the information available for these systems combined with the difference in structure across them would reverse whether stoichiometric or substrate use efficiency measurements were better at constraining flows. By addressing these hypotheses, we (1) demonstrate the value of stoichiometric data for improving our understanding of SOM cycling, (2) provide upper and lower bounds for feasible element flows across different ecosystem types, which can be used to evaluate the performance of predictive SOM models, and (3) identify high-value targets for future theoretical and empirical research efforts.
Stoichiometry and SOM Formation
The structure of the LSD reflects our current understanding of SOM cycling. Following the new generation of SOM models, we focused on microbial productivity and mineral sorption as primary pathways of SOM stabilization. We also included other processes, like physical protection, that are important contributors to SOM formation, transformation, and turnover (Six et al., 2002).
In this section, we provide a qualitative overview of stoichiometry in four important SOM pathways represented in the LSD: litter losses through abiotic processes and soil animals, belowground inputs of organic matter, microbial productivity and CUE, and the stabilization of MAOM. Other processes important for SOM formation, transformation, and loss have been reviewed elsewhere (e.g., stoichiometry and leaf litter decomposition by soil microorganisms; Manzoni et al., 2010). Figure 1 provides a simplified visualization of the pools and flows reviewed here (see Figure S1 for a diagram of the entire system in the LSD). In each subsection, we identify both how a particular process is dependent on stoichiometry and how that process itself can alter stoichiometry.
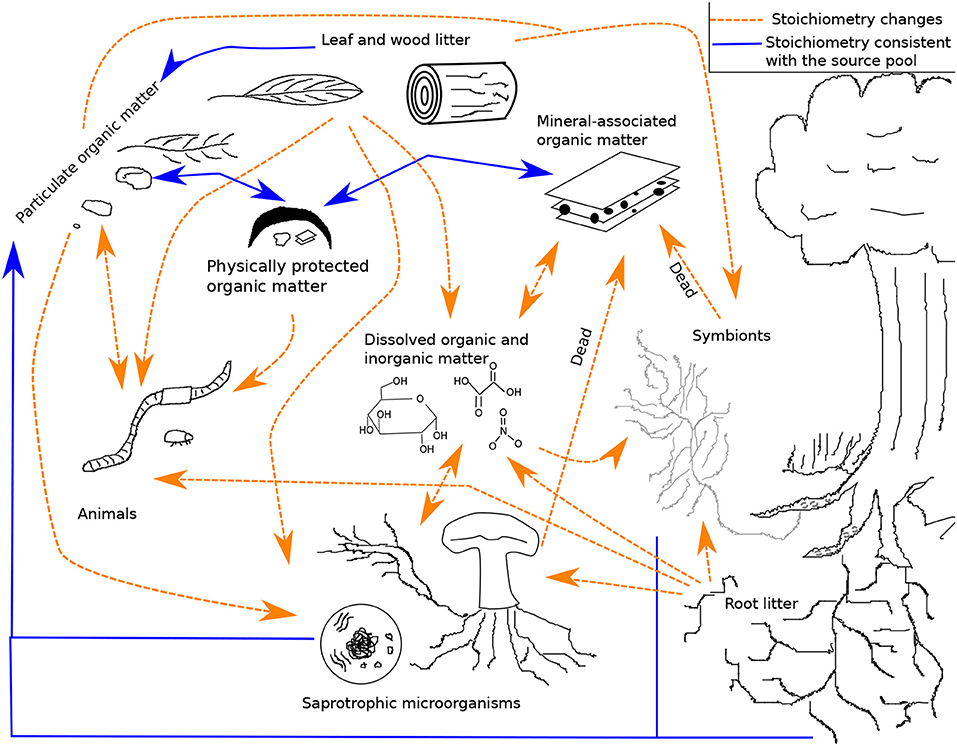
Figure 1. A framework for the formation and loss of soil organic matter. Dashed orange arrows represent pathways with a stoichiometric bias, while solid blue arrows represent pathways with stoichiometry matching the source pools. This is not a model diagram and for readability does not show that most pools have variable chemical quality, multiple species, and multiple elements. The diagram also does not show inputs (root exudates, carbon to symbionts, nitrogen fixation, leaf, wood, and root litter) or outputs (leaching and respiration). See the model diagram in the supplemental (Figure S1; Table S1).
Aboveground Litter Fragmentation and Decomposition
Plants contribute large pulses of C, N, P, and S into soil ecosystems through litterfall (Schlesinger and Bernhardt, 2013). Leaf litter can be incorporated into the soil through abiotic and biotic pathways, each of which has the potential to alter the stoichiometry of SOM inputs (Figure 1). Here, we focus on abiotic pathways of litter losses and processing of litter by soil animals.
Abiotic Litter Loss
Litter losses through abiotic processes can change stoichiometry or be stoichiometrically neutral. For example, physical fragmentation caused by freeze-thaw or animal movement isn't associated with stoichiometric changes (Fahey et al., 2013). Because fragmented litter is more easily incorporated into the particulate organic matter (POM) pool, this process helps to transfer higher C:N:P:S compounds from litter into SOM. In contrast, photodegradation preferentially degrades lignin (Austin and Ballare, 2010; Brandt et al., 2010; Austin et al., 2016). Limited data suggest that changes in litter stoichiometry across the first year of decomposition are similar between photodegradation and degradation by microbial exoenzymes (Frouz et al., 2011; Wang et al., 2015). Photodegradation is not, however, independent of microbial decomposition; photodegraded litter is more accessible to microbial decomposers, which facilitates subsequent transformation and incorporation into microbial biomass or leaching into dissolved organic matter once it is broken into small enough molecules (DOM; Kaiser and Kalbitz, 2012; Cotrufo et al., 2015; Austin et al., 2016).
DOM lost from leaf litter can be incorporated into the MAOM pool as it moves into the soil profile. Once adsorbed, DOM can desorb, partially as a function of redox-sensitive elements, and undergo processing by microbes (Fahey et al., 2011; Kaiser and Kalbitz, 2012). As a result, DOM stoichiometry in upper soil profiles more closely matches the original litter, while DOM in lower soil profiles has a lower C:N because of microbial processing (Cotrufo et al., 2015). In some ecosystems, the DOM pathway can account for losses of up to a third of litter C (Cotrufo et al., 2015). Carbon and nutrients in litter that are not photodegraded or leached out are instead decomposed by soil animals and microorganisms.
Litter Consumption by Soil Animals
Through consumption and digestion, soil animals alter the stoichiometry of leaf litter entering the soil (Kautz et al., 2002; David, 2014; Frouz et al., 2015). However, their effects are extremely variable because soil animals have a wide range of stoichiometric requirements (Teuben and Verhoef, 1992; Martinson et al., 2008). For example, soil macrofauna, like isopods and millipedes, usually lower the C:N ratios of their food when converting them to feces (Kautz et al., 2002; Bastow, 2011; Frouz et al., 2015). However, soil mesofauna, like collembola, can raise the C:N ratio of leaf litter passing through their guts (Teuben and Verhoef, 1992). Data on the assimilation of P and S by soil animals are sparse, but studies on isopods and collembola indicate that gut passage tends to increase bulk C:P and C:S ratios, as well as the amount of P and S in dissolved forms (Morgan and Mitchell, 1987; Teuben and Verhoef, 1992). Some animals may reduce C: nutrient ratios because easily degradable C-rich compounds in the leaf litter are decomposed and assimilated in their guts (David, 2014). If this is true, understanding the impact of soil animals on SOM stoichiometry will require data on chemical quality as well as stoichiometry (David, 2014). These generalizations are based on limited data sets because the nutrient ratios of soil faunal feces, especially those of smaller-bodied organisms, are rarely measured (Osler and Sommerkorn, 2007). While the role of soil animal gut processing is partially dependent on the animal's nutrient requirements, it is also driven by the activity of litter-degrading microorganisms.
Belowground Inputs of Organic Matter
Our understanding of SOM inputs that originate belowground is poorly constrained compared to that of aboveground litter transformations (Sokol et al., 2019). Since a sizable portion of terrestrial ecosystem productivity is allocated belowground (Gill and Finzi, 2016), this represents a major knowledge gap hindering our ability to model SOM formation. Here, we discuss two major pathways by which belowground organic matter inputs can be incorporated into SOM: roots and mycorrhizal fungi.
Roots
A majority of the decomposition literature is devoted to leaf litter (Sokol and Bradford, 2019), despite the disproportionate importance of fine root turnover and the marked difference between foliar and root chemistry. Indeed, root-derived C may be more important to SOM formation than aboveground C inputs by a factor of 2.4–2.7 (Crow et al., 2009; Kong and Six, 2010; Clemmensen et al., 2013; Sokol et al., 2019). Roots also have a longer mean residence time (Rasse et al., 2005) and are more likely to be incorporated into stable SOM. Like annual inputs of leaf litter, fine root litter chemical quality strongly influences initial (<1 year) litter decomposition dynamics (Adair et al., 2008; Cotrufo et al., 2013; See et al., 2019).
In the first stage of decomposition, fine roots decompose slowly (See et al., 2019). This is a function of chemical recalcitrance, which summarizes not only stoichiometry but also the composition of chemical constituents in organic matter. Therefore, the impact of chemical quality and stoichiometry in roots matches trends for leaf litter (Aerts, 1997; Hobbie, 2005; Adair et al., 2008; Harmon et al., 2009; Keiser and Bradford, 2017). However, while foliar litter inputs tend to be nutrient poor, with a global average C:N:P of 3007:45:1 (McGroddy et al., 2004), fine roots (<2 mm) are relatively nutrient rich, with a global average C:N:P of 522:12:1 (Gordon and Jackson, 2000). Fine root litter maintains the C:N of fine roots, but has higher C:P because, unlike leaf litter, only modest P resorption has been identified in fine roots (Gordon and Jackson, 2000; Yuan et al., 2011).
The finest roots have extremely slow decomposition rates despite their low C:N ratios (~21) and high turnover rates (Sun et al., 2018). The chemical structure of roots is important for determining decomposition rates, because microbes need to depolymerize these compounds to metabolize them. Organic matter with less favorable stoichiometry (e.g., high C:N ratio) and high glucose content, for example, is more easily degraded than organic matter with favorable stoichiometry (e.g., lower C:N ratio) and a high portion of lignin and suberin. Therefore, stoichiometry is one indicator of the chemical quality and decomposition of fine roots, but cannot be totally separated from differences in other dimensions of chemical quality (Sugai and Schimel, 1993). As in leaf litter, where higher proportions of structural (i.e., lignin) and inhibitory compounds decrease microbial decomposition and the assimilation of C and nutrients (Manzoni et al., 2010; Sinsabaugh et al., 2013), many first order roots contain low energy C compounds that limit their decomposition rates, and may contribute to C limitation in soil microbes (Mooshammer et al., 2014; Sun et al., 2018).
Root litter is an important belowground input, but several other classes of root-derived C also make large contributions to SOM (Crow et al., 2009; Kong and Six, 2010; Clemmensen et al., 2013; Sokol et al., 2019). These inputs include several classes of root exudates, including those that contribute to priming (Kuzyakov et al., 2000; Kuzyakov, 2010; Di Lonardo et al., 2017), desorption (Keiluweit et al., 2015), defense (Jung et al., 2012), and symbiont signaling/support (Badri and Vivanco, 2009; Jung et al., 2012).
Root exudation is an important component of belowground C inputs because it can promote the decomposition of SOM compounds that require more energy to degrade or don't have a stoichiometric ratio that matches microbial demand (Brzostek et al., 2013; Drake et al., 2013; Di Lonardo et al., 2017). Such root exudates may promote microbial N mining in some circumstances by providing the energy required to decompose N rich SOM (Dijkstra et al., 2013). By providing lower C:N inputs to mine SOM, root exudates are an indirect pathway that allows soil microorganisms to overcome C limitation (Drake et al., 2013). Exudation into rhizosphere soils occurs alongside another, more direct plant-to-microbe C exchange involving symbiotic microorganisms that support plant nutrient acquisition.
Symbionts
Mycorrhizal fungi and symbiotic N-fixing bacteria are soil microorganisms that provide nutrients to plants in exchange for photosynthetic C (Smith and Read, 2008; Menge et al., 2017). The activities of these specialized symbioses can alter soil stoichiometry. For example, by facilitating plant nutrient uptake from soil, mycorrhizal fungi could increase SOM C:nutrient ratios (Smith and Read, 2008). In contrast, by incorporating new N into the plant-soil system, N-fixers could decrease SOM C:N ratios.
Almost all plants rely on root-associated mycorrhizal fungi to obtain the soil nutrients needed for growth (Smith and Read, 2008). Most of these plants associate with one, or sometimes both, of the two most common types of mycorrhizal fungi: ectomycorrhizal and arbuscular mycorrhizal. Due to their geographic ubiquity and importance to plant nutrition, mycorrhizal fungi constitute a major pathway by which plant C enters the soil (Leake et al., 2004) and by which soil N, P, and S exit the soil, mediating changes in SOM stoichiometry (Allen and Shachar-Hill, 2009; Orwin et al., 2011; Rosling et al., 2016). Crucially, these two mycorrhizal types are functionally different, resulting in systematic variation in nutrient cycling between ecosystems where most plants associate with one or the other (Phillips et al., 2013).
In general, ectomycorrhizal fungi promote plant uptake of organic nutrients from soil more than arbuscular mycorrhizal fungi (Smith and Smith, 2011; Phillips et al., 2013; Hodge and Storer, 2014; Shah et al., 2016), which can allow ectomycorrhizal plants to increase SOM C:nutrient ratios (Orwin et al., 2011). Leaf litter from ectomycorrhizal plants also decomposes more slowly than leaf litter from arbuscular mycorrhizal plants (Cornelissen et al., 2001), reducing litter nutrient accessibility. These above- and belowground traits interact, enabling ectomycorrhizal plants to thrive in environments where slow mineralization limits nutrient availability (Steidinger et al., 2019), and, potentially, to also reinforce these conditions (Lin et al., 2017; Fernandez et al., 2019; Smith and Wan, 2019). Together, these dynamics contribute to correlations between global ectomycorrhizal plant abundance and higher SOM C:N ratios (Averill et al., 2014).
Mycorrhizal fungi also form extensive hyphal networks in soil that can directly contribute to SOM (Leake et al., 2004). In a Mediterranean poplar plantation, C derived from the turnover of mycorrhizal hyphae exceeded that of fine roots and leaf litter, forming the majority of total SOM inputs (Godbold et al., 2006). In boreal forests, a large proportion of primary productivity is allocated belowground (Gill and Finzi, 2016), and much of the SOM in these environments is derived from roots and mycorrhizal fungal biomass (Clemmensen et al., 2013). Fungal biomass has a higher nutrient content than plant roots, so inputs from mycorrhizal mycelia are likely to lower SOM C:nutrient ratios (Zhang and Elser, 2017).
In contrast to mycorrhizal fungi, which help plants acquire nutrients already present in soil, symbiotic N fixers introduce new N into the system (Menge et al., 2017). The majority of N fixation is performed by plant-associated symbionts, so these symbionts likely have the largest impact on SOM stoichiometry (Cleveland et al., 1999). Most N fixed by plant symbionts enters SOM after first traveling through the host plant; returning to the soil as root exudates and litter deposited above- or belowground (Sulman et al., 2019). Some of the fixed N, however, can enter the soil system directly through death of the symbionts themselves. This flow of nutrients may impact the stoichiometry of inputs into SOM (Brophy and Heichel, 1989).
Microbial Productivity and Carbon Use Efficiency
Microbial metabolism controls the speed at which organic matter is decomposed. Microbial CUE measures the fate of metabolites as the proportion of total C uptake that is allocated to biomass (Manzoni et al., 2012). Microbial CUE is also highly variable (Qiao et al., 2019), affected by the chemical composition of substrate (Sugai and Schimel, 1993; Frey et al., 2013), as well as by the match between resource stoichiometry and microbial stoichiometry (Sinsabaugh et al., 2013, 2016). Carbon use efficiency determines how efficiently substrate inputs are transformed into stable, microbially-derived SOM. As such, even small changes in CUE can have important downstream impacts on SOM formation (Six et al., 2006). Because CUE succinctly captures the relationship between organic matter inputs and the SOM precursors produced by microorganisms, it appears as an important parameter in the new generation of microbe-focused SOM models (Allison et al., 2010; Wieder et al., 2014; Sihi et al., 2016).
Stabilization of Mineral-Associated Organic Matter
Soil organic matter can be stabilized by association with mineral surfaces. The strength and nature of organo-mineral interactions varies with edaphic conditions like soil mineralogy and texture (Dungait et al., 2012; Lehmann and Kleber, 2015; Kallenbach et al., 2016; Jilling et al., 2018). Soil pH also plays an important role in SOM stabilization. Organo-metal complexes are associated with aluminum- and iron-dominated clay minerals in acidic systems and with calcium in alkaline systems (Rasmussen et al., 2018). The MAOM pool can persist over long time scales when physically protected within soil aggregates (Tipping et al., 2016), even if the organic compounds that are attached to mineral surfaces would otherwise be prone to microbial degradation. Predicting the stoichiometry of MAOM thus requires an understanding of which compounds are adsorbed onto mineral surfaces under what conditions.
The quantity, stability, chemistry, and distribution of MAOM in an ecosystem is determined by the relative dominance of biotic vs. abiotic pathways to sorption, whether DOM is adsorbed directly to mineral surfaces or after it is processed by soil microbes (Mikutta et al., 2019; Sokol et al., 2019). Because microbes tend to outcompete minerals for organic matter (Fischer et al., 2010), the biotic pathway increases in prevalence with microbial biomass such that sorption of microbially-processed compounds dominates in surface soil horizons and rhizosphere soils (Sokol et al., 2019). In the rhizosphere, sugars and amino acids exuded by roots can release SOM from mineral associations, allowing for microbial processing and turnover of previously adsorbed compounds (Keiluweit et al., 2015). However, the high-quality substrates exuded into the rhizosphere also promote the production of large quantities of microbial necromass, which can be readily converted into stable MAOM and aggregates (Knicker, 2011; Cotrufo et al., 2013; Schrumpf et al., 2013; Craig et al., 2018). The balance of decomposition and formation of MAOM in the rhizosphere appears to produce a net increase in stable MAOM, likely because root exudates provide plenty of C and nutrients for sorption (Sokol et al., 2019).
The two classes of biomolecules most susceptible to sorption on mineral surfaces are proteins (peptide compounds) and inositol phosphates (Sollins et al., 2006; Celi and Barberis, 2007; Kleber et al., 2007; Tipping et al., 2016; Newcomb et al., 2017), both of which can introduce strong stoichiometric biases. The accumulation of N-rich proteins lowers MAOM C:N while the accumulation of inositol phosphates strongly (and variably) lowers MAOM C:P (Celi and Barberis, 2007; Tipping et al., 2016; Jilling et al., 2018). Inositol phosphates are the most common phosphate monoesters, making them the most abundant, highest-affinity organic P compounds in soils (Turner et al., 2002). Though they interact with exchange sites via their phosphate groups much like inorganic phosphates (Goldberg and Sposito, 1985), each inositol phosphate can have one to six phosphate groups. Many minerals, especially iron oxides, have a much higher affinity for these organic P compounds than their inorganic counterparts (Celi et al., 1999; Celi and Barberis, 2007). However, the extent of MAOM P enrichment resulting from the sorption of inositol phosphates (Adams et al., 2018) depends on the minerals in a given soil (Celi and Barberis, 2007). The flow of organic matter into the MAOM pool is thus subject to a variable stoichiometric filter, which generally concentrates nutrients relative to C and specifically concentrates N and/or P according to soil mineralogy.
The Linear SOM Description
The LSD is a static description of the soil system (van Oevelen et al., 2010; Liang et al., 2011) with pools and processes included in recent dynamic SOM models as well as several new additions identified in our review (Wieder et al., 2014; Robertson et al., 2019; Sulman et al., 2019). It contains leaf/wood litter, root litter, soil animals, POM, DOM, saprotrophic microorganisms, symbiotic microorganisms, MAOM, and inorganic nutrients, as well as pools of POM and MAOM that are physically protected (Figure 1; Figure S1). We track the possible flows of four elements (C, N, P, and S) through these pools. We chose to include N, P, and S in addition to C because they are often in high demand relative to their supply in soil (Sterner and Elser, 2002; Brady and Weil, 2007). However, rather than tracking the mass of C, N, P, and S in these pools, we instead use pool stoichiometry to constrain the ranges of possible C and nutrient flows between them.
Most SOM models use a dynamic approach (e.g., Jenkinson et al., 1987; Parton et al., 1987; Wang et al., 2013; Sulman et al., 2014; Wieder et al., 2014; Abramoff et al., 2018), where pool sizes are explicitly modeled so that flows or fluxes between them can be quantified (Equation 1). We will use the term flow to describe the rate of carbon and nutrient movement between pools (van Oevelen et al., 2010), but note that the term flux is used interchangeably in the ecosystem literature (Chapin et al., 2011). In a linear dynamic model, flows (y; mass • time−1) are calculated by multiplying a rate constant (k; time−1) by the pool size (X; mass):
In contrast to dynamic linear models like CENTURY (Parton et al., 1987) or Roth-C (Jenkinson et al., 1987), the LSD is always at equilibrium, so neither rate constants (k) nor pool sizes (X) are explicitly modeled over time. The LSD does not include equations like Equation 1. Instead, equations setting mass balance, stoichiometry, and substrate use efficiency relationships are used to constrain flows (see Model Example; Equation 2). By constraining possible flows, the LSD indirectly determines the reasonable combinations of rate constants and equilibrium pool sizes (Equation 1). The flows in the LSD are comparable to those that would be reached at equilibrium in a linear model such as CENTURY (Parton et al., 1987) or a non-linear SOM model such as MIMICS or the Millennial model (Wieder et al., 2014; Abramoff et al., 2018).
Our approach has three major benefits. First, a linear system can effectively account for the interaction between flows that have stoichiometric constraints placed upon them (van Oevelen et al., 2010; Yang et al., 2017). Second, linear systems at equilibrium can be solved in high dimensions, allowing us to evaluate many structural and parameter changes (van Oevelen et al., 2010). Third, a linear system built with minimal assumptions yields the set of equilibria obtainable from structurally analogous non-linear models (Stevens, 2009). An equilibrium approach does not simulate or predict how systems evolve over time, which means that the LSD does not replicate the efforts of new non-linear models that include many of the same processes (Wieder et al., 2014; Abramoff et al., 2018; Sulman et al., 2019). Instead, it is useful for comparing equilibrium scenarios and evaluating what new data would provide the most effective constraints on equilibrium soil C and nutrient cycling.
Model Constraints
We imposed a few initial constraints to capture the biologically feasible range of state space in the absence of stoichiometric information. The baseline model conditions were:
1. System inputs, defined as leaf/wood litter, root litter, plant root exudates to DOM, and plant C to microbial symbionts, are constrained between 180 and 2,500 g C m−2 year−1 (Chapin et al., 2011).
2. There are two pools each of leaf/wood litter, root litter, DOM, POM, and MAOM that arbitrarily divide the multivariate differences in chemical quality into categories with different stoichiometry and CUE (see below; Cotrufo et al., 2013).
3. There are bacterial, saprotrophic fungal, ectomycorrhizal fungal, arbuscular mycorrhizal fungal, and nitrogen fixer microbial pools (Smith and Read, 2008; Waring et al., 2013; Wieder et al., 2014), as well as primary and secondary detritivores (Scheu, 2002).
4. Unless otherwise stated, substrate use efficiencies are between 5 and 95%, and CUE values are lower for the pools with higher chemical recalcitrance (Qiao et al., 2019).
5. The rate of physical protection of POM and MAOM pools cannot exceed their fresh input rates.
6. The rate of DOM sorption onto MAOM cannot exceed the rate of depolymerization.
7. Microorganisms cannot immobilize inorganic nutrients faster than they enter the system.
Constraint 1 places the model output within a realistic range of elemental flows for ecosystems. Constraints 2 and 3 establish a reasonable model structure for soil elemental cycling including the important components discussed in our review. Finally, constraints 4–7 prevent infinite cycling between pools that exchange nutrients (e.g., microorganisms and inorganic N). These constraints are not necessary in models like CENTURY that mass balance pools, but are necessary in systems like the LSD, which mass balances flows (van Oevelen et al., 2010).
The pools with different chemical qualities defined in constraint 2 capture important mechanisms linking organisms to soil elemental cycling. They also help confirm that the importance of stoichiometry is not nullified by adding a categorical difference in chemical quality to our accounting. Many SOM models include some measure of quality, but two general strategies predominate: ontogeny models track the quality change of each unit of organic matter as it is processed, effectively treating quality as a continuous variable (Bosatta and Agren, 1991; Moore et al., 2004). Other models divide organic matter into discrete quality pools (Parton et al., 1998; Adair et al., 2008; Wieder et al., 2014). Because tractability is one of our primary goals, we chose to follow the latter approach. We include two pools with different levels of chemical recalcitrance, which are distinguished by their stoichiometry and the CUE with which they can be used (Moore et al., 2004; David, 2014). We recognize there are limitations in defining chemical recalcitrance purely on stoichiometry and differences in CUE, as opposed to a metric which also includes constituent compounds like lignin:N. Future expansions of the LSD could include many more biochemical categories, allowing it to track molecular differences in CUE that extend beyond stoichiometry (Yang et al., 2017).
Analytical models of SOM decomposition use different strategies to constrain the cycling of nutrients through microbial biomass. Many models combine the stoichiometric imbalance between organic matter, microorganisms, and their exoenzymes with flexible microbial CUE (Manzoni and Porporato, 2009; Moorhead et al., 2012, 2013; Manzoni, 2017) and overflow respiration (Schimel and Weintraub, 2003). Others represent stoichiometric biases in SOM decomposition by shifting microbial community composition or microbial community homeostasis (Sinsabaugh and Shah, 2012; Sinsabaugh et al., 2013, 2015; Waring et al., 2013; Warton et al., 2015; Hartman et al., 2017). Both of these modeling approaches demonstrate that stoichiometric constraints, soil community composition, and substrate use efficiencies are intertwined. In the LSD, we impose stoichiometry and substrate use efficiency as constraints that set a range of possible values (e.g., minimum to maximum of CUE or C:N ratio for bacteria). Since these constraints act in similar ways, we can identify the relative ability of either stoichiometry or substrate use efficiency to constrain the range of possible flows.
Model Example
In Figure 2, we illustrate how the LSD works by following C and N partitioning through ectomycorrhizal fungi. This example demonstrates how the flow changes as new constraints (i.e., substrate use efficiency or stoichiometric data) are added. It also highlights that the LSD does not currently incorporate empirical data on the flows between specific SOM pools or track the dynamics of SOM pool sizes, but instead uses C and nutrient input rates plus stoichiometry and substrate use efficiency to derive the range of possible flows.
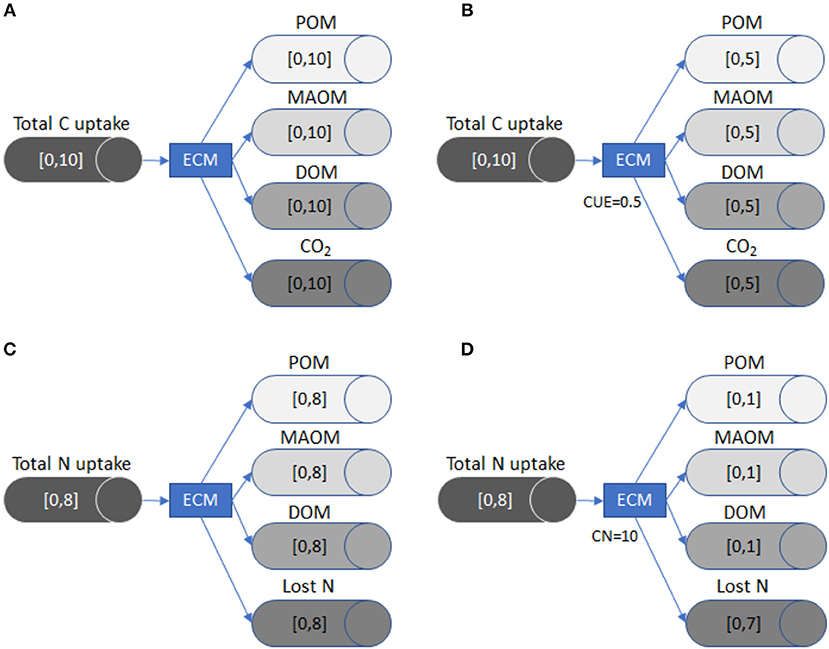
Figure 2. A visual representation of how LSD works using ectomycorrhizal fungi (ECM) as an example. Each tube and arrow represent the C or nutrient transfer to a specific pool (i.e., POM), while the brackets inside each tube define the minimum and maximum flow. The general model (A) shows the possible range of C flows in the absence of stoichiometric or substrate use efficiency constraints. Once the CUE of the fungi is defined in (B), the maximum flow for CO2 (respiration) is constrained, which also reduces the potential maximum flow of C for the three remaining pools because the system is at equilibrium and mass balanced. The general model (C) shows the possible range of N flow in the absence of stoichiometric or substrate use efficiency constraints. In (D), we define the C:N of ECM as 10:1. Because the maximum total C uptake is 10 (A/B), the maximum size of the N flows to POM, MAOM, DOM N pools is reduced to 1. The N flow is constrained due to stoichiometric limitations, since the ECM pool must have ten units of C for every unit of N. The Lost N flow (i.e., transfer to plants) now has a maximum flow size of 7, because the system must remain mass balanced.
Total C taken up by the ectomycorrhizal fungi (EYc) is equal to losses, since the model is mass balanced and static. Carbon lost from ectomycorrhizal fungi can exit the system through respiration (YEc), or can be partitioned into the MAOM pool (YMc + YJc), the POM pool (YPc + YQc), or the DOM pool (YDc + YUc), each with two levels of chemical quality:
When applicable, CUE constrains the proportion of C uptake (EYc) that ectomycorrhizal fungi respire (YEc). Respiration is equal to 1-CUE multiplied by the total quantity of C taken up (EYc):
In the example given by Figure 2A, the quantity of C taken up by ectomycorrhizal fungi (EYc) is between 0 and 10 g C m−2 y−1. If neither CUE nor stoichiometric constraints are imposed, the C partitioned to respiration (YEc), DOM (YDc+YUc), MAOM (YMc +YJc), or POM (YPc + YQc) all have the same potential size range, which is also 0–10 g C m−2 y−1. However, all pathways must sum to inputs (Equation 2), which means that as one flow grows, all others must shrink.
If we define CUE as 0.5 (Figure 2B), the size of the respiration flow, YEc, becomes 0.5 * EYc, which constrains it between 0 and 5 g C m−2 y−1. Because the flows are mass balanced (Equation 3), the other three flows must now be between 0 and 5 g C m−2 y−1. In this way, including CUE reduces the uncertainty, i.e., the range between minimum and maximum flows, in the system.
The LSD can also be constrained by imposing stoichiometric ratios, such as a fixed C:N ratio, as follows (van Oevelen et al., 2010):
Here, net C gain by the ectomycorrhizal fungi (EYc–YEc) is equal to the C:N ratio of the ectomycorrhizal pool (YCN) multiplied by its net N gain. Net N gain is calculated by adding up N acquired from leaf/wood litter (LYN + RYN), root litter (VYN + WYN), DOM (DYN + UYN), POM (PYN + QYN), and inorganic N (IYN), and subtracting inorganic N losses through mineralization (YIN), and N provided to plants (YEN; Equation 4). In the example given in Figure 2C, no substrate use efficiency or stoichiometric constraints are imposed and the net N gain is constrained between 0 and 8 g N m−2 y−1. This means that without a fixed C:N ratio, the range of flows to POM, MAOM, and DOM as well as the quantity of N lost can be between 0 and 8 g N m−2 y−1. In contrast, if we define the C:N ratio of ectomycorrhizal fungi as 10 (Figure 2D), the potential flows for N lost to POM, MAOM, and DOM have a maximum of only 1 g N m−2 y−1. This change occurs because ectomycorrhizal fungi mineralize or send to plants up to 7 g N m−2 y−1 to maintain their C:N ratio.
With each additional stoichiometric relationship defined in the model (i.e., going from C:N to C:N:P), a further equation of the same form as Equations 3 or 4 is added to represent the partitioning of each element. Each additional equation is likely to shrink the difference between the minimum and maximum flows, thus reducing uncertainty. However, the impact of each constraint on the entire LSD network is not obvious a priori because not all constraints will be binding. For example, the C:N constraint we described does not reduce uncertainty in C flow, because there is enough N to span the entire range of available C (i.e., N is limiting; Figure 2). Consequently, we can use the LSD as a tool to determine if and when stoichiometry and substrate use efficiency matter in the network of ~400 flows that we consider (Figure S1).
Application of the LSD
We used the LSD to consider three fundamental stoichiometric biases: soil organism homeostasis (stoichiometric demands), mineral sorption biases, and abiotic litter loss biases (i.e., leaching through DOM). We then evaluated how three classes of empirical information constrained the state-space in which our linear system could exist. First, we considered the effects of broad stoichiometric ranges (e.g., animal C:N ratio is between 4 and 25; Sterner and Elser, 2002). Second, we considered specific stoichiometric constraints, where the exact C:N:P:S ratios of each process are known (e.g., animal C:N ratio is 6; Equation 4). Finally, we considered the case where substrate use efficiency is a set as at exact value (Equation 3). For each, we assessed the effect of these data on model uncertainty, defined as the range between the minimum and maximum flows possible under the prescribed constraints.
We also quantified the value of stoichiometry and substrate use efficiency information across 27 different biome × ecosystem type combinations. These systems have different animal and microbial communities, as well as different mineral properties, albeit with varying levels of data to constrain them (Chapin et al., 2011; Bond-Lamberty and Thomson, 2014; Adams et al., 2018; Steidinger et al., 2019). We first confirmed that the LSD was producing reasonable flows by comparing its litter inputs and heterotrophic respiration estimates to values from the SRDB (version 3.0) dataset (Bond-Lamberty and Thomson, 2014; Figure S6). Then, we used the LSD to examine how stoichiometric vs. substrate use efficiency information constrained the range of possible C and nutrient flows into stabilized pools across ecosystem types.
Solving the LSD and Quantifying Uncertainty
We solved the LSD using inverse linear programming in R (van Oevelen et al., 2010; R Core Team, 2014; see section Model Example for a case study on one pool). We explored the importance of stoichiometry and substrate use efficiency in the LSD across differences in structure, parameterization, and type of stoichiometric information available, as detailed above. Structures varied the number of microbial pools or the presence of different stabilization pathways. Modifying parameters allowed us to confirm that our results were general across possible parameter ranges, and modifying the pools that receive constraints allowed us to assess the impact of stoichiometric or substrate use efficiency information for different pools.
We present these data at the level of overall uncertainty to test whether changes in structural conditions or parameters influence the value of stoichiometric information. Here, overall uncertainty means the range of possible flows across the entire linear system. To calculate a value of overall uncertainty (Equation 6), we solved for the individual flows that maximize (ymax) and minimize (ymin) the total flow throughout the linear system. Uncertainty is the overall difference between all i flows in the maximum and minimum cases for each element.
Given that the LSD is static and does not explicitly account for pool sizes and rate constants, our uncertainty estimates are not directly comparable with those derived from dynamic SOM (and carbon cycle) models, which do not always operate at equilibrium (Sihi et al., 2018; Sulman et al., 2018). Instead, the magnitude of uncertainty in the LSD indicates the precision of each flow at equilibrium. Although this metric may differ from the general measure of uncertainty used within the soil (and terrestrial) ecology community, inverse linear programming has been extensively used to solve network flow problems and their associated uncertainties in community ecology, metabolic networks, engineering, nutrition, and transport planning (Dantzig, 1963; van Oevelen et al., 2010; Yang et al., 2017; Goldford et al., 2018).
Results
The general model scenario constrained soil processes within ranges set by the described structural conditions (see section Model Constraints) and by mass balance. The uncertainty calculated for the base model was at least two orders of magnitude higher than the system inputs (i.e., 180–2,500 g C m−2 y−1; assumption 1). Uncertainty was higher than the system inputs because many flows recycled C and nutrients among pools in the soil system (This does not occur in the one pool example provided; Figure 2).
Specific stoichiometric constraints, such as an exact C:P ratio for bacteria, had a much more important impact on uncertainty than broad stoichiometric ranges (Figure 3A). Adding broad constraints on the relationship between C, N, P, and S encompassing all potential minimum to maximum ratios had a negligible impact on uncertainty in C (Figure 3A), but reduced uncertainty in N, P, and S flows whenever that nutrient was included (Figure S2). We tested the system using specific stoichiometric constraints (fixed C:N:P:S ratios across all pools) and found that they reduced the uncertainty in C flow by 20% when we included only C:N and by 80% when we included at least C:N:P (Figure 3A).
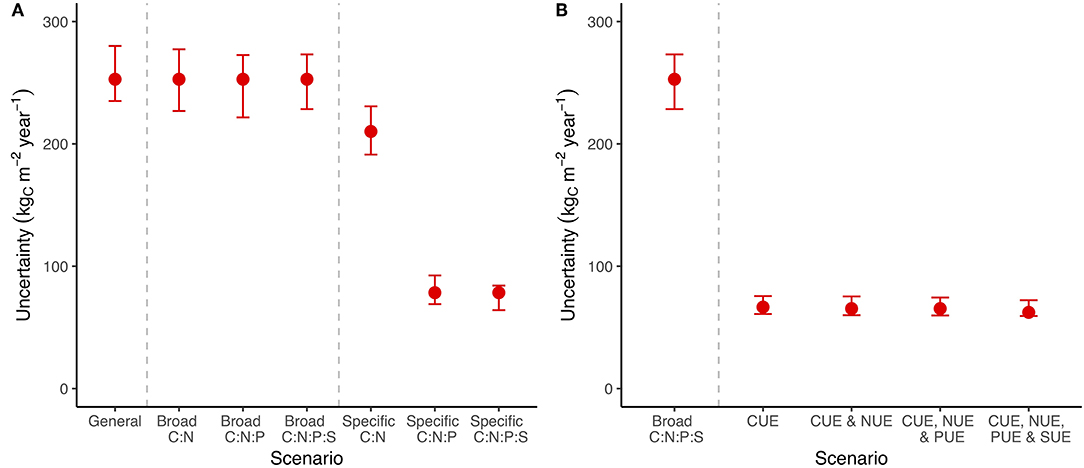
Figure 3. A summary of C cycle uncertainty in the LSD using different amounts of stoichiometry and substrate use efficiency information. (A) The scenarios represent an increasing number of links between element cycles, ranging from entirely independent to linkage between “C:N,” “C:N:P,” and “C:N:P:S.” The general scenario has the widest possible bounds, while still avoiding infinite recycling between pools. Broad scenarios are constrained by a wide range of potential ratios between C and the indicated nutrients, while specific scenarios are constrained to a point estimate of that ratio. (B) Scenarios with CUE, NUE, PUE, and SUE are constrained to a point estimate of C, N, P, and S use efficiency, respectively. Uncertainty is shown for the general model containing all pools and information along with error bars that span the 25th−75th quantiles of 100 random parameters draws within ± 20% of the base value. Uncertainty is calculated as the sum of the absolute difference in flows between the minimum and maximum flow scenarios. See Figure S2 for N, P, and S.
We then tried including substrate use efficiency for C, N, P, and S rather than imposing stoichiometry (Figure 3B). Information on CUE for microorganisms and soil animals was effective at reducing the uncertainty in C flows (Figure 3B) but the substrate use efficiency of other nutrients (i.e., N, P, and S) did not provide additional benefits (Figure 3B; Figure S2). Unlike specific stoichiometric information, which became more useful with additional elements, most of the value of substrate use efficiency data came from CUE (Figure 3B; Figure S2). The general trends in uncertainty across stoichiometry and substrate use efficiency were robust to changes in the parameter values (Figure 3: error bars). These results show that stoichiometry, especially precise C:N:P ratios, is on par with substrate use efficiency at constraining C flows (Figure 3).
Modifying the model structure (see section Model Example) altered the overall uncertainty and, in certain cases, altered the value of stoichiometric and substrate use efficiency information. Removing differences in chemical quality and microbial pools dramatically reduced the overall uncertainty, while removing MAOM pools and physical protection had a more modest effect (Figure 4A: inset). The fact that differences in chemical quality, microbial biomass, and MAOM increased uncertainty in the model is consistent with our new understanding of them as central to SOM formation and loss (Lehmann and Kleber, 2015). When microbial pools were taken out of the budget, substrate use efficiency information had no effect on uncertainty even though animals were still included (Figure 4B). Removing chemical quality from the budget also made substrate use efficiency information less useful. Similarly, stoichiometric ratios were much less important without differences in chemical quality, MAOM pools, or saprotrophic microbial pools (Figure 4A). Since recent empirical findings indicate that such interactions drive the formation of large pools of stable SOM (Lehmann and Kleber, 2015), our results establish stoichiometry as a necessary component of SOM models that focus on microbial and mineral SOM formation. These results highlight an important interaction between stoichiometry and the structural assumptions used to build predictive models of SOM formation and loss.
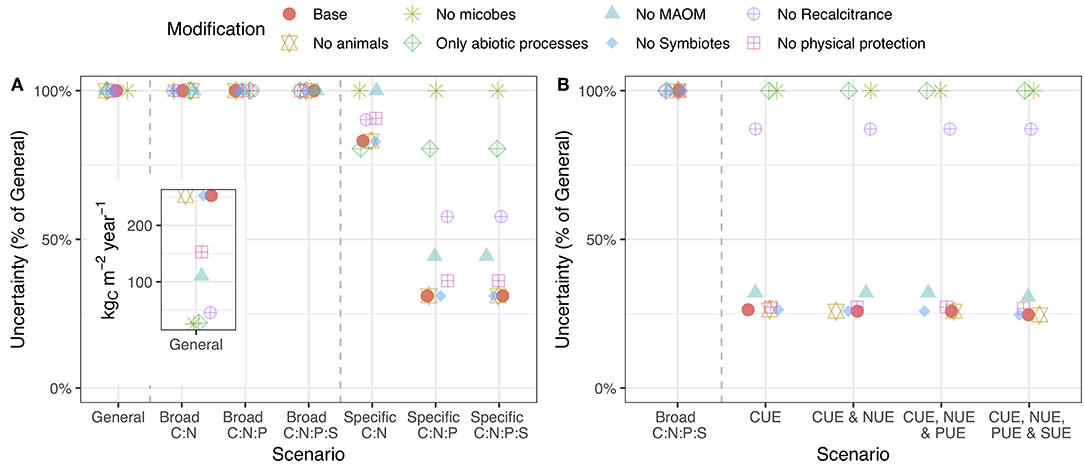
Figure 4. Uncertainty in C cycling when the model structure is changed by removing the indicated pool(s). Points higher on the y-axis indicate that the addition of stoichiometric (A) or substrate use efficiency (B) information less effectively reduces model uncertainty. The inset shows raw uncertainty values in the general case. The caption for Figure 3 provides a description of the axes. A version of this plot for N, P, and S is presented in the supporting information (Figure S3).
Changing the organisms or pools that received stoichiometric or substrate use efficiency constraints altered their impact on uncertainty. For reducing C flow uncertainty, stoichiometric and substrate use efficiency constraints on saprotrophic microorganisms (i.e., bacteria and fungi) were the most important (Figure 5). Stoichiometric constraints on MAOM also reduced uncertainty, but were much less impactful (Figure 5A). For N flow, constraints on symbionts were also important. For P and S, constraints on MAOM stoichiometry reduced uncertainty (Figure S4). Overall, specific stoichiometric data for microbial C:N:P ratio was the most useful for reducing model uncertainty (by > 50%).
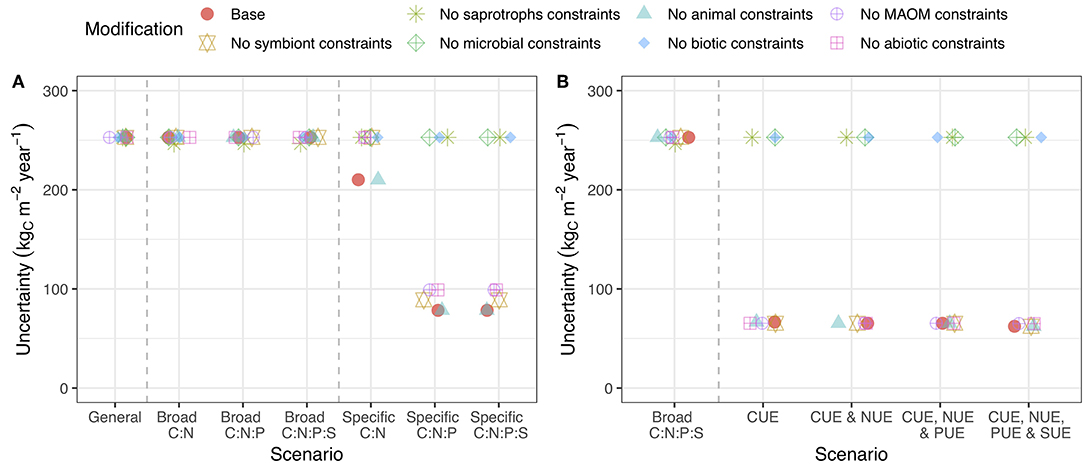
Figure 5. Uncertainty in C cycling when stoichiometric and substrate use efficiency constraints are applied to all pools except the focal. Stoichiometric (A) or substrate use efficiency (B) information for the focal pool is most important when the line associated with that pool remains high on the graph. See caption for Figure 3 for a description of the axes. Versions of this plot for N, P, and S are presented in the supporting information (Figure S4).
Nutrient flows responded differently to a reduction in the possible range of pool stoichiometry and organism CUE across ecosystem types. The differences reflect both the pathways present in a given ecosystem (analogous to structural changes) and starting uncertainty in the potential range of CUE or C:N:P:S for each ecosystem type (Table S2). For example, we found that stoichiometric information is much more effective at constraining flows in tropical systems, where uncertainty in stoichiometric ratios is high and all three plant symbionts can occur (Figure 6; Steidinger et al., 2019). In contrast, stoichiometry and CUE could both reduce uncertainty in temperate systems, with CUE being particularly effective given the wide range of CUE estimates available for temperate forests (Figure 6; Qiao et al., 2019). In general, specific stoichiometric information was more effective than substrate use efficiency at constraining the flows of all elemental cycles (Figure 6). Microbial and animal CUE was most effective at constraining C (Figure 6). Even though temperate forests have more data with which to estimate CUE, the trend in Figure 6 held when we made the range of initial CUE values the same for temperate and tropical systems.
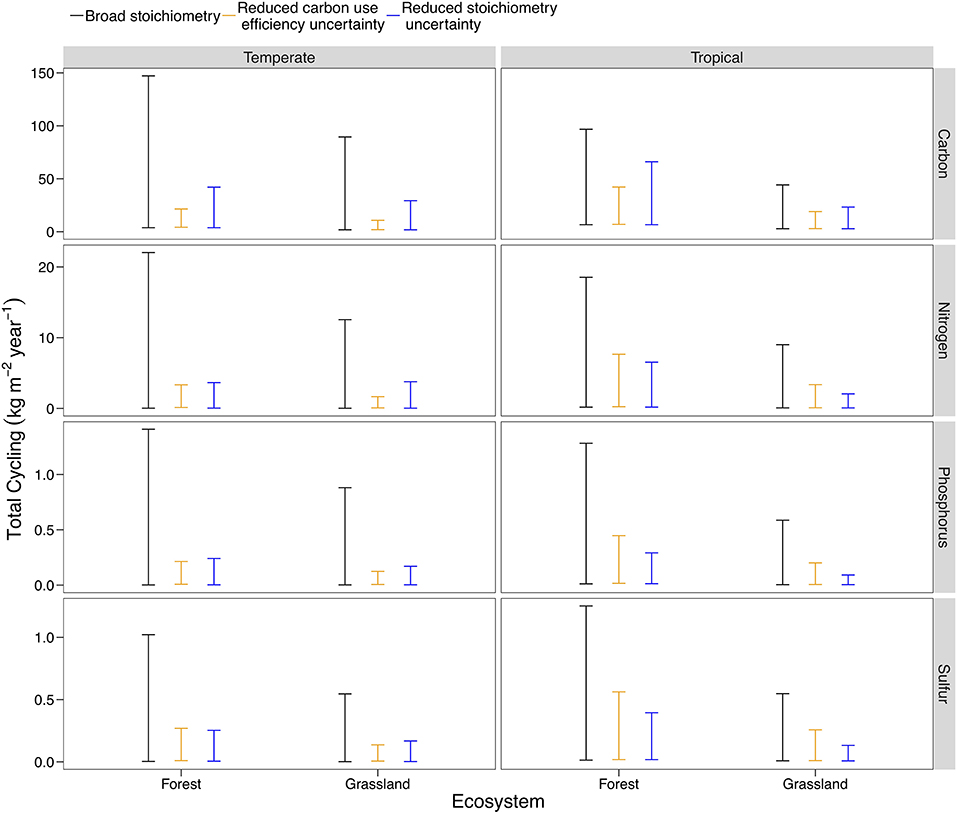
Figure 6. A comparison of model behavior across ecosystem types, using temperate and tropical, forests, and grasslands as an example. The baseline uncertainty corresponds to the broad C:N:P:S scenario in earlier model results (Figure 3), but is different across ecosystem types due to stricter constraints on the range of possible C:N:P:S ratios and CUE. The base scenario is compared with a 90% reduction in the uncertainty of stoichiometry (analogous to the minimum of the error bars in Figure 1: Broad C:N:P:S) and a 90% reduction in the uncertainty of CUE. Plots for the 27 different ecosystem-biome combinations are presented Figure S5.
In general, our analysis indicated that acquiring more precise stoichiometric data will reduce uncertainty in soil nutrient cycling, confirming our hypothesis and the conclusions of our qualitative review (Figure 6; Figure S5). We also found that a budgeting approach, like the LSD, can quantify the usefulness of new stoichiometry and CUE data for a particular system.
Conclusions and Future Directions
Our review traced several of the many stoichiometric changes that can occur along the path separating soil inputs from SOM. With the LSD, we quantified whether these stoichiometric relationships could constrain uncertainty in the size of SOM flows at equilibrium. We discovered that adding stoichiometric information narrowed the range of possible flows, and that the inclusion of elements other than C and N substantially improved the precision of overall flow patterns. In fact, stoichiometric data allowed us to constrain all elemental cycles, improving our representation not only of nutrient flows but also of C flows.
The new generation of SOM models generally use CUE parameters, either fixed or as a function of abiotic conditions, to constrain the flow of C inputs into microbially-derived SOM pools (Allison et al., 2010; Wieder et al., 2014). Though appealing for its simplicity, this approach cannot capture the dependency of CUE on resource availability and often relies on empirical point measurements, which can obscure the variability inherent in CUE (Manzoni et al., 2012). Fixed parameters also do not capture the changes in CUE at different levels of mineral nutrient availability, meaning that models relying on prescribed CUE parameters instead make implicit stoichiometric assumptions. By contrast, stoichiometrically explicit models allow this component of CUE to emerge dynamically as a function of nutrient availability. Our findings demonstrate that a stoichiometric approach can effectively reduce uncertainty in C flow to SOM, justifying the addition of multiple elements into a dynamic accounting of SOM (Schimel and Weintraub, 2003; Buchkowski et al., 2015, 2017; Sulman et al., 2019). Parameterizing such a model would require stoichiometric measurement of important pools, but this is likely to be both more cost-effective and more consistent than measuring substrate use efficiencies at a large scale. Our results also show that such SOM models could be effectively constrained with open-source C and nutrient data on soil and plant inputs available from environmental research and observation networks (Weintraub et al., 2019).
Measurement of SOM pool stoichiometry is a clear opportunity for high-value empirical work. For instance, our review and analysis strongly support several recent theoretical advances (Lehmann and Kleber, 2015; Jilling et al., 2018) highlighting the importance of the microbial to MAOM transition as a hub of C and nutrient exchange in the SOM system. Unfortunately, data on the nutrient content of the MAOM pool remain sparse, especially outside of agricultural and temperate forest ecosystems and for ratios other than C:N. While flows into this pool are predicted to be nutrient-enriched, the quality and extent of this enrichment is highly dependent upon soil characteristics and processes, such as sorption, that are non-linear and require data across substrate × mineral combinations to parameterize SOM models.
Despite the fact that stoichiometry is more consistent than CUE (Cleveland and Liptzin, 2007), the stoichiometry of MAOM and other large soil pools can be sensitive to disturbance, and may therefore be vulnerable to global change. For example, fire (e.g., Butler et al., 2019), warming (e.g., Sihi et al., 2019), and nutrient addition (e.g., Crowther et al., 2019) have been known to influence the stoichiometry of soil, invertebrate, saprotrophic microorganisms, mycorrhizal fungi, and enzyme kinetic activities, which in turn can affect SOM pools and flows. Likewise, MAOM stoichiometry is likely to change with soil pH and associated organo-metal complexation with sesquioxides (Fe and Al oxides) and exchangeable Ca (Rasmussen et al., 2018). Adding these stoichiometric mechanisms into dynamic SOM models may help them replicate larger-scale changes in soil stoichiometry and resolve global patterns.
By synthesizing recent advances in SOM cycling and developing a simple, stoichiometrically explicit budget, we were able to quantify the size of organic matter flows in soil and identify which SOM flows were well-constrained by new data across 27 different ecosystem × biome combinations. Information not only on soil organic C and N but also on P and S was central to achieving this goal, which indicates that collecting data on the distribution of these soil nutrients is an effective way to strengthen our capacity to predict SOM stocks and flows. With our work, we have provided a foundation for incorporating these new stoichiometric data into dynamic SOM models, where they have the potential to significantly enhance accuracy. Together, empirical and theoretical advances like these can allow us to move away from equilibrium and toward a better understanding of the non-linear dynamics that characterize our changing world.
Data Availability Statement
The model code and data necessary to recreate our analyses is available on Zenodo at https://doi.org/10.5281/zenodo.3464585.
Author Contributions
RB initiated the project. RB and DS ran the linear model analyses. All authors defined the scope of the project, synthesized the available data, and wrote and revised the manuscript.
Funding
The work of RB was supported by the Yale School of Forestry & Environmental Studies. The work of AS was supported by NSF grant DEB-1556643. The work of DS was funded by the U.S. Department of Energy Office of Biological and Environmental Research through the ORNL TES SFA program and an Early Career Award. ORNL is managed by the University of Tennessee-Battelle, LLC, under contract DE-AC05–00OR22725 with the US DOE. The work of GS was funded by a US NSF Graduate Research Fellowship. The work of AK was funded by a NatureNet Science Fellowship.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor declared a shared affiliation, though no collaboration, with one of the author AS.
Acknowledgments
The ideas in this manuscript were synthesized at the Woodstoich 4 workshop, funded by the National Science Foundation under the award DEB-1840408. The authors are grateful to Jim Elser, Michelle A. Evans-White, Jen Schweitzer, Eli Fenichel, Craig See, Paul Julian, Joe Vanderwall, and all the participants in the Woodstoich 4 workshop for their valuable advice and feedback. The final paper was substantially improved by invaluable comments from Josh Schimel and two reviewers.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2019.00382/full#supplementary-material
References
Abramoff, R., Xu, X., Hartman, M., O'Brien, S., Feng, W., Davidson, E., et al. (2018). The Millennial model: in search of measurable pools and transformations for modeling soil carbon in the new century. Biogeochemistry 137, 51–71. doi: 10.1007/s10533-017-0409-7
Abramoff, R. Z., Davidson, E. A., and Finzi, A. C. (2017). A parsimonious modular approach to building a mechanistic belowground carbon and nitrogen model. J. Geophys. Res. 122, 2418–2434. doi: 10.1002/2017jg003796
Adair, E. C., Parton, W. J., Del Grosso, S. J., Silver, W. L., Harmon, M. E., Hall, S. A., et al. (2008). Simple three-pool model accurately describes patterns of long-term litter decomposition in diverse climates. Glob. Chang. Biol. 14, 2636–2660. doi: 10.1111/j.1365-2486.2008.01674.x
Adams, J. L., Tipping, E., Thacker, S. A., and Quinton, J. N. (2018). An investigation of the distribution of phosphorus between free and mineral associated soil organic matter, using density fractionation. Plant Soil 427, 139–148. doi: 10.1007/s11104-017-3478-4
Aerts, R. (1997). Climate, leaf litter chemistry and leaf litter decomposition in terrestrial ecosystems: a triangular relationship. Oikos 79, 439–449. doi: 10.2307/3546886
Allen, J. W., and Shachar-Hill, Y. (2009). Sulfur transfer through an arbuscular mycorrhiza. Plant Physiol. 149, 549–560. doi: 10.1104/pp.108.129866
Allison, S. D., Wallenstein, M. D., and Bradford, M. A. (2010). Soil-carbon response to warming dependent on microbial physiology. Nat. Geosci. 3, 336–340. doi: 10.1038/ngeo846
Austin, A. T., and Ballare, C. L. (2010). Dual role of lignin in plant litter decomposition in terrestrial ecosystems. Proc. Natl. Acad. Sci. U.S.A. 107, 4618–4622. doi: 10.1073/pnas.0909396107
Austin, A. T., Méndez, M. S., and Ballaré, C. L. (2016). Photodegradation alleviates the lignin bottleneck for carbon turnover in terrestrial ecosystems. Proc. Natl. Acad. Sci. U.S.A. 113, 4392–4397. doi: 10.1073/pnas.1516157113
Averill, C., Turner, B. L., and Finzi, A. C. (2014). Mycorrhiza-mediated competition between plants and decomposers drives soil carbon storage. Nature 505, 543–545. doi: 10.1038/nature12901
Badri, D. V., and Vivanco, J. M. (2009). Regulation and function of root exudates. Plant Cell Environ. 32, 666–681. doi: 10.1111/j.1365-3040.2009.01926.x
Bastow, J. L. (2011). Facilitation and predation structure a grassland detrital food web: the responses of soil nematodes to isopod processing of litter. J. Anim. Ecol. 80, 947–957. doi: 10.1111/j.1365-2656.2011.01853.x
Blankinship, J. C., Berhe, A. A., Crow, S. E., Druhan, J. L., Heckman, K. A., Keiluweit, M., et al. (2018). Improving understanding of soil organic matter dynamics by triangulating theories, measurements, and models. Biogeochemistry 140, 1–13. doi: 10.1007/s10533-018-0478-2
Bond-Lamberty, B. P., and Thomson, A. M. (2014). A Global Database of Soil Respiration Data, Version 3.0. Data set. Available online at: http://daac.ornl.gov from Oak Ridge National Laboratory Distributed Active Archive Center, Oak Ridge, Tennessee, USA.
Bosatta, E., and Agren, G. I. (1991). Dynamics of carbon and nitrogen in the organic matter of the soil: a generic theory. Am. Natural. 138, 227–245. doi: 10.1086/285213
Bradford, M. A., Keiser, A. D., Davies, C. A., Mersmann, C. A., and Strickland, M. S. (2013). Empirical evidence that soil carbon formation from plant inputs is positively related to microbial growth. Biogeochemistry 113, 271–281. doi: 10.1007/s10533-012-9822-0
Brady, N. C., and Weil, R. R. (2007). The Nature and Properties of Soils. Fourteenth. Upper Saddle River, NJ: Prentice Hall.
Brandt, L. A., King, J. Y., Hobbie, S. E., Milchunas, D. G., and Sinsabaugh, R. L. (2010). The role of photodegradation in surface litter decomposition across a grassland ecosystem precipitation gradient. Ecosystems 13, 765–781. doi: 10.1007/s10021-010-9353-2
Brophy, L. S., and Heichel, G. H. (1989). Nitrogen release from roots of alfalfa and soybean grown in sand culture. Plant Soil 116, 77–84.
Brzostek, E. R., Greco, A., Drake, J. E., and Finzi, A. C. (2013). Root carbon inputs to the rhizosphere stimulate extracellular enzyme activity and increase nitrogen availability in temperate forest soils. Biogeochemistry 115, 65–76. doi: 10.1007/s10533-012-9818-9
Buchkowski, R. W., Bradford, M. A., Grandy, A. S., Schmitz, O. J., and Wieder, W. R. (2017). Applying population and community ecology theory to advance understanding of belowground biogeochemistry. Ecol. Lett. 20, 231–245. doi: 10.1111/ele.12712
Buchkowski, R. W., Schmitz, O. J., and Bradford, M. A. (2015). Microbial stoichiometry overrides biomass as a regulator of soil carbon and nitrogen cycling. Ecology 96, 1139–1149. doi: 10.1890/14-1327.1
Butler, O. M., Lewis, T., Rezaei Rashti, M., Maunsell, S. C., Elser, J. J., and Chen, C. (2019). The stoichiometric legacy of fire regime regulates the roles of micro organisms and invertebrates in decomposition. Ecology 100:e02732. doi: 10.1002/ecy.2732
Celi, L., and Barberis, E. (2007). “Chapter 13: abiotic reactions of inositol phosphates in soil,” in Inositol Phosphates: Linking Agriculture and the Environment, eds B. L. Turner, A. E. Richardson, and E. J. Mullaney 207–221. doi: 10.1079/9781845931520.0207
Celi, L., Lamacchia, S., Marsan, F. A., and Barberis, E. (1999). Interaction of inositol hexaphosphate on clays: adsorption and charging phenomena. Soil Sci. 164, 574–585. doi: 10.1097/00010694-199908000-00005
Chapin, F. S., Matson, P. A., and Vitousek, P. M. (2011). Principles of Terrestrial Ecosystem Ecology. New York, NY: Springer New York.
Clemmensen, K. E., Bahr, A., Ovaskainen, O., Dahlberg, A., Ekblad, A., Wallander, H., et al. (2013). Roots and associated fungi drive long-term carbon sequestration in boreal forest. Science 339, 1615–1618. doi: 10.1126/science.1231923
Cleveland, C. C., and Liptzin, D. (2007). C: N: P stoichiometry in soil: is there a “Redfield ratio” for the microbial biomass? Biogeochemistry 85, 235–252. doi: 10.1007/s10533-007-9132-0
Cleveland, C. C., Townsend, A. R., Schimel, D. S., Fisher, H., Howarth, R. W., Hedin, L. O., et al. (1999). Global patterns of terrestrial biological nitrogen (N2) fixation in natural ecosystems. Global Biogeochem. Cycles 13, 623–645. doi: 10.1029/1999GB900014
Cornelissen, J., Aerts, R., Cerabolini, B., Werger, M., and Van Der Heijden, M. (2001). Carbon cycling traits of plant species are linked with mycorrhizal strategy. Oecologia 129, 611–619. doi: 10.1007/s004420100752
Cotrufo, M. F., Soong, J. L., Horton, A. J., Campbell, E. E., Haddix, M. L., Wall, D. H., et al. (2015). Formation of soil organic matter via biochemical and physical pathways of litter mass loss. Nat. Geosci. 8, 776–779. doi: 10.1038/ngeo2520
Cotrufo, M. F., Wallenstein, M. D., Boot, C. M., Denef, K., and Paul, E. (2013). The microbial efficiency-matrix stabilization (MEMS) framework integrates plant litter decomposition with soil organic matter stabilization: do labile plant inputs form stable soil organic matter? Glob. Chang. Biol. 19, 988–995. doi: 10.1111/gcb.12113
Craig, M. E., Turner, B. L., Liang, C., Clay, K., Johnson, D. J., and Phillips, R. P. (2018). Tree mycorrhizal type predicts within-site variability in the storage and distribution of soil organic matter. Glob. Chang. Biol. 24, 3317–3330. doi: 10.1111/gcb.14132
Crow, S. E., Lajtha, K., Filley, T. R., Swanston, C. W., Bowden, R. D., and Caldwell, B. A. (2009). Sources of plant-derived carbon and stability of organic matter in soil: implications for global change. Glob. Chang. Biol. 15, 2003–2019. doi: 10.1111/j.1365-2486.2009.01850.x
Crowther, T. W., Riggs, C., Lind, E. M., Borer, E. T., Seabloom, E. W., Hobbie, S. E., et al. (2019). Sensitivity of global soil carbon stocks to combined nutrient enrichment. Ecol. Lett. 22, 936–945. doi: 10.1111/ele.13258
Dantzig, G. B. (1963). Linear Programming and Extensions. Princeton, NJ: Princeton University Press.
David, J. F. (2014). The role of litter-feeding macroarthropods in decomposition processes: a reappraisal of common views. Soil Biol. Biochem. 76, 109–118. doi: 10.1016/j.soilbio.2014.05.009
Di Lonardo, D. P., De Boer, W., Gunnewiek, P. K., Hannula, S. E., and Van der Wal, A. (2017). Priming of soil organic matter: chemical structure of added compounds is more important than the energy content. Soil Biol. Biochem. 108, 41–54. doi: 10.1016/j.soilbio.2017.01.017
Dijkstra, F. A., Carrillo, Y., Pendall, E., and Morgan, J. A. (2013). Rhizosphere priming: a nutrient perspective. Front. Microbiol. 4:216. doi: 10.3389/fmicb.2013.00216
Drake, J. E., Darby, B. A., Giasson, M. A., Kramer, M. A., Phillips, R. P., and Finzi, A. C. (2013). Stoichiometry constrains microbial response to root exudation-insights from a model and a field experiment in a temperate forest. Biogeosciences 10, 821–838. doi: 10.5194/bg-10-821-2013
Dungait, J. A. J., Hopkins, D. W., Gregory, A. S., and Whitmore, A. P. (2012). Soil organic matter turnover is governed by accessibility not recalcitrance. Glob. Chang. Biol. 18, 1781–1796. doi: 10.1111/j.1365-2486.2012.02665.x
Fahey, T. J., Yavitt, J. B., Sherman, R. E., Groffman, P. M., Fisk, M. C., and Maerz, J. C. (2011). Transport of carbon and nitrogen between litter and soil organic matter in a northern hardwood forest. Ecosystems 14, 326–340. doi: 10.1007/s10021-011-9414-1
Fahey, T. J., Yavitt, J. B., Sherman, R. E., Maerz, J. C., Groffman, P. M., Fisk, M. C., et al. (2013). Earthworm effects on the incorporation of litter C and N into soil organic matter in a sugar maple forest. Ecol. Appl. 23, 1185–1201. doi: 10.1890/12-1760.1
Fernandez, C. W., See, C. R., and Kennedy, P. G. (2019). Decelerated carbon cycling by ectomycorrhizal fungi is controlled by substrate quality and community composition. bioRxiv. doi: 10.1101/716555
Fischer, H., Ingwersen, J., and Kuzyakov, Y. (2010). Microbial uptake of low-molecular-weight organic substances out-competes sorption in soil. Eur. J. Soil Sci. 61, 504–513. doi: 10.1111/j.1365-2389.2010.01244.x
Frey, S. D., Lee, J., Melillo, J. M., and Six, J. (2013). The temperature response of soil microbial efficiency and its feedback to climate. Nat. Clim. Chang. 3:395. doi: 10.1038/nclimate1796
Frouz, J., Cajthaml, T., and Mudrák, O. (2011). The effect of lignin photodegradation on decomposability of Calamagrostis epigeios grass litter. Biodegradation 22, 1247–1254. doi: 10.1007/s10532-011-9479-8
Frouz, J., Špaldonová, A., Lhotáková, Z., and Cajthaml, T. (2015). Major mechanisms contributing to the macrofauna-mediated slow down of litter decomposition. Soil Biol. Biochem. 91, 23–31. doi: 10.1016/j.soilbio.2015.08.024
Gill, A. L., and Finzi, A. C. (2016). Belowground carbon flux links biogeochemical cycles and resource-use efficiency at the global scale. Ecol. Lett. 19, 1419–1428. doi: 10.1111/ele.12690
Godbold, D. L., Hoosbeek, M. R., Lukac, M., Cotrufo, M. F., Janssens, I. A., Ceulemans, R., et al. (2006). Mycorrhizal hyphal turnover as a dominant process for carbon input into soil organic matter. Plant Soil 281, 15–24. doi: 10.1007/s11104-005-3701-6
Goldberg, S., and Sposito, G. (1985). On the mechanism of specific phosphate adsorption by hydroxylated mineral surfaces: a review. Commun. Soil Sci. Plant Anal. 16, 801–821. doi: 10.1080/00103628509367646
Goldford, J. E., Lu, N., Bajić, D., Estrela, S., Tikhonov, M., Sanchez-Gorostiaga, A., et al. (2018). Emergent simplicity in microbial community assembly. Science 361, 469–474. doi: 10.1126/science.aat1168
Gordon, W. S., and Jackson, R. B. (2000). Nutrient concentrations in fine roots. Ecology 81, 275–280. doi: 10.1890/0012-9658(2000)081[0275:NCIFR]2.0.CO;2
Griffiths, B. S., Spilles, A., and Bonkowski, M. (2012). C:N:P stoichiometry and nutrient limitation of the soil microbial biomass in a grazed grassland site under experimental P limitation or excess. Ecol. Proc. 1:6. doi: 10.1186/2192-1709-1-6
Harmon, M. E., Silver, W. L., Fasth, B., Chen, H., Burke, I. C., Parton, W. J., et al. (2009). Long-term patterns of mass loss during the decomposition of leaf and fine root litter: an intersite comparison. Glob. Chang. Biol. 15, 1320–1338. doi: 10.1111/j.1365-2486.2008.01837.x
Hartman, W. H., Ye, R., Horwath, W. R., and Tringe, S. G. (2017). A genomic perspective on stoichiometric regulation of soil carbon cycling. ISME J. 11:2652. doi: 10.1038/ismej.2017.115
Hobbie, S. E. (2005). Contrasting effects of substrate and fertilizer nitrogen on the early stages of litter decomposition. Ecosystems 8, 644–656. doi: 10.1007/s10021-003-0110-7
Hodge, A., and Storer, K. (2014). Arbuscular mycorrhiza and nitrogen: implications for individual plants through to ecosystems. Plant Soil 386, 1–19. doi: 10.1007/s11104-014-2162-1
Iversen, C. M., McCormack, M. L., Powell, A. S., Blackwood, C. B., Freschet, G. T., Kattge, J., et al. (2017). A global fine-root ecology database to address below-ground challenges in plant ecology. N. Phytol. 215, 15–26. doi: 10.1111/nph.14486
Jenkinson, D. S., Hart, P. B. S., Rayner, J. H., and Parry, L. C. (1987). Modell. Turnover Org. Matter Long.-Term Exp. Rothamsted. INTECOL Bull. 15, 1–8.
Jilling, A., Keiluweit, M., Contosta, A. R., Frey, S., Schimel, J., Schnecker, J., et al. (2018). Minerals in the rhizosphere: overlooked mediators of soil nitrogen availability to plants and microbes. Biogeochemistry 139, 103–122. doi: 10.1007/s10533-018-0459-5
Jung, S. C., Martinez-Medina, A., Lopez-Raez, J. A., and Pozo, M. J. (2012). Mycorrhiza-induced resistance and priming of plant defenses. J. Chem. Ecol. 38, 651–664. doi: 10.1007/s10886-012-0134-6
Kaiser, K., and Kalbitz, K. (2012). Cycling downwards – dissolved organic matter in soils. Soil Biol. Biochem. 52, 29–32. doi: 10.1016/j.soilbio.2012.04.002
Kallenbach, C., Grandy, A., Frey, S., and Diefendorf, A. (2015). Microbial physiology and necromass regulate agricultural soil carbon accumulation. Soil Biol. Biochem. 91, 279–290. doi: 10.1016/j.soilbio.2015.09.005
Kallenbach, C. M., Frey, S. D., and Grandy, A. S. (2016). Direct evidence for microbial-derived soil organic matter formation and its ecophysiological controls. Nat. Commun. 7:13630. doi: 10.1038/ncomms13630
Kautz, G., Zimmer, M., and Topp, W. (2002). Does Porcellio scaber (Isopoda: Oniscidea) gain from coprophagy? Soil Biol. Biochem. 34, 1253–1259. doi: 10.1016/S0038-0717(02)00065-2
Keiluweit, M., Bougoure, J. J., Nico, P. S., Pett-Ridge, J., Weber, P. K., and Kleber, M. (2015). Mineral protection of soil carbon counteracted by root exudates. Nat. Clim. Chang. 6, 588–595. doi: 10.1038/nclimate2580
Keiser, A. D., and Bradford, M. A. (2017). Climate masks decomposer influence in a cross-site litter decomposition study. Soil Biol. Biochem. 107, 180–187. doi: 10.1016/j.soilbio.2016.12.022
Kleber, M., Sollins, P., and Sutton, R. (2007). A conceptual model of organo-mineral interactions in soils: self-assembly of organic molecular fragments into zonal structures on mineral surfaces. Biogeochemistry 85, 9–24. doi: 10.1007/s10533-007-9103-5
Knicker, H. (2011). Pyrogenic organic matter in soil: its origin and occurrence, its chemistry and survival in soil environments. Quat. Int. 243, 251–263. doi: 10.1016/j.quaint.2011.02.037
Kong, A. Y., and Six, J. (2010). Tracing root vs. residue carbon into soils from conventional and alternative cropping systems. Soil Sci. Soc. Am. J. 74, 1201–1210. doi: 10.2136/sssaj2009.0346
Kuzyakov, Y. (2010). Priming effects: interactions between living and dead organic matter. Soil Biol. Biochem. 42, 1363–1371. doi: 10.1016/j.soilbio.2010.04.003
Kuzyakov, Y., Friedel, J. K., and Stahr, K. (2000). Review of mechanisms and quantification of priming effects. Soil Biol. Biochem. 32, 1485–1498. doi: 10.1016/S0038-0717(00)00084-5
Leake, J., Johnson, D., Donnelly, D., Muckle, G., Boddy, L., and Read, D. (2004). Networks of power and influence: the role of mycorrhizal mycelium in controlling plant communities and agroecosystem functioning. Can. J. Bot. 82, 1016–1045. doi: 10.1139/b04-060
Lehmann, J., and Kleber, M. (2015). The contentious nature of soil organic matter. Nature 528, 60–68. doi: 10.1038/nature16069
Liang, C., Cheng, G., Wixon, D. L., and Balser, T. C. (2011). An Absorbing Markov Chain approach to understanding the microbial role in soil carbon stabilization. Biogeochemistry 106, 303–309. doi: 10.1007/s10533-010-9525-3
Lin, G., McCormack, M. L., Ma, C., and Guo, D. (2017). Similar below-ground carbon cycling dynamics but contrasting modes of nitrogen cycling between arbuscular mycorrhizal and ectomycorrhizal forests. N. Phytol. 213, 1440–1451. doi: 10.1111/nph.14206
Ludwig, M., Achtenhagen, J., Miltner, A., Eckhardt, K.-U., Leinweber, P., Emmerling, C., et al. (2015). Microbial contribution to SOM quantity and quality in density fractions of temperate arable soils. Soil Biol. Biochem. 81, 311–322. doi: 10.1016/j.soilbio.2014.12.002
Manzoni, S. (2017). Flexible carbon-use efficiency across litter types and during decomposition partly compensates nutrient imbalances—results from analytical stoichiometric models. Front. Microbiol. 8:661. doi: 10.3389/fmicb.2017.00661
Manzoni, S., and Porporato, A. (2009). Soil carbon and nitrogen mineralization: theory and models across scales. Soil Biol. Biochem. 41, 1355–1379. doi: 10.1016/j.soilbio.2009.02.031
Manzoni, S., Taylor, P., Richter, A., Porporato, A., and Ågren, G. I. (2012). Environmental and stoichiometric controls on microbial carbon-use efficiency in soils: research review. N. Phytol. 196, 79–91. doi: 10.1111/j.1469-8137.2012.04225.x
Manzoni, S., Trofymow, J. A., Jackson, R. B., and Porporato, A. (2010). Stoichiometric controls on carbon, nitrogen, and phosphorus dynamics in decomposing litter. Ecol. Monogr. 80, 89–106. doi: 10.1890/09-0179.1
Martinson, H. M., Schneider, K., Gilbert, J., Hines, J. E., Hamback, P. A., and Fagan, W. F. (2008). Detritivory: stoichiometry of a neglected trophic level. Ecol. Res. 23, 487–491. doi: 10.1007/s11284-008-0471-7
McGroddy, M. E., Daufresne, T., and Hedin, L. O. (2004). Scaling of C: N: P stoichiometry in forests worldwide: implications of terrestrial redfield-type ratios. Ecology 85, 2390–2401. doi: 10.1890/03-0351
Menge, D. N. L., Batterman, S. A., Hedin Lars, O., Wenying, L., Pacala, S. W., and Benton, T. (2017). Why are nitrogen-fixing trees rare at higher compared to lower latitudes? Ecology 98, 3127–3140. doi: 10.1002/ecy.2034
Mikutta, R., Turner, S., Schippers, A., Gentsch, N., Meyer-Stüve, S., Condron, L. M., et al. (2019). Microbial and abiotic controls on mineral-associated organic matter in soil profiles along an ecosystem gradient. Sci. Rep. 9:10294. doi: 10.1038/s41598-019-46501-4
Moore, J. C., Berlow, E. L., Coleman, D. C., de Ruiter, P. C., Dong, Q., Hastings, A., et al. (2004). Detritus, trophic dynamics and biodiversity. Ecol. Lett. 7, 584–600. doi: 10.1111/j.1461-0248.2004.00606.x
Moorhead, D. L., Lashermes, G., and Sinsabaugh, R. L. (2012). A theoretical model of C-and N-acquiring exoenzyme activities, which balances microbial demands during decomposition. Soil Biol. Biochem. 53, 133–141. doi: 10.1016/j.soilbio.2012.05.011
Moorhead, D. L., Rinkes, Z. L., Sinsabaugh, R. L., and Weintraub, M. N. (2013). Dynamic relationships between microbial biomass, respiration, inorganic nutrients and enzyme activities: informing enzyme-based decomposition models. Front. Microbiol. 4:223. doi: 10.3389/fmicb.2013.00223
Mooshammer, M., Wanek, W., Hämmerle, I., Fuchslueger, L., Hofhansl, F., Knoltsch, A., et al. (2014). Adjustment of microbial nitrogen use efficiency to carbon: nitrogen imbalances regulates soil nitrogen cycling. Nat. Commun. 5:3694. doi: 10.1038/ncomms4694
Morgan, C. R., and Mitchell, M. J. (1987). The effects of feeding by Oniscus asellus on leaf litter sulfur constituents. Biol. Fertil. Soils 3, 107–111. doi: 10.1007/BF00260589
Newcomb, C. J., Qafoku, N. P., Grate, J. W., Bailey, V. L., and De Yoreo, J. J. (2017). Developing a molecular picture of soil organic matter–mineral interactions by quantifying organo–mineral binding. Nat. Commun. 8:396. doi: 10.1038/s41467-017-02125-8
Orwin, K. H., Kirschbaum, M. U. F., St. John, M. G., and Dickie, I. A. (2011). Organic nutrient uptake by mycorrhizal fungi enhances ecosystem carbon storage: a model-based assessment. Ecol. Lett. 14, 493–502. doi: 10.1111/j.1461-0248.2011.01611.x
Osler, G. H. R., and Sommerkorn, M. (2007). Toward a complete soil C and N cycle: incorporating the soil fauna. Ecology 88, 1611–1621. doi: 10.1890/06-1357.1
Parton, W. J., Hartman, M., Ojima, D., and Schimel, D. (1998). DAYCENT and its land surface submodel: description and testing. Glob. Planet. Chang. 19, 35–48. doi: 10.1016/S0921-8181(98)00040-X
Parton, W. J., Schimel, D. S., Cole, C. V., and Ojima, D. S. (1987). Analysis of factors controlling soil organic matter levels in great plains grasslands1. Soil Sci. Soc. Am. J. 51, 1173–1179. doi: 10.2136/sssaj1987.03615995005100050015x
Phillips, R. P., Brzostek, E., and Midgley, M. G. (2013). The mycorrhizal-associated nutrient economy: a new framework for predicting carbon–nutrient couplings in temperate forests. N. Phytol. 199, 41–51. doi: 10.1111/nph.12221
Prescott, C. E. (2010). Litter decomposition: what controls it and how can we alter it to sequester more carbon in forest soils? Biogeochemistry 101, 133–149. doi: 10.1007/s10533-010-9439-0
Qiao, Y., Wang, J., Liang, G., Du, Z., Zhou, J., Zhu, C., et al. (2019). Global variation of soil microbial carbon-use efficiency in relation to growth temperature and substrate supply. Sci. Rep. 9:5621. doi: 10.1038/s41598-019-42145-6
R Core Team (2014). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. Available online at: http://www.R-project.org/
Rasmussen, C., Heckman, K., Wieder, W. R., Keiluweit, M., Lawrence, C. R., Berhe, A. A., et al. (2018). Beyond clay: towards an improved set of variables for predicting soil organic matter content. Biogeochemistry 137, 297–306. doi: 10.1007/s10533-018-0424-3
Rasse, D. P., Rumpel, C., and Dignac, M. F. (2005). Is soil carbon mostly root carbon? Mechanisms for a specific stabilisation. Plant Soil 269, 341–356. doi: 10.1007/s11104-004-0907-y
Robertson, A. D., Paustian, K., Ogle, S., Wallenstein, M. D., Lugato, E., and Cotrufo, M. F. (2019). Unifying soil organic matter formation and persistence frameworks: the MEMS model. Biogeosciences 16, 1225–1248. doi: 10.5194/bg-16-1225-2019
Rosling, A., Midgley, M. G., Cheeke, T., Urbina, H., Fransson, P., and Phillips, R. P. (2016). Phosphorus cycling in deciduous forest soil differs between stands dominated by ecto- and arbuscular mycorrhizal trees. N. Phytol. 209, 1184–1195. doi: 10.1111/nph.13720
Scheu, S. (2002). The soil food web: structure and perspectives. Eur. J. Soil Biol. 38, 11–20. doi: 10.1016/S1164-5563(01)01117-7
Schimel, J. P., and Weintraub, M. N. (2003). The implications of exoenzyme activity on microbial carbon and nitrogen limitation in soil: a theoretical model. Soil Biol. Biochem. 35, 549–563. doi: 10.1016/S0038-0717(03)00015-4
Schlesinger, W. H., and Bernhardt, E. S. (2013). Biogeochemistry: An Analysis of Global Change. Waltham, MA: Academic Press.
Schrumpf, M., Kaiser, K., Guggenberger, G., Persson, T., Kögel-Knabner, I., and Schulze, E. D. (2013). Storage and stability of organic carbon in soils as related to depth, occlusion within aggregates, and attachment to minerals. Biogeosciences 10, 1675–1691. doi: 10.5194/bg-10-1675-2013
See, C. R., Luke McCormack, M., Hobbie, S. E., Flores-Moreno, H., Silver, W. L., and Kennedy, P. G. (2019). Global patterns in fine root decomposition: climate, chemistry, mycorrhizal association and woodiness. Ecol. Lett. 22, 946–953. doi: 10.1111/ele.13248
Shah, F., Bentzer, J., Ellstr, M., Floudas, D., Carleer, R., Lackner, G., et al. (2016). Ectomycorrhizal fungi decompose soil organic matter using oxidative mechanisms adapted from saprotrophic ancestors. N. Phytol. 209, 1705–1719. doi: 10.1111/nph.13722
Sihi, D., Davidson, E. A., Chen, M., Savage, K. E., Richardson, A. D., Keenan, T. F., et al. (2018). Merging a mechanistic enzymatic model of soil heterotrophic respiration into an ecosystem model in two AmeriFlux sites of northeastern USA. Agricul. For. Meteorol. 252, 155–166. doi: 10.1016/j.agrformet.2018.01.026
Sihi, D., Gerber, S., Inglett, P. W., and Inglett, K. S. (2016). Comparing models of microbial-substrate interactions and their response to warming. Biogeosciences 13, 1733–1752. doi: 10.5194/bg-13-1733-2016
Sihi, D., Inglett, P. W., and Inglett, K. S. (2019). Warming rate drives microbial nutrient demand and enzyme expression during peat decomposition. Geoderma 336, 12–21. doi: 10.1016/j.geoderma.2018.08.027
Simpson, A. J., Simpson, M. J., Smith, E., and Kelleher, B. P. (2007). Microbially derived inputs to soil organic matter: are current estimates too low? Environ. Sci. Technol. 41, 8070–8076. doi: 10.1021/es071217x
Sinsabaugh, R. L., Benjamin, L., Turner, J. M., Talbot, B. G., Waring, J. S., Powers, C. R., et al. (2016). Stoichiometry of microbial carbon use efficiency in soils. Ecol. Monogr. 86, 172–189. doi: 10.1890/15-2110.1
Sinsabaugh, R. L., Manzoni, S., Moorhead, D. L., and Richter, A. (2013). Carbon use efficiency of microbial communities: stoichiometry, methodology and modelling. Ecol. Lett. 16, 930–939. doi: 10.1111/ele.12113
Sinsabaugh, R. L., and Shah, J. J. F. (2012). Ecoenzymatic stoichiometry and ecological theory. Annu. Rev. Ecol. Evol. Syst. 43, 313–343. doi: 10.1146/annurev-ecolsys-071112-124414
Sinsabaugh, R. L., Shah, J. J. F., Findlay, S. G., Kuehn, K. A., and Moorhead, D. L. (2015). Scaling microbial biomass, metabolism and resource supply. Biogeochemistry 122, 175–190. doi: 10.1007/s10533-014-0058-z
Six, J., Conant, R. T., Paul, E. A., and Paustian, K. (2002). Stabilization mechanisms of soil organic matter: Implications for C-saturation of soils. Plant Soil 241, 155–176. doi: 10.1023/A:1016125726789
Six, J., Frey, S., Thiet, R., and Batten, K. (2006). Bacterial and fungal contributions to carbon sequestration in agroecosystems. Soil Sci. Soc. Am. J. 70, 555–569. doi: 10.2136/sssaj2004.0347
Smith, G. R., and Wan, J. (2019). Resource-ratio theory predicts mycorrhizal control of litter decomposition. N. Phytol. 223, 1595–1606. doi: 10.1111/nph.15884
Smith, S. E., and Smith, F. A. (2011). Roles of arbuscular mycorrhizas in plant nutrition and growth: new paradigms from cellular to ecosystem scales. Annu. Rev. Plant Biol. 62, 227–250. doi: 10.1146/annurev-arplant-042110-103846
Sokol, N. W., and Bradford, M. A. (2019). Microbial formation of stable soil carbon is more efficient from belowground than aboveground input. Nat. Geosci. 12, 46–53. doi: 10.1038/s41561-018-0258-6
Sokol, N. W., Sanderman, J., and Bradford, M. A. (2019). Pathways of mineral-associated soil organic matter formation: integrating the role of plant carbon source, chemistry, and point of entry. Glob. Chang. Biol. 25, 12–24. doi: 10.1111/gcb.14482
Sollins, P., Swanston, C., Kleber, M., Filley, T., Kramer, M., Crow, S., et al. (2006). Organic C and N stabilization in a forest soil: evidence from sequential density fractionation. Soil Biol. Biochem. 38, 3313–3324. doi: 10.1016/j.soilbio.2006.04.014
Steidinger, B. S., Crowther, T. W., Liang, J., Van Nuland, M. E., Werner, G. D. A., Reich, P. B., et al. (2019). Climatic controls of decomposition drive the global biogeography of forest-tree symbioses. Nature 569, 404–408. doi: 10.1038/s41586-019-1128-0
Sterner, R., and Elser, J. (2002). Ecological Stoichiometry: the Biology of Elements From Molecules to the Biosphere. Princeton: Princeton University Press.
Sugai, S. F., and Schimel, J. P. (1993). Decomposition and biomass incorporation of 14C-labeled glucose and phenolics in taiga forest floor: effect of substrate quality, successional state, and season. Soil Biol. Biochem. 25, 1379–1389. doi: 10.1016/0038-0717(93)90052-D
Sulman, B. N., Moore, J. A., Abramoff, R., Averill, C., Kivlin, S., Georgiou, K., et al. (2018). Multiple models and experiments underscore large uncertainty in soil carbon dynamics. Biogeochemistry 141, 109–123. doi: 10.1007/s10533-018-0509-z
Sulman, B. N., Phillips, R. P., Oishi, A. C., Shevliakova, E., and Pacala, S. W. (2014). Microbe-driven turnover offsets mineral-mediated storage of soil carbon under elevated CO2. Nat. Clim. Chang. 4, 1099–1102. doi: 10.1038/nclimate2436
Sulman, B. N., Shevliakova, E., Brzostek, E. R., Kivlin, S. N., Malyshev, S., Menge, D. N. L., et al. (2019). Diverse mycorrhizal associations enhance terrestrial c storage in a global model. Glob. Biogeochem. Cycles 2018:GB005973. doi: 10.1029/2018GB005973
Sun, T., Hobbie, S. E., Berg, B., Zhang, H., Wang, Q., Wang, Z., et al. (2018). Contrasting dynamics and trait controls in first-order root compared with leaf litter decomposition. Proc. Nat. Acad. Sci. U.S.A. 115, 10392–10397. doi: 10.1073/pnas.1716595115
Teuben, A., and Verhoef, H. A. (1992). Direct contribution by soil arthropods to nutrient availability through body and fecal nutrient content. Biol. Fertil. Soils 14, 71–75. doi: 10.1007/BF00336253
Tipping, E., Somerville, C. J., and Luster, J. (2016). The C:N:P:S stoichiometry of soil organic matter. Biogeochemistry 130, 117–131. doi: 10.1007/s10533-016-0247-z
Turner, B. L., Papházy, M. J., Haygarth, P. M., and McKelvie, I. D. (2002). Inositol phosphates in the environment. Philos. Transact. R. Soc. Lond. Seri. B 357, 449–469. doi: 10.1098/rstb.2001.0837
van Oevelen, D., Van den Meersche, K., Meysman, F. J. R., Soetaert, K., Middelburg, J. J., and Vézina, A. F. (2010). Quantifying food web flows using linear inverse models. Ecosystems 13, 32–45. doi: 10.1007/s10021-009-9297-6
Wang, G., Post, W. M., and Mayes, M. A. (2013). Development of microbial-enzyme-mediated decomposition model parameters through steady-state and dynamic analyses. Ecol. Appl. 23, 255–272. doi: 10.1890/12-0681.1
Wang, J., Liu, L., Wang, X., and Chen, Y. (2015). The interaction between abiotic photodegradation and microbial decomposition under ultraviolet radiation. Glob. Chang. Biol. 21, 2095–2104. doi: 10.1111/gcb.12812
Waring, B. G., Averill, C., and Hawkes, C. V. (2013). Differences in fungal and bacterial physiology alter soil carbon and nitrogen cycling: insights from meta-analysis and theoretical models. Ecol. Lett. 16, 887–894. doi: 10.1111/ele.12125
Warton, D. I., Shipley, B., and Hastie, T. (2015). CATS regression–a model-based approach to studying trait-based community assembly. Methods Ecol. Evol. 6, 389–398. doi: 10.1111/2041-210X.12280
Weintraub, S. R., Flores, A. N., Wieder, W. R., Sihi, D., Cagnarini, C., Gonçalves, D. R. P., et al. (2019). Leveraging environmental research and observation networks to advance soil carbon science. J. Geophys. Res. 124:1047–1055. doi: 10.1029/2018JG004956
Wieder, W. R., Bonan, G. B., and Allison, S. D. (2013). Global soil carbon projections are improved by modelling microbial processes. Nat. Clim. Chang. 3:909. doi: 10.1038/nclimate1951
Wieder, W. R., Grandy, A. S., Kallenbach, C. M., and Bonan, G. B. (2014). Integrating microbial physiology and physio-chemical principles in soils with the MIcrobial-MIneral Carbon Stabilization (MIMICS) model. Biogeosciences 11, 3899–3917. doi: 10.5194/bg-11-3899-2014
Yang, Y., Hu, X., and Ma, B. (2017). Construction and simulation of the Bradyrhizobium diazoefficiens USDA110 metabolic network: a comparison between free-living and symbiotic states. Molecul BioSyst. 13, 607–620. doi: 10.1039/C6MB00553E
Yuan, Z. Y., Chen, H. Y. H., and Reich, P. B. (2011). Global-scale latitudinal patterns of plant fine-root nitrogen and phosphorus. Nat. Commun. 2:344. doi: 10.1038/ncomms1346
Keywords: soil organic matter, ecological stoichiometry, carbon, nutrients, litter decomposition, soil organisms, stabilization, mineral associated organic matter
Citation: Buchkowski RW, Shaw AN, Sihi D, Smith GR and Keiser AD (2019) Constraining Carbon and Nutrient Flows in Soil With Ecological Stoichiometry. Front. Ecol. Evol. 7:382. doi: 10.3389/fevo.2019.00382
Received: 22 July 2019; Accepted: 24 September 2019;
Published: 10 October 2019.
Edited by:
James Joseph Elser, University of Montana, United StatesReviewed by:
Joshua Schimel, University of California, Santa Barbara, United StatesChengrong Chen, Griffith University, Australia
Michael Kaspari, University of Oklahoma, United States
Copyright © 2019 Buchkowski, Shaw, Sihi, Smith and Keiser. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Robert W. Buchkowski, cm9iYnVjaGtvQGdtYWlsLmNvbQ==
 Robert W. Buchkowski
Robert W. Buchkowski Alanna N. Shaw
Alanna N. Shaw Debjani Sihi
Debjani Sihi Gabriel R. Smith
Gabriel R. Smith Ashley D. Keiser
Ashley D. Keiser