Second-Generation P-Values, Shrinkage, and Regularized Models

Second-generation p-values (SGPVs) are a novel and intuitive extension of classical p-values that better summarize the degree to which data support scientific hypotheses. SGPVs measure the overlap between an uncertainty interval for the parameter of interest and an interval null hypothesis that represents the set of null and practically null hypotheses. Although SGPVs are always in the unit interval, they are not formal probabilities. Rather, SGPVs are summary measures of when the data are compatible with null hypotheses (SGPV = 1), compatible with alternative hypotheses (SGPV = 0), or inconclusive (0 < SGPV < 1). Because second-generation p-values differentiate between inconclusive and null results, their Type I Error rate converges to zero along with the Type II Error rate. The SGPV approach is also inferentially agnostic: it can be applied to any uncertainty interval about a parameter of interest such as confidence intervals, likelihood support intervals, and Bayesian highest posterior density intervals. This paper revisits the motivation for using SGPVs and explores their long-run behavior under regularized models that provide shrinkage on point estimates. While shrinkage often results in a more desirable bias-variance trade-off, the impact of shrinkage on the error rates of SGPVs is not well-understood. Through extensive simulations, we find that SPGVs based on shrunken estimates retain the desirable error rate behavior of SGPVs that we observe in classical models—albeit with a minor loss of power—while also retaining the benefits of bias-variance tradeoff.

Introduction

Despite decades of controversy, p-values remain a popular tool for assessing when observed data are incompatible with the null hypothesis. While p-values are widely recognized as imperfect, they continue to flourish in the scientific literature even when their shortcomings have real consequences. This reluctance to change occurs, in large part, because p-values are being used as quick-and-dirty summary assessments of the underlying data (instead of as a perfectly precise measure of evidence for a statistical hypothesis). In some cases, p-values are undeniably misused, abused and selectively misinterpreted. However, most researchers look to the p-value for an objective assessment of when the data are worthy of further detailed inspection. Given the large amount of information published on a daily basis, there is a critical role for a summary statistic to do just that. Blume et al. (2018, 2019) proposed the second-generation p-value (SGPV) as an improved p-value as used in practice. The SGPV is intended to serve as a summary measure of the data at hand, regardless of the statistical approach.

The SGPV is a formalization of today's best practices for interpreting data. According to the American Statistical Association (Wasserstein and Lazar, 2016), “best practice” amounts to de-emphasizing the magnitude of the p-value and inspecting the associated uncertainty interval (typically a confidence interval) to see if contains only scientifically meaningful effects. That is, researchers are supposed to check to see if the uncertainty interval rules out the null hypothesis and all other trivial, scientifically uninteresting effects. The problem with this approach is that it is post-hoc; the assessment of scientific meaningfulness is conducted after examining the data. As a result, the researcher's post-hoc assessments are influenced by results at hand, and this leads to the embellishment of effectively inconclusive data that supports practically null effects simply because the classical p-value is small. Given this, it should be no surprise that many “findings” fail to replicate; those “findings” were often mischaracterized in the first place.

A straightforward remedy for this is to require researchers to specify interesting and uninteresting effect sizes before the data are collected. This is routinely done in clinical trials, for example. The observed results can then be contrasted against initial benchmarks, uncorrupted by the observed data. Findings that fail to meet those benchmarks should still be reported, of course. But now they will be correctly reported as exploratory results and not as confirmatory ones. This is a critical step toward reproducibility: requiring the experimenter to define what constitutes a “successful experiment” before data are collected and interpreted.

The second-generation p-value (SGPV) is an improved p-value that has been adapted to this new level of exactness. It depends on the researcher's a priori definition of what constitutes an interesting or uninteresting effect and it indicates when the experiment has met that pre-specified benchmark. Blume et al. (2018, 2019) showed that this formalization leads to improved statistical properties in terms of a reduced Type I Error rate (it converges to zero as the sample size grows, much like the Type II error rate) and reduced false discovery rates.

The SGPV also depends on an uncertainty interval that characterizes the effect sizes that are supported by the data. Blume et al. (2018) shows how the SGPV's frequency properties are derived from the uncertainty interval. Blume et al. (2018, 2019) show than if a (1 − α)100% confidence interval or properly calibrated likelihood support interval is used, then the SGPV has desirable error rate behavior, with a Type I Error rate that remains bounded by α. The SGPV can just as easily be based on a Bayesian credible interval. The ability to incorporate an uncertainty interval from any of the three inferential schools of thought is why the SGPV is “method-agnostic.” This also highlights the SGPVs role as a global indicator of when the study has collected sufficient data to draw conclusions, regardless of the underlying inferential approach used in the analysis.

In this paper, we examine what happens when the uncertainty interval upon which the SGPV is based comes from a model that is regularized. This is most easily thought of as using a Bayes or credible interval with a pre-specified prior. The Bayes approach provides shrinkage, which often results in reduced mean square error because the added bias is offset by a larger reduction of variance (confidence intervals, on the other hand, are routinely based on unbiased estimates). The question of interest is what happens to the frequency properties of the SGPV when uncertainty intervals are derived from a procedure that adds bias to reduce the variance. We investigate this by examining the behavior of SGPVs based on Bayes uncertainty intervals in a variety of simulations. We find that the SGPV easily incorporates these intervals while maintaining the improved Type I/Type II Error rate tradeoff. That is, the Type I error rate still converges to zero and the associated reduction of power tends to be minor. As a result, SGPVs based on Bayes intervals are similarly reliable inferential tools.

Background: The Second-Generation p-value

Blume et al. (2018) present Figure 1 (below) to illustrate the SGPV. The top diagram depicts the typical scenario: an estimated effect (denoted by Ĥ), the traditional null hypothesis (denoted by H₀) and a confidence interval (CI) for the uncertainty interval. Here we take the uncertainty interval to be a collection of hypotheses, or effect sizes, that are supported by the data by some criteria (in this case at the 95% level). Classical hypothesis testing follows by simply checking if H₀ is in the CI or not.

FIGURE 1

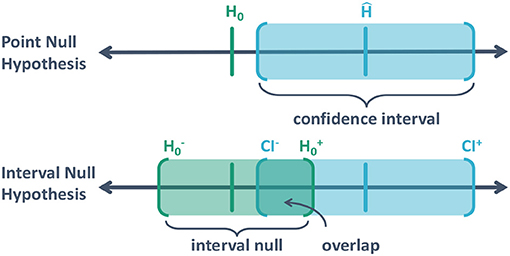
Figure 1. Illustration of a point null hypothesis, H₀; the estimated effect that is the best supported hypothesis, Ĥ; the a confidence interval (CI) for the estimated effect [CI⁻, CI⁺]; and the interval null hypothesis $\left[H_0^{-}{H}_0^{+}\right]$.

There will always be a set of distinct hypotheses that are close to the null hypothesis but are scientifically inconsequential. This group represents null effects and practically null results, which we sometimes call trivial hypotheses, so it makes sense to group them together. This collection of hypotheses represents an indifference zone or interval null hypothesis. The bottom diagram depicts what happens when the null hypothesis is an interval instead of a single point. The null zone contains effect sizes that are indistinguishable from the null hypothesis, due to limited precision or practicality.

An interval null always exists, even if it is narrow, which is why the inspection of a CI for scientific relevance is essential and considered best practice. It is not sufficient to simply rule out the mathematically exact null; one must also rule similarly inconsequential scientific hypotheses/models. At its core, the problem of statistical significance not implying clinical significance boils down to this very issue. It is a matter of scale; the SGPV forces the experimenter to anchor that scale. As we will see, the reward for doing this is a substantially reduced false discovery rate.

Note that the experimental precision, which is finite, can serve as a minimum set for the interval null hypothesis. Finite experimental precision means there is some resolution along the x-axis (Figure 1) within which it is impossible to distinguish between hypotheses. This is a constraint of the experimental design, not the statistical methods. For example, when measuring income, hypotheses differing by <1 cent cannot be compared because the data on income are only measured to within 1 cent. Hypotheses differing by <1 cent are within the fundamental measurement error of the experiment. Typically, however, we are interested in hypotheses that are less precise than the experimental precision, e.g., income differences at the level of 1 dollar. It is this scientific determination that sets the indifference zone around the null interval.

The SGPV is a scaled measurement of the overlap between the two intervals. If there is no overlap, the SGPV is zero. The data only support meaningful non-null hypotheses. If the overlap is partial, so that some of hypotheses supported by the data are in the interval null and some are out, we say the data are inconclusive. The degree of inconclusivity is directly related to the degree of overlap. But the general message is clear: more data are required for a definitive result. If the uncertainly interval is completely contained within the null zone—so the SGPV is 1—then the data support only null or scientifically trivial effects. This is how the SGPV indicates support for alternative hypotheses or null hypotheses, or indicates the data are inconclusive.

An important side note is that a SGPV of 0 or 1 is an endpoint in the sense that the study has completed its primary objective. It has collected sufficient information to screen out/in the null hypothesis. This does not imply that the data have achieved sufficient precision for policy implementation; the resulting uncertainty intervals can still be wide.

Formally, let interval I represent an uncertainty interval, e.g., a 95% CI or 95% credible interval, and let H₀ represent the interval null hypothesis. If I = [a, b] where a < b are real numbers, then its length is |I| = b − a. The second-generation p-value, denoted by p_δ, is defined as

$\begin{array}{ll}{p}_{\delta }=\frac{|I\cap H_0|}{\left|I\right|}\times max\left\{\frac{\left|I\right|}{2\left|H_0\right|},1\right\}& (1)\end{array}$

where I ∩ H₀ is the overlap between intervals I and H₀. The subscript δ signals the reliance of the second-generation p-value on an interval null. Often δ represents the half-width of the interval null hypothesis. The value of δ is driven by scientific context and should be specified prior to conducting the experiment. The SGPV is often referred to as “p-delta.”

The first term in Equation (1) is the fraction of best supported hypotheses that are also null hypotheses. The second term is a small-sample correction factor, which forces the second-generation p-value to indicate inconclusiveness when the observed precision is insufficient to permit valid scientific inferences about the null hypotheses. The second term applies whenever the uncertainty interval is more than twice as long as the null interval. It is this device that allows the SGPV to distinguish inconclusive results from those that support the null premise. See Blume et al. (2018) for a discussion of the correction factor. When the uncertainty interval is a traditional confidence interval, it is straightforward to determine the error rates and subsequent false discovery rates. Blume et al. (2018, 2019) provide these computations. Here we consider what happens when one uses an uncertainty interval from a regularized model, or a Bayes interval, for the basis of the SGPV and how that affects the statistical properties of the SGPV.

The use of an interval null hypothesis is not new in statistics. It is featured in equivalence testing (Schuirmann, 1987), non-inferiority testing (Wang and Blume, 2011), and the Bayesian Region of Practical Equivalence procedure [ROPE; Kruschke, 2014, chapter 12; Kruschke and Liddell, 2017]. Despite 30+ years of existence, equivalence tests have not garnered a large following in the statistical community. Factors contributing to this are the equivalence test's general behavior and non-optimality (Perlman and Wu, 1999) and a well-respected paper calling for the abandonment of a popular variant of equivalence tests—the two one-sided tests (Berger and Hsu, 1996). Of course, equivalence and non-inferiority tests are classical hypothesis tests. As a result, they inherit the shortcomings of the general approach. Flipping the null and alternative hypotheses does not alleviate the ills of hypothesis testing. For example, a p-value cannot measure the evidence for a null hypothesis; flipping the null and alternative hypotheses does not solve this problem, as support for the new null (the old alternative) can no longer be assessed. On the other hand, the SGPV is something different; it is not rooted in classical testing. The similarity between equivalence testing and SGPVs begins and ends in the mathematical formalization of the hypotheses. To the point, the SGPV easily indicates when the data support the null or alternative hypotheses, or when the data are inconclusive; there is no need to flip the hypotheses.

Background: Regularized Models

Regularized models are commonly used in quantitative research. These models can be generated using a wide variety of methods. Some common examples are LASSO (Tibshirani, 1996), elastic-net (Zou and Hastie, 2005), support vector machines (SVM) (Cortes and Vapnik, 1995), Bayesian regression models (Gelman et al., 2013), and even simple continuity corrections of 2 × 2 tables. Because regularized models are now ubiquitous, it is important to know how the SGPV performs when calculated with an uncertainty interval generated from a regularized model.

Broadly speaking, regularization is the practice of incorporating additional structure to a model beyond the typical likelihood or loss function. The additional structure is often incorporated into the model via (a) constraints on the model parameters (LASSO, elastic-net), (b) direct addition of model complexity terms to the loss function (SVM), (c) prior distributions of the model parameters or Bayesian models, or (d) augmented data. Operationally, the contribution of the additional structure—the regularization—relative to the typical likelihood or loss function is controlled by tuning parameters e.g., the severity of the constraint, the scale of the complexity penalty, the variation in the prior distributions, or the amount of augmented data. These tuning parameters are commonly set by cross-validation, although this is not the only approach. Such regularization helps to combat over-optimistic parameter estimation in models that have sparse information relative to the (number of) parameters of interest.

Consider, for example, the classical Bayesian model. The impact of the prior distribution can be minimal if the variation of the prior distribution is large enough that the prior distribution looks essentially flat relative to the likelihood function. When this happens the (flat) prior adds no additional structure to the model. In these cases, the posterior distribution looks very similar to the likelihood function. Conversely, the prior's impact can be substantial if the variation in the prior distribution is small and discordant with the likelihood. Such a prior adds considerable structure to the model; the resulting posterior is a weighted average of the likelihood and that prior.

To illustrate, consider the comparison of two group means using a Bayesian regression model. A detailed description of each regularized model is beyond the scope of this paper, but a simple summary is that the prior and likelihood are combined to yield uncertainty intervals from the posterior (regularized credible intervals). In this example, let β = μ₁ − μ₀ denote the difference in means between the two groups. In Figure 2, data collected from two groups is displayed as overlapping histograms, and the observed sample means are shown as X₁ and X₀. In the bottom of Figure 2, the impact of the prior on the posterior is evident. Note that the 95% credible interval and posterior point estimate of β (displayed as a blue line and point overlaid on the posterior) are pulled toward zero. The data are not changing in this example; the different credible intervals are the result of changing the prior distribution.

FIGURE 2

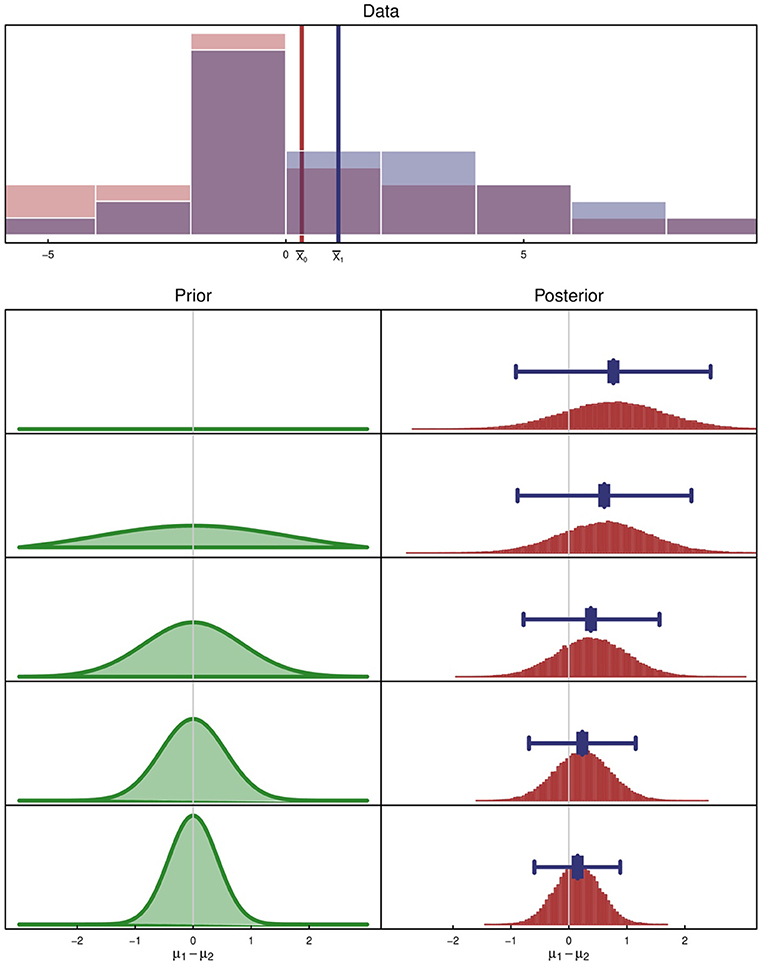
Figure 2. An illustration of shrinkage when additional structure is incorporated into a model by regularization. In this illustration, regularization is achieved with a Bayesian prior, which ranges from flat to peaked. The top figure is the hypothetical data collected from two groups. N (per group) is 30. The observed sample means are shown as X₁ and X₀. The bottom panel shows the posterior distributions (right column) resulting from the choice of prior for the difference in means (left column). As variation in the prior decreases, the resulting interval estimate and point estimate (shown as a blue line and point overlaid on the posterior) are shrunk toward 0.

The phenomenon evident in Figure 2, where posterior point estimates are pulled toward to the mean of the prior (usually 0), is called shrinkage. Shrinkage is natural a consequence of adding structure or information to the model. Notice also that the interval widths become narrower as the degree of regularization becomes larger. The shrunken point estimates are statistically biased but the standard errors of the estimates are smaller. The bias typically vanishes as the sample size grows if the added structure does not change as data accumulate (e.g., the prior is prespecified and remains fixed). Shrinkage often reduces the mean squared error (MSE, i.e., bias² + variance), which is why regularized methods are typically used on prediction models. The trade-off of bias and variance is an important one; smaller MSE is often a desirable operating characteristic.

However, there is no guarantee that regularization will generate smaller MSE. Figure 3 shows the impact on MSE as outcome variation increases under various degrees of regularization. (The operational definition of the degree of regularization is described in section Methods: Simulation Setup.) For a given level of regularization, MSE is improved if the standard deviation of the outcome somewhat exceeds β (in standard deviation units) as depicted in Figure 3. However, regularization tends to increase MSE when the standard deviation of the outcome was comparable to, or less than, the effect size. This phenomenon becomes exaggerated as the degree of regularization increases.

FIGURE 3

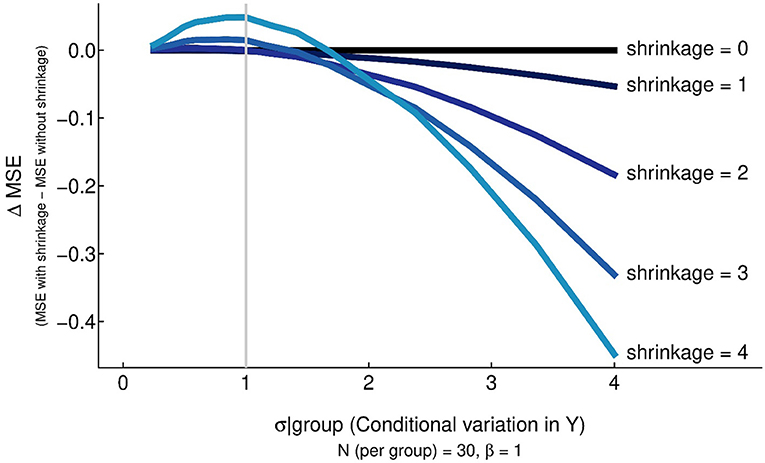
Figure 3. An illustration of the relationship between the conditional variance, the degree of regularization/shrinkage, and the change in MSE when estimating the difference in means. The gray vertical line represents the effect size of the difference in means (1 SD). Shrinkage improves MSE when the conditional variance is large relative to the effect size, but it may increase MSE when the conditional variance is relatively comparable or smaller to the effect size.

The take home message from Figure 3 is that regularization works well when the magnitude of the noise is substantially larger than the signal strength. But when the signal is larger than the noise, regularization can be counterproductive and increase the mean squared error (reduce predictive ability). It should also be said that some models cannot be estimated uniquely without regularization. That is, often the data do not provide enough information to identify a model by themselves. In such cases, adding structure to the model allows the enhanced model to be fit with the data. For example, when the number of predictor variables exceeds the number of observations, regularization can add sufficient structure to permit unique model estimation. LASSO regression and ridge regression are often used in these settings.

Because the SGPV is predicated upon the concept of interval estimates and interval nulls, the SGPV can be immediately applied to parameter estimates and uncertainty intervals constructed from regularized models. In the sections that follow, we examine how the SGPV performs when applied to a Bayesian regression model that estimates the difference in means between two groups. The Bayesian setting is quite flexible and generalizable, as virtually all popular regularization techniques can be re-written as a Bayesian model (albeit sometimes with empirical or specialized prior). Lasso, Ridge Regression, and the James-Stein estimator are some prominent examples. Other penalized likelihood formulations can be framed in a Bayesian context, although the corresponding prior may not be proper, smooth, or as well-behaved as the Lasso, Ridge, and JS estimation.

An Introductory Example: Loggerhead Shrike and Horned Lizard

Data presented in Young (2004) and made public as part of the textbook Analysis of Biological Data (Whitlock and Schluter, 2015) compared the horn length of 30 dead and 154 alive lizards, Phrynosoma mcalli. Researchers hypothesized that larger horn length might be protective against the attack of the loggerhead shrike, Lanius ludovicianus. Here we present a reanalysis of the data in the context of regularization and SGPVs.

The model for the difference in mean horn length can be parameterized with β in the following linear model. In this model, I(Alive) is an indicator variable which is equal to 1 if the lizard was alive at the time of measurement and 0 otherwise.

$\begin{array}{l}E\left[HornLength|Alive\right]=\alpha +\beta I(Alive)\\ V\left[Y|G\right]={\sigma }^2\end{array}$

We set the Bayesian priors as follows:

$\begin{array}{lll}\beta & \sim & N(0,4.25)\\ \alpha & \sim & ImproperFlatPrior\end{array}$

Prior to the analysis, we set the null region from −0.5 to 0.5 mm, indicating that a mean difference <0.5 mm is scientifically equivalent to no difference. The null region should be based on researcher expertise. It is not a quantity driven by data; rather it is driven by scientific understanding of the subject matter. In this example, it is quite possible that different researchers will arrive at different null regions. The variance of the prior for beta was selected to be wide enough to be non-informative, but not so wide to allow implausible values of the treatment effect. There are different approaches to selecting a prior in a Bayesian analysis (Gelman et al., 2013). The approach used will impact the degree of regularization, and it is not a primary concern in this investigation because our focus is on the SGPV's behavior after regularization. However, in our experience, using an empirically derived prior, as we done here, often provides sensible shrinkage behavior.

In Figure 4, we show the prior, the likelihood for the observed data, and the resulting posterior and 95% credible interval for three different version of this analysis. Credible intervals were generated from 50,000 draws from the posterior distribution and an empirical calculation of the 95% highest posterior density. The null region is also shown. In the first panel (column), the null region and the credible interval do not overlap, so the SGPV is 0. A larger null region from −1 to 1 mm is needed to have any chance of overlapping.

FIGURE 4

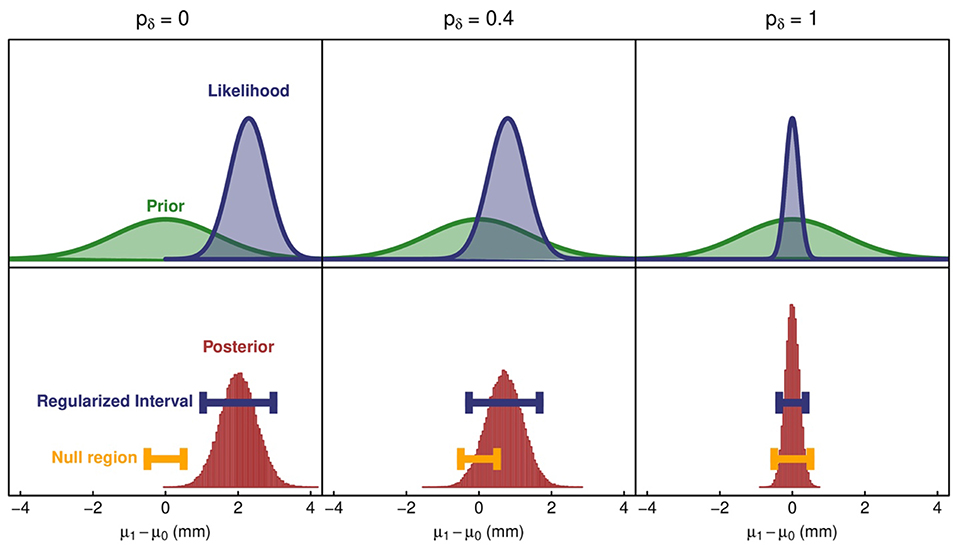
Figure 4. A demonstration of three possible study results in the context of the horned lizard data. The left column shows an interval estimate that does not overlap with the null region, resulting in a second-generation p-value of 0. The middle column shows an interval estimate that straddles the null region, resulting in a second-generation p-value of 0.4. The right column shows an interval estimate that falls entirely within the null region, so the second-generation p-value is 1. The left column results from the unaltered data; whereas data for the middle and right column have been altered for demonstration purposes.

To demonstrate how the analysis might proceed for different effect sizes, we artificially shifted the outcome values for the living lizards by 1.5 mm so that differences in mean horn length are much smaller than the original data. After shifting the data, we see a different result, which is shown in the middle panel (column). The regularized interval straddles the boundary of the null region, so the analysis of this data generates an inconclusive result. The data support both null and meaningful effect sizes, and the second-generation p-value is 0.4.

We also artificially altered the dataset to demonstrate an analysis that results in a conclusive similarity between groups (last panel/column, Figure 5). First, we shifted the horn length for living lizards to match the mean horn length of dead lizards. Second, we increased the sample size of the dataset by a factor of 8 by resampling rows. As one would expect, the likelihood and posterior terms are tighter because of the increased sample size. The resulting interval calculated from the posterior is shorter and falls completely within the null region. The second-generation p-value is 1 in this case, which is an indication of a conclusive similarity.

FIGURE 5

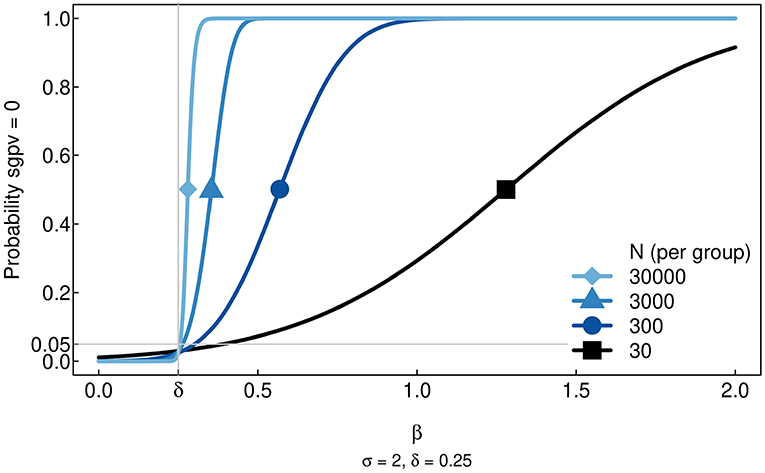
Figure 5. Simulation results showing the Type I and Type II Errors rates for the SGPV as the sample size (N) increases. Within the null region (i.e., all values of beta less than delta), the probability that the SGPV = 0 gets increasingly small as N gets larger. In contrast, for beta values beyond the null region, the probability that the SGPV = 0 goes to 1 as N gets larger. At delta, the boundary of the null region, the probability that SGPV = 0 is controlled at α = 0.05 or less. Hence, the Type I Error rate goes to 0 as N increases. For non-zero values of beta within the null region, the Type II Error rate goes to 1.

We now understand how to compute and use SGPVs. The question that remains is whether the SGPV is reliable in a repeated sampling sense. In the following sections, we simulate similar types of data and perform similar analyses under a wide variety of settings in order to understand the operating characteristics of the SGPV with (smooth) regularization.

Methods: Simulation Setup

In order to better understand the properties of SGPV, we generated Gaussian outcome data for two groups of size N. The difference in means between the groups was β, and the conditional standard deviation was σ. Depending on the simulation, we varied N, β, and σ. In mathematical notation, the data generation procedure was:

$\begin{array}{l}Fori=1,\dots ,N,\dots ,2N\\ Let{G}_i=\{\begin{array}{c}0,i\le N\\ 1,i>N\end{array}\\ Draw{ϵ}_i\sim N\left(0,\sigma \right)\\ Calculate{Y}_i=\beta G_i+ϵ.\end{array}$

G_i is the group indicator and the linear regression model for estimating β was

$\begin{array}{l}E\left[Y|G\right]=\alpha +\beta G\\ V\left[Y|G\right]={\sigma }^2.\end{array}$

When fitting a Bayesian regression model, the prior for the two mean parameters (α, β) was

$\begin{array}{l}\beta \sim N\left(0,\frac{3\widehat{\sigma }}{1.96}\times \frac{1}{shrinkage}\right)\\ \alpha \sim ImproperFlatPrior.\end{array}$

where shrinkage is a variable set for each simulation. Setting shrinkage to 0 is equivalent to ordinary least squares. The prior for β is calibrated so that 95% of its probability mass is within $\pm \frac{3\widehat{\sigma }}{shrinkage}$ (Gelman et al., 2008). The value $\widehat{\sigma }$ is the unconditional standard deviation of the outcome. In a typical analysis setting, the prior for the treatment effect coefficient would be driven by expert opinion. In the simulation setting, we resort to an empirically driven prior. The resulting prior without shrinkage is non-informative without admitting implausible values (Gelman et al., 2008). As shrinkage increases, the probability mass becomes more concentrated around 0. We varied the shrinkage parameter from 0 to 9 in our simulations. For computing the SGPV, we used a null interval of [−0.25, 0.25] or equivalently δ = 0.25 (we used a relatively narrower null interval than in the example to account for possibly strong shrinkage in the simulations).

For each combination of simulation parameters, 5,000 replicate datasets were generated and analyzed. Credible intervals in each analysis were generated from 1,000 draws from the posterior distribution and an empirical calculation of the 95% highest posterior density. Power was calculated as the proportion of replicates where the SGPV equaled zero. If the interval null had been specified as a point, then this procedure would be equivalent to a standard two-sided t-test. MSE was calculated as the mean squared error of the difference between the known β (set by simulation) and estimated $\widehat{\beta }$ (from simulated replicates).

Results

Simulation 1: Power of SGPV as N Increases

As a starting point, we consider the traditional case of least squares to demonstrate the default trade-off of Type I and Type II/power rates for the SGPV. Data were generated under a range of effect sizes, β values, with an increasing number of observations in each group. The conditional standard deviation and null interval were held constant as indicated above.

The results are reported in Figure 5. The most noticeable feature of the figure is that errors within the null region tend toward 0, especially as N increases. Rather than an error rate of 5% at β = 0, there is an approximate error rate of 5% at β = δ, the boundary of the null region. Consequently, power for values of β outside the null region is less than what would be observed with the traditional t-test. This agrees with the results in Blume et al. (2018). The SGPV's reduction in power is traded for a similar reduction in the Type I Error rate for clinically meaningless effect sizes. The reduction in power here is not substantial, but it might be larger in other cases. This is should be checked when planning studies.

Simulation 2: Power, Interval Null, Shrinkage

At the heart of this simulation study is the question of how SGPVs generated with intervals from regularized models compare to SGPVs generated without regularization. To that end, we simulated power curves for all four possible combinations of interval types and degree of shrinkage. In the top panel of Figure 6 we see that mild shrinkage has negligible impact on the Type I and Type II error rates. The primary feature in the top panel is that SGPVs with an interval null spend power to reduce the Type I error rate. In the bottom panel of the same figure, the degree of shrinkage is exceedingly large, much larger than one would typically use in an actual analysis. Interestingly, even in this case, there is a real separation of the power curves when comparing regularized and non-regularized approaches. Given the extreme nature of the shrinkage, it is surprising that the differences are not larger.

FIGURE 6

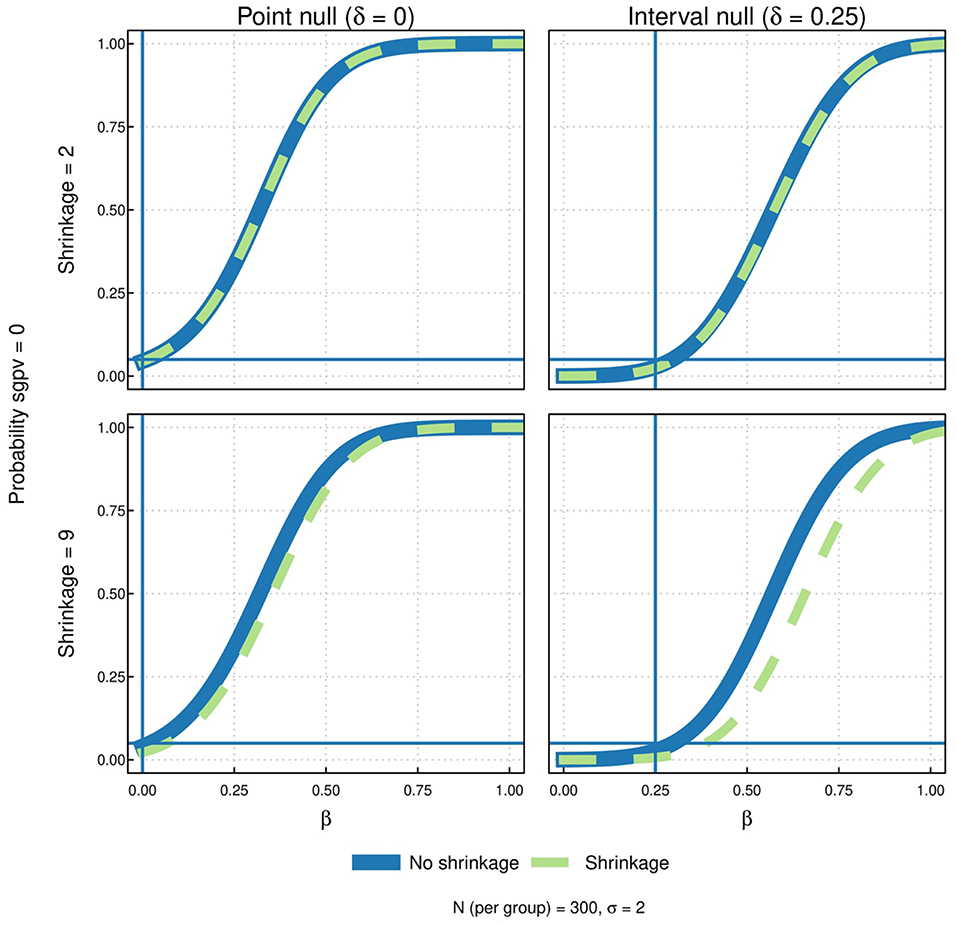
Figure 6. Results of the simulation study with the following factors: degree of shrinkage [mild vs. none (row 1) and extreme vs. none (row 2)] and type of null [point (column 1) and interval (column 2)]. In each of the four graphs, the probability that the SGPV = 0 is plotted as a function of beta for both the shrinkage and no shrinkage intervals. Comparing column 1 to column 2, the estimated probability curves cross 0.05 at the boundary of the respective nulls (0 for the point null and 0.25 for the interval null). For mild shrinkage (row 1), there is little noticeable difference between probability curve estimates with or without shrinkage (solid blue vs. dashed green). More noticeable differences between shrinkage and no shrinkage occur with more extreme shrinkage (row 2).

Simulation 3: MSE, Interval Null, and Shrinkage

This final simulation reinforces that the MSE benefits of regularization are retained when SGPV is used as a summary measure. Because MSE is a function of the estimated and true β–values which are not altered when calculating or interpreting the SGPV—MSE will not change when a null interval is used for inference. In the simulation results below (Figure 7), the red line represents the difference between the MSE of a regularized model with an interval null compared to the same regularized model with a point null. As is clear from the plot, this difference in MSE is 0. As a point of reference, the black line shows that in this simulation setting, regularization does in fact lower MSE. This shows that using an interval null also yields the typical benefits seen with standard shrinkage estimators of improved prediction via lower MSE.

FIGURE 7

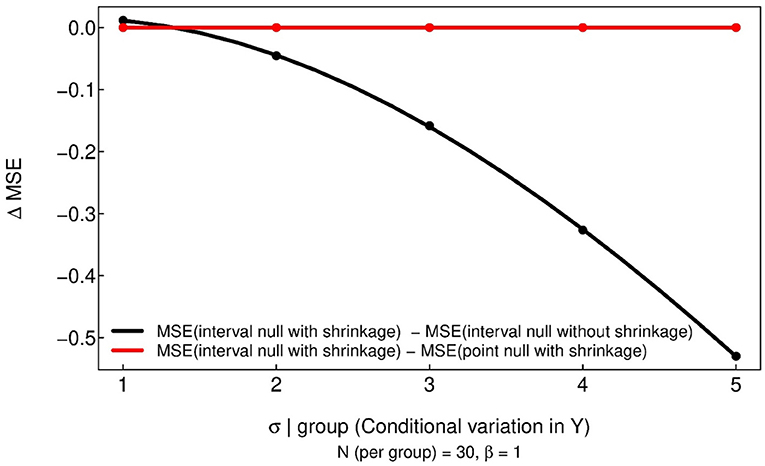
Figure 7. Simulation results showing that MSE is not altered when using a point null or a region null (red line). The black line is a reference to show the change in MSE when incorporating shrinkage.

Discussion

The SGPV promotes good scientific practice by encouraging researchers to a priori establish what are, and what are not, scientifically meaningful effects. By establishing the null interval at the start of the analysis, the SGPV can provide a summary of how consistent the data are with the null hypothesis or how consistent the data are with meaningful effects. Better Type I Error rates are achieved at the expense of power in the region outside the null interval. Because regularized models are now widely used, it is important to understand how the SGPV operates when applied to intervals impacted by shrinkage. Based on our simulations, SPGVs based on credible intervals retain their desirable Type I/Type II error rate tradeoff at a modest cost in power. Likewise, the same gains in MSE observed with Bayesian estimation are observed when a null interval and the SGPV are used. Consequently, SPGVs may be applied to Bayesian analyses (where classical p-values are currently not available) and to regularized models that exhibit some degree of natural and smooth shrinkage.

The simulation study in this manuscript focuses on shrinkage intervals constructed using a prior and a Bayesian posterior distribution. Because regularized likelihood and regularized machine learning methods can often be couched as special cases of Bayesian modeling, the focus on shrinkage-by-prior is a natural place to start. We note, however, that in focusing on the Bayesian approach in the simulations, we are really focusing on the subset of priors that induce shrinkage in the natural way; overly informative priors or priors which lead to pathological shrinkage are outside the scope of our investigation.

Statements regarding Type I or Type II error rates and Bayesian credible intervals may seem odd to some readers because some authors do not consider p-values or null hypothesis testing to fit within the Bayesian paradigm. Likewise, it can seem odd to estimate a posterior distribution in order to calculate a second-generation p-value. However, this highlights an important point: the SGPV is not a probability. It is a summary measure—applicable to any inferential framework—for indicating the degree of conclusiveness of the analysis. An SGPV of 0 indicates a conclusive difference, a value near 1 indicates a conclusive similarity, and values between 0 and 1 indicate differing degrees of inconclusive results with a value at 0.5 indicating a maximum degree of inconclusiveness.

One might wonder why this summary measure is called a second-generation p-value if it is not a probability. It is our contention that the practical, every-day use of traditional p-values is as a marker for results deserving of increased scrutiny. That is, the traditional p-value and 0.05 threshold is used to answer the question: “Should I dive deeper into this hypothesis?” As many have noted, the traditional p-value is not a good filter for this in practice. The SGPV, in contrast, is designed to filter results that deserve greater attention vs. results that need more data and are currently inconclusive. So, the SGPV is a second generation of the p-value as it is used in practice; it is not an extension of the probability calculation for a null hypothesis test.

Evaluating the operating characteristics of the SGPV is routine step that is intended to be paradigm-agnostic. It is common these days to see a statistical approach, regardless of paradigm of origin, evaluated in this long-run sense. The Food and Drug Administration (FDA) which approves drugs and medical devices for commercial use in the United States requires evaluation of operating characteristics as part of drug and device applications even when the submitted data analysis is a set of posterior probabilities from a Bayesian analysis (or set of likelihood ratios or p-values). In “Guidance for the Use of Bayesian Statistics in Medical Device Clinical Trials¹” (Young, 2004), the FDA recommends and provides guidance for computing Type I and Type II Error rates regardless of the analysis paradigm. Note that even when prominent Bayesian statisticians propose a new Bayesian clinical trial design, as with the “Bayesian decision-theoretic group sequential clinical trial design” (Lewis et al., 2007) or with “Phase II oncology clinical trials” (Berry et al., 2013), the analysis is calibrated so that the Type I Error rate is controlled. The SGPV is a tool for deciding when an analysis shows a conclusive difference, a conclusive similarity, or is not conclusive. As such, it is appropriate to explore the operating characteristics of this tool even if the interval is calculated from a Bayesian posterior or from a statistical learning method with regularization.

The calculation of the SGPV is simple and intuitive. Specifying the null region, however, is challenging. Ideally, the null region should reflect subject matter expertise of effect sizes that are not meaningful. Agreement among subject-matter experts on what the null region should be is potentially hard to achieve. Further, some research areas may be so new, there is no prior information to guide the decision. Some users may want to punt on deciding what the null region should be and may seek a “data-driven null region.” Unfortunately, there is no such thing, at least not with data from the same dataset that one intends to analyze. The challenge of specifying a null region is, in our opinion, the biggest obstacle and limitation of the SGPV. However, it is the step that anchors the statistical analysis to the scientific context; it is the step that pushes that research team to decide what it means to be similar and what it means to be different for their particular research question, all prior to the analysis. These questions are exactly where discussion should focus; and they are precisely the questions that subject matter experts are best equipped to debate. Specifying the null region is a challenging task, but it is a scientific one worth the effort it requires.

There is still a lot to learn about the SGPV and a number of potentially fruitful areas of investigation or expansion. One outstanding question, for example, is what impact cross-validation of shrinkage parameters may have on the operating characteristics of the SGPV when used with intervals constructed with machine learning methods. Dezeure et al. (2015) show that this impact can be real. Another possible extension of particular interest to those analysts that use Bayesian methods is to expand the meaning of the null region. The null region as currently used with the SGPV treats all values in the region as equally unimportant. One may want to incorporate the idea that some values in the null region are more null than others. One approach would be to represent the relative “nullness” of the values by borrowing structure from mathematical distributions, similar in spirit to the likelihood. For example, the simple null region of the current SGPV can be described as a uniform null region in reference to the uniform distribution. A null region in which the relative “nullness” is maximized at zero but then fades to the interval endpoints might be represented with a beta distribution. This is an intriguing next step of research.

The SGPV is intended to be a method-agnostic indicator of when a prespecified evidential benchmark is achieved. Assessing the overlap of the null and uncertainty interval is easily mapped back to classical measures of statistical evidence like the likelihood ratio. For example, a SGPV that is based on a 1/k likelihood support interval is set to zero whenever the likelihood ratio for the MLE vs. the nearest hypothesis in the null interval is >k [most 95% CIs can be mapped to a 1/6.83 SI, see (Blume, 2002)]. A similar condition can be formulated for Bayes factors when SGPVs are based on credible intervals. In this sense, the SGPV just indicates when the observed evidence is sufficiently strong against the hypotheses in the interval null hypothesis.

Conclusions

The second-generation p-value is an intuitive summary of analysis results that is based on an uncertainty interval about the parameter of interest and a pre-specified null region. Previous publications on SGPVs focused on 95% confidence intervals and 1/8 likelihood support intervals. In the current manuscript, we explored the performance of SGPVs based on uncertainty intervals from a regularized model, specifically Bayesian credible intervals. While we considered intervals generated with Bayes regression, this framework is readily generalizable to many different types of regularization schemes. We saw nearly the same trade-off of Type I and Type II Error rates in SGPVs based on Bayesian credible intervals as SGPVs based on classical confidence intervals. Our results indicate that SPGVs based on regularized intervals retain this desirable error rate trade-off, at a slight loss in power, while benefiting from the bias-variance tradeoff imparted by regularization. Consequently, the SPGV is a meaningful summary of study results, even when applied in a Bayesian framework or other contexts that incorporate regularization.

Data Availability Statement

Publicly available datasets were analyzed in this study. These data can be found here: http://whitlockschluter.zoology.ubc.ca/wp-content/data/chapter12/chap12e3HornedLizards.csv.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnote

1. ^Guidance for the Use of Bayesian Statistics in Medical Device Clinical Trials. Available online at: https://www.fda.gov/regulatory-information/search-fda-guidance-documents/guidance-use-bayesian-statistics-medical-device-clinical-trials#7

References

Berger, R. L., and Hsu, J. C. (1996). Bioequivalence trials, intersection-union tests and equivalence confidence sets. Stat. Sci. 11, 283–319. doi: 10.1214/ss/1032280304

CrossRef Full Text | Google Scholar

Berry, S. M., Broglio, K. R., Groshen, S, and Berry, DA. (2013). Bayesian hierarchical modeling of patient subpopulations: efficient designs of Phase II oncology clinical trials. Clin. Trials 10, 720–734. doi: 10.1177/1740774513497539

PubMed Abstract | CrossRef Full Text | Google Scholar

Blume, J. D. (2002). Likelihood methods for measuring statistical evidence. Stat. Med. 21, 2563–2599. doi: 10.1002/sim.1216

PubMed Abstract | CrossRef Full Text | Google Scholar

Blume, J. D., D'Agostino McGowan, L., Dupont, W. D., and Greevy, R. A. Jr. (2018). Second-generation p-values: improved rigor, reproducibility, & transparency in statistical analyses. PLoS ONE 13:e0188299. doi: 10.1371/journal.pone.0188299

PubMed Abstract | CrossRef Full Text | Google Scholar

Blume, J. D., Greevy, R. A. Jr., Welty, V. F., Smith, J. R., and Dupont, W. D. (2019). An introduction to second-generation p-values. Am. Stat. 73, 157–167. doi: 10.1080/00031305.2018.1537893

CrossRef Full Text | Google Scholar

Cortes, C., and Vapnik, V. N. (1995). Support-vector networks. Mach. Learn. 20, 273–297. doi: 10.1007/BF00994018

CrossRef Full Text | Google Scholar

Dezeure, R., Bühlmann, P., Meier, L., and Meinshausen, N. (2015). High-dimensional inference: confidence intervals, p-values and R-software Hdi. Stat. Sci. 30, 533–558. doi: 10.1214/15-STS527

CrossRef Full Text | Google Scholar

Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D., Vehtari, A., and Rubin, D. B. (2013). Bayesian Data Analysis, 3rd Edn. Boca Raton, FL: Chapman & Hall/CRC.

Google Scholar

Gelman, A., Jakulin, A., Pittau, M. G., and Su, Y. S. (2008). A weakly informative default prior distribution for logistic and other regression models. Ann. Appl. Stat. 2, 1360–1383. doi: 10.1214/08-AOAS191

CrossRef Full Text | Google Scholar

Kruschke, J. (2014). Doing Bayesian Data Analysis, Second Edition: A Tutorial With R, JAGS, and Stan, 2nd Edn. Boston, MA: Academic Press.

Kruschke, J., and Liddell, T. M. (2017). The Bayesian new statistics: hypothesis testing, estimation, meta-analysis, and power analysis from a Bayesian perspective. Psychon. Bull. Rev. 25, 178–206. doi: 10.3758/s13423-016-1221-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Lewis, R. J., Lipsky, A. M., and Berry, D. A. (2007). Bayesian decision-theoretic group sequential clinical trial design based on a quadratic loss function: a frequentist evaluation. Clin. Trials 4, 5–14. doi: 10.1177/1740774506075764

PubMed Abstract | CrossRef Full Text | Google Scholar

Perlman, M. D., and Wu, L. (1999). The Emperor's new tests. Stat. Sci. 14, 355–369. doi: 10.1214/ss/1009212517

CrossRef Full Text | Google Scholar

Schuirmann, D. J. (1987). A comparison of the two one-sided tests procedure and the power approach for assessing the equivalence of average bioavailability. J. Pharm. Biopharm. 15, 657–680. doi: 10.1007/BF01068419

PubMed Abstract | CrossRef Full Text | Google Scholar

Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B 58, 267–288. doi: 10.1111/j.2517-6161.1996.tb02080.x

CrossRef Full Text | Google Scholar

Wang, S. J., and Blume, J. D. (2011). An evidential approach to noninferiority clinical trials. Pharm. Stat. 10, 440–447. doi: 10.1002/pst.513

PubMed Abstract | CrossRef Full Text | Google Scholar

Wasserstein, R. L., and Lazar, N. A. (2016). The ASA's Statement on p-values: context, process, and purpose. Am. Stat. 70, 129–133. doi: 10.1080/00031305.2016.1154108

CrossRef Full Text | Google Scholar

Whitlock, M. C., and Schluter, D. (2015). The Analysis of Biological Data. New York, NY: W.H. Freeman and Company.

Google Scholar

Young, K. V. (2004). How the horned lizard got its horns. Science 304, 65–65. doi: 10.1126/science.1094790

PubMed Abstract | CrossRef Full Text | Google Scholar

Zou, H., and Hastie, T. (2005). Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B 67, 301–320. doi: 10.1111/j.1467-9868.2005.00503.x

CrossRef Full Text | Google Scholar