Ignoring Fossil Age Uncertainty Leads to Inaccurate Topology and Divergence Time Estimates in Time Calibrated Tree Inference

1. Introduction

Estimating phylogenetic relationships and divergence times among species are key components of piecing together evolutionary and geological history. Approaches to building time trees in paleobiology have traditionally involved estimating the topology and branch lengths scaled to time in separate, sequential analyses (Bapst and Hopkins, 2017). Bayesian phylogenetic models make it possible to estimate these parameters in combination. An advantage of this joint inference is that temporal evidence can be used to inform the tree topology, in combination with character data, and the posterior output will better reflect the uncertainty associated with the results (Ronquist et al., 2012).

Statistically coherent models for incorporating extinct species into time calibrated tree inference only recently became available. In particular, the fossilized birth-death (FBD) process provides a joint description of the diversification and fossil sampling processes (Stadler, 2010; Heath et al., 2014). Under this model, extinct dated samples are considered as part of the tree, therefore contributing temporal information, and their phylogenetic position can be recovered, either as terminal branches (tips) or ancestral to other samples (sampled ancestors). This modeling framework has created enormous potential for incorporating more paleontological data into divergence time analyses and we are only just beginning to explore the impact and existing limitations of this approach.

Analyses using the FBD process can be divided into two categories depending on the amount of data available. The first category uses topological constraints which assign fossils to specific clades (Gavryushkina et al., 2014; Heath et al., 2014). In these analyses the position of the fossils in the tree is thus not part of the inference. The second category are so-called “total-evidence” approaches, which use morphological data to place the fossils on the tree as part of the inference (Ronquist et al., 2012; Zhang et al., 2015; Gavryushkina et al., 2017). Total-evidence analyses better reflect the uncertainty associated with fossil placement than analyses that fix the position of fossils and thus may lead to more accurate results, particularly in clades where the fossil taxonomy is contested. This approach can also be applied to entirely extinct groups, for which only morphological and no molecular data are available (Lee et al., 2014; Slater, 2015; Wright, 2017b; Wright and Toom, 2017; Paterson et al., 2019).

Simulations play an important role in testing the limits of tree inference methods. Different taxonomic groups and time periods are associated with different issues that contribute to challenges inferring topology and time, and a growing number of studies have sought to explore the performance of phylogenetic inference under the FBD model in different scenarios. Several studies have focused on specific model violations, including the impact of non-uniform sampling among living taxa (Zhang et al., 2015; Matschiner, 2019), non-uniform sampling of fossil taxa over time (Heath et al., 2014; Zhang et al., 2015; O'Reilly and Donoghue, 2019) or across lineages (Heath et al., 2014; Matschiner et al., 2017), as well as the effect of ignoring sampled ancestors (Gavryushkina et al., 2014). A clear consensus that emerges from this work is that higher sampling rates of taxa and characters result in better estimates of time and (when co-estimated) topology, provided model violation is not extreme. In an extensive set of simulations, Luo et al. (2019) examined the performance of total-evidence inference under the FBD model. This work indicated that a large degree of uncertainty is anticipated to be associated with the placement of extinct samples, for which only morphology is available, and that fossil sampling may ultimately outweigh the significance of other issues encountered in dating analyses, including character sampling and among-lineage rate variation.

Barido-Sottani et al. (2019a) focused on one particular aspect of the fossil record, namely the uncertainty associated with the age assigned to each fossil sample. As the age of fossils is established in reference to the geological record, fossil samples are not dated to a single numerical value but rather to an interval of time; this is referred to hereafter as the “age range” of the sample. This uncertainty can be handled in FBD analyses by sampling fossil ages as part of the inference (Drummond and Stadler, 2016), but many studies in the existing literature chose instead to fix fossil ages to a single value, usually the midpoint of the age range (e.g., Larabee et al., 2016) or an age sampled uniformly at random inside the range (e.g., Grimm et al., 2015). Barido-Sottani et al. (2019a) tested these different approaches of handling fossil age uncertainty in analyses using topological constraints to place fossils and found that fixing the fossil ages to incorrect values led to important errors in divergence times estimates. Here, we extend the Barido-Sottani et al. (2019a) study to time calibrated tree inference using morphological data only. Using simulated datasets, we explore the impact of character and taxon sampling, approaches to handling fossil age uncertainty, and clock model priors on estimates of topology and divergence times. We also compare our results to those obtained using temporally unconstrained (i.e., non-time calibrated) Bayesian tree inference. Finally, we apply the FBD model and several different methods for handing fossil age uncertainty to an empirical dataset that is typical of those available for Paleozoic marine invertebrates.

2. Methods

2.1. Simulated Datasets

The design of our simulation study is broadly based on features that are typical for datasets of Paleozoic marine invertebrates. In order to select parameter values that would reflect the size and scale of these datasets (in terms of taxon and character sampling) we first tallied 81 studies of Paleozoic invertebrate groups, which included trilobites (67%), brachiopods (18%), and crinoids (15%). The majority of these studies used species as operational taxonomic units (OTUs) (77%), while the rest coded genera (23%). The results are summarized in Figure S1 and Appendix Table 1. The typical size of these datasets was 25–35 taxa, at both taxonomic levels (mean for species OTUs = 25, mean for genus OTUs = 32), with a maximum of 85. For 63 of these studies we were able to estimate approximate time spans in millions of years (Myr). Across all studies, the typical time span was 50 Myr, with 85% <75 Myr. However, there was a large difference between taxonomic scales: the mean total time span for studies using species OTUs was 37 Myr, while the mean total time span for studies using genus OTU studies was 88 Myr. Interestingly, no relationship was observed between the number of taxa in the study and the total time span. Intuitively, we might expect sampling taxa over longer intervals to lead to datasets containing larger numbers of taxa, i.e., because the number of opportunities for sampling increases. However, it is not clear whether this observation reflects a genuine lack of correlation between time and the number of taxa sampled, or the fact that studies chose not to include all available taxa in phylogenetic studies for practical reasons, e.g., due to the intense effort required to collect morphological characters. The average number of characters was 35 for both species and genus levels, with an average of 60% binary characters.

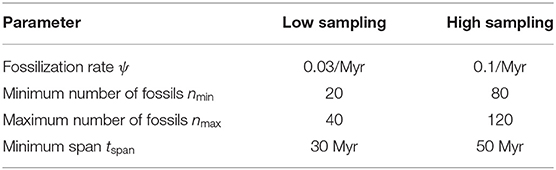
Based on these empirical data characteristics, we established two main parameter settings that determined the number of fossils sampled during simulation, one based on the average size of empirical datasets (referred to as low sampling) and the other based on a more optimistic sampling scenario (referred to as high sampling). We also explored the effect of morphological matrix length (30, 300, or 3,000 characters), where the lowest value was based on our sample of empirical studies and the higher values represented more optimistic scenarios. The optimistic scenarios are more similar to previous simulation studies that have focused on morphology based tree inference (Wright and Hillis, 2014; O'Reilly and Donoghue, 2017; Puttick et al., 2017). Note that a priori we do not expect to recover good results under the low sampling scenario and with the small number of characters typical of empirical datasets. The more optimistic scenarios were necessarily included to gain robust insights into the behavior of our inference framework. For each set of parameter values we simulated 50 replicates.

2.1.1. Simulation of Phylogenies and Fossil Samples

Trees were simulated under a constant rate birth-death process with speciation rate λ = 0.06/Myr and extinction rate μ = 0.045/Myr, using the R package TreeSim (Stadler, 2011). These estimates were taken from an empirical study of Paleozoic crinoids (Wright, 2017a), which is the only one of the 81 datasets evaluated that has been the subject of an analysis using the FBD model, and for which empirical estimates of these parameters were readily available. The birth-death simulation was allowed to run for 130 Myr, which approximates the temporal duration (Ordovician to Devonian) of the crinoid clade of Wright (2017a).

Fossils were sampled on the complete phylogeny following a Poisson process with a constant fossilization rate ψ, using the R package FossilSim (Barido-Sottani et al., 2019b). We rejected phylogenies with less than the minimum number n_min or more than the maximum number n_max of sampled fossils, and phylogenies for which the fossils spanned less than the minimum time span t_span Myr. Values for ψ, n_min, n_max, and t_span depended on the fossil sampling setting (high vs. low sampling) and are detailed in Table 1. The average time span of simulated datasets was 111 Myr in the low sampling scenario, and 123 Myr in the high sampling scenario, consistent with our assumption of constant fossilization rate over the entire simulated period.

TABLE 1

Table 1. Parameters values for low and high fossil sampling settings.

2.1.2. Simulation of Fossil Age Uncertainty

Fossil age uncertainty was simulated using the procedure described in Barido-Sottani et al. (2019a). Realistic age ranges for simulated data are based on empirical ranges of fossil crinoids obtained from the Paleobiology Database (PBDB) using the following parameters: time intervals = from Ordovician to Devonian, scientific name = Crinoidea (download date: 07/03/2018). Each simulated fossil sample was assigned to an interval based on its true age. If a simulated fossil age could be assigned to multiple intervals, a single interval was selected at random by weighting all possible intervals by their frequency of appearance in the PBDB data. If no intervals appeared in the PBDB data for a simulated fossil age, a random interval containing the true age was drawn, with a length equal to the average length of all intervals in the PBDB data, i.e., 12 Myr. Thus, the simulated interval for each fossil always included the correct age of the fossil.

2.1.3. Simulation of Morphological Data

As the majority of the characters used in our sample of empirical studies were binary and the number of character states was not the focus of our study, we chose to simulate binary characters only. These characters were simulated for each fossil using the function sim.char from the R package geiger (Pennell et al., 2014). A strict clock model was used and the rate of character state change was set to 0.033/Myr, based on the rate obtained by Wright (2017a). For both fossil sampling settings, character matrices of length 30, 300, and 3,000 were simulated. We did not filter the resulting matrices to remove uninformative characters. However, the proportion of uninformative characters was low: 0% for the matrices with 30 characters, 0.07% for the matrices with 300 characters, and 0.04% for the matrices with 3,000 characters.

2.1.4. Bayesian Inference

Markov Chain Monte-Carlo (MCMC) inference using the FBD process is implemented in the Sampled Ancestors package (Gavryushkina et al., 2014) for the software BEAST2 (Bouckaert et al., 2014). We extended this package to be able to use a tree with no extant samples. This extension made no changes to the FBD model or to the likelihood function, and was done simply to allow for sampling fossil ages on a fully extinct tree. This package was used to perform Bayesian phylogenetic inference on the simulated datasets. The fossil ages were handled using five different methods, detailed here and illustrated in Figure 1.

• Correct ages: the fossil ages are fixed to the true ages as simulated.

• Interval ages: the fossil ages are not fixed, but are sampled along with the other parameters within the simulated age range.

• Median ages: the fossil ages are fixed to the midpoint of their simulated age range.

• Random ages: the fossil ages are fixed to an age sampled uniformly at random inside of their simulated age range.

• Symmetric interval ages: the fossil ages are not fixed, but are sampled along with the other parameters. Each fossil age is sampled within a symmetric interval of length 12 Myr (i.e., equal to the average length of all intervals in the PBDB data) around the true age of the fossil. The purpose of this setting was to evaluate whether the position of the interval relative to the true age affected the resulting estimates.

FIGURE 1

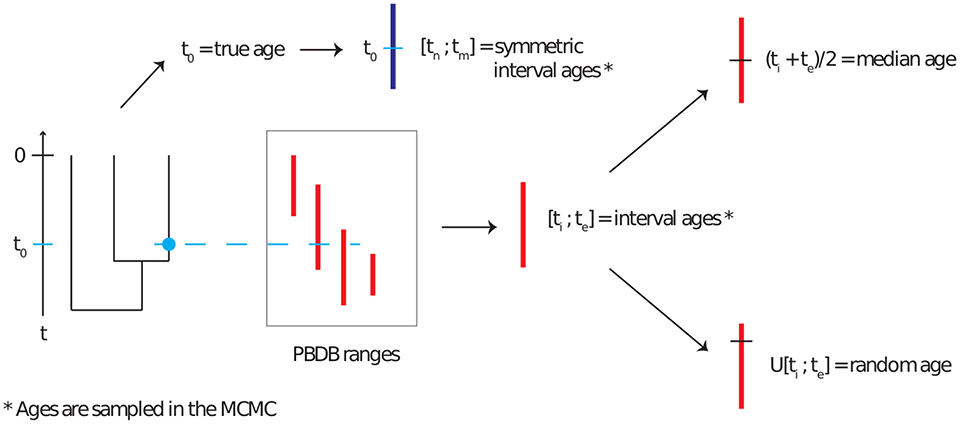
Figure 1. Representation of the age uncertainty simulation process, reproduced from Barido-Sottani et al. (2019a). Phylogenies with fossils are simulated according to a birth-death-fossilization process. The correct age of each fossil is used to draw an age interval for that fossil from the set obtained from PBDB. This age interval is then used as the basis for the median and random age assignment. A symmetric age interval is also drawn from the correct age.

Note that for the interval age methods, we sample trees as in Drummond and Stadler (2016), i.e., we set the probability density of the proposed tree to the FBD probability density if all fossil ages are within their intervals, and 0 otherwise. The effective prior on fossil ages, i.e., the fossil age distribution when using all information excluding sequence data, is thus not a uniform prior, as the FBD model already induces a distribution on fossil ages.

The Lewis Mk model of morphological character evolution was used (Lewis, 2001). The strict clock model was used with three different priors on the clock rate: an unbounded uniform prior, a lognormal prior with median = 0.033/Myr, equal to the true rate [i.e., LogNormal(−3.4, 0.3)] and a lognormal prior with median = 1.220/Myr, different from the true rate [i.e., LogNormal(0.2, 1.25)]. The inference was run for at least 100,000,000 iterations, or until convergence was considered satisfactory, and sampled every 10,000 steps. Convergence was assessed in the software Tracer v. 1.7 (Rambaut et al., 2018) and considered satisfactory if the effective sample sizes were more than 200. Datasets that did not converge after 120 h were excluded (<5% of runs).

Additionally, unconstrained Bayesian phylogenetic inferences were performed on the simulated datasets using the RevBayes framework (Höhna et al., 2016) without including any fossil age information. These inferences were performed on all simulated datasets for both low and high fossil sampling and, with character data simulated under the strict clock model. We used the Lewis Mk model, a uniform prior on the tree topology and an exponential prior on the branch lengths. The mean of the distribution on the branch lengths, which is determined by the rate parameter λ, was estimated using an exponential hyperprior with mean = 1. The use of alternative branch length priors did not impact estimates of tree accuracy. See Supplementary Material Section 3 and Figure S4 for more details. Convergence and MCMC diagnostics were assessed using identical guidelines as those described above.

2.1.5. Assessing Inference Results

We assessed the accuracy of the FBD model parameters by measuring the relative error of the median posterior estimates, where the relative error was defined as the difference between the true value and the estimated value, divided by the true value. The relative error was averaged over all replicates. We also calculated the coverage, i.e., the proportion of analyses in which the true parameter value was included in the 95% highest posterior density (HPD) interval. In order to evaluate the accuracy of the divergence time estimates, we considered nodes defined as the most recent common ancestor (MRCA) of samples t₁ and t₂, for all pairs of samples. This definition allowed us to obtain nodes which were always present in the inferred tree, regardless of the accuracy of the topology. Similarly to the FBD model parameters, we calculated the relative error of the median posterior estimates and the coverage of the divergence times, averaged across all nodes and replicates.

To assess the accuracy of inferred topologies we calculated the mean normalized Robinson-Foulds (RF) distance (Robinson and Foulds, 1981) between simulated trees and tree samples from the posterior distribution. The RF distance only depends on the topology of the trees. The normalized RF distance between two trees with n tips is computed by dividing the RF distance between these trees by the maximum possible RF distance between two trees with n tips, thus scaling the distances between 0 and 1.

The normalized RF distances were calculated using the RF.dist function from the R package phangorn (Schliep, 2010), and averaged over all the trees sampled during the MCMC (ignoring the first 10% of the samples as burn-in), and averaged over all replicates for each parameter combination.

All trees were unrooted prior to calculating the RF distance to facilitate comparison between the time constrained and unconstrained analyses.

2.2. Empirical Dataset

To explore the impact of different approaches to handling stratigraphic age uncertainty on empirical estimates of divergence times, Bayesian phylogenetic inference was performed on a dataset of North American Devonian brachiopod species (Stigall Rode, 2005). This dataset was chosen because, with 18 taxa and 36 characters, it represents the average size of the 81 studies we evaluated (Figure S1). Among datasets of similar size, it also comprised OTUs sampled across geologic stages. The latter criterion is important because at global scales, the geologic time scale is generally coarse enough that closely related species occur within the same geologic stage, and obtaining a finer resolution time scale is not straightforward, or even possible, in many instances (Hopkins et al., 2018).

Fossil occurrences were assigned to geologic stages based on vetted occurrences in the Paleobiology Database and additional literature (Stigall Rode, 2005; Menning et al., 2006). Minimum and maximum ages for stage boundaries were assigned following the International Commission on Stratigraphy 2018 chart (www.stratigraphy.org). Species for which all specimens were recovered from the same geological stage were treated as a single OTU. Three species had specimens which were sampled from more than one stage and were treated as multiple OTUs, corresponding to one OTU for each stage. For these species, the species was constrained to be monophyletic and morphology was included for the oldest specimen only. This approach was taken in order to avoid having multiple specimens associated with the same morphology over long intervals of time, which would represent a strong violation of the Mk model. The analysis used the same model parameterization and priors as the simulated data. The clock rate prior was set to a lognormal distribution [LogNormal(−3.4, 0.3)]. As the true ages of the fossils in this dataset are unknown, we limited our comparison to the median, random, and interval ages in BEAST2, and the unconstrained analysis in RevBayes. To facilitate comparison between constrained and unconstrained topologies, unconstrained trees were rooted using Xystostrophia umbraculum as the outgroup taxon (Stigall Rode, 2005). The FBD analyses were run both excluding and including the outgroup. This choice did not impact the overall results but we note that the inclusion of an outgroup taxon represents a violation of the assumption of uniform taxon sampling throughout the tree.

3. Results

3.1. Simulated Datasets

3.1.1. Impact of the Clock Rate Prior

The use of different clock rate priors had a minor impact on the results. For most parameters, including divergence times, estimates of coverage and relative error were similar or even identical for different clock priors, particularly when character and fossil sampling were both high (Figures S2, S3). The use of different priors on the clock rate also had little impact on the topological accuracy based on RF distances (Figure 2). The largest impact was observed on the clock rate itself. When character and fossil sampling were low, there was less signal in the data to inform this parameter. Running the analysis with an unbounded uniform prior (i.e., from 0 to ∞) on the clock rate in the low sampling scenario produced rate estimates of ≈10³⁰⁷ (i.e., the numerical upper limit of the software) in approximately 20% of replicates, as the posterior followed the prior. Thus, we excluded this condition from Figure S2 (lower panel).

FIGURE 2

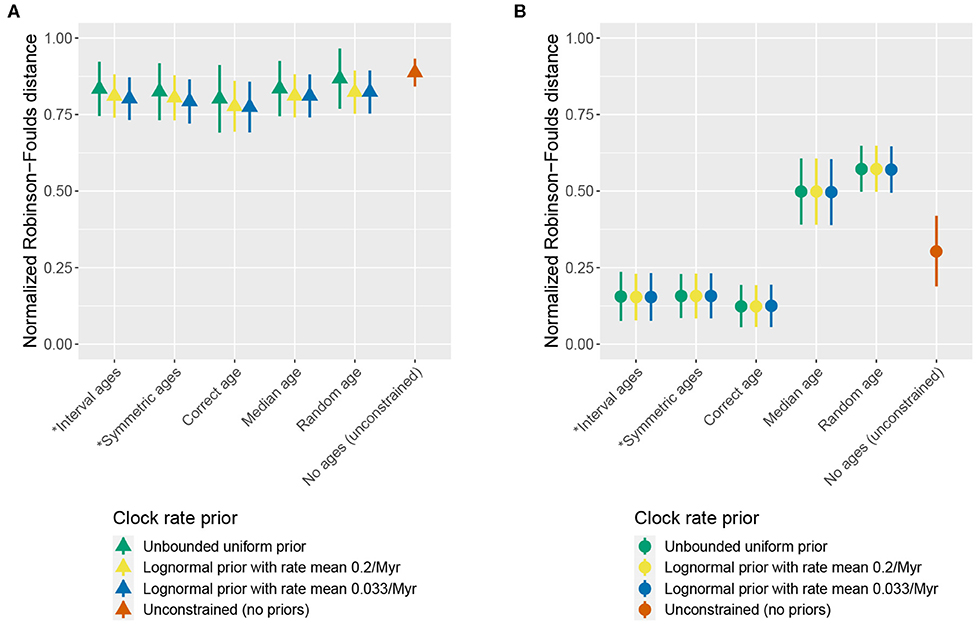
Figure 2. Impact of the clock prior on topology. The mean and standard deviation of the normalized Robinson-Foulds distance between the true simulated tree and trees inferred during MCMC across all replicates are shown for different clock rate priors, different age handling methods, and different fossil sampling settings [low (A) vs. high (B)]. Ages sampled as part of the MCMC are marked by (*). (A) Low fossil sampling and character length 30. (B) High fossil sampling and character length 300.

As the clock rate prior exerted a negligible impact on parameter estimates, for the remainder of the results we focus on describing the output obtained using a lognormal prior on the clock rate with a median that differs from the true rate. This setting best matches a plausible scenario for empirical studies and avoids the issues encountered using the unbounded prior.

3.1.2. The Combined Effects of Stratigraphic Age Uncertainty, Fossil Sampling, and Character Sampling

Figures 3–5 present the results obtained under different character and fossil sampling settings when running the analysis using the lognormal clock rate prior with a median that differs from the true rate. Using symmetric interval ages results in very similar estimates compared to interval ages, showing that the accuracy of the estimates is not affected by the position of the interval relative to the true age of the fossil. Thus, in the following we will refer to these two conditions together.

FIGURE 3

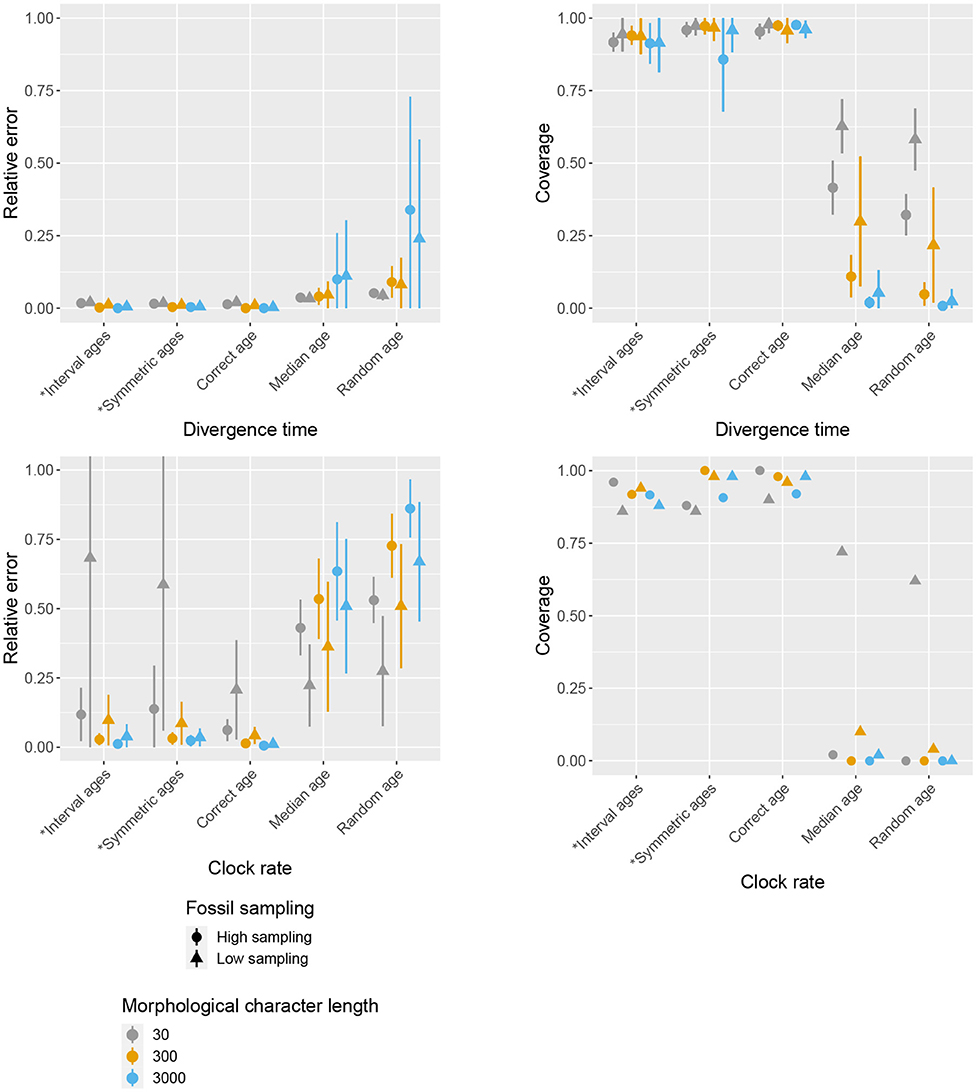
Figure 3. Impact of character and fossil sampling on divergence times and clock rate. The mean and standard deviation of the relative error of median posterior estimates (left), and the mean 95% HPD coverage (right) are shown for different age handling methods, different character sampling, and different fossil sampling settings. Ages sampled as part of the MCMC are marked by (*).

FIGURE 4

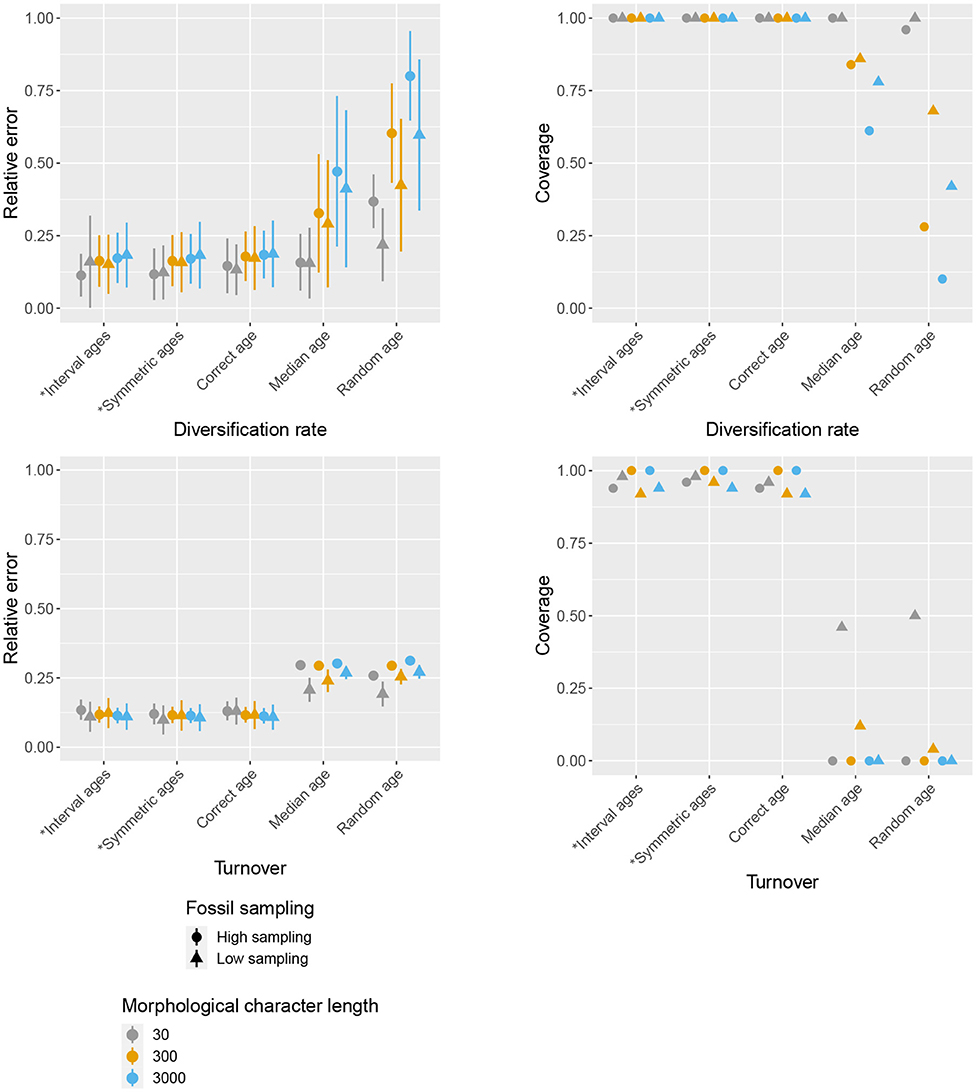
Figure 4. Impact of character and fossil sampling on diversification and turnover. The mean and standard deviation of the relative error of median posterior estimates (left), and the mean 95% HPD coverage (right) are shown for different age handling methods, different character sampling and different fossil sampling settings. Ages sampled as part of the MCMC are marked by (*).

FIGURE 5

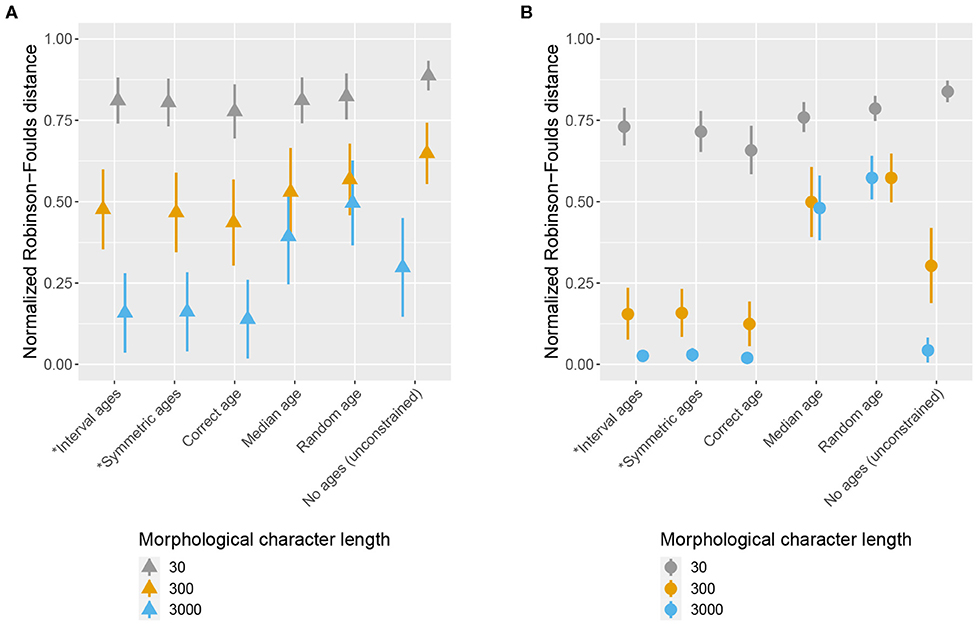
Figure 5. Impact of character and fossil sampling on topology. The mean and standard deviation of the normalized Robinson-Foulds distance between the true simulated tree and trees inferred during MCMC across all replicates are shown for shown for different age handling methods, different character sampling, and different fossil sampling settings [low (A) vs. high (B)]. Ages sampled as part of the MCMC are marked by (*). (A) Low fossil sampling, (B) High fossil sampling.

The accuracy of inferred divergence times, in terms of coverage and relative error, show similar behavior across fossil and character sampling settings (Figure 3). In particular, we obtained high accuracy (i.e., high coverage and low relative error) when the fossil ages were fixed to the correct ages or sampled from within the known interval of uncertainty as part of the MCMC, irrespective of fossil or character sampling. In contrast, we obtained low accuracy when the ages were fixed to incorrect (median or random) ages, but the extent to which the results were worse depended on both fossil and character sampling. In the case of fixed incorrect ages, increased fossil, and character sampling decreased the accuracy of divergence time estimates. A similar trend is observed for the diversification and turnover parameters (Figure 4). The clock rate parameter showed the same trends for coverage (i.e., higher fossil and character sampling lead to lower coverage with median or random fossil ages), but a different trend was recovered for relative error (Figure 3). Specifically, when fossil and character sampling were low, relative error was higher when fossil ages were co-estimated compared to when the ages were fixed to either the correct or incorrect ages. However, coverage was consistently lower with incorrect fossil ages.

The accuracy of inferred trees follow a pattern which is similar overall to the divergence times estimates, across fossil age handling approaches and fossil sampling settings. However, character sampling had a large impact on the magnitude of the differences observed under different age handling and fossil sampling scenarios (Figure 5). In particular, when character sampling was low (n = 30) the inferred trees were relatively far from the true tree, as measured by RF distance, irrespective of fossil age handling approach or fossil sampling parameters. Overall, higher character and fossil sampling both led to increased accuracy (i.e., lower RF distances) across all scenarios, with the best estimates obtained when both character and fossil sampling were high (Figure 5). The positive effects of increased fossil or character sampling were also greater when fossil ages were fixed to the truth or co-estimated, while estimates obtained when fossil ages were fixed to median or random ages remained inaccurate even with high sampling. When fossil and character sampling were both high, using the correct fossil ages or estimating the ages performed much better than using incorrect fossil ages.

Differences in accuracy between time calibrated and unconstrained tree inferences were also linked to variation in character sampling (Figure 2). For low or intermediate character sampling (n = 30 or 300) combined with low fossil sampling, or for low character sampling (n = 30) combined with high fossil sampling, the FBD inference outperformed the unconstrained inference, irrespective of the fossil age handling method. In contrast, for increased character or fossil sampling (n = 3, 000 combined with low fossil sampling and n = 300 or 3, 000 combined with high fossil sampling), the unconstrained inference outperformed the FBD model when fossil ages were fixed to incorrect ages. The FBD model outperformed the unconstrained inference under intermediate sampling scenarios (n = 3, 000 combined with low fossil sampling and n = 300 combined with high fossil sampling) when fossil ages were fixed to the correct ages or co-estimated. When fossil and character sampling were both high the results obtained using both constrained and unconstrained analyses converged on the true tree, provided fossil ages were fixed to correct ages or co-estimated.

The results are summarized in Table 2. Overall, these results indicate that increasing the amount of data does not compensate for the errors introduced by fixing fossil ages to incorrect values. On the contrary, these errors have a much larger impact when using larger datasets, to the point that discarding the fossil ages entirely leads to better estimates of the topology than using incorrect fixed ages.

TABLE 2

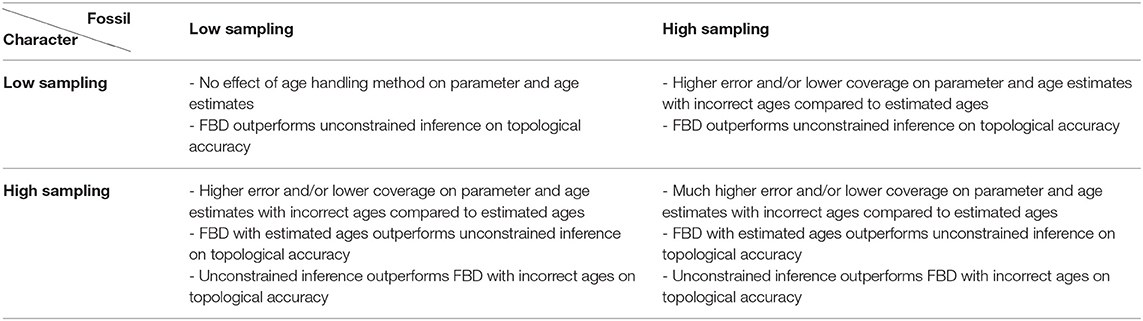
Table 2. Impact of fossil and character sampling on the estimates obtained using the FBD model with different age handling methods vs. unconstrained (i.e., non-clock) inference.

3.2. Empirical Dataset

The Maximum Clade Credibility (MCC) trees obtained with interval ages, median ages, random ages or unconstrained analysis using our empirical brachiopod dataset are shown in Figure 6. The parameter estimates obtained under different age handling methods are shown in Figure S5. All OTUs belonging to the same species were constrained to be monophyletic. However, the posterior support for these nodes may be lower than 1.0. This is due to the fact that the clade [A1(A2)], where A1 is a sampled ancestor of A2, represents a different realization of the FBD process than the clade (A1,A2), and so they are counted separately when calculating the posterior support of nodes using an MCC tree summary method such as TreeAnnotator.

FIGURE 6

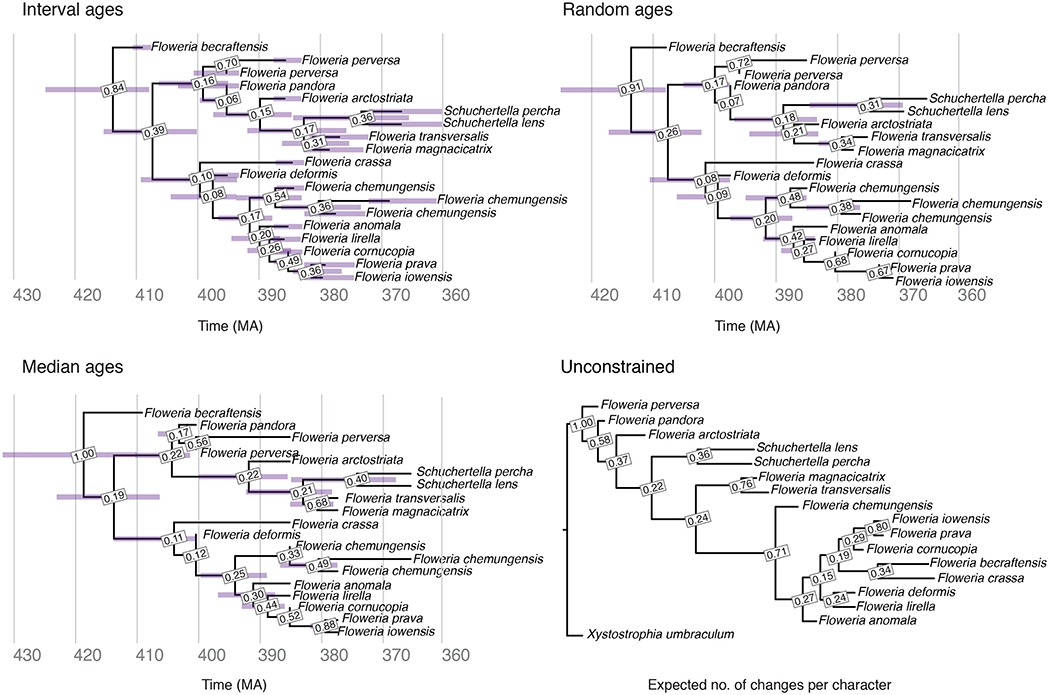
Figure 6. Brachiopod MCC trees obtained using the FBD analysis with interval ages, median ages and random ages, and unconstrained analysis. Posterior support is shown for each node for all trees. Error bars on the FBD trees show the 95% HPD interval for the age of each node, as well as the age of each fossil in the tree with interval ages.

The MCC trees obtained with the three methods for handling fossil ages are all almost identical in terms of their topology, with the exception of the placement of Floweria arctostriata in the random ages tree, and the node support is consistent across all three analyses. The median root ages are slightly different, with the median root age for the interval ages analysis the youngest, but only by a few million years (Figure 6, Figure S2). The MCC for the unconstrained analysis supports some of the same sister taxa with similar support values, and larger subclades are broadly consistent with several exceptions for specific taxa. Particularly notable is the derived placement of Floweria becraftensis in the unconstrained analysis. This species is among the oldest of the clade, and when fossil ages are included in the analysis, it is commonly placed as sister to the rest. Including the outgroup in the FBD analyses did not impact the estimated ingroup topology or divergence times (Figure S6). Overall, these results match the output expected based on our simulations, given the low taxon and character sampling, and fossil age uncertainty associated with this dataset.

4. Discussion

The FBD model can be used to estimate time-calibrated trees under a range of scenarios. Our goal was to examine the impact of stratigraphic age uncertainty in FBD model analyses for datasets that are characteristic of fully extinct clades, such as Paleozoic marine invertebrate groups. Our survey of empirical data confirms that datasets associated with taxonomic groups from this time period typically have a small number of both taxa and phylogenetic characters. The age uncertainty associated with fossil samples from this time period is also relatively high (12 Myr on average, compared with a typical time span of 50 Myr for the full dataset in our example studies). Our results demonstrate the importance of incorporating stratigraphic age uncertainty into phylogenetic dating analyses on these datasets, rather than the popular practice of fixing fossil ages to a value from within the known interval of uncertainty, e.g., using the mean or a random value (Figures 3, 4, Figures S2, S3).

Our results build on the findings of previous work, where it was shown that fixing fossil ages to incorrect values can lead to inaccurate estimates of divergence times under the FBD model when using topological constraints to place the fossils (Barido-Sottani et al., 2019a). This previous study focused on a scenario where the aim was to estimate divergence times among extant species using molecular data. No character data was available for fossil samples but it was assumed that strong prior information was available to constrain the topology. Here, we assumed that the phylogenetic position of fossil samples was unknown and used morphological data to co-estimate topology along with divergence times. The results of our simulations show that in addition to recovering inaccurate divergences times, mishandling fossil age uncertainty can also result in the wrong tree (Figures 2, 5).

We did not examine the impact of non-uniform fossil recovery, though this is known to decrease performance of the FBD model if unaccounted for (Heath et al., 2014; Luo et al., 2019; O'Reilly and Donoghue, 2019). Overall, our simulated datasets were designed to represent a best-case scenario for a fully extinct Paleozoic clade. We anticipate that additional, unaccounted-for model violations, such as non-uniform fossil recovery, would increase the errors in topology and divergence times estimates reported in this study.

Similarly, we did not examine the impact of morphological model violations such as rate heterogeneity among characters or the effects of non-uniform missing character data. A recent study suggested that even large deviations from the true model may have limited impact on divergence time estimates using total-evidence dating under the uniform tree model (Klopfstein et al., 2019). However, none of their simulation scenarios excluded molecular data and thus these findings may not be applicable to fully extinct clades. That said, the overall number of phylogenetic characters may be more of a concern for extinct clades, given the large degree of uncertainty associated with small matrices.

Small character matrices can be due to low taxon sampling, low character sampling, or both. The effect of both has been examined in previous studies. For example, simulations focused on unconstrained (i.e., non time-calibrated) Bayesian inference have shown that small morphological matrices (e.g., 100 characters or less) will result in highly uncertain trees (O'Reilly and Donoghue, 2017; Puttick et al., 2017). Similarly, several simulation studies have demonstrated the importance of having sufficient fossil sampling in order to recover reliable estimates of divergence times using the FBD model (Heath et al., 2014; O'Reilly and Donoghue, 2019). Luo et al. (2019) examined the combined effects of fossil and character sampling on total-evidence estimates of time and topology, including a scenario that used morphological data only. Similar to our findings, their results show that increasing both the number of fossil samples and morphological characters leads to better estimates of time and topology, in terms of accuracy and precision. They also compared the use of fixed vs. co-estimated fossil ages, where the age of fossils were fixed to the truth or ages were estimated from within the known interval of uncertainty. They found no strong differences in the estimated node ages when co-estimating fossil ages, which is coherent with our simulation scenarios, in which we observe very little difference in accuracy when comparing true vs. co-estimated fossil ages.

Our simulations also show that the inclusion of fossil age information can improve the inferred topology regardless of the size of the matrix, if fossil age uncertainty is handled appropriately (Figures 2, 5). On the other hand, excluding age information is preferable to using incorrect fossil ages even when using large morphological matrices. Thus, stratigraphic age uncertainty must be taken into account in order to fully benefit from the inclusion of fossil sampling times in the analysis. Note that we focus on the impact of stratigraphic age uncertainty, and not any uncertainty associated with the total duration over which a species is observed in the fossil record—that is, the stratigraphic range of a species (Hopkins et al., 2018). Different approaches to handling stratigraphic range durations have been shown recently to introduce errors into phylogenetic dating using the uniform tree model (Püschel et al., 2020). This type of data may be more appropriately modeled using the FBD range process (Stadler et al., 2018). However, we emphasize that the start and end of species ranges will also be associated with fossil age uncertainty, which will be essential to consider, regardless of the tree model (see also O'Reilly et al., 2015).

Assuming that fossil age uncertainty is handled appropriately, our results based on simulated and empirical data indicate that the priority for improving topology and divergence times should be to increase matrix size. However, some clades are naturally small or rare. For these clades, even with complete taxon sampling, the size of the dataset will remain small. The best course of action then may be to increase the taxonomic scope of the study and to sample more broadly. In the case of fossil clades, small numbers of characters may reflect the paucity of morphological trait data available from some groups whose record is characterized by exoskeletal or shell elements exhibiting minimal morphological variation. However, small matrix size might also reflect the historical circumstances in which these data were generated: many matrices surveyed (Appendix S1) were constructed for parsimony analysis where the focus was on the selection of phylogenetically informative characters and not necessarily intended to represent an exhaustive survey of the preserved variation. Moreover, some previous studies excluded a subset of characters from consideration because of a priori concerns about homoplasy (Guensburg and Sprinkle, 2003), and therefore only sampled characters they considered relevant or taxonomically significant. In this regard, it is conceivable that many published matrices may be expanded by a resurvey of the taxa of interest.

In addition, continuous trait data could provide an additional source of morphological information to complement matrices of discrete characters. Models of continuous trait evolution can be used to infer topology (Parins-Fukuchi, 2017) and divergence times (Alvarez-Carretero et al., 2019). Continuous data has also been shown to capture higher phylogenetic signal compared to discrete characters and can result in more accurate trees (Parins-Fukuchi, 2018). It is worth noting that >30% of the characters in our empirical example using brachiopods are continuous characters broken down into discrete states. If the process of discretization results in a loss of phylogenetic information, then tree inference and divergence time estimation could potentially be improved by modeling discrete and continuous characters separately.

We note that previous simulations examining the performance of both unconstrained vs. time calibrated Bayesian phylogenetic inference tend to use a minimum of 100 characters, which is >3 times the size of datasets available for many fossil invertebrate groups. Matrices of only 20–30 characters, which are widely used in the literature, may contain too much uncertainty for other methodological choices to matter. Thus, we must be realistic about the degree of uncertainty expected when the number of phylogenetic characters sampled is low. All approaches to constructing summary trees are problematic when there is a lot of uncertainty in the posterior and all summary trees should be interpreted with caution (O'Reilly and Donoghue, 2017). In conclusion, we show that as more phylogenetically informative data become available, fixing the fossil ages to incorrect values can lead to important errors. Sampling fossil ages as part of the inference recovers estimates similar to those obtained when fixing the ages to the correct values. Consequently, we recommend incorporating stratigraphic age uncertainty when conducting analyses using the FBD process.

Data Availability Statement

The extended SA package is available on GitHub, https://github.com/CompEvol/sampled-ancestors and via the BEAST2 package manager. The R scripts used to simulate and analyse the data, as well as the configuration files used to run BEAST2 and RevBayes, are available on Zenodo, https://doi.org/10.5281/zenodo.3825626.

Author Contributions

JB-S and NT implemented the study, ran the simulations, and analyzed the results. MH and DW assembled the empirical datasets and analyzed the empirical results. TS provided feedback on the study design and results. RW designed the study and interpreted the results. All authors contributed to writing the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This is Paleobiology Database official publication #373. JB-S was supported by funds from the National Science Foundation (US), grant DBI-1759909. DW acknowledges support from the Gerstner Scholars Fellowship and the Gerstner Family Foundation, the Lerner-Gray Fund for Marine Research, and the Richard Gilder Graduate School, American Museum of Natural History, as well as a Norman Newell Early Career Grant from the Paleontological Society. RW was funded by the ETH Zürich Postdoctoral Fellowship and Marie Curie Actions for People COFUND programme.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2020.00183/full#supplementary-material

References

Alvarez-Carretero, S., Goswami, A., Yang, Z., and Dos Reis, M. (2019). Bayesian estimation of species divergence times using correlated quantitative characters. Syst. Biol. 68, 967–986. doi: 10.1093/sysbio/syz015

PubMed Abstract | CrossRef Full Text | Google Scholar

Bapst, D. W., and Hopkins, M. (2017). Comparing cal3 and other a posteriori time-scaling approaches in a case study with the pterocephaliid trilobites. Paleobiology 43, 49–67. doi: 10.1017/pab.2016.34

CrossRef Full Text | Google Scholar

Barido-Sottani, J., Aguirre-Fernández, G., Hopkins, M. H., Stadler, T., and Warnock, R. (2019a). Ignoring stratigraphic age uncertainty leads to erroneous estimates of species divergence times under the fossilized birth-death process. Proc. R. Soc. Lond. B Biol. Sci. 286:20190685. doi: 10.1098/rspb.2019.0685

PubMed Abstract | CrossRef Full Text | Google Scholar

Barido-Sottani, J., Pett, W., O'Reilly, J. E., and Warnock, R. C. (2019b). Fossilsim: an r package for simulating fossil occurrence data under mechanistic models of preservation and recovery. Methods Ecol. Evol. 10, 835–840. doi: 10.1111/2041-210X.13170

CrossRef Full Text | Google Scholar

Bouckaert, R., Heled, J., Kühnert, D., Vaughan, T., Wu, C.-H., Xie, D., et al. (2014). Beast 2: A software platform for Bayesian evolutionary analysis. PLoS Comput. Biol. 10:e1003537. doi: 10.1371/journal.pcbi.1003537

PubMed Abstract | CrossRef Full Text | Google Scholar

Drummond, A. J., and Stadler, T. (2016). Bayesian phylogenetic estimation of fossil ages. Philos. Trans. R. Soc. B Biol. Sci. 371:20150129. doi: 10.1098/rstb.2015.0129

PubMed Abstract | CrossRef Full Text | Google Scholar

Gavryushkina, A., Heath, T. A., Ksepka, D. T., Stadler, T., Welch, D., and Drummond, A. J. (2017). Bayesian total-evidence dating reveals the recent crown radiation of penguins. Syst. Biol. 66, 57–73. doi: 10.1093/sysbio/syw060

PubMed Abstract | CrossRef Full Text | Google Scholar

Gavryushkina, A., Welch, D., Stadler, T., and Drummond, A. J. (2014). Bayesian inference of sampled ancestor trees for epidemiology and fossil calibration. PLoS Comput. Biol. 10:e1003919. doi: 10.1371/journal.pcbi.1003919

PubMed Abstract | CrossRef Full Text | Google Scholar

Grimm, G. W., Kapli, P., Bomfleur, B., McLoughlin, S., and Renner, S. S. (2015). Using more than the oldest fossils: dating osmundaceae with three bayesian clock approaches. Syst. Biol. 64, 396–405. doi: 10.1093/sysbio/syu108

PubMed Abstract | CrossRef Full Text | Google Scholar

Guensburg, T., and Sprinkle, J. (2003). The oldest known crinoids (early ordovician, utah) and a new crinoid plate homology system. Bull. Am. Paleontol. 364:1–43. Available online at: https://www.biodiversitylibrary.org/page/27980785#page/677/mode/1up

Heath, T. A., Huelsenbeck, J. P., and Stadler, T. (2014). The fossilized birth-death process for coherent calibration of divergence-time estimates. Proc. Natl. Acad. Sci. U.S.A. 111, E2957–E2966. doi: 10.1073/pnas.1319091111

PubMed Abstract | CrossRef Full Text | Google Scholar

Höhna, S., Landis, M. J., Heath, T. A., Boussau, B., Lartillot, N., Moore, B. R., et al. (2016). RevBayes: bayesian phylogenetic inference using graphical models and an interactive model-specification language. Syst. Biol. 65, 726–736. doi: 10.1093/sysbio/syw021

PubMed Abstract | CrossRef Full Text | Google Scholar

Hopkins, M. J., Bapst, D. W., Simpson, C., and Warnock, R. C. (2018). The inseparability of sampling and time and its influence on attempts to unify the molecular and fossil records. Paleobiology 44, 561–574. doi: 10.1017/pab.2018.27

CrossRef Full Text | Google Scholar

Klopfstein, S., Ryser, R., Corio, M., and Spasejovic, T. (2019). Mismatch of the morphology model is mostly unproblematic in total-evidence dating: insights from an extensive simulation study. bioRxiv 679084. doi: 10.1101/679084

CrossRef Full Text | Google Scholar

Larabee, F. J., Fisher, B. L., Schmidt, C. A., Matos-Maraví, P., Janda, M., and Suarez, A. V. (2016). Molecular phylogenetics and diversification of trap-jaw ants in the genera Anochetus and Odontomachus (Hymenoptera: Formicidae). Mol. Phylogenet. Evol. 103, 143–154. doi: 10.1016/j.ympev.2016.07.024

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, M. S., Cau, A., Naish, D., and Dyke, G. J. (2014). Morphological clocks in paleontology, and a mid-cretaceous origin of crown aves. Syst. Biol. 63, 442–449. doi: 10.1093/sysbio/syt110

PubMed Abstract | CrossRef Full Text | Google Scholar

Lewis, P. O. (2001). A likelihood approach to estimating phylogeny from discrete morphological character data. Syst. Biol. 50, 913–925. doi: 10.1080/106351501753462876

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, A., Duchêne, D. A., Zhang, C., Zhu, C.-D., and Ho, S. (2019). A simulation-based evaluation of tip-dating under the fossilized birth-death process. Syst. Biol. 69, 325–344. doi: 10.1093/sysbio/syz038

PubMed Abstract | CrossRef Full Text | Google Scholar

Matschiner, M. (2019). Selective sampling of species and fossils influences age estimates of the fossilized birth-death model. Front. Genet. 10:1064. doi: 10.3389/fgene.2019.01064

PubMed Abstract | CrossRef Full Text | Google Scholar

Matschiner, M., Musilová, Z., Barth, J. M., Starostová, Z., Salzburger, W., Steel, M., and Bouckaert, R. (2017). Bayesian phylogenetic estimation of clade ages supports trans-atlantic dispersal of cichlid fishes. Syst. Biol. 66, 3–22. doi: 10.1093/sysbio/syw076

PubMed Abstract | CrossRef Full Text | Google Scholar

Menning, M., Alekseev, A., Chuvashov, B., Davydov, V., Devuyst, F.-X., Forke, H., et al. (2006). Global time scale and regional stratigraphic reference scales of central and West Europe, East Europe, Tethys, South China, and North America as used in the devonian-carboniferous-permian correlation chart 2003 (dcp 2003). Palaeogeogr. Palaeoclimatol. Palaeoecol. 240, 318–372. doi: 10.1016/j.palaeo.2006.03.058

CrossRef Full Text | Google Scholar

O'Reilly, J. E., and Donoghue, P. C. (2017). The efficacy of consensus tree methods for summarizing phylogenetic relationships from a posterior sample of trees estimated from morphological data. Syst. Biol. 67, 354–362. doi: 10.1093/sysbio/syx086

PubMed Abstract | CrossRef Full Text | Google Scholar

O'Reilly, J. E., and Donoghue, P. C. (2019). The effect of fossil sampling on the estimation of divergence times with the fossilised birth death process. Syst. Biol. 69, 124–138. doi: 10.1093/sysbio/syz037

PubMed Abstract | CrossRef Full Text | Google Scholar

O'Reilly, J. E., dos Reis, M., and Donoghue, P. C. (2015). Dating tips for divergence-time estimation. Trends Genet. 31, 637–650. doi: 10.1016/j.tig.2015.08.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Parins-Fukuchi, C. (2017). Use of continuous traits can improve morphological phylogenetics. Syst. Biol. 67, 328–339. doi: 10.1093/sysbio/syx072

PubMed Abstract | CrossRef Full Text | Google Scholar

Parins-Fukuchi, C. (2018). Bayesian placement of fossils on phylogenies using quantitative morphometric data. Evolution 72, 1801–1814. doi: 10.1111/evo.13516

PubMed Abstract | CrossRef Full Text | Google Scholar

Paterson, J. R., Edgecombe, G. D., and Lee, M. S. (2019). Trilobite evolutionary rates constrain the duration of the Cambrian explosion. Proc. Natl. Acad. Sci. U.S.A. 116, 4394–4399. doi: 10.1073/pnas.1819366116

PubMed Abstract | CrossRef Full Text | Google Scholar

Pennell, M. W., Eastman, J. M., Slater, G. J., Brown, J. W., Uyeda, J. C., FitzJohn, R. G., et al. (2014). geiger v2. 0: an expanded suite of methods for fitting macroevolutionary models to phylogenetic trees. Bioinformatics 30, 2216–2218. doi: 10.1093/bioinformatics/btu181

PubMed Abstract | CrossRef Full Text | Google Scholar

Püschel, H. P., O'Reilly, J. E., Pisani, D., and Donoghue, P. C. (2020). The impact of fossil stratigraphic ranges on tip-calibration, and the accuracy and precision of divergence time estimates. Palaeontology 63, 67–83. doi: 10.1111/pala.12443

CrossRef Full Text | Google Scholar

Puttick, M. N., O'Reilly, J. E., Tanner, A. R., Fleming, J. F., Clark, J., Holloway, L., et al. (2017). Uncertain-tree: discriminating among competing approaches to the phylogenetic analysis of phenotype data. Proc. R. Soc. B Biol. Sci. 284:20162290. doi: 10.1098/rspb.2016.2290

PubMed Abstract | CrossRef Full Text | Google Scholar

Rambaut, A., Drummond, A. J., Xie, D., Baele, G., and Suchard, M. A. (2018). Posterior summarization in bayesian phylogenetics using tracer 1.7. Syst. Biol. 67, 901–904. doi: 10.1093/sysbio/syy032

PubMed Abstract | CrossRef Full Text | Google Scholar

Robinson, D., and Foulds, L. (1981). Comparison of phylogenetic trees. Math. Biosci. 53, 131–147. doi: 10.1016/0025-5564(81)90043-2

CrossRef Full Text | Google Scholar

Ronquist, F., Klopfstein, S., Vilhelmsen, L., Schulmeister, S., Murray, D. L., and Rasnitsyn, A. P. (2012). A total-evidence approach to dating with fossils, applied to the early radiation of the hymenoptera. Syst. Biol. 61, 973–979. doi: 10.1093/sysbio/sys058

PubMed Abstract | CrossRef Full Text | Google Scholar

Schliep, K. P. (2010). phangorn: phylogenetic analysis in R. Bioinformatics 27, 592–593. doi: 10.1093/bioinformatics/btq706

CrossRef Full Text | Google Scholar

Slater, G. J. (2015). Iterative adaptive radiations of fossil canids show no evidence for diversity-dependent trait evolution. Proc. Natl. Acad. Sci. U.S.A. 112, 4897–4902. doi: 10.1073/pnas.1403666111

PubMed Abstract | CrossRef Full Text | Google Scholar

Stadler, T. (2010). Sampling-through-time in birth-death trees. J. Theor. Biol. 267, 396–404. doi: 10.1016/j.jtbi.2010.09.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Stadler, T. (2011). Simulating trees with a fixed number of extant species. Syst. Biol. 60, 676–684. doi: 10.1093/sysbio/syr029

PubMed Abstract | CrossRef Full Text | Google Scholar

Stadler, T., Gavryushkina, A., Warnock, R. C., Drummond, A. J., and Heath, T. A. (2018). The fossilized birth-death model for the analysis of stratigraphic range data under different speciation modes. J. Theor. Biol. 447, 41–55. doi: 10.1016/j.jtbi.2018.03.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Stigall Rode, A. L. (2005). Systematic revision of the middle and late devonian brachiopods schizophoria (schizophoria) and “schuchertella” from North America. J. Syst. Palaeontol. 3, 133–167. doi: 10.1017/S1477201905001537

CrossRef Full Text | Google Scholar

Wright, A. M., and Hillis, D. M. (2014). Bayesian analysis using a simple likelihood model outperforms parsimony for estimation of phylogeny from discrete morphological data. PLoS ONE 9:e109210. doi: 10.1371/journal.pone.0109210

PubMed Abstract | CrossRef Full Text | Google Scholar

Wright, D. F. (2017a). Bayesian estimation of fossil phylogenies and the evolution of early to middle paleozoic crinoids (echinodermata). J. Paleontol. 91, 799–814. doi: 10.1017/jpa.2016.141

CrossRef Full Text | Google Scholar

Wright, D. F. (2017b). Phenotypic innovation and adaptive constraints in the evolutionary radiation of palaeozoic crinoids. Sci. Rep. 7:13745. doi: 10.1038/s41598-017-13979-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Wright, D. F., and Toom, U. (2017). New crinoids from the baltic region (estonia): fossil tip-dating phylogenetics constrains the origin and Ordovician–silurian diversification of the flexibilia (echinodermata). Palaeontology 60, 893–910. doi: 10.1111/pala.12324

CrossRef Full Text | Google Scholar

Zhang, C., Stadler, T., Klopfstein, S., Heath, T. A., and Ronquist, F. (2015). Total-evidence dating under the fossilized birth-death process. Syst. Biol. 65, 228–249. doi: 10.1093/sysbio/syv080

PubMed Abstract | CrossRef Full Text | Google Scholar