Tenors Not Sopranos: Bio-Mechanical Constraints on Calling Song Frequencies in the Mediterranean Field-Cricket

Male crickets and their close relatives bush-crickets (Gryllidae and Tettigoniidae, respectively; Orthoptera and Ensifera) attract distant females by producing loud calling songs. In both families, sound is produced by stridulation, the rubbing together of their forewings, whereby the plectrum of one wing is rapidly passed over a serrated file on the opposite wing. The resulting oscillations are amplified by resonating wing regions. A striking difference between Gryllids and Tettigoniids lies in wing morphology and composition of song frequency: Crickets produce mostly low-frequency (2–8 kHz), pure tone signals with highly bilaterally symmetric wings, while bush-crickets use asymmetric wings for high-frequency (10–150 kHz) calls. The evolutionary reasons for this acoustic divergence are unknown. Here, we study the wings of actively stridulating male field-crickets (Gryllus bimaculatus) and present vibro-acoustic data suggesting a biophysical restriction to low-frequency song. Using laser Doppler vibrometry (LDV) and brain-injections of the neuroactivator eserine to elicit singing, we recorded the topography of wing vibrations during active sound production. In freely vibrating wings, each wing region resonated differently. When wings coupled during stridulation, these differences vanished and all wing regions resonated at an identical frequency, that of the narrow-band song (∼5 kHz). However, imperfections in wing-coupling caused phase shifts between both resonators, introducing destructive interference with increasing phase differences. The effect of destructive interference (amplitude reduction) was observed to be minimal at the typical low frequency calls of crickets, and by maintaining the vibration phase difference below 80°. We show that, with the imperfect coupling observed, cricket song production with two symmetric resonators becomes acoustically inefficient above ∼8 kHz. This evidence reveals a bio-mechanical constraint on the production of high-frequency song whilst using two coupled resonators and provides an explanation as to why crickets, unlike bush-crickets, have not evolved to exploit ultrasonic calling songs.

Introduction

Male crickets (Ensifera, Gryllidae) produce loud musical songs to attract conspecific females by rubbing their raised forewings together, a process known as stridulation. During stridulation, the plectrum – a sharp sclerotised region at the anal edge of the left wing (LW) – engages with the file, a row of teeth on a modified, serrated vein on the underside of the right wing (RW) in a clockwork-like manner (Elliott and Koch, 1985; Prestwich et al., 2000). In Gryllidae, the RW usually sits on top of the LW, and during stridulation, both wings open and close in a rhythmic cycle, with sound being generated during the closing phase only (Koch et al., 1988; Bennet-Clark, 1999). The dorsal field of each bilaterally symmetric wing displays a number of clearly delineated wing cells involved in sound radiation. These are the harp, mirror, chord, and the hardened, non-membranous anal surface (Montealegre-Z et al., 2011) (Figure 1).

FIGURE 1

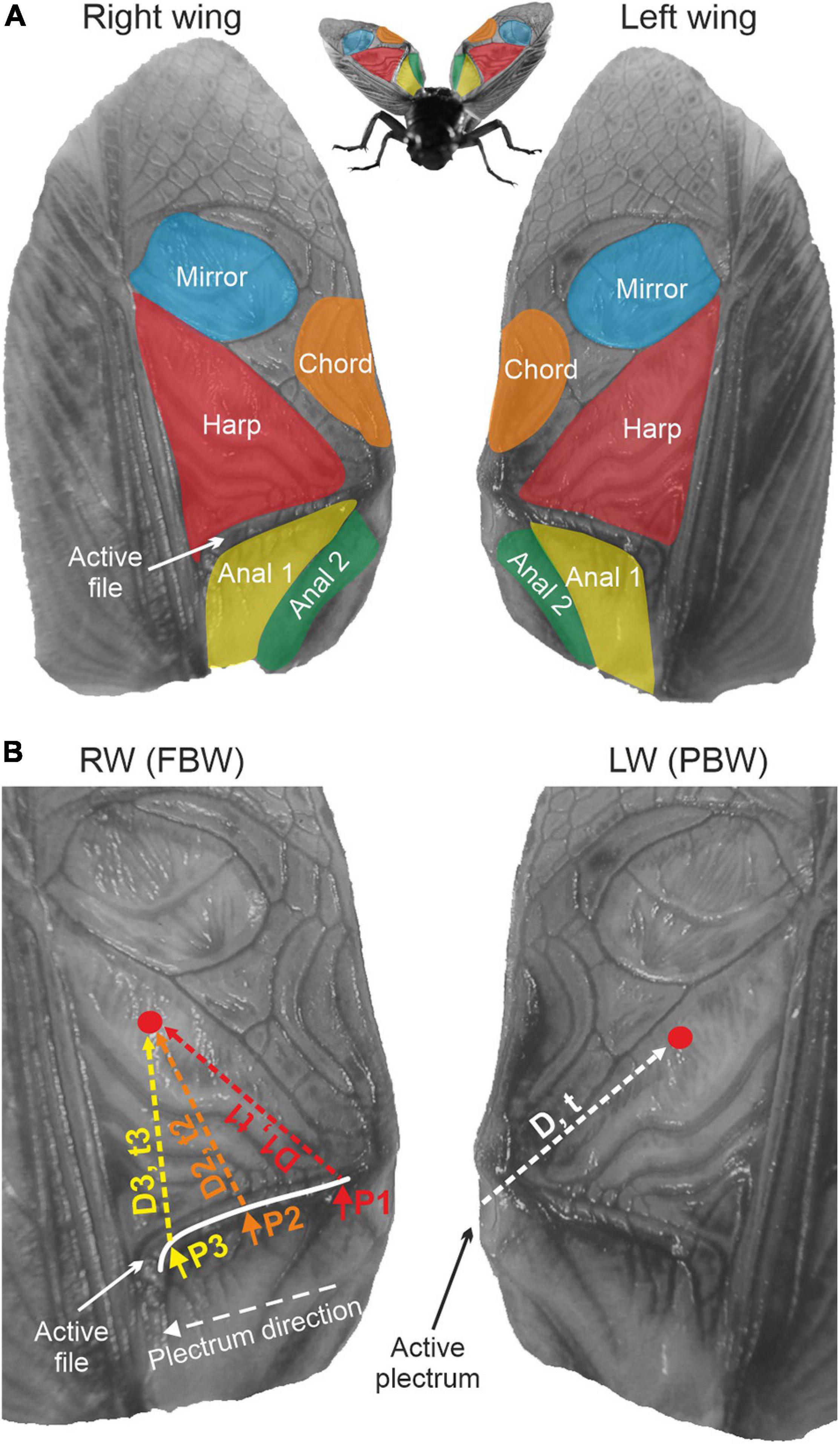
Figure 1. Extended tegmina of Gryllus bimaculatus. (A) The main regions involved in sound production are highlighted. Nomenclature of wing regions follows Montealegre-Z et al. (2011). (B) The problem of phase interference during tegmino-tegminal stridulation. For the left, plectrum-bearing wing (PBW), energy from tooth impacts will travel a constant distance (D) from the plectrum region to a specific region of the same wing (e.g., the red dot; arbitrarily chosen). Conversely, for the file-bearing right wing (FBW), the point of energy input will change as the scraper moves over the file. Energy will travel different distances (D1–D3), reaching the red dot at variable times t, resulting in varying phases of vibration as the scraper moves.

The male is under strong sexual selection to sing at a high amplitude in order to effectively attract and provide phonotactic information for distant females (Forrest and Green, 1991; Römer, 1998). In most cricket species, acoustic energy is concentrated within a narrow-band, pure-tone signal centred on a single low-frequency carrier (∼5 kHz in the case of the field-cricket Gryllus bimaculatus De Geer) which is amplified and radiated by wing regions functioning as natural resonators (Bennet-Clark, 1999, 2003). A loud, pure-tone calling song extends the signal range, aiding the females in determining the direction of the sound source through the enhancement of binaural hearing (Kostarakos et al., 2008; Michelsen and Larsen, 2008) and makes it possible to obtain a large signal-to-noise ratio for transmission across the environment (Michelsen, 1998; Warren et al., 2006; Wiley, 2006). For optimal power transfer from sound source to the surrounding medium, a resonator like the cricket wing should have a radius of at least 1/6 of the sound wavelength λ (λ = ∼7 cm at 5 kHz; assuming a monopole radiator; the radius increases to 1/4–1/3λ for dipoles) (Fletcher, 1992; Bennet-Clark, 1998). Small, sound-producing insects like crickets with wings about 0.5–1 cm in size are therefore under strong selection to optimize power output in order to maximize signal range. Crickets approach this optimization problem by using both symmetric forewings together as sound radiators during stridulation to increase the sound radiating surface for low-frequency songs (Bennet-Clark, 1999, 2003; Montealegre-Z et al., 2011). In contrast, their close relatives bush-crickets (Tettigoniidae) have evolved high-frequency singing using asymmetric wings as a derived trait where the overlying LW bears the file and is usually mechanically dampened, while the plectrum-bearing RW is highly adapted for efficient sound radiation (e.g., Montealegre-Z and Postles, 2010; Sarria-S et al., 2016; Song et al., 2020). The drivers for the evolution of this asymmetry are unknown but it has been hypothesised to be linked to ultrasonic sound production and signal purity (Montealegre-Z, 2005; Gu et al., 2012).

Signal transmission is facilitated by resonance – an inexpensive way of enhancing sound output while conserving metabolic energy – whereby the call’s carrier frequency (f_c) is determined by the resonance frequency f₀ of the wings, which implies that both wings in a symmetric system should resonate at similar f₀. Reliance on two coupled resonant structures requires that crickets have to achieve and maintain a high degree of phase locking between the two wings in order to add vibrations constructively (Prestwich et al., 2000). Only when the two resonators are vibrating at similar f₀ with minimal phase differences (ϕ) is constructive wave superposition providing the desired effect of increasing the amplitude of radiated sound energy. When optimal (ϕ = 0), this constructive interference results in a doubling of the amplitude of the combined output (Rossing, 1990). How can this behaviour, defined here as in-phase, take place?

The in-phase resonance between wings is facilitated by an escapement mechanism that allows both wings to vibrate together and radiate sound efficiently (Koch et al., 1988). However, prior mechanical analyses of cricket stridulation showed that the mechanism of sound production is asymmetrical (Bennet-Clark, 2003; Montealegre-Z, 2005; Montealegre-Z et al., 2011): While the RW receives its energy input along the file’s ca. 200 teeth distributed over a distance of some 4 mm, the underlying LW receives energy only through the small region of the plectrum (0.1 mm², Figure 1B). Figure 1B shows that as the plectrum is dragged on the file from left to right, it generates mechanical impacts at different locations along the file. The input of mechanical energy therefore varies in time and location, potentially resulting in a complicated dispersion of substrate-borne waves across the surface area of the RW (Figure 1B, left). On the other hand, the LW has only one input, the plectrum, and vibrations will travel constantly to the various LW regions from that input (Figure 1B, right). Therefore, the LW should vibrate with constant phase, independently of the plectrum’s position on the RW. In contrast, the RW should be more vulnerable to phase changes as the moving plectrum delivers energy impulses along the file. If these assumptions hold true, the constant phase generator (LW) and the variable phase generator (RW) are expected to interact and generate beats in their summed acoustic output, in particular at locations where LW and RW vibrations cancel each other out (Sismondo, 1993). Yet, the natural song of the male does not exhibit such beats; instead, song pulses have sustained and regular amplitude and phase profiles.

In addition, it is also implied that the wings’ resonances are perfectly in tune with the input stimulus, each wings’ f₀ is equal to the song carrier frequency f_c. However, previous studies revealed that the left and RWs exhibit different f₀, above and below the output f_c (<5 kHz>) (Nocke, 1971; Bennet-Clark, 2003; Montealegre-Z et al., 2011). Non-contact laser Doppler vibrometry (LDV) measurements showed that the left and RWs of field-crickets are mechanically different, with resonant frequencies differing by as much as 2 kHz (f_0left < f_0right; Montealegre-Z et al., 2011). It remains unclear how the seemingly imperfect and differently tuned resonators can generate the high quality pure-tones observed in crickets.

Using LDV, focal microinjection of the neuropharmacological neuroactivator eserine, and specialised acoustic equipment, we measured wing vibrations in actively stridulating Mediterranean field-crickets (G. bimaculatus). From physical acoustics, we hypothesise that efficient, high gain, pure-tone radiation results from the in-phase oscillation of both wings when coupled during the stridulation process. We furthermore formulate and test a second hypothesis: different wing regions vibrate in phase, despite differential tuning and inputs, and thereby generate the coherent acoustic radiation typical of field-cricket songs. As a consequence, any imperfections in the coupling of the wings that lead to temporal and phase shifts between the resonators should result in sub-optimal amplitude of the output signal and ultimately impose constraints on signal frequency.

Materials and Methods

Animals

Adult male crickets (G. bimaculatus) obtained from a breeding colony maintained at the University of Bristol were used. Animals were kept at room temperature (20–22 °C) under a 12 h:12 h light:dark cycle and were fed with oats, dry dog food and water ad libitum. Adult males were randomly taken from the colony, their wings inspected for damage and kept individually in cages prior to the experiments. After isolation, 18 males that sang for prolonged periods of time were chosen for the experiments, as these animals usually responded better to pharmacological stimulation. All males recorded were singing with the usual wing overlap (RW over LW).

Neuropharmacological Stimulation

To elicit persistent stridulation in tethered crickets, we followed methods established and described in detail in earlier studies (Hedwig and Becher, 1998; Wenzel et al., 1998; Wenzel and Hedwig, 1999; Montealegre-Z et al., 2011). In short, we used borosilicate glass microcapillaries (1B120F-3; ID = 0.68 mm; World Precision Instruments, Inc., Sarasota, FL, United States) pulled with a Sutter microelectrode puller (Sutter Instrument Company, Novato, CA, United States) to produce ca. 10 μm wide tips. These microcapillaries were then filled with eserine/ringer solution (10^–2 mol l^–1; Sigma-Aldrich Company Ltd., Dorset, United Kingdom) and connected to a picospritzer (Picospritzer II, Parker Hannifin, Pneutronics Division (formerly General Valve, NJ, United States). Small quantities of eserine (an acetylcholinesterase inhibitor) were injected into a brain neuropil, located between the pedunculus and the α-lobe of the mushroom bodies. Successful procedures elicited sustained stridulation in the typical calling song pattern (see Supplementary Video 1). Crickets were removed from the study if we recorded no singing activity within 1 h after the first injection.

Crickets exhibit frequency modulation (FM) in their calls, and the envelope of this modulation has been shown to be a fingerprint of each individual (Montealegre-Z et al., 2011). The quality of the pharmacologically elicited calls was examined by correlating their FM pattern with that of the natural calls obtained by zero-crossing analysis. Calls were judged of sufficient quality when the correlation was higher than 0.85 (see Montealegre-Z et al., 2011, for more experimental details).

Recordings of Wing Vibrations in Stridulating Animals (Wings Engaged)

Vibrations from the tegminal surface were successfully quantified from 11 of the 14 stridulating animals using two coupled laser Doppler vibrometers (Polytec PSV-300-F, and a PSV-400; Polytec GmBH, Waldbronn, Germany) and corresponding scanning heads (OFV-056) fitted with close-up attachments. The velocity output of the PSV-300-F served as an input channel for the PSV-400 vibrometer, thus allowing for synchronization of the recordings. Sound signals were recorded using a 1/8″ condenser microphone Brüel & Kjær Type 4138, connected to a Brüel & Kjær 2633 preamplifier and a Type 5935L amplifier (Brüel & Kjær, Nærum, Denmark), which was in turn connected to the PSV-400 acquisition system. Measurements were performed in single-shot mode (one recording per chosen spot on the wing, no averaging) in the temporal domain (1,024 samples at 512 kHz sampling rate, leading to recordings with 2 ms duration and a temporal resolution of ∼1.95 μs). Acoustic and vibrational measurements were recorded with Polytec Scanning Vibrometer software (PSVSoft, Version 8, Polytec GmbH, Waldbronn, Germany). The microphone was positioned posterior to the specimen, 3–4 cm away from the wings as to not interfere with the laser beams. Simultaneously, wing vibrations were recorded with the laser beams focused on the anal regions, harps, chords, and mirrors (Figure 1 and see Supplementary Video 1 showing a singing male after pharmacological stimulation). Through the video feed of the two LDVs, we were able to visually place the laser points with some acuity within the regions in question, ensuring that the recordings from left and RW came from equivalent locations. Results for the chord regions are shown in the Supplementary Material but are not included in the main results as we were able to obtain chord recordings in only 7 out of the 11 animals used (the left chord regions are usually covered by the RW during stridulation and thus not easily accessible). The laser spot position and signal strength (the amount of laser light reflected from the target) was monitored and controlled via the live video feeds to the controlling computers of both laser systems. Using earlier LDV systems, signal strength often had to be increased by applying minute reflecting beads or powder to the wing surfaces. This was not the case here as the focussed laser light (λ∼ 630 nm) was well reflected by the wing cuticle, which allowed us to perform contactless vibration measurements without further manipulation of the wings.

The microphone signal was used as a measurement trigger, so only wing vibrations involved in sound production were recorded. Data acquisition was programmed to last for 2 ms during the maximum amplitude event of a song pulse. This duration was chosen to minimise the movement of the wings during recording (∼ 8–10 teeth) while still gathering sufficient data for analysis (see also Montealegre-Z et al., 2011).

Individual Resonances of Unengaged Fixed Wings (Free Vibration)

After the previous experiment, each of the wings of each live specimen (n = 14) were extended and separated from each other by fixing the axillary sclerites with a bee’s wax (Fisher Scientific United Kingdom, Limited, Leicestershire; product code W/0200/50), and Colophony (Sigma-Aldrich Co. St. Louis, MO, United States; Product No. 60895-250G) mixture (1:1). The wings were extended to not be in contact with the pronotal lateral and posterior edges. A loudspeaker (ESS AMT-1; ESS Laboratory Inc., Sacramento, CA, United States) was used to broadcast periodic chirps in the range 1–20 kHz, with a flat (55 dB SPL ± 1.5 dB) spectrum. The microphone was placed dorsally in the middle of both extended wings (Figure 2). The laser system was set to record in the scan mode. A complete scan of the extended wings in response to the periodic chirps was performed with the PSV-400 LDV, using 250–300 scanning points per wing with 10 measurements averaged per point. Fast Fourier transforms (FFT) with a rectangular window and a sampling rate of 512 kHz, 128 ms sampling time, and a frequency resolution of 7.81 Hz were generated for each point.

FIGURE 2

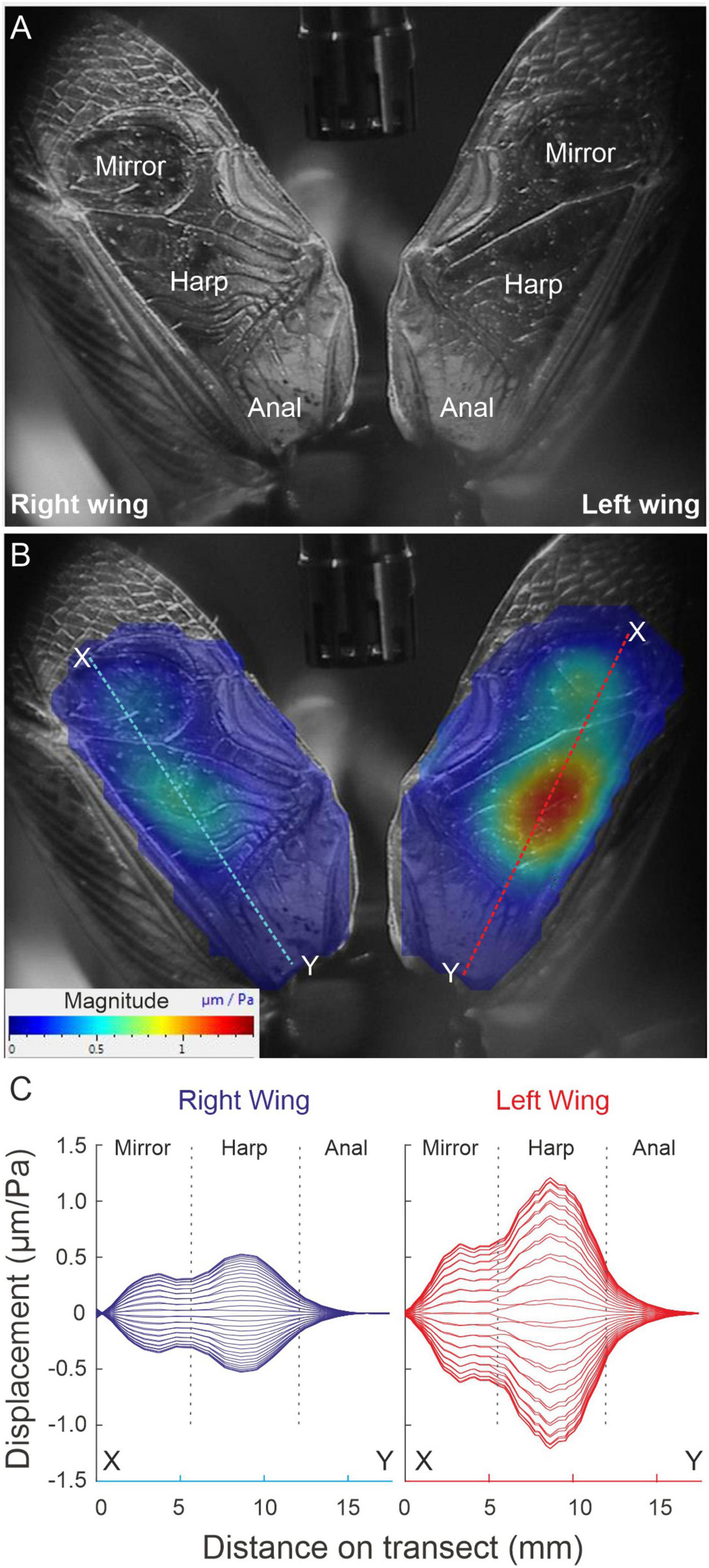
Figure 2. Amplitude response of extended wings to sympathetic acoustic stimulation. (A) Orientation image relating tegmen topography to the position of the scanning lattice. (B) Scanned area and deflection shapes of the tegmen dorsal surface (harp and mirror). Dashed lines illustrate the sections through which the deflection envelopes in panel (C) were built. (C) Envelope of mechanical deflections along transects shown in B for a series of phases (in steps of 10°) in the full oscillation cycle. For this specimen: RW f₀ = 4.71 kHz, LW f₀ = 4.62 kHz).

Data Analysis

Experimental data was either analysed directly with the PSV software or with custom written scripts in MATLAB (R2019a; The MathWorks Inc., Natick, MA, United States). Instantaneous phase in the time domain was obtained with Hilbert transform using custom MATLAB code (Hartmann, 1997). We tested whether the frequency differed between left and RWs, and between areas (mirror, harp, chord, anal) using linear mixed effects models run in R 4.0.0 (R Core Team, 2020). Models were run separately for free and engaged wings, with male ID included as a random effect. Models were run using lme4 (Bates et al., 2015) and lmerTest (Kuznetsova et al., 2017), with post hoc testing carried out using emmeans (Lenth, 2020). We also tested the difference in the normalised amplitude of the mechanical response (μm/Pa), between left and RWs using a paired t-test.

Results

Using focal microinjection of the neuroactivator eserine into the cricket’s brain (Wenzel et al., 1998; Hedwig, 2000), long-lasting and stable stridulation was elicited in 14 restrained males (Supplementary Video 1). Using two synchronised micro-scanning LDVs, we successfully measured the spatially resolved vibration of both wings simultaneously during the “engaged” phase of the stridulation process in 11 of the 14 actively singing males, following a previously established protocol (Montealegre-Z et al., 2011). After the cessation of singing, the wings of each specimen were extended and fixed basally and stimulated with sweeps of broadband sound to reveal their natural resonances f₀ and relative magnitudes of vibration. The surface area of these “unengaged” wings was scanned in its entirety, providing a detailed map of vibrational patterns (Figures 2, 3 and Supplementary Video 2, showing wing vibrations of one male at resonance of 4.6 kHz).

FIGURE 3

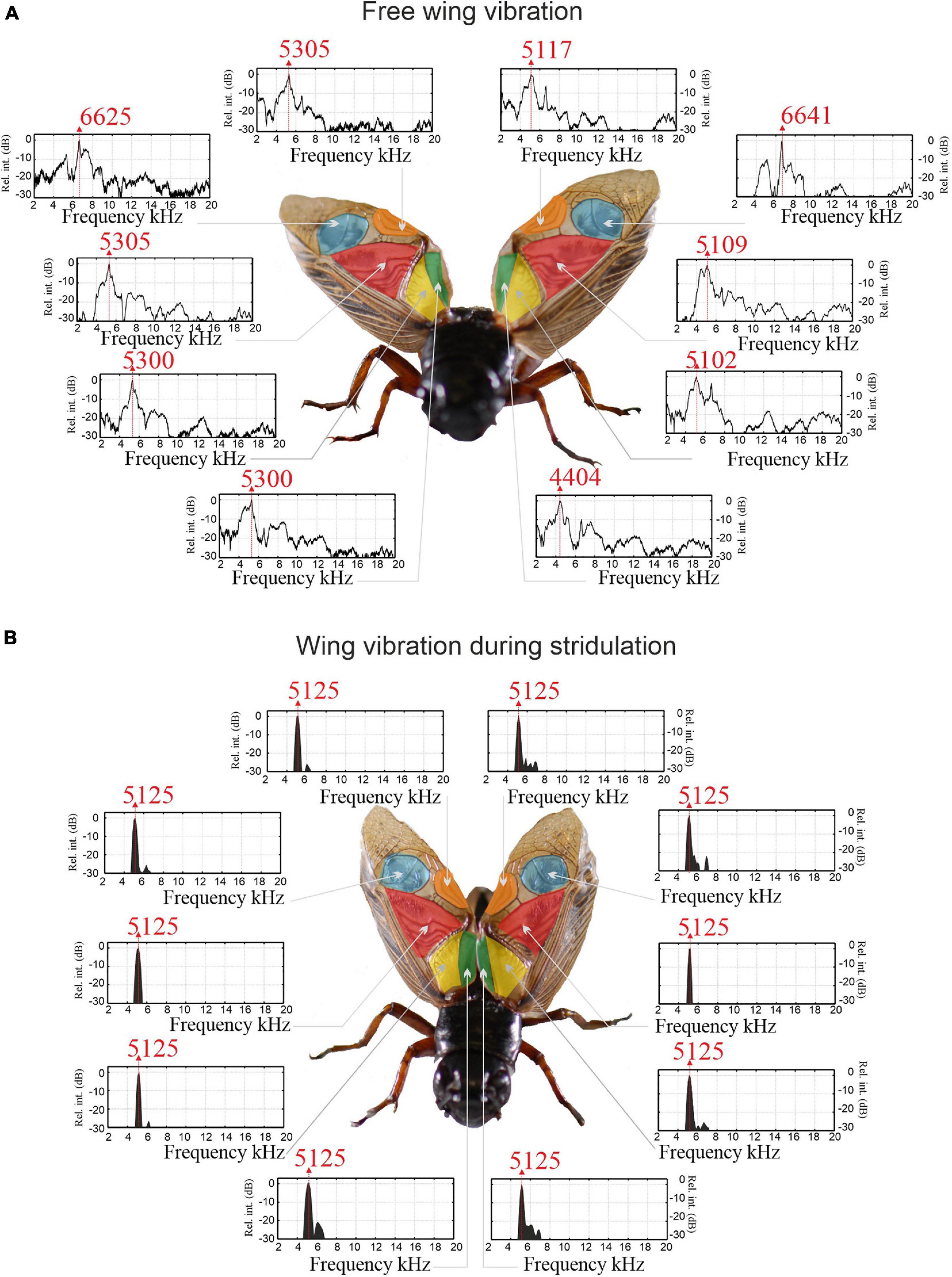
Figure 3. Wing region resonances of unengaged and engaged wings of a male Gryllus bimaculatus. (A) Natural resonances of wing regions measured with LDV in unengaged wings. (B) Wing resonances measured in the same individual during stridulation (engaged). Vibration amplitudes have been normalised to a relative dB scale.

Natural Frequencies of Wing Vibrations

Full wing scan recordings of unengaged (extended and fixed) wings show that the RW f₀ is significantly higher than the LW (RW = 5.168 ± 0.434 kHz, SE 0.116; LW = 4.827 ± 0.396 kHz, SE 0.106; LMM: F_1,152.60 = 15.93, p < 0.001). However, when comparing vibration amplitudes at the average f₀ of both wings, no difference between left and RWs was found. This was true for both average vibration amplitudes per wing and maximum vibration amplitudes of the harp areas alone (RW_harp = 0.32 ± 0.24 μm/Pa; LW_harp = 0.40 ± 0.35 μm/Pa; t = 0.988, df = 13, p = 0.34). When each wing is stimulated at its average f₀, one always exhibits a higher vibration amplitude (on average by a factor of ∼1.7; Figures 2B,C), but this dominant wing can be either LW or RW (cf. Supplementary Video 2, where the animal’s LW vibrates with higher amplitude). In a previous study, we reported a trend of LW dominance which we could not identify here, which is most likely due to our low sample size (n = 44 in Montealegre-Z et al., 2011).

Examining wing vibrations in more detail, LDV measurements reveal that each wing region exhibits its own resonance spectra with varying peak frequencies (Figure 3A); there were significant differences in the f₀ between areas (LMM: F_4,152.56 = 72.55, p < 0.001). Post hoc testing revealed that the mirror of each wing consistently showed higher f₀ than the average wing f₀ (LW_mirror = 6.858 ± 0.540 kHz, SE 0.127 kHz; LW average f₀ of other areas = 4.827 ± 0.396 kHz, SE 0.106; RW_mirror = 7.007 ± 0.865 kHz, SE 0.204 kHz; RW average f₀ of other areas = 5.168 ± 0.434 kHz, SE 0.116; n = 18) (Figure 3A), with other areas of the wing not significantly different from each other.

Wing Vibrations in Stridulating Animals

Wing vibrations were recorded during active stridulation using two LDVs in single shot mode, enabling vibration measurement at defined locations and times (see Supplementary Video 2). Remarkably, vibrations of engaged wings during stridulation (Figure 3B) differ from sound-evoked vibrations in unengaged wings (Figure 3A). When the wings are engaged, all regions exhibit near identical, narrow vibrational frequency spectra with maximum power concentrated at the carrier frequency f_c of the calling song (here 5.125 kHz; LMM: F_3,66.29 = 1.56, p = 0.208; Figure 3B). There is also no difference between the left or RW (LMM: F_1,65.20 = 0.77, p = 0.383). The convergence of all resonators toward one very narrow frequency band of oscillation is reminiscent of entrainment, a process similar to synchronization between Huygens’ clocks (Peña Ramirez et al., 2016).

Apart from identical oscillation frequency, an additional key feature of synchronised resonators is their phase relationship. Time-resolved LDV data were obtained by recording vibrations from different regions of both wings at synchronised points during stridulation (see methods). Results across 11 specimens show that the wings are not perfectly in phase during sound production, but that phase lags ϕ exist over a wide range between left and RWs (Figure 4). In some individuals, ϕ is small and relatively constant between wings (both over time and between regions, Figure 4A), while others show larger differences in phase (Figure 4B and Supplementary Figure 1). Within an individual, average phase lags across wing regions seem to be relatively consistent, although considerable variation exists (see Supplementary Figure 1).

FIGURE 4

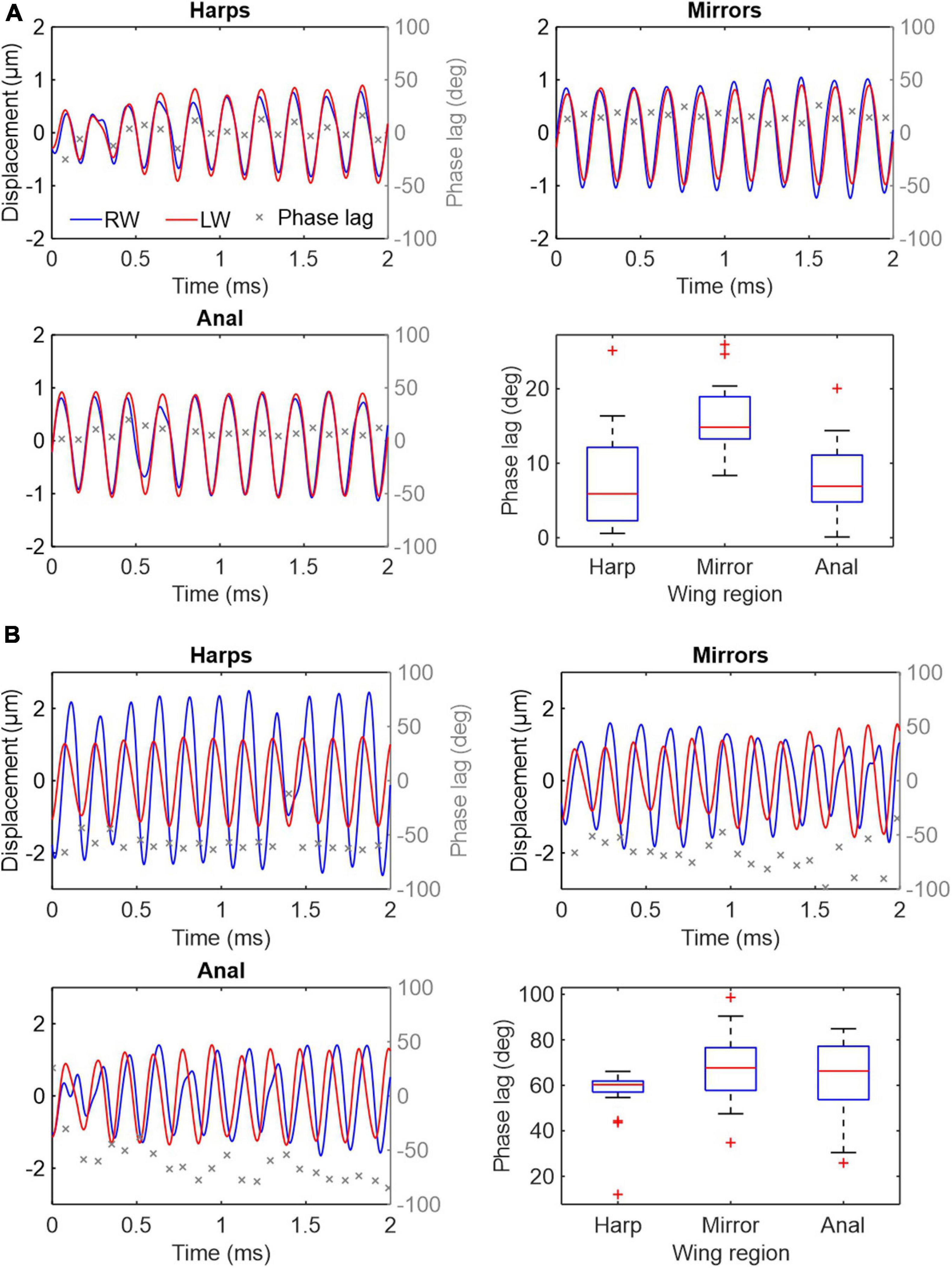
Figure 4. Vibration displacements and phase relation in three major wing regions during stridulation in two Gryllus bimaculatus males. Wing vibration measurements were obtained simultaneously from two homologous wing regions using two LDVs. (A) An individual with nearly perfect phasing of the wings (median ϕ between 6° and 15°). (B) An individual with more prominent phase differences and variation between the wings (median ϕ between 60° and 68°). Each panel represents an independent recording showing RW in blue, LW in red and phase lag ϕ in grey. ϕ is measured as the difference in phase between LW and RW at the LW local maxima and minima. Boxplots show the median (red line), 25th, 75th percentiles (box) and 1 IQR whiskers for all ϕ per wing region. Outliers are marked as red +.

Time domain recordings of single point measurements at the harps, anal regions and mirrors also show that LW vibration amplitudes are mostly higher than RW amplitudes (red and blue lines in Figure 4A, respectively) but there is also considerable variation in amplitudes across animals and wing regions (Figure 4B). The high variation in vibration amplitude can be explained by the limitations of the experimental set up. As two lasers had to be manually aligned on the stridulating animals, space restrictions and changes in the way the animals held their wings during stridulation often prevented a perfect orthogonal alignment of the laser beams to the vibrating surfaces, resulting in absolute displacement amplitudes that are hard to compare between wings. Relative phase relationships between the wings, however, can be measured with high accuracy, as they are not affected by laser beam–target orthogonality. In theory, mathematical superposition of LW and RW vibrations allows estimating the resulting combined output vibration. For example, the net vibratory response at a given place and time caused by the two harps is the sum of the responses which would have been caused by each harp individually (Figures 5A,B). These calculations show that the greater the phase lag ϕ (and thus time lag Δt for a given frequency; cf. Supplementary Figures 1, 2) between LW and RW, the lower the amplitude of the resulting vibration and therefore the gain as compared to using only one wing (Figures 5A–C). Without exact amplitude information for engaged wings, we can nevertheless show the effect of phase shifts between wings on the overall output amplitude assuming that vibration amplitudes are equal for both wings (as shown in Figure 5A). Thus, Figure 5C shows normalised RMS (root mean square) gain as a function of phase lag ϕ of three different wing regions using normalised vibration velocity amplitudes. In ideal conditions, where both wings exhibit equal vibration amplitudes at equal frequencies, perfect phase locking (ϕ = 0°) produces a gain of 2, while a phase lag of 120° (Δt = 67 μs at 5 kHz) would produce a gain of 1 or no amplification of the resulting output as compared to using only one resonating wing. For example, the phase lags recorded from left and right harps (median values ranging from 6° to 79° across all specimens; this equates to Δt values between 3 and 43 μs; see Supplementary Figures 1, 2) produce relative amplitude gains ranging from 1.97 to 1.34 (Figure 5C, blue stars). Other wing regions (mirror and anal regions, red circles and yellow squares, respectively), exhibit similar values.

FIGURE 5

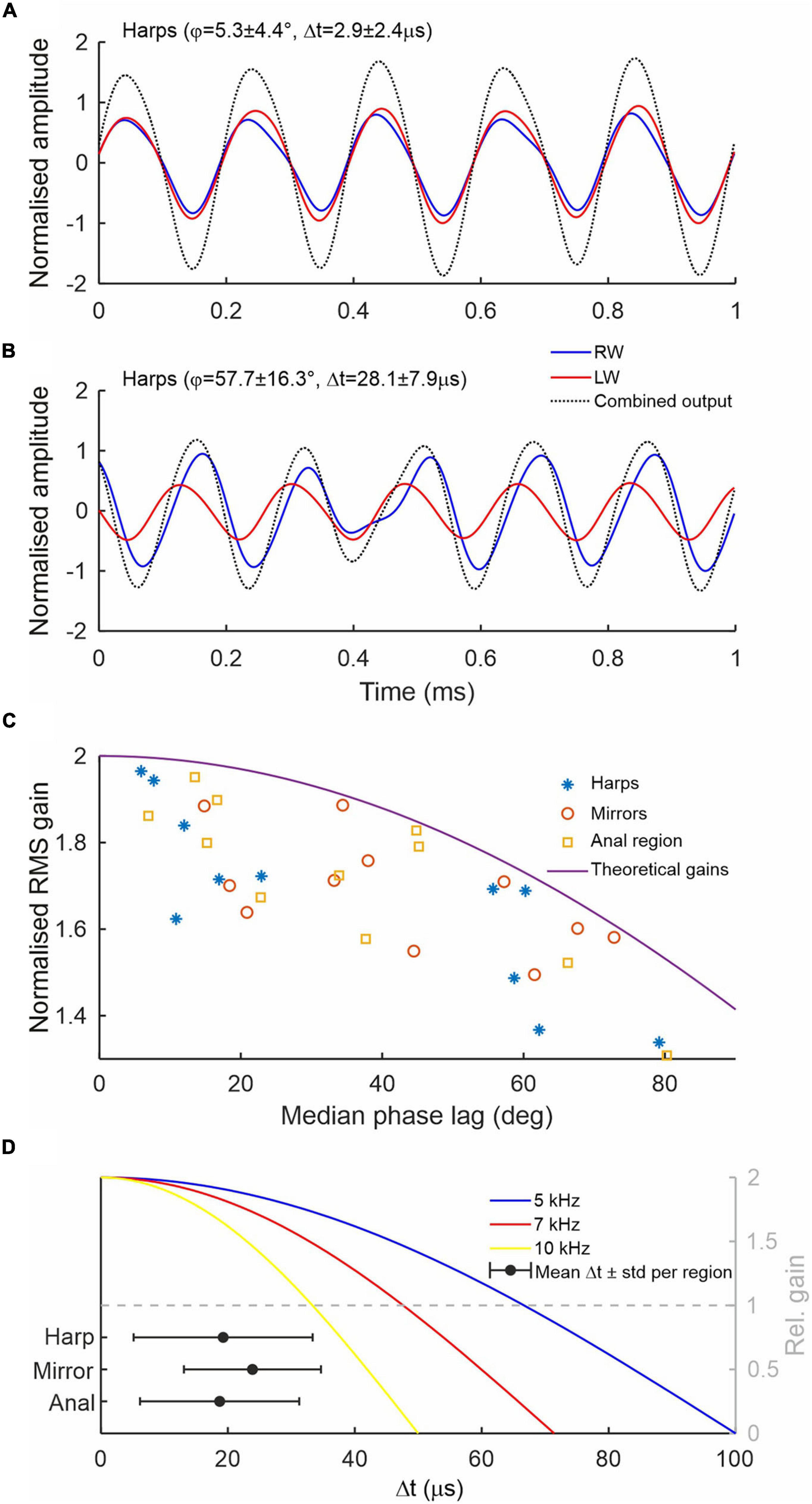
Figure 5. Sound wave superposition to illustrate amplitude gains. (A) Theoretical harp output calculated from a Gryllus bimaculatus showing small phase differences between both harps (ϕ∼5°; Δt∼3 μs; f_c = 5.07 kHz). (B) Harp output from an individual with large phase differences (ϕ∼58°; Δt∼28 μs; f_c = 5.7 kHz). Note that in spite of large phase differences, the output (black dotted line) shows a gain, which is larger in A. In both cases, tracks have been normalised to the highest amplitude. (C) Comparison of median absolute phase lag per specimen and RMS gain of three major wing regions. Vibrations were obtained simultaneously from the paired respective regions (harps, mirrors, and anal) of LW and RW. RMS gains were calculated from the superposition of normalised LW and RW displacement responses measured with each laser. Each data point per region represents one individual; n = 11. The solid line shows theoretical gains with increasing ϕ assuming equal vibration amplitudes and frequencies. (D) Mean absolute time lags Δt (black circles) and standard deviation between LW and RW for three major wing regions and 11 animals. Coloured solid lines show the theoretical amplitude gains (right y-axis in grey; equal amplitudes and frequencies) as function of Δt for three different carrier frequencies (blue, red, and yellow for 5, 7, and 10 kHz, respectively). Values below 1 (dashed grey line) signify lower combined output amplitudes compared to using only one resonator.

Figure 5D illustrates the effect imperfect coupling of the wings has on the overall combined output amplitudes at different song carrier frequencies (assuming both wings vibrate with the same frequency and amplitude). While animals producing pure-tones at 5 kHz can afford to have relatively uncoupled wings with time lags up to ∼67 μs before destructive interference occurs (Figure 5D, intersection of blue and grey dashed lines), Δt at which destructive interference starts is reduced to ∼48 and 34 μs when singing at 7 or 10 kHz, respectively (red and yellow lines). The inset in Figure 5D showing the average time differences and standard deviations between wings for the 11 specimens recorded shows that the span of Δt values (like ϕ) is generally small enough to ensure amplitude gains well over 1.5 when singing with a 5 kHz carrier frequency.

Discussion

Here, we have revealed the presence of an elegant additional mechanism at work in crickets that contributes to generating high amplitude, pure tone signals using distinct yet coupled sound generators: the two forewings and their individual wing cells. Although the wings appear to be mirror images of each other (Figure 1), they are asymmetrical in their mechanical properties and structure (Figure 2A), as previously reported (Simmons and Ritchie, 1996; Bennet-Clark, 2003; Montealegre-Z et al., 2011). For G. bimaculatus, it is known that the RW on top is slightly larger in surface area and exhibits a higher f₀ than the LW (Montealegre-Z et al., 2011).

In addition, differences in resonant properties between both wings and among single wing regions are characterised in some detail. The biomechanical data demonstrate that, within a single wing, different regions have variable resonance peaks close to that of the harp f₀ value (apart from the mirror, which generally resonates several kHz higher) and overall resonance curves also differ in their spectral composition (Figure 3). Interestingly, the observed differences between both the individual wing regions and between the wings themselves (Figure 3A), vanish when the wings engage in active stridulation (Figure 3B). These results confirm for the first time that all regions of both wings actively radiate sound at the carrier frequency during stridulation and that the resonance properties of the LW dominate the frequency output. This suggests that, during stridulation, the LW harp vibrations, generated through plectrum-teeth impacts, drive the vibrations of all other wing regions, including those of the RW, so that the engaged wings vibrate together at the LW f₀.

In order to produce the best possible signal output from both coupled resonators, we hypothesised that both wings and the wing regions therein should not only oscillate at one common frequency, but also, ideally, in-phase (ϕ = 0°), thereby creating maximal constructive interference (and thus a two-fold amplitude gain as compared to using only one wing). Whilst the whole system is indeed driven and oscillating at one specific frequency, we find considerable incoherence in the phase relationships between LW and RW and their respective regions. Figures 4, 5 clearly show that individual wing regions are not phase-locked to each other but exhibit average phase differences ϕ ranging from ca. 6° to 79°, equating to temporal differences Δt between the wings of 3–43 μs at the carrier frequency (f_c = 5.125 kHz). Figure 4 and Supplementary Figure 1 also show that individuals exhibit roughly similar phase differences within their wing regions but phase shifts between individuals are quite variable. This leads us to suggest that the ability to tightly control the wing movements and the coupling of the resonators is an individual trait depending on either wing morphology or neuro-muscular control of the stridulation process or a combination thereof. As a consequence, the phase differences ϕ and corresponding time lags Δt seen across the recorded individuals would approach the distribution of this trait over the population.

Figures 5A,B depicts the consequences of these phase shifts in two male crickets on the opposite sides of the range of observed ϕ. While the lower ϕ of Male 1 (ϕ = 5.3°, Δt = 2.9 μs, Figure 5A) results in a considerable output gain in comparison to the individual harp amplitudes (ca. 1.85 times the highest LW amplitude), the higher phase differences of Male 2 (ϕ = 58°, Δt = 28 μs, Figure 5B) result in only a moderate gain (ca. 1.3). For this animal, a further increase in ϕ and consequently Δt would result in destructive interference, whereby the combined output of both wings would be less than the output of one wing alone, negating the advantage of using coupled resonators. This is shown in more detail for three major wing regions over all animals in Figure 5C. It is noteworthy that no instance of destructive interference was observed in the specimens studied.

Figure 5D shows the effect frequency has on the overall gain of this imperfect coupling in the temporal domain. While a cricket singing at 5 kHz will experience an increase in combined output amplitude (gain > 1, above dashed grey line, Figure 5D) for temporal differences between the wings of up to 67 μs (corresponding to a 120° phase shift and assuming equal vibration amplitudes), crickets singing at higher frequencies will encounter this threshold much earlier (at 48 μs and 33 μs for 7 kHz and 10 kHz, respectively). Consequently, the animals’ observed inability to tightly synchronise the wing movements in time will act as an acoustic constraint for crickets to exploit higher song frequencies using two (imperfectly) coupled resonators. In addition, Figures 5C,D demonstrate that the observed imperfections in wing coupling in G. bimaculatus are still sufficiently low to ensure theoretical amplitude gains well above 1.5 times in comparison to the output of one wing alone. It is unknown, however, if ϕ and Δt are, for example, dependent on temperature. Due to the clockwork escapement mechanism involved in stridulation (and different from wing motion dynamics; Prestwich and Walker, 1981) tooth strike rates and f_c are largely independent of temperature in many Gryllidae, as are the resonant properties of the wings (Elliott and Koch, 1985; Bennet-Clark and Bailey, 2002). However, some species can show slight changes in f_c with temperature. Furthermore, the temporal song patterns, including syllable duration, are often affected by changes in ambient temperature (Walker, 1962; Pires and Hoy, 1992; Walker and Cade, 2003). It would therefore be conceivable that ϕ is also temperature dependent, potentially increasing with temperature and changes in singing behaviour. Further experiments including other cricket species and varying recording temperatures are planned to address inter-species variability and temperature dependence of the animals’ wing coupling abilities.

If the higher values of Δt we observe in G. bimaculatus (Figure 5D for averages and SD; see Supplementary Figure 2 for a depiction of the range of observed values across all animals) are an indicator for the minimal amount of temporal control crickets in general are able to exert during stridulation, then one can attempt to calculate a cut-off frequency above which the sound production with two symmetrical and coupled wings becomes inefficient. The highest median value for ϕ we measured for the three wing regions were between 72° and 80°, equating to Δt values between 38 and 43 μs at f_c = 5.125 kHz. Using simple trigonometric relationships between phase, amplitude, Δt and frequency of waves and under the simplified assumption that both waves have the same frequency and amplitude, one can calculate the frequency f_max at which the gain of the combined output of the superimposed waves becomes 1:

$$f_{\text{max}}=\arccos \left(\frac{Gain}{2}\right)/(\mathrm{\pi }*\mathrm{△}t)(1)$$

Using Eq. (1) and the range of Δt stated above, theoretical f_max values range from 7.8 to 8.8 kHz (for 43 and 38 μs, respectively), denoting frequencies above which stridulation using the mechanism described above becomes inefficient for some animals in the population. Taking the mean and standard deviation values for Δt shown in Figure 5D as rough population measure (harp: 19.3 ± 14.1 μs; mirror: 23.9 ± 10.8 μs; anal region: 18.7 ± 12.5 μs; see also Supplementary Figures 2, 3), one could state that ∼16% of males would not be able to produce song above ∼10 kHz with an amplitude gain above 1 when using both wings as active resonators.

These cut-off frequencies correspond very well with maximal carrier frequencies observed in the majority of Gryllidae, which lie between 2 and 8 kHz (Bennet-Clark, 1989; Robillard et al., 2015). A notable exception are members of the subfamily Eneopterinae, which produce calling songs with frequencies of up to 26 kHz (Robillard et al., 2013). Interestingly, in this subfamily, there is a clear gap between species singing at low frequencies and species singing at high frequencies. This gap is located between 7.9 and 12.2 kHz and members of the high-singing species form a distinct clade within the Eneopterinae (the Lebinthini) (Desutter-Grandcolas and Robillard, 2004). Additionally, Robillard et al. (2013) found that these species exhibit resonance patterns and stridulation mechanisms quite different to the ones employed by other Gryllids and other Eneopterinae. Here, the resonances in the LW and RW are clearly asymmetrical, only partly (or not at all) overlapping the carrier frequencies and they generally show lower vibration magnitudes when compared to, e.g., the wings of G. bimaculatus. Furthermore, instead of employing constant tooth strike rates (like G. bimaculatus and most other Gryllids), some Lebinthini employ a stridulation mechanism (resembling those commonly observed in bush-crickets) whereby the wing stops during the closing phase to build up elastic energy which is then quickly released to produce highly increased tooth strike rates and therefore higher frequency calls (Robillard et al., 2013). These adaptations for high-frequency song production are similar to those encountered in bush-crickets. In bush-crickets, the wings are generally highly asymmetric as well, both morphologically and acoustically: The LW (lying on top of the RW and bearing the active stridulatory file) is often thicker, usually shows no clear stridulatory fields and is highly damped, therefore playing only a minor role in sound radiation (Montealegre-Z and Postles, 2010; Baker et al., 2017). The RW on the other side (which receives its mechanical input vie the plectrum) often exhibits extremely thin to translucent stridulatory fields with clear resonance properties, thus constituting the acoustically active wing (e.g., Sarria-S et al., 2014; Baker et al., 2017). Thus, the sound production system in Tettigoniidae only contains one resonator, reducing the surface for sound radiation, whilst eliminating the problems inherent to two imperfectly coupled resonators as described here for crickets. This allows for a shift to higher song frequencies (and shorter wavelengths) without destructive interference from a second resonator, and simultaneously ensures that the size of the remaining resonator is still (closer to) optimal for pure tone sound radiation.

In conclusion, the results presented here suggest a mechano-acoustical constraint on the bilateral near-symmetrical, dual resonator sound production mechanism common to most Gryllidae which prevents the exploitation of higher song frequencies above ∼8–9 kHz whilst still being able to produce loud and pure-tone calling songs to effectively attract mates. This could have been an important constraint for the majority of Gryllidae (restricting them to the role of tenors) which the Tettigoniidae (the sopranos within the Ensifera) seem to have overcome by evolving a highly asymmetric singing mechanism (Montealegre-Z et al., 2017; Song et al., 2020) which allows them to produce high-frequency songs without the drawback of undesirable destructive interference reducing song amplitude.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

FM-Z, TJ, and DR designed the research and wrote the manuscript. FM-Z and TJ performed the experiments. CS conducted the statistics. FM-Z, TJ, and CS analysed the data. All authors contributed to the article and approved the submitted version.

Funding

This research was supported by a Leverhulme Trust grant (grant RPG-2014-284 to FM-Z and DR), a Human Frontier Science Programme (Cross Disciplinary Fellowship LT00024/2008-C to FM-Z) and a National Geographic grant (National Geographic Explorer’s grant RG120495 to FM-Z). DR acknowledges the support of the Royal Society of London, by the United Kingdom–India Education and Research Initiative (grant no. SA06-169E to DR) and the Biotechnology and Biological Sciences Research Council (grant no. BB/I009671/1). TJ was supported through a Human Frontier Science Programme grant during the experimental phase and has received funding from the European Union’s Horizon 2020 Research and Innovation Programme under the Marie Skłodowska-Curie grant agreement (no. 829208, InWingSpeak). TJ also acknowledges financial support from the publication fund of the University of Graz.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank the editor and reviewers for their helpful comments on the manuscript. FMZ and TJ would like to dedicate this article to Henry Bennet-Clark, Berthold Hedwig, Uwe Koch, Ken Prestwich, and Thomas Walker for their pioneering and inspiring works in cricket bioacoustics.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2021.647786/full#supplementary-material

Supplementary Video 1 | A male Gryllus bimaculatus producing calling song in the experimental setup after pharmacological injection of Eserine (10^–2 mol/l) into the brain. The cricket is mounted and fixed on a holder in front of the LDV. The LDV’s laser dot is visible on the harp area of the right wing.

Supplementary Video 2 | Animation of the vibration map of unengaged left and right wing of a male Gryllus bimaculatus as derived from LDV recordings. The wings are elevated upward from the animal’s body at a similar angle to the natural singing position, spaced apart and imaged from the front; the reference microphone is visible between and slightly behind the wings. The overlaid vibration map shows the colour-coded relative displacement (μm/Pa; red = max. positive displacement; blue = max. negative displacement) of the wing surface as a response to acoustic stimulation at the wings’ overall resonance frequency (4.62 kHz). Here, the LW displacement amplitude is higher than the RW’s.

References

Baker, A., Sarria-S, F. A., Morris, G. K., Jonsson, T., and Montealegre-Z, F. (2017). Wing resonances in a new dead-leaf-mimic katydid (Tettigoniidae: Pterochrozinae) from the Andean cloud forests. Zool. Anz. 270, 60–70. doi: 10.1016/j.jcz.2017.10.001

CrossRef Full Text | Google Scholar

Bates, D., Mächler, M., Bolker, B., and Walker, S. (2015). Fitting linear mixed-effects models using Lme4. J. Stat. Softw. 67, 1– 48. doi: 10.18637/jss.v067.i01

CrossRef Full Text | Google Scholar

Bennet-Clark, H. C. (1989). “Songs and the physics of sound production,” in Cricket Behavior and Neurobiology, eds F. Huber, T. E. Moore, and W. Loher (Ithaca, NY: Comstock Publishing Associates), 227–261.

Google Scholar

Bennet-Clark, H. C. (1998). Size and scale effects as constraints in insect sound communication. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 353, 407–419. doi: 10.1098/rstb.1998.0219

CrossRef Full Text | Google Scholar

Bennet-Clark, H. C. (1999). Resonators in insect sound production: how insects produce loud pure-tone songs. J. Exp. Biol. 202, 3347–3357.

Google Scholar

Bennet-Clark, H. C. (2003). Wing resonances in the Australian field cricket Teleogryllus oceanicus. J. Exp. Biol. 206, 1479–1496. doi: 10.1242/jeb.00281

PubMed Abstract | CrossRef Full Text | Google Scholar

Bennet-Clark, H. C., and Bailey, W. J. (2002). Ticking of the clockwork cricket: the role of the escapement mechanism. J. Exp. Biol. 205, 613–625.

Google Scholar

Desutter-Grandcolas, L., and Robillard, T. (2004). Acoustic evolution in crickets: need for phylogenetic study and a reappraisal of signal effectiveness. An. Acad. Bras. Ciênc. 76, 301–315.

Google Scholar

Elliott, C. J. H., and Koch, U. T. (1985). The clockwork cricket. Naturwissenschaften 72, 150–153. doi: 10.1007/BF00490404

CrossRef Full Text | Google Scholar

Fletcher, N. H. (1992). Acoustic Systems in Biology. Oxford: Oxford University Press.

Google Scholar

Forrest, T. G., and Green, D. M. (1991). Sexual selection and female choice in mole crickets (Scapteriscus: Gryllotalpidae): modelling the effects of intensity and male spacing. Bioacoustics 3, 93–109. doi: 10.1080/09524622.1991.9753166

CrossRef Full Text | Google Scholar

Gu, J.-J., Montealegre-Z, F., Robert, D., Engel, M. S., Qiao, G.-X., and Ren, D. (2012). Wing stridulation in a jurassic katydid (Insecta, Orthoptera) produced low-pitched musical calls to attract females. Proc. Natl. Acad. Sci. U.S.A. 109, 3868–3873. doi: 10.1073/pnas.1118372109

PubMed Abstract | CrossRef Full Text | Google Scholar

Hartmann, W. M. (1997). Signals, Sound, and Sensation. Woodbury, NY: American Institute of Physics.

Google Scholar

Hedwig, B. (2000). Control of cricket stridulation by a command neuron: efficacy depends on the behavioral state. J. Neurophysiol. 83, 712–722.

Google Scholar

Hedwig, B., and Becher, G. (1998). Forewing movements and intracellular motoneurone stimulation in tethered flying locusts. J. Exp. Biol. 201, 731–744.

Google Scholar

Koch, U. T., Elliott, C. J. H., Schäffner, K.-H., and Kleindienst, H.-U. (1988). The mechanics of stridulation of the cricket Gryllus campestris. J. Comp. Physiol. 162, 213–223. doi: 10.1007/BF00606086

CrossRef Full Text | Google Scholar

Kostarakos, K., Hartbauer, M., and Römer, H. (2008). Matched filters, mate choice and the evolution of sexually selected traits. PLoS One 3:e3005. doi: 10.1371/journal.pone.0003005

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuznetsova, A., Brockhoff, P. B., and Christensen, R. H. B. (2017). lmertest package: tests in linear mixed effects models. J. Stat. Softw. 82, 1–26. doi: 10.18637/jss.v082.i13

CrossRef Full Text | Google Scholar

Lenth, R. (2020). emmeans: Estimated Marginal Means, Aka Least-Squares Means.

Google Scholar

Michelsen, A. (1998). The tuned cricket. News Physiol. Sci. 13, 32–38.

Google Scholar

Michelsen, A., and Larsen, O. N. (2008). Pressure difference receiving ears. Bioinspir. Biomim. 3:011001.

Google Scholar

Montealegre-Z, F. (2005). Biomechanics of Musical Stridulation in Katydids (Orthoptera: Ensifera: Tettigoniidae): An Evolutionary Approach. Ph.D. thesis, University of Toronto, Canada.

Google Scholar

Montealegre-Z, F., Jonsson, T., and Robert, D. (2011). Sound radiation and wing mechanics in stridulating field crickets (Orthoptera: Gryllidae). J. Exp. Biol. 214, 2105–2117. doi: 10.1242/jeb.056283

PubMed Abstract | CrossRef Full Text | Google Scholar

Montealegre-Z, F., and Postles, M. (2010). Resonant sound production in Copiphora gorgonensis (Tettigoniidae: Copiphorini), an endemic species from parque nacional natural Gorgona, Colombia. J. Orthoptera Res. 19, 347–355. doi: 10.1665/034.019.0223

CrossRef Full Text | Google Scholar

Montealegre-Z, F., Ogden, J., Jonsson, T., and Soulsbury, C. D. (2017). Morphological determinants of signal carrier frequency in katydids (Orthoptera): a comparative analysis using biophysical evidence of wing vibration. J. Evol. Biol. 30, 2068–2078. doi: 10.1111/jeb.13179

PubMed Abstract | CrossRef Full Text | Google Scholar

Nocke, H. (1971). Biophysik der Schallerzeugung durch die Vorderflügel der Grillen. Z. Vgl. Physiol. 74, 272–314. doi: 10.1007/bf00297730

CrossRef Full Text | Google Scholar

Peña Ramirez, J., Olvera, L. A., Nijmeijer, H., and Alvarez, J. (2016). The sympathy of two pendulum clocks: beyond Huygens’ observations. Sci. Rep. 6:23580. doi: 10.1038/srep23580

PubMed Abstract | CrossRef Full Text | Google Scholar

Pires, A., and Hoy, R. R. (1992). Temperature coupling in cricket acoustic communication. I. Field and laboratory studies of temperature effects on calling song production and recognition in Gryllus firmus. J. Comp. Physiol. 171, 69–78. doi: 10.1007/bf00195962

PubMed Abstract | CrossRef Full Text | Google Scholar

Prestwich, K. N., Lenihan, K. M., and Martin, D. M. (2000). The Control of carrier frequency in cricket calls: a refutation of the subalar-tegminal resonance / auditory feedback model. J. Exp. Biol. 203, 585–596.

Google Scholar

Prestwich, K. N., and Walker, T. J. (1981). Energetics of Singing in crickets: effect of temperature in three trilling species (Orthoptera: Gryllidae). J. Comp. Physiol. 143, 199–212. doi: 10.1007/BF00797699

CrossRef Full Text | Google Scholar

R Core Team (2020). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.

Google Scholar

Robillard, T., Montealegre-Z, F., Desutter-Grandcolas, L., Grandcolas, P., and Robert, D. (2013). Mechanisms of high-frequency song generation in brachypterous crickets and the role of ghost frequencies. J. Exp. Biol. 216, 2001–2011. doi: 10.1242/jeb.083964

PubMed Abstract | CrossRef Full Text | Google Scholar

Robillard, T., ter Hofstede, H. M., Orivel, J., and Vicente, N. M. (2015). Bioacoustics of the neotropical eneopterinae (Orthoptera, Grylloidea, Gryllidae). Bioacoustics 24, 123–143. doi: 10.1080/09524622.2014.996915

CrossRef Full Text | Google Scholar

Römer, H. (1998). “The sensory ecology of acoustic communication in insects,” in Comparative Hearing: Insects, eds R. R. Hoy, A. N. Popper, and R. R. Fay (New York, NY: Springer), 63–96.

Google Scholar

Rossing, T. D. (1990). The Science of Sound. Reading, MA: Addison-Wesley.

Google Scholar

Sarria-S, F. A., Buxton, K., Jonsson, T., and Montealegre-Z, F. (2016). Wing mechanics, vibrational and acoustic communication in a new bush-cricket species of the genus Copiphora (Orthoptera: Tettigoniidae) From Colombia. Zool. Anz. 263, 55–65. doi: 10.1016/j.jcz.2016.04.008

CrossRef Full Text | Google Scholar

Sarria-S, F. A., Morris, G. K., Windmill, J. F. C., Jackson, J., and Montealegre-Z, F. (2014). Shrinking wings for ultrasonic pitch production: hyperintense ultra-short-wavelength calls in a new genus of neotropical katydids (Orthoptera: Tettigoniidae). PLoS One 9:e98708. doi: 10.1371/journal.pone.0098708

PubMed Abstract | CrossRef Full Text | Google Scholar

Simmons, L. W., and Ritchie, M. G. (1996). Symmetry in the Songs of Crickets. Proc. R. Soc. Lond. B Biol. Sci. 263, 1305–1311. doi: 10.1098/rspb.1996.0191

CrossRef Full Text | Google Scholar

Sismondo, E. (1993). Ultrasubharmonic resonance and nonlinear dynamics in the song of Oecanthus nigricornis F. Walker (Orthoptera: Gryllidae). Int. J. Insect Morphol. Embryol. 22, 217–231. doi: 10.1016/0020-7322(93)90011-O

CrossRef Full Text | Google Scholar

Song, H., Béthoux, O., Shin, S., Donath, A., Letsch, H., Liu, S., et al. (2020). Phylogenomic analysis sheds light on the evolutionary pathways towards acoustic communication in Orthoptera. Nat. Commun. 11:4939. doi: 10.1038/s41467-020-18739-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Walker, T. J. (1962). Factors responsible for intraspecific variation in the calling songs of crickets. Evolution 16:407. doi: 10.2307/2406176

CrossRef Full Text | Google Scholar

Walker, S. E., and Cade, W. H. (2003). The effects of temperature and age on calling song in a field cricket with a complex calling song, Teleogryllus oceanicus (Orthoptera: Gryllidae). Can. J. Zool. 81, 1414–1420. doi: 10.1139/z03-106

CrossRef Full Text | Google Scholar

Warren, P. S., Katti, M., Ermann, M., and Brazel, A. (2006). Urban bioacoustics: it’s not just noise. Anim. Behav. 71, 491–502. doi: 10.1016/j.anbehav.2005.07.014

CrossRef Full Text | Google Scholar

Wenzel, B., Elsner, N., and Hedwig, B. (1998). Microinjection of neuroactive substances into brain neuropil controls stridulation in the cricket Gryllus bimaculatus (De Geer). Naturwissenschaften 85, 452–454.

Google Scholar

Wenzel, B., and Hedwig, B. (1999). Neurochemical control of cricket stridulation revealed by pharmacological microinjections into the brain. J. Exp. Biol. 202, 2203–2216.

Google Scholar

Wiley, R. H. (2006). “Signal detection and animal communication,” in Advances in the Study of Behavior, eds H. J. Brockmann, P. J. Slater, and C. T. Snowdon (London: Academic Press), 217–247.

Google Scholar