Estrogen as an Essential Resource and the Coexistence of ER+ and ER– Cancer Cells

Kareva, Irina; Brown, Joel S.

doi:10.3389/fevo.2021.673082

ORIGINAL RESEARCH article

Front. Ecol. Evol., 17 August 2021

Sec. Behavioral and Evolutionary Ecology

Volume 9 - 2021 | https://doi.org/10.3389/fevo.2021.673082

This article is part of the Research Topic From Ecology to Cancer Biology and Back Again View all 18 articles

Estrogen as an Essential Resource and the Coexistence of ER⁺ and ER^– Cancer Cells

$\r\nIrina Kareva*$ Irina Kareva^1*

Joel S. Brown²

¹Computational and Modeling Sciences Center, Arizona State University, Tempe, AZ, United States
²Department of Integrated Mathematical Oncology, Moffitt Cancer Center, Tampa, FL, United States

Diagnosis of estrogen sensitivity in breast cancer is largely predicated on the ratio of ER⁺ and ER^– cancer cells obtained from biopsies. Estrogen is a growth factor necessary for cell survival and division. It can also be thought of as an essential resource that can act in association with other nutrients, glucose, glutamine, fatty acids, amino acids, etc. All of these nutrients, collectively or individually, may limit the growth of the cancer cells (Liebig’s Law of the Minimum). Here we model estrogen susceptibility in breast cancer as a consumer-resource interaction: ER⁺ cells require both estrogen and glucose as essential resources, whereas ER^– only require the general resource. The model predicts that when estrogen is the limiting factor, other nutrients may go unconsumed and available at higher levels, thus permitting the invasion of ER^– cells. Conversely, when ER^– cells are less efficient on glucose than ER⁺ cells, then ER^– cells limited by glucose may be susceptible to invasion by ER⁺ cells, provided that sufficient levels of estrogen are available. ER⁺ cells will outcompete ER^– cells when estrogen is abundant, resulting in low concentrations of interstitial glucose within the tumor. In the absence of estrogen, ER^– cells will outcompete ER⁺ cells, leaving a higher concentration of interstitial glucose. At intermediate delivery rates of estrogen and glucose, ER⁺ and ER^– cells are predicted to coexist. In modeling the dynamics of cells in the same tumor with different resource requirements, we can apply concepts and terms familiar to many ecologists. These include: resource supply points, R^∗, ZNGI (zero net growth isoclines), resource depletion, and resource uptake rates. Based on the circumstances favoring ER⁺ vs. ER^– breast cancer, we use the model to explore the consequences of therapeutic regimens that may include hormonal therapies, possible roles of diet in changing cancer cell composition, and potential for evolutionarily informed therapies. More generally, the model invites the viewpoint that cancer’s eco-evolutionary dynamics are a consumer-resource interaction, and that other growth factors such as EGFR or androgens may be best viewed as essential resources within these dynamics.

Introduction

Food-webs within ecosystems describe the trophic relationship between species of an ecological community. There can be predators, prey and resources, where different species find themselves consuming those on a lower trophic level, while being consumed by those on a higher one (Rosenzweig, 1971; Oksanen et al., 1981). Predators exploit prey, prey exploit resources, and resource renewal fuels the food-web. For species on the same trophic level, competition is often indirect. One individual competes with another by consuming and depressing the availability of shared resources. Such ecosystems may have two, three, four, or possibly even more trophic levels (Oksanen and Oksanen, 2000).

A key element of consumer-resource dynamics is the nutritional relationship of resources to the consumer, often showcased by the “beer and pretzel” example of complementary resources. To a consumer, two resources may be perfect substitutes, complementary, hemi-essential or essential (Tilman, 1980). Two nutrients are perfect substitutes if the value of a given diet is a linear, weighted average of the two nutrients in the diet. They are complementary if there are diminishing returns to fitness from consuming more of one of the resources. They are hemi-essential if (i) a non-zero amount of each must be consumed, (ii) there are diminishing returns to consuming more of one, and (iii) consuming more of one resource increases the value of consuming the other (Letnic and Crowther, 2013).

Two resources are essential if some ratio of the two must be consumed to achieve higher reward. That is, increasing consumption of the first resource has no value if consumption of the second resource limits the diet’s value, and vice-versa. Such resources conform to Liebig’s Law of the Minimum (Liebig, 1876). In the context of agriculture, Justus Freiherr von Liebig (von Liebig, 1840; Liebig, 1876) noted that beyond a certain point adding more of one nutrient, such as nitrogen, did not increase yields as some other nutrient, such as phosphorus, was now the limiting resource. With two resources, at any given time just one or the other resource is limiting unless they conform to a specific ratio in the diet. Essential resources impact the dynamics of both more traditional ecosystems, such as plants or microbes, as well as the dynamics within the ecosystem of the human body. Essential resources may characterize the nutrient or molecular requirements of normal cells, as well as cancer cells within their host.

While normal cells are not free-living single celled organisms, they do rely on consumption of blood-born or tissue-generated nutrients that can serve as fuel, as structural molecules, or as functional molecules (Thompson, 2011). Some of these nutrients can be thought of as general resources that are used by all cells in the human body (Palm and Thompson, 2017; Amend et al., 2018). These can include glucose, oxygen, and amino acids. Among these, some are essential, such as the essential amino acids (e.g., lysine) that cannot be synthesized from other amino acids or obtained in another way. Many other molecules can be used as fuel or metabolically transformed into the building blocks for structural and functional purposes (Hosios et al., 2016).

Some nutrients can be described as specific resources in that only a subset of cell types or tissues need and use them. For instance, in humans only a subset of cells in the liver and brain can, in general, take up and metabolize fructose; most of our cells cannot (Oppelt et al., 2017). Furthermore, in some cases, the need for a specific resource by a subset of cell types has evolved as an adaption for the whole organism to control the proliferation or metabolic activity of these cell subsets without impacting other cells. Hormones are examples of such specific resources that serve to regulate specific cells within specific tissues; examples of such resources include estrogen for glandular tissue in the breast and testosterone for glandular tissue in the prostate that are necessary for these cells to proliferate. Even as all other nutrients are in ample supply, proliferation of subsets of cells can be controlled by regulating the hormone supply. Hormones, therefore, serve as essential resources relative to the pool of other resources. Yet, as growth factors, they do not provide fuel or material for the cell. Nevertheless, specific cells have evolved to be metabolically wired to require these growth factors as keys (they generally form a dimer with another molecule within the cell (Duffy, 2006; Razandi et al., 2004; Lallous et al., 2013) to initiate metabolic pathways, including the possibility of cell division. They are used up in the process and metabolically broken down. As such, they are a faux resource, whose adaptive value is for the whole organism and not for the individual cell (Tilman, 1982).

Breast cancer cells, at least initially, carry the ancestral trait of requiring estrogen as an essential resource. The ability of cells to recognize and utilize estrogen is mediated through estrogen receptors (ER), which have been an appealing therapeutic target for patients with breast cancer since their discovery over a century ago. Beatson (1896) first observed in 1896 that removing the ovaries can lead to breast cancer remission. Over half a century later, estrogen and its receptors were confirmed as key actors in breast cancer (Jensen et al., 1971), marking the beginning of therapies to interfere with ER signaling to treat the disease.

Once a patient’s breast cancer is clinically detectable, cells of the tumor can be classified as ER⁺ (requiring estrogen) or ER^– (lacking estrogen receptors) by immunohistochemical staining of tumor biopsies. Most primary breast cancers possess both types of cells coexisting within the tumor. Breast cancers are scored pathologically as ER⁺ or ER^– based on the percentage of cells exhibiting the estrogen receptor. Patients with ER⁺ breast cancer typically have a more favorable prognosis compared to ER^– patients, with the arsenal of therapeutic interventions expanded to include therapies that interfere with estrogen production or estrogen signaling. Women that score as ER^– have fewer therapy options (Hammond et al., 2010).

Ecologically, within a breast cancer tumor we expect to observe at least three distinct types of communities: all ER⁺, all ER^– or a community of the two coexisting together. Coexistence seems to be the norm (Jensen et al., 1971; Harvey et al., 1999; Caruana et al., 2020). Here, we want to leverage ecological insights about consumer-resource dynamics and resource subsistence levels to explore the circumstances favoring ER⁺ vs. ER^– breast cancer. We explore the possibilities for evolutionarily steering cancer cell frequencies through nutrient manipulations. To achieve this goal, we model interactions of cancer cells with a general (glucose) and a specific (estrogen) resource subject to Liebig’s Law of the Minimum as a consumer-resource interaction. We consider nutrient uptake rates, resource supply rates, and the proliferation and survival consequences to cancer cells of their nutrient uptake. We identify conditions favoring ER⁺ or ER^– cancer cells in the tumor microenvironment and discuss strategies that may impact success of hormone-based therapeutic interventions.

Model Description

In our modeling framework, we consider two types of consumers. Consumers using strategy 1, S₁, use both specific and general resources (ER⁺ cells), while consumers using strategy 2, S₂, rely only on general resources (ER^– cells). Evidence suggests that in some cases these consumer strategies are heritably distinct and as such are pure strategies that breed true. In other cases, cancer cells can switch between the strategies.

Let the individuals within the population of cancer cells be denoted as x_α(t), where α represents a mixed strategy of using S₁ with probability α. If α = 1, cells only use S₁, and if α = 0, cells only use S₂.

Cells utilizing strategy S₁ depend on both the specific resourceR₁(t), such as estrogen, and the general resourceR₂(t), such as glucose, as essential resources to the cell. Parameters a_ij (per time) represent the probability of encountering a given item of the resource, while parameters b_ijrepresent the conversion rate of resources into the proliferation daughter cells; we also assume that there exists some intrinsic cell death rate δ. Finally, we can describe the fitness (per capita proliferation rate), F₁(t), of cells using strategy S₁ based on Liebig’s Law of the Minimum as F₁(t) = min⁡(b₁₁a₁₁R₁(t),a₂₁b₂₁R₂(t)). Cells that use strategy S₂ depend only on general resource R₂(t) and grow at a rate F₂(t) = a₂₂b₂₂R₂(t). Together, the change over time in a population with ER⁺ (x_{α = 0}) and ER^– (x_{α = 1}) cancer cells can be described as:

x_{α = 1}^{'} = x_{α = 1} F_{1} (R_{1}, R_{2}) - δ x_{α = 1}

x_{α = 0}^{'} = x_{α = 0} F_{2} (R_{2}) - δ x_{α = 0} . (1)

Next, we assume that resources R₁(t) and R₂(t) have constant inflow rates R₀₁ and R₀₂, respectively, and are cleared or consumed by normal cells at rates k₁ and k₂ per unit of the resources R₁(t) andR₂(t), respectively. Resource R₂(t) can be consumed by cells using strategy S₁ or strategy S₂, while R₁(t) can only be consumed by cells using strategy S₁. These assumptions are captured by the following system of equations:

\frac{d x_{α = 1} (t)}{d t} = x_{α = 1} (t) \min (a_{11} b_{11} R_{1} (t), a_{21} b_{21} R_{2} (t))

- δ x_{α = 1} (t)

\frac{d x_{α = 0} (t)}{d t} = x_{α = 0} (t) a_{22} b_{22} R_{2} (t) - δ x_{α = 0} (t)

N (t) = x_{α = 1} (t) + x_{α = 0} (t)

\frac{d R_{1} (t)}{d t} = R_{01} - k_{1} R_{1} (t) - α x_{α = 0} (t) \min

(a_{11} R_{1} (t), a_{21} R_{2} (t) \frac{b_{21}}{b_{11}})

\frac{d R_{2} (t)}{d t} = R_{02} - k_{2} R_{2} (t) - α x_{α = 0} (t) a_{21} \min (a_{11} R_{1} (t)

\frac{b_{11}}{b_{21}}, a_{21} R_{2} (t)) - (1 - α) x_{α = 1} (t) a_{22} R_{2} (t) (2)

In formulating these dynamics, we assume that cancer cells using strategy S₁ do not overconsume either of the essential resources. If resource 1 is limiting, then the cancer cell will consume all encountered items of resource 1 but only some of the encountered items of resource 2. The amount of resource 2 consumed when it is not limiting is just that amount needed to fully utilize resource 1. And vice-versa if resource 2 is limiting.

Equilibrium Conditions

In the absence of consumption by the cancer cells, resources will achieve a steady state level at $R_{1}^{'} = \frac{R_{01}}{k_{1}}$ for specific resource R₁, and $R_{2}^{'} = \frac{R_{02}}{k_{2}}$ for general resource R₂. In consumer-resource theory, these levels are referred to as resource supply points. This represents the highest standing crop of resources that is achievable within the tumor.

Each consumer strategy, S₁ and S₂, will have a subsistence level of resource abundance, R₁^∗ and R₂^∗, below which it will have negative fitness (declining numbers) and above which fitness will be positive (increasing numbers). The subsistence level of resources can be found by setting the fitness of a consumer strategy equal to zero and solving for the associated R^∗.

When α = 1, cells require both resources (ER⁺ cells), and thus subsistence levels for both resources are $R_{1}^{*} = \frac{δ}{a_{11} b_{11}}$ when $R_{2} \geq \frac{δ}{a_{21} b_{21}}$ , or $R_{2}^{*} = \frac{δ}{a_{21} b_{21}}$ when $R_{1} \geq \frac{δ}{a_{11} b_{11}}$ . That is, these are the minimal levels of both resources that an ER⁺ cell requires for survival. In consumer resource theory, the graph of this in the state space of R₂ vs. R₁ forms an elbow, and it describes the zero net growth isocline (ZNGI) for a consumer harvesting essential resources (see Figure 1).

FIGURE 1

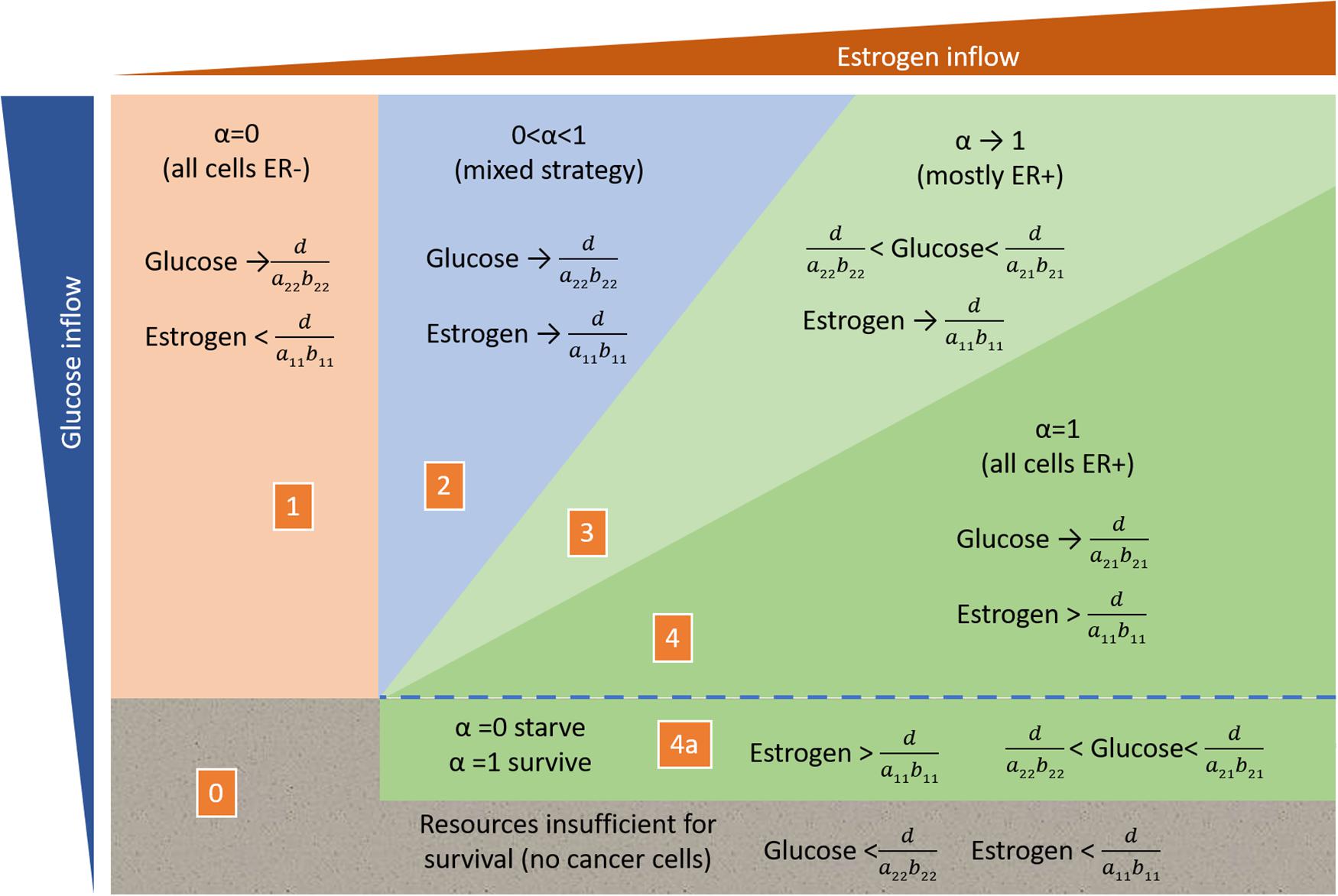
Figure 1. Outcome of consumer resource dynamics as influenced by the resource supply point. The five regions show the qualitatively different outcomes described by System (Rosenzweig, 1971).

Conversely, for cells with α = 0, which depend only on the general resource R₂, the resource subsistence level is given by $R_{2}^{*} = \frac{δ}{a_{22} b_{22}}$ . In the state space of R₂ vs. R₁, this describes a horizontal line, and it is the zero net growth isocline of strategy S₂ (Figure 1). Above this line, cells with strategy S₂ have positive fitness and below this line their fitness is negative. By the definition of this strategy, the fitness of individuals with S₂ is independent of the availability of the specific resource, R₁.

In a consumer-resource model there are limits to growth for the consumers. Consumers, intra- and inter-specifically, compete with each other. This competition is indirect via depletion of the standing crop of resources. This means that each species has a carrying capacity determined by the population size that depresses resource availability to its R^∗. At population sizes above this level, R will be driven below R^∗ and the consumer’s population growth will be negative, and vice-versa for population sizes below this level.

Role of Tradeoff

For there to be any possibility for the two consumer strategies to coexist, their ZNGIs must intersect at positive values of R₁ and R₂ as shown in Figure 1. The only way for the ZNGIs to not intersect is if the subsistence level of the general resource is lower for S₂ than for S₁. In this case, cancer cells with strategy S₂ will drive the level of the general resource to the point, where consumers using strategy S₁ will starve no matter what the abundance of the specific resource, R₁. Thus, for ER⁺ cancer cells to persist in the tumor, there must be a tradeoff, such that the ER^– cells free of the specific resource pay the price by having a higher subsistence level on the general resource compared to the ER⁺ cells: $\frac{δ}{a_{21} b_{21}} < \frac{δ}{a_{22} b_{22}}$ , which means a₂₁b₂₁ > a₂₂b₂₂. It is noteworthy that if hormone therapy or time permit ER^– cancer cells to break free of this constraint, then all the cancer cells will be ER^– and unaffected and essentially resistant to all forms of hormonal therapies.

ER^– breast cancers or ER⁺ cell lines such as MCF-7 that have been selected in the lab to be ER^– exhibit a rewiring of various metabolic pathways (Leung et al., 2010; Nayar et al., 2019). These can include the MAPK/ERK signaling pathways that seem to bypass the estrogen receptor pathway in normal cells of ER⁺ breast cancer cells (Peng et al., 2017). The rewired metabolic pathways are associated with upregulation of glucose transporters, GLUT1, and increased glycolysis (faster but less efficient use of glucose). Of relevance to our parameter selection, the relative availability of estrogen and glucose alters glucose uptake and metabolism by ER⁺ MCF-7 cells. In support of the idea that these are essential resources, increased estrogen for MCF-7 cells results in increased glucose uptake and metabolism (Kulkoyluoglu-Cotul et al., 2019). This suggests that the MCF-7 cells had been limited by estrogen, and so had suppressed utilization of glucose. With more estrogen, the amount of glucose that could be usefully utilized was thus increased. For these reasons, we assigned the ER^– a higher encounter rate on glucose than ER⁺ (a₂₂ > a₂₁), a lower conversion efficiency (b₂₁ > b₂₂), and a lower overall product (a₂₁b₂₁ > a₂₂b₂₂). Beyond satisfying these conditions, the selection of relative magnitudes was arbitrary.

With this tradeoff, ER⁺ cells have a lower R^∗ on glucose (= general resource) than ER^– cells when estrogen has a sufficiently high resource supply. With a surplus of estrogen, ER⁺ cells can achieve a higher population size than ER^– cells for a given resource supply of glucose. Furthermore, increasing the resource supply of glucose will raise the equilibrium population size of cancer cells. Some evidence supports this prediction. For instance, when grown as mono-cultures in 3-D spheroids, ER⁺ MCF-7 cells had higher carrying capacities than ER^– MDA-MB-231 cells (Freischel et al., 2020). Whether biopsies of women with ER⁺ breast cancer exhibit higher densities of cancer cells than those with ER^– breast cancer remains, to our knowledge, an open and interesting question.

The Role of Resource Supply Points

From here onwards we will assume that this tradeoff exists and that the ZNGIs do cross, as shown in Figure 1. The outcomes of the consumer-resource interactions now depend on the resource supply points. Even without competition from consumers using strategy S₁, consumer strategy S₁ will be absent if the supply points of either of the resources is below subsistence level. Similarly, even in the absence of competition from consumers using S₁, consumer strategy S₂ will be absent if the resource supply point for the general resource is below its subsistence level.

Region 0 of Figure 1: The cancer cell population cannot sustain itself and will go extinct if the resource supply points are below the subsistence levels of both consumer strategies.

Region 1 of Figure 1: Only consumer ER^– cells (α = 0) will be present in the cancer cell population if the resource supply point of glucose (general resource) is above S₂’s R^∗ but the resource supply point of estrogen (specific resource) is below the R^∗ of the ER⁺ cells.

Region 4a of Figure 1: Only ER⁺ cells can be present if the resource supply point is above their subsistence levels of glucose and estrogen, and the resource supply point on glucose is below the R^∗ of the ER^– strategy.

When the resource supply point, R’, is above the subsistence R^∗’s for both the ER⁺ and ER^– strategies, then there are 3 possible outcomes. In all cases, both strategies could exist in the absence of the other, but the presence of cancer cells using a particular strategy can influence resource depletion in a manner that does not permit both consumer strategies to be present.

Region 2 of Figure 1: A mix of ER⁺ and ER^– cells (0 < α < 1) becomes the expected outcome, when the ER⁺ cells are limited by estrogen and consume so little of the available glucose that they would leave a standing crop of glucose above the R^∗ of the ER^– cells. This outcome becomes likely when the resource supply point exhibits a high ratio of glucose to estrogen. The resulting equilibrium sees the coexistence of both cell types and the depletion of resources to the intersection of the ZNGIs. Namely, the level of estrogen matches the R^∗ of the ER⁺ cells, and the level of glucose matches the R^∗ of the ER^– cells.

Region 3 of Figure 1: With a moderate ratio of glucose to estrogen, the ER⁺ cells will still be limited by estrogen. This means that they leave a level of glucose above their R^∗; however, if this level of glucose is below the R^∗ of the ER^– cells, they will slowly and eventually be excluded from the community of cancer cells. In this region, the cancer will tend toward all ER⁺ (α = 1). The standing crop of resources will have estrogen at the R^∗ of the ER⁺ cells, and the standing crop of glucose will be above that of the ER⁺ cells and below that of the ER^– cells.

Region 4 of Figure 1: With a low ratio of glucose to estrogen at the resource supply point, the ER⁺ cells will be glucose limited and not estrogen limited. When this happens, they will drive glucose levels down to their R^∗ for glucose. Since this is lower than the R^∗ on glucose for the ER^– cells, the ER^– cells will be outcompeted from this community. One should see a rapid equilibration on a community of just ER⁺ cancer cells (α = 1).

All of the qualitatively different regions shown in Figure 1 can be solved for analytically from the consumer resource dynamics as summarized in the figure. This analysis allows us to predict the resource-dependent boundaries between different population compositions. Specifically, we can predict resource steady state levels given a fixed population composition with respect to resource consumption strategy. Next, we perform the inverse analysis and predict what composition the population will evolve toward, subject to variations in resource availability and initial population composition.

Introducing Population Heterogeneity With Respect to Strategy Selection

In this section we address the question of how a population that is heterogeneous with respect to resource consumption strategy will evolve over time with respect to both its initial composition and properties of cells and the environment, i.e., with respect to variations in parameters R₀₁,R₀₂,a_ij,b_ij as defined in Table 1. For that, we assume that each individual cell in the population possesses a strategy parameter of α that belongs to the interval [0,1]. With this assumption, the population can consist of individuals that use either the pure strategy (cases analyzed in the previous section), or any mixture of the two pure strategies. There is value in allowing for both possibilities: a mix of two pure strategies vs. a continuum of mixed strategies. In the case of estrogen receptor status in breast cancer, evidence suggests cases in which ER⁺ and ER^– are heritably distinct and other cases where the trait is phenotypically plastic (Polyak, 2007; Dai et al., 2017; Sahoo et al., 2021).

TABLE 1

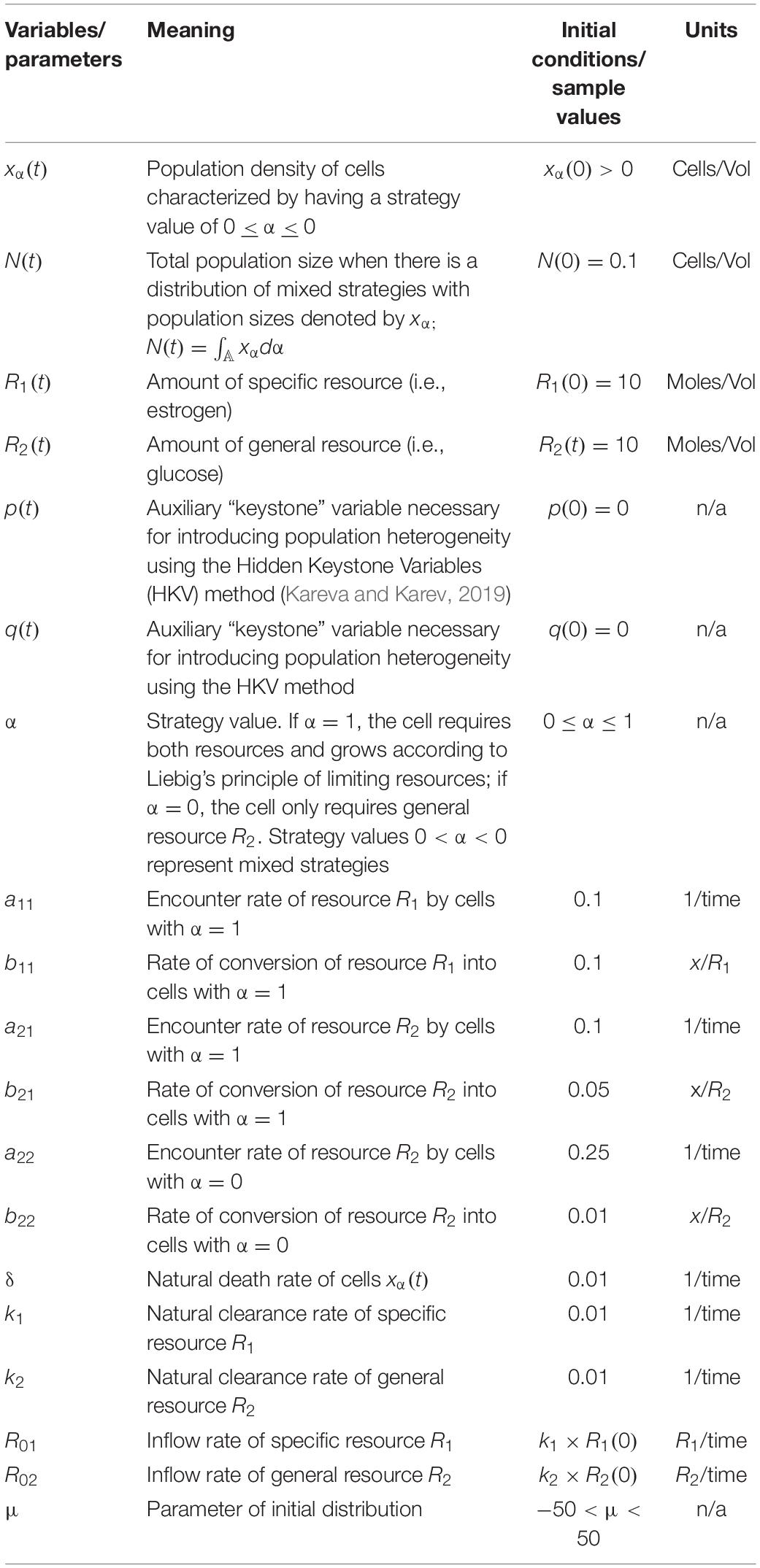
Table 1. Variables and parameters used when there are 2 pure strategies, System (Rosenzweig, 1971), and when there is a distribution of mixed strategies, System (Oksanen and Oksanen, 2000).

We can consider the dynamics of any starting distribution of mixed strategies through the application of the Hidden Keystone Variable (HKV) method (Kareva and Karev, 2019); the specific details of transformations necessary to apply the HKV method to this system of equations are given in Supplementary Appendix. The final system of equations reads as follows:

\frac{d R_{1} (t)}{d t} = R_{01} - k_{1} R_{1} (t) - E^{t} [α] N (t) \min

(a_{11} R_{1} (t), \frac{a_{21} b_{21} R_{2} (t)}{b_{11}})

\frac{d R_{2} (t)}{d t} = R_{02} - k_{2} R_{2} (t) - E^{t} [α] N (t) \min

(\frac{a_{11} b_{11} R_{1} (t)}{b_{21}}, a_{21} R_{2} (t)) - (1 - E^{t} [α]) N (t) a_{22} R_{2} (t) (3)

where E^t[α] is the expected value of the strategy parameter that changes over time as the population evolves, and N(t) is the total population size of all the cells. Derivations for expression describing E^t[α] and N(t) are given in Supplementary Appendix. Using this transformed system of equations we can now calculate change in population size, expected value and variance of α over time, thus enabling us to track evolution of the population with respect to resource consumption strategy subject to variations in environmental conditions.

Results

Model Analysis

We use equations (Oksanen and Oksanen, 2000) to firstly demonstrate the existence of the 4 qualitatively different regimes of coexistence of consumers with the resource, and the resulting final strategy, that are shown in Figure 1. The results of our simulations are given in Figure 2. We change the inflow rate R₀₁ of the specific resource, R₁, keeping all other parameter values constant as reported in Table 1; the initial distribution is assumed to be truncated exponential on the interval [0,1]; other truncated initial distributions can be chosen subject to data availability. We then evaluate changes in total population size N(t) (Figure 2A), changes in the standing crop of the specific resource R₁ (Figure 2B) and the general resource R₂ (Figure 2C); change in the mean value of the cancer cells’ strategy parameter α (Figure 2D), changes in the variance of α and change in the population composition over time. Equations used for these calculations are derived in Supplementary Appendix.

FIGURE 2

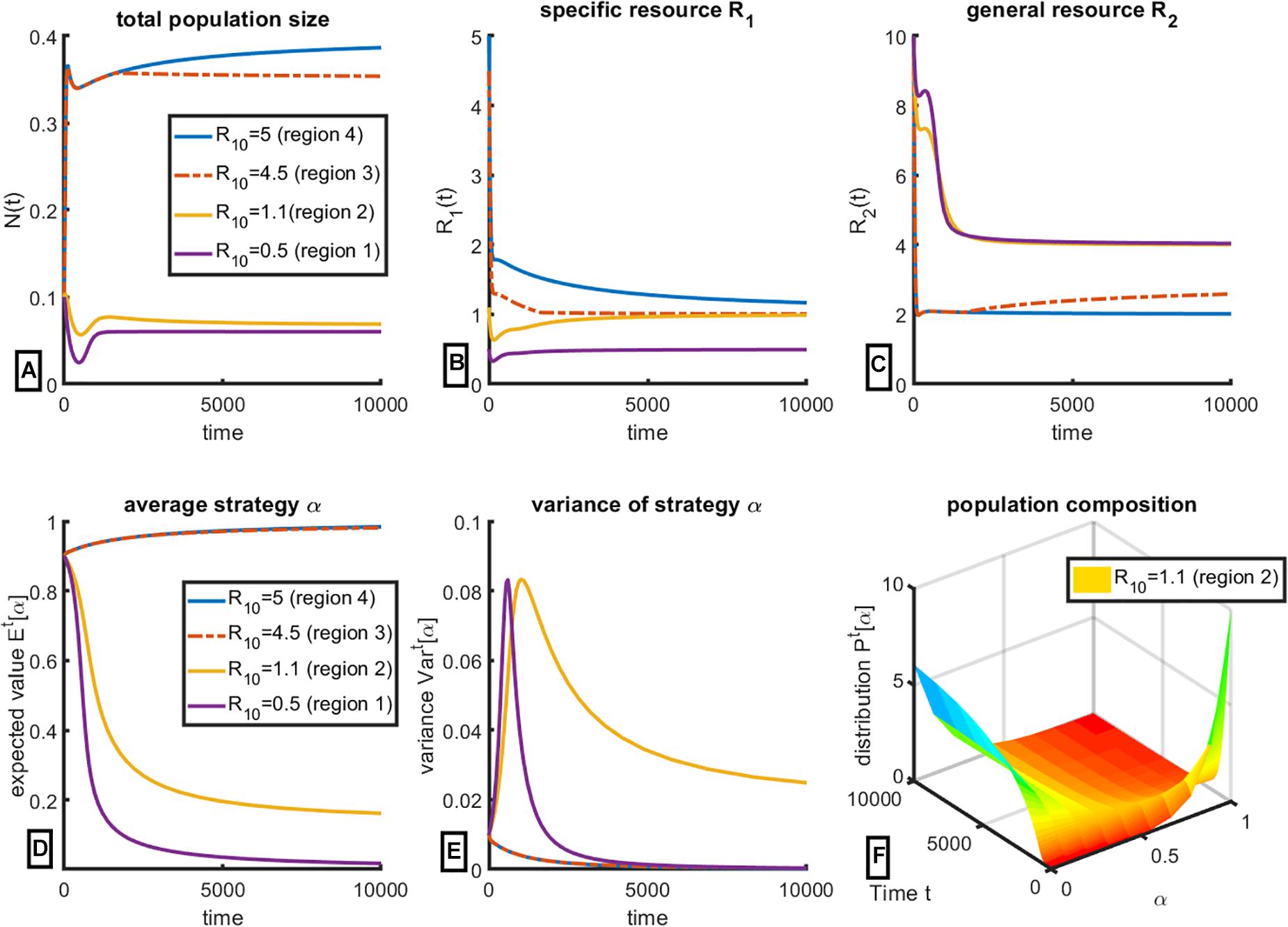
Figure 2. Evolution of the population of consumers over time with respect to resource consumption strategy subject to change in resource availability. Initial values of R₀₁ were chosen to provide representative plots of the 4 key regions of Figure 1. (A) Change in total population size N(t); (B) Equilibrium level of specific resource R₁ (here interpreted as estrogen) and (C) equilibrium level of general resource R₂, here interpreted as glucose, calculated from System (Oksanen and Oksanen, 2000); (D) change in mean strategy α ∈ [0,1]; (E) change in variance of α over time; (F) a representative plot of change in population composition changes over time, for R₀₁ = 1.1, corresponding to region 2 of Figure 1. All other parameter values are held constant at values given in Table 1.

For the set of parameter values given in Table 1, R₀₁ = 5 corresponds to region 4, where over time the population evolves toward Strategy 1; α→1, and therefore all the cells in the population require both resources (for the case when R₁ represents estrogen, this corresponds to all ER⁺ cells); the variance (Figure 2E) tends to 0 over time, confirming that at steady state, the population is indeed homogeneous with respect to strategy α. It is easy to confirm that the equilibrium levels of the specific resource R₁ is greater than $\frac{δ}{a_{11} b_{11}}$ , while the equilibrium level of the general resource R₂ tends toward S₁’s R^∗ of $\frac{δ}{a_{21} b_{21}}$ , as expected (see Figure 1).

Here the model predicts an initially counterintuitive observation: even though the population is composed solely of ER⁺ cells, there exists a surplus of estrogen (resource R₁). However, this makes sense within the framework of Liebig’s Law of the Minimum: the general resource R₂ is limiting, which results in a surplus of the specific resource R₁. This prediction can also have important diagnostic implications, as will be discussed later.

Decreasing the value of R₀₁ to 4.5 corresponds to region 3, where final population composition still tends to α→1 (Figures 2D,E). However, the final levels of both resources are different, as can be seen in Figures 2B,C. General resource R₂ is no longer limiting, and thus its equilibrium levels are higher than in the previous case, while the equilibrium levels of the specific resource R₁ are lower. Notably, final population size (Figure 2A) is lower in region 3 than in region 4, even though final population composition is nearly identical. In this region, estrogen is the limiting resource for the population of ER⁺ cells.

Further reducing the value of R₀₁ = 1.1 corresponds to region 2, which predicts the coexistence of ER⁺ and ER^– negative cells as a mixed strategy (Figure 2D). Notably, this population is heterogeneous at steady state, since its variance over time is non-zero (Figure 2E). The change in population composition can also be shown in Figure 2F, which plots distribution of cell clones with respect to α over time. As one can clearly see, the population composition changes over time but does not become concentrated at a single value of α, as happens for the other cases (not shown). Here, specific resource R₁ is limiting for ER⁺ cells (Figure 2B), and thus the level of general resource R₂ is at the highest level possible. This level corresponds to the R^∗ of the ER^– cells.

Finally, reducing R₀₁ to 0.5, effectively minimizing the level of specific resource R₁ below subsistence levels, predictably results in a population that consists entirely of ER^– cells (α→0). This population has the smallest final population size (Figure 2A) and is fully limited by the general resourceR₂.

These simulations confirm that the model described by System (Oksanen and Oksanen, 2000) exhibits the outcomes predicted and summarized in Figure 1. The simulations show the consumer-resource dynamics toward these outcomes and equilibria. The model tracks changes in the strategy distribution and the final population composition. The simulations verify that changing the ratio of the resource supply points of the two resources results in corresponding changes in the standing crop of the two resources, determining whether the tumor is expected to have all ER⁺, all ER^– or a mix of both cell types. We additionally demonstrate that populations with mixed equilibrium strategy are heterogeneous at steady state (rather than being composed of a single cell clone). Finally, we note that final population size of cancer cells is largest when ER⁺ cells dominate the tumor, i.e., cells with largest values of α. This last result happens because ER⁺ dominated tumors occur when the ER⁺ cells are limited by the general resource and not the specific resource. Since ER⁺ cells are more efficient on the general resources (lower R^∗), they can support a larger population size than if it were a tumor composed of ER^–. Whether cancers scored as ER⁺ have a higher overall density of cancer cells than those scored ER^– provides a testable prediction of the model.

Next, we evaluate how composition of the initial population affects the steady state strategy distribution.

Final Population Composition Is Invariant to Initial Distribution of Cell Clones in the Population

In the previous section we demonstrated that relative levels of specific and general resources affect final population composition. Now we evaluate the impact of initial population composition on final strategy distribution.

For that, we change the value of parameter μ in Equation (Thompson, 2011) that dictates the initial distribution of mixed strategies in the cancer cell population to see how populations with different initial mean values of α change over time. In the following we hold all other parameters constant at values given in Table 1 unless indicated otherwise. A representative plot of a population in region 2 of Figure 1 is given in Figure 3.

FIGURE 3

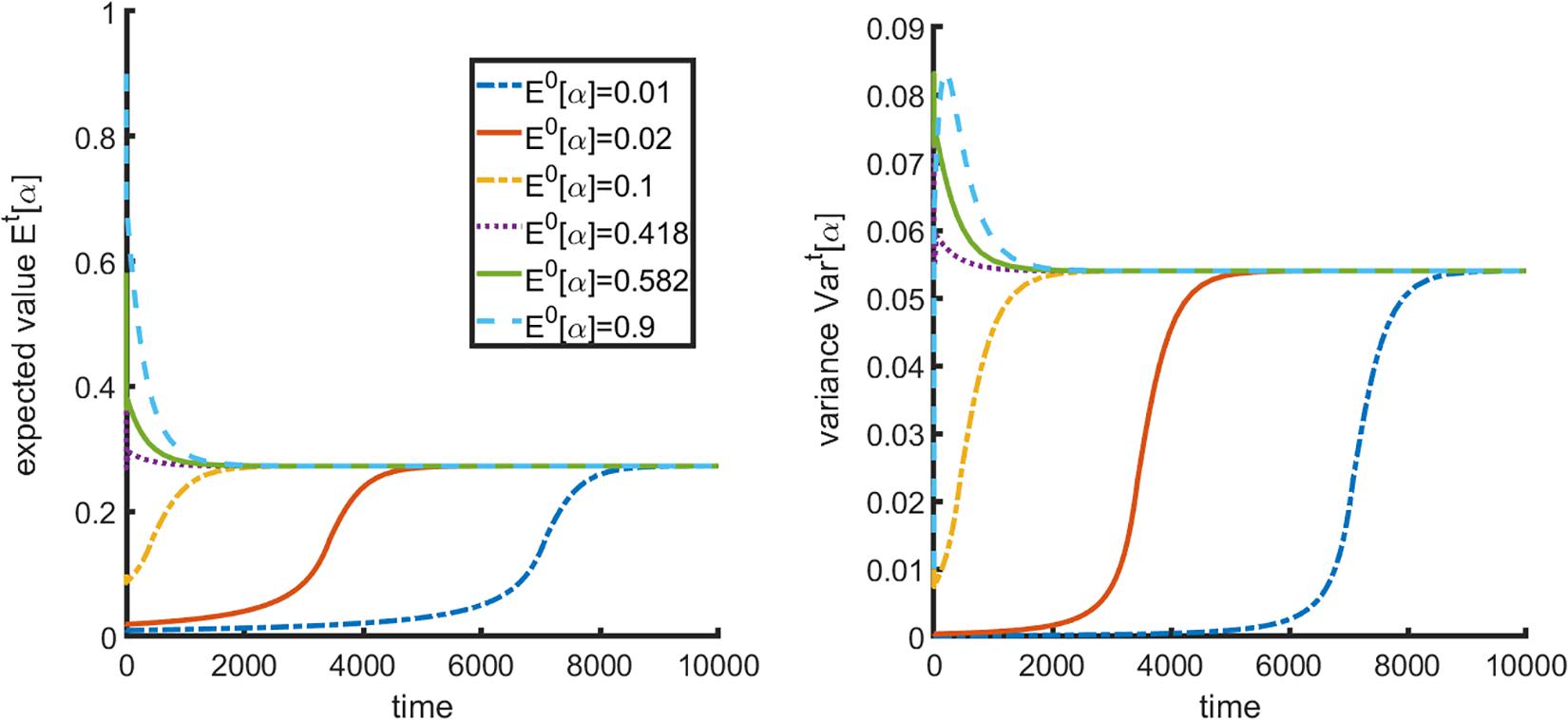
Figure 3. Impact of initial distribution on final population composition. (A) Final mean strategy α and (B) variance are invariant to initial distribution.

As one can see, changes in initial population composition do not affect the steady state value of α or the variance of the population; they only affect time necessary to reach the steady state, which is expected. From this we can conclude that within the frameworks of the proposed model, it is the relative resource supply points that will drive the evolution of the population over time, and thus it may be possible to steer population composition by manipulating resources.

Evolution of Population With Respect to Resource Availability

Next, we construct a more integrated picture of the dependence of population composition and resource availability on final strategy at steady state. The data were collected as follows: for various combinations of resource supply rates R₀₁ ∈ [0.1, 20] and R₂₀ ∈ [0.1, 10], the simulation was run until the population reached a steady state, at which point the corresponding values for total population size (Figure 4A), specific resource R₁ (Figure 4B), general resource R₂ (Figure 4C), average strategy α (Figure 4D), and average variance of α (Figure 4E) were noted. Additionally, we plotted the relationship between final population size and final average strategy at steady state in Figure 4F, showing clearly that final population size increases as α→1.

FIGURE 4

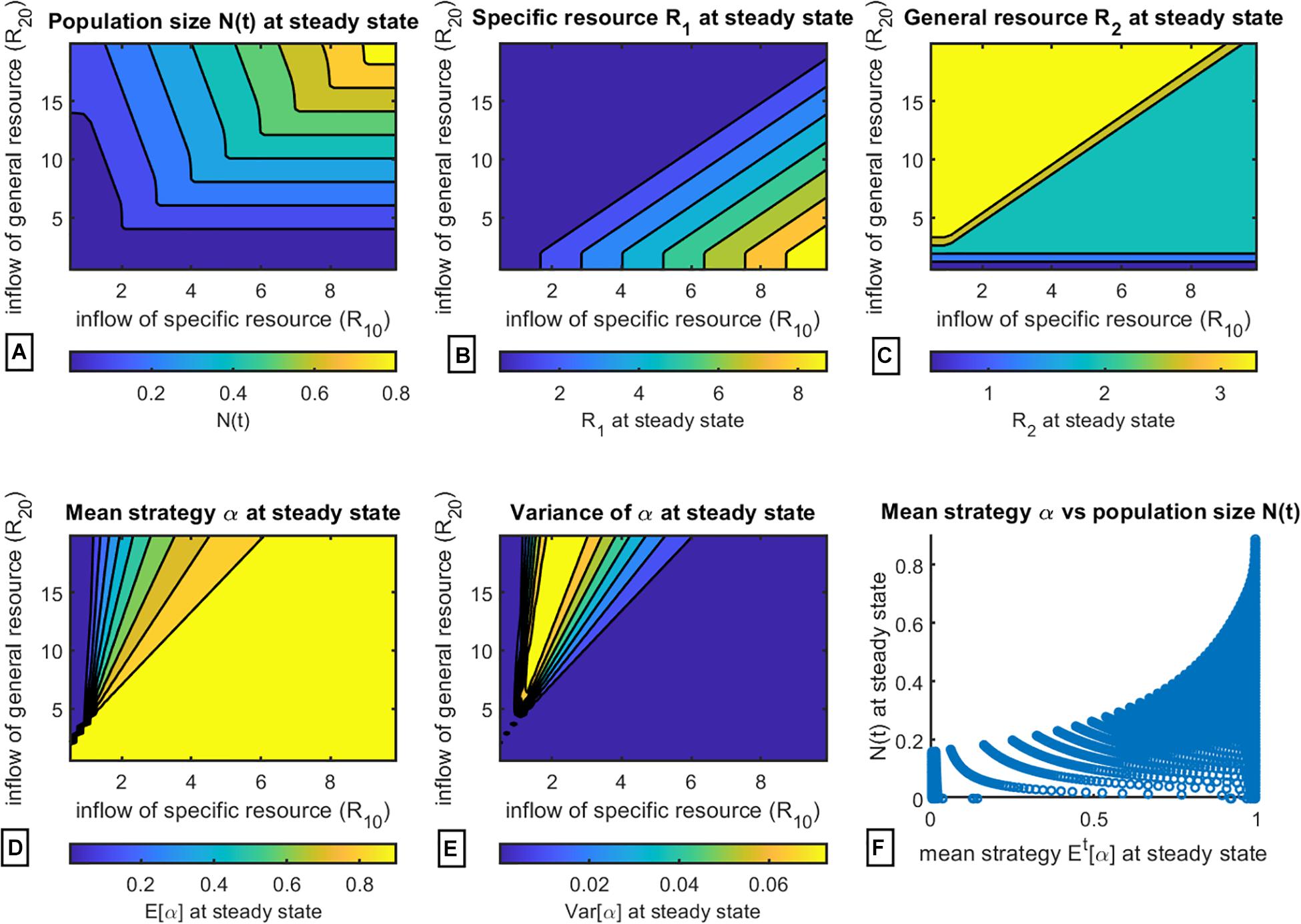
Figure 4. Evaluation of population composition and equilibrium values at steady state subject to variation of resource inflow rates. (A) population size N(t); (B) equilibrium levels of specific resource R₁; (C) equilibrium levels of general resource R₂; (D) mean strategy E^t[α] ∈ [0,1]; (E) variance Var^t[α]; (F) mean strategy E^t[α] vs. population size N(t) at steady state.

As expected, final population size is predicted to be largest when both resources are most abundant (Figure 4A). The resulting equilibrium abundances of the two resources do not directly depend on the resource supply points but on the resulting community composition. When the resource supply point of the general resource is high and that of the specific resource low, a mixed strategy results. Over this region of coexistence, the specific resource will equilibrate on the subsistence level R^∗ of consumer strategy 1 (Figure 4B), and the general resource will equilibrate on the subsistence R^∗ of strategy 2 (Figure 4C). As changing the ratio of resource supply points shifts the system from mixed strategies to all S₁ (α→1), the limiting resource switches from the specific to the general resource. Once this happens, the general resource will always equilibrate on S₁’s R^∗ for that resource (Figure 4C), and the specific resource at equilibrium will continue to increase (Figure 4B) as the ratio of the general to specific resource declines. This happens because a smaller and smaller proportion of the encountered items of the specific resource will actually be consumed by the S₁ cancer cells.

In Figure 4D we can see that indeed there exists a range of intermediate mixed strategies between regions of evolution toward pure strategies α→0 and α→1, in correspondence with the theoretically predicted regions described in Figure 1. Moreover, Figure 4E shows that highest variance, and thus highest degree of population heterogeneity, is observed for populations with intermediate values of α. This may have therapeutic implications, since more heterogeneous populations of cancer cells may indicate a more aggressive cancer in terms of developing metastases or resistance to therapy (Marusyk and Polyak, 2010; Rajput et al., 2017; Marusyk et al., 2020).

Implications for Hormonal Therapies of Breast Cancer

The direct impact of nutrient inflow rates on population composition raises the possibility of “evolutionary steering” (Stanková et al., 2019), aimed at promoting a more therapeutically susceptible composition of cancer cell types. Ideally, we would devise strategies to steer the populations toward a point where neither ER⁺ nor ER^– cells can persist (Region 0 in Figure 1). However, this cannot be achieved directly through nutrient manipulation without harming the host, since the general resources (glucose) are required by all cells of the body.

An alternative approach involves steering the population composition toward the ER⁺ phenotype, which is more susceptible to therapeutic interventions. Such interventions include several endocrine-based therapies, such as tamoxifen, fulvestrant and aromatase inhibitors (AIs). Development of tamoxifen, initially a contraceptive, has been a critical advance in breast cancer treatment (Jordan, 2003; Quirke, 2017). It acts as a selective ER modulator (SERM), interfering with signaling between ER and estrogen, although it has been shown to have both antagonist and weak agonist activity. Fulvestrant acts to not only block but also downregulate ER without agonist activity (Osborne et al., 2004). Both are effective in breast cancer, yet both can select for resistant cancer cells (Riggins et al., 2007; Mills et al., 2018), namely those that are ER^– or resistant through other mechanisms. AIs are small molecules that block conversion of precursor compounds into estrogenic molecules (Smith and Dowsett, 2003). AIs, such as anastrozole, letrozole, and exemestane, have proven effective as monotherapies (Mauri et al., 2006) and in combination with tamoxifen (Johnston et al., 2005; Winer et al., 2005; Early Breast Cancer Trialists’ Collaborative Group (Ebctcg), 2015).

With a range of options available for estrogen-dependent tumors, it is particularly important to provide therapeutic options to all patients who can benefit. Breast tumors can harbor a combination of ER⁺ and ER^– cells, but what fraction of ER⁺ cells within the tumor is high enough to qualify the patient for hormone therapies? This question is not as straightforward as one might believe. One issue concerns inconsistency between testing facilities in how they classify tumors as ER⁺ or ER^–. Typically, one or several sections from a biopsy are stained for ER expression using immunohistochemistry (IHC). Tumors may show a continuum of expression levels among the constituent cancer cells, some cells showing no expression at all (ER^– cells). Generally, all cells exhibiting expression “at any intensity” are reported as positive (Hammond et al., 2010). However, Layfield et al. (2003) showed that there exists considerable variability between ER classifications on the same tissue block when analyzed by different laboratories. Similar discrepancies have been reported by Goldstein et al. (2003) and Nkoy et al. (2010) highlighting differences in laboratory protocols (Ibarra et al., 2010). A nationwide assessment of positivity rates in the Netherlands (Dooijeweert et al., 2019) identified limited variability in a more recent analysis, but absolute variations still existed.

Next, even if there were no inter-laboratory inconsistencies, another question remains: what level of ER expression within the tumor is therapeutically relevant? Two main scoring methods have been used for evaluating the extent of ER positivity: H-score and Allred score. Allred score (Allred et al., 1998) combines the proportion of positive-staining tumor cells and the intensity of staining to give a score between 0 and 8. H-score (Goulding et al., 1995) aims to capture the full range of staining percentages and intensities in tumor samples rather than just the average intensity of the Allred score. H-scores range from 1 to 300. A larger score corresponds to a higher intensity of staining. A score of 1 corresponds to up to 1% ER⁺ cells among the cancer cells within the tumor.

Some studies however suggest that there are actually few cases of tumors being weakly ER⁺ vs. entirely ER^–. They suggest that ER staining results in a bimodal distribution of tumor types (Collins et al., 2005). The lack of consistency in testing and potential misclassification of weakly ER⁺ tumors as ER⁺ tumors prompted Collins et al. (2005) to perform internal IHC analysis of immune-stains of 825 breast cancer samples, estimating proportion of ER⁺ tumor cells, and grading samples using the Allred score. The authors showed that in 817 cases (99.0%), either all of the cancer cells in the tumor showed an absence of staining (all ER^– cells) or over 70% of the cells were ER⁺. Thus, 818 cases (99.2%) exhibited Allred scores of either 0 or 7/8. These results prompted the authors to conclude that in most cases, an overwhelming number of breast cancer patients’ tumors can be classified as completely ER^– or unambiguously ER⁺, with only a small fraction of tumors showing very small frequencies of ER⁺ cells and thus appearing weakly positive. It is noteworthy that Allred scores of 7 or 8 means there are still a sizeable frequency of ER^– cancer cells within the tumor.

The question of whether even weakly positive tumors should be treated with endocrine therapies was addressed in 2010 at the American Society of Clinical Oncology (ASCO)/College of American Pathologists (CAP) meeting. A panel of experts agreed on setting a threshold of 1% ER⁺ cancer cells for reporting a patient’s breast cancer as ER positive (Hammond et al., 2010). With regards to scoring, this corresponds to a minimum Allred score of 3, which can be seen with as few as 1–10% weakly staining cells, and an H-score of over 1 (Table 10 in Hammond et al., 2010).

While the main rationale for the 1% cutoff is to expand access to treatment options to as many patients as possible, it may be too low for statistically significant efficacy. Morgan et al. (2011) showed that low levels of expression, defined as H-score ≤ 50, resulted in lower overall disease-free survival when treated with only endocrine therapy. Chen et al. (2018) showed that patients with ER⁺ staining between 1 and 9% gained no significant benefit from endocrine therapy, unlike ER⁺ tumors with over 10% positive staining. Raghav et al. (2012) also showed that patients with tumors with 1–5% ER positive expression gained no clinical benefit from endocrine therapy.

Even though weakly positive tumors are classified as eligible to receive endocrine therapies, it seems that therapeutic success would be greater if one could increase the proportion of ER⁺ cells in these tumors prior to administering endocrine therapy. Within the framework proposed here, this may be possible through resource manipulation.

As we have shown above, the proportion of ER⁺ cells that rely on both resources increases with increased estrogen inflow, or with reduced glucose inflow. Perhaps it might be feasible to externally increase estrogen concentration to favor ER⁺ cells over ER^– ones without compromising patient health, but as yet, this has not been explored experimentally. Such a therapy would fall into what has been termed an evolutionary gambit or suckers gambit (Maley et al., 2004; Gatenby and Brown, 2020). On the other hand, glucose deprivation may be able to achieve a similar effect (Barbosa and Martel, 2020), priming the tumor to becoming more receptive to hormone therapy by favoring an increase in the frequency of ER⁺ cells relative to ER^– ones (Figure 5).

FIGURE 5

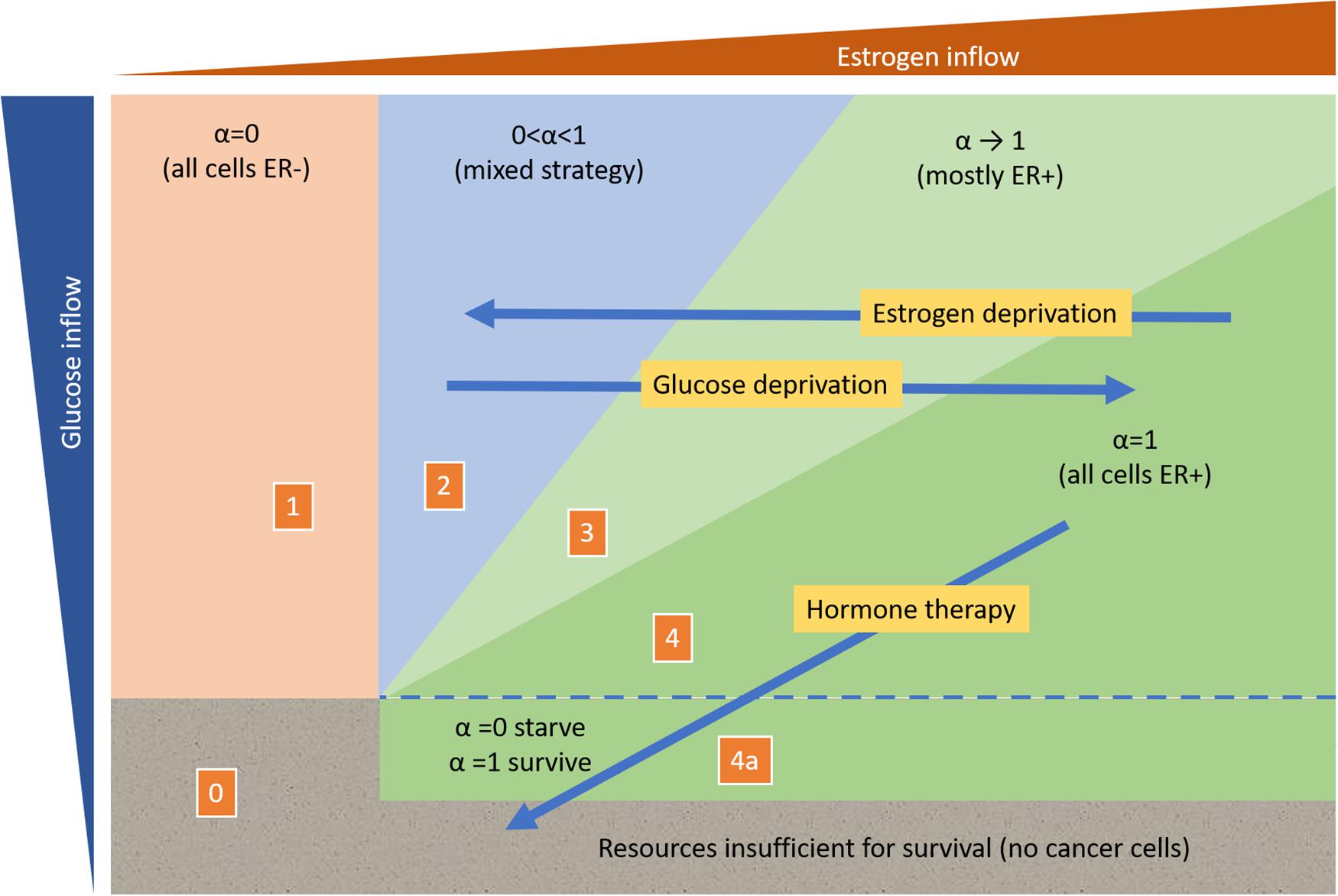
Figure 5. Impact of possible resource-dependent intervention strategies on predicted tumor composition.

If the tumor is primarily composed of ER⁺ cells, then estrogen deprivation therapies will have initial success but might eventually drive the tumor toward either all ER^– or a mixture of both ER⁺ and ER^– cells. Adding glucose deprivation or enhancing the resource supply of estrogen relative to other nutrients may set up an evolutionary double-bind (Gatenby et al., 2009), where the resulting resource dynamics force an ER⁺ tumor that is highly susceptible to hormone therapy (Figure 5).

Discussion

Here we analyzed a consumer-resource model with two resources subject to Liebig’s Law of the Minimum to describe evolution of a heterogeneous population of cancer cells as influenced by resource availability. We evaluated the impact of a general resource, such as glucose, and a specific resource, such as estrogen, on the conditions for coexistence by a phenotype that requires both, and a phenotype that only requires the general resource. Our model was intended for breast cancer, where ER⁺ and ER^– cancer cells are frequently found coexisting within the same patient’s tumor. We solved analytically for conditions under which the tumor should have pure or mixed strategies (Figure 1). This involved calculating the subsistence levels of resources (R^∗) for the ER⁺ and ER^– cancer cell strategies, there zero net growth isoclines (ZNGI), and the effect of the resource supply points of glucose and estrogen on the composition of cancer cell strategies.

We then confirmed theoretical predictions these results by showing that if a heterogeneous population can evolve over time, it will evolve toward the predicted population composition and resource equilibrium levels. We assessed population evolution by changes in the mean and variance of a distribution of mixed strategies, where a given strategy gives the probability of exhibiting the ER^– or ER⁺ phenotype (Figure 2). We showed that in this system, population evolution is invariant to initial distribution of cell clones in the populations, and that over time the final population composition is dictated only by the supply of each resource (Figure 3), suggesting that resource manipulation can be used to impact the composition of the population (Figure 5).

To test this hypothesis, we varied relative inflow rates for both the general and specific resource and evaluated where the population evolved over time (Figure 4). Specifically, in our simulations we allowed the population to evolve to steady state, at which point we evaluated composition of the population (mean strategy and variance of strategies), as well as equilibrium abundances of resources. In addition to confirming predicted levels of both resources at a steady state, the model analysis revealed that the highest variance in the mixed strategies found among the cell lineages occurs for populations that have a mix of ER⁺ and ER^– cells.

In Lloyd et al. (2014) examined the frequency of ER⁺ and ER^– cancer cells from the biopsies of 24 patients; all biopsies were obtained from the primary tumor. Six exhibited 100% ER^– cells (corresponding to Region 1 of Figure 5), seven had both phenotypes at 5–10% ER^– cells (corresponding to Region 2 of Figure 5) and 11 were 100% ER⁺ cells (corresponding to Regions 3 or 4 of Figure 5). The authors found that ER^– tumors exhibit less vasculature. Lack of vasculature may reduce the inflow of both glucose (and other general resources) and estrogen, but the level of estrogen may drop below the subsistence level of the ER⁺ cells, leaving a higher standing crop of underutilized general resources, thereby favoring ER^– cells (to our knowledge, this prediction remains untested). The authors hypothesize that anti-estrogen therapy (e.g., Tamoxifen) can select for ER^–independent cells, while “cyclic introduction of estrogen may improve survival rate by continually altering, rather than unilaterally shifting, toward an ER^– population.” The authors suggest that “modulation (and not eradication or extinction of certain population) may prove to be an advantageous treatment strategy,” a hypothesis that is supported by the proposed mathematical model.

The proposed model is built on the underlying theory of essential resources and Liebig’s Law of the Minimum. For ER⁺ cells, estrogen may be a hemi-essential resource (it certainly is not a perfectly substitutable one). Had we modeled estrogen as a hemi-essential resource for ER⁺ cancer cells, our results would remain qualitatively unchanged. The model, however, would lose much of its analytic tractability as fitness would now involve the product of consumption rates of estrogen and the general resource.

Direct evidence for estrogen acting as an essential resource is that ER⁺ cells cannot survive and proliferate in the absence of estrogen, no matter the abundance of other nutrients (Martin et al., 2003; Comsa et al., 2015). Furthermore, in the absence of sufficient quantities of other nutrients such as glucose, fatty acids and amino acids, cancer cells cannot survive or proliferate regardless of the availability of estrogen. Finally, like other resources, estrogen becomes depleted and used up by the cells rather than continuously being recycled (Gudas et al., 1995).

Indirect evidence suggests that estrogen may act as an essential or hemi-essential resource in line with Liebig’s Law. Mathews et al. (2020) quantified the effect of long-term glucose deprivation on various cancer cell lines in vitro. Cell lines were stabilized at typical human glucose level of 6 mmol/L, with the intervention group then receiving 3 mmol/L of glucose for 90 days. The authors observed that glucose deprivation had different effect on different cell lines, with MDA-MB-231 cell line (ER^–), the highly aggressive triple negative breast cancer cell line, being most sensitive to the metabolic intervention, while the non-tumorigenic epithelial cell line MCF 10A (ER⁺) was least affected. For the purposes of model validation, more decisive experiments involving ER⁺ and ER^– cell lines should include varying resource availabilities, and mono- vs. co-culturing to then quantify changes in population composition over time (Freischel et al., 2020). If estrogen and general nutrients function as essential resources, then nutrient modulation may be an effective strategy for cancer modulation.

The potential benefit on cancer therapy of glucose deprivation through a ketogenic diet has been discussed extensively in the last several years (Klement, 2017; Weber et al., 2018). Khodabakhshi et al. (2020) reported results of a randomized controlled clinical trial, evaluating the effects of ketogenic diet on patients with breast cancer undergoing chemotherapy. In neoadjuvant patients, they found that overall survival increased in the intervention group compared to the control group. In another trial by the same authors (Khodabakhshi et al., 2021) evaluated changes in biomarkers of breast cancer patients undergoing chemotherapy. Patients on a ketogenic diet showed significant decreases in TNF-alpha and insulin levels after 12 weeks of treatment, as well as increase in IL-10. All of these changes are associated with better patient outcomes. Additional experiments are needed to evaluate relative contributions of different mechanisms triggered by glucose deprivation in the presence and absence of estrogen. In addition to manipulating cancer-cell population composition and density, glucose deprivation may also influence immune modulation (Chang et al., 2015; Buck et al., 2017; Klein Geltink et al., 2018) and vasculature (Lloyd et al., 2014).

Broader Context Within Cancer

The model applies to any cancer that is dependent on specific growth factors including androgen-dependent prostate cancers. Epidermal growth factors (EGF) are typical regulators of many tissue types and they can influence cell proliferation and cell differentiation. Cancers that are wildtype for EGFR (epidermal growth factor receptor) require EGF as an essential resource. Other cancer cells, such as EGFR mutant lung cancer, mutate so that the receptor is permanently turned on, produce their own growth factors or stimulate neighboring normal cells, such as fibroblasts, to produce growth factors for them.

In most of these cases, the growth factor serves as an essential resource necessary for survival and proliferation. The need for these growth factors or hormones derives from the ancestry of the cancer cells. They retain the primitive trait of the normal cells of that tissue type. The need for these growth factors is part of the organism-wide homeostatic control of tissue-specific cell proliferation and activity. Because these hormones and growth factors are not strictly necessary for the survival of an individual cell, there can be strong selection, accelerated by therapy, for a subset of the cancer cells to evolve independence from these. Cancer cell types that are growth factor independent may either replace the others or coexist as a mixed strategy of different phenotypes. We believe our model provides a simple mechanistic explanation for when growth factor independent cancer cell types will either outcompete, coexist with, or be outcompeted by the cancer cell type that requires the growth factor.

Broader Context Within Consumer-Resource Models

Our model falls well within the class of consumer-resource models proposed and developed by Tilman (1980, 1982). As mentioned in the introduction, in these models, resources can be perfect substitutes, complementary, hemi-essential, or essential. The resources themselves may be co-occurring and encountered at random or distributed in separate patches or habitats (Hunt and Brown, 2018). The nutritional relationship between the resources and their distribution in space strongly influence the potential for the coexistence of different consumers (Vincent et al., 1996).

The analysis of these models has general features described by the resource supply point of the nutrients (inflows), ZNGIs of the consumer species, and the depletion of the resource by the consumers. For models like ours that are non-spatial and achieve a steady-state, coexistence requires that the ZNGIs of the consumers intersect, meaning that there is a tradeoff among consumers between the subsistence levels of the resources. Furthermore, the resource supply points must lie in an intermediate range of the state space of resource abundances but outside of each consumer species’ ZNGI. Finally, the consumers must deplete the resources along different trajectories. For a two-resource two-consumer species system, when coexistence is possible, the equilibrium abundance of resources generally lies at the intersection of the two ZNGIs; and the equilibrium population sizes of the two species is what will drive the resource abundances form the supply point to this intersection.

An extensive theoretical and empirical body of literature exists in ecology on consumer-resource dynamics, including essential resources (Abrams, 1987; Fox and Vasseur, 2008). Much of this work is in the context of phytoplankton under chemostat (batch or continuous flow) conditions (Harmand et al., 2017; De Rijcke et al., 2020). The essential resources can be either light and other nutrients, or the nutrients themselves such as nitrogen and phosphorus. Model extensions can include resource pulsing, diffusion gradients within the medium or water column, and large numbers of consumer species and nutrient conditions (Dubinkina et al., 2019; Stojsavljevic et al., 2019).

Tumors can be thought of as rather viscous chemostats, where blood delivers nutrients and removes both residual nutrients and metabolites. In this work, our system was quite simple, with two co-occurring essential resources, applicable to cancers requiring growth hormones or growth factors. More generally, cancers provide a relatively unexplored opportunity to apply and test consumer-resource theory (Palmer et al., 2011; Seynhaeve and Ten Hagen, 2018). Such applications could include ecological “priming” of tumors to be most receptive to therapy, although tracking resource dynamics, cancer cell compositions, and interactions within the tumor is not yet possible. It can at best be inferred from radiographic imaging (MRI, PET scans, CT scans). Jarrett et al. (2020) showed the value of combining MRI and PET scans for inferring cancer cell densities, the distribution of cancer cells with respect to expression of HER2, and mathematically modeling breast-cancer patient responses to neoadjuvant therapies targeting HER2. Their model, like ours, considers the importance of a growth factor (Human epidermal growth factor). Unlike ours, they use a logistic growth model instead of a consumer-resource model; and theirs explicitly considers space using partial differential equations and a diffusion term representing cell dispersal.

Mouse experiments provide greater control and the opportunity to track dynamics more closely, especially using window chamber mouse models (Amend et al., 2018). Culture experiments provide a promising way to compete different cell lines under different nutrient conditions, particularly when grown in 3-D spheroids, where nutrients rather than space become limiting (Freischel et al., 2020). In such experiments the Seahorse Extracellular Flux Analyzers can be used to measure cellular metabolic processes, such as ATP production, glucose consumption, oxygen uptake, lactic acid production and other nutrient fluxes (Cheng et al., 2014; Zhang and Zhang, 2019). Such measure may highlight tradeoffs and differences among cancer cells in uptake and utilization strategies (e.g., glycolytic vs. non-glycolytic cancer cell types) (Persi et al., 2018; Damaghi et al., 2021).

As part of the ecological system of the human body, cancer cells require diverse nutrients, drawing fatty acids, amino acids, trace nutrients, and macromolecules from the blood and interstitial fluid. These nutrients serve as both fuel and as building blocks for structural and functional molecules. Some will be essential, but many will be substitutable or complementary. There is much opportunity to apply consumer-resource dynamics to investigate the ecology, evolution and diversification of cancer cells within and between tumors of a patient, between patients with the same cancer or patients with diverse cancers.

Conclusion

When a patient is diagnosed with breast cancer, it is standard approach to classify the tumor and start tumor treatment as expeditiously as possible, with tumor burden reduction being the goal of each step of the treatment. However, it may be more effective to first prime the tumor following the initial assessment of the frequency of ER⁺ and ER^– cancer cells. The first step in the treatment cascade could be aimed at modifying the tumor environment to favor ER⁺ cancer cells. By developing a long-term strategy rather than relying on short-term tumor burden reduction, it may be possible to expand the pool of patients that can maximally benefit from endocrine-based therapy through application of ecological principles to cancer.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

IK conducted MATLAB simulations. Both authors contributed to study design and manuscript preparation.

Funding

This research was partially supported by the grants U54 CA143970, R01 CA077575, and U01CA232382 (to JB).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling Editor declared a past co-authorship with one of the authors IK.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2021.673082/full#supplementary-material

References

Abrams, P. A. (1987). The nonlinearity of competitive effects in models of competition for essential resources. Theor. Popul. Biol. 32, 50–65. doi: 10.1016/0040-5809(87)90039-6

CrossRef Full Text | Google Scholar

Allred, D., Harvey, J. M., Berardo, M., and Clark, G. M. (1998). Prognostic and predictive factors in breast cancer by immunohistochemical analysis. Mod. Pathol. 11:155.