Kelp Forests: Catastrophes, Resilience, and Management

Resilient kelp forests provide foundation habitat for marine ecosystems and are indicators of the ecosystems’ sustainable natural capital. Loss of resilience and imperfectly reversible catastrophic shifts from kelp forests to urchin barrens, due to pollution or loss of a top predator, are part of an ecological tipping point phenomenon, and involve a loss in sustainable natural capital. Management controls to prevent or reverse these shifts and losses are classified in a number of ways. Systemic controls eliminate the cause of the problem. Symptomatic controls use leverage points for more direct control of the populations affected, urchin harvesting or culling, or kelp enhancement. There is a distinction between ongoing structural (press) controls versus temporary or intermittent perturbation (pulse) controls, and one between shift preventing versus shift reversing or restorative controls. Adaptive management and the options it creates both focus on reductions in uncertainty and control policies with the flexibility to take advantage of those reductions. The various management distinctions are most easily understood by modeling the predator-urchin-kelp marine ecosystem. This paper develops a mathematical model of the ecosystem that has the potential for two different catastrophic shifts between equilibria. Pulse disturbances, originating from exogenous abiotic factors or population dynamics elsewhere in the metacommunity, can activate shifts. A measure of probabilistic resilience is developed and used as part of an assessment of the ecosystem’s sustainable stock of natural capital. With perturbation outcomes clustered around the originating equilibrium, hysteresis is activated, resulting imperfect reversibility of catastrophic shifts, and a loss in natural capital. The difficulty of reversing a shift from kelp forest to urchin barren, with an associated loss in sustainable natural capital, is an example. Management controls are modeled. I find that systemic and symptomatic, and press and pulse, controls can be complementary. Restorative controls tend to be more difficult or costly than preventative ones. Adaptive management, favoring flexible, often preventative, controls, creates option value, lowering control costs and/or losses in sustainable natural capital. Two cases are used to illustrate, Tasmania, Australia and Haida Gwaii, Canada.

Introduction

Healthy marine ecosystems are rich in natural capital (Mäler and Li, 2010; Bennett et al., 2016; Wernberg et al., 2019). In an ecologically resilient kelp forest community, kelp (order Laminariales) are the foundation species whose physical characteristics provide the habitat for a healthy marine ecosystem (Miller et al., 2018). The density of kelp is an indicator of the richness of the community’s stock of natural capital, and the kelp forest’s ecological resilience (Holling, 1973) is an indicator of the stock’s sustainability (Graham, 2004; Ellison et al., 2005; Small, 2018). A sustained stock has value through the ongoing human life support services provided (e.g., harvestable fish and other food products) (Boyd and Krupnick, 2013; Fenichel and Abbott, 2014; Bond, 2017). However, kelp are consumed by urchins (order Echinoida or Diadematoida), and the kelp forest regime, with cryptic (i.e., low density) urchin herbivores whose density is limited by the availability of safe hiding spaces, typically exists in an ecosystem in which its resilience (Walker et al., 2004) can be compromised. Decreased resilience increases the probability of a catastrophic (abrupt, perhaps over decades) shift from a cryptic urchin-kelp forest regime to a kelp depauperate-urchin barren regime with a much poorer stock of natural capital (Petraitis and Dudgeon, 2004; Ling et al., 2015; Krumhansl et al., 2016; Wernberg et al., 2016; Filbee-Dexter and Wernberg, 2018; Wernberg et al., 2019).

To address the loss of resilience and depletion of kelp forests, this paper develops a mathematical model that integrates what is known about the predator-urchin-kelp ecosystem to analyze catastrophic shifts in urchin and kelp densities. While empirical evidence to support such a model is not definitive, low urchin kelp-forests and kelp depauperate-urchin barrens are prime candidates for alternative regimes (Petraitis and Dudgeon, 2004). The model is a recursively decoupled catastrophe model with two trophic interactions and the potential for two catastrophic shifts, one at the level of the predator-urchin trophic interaction and one at the level of the urchin-kelp interaction. It incorporates the concept of resilience at both levels and uses resilience probabilities and hysteresis as part of a definition of the sustainable natural capital stock as expected kelp density. The key concepts used in the model are described in Supplementary Appendix A. Two cases are used to illustrate, Tasmania, Australia and Haida Gwaii, Canada (Lee et al., 2018; Tasmanian Government, 2019). The first is an ocean warming induced invasion of long spined sea urchins (Centrostephanus rodgersii) to coastal Tasmania and subsequent overgrazing of kelp forests (Edgar et al., 2004). The second is the absence of the sea otter predator (Enhydra lutris) in Haida Gwaii and lack of kelp forest recovery. Supplementary Appendix B provides details for both cases. The model is used to assess a range of management controls. See Supplementary Appendix A for details about the controls. I find that there is often complementarity in that combinations of control types can be more successful than one type alone. Moreover, in the face of hysteresis and uncertain restoration costs, preventative controls tend to have an advantage over restorative ones in that they require less investment and are often more amenable to adaptive management with the flexible decision process that creates option value.

The section “Materials and Methods” presents the formal definitions of catastrophe theory, trophic cascades, pulse disturbances, resilience, and hysteresis as they apply to the model of the predator-urchin-kelp ecosystem. It also develops the top-down recursively decoupled catastrophe model (Brummitt et al., 2015). The model is intended to be demonstrative or illustrative. The parameter values used for the catastrophe model and the pulse disturbances are not meant to be precisely correct, but to capture the essence of the various interactions so as to better understand their outcomes and the influence of alternative management policies (Murray, 2002). Finally it characterizes kelp forests and their resilience as sustainable natural capital (Mäler and Li, 2010). The section “Results” uses the catastrophe model, probabilistic resilience, and natural capital to characterize the losses in sustainable natural capital that may occur, or have occurred, in Tasmania and Haida Gwaii. It also examines the use of systemic versus symptomatic controls and press versus pulse controls, and assesses adaptive management control and the option value of preventative versus restorative controls. The section “Discussion” summarizes, considers limitations and extensions, and concludes.

Materials and Methods

Trophic Cascades, Catastrophic Shifts, Resilience, and Hysteresis

Trophic Cascades

The predator-urchin-kelp model has been characterized as one of best examples of a strong top-down trophic cascade (Estes and Palmisano, 1974; Sala et al., 1998; Hereu Fina, 2004; Borer et al., 2005; Halpern et al., 2006; Sommer, 2008). A top-down trophic cascade describes a set of relationships for which there is a negative relationship between the biomass density of adjacent trophic levels and a positive one between those that are once removed (Carpenter et al., 1985; Sommer, 2008). Predation or grazing mortality, or release from it, is the dominant response (Holling, 1959a, b; Nowak et al., 2008). Due to factors such as larger body size and slower change at higher trophic levels, a trophic cascade exhibits weak numerical responses, and bottom-up effects, focusing on numerical responses (the response of predator or grazer), play a minimal role (Sommer, 2008).

While factors such as loss of top predators, storms or pollution may interfere (Foster and Schiel, 2010; Reed et al., 2011; Dunn and Hovel, 2019), there is statistical analysis supporting the dominance of top-down influence (Halpern et al., 2006), and there is evidence for the absence of numerical response in the behavior of urchins and predators. At the urchin-kelp level, urchin grazers use alternative food resources. With no kelp, urchins in high density barrens consume biofilms and crustose coralline algae (Lyons and Scheibling, 2007; Kraufvelin, 2017). Urchin density in barrens doesn’t decline with absence of kelp, instead urchins adapt to less nutritious food sources (Konar and Estes, 2003; Ling and Johnson, 2009; Ling et al., 2009; Stewart and Konar, 2012). Evidence also suggests that while urchin reproductive potential is higher in kelp forests, the pattern of larval dispersal and settlement is such that settlement in barrens is possible, and is enhanced by chemical cues from coralline algae found in barrens (Rowley, 1989, 1990; Baskett and Salomon, 2010; Wilson et al., 2013). In addition, dense kelp forests provide habitat for urchin predators and are able to physically beat back grazing (Andrew, 1993; Konar and Estes, 2003). At the predator-urchin level, both sea otters and lobster are generalist predators, making them less sensitive to changes in urchin density (Edyvane, 2003; Estes et al., 2003; Tinker et al., 2008; Marzloff, 2012; Butler et al., 2016). At high densities, urchins themselves becomes less nutritious and more difficult prey (e.g., longer spines and flight), avoiding encouraging greater predator density (Konar and Estes, 2003; Ling and Johnson, 2009; Watson and Estes, 2011). Ling et al. (2019) find the highest lobster predation to be on small urchins within kelp beds.

Urchin-Kelp Interactions

First consider only the lower-level trophic interaction, with urchin as grazers of kelp, and equilibrium urchin density from the predator-urchin subsystem as an exogenous input to the urchin-kelp system. At the urchin-kelp trophic interaction level, kelp forests (high kelp density) and kelp depauperate communities (low kelp density) are examples of alternate states. A forward shift from a kelp forest equilibrium to a kelp depauperate equilibrium can occur, as well as a reverse shift from depauperate equilibrium to kelp forest. Starting from a high kelp density equilibrium, gradual increases in an ecosystem’s exogenous parameter (urchin density), which may be result of species invasion encouraged by environmental changes such as ocean warming, or human over-harvesting of urchin predators, causes reductions in kelp density, and some combination of abrupt and gradual decreases in the resilience of the kelp forest equilibrium (Wernberg et al., 2016; Filbee-Dexter and Wernberg, 2018). Reduced resilience for the kelp forest equilibrium lessens the propensity of the state variable (kelp density) to return to the original equilibrium after a stochastic perturbation such as a kelp destroying storm event, and increases the probability of a forward tip to a kelp depauperate one (Filbee-Dexter and Scheibling, 2014). Once the kelp forest equilibrium has lost all its resilience, the forward tip becomes unavoidable.

To illustrate, Figure 1 shows, in blue, an isocline of urchin-kelp steady state equilibria (the model producing this isocline will be presented in section “Urchin-Kelp Model”). With U as exogenously determined urchin density (in 100 g/m²), and K as the state variable, kelp density (in g/m²), the upper arm, K ≥ 5, contains stable kelp forest equilibria, and the lower arm, K ≤ 0.1, contains stable kelp depauperate equilibria. The upward sloping portion of the curve, from (U, K) = (0.6, 0.1) to (7.7, 5), contains unstable kelp equilibria. For a given U, the unstable kelp equilibrium is a boundary point between the basins of attraction of the stable kelp equilibrium on the upper arm versus one on the lower arm. The inevitable tip points are indicated by vertical solid black arrows.

FIGURE 1

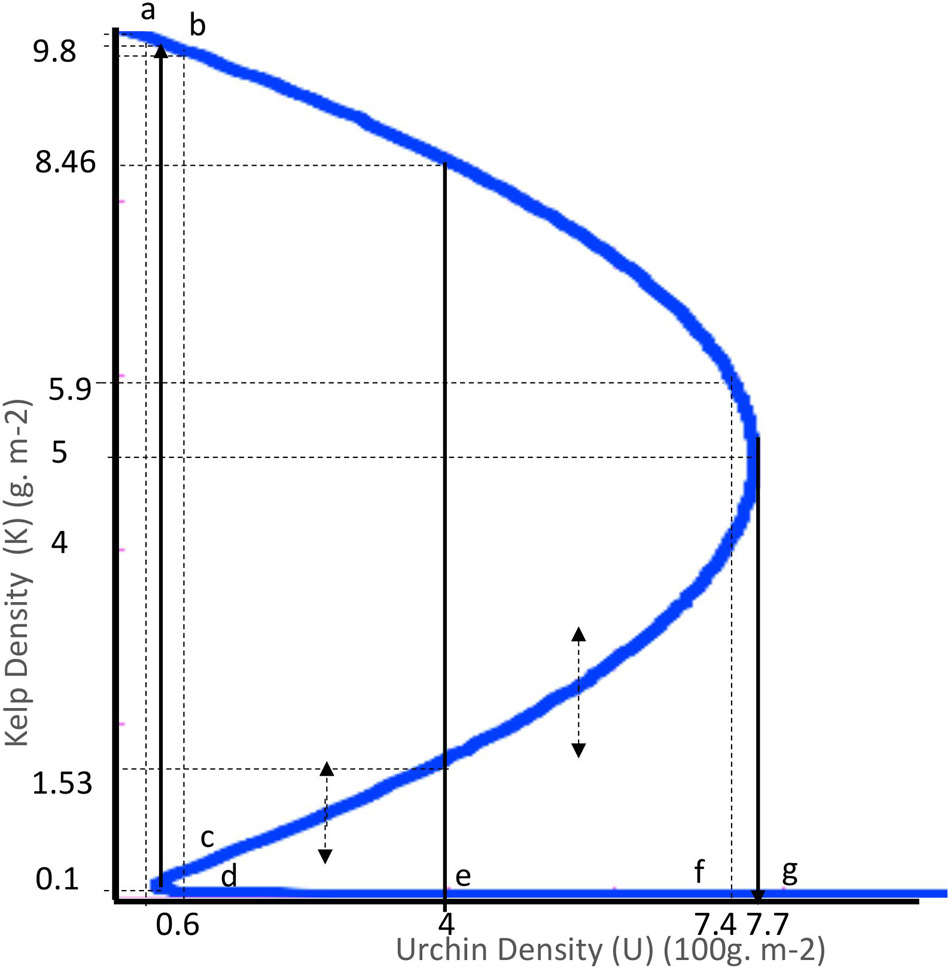
Figure 1. Urchin-kelp subsystem isocline: The cubic equation for the $\stackrel{.}{K}=0$ isocline is K³−10K² + (0.01 + 3.25U)K−0.1 = 0. Arrows indicate movement away from equilibria on the unstable arm and toward equilibria on the stable arms. The (U, K) coordinates for the letters are: a– (0.4,9.9), b– (0.7,9.7), c– (0.7,0.17), d– (0.7,0.06), e– (4,0.008), f– (7.4,0.004), and g– (7.7,0.004).

Kelp Resilience and Catastrophic Shifts

At a given urchin density, a kelp forest equilibrium’s resilience is the tendency for a pulse perturbation in kelp density from that equilibrium to be attracted back to it, rather than being induced toward a kelp depauperate equilibrium. See Supplementary Appendix A for more on catastrophic shifts and resilience. Resilience can be translated into a resilience probability that depends on the size of the equilibrium’s basin of attraction and on the probability distribution for the size of the perturbation or, equivalently, the distribution of perturbation displacement locations (Carpenter et al., 2001). If U ≤ 0.6, there is a fully resilient kelp forest equilibrium, and any kelp density perturbation has a probability of one of returning to it. If U ≥ 7.7, the kelp forest equilibrium loses all resilience and disappears. When the kelp forest equilibrium vanishes, the kelp depauperate equilibrium achieves full resilience, and any kelp density perturbation has a probability of one of returning to it. The zone of partial resilience extends over the range 0.6 < U < 7.7 Over that range, there is a change from a fully resilient kelp forest to a fully resilient kelp depauperate regime. At any given urchin density in the partial resilience zone, there are two stable equilibria and two basins of attraction, separated by a boundary point consisting of the unstable equilibrium. Within the zone of partial resilience, the resilience of a stable equilibrium depends on the magnitude of perturbations away from it relative to the size of its basin of attraction (Carpenter et al., 2001). Given a probability density function for perturbation induced displacement locations, the resilience of a kelp forest/depauperate equilibrium can be translated into probabilistic resilience, or the probability that, given a perturbation from a stable kelp forest/depauperate equilibrium, the displacement location will be in the basin of attraction of the stable kelp forest/depauperate equilibrium, and attracted back to it. Otherwise, the perturbation will land in the basin of attraction of the stable depauperate/kelp forest equilibrium, and there will be a shift to the alternative equilibrium.

Designating a stable upper arm equilibrium as a function of U, K_h/U = K_h(U), a stable lower arm equilibrium as K_l/U = K_l(U), and an unstable equilibrium boundary point as K_b/U = K_b(U), the basin of attraction of the uppper arm equilbrium is the vertical distance K_h/U−K_b/U (Carpenter et al., 2001; Standish et al., 2014; Baho et al., 2017). For the lower arm equilibrium, it is K_b/U−K_l/U. With urchin density fixed at U = 4 in Figure 1, consider a pulse disturbance in kelp density from either of the two stable equilibria that lands at a point somewhere along the vertical line between K_l/4 = 0.008 (point e) and K_h/4 = 8.46, including the endpoints. The basins of attraction are K_h/4−K_b/4 = 6.93 and K_b/4−K_l/4 = 1.522. From each stable equilibrium in the partial resilience zone, a perturbation’s displacement location may or may not be within that equilibrium’s basin of attraction.

Specifically, I model the displacement locations of a perturbation from the kelp forest equilibrium in the partial resilience zone as following a combination of two piecewise linear probability density functions. The first, representing the clustering of very small or zero disturbances, gives a displacement location K_h/U and occurs with a probability of π_h. The second, covering the full range of disturbance locations K_h/U to K_l/U, is the uniform distribution with a probability density of u_h(K_h/U, K_l/U) (Schultz et al., 2017). The latter occurs with a probability 1−π_h. Zero disturbances will always end up at K_h/U. Each non-zero perturbation outcome will eventually end up at either K_h/U or K_l/U, depending on the basin of attraction into which it is perturbed. For a given urchin density, negative perturbations from an equilibrium on the high kelp arm toward an equilibrium on the low kelp arm, will have a probability, P(K_h/h/U), of returning to the upper arm. This probability depends on the probability of a zero perturbation, and the probability, from the uniform distribution, of a perturbation being small enough that its displacement location remains within the basin of attraction of the upper arm equilibrium. The probability of a perturbation from an equilibrium on the high kelp arm ending up on the lower arm is P(K_l/h/U) = 1−P(K_h/h/U).

Taking into account all three resilience zones (full, partial, and no resilience), and assuming partial resilience zone perturbations are no greater than K_h/U−K_l/U, the probability a perturbation from K_h/U ending up at K_h/U versus K_l/U is given as Eq. 1.

$$\begin{array}{l}P\left(K_{h/h/U}\right)=\{\begin{array}{l}1\hfill \\ if0\le U\le 0.6,\text{ only }{K}_{h/U}\text{ equilibria}\hfill \\ {\text{π}}_h+\left(1-{\text{π}}_h\right)\frac{K_{h/U}-K_{b/U}}{K_{h/U}-K_{l/U}}\hfill \\ if0.6<U<7.7,0<K_{h/U}-K_{b/U}<K_{h/U}-K_{l/U}\hfill \\ 0\hfill \\ if10\ge U\ge 7.7,\text{ only }{K}_{l/U}\text{ equilibria}\hfill \end{array}\hfill \\ P\left(K_{l/h/U}\right)=1-P\left(K_{h/h/U}\right)\hfill \end{array}(1)$$

Starting from a kelp depauperate equilibrium on the lower arm, K_l/U, and assuming the probability, π_l, of zero perturbations from K_l/U, the probability of ending up at K_h/U versus K_l/U over three resilience zones is given by Eq. 2.

$$\begin{array}{l}P\left(K_{l/l/U}\right)=\{\begin{array}{l}1\hfill \\ if10\ge U\ge 7.7\text{, only }{K}_{l/U}\text{ equilibria}\hfill \\ {\text{π}}_1+\left(1-{\text{π}}_1\right)\frac{K_{b/U}-K_{l/U}}{K_{h/U}-K_{l/U}}\hfill \\ if0.6<U<7.7,0<K_{b/U}-K_{l/U}<K_{h/U}-K_{l/U}\hfill \\ 0\hfill \\ if0\le U\le 0.6\text{, only }{K}_{h/U}\text{ equilibria}\hfill \end{array}\hfill \\ P\left(K_{h/l/U}\right)=1-P\left(K_{l/l/U}\right)\hfill \end{array}(2)$$

Over the partial resilience range, 0.6 < U < 7.7, the probability of returning to the original equilibrium will vary between zero and one. The abruptness of the changes in probability in response to changes in U is directly related to the degree of clustering in the perturbation distributions, as is the degree of hysteresis.

Hysteresis, or hysteretic memory, is closely related to resilience. If the system has hysteric memory, the probability of a perturbed point landing in one or the other basin of attraction will depend not just on the relative sizes of the basins, but also on which equilibrium it was perturbed from. Supplementary Appendix A contains a diagrammatic example of hysteresis. With displacement locations bounded by K_l/4 = 0.008 and K_h/4 = 8.46, hysteretic memory is provoked by the perturbation’s probability distribution of displacement locations clustering around the perturbation generating equilibrium (Paine et al., 1998). As a result, a perturbation from a kelp forest equilibrium, which lands in the basin of attraction of, and is absorbed by, the kelp depauperate equilibrium, will have an increased probability of returning to the depauperate equilibrium following future perturbations from it (Walker et al., 2004).

The magnitudes of π_h and π_l in Eqs. 1, 2 determine the degree of clustering around the kelp forest and kelp depauperate equilibrium, respectively. Hysteresis requires that P(K_h/h/U) > P(K_h/l/U), or equivalently that P(K_l/l/U) > P(K_l/h/U). Disturbance locations in a kelp forest/kelp depauperate equilibrium’s basin of attraction more probably were perturbed from that equilibrium than from the kelp depauperate/kelp forest equilibrium. From Eqs 1, 2, π_h + π_l > 0 will produce some hysteresis (see the Supplementary Appendix C for proof). I define a moderate amount of clustering and hysteresis as 0 < π_h + π_l < 2. I use a moderate degree of clustering and hysteresis with π_h = π_l = 0.5. Exteme clustering, $\mathrm{\pi }{}_l={\mathrm{\pi }}_h=1$, yields strong hystersis, making P(K_h/h/U) = P(K_l/l/U) = 1 and P(K_h/l/U) = P(K_l/h/U) = 0. No clustering, $\mathrm{\pi }{}_l={\mathrm{\pi }}_h=0$, yields no hysteresis, P(K_h/h/U) = P(K_h/l/U) and P(K_l/l/U) = P(K_h/l/U). The extreme and no clustering cases are presented in more detail in Supplementary Appendix C.

Predator-Urchin Interactions

The urchin-kelp system is the lower part of a dynamic trophic cascade. The higher-level trophic interaction in the cascade is the predator-urchin linkage. While predator size relative to prey size has also been shown to be important (Ling et al., 2009; Dunn et al., 2017), it need not always be, so I simply use predator density as the exogenous driver, and urchin density as the state variable. Depletion of the predator through human harvesting creates greater densities of its prey (urchin) and, reverberating down the food chain, the overgrazing of the lower level food source (kelp) (Estes and Palmisano, 1974; Estes and Duggins, 1995; Steneck et al., 2002; Lafferty, 2004; Estes et al., 2011; Ling et al., 2015; Ripple et al., 2016; Filbee-Dexter and Wernberg, 2018). The overharvesting of sea-otter drove the switch from cryptic urchin-kelp forest to kelp depauperate-urchin barren off Haida Gwaii (Estes and Palmisano, 1974; Sloan and Dick, 2012), and the harvesting of spiny lobster off the Tasmanian coast has reduced the capacity of predation to control urchin density and to maintain kelp bed resilience (Ling et al., 2009; Ling and Johnson, 2012). Resilience and hysteresis for a cryptic urchin versus urchin barren equilibria can characterized as described above for the kelp forest versus kelp depauperate equilibria. Catastrophic shifts are possible at the predator-urchin level as well as at the urchin-kelp level (Soulé et al., 2003; Brummitt et al., 2015; Ling et al., 2015), and it is the combined catastrophic shifts that matter in managing the overall system to prevent kelp loss.

Modeling

Modeling Assumptions

Using what is known about the predator-urchin-kelp ecosystem off the Tasmanian Coast (Edgar et al., 2004; Ling et al., 2009; Johnson et al., 2011; Marzloff, 2012; Tasmanian Government, 2019) and that in Haida Gwaii (Lee et al., 2016; Lee et al., 2018), I develop a recursively decoupled mathematical model that allows for both predator-urchin and urchin-kelp interactions with the possibility for hysteresis and catastrophic shifts at both trophic interaction levels (Ludwig et al., 1997; Scheffer et al., 2001; Soulé et al., 2003; Pearse, 2006; Flukes et al., 2012; Ling et al., 2015; Johnson et al., 2017; Kenner and Tinker, 2018). Both environmental factors such as ocean warming (Edgar et al., 2004; Gorman et al., 2009; Filbee-Dexter et al., 2016), and predator density, are top level parameters that can drive the system to shift from a kelp forest with cryptic urchin to a kelp depauperate urchin barren.

I follow Scheffer et al. (2001) and specify the minimal model consistent with gradual increases in urchin density triggering a catastrophic decline in kelp density (Ling et al., 2015) and with gradual changes in an environmental factor, or decreases in predator density, triggering an explosion in urchin density (Selkoe et al., 2015). Since there are at most very weak numerical responses of urchin density to kelp density and of predator density to urchin density, my model treats them as zero, allowing me to use a downwardly recursively decoupled model; a top down cascade approach with no reciprocal effect (Ludwig et al., 1978; Walker et al., 2012; Brummitt et al., 2015; Pershing et al., 2015; Winnie and Creel, 2017). Changes in the density of urchin prey are driven by environmental factors and predator (lobster or sea otter) density, assumed to be the slower, or exogenous, variables, affecting urchin density but unaffected by it (Estes and Duggins, 1995; Ling et al., 2009; Dunn et al., 2017). In the same vein, urchins, as grazers of kelp, are drivers of changes in kelp cover, and urchin density can be treated as a slow, or exogenous, variable, affecting kelp density but unaffected by it, allowing changes at higher trophic levels cascade down the food chain (Paine, 1980; McLaren and Peterson, 1994; Ripple et al., 2016).

For the lower-level trophic interaction, the urchin-kelp model, I assume that kelp exhibit logistic growth in the absence of grazing. The potential for hysteresis and catastrophic shifts comes from a non-linear relationship between urchins and kelp. Specifically, urchin grazing on kelp is modeled as a Holling type-III functional response for which the proportion of kelp consumed per urchin (grazing efficiency or proportion of available kelp consumed per urchin or the average product of kelp density) depends on kelp density, starting off very low at very low kelp densities, increasing at a decreasing rate at low kelp densities, reaching a maximum, and decreasing, at first at an increasing and then at a decreasing absolute rate, approaching zero at very high kelp densities (Holling, 1959a, b; Ludwig et al., 1997; Scheffer et al., 2001). While a Holling type IV function, which at high kelp densities, exhibits declining total (not just the proportion of) kelp consumption per urchin, has been used (Karatayev et al., 2019), a type III is preferred here because it allows both grazer switching and satiation. Support for the type III functional response is provided by the same factors that dampen the numerical response. At the predator-urchin level, I also use a logistic growth function for urchin density, and a Holling type III predation function to model the predator-urchin relationship. As for the urchin-kelp model, the arguments supporting a damped numerical response also support the Holling type III predation function.

The literature contains some ecological modeling, and some empirical work on the possibility of alternative stable equilibria (kelp forest versus urchin barrens) (see the Supplementary Appendix F). I ignore some of the details in the models mentioned in the literature, but non-linearities, such as the recruitment facilitation posited by Baskett and Salomon (2010), or differing density dependence of predation across kelp beds versus barrens (Dunn and Hovel, 2019), are accommodated by the use of Holling type III grazing and predation functions (Ludwig et al., 1997). The long spined urchin invasion resulting from changed environmental factors (ocean warming) is modeled as a discrete increase in the maximum urchin density growth rate in the predator-urchin model.

Predator-Urchin Model

For the predator-urchin part of the model, with U as the urchin density, $\stackrel{.}{U}$ as its time derivative, and S as exogenous predator density (in g/m²), a minimal dynamic model is given by Eq. 3.

$$\stackrel{.}{U}=\left(\mathrm{\alpha }-\mathrm{\beta }U\right)U-\frac{\mathrm{\gamma }S{U}^2}{\left(\mathrm{\theta }+U^2\right)}(3)$$

The first right hand side terms represent the natural growth of urchin density, with α and β as parameters. For the sea-otter case the maximum growth rate, α, is set at 0.8. For the lobster case, environmental change of the warm East Australian Current has occasioned the invasion of long spined urchins. Treating all urchins as part of the same population, I follow the approach used for migration in population models (Preston and Wang, 2007), and model this as an exogenous increase in maximum urchin population growth. I give the maximum growth parameter, a, a pre-invasion level of 0.42, increasing to 0.66 and 0.8 as the invasion proceeds. The second term in Eq. 3 represents the loss in urchin biomass from sea otter or lobster predation, with γ and θ as parameters. It is a sigmoid function that represents grazing by a given predator population, S, as a function of urchin biomass. Although the predator population is treated as fixed, its predation efficiency, defined as probability per predator of an urchin being consumed, or γU/(θ + U²), changes as the urchin density changes. When U = 0, predation efficiency is zero. When U > 0 but low, predation efficiency will be very low as predators will focus on other types of prey. At higher urchin densities, predation efficiency increases at a positive but declining rate, as predators shift more attention on urchin prey. Predation efficiency reaches a maximum, and then decreases as predators become overwhelmed by the higher prey density, as the nutritional quality of the prey decreases, or (for lobsters) as the spine length increases (Stewart and Konar, 2012; Eurich et al., 2014; Ling et al., 2015; Dunn et al., 2017; Dunn and Hovel, 2019). Watson and Estes (2011) also documented, at high urchin densities, an urchin flight response to evidence of a predation threat (urchin tests discarded by sea otters).

To find the steady states I set $\stackrel{.}{U}=0$ from Eq. 3. Since it is not expected that urchins will be completely extirpated in an area, I assume that, although it may get very small, U > 0. With exogenous S the isocline of steady state equilibria can be characterized as the real roots of the cubic Eq. 4.

$$U^3-\frac{\mathrm{\alpha }}{\mathrm{\beta }}{U}^2+\left(\mathrm{\theta }+\frac{\mathrm{\gamma }}{\mathrm{\beta }}S\right)U-\frac{\mathrm{\alpha }\mathrm{\theta }}{\mathrm{\beta }}=0(4)$$

Figure 2 shows multiple isoclines for Eq. 4, with different values for α, with β = 0.08, θ = 1 and γ = 0.26. For given S and a, there can be either one or three real roots, and one or three equilibria. If there is only one equilibrium, it will be either on the upper or lower arm and locally stable. If there are three, there will be one on each of the three arms, $U_h^{S,\mathrm{\alpha }}=U_h(S,\mathrm{\alpha })$ on the upper stable arm, $U_l^{S,\mathrm{\alpha }}=U_l(S,\mathrm{\alpha })$ on the lower stable arm, and $U_b^{S,\mathrm{\alpha }}=U_b(S,\mathrm{\alpha })$ on the unstable arm (see Supplementary Appendix A for local stability conditions).

FIGURE 2

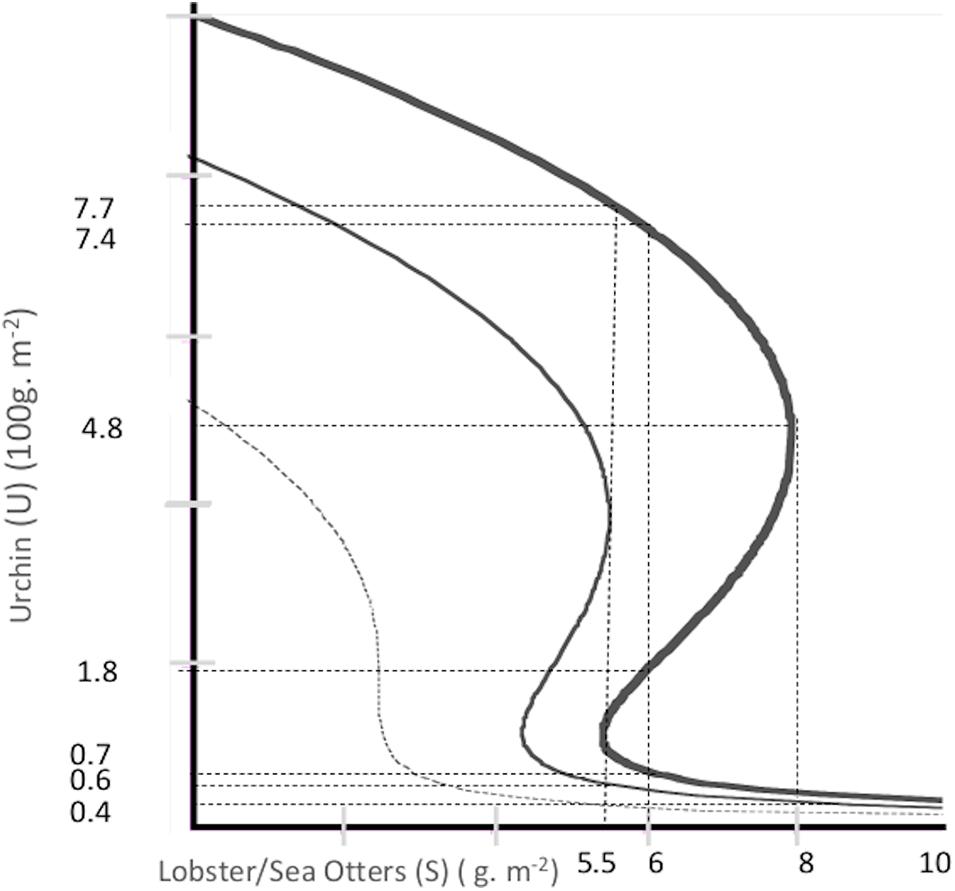
Figure 2. Predator-urchin subsystem isoclines: The cubic equation for the $\stackrel{.}{U}=0$ isocline is U³ − 12.5αU² + (1 + 3.25S)U + 1.25α = 0. Varying α, α = 0.42- lower dashed curve, α = 0.66-middle normal weight curve, α = 0.8-upper heavy weight curve.

The α = 0.8 isocline, the upper heavy weight curve, applies to the sea otter case. The vertical arrows indicate the inevitable forward and reverse shift thresholds for α = 0.8. If the initial equilibrium is a cryptic (low density) urchin equilibrium the resilience probability is described by Eq. 5, and if the initial equilibrium is an urchin barren (high density), by Eq. 6 (Carpenter et al., 2001; Standish et al., 2014; Baho et al., 2017). Consider the example of an equilibrium, $U_l^{S,0.8}$, on the cryptic urchin (lower) arm of the α = 0.8 isocline of Figure 2. In the full resilience zone (S ≥ 8), perturbations from that equilibrium always return to the cryptic equilibrium. In the zero-resilience zone (S ≤ 5.5) the cryptic equilibrium does not exist. Instead, there is a fully resilient urchin barren. In the partial resilience zone (8 > S > 5.5), perturbations from the cryptic equilibrium are non-negative and bounded by the two stable equilibria. Assuming that perturbation outcomes from a cryptic urchin equilibrium in the partial resilience zone land at the originating equilibrium with a probability of ω_l, or follow a uniform distribution, $u(U_l^{S,0.8},U_h^{S,0.8})$, with a probability 1−ω_l, the probabilistic resilience for ending up on the lower arm versus upper arm equilibrium is given by Eq. 5.

$$\begin{array}{l}Q\left(U_{l/l}^{S,0.8}\right)=\{\begin{array}{l}1\hfill \\ if0\ge S\ge 8\text{, only }{U}_l^{S,0.8}\text{as real root}\hfill \\ {\text{ω}}_l+\left(1-{\text{ω}}_l\right)\left(\frac{U_b^{S,0.8}-U_l^{S,0.8}}{U_h^{S,0.8}-U_l^{S,0.8}}\right)\hfill \\ if8>S>5.5,0<U_b^{S,0.8}-U_l^{S,0.8}<U_h^{S,0.8}-U_l^{S,0.8}\hfill \\ 0\hfill \\ if0\le S\le 5.5\text{, only }{U}_h^{S,0.8}\text{ as real root}\hfill \end{array}\hfill \\ Q\left(U_{h/l}^{S,0.8}\right)=1-Q\left(U_{l/l}^{S,0.8}\right)\hfill \end{array}(5)$$

If, instead, the original equilibrium is an urchin barren, $U_h^{S,0.8}$, on the upper arm of Figure 2, and the probability of a zero disturbance is ω_h, the probability of return to $U_h^{S,0.8}$ is given by Eq. 6.

$$\begin{array}{l}Q\left(U_{h/h}^{S,0.8}\right)=\{\begin{array}{l}1\hfill \\ if0\le S\le 5.5,\text{ only }{U}_h^{S,0.8}\text{ as real root }\hfill \\ {\text{ω}}_h+\left(1-{\text{ω}}_h\right)\left(\frac{U_h^{S,0.8}-U_b^{S,0.8}}{U_h^{S,0.8}-U_l^{S,0.8}}\right)\hfill \\ if8>S>5.5,0<U_h^{S,0.8}-U_b^{S,0.8}<U_h^{S,0.8}-U_l^{S,0.8}\hfill \\ 0\hfill \\ if10\ge S\ge 8,\text{ only }{U}_h^{S,0.8}\text{ as real root}\hfill \end{array}\hfill \\ Q\left(U_{l/h}^{S,0.8}\right)=1-Q\left(U_{h/h}^{S,0.8}\right)\hfill \end{array}(6)$$

If 0 < ω_l + ω_h < 2, there is moderate clustering and some hysteresis, giving $Q\left(U_{l/l}^{S,0.8}\right)>Q\left(U_{l/h}^{S,0.8}\right)$ and $Q\left(U_{h/h}^{S,0.8}\right)>Q\left(U_{h/l}^{S,0.8}\right)$. I use ${\mathrm{\omega }}_h=\mathrm{\omega }{}_l=0.5$.

In the partial resilience zone for both Eqn 5 and 6, 5.5 < S < 8, with hysteretic memory induced by clustering in the probability density function for the perturbation-initiated displacement location, the probability of a perturbation ending up at cryptic urchin/urchin barren equilibrium is greater if it originated from that equilibrium. There is only imperfect reversibility.

Urchin-Kelp Model

Turning to the urchin-kelp subsystem, I now treat the equilibrium urchin density from the predator-urchin subsystem as an exogenous parameter. With K as kelp biomass density, $\stackrel{.}{K}$ as its time derivative, and U as urchin biomass, the minimal dynamic model is given by Eq. 7.

$$\stackrel{.}{K}=\left(\mathrm{\varphi }-\mathrm{\lambda }K\right)K-\frac{\mathrm{\mu }U{K}^2}{\left(K^2+\mathrm{\psi }\right)}(7)$$

The first right hand side term of Eq. 7 represents the natural growth of kelp, with ϕ and λ as parameters. The second right hand side term represents the loss of kelp from urchin grazing with μ and ψ as parameters. Although some researchers have used a linear grazing function (Marzloff, 2012), others have proposed a sigmoid one (Ling et al., 2015). I use a sigmoid, or Holling type III, function because it best represents the urchin-kelp relationship described in most of the literature. With no numerical response, urchin biomass is treated as exogenous. However, the grazing efficiency of urchins (proportion of kelp being consumed per unit of urchin density), (μK)/(K² + ψ), changes as the kelp density changes. When K = 0, grazing efficiency per urchin is zero. When K > 0 but low, grazing efficiency is low as urchins focus on other resources, like detritus (Konar and Estes, 2003). With greater kelp density, grazing efficiency first increases at decreasing rate, reaches a maximum, and then declines toward zero. Increased urchin grazing efficiency at low kelp levels may be due to urchin recruitment facilitation by crustose coralline algae (a kelp competitor) (Baskett and Salomon, 2010) and/or urchins switching from detritus to living plants (Konar and Estes, 2003). At the highest levels of kelp biomass, there is evidence that the motion of kelp inhibits urchin grazing efficiency (Konar and Estes, 2003).

From Eq. 7, assuming that although kelp density may get very small kelp will not be completely extirpated (K > 0), the K = 0 isocline contains the kelp-urchin combinations that are real roots of Eq. 8. As with Eq. 4, there are either one or three real roots.

$$K^3-\frac{\mathrm{\varphi }}{\mathrm{\lambda }}{K}^2+\left(\mathrm{\psi }+\frac{\mathrm{\mu }}{\mathrm{\lambda }}U\right)K-\frac{\mathrm{\psi }\mathrm{\varphi }}{\mathrm{\lambda }}=0(8)$$

Some research shows that kelp forests are extremely difficult to restore, there is very large amount of hysteresis in the urchin kelp system, and nearly all urchins may have to be eradicated for kelp forests to inevitably recover on barrens (Ling et al., 2015; Marzloff et al., 2016; Eger et al., 2020). To mimic these findings, I use most of the same parameter values as above (ϕ = 0.8, λ = 0.08, μ = 0.26), but with ψ = 0.01.

Figure 1 shows the isocline with the arrowed lines indicating inevitable regime shift thresholds. With K_h/U, K_l/U, and K_b/U as the upper, lower, and unstable arm equilibria. Local stability conditions are presented in Supplementary Appendix A for the predator-urchin model. The probability of return to an equilibrium on the high kelp arm is given in Eq. 1, and on the low kelp arm by Eq. 2. Fully resilient high kelp equilibria occur only if U ≤ 0.6. The partial resilience zone is 0.6 < U < 7.7, and in the range 7.7 ≤ U there are only low kelp equilibria, and zero high kelp resilience.

For a given predator density, S, and environmental state, α, over the two tropic relationships, depending on whether each relationship is in its partial resilience zone, there are up to four possible joint stable equilibria. For the predator-urchin system, partial resilience gives two urchin density equilibria, the low-density cryptic urchin equilibrium, $U_l^{S,\mathrm{\alpha }}$, and the high-density urchin barren, $U_h^{S,\mathrm{\alpha }}$. Conditional on the cryptic urchin equilibrium, designated C, partial resilience in the urchin-kelp system gives two kelp density equilibria, the high-density kelp forest, $K_{h/U_l}^{S,\mathrm{\alpha }}$ (KC), and the low- density kelp depauperate community, $K_{l/U_l}^{S,\mathrm{\alpha }}$ (DC). Conditional on an urchin barren, designated B, partial resilience for kelp gives either a low-density kelp depauperate community, $K_{l/U_h}^{S,\mathrm{\alpha }}$ (DB), or a kelp forest with lots of urchins, $K_{h/U_h}^{S,\mathrm{\alpha }}$ (KB). KB and DC are lower resilience versions of KC and DB, respectively. The KB can be characterized as a kelp forest with lower resilience because higher urchin density puts it closer to its inevitable tipping point to DB. It is an example of what Tracey et al. (2015) call an incipient barren. The DC is a kelp depauperate community with low resilience because the urchin density is low enough to put it close to its tipping point back to KC. All four joint equilibria exist if both the urchin and kelp equilibria are in their partial resilience zones. For S = 6 and α = 0.8, the equilibrium kelp density for KC is $K_{h/0.7}^{6,0,8}=9.7$, for DC is $K_{l/0.7}^{6,0,8}=0.06$, for DB is $K_{l/7.4}^{6,0.8}=0.004$, and for KB is $K_{h/7.4}^{6,0.8}=5.9$. Figure 2 shows the two urchin equilibria, and Figure 1 shows the conditional kelp equilibria.

Outside the zones of partial resilience, not all four joint equilibria exist. At very high or very low predator densities here may be full resilience for both the cryptic urchin and kelp forest (KC), or for both the urchin barren and depauperate kelp equilibria (DB). In each case there is only one joint equilibrium, a KC at very high predator density, or a DB at very low predator density. There is also the possibility of two partially resilient kelp equilibria, conditional on one fully resilient urchin equilibrium, yielding two joint equilibria, either DB and KB, or DC and KC. Finally, there can be two partially resilient urchin equilibria, one or both of which condition a fully resilient kelp equilibrium. Supplementary Appendix E has an example of the former, with three joint stable equilibria, KC, DB and KB.

Sustainable Natural Capital

Kelp Density, Resilience, and Hysteresis

Kelp density, resilience, and hysteresis are all important to the measurement of sustainable natural capital. Although I use equilibrium kelp density as the resource input to the indicator of the sustainable stock of natural capital, it is conditional on urchin density, which is in turn conditional on predator density. The resilience probabilities and hysteresis for both the kelp and urchin equilibria, which describe their ability to persist, are the sustainability inputs.

Resilience probabilities are tied to pulse perturbations in both the urchin and kelp systems. If any joint equilibrium has full resilience in both the urchin and kelp systems, all perturbations return to it and the kelp at that equilibrium is sustained. If the initial joint equilibrium is a fully resilient KC, its kelp density or natural capital will be sustained at a high level. If that KC does not exhibit full resilience in both systems, the kelp density at the KC equilibrium is not sustainable, and a perturbation can cause a shift to another stable joint equilibrium with a lesser amount of natural capital. For a measure of sustainable natural capital, I consider multiple rounds of perturbations, giving the ability to look at multiple generations of shifts from an originating equilibrium.

For any given perturbation round, there is both an urchin density perturbation and a kelp density perturbation. I assume that the urchin density perturbation occurs first, and that urchin density has settled at its post-perturbation equilibrium before kelp density is perturbed. Kelp density adjusts to shifts in urchin density along the upper (kelp forest) or lower (kelp depauperate) arm of Figure 1 but then faces separate perturbations. A round of pertubations allows for transitions between the joint equilibrium states, with the resiience probabilites determining the transition probabilities. If a perturbation round starts at $U_l^{S,\mathrm{\alpha }}$, there is a probability of $Q\left(U_{l/l}^{S,\mathrm{\alpha }}\right)$ of returning to that equilibrium following the round, and a probabilty of $Q\left(U_{h/l}^{S,\mathrm{\alpha }}\right)=1-Q\left(U_{l/l}^{S,\mathrm{\alpha }}\right)$ of transitioning to $U_h^{S,\mathrm{\alpha }}$. Similarly, starting at an equilibrium of $U_h^{S,\mathrm{\alpha }}$, there is a probability of $Q\left(U_{h/h}^{S,\mathrm{\alpha }}\right)$ of returning to $U_h^{S,\mathrm{\alpha }}$ after the pertubation round and a probability of $Q\left(U_{l/h}^{S,\mathrm{\alpha }}\right)=1-Q\left(U_{h/h}^{S,\mathrm{\alpha }}\right)$ of transitioning to $U_l^{S,\mathrm{\alpha }}$. There are four possible transition probabilities, all defined by Eqs 5 or 6.

Now consider perturbations in kelp density. With the subscript l/h/U_h representing a post-perturbation urchin equilibrium of U_h and a switch of the kelp equilibrium from h to l during the perturbation round, there are four transition probabilities for each of the two urchin equilibria outcomes, for a total of eight; $P\left(K_{h/h/U_h}^{S,\mathrm{\alpha }}\right)$, $P\left(K_{l/h/U_h}^{S,\mathrm{\alpha }}\right)$, $P\left(K_{l/l/U_h}^{S,\mathrm{\alpha }}\right)$, $P\left(K_{h/l/U_h}^{S,\mathrm{\alpha }}\right)$, $P\left(K_{h/h/U_l}^{S,\mathrm{\alpha }}\right)$, $P\left(K_{l/h/U_l}^{S,\mathrm{\alpha }}\right)$, $P\left(K_{l/l/U_l}^{S,\mathrm{\alpha }}\right)$, $P\left(K_{h/l/U_l}^{S,\mathrm{\alpha }}\right)$. They are all defined by Eqs 1 or 2. With four joint equilibrium states, there are sixteen transition probabilities. With the substript DBKC representing a transition fron KC to DB, the transition probabilty matrix is Eq. 9.

$$\begin{array}{l}A=\left(\begin{array}{llll}{a}_{KCKC}\hfill & a_{DCKC}\hfill & a_{DBKC}\hfill & a_{KBKC}\hfill \\ a_{KCDC}\hfill & a_{DCDC}\hfill & a_{DBDC}\hfill & a_{KBDC}\hfill \\ a_{KCDB}\hfill & a_{DCD\text{}B}\hfill & a_{DBDB}\hfill & a_{KBDB}\hfill \\ a_{KCKB}\hfill & a_{DCKB}\hfill & a_{DBKB}\hfill & a_{KBKB}\hfill \end{array}\right)\hfill \\ =(\begin{array}{ll}Q\left(U_{l/l}^{S,\alpha }\right)P\left(K_{h/h/U_l}^{S,\alpha }\right)\hfill & Q\left(U_{l/l}^{S,\alpha }\right)P\left(K_{l/h/U_l}^{S,\alpha }\right)\hfill \\ Q\left(U_{l/l}^{S,\alpha }\right)P\left(K_{h/l/U_l}^{S,\alpha }\right)\hfill & Q\left(U_{l/l}^{S,\alpha }\right)P\left(K_{l/l/U_l}^{S,\alpha }\right)\hfill \\ Q\left(U_{l/h}^{S,\alpha }\right)P\left(K_{h/l/U_l}^{S,\alpha }\right)\hfill & Q\left(U_{l/h}^{S,\alpha }\right)P\left(K_{l/l/U_h}^{S,\alpha }\right)\hfill \\ Q\left(U_{l/h}^{S,\alpha }\right)P\left(K_{h/h/U_l}^{S,\alpha }\right)\hfill & Q\left(U_{l/h}^{S,\alpha }\right)P\left(K_{l/h/U_l}^{S,\alpha }\right)\hfill \end{array}\hfill \\ \begin{array}{ll}Q\left(U_{h/l}^{S,\alpha }\right)P\left(K_{l/h/U_h}^{S,\alpha }\right)\hfill & Q\left(U_{h/l}^{S,\alpha }\right)P\left(K_{h/h/U_h}^{S,\alpha }\right)\hfill \\ Q\left(U_{h/l}^{S,\alpha }\right)P\left(K_{l/l/U_h}^{S,\alpha }\right)\hfill & Q\left(U_{h/l}^{S,\alpha }\right)P\left(K_{h/l/U_h}^{S,\alpha }\right)\hfill \\ Q\left(U_{h/h}^{S,\alpha }\right)P\left(K_{l/l/U_h}^{S,\alpha }\right)\hfill & Q\left(U_{h/h}^{S,\alpha }\right)P\left(K_{h/l/U_h}^{S,\alpha }\right)\hfill \\ Q\left(U_{h/h}^{S,\alpha }\right)P\left(K_{l/h/U_h}^{S,\alpha }\right)\hfill & Q\left(U_{h/h}^{S,\alpha }\right)P\left(K_{h/h/U_h}^{S,\alpha }\right)\hfill \end{array})\hfill \end{array}(9)$$

Assuming S = 6 and α = 0.8, other parameters as in Figures 1, 2, and with the resilience probabilities from Eqs 1, 2, 5, 6 with π_h = π_l = ω_h = ω_l = 0.5, Eq. 9 becomes Eq. 10.

$$\begin{array}{l}A=\left(\begin{array}{llll}{a}_{KCKC}\hfill & a_{DCKC}\hfill & a_{DBKC}\hfill & a_{KBKC}\hfill \\ a_{KCDC}\hfill & a_{DCDC}\hfill & a_{DBDC}\hfill & a_{KBDC}\hfill \\ a_{KCDB}\hfill & a_{DCDB}\hfill & a_{DBDB}\hfill & a_{KBDB}\hfill \\ a_{KCKB}\hfill & a_{DCKB}\hfill & a_{DBKB}\hfill & a_{KBKB}\hfill \end{array}\right)\hfill \\ =\left(\begin{array}{llll}0.594\hfill & 0.006\hfill & 0.136\hfill & 0.264\hfill \\ 0.294\hfill & 0.306\hfill & 0.336\hfill & 0.064\hfill \\ 0.049\hfill & 0.051\hfill & 0.756\hfill & 0.144\hfill \\ 0.099\hfill & 0.001\hfill & 0.306\hfill & 0.594\hfill \end{array}\right)\hfill \end{array}(10)$$

Let (Π_KC0  Π_DC0 Π_DB0 Π_KB0) be the initial vector of probabilities for the four possible joint equilibria, with Π_KC0 + Π_DC0 + Π_DB0 + Π_KB0 = 1. Starting from a KC equilibrium gives an initial probabilty of Π_KC0 = 1. After one perturbation round, using the transition matrix in Eq. 10, the probabilties of each equilibrium are given by the right most vector in Eq. 11.

$$\begin{array}{l}\left(\begin{array}{cccc}{\Pi }_{KC1}& {\Pi }_{DC1}& {\Pi }_{DB1}& {\Pi }_{KB1}\end{array}\right)\hfill \\ =\left(\begin{array}{cccc}{\Pi }_{KC0}& {\Pi }_{DC0}& {\Pi }_{DB0}& {\Pi }_{KB0}\end{array}\right)A\hfill \\ =\left(\begin{array}{cccc}1& 0& 0& 0\end{array}\right)A=\left(\begin{array}{cccc}0.594& 0.006& 0.136& 0.264\end{array}\right)\hfill \end{array}(11)$$

With the equilbrium kelp densities for KC, DC, DB, and KB, expected kelp density after one round of perturbations from a KC equilbrium is Eq. 12.

$$\begin{array}{c}{K}_{EKC1}^{6,0.8}=\left({\mathrm{\Pi }}_{KC1}{\mathrm{\Pi }}_{DC1}{\mathrm{\Pi }}_{DB1}{\mathrm{\Pi }}_{KB1}\right)\left(\begin{array}{c}{K}_{h/0.7}^{6,0.8}\hfill \\ K_{l/0.7}^{6,0.8}\hfill \\ K_{l/7.4}^{6,0.8}\hfill \\ K_{h/7.4}^{6,0.8}\hfill \end{array}\right)\hfill \\ =\left(\mathrm{0.594\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0.006\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0.136\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0.264}\right)\left(\begin{array}{c}9.7\hfill \\ 0.06\hfill \\ 0.004\hfill \\ 5.9\hfill \end{array}\right)\hfill \\ =7.32\hfill \end{array}(12)$$

Expected kelp has declined from its pre-perturbation KC level of $K_{h/0.7}^{6,0.8}$ = 9.7 because partial resilience allows there to be non-zero probabilities of displacement to the basins of attraction of other equilibria with lower kelp densities.

If perturbation rounds continue, hysteresis will limit the ability to return to the KC equilibrium. Starting from KC, after two rounds the expected kelp density will be Eq. 13.

$$\begin{array}{c}{K}_{EKC2}^{6,0.8}=\left({\mathrm{\Pi }}_{KC1}{\mathrm{\Pi }}_{DC1}{\mathrm{\Pi }}_{DB1}{\mathrm{\Pi }}_{KB1}\right)A\left(\begin{array}{c}{K}_{h/0.7}^{6,0.8}\hfill \\ K_{l/0.7}^{6,0.8}\hfill \\ K_{l/7.4}^{6,0.8}\hfill \\ K_{h/7.4}^{6,0.8}\hfill \end{array}\right)\hfill \\ =\left({\mathrm{\Pi }}_{KC2}{\mathrm{\Pi }}_{DC2}{\mathrm{\Pi }}_{DB2}{\mathrm{\Pi }}_{KB2}\right)\left(\begin{array}{c}{K}_{h/0.7}^{6,0.8}\hfill \\ K_{l/0.7}^{6,0.8}\hfill \\ K_{l/7.4}^{6,0.8}\hfill \\ K_{h/7.4}^{6,0.8}\hfill \end{array}\right)\hfill \\ =\left(\mathrm{0.387\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0.013\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0.266\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0.334}\right)\left(\begin{array}{c}9.7\hfill \\ 0.06\hfill \\ 0.004\hfill \\ 5.9\hfill \end{array}\right)=5.73\hfill \end{array}(13)$$

At some point there will be a stationary probability vector, which remains the same from one round to the next and depends only on the transition probabilities, not on the originating equilibrium. The equilibrium probabilities for this case are given by Eq. 14.

$$\begin{array}{c}\left({\mathrm{\Pi }}_{K{C}^{*}}{\mathrm{\Pi }}_{D{C}^{*}}{\mathrm{\Pi }}_{D{B}^{*}}{\mathrm{\Pi }}_{K{B}^{*}}\right)A\hfill \\ =\left({\mathrm{\Pi }}_{K{C}^{*}}{\mathrm{\Pi }}_{D{C}^{*}}{\mathrm{\Pi }}_{D{B}^{*}}{\mathrm{\Pi }}_{K{B}^{*}}\right)\hfill \\ =\left(\mathrm{0.161\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0.039\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0.507\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0.292}\right)\hfill \end{array}(14)$$

Using the equilbrium probabilities, there will be an equilibrium expected kelp density, Eq. 15.

$$\begin{array}{c}{K}_{E^{*}}^{6,0.8}=\left({\mathrm{\Pi }}_{K{C}^{*}}{\mathrm{\Pi }}_{D{C}^{*}}{\mathrm{\Pi }}_{D{B}^{*}}{\mathrm{\Pi }}_{K{B}^{*}}\right)\left(\begin{array}{c}{K}_{h/0.7}^{6,0.8}\hfill \\ K_{l/0.7}^{6,0.8}\hfill \\ K_{l/7.4}^{6,0.8}\hfill \\ K_{h/7.4}^{6,0.8}\hfill \end{array}\right)\hfill \\ =\left(\mathrm{0.161\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0.039\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0.507\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0.0.292}\right)\left(\begin{array}{c}9.7\hfill \\ 0.06\hfill \\ 0.004\hfill \\ 5.9\hfill \end{array}\right)\hfill \\ =3.29\hfill \end{array}(15)$$

The factors potentially affecting the expected kelp measures are: (i) kelp densities at the four stable equilibrium, (ii) the probabilty vector for the initial equilibrium, and (iii) the transition probability matrix, whose elements are affected by both the resilience of the four stable equilibria and the degree of hysteresis present. A more highly resilient KC equilbirum would mean a larger a_KCKC in the northwest corner of the A matrix in Eq. 10 and smaller entries in the rest of the row. This would increase $K_{EKC1}^{6,0.8}$, $K_{EKC2}^{6,0.8}$, through to $K_{E*}^{6,0.8}$. Hystersis also influences the A matrix. Strong hystersis (π_h = π_l = ω_h = ω_l = 1) would produce an identity matrix for A, causing the probabilty vector for the initial equilibrium to be repeated after each round of perturbations, and expected kelp density to remain at the initial level. There would be no convergence to a common equilibrium. If the intitial equilibrium was a KC, $K_{h/0.7}^{6,0.8}=K_{EKC1}^{6,0.8}=K_{EKC2}^{6,0.8}=K_{EKC*}^{6,0.8}=9.7$. If it was a DB, $K_{l/7.4}^{6,0.8}=K_{EDB1}^{6,0.8}=K_{EDB2}^{6,0.8}=K_{EDB*}^{6,0.8}=0.004$. With more moderate hysteresis, there is convergence, but, depending on hysteresis strength, it may take a large number of perturbations rounds to achieve. The case in Eqs 14 and 15 takes around ten perturbation rounds. With no hysteresis, the probability of ending up at any equilibrium will be independent of the perturbing equilibrium, and the A matrix will have identical rows. The result is immediate convergence to $K_{E*}^{6,0.8}=5.1$. Supplemental Appendix C shows the transition matrices and outcomes for the strong and no hysteresis cases. Whether the better measure of expected kelp density involves few or many rounds of perturbations, depends on the context in which it is being used.

Results

Losses in Sustainable Natural Capital

Natural capital, as measured by expected kelp density, can be lost through a decrease in the predator density parameter, S, or an increase in the urchin growth rate, α. For the Haida Gwaii case, a decrease in S (or loss of sea-otters) caused the loss in expected kelp. The urchin growth parameter, α, remained fixed at 0.8, while the fur trade caused sea otter extirpation is modeled as reducing S from S ≥ 8 to S ≤ 5.5. For the Tasmanian case predator density remains fixed at S = 5.5, but α, reflecting the urchin invasion, increases from 0.42 to 0.8.

First, consider the Haida Gwaii case. The situation prior to the post-contact sea otter fur trade would have been a low urchin density equilibrium in which both the sea-otter population and kelp beds were largely intact and which exhibited a high degree of resilience (Sloan and Bartier, 2000; Sloan and Dick, 2012). In Figure 2, this suggests S ≥ 8. With S ≥ 8 and α = 0.8 there was a fully resilient low urchin equilibrium at $U_l^{\ge 8,0.8}\le 0.4$ (Figure 2), and with $U_l^{\ge 8,0.8}\le 0.4$ there was a fully resilient high kelp equilibrium at $K_{h/\le 0.4}^{\ge 8,0.8}\ge 9.8$ (Figure 1). Since both the low urchin and high kelp equilibria were in their full resilience zones, there was only a KC equilibrium, with $A=a_{KFKF}=Q\left(U_{l/l}^{>8,0.8}\right)=P\left(K_{h/h/\le 0.4}^{\ge 8,0.8}\right)=1$. This ensured sustainable expected kelp, $K_{h/\le 0.4}^{\ge 8,0.8}=K_{EKC1}^{\ge 8,0.8}=K_{EKC2}^{\ge 8,0.8}=K_{EKC*}^{\ge 8,0.8}\ge 9.8$.

The fur trade reduced S below the reverse shift threshold of S = 8, and, as that happened, the low urchin equilibrium lost some if its resilience to perturbations. In the range 8 > S > 5.5, large enough perturbations from the cryptic urchin equilibrium would have had the potential to land in basin of attraction of the urchin barren equilibrium and cause a move to that equilibrium.

For example, if S was reduced to S = 6, the initial equilibrium would have been a KC with a slightly lower kelp density, $K_{h/{0.7}_l}^{6,0.8}=9.7$. But, due to a lack of resilience and hysteresis, π_l = π_h = ω_l = ω_h = 0.5, there would have been a much lower sustainable expected kelp density, $K_{EKC1}^{6,0.8}=7.32>K_{EKC2}^{6,0.8}=5.73>K_{EKC*}^{6,0.8}\ge 3.29$. Further decreases in sea otter density past the forward shift threshold of S = 5.5 would have caused low urchin resilience to be completely lost, the low urchin equilibrium to disappear, and would have made the shift to an equilibrium on the high urchin arm inevitable. In the urchin-kelp system, the urchin shift would have caused an inevitable shift to the lower kelp arm. Once S had been reduced to S ≤ 5.5, there was only fully resilient DB equilibrium, with $A=a_{DBDB}=Q\left(U_{h/h}^{\le 5.5,0.8}\right)P\left(K_{l/l/\ge 7.7}^{\le 5.5,0.8}\right)=1$ and $K_{l/\ge 7.7}^{\le 5.5,0.8}=K_{EDB1}^{\le 5.5,0.8}=K_{EDB2}^{\le 5.5,0.8}=K_{EDB*}^{\le 5.5,0.8}\le 0.004$. Further decreases in S resulted in further gradual increases in urchin density along the high urchin arm and gradual decreases in kelp density along the lower kelp arm. There the system has remained (Sloan et al., 2001).

For the Tasmanian lobster-urchin case, the pre-invasion locus assumes α = 0.42, the lowest (dashed) isocline in Figure 2. This isocline does not bend back on itself, leaving no possibility for an abrupt regime shift or hysteresis. With S = 5.5, $U_{/}^{5.5,0.42}=0.4$, and $K_{h/0.4}^{5.5,0.42}=9.9$ (Figures 1, 2), with all equilibria stable and fully resilient. The long spined urchin invasion transformed the isocline in Figure 2 from the dashed α = 0.42 locus, to the normal thickness α = 0.66 locus and is causing it to approach the heavier weight α = 0.8 locus. With S constant at S = 5.5, the result of the shift from α = 0.42 to α = 0.66 was a move from a fully resilient KC equilibria at $U_{/}^{5.5,0.42}=0.4,K_{h/0.4}^{5.5,0.42}=9.9$ to another fully resilient equilibrium just inside the boundaries of the full resilience zones for both urchin and kelp at $U_{/}^{5.5,0.66}=0.6,K_{h/0.6}^{5.5,0.66}=9.8$. Once α > 0.66, the equilibria moved into the zones of partial resilience, and there was the possibility for a perturbation to kick the urchin equilibrium from the lower arm to the upper arm, and/or the kelp equilibrium from the upper arm to the lower arm. As shown in the Supplemental Appendix D, α = 0.7, arrived at via increasing a, gave a partially resilient KC equilibrium at $K_{h/0.64}^{5.5,0.7}=9.75$. With perturbations clustered according to π_l = π_h = ω_l = ω_h = 0.5, hysteresis results in lower expected kelp, $K_{EKC1}^{5.5,0.7}=8.37$, $K_{EKC2}^{5.5,0.7}=7.7$, and $K_{EKC*}^{5.5,0.7}=6.5$. When α passes 0.8, there will be only a high urchin equilibrium, $U_h^{5.5,\ge 0.8}\ge 7.7$, and a low kelp equilibrium, $K_{l/\ge 7.7}^{5.5,\ge 0.8}\le 0.004$. Both will be fully resilient, giving a DB equilibrium with A = a_DBDB = 1 and sustainable natural capital of $K_{EDB*}^{5.5,\ge 0.8}\le 0.004$.

Management Controls

Systemic, Symptomatic, Press, Pulse, Preventative, and Restorative Controls

I consider management controls in the context of the two cases, Tasmania and Haida Gwaii. Management controls are necessary to prevent or reverse losses in sustainable natural capital. These controls may be systemic, symptomatic, press, pulse, preventative, or restorative (Scheffer et al., 2001; Lessard et al., 2005; Layton et al., 2020). Systemic controls aim to remove the ultimate causes of the losses. They are typically ongoing press controls (like permanent reductions in the harvesting of predators). In contrast, symptomatic control implies using leverage points for more direct control of affected populations, urchin harvesting or culling, or kelp enhancement (seeding or transplantation) (Lessard et al., 2005). Symptomatic controls may be either pulse (like one time or intermittent urchin culling in response to perturbations in urchin density) or press. Preventative controls aim to prevent a loss of kelp forest, and restorative controls to restore it after the loss has occurred. See Supplementary Appendix A for background on these controls.

In the Tasmanian case, the ulimate cause or threat is ocean warming, which for scientific and governance reasons, is not easily removable (Ling and Johnson, 2009). Harvesting of the lobster predator is an exacerbating factor (Ling et al., 2009), but there are questions as to whether restrictions on lobster harvest, be they systemic or symptomatic press controls, can be sufficent to prevent significant kelp forest losses (Tracey et al., 2015). Starting from a KC equilibrium, if the long spined urchin invasion proceeds to α = 0.8 in Figure 2, imposing lobster harvesting restrictions to ensure S > 5.5, will keep the equilibrium in the partial resilience zone. But, in that zone, natural perturbations in urchin and/or kelp density have the potential to initiate a shift away from the KC equilibrium.

In the Haida Gwaii case, the cause of the decrease in sustainable natural capital was overharvesting and extirpation of the sea otter predator (Sloan and Dick, 2012). The post-extirpation equilibrium is effectively a fully resilient DB. Systemic press control would have to produce a significant increase in effective sea otter density (supplemented by press uchin harvesting or culling to mimic sea otter predation) to move to the partial resilience zone, and a likely infeasible increase to get to a fully resilient KC equilibrium. While the sea otter has been reintroduced in the Pacific Northwest, only recently have there been indications that it will return to Haida Gwaii (Gwaii Haanas Archipelago Management Board, 2020). Press human harvesting of urchins is difficult or costly, and the pending return of the sea otter is not necessarily encouraged by human harvesters of other sea otter prey like abalone (Lee et al., 2016). Systemic control seems unlikely to be successful on its own.

While systemic or symtomatic press controls may be necessary to move into, and remain in, the zone of partial resilience (Layton et al., 2020), in that zone pulse controls may provide a cost effective way to cushion or enhance perturbations, disuading or encouraging a kick to an alternative equilibrium. Since both the Tasmanian and Haida Gwaii probrems are difficult to solve with press controls alone, pulse controls are useful complements that are designed to produce one time or periodic changes in the transition probability matrix. For simplicity of exposition, I illustrate with changes that increase crucial transition probabilities to one.

In the Tasmanian case, suppose press lobster harvesting restrictions have increased S to S = 6 while the long spined urchin invasion has produced α = 0.8. Assuming the KC equilibrium still prevails, Π_KC0 = 1. Even if press lobster harvest controls can maintain S = 6 in the partial resilience zone, perturbations still have the potential to kick the system to other equilibria, including a DB equilibrium. Over many perturbation rounds sustainable natural capital would be reduced to $K_{EKC*}^{6,0.8}=3.29$. However, supplementing press lobster harvest controls with others that are symptomatic, pulse and preventative may be able to sustain natural capital at $K_{EKC*}^{6,0.8}=9.7$. These would be periodic uchin culling, perhaps supplemented by periodic kelp enhancement (Flukes et al., 2012; Tracey et al., 2015). Pulse urchin culling could be used to counteract positive urchin perturbations from the low urchin equilibrium in both fthe first and subsequent rounds. ideally increasing $Q\left(U_{l/l}^{6,0.8}\right)$ from 0.6 to 1. Pulse kelp enhancement could counteract and negative perturbations from the hign kelp equilibrium in multiple rounds, ideally raising $P\left(K_{h/h/0.7}^{6,0.8}\right)$ from 0.99 to 1, and producing an increase in overall transition probability, $a_{KCKC}=Q\left(U_{l/l}^{6,0.8}\right)P\left(K_{h/h/0.7}^{6,0.8}\right)$, from 0.594 to 1. This changes the transition probabilty matrix from Eq. 10 to A′ in Eq. 16. With culling and kelp enhancement used to offset successfully all urchin and kelp perturbations, from KC, $K_{h/U_l}^{6,0.8}=K_{EKC1}^{6,0.8}=K_{ELC2}^{6,0.8}=K_{EKC*}^{6.0;8}=9.7$, and natural capital would be preserved.

$$\begin{array}{r}A{}^{\prime }=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0.294& 0.306& 0.336& 0.064\\ 0.049& 0.051& 0.756& 0.144\\ 0.099& 0.001& 0.306& 0.594\end{array}\right)\end{array}(16)$$

Turing to the Haida Gwaii case, if effective sea otter density can be increased to S = 6, the intitial equilbrium is a DB in the partial resilience zone. With no further action, other than maintaining S = 6, $K_{l/7.4}^{6,0.8}=0.004<K_{EDB1}^{6,0.8}=1.33<K_{EDB2}^{6,0.8}=2.17<K_{EDB*}^{6.0;8}=3.29$. The restoration of a kelp forest would required pulse urchin culling to create or enhance negative urchin density perturbations, possibly paired with pulse kelp enhancement. Starting at a DB equilibrium (Π_DB0 = 1), urchin culling could ideally increase $Q\left(U_{l/h}^{6,0.8}\right)$ from 0.1 to 1, and pulse kelp enhancment would ideally create positive perturbation in kelp density to increase $P\left(K_{h/l/0.7}^{6,0.8}\right)$ from 0.49 to 1. Overall the increase in $a_{KCDB}=Q\left(U_{l/h}^{6,0.8}\right)P\left(K_{h/l/0.7}^{6,0.8}\right)$ would be from 0.049 to 1. The transition probabilty matrix becomes A″ in Eq. 17.

$$A^{\mathrm{"}}=\left(\begin{array}{ccc}\hfill 0.594\hfill & \hfill 0.006\hfill & \hfill \mathrm{0.136\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0.264}\hfill \\ \hfill 0.294\hfill & \hfill 0.306\hfill & \hfill \mathrm{0.336\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0.064}\hfill \\ \hfill \begin{array}{c}\mathrm{\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}1}\hfill \\ 0.099\hfill \end{array}\hfill & \hfill \begin{array}{c}\mathrm{\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0}\hfill \\ 0.001\hfill \end{array}\hfill & \hfill \begin{array}{c}\mathrm{\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0}\hfill \\ \mathrm{0.306\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0.594}\hfill \end{array}\hfill \end{array}\right)(17)$$

The restoration involves a shift from a DB to a KC. Since S remains in the partial resilience zone, there would need to be pulse preventative culling and enhancement to maintain the KC equilibrium. Maintaining a kelp forest equilbrrium is not as hard as restoring it, requiring only an sustained increase in a_KCKC from 0.549 to 1 as in Eq. 16. Using restorative control followed by ongoing, but intermittent, preventative control, expected kelp density will increase from $K_{l/7.4}^{6,0.8}=0.004<K_{EDB1}^{6,0.8}=1.33<K_{EDB2}^{6,0.8}=2.17<K_{EDB*}^{6.0;8}=3.29$ to $K_{h/7.4}^{6,0.8}=K_{EKC1}^{6,0.8}=K_{ELC2}^{6,0.8}=K_{EKC*}^{6.0;8}=9.7$.

Preventative Control as Adaptive Management

Although sometimes restorative controls are necessary, when there is a choice preventative controls are usually preferable to restorative ones (Young, 2000). I show this in the context of pulse controls, although similar aguments can be made for press controls. There are three arguments to be made. First, due to hysterisis, getting back to a KC from an equilibrium like a DB, involves a larger transition probability increase than preventing the loss of the KC. Second, the cost function for transition probability increases (via urchin culling and kelp enhancement) may be strictly convex, with the increasing marginal cost for the probabilty increases required to restore a KC, making resoration of badly degraded barrens prohibitively costly (Layton et al., 2020). Third, a control which prevents a shift away from a KC can be used as adaptive management, providing more flexibilty for subsequent controls than doing nothing and allowing the shift. In the presence of current uncertainty about whether innovations will bring down restoration costs (Sunnset et al., 2010; Fredriksen et al., 2020), research to reduce the uncertainty, combined with the flexibility to resort to the option of restortative control only if it can be done cheaply and effectively, can be worthwhile. The extra benefit provided by using preventative control as adaptive management is its option value.

Using the Tasmanian case with S = 6 and α = 0.8, I first compare a pure preventative control plan (three round prevention controls) versus restorative control plan (after a first round of prevention there is a round of no control followed by a round of restoration control). Starting at a KC equilibrium, Π_KC0 = 1, both plans put us back at a a KC after three rounds, Π_KC3 = 1. This allows us to make comparisons on the basis of the first three rounds alone. With the initial probability of a KC equilibrium at Π_KC0 = 1 and Eq. 10 as the no control transition matrix, the pure preventative plan requires increasing the probability of a return to the KC from 0.594 to 1 in round one. This changes the transition matrix from Eqs 10–16. Continuing preventative control sustains the KC equilibrium.

The restoration plan also starts at a KC equilibrium, Π_KC0 = 1. With preventative control in round one, Eq. 16 is the transition matrix and the outcome is Π_KC1 = 1. With no control on the second round, the transition matrix reverts to A in Eq. 10, and the outcome vector is (Π_KC2 Π_DC2 Π_DB2 Π_KB2) = (0.594 0.006 0.136 0.264). Expected kelp after a round of perturbations with no control drops to $K_{EKC1}^{6,0.8}=7.32$. Restoration occurs in round three, with the goal that Π_KC3 = 1, with $K_{h/0.7}^{6,0.8}=9.7$. To generate this outcome, restoration must change the transition matrix from A to A‴ in Eq. 18, with a left-hand column of ones.

$$\begin{array}{c}\left({\mathrm{\Pi }}_{KC2}{\mathrm{\Pi }}_{DC2}{\mathrm{\Pi }}_{DB2}{\mathrm{\Pi }}_{KB2}\right)\hfill \\ A^{‴}=\left(\mathrm{0.594\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0.006\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0.136\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0.264}\right)\left(\begin{array}{c}\mathrm{1\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0}\hfill \\ \mathrm{1\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0}\hfill \\ \mathrm{1\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0}\hfill \\ \mathrm{1\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0}\hfill \end{array}\right)\hfill \\ =\left({\mathrm{\Pi }}_{KC3}{\mathrm{\Pi }}_{DC3}{\mathrm{\Pi }}_{DB3}{\mathrm{\Pi }}_{KB3}\right)=\left(\mathrm{1\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}0}\right)\hfill \end{array}(18)$$

Now consider the adaptive plan that is useful when there is uncertainty about an important decision factor like restoration costs. It is structured to allow for adaptive management and the creation of option value. It uses research to reduce uncertainty and a decision structure that has the flexibility to take advantage of the reduction in uncertainty. The first-round choice is crucial. To be useful research must be undertaken early, and the first-round choice should be one that is not difficult to change in the second round. For example, doing nothing in the first round may make it impossible to use prevention in the second round. Successful kelp forest restoration would have to be undertaken first. However, prevention in the first round can easily be changed to doing nothing in the second round. The adaptive plan combines first round preventative control with research which, by the beginning of the second round, reveals whether restoration costs are strictly convex (high) or linear (low). Once the restoration costs are known, the second-round decision, to continue prevention in rounds two and three (like the pure prevention plan) or to do nothing in round two and pursue restoration in round three (like the restoration plan), both followed from then on by prevention, can be taken.

Like the other two plans, the adaptive plan starts with Π_KC0 = 1. In round one, prevention changes A in Eq. 10 to A′ in Eq. 16, producing Π_KC1 = 1. With research into restoration costs yielding cost certainty by the beginning of round two, at this point there is a choice to be made between continued prevention versus a sequence of no control followed by restoration. The former maintains the transition probabilities as A′ and yields Π_KC2 = Π_KC3 = 1. The latter goes back toA for the second round yielding (Π_KC2 Π_DC2Π_DB2Π_KB2) = (0.594   0.006   0.136   0.264), and a switch from A to A‴ in (18) is required for restoration to Π_KC3 = 1 in the third round.

To compare the costs of the three plans, it is necessary to model cost function uncertainty. I assume the cost of increasing a transition probability, a_KCKC, a_KCDC, a_KCDB, or a_KCKB, to certainty, through a combination of pulse urchin culling and kelp enhancement, has a 0.5 probability of being given by a strictly convex cost function and a 0.5 probability of being given by a linear one. With KC as the original equilibrium, the convex and linear functions are C_c = 6.06(1−a_KCKC)³ and C_n = (1−a_KCKC), respectively. For the smaller transition probability increase required for preventative control, an increase in a_KCKC from 0.594 in A in Eq. 10 to 1 in A′ in Eq. 16, uncertainty with respect to the cost function doesn’t matter. Figure 3 shows 1−a (without the subscript) on the horizontal axis versus the cost, C. As shown in Eq. 19 and Figure 3, with 1−a = 0.406 the prevention cost is C^P = 0.406 (at point b) regardless of the shape of the cost function. The per round costs of prevention are the same regardless of whether the cost function is strictly convex or linear.

$$\begin{array}{c}{C}^P=C_c^P=6.06{\left(1-a_{KCKC}\right)}^3=6.06{\left(1-0.594\right)}^3\hfill \\ =C_n^P=\left(1-0.594\right)=0.406\hfill \end{array}(19)$$

FIGURE 3

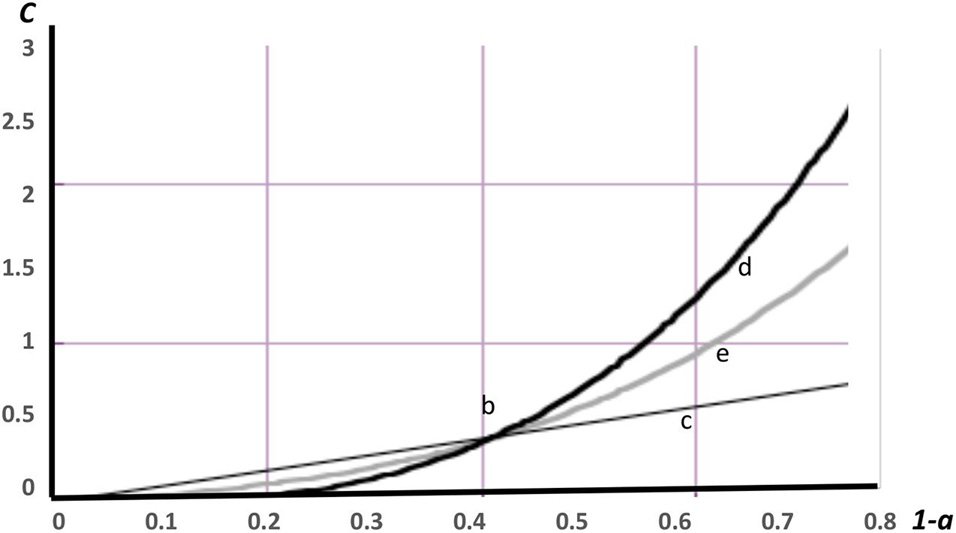
Figure 3. Cost functions for prevention and restoration: C_n = 1−a-linear cost function-normal black line, C_c = 6.06(1−a)³ -convex cost function-heavy black line, E(C) = 0.5C_n + 0.5C_c -expected cost-heavy gray line, b = (0.406,0.406), c = (0.559,0.559), d = (0.620,1.466), e = (0.613,1.003). Note that the 1−a coordinates for c, d, and e are certainty equivalents.

However, with restoration from A in Eq. 10 to A‴ in Eq. 18 it does matter whether the cost function is strictly convex or linear. Other equilibria, such as a DB, have positive probability (Π_KC2 Π_DC2 Π_DB2 Π_KB2) = (0.549 0.006 0.136 0.264), and all three of them require a larger probability increase to restore a KC than is required to maintain it. For the strictly convex cost outcome, the expected one-time restoration cost is Eq. 20.

$$\begin{array}{c}{C}_c^R=6.06\left[{\mathrm{\Pi }}_{KC2}{\left(1-a_{KCKC}\right)}^3+{\mathrm{\Pi }}_{DC2}{\left(1-a_{KCDC}\right)}^3\right]\hfill \\ +6.06\left[{\mathrm{\Pi }}_{DB2}{\left(1-a_{KCDB}\right)}^3+{\mathrm{\Pi }}_{KB2}{\left(1-a_{KCKB}\right)}^3\right]\hfill \\ =6.06\left[0.594{\left(1-0.594\right)}^3+0.006{\left(1-0.006\right)}^3\right]\hfill \\ +6.06\left[0.136{\left(1-0.136\right)}^3+0.264{\left(1-0.264\right)}^3\right]=1.446\hfill \end{array}(20)$$

For the linear cost outcome, it is Eq. 21.

$$\begin{array}{c}{C}_n^R=\left[{\mathrm{\Pi }}_{KC2}\left(1-a_{KCKC}\right)+{\mathrm{\Pi }}_{DC2}\left(1-a_{KCDC}\right)\right]\hfill \\ \mathit{\hspace{1em}\hspace{0.5em} }+\left[{\mathrm{\Pi }}_{DB2}\left(1-a_{KCDB}\right)+{\mathrm{\Pi }}_{KB2}\left(1-a_{KCKB}\right)\right]\hfill \\ =\left[0.594\left(1-0.594\right)+0.006\left(1-0.006\right)\right]\hfill \\ +\left[0.136\left(1-0.136\right)+0.264\left(1-0.264\right)\right]=0.559\hfill \end{array}(21)$$

With a 0.5 probability of each of the two cost function outcomes, one-time expected restoration costs are $E\left(C^R\right)=0.5\left(C_c^R+C_n^R\right)=1.003$. Figure 3 shows C^P = 0.406, $C_n^R=0.559$, $C_c^R=1.446$, and E(C^R) = 1.003 as b c, d, and e, respectively.

Now consider the cost of the three alternative plans for the Tasmanian case, starting from a KC and considering three potential rounds of perturbations. I use no discounting, as it would not affect the nature of the results, only their magnitude. The goal is to minimize the cost of returning to KC by the end of the third round. If there is no control during a round, the cost includes losses of services from the temporary loss of natural capital.

The pure preventative policy is a continuing preventative policy that always brings the system back to a KC equilibrium. Over three perturbation rounds, the control cost is C^PPP = 3C^P = 1.218, with natural capital sustained at $K_{EKC*}^{6,0.8}=9.7$. The restorative policy is to revert to no control for the second round of perturbations, letting natural capital temporarily drop from $K_{h/0.7}^{6,0.8}=9.7$ to a level of $K_{EKC1}^{6,0.8}=7.32$, for a lost value of services in round two of L. In round three, restoration to the kelp forest state is undertaken at an expected cost of E(C^R) = 1.003 and there is a return to a sustained $K_{h/0.7}^{6,0.8}=K_{EKC*}^{6,0.8}=9.7$. The three-round expected cost of the restorative policy is Eq. 22.

$$C^{PLR}=C^P+L+E\left(C^R\right)=0.406+L+1.003=L+1.409(22)$$

Comparing the costs of the purely preventative and restoration plans gives C^PLR − C^PPP = L + E(C^R) − 2C^p = L + 0.191. In Figure 3, L = 0, but E(C^R) = 1.003 (point e) is high enough to exceed 2C^P = 0.812 (double the height of point b). The pure prevention plan is clearly more cost effective. The crucial difference is that E(C^R) > C^P by a substantial amount. The two factors accounting for this difference are the greater probability increases required for restoration, and the increasing marginal cost in the event that $C_c^R$ is the cost function outcome. A large loss in natural capital services, L, would mitigate even more strongly in favor of the preventative control policy.

Now consider the adaptive plan. It uses research to reduce uncertainty and a decision structure that has the flexibility to take advantage of the reduction in uncertainty. The first-round choice is crucial. The adaptive plan combines first round preventative control with research which, by the beginning of the second round, reveals whether restoration costs are strictly convex (high) or linear (low). Once the restoration costs are known, the second-round decision can be taken, to continue prevention in rounds two and three (like the pure prevention plan) or to do nothing in round two and pursue restoration in round three, (like the restoration plan). Including research costs, W, the first-round cost is C^P = 0.406 + W. In the second round, the choice involves using the flexibility built into the preventative control to minimize costs for the second and third rounds based on newly acquired certainty about restoration costs. Over three rounds the costs for the adaptive plan are given by Eq. 23.

$$\begin{array}{c}{C}^{PAA}=C^P+0.5\left(\min [2C^P,L+C_c^R]\right)\hfill \\ +0.5\left(\min [2C^P,L+C_n^R]\right)\hfill \\ =0.406+W\hfill \\ +0.5\left(\min [0.812,L+1.446]\right)\hfill \\ +0.5\left(\min [0.812,L+0.559]\right)\hfill \end{array}(23)$$

The difference, V = C^PPP−C^PAA = 1.218−C^PAA, is the option value generated by the combination of knowledge about restoration costs and flexibility to change control options. Whether V > 0 depends upon whether the cheap restoration option, including the lost natural capital services and the cost of research, is less than the cost of continuing prevention. In Eq. 23 this requires 0.5L < 0.1265−W. If 0.5L < 0.1265−W, knowing after the first round that there will be cheap restoration costs, makes it worthwhile to do nothing in round two and then undertake restoration, giving C^PAA = 1.0915 + W + 0.5L and an option value, V = C^ppp−C^PAA = 0.1265−W−0.5L. In Figure 3, L = 0 and V = 0.1265−W. The possibility for a positive V comes from being able to choose one later round of cheap restoration (point c in Figure 3 with a restoration cost of 0.559) if it ends up being available (0.5 probability), rather than two more rounds of prevention costs for a total of 0.812 (double the height of point b in Figure 3) if cheap restoration is not available (0.5 probability). As long as L and the cost of research, W, are not too great, V > 0 and research to ascertain restoration costs is worthwhile. The adaptation plan provides an extra argument, based on flexibility, for current use of preventative controls. The overall conclusion is that initial prevention is always preferred. If it is paired with research that is not too costly, and it turns out that restoration costs, including lost natural capital services, are small, prevention can be abandoned in favor of later restoration. Otherwise prevention should continue to be used as needed.

Adaptive Manegement as Part of Restorative Control

For the Haida Gwaii case, the system is better characterized as already in a fully resilient DB state, with restorative control the only alternative to shift back to a KC. In a fully resilient DB state, all perturbations return to the DB, and pulse controls alone will not be helpful in producing the shift. Until the sea otter predator returns in sufficient numbers, there must also be ongoing press urchin culling control, simulating sea otter predation and pushing the system back at least into the partial resilience zones, where pulse urchin culling, with or without kelp enhancement, can kick the system back to a KC. Whether a given amount of press urchin culling will move the effective S from a fully resilient urchin barren into the partial resilience zone depends on the rate of sea otter recovery, and the thresholds at which the urchin density shifts from high to low and kelp density shifts from low to high, all of which are uncertain (Goldman, 2020). Here I simplify by characterizing the uncertainty as doubt about how much resilience the urchin barren equilibrium will lose for a given amount of press culling. Hypothetically, assume there is a 0.5 probability that otter recovery, combined with some fixed amount of press urchin culling, will increase S to S = 6, with a DB equilibrium and a transition probability a_KCDB = 0.049 (from Eq. 10) of ending up at KC following negative urchin and positive kelp pulse perturbations. Or there is a probability of 0.5 that press culling alone will increase S to S = 9, with a_KCDB = 1, a move to a fully resilient kelp forest equilibrium. Without strong monitoring of either sea-otter numbers or kelp and urchin abundance (Estes et al., 2010; Williams et al., 2018), we will not know whether we are approaching S = 6, requiring a pulse of urchin culling and kelp enhancement to get to a KC, or S = 9, requiring none. Instead, we know only that we have fifty-fifty chance of approaching either S = 6or S = 9 for an expected predator density of E(S) = 7.5. Adaptive management can be beneficial here as well. Knowing whether S = 6 or S = 9 enables the policy maker to tailor investment in pulse culling and enhancement control to the sea-otter recovery level, with the possibility of making that investment more cost effective and generating positive option value. Details are presented in the Supplementary Appendix D.

Discussion

Addressing the loss of resilience and depletion of kelp forests as a foundation species in an important marine ecosystem, this paper developed a mathematical model to analyze catastrophic shifts in urchin and kelp densities. The recursively decoupled catastrophe model has two trophic interactions, with the potential for two catastrophic shifts, one at the level of the predator-urchin trophic interaction and one at the level of the urchin-kelp trophic interaction. It incorporates the concept of resilience at both levels and uses resilience probabilities and hysteresis to describe the probabilities of shift patterns between alternative urchin and kelp equilibria and as part of a definition of a sustainable natural capital stock as expected kelp density. To prevent or reverse losses in the sustainable natural capital stock, I consider systemic versus symptomatic, press versus pulse, and preventative versus restorative controls. There is often complementarity in that combinations of controls can be more successful than one type alone. Pulse controls alone cannot be successful in converting a DB to a KC unless the originating equilibrium is in the partial resilience zone. But they may provide a cost-effective complement to a systemic or symptomatic press control that moves the originating equilibrium into, and keeps it in, that zone. With hysteretic memory activated by clustered perturbations, and convex cost function for controls like urchin culling and kelp enhancement, it is likely to be more difficult and costly to restore a kelp forest, than to prevent its loss. I also suggest a role for adaptive management, in that improving knowledge about such uncertain factors as restoration cost or the rate of sea otter recovery can, if control policies are flexible, create an option value that reduces the cost of maintaining or restoring a kelp forest state.

The mathematical model has some limitations. The pure top-down predator-urchin-kelp cascade is often used in the literature and makes the modeling more straight forward, but also ignores some ecological complexity (Wallington et al., 2005). This may limit application to other systems, particularly those where the downward cascade is less prominent. Exogenous factors, such as climatic changes or ongoing pollution, can be incorporated by parameter manipulation, as was done for the invasive long spined sea urchin, but complexity may be compromised here as well (Mooney and Cleland, 2001; Karatayev and Baskett, 2020). Because it generates multiple stable equilibria, the Holling-type III predation function plays a critical role in the model. While findings of alternative stable states with different shift thresholds (hysteresis) support type III (Ling et al., 2019), direct empirical estimates of functional form do not always do so (Dunn and Hovel, 2019; Karatayev et al., 2019). Another crucial assumption is the treatment of pulse perturbations and hysteresis. While pulse perturbations clearly have a role in initiating shifts between equilibria, and in creating hysteresis, there has been little or no incorporation of them into mathematical models. The piecewise approach is an initial attempt. For both predation functions, and pulse perturbations, future model adjustments are possible depending on what scientific evidence suggests. Other case studies, such as the California marine heat wave that combines climate perturbations with predator decline (Rogers-Bennett and Catton, 2019; McPherson et al., 2021), could be usefully explored. Finally, while sustainable natural capital is a clear enough concept, both physical and value measures are mostly missing (Loomis, 2006). Overall, improved empirical evidence, both ecologic and economic, is needed to give more substance to the final verdict. Nevertheless, despite its limitations, the model is based on available scientific evidence and does generate important implications for control policies. Pairing with the economic concepts of sustainable natural capital and the cost functions for controls, enriches the policy conclusion.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2021.674792/full#supplementary-material

References

Andrew, N. (1993). Spatial heterogeneity, sea urchin grazing, and habitat structure on reefs in temperate Australia. Ecology 74, 292–302. doi: 10.2307/1939293

CrossRef Full Text | Google Scholar

Baho, D. L., Allen, C. R., Garmestani, A. S., Fried-Petersen, H. B., Renes, S. E., Gunderson, L. H., et al. (2017). A quantitative framework for assessing ecological resilience. Ecol. Soc. 22, 1–17. doi: 10.5751/ES-09427-220317

PubMed Abstract | CrossRef Full Text | Google Scholar

Baskett, M. L., and Salomon, A. K. (2010). Recruitment facilitation can drive alternative states on temperate reefs. Ecology 91, 1763–1773. doi: 10.1890/09-0515.1

CrossRef Full Text | Google Scholar

Bennett, S., Wernberg, T., Connell, S. D., Hobday, A. J., Johnson, C. R., and Poloczanska, E. S. (2016). The ‘Great Southern Reef’: social, ecological and economic value of Australia’s neglected kelp forests. Mar. Freshw. Res. 67, 47–56. doi: 10.1071/MF15232

CrossRef Full Text | Google Scholar

Bond, C. A. (2017). Valuing coastal natural capital in a bioeconomic framework. Water Econ. Policy 3:1650008. doi: 10.1142/S2382624X16500089

CrossRef Full Text | Google Scholar

Borer, E., Seabloom, E., Shurin, J., Anderson, K., Blanchette, C., Broitman, B., et al. (2005). What determines the strength of a trophic cascade? Ecology 86, 528–537. doi: 10.1890/03-0816

CrossRef Full Text | Google Scholar

Boyd, J., and Krupnick, A. (2013). Using ecological production theory to define and select environmental commodities for nonmarket valuation. Agric. Resour. Econ. Rev. 42, 1–32. doi: 10.1017/S1068280500007590

CrossRef Full Text | Google Scholar

Brummitt, C. D., Barnett, G., and D’Souza, R. M. (2015). Coupled catastrophes: sudden shifts cascade and hop among interdependent systems. J. R. Soc. Inter. 12:20150712. doi: 10.1098/rsif.2015.0712

PubMed Abstract | CrossRef Full Text | Google Scholar

Butler, I., Mark, J., and Kintzing, M. D. (2016). An exception to the rule: top-down control of a coral reef macroinvertebrate community by a tropical spiny lobster. Bull. Mar. Sci. 92, 137–152. doi: 10.5343/bms.2015.1045

PubMed Abstract | CrossRef Full Text | Google Scholar

Carpenter, S., Walker, B., Anderies, J. M., and Abel, N. (2001). From metaphor to measurement: resilience of what to what? Ecosystems 4, 765–781. doi: 10.1007/s10021-001-0045-9

CrossRef Full Text | Google Scholar

Carpenter, S. R., Kitchell, J. F., and Hodgson, J. R. (1985). Cascading trophic interactions and lake productivity. BioScience 35, 634–639. doi: 10.2307/1309989

CrossRef Full Text | Google Scholar

Dunn, R. P., Baskett, M. L., and Hovel, K. A. (2017). Interactive effects of predator and prey harvest on ecological resilience of rocky reefs. Ecol. Appl. 27, 1718–1730. doi: 10.1002/eap.1581

PubMed Abstract | CrossRef Full Text | Google Scholar

Dunn, R. P., and Hovel, K. A. (2019). Experiments reveal limited top-down control of key herbivores in southern California kelp forests. Ecology 100:e02625. doi: 10.1002/ecy.2625

PubMed Abstract | CrossRef Full Text | Google Scholar

Edgar, G. J., Barrett, N. S., Morton, A. J., and Samson, C. R. (2004). Effects of algal canopy clearance on plant, fish and macroinvertebrate communities on eastern Tasmanian reefs. J. Exp. Mar. Biol. Ecol. 312, 67–87. doi: 10.1016/j.jembe.2004.06.005

CrossRef Full Text | Google Scholar

Edyvane, K. (2003). Conservation, Monitoring & Recovery of Threatened Giant Kelp (Macrocystis pyrifera) Beds in Tasmania – Final Report. Hobart, TAS: Dept. of Primary Industries, Water and Environment.

Google Scholar

Eger, A., Vergés, A., Choi, C. G., Christie, H., Coleman, M. A., Fagerli, C. W., et al. (2020). Financial and institutional support are important for large-scale kelp forest restoration. Front. Mar. Sci. 7:535277. doi: 10.3389/fmars.2020.535277

CrossRef Full Text | Google Scholar

Ellison, A. M., Bank, M. S., Clinton, B. D., Colburn, E. A., Elliott, K., Ford, C. R., et al. (2005). Loss of foundation species: consequences for the structure and dynamics of forested ecosystems. Front. Ecol. Environ. 3:479. doi: 10.2307/3868635

CrossRef Full Text | Google Scholar

Estes, J., Riedman, M., Staedler, M., Tinker, M., and Lyon, B. (2003). Individual variation in prey selection by sea otters: patterns, causes and implications. J. Anim. Ecol. 72, 144–155. doi: 10.1046/j.1365-2656.2003.00690.x

CrossRef Full Text | Google Scholar

Estes, J. A., and Duggins, D. O. (1995). Sea otters and kelp forests in Alaska: generality and variation in a community ecological paradigm. Ecol. Monogr. 65, 75–100. doi: 10.2307/2937159

CrossRef Full Text | Google Scholar

Estes, J. A., and Palmisano, J. F. (1974). Sea otters: their role in structuring nearshore communities. Science 185, 1058–1060. doi: 10.1126/science.185.4156.1058

PubMed Abstract | CrossRef Full Text | Google Scholar

Estes, J. A., Terborgh, J., Brashares, J. S., Power, M. E., Berger, J., Bond, W. J., et al. (2011). Trophic downgrading of planet Earth. Science 333, 301–306. doi: 10.1126/science.1205106

PubMed Abstract | CrossRef Full Text | Google Scholar

Estes, J. A., Tinker, M. T., and Bodkin, J. L. (2010). Using ecological function to develop recovery criteria for depleted species: sea otters and kelp forests in the Aleutian archipelago. Conserv. Biol. 24, 852–860. doi: 10.1111/j.1523-1739.2009.01428.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Eurich, J. G., Selden, R. L., and Warner, R. R. (2014). California spiny lobster preference for urchins from kelp forests: implications for urchin barrens persistence. Mar. Ecol. Prog. Ser. 498, 217–225. doi: 10.3354/meps10643

CrossRef Full Text | Google Scholar

Fenichel, E. P., and Abbott, J. K. (2014). Natural capital: from metaphor to measurement. J. Assoc. Environ. Resour. Econ. 1, 1–27. doi: 10.1086/676034

CrossRef Full Text | Google Scholar

Filbee-Dexter, K., Feehan, C. J., and Scheibling, R. E. (2016). Large-scale degradation of a kelp ecosystem in an ocean warming hotspot. Mar. Ecol. Prog. Ser. 543, 141–152. doi: 10.3354/meps11554

CrossRef Full Text | Google Scholar

Filbee-Dexter, K., and Scheibling, R. E. (2014). Sea urchin barrens as alternative stable states of collapsed kelp ecosystems. Mar. Ecol. Prog. Ser. 495, 1–25. doi: 10.3354/meps10573

CrossRef Full Text | Google Scholar

Filbee-Dexter, K., and Wernberg, T. (2018). Rise of turfs: a new battlefront for globally declining kelp forests. BioScience 68, 64–76. doi: 10.1093/biosci/bix147

CrossRef Full Text | Google Scholar

Flukes, E., Johnson, C., and Ling, S. (2012). Forming sea urchin barrens from the inside out: an alternative pattern of overgrazing. Mar. Ecol. Prog. Ser. 464, 179–194. doi: 10.3354/meps09881

CrossRef Full Text | Google Scholar

Foster, M. S., and Schiel, D. R. (2010). Loss of predators and the collapse of southern California kelp forests (?): alternatives, explanations and generalizations. J. Exp. Mar. Biol. Ecol. 393, 59–70. doi: 10.1016/j.jembe.2010.07.002

CrossRef Full Text | Google Scholar

Fredriksen, S., Filbee-Dexter, K., Norderhaug, K. M., Steen, H., Bodvin, T., Coleman, M. A., et al. (2020). Green gravel: a novel restoration tool to combat kelp forest decline. Sci. Rep. 10, 1–7. doi: 10.1038/s41598-020-60553-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Goldman, J. S. (2020). Restoring Harmony in Haida Gwaii. Yes!. Available online at: https://www.biographic.com/restoring-harmony-in-haida-gwaii (accessed September 18, 2021).

Google Scholar

Gorman, D., Russell, B. D., and Connell, S. D. (2009). Land-to-sea connectivity: linking human-derived terrestrial subsidies to subtidal habitat change on open rocky coasts. Ecol. Appl. 19, 1114–1126. doi: 10.1890/08-0831.1

CrossRef Full Text | Google Scholar

Graham, M. H. (2004). Effects of local deforestation on the diversity and structure of southern California giant kelp forest food webs. Ecosystems 7, 341–357. doi: 10.1007/s10021-003-0245-6

CrossRef Full Text | Google Scholar

Gwaii Haanas Archipelago Management Board (2020). Sharing our waters with kuu once again. Land Sea People Plan. Available online at: https://www.pc.gc.ca/en/pn-np/bc/gwaiihaanas/culture/terre-mer-gens-land-sea-people (accessed September 18, 2021).

Google Scholar

Halpern, B. S., Cottenie, K., and Broitman, B. R. (2006). Strong top-down control in southern California kelp forest ecosystems. Science 312, 1230–1232. doi: 10.1126/science.1128613

PubMed Abstract | CrossRef Full Text | Google Scholar

Hereu Fina, B. (2004). The Role of Trophic Interactions Between Fishes, Sea Urchins and Algae in the Northwestern Mediterranean Rocky Infralittoral. Ph.D dissertation. Barcelona: Universitat de Barcelona.

Google Scholar

Holling, C. S. (1959a). Some characteristics of simple types of predation and parasitism. Can. Entomol. 91, 385–398. doi: 10.4039/Ent91385-7

CrossRef Full Text | Google Scholar

Holling, C. S. (1959b). The components of predation as revealed by a study of small-mammal predation of the European pine sawfly. Can. Entomol. 91, 293–320. doi: 10.4039/Ent91293-5

CrossRef Full Text | Google Scholar

Holling, C. S. (1973). Resilience and stability of ecological systems. Annu. Rev. Ecol. Syst. 4, 1–23. doi: 10.1146/annurev.es.04.110173.000245

CrossRef Full Text | Google Scholar

Johnson, C. R., Banks, S. C., Barrett, N. S., Cazassus, F., Dunstan, P. K., Edgar, G. J., et al. (2011). Climate change cascades: shifts in oceanography, species’ ranges and subtidal marine community dynamics in eastern Tasmania. J. Exp. Mar. Biol. Ecol. 400, 17–32. doi: 10.1016/j.jembe.2011.02.032

CrossRef Full Text | Google Scholar

Johnson, C. R., Chabot, R. H., Marzloff, M. P., and Wotherspoon, S. (2017). Knowing when (not) to attempt ecological restoration. Restor. Ecol. 25, 140–147. doi: 10.1111/rec.12413

CrossRef Full Text | Google Scholar

Karatayev, V. A., and Baskett, M. L. (2020). At what spatial scales are alternative stable states relevant in highly interconnected ecosystems? Ecology 101:e02930. doi: 10.1002/ecy.2930

PubMed Abstract | CrossRef Full Text | Google Scholar

Karatayev, V. A., Baskett, M. L., Kushner, D. J., Shears, N. T., Caselle, J. E., and Boettiger, C. (2019). Grazer behavior can regulate large-scale patterns of community states. bioRxiv[Preprint] 722215, doi: 10.1101/722215

CrossRef Full Text | Google Scholar

Kenner, M. C., and Tinker, M. T. (2018). Stability and change in kelp forest habitats at San Nicolas Island. West. N. Am. Nat. 78, 1–11. doi: 10.3398/064.078.0407

CrossRef Full Text | Google Scholar

Konar, B., and Estes, J. A. (2003). The stability of boundary regions between kelp beds and deforested areas. Ecology 84, 174–185. doi: 10.1890/0012-9658(2003)084[0174:TSOBRB]2.0.CO;2

CrossRef Full Text | Google Scholar

Kraufvelin, P. (2017). Macroalgal grazing by the green sea urchin: born to consume resources. Mar. Biol. 164:132. doi: 10.1007/s00227-017-3161-6

CrossRef Full Text | Google Scholar

Krumhansl, K. A., Okamoto, D. K., Rassweiler, A., Novak, M., Bolton, J. J., Cavanaugh, K. C., et al. (2016). Global patterns of kelp forest change over the past half-century. Proc. Natl. Acad. Sci. U. S. A. 113, 13785–13790. doi: 10.1073/pnas.1606102113

PubMed Abstract | CrossRef Full Text | Google Scholar

Lafferty, K. D. (2004). Fishing for lobsters indirectly increases epidemics in sea urchins. Ecol. Appl. 14, 1566–1573. doi: 10.1890/03-5088

CrossRef Full Text | Google Scholar

Layton, C., Coleman, M. A., Marzinelli, E. M., Steinberg, P. D., Swearer, S. E., Vergés, A., et al. (2020). Kelp forest restoration in Australia. Front. Mar. Sci. 7:74. doi: 10.3389/fmars.2020.00074

CrossRef Full Text | Google Scholar

Lee, L., Irvine, R., and Wilson, N. (2018). Chiixuu Tll Iinasdll-Nurturing Seafood to Grow. Gwaii Haanas: Gwaii Haanas National Park Reserve.

Google Scholar

Lee, L., Watson, J., Trebilco, R., and Salomon, A. (2016). Indirect effects and prey behavior mediate interactions between an endangered prey and recovering predator. Ecosphere 7:e01604. doi: 10.1002/ecs2.1604

CrossRef Full Text | Google Scholar

Lessard, R. B., Martell, S. J., Walters, C. J., Essington, T. E., and Kitchell, J. F. (2005). Should ecosystem management involve active control of species abundances? Ecol. Soc. 10:1. doi: 10.5751/ES-01313-100201

PubMed Abstract | CrossRef Full Text | Google Scholar

Ling, S., and Johnson, C. (2009). Population dynamics of an ecologically important range-extender: kelp beds versus sea urchin barrens. Mar. Ecol. Prog. Ser. 374, 113–125. doi: 10.3354/meps07729

CrossRef Full Text | Google Scholar

Ling, S., and Johnson, C. (2012). Marine reserves reduce risk of climate-driven phase shift by reinstating size-and habitat-specific trophic interactions. Ecol. Appl. 22, 1232–1245. doi: 10.1890/11-1587.1

CrossRef Full Text | Google Scholar

Ling, S., Johnson, C., Frusher, S., and Ridgway, K. (2009). Overfishing reduces resilience of kelp beds to climate-driven catastrophic phase shift. Proc. Natl. Acad. Sci. U. S. A. 106, 22341–22345. doi: 10.1073/pnas.0907529106

PubMed Abstract | CrossRef Full Text | Google Scholar

Ling, S., Scheibling, R., Rassweiler, A., Johnson, C., Shears, N., Connell, S., et al. (2015). Global regime shift dynamics of catastrophic sea urchin overgrazing. Philos. Trans. R. Soc. B Biol. Sci. 370:20130269. doi: 10.1098/rstb.2013.0269

CrossRef Full Text | Google Scholar

Ling, S. D., Kriegisch, N., Woolley, B., and Reeves, S. E. (2019). Density-dependent feedbacks, hysteresis, and demography of overgrazing sea urchins. Ecology 100:e02577. doi: 10.1002/ecy.2577

PubMed Abstract | CrossRef Full Text | Google Scholar

Loomis, J. (2006). Estimating recreation and existence values of sea otter expansion in California using benefit transfer. Coast. Manag. 34, 387–404. doi: 10.1080/08920750600860282

CrossRef Full Text | Google Scholar

Ludwig, D., Jones, D. D., and Holling, C. S. (1978). Qualitative analysis of insect outbreak systems: the spruce budworm and forest. J. Anim. Ecol. 47, 315–332. doi: 10.2307/3939

CrossRef Full Text | Google Scholar

Ludwig, D., Walker, B., and Holling, C. S. (1997). Sustainability, stability, and resilience. Conserv. Ecol. 1:7. doi: 10.5751/ES-00012-010107

PubMed Abstract | CrossRef Full Text | Google Scholar

Lyons, D. A., and Scheibling, R. E. (2007). Differences in somatic and gonadic growth of sea urchins (Stronglyocentrotus droebachiensis) fed kelp (Laminaria longicruris) or the invasive alga Codium fragile ssp. tomentosoides are related to energy acquisition. Mar. Biol. 152, 285–295. doi: 10.1007/s00227-007-0682-4

CrossRef Full Text | Google Scholar

Mäler, K.-G., and Li, C.-Z. (2010). Measuring sustainability under regime shift uncertainty: a resilience pricing approach. Environ. Dev. Econ. 15, 707–719. doi: 10.1017/S1355770X10000318

CrossRef Full Text | Google Scholar

Marzloff, M. P. (2012). Towards Ecosystem-Based Management of Tasmanian Temperate Rocky Reefs: Community Dynamics Models Indicate Alternative Community States and Management Strategies. Hobart TAS: University of Tasmania.

Google Scholar

Marzloff, M. P., Little, L. R., and Johnson, C. R. (2016). Building resilience against climate-driven shifts in a temperate reef system: staying away from context-dependent ecological thresholds. Ecosystems 19, 1–15. doi: 10.1007/s10021-015-9913-6

CrossRef Full Text | Google Scholar

McLaren, B., and Peterson, R. (1994). Wolves, moose, and tree rings on Isle Royale. Science 266, 1555–1558. doi: 10.1126/science.266.5190.1555

PubMed Abstract | CrossRef Full Text | Google Scholar

McPherson, M. L., Finger, D. J., Houskeeper, H. F., Bell, T. W., Carr, M. H., Rogers-Bennett, L., et al. (2021). Large-scale shift in the structure of a kelp forest ecosystem co-occurs with an epizootic and marine heatwave. Commun. Biol. 4, 1–9. doi: 10.1038/s42003-021-01993-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Miller, R. J., Lafferty, K. D., Lamy, T., Kui, L., Rassweiler, A., and Reed, D. C. (2018). Giant kelp, Macrocystis pyrifera, increases faunal diversity through physical engineering. Proc. R. Soc. B Biol. Sci. 285:20172571. doi: 10.1098/rspb.2017.2571

PubMed Abstract | CrossRef Full Text | Google Scholar

Mooney, H. A., and Cleland, E. E. (2001). The evolutionary impact of invasive species. Proc. Natl. Acad. Sci. U. S. A. 98, 5446–5451. doi: 10.1073/pnas.091093398

PubMed Abstract | CrossRef Full Text | Google Scholar

Murray, J. D. (2002). Mathematical Biology. I, An Introduction, 3rd Edn. New York, NY: Springer. doi: 10.1007/b98868

CrossRef Full Text | Google Scholar

Nowak, E. M., Theimer, T. C., and Schuett, G. W. (2008). Functional and numerical responses of predators: where do vipers fit in the traditional paradigms? Biol. Rev. 83, 601–620. doi: 10.1111/j.1469-185X.2008.00056.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Paine, R. T. (1980). Food webs: linkage, interaction strength and community infrastructure. J. Anim. Ecol. 49, 667–685. doi: 10.2307/4220

CrossRef Full Text | Google Scholar

Paine, R. T., Tegner, M. J., and Johnson, E. A. (1998). Compounded perturbations yield ecological surprises. Ecosystems 1, 535–545. doi: 10.1007/s100219900049

CrossRef Full Text | Google Scholar

Pearse, J. S. (2006). Ecological role of purple sea urchins. Science 314, 940–941. doi: 10.1126/science.1131888

PubMed Abstract | CrossRef Full Text | Google Scholar

Pershing, A. J., Mills, K. E., Record, N. R., Stamieszkin, K., Wurtzell, K. V., Byron, C. J., et al. (2015). Evaluating trophic cascades as drivers of regime shifts in different ocean ecosystems. Philos. Trans. R. Soc. B Biol. Sci. 370:20130265.

Google Scholar

Petraitis, P. S., and Dudgeon, S. R. (2004). Detection of alternative stable states in marine communities. J. Exp. Mar. Biol. Ecol. 300, 343–371. doi: 10.1016/j.jembe.2003.12.026

CrossRef Full Text | Google Scholar

Preston, S. H., and Wang, H. (2007). Intrinsic growth rates and net reproduction rates in the presence of migration. Popul. Dev. Rev. 33, 357–666. doi: 10.1111/j.1728-4457.2007.00192.x

CrossRef Full Text | Google Scholar

Reed, D. C., Rassweiler, A., Carr, M. H., Cavanaugh, K. C., Malone, D. P., and Siegel, D. A. (2011). Wave disturbance overwhelms top-down and bottom-up control of primary production in California kelp forests. Ecology 92, 2108–2116. doi: 10.1890/11-0377.1

CrossRef Full Text | Google Scholar

Ripple, W. J., Estes, J. A., Schmitz, O. J., Constant, V., Kaylor, M. J., Lenz, A., et al. (2016). What is a trophic cascade? Trends Ecol. Evol. 31, 842–849. doi: 10.1016/j.tree.2016.08.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Rogers-Bennett, L., and Catton, C. (2019). Marine heat wave and multiple stressors tip bull kelp forest to sea urchin barrens. Sci. Rep. 9, 1–9. doi: 10.1038/s41598-019-51114-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Rowley, R. (1989). Settlement and recruitment of sea urchins (Strongylocentrotus spp.) in a sea-urchin barren ground and a kelp bed: are populations regulated by settlement or post-settlement processes? Mar. Biol. 100, 485–494. doi: 10.1007/BF00394825

CrossRef Full Text | Google Scholar

Rowley, R. (1990). Newly settled sea urchins in a kelp bed and urchin barren ground: a comparison of growth and mortality. Mar. Ecol. Prog. Ser. 62, 229–240. doi: 10.3354/meps062229

CrossRef Full Text | Google Scholar

Sala, E., Boudouresque, C., and Harmelin-Vivien, M. (1998). Fishing, trophic cascades, and the structure of algal assemblages: evaluation of an old but untested paradigm. Oikos 83, 425–439. doi: 10.2307/3546364

CrossRef Full Text | Google Scholar

Scheffer, M., Carpenter, S., Foley, J. A., Folke, C., and Walker, B. (2001). Catastrophic shifts in ecosystems. Nature 413:591. doi: 10.1038/35098000

PubMed Abstract | CrossRef Full Text | Google Scholar

Schultz, P., Menck, P. J., Heitzig, J., and Kurths, J. (2017). Potentials and limits to basin stability estimation. New J. Phys. 19:023005. doi: 10.1088/1367-2630/aa5a7b

CrossRef Full Text | Google Scholar

Selkoe, K. A., Blenckner, T., Caldwell, M. R., Crowder, L. B., Erickson, A. L., Essington, T. E., et al. (2015). Principles for managing marine ecosystems prone to tipping points. Ecosyst. Health Sustain. 1, 1–18. doi: 10.1890/EHS14-0024.1

CrossRef Full Text | Google Scholar

Sloan, N., and Bartier, P. (2000). Living Marine Legacy of Gwaii Haanas. I: Marine Plant Baseline to 1999 and Plant-Related Management Issues. Halifax : Department of Canadian Heritage.

Google Scholar

Sloan, N. A., Bartier, P. M., and Austin, W. C. (2001). “Living marine legacy of Gwaii Haanas. II: marine invertebrate baseline to 2000 and invertebrate-related management issues,” in Parks Canada-Technical Reports in Ecosystem Science, (Queen Charlotte, BC: Gwaii Haanas National Park Reserve). Available online at: https://ceaa-acee.gc.ca/050/documents_staticpost/cearref_21799/83896/Marine_Invertebrate_Report.pdf (accessed September 18, 2021).

Google Scholar

Sloan, N. A., and Dick, L. (2012). Sea Otters of Haida Gwaii. Icons in Human–Ocean Relations. Queen Charlotte, BC: Archipelago Management Board.

Google Scholar

Small, E. (2018). 56. Kelps: the key to sustainable harvest of marine biodiversity. Biodiversity 19, 101–113. doi: 10.1080/14888386.2018.1438920

CrossRef Full Text | Google Scholar

Sommer, U. (2008). Trophic cascades in marine and freshwater plankton. Int. Rev. Hydrobiol. 93, 506–516. doi: 10.1002/iroh.200711039

CrossRef Full Text | Google Scholar

Soulé, M. E., Estes, J. A., Berger, J., and Del Rio, C. M. (2003). Ecological effectiveness: conservation goals for interactive species. Conserv. Biol. 17, 1238–1250. doi: 10.1046/j.1523-1739.2003.01599.x

CrossRef Full Text | Google Scholar

Standish, R. J., Hobbs, R. J., Mayfield, M. M., Bestelmeyer, B. T., Suding, K. N., Battaglia, L. L., et al. (2014). Resilience in ecology: abstraction, distraction, or where the action is? Biol. Conserv. 177, 43–51. doi: 10.1016/j.biocon.2014.06.008

CrossRef Full Text | Google Scholar

Steneck, R. S., Graham, M. H., Bourque, B. J., Corbett, D., Erlandson, J. M., Estes, J. A., et al. (2002). Kelp forest ecosystems: biodiversity, stability, resilience and future. Environ. Conserv. 29, 436–459. doi: 10.1017/S0376892902000322

CrossRef Full Text | Google Scholar

Stewart, N. L., and Konar, B. (2012). Kelp forests versus urchin barrens: alternate stable states and their effect on sea otter prey quality in the Aleutian Islands. J. Mar. Biol. 2012, 1–12. doi: 10.1155/2012/492308

CrossRef Full Text | Google Scholar

Sunnset, B. H., Strand, H. K., Moy, F., Steen, H., and Christie, H. (2010). Treatment may help kelp to recover. Mar. Resour. News 4, 1–2.

Google Scholar

Tasmanian Government (2019). “Long spined sea urchin strategy,” in Department of Primary Industries, Water and Environment, (Hobart, AU: Department of Primary Industries). Available online at: https://dpipwe.tas.gov.au/sea-fishing-aquaculture/sustainable-fisheries-management/fisheries-management-strategies/long-spined-sea-urchin-strategy (accessed September 18, 2021).

Google Scholar

Tinker, M. T., Bentall, G., and Estes, J. A. (2008). Food limitation leads to behavioral diversification and dietary specialization in sea otters. Proc. Natl. Acad. Sci. U. S. A. 105, 560–565. doi: 10.1073/pnas.0709263105

PubMed Abstract | CrossRef Full Text | Google Scholar

Tracey, S. R., Baulch, T., Hartmann, K., Ling, S. D., Lucieer, V., Marzloff, M. P., et al. (2015). Systematic culling controls a climate driven, habitat modifying invader. Biol. Invasions 17, 1885–1896. doi: 10.1007/s10530-015-0845-z

CrossRef Full Text | Google Scholar

Walker, B., Carpenter, S., Rockstrom, J., Crépin, A.-S., and Peterson, G. (2012). Drivers, “slow” variables, “fast” variables, shocks, and resilience. Ecol. Soc. 17:30. doi: 10.5751/ES-05063-170330

PubMed Abstract | CrossRef Full Text | Google Scholar

Walker, B., Holling, C. S., Carpenter, S. R., and Kinzig, A. (2004). Resilience, adaptability and transformability in social–ecological systems. Ecol. Soc. 9:5. doi: 10.5751/ES-00650-090205

PubMed Abstract | CrossRef Full Text | Google Scholar

Wallington, T. J., Hobbs, R. J., and Moore, S. A. (2005). Implications of current ecological thinking for biodiversity conservation: a review of the salient issues. Ecol. Soc. 10:16. doi: 10.5751/ES-01256-100115

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, J., and Estes, J. A. (2011). Stability, resilience, and phase shifts in rocky subtidal communities along the west coast of Vancouver Island, Canada. Ecol. Monogr. 81, 215–239. doi: 10.1890/10-0262.1

CrossRef Full Text | Google Scholar

Wernberg, T., Bennett, S., Babcock, R. C., De Bettignies, T., Cure, K., Depczynski, M., et al. (2016). Climate-driven regime shift of a temperate marine ecosystem. Science 353, 169–172. doi: 10.1126/science.aad8745

PubMed Abstract | CrossRef Full Text | Google Scholar

Wernberg, T., Krumhansl, K., Filbee-Dexter, K., and Pedersen, M. F. (2019). “Status and trends for the world’s kelp forests,” in World Seas: An Environmental Evaluation, ed. C. Sheppard (London: Elsevier), 57–78. doi: 10.1016/B978-0-12-805052-1.00003-6

CrossRef Full Text | Google Scholar

Williams, P. J., Hooten, M. B., Womble, J. N., Esslinger, G. G., and Bower, M. R. (2018). Monitoring dynamic spatio-temporal ecological processes optimally. Ecology 99, 524–535. doi: 10.1002/ecy.2120

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, J. A., Acheson, J. M., and Johnson, T. R. (2013). The cost of useful knowledge and collective action in three fisheries. Ecol. Econ. 96, 165–172. doi: 10.1016/j.ecolecon.2013.09.012

CrossRef Full Text | Google Scholar

Winnie, J. Jr., and Creel, S. (2017). The many effects of carnivores on their prey and their implications for trophic cascades, and ecosystem structure and function. Food Webs 12, 88–94. doi: 10.1016/j.fooweb.2016.09.002

CrossRef Full Text | Google Scholar

Young, T. P. (2000). Restoration ecology and conservation biology. Biol. Conserv. 92, 73–83. doi: 10.1016/S0006-3207(99)00057-9

CrossRef Full Text | Google Scholar