Relating the Strength of Density Dependence and the Spatial Distribution of Individuals

Brush, Micah; Harte, John

doi:10.3389/fevo.2021.691792

ORIGINAL RESEARCH article

Front. Ecol. Evol., 24 June 2021
Sec. Models in Ecology and Evolution
Volume 9 - 2021 | https://doi.org/10.3389/fevo.2021.691792

Relating the Strength of Density Dependence and the Spatial Distribution of Individuals

Micah Brush¹^*

John Harte²

¹Department of Physics, University of California, Berkeley, Berkeley, CA, United States
²Energy and Resources Group, University of California, Berkeley, Berkeley, CA, United States

Spatial patterns in ecology contain useful information about underlying mechanisms and processes. Although there are many summary statistics used to quantify these spatial patterns, there are far fewer models that directly link explicit ecological mechanisms to observed patterns easily derived from available data. We present a model of intraspecific spatial aggregation that quantitatively relates static spatial patterning to negative density dependence. Individuals are placed according to the colonization rule consistent with the Maximum Entropy Theory of Ecology (METE), and die with probability proportional to their abundance raised to a power α, a parameter indicating the degree of density dependence. This model can therefore be interpreted as a hybridization of MaxEnt and mechanism. Our model shows quantitatively and generally that increasing density dependence randomizes spatial patterning. α = 1 recovers the strongly aggregated METE distribution that is consistent with many ecosystems empirically, and as α → 2 our prediction approaches the binomial distribution consistent with random placement. For 1 < α < 2, our model predicts more aggregation than random placement but less than METE. We additionally relate our mechanistic parameter α to the statistical aggregation parameter k in the negative binomial distribution, giving it an ecological interpretation in the context of density dependence. We use our model to analyze two contrasting datasets, a 50 ha tropical forest and a 64 m² serpentine grassland plot. For each dataset, we infer α for individual species as well as a community α parameter. We find that α is generally larger in the tightly packed forest than the sparse grassland, and the degree of density dependence increases at smaller scales. These results are consistent with current understanding in both ecosystems, and we infer this underlying density dependence using only empirical spatial patterns. Our model can easily be applied to other datasets where spatially explicit data are available.

1. Introduction

Spatial patterns in ecology have been studied extensively (e.g., Wiegand and Moloney, 2013; Diggle, 2014), and contain useful information about what processes shape ecosystems (Law et al., 2009; Brown et al., 2011; Münkemüller et al., 2020). Quantitative understanding of these patterns can therefore be used to infer the importance of various mechanisms, and illuminate underlying processes (Levin, 1992; Rosenzweig, 1995; Brown et al., 2016). Additionally, models of spatial patterns allow us to better model and predict ecosystem response to natural and anthropogenic disturbances (Thomas et al., 2004; Newman et al., 2020), are critical in understanding the well studied species-area relationship (Arrhenius, 1921; Plotkin et al., 2000; Drakare et al., 2006; Harte and Kitzes, 2015), and have applications in reserve designs and conservation (Kitzes and Shirley, 2016).

A common approach to quantifying these patterns is the use of various summary statistics (Wiegand et al., 2013), which have been shown to be able to distinguish different ecological mechanisms (Brown et al., 2016). Here we take a slightly different approach and directly model the impact of an important mechanism in population dynamics: intraspecific negative density dependence. We focus on the effects of this ecological mechanism on spatial patterning.

More specifically, we consider the effects of intraspecific negative density dependence on the spatially explicit species-level abundance distribution. This distribution, Π(n|A, A₀, n₀), is defined as the probability that if a species has n₀ individuals in a plot of area A₀, then it has n individuals in a randomly selected subplot of area A. In this analysis, we will focus on this distribution in bisected plots where A = A₀/2. Studying bisections is well-motivated theoretically as it often leads to simpler expressions which can be easily compared across models. Here it keeps our model analytically tractable and facilitates comparison to empirical data. We note limitations to this approach in the section 4.

One prediction of the function Π(n|n₀) comes from the Maximum Entropy Theory of Ecology (METE), which successfully and simultaneously predicts many macroecological patterns (Harte, 2011; Harte and Newman, 2014) across a wide range of spatial scales, taxa, and habitats (White et al., 2012; Xiao et al., 2015). METE predicts very strong spatial aggregation, which is consistent with many observed ecosystems, and obtains the functional form of Π(n) by maximizing entropy while constraining the mean number of individuals in a subplot. However, the same functional form can be obtained using a colonization rule, which is the approach we will use in our model.

Colonization rules assign spatial locations to new individuals based on the location of existing individuals. Chapter 4.1.2 in Harte (2011) shows that using the Laplace rule of succession as a colonization rule results in the same geometric distribution for Π(n) that METE predicts. Because METE agrees well with empirical data in many cases, we will use this colonization rule in our model. Occasionally, however, we see that the empirical degree of aggregation is less than the METE prediction (Conlisk et al., 2012; McGlinn et al., 2015). To study this, Conlisk et al. (2007) added an extra parameter to the relevant colonization rule that allows Π(n) to vary, but it has no mechanistic interpretation and is used only as a free fit parameter.

We derive a new model that uses the colonization rule consistent with METE and adds a density dependent death rule. This means our model can be viewed as a density dependent extension of METE, and in that sense hybridizes MaxEnt and mechanism. Our model introduces a parameter α which quantifies the degree of intraspecific negative density dependence. This parameter can be fit to empirical spatial data to predict the strength of underlying density dependence. However, as with all models inferring process from pattern, there are many underlying mechanisms that lead to similar spatial patterns (Vellend, 2016; Leibold and Chase, 2018), and we cannot definitively attribute any pattern to a single process.

More generally, our model predicts a more random spatial arrangement with stronger negative density dependence and more spatial aggregation with weaker density dependence. While empirically there is an apparent qualitative relationship between species density and aggregation (Condit et al., 2000; Bagchi et al., 2011; Comita et al., 2014), our aim here is to establish a general quantitative statement relating density dependence and spatial aggregation.

2. Materials and Methods

In this section, we review the Maximum Entropy Theory of Ecology (METE) and its prediction for the species-level abundance distribution, Π(n). We then contrast this prediction of strong aggregation to the well-known random placement model (Coleman, 1981), which predicts no spatial aggregation. Given that most species are aggregated (He and Gaston, 2000; Kitzes, 2019), but not all are as aggregated as predicted by METE (Conlisk et al., 2012), the aggregation of most species should fall somewhere between these two predictions for Π(n).

We then introduce a density dependent death rule to combine with the colonization rule consistent with METE, and derive the resulting Π(n) distribution. This derivation assumes a steady state between deaths and new individuals in a single species, but our results should hold if this assumption is relaxed (see section 4).

Finally, we discuss the techniques used to compare our predicted distribution to data, and describe the datasets used in our analysis.

Relevant code for the resulting Π(n) distribution and data analysis is available at https://github.com/micbru/density_dependence_public.

2.1. The Maximum Entropy Theory of Ecology (METE)

In METE, the Π(n) function is given by maximizing the information entropy of the Π(n) distribution given the following constraint (Harte et al., 2008; Harte, 2011, Chapter 7.4):

\begin{array}{l} \sum_{n = 0}^{n_{0}} n Π (n | A, A_{0}, n_{0}) = \frac{n_{0} A}{A_{0}} . & (1) \end{array}

This leads to the following distribution

\begin{array}{l} Π (n | A, A_{0}, n_{0}) = \frac{e^{- λ_{Π} n}}{Z_{Π}} & (2) \end{array}

where Z_Π is a normalization factor, and λ_Π is the Lagrange multiplier determined by the constraint condition.

In the case of a bisection, A = A₀/2 and the Π function simplifies to

\begin{array}{l} Π (n | n_{0}) = \frac{1}{n_{0} + 1}, & (3) \end{array}

which is independent of n. This means that given n₀ individuals, any arrangement of them on the two sides of a bisected plot or quadrat is just as likely as any other. In other words, this is equivalent to equal probability for each unique spatial arrangement of unlabeled individuals (Haegeman et al., 2010).

Ecologically this prediction translates to very strong spatial aggregation, as individuals are equally as likely to all be on one side of the bisection as to be evenly divided on each half. This is in agreement with many datasets (Harte et al., 2008; Harte, 2011, Chapter 8.3) but fails in others, where the theory over-predicts aggregation (Conlisk et al., 2007; McGlinn et al., 2015). This empirical agreement is why we choose the METE distribution as our starting point.

The prediction from METE is equivalent to the distribution obtained from using the Laplace rule of succession as a colonization rule (Harte, 2011, Chapter 4.1.2). This rule states that in a colonization process, the probability of placing an individual on one side of the bisected area is roughly proportional to the fraction of individuals already there. This “rich get richer” effect results in strong spatial aggregation. The probability for placing an individual on the left half of a bisected plot with n_L individuals on the left and n_R individuals on the right is

p_{L} = \frac{n_{L} + 1}{n_{L} + n_{R} + 2} .

To make our notation consistent with that above, let the number on the left be n and the total number to be n₀. The probabilities of a new individual arriving on the left or on the right are then:

\begin{array}{l} \begin{array}{l} p_{L} (n | n_{0}) = \frac{n + 1}{n_{0} + 2}, \\ p_{R} (n | n_{0}) = \frac{n_{0} - n + 1}{n_{0} + 2} . \end{array} & (4) \end{array}

If we place n₀ individuals using this rule, the resulting probability distribution is given by Equation (3).

2.2. Random Placement

Another model for spatial ecology, perhaps the simplest, is the random placement model (Coleman, 1981). Instead of the placement rules in Equation (4), each individual is placed randomly. In a bisected plot this means each individual has a 50 percent chance of being placed on either side, p_L = p_R = 0.5. Placing n₀ individuals this way gives the binomial distribution

\begin{array}{l} Π_{RP} (n | n_{0}) = (\begin{matrix} n_{0} \\ n \end{matrix}) {(\frac{1}{2})}^{n_{0}} & (5) \end{array}

which, if n₀ is large, means we are very likely to have roughly half the individuals on each side. This is equivalent to having no spatial aggregation; there is no preference for any new individual to stay close to any previous individual as each placement is a random coin flip.

2.3. Deriving the Π(n) Distribution With a Density Dependent Death Rule

We now introduce an intraspecific density dependent death rule in addition to the METE colonization rule in Equation (4). To allow for general density dependence, we set the death rate proportional to n^α. The parameter α determines the strength of the density dependence, and can be inferred from the data. Density dependence may result from resource limitation, or some other mechanism (e.g., the Janzen-Connell effect, Janzen, 1970; Connell, 1971).

In the case of a bisected plot, each death must be on the left or right. Thus, given that we have one death in a species, the probabilities that the death is on the left, p_{D, L}, or on the right, p_{D, R}, are

\begin{array}{l} \begin{array}{l} p_{D, L} (n | n_{0}) = \frac{n^{α}}{n^{α} + {(n_{0} - n)}^{α}} \\ p_{D, R} (n | n_{0}) = \frac{{(n_{0} - n)}^{α}}{n^{α} + {(n_{0} - n)}^{α}} . \end{array} & (6) \end{array}

Now that we have the colonization and death rules (Equations 4 and 6), we can derive the general Π_α(n|n₀) for bisections. We will assume the population size of the species is constant and step the model forward over time, where at each step in the model we will have one death followed by the placement of one new individual within a species. Each placement can be interpreted ecologically as a birth or as the immigration of an individual from the same species. We can then solve for the resulting steady state distribution where we reach an equilibrium in the spatial pattern.

There are several approaches for deriving the steady state solution for such a system. Here, we equate the rates leaving and entering any individual state Π_α(n|n₀). We take the probability that we start with n individuals on the left, one on the right dies and then one is placed on the left resulting in n + 1 individuals on the left, and equate that to the probability that we have n + 1 individuals on the left, one on the left dies and then one is placed on the right resulting in n individuals on the left. We could have equivalently done the same thing with n and n − 1. Equating these rates using the probabilities in Equations (4) and (6) leads to a recursion relation. Solving it gives a general stationary solution for Π_α with a given n₀ and α:

\begin{array}{l} Π_{α} (n | n_{0}) = \frac{n^{α} + {(n_{0} - n)}^{α}}{C (n_{0}, α) n_{0}^{α}} {(\begin{matrix} n_{0} \\ n \end{matrix})}^{α - 1} & (7) \end{array}

where C(n₀, α) is the overall normalization that does not have a closed analytic form. In the case that n₀(α − 1) is large, an approximate form for the normalization is

\begin{array}{l} C = \frac{2^{n_{0} (α - 1)} π n_{0}}{\sqrt{α - 1}} {(\frac{1}{2 π n_{0}})}^{α / 2} . & (8) \end{array}

See Supplementary Material 1 for the details of this derivation.

If α = 2, we can solve for the normalization explicitly to get

\begin{array}{l} Π_{α = 2} (n | n_{0}) = \frac{n^{2} + {(n_{0} - n)}^{2}}{2^{n_{0} - 1} n_{0} (n_{0} + 1)} (\begin{matrix} n_{0} \\ n \end{matrix}), & (9) \end{array}

and if α = 1, we recover the METE prediction $Π_{α = 1} (n | n_{0}) = \frac{1}{n_{0} + 1}$ .

2.4. Comparing to Data

Inferring the degree of intraspecific density dependence in empirical data requires obtaining a value of α consistent with the data. Bisection predictions can be compared to data by rank ordering the fraction of individuals present in one half of the plot for each species (e.g., Harte, 2011). This method, however, ignores species abundance and does not account for the likelihood of individual data points. This can lead to incorrect conclusions about which model is preferred (see Supplementary Material 2).

We instead find the maximum likelihood α given the data, where we minimize the sum of the negative logs of the probabilities given data points n_i and n_{0, i}, where i labels each quadrat for a given species. Inferring α using this method gives us the values that are the most consistent with the data, even if they may not look like they agree with the rank ordered fractions (Supplementary Figure 1 and Supplementary Table 1).

The statistical error in estimating α this way goes as $1 / \sqrt{p}$ where p is the sample size (see Supplementary Material 3). We can also get some idea of error from the maximum likelihood estimate itself by considering the width of the likelihood distribution, however for Figures 3, 4, we do not include these error bars as they are smaller than the data points.

For determining α for individual species, we will require multiple bisections and the sample size p will be roughly the number of cell pairings, p ≈ 2^b−1, where b is the number of bisections. There will be fewer data points in practice as some cell pairings will be empty.

We can also define a community α, assuming each species follows the same death rule with identical α. In this case, we will have a larger sample size. For a single bisection, we will have a sample size p equal to the number of species, p = S₀. For multiple bisections where we consider the species on aggregate, the sample size will be roughly equal to the number of species multiplied by the number of cells, $p \approx S_{0} 2^{b - 1}$ . Again, the equality is not exact as not all cell pairings beyond the first bisection will have all of the species present at the single bisection level.

In both the case of the species-level and community-level α, we will bisect single plots more than once (into quadrants, then into 8 cells, etc.) when comparing the model to data. In our analysis, we begin by bisecting the plot in half in one direction, then bisecting each of the resulting plots in the opposite direction. We alternate this bisection pattern until we have 2^b cells. We can then combine adjacent cells (either left/right or up/down) as if they were single plots with abundance n_{0, i}, where i will index the plots and range from 1 to 2^b−1. We then choose the abundance on one half to be n_i. This method gives us 2^b−1 points.

Additionally, in this analysis we will only consider species that could have at least one individual per bisection ( $n_{0} > 2^{b - 1}$ ). The smallest scale we consider in our datasets is b = 8, so when we bisect the plot more than once we will only consider species with more than 128 individuals. This restriction ensures that we do not have too many plots with only a few individuals present. If n₀ is very small, Π_α(n) is not particularly sensitive to α and it becomes very difficult to reliably infer α from the data. For n₀ ≤ 2, Π_α(n) does not depend on α.

2.5. Data Used

We will compare our results to two contrasting datasets. First, we will use data from a sparse Californian serpentine grassland site (Green et al., 2003, 2019) at the McLaughlin University of California Natural Reserve censused in 1998. This is a 64 m² plot divided into 256 cells with 24 species and 37 182 individuals. There are 10 species with abundance greater than 128 individuals that constitute 36 783 individuals.

Second, we will use data from Barro Colorado Island (BCI) in Panama (Condit, 1998; Hubbell et al., 1999, 2005; Condit et al., 2019), a 50 ha plot in a moist tropical forest. We will work with the 2005 census and consider plants with a diameter at breast height (dbh) greater than 10 cm. This dataset has 229 species and 20,852 individuals, and 40 species with abundance greater than 128 individuals that constitute 15,960 individuals.

3. Results

3.1. Comparison to METE and Random Placement

Figure 1 compares the bisection predictions for Π(n) from METE, random placement, and our density dependent model for various α, at n₀ = 10 and 50. In general, our model predicts that increasing negative density dependence (larger α) leads to more random spatial patterning, and less density dependence (smaller α) leads to stronger aggregation.

FIGURE 1

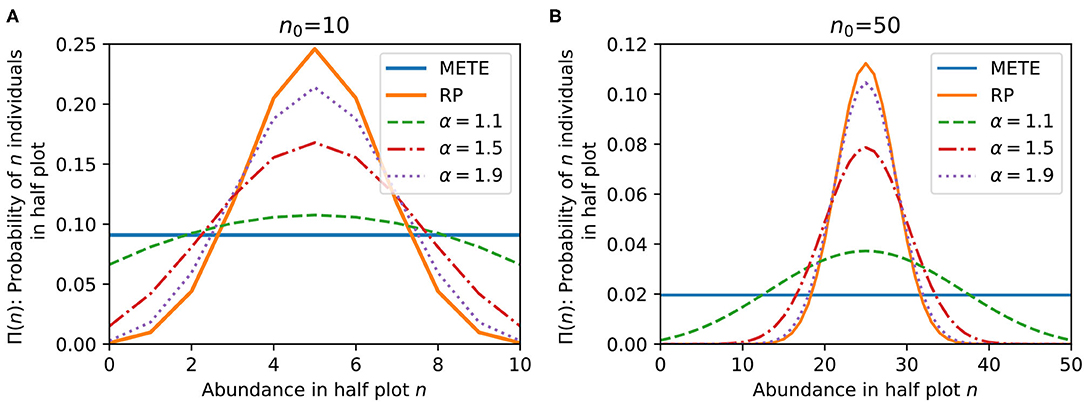
Figure 1. Comparison of the bisection probability distributions Π(n) from METE, random placement (RP), and our density dependent model with varying α at (A) n₀ = 10 and (B) n₀ = 50. At α = 1, our model corresponds exactly to METE. At larger n₀, α → 2 approaches the random placement distribution. Our model varies continuously between METE and random placement for 1 < α < 2.

We can relate our distribution directly to both the METE and random placement distributions for different values of α. α = 1 corresponds exactly to the METE solution, which makes sense given that the placement and death rules are both linear in n. As α → 2, our distribution approaches the random placement prediction if n₀ is large enough (Supplementary Material 4 shows this result analytically). For 1 < α < 2, we vary continuously between METE and random placement. We can make the distribution even more spatially aggregated than METE with α < 1 and even less than random placement (overdispersed) with α > 2.

We can also relate this distribution to the commonly used conditional negative binomial distribution (Bliss and Fisher, 1953; He and Gaston, 2000, 2003; Green and Plotkin, 2007) in the limit of large n₀, assuming that matching the peak of the distributions is a good approximation for the entire distribution. In that limit, the aggregation parameter k is approximately related to the density dependent parameter α by

\begin{array}{l} k \approx \frac{n_{0}}{2} (\frac{α - 1}{2 - α}) + 1 . & (10) \end{array}

Note that this approximation holds for 1 ≤ α ≤ 2, which should be the ecologically relevant range for most species as most species will be more aggregated than random placement, and less aggregated than METE. This also allows the aggregation parameter k to be interpreted mechanistically as the degree of density dependence, in that higher k corresponds to higher α and greater density dependence. See Supplementary Material 5 for the derivation.

3.2. Individual Species

Since the Π function is defined on the species level, we can consider each species separately and find the maximum likelihood α for each. To do this we have to go beyond the first bisection to get multiple data points for the same species at smaller scales.

For the serpentine data, we exclude Eriogonum nudum from the following figures as an outlier (see section 4). This leaves 9 species with abundance greater than 128 individuals.

Figure 2 shows the distribution of α values among the species at each scale, for both the serpentine and BCI data. The median α increases at smaller scales for both datasets, and is higher overall at the BCI dataset, even though the absolute scale is much larger. The spread in α is quite large, but this variation is expected considering the small number of data points, especially for rarer species. Most species have an α between 1 and 2, which is somewhere between the aggregation predicted by METE and random placement.

FIGURE 2

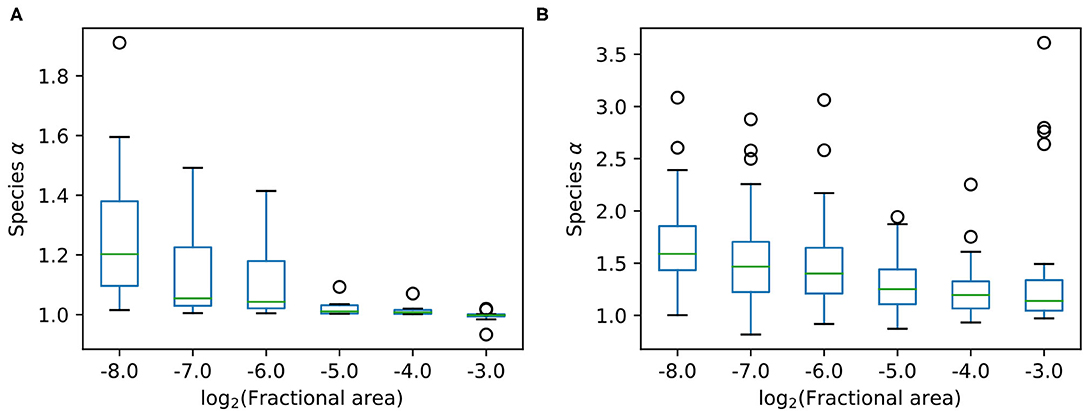
Figure 2. Boxplots for α among the species at different scales at both sites, where panel (A) shows 10 species from the Serpentine dataset, and panel (B) shows 40 species from the BCI dataset. In both cases at smaller scales α is larger, and we see a relatively large spread in α across species at the same scale. The boxplots show boxes from quartile 1 (Q1) to quartile 3 (Q3) with a line at the median. The whiskers extend to 1.5 × (Q3-Q1). The remaining points are plotted as individual circles.

3.3. Community α

We can instead treat α as a community parameter, using each species as a single data point to recover a community α. Figure 3 shows the direct comparison between our model prediction and the serpentine and BCI datasets at the single bisection level. Each data point is the observed fraction of individuals in one half of the plot vs. the species abundance. The curves in this figure show the 95% contour intervals for the Π(n|n₀) distributions predicted by METE, random placement, and our density dependent model with the maximum likelihood α value. We can see that with increasing n₀, the random placement model narrows quickly to having most of its probability weight around 0.5, whereas the METE contours are very wide.

FIGURE 3

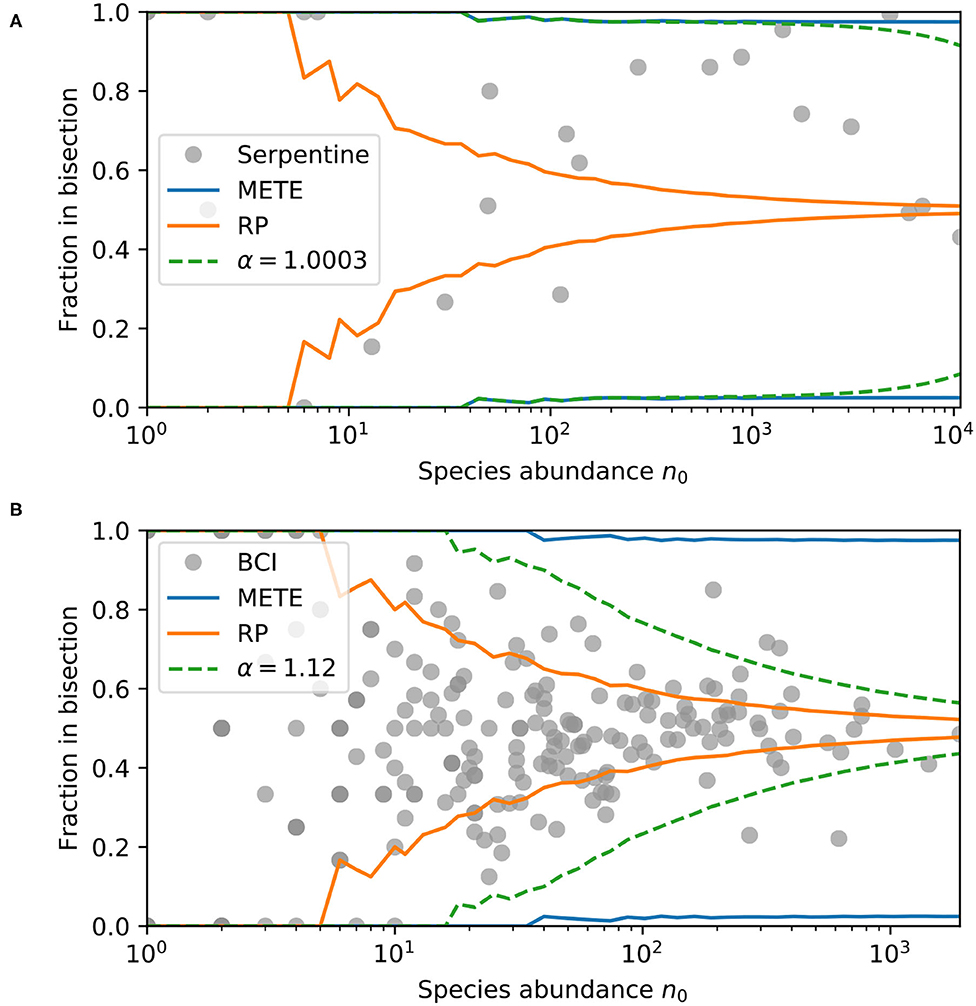
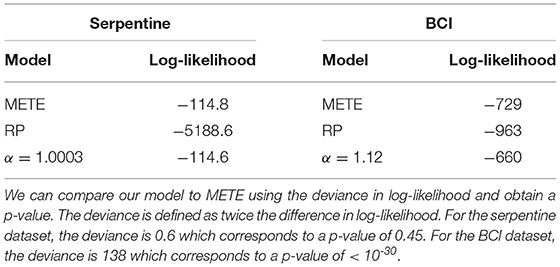
Figure 3. Ninety-five percent contour intervals for the predicted bisection probability distributions Π(n|n₀) from METE, random placement, and our density dependent model with maximum likelihood community α, and bisection data for each species in (A) the serpentine dataset, and (B) the BCI dataset. The data is plotted for each species, where the y-axis is the fraction in one half plot and the x-axis is the total species abundance in that plot. The contours are calculated at each n₀. For our density dependent model with a community α, α = 1.0003 maximizes the log-likelihood for the serpentine dataset, and α = 1.12 maximizes log-likelihood for BCI dataset.

At the single bisection level, the maximum likelihood result for the serpentine dataset is nearly indistinguishable from α = 1, so the confidence interval curves on the plot for METE and the density dependent model overlap for most n₀. For the BCI data, the maximum likelihood value is α = 1.12, slightly larger than 1. In this case, where 1 < α < 2, we see the width of the predicted distribution is between METE and random placement. The likelihoods for each of the models are shown in Table 1.

TABLE 1

Table 1. Log-likelihood values for the three different models, with α as a community parameter.

3.4. Scale Dependence in Community α

Going beyond the first bisection allows us to see how α varies depending on the scale of our plot. Figure 4 shows how α scales with fractional area for both the serpentine and BCI plots. Density dependence increases at smaller scales in both datasets. The trend in community α across scales is similar to the median α in the single species analysis, though the median α is in general slightly larger than the community α. Note that here we restrict our analysis to species with n₀ > 128 for all scales so that we are including the same species across scales.

FIGURE 4

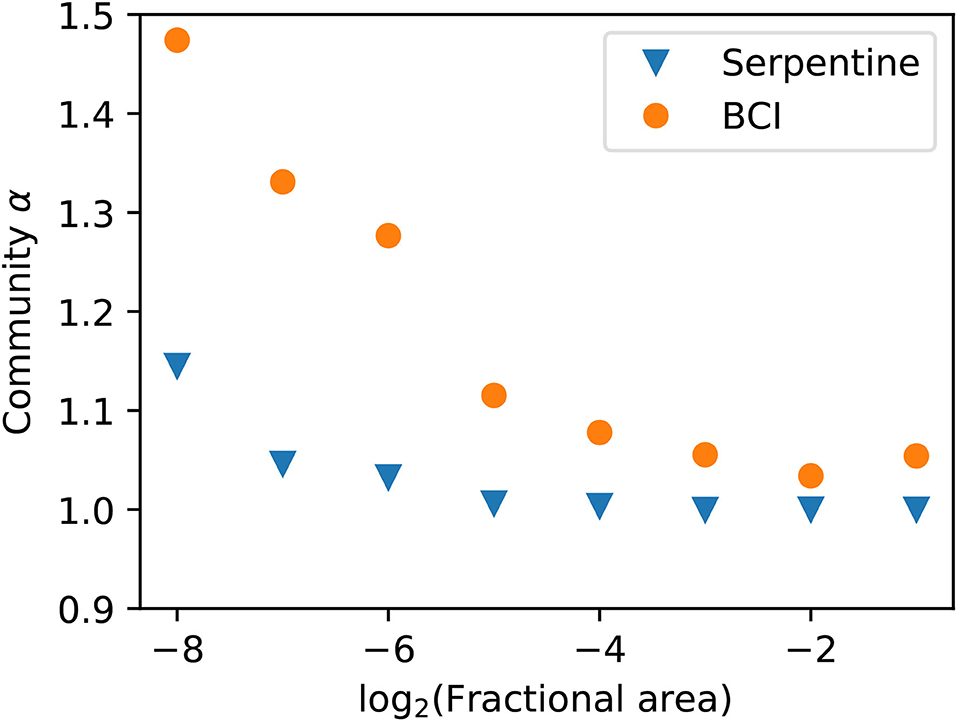
Figure 4. Community α scaling with area for species with abundance n₀ > 128. The density dependence again increases at smaller scales and the trend is similar to the single species analysis. The serpentine dataset has 36,783 individuals and the BCI dataset has 15,960 individuals.

4. Discussion

Our model establishes a quantitative relationship between the spatially explicit distribution Π(n) and the parameter α, which measures the strength of negative density dependence. This can be seen in Figure 1, where the Π_α(n) distribution flattens with smaller α, indicating greater aggregation, and broadens as α increases. Importantly, the parameter α has a direct interpretation as quantifying the strength of negative density dependence. Further, our relationship in Equation (10) allows us to interpret the parameter k in the negative binomial distribution in the same intuitive way.

4.1. Comparing Species and Community α

In our analysis, we consider α both as a separate parameter for each species (as in Figure 2), and as a community parameter where each species has the same α (as in Figures 3, 4). The community α is harder to interpret ecologically, but we include it to allow for comparisons with models with community level aggregation parameters (e.g., Volkov et al., 2005; Conlisk et al., 2007). To analyze and compare the accuracy of the species-level α and the community α, we considered the Akaike Information Criterion (AIC) in both cases across scales (Table 2). This was calculated for single species as the negative log-likelihood summed over each species with the number of parameters equal to the number of species, whereas for the community α there was only a single α parameter. For both serpentine and BCI at all scales considered, we find that the AIC is lower with species-level α compared to a single community α, despite the inclusion of 9 more parameters in the case of the serpentine data and 228 more parameters in the case of the BCI data. We therefore conclude that a separate α for each species describes the data better than a single community α.

TABLE 2

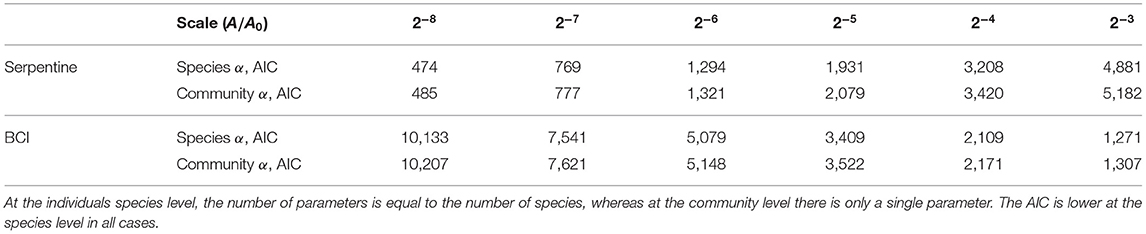
Table 2. Comparison of the Akaike Information Criterion (AIC) for α defined at the individual species level and at the community level in both the serpentine and BCI data and across scales.

4.2. Comparing Serpentine and BCI

We use our model to directly compare our results between our two contrasting datasets, serpentine and BCI. Because the serpentine site was very sparse, whereas the BCI forest is tightly packed, we expect higher α values and greater density dependence at BCI than at the serpentine site. This is consistent with our inferred values of α at both the individual species level and at the community level.

Another difference between the serpentine and BCI sites is how well other macroecological distributions agree with METE. METE well describes other patterns at the serpentine site, and does less well at explaining the BCI data. Given that α = 1 corresponds to the METE prediction for Π(n), we might expect that ecosystems well-described by other METE predictions will have α ≈ 1, as these systems will generally be consistent with METE. This is consistent with our analysis here as the median and community αs for the serpentine data are approximately 1 at the largest scale, whereas at BCI the median and community αs are larger than 1.

Because METE predictions seem to hold for relatively static and undisturbed ecosystems (Newman et al., 2020), this suggests interpreting an increase in density dependence away from METE (α>1) as a kind of ecological disturbance. A biological example of strong density dependent mortality as a result of disturbance could be the self-thinning of trees in forest recovery from wildfire, such as bishop pines in coastal California (Harvey et al., 2014). This interpretation is in line with the recently proposed DynaMETE theory (Harte et al., 2021), which models specific mechanistic disturbances away from METE to predict macroecological patterns.

4.3. Scaling

Our scaling results in both Figures 2, 4 make ecological sense. We expect that at smaller scales, the density dependence would be larger as individuals compete more for resources at that scale. At large scales, we expect α to be close to 1 as the individuals do not compete over large distances. This means that the spatial distributions look more aggregated on large scales than on small scales as the individuals within species broadly group together, but repel each other at small scales. We see this trend at the individual level in Figure 2 as the medians increase at smaller scales, and for the community α in Figure 4.

Our repeated bisection analysis also indicates at which scale density dependence becomes important. This will appear as a shoulder in the data where α moves away from ≈1. We could do this for individual species by tracing α and looking for a shoulder in Figure 2, but here we will look at the community results in order to compare to Conlisk et al. (2007) and Volkov et al. (2005). Looking at Figure 4, we find that the shoulder in absolute scale corresponds to <0.5 m² for the serpentine plot and <1.6 ha for the BCI dataset. This again makes sense given that the serpentine grassland is much more sparse than the BCI forest.

We first compare to Conlisk et al. (2007), who introduce a fit parameter ϕ that modifies the colonization rule Equation (4) and allows the Π distribution to vary continuously between random placement and METE. They compare their estimated community ϕ parameter to both the serpentine and BCI data in their Figure 6. For the serpentine data, they find that at scales larger than around 0.5 m² (the 8th bisection), ϕ approaches 0.5, which corresponds to the METE prediction. At scales around 0.5 m² or smaller, ϕ ≈ 0.25, where ϕ = 0 corresponds to random placement. This is consistent with our scaling results in Figure 4. For BCI, they find that at all but the largest scales ϕ ≈ 0.25. Our result that α is larger at BCI than at the serpentine site across scales, which corresponds to less spatial aggregation, is not consistent with their findings. We believe this is due to a difference in how the data are analyzed.

In Conlisk et al. (2007), the species abundance n₀ is measured at the scale of the full plot, and the bisection prediction is recursively iterated to smaller scales (see their Theorem 2). Here, we treat each bisection at smaller scales separately. For example, after dividing the plot into 128 quadrants (8 bisections), we look at the species abundance in each individual quadrat without considering n₀ at the scale of the entire plot. In principle, we could conduct our analysis in the same way and anchor at the largest scale, though this would be difficult analytically, and our approach makes use of the empirical data available at each scale rather than only at the largest scale. Further, the method in Conlisk et al. (2007) depends implicitly on the chosen size of the overall study plot. This is not true in our analysis as a bisection studied at any scale does not depend on information at any other scale. In practice, this means that in our analysis there is no difference between studying species in a 1 m² subplot embedded in a 100 m² plot vs. studying the same 1 m² plot independently. This difference in how n₀ is treated across scales could lead to different predictions for α (or ϕ).

We can further compare our results to Conlisk et al. (2007) by relating our α to ϕ, using their relationship between ϕ and k and our Equation (10). This relationship depends on n₀, which may affect comparisons between these parameters across scales. Finally, an additional difference between our analyses is our different cutoff of n₀>128, and for BCI, dbh >100 mm, however this does not explain all of the difference between our results. Supplementary Material 6 derives an approximate relationship between α and ϕ, Supplementary Figure 4 uses that relationship to transform our Figure 4 to a relationship in ϕ, and Supplementary Figure 5 shows how our result changes if we remove our abundance threshold. A takeaway from this comparison is that these scaling results depend at least in part on the choice of model and the data analysis methods.

Volkov et al. (2005) showed that intraspecfic and symmetric density dependence can explain different shapes for the species-abundance distribution. Their added parameter c is interpreted as a measure of the strength of symmetric density dependence, where c = 0 corresponds to no density dependence. This parameter is therefore similar to our community α in that all species have the same degree of negative density dependence. They then show at what density these effects become important in their Figure 3. For BCI, they find c = 1.80, and the density dependent effects are visible for species with n>27. To convert this to area, we need to look at scales of the total area divided by the abundance where density dependent effects become visible. Thus, this corresponds to density dependence entering at scales smaller than a fractional area of 1/27 = 1/2^4.75, which is close to the same scale where we see α increase away from 1 in Figure 4.

Across these results, we interpret increasing α at small scale as an increase in density dependence. However, at smaller spatial scales where there are fewer individuals it becomes more difficult to distinguish between different patterns of aggregation. In particular, when n₀A/A₀ << 1, it is difficult to determine if the empirical pattern is due to noise or a specific clustering process (Harte, 2011, p. 63). This sampling effect should be small here, as even at the smallest scale the median n₀A/A₀ is greater than 1 for both datasets (Supplementary Material 7).

4.4. Trends for Individual Species at BCI

At the individual species level at BCI, we find overall that most species at all scales are more aggregated than random (α < 2 in Figure 2). This is consistent with results from Condit et al. (2000). We also find that species tend to be more aggregated at large scales than at small scales (median α>1 at small scales and α ≈ 1 at large scales in Figure 2), which makes sense as we expect some species to only be present in certain areas of the plot.

More broadly, we might expect to find trends in inferred density dependence with species abundance or size. More abundant species may be competing more for the same resources, or larger species may compete over larger distances. For example, Condit et al. (2000) find that both rarer species and smaller individuals tend to be more aggregated, however at a much smaller scale (within a 10 m radius). We looked for trends in abundance, mean dbh, and total energy for each species at BCI with n₀ > 128 across all scales considered (as in Figure 2).

In terms of abundance (Supplementary Figure 7 and Supplementary Table 2), we do not find any species with high α and high abundance (no highly density dependent high abundance species), and we find that the variance in α decreases with abundance. We also find that at all scales except the two smallest, α decreases slightly with increasing log of abundance. Thus, we find that at larger scales, more abundant species are slightly more aggregated than less abundant species.

We find no evidence of a trend with species' mean dbh (Supplementary Figure 8 and Supplementary Table 3), though it is possible this trend is obscured by variance in individual size within a species, or that the range of mean dbh we considered (about 100 − 500 mm) is too small to see its effect. Finally, we looked for an overall energy effect. Considering that the most abundant species tend to be smaller, it may be that density dependence depends on the total metabolic rate of a species. Plotting this relationship (Supplementary Figure 9 and Supplementary Table 4) again does not reveal a significant scaling relationship at all scales except one (log₂(A/A₀) = −6).

A plausible mechanism for the observed density dependence at BCI is the Janzen-Connell effect (Janzen, 1970; Connell, 1971), whereby areas near parent trees are inhospitable for offspring, resulting in density dependence. Various studies (Harms et al., 2000; Carson et al., 2008; Comita et al., 2014) have observed this effect at BCI, which is consistent with our result that α>1 for most species at smaller scales there.

See Supplementary Material 8 for more information on these trends.

4.5. Notable Species

For individual species at the BCI dataset, Gustavia superba stood out with an average α of 1.001 across scales. This species is largely limited to 2 hectares of young secondary forest along the edge of the plot, (J. Wright, personal communication, 2019) making it look especially aggregated and resulting in a maximum likelihood α close to 1.

In the serpentine dataset, we excluded Eriogonum nudum as an outlier for part of our analysis. The maximum likelihood α was > 6 at the smallest scale and the maximum itself was very shallow. This species has a large canopy compared to the other grassland plants, and tends to be found far from other individuals. It makes sense that it would be overdispersed with α > 2.

4.6. Implications for the Species-Area Relationship

In METE, the spatial distribution is used together with the species-abundance distribution to predict the species-area relationship (Harte, 2011, Chapter 7.5), and to upscale predictions of biodiversity (Harte and Kitzes, 2015). These predictions should hold in ecosystems like the serpentine grassland analyzed here, as the observed species aggregation agrees with the METE prediction. However, different levels of aggregation will impact the species-area relationship. The impact of aggregation is discussed in Wilber et al. (2015). They find that increasing randomization decreases the predicted slope of the species-area relationship at the same scale, and therefore upscaling METE will overpredict species richness. In addition, they analyze the effect of variation in aggregation among species, which slightly decreases the slope at small scales and increases the slope at larger scales. This results in a species-area relationship that more closely resembles a power law. They also consider the effect of decreasing aggregation across scale, which results in a species-area relationship that no longer displays scale collapse. We observe both of these effects here.

4.7. Limitations and Assumptions

As with all models inferring process from pattern, we can never be sure the pattern we observe can be completely attributed to the process we model. There are many different underlying processes that can lead to aggregation, including environmental filtering and dispersal limitation (Vellend, 2016; Leibold and Chase, 2018), and it is not possible for any one model to include every effect. Our empirical results here are consistent with our interpretation of α as a parameter that relates to the strength of intraspecific negative density dependence, however there are certainly other important mechanisms in these datasets. Regardless of our ability to infer process from pattern, our theoretical result that increasing density dependence increases spatial randomization holds.

Our model is also limited in that it only considers bisections, and it would be useful to extend it to be more general. There are many spatial arrangements that can not be accurately captured by dividing plots into bisection, and in general a single functional summary statistic does not completely describe the observed spatial pattern (Wiegand et al., 2013). For example, if we divide our plot into an m by m grid, and have one individual per cell, we would see exactly 0.5 as the fraction for each bisection. This result would be consistent with random placement with a large number of individuals, which does not well describe this exceptionally uniform arrangement. There could also be different degrees of spatial aggregation within a cell that we will not accurately capture with a bisection. Despite these limitations, bisections are useful for understanding commonly observed macroscopic spatial patterns.

A conceptually simple extension to our model is to divide plots into quadrisections rather than bisections. The colonization and death rules then have three unknowns rather than one (the number of individuals in each quadrant, where the fourth is determined by constraining the sum to be n₀). This makes it hard to solve analytically, however we can simulate the birth-death process until it reaches steady state. We find no significant difference in our simulation compared to our prediction from two bisections, and find that a community α = 1.12 is still consistent with the BCI data.

Because we consider the steady state solution in our model, we are assuming that the density dependence time scale is longer than the time scale of individual births or deaths. That is, α must not change too rapidly in time. This assumption is justified for many systems roughly in steady state with their environment and not undergoing rapid change (Newman et al., 2020).

Solving for the steady state solution also assumes that births and deaths are in balance. We assume here that there is a single death followed by a placement, however simulating two deaths followed by two placements gives a probability distribution consistent with our analytic prediction. We expect our result to hold with other numbers of deaths and placements. Assuming that births and deaths are in balance also implicitly assumes some amount of negative density dependence, and here α provides a quantitative measure of the degree of density dependence.

Another assumption in our model is the choice of colonization rule itself, though if we had chosen a different colonization rule many of our conclusions would remain the same. We use the colonization rule consistent with METE because of its good empirical agreement (Harte, 2011, Chapter 8.3). This allows us to interpret the α = 1 case as consistent with METE. This is useful as METE can be thought of as a null theory that holds in ecosystems that are undisturbed and relatively static (White et al., 2012; Xiao et al., 2015; Harte et al., 2017; Newman et al., 2020), and α ≠ 1 can be thought of as a density dependent correction, away from the MaxEnt distribution. In this sense, this model hybridizes MaxEnt and mechanism.

Instead, as an example, we could have chosen the colonization rule resulting in the random placement distribution. For a bisection this rule is just p_L = p_R = 0.5. In this case, α = 1 would recover the binomial distribution, which we know does not well describe most spatial data (Condit et al., 2000; He and Gaston, 2000), and so we cannot interpret α ≠ 1 as a density dependent correction. As another example, if we had chosen the more general colonization rule in (Conlisk et al., 2007) we would have two parameters to tune, making it difficulty to differentiate between colonization and death. In ecosystems where we suspect a different colonization rule may be in play, we could modify our theory appropriately. In any of these cases, our general results would remain largely unchanged.

4.8. Future Work

One advantage of the bisection approach is that it can make predictions about inter-quadrat correlations. McGlinn et al. (2015) examined these correlations and compared empirical distance-decay relationships with the spatial predictions of METE (α = 1 in this model). They found that the predicted distance-decay was much stronger than observed. We would expect the predicted distance-decay relationship to be weaker with α>1 in our model. Conlisk et al. (2007) note that ϕ>0 in their model produces more realistic looking distance-decay than random placement. Together, this means that with 1 < α < 2 our model should predict a more realistic shape for the distance-decay relationship compared to random placement, but with less steep of a slope than predicted by METE. However, Conlisk et al. (2007) also note that the analysis of these inter-quadrat correlations makes use of distance between cell pairs rather than physical distance, which limits the analysis [though note Ostling et al. (2004) provides a set of user rules to reduce this effect]. This issue is also present in our model. Future comparisons to empirical distance-decay relationships could provide another method of estimating α and testing this framework.

Another advantage of our approach is that it only requires static spatial data. However, analyzing a single dataset over time could provide an interesting test of our interpretation of α as a measure of density dependence. This would be particularly appropriate with data where strong density dependent mortality is known to occur, for example a self-thinning forest recovering from wildfire (Harvey et al., 2014; Newman et al., 2020).

Finally, while our analysis here compares two contrasting datasets, future work could analyze more ecosystems to look for effects of habitat type, species richness, or average density.

5. Conclusion

Our model robustly predicts that increased intraspecific negative density dependence leads to more random spatial patterning, and establishes a quantitative relationship between the degree of density dependence described by the parameter α and spatial patterning described by the metric Π(n). We predict that this result is general across ecosystems and taxonomic groups. We find that at all but the smallest scales, the serpentine grassland site is consistent with the absence of a density dependent correction and has the strong spatial aggregation predicted by METE. This is true for both the median individual species and at the community level. At the tropical forest site, our results indicate that negative density dependence is important: the median species α and the community α are both greater than 1 at even the largest scales. Both ecosystems show scaling of α consistent with its interpretation as the strength of negative density dependence. Median species α and community α are larger at smaller scales, and increase away from 1 at scales consistent with other analyses. Overall, our analysis of α is consistent with the interpretation of density dependence at both sites. Because this model uses only static spatial patterning, it can be applied in any ecosystem with spatially explicit data.

Data Availability Statement

The serpentine data are available from the Dryad Digital Repository at https://doi.org/10.6078/D1MQ2V. The BCI data can be found at https://forestgeo.si.edu/explore-data and are available from the Dryad Digital Repository at https://doi.org/10.15146/5xcp-0d46. Relevant code is available at https://github.com/micbru/density_dependence_public. The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

MB conducted the formal analysis and led the writing of the manuscript. Both authors were involved in conceptualization.

Funding

This work was supported by the National Science Foundation under Grant no. DEB-1751380. MB acknowledged the support of the Natural Sciences and Engineering Research Council of Canada (NSERC) [PGSD2-517114-2018]. Publication made possible in part by support from the Berkeley Research Impact Initiative (BRII) sponsored by the UC Berkeley Library.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

JH thanks the Santa Fe Institute and the Rocky Mountain Biological Laboratory for their hospitality. We thank Kaito Umemura for valuable discussion and feedback, and Egbert Leigh and Joseph Wright for their help with the BCI dataset. We thank Jessica Green for the serpentine data. The BCI forest dynamics research project was founded by S. P. Hubbell and R. B. Foster and is now managed by R. Condit, S. Lao, and R. Perez under the Center for Tropical Forest Science and the Smithsonian Tropical Research in Panama. Numerous organizations have provided funding, principally the U.S. National Science Foundation, and hundreds of field workers have contributed.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2021.691792/full#supplementary-material

References

Arrhenius, O. (1921). Species and area. J. Ecol. 9, 95–99. doi: 10.2307/2255763

ORIGINAL RESEARCH article

Relating the Strength of Density Dependence and the Spatial Distribution of Individuals

1. Introduction

2. Materials and Methods

2.1. The Maximum Entropy Theory of Ecology (METE)

2.2. Random Placement

2.3. Deriving the Π(n) Distribution With a Density Dependent Death Rule

2.4. Comparing to Data

2.5. Data Used

3. Results

3.1. Comparison to METE and Random Placement

3.2. Individual Species

3.3. Community α

3.4. Scale Dependence in Community α

4. Discussion

4.1. Comparing Species and Community α

4.2. Comparing Serpentine and BCI

4.3. Scaling

4.4. Trends for Individual Species at BCI

4.5. Notable Species

4.6. Implications for the Species-Area Relationship

4.7. Limitations and Assumptions

4.8. Future Work

5. Conclusion

Data Availability Statement

Author Contributions

Funding

Conflict of Interest

Acknowledgments

Supplementary Material

References

This article is part of the Research Topic

People also looked at