- 1Ecology Center and Department of Biology, Utah State University, Logan, UT, United States
- 2Department of Integrated Mathematical Oncology, Moffitt Cancer Center, Tampa, FL, United States
- 3Inspirata, Inc., Tampa, FL, United States
Over 40 years ago, seminal papers by Armstrong and McGehee and by Levins showed that temporal fluctuations in resource availability could permit coexistence of two species on a single resource. Such coexistence results from non-linearities or non-additivities in the way resource supply translates into fitness. These reflect trade-offs where one species benefits more than the other during good periods and suffers more (or does less well) than the other during less good periods, be the periods stochastic, unstable population dynamics, or seasonal. Since, coexistence based on fluctuating conditions has been explored under the guises of “grazers” and “diggers,” variance partitioning, relative non-linearity, “opportunists” and “gleaners,” and as the storage effect. Here we focus on two phenotypes, “cream skimmers” and “crumb pickers,” the former having the advantage in richer times and the latter in less rich times. In nature, richer and poorer times, with regular or stochastic appearances, are the norm and occur on many time scales. Fluctuations among richer and poorer times also appear to be the norm in cancer ecosystems. Within tumors, nutrient availability, oxygen, and pH can fluctuate stochastically or periodically, with swings occurring over seconds to minutes to hours. Despite interest in tumor heterogeneity and how it promotes the coexistence of different cancer cell types, the effects of fluctuating resource availability have not been explored for cancer. Here, in the context of pulsed resources, we (1) develop models of foraging consumers who experience pulsed resources to examine four types of trade-offs that can promote coexistence of phenotypes that do relatively better in richer versus in poorer times, (2) establish that conditions in tumors are conducive for this mechanism, (3) propose and empirically explore biomarkers indicative of the two phenotypes (HIF-1, GLUT-1, CA IX, CA XII), and (4) and compare cream skimmer and crumb picker biology and ecology in nature and cancer to provide cross-disciplinary insights into this interesting, and, we argue, likely very common, mechanism of coexistence.
Introduction
Biodiversity, the presence of many phenotypes and species, is a ubiquitous feature of nature. Species coexist by preferentially consuming different foods (diet separation), occupying different times and places (habitat separation), or varying in their capacities to avoid hazards and exploit opportunities (predation-based or food-safety trade-offs) (e.g., Pulliam, 1974; Schoener, 1974; Werner and Hall, 1977; Kotler and Brown, 1988; Huntly, 1991; Morris, 2003). Community ecologists construct theories and models to understand how biodiversity might exist, and then test empirically what mechanisms do promote coexistence of different species. Diversity also seems the norm in cancers, where cancer biologists recognize much variety among the cancer cells that inhabit tumor ecosystems within patients. Metrics generally involve genetic and molecular variation, but much of this can be clustered into what appear to be distinct cancer cell phenotypes (e.g., Amaro et al., 2016; Yeo and Guan, 2017; Wooten et al., 2019; Iravani et al., 2021). These types may coexist within tumor microenvironments, across whole tumors, or among tumors within a single patient (Lloyd et al., 2016). We suggest here that the different cancer cell types may equate to biodiversity in nature. Kotler and Brown (2020) have proposed cancer community ecology as a parallel to community ecology in nature to study the mechanisms that promote a diversity of cancer cell types.
The competitive exclusion principle (Hardin, 1961) has provided a basis for understanding how species coexist. It states that no two species can coexist by occupying the same niche at the same place and time. To add rigor, ecologists have noted that for two species to coexist there must be at least two (or a continuum of) limiting factors. These limiting factors can take the form of resources or hazards. For instance, two consumer species can coexist if one is more successful at exploiting resource A, the other is the more successful with resource B, and both A and B are sufficiently abundant to support the species. The two species coexist by trade-offs in their abilities to harvest and use the two resources. Alternatively, the two species can coexist if the species that is better at exploiting resource A is also more vulnerable to predation risk, promoting coexistence by a food-safety trade-off.
An early challenge to the competitive exclusion principle was the Paradox of the Plankton (Hutchinson, 1961). In many aquatic ecosystems, the number of limiting resources (e.g., nitrogen, phosphorus, organic carbon, carbon dioxide) seemed much less than the number of coexisting phytoplankton species. Subtle habitat selection, trade-offs in absorbing different sizes and states of micro- and macro-molecules, and threats from numerous species of predators have been proposed to reconcile the paradox (e.g., Litchman and Klausmeier, 2008; Salcher, 2014). However, Hutchinson suggested that fluctuation in conditions over time might itself contribute to coexistence of biodiverse plankton. Fluctuations are reflected in the higher statistical moments of resource availabilities, the variance and covariance, which can be viewed as reflecting potentially separate “resources” (Levins, 1979; Chesson and Huntly, 1989; Chesson, 1994). Such resources could include, for instance, seeds, for a granivore, at high versus low abundance (Brown, 1989b; Kotler et al., 1993), abiotic essential nutrients for plankton at different seasonal temperatures (Descamps-Julien and Gonzalez, 2005), the prey of cold versus warm water fishes in summer versus winter (McMeans et al., 2020), or water in a year of early abundant rainfall or of drought (Chesson et al., 2004, 2013; Hallett et al., 2019).
Armstrong and McGehee (1976, 1980) provided early mathematical models of how temporal resource fluctuations could permit coexistence of more species than resources, even when both rank good and bad times the same (see Koch, 1974). Trade-offs between the relative foraging, recruitment, or survival success of two species over temporal fluctuations in environmental conditions make coexistence of two species on a single resource possible. One species does better than the other during more favorable periods, while doing worse than the other during less favorable periods. Various models have explored behaviors that can underly species coexistence when resource availability fluctuates over time. These models have taken a number of forms. including endogenously generated non-equilibrium consumer-resource dynamics, exogenously generated seasonal or pulsed resource renewal, and the storage effect (e.g., Armstrong and McGehee, 1976, 1980; Chesson and Warner, 1981; Chesson and Huntly, 1988, 1997; Brown, 1989a; Abrams and Holt, 2002; Abrams et al., 2003; Abrams, 2004; Xiao and Fussmann, 2013). All of these models include times of relatively richer and relatively poorer conditions. The contrasting phenotypes have been referred to as “opportunist” and “gleaner” (Grover, 1990), “grazers” and “diggers” (Richards et al., 2000), or “cream skimmers” and “crumb pickers” (Brown et al., 1994; Jones et al., 2001; Bonsall et al., 2002). We shall use the last of these three as has previously been used in the cancer literature (Gillies et al., 2018; Kotler and Brown, 2020). Here, we are specifically interested in fluctuations in resource availability as a mechanism of coexistence in nature and in the potential of this mechanism to explain some of the variation in coexisting phenotypes of cancer cells.
In general, coexistence on seasonal or otherwise pulsed resources can happen in at least two ways. First, the coexistence of two consumer species is possible if one has the higher foraging efficiency at high resource abundances, while the other has the higher efficiency at low resource abundances (Stewart and Levin, 1973; Abrams, 1984). Foraging efficiency in this case is the ratio of foraging benefits to total foraging costs. Second, foraging costs may be divisible into fixed and variable costs whereby a forager can avoid the variable costs of foraging through resting, ceasing activity, or dormancy. Coexistence on pulsed resources becomes possible if there is a trade-off between fixed and variable costs (Brown, 1989a). Under the circumstances, these tradeoffs are necessary but not sufficient. Coexistence also requires that each species depletes resources in a manner that is more favorable for the other species than itself.
We center in this paper on foraging trade-offs that could promote coexistence of cream-skimmer versus crumb-picker consumer phenotypes when the environment has pulsed resource supply followed by depletion through consumption. We explore the potential for behavioral trade-offs along a continuum of environmental favorability that make a cream skimmer and crumb picker relatively better than the other during richer and poorer times, respectively. In nature, many examples of such rich/poor environmental conditions and cream-skimmer/crumb-picker phenotypes or species have been identified, including hummingbirds and bees, nectar yeasts, woodland rodents, large and small desert rodents, annual and perennial plants, grasses and forbs, slow- and fast-growing mosses, and various planktonic and intertidal organisms (Schaffer et al., 1979; Brown et al., 1981; Kotler and Brown, 1990; Wolfe, 1996; Wilson et al., 1999; Descamps-Julien and Gonzalez, 2005; Cermeno et al., 2011; McNickle et al., 2016; Letten et al., 2018; Oke and Turetsky, 2020). The basic idea of cream skimmer and crumb picker trade-offs can generalize to continua of richer and poorer conditions and to larger numbers of coexisting species, for which examples include diverse desert annuals (Angert et al., 2009; Chesson et al., 2013), grassland plants (Zepeda and Martorell, 2019), plankton (Huisman and Weissing, 1999; Huisman et al., 2001), and acorn-inhabiting weevils (Venner et al., 2011).
In cancer ecosystems, variation in environmental favorability and resource abundances also appears to be the norm. Within tumors, nutrient availability, oxygen, and pH can fluctuate stochastically or periodically, with swings occurring on scales of seconds to minutes to hours and varying among spatial locations (Michiels et al., 2016; Gillies et al., 2018; Saxena and Jolly, 2019). Also in cancer ecosystems, diversity or heterogeneity of cell types within tumors is the norm and correlates with resistance of tumors to therapies (Marusyk and Polyak, 2010; Robertson-Tessi et al., 2015; Lloyd et al., 2016). Despite considerable interest in tumor heterogeneity and how it may promote coexistence of different cell types, coexistence of cancer cell types as cream skimmers and crumb pickers has not been explored. Here, we (1) use consumer-resource models to examine several types of trade-offs that can promote coexistence, (2) establish the conditions in tumors conducive for such a mechanism, (3) propose and explore biomarkers indicative of cream-skimmer and crumb-picker phenotypes (HIF-1; GLUT-1; CA IX; CA XII, and others), and (4) and compare actual and potential examples of these phenotypes in nature around us and in cancer.
Methods and Results: Analysis of a Consumer-Resource Model
Continuous Resource Renewal
We imagine two consumer species (cancer cell phenotypes) harvesting (nutrient uptake in cancer) a single resource. We start with continuous resource renewal and the following consumer-resource dynamics:
where xi are the population densities of consumer species i = 1,2, and R is the density of resources (see Table 1 for list of model variables and parameters).
Net profit rate, the difference between resource harvest rate and the cost of existence, ci (in units of resources per time), determines whether the per capita population growth rate of a consumer species is positive or negative. The conversion factor of net profit rate into per capita growth, bi, scales the rate of growth or decline. The consumers harvest resources by encountering and then handling them, where ai describes the probability of resource encounter per unit time (encounter rate, or attack rate), and hi describes the time taken to handle an encountered resource item. In cancer cells, encounter rates (per time) and handling times (time per item or molecule) with extracellular molecules vary and are mediated by the presence, number, and speed of carrier and channel proteins (in the case of facilitated diffusion) or transporter molecules (in the case of active transport) (e.g., Perfahl et al., 2013; Lisan and Langhans, 2015). Other forms of encounter and uptake that require even more handling effort include receptor-mediated endocytosis and pinocytosis involving the formation of vesicles and engulfment, respectively.
We assume that the consumers’ harvest rates, H (R), follow Holling’s (1959) disc equation (type II functional response), taking the form of a Michaelis Menten or Monod equation:
With continuous resource renewal, we have something akin to a chemostat where the resource flows into the system at some rate, r, and at some concentration, K. Resources (but not the consumers) are lost via outflow and consumption by the consumers. In the absence of consumers, the resource density (or concentration) would equilibrate at R = K. With consumption, the resource equilibrates at a lower density. For solid tumor cancers, the tumor can be viewed as a somewhat viscous chemostat, with blood flow providing and removing resources (among other bloodborne normal cells and metabolites).
Each consumer species will have a subsistence level of resource, Ri∗, above which it experiences a positive growth rate and below which its population declines. This subsistence level is species-specific. It is the value of R such that a species’ net profit rate from foraging is 0:
This subsistence level increases with handling time, hi, and the cost of existence, ci, and decreases with encounter rate, ai. Note that for the resource to have any value to the consumer cihi < 1.
With just a single consumer species, its population size will achieve an equilibrium, xi∗ (when xj = 0), such that the equilibrium resource availability has been driven to the consumer species’ Ri∗:
As expected, the equilibrium number of a single consumer species will increase linearly with the flow rate of resources into the system, r, and the concentration of those resources, K. For xi∗ > 0, the incoming resource concentration must be higher than the consumer species’ Ri∗: K > Ri∗.
Key Results
If the incoming resource concentration is too low, K < Ri∗ for i = 1,2, then neither consumer species can exist (i.e., the necrotic zone in a tumor). If the R2∗ < K < R1∗, then by default only consumer species 2 can exist in the community. If K > Ri∗ for i = 1,2, then the consumer with the lower R∗ will outcompete the other. Hence, at most, just one consumer species can exist in this community.
Significance
All of the above are well-known results from consumer-resource theory. But, they provide the jumping off point for considering the effect of a pulsed (batch chemostat) rather than continuously supplied (continuous flow chemostat) resource. All of these results emanate from three foraging parameters: encounter rate, handling time, and cost of existence. This consumer-resource approach is relatively unexplored in cancer (Amend et al., 2018), and may be quite applicable to 3-D spheroid (Carvalho et al., 2015; Ravi et al., 2015; Agrawal et al., 2021) and organoid culture experiments (Lo et al., 2020; Schuster et al., 2020), and to mouse experiments involving competition between different cancer cell lines (Di Gregorio et al., 2016; Parker et al., 2020).
Pulsed Resource: Encounter Rate and Handling Time Trade-Off
Pulsed nutrient renewal is a feature of nature (daily or seasonal pulses), tumors (intra-tumoral cycles of blood flow, resource availability, and hypoxia), and cell culture experiments (regular changes to the growth medium every so many days). We evaluate these conditions for coexistence in terms of the foraging and cost parameters (a, h, and c). In doing so, we will refer to the cream skimmer (species 1) as the species with a higher positively valued profit than the crumb picker (species 2) at high values of resource availability, and the crumb picker as vice-versa. Thus, the crumb picker has the lower R∗. In the absence of such a trade-off, yet again, the species with the lowest R∗ would outcompete the other.
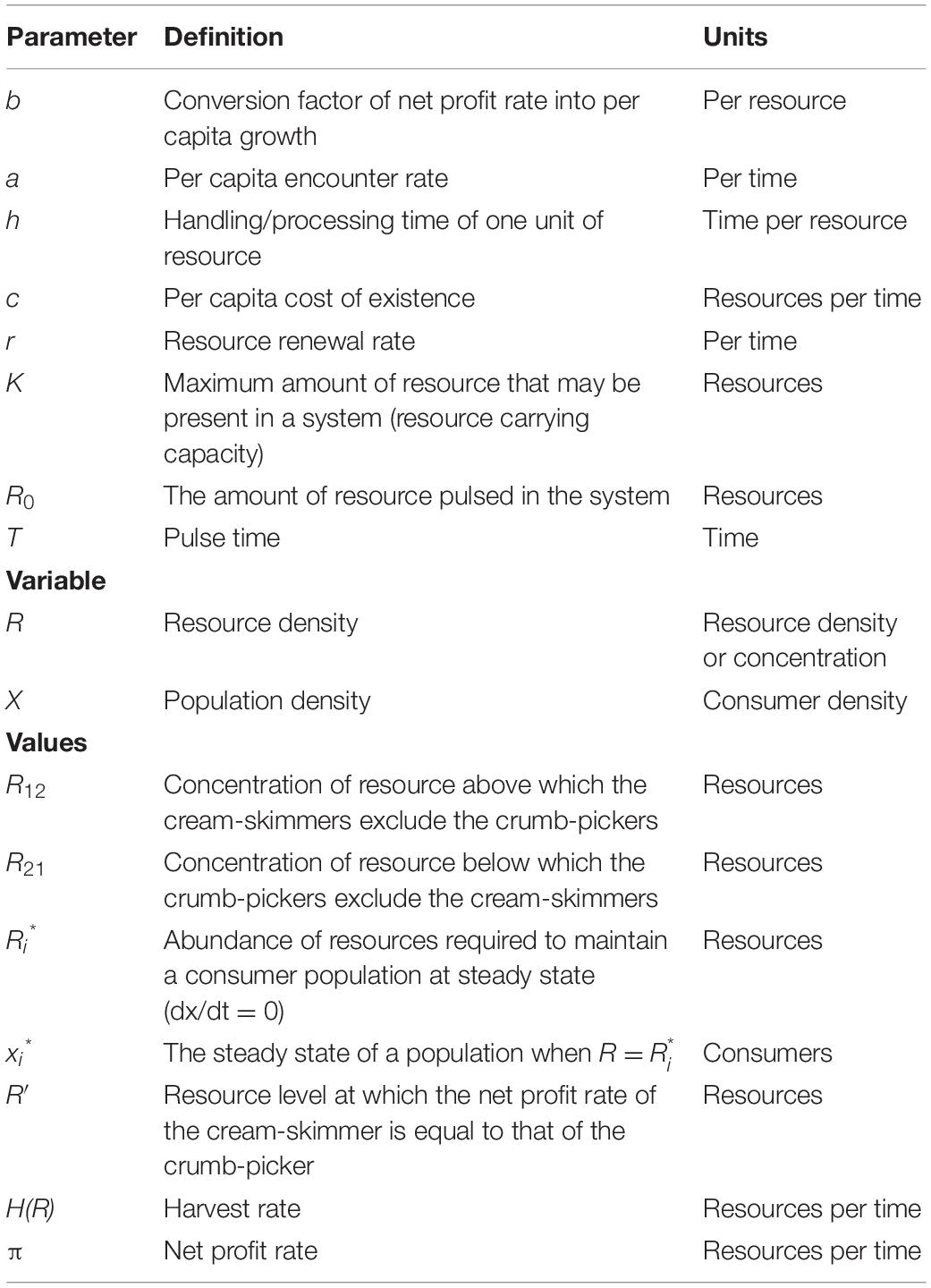
A trade-off between encounter rate and handling time can fulfill the assumptions for coexistence on a pulsed resource. The cream skimmer has the lower values for handling time and encounter rate than the crumb picker: a1 < a2 and h1 < h2. We will assume that they share the same values for conversion efficiency, b, and cost of existence, c. So long as consuming the resource is profitable for both (1 > chi), then: (1) the crumb picker has the lower R∗, (2) the cream skimmer has a higher net profit rate than the crumb picker at high values of R (as R gets very large, a consumer’s harvest rate converges on 1/h, and 1/h1 > 1/h2), and (3) the crumb picker has a higher net profit rate than the cream skimmer at low values of R (as R gets very low, a consumer’s harvest rate converges on a, and a2 > a1) (Figure 1A). Thus there will exist a unique R′ where both consumer species have the same net profit rate:
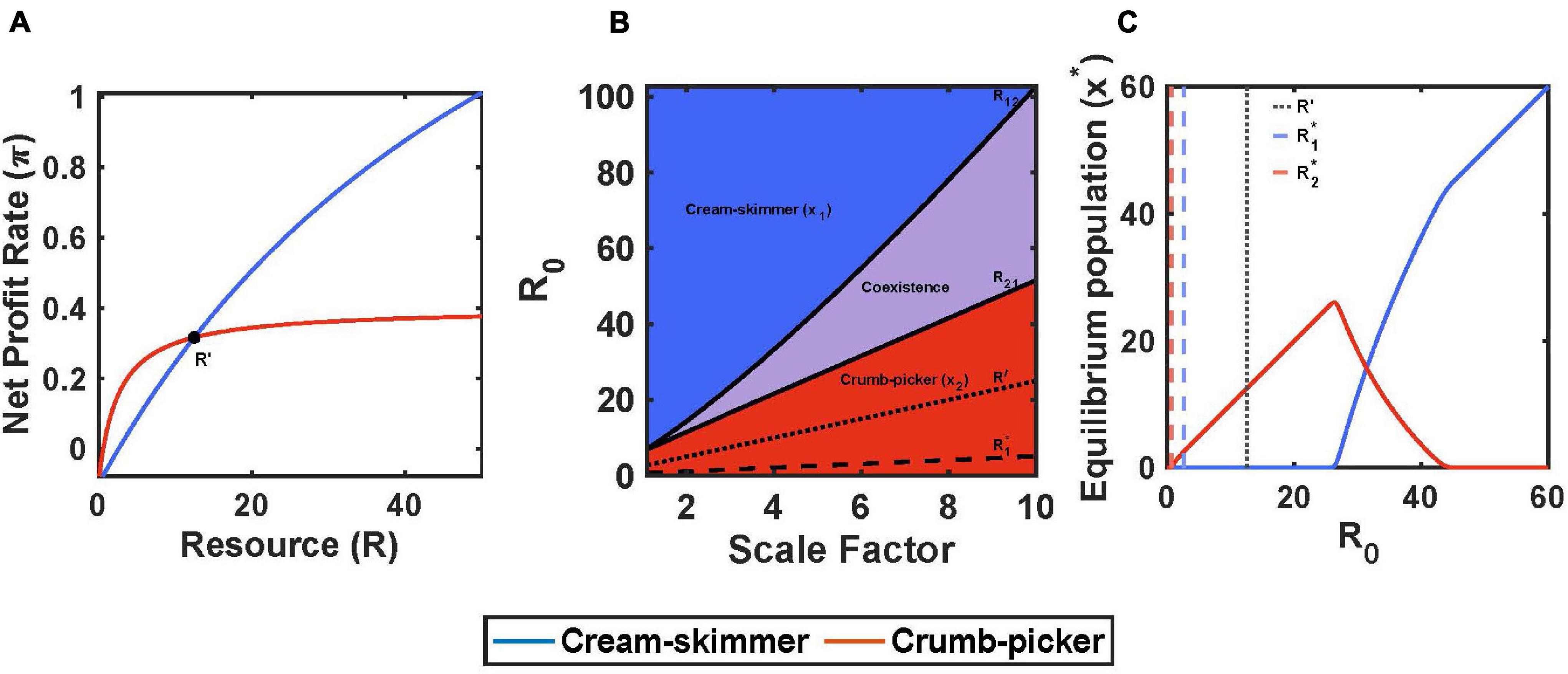
Figure 1. Encounter rate and handling time trade-off with pulsed resource. (A) The crumb-picker has the higher net profit rate than the cream-skimmer at low values of R. R′ represents the resource level where both species have the same net profit rate. (B) Regions of competitive exclusion and coexistence change due to initial pulse size R0 and the scale factor μ. (C) For μ = 5, equilibrium populations change as a function of R0. Intermediate values of R0 show species coexistence. Parameters: a2 = 0.2, a1 = a2/μ, h2 = 2, h1 = h2/μ, b1 = b2 = 0.5, c1 = 0.1, T = 10, x1(0) = 10, x2(0) = 10.
We assume that every T time units there occurs a new pulse of resources that achieves a concentration of R0. The consumers can deplete this resource, but renewal does not occur until the next pulse which achieves the same level regardless of leftover resources from the prior pulse (Figure 2B).
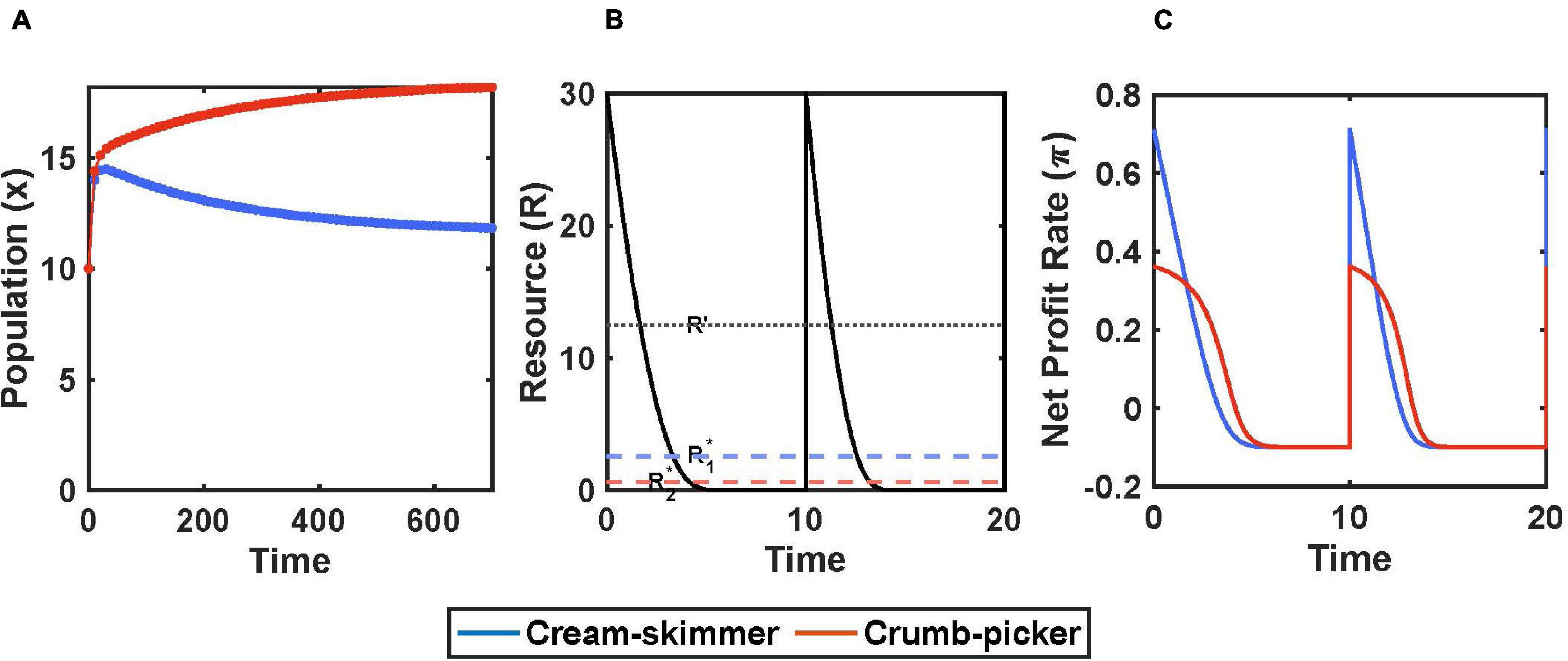
Figure 2. Encounter rate and handling time trade-off with pulsed resource. (A) Species coexist when R0 = 30 and μ = 5. (B) There is a pulse of resource every T = 10 units of time. The crumb picker has the lower subsistence level of resource, R*2. (C) Net profit rate of consumers in response to pulse of resource. Parameters: a1 = a2/μ, a2 = 0.2, h1 = h2/μ, h2 = 2, b1 = b2 = 0.7, c1 = c2 = 0.1, x1(0) = 10, x2(0) = 10.
We assume that changes in population sizes of the consumers occur at the end of each pulse based on the integral of their net profit rate over the course of the interval. Thus, resource levels, R(t), change continuously over the interval t = 0 to t = T, but consumer population sizes do not (semi-discrete consumer-resource model; Pachepsky et al., 2008):
There are several immediate results. For coexistence, the initial pulse size R0 must be greater than the consumer species’ R∗. To have the lower R∗, the crumb picker’s R∗ must lie in the region where it has a higher profit gain than the cream skimmer: R2∗ < R′. The cream skimmer’s R∗ may be greater than or less than R′; but for our simulations we shall assume that both species R∗’s are less than R′ and in the region of R(t) where the crumb picker has the higher net profit rate.
At equilibrium population sizes, the integral of a consumer’s net profit rate must be zero. Hence, there must be earlier times during the pulse where resource abundances yield positive profits that are canceled out by later times when resource abundances yield negative profits. Thus, at a single species x∗: R0 > R∗ > R(T). This generates an interesting result. The equilibrium population size of a single consumer species must lie along this interval:
The advantage of this relationship is that R0 is known and R∗ can be solved analytically while R(T) cannot be solved for analytically. Additionally, as R0 increases and becomes very large, the leftover resources at the end of the pulse, R(T), decline and converge on R(T) = 0 as R0 goes to infinite.
The value of R0 determines the community of consumer species. When R0 is less than the crumb picker’s R∗, then neither consumer species can exist. Then there is a critical value of R0 = R12 > R2∗ below which either the cream skimmer is outcompeted by the crumb picker, or it cannot persist at all. Above this level, R12 > R0, the cream skimmer will be present in the community, as it is able to invade a community of crumb pickers at their equilibrium. Then there is another critical value of R0 = R12 > R21, below which the crumb picker can invade a community of cream skimmers at their equilibrium and above which the cream skimmers will outcompete the crumb pickers (Figures 1B,C). As R0 increases, the equilibrium population size of crumb pickers steadily increases, but as soon as the cream skimmer is present, further increases in R0 lead to an increase in the cream skimmer population size at the expense of the crumb pickers (Figure 1C).
We can use simulations to illustrate all of this. We fixed the parameter values of the crumb picker and then used a scaling factor to create a continuum of possible cream skimmer species. To do this, we define a scaling factor μ > 1, where a1 = a2/μ and h1 = h2/μ. The divergence between the crumb picker and the cream skimmer increases with μ. As μ increases, the cream skimmers R∗ increases (this will always be true for μ > 2; and for all μ > 1, so long as ch2 < 0.5) and the value of R′, the resource abundance where the cream skimmer and crumb picker have the same profit rate, increases. As the cream skimmer becomes more so relative to the crumb picker (increasing μ), both the upper and lower bounds of R0 that produce coexistence increase, even as the region of coexistence expands (Figure 1B). Figure 2 shows an example of coexistence for μ = 5 and an intermediate value of initial pulse size (R0 = 30) (see Supplementary Figures 1, 2 for examples of population dynamics when coexistence is precluded).
Key Results
The species with the higher encounter rate, relative to the cost of existence, will have the lower R∗ and be the crumb picker, and the one with the lower handling time, relative to the cost of existence, will have the higher R∗ and be the cream skimmer. At intermediate values for pulse sizes, coexistence of a crumb picker with a cream skimmer species (or cancer cell type) is expected. At pulse sizes below or above this range, the crumb picker or the cream skimmer should outcompete the other, respectively, thus forming single species communities. As the trade-off in encounter rate and handling time become more extreme, the range of pulse sizes permitting coexistence expands, even as the cream skimmer requires higher pulse sizes to be present in the community. This result emerges from how foraging efficiencies change with resource level, H(R)/c. As long as 1/(h1c1) > 1/(h2c2), then there will always exist a resource level below which the crumb picker is the more efficient forager (because of a2/c2 > a1/c1) and above which the cream skimmer is the more efficient one.
Significance
Variability in resource levels can serve as a consumable resource, thus permitting coexistence (Levins, 1979; Armstrong and McGehee, 1980; Chesson, 1994). Here, we place this into a foraging framework where the cream skimmer benefits more from the variance of abundances, while promoting a higher mean level of resources. The crumb picker benefits more from the mean, while promoting a higher variance in temporal resource availabilities. Body size in mammals may represent such a trade-off between cost-adjusted handling times and encounter rates (Brown et al., 2017). In cancer, most cell culture experiments include refreshing the growth medium every 3–6 days, creating regular pulses of resources. The implications of such pulsing have not been investigated for cancer cells’ uptake dynamics, competition between difference cell lines, or as a system for testing for cream skimmers and crumb pickers. The functional response curves, H(R), of cancer cells have not been measured. Furthermore, the way a cell line is cultured drives evolution (Burdall et al., 2003). Based on the possibility of an encounter rate versus handing time trade-off, it would be interesting to see whether low resource media (usually in the form of diluted fetal bovine serum) that is changed frequently selects for higher uptake rates at low resource levels at the expense of uptake rates at high levels, and vice-versa for high concentration media changed infrequently.
Pulsed Resource: Handling Time and Cost of Existence Trade-Off
Cream skimmers and crumb pickers also can be generated from a trade-off between handling time, h, and the cost of existence, c. Here, we will assume that both species have the same encounter rate with resources, a, but that the cream skimmer has a lower handling time and higher cost of existence. This will cause the profit curves as a function of resource abundance to cross at some value of R. This happens because the cream skimmer has a lower y-intercept because of a larger cost of existence, yet the cream skimmer has a higher maximum profit by virtue of the lower handling time (Figure 3A).
Figure 3. Handling time and cost of existence trade-off with pulsed resource. (A) The crumb-picker has the higher net profit rate than the cream-skimmer at low values of R. R′ represents the resource level where both species have the same net profit rate. (B) Regions of competitive exclusion and coexistence change due to initial pulse size R0 and the scale factor μ. (C) For μ = 5, equilibrium populations change as a function of R0. Intermediate values of R0 show species coexistence. Parameters: μ = 5, h2 = 2, h1 = h2/μ, c2 = 0.1, c1 = c2+(0.025*μ), b1 = b2 = 0.5, a1 = a2 = 0.2, T = 10, R0 = 10, x1(0) = 10, x2(0) = 10.
When setting the net profit rate of the crumb picker equal to that of the cream skimmer to solve for R′, one finds a more complicated relationship than for the case of a versus h. The solution is quadratic on R′ (see Supplementary Material). One solution will always involve negative values for both R′ and the net profit rate. The other solution is relevant and involves a positive value for R′, though at R′ the net profit rate may be positive or negative depending upon the magnitudes of a, h1, h2, c1, and c2.
If the positive solution for R′ is greater than the crumb pickers R2∗ and the foraging efficiency of the cream skimmer is higher at some level of resource (1/(h1c1) > 1/(h2c2)), then there will exist an initial pulse size R21 below which the crumb picker will outcompete the cream skimmer and above which there will be coexistence. Furthermore, there will also be an R12 below which coexistence occurs and above which the cream skimmer outcompetes the crumb picker (Figures 3B,C). Coexistence will occur when the initial pulse size falls between these two values: R21 < R0 < R12.
To illustrate these outcomes we scaled the trade-off using a scaling factor μ > 1 where h1 = h2/μ and c1 = c2 + 0.025 μ. The values for R21 and R12 at first decline and then increase with the magnitude of the trade-off, μ. Regardless, the region of coexistence increases with the magnitude of the trade-off (Figure 3B). Otherwise the patterns of coexistence resemble closely those for the a versus h trade-off.
Key Results
Like the a versus h trade-off, an h versus c trade-off provides the necessary conditions for coexistence on a pulsed resource. While the cream skimmer always has a higher harvest rate than the crumb picker for all resource abundances, its higher cost of foraging drives the intersection of the two species profit curves with resource abundance. The actual conditions require: h1 < h2; c1 > c2 and (1/h1 – c1) > (1/h2 – c2) where this last term is the asymptotic maximum profit as the initial pulse size becomes very large. As the more efficient forager, the crumb picker can always achieve a higher equilibrium population size when alone than can the cream skimmer species. This trade-off represents a foraging speed versus foraging efficiency trade-off.
Significance
Speed versus efficiency trade-offs are ubiquitous in nature. They can involve different taxa such as reptiles versus mammals, or strategies of plants of more xeric versus more mesic conditions, including varying water use efficiencies (Miller-Rushing et al., 2009; Lanning et al., 2020). An intriguing possibility may be coexisting pinon pine and juniper (Limousin et al., 2015). The pine has more roots that extend less far and less deep (Schwinning et al., 2020) and respond quickly to short pulses of summer rain (West et al., 2007). Thus the pinon pine (cream skimmer) may have a lower overall encounter rate with water, but a rapid and efficient means for handling water and nutrient uptake. A speed versus efficiency trade-off may be particularly relevant to cancer cells in the context of the Warburg effect (Gillies and Gatenby, 2007; Bhattacharya et al., 2016). Cells showing this effect maintain anaerobic glycolysis even in the presence of oxygen. Anaerobic glycolysis permits rapid, yet inefficient, use of glucose; whereas oxidative phosphorylation, through mitochondria, represents a slower but more efficient use of glucose (Epstein et al., 2017).
Pulsed Resource: Encounter Rate Versus Cost of Existence Trade-Off
A trade-off between encounter rate, a, and cost of existence, c, provides similar opportunities for coexistence as do the a versus h or h versus c trade-offs. But, coexistence requires that there be a positive handling time: h > 0.
With h = 0, the species with the lowest R∗ will outcompete the other, regardless of the initial pulse size, R0. This is because relative foraging efficiency is now independent of resource abundance. It is everywhere given by a/c. The curves of net profit rate, π, versus resource abundance, R, are straight lines with y-intercepts of –c, x-intercepts of R∗ and slopes of encounter rate a. The species with the higher a/c, has the lower R∗ and it will always outcompete the other (Supplementary Figure 3).
When h > 0 and equal between the two species, a trade-off between a and c can promote coexistence. The species with the higher a must have a higher c that is not proportionately larger than it’s a relative to the other species. Furthermore, the species with the higher encounter rate and higher cost of existence (all relative to the fixed h) is in fact the crumb picker (species 2): a1 < a2, c1 < c2. Coexistence between the two species is possible if R1∗ > R2∗, and a2/a1 > c2/c1 > 0. With these conditions, the crumb picker has the higher foraging efficiency at very low resource abundances (a2/c2 > a1/c1), and the cream skimmer at high (1/(h1c1) > 1/(h2c2)). Under these conditions, the profit curves with resource abundance are non-linear, have y-intercepts at –c, x-intercepts at R∗, and asymptotes at (1/h – c) (Figure 4A; see Supplementary Material).
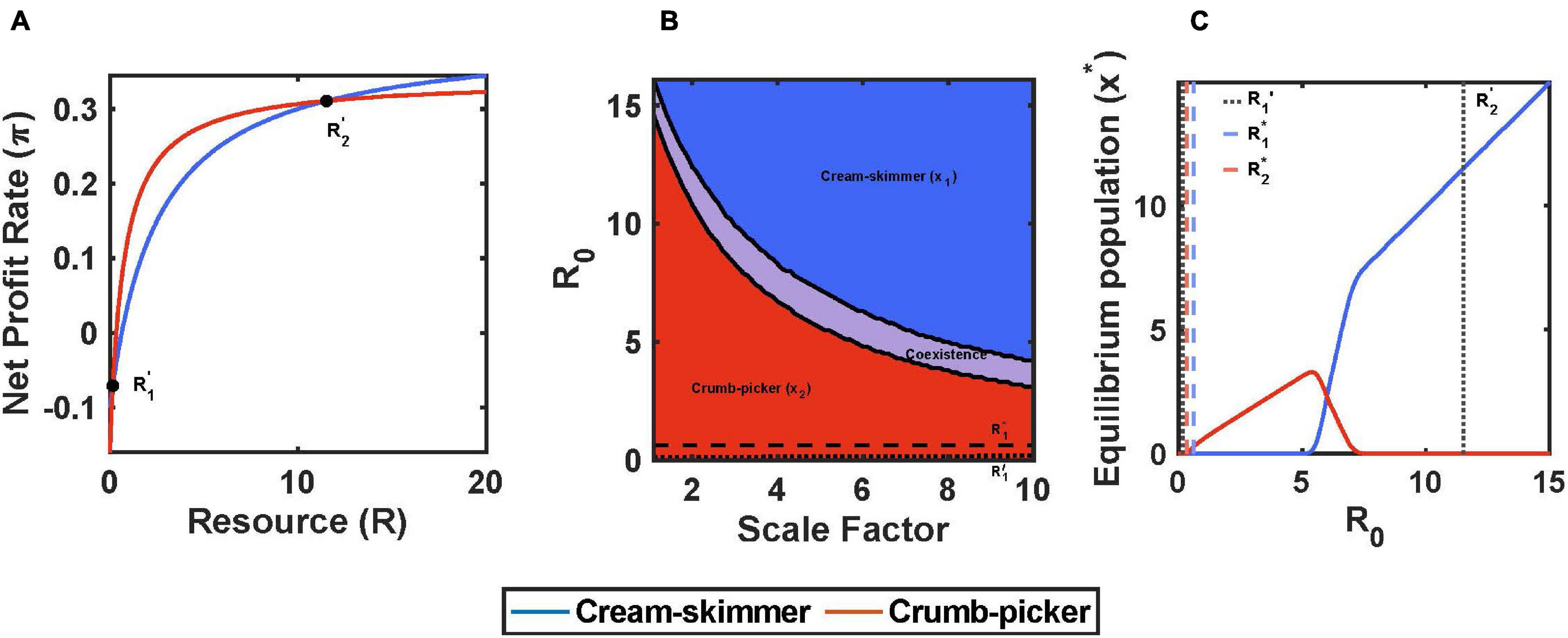
Figure 4. Encounter rate and cost of existence trade-off with pulsed resource, h1 = h2 = 2. (A) The crumb-picker has the higher net profit rate than the cream-skimmer for R′1 < R < R′2. (B) Regions of competitive exclusion and coexistence change due to initial pulse size R0 and the scale factor μ. (C) For μ = 5, equilibrium populations change as a function of R0. Intermediate values of R0 show species coexistence. Parameters: μ = 5, a1 = 0.2, a2 = 0.1 μ+a1, c1 = 0.1, c2 = 0.012 μ+c1, b1 = b2 = 0.5, T = 10, R0 = 10, x1(0) = 10, x2(0) = 10.
For the coexistence of the cream skimmer with the crumb picker, the species’ profit curves intersect twice at positive values of R. At very low values of R the cream skimmer actually has the higher profit. Beyond the first intersection point, R, the crumb picker now has the higher profit, though at this intersection point both species experience negative profits. At a still higher value of R, there is the second intersection point, R, above which the cream skimmer retains a higher profit rate than the crumb picker for all values of R > R (Figure 4A). As the initial pulse size increases, there is the region where no consumer species can exist (necrotic zone in cancer; R0 < R2∗), a region where the crumb picker outcompetes the cream skimmer (R0 < R21), a region of coexistence (R21 < R0 < R12), and then a region where the cream skimmer outcompetes the crumb picker (R0 > R12). Figure 4B shows how the abundances of resources at which communities switch from one to another (R21 and R12) decline with a scaling factor that makes the difference between the cream skimmer and crumb picker more extreme with respect to a and c. Thus, the cream skimmer actually becomes favored at lower and lower pulse sizes as the two species’ trade-off becomes more extreme. Figure 4C shows how the equilibrium population sizes of crumb pickers and cream skimmers change with R0.
Key Results
A trade-off between encounter rate and the cost of existence leads to similar opportunities for coexistence as the a versus h, and h versus c trade-offs with a twist. When handling times are equal, it is the species with the higher a and c that is the crumb picker. Relative to the cream skimmer, the crumb picker’s proportional increase in a must be greater than its proportional increase in c. If there is no handling time, then coexistence is not possible. The species with the higher a/c will always outcompete the other.
Significance
Mechanisms that change encounter rates in plants include stomatal number, root area, and leaf area. For example, the widespread desert perennial sagebrush produces short-lived “extra” leaves in spring, when water pulses into the desert ecosystem. These leaves increase the encounter rates with light and CO2, have high photosynthetic carbon fixation but low water use efficiency, and are shed before water becomes limiting and costly to use (Evans and Black, 1993). A similar potential mechanism for cancer cell types could be the number of glucose transporters (GLUT1) (Younes et al., 1997; Loponte et al., 2019; Kondo et al., 2021). Upregulating more transporters should increase a cancer cell’s encounter rate with glucose molecules, while raising the metabolic costs of producing and maintaining these transporters. This mechanism could be further enhanced by (1) changing the functional response, for instance, a Type 3 functional response (Morozov, 2010), where γi > 0:
or, (2) making encounter rates dependent on resource abundance, ai(R), as might occur when foragers develop a search image (Dukas and Kamil, 2001).
Environmental heterogeneity and trade-offs in foraging parameters form the basis for many mechanisms of coexistence. But, not all trade-offs in foraging parameters will result in coexistence (see Vincent et al., 1996). For our model, appropriate trade-offs between any of the three profit parameters can promote coexistence of a cream skimmer and crumb picker on a pulsed resource.
Pulsed Resource: Trade-Offs Between Fixed and Total Costs
Virtually all organisms, including microbes, incur an additional variable cost, v, when actively foraging or taking up nutrients. Being inactive allows the organism to forgo this cost while still incurring some fixed cost of existence, f. Thus, we can break the cost of existence into these two components: c = v + f. When actively harvesting resources, the consumer expends both the fixed and variable costs; but, if the consumer so chooses, it can rest. When resting it harvests no resources but only expends the fixed cost. If the consumer’s harvest rate is less than the variable cost of foraging, it would be best to rest. Hence, be active when H(R) > v and remain inactive when H(R) < v:
where π is the consumer’s net profit rate.
In the prior models all costs were fixed costs (v = 0) and so the consumers never rested. With a pulsed resource and a variable cost greater than zero, v > 0, there is now a switch density, Rs, where the forager should become inactive when R(t) < Rs. This switch can be found by setting the change in profit from foraging equal to that when resting:
Note that Rs < R∗ for f > 0, meaning that consumers will switch to resting at a resource abundance less than their subsistence level. It pays to operate at a loss of profit so long as the harvest rate covers the variable cost of foraging.
Cancer cells are known to have quiescent states that can include cell cycle arrest, reduced nutrient uptake, and reduced metabolic expenditures (Valcourt et al., 2012; Miller et al., 2021). While quiescence can be induced by nutrient deprivation, it remains an open research question whether cancer cells behaviorally shift from active feeding to a non-feeding resting state in response to the profitability of each activity (White et al., 2020). If they do, a pulsed resource with a trade-off between fixed costs and total costs, f versus c, can promote the coexistence of a cream skimmer and crumb picker.
For this model, we will assume that encounter rates and handling times are the same for both consumer species. We identify the cream skimmer as the species with the higher total cost of existence, c, the lower fixed cost, f, and the higher R∗. For simplicity, we assume that the crumb picker has no variable cost and hence remains active all of the time; its switch density is R2s = 0. Under these circumstances, the profit curve of the crumb picker as a function of resource availability has a y-intercept of –c2, an x-intercept of R2∗, and a profit rate at maximum harvest rate of (1/h2 – c2). The cream skimmer’s profit curve has a discontinuity at R1s. Below this switch value, profit as a function of R is simply –f1 because it is resting. Above this value, the cream skimmer is active and has the same curve as the crumb picker’s, but shifted downwards by c1 – c2, with an x-intercept of R1∗ and a maximum profit rate of (1/h1 – c1). The intersection of the crumb picker’s and cream skimmer’s profit curves, R′, occurs at a value less than the cream skimmer’s switch density and in the region of negative profit gain (Figure 5A).
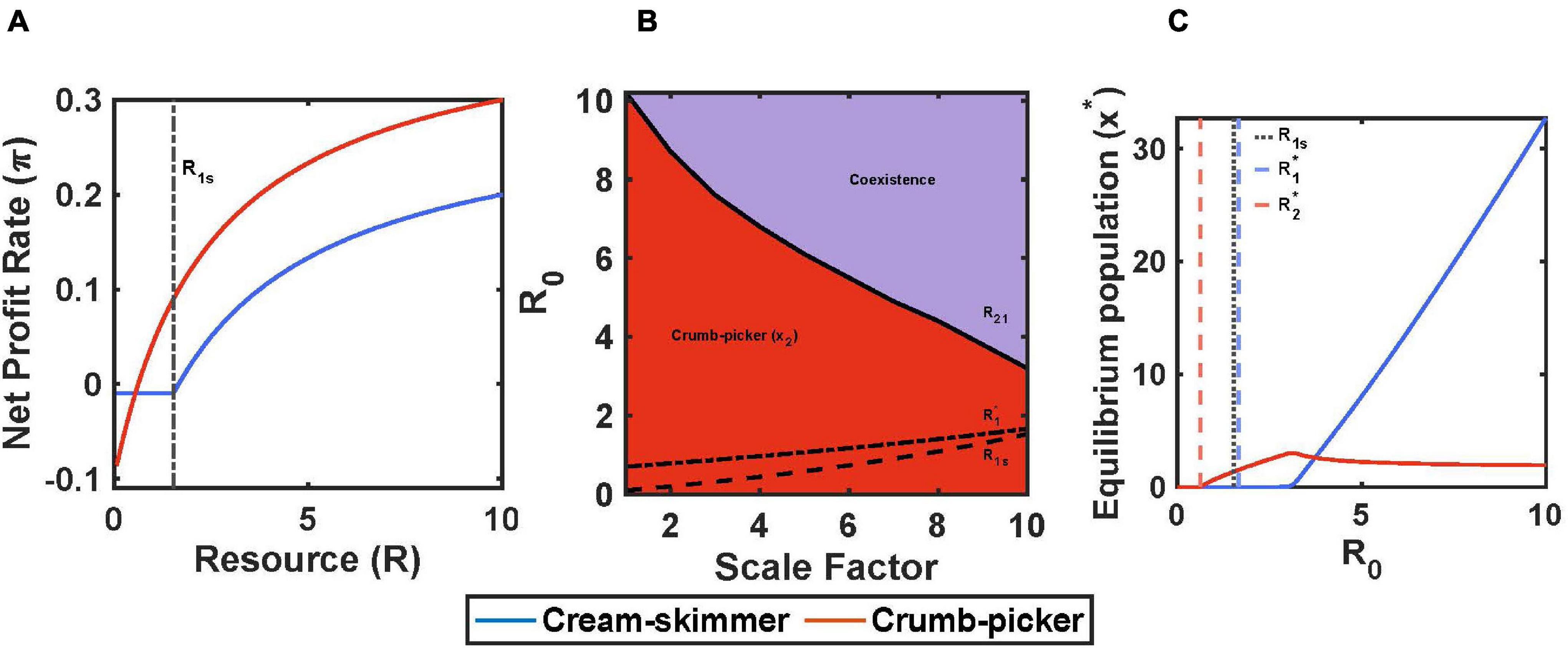
Figure 5. Fixed and total costs trade-off with pulsed resource. (A) The cream-skimmer’s net profit rate has a discontinuity at R1s: For R < R1s the cream-skimmer is resting, for R > R1s the cream-skimmer is active. (B) Regions of competitive exclusion and coexistence change due to initial pulse size R0 and the scale factor μ. (C) For μ = 10, equilibrium populations change as a function of R0. Parameters: μ = 5, f1 = 0.1–0.009*μ, f2 = 0.1, c1 = 0.1+0.01*μ, c2 = 0.1, b1 = b2 = 0.5, a1 = a2 = 0.2, h1 = h2 = 2, v1 = c1-f1, v2 = c2-f2, T = 10, R0 = 10, x1(0) = 10, x2(0) = 10.
As shown in the simulations, the success of the crumb picker can be insured so long as R1s > R2∗. If the cream skimmers become inactive at a level of resource at which the crumb pickers still make a positive profit, then there are always profitable resources to be had, no matter the population size of cream skimmers or the initial pulse size (so long as R0 > R2∗). In the truest sense, the cream skimmers leave “crumbs” that are valuable to the crumb picker. Thus, there is no pulse size above which the cream skimmers can competitively exclude the crumb pickers. There still remains a pulse size, R21, above which the cream skimmers will be present and coexist with the crumb pickers (Figure 5B). Above the point where the cream skimmers can join a community of crumb pickers, the population size of cream skimmers increases rapidly with pulse size, as that of the crumb pickers declines to a positive asymptote determined by how many crumb pickers can be supported from effectively having just R1s to work with (Figure 5C). The cream skimmers succeed because their low fixed cost allows them to travel inexpensively through time from the point of too few resources to the next resource pulse. If we let t1s be the time at which the cream skimmers switch from foraging to resting during the intra-pulse period, we see that it takes fewer resources to support a cream skimmer than a crumb picker. In the region of coexistence, c1t1s + (T-t1s)f1 < c2T.
Key Points
Coexistence of a cream skimmer and crumb picker becomes highly likely on a pulsed or seasonal resource when (1) foragers can choose to be active or to rest or remain dormant, and when there is a trade-off between maintenance efficiency (H/f = efficiency of traveling through time from one good period to the next) and (2) foraging efficiency (H/c = ability to profitably forage resources to a low level). This applies where the forager will switch from foraging to some form of resting when resource abundances have become sufficiently depleted.
Significance
In nature, this ubiquitous mechanism of coexistence can apply to annual or ephemeral plants (cream skimmers) versus perennials (crumb pickers) (Brown, 1989a), hummingbirds and bees (Brown et al., 1981), colonial bees versus solitary bees (Schaffer et al., 1979), mosses (McNickle et al., 2016), phytoplankton (Litchman and Klausmeier, 2001), and more, and can extend to more species along resource continua (e.g., Chesson et al., 2004, 2013; Angert et al., 2009). While the conditions for this mechanism appear to be met in cancer, it has not been tested or verified. As discussed, the trade-off between anaerobic and aerobic metabolism may allow a Warburg phenotype to coexist with cancer cells that have near-normal metabolism. While expensive, much of the machinery for glycolysis is variable cost and can be down-regulated, while the maintenance of mitochondria entails a high fixed cost. Such a trade-off may manifest between two of the most studied breast cancer cell lines, MDA-MB-231 (elevated glycolysis) and MCF-7 (normal aerobic metabolism). Furthermore, cancer cell dormancy has been documented for many cancer types and can provide the basis for this mechanism of coexistence (Miller et al., 2020, 2021).
Freischel et al. (2021), in Gause-style competition experiments using 3-D spheroid cell cultures, found that MDA-MB-231 cells had a stronger competitive effect on MCF-7 cells than vice-versa, even as MCF-7 had the higher intrinsic growth rates and carrying capacities. As cream skimmers, MDA-MB-231 may have a harvest rate advantage at high resource levels (either through a higher a or lower h), have a lower foraging efficiency (higher c), and lower fixed cost (lower f) as compared to the MCF-7 cells. In these cell cultures, the medium was changed every 4 days, providing a new pulse of resources. Such a system holds much promise for testing for coexistence on a pulsed resource. However, at present we do not know each cancer cell line’s profit curves with resource abundance, whether they cease activity when resources become scarce, or how quickly and thoroughly they depress the resources of the culture medium prior to the next pulse.
Cream Skimmers and Crumb Pickers in Cancer: How and Where to Look?
Tumor heterogeneity, both in micro-environmental conditions and in the genetic and phenotypic composition of the cancer cells themselves, is the norm. Such heterogeneities increase with tumor growth and disease spread. Tumor heterogeneity is generally, though not always (Yu et al., 2017), associated with a poor prognosis for the patient. Histologies with immunohistochemical staining provide one method for identifying cancer cell phenotypes and identifying the diversity of “Darwin’s finches” comprising the community of coexisting cancer cell types.
Our model applies to circumstances, likely in tumors, where the pulsing and depletion of resources occurs on a faster time scale than the population dynamics of the consumers. Small scale fluctuations in blood flow, oxygen levels, pH and nutrient supplies give rise to heterogeneity in the microenvironment (Gillies et al., 2018). These temporal variabilities can be stochastic or cyclic (Cárdenas-Navia et al., 2008; Dewhirst, 2009). Scale also plays a role in how nutrient fluctuations occur in the tumor. Recently, Pressley et al. (2021) found approximately 4- to 5-min cycles of O2 levels (and presumably the levels of other nutrients) at small spatial scales within a pancreatic cancer cell line subcutaneously implanted into mice. These results indicate that pulsation and fluctuations of nutrients, the first condition for the coexistence of cream skimmers with crumb pickers, is met in many if not all solid tumors. Furthermore, these changes happen at time scales faster than cancer cell generation times, motivating the use of our semi-discrete consumer-resource model.
The geno- and phenotypic heterogeneity of cancer cells also indicate the potential presence of “cream-skimmer” and “crumb-picker” like cancer cells. Cancer cells expressing hormone receptors are easily characterized with histology. In breast and prostate cancers, estrogen positive or testosterone positive cancer cells require their respective hormones for survival and growth. The frequent coexistence of estrogen positive or testosterone positive cancer cells with estrogen negative or testosterone negative ones that do not require consumption of estrogen or testosterone, respectively, represents a fairly clear case of diet choice (Kareva and Brown, 2021). Furthermore, the different composition of breast cancer cells near vasculature versus away represents spatial separation akin to mesic versus xeric habitats and their associated plant communities (Alfarouk et al., 2013). Finally, coexistence of cell types based on food-safety trade-offs manifest in the different cell types associated with “hot” and “cold” regions of tumors based on high and low immune cell infiltration, respectively (Shembrey et al., 2019; Gatenbee et al., 2020).
Non-hormonal cancers also display differing bio-markers distinguishable in histological studies using a variety of nutrient receptors and metabolic markers. Commander et al. (2020) found that clusters of tumor cells could be divided into leader and follower cells. These two phenotypes displayed distinct metabolic phenotypes. What they referred to as leader cells relied heavily on oxidative phosphorylation with decreased glucose uptake. Conversely, the follower cells relied on glycolysis and required high glucose uptake. This difference could be identified using staining for the glucose transporter, GLUT1, where cream skimmers and crumb pickers would have high and low expression levels, respectively.
Hypoxia markers such as HIF1-α, CAIX, and CAXII also show intra-tumor variation between cancer cells and provide valuable identifiers of cancer stage and prognosis (Chen et al., 2010, 2018; Ilie et al., 2011; Rademakers et al., 2011). Collective production of HIF1-α can promote angiogenesis and increased blood flow to the microenvironment (Yang et al., 2013). To the individual cancer cells it also permits survival and metabolic activity under hypoxic conditions (Kaidi et al., 2007). CAXII is a transmembrane protein often over-expressed in cancers and associated with buffering intra-cellular pH and also permitting survival and activity at low oxygen and nutrient levels (Chiche et al., 2009). We hypothesize that high expression of HIF1-α or CAXII may identify crumb pickers, and at the very least be indirectly associated with our models’ foraging parameters.
Diversity of cancer cell metabolism, indicated by upregulated glycolysis (cream skimmer?) or upregulated oxidative phosphorylation (crumb picker?), suggests a speed versus efficiency trade-off. The Warburg effect is likely characteristic of cream-skimmers. These cells maintain high levels of glycolysis (anaerobic respiration) even in the presence of oxygen. In addition to lowering pH, such a strategy increases nutrient uptake, and decreases handling time; but produces much less ATP per respired glucose molecule. Such a strategy entails a low fixed but high variable cost of foraging relative to aerobic respiration via the mitochondria. The transmembrane protein CAIX can provide a marker for cells with upregulated glycolysis (Mboge et al., 2019). CAIX protects against extracellular low pH by creating a protective buffer around the cell, and reducing intra-cellular stress caused by the toxic metabolites from glycolysis. It also may play a role in immune evasion and also represent a food safety trade-off (Lloyd et al., 2016). Upregulated CAIX may provide a biomarker of a cream skimmer strategy.
Genomic analyses (whole genome sequencing for mutations or RNAseq for gene expression) can also identify cancer cell types. Neftel et al. (2019) found four identifiable types of brain cancer cells (glioblastoma). While the frequency of the four types varied with patient and tumor; within a tumor these cell types could be found coexisting in close proximity. One type exhibited traits that were mesenchymal (high motility) and highly glycolytic. This could be a cream skimmer. Any of the other three types might, with further investigation, fit a crumb picker strategy with a slower rate of nutrient uptake and use, but at a lower cost. Sasmita et al. (2018) provide an extensive review of biomarkers and classification schemes for the different subtypes of glioblastomas between patients and of the cancer cell types coexisting within a patient’s tumor. The recognized mesenchymal cell type, and the proneural and neural subtypes of cells, may correspond to cream skimmers and crumb pickers, respectively (Verhaak et al., 2010).
Data From Cancer Patients
We used histologies from 10 breast cancer patients that had been previously stained and scored in Lloyd et al. (2016). Here, we are interested in whether cells with low and high expression of GLUT1, HIF1-α, CAIX or CAXII can be found coexisting in close proximity (unfortunately, the data do not permit examination of how an individual cell scores simultaneously on all four of these stains). Figure 6 shows an entire biopsy slide for one of the patients and how it can be imaged to highlight the whereabouts of cancer cells. For each of the stains, we identified a subsample in a region with numerous cancer cells. From this cancerous region we created a smaller quadrat 150 μm on a side. For each stain, we found coexisting cancer cells with high and low expression occurring side by side at this small spatial scale (Figure 7). For CAIX, CAXII, GLUT1, and HIF1-α, their respective quadrats had 27 versus 20 (57%), 22 versus 38 (33%), 42 versus 73 (37%), and 11 versus 91 (89%) cancer cells showing high versus low expression (the bolded numbers and % occurrence are the putative cream skimmers). This pattern of coexistence was manifest across most patients.
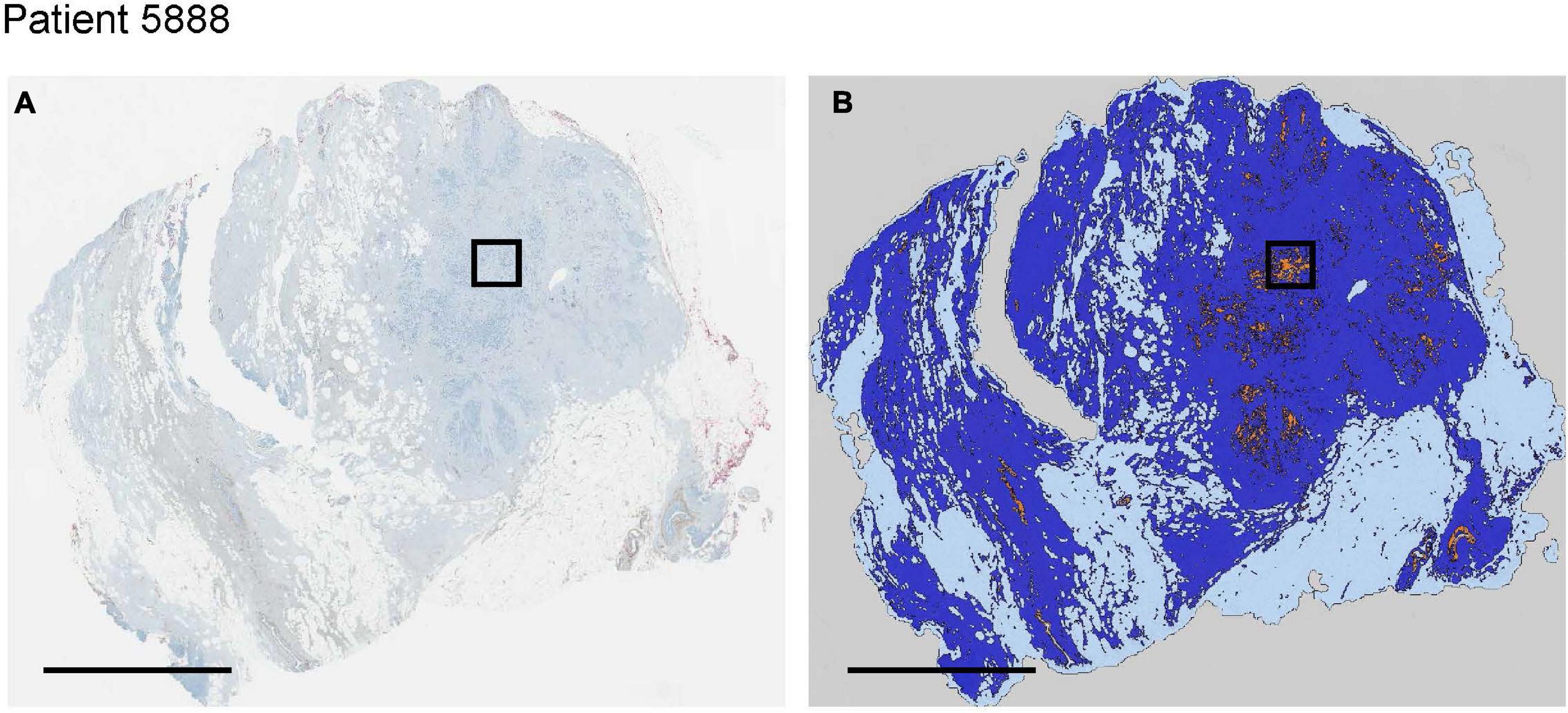
Figure 6. For a single invasive breast cancer patient (A), image analysis techniques we used to segment and classify cancer (orange), normal breast tissue (dark blue) and normal adipose tissue (light blue) regions of interest (B). Black bounding box represents the region of interest evaluated in more detail in Figure 7. All scale bars = 5 mm.
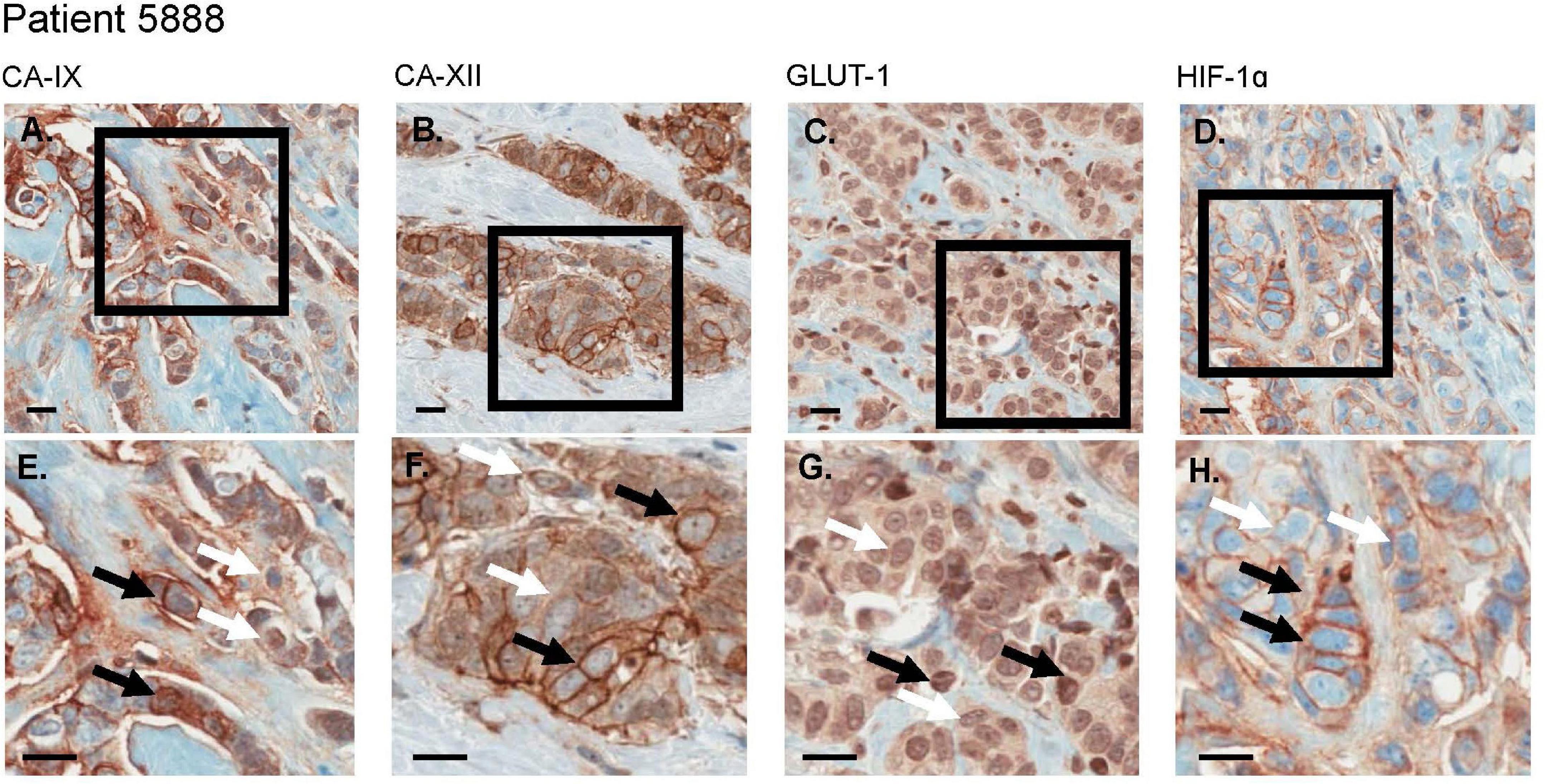
Figure 7. For an invasive breast cancer patient, CA-IX, CA-XII, Glut-1, and HIF-1α each demonstrate regions of variable biomarker expression. (A–D) display a larger number of cells wherein (E–H) are expanded views of selected regions of interest (black bounding boxes). (E–H) demonstrate both high (black arrows) and low (white arrows) expression levels (brown stain) in co-mingled populations of cancer cells. All scale bars = 20 μm.
We reexamined Lloyd et al.’s (2016) data for frequencies of cell types based on biomarker expression. These data generally provide 60 500 × 500 μm sample quadrats (10 patients × edge versus interior habitats of the tumor × 3 replicates per habitat). CAIX and CAXII data are only available for 9 patients and thus 54 quadrats. The percentages of cells with high expression of the stain within a sample are shown in Table 2. High-expressing CAIX cells, perhaps indicative of cream skimmers, were virtually absent (<5%), rare (5–10%), and common in 18, 8, and 1, respectively, of the 27 quadrats at the interior of the tumor (low resources), while 0, 2, and 25, respectively, at the edge of the tumor (high resources) (Supplementary Table 1). Low expressing CAIX cells always comprised at least 10% of the cancer cell population. Low CAXII expressing cells, perhaps indicative of cream skimmers, always comprised > 10% of the cancer cell populations both in the interior and edge of the tumors (Supplementary Table 2). High expressing CAXII cells (crumb pickers?) always comprised > 10% of cancer cells in the tumors’ interiors, but at the edge were <1% in 2 samples, between 1 and 5% in 7 samples, and 5–10% in 6 samples. For GLUT1, high expression (cream skimmers?) was prevalent at the edge of the tumor, but not the interior (Supplementary Table 3). At the edge, of the 30 samples, 7 had < 5%, and 5 samples had between 5 and 10%. In the interior, of the 30 samples, 9 had < 1%, 9 between 1 and 5%, 8 between 5 and 10%, and only 4 > 10%. For HIF1α, low expression cells (cream skimmers) were always > 10% of the cells for all samples irrespective of habitat (Supplementary Table 4). High expression cells (crumb pickers?) were more common in the interior than edge of the tumor. In the interior, they comprised < 5% in 3 samples, between 5 and 10% in 5 samples, and > 10% in 22 samples. At the edge, they comprised < 5% in 5 samples, between 5 and 10% in 10 samples, and > 10% in 15 samples. Besides opportunities for coexistence of cream skimmers and crumb pickers within specific regions of the tumor, the results also speak to the importance of spatial variation in habitats within tumors in promoting cancer cell heterogeneity (Hoefflin et al., 2016).
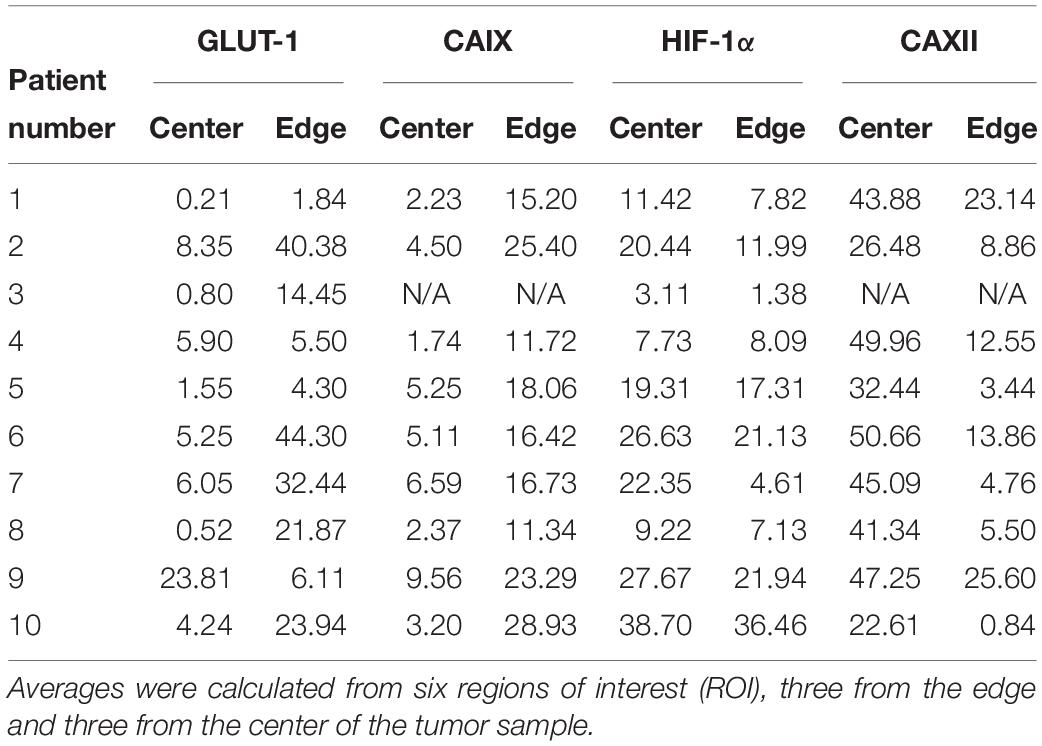
Table 2. Average percent positive expression of GLUT-1, CAIX, HIF-1α, and CAXII in the center and edge of the tumor.
For each of these biomarkers there are significant patient-to-patient variation and significant differences between habitats (edge and interior) as originally noted by Lloyd et al. (2016). Furthermore, if any of these biomarkers are indicative of cream skimmers and crumb pickers, then patients, habitats or samples may exhibit examples of just one or the other type, and, in most cases, the coexistence of both types.
As a caveat, note that such histology data might confound true differences in cell types because of overlaps between stain expression and natural variation in the cell’s expression that might vary between patients and between tumor habitats within a patient. Furthermore, differences in staining between cells might represent phenotypic plasticity rather than heritable differences. Regardless, we do see strong differences between cancer cells in these stains, with many having near to complete absence and others showing very strong expression. And, the mechanism of coexistence can serve to explain coexisting phenotypes whether the basis is plasticity or inheritance.
Discussion
Temporal variation in resource abundance, or in environmental conditions that affect availability of resources to a consumer, can provide a mechanism of coexistence. These may accompany the more familiar ones of coexisting species partitioning different resources or habitats. Here, we developed and operationalized a model of coexistence on a temporally pulsed resource. We explicitly considered trade-offs in key foraging parameters that can be measured or observed, namely a consumer’s encounter rate with resources, a (a measure of foraging speed at low resource abundance), handling time, h (a measure of foraging speed at high resource abundances, where lower is better), and cost of existence, c (a term that determines foraging efficiency at low, a/c, versus high, 1/(hc), resource abundances). Additionally, we considered the trade-off that can occur when the cost of existence includes a fixed, f (unavoidable cost of being alive), and a variable, v (avoidable if the organism chooses to be inactive), component.
We imagined a pulsed resource, a reasonable proxy to aspects of nature and cancer. Every so many time units, the abundance of resource for the consumers renews to a fixed starting level. Following the pulse, resource abundance declines as consumers consume the resource, and this decline continues until the next pulse. For broad ranges of pulse sizes and trade-offs between two consumer species in foraging parameters (a, h, and c), coexistence is possible between a crumb picker (with the higher a/c) and a cream skimmer (with the higher 1/(hc)). For the fixed and variable cost model, coexistence occurs when the crumb picker has the higher combined foraging efficiency (H/c, where H is harvest rate as a function of resource abundance) and the cream skimmer has the higher maintenance efficiency (H/f). Both consumer species benefit, when alone, from larger pulse sizes. But, cream skimmers see an increase in their competitive advantage over crumb pickers as the pulse size increases. Throughout, we mention examples from nature around us and suggest putative cancer examples. While well-documented examples exist in the literature on natural ecosystems, the cream-skimmer/crumb-picker trade-off, in its several manifestations, remains untested as a possible explanation for coexisting cancer cell types within a tumor.
Several realistic additional aspects could hamper or facilitate coexistence of a cream skimmer with a crumb picker and might be incorporated into the models we have analyzed here. These include stochastic variation in the timing and sizes of pulses, intra-pulse births and deaths within the consumer species’ populations, and some small trickle of resource renewal during the interval following a pulse. A likely important additional factor is the value of a resource item to a consumer, e. In effect, we held this constant at unity for both consumers, but there can be trade-offs associated with value. A more complete model would allow for a net profit rate of eH – c. Examples of value-dependent net profit can emerge from digestive physiology that create a trade-off between e and h (handling time). For instance, zebra and Canada geese, relative to wildebeest and cottontail rabbits, respectively, are cream skimmers. They do not efficiently digest cellulose. Rather, they consume large amounts of herbage (low h), while their digestive system absorbs only a small fraction of the caloric value (low c). Wildebeest (ruminants) and cottontails (hindgut fermenters) eat less and take much longer to digest the material (high h), but have a higher digestion efficiency (higher e). Like the other trade-offs in the consumer-resource model, an e versus h trade-off can promote coexistence if the crumb picker has the higher ea/c and the cream skimmer has the higher e/hc. This may be relevant to cancer in that cancer cells with high glycolysis (cream skimmers) versus high oxidative phosphorylation (crumb pickers) may be best represented as having a low e (2 ATPs versus 36 ATPs per glucose molecule) and a low h, in addition to other trade-offs associated with a, c, or f.
Cancer may provide a good model for testing the mechanisms we have described. Cancer biologists generally do not measure the key foraging parameters of the consumer-resource model (see Amend et al., 2018; Mallin et al., 2020), but some tools for such measurement are available and can be quite sophisticated. The Seahorse XF Analyzer (de Moura and Van Houten, 2014) can analyze the extracellular flux of a small population or aliquot of cells (normal or cancerous) for oxygen, lactate production, glucose uptake, etc. While used extensively in cancer research, this technique has not yet been used specifically to measure things like a cancer cell’s functional response (H versus R) in terms of a and h. Furthermore, 2-D and 3-D culture experiments are generally run as batch chemostats where the culture medium is removed and replaced every so many days. Careful calibration with respect to cell type, cell numbers, cell proliferation rates, initial resource concentration, ending resource concentration, and pulse frequency could be used to not only estimate model parameters, but also to test for coexistence when competing multiple cell lines (Freischel et al., 2021).
Our modeling results have implications for conducting appropriate cell culture experiments. In general, culture medium, rich in fetal bovine serum and sometimes augmented with additional resources, is changed every few days. The change is often made with reference to a pH marker to ensure little change in pH via cell metabolites. Furthermore, in 2-D and some 3-D cultures, cells are passaged prior to reaching some level of confluency, meaning they may not reach a true equilibrium with their resource availabilities. As such, we may inadvertently be selecting for cream skimmers or species that speedily but inefficiently turn resources into proliferation. The timing of nutrient pulses and the passaging of cells in culture experiments may be far from what meaningfully occurs in patient tumors or mouse models. Imposing a given pulsing of nutrient renewal may change the whole ecology of the tumor, which may possibly undermine the validity of the interpretation of the results. Our modeling and that of others on consumer resource dynamics invites researchers to be mindful of the ecological conditions of their cell cultures and whether the ecology is realistic or useful for the objectives of the study.
Therefore, it is reasonable to postulate that cell culture experimentation may be used to further elucidate tangible differences in cell survival strategies. Under the lens of live cell, time lapse microscopy, one may observe how resource dynamics affect cell survival strategies and discern if cells are establishing heritable variation versus phenotypic plasticity. Non-invasive live cell microscopy is now possible within incubation conditions which can facilitate multiple generations of cellular growth to confluency, splitting and repeating. Future experiments may be designed to select for cells in resource rich and resource poor environments and observe cellular population growth upon changes in resource allocation after multiple passages.
For cancer, one often is interested in implications of ecological models for cancer therapies. We cannot provide specific recommendations in terms of cancer therapy based on the mechanisms we have described for coexistence of cream skimmer and crumb picker phenotypes. But, more broadly, it is known that tumors that are heterogeneous, including diverse cancer cell types, tend to be associated with worse prognoses. This is generally thought to result from higher levels of heritable variation among the cancer cells and hence a higher likelihood that one or several variants will be resistant to therapy. This may be so. Additionally, therapy failure may result from the consequences of using one or several therapeutic regimens to treat a community of cancer cells, not just a single cancer. If cancer cells are diversifying and filling niches, as in an ecological community, then therapy may be more effective at killing one type of cancer cell and not another. Kotler and Brown (2020) provide thoughts on how therapy strategizing should take into consideration within-patient mechanisms of coexistence among cancer cell types.
With respect to cream skimmers and crumb pickers, a variety of therapies may directly or indirectly influence competitive balance and treatment efficacy. For instance, many chemotherapies target rapidly dividing cells, which may favor crumb-picker strategies among the survivors. Radiation therapy, use of a variety of therapies, and diets that modify the tumor microenvironment (anti-angiogenics, bicarbonate therapies, fasting, ketogenic diets, etc.) may alter the amount and temporal pulsing of nutrients (Gatenby and Brown, 2020). This might harm all cancer cells or might simply tip the competitive scales away from or toward a cream skimmer. Finally, knowing that some of the tumor microenvironment is composed of coexisting cream skimmers and crumb pickers may suggest double-bind therapies (Gatenby et al., 2009; Basanta et al., 2012), where one begins with a therapy that favors one of these types and would lead to competitive exclusion of the other. Upon shifting the cancer community with the first therapy, one then would apply a second therapy to target the remaining and now dominant cancer cell type (Maley et al., 2004).
In this study, we examined temporal variation in resource abundances. Spatial variation can provide an extension of the mechanisms we discussed (Chesson, 2000a). Spatial variation can provide both additional trade-off terms (higher travel speed or lower costs can now define a cream skimmer) and an additional way that the foraging activities of consumers can create temporal variability, particularly if a consumer locally depletes resources faster than they can renew (Richards et al., 2000; Abrams and Wilson, 2004; Bolin et al., 2018). Examples include freshwater snails (Chase et al., 2001), sunbirds (Oyugi et al., 2012), and bees (Aizen et al., 2011). Furthermore, the trade-off between cream skimmers and crumb pickers can include the ability to accurately assess local resource abundances, but at a cost of supporting a higher cognitive ability (Olsson and Brown, 2010). Despite these examples from the ecosystems around us, we anticipate that this spatial form of cream skimmer/crumb picker trade-offs is less likely in cancer, given the limited motility of cancer cells relative to the scale of spatial variation in resources. Even though cancer cells have motile phenotypes (with amoeboid, pseudopodial, and lobopodial movement; Paul et al., 2017; Jun et al., 2020), they do not move very fast and are quite slow compared to free-living unicells such as yeast. Travel speeds in a 3-D collagen matrix were 4.5 μm/h and 2.1 μm/h for a “fast” mesenchymal and “slow” epithelial cancer cell type, respectively. Populations of such cancer cells can have mean diameters of 19–25 μm (Connolly et al., 2020), meaning that it could take at best 4 h to move one body length, and likely much longer. However, we could be wrong about how spatial variation is realized by cancer cells. In reality, biodiversity is affected simultaneously by more than a single mechanism of coexistence, and these operate simultaneously over many temporal and spatial scales; the relative strengths of mechanisms also no doubt vary over time, and which mechanisms are visible will depend on the scales at which we sample and analyze information (Chesson and Huntly, 1993, 1997; Chesson, 2000b, 2009; Chesson et al., 2013; Letten et al., 2018). The cancer ecosystem provides an interesting potential model in which to examine the many temporal and spatial scales and mechanisms that could simultaneously affect coexistence of cream skimmers and crumb pickers.
In conclusion, we think that a mechanism of coexistence of cream skimmers with crumb pickers has broad applicability to all of nature, including cancer. Identifying and studying this mechanism in cancer would provide (1) direct applications and tests of ecological principles in a simpler yet complete ecosystem, (2) applications of consumer-resource models to the diversification of cancer cells within and between patients, (3) explicit uptake and cost parameters that have not been, but can be, measured for cancer cells, and (4) insights to possible therapeutic implications.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Ethics Statement
The studies involving human participants were reviewed and approved by the University of South Florida Institutional Review Board; Moffitt Scientific Review Committee. The patients/participants provided their written informed consent to participate in this study.
Author Contributions
JB and NH conceived the study. AF, AM, and JB analyzed the model and conducted simulations. ML and JB provided and analyzed in vivo data. AF, AM, and ML created the figures and tables. JB, NH, and ML wrote portions of the first draft. All authors contributed substantially to revisions, contributed to the article, and approved the submitted version.
Funding
JB gratefully acknowledges funding by NIH/NCI 1U54CA 193489-01A1, “Cancer as a Complex Adaptive System,” NIH/NCI U54 Supplement, “The tumor-host evolutionary arms race.” DB and AM were partially funded by an NCI PSON U01 CA244101. The data acquisition was sponsored in part by the Moffitt Cancer Center PSOC NIH/NCI U54CA143970. Partial funding was provided by the Utah State University Ecology Center.
Conflict of Interest
ML was employed by the company Inspirata, Inc.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors thank Tatiana Miti for discussion and insights on the modeling, Jeffrey West for help with figures, and the Moffitt Tissue Core and the Analytic Microscopy Core for their expertise.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2021.697618/full#supplementary-material
References
Abrams, P. A. (1984). Variability in resource consumption rates and the coexistence of competing species. Theor. Popul. Biol. 25, 106–124. doi: 10.1016/0040-5809(84)90008-x
Abrams, P. A. (2004). When does periodic variation in resource growth allow robust coexistence of competing consumer species. Ecology 85, 372–382. doi: 10.1890/02-0684
Abrams, P. A., and Wilson, W. G. (2004). Coexistence of competitors in metacommunities due to spatial variation in resource growth rates; does R∗ predict the outcome of competition? Ecol. Lett. 7, 929–940. doi: 10.1111/j.1461-0248.2004.00644.x
Abrams, P. S., Brassil, C. E., and Holt, R. D. (2003). Dynamics and responses to mortality rates of competing predators undergoing predator-prey cycles. Theor. Popul. Biol. 64, 163–176. doi: 10.1016/S00040-5809(03)00067-4
Abrams, P. S., and Holt, R. D. (2002). The impact of consumer-resource cycles on the coexistence of competing consumers. Theor. Popul. Biol. 62, 281–295. doi: 10.1006/tpbi.2002.1614
Agrawal, G., Ramesh, A., Aishwarya, P., Sally, J., and Ravi, M. (2021). Devices and techniques used to obtain and analyze three-dimensional cell cultures. Biotechnol. Progress 2021:e3126. doi: 10.1002/btpr.3126
Aizen, M. A., Lozada, M., and Morales, C. L. (2011). Comparative nectar-foraging behaviors and efficiencies of an alien and a native bumble bee. Biol. Invas. 13, 2901–2909. doi: 10.1007/s10530-011-9972-3
Alfarouk, K. O., Ibrahim, M. E., Gatenby, R. A., and Brown, J. S. (2013). Riparian ecosystems in human cancers. Evol. Appl. 6, 46–53. doi: 10.1111/eva.12015
Amaro, A., Chiara, S., and Pfeffer, U. (2016). Molecular evolution of colorectal cancer: from multistep carcinogenesis to the big bang. Cancer Metastasis Rev. 35, 63–74. doi: 10.1007/s10555-016-9606-4
Amend, S. R., Gatenby, R. A., Pienta, K. J., and Brown, J. S. (2018). Cancer foraging ecology: diet choice, patch use, and habitat selection of cancer cells. Curr. Pathobiol. Rep. 6, 209–218. doi: 10.1007/s40139-018-0185-7
Angert, A. L., Huxman, T. E., Chesson, P., and Venable, D. L. (2009). Functional trade-offs determine species coexistence via the storage effect. Proc. Nat. Acad. Sci. U.S.A. 106, 11641–11645. doi: 10.1073/pnas.0904512106
Armstrong, R. A., and McGehee, R. P. (1976). Coexistence of two competitors on one resource. J. Theor. Biol. 56, 499–502. doi: 10.1016/s0022-5193(76)80089-6
Basanta, D., Gatenby, R. A., and Anderson, A. R. (2012). Exploiting evolution to treat drug resistance: combination therapy and the double bind. Mol. Pharm. 9, 914–921. doi: 10.1021/mp200458e
Bhattacharya, B., Mohd Omar, M. F., and Soong, R. (2016). The Warburg effect and drug resistance. Br. J. Pharm. 173, 970–979. doi: 10.1111/bph.13422
Bolin, A., Smith, H. G., Lonsdorf, E. V., and Olsson, O. (2018). Scale-dependent foraging tradeoff allows competitive coexistence. Oikos 127, 1575–1585. doi: 10.1111/oik.05072
Bonsall, M. B., Hassell, M. P., and Asefa, G. (2002). Ecological trade-offs, resource partitioning, and coexistence in a host–parasitoid assemblage. Ecology 83, 925–934. doi: 10.2307/3071902
Brown, J. H., Kodric-Brown, A., Whitham, T. G., and Bond, H. W. (1981). Competition between hummingbirds and insects for the nectar of two species of shrubs. Southwest. Nat. 26, 133–145. doi: 10.2307/3671109
Brown, J. S. (1989a). Coexistence on a seasonal resource. Am. Nat. 133, 168–182. doi: 10.1086/284908
Brown, J. S. (1989b). Desert rodent community structure: a test of four mechanisms of coexistence. Ecol. Monogr. 59, 1–20. doi: 10.2307/2937289
Brown, J. S., Kotler, B. P., and Mitchell, W. A. (1994). Foraging theory, patch use, and structure of a Negev Desert granivore community. Ecology 75, 2286–2300. doi: 10.2307/1940884
Brown, J. S., Kotler, B. P., and Porter, W. P. (2017). How foraging allometries and resource dynamics could explain Bergmann’s rule and the body-size diet relationship in mammals. Oikos 126, 224–230.
Burdall, S. E., Hanby, A. M., Lansdown, M. R., and Speirs, V. (2003). Breast cancer cell lines: friend or foe? Breast Cancer Res. 5, 1–7.
Cárdenas-Navia, L. I., Mace, D., Richardson, R. A., Wilson, D. F., Shan, S., and Dewhirst, M. W. (2008). The pervasive presence of fluctuating oxygenation in tumors. Cancer Res. 68, 5812–5819. doi: 10.1158/0008-5472.CAN-07-6387
Carvalho, M. R., Lima, D., Reis, R. L., Correlo, V. M., and Oliveira, J. M. (2015). Evaluating biomaterial-and microfluidic-based 3D tumor models. Trends Biotech. 33, 667–678. doi: 10.1016/j.tibtech.2015.09.009
Cermeno, P., Lee, J.-B., Wyman, K., Schofield, O., and Falkowski, P. G. (2011). Competitive dynamics in two species of marine phytoplankton under non-equilibrium conditions. Mar. Ecol. Prog. Ser. 429, 19–28. doi: 10.3354/meps09088
Chase, J. M., Wilson, W. G., and Richards, S. A. (2001). Foraging trade-offs and resource patchiness: theory and experiments with a freshwater snail community. Ecol. Lett. 4, 304–312. doi: 10.1046/j.1461-0248.2001.00216.x
Chen, C.-L., Chu, J.-S., Su, W.-C., Huang, S.-C., and Lee, W.-Y. (2010). Hypoxia and metabolic phenotypes during breast carcinogenesis: expression of HIF-1α, GLUT1, and CAIX. Virchows Arch. 457, 53–61. doi: 10.1007/s00428-010-0938-0
Chen, Z., Ai, L., Mboge, M. Y., Tu, C., McKenna, R., Brown, K. D., et al. (2018). Differential expression and function of CAIX and CAXII in breast cancer: a comparison between tumorgraft models and cells. PLoS One 13:e0199476. doi: 10.1371/journal.pone.0199476
Chesson, P. (1994). Multispecies competition in variable environments. Theor. Popul. Biol 45, 227–276. doi: 10.1006/tpbi.1994.1013
Chesson, P. (2000a). General theory of competitive coexistence in spatially-varying environments. Theor. Popul. Biol. 58, 211–237. doi: 10.1006/tpbi.2000.1486
Chesson, P. (2009). Scale transition theory with special reference to species coexistence in a variable environment. J. Biol. Dyn. 3, 149–163. doi: 10.1080/17513750802585491
Chesson, P., Gebauer, R. L. E., Schwinning, S., Huntly, N., Weigand, K., Ernest, M. S. K., et al. (2004). Resource pulses, species interactions, and diversity maintenance in arid and semi-arid environments. Oecologia 141, 236–253. doi: 10.1007/s00442-004-1551-1
Chesson, P., and Huntly, N. (1988). Community consequences of life history traits in a variable environment. Ann. Zool. Fennici 25, 5–16.
Chesson, P., and Huntly, N. (1989). How do short-term instabilities affect long-term community dynamics? Tree 4, 293–298. doi: 10.1016/0169-5347(89)90024-4
Chesson, P., and Huntly, N. (1993). Temporal hierarchies of variation and the maintenance of diversity. Plant Species Biol. 8, 195–206. doi: 10.1111/j.1442-1984.1993.tb00070.x
Chesson, P., and Huntly, N. (1997). The roles of harsh and fluctuating conditions in the dynamics of ecological communities. Am. Nat. 150, 519–553. doi: 10.1086/286080
Chesson, P., Huntly, N. J., Roxburgh, S. H., Pantastico-Caldas, M., and Facelli, J. M. (2013). “The storage effect: definitions and tests in two plant communities,” in Temporal Dynamics and Ecological Process, eds C. Kelly, M. Bowler, and G. Fox (New York, NY: Cambridge University Press), 11–40. doi: 10.1017/cbo9781139048170.003
Chesson, P., and Warner, R. R. (1981). Environmental variability promotes coexistence in lottery competitive systems. Am. Nat. 117, 923–943. doi: 10.1086/283778
Chiche, J., Ilc, K., Laferrière, J., Trottier, E., Dayan, F., Mazure, N. M., et al. (2009). Hypoxia-inducible carbonic anhydrase IX and XII promote tumor cell growth by counteracting acidosis through the regulation of the intracellular pH. Cancer Res. 69, 358–368. doi: 10.1158/0008-5472.CAN-08-2470
Commander, R., Wei, C., Sharma, A., Mouw, J. K., Burton, L. J., Summerbell, E., et al. (2020). Subpopulation targeting of pyruvate dehydrogenase and GLUT1 decouples metabolic heterogeneity during collective cancer cell invasion. Nat. Commun. 11:1533. doi: 10.1038/s41467-020-15219-7
Connolly, S., McGourty, K., and Newport, D. (2020). The in vitro inertial positions and viability of cells in suspension under different in vivo flow conditions. Sci. Rep. 10:1711. doi: 10.1038/s41598-020-58161-w
de Moura, M. B., and Van Houten, B. (2014). “Bioenergetic analysis of intact mammalian cells using the Seahorse XF24 Extracellular Flux analyzer and a luciferase ATP assay,” in Molecular Toxicology Protocols, eds P. Keohavong and S. G. Grant (Totowa, NJ: Humana Press), 589–602. doi: 10.1007/978-1-62703-739-6_40
Descamps-Julien, B., and Gonzalez, A. (2005). Stable coexistence in a fluctuating environment: an experimental demonstration. Ecology 86, 2815–2824. doi: 10.1890/04-1700
Dewhirst, M. W. (2009). Relationships between cycling hypoxia, HIF-1, angiogenesis and oxidative stress. Radiat. Res. 172, 653–665. doi: 10.1667/rr1926.1
Di Gregorio, A., Bowling, S., and Rodriguez, T. A. (2016). Cell competition and its role in the regulation of cell fitness from development to cancer. Dev. Cell 38, 621–634. doi: 10.1016/j/devcel.2016.08.012
Dukas, R., and Kamil, A. C. (2001). Limited attention: the constraint underlying search image. Behav. Ecol. 12, 192–199. doi: 10.1093/beheco/12.2.192
Epstein, T., Gatenby, R. A., and Brown, J. S. (2017). The Warburg effect as an adaptation of cancer cells to rapid fluctuations in energy demand. PLoS One 12:e0185085. doi: 10.1371/journal.pone.0185085
Evans, R. D., and Black, R. A. (1993). Growth, photosynthesis, and resource investment for vegetative and reproductive modules of Artemisia tridentata. Ecology 74, 1516–1528. doi: 10.2307/1940079
Freischel, A. R., Damaghi, M., Cunningham, J. J., Ibrahim-Hashim, A., Gillies, R. J., Gatenby, R. A., et al. (2021). Frequency-dependent interactions determine outcome of competition between breat cancer cell lines. Sci. Rep. 11:4908. doi: 10.1038/s41598-021-84406-3
Gatenbee, C. D., Minor, E. S., Slebos, R. J., Chung, C. H., and Anderson, A. R. (2020). Histoecology: applying ecological principles and approaches to describe and predict tumor ecosystem dynamics across space and time. Cancer Control 27:1073274820946804.
Gatenby, R. A., Brown, J., and Vincent, T. (2009). Lessons from applied ecology: cancer control using an evolutionary double bind. Cancer Res. 69, 7499–7502. doi: 10.1158/0008-5472.can-09-1354
Gatenby, R. A., and Brown, J. S. (2020). Integrating evolutionary dynamics into cancer therapy. Nat. Rev. Clin. Oncol. 17, 675–686. doi: 10.1038/s41571-020-0411-1
Gillies, R. J., Brown, J. S., Anderson, A. R. A., and Gatenby, R. A. (2018). Ecoevolutionary causes and consequences of temporal changes in intratumoural blood flow. Nat. Rev. Cancer 18, 576–585. doi: 10.1038/s41568-018-0030-7
Gillies, R. J., and Gatenby, R. A. (2007). Adaptive landscapes and emergent phenotypes: why do cancers have high glycolysis? J. Bioenerg. Biomembr. 39, 251–257. doi: 10.1007/s10863-9085-y
Grover, J. P. (1990). Resource competition in a variable environment: phytoplankton growing according to Monod’s model. Am. Nat. 136, 771–789. doi: 10.1086/285131
Hallett, L. M., Shoemaker, L. G., White, K. T., and Suding, K. N. (2019). Rainfall variability maintains grass-forb species coexistence. Ecol. Lett. 22, 1658–1667. doi: 10.1111/ele.13341
Hardin, G. (1961). The competitive exclusion principle. Science 131, 1292–1297. doi: 10.1126/science.131.3409.1292
Hoefflin, R., Lahrmann, B., Warsow, G., Hübschmann, D., Spath, C., Walter, B., et al. (2016). Spatial niche formation but not malignant progression is a driving force for intratumoural heterogeneity. Nat. Commun. 7:ncomms11845.
Holling, C. S. (1959). Some characteristics of simple types of predation and parasitism. Can. Entom. 91, 385–398. doi: 10.4039/ent91385-7
Huisman, J., Johansson, A. M., Folmer, E. O., and Weissing, F. J. (2001). Towards a solution of the plankton paradox: the importance of physiology and life history. Ecol. Lett. 4, 408–411. doi: 10.1046/j.1461-0248.2001.00256.x
Huisman, J., and Weissing, F. J. (1999). Biodiversity of plankton by species oscillations and chaos. Nature 402, 407–410. doi: 10.1038/46540
Huntly, N. (1991). Herbivores and the dynamics of communities and ecosystems. Ann. Rev. Ecol. Syst. 22, 477–503. doi: 10.1146/annurev.es.22.110191.002401
Ilie, M. I., Hofman, V., Ortholan, C., Ammadi, R. E., Bonnetaud, C., Havet, K., et al. (2011). Overexpression of carbonic anhydrase XII in tissues from resectable non-small cell lung cancers is a biomarker of good prognosis. Int. J. Cancer 128, 1614–1623. doi: 10.1002/ijc.25491
Iravani, A., Mitchell, C., Akhurst, T., Sandhu, S., Hofman, M. S., and Hicks, R. J. (2021). Molecular imaging of neuroendocrine differentiation of prostate cancer: a case series. Clin. Genitourin. Cancer 19, e200–e205. doi: 10.1016/j.dgc.2021.01.008
Jones, M., Mandelik, Y., and Dayan, T. (2001). Coexistence of temporally partitioned spiny mice: roles of habitat structure and foraging behavior. Ecology 82, 2164–2176. doi: 10.1890/0012-9658(2001)082[2164:cotpsm]2.0.co;2
Jun, B. H., Guo, T., Libring, S., Chanda, M. K., Paez, J. S., Shinde, A., et al. (2020). Fibronectin-expressing mesenchymal tumor cells promote breast cancer metastasis. Cancers 12:2553. doi: 10.3390/cancers12092553
Kaidi, A., Williams, A. C., and Paraskeva, C. (2007). Interaction between β-catenin and HIF-1 promotes cellular adaptation to hypoxia. Nat. Cell Biol. 9, 210–217. doi: 10.1038/ncb1534
Kareva, I., and Brown, J. S. (2021). Estrogen as an essential resource and the coexistence of ER+ and ER- cancer cells. Front. Ecol. Evol. 9:673082. doi: 10.3389/fevo.2021.673082
Koch, A. L. (1974). Coexistence resulting from an alternation of density dependent and density independent growth. J. Theor. Biol. 44, 373–386. doi: 10.1016/0022-5193(74)90168-4
Kondo, H., Ratcliffe, C. D., Hooper, S., Ellis, J., MacRae, J. I., Hennequart, M., et al. (2021). Single-cell resolved imaging reveals intra-tumor heterogeneity in glycolysis, transitions between metabolic states, and their regulatory mechanisms. Cell Rep. 34:108750. doi: 10.1016/j/celrep/2021/108750
Kotler, B. P., and Brown, J. S. (1988). Environmental heterogeneity and the coexistence of desert rodents. Ann. Rev. Ecol. Syst. 19, 281–307. doi: 10.1146/annurev.es.19.110188.001433
Kotler, B. P., and Brown, J. S. (1990). Rates of seed harvest by two species of gerbilline rodents. J. Mamm. 71, 591–596. doi: 10.2307/1381798
Kotler, B. P., and Brown, J. S. (2020). Cancer community ecology. Cancer Control 27:1073274820951776. doi: 10.1177/1073274820951776
Kotler, B. P., Brown, J. S., and Subach, A. (1993). Mechanisms of species coexistence of optimal foragers: temporal partitioning by two species of sand dune gerbils. Oikos 67, 548–556. doi: 10.2307/3545367
Lanning, M., Wang, L., Benson, M., Zhang, Q., and Novick, K. (2020). Canopy isotopic investigation reveals different water uptake dynamics of maples and oaks. Phytochemistry 175:112389. doi: 10.1016/j.phytochem.2020.112389
Letten, A. D., Dhami, M. K., Je, P.-J., and Fukami, T. (2018). Species coexistence through simultaneous fluctuation-dependent mechanisms. Proc. Natl. Acad. Sci. U.S.A. 115, 6745–6750. doi: 10.1073/pnas.1801846115
Levins, R. (1979). Coexistence in a variable environment. Am. Nat. 114, 765–783. doi: 10.1086/283527
Limousin, J. M., Yepez, E. A., McDowell, N. G., and Pockman, W. T. (2015). Convergence in resource use efficiency across trees with differing hydraulic strategies in response to ecosystem precipitation manipulation. Func. Ecol. 29, 1125–1136. doi: 10.1111/1365-2435.12426
Lisan, A., and Langhans, S. A. (2015). Cancer as a channelopathy: ion channels and pumps in tumor development and progression. Front. Cell. Neurosci. 9:86. doi: 10.3389/fncel.2015.00086
Litchman, E., and Klausmeier, C. A. (2001). Competition of phytoplankton under fluctuating light. Am. Nat. 157, 170–187. doi: 10.2307/3079257
Litchman, E., and Klausmeier, C. A. (2008). Trait-based community ecology of phytoplankton. Ann. Rev. Ecol. Syst. 39, 615–639. doi: 10.1146/annurev.ecolsus.39.110707.173549
Lloyd, M. C., Cunningham, J. J., Bui, M. M., Gillies, R. J., Brown, J. S., and Gatenby, R. A. (2016). Darwinian dynamics of intratumoral heterogeneity: not solely random mutations but also variable environmental selection forces. Cancer Res. 76, 3136–3144. doi: 10.1158/0008-5472.CAN-15-2962
Lo, Y. H., Karlsson, K., and Kuo, C. J. (2020). Applications of organoids for cancer biology and precision medicine. Nat. Cancer 1, 761–773. doi: 10.1038/s43018-020-0102-y
Loponte, S., Lovisa, S., Deem, A. K., Carugo, A., and Viale, A. (2019). The many facets of tumor heterogeneity: is metabolism lagging behind? Cancers 11:1574. doi: 10.390/cancers11101574
Maley, C. C., Reid, B. J., and Forrest, S. (2004). Cancer prevention strategies that address the evolutionary dynamics of neoplastic cells: simulating benign cell boosters and selection for chemosensitivity. Cancer Epidemiol. Prevent. Biomarkers 13, 1375–1384.
Mallin, M. M., Pienta, K. J., and Amend, S. R. (2020). Cancer cell foraging to explain bone-specific metastatic progression. Bone 2020:115788. doi: 10.1016/j.bone.2020.115788
Marusyk, A., and Polyak, K. (2010). Tumor heterogeneity: causes and consequences. Biochim. Biophys. Acta. 1805, 105–117. doi: 10.1016/j.bbcan.2009.11.002
Mboge, M. Y., Chen, Z., Khokhar, D., Wolff, A., Ai, L., Heldermon, C. D., et al. (2019). A non-catalytic function of carbonic anhydrase IX contributes to the glycolytic phenotype and pH regulation in human breast cancer cells. Biochem. J. 476, 1497–1513. doi: 10.1042/BCH20190177
McMeans, B. C., McCann, K. S., Guzzo, M. M., Bartley, T. J., Bieg, C., Blanchfield, P. J., et al. (2020). Winter in water: differential responses and the maintenance of biodiversity. Ecol. Lett. 23, 922–938. doi: 10.1111/ele.13504
McNickle, G. G., Wallace, C., and Baltzer, J. L. (2016). Why do mosses have height? Moss production as a tragedy of the commons game. Evol. Ecol. Res. 17, 75–93.
Michiels, C., Tellier, C., and Feron, O. (2016). Cycling hypoxia: a key feature of the tumor microenvironment. Biochim. Biophys. Acta. 1866, 78–86. doi: 10.1016/j.bbcan.2016.06.004
Miller, A. K., Brown, J. S., Basanta, D., and Huntly, N. (2020). What is the storage effect, why should it occur in cancers, and how can it inform therapy? Cancer Control 27:1073274820941968. doi: 10.1177/1073274820941068
Miller, A. K., Brown, J. S., Enderling, H., Basanta, D., and Whelan, C. J. (2021). The evolutionary ecology of dormancy in nature and in cancer. Front. Ecol. Evol. 9:676802. doi: 10.2289/fevo.2021.676802
Miller-Rushing, A. J., Primack, R. B., Templer, P. H., Rathbone, S., and Mukunda, S. (2009). Long-term relationships among atmospheric CO2, stomata, and intrinsic water use efficiency in individual trees. Am. J. Bot. 96, 1779–1786. doi: 10.3732/ajb.0800410
Morozov, A. Y. (2010). Emergence of Holling type III zooplankton functional response: bringing together field evidence and mathematical modelling. J. Theor. Biol. 265, 45–54. doi: 10.1016/j.jtbi.2010.04.016
Morris, D. W. (2003). Toward an ecological synthesis: a case for habitat selection. Oecologia 136, 1–13. doi: 10.1007/s00442-003-1241-4
Neftel, C., Laffy, J., Filbin, M. G., Hara, T., Shore, M. E., Rahme, G. J., et al. (2019). An integrative model of cellular states, plasticity, and genetics for glioblastoma. Cell 178, 835–849.
Oke, T. A., and Turetsky, M. R. (2020). Evaluating Sphagnum traits in the context of resource economics and optimal partitioning theories. Oikos 129, 1204–1215. doi: 10.1111/oik.07195
Olsson, O., and Brown, J. S. (2010). Smart, smarter, smartest: foraging information states and coexistence. Oikos 119, 292–303. doi: 10.1111/j.1600-0706.2009.17784.x
Oyugi, J. O., Brown, J. S., and Whelan, C. J. (2012). Foraging behavior and coexistence of two sunbird species in a Kenyan woodland. Biotropica 44, 262–269. doi: 10.1111/j.1744-7429.2011.00785.x
Pachepsky, E., Nisbet, R. M., and Murdoch, W. W. (2008). Between discrete and continuous: consumer–resource dynamics with synchronized reproduction. Ecology 89, 280–288. doi: 10.1890/07-0641.1
Parker, T. M., Henriques, V., Beltran, A., Nakshatri, H., and Gogna, R. (2020). Cell competition and tumor heterogeneity. Sem. Cancer Biol. 63, 1–10. doi: 10.1016/j.semcan.2019.09.003
Paul, C. D., Mistriotis, P., and Konstantopoulos, K. (2017). Cancer cell motility: lessons from migration in confined spaces. Nat. Rev. Cancer 17, 131–140. doi: 10.1038/nrc.2016.123
Perfahl, H., Byrne, H. M., Chen, T., Estrella, V., Alarcon, T., Lapin, A., et al. (2013). “Multiscale modelling of angiogenesis and vascular tumour growth,” in Micro and Nano Flow Systems for Bioanalysis (Advanced Materials, Methods, and Devices), vol. 2, eds. M. Collins, and C. Koenig (New York, NY: Springer), 29–48. doi: 10.1007/978-1-4614-4376-6_3
Pressley, M., Gallaher, J. A., Brown, J. S., Tomaszewski, M. R., Borad, P., Damaghi, M., et al. (2021). Cycling hypoxia selects for constitutive HIF stabilization. Sci. Rep. 11:5777. doi: 10.1038/s414598-021-85184-8
Rademakers, S. E., Lok, J., van der Kogel, A. J., Bussink, J., and Kaanders, J. H. A. M. (2011). Metabolic markers in relation to hypoxia; staining patterns and colocalization of pimonidazole, HIF-1α, CAIX, LDH-5, GLUT-1, MCT1 and MCT4. BMC Cancer 11:167. doi: 10.1186/1471-2407-11-167
Ravi, M., Paramesh, V., Kaviya, S. R., Anuradha, E., and Solomon, F. P. (2015). 3D cell culture systems: advantages and applications. J. Cell. Phys. 230, 16–26. doi: 10.1002/jcp.24683
Richards, S. A., Nisbet, R. M., Wilson, W. G., and Possingham, H. P. (2000). Grazers and diggers: exploitation competition and coexistence among foragers with different feeding strategies on a single resource. Am. Nat. 155, 266–279. doi: 10.1086/303316
Robertson-Tessi, M., Gillies, R. J., Gatenby, R. A., and Anderson, A. R. A. (2015). Impact of metabolic heterogeneity on tumor growth, invasion, and treatment outcomes. Cancer Res. 75, 1567–1579. doi: 10.1158/0008-5472.CAN-14-1428
Salcher, M. M. (2014). Same same but different: ecological niche partitioning of planktonic freshwater prokaryotes. J. Limnol. 73, 74–87.
Sasmita, A. O., Wong, Y. P., and Ling, A. P. K. (2018). Biomarkers and therapeutic advances in glioblastoma multiforme. Asia Pac. J. Clin. Oncol. 14, 40–51. doi: 10.1111/ajco.12756
Saxena, K., and Jolly, M. K. (2019). Acute vs. chronic vs. cyclic hypoxia: their differential dynamics, molecular mechanisms, and effects on tumor progression. Biomolecules 9:339. doi: 10.3390/biom9080339
Schaffer, W. M., Jensen, D. B., Hobbs, D. E., Gurevitch, J., Todd, J. R., and Schaffer, M. V. (1979). Competition, foraging energetics, and the cost of sociality in three species of bees. Ecology 60, 976–987. doi: 10.2307/1936866
Schoener, T. W. (1974). Resource partitioning in ecological communities. Science 5, 27–39. doi: 10.1126/science.185.4145.27
Schuster, B., Junkin, M., Kashaf, S. S., Romero-Calvo, I., Kirby, K., Matthews, J., et al. (2020). Automated microfluidic platform for dynamic and combinatorial drug screening of tumor organoids. Nat. Commun. 11:5271.
Schwinning, S., Litvak, M. E., Pockman, W. T., Pangle, R. E., Fox, A. M., Huang, C. W., et al. (2020). A 3-dimensional model of Pinus edulis and Juniperus monosperma root distributions in New Mexico: implications for soil water dynamics. Plant Soil 450, 337–355. doi: 10.1007/s11104-020-04446-y
Shembrey, C., Huntington, N. D., and Hollande, F. (2019). Impact of tumor and immunological heterogeneity on the anti-cancer immune response. Cancers 11:1217. doi: 10.3390/cancers11091217
Stewart, F. M., and Levin, B. R. (1973). Partitioning of resources and the outcome of interspecific competition: a model and some general considerations. Am. Nat. 954, 171–198. doi: 10.1086/282825
Valcourt, J. R., Lemons, J. M., Haley, E. M., Kojima, M., Demuren, O. O., and Coller, H. A. (2012). Staying alive: metabolic adaptations to quiescence. Cell Cycle 11, 1680–1696. doi: 10.4161/cc.19879
Venner, S., Pélisson, P. F., Bel-Venner, M. C., Débias, F., Rajon, E., and Menu, F. (2011). Coexistence of insect species competing for a pulsed resource: toward a unified theory of biodiversity in fluctuating environments. PLoS One 6:e18039. doi: 10.1371/journal.pone.0018039
Verhaak, R. G. W., Hoadley, K. A., and Purdom, E. (2010). Integrated genomic analysis identifies clinically relevant subtypes of glioblastoma characterized by abnormalities in PDGFRA, IDH1, EGFR, and NF1. Cancer Cell 17, 98–110. doi: 10.1016/j.ccr.2009.12.020
Vincent, T. L. S., Scheel, D., Brown, J. S., and Vincent, T. L. (1996). Trade-offs and coexistence in consumer-resource models: it all depends on what and where you eat. Am. Nat. 148, 1038–1058. doi: 10.1086/285970
Werner, E. E., and Hall, D. J. (1977). Competition and habitat shift in two sunfishes (Centrarchidae). Ecology 58, 869–876. doi: 10.2307/1936222
West, A. G., Hultine, K. R., Jackson, T. L., and Ehleringer, J. R. (2007). Differential summer water use by Pinus edulis and Juniperus osteosperma reflects contrasting hydraulic characteristics. Tree Phys. 27, 1711–1720. doi: 10.1093/treephys/27.12.1711
White, E. Z., Pennant, N. M., Carter, J. R., Hawsawi, O., Odero-Marah, V., and Hinton, C. V. (2020). Serum deprivation initiates adaptation and survival to oxidative stress in prostate cancer cells. Sci. Rep. 10:12505. doi: 10.1038/s41598-020-68668-x
Wilson, W. G., Osenberg, C. W., Schmitt, R. J., and Nisbet, R. M. (1999). Complementary foraging behaviors allow coexistence of two consumers. Ecology 80, 2358–2372. doi: 10.1890/0012-9658(1999)080[2358:cfbaco]2.0.co;2
Wolfe, J. O. (1996). Coexistence of white-footed mice and deer mice may be mediated by fluctuating environmental conditions. Oecologia 108, 529–533. doi: 10.1007/bf00333730
Wooten, D. J., Groves, S. M., Tyson, D. R., Liu, Q., Lim, J. S., Albert, R., et al. (2019). Systems-level network modeling of small cell lung cancer subtypes identifies master regulators and destabilizers. PLoS Comp. Biol 15:e1007343. doi: 10.1371/journal.pcbi.1007343
Xiao, X., and Fussmann, G. F. (2013). Armstrong-McGehee mechanism revisited: competitive exclusion and coexistence of nonlinear consumers. J. Theor. Biol. 339, 26–35. doi: 10.1016/j.jtbi.2013.05.025
Yang, Y., Sun, M., Wang, L., and Jiao, B. (2013). HIFs, angiogenesis, and cancer. J. Cell. Biochem. 114, 967–974. doi: 10.1002/jcb.24438
Yeo, S. K., and Guan, J. L. (2017). Breast cancer: multiple subtypes within a tumor? Trends Cancer 3, 753–760. doi: 10.1016/j.trecan.2017.09.001
Younes, M., Brown, R. W., Stephenson, M., Gondo, M., and Cagle, P. T. (1997). Overexpression of Glut1 and Glut3 in stage I nonsmall cell lung carcinoma is associated with poor survival. Cancer 80, 1046–1051. doi: 10.1002/(sici)1097-0142(19970915)80:6<1046::aid-cncr6>3.0.co;2-7
Yu, M., Yongzhi, H., Chen, S., Luo, X., Lin, Y., Zhou, Y., et al. (2017). The prognostic value of GLUT1 in cancers: a systematic review and meta-analysis. Oncotarget 8, 43356–43367. doi: 10.18632/oncotarget.17445
Keywords: coexistence, biodiversity, foraging behavior, fixed and variable costs, fluctuating environment, cream skimmer, crumb picker, non-equilibrium coexistence
Citation: Huntly N, Freischel AR, Miller AK, Lloyd MC, Basanta D and Brown JS (2021) Coexistence of “Cream Skimmer” and “Crumb Picker” Phenotypes in Nature and in Cancer. Front. Ecol. Evol. 9:697618. doi: 10.3389/fevo.2021.697618
Received: 20 April 2021; Accepted: 03 September 2021;
Published: 29 September 2021.
Edited by:
Jason Somarelli, Duke University Medical Center, United StatesReviewed by:
Andrew Letten, The University of Queensland, AustraliaFrancisco Garcia-Gonzalez, Estación Biológica de Doñana (EBD), Spain
Copyright © 2021 Huntly, Freischel, Miller, Lloyd, Basanta and Brown. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nancy Huntly, bmFuY3kuaHVudGx5QHVzdS5lZHU=
 Nancy Huntly
Nancy Huntly Audrey R. Freischel
Audrey R. Freischel Anna K. Miller
Anna K. Miller Mark C. Lloyd
Mark C. Lloyd David Basanta2
David Basanta2 Joel S. Brown
Joel S. Brown