- 1Department of Biology, University of Maryland, College Park, MD, United States
- 2Biodesign Institute, Arizona State University, Tempe, AZ, United States
Perception is central to the survival of an individual for many reasons, especially as it affects the ability to gather resources. Consequently, costs associated with perception are partially shaped by resource availability. Understanding the interplay of environmental factors (such as the density and distribution of resources) with species-specific factors (such as growth rate, mutation, and metabolic costs) allows the exploration of possible trajectories by which perception may evolve. Here, we used an agent-based foraging model with a context-dependent movement strategy in which each agent switches between undirected and directed movement based on its perception of resources. This switching behavior is central to our goal of exploring how environmental and species-specific factors determine the evolution and maintenance of perception in an ecological system. We observed a non-linear response in the evolved perceptual ranges as a function of parameters in our model. Overall, we identified two groups of parameters, one of which promotes evolution of perception and another group that restricts it. We found that resource density, basal energy cost, perceptual cost and mutation rate were the best predictors of the resultant perceptual range distribution, but detailed exploration indicated that individual parameters affect different parts of the distribution in different ways.
Introduction
Locating resources and gathering information about immediate surroundings are crucial for the survival of an individual, and this makes perception an important nexus for behavior, ecology and evolution. What an individual can detect and respond to is dictated by its perceptual or sensory systems and how these systems are constructed and constrained over species-specific evolution (Stevens, 2013). This evolution of the perceptual apparatus is regulated by interactions of the species with its immediate environment and via inter and intra-specific interactions. Such evolution can sometimes completely redefine the ecological dynamics of a system. This is particularly apparent in the evolution of sensory systems, in tandem with major evolutionary transitions and species radiations (Plotnick et al., 2010). For example, a marked increase in spatial heterogeneity of resources and evolution of mobile organisms as well as new ecological lifestyles changed the information landscape of the Cambrian period. This ushered in a major sensory transition, along with major changes in feeding and predation modes (Dzik, 2005; Plotnick et al., 2010).
Possessing greater sensory input is always valuable as it gives a better model of the surrounding world. However, the sensory apparatus is not without its context and costs: changes in habitat and surrounding environmental conditions can force organisms to adapt their perceptual apparatus due to inherent biological costs (Laughlin, 2001; Niven and Laughlin, 2008; Stevens, 2013). Loss of eyes in animals dwelling in caves or other light-limited habitats has been widely documented, especially various forms of cavefish (Jeffery, 2009; Protas and Jeffery, 2012; Wilkens and Strecker, 2017). A similar loss of visual acuity has been studied in Drosophila across multiple generations in captivity (Tan et al., 2005). Likewise, researchers have investigated the weakening of electric organ discharges in electric fish in oxygen-stressed habitats (Salazar and Stoddard, 2008; Stoddard and Salazar, 2011), which may represent an adaptation for saving energy under adverse conditions. Clearly, interactions between species-specific and environmental factors mold the sensory systems of organisms and how they relate to movement and behavior. A theoretical framework that facilitates systematic exploration of these costs and benefits would help clarify the process of perceptual evolution.
Extensive theoretical and empirical work has been undertaken to explore the interplay of movement and perception at various spatio-temporal scales, especially in the context of foraging (Hastings, 1983; Johnson and Gaines, 1990; McPeek and Holt, 1992; Perry and Pianka, 1997; Farnsworth and Beecham, 1999; Beecham, 2001; Cressman and Křivan, 2006; Cantrell et al., 2010; Averill et al., 2012; Bracis et al., 2015). Among the theoretical approaches, there is a great amount of variation in the assumptions regarding information gathering capabilities of individuals based on the mathematical frameworks that the researchers decide to use (Fagan et al., 2017; O’Dwyer, 2020; Martinez-Garcia et al., 2020). Patch models generally assume omniscience about the environment (Fretwell, 1969; Pyke, 1984; Pleasants, 1989; Houston and McNamara, 1999) whereas other modeling frameworks allow for complete environmental information to be learned through sampling (Cressman and Křivan, 2006). In contrast, many partial differential equation (PDE) (Okubo, 1980; Cosner, 2005; Cantrell et al., 2006) models typically make foragers follow a resource gradient, with movement dependent on purely local information from their immediate vicinity. Certain integrodifference/integrodifferential equation (IDE) frameworks, although permitting for extensive non-local movement (through longer-tailed dispersal kernels), allow for the perception of strictly local information, while some other IDE models use patch-level knowledge or full-omniscience (Cosner et al., 2012). The same is true for many agent-based models where agents get information on a strictly local scale (either spatially, temporally or spatio-temporally; i.e., information only about where they currently exist in a model scenario) and do not have access to any form of non-local knowledge in the context of foraging and decision-making (Ranta et al., 2000; Matsumura et al., 2010; Fraker and Luttbeg, 2012; Nabe-Nielsen et al., 2013; Swain and Fagan, 2019). Between these extremes, only a few formalisms exploit the concept of limited but possibly non-local information (Berec, 2000; Hillen et al., 2007; Barnett and Moorcroft, 2008; Martínez-García et al., 2013; Fagan et al., 2017). Using these frameworks, past research has described information gathering and resource tracking in static landscapes (Viswanathan et al., 1999; Edwards et al., 2007; Vergassola et al., 2007; Bartumeus and Levin, 2008; Hein and McKinley, 2012), but equivalent questions in dynamic landscapes remain less explored (but see Torney et al., 2011; Berdahl et al., 2013).
The limits of information gathering and perception lead to alterations in behavior and movement strategies over different spatio-temporal scales, as outlined by previous research (Zollner and Lima, 1999; Zollner, 2000; Gehring and Swihart, 2003; Calabrese and Fagan, 2004; Olden et al., 2004; Prevedello et al., 2011; Fletcher et al., 2013; Fagan et al., 2019). This limit—the maximum distance at which landscape elements can be identified by an organism—is often called its perceptual range (Fagan et al., 2017). The spatial size of the perceptual range varies widely, with magnitudes depending on species, individual state, sensory mode, and spatial context (Zollner and Lima, 1997; Zollner, 2000; Mech and Zollner, 2002; Fletcher et al., 2013). Encoding and exploration of perceptual ranges in ecological systems has been done more through agent-based models (Ranta et al., 2000; Matsumura et al., 2010; Fraker and Luttbeg, 2012) than through equation-based frameworks (Skalski and Gilliam, 2003; Tyson et al., 2011; Martinez-Garcia et al., 2020) due to the complexity of incorporating them in the latter (Fagan et al., 2019). Both modeling frameworks have provided important clues about the interplay among resource detection, movement patterns, swarming dynamics and other phenomena (Grünbaum and Okubo, 1994; Berec, 2000; Barnett and Moorcroft, 2008; Martínez-García et al., 2013; Fagan et al., 2017, 2019), but most of these previous models have focused primarily on changes in perceptual range and how it affects population-level performance. In this work, our objective is instead to explore what environmental and species-specific factors might result in the emergence, evolution, and maintenance of perception in a species. In other words, we are more interested in the evolutionary timescale, rather than the near-term ecology of the system.
We use a simple agent-based model in a semi-dynamic resource system to understand how the interplay of environmental factors with species-specific factors can allow for population trajectories by which perception may evolve. Environmental factors such as the availability and heterogeneity of resources help regulate the range of perception in organisms as well as its usage and efficacy (Plotnick et al., 2010; Stevens, 2013). Metabolic costs to maintain sensory apparatus as well as basal energy requirement and reproductive costs can affect the perceptual range and its evolution in organisms (Laughlin, 2001; Niven and Laughlin, 2008; Stevens, 2013; Tan et al., 2005). We introduce a basic set of parameters in our model that represent these environmental and species-specific factors, but we avoid bringing in too many details to balance biological realism with breadth of applicability to a variety of organisms with different sensory modalities. More such details can be added above the current model in further explorations of the work.
We incorporate a context-dependent movement strategy for each agent where it switches between undirected (random walk) and directed (advective) movement based on its perception of resources. Behavioral switching has been demonstrated in a wide range of species at different spatial scales of foraging, such as opossums (Prevedello et al., 2011), woodpeckers (Vergara et al., 2019), tuna (Newlands et al., 2004), and even mosquitoes (Raji and DeGennaro, 2017). Such a switching pattern has been shown to better describe empirical behavioral patterns in bees and caribou than a more straightforward blending of movement strategies (Tyson et al., 2011). We also opted to use a movement model that involves switching between random walk and advective motion because models with such switching have already identified a clear role for non-zero perceptual ranges to enhance foraging success (Fagan et al., 2019). Alternative models of movement exist certainly, such as ballistic movement for agents with no information and increased tortuosity when near resources (see Gurarie and Ovaskainen, 2013; Bartumeus et al., 2016), but these and other foraging models are frequently couched in terms of what is optimal (i.e., what strategy or combination of strategies will yield the greatest uptake of resources), which provides a poor baseline for consideration of issues hypothesized to occur early in evolutionary history. To supply additional biological realism, we investigated evolution in a reproductive context, imposing limits on the amount of resource an individual can gather and store and exploring a wide range of initial conditions and parametric scenarios.
Focusing on the evolved distribution of perceptual range, we assigned the parameters in the model to two categories based on their effects: activation and deactivation parameters (i.e., parameters which generally promote evolution of perception and that restrict it, respectively, in a simulated population). We observed a non-linear, non-monotonic response as a function of resource density, which interacts with other parameters. Resources play a major role in determining the stability of equilibria of the system, controlling whether or not perceptual ranges emerge at all. In addition, we found that the system’s behavior mirrored some biological aspects, with the evolution of perceptual abilities depending on their costs.
Materials and Methods
Model Description
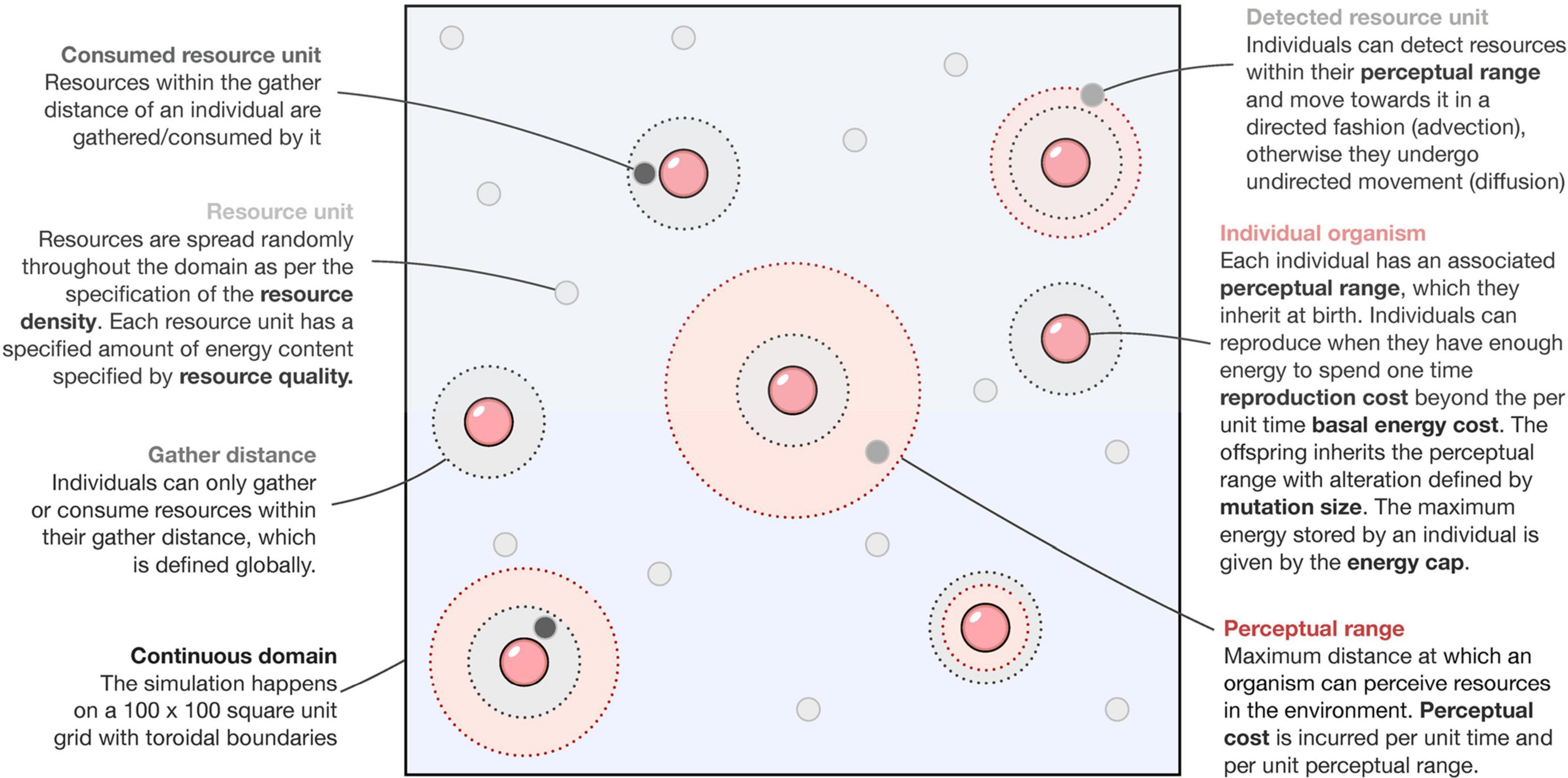
We model the dynamics of the system using an agent-based approach (see Figure 1). The computational spatial domain is a 100 unit by 100 unit continuous square with parallel sides identified (toroidal boundary conditions). Each simulation starts with all individuals having zero perceptual range. Through selection (enforced by environmental and species-specific parameters) and neutral processes (brought about by mutation) (Table 1), we observe the shape of the perceptual range distribution in the population over time. Before the simulation begins, a constant amount of total resource is specified according to two parameters: resource density and resource quality.
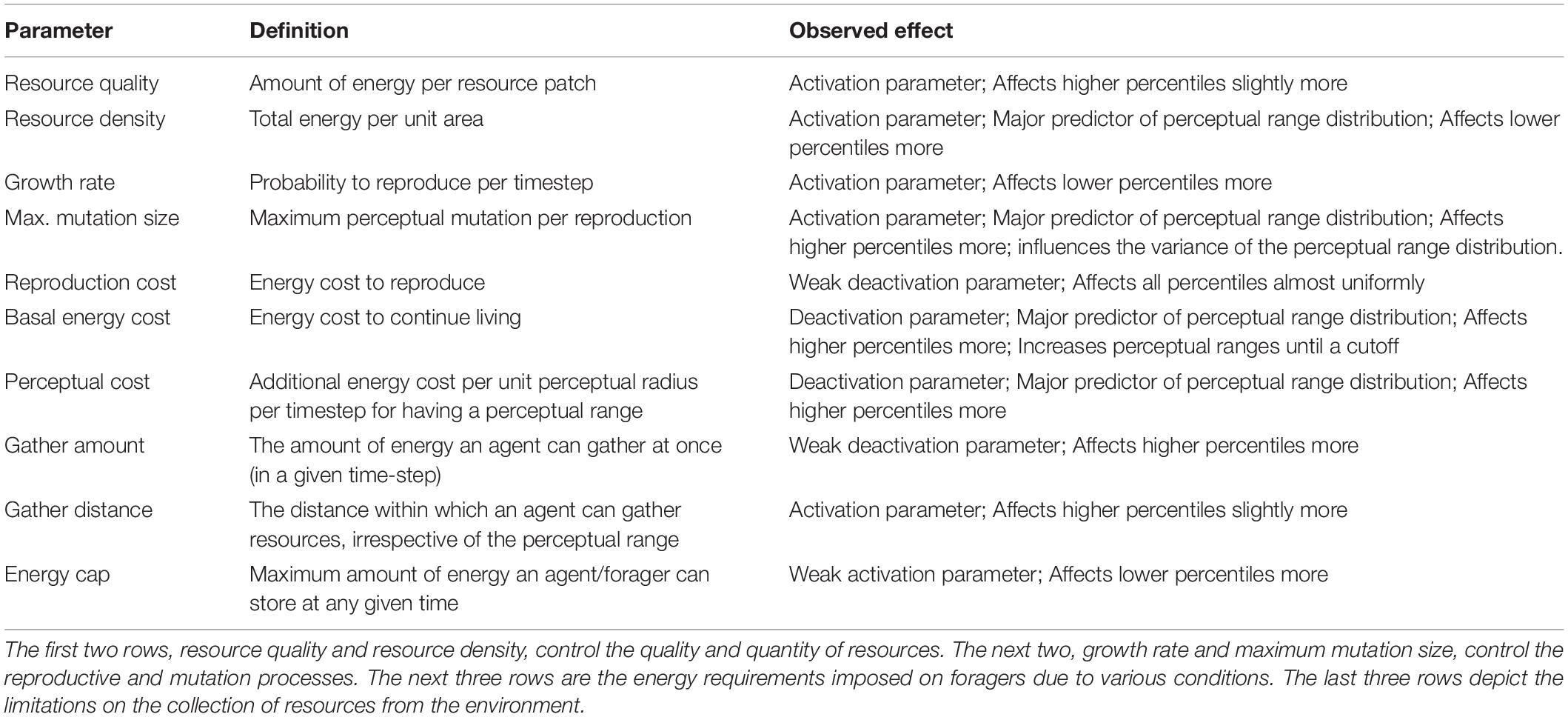
Table 1. Summary of various parameters used in the model, their definitions and their effects on the perceptual range distribution.
Resource density is defined as the amount of resource patches per unit area in the domain; thus, the number of patches where resources are present is equal to the resource density times the area of the domain. The resource patches are then distributed randomly on the domain with each patch containing an amount of resource equal to the resource quality (or the energy quantity per resource), ensuring a spatial heterogeneity in resource availability to mimic natural scenarios. At every time step, the code checks the resource distribution and adds more resource patches with the same resource quality if the total amount of resources is less than the initial amount. This way, the total amount of resources is held constant over time for simplicity.
Individual agents (foragers) default to undirected movement (a random walk) until resources enter their perceptual range, at which point they switch movement modes and move along a straight line (advective movement) to the nearest resource patch and gather resources from it (see Figure 1). All foragers have the same constant movement speed of one spatial unit per time step. This simulates the mode of movement observed in organisms in natural settings during foraging (Tyson et al., 2011). Foragers having a non-zero perceptual range incur an additional cost every timestep per unit perceptual range, termed as the perceptual cost. We assume the relation between perceptual range and its cost to be linear for simplicity: increased perception translated directly into higher costs (Protas et al., 2007; Moran et al., 2015). This cost is above the basal metabolic cost incurred per timestep for survival, irrespective of the perceptual range. A forager can gather an amount of resources equal to the gather amount parameter only if the resources are within its gather distance (irrespective of its perceptual range) and the forager is not exceeding its energy cap, which defines the maximum amount of resource that an individual can consume. A special case arises when the gather distance is lesser than an agent’s perceptual range, and in such a case, the gathering action can be understood as a rudimentary detection, which we assume, can occur irrespective of complex perceptual systems.
Once a forager has sufficient resources, it can randomly reproduce asexually according to a threshold growth rate parameter. Should an individual reproduce, it incurs a one-time cost associated with reproduction (reproduction cost) and transfers that energy/resources to the offspring (new individual). The offspring also undergoes a mutation in its perceptual range, changing its parent’s perceptual range by an amount randomly drawn from a uniform distribution on the interval [−m,m] where m is the maximum mutationsize parameter. In implementation, we ensured that perceptual ranges were always non-negative. Death only occurs when the foragers run out of energy. From our numerical experiments, we found that this causes the population size to be regulated by the resource availability (similar to the idea of carrying capacity), although the exact values can depend upon other parameters such as metabolic costs.
Model Implementation and Analysis
We implemented the model in the Go programming language using its standard libraries (see the code and data availability section for details). A detailed account of all parameters appears in Supplementary Table 1. To obtain a representative behavior in the ensemble of simulations, we performed 10 million runs, involving parameter combinations chosen using a Latin hypercube sampling (LHS) procedure. Each simulation was run for 150 time-steps and had a starting population of 100 zero-perceptual range individuals. From a set of preliminary simulations over a wide variety of parameters, we found that simulations stabilized to almost a constant distribution (less than 5 percent difference) in under 150 timesteps and remained stable afterward (see Supplementary Figure 1 and Supplementary Video).
Each simulation begins by randomly placing 100 foragers on the computational domain and initializing their energy levels to 1.0. At each time step, a sequence of events occur: (1) all individuals check their perceptual radii for resources; (2) foragers move in a random manner (if they cannot perceive any resources) or a directed manner to the closest resource (if they can perceive one or more resources); (3) If possible, foragers gather resources from the locations harboring resources; (5) All foragers pay their cost penalties; (6) if they have sufficient resources, foragers reproduce with a probability prescribed by the growth rate parameter with their offspring placed at a random location adjacent to their parents (randomly within a distance of 5 units), and lastly, (7)resources are replenished according to the parameters in the code.
Each parameter combination was replicated 10 times and then the end time perceptual ranges were aggregated (for each combination) to obtain an averaged, statistically robust distribution of perceptual ranges (i.e., 10 replicates times 100 randomly placed individuals at the start of each simulation) from which we could calculate percentiles of interest (2.5, 25, 50, 75, and 97.5). We focus on these percentiles rather than a simple mean because we anticipate that different factors may influence the structure of the perceptual range distribution in different ways. For example, the degrees to which the parameters affect the lowest perceptual range values would be different from how they affect the highest perceptual ranges in the system. After accumulating all the data, we performed further analysis in Python and R. Preliminary analyses justified our choice of 10 replicates per parameter combination. To do this we ran 100 replicates for 100 randomly selected parameter combinations and then calculated the Bhattacharyya distance among replicates for various subsets from 1 to 100, discovering that 10 was an optimal number with respect to computational time and statistical robustness (see Supplementary Figure 2 for details). Bhattacharyya distance is a standard statistical metric for quantifying the similarity of two probability distributions; it reflects the amount of overlap between two statistical samples or populations (see Bhattacharyya, 1943), and is measured between 0 and 1, where 1 denotes complete similarity.
One might argue that assuming the probability of mutation to be 1 on reproduction, irrespective of mutation size, is not a biologically relevant scenario, and instead the probability of mutation should vary depending upon environmental conditions and species-specific factors. However, we found that a mutation probability of 1 was appropriate for our purposes, by conducting a series of numerical experiments in which we considered 1,000 parameter combinations at each of ten mutation probabilities. These simulations show that the probability of mutations (independent of the mutation size) only affects the timescale of the simulations. It does not affect the final distribution of perceptual ranges (see Supplementary Figure 3 for details). Therefore, to be computationally efficient we assume mutation probability to be 1 and focus our analyses of mutational dynamics on maximum mutation size.
To obtain a simplified dependence structure of various parameters on the evolution of the perceptual range distribution, we determined the partial rank correlation coefficient (PRCC) of various parameters with respect to the 2.5, 25, 50, 75, and 97.5 percentiles of the distribution, using the sensitivity package (Iooss et al., 2020) in R. We also performed a Random Forest (RF) regression, using the random Forest package (Liaw and Wiener, 2002) in R, to identify which parameters are the strongest predictors of the patterns in different percentiles of the perceptual distribution. We optimized the number of parameters available for splitting at each tree node in the RF using out-of-bag error (OOB) (Liaw and Wiener, 2002). We use the IncNodePurity statistic (another standard statistical metric defined as the total decrease in node impurities from splitting on a given parameter, averaged over all trees; Impurity is measured by residual sum of squares and is calculated only at the node at which a given parameter is used for a split; see Liaw and Wiener, 2002) for comparing variable importance scores in RF models. Higher values of IncNodePurity denote higher importance of a parameter in predicting a given variable.
To further analyze the details in the patterns of perceptual evolution and identify how perceptual evolution depended on resource availability, we fixed a standard set of parameters (see Supplementary Table 1 for details) and plotted the distributions by altering one parameter at a time in three different resource regimes (low, medium, and high; see Supplementary Table 1).
Results
Classifying Parameters and Their Impact
Figure 2A summarizes results from the PRCC analysis investigating how model parameters affect the percentiles of the distributions of perceptual ranges. To understand the impact of various parameters, we categorized all parameters into two groups: activating, which are the ones with PRCC greater than 0.0 (i.e., a positive effect on the distribution of perceptual ranges) and deactivating, with PRCC less than 0.0 (i.e., a negative effect). This categorization groups resource quality, growth rate, maximum mutation size, resource density, gather distance, and energy cap as activating parameters because these parameters positively affect and/or aid the evolution of non-zero perceptual ranges. On the other hand, basal energy cost, perceptual cost, reproduction cost and gather amount fall into our deactivating category and affect the evolution of non-zero perceptual ranges negatively.
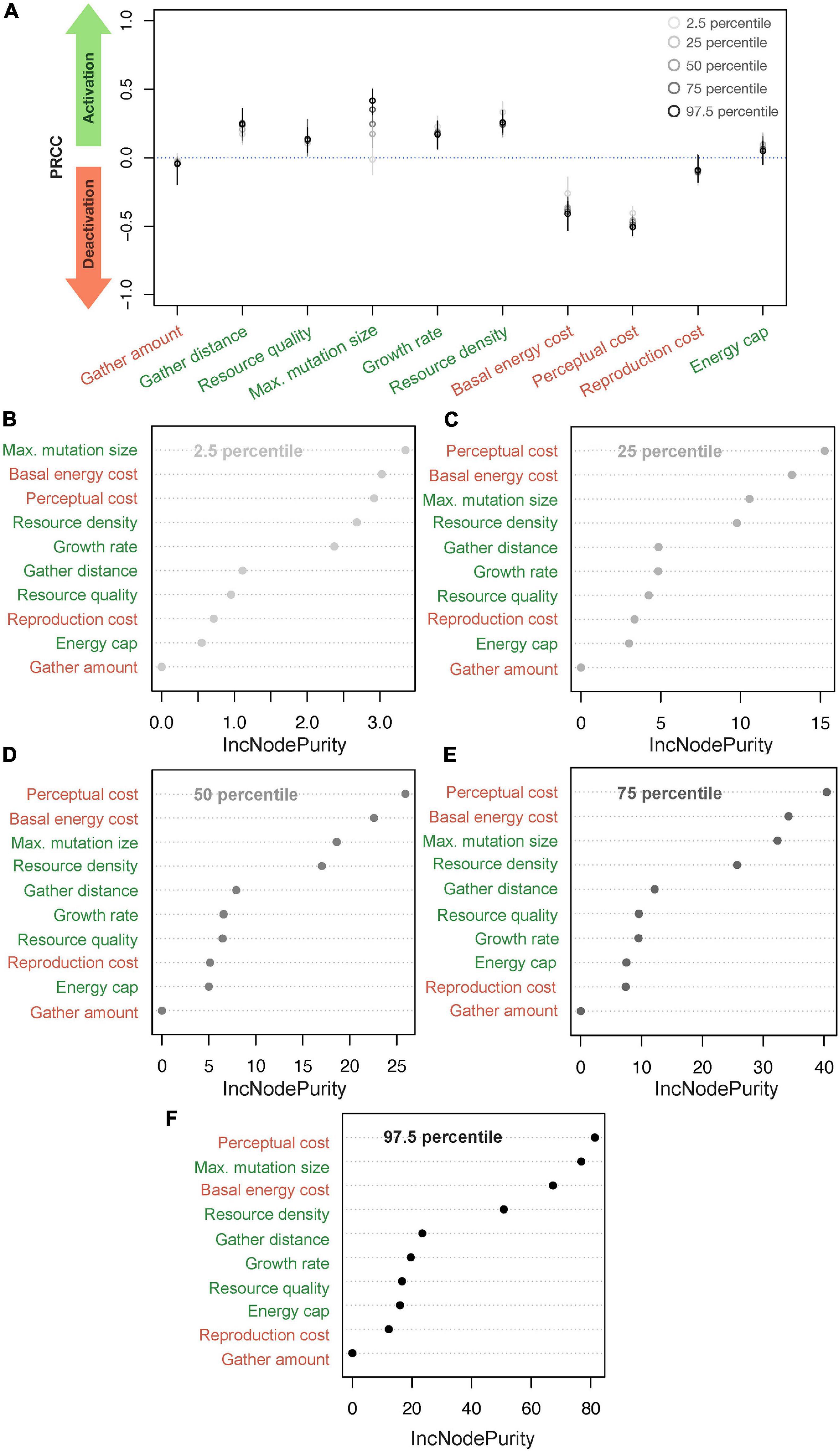
Figure 2. Finding critical parameters. (A) Classifying parameters into activating and deactivating groups using partial rank correlation coefficient (PRCC); parameters where the mean PRCC is above 0.0 are activating and those with mean PRCC below 0.0 are termed deactivating. (B–F) Represent a Random Forest (RF) Regression of different parts of the resultant perceptual range distribution from the parameter values where (B–F) represent the results for 2.5, 25, 50, 75, and 97.5 percentiles, respectively (and percentage of variance explained: 74.84, 70.03, 70.25, 70.16 and 72.92%, respectively). The labels in green are activating parameters and those in red are deactivating. The x-axis in (B–F), IncNodePurity, refers to the total decrease in node impurities from splitting on a given parameter, averaged over all trees. Higher IncNodePurity means higher variable importance.
Although this broad classification is helpful, the impact of each parameter within the categories differs substantially, and for some parameters (e.g., maximum mutation size) the impact differs across the parts of the perceptual distribution (Figure 2A). To further elucidate parameter impacts on perceptual range, we can examine the variable impact scores from RF regression models and quantify how individual parameters affect perceptual ranges when all others are held constant.
Parameters as Predictors of the Perceptual Distribution
We plot the variable importance scores through the IncNodePurity statistic from the RF regression models, with all parameters as predictor variables and percentiles of the perceptual range distribution as the outcome variable (Figures 2B–F). See Supplementary Figure 4 for RF optimization. These results echo the findings from the PRCC plot (Figure 2A) and describe more than 70% of the variance in each of the five perceptual percentile levels. Specifically, RF could explain 74.84, 70.03, 70.25, 70.16, and 72.92% of the variance for the 2.5, 25, 50, 75, and 97.5 percentiles, respectively).
Perceptual cost, basal energy cost, maximum mutation size, and resource density, which have the highest PRCC values for almost all the percentile perceptual values, are consistently the best predictors of evolved perceptual range. Only the relative ranking of the importance of these four parameters changes in the RF regression across the percentile levels. In the case of the 2.5 percentiles, growth rate approaches a similar range as the top four parameters listed above, but in all other cases, growth rate’s PRCC value remains low. Although gather distance positively affects the perceptual evolution and affects its variation as evident in PRCC values (Figure 1), it is not a good predictor of the percentile perceptual values.
Detailed Discussion About Parameters
To gain more insights into the model’s evolutionary dynamics, we plotted the mean perceptual radius of simulations where we tuned one parameter and kept the others constant at standard values (Supplementary Table 1). We did this for each of three resource regimes in Figure 3 to uncover broad scale patterns associated with changing resource density. For a more detailed structure of the distribution, please refer to Supplementary Figures 5, 6.
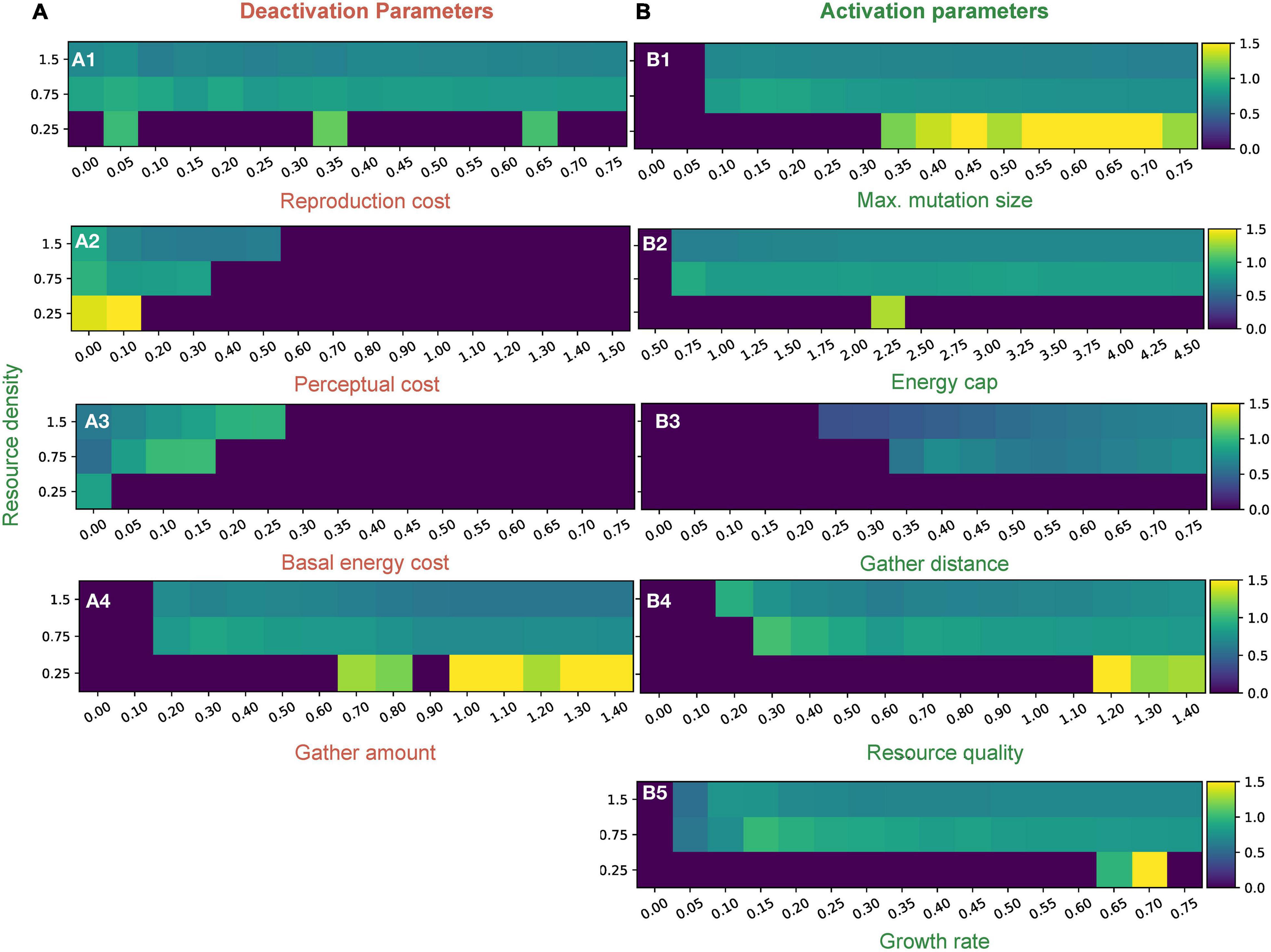
Figure 3. Mean distribution values of perceptual range for different parameters in three different resource density regimes. Column A (A1–4) represents deactivation parameters and column B (B1–5) represents activation parameters (The labels in red are deactivation parameters and those in green are activation). Resource densities of 0.25, 0.75, and 1.5 correspond to the “low,” “medium,” and “high” resource conditions, respectively. Detailed distributions of the perceptual ranges and how they are affected by various parameters can be found in Supplementary Figures 5, 6.
Activation Parameters
Activation parameters allow perceptual ranges to evolve and persist in the population. Resource quality, growth rate, maximum mutation size, resource density, gather distance, and energy cap are activating parameters. Each of these parameters has a threshold value such that when the parameter is below the threshold, conditions are sufficiently harsh that no perceptual range evolution is possible. Once above the threshold, however, the parameter creates a setting that activates perceptual range evolution (see Figure 3B and Supplementary Figure 5).
Threshold values vary among the activation parameters, and across the parameter space. Regimes where positive perceptual ranges reliably exist are usually characterized by a resource density of around 0.5 or more, showing an important dependence on resource availability. In the low resource case (resource density is 0.25), we see interesting patterns: populations with non-zero perception exist only sporadically and by chance; but when they do exist, they create higher mean perceptual ranges than higher resource density cases for similar parameter values (Figure 3). The maximum mutation size parameter is unique among the activation parameters, as it allows populations to thrive more reliably in low resource regimes than other parameters (Figure 3). The perceptual range distribution exhibits high variation in harsh or low resource environments for all parameters as compared to those in medium and high resource environments (Supplementary Figure 5).
Deactivation Parameters
Deactivation parameters, such as basal energy cost, perceptual cost, reproduction cost, and gather amount, make it more difficult for perceptual ranges to evolve and persist in a population. Instead of having thresholds, these parameters have cutoffs after which no non-zero perceptual ranges generally evolve (Figure 3 and Supplementary Figure 6).
The perceptual range distribution is very sensitive to changes in perceptual cost (Figures 2, 3A2). We see a quick decrease in perceptual ranges as perceptual costs go up, but greater perceptual costs are tolerated in high resource scenarios (Figure 3A2). For basal energy cost, which is another strong predictor of perceptual range (Figure 2), we see an increase in perceptual range until the cutoff is reached (Figure 3A3). Although reproduction cost reduces the distribution of perceptual ranges, its impacts are relatively small (Figures 2, 3A1). Gather amount behaves like an activation parameter, in having a threshold rather than a cutoff, and has a small negative impact on perceptual evolution (Figure 3A4).
Discussion
Understanding the evolution of perception in a given ecological setting sheds light on the interplay between environmental and species-specific factors in structuring the sensory spaces of organisms. Using our simple agent-based model, with assumptions pertaining to biological scenarios, we can predict possible effects of various environmental and biological factors on perceptual evolution. Moreover, our simulations include both neutral and adaptive processes of change (i.e., through mutation size and selective pressure to survive and reproduce), which allows for exploration of how such evolutionary changes may take place.
The simulations draw a stage where the foragers try to maximize their temporal energy gain while trying to minimize the risk of running out of energy, under various starting conditions and a spatially heterogeneous (but controlled) environment. Although it would be interesting to understand conditions and evolutionary strategies through which one can view the emergence and maintenance of various perceptual range distributions, the complex form of density dependence and continuous space of possible pathways or strategies present in our model mean that such investigation is not at all straightforward. Therefore, we focus here on a higher-level correlative view of the emergent patterns of perceptual range distributions.
Results from the simulations suggest a few major patterns. From the RF analysis and PRCC estimation, we found the four major predictors of perceptual range evolution to be resource density, maximum mutation size, perceptual cost, and basal energy cost, with resource density providing the uniformly strongest effects (Figure 2A). From basic ecological principles, one expects factors akin to resource density to affect the evolution of perception, either directly or indirectly. A good example involves the reduction of sensory apparatus in a variety of organisms in resource-limited environments in both natural settings and in well-controlled experimental systems (Stevens, 2013; Brandon and Dudycha, 2014; Brandon et al., 2015). For example, caves have resource-limited conditions, and the reduction in visual organs of cavefish, as compared to their above-ground relatives (Jeffery, 2009; Borowsky, 2008), may be driven by the relatively high energetic costs of the visual system coupled with minimal benefit of vision (Niven and Laughlin, 2008), in addition to other developmental constraints. Likewise, in benthic decapods, eye size increases with increasing depth, as expected from the fact that larger eye size improves vision in dimmer environments (Hiller-Adams and Case, 1985). However, the opposite trend was observed in pelagic crustaceans (Hiller-Adams and Case, 1984, 1988), indicating that large eyes are an energetic burden in the resource-limited pelagic zone. These comparative examples suggest the evolution (or loss) of visual apparatus depends not only on the perceptual environment but may also (directly or indirectly) depend on resource availability (although a strong mechanistic link is still lacking). Evolutionary effects and generational plasticity in perceptual apparatus investment due to limited resources and allocation to other body parts have also been observed in a number of organisms including Daphnia (Brandon and Dudycha, 2014; Brandon et al., 2015), beetles (Nijhout and Emlen, 1998), and butterflies (Merry et al., 2011). Although resource availability has been implicated or hypothesized in perceptual loss or gain in these systems, the mechanistic link is still missing, and the observed effects might be due to other secondary factors.
Naively, one might expect that the strongest selection on perceptual ranges would happen under intermediate resource densities, because at high densities, there might be little to no benefit of increased ranges as resources are likely to be encountered under random movement patterns and at low resource densities, the benefits of findings resources may not necessarily offset the costs of the systems necessary to detect them. Interestingly, in our model lower resource density environments sometimes produced noticeably larger perceptual ranges than those of higher resource density environments, even though the threshold for attaining non-zero perception in the latter environments was lower (Figure 2 and Supplementary Figures 5, 6). This effect was, however, sporadic and depended on chance: low resource environments can also lead to smaller perceptual ranges. This diversity of successful strategies seems to be true for some low resource environments like the deep-sea, where certain organisms have exceptionally well-developed sensory capabilities whereas others feature extensive reductions in sensory systems (Drazen and Sutton, 2017). Moreover, although resource density had an overall positive impact on the whole perceptual distribution, it had a higher impact in increasing the lower percentiles of the perceptual range distribution (Figure 2A), and therefore might play a critical role in early stages of perception evolution.
Maximum mutation size facilitated evolution of more diverse perceptual ranges in all scenarios. The notion that large mutations might aid in the formation of complex morphological features, such as sensory systems, is well-developed both experimentally (Weng, 2014) and theoretically (Lenski et al., 2003). For example, mutation rate affects the time required for eye evolution (Nilsson and Pelger, 1994). In addition, we observed that maximum mutation size allowed for a more stable persistence of perception in low resource environments and led to the evolution of larger perceptual ranges (Figure 3B1 and Supplementary Figure 5). Such an observation may be related to the fact that there is bistability in the system (here, bistability corresponds to situations where the equilibrium distribution of perceptual ranges included both zero and non-zero values; Supplementary Figures 5A2–A4, 6A3–A4). Bistability would be expected to emerge only when sufficient temporal and spatial conditions are met, and near such points, we would expect to see a transition to situations in which a portion of the population has non-zero perceptual ranges. For example, under standard conditions of our model and low resources, mutation size was the major parameter that led to apparent bistable states. In this case, sufficiently high mutation size helps create larger perceptual ranges, which can aid survival under low resource conditions while also meeting the perceptual costs. Otherwise, zero-perceptual range is the stable state where random walk foraging and low energetic costs can sustain the population. In other scenarios, we might have such bistability as a complex function of many parameters. As this work provides a path for thinking about evolution of perceptual ranges and the parameters that affect their stable distributions under various conditions, future work, using non-agent-based approaches, should investigate bistability more fully.
Maximum mutation size affected various parts of the perceptual distribution differentially (Figure 2A). In particular, the effect of this parameter increased with increasing percentiles of the perceptual range distribution, meaning that higher maximum mutation sizes allowed for higher upper bounds on the possible perceptual ranges but did not affect the lower bounds as much.
As expected, an increase in perceptual cost decreased the prevalence of non-zero perceptual ranges (Figures 2A, 3A2) as the foragers became unable to afford the energy loss incurred by increasing their perceptual range. Such a phenomenon is known from a wide range of species in both natural and captive settings and from physiological experiments (Niven et al., 2007; Niven and Laughlin, 2008; Stevens, 2013). For example, the production of electric organ discharges (EODs) (in weakly electric fish) is metabolically expensive (Salazar and Stoddard, 2008; Stoddard and Salazar, 2011). Fish living in waters with sufficient oxygen show no correlation between metabolic rate and EOD, but those in oxygen depleted waters show reduced EOD (Reardon et al., 2011). In sticklebacks, where divergence into two forms occurs during lake habitat acclimatation—benthic (bottom dwelling, invertivorous) individuals, which live in lower light conditions and have higher perceptual costs, possess diminished eyes, whereas limnetic (open water dwelling, zooplanktivorous) individuals have larger eyes (Willacker et al., 2010). In ray-finned fish, eye size decreases as a function of turbidity of waters they inhabit—pointing to increased perceptual cost in more turbid waters (i.e., reduced visibility) affecting eye size and acuity (Caves et al., 2017). We also note that perceptual cost had the strongest effect on the higher percentiles of the perceptual range distribution (Figure 2A).
Basal energy cost also had an overall intuitive trend. At low levels, it is easier for foragers to evolve perceptual range, while at higher levels the foragers are unable to meet the cost; this cutoff increased with increasing resources (Figure 3A3). But on a finer scale, we observed an increase in perceptual ranges with increasing basal energy cost, until the cutoff value, where it abruptly crashed (Supplementary Figure 5). Increases in basal energy cost forced foragers to find a better way to gather resources and thus, perceptual ranges increased (Supplementary Figure 5). This process continued, in increasing strength, until the point where foragers cannot sustain themselves due to a high metabolic cost—which results in the cutoff. Predation and competitive interactions both increase basal energy costs (Hawlena and Schmitz, 2010; DeLong et al., 2014), and larger sensory apparatus can occur in situations featuring greater predation and competition (Beston and Walsh, 2019). But beyond a certain threshold rate of predation, reduced visual apparatus might happen due to higher costs as documented in Eurasian perch (Svanbäck and Johansson, 2019), similar to our results (see Figure 3A3 and Supplementary Figure 5). Another intriguing example of the phenomena involves cylindroleberidid ostracods, in which species with eyes living in the photic zone have larger carapaces (and therefore higher basal energy costs) and may possess a larger number of ommatidia when living at greater depths were resources are fewer (Juarez et al., 2019). In the same group, neither body size nor absolute metabolic rate changes as depth increases in the disphotic zone. However, food availability does decrease with depth (and therefore, relative metabolic rate increases) and eyes have more ommatidia (Juarez et al., 2019). In other words, evolution of better perceptual apparatus is possible over a range of conditions, even with increasing relative metabolic costs.
Beyond these four major predictors, the remaining parameters had smaller or more restricted effects. For example, growth rate played an important role in determining the lower bound of the perceptual distribution (Figures 2A,B), although it did not impact other parts of the distribution as much (Figures 2C–F). Previous works have reported enhanced growth rate being correlated with larger eyes in Trinidadian killifish (Beston and Walsh, 2019) and in amblyopsid fishes (Poulson, 1963).
Reproduction cost negatively affected all percentiles uniformly, although the impact was weak (Figure 2A). Although we only modeled asexual reproduction, we take this result as a weak indicator of reproductive investment affecting perception. An example of this can be seen in scarab beetles where there is a strong trade-off between anatomical investments that help in reproduction, such as horns, and eye size (Nijhout and Emlen, 1998).
The rest of the parameters that we introduced to make our model more biologically realistic gave us important insights about perceptual evolution but have limited experimental and observational evidence for validation. For example, resource quality was a weak activation parameter, which affected the higher percentiles of perceptual range distribution slightly more than the lower percentiles (Figure 2A). Energy cap is another parameter of weak influence, but it impacted perceptual evolution in a positive way, and had greater impacts on the lower percentiles of the distribution (Figure 2A).
Gather amount is an intriguing parameter, it behaved like an activation parameter (in the sense of having a threshold), but it had a deactivating influence on the perceptual range distribution (Figure 2A). When gather amount increased beyond a certain value, larger perceptual ranges were possible as the foragers were able to meet biological costs. At the same time, however, foragers with lower perception ranges obtained an advantage by not having to spend much energy on perception, leading to a net weak decrease in perceptual ranges (Figure 2A). This could be evidence that gather amount is leading to increased greediness among the foragers, resulting in a more equal spreading of resources and decreased efficacy of the evolutionary process.
Gather distance improved the foraging ability of larger perceptual ranges, and therefore affected the higher percentiles of the perceptual range distribution in a more positive way than the lower percentiles (Figure 2A). Foragers with small or zero perceptual ranges also would be able to collect resources easily with increasing gather distance, but they would do so in a diffusive movement pattern. This means they would consume more energy per timestep—making them less competitive than foragers able to employ advective movement on the basis of their perceptual ranges. Gather distance is especially useful at lower resource densities (beyond a threshold which will allow for survival; Figure 3B3 and Supplementary Figure 5).
Exploring the effects of parameters in our model facilitates understanding of the evolution of perception by identifying how environmental and species-specific attributes (and their interactions) influence the development and maintenance of perceptual range. Such investigations are also beneficial because they suggest patterns of perceptual evolution that might have occurred under various circumstances in the past. In particular, this work suggests the existence of certain “minimal conditions” that are necessary for the evolution and persistence of perception. These conditions, in the form of cut-offs in the case of deactivation parameters and thresholds in activation ones, give us a basic framework to hypothesize about evolutionary trajectories of perception and perceptual ranges. Moreover, given the general nature of this simple model, it is relevant to the evolution of perception for organisms of any size and sensory perception of any modality. Even though we focus on only one type of perception in our model, it can be easily expanded in a future work to involve multiple sensory inputs and their relative trade-offs to better understand the evolutionary trajectories of multiple sensory modalities (Howarth and Moldovan, 2018; Keesey et al., 2019).
In addition, we have not explored the ways in which “dispersal distance” or “mobility” during the reproductive process might affect the system dynamics in the current set of simulations. This topic is a complex one and exceeds the scope of the current paper, but we are able to draw a few conclusions based on pilot results and extrapolations. Small “dispersal distance” leads to agents with similar phenotypes being spatially localized. This does not, however, have a direct impact on the phenotypic distribution because reproduction is purely asexual in the current model. In contrast, dispersal distance could have an impact via resource consumption. Specifically, because agents with higher perceptual range are more effective at removing resources from the environment, spatial clustering resulting from “dispersal distance” can indirectly result in subregions in the simulation space that are less resource-dense because they are inhabited by clusters of highly perceptive agents.
In its current form, our work has provided one way of exploring the evolution of perception in a spatially explicit agent-based model, something that has not been done in the past. Instead, past work on the evolution of perception has used different approaches and considered different themes. For example, researchers have investigated the evolution of perception from a Bayesian perspective to explore the formal link between the statistics of the environment and species-specific characteristics through the lens of genetics (see Geisler and Diehl, 2002, 2003). Those authors used the concept of a maximum fitness ideal observer (a standard Bayesian ideal observer with a utility function) appropriate for natural selection (with a utility function for fitness) and a formal version of natural selection based upon Bayesian statistical decision theory, to explore perceptual systems (Geisler and Diehl, 2003). Others have approached the evolution of perception from a sensory ecology perspective – through the interplay of signals, signaling behaviors and sensory drives (Endler, 1992), where the focus in on how the environment influences the production, propagation, and detection of signals. Our work is complementary to both of these frameworks, as we created a system incorporating important paradigms from movement ecology (foraging, perceptual ranges, and switching between random search and directional movements) to answer the same questions, but with biologically inspired and tunable parameters. Our model is very simple in terms of its treatment of perception and its properties and provides only a crude representation of forager-resource interactions. Nevertheless, it is a first step in the direction of building more sophisticated models of the evolution of perception. Limitations of the current study include (1) our binary treatment of perceptual acuity (we model acuity simply as 1 inside the perceptual range and 0 otherwise, such that a forager isomniscient about resources inside its perceptual range); (2) our lack of attention to sexual reproduction (we assume only asexual reproduction for simplicity because consideration of sexual reproduction would require attention to a great deal behavioral complexity and many further assumptions); (3) our lack of a role for memory; and (4) rudimentary treatment of perception that does differentiates among different modalities.
In the future, we plan to investigate speciation as a function of changing perceptual range. Such inquiry is not possible here because aggregated data obscures our ability to distinguish fine patterns that might indicate “perceptual speciation” and bistability in our scenarios. Understanding such phenomena might be important in exploring patterns of sympatric speciation seen in many subterranean habitats (Segherloo et al., 2018), and perhaps in Drosophila (Keesey et al., 2019) and hypogean spiders (Mammola and Isaia, 2017). Moreover, due to our focus on foraging in this model, we did not consider mating signals and interactions, which also play a major role in perceptual evolution (Endler, 1992). Perception of sexual signaling would be a new direction in which our model could be remodeled and explored in the future.
To make this line of modeling more biologically realistic and explore prey-predator interactions (see Hein and Martin, 2020), future studies will include moving resource (or prey) items, different foraging strategies and scale of movement (see Farnsworth and Beecham, 1999; Beecham, 2001). Such a model can also account for co-evolution of perception in multiple interacting species such as the coevolution of hearing in bat-moth systems (Fullard, 1998), and evolution of alternative “cognitive” strategies for movement and foraging (Farnsworth and Beecham, 1999; Beecham, 2001). We also would like to explore more than one type of sensory perception (and its associated range) and incentivize the development of perceptual modalities with different resources. Future work could also explore other properties of perception, such as acuity and memory to increase the model’s biological realism. Taken together, such a system of models can help us understand the evolution of perception and the interplay between sensory modalities (Howarth and Moldovan, 2018; Keesey et al., 2019), allowing investigation of the biological and environmental factors that facilitate or hinder such evolutionary changes.
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: github.com/anshuman 21111/vision-evo.
Author Contributions
AS, KL, and WF conceptualized the project. KL and TH wrote the model code. AS and TH performed statistical analyses. AS and WF performed the interpretation of the results and data. AS, TH, and WF wrote the manuscript. All authors contributed to the article and approved the submitted version.
Funding
AS and WF would like to thank NSF Award DMS1853465 and the University of Maryland for support. KL would like to thank NSF (IOS-8044276,CCF-1908633) and the Arizona State University Biodesign Institute for training.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to thank Karen Carleton, Bill Jeffery, Jake Weissman, and Elie Gurarie for their comments that helped to improve this work.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2021.698041/full#supplementary-material
References
Averill, I., Lou, Y., and Munther, D. (2012). On several conjectures from evolution of dispersal. J. Biol. Dyn. 6, 117–130. doi: 10.1080/17513758.2010.529169
Barnett, A. H., and Moorcroft, P. R. (2008). Analytic steady-state space use patterns and rapid computations in mechanistic home range analysis. J. Math. Biol. 57, 139–159. doi: 10.1007/s00285-007-0149-8
Bartumeus, F., Campos, D., Ryu, W. S., Lloret-Cabot, R., Méndez, V., and Catalan, J. (2016). Foraging success under uncertainty: search tradeoffs and optimal space use. Ecol. Lett. 19, 1299–1313. doi: 10.1111/ele.12660
Bartumeus, F., and Levin, S. A. (2008). Fractal reorientation clocks: linking animal behavior to statistical patterns of search. Proc. Natl. Acad. Sci. U. S. A. 105, 19072–19077. doi: 10.1073/pnas.0801926105
Beecham, J. A. (2001). Towards a cognitive niche: divergent foraging strategies resulting from limited cognitive ability of foraging herbivores in a spatially complex environment. Biosystems 61, 55–68. doi: 10.1016/s0303-2647(01)00129-0
Berdahl, A., Torney, C. J., Ioannou, C. C., Faria, J. J., and Couzin, I. D. (2013). Emergent sensing of complex environments by mobile animal groups. Science 339, 574–576. doi: 10.1126/science.1225883
Berec, L. (2000). Mixed encounters, limited perception and optimal foraging. Bull. Math. Biol. 62, 849–868. doi: 10.1006/bulm.2000.0179
Beston, S. M., and Walsh, M. R. (2019). Natural selection favours a larger eye in response to increased competition in natural populations of a vertebrate. Funct. Ecol. 33, 1321–1331. doi: 10.1111/1365-2435.13334
Bhattacharyya, A. (1943). On a measure of divergence between two statistical populations defined by their probability distributions. Bull. Calcutta Math. Soc. 35, 99–109.
Bracis, C., Gurarie, E., Van Moorter, B., and Goodwin, R. A. (2015). Memory effects on movement behavior in animal foraging. PLoS One 10:e0136057. doi: 10.1371/journal.pone.0136057
Brandon, C. S., and Dudycha, J. L. (2014). Ecological constraints on sensory systems: compound eye size in Daphnia is reduced by resource limitation. J. Comp. Physiol. A 200, 749–758.
Brandon, C. S., James, T., and Dudycha, J. L. (2015). Selection on incremental variation of eye size in a wild population of Daphnia. J. Evol. Biol. 28, 2112–2118. doi: 10.1111/jeb.12711
Calabrese, J. M., and Fagan, W. F. (2004). A comparison-shopper’s guide to connectivity metrics. Front. Ecol. Environ. 2:529–536. doi: 10.1890/1540-92952004002[0529:ACGTCM]2.0.CO;2
Cantrell, R. S., Cosner, C., and Lou, Y. (2006). Movement toward better environments and the evolution of rapid diffusion. Math. Biosci. 204, 199–214. doi: 10.1016/j.mbs.2006.09.003
Cantrell, R. S., Cosner, C., and Lou, Y. (2010). Evolution of dispersal and the ideal free distribution. Math. Biosci. Eng. 7, 17–36. doi: 10.3934/mbe.2010.7.17
Caves, E. M., Sutton, T. T., and Johnsen, S. (2017). Visual acuity in ray-finned fishes correlates with eye size and habitat. J. Exp. Biol. 220, 1586–1596.
Cosner, C. (2005). A dynamic model for the ideal-free distribution as a partial differential equation. Theor. Popul. Biol. 67, 101–108. doi: 10.1016/j.tpb.2004.09.002
Cosner, C., Dávila, J., and Martínez, S. (2012). Evolutionary stability of ideal free nonlocal dispersal. J. Biol. Dyn. 6, 395–405. doi: 10.1080/17513758.2011.588341
Cressman, R., and Křivan, V. (2006). Migration dynamics for the ideal free distribution. Am. Nat. 168, 384–397. doi: 10.2307/3844696
DeLong, J. P., Hanley, T. C., and Vasseur, D. A. (2014). Competition and the density dependence of metabolic rates. J. Anim. Ecol. 83, 51–58. doi: 10.1111/1365-2656.12065
Drazen, J. C., and Sutton, T. T. (2017). Dining in the deep: the feeding ecology of deep-sea fishes. Ann. Rev. Mar. Sci. 9, 337–366. doi: 10.1146/annurev-marine-010816-060543
Dzik, J. (2005). Behavioral and anatomical unity of the earliest burrowing animals and the cause of the “cambrian explosion”. Paleobiology 31, 503–521. doi: 10.1666/0094-8373(2005)031[0503:baauot]2.0.co;2
Edwards, A. M., Phillips, R. A., Watkins, N. W., Freeman, M. P., Murphy, E. J., Afanasyev, V., et al. (2007). Revisiting Lévy flight search patterns of wandering albatrosses, bumblebees and deer. Nature 449, 1044–1048. doi: 10.1038/nature06199
Endler, J. A. (1992). Signals, signal conditions, and the direction of evolution. American Nat. 139, S125–S153.
Fagan, W. F., Gurarie, E., Bewick, S., Howard, A., Cantrell, R. S., and Cosner, C. (2017). Perceptual ranges, information gathering, and foraging success in dynamic landscapes. Am. Nat. 189, 474–489. doi: 10.1086/691099
Fagan, W. F., Hoffman, T., Dahiya, D., Gurarie, E., Cantrell, R. S., and Cosner, C. (2019). Improved foraging by switching between diffusion and advection: benefits from movement that depends on spatial context. Theor. Ecol. 13, 127–136. doi: 10.1007/s12080-019-00434-w
Farnsworth, K. D., and Beecham, J. A. (1999). How do grazers achieve their distribution? A continuum of models from random diffusion to the ideal free distribution using biased random walks. Am. Nat. 153, 509–526. doi: 10.2307/2463665
Fletcher, R. J., Maxwell, C. W., Andrews, J. E., and Helmey-Hartman, W. L. (2013). Signal detection theory clarifies the concept of perceptual range and its relevance to landscape connectivity. Landsc. Ecol. 28, 57–67. doi: 10.1007/s10980-012-9812-6
Fraker, M. E., and Luttbeg, B. (2012). Effects of perceptual and movement ranges on joint predator–prey distributions. Oikos 121, 1935–1944. doi: 10.1111/j.1600-0706.2012.20496.x
Fretwell, S. D. (1969). On territorial behavior and other factors influencing habitat distribution in birds. Acta Biotheoretica 19, 45–52. doi: 10.1007/bf01601955
Fullard, J. H. (1998). “The sensory coevolution of moths and bats,” in Comparative Hearing: Insects, eds R. R. Hoy, A. N. Popper, and R. R. Fay (New York, NY: Springer), 279–326. doi: 10.1007/978-1-4612-0585-2_8
Gehring, T. M., and Swihart, R. K. (2003). Body size, niche breadth, and ecologically scaled responses to habitat fragmentation: mammalian predators in an agricultural landscape. Biol. Conserv. 109, 283–295. doi: 10.1016/s0006-3207(02)00156-8
Geisler, W. S., and Diehl, R. L. (2002). Bayesian natural selection and the evolution of perceptual systems. Philos. Trans. R. Soc. Lond. B Biol. Sci. 357, 419–448. doi: 10.1098/rstb.2001.1055
Geisler, W. S., and Diehl, R. L. (2003). A Bayesian approach to the evolution of perceptual and cognitive systems. Cogn. Sci. 27, 379–402. doi: 10.1207/s15516709cog2703_3
Grünbaum, D., and Okubo, A. (1994). “Modelling social animal aggregations,” in Frontiers in Mathematical Biology, ed. S. A. Levin (Berlin: Springer), 296–325. doi: 10.1007/978-3-642-50124-1_18
Gurarie, E., and Ovaskainen, O. (2013). Towards a general formalization of encounter rates in ecology. Theor. Ecol. 6, 189–202. doi: 10.1007/s12080-012-0170-4
Hastings, A. (1983). Can spatial variation alone lead to selection for dispersal? Theor. Pop. Biol. 24, 244–251. doi: 10.1016/0040-5809(83)90027-8
Hawlena, D., and Schmitz, O. J. (2010). Herbivore physiological response to predation risk and implications for ecosystem nutrient dynamics. Proc. Natl. Acad. Sci. U. S. A. 107, 15503–15507. doi: 10.1073/pnas.1009300107
Hein, A. M., and Martin, B. T. (2020). Information limitation and the dynamics of coupled ecological systems. Nat. Ecol. Evol. 4, 82–90. doi: 10.1038/s41559-019-1008-x
Hein, A. M., and McKinley, S. A. (2012). Sensing and decision-making in random search. Proc. Natl. Acad. Sci. U. S. A. 109, 12070–12074. doi: 10.1073/pnas.1202686109
Hillen, T., Painter, K., and Schmeiser, C. (2007). Global existence for chemotaxis with finite sampling radius. Discrete Contin. Dyn. Syst. B 7:125. doi: 10.3934/dcdsb.2007.7.125
Hiller-Adams, P., and Case, J. F. (1984). Optical parameters of euphausiid eyes as a function of habitat depth. J. Comp. Physiol. A 154, 307–318. doi: 10.1007/bf00605230
Hiller-Adams, P., and Case, J. F. (1985). Optical parameters of the eyes of some benthic decapods as a function of habitat depth (Crustacea, Decapoda). Zoomorphology 105, 108–113. doi: 10.1007/bf00312145
Hiller-Adams, P., and Case, J. F. (1988). Eye size of pelagic crustaceans as a function of habitat depth and possession of photophores. Vision Res. 28, 667–680. doi: 10.1016/0042-6989(88)90047-8
Houston, A. I., and McNamara, J. M. (1999). Models of Adaptive Behaviour: An Approach Based on State. Cambridge: Cambridge University Press.
Howarth, F. G., and Moldovan, O. T. (2018). “The ecological classification of cave animals and their adaptations,” in Cave Ecology, eds O. Moldovan, Ĺ Kováč, and S. Halse (Cham: Springer), 41–67. doi: 10.1007/978-3-319-98852-8_4
Iooss, B., Da Veiga, S., Janon, A., Pujol, G., Broto, B., Boumhaout, K., et al. (2020). Sensitivity: Global Sensitivity Analysis of Model Outputs. R package version 1.20.0. Available online at: https://CRAN.R-project.org/package=sensitivity (accressed March 20, 2021).
Jeffery, W. R. (2009). Evolution and development in the cavefish Astyanax. Curr. Top. Dev. Biol. 86, 191–221. doi: 10.1016/s0070-2153(09)01008-4
Johnson, M. L., and Gaines, M. S. (1990). Evolution of dispersal: theoretical models and empirical tests using birds and mammals. Ann. Rev. Ecol. Syst. 21, 449–480. doi: 10.1146/annurev.es.21.110190.002313
Juarez, B. H., Speiser, D. I., and Oakley, T. H. (2019). Context-dependent evolution of ostracod morphology along the ecogeographical gradient of ocean depth. Evolution 73, 1213–1225. doi: 10.1111/evo.13748
Keesey, I. W., Grabe, V., Gruber, L., Koerte, S., Obiero, G. F., Bolton, G., et al. (2019). Inverse resource allocation between vision and olfaction across the genus Drosophila. Nat. Commun. 10, 1–16.
Laughlin, S. B. (2001). Energy as a constraint on the coding and processing of sensory information. Curr. Opin. Neurobiol. 11, 475–480. doi: 10.1016/s0959-4388(00)00237-3
Lenski, R. E., Ofria, C., Pennock, R. T., and Adami, C. (2003). The evolutionary origin of complex features. Nature 423, 139–144. doi: 10.1038/nature01568
Mammola, S., and Isaia, M. (2017). Spiders in caves. Proc. R. Soc. B Biol. Sci. U. S. A. 284:20170193. doi: 10.1098/rspb.2017.0193
Martínez-García, R., Calabrese, J. M., Mueller, T., Olson, K. A., and López, C. (2013). Optimizing the search for resources by sharing information: mongolian gazelles as a case study. Phys. Rev. Lett. 110:248106.
Martinez-Garcia, R., Fleming, C. H., Seppelt, R., Fagan, W. F., and Calabrese, J. M. (2020). How range residency and long-range perception change encounter rates. J. Theor. Biol. 498:110267. doi: 10.1016/j.jtbi.2020.110267
Matsumura, S., Arlinghaus, R., and Dieckmann, U. (2010). Foraging on spatially distributed resources with sub-optimal movement, imperfect information, and travelling costs: departures from the ideal free distribution. Oikos 119, 1469–1483. doi: 10.1111/j.1600-0706.2010.18196.x
McPeek, M. A., and Holt, R. D. (1992). The evolution of dispersal in spatially and temporally varying environments. Am. Nat. 140, 1010–1027. doi: 10.1086/285453
Mech, S. G., and Zollner, P. A. (2002). Using body size to predict perceptual range. Oikos 98, 47–52. doi: 10.1034/j.1600-0706.2002.980105.x
Merry, J. W., Kemp, D. J., and Rutowski, R. L. (2011). Variation in compound eye structure: effects of diet and family. Evolution 65, 2098–2110. doi: 10.1111/j.1558-5646.2011.01285.x
Moran, D., Softley, R., and Warrant, E. J. (2015). The energetic cost of vision and the evolution of eyeless Mexican cavefish. Sci. Adv. 1:e1500363. doi: 10.1126/sciadv.1500363
Nabe-Nielsen, J., Tougaard, J., Teilmann, J., Lucke, K., and Forchhammer, M. C. (2013). How a simple adaptive foraging strategy can lead to emergent home ranges and increased food intake. Oikos 122, 1307–1316. doi: 10.1111/j.1600-0706.2013.00069.x
Newlands, N. K., Lutcavage, M. E., and Pitcher, T. J. (2004). Analysis of foraging movements of Atlantic bluefin tuna (Thunnus thynnus): individuals switch between two modes of search behaviour. Pop. Ecol. 46, 39–53. doi: 10.1007/s10144-004-0169-9
Nijhout, H. F., and Emlen, D. J. (1998). Competition among body parts in the development and evolution of insect morphology. Proc. Natl. Acad. Sci. 95, 3685–3689. doi: 10.1073/pnas.95.7.3685
Nilsson, D. E., and Pelger, S. (1994). A pessimistic estimate of the time required for an eye to evolve. Proc. Biol. Sci. 256, 53–58. doi: 10.1098/rspb.1994.0048
Niven, J. E., Anderson, J. C., and Laughlin, S. B. (2007). Fly photoreceptors demonstrate energy-information trade-offs in neural coding. PLoS Biol. 5:e116. doi: 10.1371/journal.pbio.0050116
Niven, J. E., and Laughlin, S. B. (2008). Energy limitation as a selective pressure on the evolution of sensory systems. J. Exp. Biol. 211, 1792–1804. doi: 10.1242/jeb.017574
O’Dwyer, J. P. (2020). Beyond an ecological ideal gas law. Nat. Ecol. Evol. 4, 14–15. doi: 10.1038/s41559-019-1066-0
Okubo, A. (1980). Diffusion and Ecological Problems: Mathematical Models. Lecture Notes in Biomechanics, Vol. 10. New York, NY: Springer-Verlag.
Olden, J. D., Schooley, R. L., Monroe, J. B., and Poff, N. L. (2004). Context-dependent perceptual ranges and their relevance to animal movements in landscapes. J. Anim. Ecol. 73, 1190–1194. doi: 10.1111/j.0021-8790.2004.00889.x
Perry, G., and Pianka, E. R. (1997). Animal foraging: past, present and future. Trends Ecol. Evol. 12, 360–364. doi: 10.1016/s0169-5347(97)01097-5
Pleasants, J. M. (1989). Optimal foraging by nectarivores: a test of the marginal-value theorem. Am. Nat. 134, 51–71. doi: 10.1086/284965
Plotnick, R. E., Dornbos, S. Q., and Chen, J. (2010). Information landscapes and sensory ecology of the Cambrian Radiation. Paleobiology 36, 303–317. doi: 10.1666/08062.1
Poulson, T. L. (1963). Cave adaptation in amblyopsid fishes. Am. Midl. Nat. 70, 257–290. doi: 10.2307/2423056
Prevedello, J. A., Forero-Medina, G., and Vieira, M. V. (2011). Does land use affect perceptual range? Evidence from two marsupials of the Atlantic Forest. J. Zool. 284, 53–59. doi: 10.1111/j.1469-7998.2010.00783.x
Protas, M., Conrad, M., Gross, J. B., Tabin, C., and Borowsky, R. (2007). Regressive evolution in the Mexican cave tetra. Astyanax mexicanus. Curr. Biol. 17, 452–454. doi: 10.1016/j.cub.2007.01.051
Protas, M., and Jeffery, W. R. (2012). Evolution and development in cave animals: from fish to crustaceans. Wiley Interdiscip. Rev. Dev. Biol. 1, 823–845. doi: 10.1002/wdev.61
Pyke, G. H. (1984). Optimal foraging theory: a critical review. Ann. Rev. Ecol. Syst. 15, 523–575. doi: 10.1146/annurev.es.15.110184.002515
Raji, J. I., and DeGennaro, M. (2017). Genetic analysis of mosquito detection of humans. Curr. Opin. Insect Sci. 20, 34–38. doi: 10.1016/j.cois.2017.03.003
Ranta, E., Lundberg, P., and Kaitala, V. (2000). Size of environmental grain and resource matching. Oikos 89, 573–576. doi: 10.1034/j.1600-0706.2000.890317.x
Reardon, E. E., Parisi, A., Krahe, R., and Chapman, L. J. (2011). Energetic constraints on electric signalling in wave-type weakly electric fishes. J. Exp. Biol. 214, 4141–4150. doi: 10.1242/jeb.059444
Salazar, V. L., and Stoddard, P. K. (2008). Sex differences in energetic costs explain sexual dimorphism in the circadian rhythm modulation of the electrocommunication signal of the gymnotiform fish Brachyhypopomus pinnicaudatus. J. Exp. Biol. 211, 1012–1020. doi: 10.1242/jeb.014795
Segherloo, I. H., Normandeau, E., Benestan, L., Rougeux, C., Coté, G., Moore, J. S., et al. (2018). Genetic and morphological support for possible sympatric origin of fish from subterranean habitats. Sci. Rep. 8, 1–13. doi: 10.1093/oso/9780198820765.003.0001
Skalski, G. T., and Gilliam, J. F. (2003). A diffusion-based theory of organism dispersal in heterogeneous populations. Am. Nat. 161, 441–458. doi: 10.1086/367592
Stoddard, P. K., and Salazar, V. L. (2011). Energetic cost of communication. J. Exp. Biol. 214, 200–205. doi: 10.1242/jeb.047910
Svanbäck, R., and Johansson, F. (2019). Predation selects for smaller eye size in a vertebrate: effects of environmental conditions and sex. Proc. Biol. Sci. 286:20182625. doi: 10.1098/rspb.2018.2625
Swain, A., and Fagan, W. F. (2019). Group size and decision making: experimental evidence for minority games in fish behaviour. Anim. Behav. 155, 9–19. doi: 10.1016/j.anbehav.2019.05.017
Tan, S., Amos, W., and Laughlin, S. B. (2005). Captivity selects for smaller eyes. Curr. Biol. 15, R540–R542.
Torney, C. J., Berdahl, A., and Couzin, I. D. (2011). Signalling and the evolution of cooperative foraging in dynamic environments. PLoS Comput. Biol. 7:e1002194. doi: 10.1371/journal.pcbi.1002194
Tyson, R. C., Wilson, J. B., and Lane, W. D. (2011). Beyond diffusion: modelling local and long-distance dispersal for organisms exhibiting intensive and extensive search modes. Theor. Pop. Biol. 79, 70–81. doi: 10.1016/j.tpb.2010.11.002
Vergara, P. M., Soto, G. E., Rodewald, A. D., and Quiroz, M. (2019). Behavioral switching in magellanic woodpeckers reveals perception of habitat quality at different spatial scales. Landsc. Ecol. 34, 79–92. doi: 10.1007/s10980-018-0746-5
Vergassola, M., Villermaux, E., and Shraiman, B. I. (2007). ‘Infotaxis’ as a strategy for searching without gradients. Nature 445, 406–409. doi: 10.1038/nature05464
Viswanathan, G. M., Buldyrev, S. V., Havlin, S., Da Luz, M. G. E., Raposo, E. P., and Stanley, H. E. (1999). Optimizing the success of random searches. Nature 401, 911–914. doi: 10.1038/44831
Weng, J. K. (2014). The evolutionary paths towards complexity: a metabolic perspective. New Phytol. 201, 1141–1149. doi: 10.1111/nph.12416
Willacker, J. J., Von Hippel, F. A., Wilton, P. R., and Walton, K. M. (2010). Classification of threespine stickleback along the benthic–limnetic axis. Biol. J. Linn. Soc. 101, 595–608. doi: 10.1111/j.1095-8312.2010.01531.x
Zollner, P. A. (2000). Comparing the landscape level perceptual abilities of forest sciurids in fragmented agricultural landscapes. Landsc. Ecol. 15, 523–533.
Zollner, P. A., and Lima, S. L. (1997). Landscape-level perceptual abilities in white-footed mice: perceptual range and the detection of forested habitat. Oikos 80, 51–60. doi: 10.2307/3546515
Keywords: perceptual evolution, agent-based model, resource-dependent movement, perceptual range, perception
Citation: Swain A, Hoffman T, Leyba K and Fagan WF (2021) Exploring the Evolution of Perception: An Agent-Based Approach. Front. Ecol. Evol. 9:698041. doi: 10.3389/fevo.2021.698041
Received: 20 April 2021; Accepted: 23 June 2021;
Published: 21 July 2021.
Edited by:
Tal Avgar, Utah State University, United StatesReviewed by:
Tomoko Sakiyama, Sōka University, JapanClaire Hemingway, University of Texas at Austin, United States
Copyright © 2021 Swain, Hoffman, Leyba and Fagan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Anshuman Swain, YW5zd2FpbkB0ZXJwbWFpbC51bWQuZWR1
†These authors have contributed equally to this work and share first authorship
 Anshuman Swain
Anshuman Swain Tyler Hoffman
Tyler Hoffman Kirtus Leyba
Kirtus Leyba William F. Fagan
William F. Fagan