Design for an Individual: Connectionist Approaches to the Evolutionary Transitions in Individuality

The truly surprising thing about evolution is not how it makes individuals better adapted to their environment, but how it makes individuals. All individuals are made of parts that used to be individuals themselves, e.g., multicellular organisms from unicellular organisms. In such evolutionary transitions in individuality, the organised structure of relationships between component parts causes them to work together, creating a new organismic entity and a new evolutionary unit on which selection can act. However, the principles of these transitions remain poorly understood. In particular, the process of transition must be explained by “bottom-up” selection, i.e., on the existing lower-level evolutionary units, without presupposing the higher-level evolutionary unit we are trying to explain. In this hypothesis and theory manuscript we address the conditions for evolutionary transitions in individuality by exploiting adaptive principles already known in learning systems. Connectionist learning models, well-studied in neural networks, demonstrate how networks of organised functional relationships between components, sufficient to exhibit information integration and collective action, can be produced via fully-distributed and unsupervised learning principles, i.e., without centralised control or an external teacher. Evolutionary connectionism translates these distributed learning principles into the domain of natural selection, and suggests how relationships among evolutionary units could become adaptively organised by selection from below without presupposing genetic relatedness or selection on collectives. In this manuscript, we address how connectionist models with a particular interaction structure might explain transitions in individuality. We explore the relationship between the interaction structures necessary for (a) evolutionary individuality (where the evolution of the whole is a non-decomposable function of the evolution of the parts), (b) organismic individuality (where the development and behaviour of the whole is a non-decomposable function of the behaviour of component parts) and (c) non-linearly separable functions, familiar in connectionist models (where the output of the network is a non-decomposable function of the inputs). Specifically, we hypothesise that the conditions necessary to evolve a new level of individuality are described by the conditions necessary to learn non-decomposable functions of this type (or deep model induction) familiar in connectionist models of cognition and learning.

Introduction: Evolutionary Transitions in Individuality

All complex individuals are made of parts that used to be individuals themselves (e.g., the transition from single-celled life to multicellular organisms). Such evolutionary transitions in individuality have occurred at many levels of biological organisation, and have been fundamental to the origin of biological complexity, but how they occurred is not well understood (Maynard Smith and Szathmary, 1997; Michod, 2000; Okasha, 2006; Godfrey-Smith, 2009; Szathmary, 2015; West et al., 2015). Before a transition, adaptations under natural selection support component entities in acting to maintain their individual survival and reproduction. But after a transition, natural selection supports components in acting to serve the development, survival and reproduction of an individual at higher level of organisation (e.g., the multicellular organism), even when it conflicts with or suppresses the survival and reproduction of these component parts (e.g., somatic cells) (Maynard Smith and Szathmary, 1997; Godfrey-Smith, 2009).

How do they come to work together in this way? The form and function of the many different parts within an individual, and their working together as a coordinated whole, is consistent with natural selection acting at the higher level. When the higher-level individual is established as an evolutionary unit, i.e., after a transition, this can even explain self-sacrifice at the level of component parts – as they are no longer effective evolutionary units as individuals. But this presupposes the higher-level individual as an evolutionary unit and does not explain the process of the transition. The evolutionary changes involved in the creation and maintenance of a new level of individuality are complex and can involve many evolutionary steps in multiple dimensions including population structure, functional interdependence and reproductive specialisation (Godfrey-Smith, 2009). For example, these may include: a new kind of compartmentalisation (e.g., cell membrane) that limits the distribution of public goods or provides physical protection that binds selective fates together; new social relationships that create irreversible fitness dependencies between ecological partners (e.g., from ecological “trade” to division of labour); the synchronisation and centralisation of reproductive machinery (e.g., as in the origin of chromosomes and the eukaryote cell); changes to physical population structure that implement genetic assortment (e.g., a reproductive bottleneck in the origin of multicellular animals) and/or reproductive specialisation (with early-determination and sequestration of a germ line) (Margulis and Fester, 1991; Maynard Smith and Szathmary, 1997; Michod, 2000; Okasha, 2006; Godfrey-Smith, 2009; Buss, 2014; Szathmary, 2015; West et al., 2015). Such changes cannot be explained as adaptations of the higher-level unit because the higher-level unit does not exist until after (some sufficient subset of) these adaptations have taken place. Rather they must be a result of selection on the extant lower-level units changing their functional relationships with one another. That is, evolutionary transitions in individuality must be understood as evolved or coevolved changes to relationships between existing evolutionary units – not as some kind of instantaneous jump in the unit of selection (followed by the evolutionary complexification of internal relationships and mechanisms) (Black et al., 2020; Veit, 2021).

This presents an evolutionary puzzle because, whilst the collective benefit of adaptations at the higher level may be significant in the long term, natural selection is famously short-sighted and self-interested. That is, characteristics that decrease immediate benefit, or differentially benefit others, do not increase in frequency. Selection at the higher level of organisation necessary to overcome this is not effective until after the new level of individuality is constructed, and selection at the lower level will not favour any changes that decrease short-term individual fitness (Veit, 2021). Assuming the new evolutionary unit did not spring into existence “all at once,” with the necessary organised relationships already in place, the multiple changes involved in its creation must have been driven “bottom-up” by the selective interests of the extant, lower-level units – even though these same units are consequently caused to give-up their self-interest in the process. A key question in the transitions is thus:

How do multiple short-sighted, self-interested entities organise their relationships with one another to create a new level of individuality, meaning that they are caused by these relationships to act in a manner that is consistent with long-term collective interest?

To answer this, a theory of ETIs needs to describe (a) what kind of functional relationships between components are needed to make a new individual, and how they need to be organised; and (b) how the organisation of these relationships arises “bottom-up,” i.e., without presupposing the higher-level individual we are trying to explain.

Existing evolutionary theory struggles with these questions. Specifically, a conventional evolutionary framework cannot explain adaptations in systems that are not evolutionary units. After the transition, when the higher-level individual is established as an evolutionary unit, selection at this higher level can explain complex relationships and even altruistic behaviours among the component parts. But before the transition, we cannot invoke natural selection to explain the adaptation of such system-level relationships or behaviours. Thus, if these are adaptations required to create the new level of individuality, how can selection explain them? Questions about how new units are created, or transition from one level of organisation to another, cannot be addressed within a framework that presupposes the unit it is trying to explain. As Veit puts it, the problem is one of circular reasoning: “how to explain the origins of Darwinian properties without already invoking their presence at the level they emerge?” (Veit, 2021). So the process of ETIs under bottom-up selection creates a chicken-and-egg problem for conventional thinking; Which came first, the higher-level unit of selection required for complex adaptations, or the complex adaptations required to create the higher-level unit of selection? (Griesemer, 2005; Clarke, 2016).

In this manuscript, we outline the existing theoretical frameworks and hypotheses regarding the ETIs, and discuss their limitations – in particular, the problem of creating fitness differences at the collective level that are not just a by-product of fitness differences among particles, and how to explain the selective mechanisms by which the structures necessary to produce this transition can evolve bottom-up.

We then introduce some new experimental findings in developmental biology – namely, “basal cognition” and the separation of organismic individuality from genetics (Manicka and Levin, 2019a; Lyon et al., 2021a) and new perspectives on evolutionary processes, namely “evolutionary connectionism” (Watson et al., 2016), which deepens and expands the formal links between evolution and learning. The link between evolution and simple types of learning has often been noted (Skinner, 1981; Watson and Szathmary, 2016) but is sometimes interpreted in an uninteresting way; as if to say Some types of learning are no more clever than random variation and selection. But the formal equivalence between evolution and learning (Frank, 2009; Harper, 2009; Shalizi, 2009; Valiant, 2013; Chastain et al., 2014) also has a much more interesting implication, namely: Evolution is more intelligent than we realised (Watson and Szathmary, 2016). Evolutionary connectionism addresses the two questions above by utilising (a) the principles of distributed cognition, familiar in neural network models, to explain how the relationships between evolutionary units can produce something that is “more than the sum of the parts” in a formal sense, and b) the principles of distributed learning to address how evolving relationships can be organised bottom-up, without presupposing system-level feedback. This provides new ways of thinking about these questions, leading to a new hypothesis for what ETIs are and how the ETIs occur.

The core of the idea is that ETIs are the evolutionary equivalent of deep learning (LeCun et al., 2015) (i.e., multi-level model induction), familiar in connectionist models of cognition and learning (Watson et al., 2016; Watson and Szathmary, 2016; Czégel et al., 2018, 2019; Vanchurin et al., 2021). We hypothesise that this is not merely a descriptive analogy, but a functional equivalence (Watson and Szathmary, 2016) that describes the types of relationships required to support a new level of individuality and the selective conditions required for these relationships to arise bottom-up. Specifically, we hypothesise that (i) the type and organisation of functional relationships between components required for a new level of individuality are those which encode a specific but basic type of non-decomposable computational function (i.e., non-linearly separable functions), (ii) these relationships are enacted by the mechanisms of information integration and collective action (“basal cognition”) observed in the developmental processes of organismic individuality, and (iii) the conditions necessary for natural selection to produce these organisations are described by the conditions for deep model induction.

Existing Approaches to the Problem of the Evolutionary Transitions in Individuality

The evolutionary transitions in individuality, ETIs, have been some of the most important innovations in the history of biological complexity (Maynard Smith and Szathmary, 1997; Michod, 2000; Godfrey-Smith, 2009; West et al., 2015). These include the transition from individual autocatalytic molecules to the first protocells, individual self-replicating genes to chromosomes, from simple bacterial cells to eukaryote cells containing multiple organelles, and from unicellular life to multicellular organisms (Maynard Smith and Szathmary, 1997; Michod, 2000). Each transition is characterised by the “de-Darwinisation” of units at the existing level of organisation and the “Darwinisation” of collectives at a higher-level of organisation (Godfrey-Smith, 2009). That is, at the lower level, each component part loses its ability to replicate independently – the most fundamental property of a Darwinian unit – and after the transition, can replicate only as part of a larger whole (Maynard Smith and Szathmary, 1997). Conversely, before the transition, reproduction does not occur at the collective level; and after the transition the collective exhibits heritable variation in fitness that belongs properly to this new level of organisation (Maynard Smith and Szathmary, 1997; Okasha, 2006).

Whereas conventional evolutionary theory takes individuality for granted, and assumes the unit of selection is fixed, it is now recognised that Darwinian individuality is a matter of degree in many dimensions (e.g., degree of genetic homogeneity, degree of functional integration, degree of reproductive specialisation) (Godfrey-Smith, 2009). The research programme of the ETIs seeks to understand the processes, mechanisms and drivers that cause evolutionary processes to move through this space of possibilities (Okasha, 2006; Godfrey-Smith, 2009).

Social Evolution Theory and Kin Selection

Social evolution theory, a general approach to explain social behaviour, notes that it is evolutionarily rational to cooperate with someone that makes more copies of you (or your genes). Thus, in the case that interactors are genetically related or homogeneous, as they can be in the case of the cells within a multicellular organism, for example, this can explain the altruism of the somatic cells (West et al., 2015; Birch, 2017). The inclusive fitness perspective on ETIs, derived from this kind of social evolution theory, also offers a viewpoint that side-steps the whole problem. The question, as we posed it, asked why short-sighted self-interested individuals would act in a manner that opposes their individual interest to serve the interests of the whole. But an inclusive fitness perspective suggests this is wrong-headed because they were never different individuals in the first place – they were always of one genotype, and the multicellular organism is just a phenotype of this singular evolutionary unit. Problem solved?

For some purposes, it might be appropriate to view ETIs as an extreme point on the same continuum as other social behaviours. But genetic relatedness, kin selection or inclusive fitness do not explain all ETIs or even key examples such as multicellularity with homogeneous genetics.

First, acting with unity of purpose in multicellular organisms does not require genetic homogeneity (Grossberg, 1978; Levin, 2019, 2021b; Levin et al., 2019; Bechtel and Bich, 2021). Second, other transitions in individuality involve components that are genetically unrelated, for example, the transition from self-replicating molecules to chromosomes, and the transition from bacterial cells to eukaryote cells with multiple organelles (Maynard Smith and Szathmary, 1997). Third, and perhaps most important, social evolution theory only explains the cooperation that is expected given a certain interaction structure (i.e., determining whether those that interact are related). It does not explain changes in interaction structures that are necessary to increase or decrease genetic assortment, let alone to reach such extremes. Moreover, the genetic definition of individuality fails to address all the questions that are really interesting about individuality – not least how individuality changes from one level of organisation to another. By asserting that, both before and after the transition, the only relevant individual was the gene, this approach fails to address the meaning of the individual at all. Of course, it is common that the cells of multicellular organisms, especially animals, are for the most part genetically homogeneous. And given that they are, this can explain the apparently altruistic behaviours of soma. But this does not explain how this situation evolved, nor other instances of individuality that are not genetically homogeneous.

Evolved Change in Interaction Structure: Ecological Scaffolding and Social Niche Construction

One recent approach to explain how new interaction structures might evolve is ecological scaffolding (Black et al., 2020; Veit, 2021). That is, extrinsic ecological conditions, that are not in themselves adaptations and do not require selective explanation, create conditions where individuals live in a grouped or meta-population structure, e.g., microbial mats aggregated around water reed stems (Veit, 2021). The differential survival and reproduction of such sub-populations, e.g., in recolonising vacant locations, affords the possibility of higher-level selection (Wilson, 1975; Wade, 2016). Thus far in this account, nothing has evolved to support or maintain these structures; It is simply an assumption of fortuitous extrinsic conditions that alter population structure to create these different selective pressures. But from there it becomes more interesting. Given these conditions, individual selection at the lower level supports the evolution of characters that access synergistic fitness interactions, changing the relationships among the particles, and given that synergistic fitness interactions among particles have evolved, it is subsequently advantageous for particles to evolve traits that actively support this grouped population structure. Now the original extrinsic ecological conditions might change or cease, but the population structure necessary to support higher-level selection is nonetheless maintained, supported by the adaptations of the particles. That is, the ecological scaffolding becomes redundant, and is replaced by endogenous effects of characters produced by selection at the particle level. This ecological scaffolding thus provides a way to overcome the chicken-and-egg problem of the ETIs (by temporarily assuming the presence of a “chicken”). It does, however, depend on the initial assumption of extrinsic ecological conditions that happen to support higher-level selection in the first place. Moreover, if population structure changes evolutionary outcomes for individuals, and individuals have the ability to alter population structure, we must consider the possibility that rather than adapting to support the new level of selection they act to oppose or disrupt it, e.g., by evolving dispersal behaviours rather than aggregation behaviours.

These works and others in this area point to the need to explain how evolution modifies the parameters of its own operation when these parameters exhibit heritable variation (Powers and Watson, 2011; Ryan et al., 2016; Watson and Szathmary, 2016; Watson and Thies, 2019), i.e., to endogenise the explanation of its own parameter values (Bourrat, 2021b; Okasha, 2021). For example, with or without scaffolding, suppose that organisms have heritable variation in traits that modify their interaction structure with others, such as compartmentalisation or group size, reproductive synchronisation, or reproductive specialisation. These traits can modify relatedness – they change how related interactors are [not by changing anyone’s genetics but by changing who interacts with whom (Taylor and Nowak, 2007; Jackson and Watson, 2013)]. How does natural selection act on these traits? For example, initial group size is known to be an important factor in modifying the efficacy of (type 1) group selection (Wilson, 1975; Powers et al., 2009, 2011), and individuals may have traits that modify initial group size (e.g., propagule size) (Powers et al., 2011). The term “social niche construction” refers to the evolution of traits that alter interaction structure, i.e., who you interact with and how much (Powers et al., 2011; Ryan et al., 2016). In some circumstances, natural selection will act to modify such traits toward structures that increase cooperation (Santos et al., 2006; Powers et al., 2011; Jackson and Watson, 2013). This social niche construction has potential advantages over ecological scaffolding because it does not presuppose exogeneous reasons for favourable population structure (that is later canalised by endogenous traits), but shows conditions where such population structure can evolve de novo.

Multi-Level Selection and Individuation Mechanisms

In contrast to the kin selection approach (i.e., focussing on the lower-level units and whether they interact with other units that are related), the multi-level selection approach conceives higher-level organisations (collectives) as units of a higher-level evolutionary process (Wilson, 1997; Okasha, 2006; O’Gorman et al., 2008). The multi-level Price approach, for example, attempts to divide the covariance of character and fitness into “between collective selection” (acting at the higher level) and “within collective selection” (acting at the particle level) (e.g., Bourrat, 2021b). Clarke (2016) proposes that we might assess the degree of individuality as “the proportion of the total change that is driven by selection at the higher level,” and like Okasha (2006), suggests that an ETI involves a decrease in the proportion of selection driven by the lower level and an increase in the proportion driven by selection at the higher level. In the limit of complete Darwinisation of the collective, and complete de-Darwinisiation of the particles, this becomes maximal.

One problem with this analysis is that, as Wimsatt (1980) points out, the presence of heritable variation in reproductive success at the collective level is not in itself “sufficient for the entity to be a unit of selection, however, for they guarantee only that the entity in question is either a unit of selection or is composed of units of selection.” Moreover, Bourrat argues that “there is no fact of the matter as to whether natural selection occurs at one level or another” because “when evolution by natural selection occurs at one level, it does so concomitantly at many other levels, even in cases where, intuitively, these levels do not count as genuine levels of selection” (Bourrat, 2021a). Collectives can be defined at any level and with any boundary, and their character-fitness covariance can be measured, and yet we could have equally well drawn boundaries in any other way. We would have got different quantities (if the interactions among particles are non-linear), but nothing about these quantities tells us how to identify which units are playing a factually causal role in the evolutionary process. Thus, even when there are salient functional interactions among the particles within a collective, it can be hard to disentangle what is happening at one level and what is happening at another, or more exactly, what caused things to happen at one level or another (see also cross-level by-products (Okasha, 2006).

Bourrat (2021a) goes on to provide an extension to the multi-level Price approach which divides the response to selection (the product of selection and heritability) into a component that is functionally additive (aggregative) and a non-additive component. The latter non-aggregative component is associated with the collective response to selection that is not explained by the particle response to selection Thies and Watson (2021). This is useful in drawing attention to the nature of the interactions among particles and its significance in identifying the salient level of causal processes. It also emphasises how a change in heritability at the collective level could alter the ability to respond to selection at the collective level. We will develop related ideas below (but argue that in order for higher-level selection to alter evolutionary outcomes, the type of non-aggregative interaction needs to be more specific).

Beyond matters of quantifying individuality, we also aim to better understand the mechanisms that cause these changes (e.g., changes in the ability to produce heritable fitness differences at the collective level) and how selection acts on these mechanisms. In other words, in addition to knowing whether the evolutionary change in a character is explained by lower-level or higher-level evolutionary units, and quantifying how this balance might alter in the course of a transition, we also want to explain how and why this balance changes. We want to explain the mechanisms by which natural selection changes the identity of the evolutionary unit. Here theory is less well developed.

Clarke offers the concept of “individuation mechanisms” that influence “the extent to which objects are able to exhibit heritable variance in fitness” (see also Godfrey-Smith, 2009). These might include developmental bottlenecks, sexual reproduction, egg-eating behaviours, germ separation, immune regulation and physical boundaries (Clarke, 2014, 2016). In general such mechanisms may affect genetic variance (by affecting the extent to which genetic variation is heritable at the collective level), the fitness effects of that variation, or other (non-genetic) sources of heritable variance in fitness. But still, we want to know how selection, more specifically, bottom-up selection, acts on such traits. For example, we need to be able to explain why lower-level selection would act on such traits in a manner that increases non-aggregative components of the collective heritability and response to selection, and not in a manner that decreases it. Intuitively, one might imagine that the reason the traits evolve, the source of their selective advantage, derives specifically from the change in the collective-level response to selection – e.g., the non-aggregative component identified by Bourrat. The models of social niche construction demonstrate that this is possible in some circumstances. However, we cannot assume that it is in the interest of particles to reduce their ability to respond to selection independently, and make themselves dependent on the collective to respond to selection. Given that such traits must be evolved through a particle-level response to selection (since a collective-level response to selection does not exist until after the transition), and that a collective-level response to selection may ultimately create a situation that opposes their direct fitness (e.g., that of somatic cells), this direction of travel is not at all for granted. As yet, these approaches do not tie together the effects that such traits have on the level of individuality with the selection that causes such traits to evolve.

Types of Fitness Interactions: Emergence, Non-aggregative Interactions and Collectives That Change Evolutionary Outcomes

In order for a new level of biological organization to have a meaningful causal role as an evolutionary unit, evolutionary outcomes of the collective must not be simply summary statistics over the lower level units they contain (Okasha, 2006; Bourrat, 2021a). Being a bone fide evolutionary unit requires heritable variation in fitness (Lewontin, 1970; Okasha, 2006), and being a new evolutionary unit (that is “more than the sum of the parts”) requires heritable fitness differences at the new level that are not just the average of heritable fitness differences at the lower level (Okasha, 2006). Otherwise, how can it be that collective characters, and not particle characters, determine particle fitness? If particle characters determine collective characters, and collective characters determine the fitness of the particles they contain, then particle characters determine particle fitness. We can write this as follows. If the sum (or other aggregative property) of particle characters (Σz) in a collective determines (linearly) the reproductive output of the collective (Ω), and the reproductive output of the collective determines (linearly) the fitness of a particular particle therein (ω₁), then the value of that particle determines its fitness (z₁ → ω₁), and hence the collective is explanatorily redundant in describing the selection on particles (Eq. 1).

$[\sum \text{z}\to \mathrm{\Omega }\to {\mathrm{\omega }}_1]\Rightarrow [{\text{z}}_1\to {\mathrm{\omega }}_1](1)$

The point is perhaps better made by focussing on changes in characters and fitnesses. Thus if the change in a character (Δz₁) determines a change in collective fitness (ΔΩ), and a change in collective fitness determines a change in particle fitness, then changes in particle fitness are determined by changes in particle characters (Δz₁ → Δω₁), and the collective is redundant.

$[\mathrm{\Delta }{\text{z}}_1\to \mathrm{\Delta }\mathrm{\Omega }\to \mathrm{\Delta }{\mathrm{\omega }}_1]\Rightarrow [\mathrm{\Delta }{\text{z}}_1\to \mathrm{\Delta }{\mathrm{\omega }}_1](2)$

So, given that collective characters and hence collective fitness are entailed by the characters of the particles they contain, how can collectives and not particles be the reason that one particle character was selected and another was not? The means by which collectives can somehow break the association between particle character and particle fitness will be a key focus of what follows.

To create a meaningful causal role for the collective, there is often an appeal to the notion of creating something qualitatively new at a higher level of organisation, a.k.a. emergence. This can be difficult to define (Corning and Szathmary, 2015; Bourrat, 2021a), especially since we generally want to retain the assumption that salient differences at the higher level require salient differences at the lower level (supervenience). It is agreed, at least, that in order for the collective to be a meaningful evolutionary unit, fitness interactions between components cannot be linearly additive (Corning and Szathmary, 2015; Bourrat, 2021b). If the fitness-affecting character of the collective is simply the sum or average of the particles, or more generally, an aggregative property of the parts (Bourrat, 2021b), then the distinction between higher and lower levels of selection is merely conventional, not substantial (Bourrat, 2021a).

Bourrat examines cases where the relationship between z and collective character, Z (and hence Ω), is non-linear (Bourrat, 2021b). For example, suppose a change in the character of a particular particle (Δz₁) given a particular context where the sum of other particle characters has a particular value (Σz_x = p), results in a change to collective fitness and hence a change to particle fitness (Δω₁). Now consider the same change, Δz₁, in a different context where the sum of other particle characters has a different value (Σz_x ≠ p), i.e., we are at a different point on the non-linear curve relating the particle characters to collective character. If this has a different effect on collective fitness (ΔΩ′ ≠ ΔΩ) and hence a different effect on the fitness of this particular particle (Δω₁′ ≠ Δω₁) then it does not follow that this change to particle character results in a change in its fitness that is independent of context (Eq. 3). In this sense, the collective is not explanatorily redundant.

$\begin{array}{c}\hfill [\mathrm{\Delta }{\text{z}}_1:(\sum {\text{z}}_{\text{x}}=p)\to \mathrm{\Delta }\mathrm{\Omega }\to \mathrm{\Delta }{\mathrm{\omega }}_1]\text{and}[\mathrm{\Delta }{\text{z}}_1:(\sum {\text{z}}_{\text{x}}\ne p)\to \mathrm{\Delta }{\mathrm{\Omega }}^{\prime }\to \mathrm{\Delta }{\mathrm{\omega }}_1^{\prime }]\hfill \\ \hfill \nRightarrow [\mathrm{\Delta }{\text{z}}_1\to \mathrm{\Delta }{\mathrm{\omega }}_1]\text{nor}[\mathrm{\Delta }{\text{z}}_1\to \mathrm{\Delta }{\mathrm{\omega }}_1^{\prime }]\hfill \end{array}(3)$

Corning and Szathmary (2015) and Bourrat (2021b) describe some examples of possible scaling relationships, such as step functions or thresholds, and super linear curves, that effect a non-linear relationship between the characters of parts and the characters of wholes. The salient criterion of such functions is “whether or not there are combined effects that are interdependent and cannot be achieved by the “parts” acting alone.” or “produce an interdependent, qualitatively different functional result” (Corning and Szathmary, 2015).

However, although Δω₁′ and Δω may be different in any such non-linear function, they could nonetheless have the same sign. This is the case whenever the function relating Σz to Z, and Ω, is monotonic (such as a diminishing returns or economy of scale relationship). In this case it will nonetheless be the case that an increase (a particular directional change) in particle character (↑z₁) will systematically produce an increase in particle fitness (↑ω₁) regardless of context. That is, for monotonic relationships, the collective is explanatorily redundant in determining the direction of selection on particle characters (Eq. 4) (even though the collective character may be non-aggregative).

$[\uparrow {\text{z}}_1\to \uparrow \mathrm{\Omega }\to \uparrow {\mathrm{\omega }}_1]\Rightarrow [\uparrow {\text{z}}_1\to \uparrow {\mathrm{\omega }}_1](4)$

This means that, although the effect of selection at the collective level may be different from selection at the particle level, it is always affected by particle characters in the same direction. This does not describe cases where higher-level selection changes evolutionary outcomes, i.e, changes in which of two variants are favoured, only how quickly the preferred variant will fix. Such monotonic non-linearities alter only the magnitude of selection, and thus might alter how quickly selection modifies the frequency of a type, but not which type is favoured. Heritable variation in the fitness at the collective level thus remains explanatorily redundant in determining which particle character is favoured by selection.

We think this is not a minor point because altering evolutionary outcomes in this sense – where individual and collective levels of selection “want different things” - is central to ETIs. Restricting attention to monotonic relationships excludes scenarios where the creation of a higher level evolutionary unit causes the lower level units to “do something they didn’t want to do” such as evolve characters that decrease their individual fitness (e.g., somatic cells, or other reproductive division of labour), or decrease fitness differences between particles (e.g., fair meiosis, mitochondrial reproductive regulation, or other policing strategies). Although other types of non-linearity where the interaction is not monotonic are sometimes mentioned (in particular a division of labour, as developed below) there is perhaps a reason why the worked examples in previous work have not addressed this. Specifically, if the direction of selection on particle character is different under particle selection and collective selection, such that higher-level selection opposes the phenotypes favoured by lower-level selection, why would bottom-up selection create a new evolutionary unit that opposed its interests in this way?

It is relatively easy to explain why selective conditions can be different (even reversed) after a transition compared to what they were before a transition; as per scenarios of strong altruism, for example. What is not easy to explain is how traits (or the parameters of individuating mechanisms) that change evolutionary outcomes in this way themselves evolve. Before a transition the only entities that can be evolving are particles not collectives, so it must be some character of particles that explains these changes in individuality. How can individual selection favour characters that serve collective interest at the expense of the short-term self-interest of particles?

New Data and Insights

A number of current inter-related topics provide new perspectives and new data that contribute to a different way of looking at the evolutionary transitions and individuality.

When the Direction of Selection on Components Is Context Sensitive - Division of Labour Games, Nonlinearly Separable Functions, Non-decomposable Phenotypes, and Comparison With Other Non-aggregative Functions

Intuitively, collectives could alter evolutionary outcomes if the way in which the character of a particle affects the fitness of the particle depends on the other particles present. More specifically, the direction of selection produced by a change in the character of a particle must depend on the other particles present.

Interactions of this form can be written as follows. Suppose that in one context (say when a neighbouring particle, z₂, has a positive character value or a value above a given threshold, θ) increasing particle fitness requires an increase in a particular particle character, and yet in another context (e.g., z₂ < θ) increasing particle fitness requires a decrease in the same particle character. In this case, neither an increase nor a decrease in particle character reliably determines an increase in particle fitness (Eq. 5). Accordingly, although collective character determines the direction of selection on particles, particle character does not (Watson and Thies, 2019).

$\begin{array}{c}\hfill [\uparrow {\text{z}}_1:{\text{z}}_2>\mathrm{\theta }\to \uparrow \mathrm{\Omega }\to \uparrow {\mathrm{\omega }}_1]\text{and}[\downarrow {\text{z}}_1:{\text{z}}_2<\mathrm{\theta }\to \uparrow \mathrm{\Omega }\to \uparrow {\mathrm{\omega }}_1]\hfill \\ \hfill \nRightarrow [\uparrow {\text{z}}_1\to \uparrow {\mathrm{\omega }}_1]\text{nor}[\downarrow {\text{z}}_1\to \uparrow {\mathrm{\omega }}_1]\hfill \end{array}(5)$

In such cases, the sign of the relationship between particle character and particle fitness depends on what other particles are present. When interacting components are within one evolutionary unit (e.g., genes), this kind of sign change in fitness effects is known as reciprocal sign epistasis (Weinreich et al., 2005). But before a transition, the components are different evolutionary units and can instead be construed as players interacting in a game (Hofbauer and Sigmund, 1988). In this case, this kind of sign change in fitness effects is described by a division of labour game (Ispolatov et al., 2012; Tudge et al., 2013, 2016), requiring individuals to adopt complimentary heterogeneous roles (Hayek, 1980; Tudge et al., 2013; Watson and Thies, 2019) [e.g., reproductive specialisations such as germ/soma (Godfrey-Smith, 2009)]. The significance of role specialisation and division of labour (or combination of labour) in ETIs has been noted by many writers (e.g., Bonner, 2003; Kirk, 2005; Ratcliff et al., 2012; Simpson, 2012; Wilson, 2013; Corning and Szathmary, 2015), but not formally developed in the manner that follows.

In this case, and only in this case, there is no particle character that maximises particle fitness but there is nonetheless a collective character (e.g., complementarity or coordination of particles) that cannot be reduced to the character of individual particles, and this collective character confers (collective fitness and hence) particle fitness. This is a basic but fundamental way of describing a non-decomposable collective character; i.e., a collective character, entailed by particle characters, that confers particle fitness, and yet there is no particle character that systematically confers increases in particle fitness over all contexts.

For what comes later, it will be useful to note that a division of labour scenario is the game theory equivalent of a non-linearly separable function in learning theory (Box 1). This provides a formal way to characterise what is important about these functions in evolutionary terms because the distinction between linearly separable and non-linearly separable functions is fundamental in machine learning for the same reasons. That is, the effect of one input changes sign depending on the other input (Box 1). We refer to collective characters underpinned by such a function as a non-decomposable collective character (Figure 1). That is, the collective character cannot be decomposed into a sum of contributions from individual characters (non-linearity) – and more specifically, the sign of the effect of changing one particle character is not independent of its context (non-decomposable).

BOX 1. Non-linearly separable functions.

In machine learning, examples of non-linearly separable functions for two binary inputs are logical exclusive-or (XOR) and if-and-only-if (IFF), meaning that the inputs are different or the same, respectively. In such a function, the contribution of each component input to the output value changes sign depending on the value of another input. For example, if A = true then the output [A XOR B] is made true by B = false. But if A = false then the output [A XOR B] is made true by B = true (for example, if this cell is soma that cell should be germ, and vice versa) (Figure B1). In functions that are linearly separable (i.e., unitary functions IDENTITY, NOT, and other two-argument functions OR, AND, NAND, and NOR) the effect of an input “shows-through” to the output (or cannot be “decoupled” from the output). That is, if there is a context (a set of values for the other inputs) where increasing a given input increases the output, its effect cannot be the reverse in another context. Put simply, in non-linearly separable functions the sign of the effect of an input on the output depends on an interaction with other inputs. This is a simple way of defining what it means for an output to be non-decomposable or “more than the sum of the parts” in a formal sense, i.e., not decomposable into a sum of sub-functions over individual inputs. Technically, the term linearly separable refers to the idea that dividing the multidimensional input space into points where the output is true and those where the output is false, only requires one straight line (or, for more than two inputs, one hyperplane). In a non-linearly separable function, in contrast, this is not possible (Figure B1). A corollary of this is that linear directional movements through input space can traverse through regions where the output is true, then false, then true again. Put differently, getting from one point where the output is true, to another region where the output is true, without going through a region where the output is false, can require either a nonlinear trajectory or a “jump” in input space where several input variables change simultaneously in a specific manner. It is not guaranteed that there is one variable that, on its own, can be changed incrementally to reach the other region (nor any linear combination of input variables) (see also Figure B3.B). This is a simple way to formalise what is meant by a scenario that requires “coordinated action,” i.e., variability that maintains a particular output requires specific coordinated simultaneous change in multiple variables.

FIGURE B1

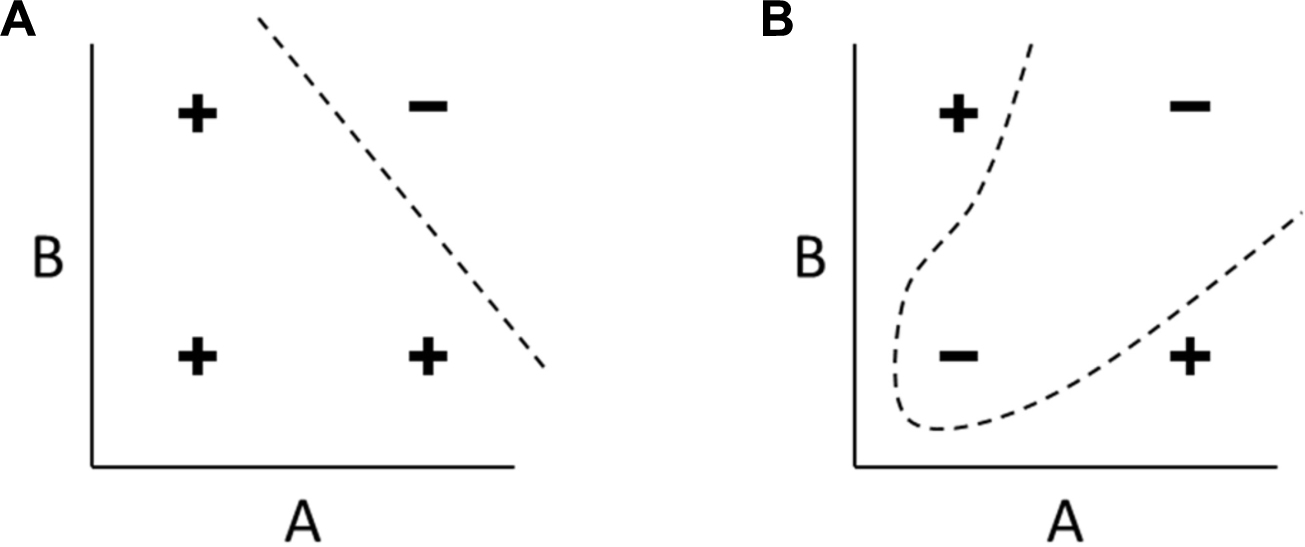
Figure B1. Linearly separable and non-linearly separable functions. (A) A linearly separable function of two inputs A and B. The four combinations of high and low values are classified as either positive or negative. In any linearly separable function, like this example representing NAND(A,B), the positive and negative examples can be separated with a linear decision boundary (another example is shown in Figure B3.B). (B) In any non-linearly separable function, like this example representing XOR(A,B), no such linear decision boundary can be drawn, and separating the two classes requires a non-linear boundary.

FIGURE 1

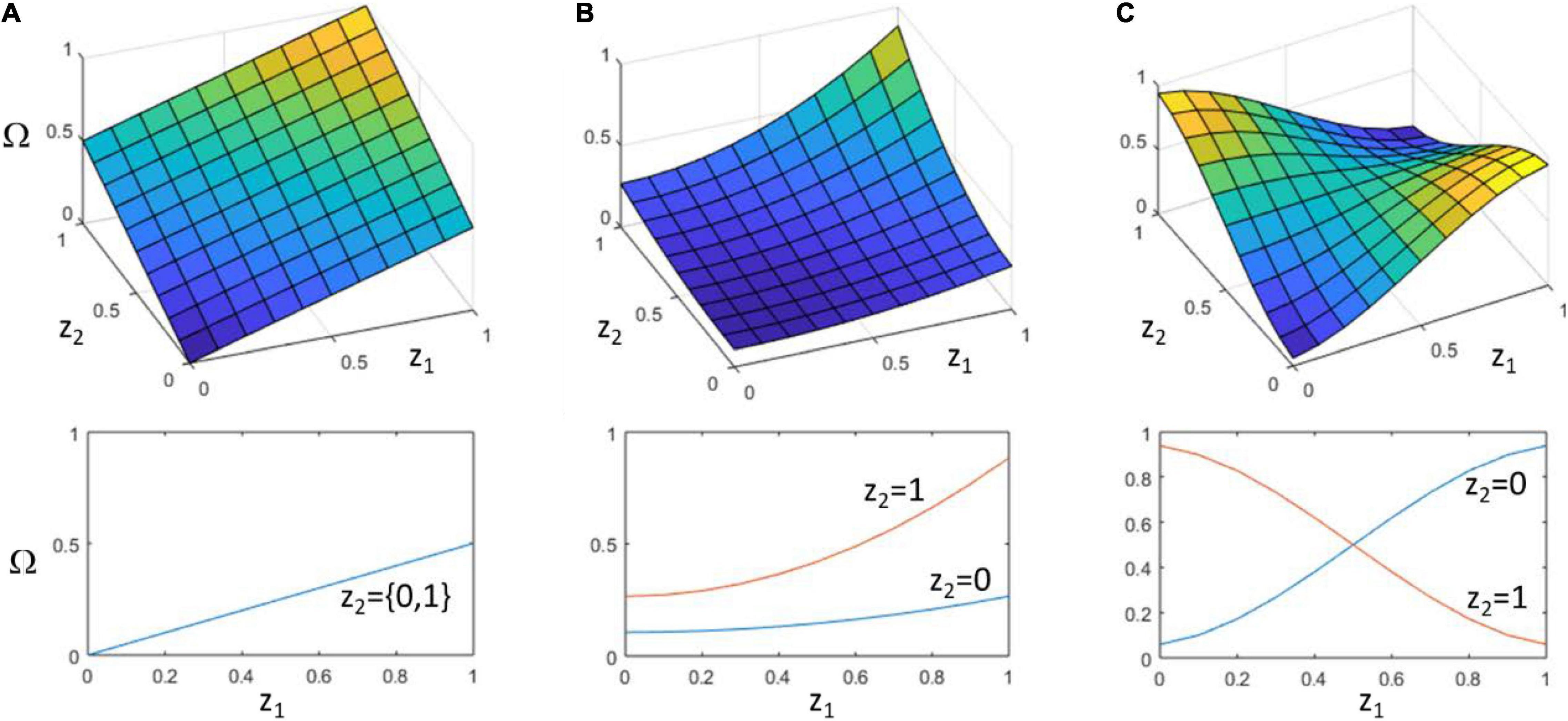
Figure 1. Different possibilities for the relationship of particle characters to collective character. (A) Additive (no interaction). Two particles, with characters z₁ and z₂, each contribute to collective character, Ω, independently. That is, changes in z₁ always have the same effect on Ω regardless of the value of z₂ and vice versa. (B) Synergistic interaction. The effect of z₁ on Ω increases with the value of z₂. The two together thus have a synergistic, i.e., super-additive, effect on collective character. (C) Non-decomposable interaction. The sign of the effect of z₁ on Ω can be reversed by the context of z₂. The class of particle character configurations that confer high values of Ω (yellow) is defined by a non-linearly separable function over z₁ and z₂, such as z₁ XOR z₂ (Box 1) (this is not the case in (B) which remains linearly separable, i.e., z₁ AND z₂). The lower panels show the value of Ω as a function of z₁. (A) insensitive to z₂, (B) slope of response depends on value of z₂ but does not change sign, (C) sign of response depends on value of z₂. Note that in both (B,C), Ω is a non-aggregative function of the particle characters, but only (C) is non-decomposable in the sense of being non-linearly separable.

Note that the statistical average of curves in Figure 1C can be flat (i.e., the context-free contribution of a single particle character to collective character is zero, averaged over all contexts). This does not mean that Ω is insensitive to particle characters; the functional interactions of particles matter significantly in determining the collective character. In this sense, non-decomposability is intimately related to the issue of separating particle character from particle fitness, and the possibility that collective character (and not particle character) determines the fitness of the particles it contains (even though collective character supervenes on particle characters). Note that, confirming the intuition of Okasha (2006), non-decomposability must be defined in terms of traits or characters not particle fitnesses. It is not logically possible for particle fitness to control collective fitness and not control its own fitness. But it is possible for particle traits to determine collective fitness and not control its own fitness. The particle character matters to its fitness, but the way it matters (the direction of selection conferred by a change in particle character) is not determined by itself independently, i.e., free from context.

Note that non-decomposability is a stronger condition than (a refinement of) non-aggregative interactions (Bourrat, 2021b). Non-aggregative interactions include both monotonic non-linear interactions and these non-linearly separable scenarios, but previous examples of non-aggregative interactions have largely been monotonic and thus linearly separable. It is easy to see why: Looked at from the particle level, if a particular change in particle character can increase its fitness in one context and the same change can decrease it in another, how can particles evolve to control and take advantage of collective benefits? Looked at from the collective level, collectives containing an appropriate complement of particle types can solve a division of labour game, and will thus be fitter than a collective that does not. But this creates a problem for the heritability of the collective – the heterogeneous functions with homogeneous fitness (HFHF) problem (Box 2). To solve this problem, and understand how selection at the lower level can find solutions to non-decomposable problems we need to look at higher-level individuals not as containers of heterogeneous but inert particles, but as dynamical systems that “calculate” collective phenotypes through the interactive behaviours of particles. The domain of such dynamics are the processes of development. How can development perform such computations?

BOX 2. The “heterogeneous functions with homogeneous fitness” (HFHF) problem.

For particle fitness to be determined by collective character and not particle character, a division of labour game is required (“When the Direction of Selection on Components Is Context Sensitive - Division of Labour Games, Nonlinearly Separable Functions, Non-decomposable Phenotypes, and Comparison With Other Non-aggregative Functions”). Solving a division of labour game requires individuals to be different to each other. But if a collective contains multiple types of individuals, how does it reproduce? If reproduction occurs through a single-celled bottleneck or unitary propagule this creates homogeneous descendant groups (and homogeneous groups cannot be solutions to a division of labour game). If reproduction occurs through fissioning the group, or any propagule greater than size one, and individuals are intrinsically different, then selection at the individual level will act on these differences, driving changes in the composition of the group. The latter appears as transmission bias opposing the ability to respond to selection at the higher level (Okasha, 2006). To remove this problem and stop selection at the lower level from interfering with selection at the collective level, the fitnesses of the components must be equalised (de-Darwinised). Individuality thus requires collectives to solve the “heterogeneous functions with homogeneous fitness” (HFHF) problem (Watson and Thies, 2019). Heterogeneous functions are necessary to create fitness differences at the collective level (a.k.a. Darwinisation of the whole); and homogeneous fitness is required to remove fitness differences at the individual level (a.k.a. de-Darwinisation of the parts) (Godfrey-Smith, 2009). But how can particles be functionally different and have the same fitness? Solving the heterogeneous functions with homogeneous fitness problem requires individuals to be plastic (Watson and Thies, 2019). This is logical; untying function from fitness requires either plasticity of function or plasticity of fitness. Functional (or phenotypic) plasticity allows individuals to be intrinsically the same (e.g., same genotype and hence same fitness) but act differently (e.g., different phenotype and function). Alternatively, reproductive plasticity (e.g., where reproduction is cued by or enacted by the context of the collective, rather than by autonomous reproductive mechanisms of the particles) allows individuals to be intrinsically different (providing functional complementarity) but reproduce the same (e.g., synchronised reproduction of chromosomes equalises fitnesses) (Watson and Thies, 2019). In evolutionary transitions, these two different ways of solving the HFHF problem are manifest in two different kinds of transitions (Queller, 1997; Watson and Thies, 2019). Fraternal transitions solve the HFHF problem with phenotypic plasticity (and homogeneous genetics) whereas egalitarian transitions utilise reproductive plasticity (and heterogeneous genetics).

New Perspectives on Organismic Individuality – Development and Basal Cognition

Organismic concepts of individuality, like evolutionary concepts of individuality, can also be hard to pin down (Clarke, 2010; Levin, 2019). Properties such as functional integration, spatial continuity or physical cohesion, coordinated action and developmental dependency, for example, may or may not be aligned with notions of evolutionary or Darwinian individuality (Godfrey-Smith, 2009). Tying individuality to an evolutionary unit identified by its genetics quickly unravels (Godfrey-Smith, 2009; Clarke, 2010). Clonal growth of a bacterial colony may be genetically homogeneous, for example, but does not constitute an organismic individual by most accounts. And even normal looking natural multicellular organisms can be profoundly genetically heterogeneous. For example, planaria are multicellular organisms that can reproduce by fissioning (without a cellular population bottleneck) and thus can accumulate somatic diversity over many generations (Lobo et al., 2012). Nonetheless, planaria exhibit development, morphology and behaviour just like genetically homogeneous multicellular organisms. At a smaller scale, the mechanisms of chromosomal reproduction and (fair) meiosis are tightly coordinated within cells but the chromosomes are genetically heterogeneous. And the behaviour of individual unicellular organisms is, of course, far from a linear combination of gene-products. At a higher level of organisation, holobionts, for example, are sometimes offered as a candidate for a higher-level individual – not because of shared genetics but because of coordinated functional integration and dependencies. Some argue for a view of the biosphere as a whole that is organismic in kind, despite the lack of conditions necessary to be an evolutionary unit. How do we distinguish a collection of multiple organisms that is merely complicated from a new level of individuality?

In multicellular organisms, morphogenesis and its disorder, the breakdown of individuality known as cancer, is intrinsic to individuality (Deisboeck and Couzin, 2009; Doursat et al., 2013; Rubenstein et al., 2014; Friston et al., 2015; Pezzulo and Levin, 2015, 2016; Slavkov et al., 2018; Pezzulo et al., 2021). In most organisms cancerous growths originate from genetically homogeneous tissue and, conversely, in planaria, despite their heterogeneity, cancers are rare. New work shows that cancerous growth can be induced by a disruption of electrical coordination signals between cells and in some cases can be reversed by re-establishing them, without genetic changes (Levin, 2021a). Meanwhile, new experiments demonstrate that artificial multicellular genetic chimera can also exhibit holistic behaviours and functions (Blackiston et al., 2021). These recent experiments and considerations add to the growing evidence that genetic homogeneity is neither necessary nor sufficient for organismic individuality. Is functional integration more important? And what kind of functional integration is necessary and sufficient?

Recent work has begun to apply the tools of collective intelligence and cognitive neuroscience to describe “the signals that turn societies into individuals?” (Lyon et al., 2021a,b). In particular, this includes consideration of behaviours and their reward structures or incentives. Like the considerations of evolutionary individuality above, if the incentives of the whole (its macro-scale reward structures and sensory-action feedbacks) are just summary statistics over the incentives of the parts (micro-scale reward structures and sensory-action feedbacks), then the individuality of the whole is conceptually degenerate. Levin recently makes the case that organismic individuality is appropriately ascribed to systems that are capable of information integration and collective action at some spatiotemporal scale (regardless of whether they are genetically related or not) (Levin, 2019, 2021b). This is a cognitive notion of “self” (“cogito, ergo sum” perhaps?). But it does not require neurons or brains; Basal cognition refers to processes of information integration and collective action that occur in non-neural substrates – such as in the development of morphological form (Pezzulo and Levin, 2015; Manicka and Levin, 2019a,b; Lyon et al., 2021a,b). It refers to cognition in an algorithmic sense that is substrate independent (Levin and Dennett, 2020). “[F]unctional data on aneural systems show that the cognitive operations we usually ascribe to brains—sensing, information processing, memory, valence, decision making, learning, anticipation, problem solving, generalization and goal directedness—are all observed in living forms that don’t have brains or even neurons” (Levin et al., 2021). What is important is the presence of functional and informational interactions (signals and responses of any nature) that facilitate information integration and the ability to orchestrate cued responses that coordinate action. In this manuscript we develop this cognitive notion of self by making explicit equivalences with computational models of individuality based on connectionist notions of cognition and learning. This provides the dynamical substrate in which interacting particles can collectively compute solutions that solve the HFHF problem.

Particle Plasticity and Collective Development

Solving the heterogeneous functions with homogeneous fitness problem requires individuals to be plastic (Watson and Thies, 2019; Box 2). Plasticity allows function and fitness to be separated such that the phenotype of the particle (e.g., whether it is type A or type B) does not determine its reproductive output (Eq. 5). Nonetheless, when this plasticity is used to coordinate phenotypes with other particles, it can access the non-decomposable component of collective fitness. Thus the ability to adopt a phenotype that is complementary to its neighbour (such as “becoming an A when with a B” or “becoming a B when with an A”) confers a consistent selective signal (toward being different for XOR, or toward being the same for IFF, Box 1). Plasticity thus pushes a collective trait like “diversity” down to a particle trait like “an ability to plastically differentiate.” This introduces the notion of a second order particle trait – a trait about relationships between things rather than the things themselves – in contrast to a first-order or context free trait. That is, a second-order trait, such as a differentiating or coordinating behaviour, controls the combinations of first-order characters. It is thus an individual character which increases the heritability of a non-decomposable collective character (e.g., phenotypic diversity necessary to solve a division of labour game).

Note that although the direction of selection on a first-order individual character will reverse depending on context in a division of labour game, the direction of selection on the second-order character (e.g., favouring being different rather than being the same) is consistent for a given game. It is then possible to attribute particle fitness to this (second-order) particle character. This appears to put us back at square one with a collective that is explanatorily redundant (Eq. 4). But note that second-order characters such as plasticity really are different from first order characters because they are about relational attributes. For example, a particle cannot be “the same” or “different” on its own, and a phenotype that is sensitive to the context of others cannot be assigned a fitness until the others are present and the plasticity is enacted (i.e., development happens). Intuitively, although the property of being able to plastically differentiate from your partner is a property that a single particle can have, the ability to solve a division of labour game is not a property that a single particle can have. This collective property is the result of a basal “calculation” performed by multiple particles within the collective in interaction with each other. When this functional outcome (a solution to the division of labour game) is a non-linearly separable function of the individual particle characters, the fitness of the particles (and more specifically, the direction of selection on particle characters) that results cannot be attributed to those individual particle characters, and accordingly, the collective is not explanatorily redundant. This view thus resolves the tension between the two desiderata of (i) collectives that are not explanatorily redundant and (ii) collective properties that are nonetheless determined by particle properties.

We thus identify particle plasticity (enabling coordinated phenotypes or coordinated reproductive behaviour between particles) as a concrete type of individuation mechanism. This is a particularly significant type because it enables access to components of selection that cannot be otherwise be accessed precisely when functional interactions between particles have a non-decomposable relationship. Because the ability to coordinate with others is a characteristic that can be heritable at the particle level, and the result of this ability is a coordinated collective phenotype that would not otherwise be heritable, this facilitates a response to selection at the collective level that was not previously present. This particular kind of particle-level trait therefore connects directly with the particular kind of non-aggregative component of selection, and the collective level heritability, required to facilitate a response to selection at the collective level (Bourrat, 2021b).

How does the necessary plasticity evolve? Given the consistent direction of selection on plastic traits, Tudge et al. (2016) showed that natural selection can evolve phenotypic plasticity that solves division of labour games in two-player collectives with homogeneous genotypes, by evolving phenotypic sensitivity to one-another to facilitate complementary differentiation (Brun-Usan et al., 2020). Plasticity of any kind requires a timescale on which it can take effect – time to go from undifferentiated types (genotypes) to differentiated types (phenotypes), with communication between one particle and another to determine the coordinated outcome. In a fraternal transition, this temporally extended process effects a minimal separation between an “embryonic group” (undifferentiated components with the same genotype) and the “group phenotype” (differentiated components with coordinated complementary functions) – and the process that separates them is a minimal model for development.² To Darwinise the collective at the same time as de-Darwinising the components thus requires the components to be plastic and a developmental process that coordinates their behaviour. The Tudge model, involves just two particles and the one connection between them. It also assumes genetic relatedness which presupposes the higher-level unit of selection and its heritability. The evolution of relationships that solve the HFHF problem in more general networks of interactions (more than two players, thus more general games), and under bottom-up selection, has not yet been shown.

Note that development is not merely a process that modifies particle phenotypes and particle fitnesses, but more specifically, to produce fitness differences that properly belong to the collective level, it must solve a division of labour game. These considerations argue that developmental interactions required for evolutionary individuality must be able to coordinate solutions to non-decomposable functions of this type. This complexity exists in the substrate of basal cognition (implicated in organismic individuality) and at the timescale of organismic development. It suggests that organismic individuality (i.e., the plasticity of particles, and the developmental interactions that coordinate their differentiation) is intrinsic to Darwinian individuality (i.e., creating non-decomposable fitness differences that properly belong to the collective level). Recent expansions on the equivalence between evolution and learning provide a new theoretical framework to make sense of and unify these observations. In particular, these develop connectionist models of cognition and learning that focus on interactions (or second-order characters) in systems of many components and many interactions.

Connectionist Models of Cognition and Learning

Connectionism explores the idea that the intelligence of a system lies not in the intelligence of its parts but in the organisation of the connections between them. Each neuron might be computationally trivial (e.g., a unit that produces an output if the sum of its inputs is strong enough), but connected together in the right way, networks of such units have computational capabilities at the system level that are qualitatively different. For example, the output of a network can be a non-linearly separable function of its inputs (Box 3), and built-up in multiple layers (the outputs of one layer being the input to the next), such networks can represent any arbitrary function of its inputs. In networks with recurrent connections (creating activation loops), the system as a whole can have multiple dynamical attractors that produce particular activation patterns. The information that produces these patterns is not held in any one neuron (or any one connection) but in the organisation of the connections between them. Patterns stored in this way can be recalled through presentation of a partial or corrupted stimulus pattern, known as an “associative memory” (Watson et al., 2014; Power et al., 2015).

BOX 3. Depth is required to represent non-linearly separable functions.

In simple artificial neural networks (e.g., the Perceptron), the output of each neuron is a function of the sum of its weighted inputs (Minsky and Papert, 1988). The shape of this function is non-linear but monotonic (e.g., sigmoidal or threshold). For a single neuron, a particular input might influence the output more or less strongly than other inputs (depending on the magnitude of the weight), it might have a positive or negative influence (depending on the sign of its weight), and because of the non-linearity of the output function, the slope of this influence can be affected by its magnitude and the magnitude of other inputs. But the influence of a particular input on the output cannot change sign. Whether it increases or decreases the output is not sensitive to other inputs [by analogy, see the difference between magnitude epistasis and sign epistasis (Weinreich et al., 2005)]. This means that when directional changes in the input “show-through” to directional changes on the output they do so in a consistent manner, i.e., there cannot be two contexts where a given change on the input has the opposite effect on the output. This property makes it easy to incrementally adjust the weights toward a desired output function because the correct direction to change a weight does not depend on the state of other inputs. However, this means that a single neuron of this type, or a network with a single layer of such neurons, cannot compute non-linearly separable functions of the inputs, where the influence of one of the inputs must be reversed depending on the value of the other input (Box 1). To represent a non-linearly separable function an intermediate level of representation (or “hidden layer”) between inputs and outputs can be employed. A multi-layer Perceptron can compute A XOR B, for example, by computing OR(AND(A, NOT(B)), AND(NOT(A),B)), i.e., (A XOR B) = “A without B or B without A.” The sub-functions used in this construction (AND, OR, and NOT) are all linearly separable functions (computable with a single Perceptron). One node in the hidden layer, let’s call it h1, can thus compute h1 = AND(A,NOT(B)) and another node can compute h2 = AND(NOT(A),B), and then an output node can be stacked on top to compute OR(h1,h2). More generally, to represent a non-linearly separable function, a network must be able to compute higher-order or multiplicative terms – not just a weighted sum of inputs.¹

FIGURE B3

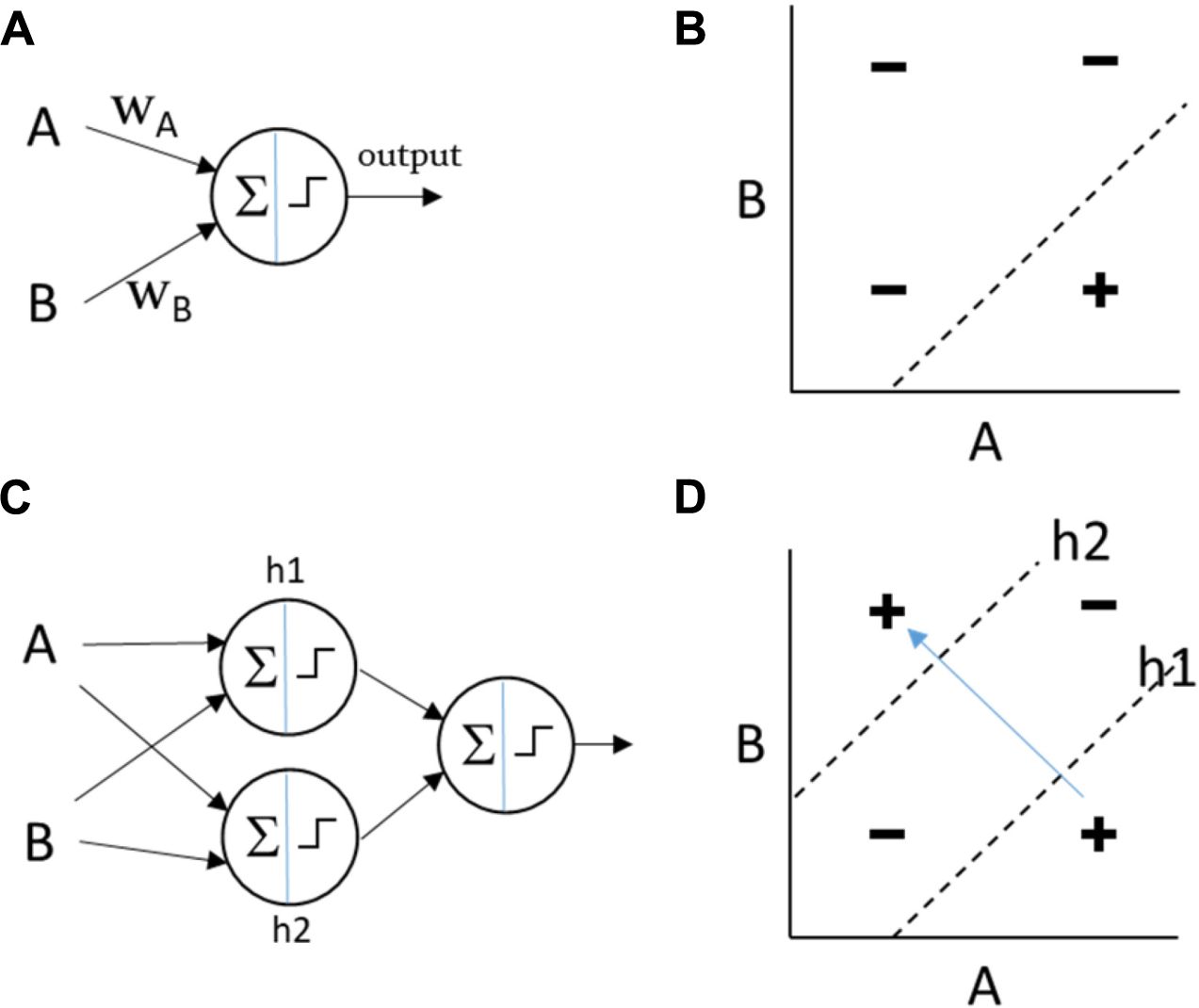
Figure B3. Shallow and deep computations. (A) A Perceptron of two inputs calculates an output that is a non-linear weighted sum of its inputs. (B) The Perceptron can represent any linearly separable function, such as this example, AND(A,NOT(B)). (C) The multi-layer Perceptron utilises “hidden” nodes to calculate intermediate functions which are fed forward to the output node. This can calculate any linearly or non-linearly separable function of its inputs. (D) In this example, h1 calculates AND(A,NOT(B)) and h2 calculates AND(NOT(A),B). The output node can calculate OR(h1,h2) such that the network as a whole represents the non-linearly separable function XOR(A,B). In a non-linearly separable function, moving between different positive regions (variation within the class without visiting regions that are not in the class) cannot be achieved by linear movements in the input space and instead requires “jumps” or coordinated “collective action” (simultaneous discontinuous changes in multiple variables).

System-Level Organisation Without System-Level Reinforcement

The organisation necessary for such distributed intelligence can arise through simple learning mechanisms – without design or selection. In most learning systems, the learning mechanism (used to adjust connections) is simply incremental adjustment that follows local improvements in an objective function. The objective function can be based on the accuracy of the output (supervised learning), the fit of the model to data (unsupervised learning), or the reward from behaviours that are generated from the model (reinforcement learning).³ Supervised learning requires an “external teacher” to define a desired output or target but reinforcement learning only requires a “warmer/colder” feedback signal and nothing more specific (reinforcement learning is commonly identified as the analogue of evolution by natural selection, but for bottom-up evolutionary processes we are particularly interested in unsupervised learning (Watson and Szathmary, 2016). Unsupervised learning does not depend on a reinforcement signal at all. It demonstrates conditions where the organisations necessary to produce system-level cognitive capabilities can arise through very simple distributed mechanisms operating without system-level feedback. A simple example is the application of Hebbian learning often paraphrased as “neurons that fire together wire together” (Watson and Szathmary, 2016). This mechanism changes relationships (under local information, i.e., using only the state of the two nodes involved in that connection) in a manner that makes the connection more compatible with the current state of the nodes it connects. Despite this simplicity, this type of learning is sufficient to produce an associative memory capable of storing and recalling multiple patterns, generalisation, data-compression and clustering, and optimisation abilities (“System-Level Optimisation Without System-Level Reinforcement”).

Learning is not the same as simply remembering something. Learning (apart from rote learning) requires generalisation – the ability to use past experience to respond appropriately to novel situations. That is, the ability to model (recognise, generate or respond to) not just the situations encountered in past experience but also novel situations that have not been encountered before. Connectionist models of cognition and learning exhibit generalisation naturally. When representing the pattern “11,” for example, the network could represent that the first neuron value is “1,” and independently, the second neuron value is “1.” But because networks can represent patterns with connections, it can also represent an association between the value of neuron 1 and the value of neuron 2 – in this case, that the values are the same. This “associative model” represents not just this particular pattern but the class of patterns where the values have the same relationship. In this example, it will also include “00.” In some situations, this might be a mistake – after all, “00” has no individual values in common with “11.” But the relationships between values (such as “sameness” or “differentness”) in a pattern are higher-order features that might represent useful underlying structures within a broader set, or “class,” of patterns. If consistent with past experience, learning such relationships enables generalisation that cannot be provided by treating individual components of the pattern as though they were unrelated. This enables neural networks, over an extraordinarily broad range of domains, to learn generalised models that capture deep underlying structural regularities from past experience and exploit this in novel situations.

System-Level Optimisation Without System-Level Reinforcement

Because of their ability to generalise, neural networks can also discover novel solutions to optimisation problems. Specifically, simple fully-distributed mechanisms of unsupervised learning, using only local information, can produce system-level optimisation abilities (Watson et al., 2011a,c). The initial weights of the network define the constraints of a problem and running the network from random initial states finds state patterns that correspond to locally optimal solutions to these constraints (Hopfield and Tank, 1986; Tank and Hopfield, 1987a,b). If the network is repeatedly shocked or perturbed, e.g., by occasionally randomising the states, with repeated relaxations in between, this causes it to visit a distribution of locally optimal solutions over time. Without learning, however, it cannot learn from past experience and may never find really good solutions. In contrast, if Hebbian learning slowly adjusts the weights of the network whilst it visits this distribution of locally optimal solutions, the dynamics of the system slowly changes. Specifically, these systems learn to solve complex combinatorial problems better with experience (Watson et al., 2009, 2011a,c). This is because the network learns an associative model of its own behaviour [known as a self-modelling dynamical system (Watson et al., 2011c)]. That is, it forms memories of the locally optimal solutions it visits, causing it to visit these patterns more often in future. This is because Hebbian changes to connections have the effect of creating a memory of the current state, making it more likely that the system dynamics visits this state in future by increasing its basin of attraction (i.e., the region of configuration space that is attracted to that state configuration by the state dynamics). Moreover, because it is an associative model, it is not simply memorising these past solutions but learning regularities that generalise. That is, any state configuration that shares that combination of states (consistent with that connection) is more likely to be visited. This means it also enlarges the dynamical attractors for other states it has not visited in the past but have similarly coordinated states. Over time, as relationships change slowly, the attractor that is enlarged the most tends to be a higher quality solution, sometimes even better than all of the locally optimal attractors visited without such learning (Mills, 2010; Watson et al., 2011a,b, c; Mills et al., 2014). The ability to improve performance at a task with experience is perhaps not unexpected in learning systems. But important for our purposes here, there is no reinforcement learning signal used in these models – system-level optimisation is produced without system-level feedback, using only unsupervised and fully-distributed Hebbian learning acting on local information, and this repeated perturbation and relaxation.

Furthermore, the principle of Hebbian learning is entirely natural; it does not require a mechanism designed or selected for the purpose of performing such learning. Specifically, Hebbian changes to connections result from incremental “relaxation” of connections, i.e., changes that reduce conflicting constraints, reduce the forces that variables exert on one another, or equivalently, decrease system energy (Watson et al., 2011a,c). This means that any network of interactions, where connections differentially deform under the stress they experience, can exhibit this type of associative learning and optimisation. The action of natural selection provides one such case in point when there is heritable variation in connections – even without system-level selection. This enables the computational framework of cognition and learning familiar in connectionist models to be unified with the evolutionary domain – hence evolutionary connectionism.

Evolutionary Connectionism

Evolutionary connectionism is a new theoretical framework which formalises the functional equivalence between the evolution of networks and connectionist models of cognition and learning (Watson et al., 2016; Watson and Szathmary, 2016). This work shows that the action of random variation and selection, when acting on heritable variation in relationships, is equivalent to simple types of associative learning. Accordingly, these models can be translated into the domain of evolutionary systems to explain the evolution of biological networks with system-level computational abilities (Watson et al., 2010; Kounios et al., 2016; Kouvaris et al., 2017; Brun-Usan et al., 2020). This work demonstrates mechanisms of information integration in biological interaction networks, equivalent to simple (but powerful) types of neural network cognition.

In some cases, these models characterise the evolution of developmental organisation (evo-devo) where the interactions are inside a single evolutionary unit (among the multiple components it contains), such as gene-regulatory interactions (Watson et al., 2010). The kind of information integration that gene-networks can evolve is the same as that which neural networks can learn and, for example, is capable of demonstrating associative memory (one genotype can store and recall multiple phenotypes, recalled from partial or corrupted selective conditions) and generalisation (networks can produce novel adaptive phenotypes that have not been produced or selected in past generations) (Watson et al., 2010; Kouvaris et al., 2017). These models demonstrate that the conditions for effective learning can be transferred into the evolutionary domain and help explain biological phenomena such as the evolution of evolvability (Kounios et al., 2016; Watson, 2021). However, these models assume that selection is applied at the system level (equivalent to reinforcement learning at the system level).

System-Level Organisation Without System-Level Selection: Evolving Organised Relationships Bottom-Up

For the ETIs, driven by bottom-up selection, we cannot assume a reward function that operates over the system as a whole; rather it must be analogous to a reward function for each individual particle (Power et al., 2015). How does reinforcement learning at the level of individual particles, in interaction with each other and acting on their relationships, change system-level behaviours?

Previous work shows that the action of fitness-based incremental change at the individual level (or individual reinforcement learning in a network of pairwise games (Davies et al., 2011; Watson et al., 2011a), when applied to relationships between agents, is equivalent to unsupervised associative learning at the system scale. That is, individual-level reinforcement learning, when given control over the strength of connections, is equivalent to unsupervised learning at the system level (Davies et al., 2011; Watson et al., 2011a; Power et al., 2015). This means that the same learning principles can be translated into evolutionary scenarios where the system is not a single evolutionary unit but a network of relationships among many evolutionary units – such as an ecological community with a network of fitness dependencies between species. These models characterise the evolution of ecological organisation (evo-eco) under individual-level natural selection (Power et al., 2015; Watson and Szathmary, 2016). Even though, in this case, selection acts at the level of the components not at the system level, the kind of information integration that community networks can evolve is also the same as that which neural networks can learn (with unsupervised learning) (Power et al., 2015). These learning principles do not depend on any centralised mechanisms, or an external teacher/system-level feedback (Watson and Szathmary, 2016). This can be used to demonstrate the evolution of ecological assembly rules that implement an associative memory that can store and recall multiple ecological attractors that have been visited in the past and recall them from partial or corrupted ecological conditions (Power et al., 2015). This is crucial in demonstrating how natural selection organises interaction networks bottom-up - before a transition.

System-Level Adaptation Without System-Level Selection: Bottom-Up Adaptation

Under suitable conditions, these models also demonstrate non-trivial problem-solving optimisation at the system level without system-level selection. As in the analogous neural systems (“System-Level Optimisation Without System-Level Reinforcement”), when the initial connections between individuals constitute a system of random constraints (or pairwise games), running the network to an attractor (i.e., repeatedly allowing all individuals to make their own decisions about the state that maximises their individual utility) increases total utility. Intuitively, each unit is incentivised to maximise their individual utility (by definition) and if each of them acts to increase their individual utility then the total utility tends to increase as well (Davies et al., 2011; Watson et al., 2011a,c) (this is guaranteed if the interactions are symmetric). However, because of the conflicts and constraints between individual incentives, the short-sightedness of their actions and the fact that individual behaviours have no system-level incentive to maximise the utility of others, the attractors found are only locally optimal (again, as analogous to the neural systems). Other attractors may exist with higher total utility but these are only found if the system happens to start from very specific initial conditions (Watson et al., 2011a).

When individual reinforcement or selection is allowed to modify the strength of the relationships between units, the system becomes a self-modelling dynamical system and its dynamics change in predictable ways, as per the distributed optimisation shown in neural models. Specifically, if the state of the system (species densities) is repeatedly shocked or perturbed, causing it to reset to different random initial conditions and repeatedly allowed to relax into different ecological attractor states, the relationships that evolve enlarge the dynamical attractors for the distribution of locally-optimal states visited. Because selection is changing the relationships between species, and associative learning can generalise, it also enlarges the dynamical attractors for other states with even higher total utility. The evolution of interactions in an ecological community can thus produce adaptive organisation at the network level without presupposing that the network is an evolutionary unit.

To provide a compelling example of what this can do, Power sets up the initial competitive ecological interactions between species to represent the constraints of a resource allocation problem equivalent to a Sudoku puzzle (Power, 2019). The profile of species densities represents assignments of numbers in a Sudoku solution, and the community matrix of fitness dependencies between them represents the rules of the puzzle (e.g., two “6”s in the same row, column or box have a strong competitive interaction). Running the initial Lotka-Volterra ecological dynamics from random initial species densities finds one of very many ecological attractors corresponding to, generally poor, locally optimal solutions (i.e., with many constraints violated). Power then showed that individual-level natural selection, acting on traits that affect inter-specific interactions, caused the attractors of the ecological dynamics to change, and showed conditions where this causes the community to form attractors that correspond to better quality solutions over evolutionary time (Power, 2019). Under these conditions, the resultant ecosystems, evolving without any system-level selection, can in many cases learn to solve Sudoku puzzles that humans find very difficult to solve.

Some comparisons with ecological scaffolding are notable. Both this effect and ecological scaffolding utilise the observation that, when a system is held in a particular state, the action of natural selection on the components therein is likely to reinforce that state – making a “memory” of that configuration. In ecological scaffolding this means that the scaffolding conditions can be removed and the organisation persists, in ecological memory (Power, 2019), the system state can be perturbed and it will, with greater probability, return to this state. In both cases this results in a system that adopts configurations of higher-total utility or higher cooperation than it would otherwise. Some important differences are that in scaffolding the one new state is (initially) created by exogenous conditions that oppose the natural attractors of the system, causing it to adopt states that are conducive to more cooperation, whereas in Power’s model of ecological adaptation, the system visits many states that are each natural local attractors, and no exogenous conditions need be changed. In scaffolding the canalisation of the new state can be any evolutionary change that maintains that state (e.g., changes to population structure that restrain the interactions in the same way), here we are interested more specifically in associative relationships that have the capability to represent underlying structural regularities that generalise over the set of states visited. This is important because (a) in scaffolding, the state that is initially imposed by exogenous factors is the state that is ultimately canalised. Insomuch as the exogenous imposition of ecological factors is not in itself an adaptive process, whatever outcome it produces is fortuitous happenstance. Though its results might have adaptive consequences, it does not require an adaptive explanation. (b) In contrast, in the effect described by Power, the ultimate outcome is a novel state that the system finds by an adaptive process of generalisation. This is a true optimising effect, explained by selection from below, not fortuitous happenstance. Nonetheless, in general cases, there is plenty of scope for exogenous ecological scaffolding, this effect, and others to interact with one another in complex ways.

Evolutionary connectionism thus translates distributed learning principles into the domain of natural selection, and demonstrates how relationships among evolutionary units can become adaptively organised by selection on the existing, lower-level units – or more exactly, on the characters of lower-level units that affect the relationships between them. This thereby demonstrates conditions where multiple short-sighted, self-interested entities organise their relationships with one another causing them to act in a manner that is consistent with long-term collective interest – increasing total welfare (the sum of individual fitnesses). Individuals do not do this because they are intrinsically motivated by long-term or pro-group interests (they are short-sighted and self-interested), but under these conditions, short-term self-interest acting on slow-changing relationships between individuals (second-order traits) produces this systematic outcome. The organisation of the whole becomes conditioned by its past experience, with distributed incremental changes to its organisation motivated to reduce individual-level conflict, and because this occurs over a distribution of many ecological equilibria, each resolving some subset from the same set of conflicting constraints, it generalises from this past experience to influence future behaviour in a manner that resolves more of these conflicts (Watson et al., 2011a,b; Power, 2019).

Thus far, however, these models have not demonstrated transitions in individuality. In the models of gene regulation networks, the evolutionary unit was already at the network level (evo-devo). In the models of ecological dynamics, the evolutionary unit was at the lower (individual) level (evo-eco) and although there are observable fitness consequences at the network level, the ecological community does not become a new reproductive unit with heritable fitness differences, nor is there a de-Darwinisation of particles. Neither model demonstrates a change in the level of individuality, or “evo-ego” (Watson and Thies, 2019). What is missing?

Hypothesis and Theory: Toward a Connectionist Framework of Individuality

The framework of evolutionary connectionism provides a basis on which to develop a different kind of theory for ETIs. Conventional evolutionary thinking suffers the chicken-and-egg problem of transitions because it attempts to explain adaptations through changes to the frequency of units, which presupposes an evolutionary unit (at the relevant level) is already defined. In contrast, a connectionist approach explains adaptations through the changing organisation of the relationships between existing lower-level units. This provides a way for the whole to become more than the sum of the parts, in a formal sense, without presupposing that the whole is already an evolutionary unit. It is a theory that focusses not on the things (and their frequencies) but on the relationships between things (and the transformation of their organisation). Connectionism provided a way for cognitive science to escape the infinite regress of homoncular thinking (i.e., the whole is intelligent only because it is composed of intelligent components), and showed that the whole can have cognitive abilities of its own (more than the sum of the parts), even though the individual components are cognitively trivial, if the relationships between them are organised appropriately. Here we aim to translate this into the evolutionary domain to provide a way for evolutionary theory to resolve the chicken-and-egg problem of individuality, and show that the whole can have individuality of its own (more than the sum of the parts), even though the components are self-interested (have no foresight or pro-social assumption), if the relationships between them are organised appropriately.

But How Exactly Do Relationships Need to Be Organised to Produce a New Level of Individuality?

What kind of interaction structures turn a society into an individual? (Lyon et al., 2021a,b). Here we develop the hypothesis that translating further principles of connectionist cognition and learning into the domain of evolutionary systems describes both the specific kind of relationships that are needed for an ETI and the conditions under which they can evolve through bottom-up selection.

Design for an Individual

Summarising the conditions discussed above, in order for an evolutionary unit to be meaningful it must explain evolutionary outcomes that cannot be explained by the summative effects of the components it contains. Collective characters must therefore be non-linearly separable functions of (embryonic) particle characters (“When the Direction of Selection on Components Is Context Sensitive - Division of Labour Games, Nonlinearly Separable Functions, Non-decomposable Phenotypes, and Comparison With Other Non-aggregative Functions”). In order for particles to effect such collective characters, particles must be plastic (either phenotypically or reproductively) (“Particle Plasticity and Collective Development”). Plasticity allows for the phenotype or the reproduction of a particle to not be determined by the intrinsic independent properties of the particle but rather by its interactions with other particles (e.g., their coordination or complementarity). Before a transition these interactions are ecological (i.e., between multiple evolutionary units) and after the transition these same interactions are developmental (i.e., among the components of a single evolutionary unit) (Watson and Thies, 2019; Fields and Levin, 2020). The dynamical process controlled by these interactions is what we recognise as the basal cognition of development - implementing information integration (computing a non-decomposable function of input states) and collective action (producing specific coordinated responses in multiple downstream variables). Ultimately, this collective action must control the reproduction of the particles involved (such that their fitness is determined by collective-level properties – properties that cannot be decomposed into the properties of the individual particles). This might result in synchronised reproduction or reproductive specialisation (the egalitarian or fraternal solutions to the HFHF problem, respectively).

Evolutionary individuality thus requires a developmental process that constitutes the computation of a non-linearly separable function (between “embryonic” collections of particles and “adult” collective phenotypes) (“Particle Plasticity and Collective Development”). When evolved interaction structures between units compute a function that is non-linearly separable, this makes collective fitness, and hence reproduction, non-decomposable in this formal sense. Natural selection, acting bottom-up, can modify relationships between units in a manner that creates adaptive organisation at the system scale. So, perhaps it might create interactions that compute the non-linearly separable functions required for a transition in individuality? However, shallow or single-level interaction structures cannot compute non-linearly separable functions (Box 3). Previous models only allowed for the evolution of shallow interaction structures – a single layer of symmetric, all-to-all relationships (e.g., a↔b, b↔c, c↔a). In order for a system to compute non-linearly separable functions, the interaction structure must have some depth⁴ (Box 3 and Figure 2).

FIGURE 2

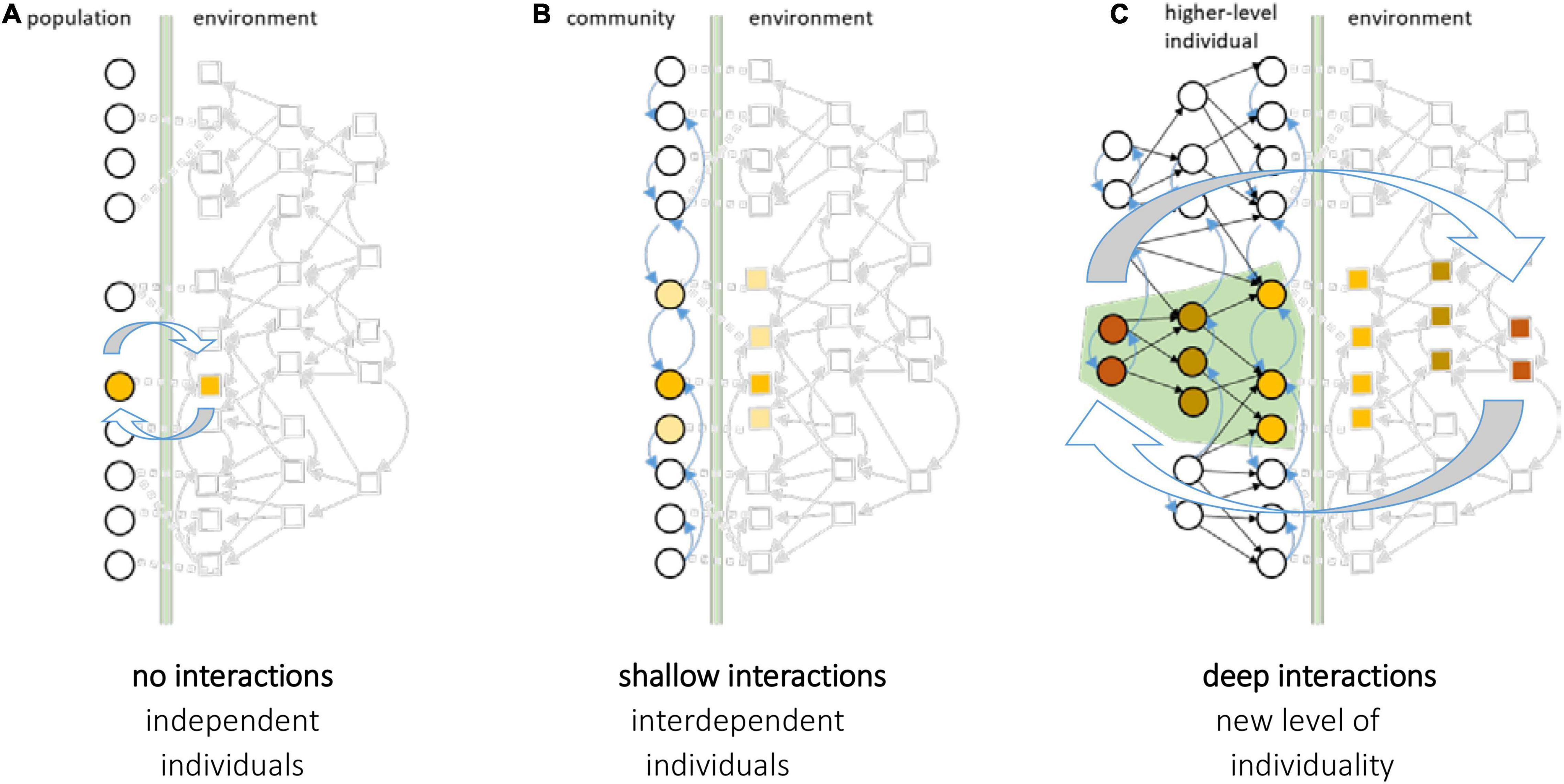
Figure B2. Overview of conventional models of evolution (A), previous work in evolutionary connectionism (B) and Hypothesis 1 (C). (A) A conventional view of evolution models individual evolutionary units in a population. The complexity of the environment is not “visible” to evolution – selection on an individual (orange circle) responds only to corresponding additive effects of selection in the environment (orange square) (large arrows). At the population level, this is formally equivalent to simple (model-free) forms of learning and inference (Frank, 2009; Harper, 2009; Shalizi, 2009). (B) When individual traits affect behavioural or phenotypic interactions with other individuals, these relationships can evolve to “mirror” dependencies among environmental variables. When interactions are reciprocal (single-level) the evolution of the community is formally equivalent to shallow models of connectionist learning (Watson et al., 2014, 2016; Power et al., 2015; Kouvaris et al., 2017). (C) We hypothesise that when functional interactions between individuals in a community are directional, creating deep interaction structures with “hidden” variables, evolution is formally equivalent to deep model induction. When evolved functions are non-linearly separable, and their outputs control the coordination of particle reproduction, the hierarchical structures so created constitute new individuals at a higher level of organisation (e.g., green). The functional interactions between component individuals constitute a developmental process for this higher-level individual, and enable information integration and collective actions at a new level of biological organisation. Adaptations under natural selection (acting on deep variables, red circles) now serve the development, survival and reproduction of the new individual (large arrows), and deep causal variables in development (red circles) mirror deep causal variables in the selective environment (red squares).

The significance of deep structure is demonstrated by further work with neural networks. An adaptive process with the ability to learn and exploit deep structure has different adaptive capabilities from an adaptive process that cannot – this is referred to as deep optimisation (Caldwell et al., 2018, 2021), or multi-scale search (Mills, 2010; Mills et al., 2014). In neural models this affords new levels of variation (coordinated action) that can access new levels of reward structure (higher-order epistatic components of fitness) (Watson et al., 2011b), i.e., coordinate changes to multiple units simultaneously. This progressive hierarchical abstraction, with each higher-level of representation building on the representations of the layer below, is familiar in machine learning and, we argue this is analogous to the way in which ETIs enable deep biological evolution (i.e., multi-scale evolutionary processes) to implement deep model induction (Mills, 2010; Mills et al., 2014; Watson and Szathmary, 2016; Czégel et al., 2018, 2019; Vanchurin et al., 2021). In the machine learning context we have shown that this coordinated collective action can find high-quality solutions to combinatorial optimisation problems that cannot be accessed by individual action (Watson et al., 2011b; Caldwell et al., 2018, 2021).

This suggests that (a) the interaction structures necessary for evolutionary individuality, (b) the interactions structures necessary for organismic individuality, and (c) the interaction structures required to compute non-linearly separable functions are intimately related. Specifically, when interactions among evolutionary units form collective phenotypes that are non-linearly separable functions of their embryonic phenotypes, and this integrated information then cues behaviours that coordinate the reproduction of the particles, this constitutes a new level of evolutionary individuality. In order for such interactions to compute non-linearly separable functions, the interaction structure cannot be shallow or reciprocal (as in previous models) but must have some depth. We thus describe a view of evolutionary processes where, given appropriate conditions, interaction structures will evolve (through bottom-up selection) in a way that “mirrors” structure in the selective environment (Wagner and Laubichler, 2004; Kounios et al., 2016; Kuchling et al., 2020) – and that when this structure is deep, this constitutes a transition in individuality (Figure 2).

This leads to our main hypothesis about the architecture of individuality:

H1. Individuality requires a dynamical process (development), mediating the plastic expression of components in the context of one another, with the specific form of computing a collective character that is a non-linearly separable function of (embryonic) particle characters, with the effect of coordinating reproduction based on this collective character.

Only under these conditions, we hypothesise, can it be true that multiple individuals have relationships that cause them to work together for long-term collective benefit despite causing behaviours that oppose their short-term individual interest. On the fine timescale we call development, we might observe this as delayed or prohibited individual reproduction of some cells within a multicellular organism, for example. Whereas on the longer timescale relevant to the reproduction of the collective, we might observe this as a coordinated or specialised reproductive behaviour that affords access to higher-order fitness differences by allowing information integration and collective action. This can be directed at the control of reproductive plasticity that coordinates reproduction timing or specialisation. For example, in individuals created by fraternal transitions, this information integration and collective action controls reproductive division of labour (i.e., which particles get to be germ). In individuals created by egalitarian transitions, it is directed at the control of reproductive centralisation and synchronisation (i.e., the timing of particle reproduction). In either case, we can see that any susceptibility to control over particle reproduction runs counter to the fitness interests of the particle – but can confer synergistic benefits to the particle via the collective character of reproductive complementarity or coordination. Whilst reproductive control of this kind can oppose the short-term fitness interests of the individual, we hypothesise that it cannot necessarily be undone by subsequent selection because of the non-decomposable nature of the control function.⁵ Thus, when information integration and collective action is directed at the control and coordination of reproductive plasticity this constitutes a new evolutionary unit. And because individual selection cannot undo this relationship, selection at the higher level can act in opposition to individual selection.

If true, how would this hypothesis inform experimental work or further theoretical development? The main impact of this hypothesis is that it makes specific predictions about the conditions for ETIs to occur that are testable either in further modelling or empirical experimentation.

Under What Conditions Can These Interaction Structures Evolve?

This hypothesis (H1) makes specific predictions about the conditions required for an ETI to occur and what would be required to build a working mechanistic model of a transition in individuality. Rather than a framework that depends on new genetic or selective structures that arise fully-formed, it suggests an approach where the ETIs can be smoothly integrated with more ordinary coevolutionary and social dynamics, and explains why ordinary evolutionary change, driven by selection from below, can result in transitions that later become qualitatively distinct.

H1 predicts that the difference between “ordinary coevolution” and ETIs depends on the particular nature of these relationships. If they have the effect of enacting a decomposable (linearly separable) function, particle character will be predictive of particle fitness, and this will not involve collective action, and will not constitute an ETI. However, if such a relationship becomes more non-linear over evolutionary time, it may become a non-linearly separable function. When this occurs collective character, and not particle character, will be predictive of particle fitness and an ETI has occurred.

Moreover, the difference between the kind of relationships that can constitute non-linearly separable functions and those that cannot is specific but not complicated – it just requires some depth. They cannot be represented by anything equivalent to a single layer Perceptron. Such networks do not need to be organised in neat layers as they often are in artificial neural networks such as the multilayer Perceptron – they could be messy. But they cannot be entirely shallow or have only symmetric interactions (Box 3).

So, how does this structure evolve? Under what conditions do deep interaction structures, computing non-linearly separable functions, evolve without presupposing the higher-level evolutionary unit we want to explain? Existing work shows several of the necessary elements (but not all in one model).

• When evolution acts on heritable variation in characters affecting the interactions between units, the effect is equivalent to connectionist models of learning (“System-Level Adaptation Without System-Level Selection: Bottom-Up Adaptation”). But, as yet, these are shallow models not deep.

• When heritable variation permits the evolution of asymmetric interaction structures, conditions exist where deep interaction structures can evolve (Nash et al., 2021). The hierarchical modularity that results mirrors the modularity of the selective environment and can consequently increase evolvability in rugged fitness landscapes. This occurs under short-term selection only, without selection for such long-term evolutionary benefits conferred by these structures. But, as yet, these models assume system-level selection.

• When individuals are given the ability to evolve symbiotic partnerships that create new reproductive units, we find that there are conditions where this permits the evolution of specific higher-level units. These units mirror the structure of the evolutionary game they are playing, and enable the discovery of high-fitness collectives that cannot be found under single-level selection (Watson et al., 2011d). These specific partnerships evolve under short-term and individual-level selection, without selection for these long-term collective benefits. But, as yet, these models assume the possibility of discrete symbiotic relationships (enacting new reproductive units) rather than collective phenotypes that develop through the signalling and plastic responses of the component particles.

• Unsupervised learning principles, acting in a decentralised manner, without system-level reward feedback or selection, demonstrate the capability to induce interaction structures that facilitate collective action and higher-level adaptation that cannot be achieved with individual action (Watson et al., 2011b). Notably this requires learned interactions to be used in a feed-forward (deep) manner rather than a symmetric recurrent manner. But, as yet, these are neural learning models not evolutionary models.

Thus, several components relevant to H1 have been demonstrated but not the whole picture in one model; we have evolutionary connectionism (in shallow models), the evolution of deep interaction structures (under system-level selection), the evolution of new selective units effective in scaling-up selection (without a developmental model), and deep models that provide collective action (in neural models). From the different components we already have, and building on H1, we hypothesise that these relationships between evolutionary individuality and deep learning models are not merely a descriptive analogy (Czégel et al., 2018, 2019) but a functional equivalence that also predicts the conditions under which bottom-up natural selection can cause these structures to evolve. Hence,

H2: The conditions necessary for the induction of deep models, familiar in connectionist models of learning and cognition, are predictive of the conditions necessary for an ETI to occur.

What are these conditions?

In addition to a basic learning mechanism,⁶ any learning system requires: A suitable model space (capable of representing the structure in the problem domain); A representative set of samples to learn from; And a suitable inductive bias (e.g., a parsimony pressure or other regularisation term). We address why each of these is needed in learning systems and how each of these corresponds to conditions for the evolution of transitions in individuality.

(1) A Model Space Capable of Representing the Structure in the Domain

If we want to learn correlations between system variables, for example, we must use a model space capable of representing correlations. In neural models, this just means that learning occurs by modifying weighted connections; We cannot learn anything interesting by altering the outputs (or the input-output function) of individual neurons as if they were a bag of independent computational units. Associative learning occurs by altering the organisation of connections in a network, not by altering the independent features of individual neural units. In learning systems this is an obvious point – but this lies in contrast to common evolutionary models, treating particles as though they are inert, and higher-selective “units” as though they are merely containers. Individuals must be modelled as non-trivial computational systems. This makes an intimate bond between organismic individuality, evolutionary individuality and cognition.

In evolutionary terms, this means that there must be heritable variation in the relationships between units – not just the independent (i.e., non-context-sensitive) features of individual particles. This means that particles must be plastic, sensitive to one-another’s phenotypes, and selection must act on the details of these signal-response connections (in whatever substrate they are implemented). Then if we want to represent non-linearly separable functions, we must use a model space that can represent these higher-order functions (e.g., a structure with some depth). In evolutionary terms, this means that a shallow network architecture with symmetric interactions (Watson et al., 2014; Power et al., 2015) (e.g., a↔b, b↔c, and c↔a) is insufficient. There must be some depth to how particles interact – with some units differentiating before others (e.g., a→b, b→c, and a→c), which then have the opportunity to coordinate the behaviour of multiple downstream units (a.k.a. development) (Figure 2C).

(2) A Representative Experience (Samples or Training Data)

It is not possible to fit the parameters of a correlation model, let alone a deep model, from a single data sample. If we simply present a single training example and allow a Hebbian learning mechanism to alter connections, the model just learns that one pattern and canalises all the relationships between all the variables (Watson et al., 2011a,c, 2014; Power et al., 2015). To learn structural relationships, i.e., that some variables are correlated and some are not, requires a training set – a distribution of training samples.

In evolutionary terms, if the interactions between units are modified by natural selection after it reaches a particular attractor state, this is analogous to the presentation of a single training sample. So, if this occurs only once then relationships fitting to correlations cannot evolve. If, in contrast, the phenotypic state of units is repeatedly shocked or reset to random configurations and each time allowed to play-out to a different attractor (whilst natural selection slowly changes the relationships between them), this is analogous to learning over a set of representative training samples. This causes the future system dynamics (modified by these learned relationships) to change in a particular way. Specifically, the evolved relationships enlarge the basin of attraction for configurations that have been visited in the past (meaning that individual selection takes the system to this configuration more often in future, from arbitrary starting conditions), and crucially, also enlarges the basin of attraction for other novel configurations with especially high total utility. In the limit, as positive feedback between the states that are visited and the states that are learned builds up, the system tends to converge on only one attractor and this tends to have much higher utility than average (“System-Level Adaptation Without System-Level Selection: Bottom-Up Adaptation”) (Kounios et al., 2016; Power, 2019). This is possible because the distributed associative model that is learned is not just a memory of past visited states, but a generalised model.

(3) A Suitable Inductive Bias

Generalisation is intrinsic to learning (“System-Level Organisation Without System-Level Reinforcement”). Of all the models that could represent the training data equally well, some will generalise differently from others, i.e., they respond differently to novel inputs. Indeed, the training set says nothing about how to respond to novel points. So, over the set of all conceivable models, it cannot be said that there are more models that categorise a novel input one way than there are that categorise it another – even if we limit this to models that agree equally well with the training set. Accordingly, the conceptual notion of “all possible models that agree with the training data” does not, in fact, afford any generalisation. Generalisation thus requires an inductive bias. Inductive bias describes the difference between all models that agree with the training data and the actual model delivered by the learning algorithm. Although in many contexts bias seems like something that should be avoided (Uller et al., 2018), in learning systems it is not – the aim is not to get rid of inductive bias, but to use an appropriate bias, that generalises well.

Accepting the idea that inductive bias is necessary for learning, the notion of a suitable inductive bias that generalises well may still seem like a cheat - a place to hide privileged knowledge that makes the system “know the right answer” despite the lack of information in the training set. It may seem like all the interesting work of a learning system is being done by this somewhat magical assumption. This is not the case. Even if we assume an appropriate inductive bias, the learning mechanism still needs to fit the model (given this bias) to the training data, and the generalisations obtained are a product of this past experience as well as the inductive bias. In fact, the form of the inductive bias can be very weak and general. For example, a bias that prefers simple models over complex models, as per Occam’s razor, a.k.a. a parsimony pressure, is an extremely simple and effective inductive bias in almost all practical learning domains. In modelling terms, this can be as simple as preferring models with less connections to models that do the same thing with more connections. In biological terms, there are many reasons that simple models may evolve more readily than complex ones that do the same job. This may arise by virtue of starting from mechanisms that constitute empty or null models and adding complexity incrementally, or through subsidiary selective pressures for material efficiency, or speed, or robustness to perturbation or damage. Whatever the reason, our hypothesis predicts that this is a necessary condition for the biological networks to learn.

Here there is an important overlap between the model space of a learning system and the inductive bias of a learning system. For example, searching in the space of single-layer networks is a different inductive bias from searching in the space of multi-layer or deep networks, even if each space is explored uniformly (with respect to their own parameters). In evolutionary terms, this means that different assumptions about the nature of interactions (whether there is heritable variation that allows for symmetric or recurrent interactions, or asymmetric, feed-forward or deep interactions, etc.) will alter whether it is possible or probable to evolve non-linearly separable functions in response to the selective conditions experienced. The previous work in evolving hierarchical gene-regulatory structure shows that we do not need to assume or force interactions to be deep (Nash et al., 2021), but it also predicts that we must allow for this possibility and suggests that a strong parsimony pressure may be important in evolving such models (Clune et al., 2013; Mengistu et al., 2016; Kouvaris et al., 2017).

Learning and Evolving Deep Structures

So, what are the particular necessary and sufficient conditions for the induction of deep models in learning systems? Actually, machine learning systems usually have their topological depth prescribed by a priori design decisions before learning begins – systems might use a single-layer network or a multi-layer network, but whichever is used is decided at the outset and does not change during learning time [otherwise we are in the advanced machine learning topic of topology search (Stanley and Miikkulainen, 2002)]. However, some simple observations are useful. Shallow architectures cannot represent deep (non-linearly separable) functions but deep architectures can represent shallow (linearly separable) functions, so deep architectures are more general. And since a deep architecture can represent linearly separable functions as well as non-linearly separable functions, the depth of the function they compute can be variable even if the topological depth of the network architecture is fixed. Moreover, this is the usual progression in learning systems – by initialising a network to weights with small uniformly random values it does not, at the outset, represent a non-linearly separable function. But over learning time, it is not difficult to alter weights incrementally such that they eventually come to represent a non-linearly separable function (Brun-Usan et al., 2020). Given the possibility of moving in a suitably general model space, incremental learning algorithms are sufficient to learn such functions.

It is notable that there are learning algorithms for the single-layer Perceptron that are guaranteed to converge on any target (linearly separable) function, but for learning models capable of representing non-linearly separable functions there are no such guarantees. Back-propagation, the standard learning algorithm for deep networks, often works well in practice but does not have such guarantees. The reason is interesting. It is because the effect on the output caused by changing an input (or a weight from an input), can change sign depending on the context of other inputs. Put differently, the way that changing inputs “shows through” to the outputs is not consistent depending on the context of other inputs. In other words, the same property that makes them an interesting class of functions (for machine learning and ETIs) also makes them difficult to learn. A different way to understand this problem is that the representation learned in the hidden nodes is under-determined by the input-output relationship.⁷ The learning process must break symmetry (arbitrarily) to identify a self-consistent internal representation. This is not particularly difficult (at least in functions over a small number of inputs), but the under-determination issues indicate the disconnect between selection on the outputs (collective phenotypes) and selection on the relationships between the parts therein (i.e., on the signals that turn societies into individuals). Our hypothesis H2 makes the prediction that evolving interactions that represent non-linearly separable functions, as required for ETIs, will be similarly sensitive to issues of non-guaranteed convergence and symmetry breaking. Indeed, we suggest that this is exactly why the conditions for evolving ETIs have been elusive thus far and difficult or impossible to characterise in conventional (additive) models of selection or social games. Nonetheless, we predict that deep interaction structures necessary for ETIs can evolve given the conditions identified above (and briefly summarised below).

Limitations and Conclusion

The topic of the evolutionary transitions in individuality has many facets, and at present, accommodates many different opinions about what is important and how they might occur. This manuscript has been a limited discussion, positioning a particular research approach and point of view within the issues of the ETIs. This is just one attempt to try to make sense of many complex issues. Some of the limitations of our approach include the following.

– The existing models of evolutionary connectionism make a strong connection between correlation learning and evolution of relational traits, and the analysis developed here shows that such traits are critical to accessing heritable fitness differences at the collective level. The need to allow for the evolution of asymmetric interactions in order (for proto-developmental dynamics) to calculate non-linearly separable functions is also well-known. However, we have not yet put these features together in a unified model.

– As yet, we have not provided a mathematical analysis that explicitly links together non-decomposable collective characters, the response to selection at the collective level, and selection on the parameters of plasticity as an individuating mechanism that increases the heritability of these collective characters. We imagine that the direction of selection on the parameters of plasticity may be equivalent to gradients in the objective function of a correlation learning system applied to a non-linearly separable function.

– Other individuating mechanisms, such as mutual policing strategies, and population structuring traits, such as dispersal radii or the severity of a population bottleneck, have not been integrated into this framework. Some of our reasoning suggests that particle plasticity is the only way to remove fitness differences at the particle level whilst creating fitness differences at the collective level, but these other mechanisms and issues are clearly fundamental to many ETIs and the interaction of plasticity with these issues is currently unclear.

– Since the evolution of adaptive organisation via connectionist principles does not require that the system is already a unit of selection, there are also potentially interesting things to say about cognition, learning and individuality in systems that are not evolutionary units such as ecological communities, social systems and the biosphere.

– The relationship between non-decomposable collective characters enacted through the phenotypic plasticity of particles, and non-decomposable collective reproduction enacted through the reproductive plasticity of particles, remains unclear. If the phenotypes we are interested in have fitness consequences, the difference between regulating phenotypes and regulating reproduction may be one of degree not kind.

– At present, our approach subsumes both egalitarian and fraternal transitions under the more general concept of reproductive regulation (namely, reproductive synchronisation and reproductive specialisation, respectively). It is notable that there are two categorically different types of non-linearly separable functions (XOR and IFF) which correspond to favouring differentiation and favouring sameness. This might be connected but is not yet developed.

– Here we have mostly developed notions of information integration, and the types of interactions required to calculate non-decomposable functions, but we have not talked much about the other key feature of organismic individuality, namely collective action (except that the consequence of collective phenotypes must ultimately be applied to collective reproduction). Our computational models of deep optimisation suggest that the ability to rescale movements in phenotype space through collective action is critical to rescaling evolutionary optimisation.

– The conceptual framework presented here depends on a separation of timescales between fast variables (game strategies, selection on first-order phenotypes) and slow variables (game pay-offs, selection on second-order plasticity parameters). These correspond to the relatively fast dynamics of cognition (neural activations) and the relatively slow dynamics of learning (changes to synaptic strengths). In some biological contexts, this separation of timescales may not be clear and the consequences of this needs investigating.

Nonetheless, we have laid out a specific set of hypotheses and predictions which we hope will prove illuminating despite these limitations. We have argued that the interaction structures necessary for organismic individuality are intimately related to those required for evolutionary individuality and non-decomposable cognitive functions. Specifically, when organismic processes of basal cognition compute a collective phenotype that is a non-linearly separable function of the embryonic particle states, and this “basal decision” is applied to the control and coordination of particle reproduction, this constitutes a new evolutionary unit. This leads to the hypothesis that the conditions for deep model induction are predictive of the conditions for a transition in individuality to evolve. The potential value of these hypotheses is the specific predictions they make about the conditions for ETIs to occur. These predictions are specific enough that they are testable in further modelling or empirical experimentation. Namely, ETIs require:

• Heritable variation in the relationships between units (requiring particle plasticity and signalling) that coordinates particle functions and reproduction.

• The ability to represent asymmetric interactions structures between units necessary for deep structure (that can represent non-linearly separable functions).

• Selective conditions that are subject to repeated shocks or perturbations.

• A sufficiently strong parsimony pressure favouring simple systems.

Notably, these predictions concern features that are quite different from those commonly addressed in ETI research. For example, although measuring genetic assortment, the severity of a population bottleneck or reproductive division of labour might all be relevant to ETIs (Godfrey-Smith, 2009), they are not in themselves sufficient nor do they identify predictions about the conditions under which they will evolve. The emphasis of our hypotheses is on a unification of organismic individuality, evolutionary individuality and the principles of distributed learning – leading to a cognitive theory of individuality. This connectionist framework focusses not on changes to the frequency of units (Darwinian fitness), at one scale or another, but on the organisation of relationships between units and the conditions under which this organisation constitutes something more than the sum of the parts in a formal sense. This cognitive framework of individuality, we believe, will provide directions for future theoretical development and experimentation that begin to overcome the inadequacies of previous theoretical approaches.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

ML and CB revised and refined the text and presented the concepts. RW, ML, and CB conceived the project together, contributed to the article, and approved the submitted version.

Funding

RW and ML gratefully acknowledge the support of Grant 62230 and Grant 62212, respectively, from the John Templeton Foundation. CB was supported by BBRSC grant BB/P022197/1.

Author Disclaimer

The opinions expressed in this publication are those of the authors and do not necessarily reflect the views of the John Templeton Foundation.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Dave Prosser, Freddy Nash, Christoph Thies, Jamie Caldwell, and Lucas Mathieu for discussion and comments on drafts of this manuscript. We are particularly grateful to Pierrick Bourrat for input that helped us position this work within existing theoretical treatments.

Footnotes

1. ^ This could be provided by a non-monotonic output function (where, for example, over-saturation of inputs depresses outputs) – but this would make it impossible to represent ordinary linearly separable relationships with the same network. Alternatively, multiplicative interactions could be implemented by synaptic connections that mediate the sign of other synaptic connections directly, e.g., via axoaxonic synapses that join directly with another incoming connection rather than the dendrites of the downstream neuron.
2. ^ In an individual resulting from an egalitarian transition, the language would be different. For example, this temporally extended process of interaction might be called collective or group reproduction, rather than development. That is, an embryonic group containing intrinsically different components (with different functions and different genotypes) is coordinated by these processes to produce undifferentiated component-reproduction (coordinated and identical reproductive opportunity).
3. ^ And may include regularisation terms that apply or modify an inductive bias, as discussed in section “System-Level Optimisation Without System-Level Reinforcement.”
4. ^ In modern neural networks, “deep” is often used to mean that there are very many computational layers, sometimes hundreds. Here we only mean that the computation cannot be single layer (simply connecting inputs to outputs directly), but must (minimally) include connections that go from inputs to outputs via hidden state variables.
5. ^ This has a natural analogue in machine learning terms. When we train a neural network to represent a given function it is advisable to start from a network that is close to neutral – e.g., with small symmetric weights. If, in contrast, we train a deep network to represent a non-linearly separable function, then try to retrain from there to a new function, the learning process can become irretrievably stuck, unable to learn the second function even though the network architecture is capable of representing it.
6. ^ The equivalence between learning and evolution shows that random variation and selection can provide a suitable learning mechanism (to adjust model parameters). This includes connectionist models of cognition and learning, and also deep models (Such et al., 2017; Brun-Usan et al., 2020; Nash et al., 2021) Back-propagation, the standard learning algorithm for the induction of deep models, is not required and a simple variation and selection process is sufficient (albeit less efficient) (Such et al., 2017).
7. ^ Even in the trivial example of learning A XOR B, the internal representation could be h1 = AND(A,NOT(B)) and h2 = AND(NOT(A),B), as described in Box 3, or it could be the other way around, i.e., h1 = AND(NOT(A),B) and h2 = AND(A,NOT(B)). Either works just as well, and other decompositions are also suitable, neither construction is more right than the other, thus symmetry breaking is required to arrive at an internally consistent representation of the function.

References

Bechtel, W., and Bich, L. (2021). Grounding cognition: heterarchical control mechanisms in biology. Philos. Trans. R. Soc. Lond. B Biol. Sci. 376:20190751. doi: 10.1098/rstb.2019.0751

PubMed Abstract | CrossRef Full Text | Google Scholar

Birch, J. (2017). The Philosophy of Social Evolution. Oxford: Oxford University Press.

Google Scholar

Black, A. J., Bourrat, P., and Rainey, P. B. (2020). Ecological scaffolding and the evolution of individuality. Nat. Ecol. Evol. 4, 426–436. doi: 10.1038/s41559-019-1086-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Blackiston, D., Lederer, E., Kriegman, S., Garnier, S., Bongard, J., and Levin, M. (2021). A cellular platform for the development of synthetic living machines. Sci. Robot. 6:eabf1571. doi: 10.1126/scirobotics.abf1571

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonner, J. T. (2003). On the origin of differentiation. J. Biosci. 28, 523–528. doi: 10.1007/BF02705126

PubMed Abstract | CrossRef Full Text | Google Scholar

Bourrat, P. (2021b). Transitions in evolution: a formal analysis. Synthese 198, 3699–3731.

Google Scholar

Bourrat, P. (2021a). Facts, Conventions, and the Levels of Selection. Elements in the Philosophy of Biology. Cambridge: Cambridge University Press.

Google Scholar

Brun-Usan, M., Thies, C., and Watson, R. A. (2020). How to fit in: the learning principles of cell differentiation. PLoS Comput. Biol. 16:e1006811. doi: 10.1371/journal.pcbi.1006811

PubMed Abstract | CrossRef Full Text | Google Scholar

Buss, L. W. (2014). The Evolution of Individuality. Princeton, NJ: Princeton University Press.

Google Scholar

Caldwell, J., Knowles, J., Thies, C., Kubacki, F., and Watson, R. (2021). “Deep optimisation: multi-scale evolution by inducing and searching in deep representations,” in Paper Presented at the International Conference on the Applications of Evolutionary Computation (Part of EvoStar) (Cham: Springer).

Google Scholar

Caldwell, J., Watson, R. A., Thies, C., and Knowles, J. D. (2018). Deep optimisation: solving combinatorial optimisation problems using deep neural networks. arXiv [Preprint]. arXiv:1811.00784

Google Scholar

Chastain, E., Livnat, A., Papadimitriou, C., and Vazirani, U. (2014). Algorithms, games, and evolution. Proc. Natl. Acad. Sci. U.S.A. 111, 10620–10623. doi: 10.1073/pnas.1406556111

PubMed Abstract | CrossRef Full Text | Google Scholar

Clarke, E. (2010). The problem of biological individuality. Biol. Theory 5, 312–325. doi: 10.1162/biot_a_00068

CrossRef Full Text | Google Scholar

Clarke, E. (2014). Origins of evolutionary transitions. J. Biosci. 39, 303–317. doi: 10.1007/s12038-013-9375-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Clarke, E. (2016). A levels-of-selection approach to evolutionary individuality. Biol. Philos. 31, 893–911. doi: 10.1007/s10539-016-9540-4

CrossRef Full Text | Google Scholar

Clune, J., Mouret, J. B., and Lipson, H. (2013). The evolutionary origins of modularity. Proc. Biol. Sci. 280:20122863. doi: 10.1098/rspb.2012.2863

PubMed Abstract | CrossRef Full Text | Google Scholar

Corning, P. A., and Szathmary, E. (2015). “Synergistic selection”: a Darwinian frame for the evolution of complexity. J. Theor. Biol. 371, 45–58. doi: 10.1016/j.jtbi.2015.02.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Czégel, D., Zachar, I., and Szathmáry, E. (2018). Major evolutionary transitions as Bayesian structure learning. bioRxiv [Preprint]. doi: 10.1101/359596

CrossRef Full Text | Google Scholar

Czégel, D., Zachar, I., and Szathmáry, E. (2019). Multilevel selection as Bayesian inference, major transitions in individuality as structure learning. R. Soc. Open Sci. 6:190202. doi: 10.1098/rsos.190202

PubMed Abstract | CrossRef Full Text | Google Scholar

Davies, A. P., Watson, R. A., Mills, R., Buckley, C., and Noble, J. (2011). “If you can’t be with the one you love, love the one you’re with”: how individual habituation of agent interactions improves global utility. Artif. Life 17, 167–181. doi: 10.1162/artl_a_00030

PubMed Abstract | CrossRef Full Text | Google Scholar

Deisboeck, T. S., and Couzin, I. D. (2009). Collective behavior in cancer cell populations. Bioessays 31, 190–197. doi: 10.1002/bies.200800084

PubMed Abstract | CrossRef Full Text | Google Scholar

Doursat, R., Sayama, H., and Michel, O. (2013). A review of morphogenetic engineering. Nat. Comput. 12, 517–535. doi: 10.1007/S11047-013-9398-1

CrossRef Full Text | Google Scholar

Fields, C., and Levin, M. (2020). Scale-free biology: integrating evolutionary and developmental thinking. Bioessays 42:e1900228. doi: 10.1002/bies.201900228

PubMed Abstract | CrossRef Full Text | Google Scholar

Frank, S. A. (2009). Natural selection maximizes Fisher information. J. Evol. Biol. 22, 231–244. doi: 10.1111/j.1420-9101.2008.01647.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Friston, K., Levin, M., Sengupta, B., and Pezzulo, G. (2015). Knowing one’s place: a free-energy approach to pattern regulation. J. R. Soc. Interface 12:20141383. doi: 10.1098/rsif.2014.1383

PubMed Abstract | CrossRef Full Text | Google Scholar

Godfrey-Smith, P. (2009). Darwinian Populations and Natural Selection. Oxford: Oxford University Press.

Google Scholar

Griesemer, J. R. (2005). “The informational gene and the substantial body: on the generalization of evolutionary theory by abstraction,” in Idealization XII: Correcting the Model, eds M. R. Jones and N. Cartwright (Leiden: Brill), 59–115.

Google Scholar

Grossberg, S. (1978). “Communication, memory, and development,” in Progress in Theoretical Biology, Vol. 5, eds R. Rosen and F. Snell (New York, NY: Academic Press).

Google Scholar

Harper, M. (2009). The replicator equation as an inference dynamic. arXiv [Preprint]. arXiv:0911.1763

Google Scholar

Hayek, F. A. (1980). Individualism and Economic Order. Chicago, IL: University of Chicago Press.

Google Scholar

Hofbauer, J., and Sigmund, K. (1988). The Theory of Evolution and Dynamical Systems: Mathematical Aspects of Selection. Cambridge: Cambridge University Press.

Google Scholar

Hopfield, J. J., and Tank, D. W. (1986). Computing with neural circuits: a model. Science 233, 625–633. doi: 10.1126/science.3755256

PubMed Abstract | CrossRef Full Text | Google Scholar

Ispolatov, I., Ackermann, M., and Doebeli, M. (2012). Division of labour and the evolution of multicellularity. Proc. Biol. Sci. 279, 1768–1776. doi: 10.1098/rspb.2011.1999

PubMed Abstract | CrossRef Full Text | Google Scholar

Jackson, A., and Watson, R. (2013). “The effects of assortment on population structuring traits on the evolution of cooperation,” in Paper Presented at the ECAL 2013: The 12th European Conference on Artificial Life September 2-6, 2013, Sicily.

Google Scholar

Kirk, D. L. (2005). A twelve-step program for evolving multicellularity and a division of labor. BioEssays 27, 299–310. doi: 10.1002/bies.20197

PubMed Abstract | CrossRef Full Text | Google Scholar

Kounios, L., Clune, J., Kouvaris, K., Wagner, G. P., Pavlicev, M., Weinreich, D. M., et al. (2016). Resolving the paradox of evolvability with learning theory: how evolution learns to improve evolvability on rugged fitness landscapes. arXiv [Preprint]. arXiv:1612.05955

Google Scholar

Kouvaris, K., Clune, J., Kounios, L., Brede, M., and Watson, R. A. (2017). How evolution learns to generalise: using the principles of learning theory to understand the evolution of developmental organisation. PLoS Comput. Biol. 13:e1005358. doi: 10.1371/journal.pcbi.1005358

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuchling, F., Friston, K., Georgiev, G., and Levin, M. (2020). Morphogenesis as Bayesian inference: a variational approach to pattern formation and control in complex biological systems. Phys. Life Rev. 33, 88–108. doi: 10.1016/j.plrev.2019.06.001

PubMed Abstract | CrossRef Full Text | Google Scholar

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learning. Nature 521, 436–444. doi: 10.1038/nature14539

PubMed Abstract | CrossRef Full Text | Google Scholar

Levin, M. (2019). The computational boundary of a “Self”: developmental bioelectricity drives multicellularity and scale-free cognition. Front. Psychol. 10:2688. doi: 10.3389/fpsyg.2019.02688

PubMed Abstract | CrossRef Full Text | Google Scholar

Levin, M. (2021b). Technological Approach to Mind Everywhere (TAME): an experimentally-grounded framework for understanding diverse bodies and minds. arXiv [Preprint]. arXiv:2201.10346

Google Scholar

Levin, M. (2021a). Bioelectric signaling: reprogrammable circuits underlying embryogenesis, regeneration, and cancer. Cell 184, 1971–1989. doi: 10.1016/j.cell.2021.02.034

PubMed Abstract | CrossRef Full Text | Google Scholar

Levin, M., and Dennett, D. C. (2020). Cognition All the Way Down. Aeon Essays. Available online at: https://aeon.co/essays/how-to-understand-cells-tissues-and-organisms-as-agents-with-agendas

Google Scholar

Levin, M., Keijzer, F., Lyon, P., and Arendt, D. (2021). Uncovering cognitive similarities and differences, conservation and innovation. Philos. Trans. R. Soc. Lond. B Biol. Sci. 376:20200458. doi: 10.1098/rstb.2020.0458

PubMed Abstract | CrossRef Full Text | Google Scholar

Levin, M., Pietak, A. M., and Bischof, J. (2019). Planarian regeneration as a model of anatomical homeostasis: recent progress in biophysical and computational approaches. Semin. Cell Dev. Biol. 87, 125–144. doi: 10.1016/j.semcdb.2018.04.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Lewontin, R. C. (1970). The units of selection. Annu. Rev. Ecol. Syst. 1, 1–18.

Google Scholar

Lobo, D., Beane, W. S., and Levin, M. (2012). Modeling planarian regeneration: a primer for reverse-engineering the worm. PLoS Comput. Biol. 8:e1002481. doi: 10.1371/journal.pcbi.1002481

PubMed Abstract | CrossRef Full Text | Google Scholar

Lyon, P., Keijzer, F., Arendt, D., and Levin, M. (2021a). Basal cognition: multicellularity, neurons and the cognitive lens. Philos. Trans. R. Soc. B Biol. Sci. 376:20190750.

Google Scholar

Lyon, P., Keijzer, F., Arendt, D., and Levin, M. (2021b). Reframing cognition: getting down to biological basics. Philos. Trans. R. Soc. Lond. B Biol. Sci. 376:20190750. doi: 10.1098/rstb.2019.0750

PubMed Abstract | CrossRef Full Text | Google Scholar

Manicka, S., and Levin, M. (2019a). The cognitive lens: a primer on conceptual tools for analysing information processing in developmental and regenerative morphogenesis. Philos. Trans. R. Soc. Lond. B Biol. Sci. 374:20180369. doi: 10.1098/rstb.2018.0369

PubMed Abstract | CrossRef Full Text | Google Scholar

Manicka, S., and Levin, M. (2019b). Modeling somatic computation with non-neural bioelectric networks. Sci. Rep. 9:18612. doi: 10.1038/s41598-019-54859-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Margulis, L., and Fester, R. (1991). Symbiosis as a Source of Evolutionary Innovation: Speciation and Morphogenesis. Cambridge, MA: MIT Press.

Google Scholar

Maynard Smith, J., and Szathmary, E. (1997). The Major Transitions in Evolution. Oxford: Oxford University Press.

Google Scholar

Mengistu, H., Huizinga, J., Mouret, J. B., and Clune, J. (2016). The evolutionary origins of hierarchy. PLoS Comput. Biol. 12:e1004829. doi: 10.1371/journal.pcbi.1004829

PubMed Abstract | CrossRef Full Text | Google Scholar

Michod, R. E. (2000). Darwinian Dynamics: Evolutionary Transitions in Fitness and Individuality. Princeton, NJ: Princeton University Press.

Google Scholar

Mills, R. (2010). How Micro-Evolution Can Guide Macro-Evolution: Multi-Scale Search via Evolved Modular Variation. Ph.D. Thesis, School of Electronics and Computer Science, University of Southampton, Southampton, United Kingdom.

Google Scholar

Mills, R., Jansen, T., and Watson, R. A. (2014). Transforming evolutionary search into higher-level evolutionary search by capturing problem structure. IEEE Trans. Evol. Comput. 18, 628–642.

Google Scholar

Minsky, M. L., and Papert, S. A. (1988). Perceptrons: Expanded Edition. Cambridge, MA: MIT press.

Google Scholar

Nash, F. K. L., Thies, C., Kouvaris, K., Tarapore, D., and Watson, R. (2021). Scaling-up variation and evolvability: the causes and consequences of developmental hierarchy. bioRxiv [Preprint].

Google Scholar

O’Gorman, R., Sheldon, K. M., and Wilson, D. S. (2008). For the good of the group? Exploring group-level evolutionary adaptations using multilevel selection theory. Group Dyn. 12, 17–26.

Google Scholar

Okasha, S. (2006). Evolution and the Levels of Selection. Oxford: Oxford University Press.

Google Scholar

Okasha, S. (2021). The strategy of endogenization in evolutionary biology. Synthese 198, 3413–3435.

Google Scholar

Pezzulo, G., Lapalme, J., Durant, F., and Levin, M. (2021). Bistability of somatic pattern memories: stochastic outcomes in bioelectric circuits underlying regeneration. Philos. Proc. R. Soc. B 376:20190765. doi: 10.1098/rstb.2019.0765

PubMed Abstract | CrossRef Full Text | Google Scholar

Pezzulo, G., and Levin, M. (2015). Re-membering the body: applications of computational neuroscience to the top-down control of regeneration of limbs and other complex organs. Integr. Biol. 7, 1487–1517. doi: 10.1039/c5ib00221d

PubMed Abstract | CrossRef Full Text | Google Scholar

Pezzulo, G., and Levin, M. (2016). Top-down models in biology: explanation and control of complex living systems above the molecular level. J. R. Soc. Interface 13:20160555. doi: 10.1098/rsif.2016.0555

PubMed Abstract | CrossRef Full Text | Google Scholar

Power, D. (2019). Distributed Associative Learning in Ecological Community Networks. Ph.D. dissertation. Southampton: University of Southampton.

Google Scholar

Power, D. A., Watson, R. A., Szathmary, E., Mills, R., Powers, S. T., Doncaster, C. P., et al. (2015). What can ecosystems learn? Expanding evolutionary ecology with learning theory. Biol. Direct 10:69. doi: 10.1186/s13062-015-0094-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Powers, S., and Watson, R. (2011). “Evolution of individual group size preference can increase group-level selection and cooperation,” in Advances in Artificial Life. Darwin Meets von Neumann, eds G. Kampis, I. Karsai, and E. Szathmáry (Berlin: Springer), 53–60. doi: 10.1111/mec.12941

PubMed Abstract | CrossRef Full Text | Google Scholar

Powers, S. T., Mills, R., Penn, A. S., and Watson, R. A. (2009). “Social environment construction provides an adaptive explanation for new levels of individuality,” in Proceedings of the ECAL 2009 Workshop on Levels of Selection and Individuality in Evolution: Conceptual Issues and the Role of Artificial Life Models (Budapest: Springer Science & Business Media).

Google Scholar

Powers, S. T., Penn, A. S., and Watson, R. A. (2011). The concurrent evolution of cooperation and the population structures that support it. Evolution 65, 1527–1543. doi: 10.1111/j.1558-5646.2011.01250.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Queller, D. C. (1997). Cooperators Since Life Began. Chicago, IL: University of Chicago Press.

Google Scholar

Ratcliff, W. C., Denison, R. F., Borrello, M., and Travisano, M. (2012). Experimental evolution of multicellularity. Proc. Natl. Acad. Sci. USA. 109, 1595–1600. doi: 10.1073/pnas.1115323109

PubMed Abstract | CrossRef Full Text | Google Scholar

Rubenstein, M., Cornejo, A., and Nagpal, R. (2014). Programmable self-assembly in a thousand-robot swarm. Science 345, 795–799. doi: 10.1126/science.1254295

PubMed Abstract | CrossRef Full Text | Google Scholar

Ryan, P., Powers, S., and Watson, R. (2016). Social niche construction and evolutionary transitions in individuality. Philos. Biol. 31, 59–79. doi: 10.1007/s10539-015-9505-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Santos, F. C., Pacheco, J. M., and Lenaerts, T. (2006). Cooperation prevails when individuals adjust their social ties. PLoS Comput. Biol. 2:e140. doi: 10.1371/journal.pcbi.0020140

PubMed Abstract | CrossRef Full Text | Google Scholar

Shalizi, C. R. (2009). Dynamics of Bayesian updating with dependent data and misspecified models. Electron. J. Stat. 3, 1039–1074. doi: 10.1890/13-0187.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Skinner, B. F. (1981). Selection by consequences. Science 213, 501–504. doi: 10.1126/science.7244649

PubMed Abstract | CrossRef Full Text | Google Scholar

Simpson, C. (2012). The evolutionary history of the division of labour. Proc. R. Soc. B 279, 116–121. doi: 10.1098/rspb.2011.0766

PubMed Abstract | CrossRef Full Text | Google Scholar

Slavkov, I., Carrillo-Zapata, D., Carranza, N., Diego, X., Jansson, F., Kaandorp, J., et al. (2018). Morphogenesis in robot swarms. Sci. Robot. 3:eaau9178. doi: 10.1126/scirobotics.aau9178

PubMed Abstract | CrossRef Full Text | Google Scholar

Stanley, K. O., and Miikkulainen, R. (2002). Evolving neural networks through augmenting topologies. Evol. Comput. 10, 99–127. doi: 10.1162/106365602320169811

PubMed Abstract | CrossRef Full Text | Google Scholar

Such, F. P., Madhavan, V., Conti, E., Lehman, J., Stanley, K. O., and Clune, J. (2017). Deep neuroevolution: genetic algorithms are a competitive alternative for training deep neural networks for reinforcement learning. arXiv [Preprint]. arXiv:1712.06567

Google Scholar

Szathmary, E. (2015). Toward major evolutionary transitions theory 2.0. Proc. Natl. Acad. Sci. U.S.A. 112, 10104–10111. doi: 10.1073/pnas.1421398112

PubMed Abstract | CrossRef Full Text | Google Scholar

Tank, D. W., and Hopfield, J. J. (1987a). Collective computation in neuronlike circuits. Sci. Am. 257, 104–114. doi: 10.1038/scientificamerican1287-104

PubMed Abstract | CrossRef Full Text | Google Scholar

Tank, D. W., and Hopfield, J. J. (1987b). Neural computation by concentrating information in time. Proc. Natl. Acad. Sci. U.S.A. 84, 1896–1900. doi: 10.1073/pnas.84.7.1896

PubMed Abstract | CrossRef Full Text | Google Scholar

Taylor, C., and Nowak, M. A. (2007). Transforming the dilemma. Evolution 61, 2281–2292. doi: 10.1111/j.1558-5646.2007.00196.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Thies, C., and Watson, R. A. (2021) Identifying causes of social evolution: contextual analysis, the price approach, and multilevel selection. Front. Ecol. Evol. 9:780508. doi: 10.3389/fevo.2021.780508

CrossRef Full Text | Google Scholar

Tudge, S., Watson, R., and Brede, M. (2013). “Cooperation and the division of labour,” in Paper Presented at the Artificial Life Conference Proceedings (Cambridge, MA: MIT Press), 13.

Google Scholar

Tudge, S. J., Watson, R. A., and Brede, M. (2016). Game theoretic treatments for the differentiation of functional roles in the transition to multicellularity. J. Theor. Biol. 395, 161–173. doi: 10.1016/j.jtbi.2016.01.041

PubMed Abstract | CrossRef Full Text | Google Scholar

Uller, T., Moczek, A. P., Watson, R. A., Brakefield, P. M., and Laland, K. N. (2018). Developmental bias and evolution: a regulatory network perspective. Genetics 209, 949–966. doi: 10.1534/genetics.118.300995

PubMed Abstract | CrossRef Full Text | Google Scholar

Valiant, L. (2013). Probably Approximately Correct: Nature’s Algorithms for Learning and Prospering in a Complex World. New York, NY: Basic Books.

Google Scholar

Vanchurin, V., Wolf, Y. I., Katsnelson, M. I., and Koonin, E. V. (2021). Towards a theory of evolution as multilevel learning. arXiv [Preprint]. arXiv:2110.14602 doi: 10.1073/pnas.2120037119

PubMed Abstract | CrossRef Full Text | Google Scholar

Veit, W. (2021). Scaffolding natural selection. Biol. Theory 1–18. doi: 10.1007/s13752-021-00387-6

CrossRef Full Text | Google Scholar

Wade, M. J. (2016). Adaptation in Metapopulations. Chicago, IL: University of Chicago Press.

Google Scholar

Wagner, G. P., and Laubichler, M. D. (2004). Rupert Riedl and the re-synthesis of evolutionary and developmental biology: body plans and evolvability. J. Exp. Zool. B Mol. Dev. Evol. 302, 92–102. doi: 10.1002/jez.b.20005

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, R. A. (2021). “Evolvability,” in Evolutionary Developmental Biology: A Reference Guide, eds L. Nuño de la Rosa and G. B. Müller (Cham: Springer), 133–148.

Google Scholar

Watson, R. A., Buckley, C., and Mills, R. (2009). The Effect of Hebbian Learning on Optimisation in Hopfield Networks. Southampton: ECS, University of Southampton.

Google Scholar

Watson, R. A., Buckley, C. L., Mills, R., and Davies, A. (2010). “Associative memory in gene regulation networks,” in Proceedings of the 12th International Conference on the Synthesis and Simulation of Living Systems (Artificial Life XII), Odense.

Google Scholar

Watson, R. A., Buckley, C. L., and Mills, R. (2011c). Optimization in “self-modeling” complex adaptive systems. Complexity 16, 17–26. doi: 10.1002/cplx.20346

CrossRef Full Text | Google Scholar

Watson, R. A., Mills, R., and Buckley, C. (2011a). Global adaptation in networks of selfish components: emergent associative memory at the system scale. Artif. Life 17, 147–166. doi: 10.1162/artl_a_00029

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, R. A., Mills, R., and Buckley, C. (2011b). Transformations in the scale of behavior and the global optimization of constraints in adaptive networks. Adapt. Behav. 19, 227–249. doi: 10.1186/s12868-016-0283-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, R. A., Palmius, N., Mills, R., Powers, S., and Penn, A. (2011d). “Can selfish symbioses effect higher-level selection?,” in Advances in Artificial Life. Darwin Meets von Neumann, eds G. Kampis, I. Karsai, and E. Szathmáry (Berlin: Springer), 27–36.

Google Scholar

Watson, R. A., Mills, R., Buckley, C., Kouvaris, K., Jackson, A., Powers, S. T., et al. (2016). Evolutionary connectionism: algorithmic principles underlying the evolution of biological organisation in evo-devo, evo-eco and evolutionary transitions. Evol. Biol. 43, 553–581. doi: 10.1007/s11692-015-9358-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, R. A., and Szathmary, E. (2016). How can evolution learn? Trends Ecol. Evol. 31, 147–157. doi: 10.1016/j.tree.2015.11.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, R. A., and Thies, C. (2019). “Are developmental plasticity, niche construction, and extended inheritance necessary for evolution by natural selection? The role of active phenotypes in the minimal criteria for Darwinian individuality,” in Evolutionary Causation: Biological and Philosophical Reflections, eds T. Uller and K. N. Laland (Cambridge, MA: MIT Press), 197–226.

Google Scholar

Watson, R. A., Wagner, G. P., Pavlicev, M., Weinreich, D. M., and Mills, R. (2014). The evolution of phenotypic correlations and ‘developmental memory. Evolution 68, 1124–1138. doi: 10.1111/evo.12337

PubMed Abstract | CrossRef Full Text | Google Scholar

Weinreich, D. M., Watson, R. A., and Chao, L. (2005). Perspective: sign epistasis and genetic costraint on evolutionary trajectories. Evolution 59, 1165–1174.

PubMed Abstract | Google Scholar

West, S. A., Fisher, R. M., Gardner, A., and Kiers, E. T. (2015). Major evolutionary transitions in individuality. Proc. Natl. Acad. Sci. U.S.A. 112, 10112–10119. doi: 10.1073/pnas.1421402112

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, D. S. (1975). A theory of group selection. Proc. Natl. Acad. Sci. U.S.A. 72, 143–146.

Google Scholar

Wilson, D. S. (1997). Altruism and organism: disentangling the themes of multilevel selection theory. Am. Nat. 150, S122–S134. doi: 10.1086/286053

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, E. O. (2013). The Social Conquest of Earth. New York, NY: Liveright Publishing Corp.

Google Scholar

Wimsatt, W. C. (1980). “The units of selection and the structure of the multi-level genome,” in Paper Presented at the PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association (Chicago, IL: University of Chicago Press).

Google Scholar