- 1Institute for Coastal and Marine Research, Nelson Mandela University, Port Elizabeth, South Africa
- 2School of Public Leadership, Stellenbosch University, Stellenbosch, South Africa
Globally, fisheries are in decline and in many parts of the world illegal fishing is a major cause of these declines. Ecological restoration of fisheries needs to be promoted, inter alia through improved enforcement, but, which method is the most successful at improving fish stocks, as well as having the highest economic returns? We compare one open-loop (without feedback) and three closed-loop (with feedback) benefit–cost models representing different restoration interventions aimed at promoting compliance. The hybrid systems methodology has been utilized, combining system dynamics, systems archetypes, mathematical differential equations and economic benefit–cost methodologies. The model is tested with reference to a case study of abalone (Haliotis midae) biomass restoration in the Table Mountain National Park marine area (Zone E), Cape Town. Stocks in Zone E have dropped to below the government’s management threshold for sustainable fisheries of 20 percent of the pre-fished levels, and urgent action is required to restore the stocks. According to the model, all proposed restoration interventions produce stock recovery to 100 percent of carrying capacity, well in excess of government targets of 40 percent. Also, all four models had a net present value of greater than zero, indicating substantial positive net benefits to restoration. Each model had specific management recommendations associated with it- greater involvement by the state, capital investment in restoration, changing poacher behavior and entrepreneurship. Although the Post Keynesian and Institutional model produced the highest net returns to restoration over 80 years (Net present value = US$12.66 million at a 6 % discount rate, 2021 prices), all the models are essentially co-evolutionary models, and have merit over different time periods, compliance rates and assumptions around discount rates. While the case study is developed for abalone the findings of the model are likely to be applicable in a wide range of fishery restoration contexts.
1. Introduction
Globally, many fisheries are in decline (Pauly et al., 2005; Pauly, 2019; Palomares et al., 2020). Developing countries are particularly vulnerable to biodiversity losses. In a recent assessment, South Africa ranked sixth worst out of 195 countries, with 40 percent of its biodiversity and ecosystem services identified as “fragile” (Retsa et al., 2020). One of the most problematic fisheries is the abalone (Haliotis midae) fishery, which has been heavily depleted, due to high levels of poaching and an over allocation of total allowable catch [DEFF (Department of Environment, Forestry and Fisheries), 2020]. Heavily depleted fish stocks can take much longer to recover, even when fish stocks are protected (Hilborn et al., 2014). Abalone may experience low fertility (Coates et al., 2013) and low dispersal (Tarr et al., 1995), which may further limit their recovery. This slow recovery is not only true for abalone, but for other demersal fish such as hake as well (Vergnon et al., 2008). Demersal finfish and shellfish are also among the taxa with the highest incidence of illegal and unreported catch (Agnew et al., 2009). Therefore, Marine Protected Areas (MPAs) alone are not enough to ensure stock recovery (Higgins et al., 2008).
Restoration is increasingly seen as a means for reversing environmental damage (Taljaard et al., 2021). In recent meta-analyses of the benefits and costs of restoration (De Groot et al., 2013; Elmqvist et al., 2015; Crookes and Blignaut, 2019), it has been demonstrated that the benefits of restoration exceed the cost, and by some considerable margin in most cases. Coastal and marine resources are, however, not well-covered in these reviews despite their very high economic and cultural values (Blignaut et al., 2016, 2017; Zhang et al., 2018). Some of the notable exceptions are reported in TEEB (2011) citing Fox et al. (2005) that estimated the benefits from coral reef restoration following blast fishing and Leschen (2007) that estimated the cost of seagrass restoration.
The Economics of Ecosystems and Biodiversity (TEEB) report also highlights a few studies with respect to the costs of mangrove restoration in estuaries in the United States (US) (Lewis Environmental Services, 2007; Francher, 2008). Barbier (2013) also discusses studies from the US documenting the valuation of ecosystem benefits from coastal system and the challenges associated with the restoration thereof. Van Dover et al. (2014) report estimates for the costs of restoration in the deep sea and indicates that these may be two to three times greater than the costs of restoration of marine systems in shallow water. These costs are for coastal systems restoration, but do not include restoration through marine enforcement activities. To contribute to the literature in this field, this study focuses on a benefit cost analysis (BCA) as applied to the improvement in abalone biomass. This is particularly important, given that in 2021, both the United Nations (UN) Decade on Ecosystem Restoration1 and the Decade of Ocean Science2 commenced. In the strategic plans for both these UN initiatives, it was indicated that investments in oceans restoration could yield benefits that are substantially greater than the costs.
The notion of restoration is mostly used within the context of an entire ecosystem. For example, Kennedy et al. (2011) consider fisheries (oyster) restoration through substrate (shell), transplanting hatchery or wild seed (juvenile oysters), bar cleaning, and bagless dredging, and Stewart-Sinclair et al. (2021) define marine restoration in terms of coral reef, mangrove, saltmarsh, and seagrass restoration. This is important, since marine ecosystems are often degraded (Nyström et al., 2012). At the same time, increasingly in the literature, the concept of the “restoration of natural capital” is being promoted. The restoration of natural capital is defined as “any activity that integrates investment in and replenishment of natural capital stocks to improve the flow of ecosystem goods and services, while enhancing all aspects of human well-being” (Aronson et al., 2007, p. 5). This definition includes all forms of natural capital restoration, including living species, ecosystems, replenishable and cultivated natural capital.
Few studies (if any) focus specifically on fisheries restoration. For the case study we consider the improvement of abalone biomass through improved enforcement effort. Other interventions that could be undertaken (but are not costed here) include reducing the Total Allowable Catch (TAC), and trans-locating west coast rock lobster away from vulnerable abalone nursery grounds [see DEFF (Department of Environment, Forestry and Fisheries), 2020]. The reason enforcement effort was focused on was because: (i) the legal landings of abalone are a small fraction of the illegally caught abalone; (ii) the Department of Environment, Forestry and Fisheries (DEFF) have identified the reduction in illegal harvests as a major management objective [DEFF (Department of Environment, Forestry and Fisheries), 2020]. But which method of ensuring compliance is best? We apply four different restoration methods based on models from four different economic schools of thought, in order to investigate which behavioral response is likely to generate the highest returns and the greatest recruitment success.
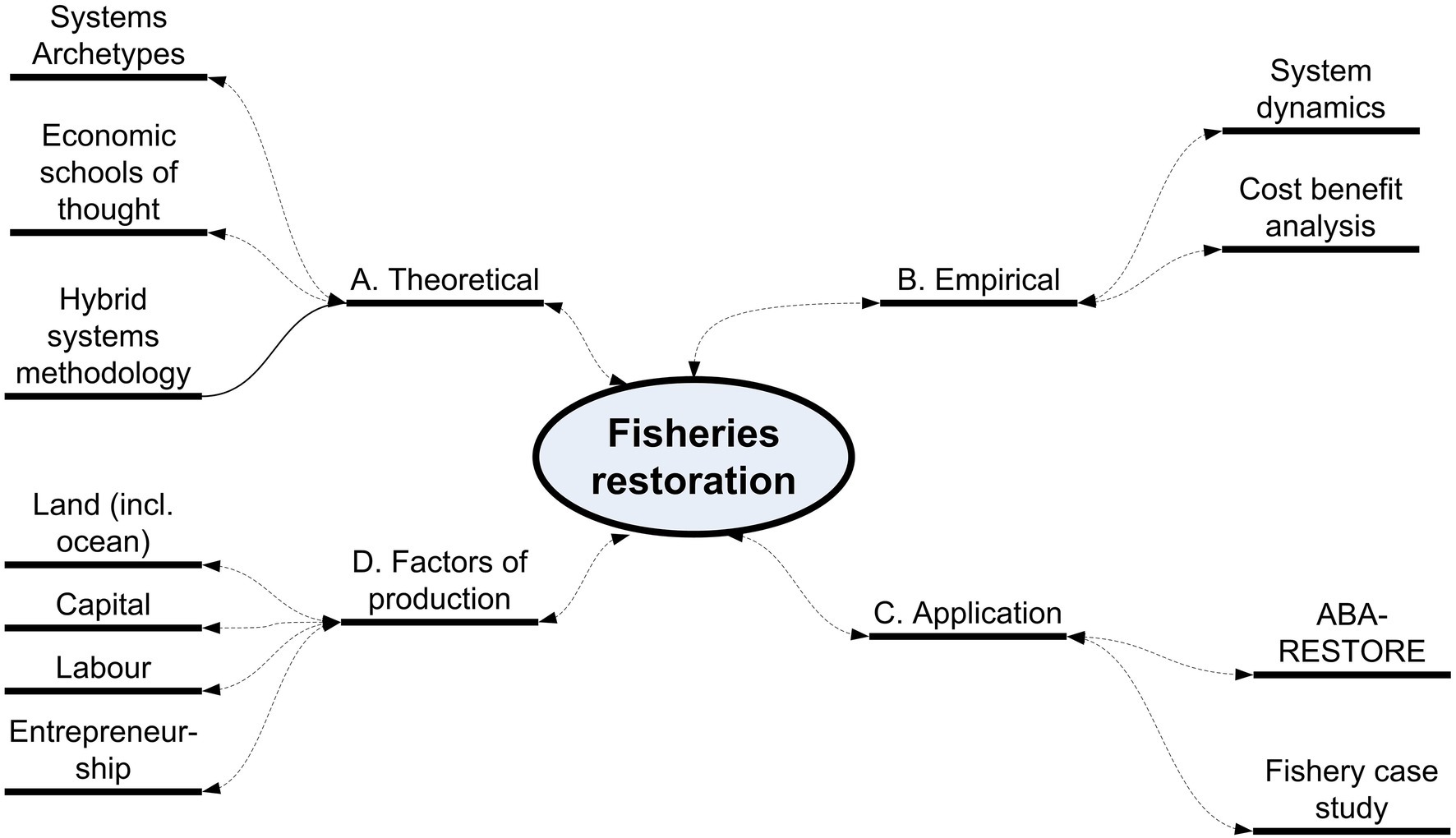
The aim of this study is to develop a framework for fisheries restoration, based on a hybrid systems approach that incorporates systems theory (archetypes), mathematics (first order differential equations), economics (benefit–cost analysis) and system dynamics modelling.
2. Materials and methods
2.1. Background
Four approaches are employed in order to analyze the benefits from fisheries restoration (Figure 1): Firstly, a theoretical approach is considered, based on a hybrid systems methodology, whereby different economic schools of thought are linked with systems archetypes. Secondly, an empirical model is developed, by converting the theoretical framework into four benefit cost models. Thirdly, a case study is proposed, where the framework is applied to a specific fishery. Finally, results of the case study are used to make inferences about fisheries restoration in general.
2.2. Classification of the economic schools of thought
We utilize a hybrid systems methodology (HSM) approach (Powell and Mustafee, 2014) to classify different economic schools of thought. The HSM approach combines methods and techniques from the systems discipline and methods from other disciplines such as economics and applied computing (Eldabi et al., 2016).
The systems discipline identifies inter alia four different types of models (or archetypes, see, e.g., Senge, 1990, Sterman, 2000). An archetype is simply a representative model, but these predefined modelling frameworks have become very influential in the systems modelling community:
1. Limits to success (growth) archetype. These are models where one entity preys on or otherwise inhibits another one.
2. The tragedy of the commons systems archetype. These models are where resource limitations prevent the expansion of an entity.
3. Drifting goals archetype. This archetype states that if there is a gap between the current state and the goal, corrective action needs to be taken to bring the current state in line with the goal.
4. Open loop models. These are models with no defined archetype, no feedback, and are usually characterized by linear systems (see Supplementary material, Annexure 1, for a further elaboration).
These four models were chosen from the list of 10 archetypes that are available in the literature due to their relevance to the abalone fishery management problem in South Africa. We utilize these didactic models in order to match the archetype to different economic schools of thought.
The economic schools of thought are summarized as follows:
1. Evolutionary economics (EV)- Law (1985) states: “evolution of the biotic environment of a population is a well-known phenomenon when the environment is composed of species for which the population has antagonistic interactions, such as predator–prey, host-pathogens and competitors”; see also Magain et al. (2017) for a more recent affirmation of this point. Although the evolutionary economics literature is vast and diverse, e.g., Van Den Bergh (2007) has linked these models to evolutionary economics. Gould and Cleveland (2018) have also coupled the “limits to success” archetype with the evolutionary system.
2. Neoclassical economics (NC)-Although there are some similarities between the EV and NC schools, one of the fundamental differences between neoclassical and evolutionary economics is its focus of the NC school on scarcity (Panayotakis, 2013). For example, Samuelson and Nordhaus (1989), a highly influential neoclassical textbook, defines economics as the study of “how people choose to use scarce or limited productive resources (land, labor, equipment, technical knowledge) to produce various commodities (such as wheat, beef)” (p.4–5). As a result, authors such as Garrity (2012) have linked the neoclassical school with the “tragedy of the commons” archetype.
3. Post Keynesians and Institutional economics (PKI)- fundamental to the understanding of Post-Keynesian economics is the concept of historical and dynamic time. Lavoie (2006) explains that: “We must always consider the transition from one dynamic time position to another and recognize that the conditions under which this transition occurs may affect the final position of equilibrium.”
A second element of Post-Keynesian economics is that it is demand driven. As Lavoie (2006) explains: “supply adapts to demand.” According to Lavoie (2006), Post-Keynesians emphasize the role of the state in stimulating effective demand, thereby seeking full employment [see also Whalen (2013) and Keller (1983) who make a similar point also with reference to the institutional school]. Although we found no other authors who have definitively linked the PKI school with the drifting goals archetype, in the context of the abalone problem discussed here it does seem particularly relevant, given that the focus in on government undertaking corrective action to solve an environmental problem.
Though we acknowledge that the PKI school could be linked to a number of different archetypes, we believe that the “drifting goals” archetype is particularly relevant to this school, since Saeed and Radzicki (1993) argue that the PKI school is a disequilibrium approach, and the drifting goals archetype is suitable for correcting imbalances between supply and demand.
1. Open loop economics (OL)- these focus on tools for appraisal that are independent of an economic ideology. These can include open loop game theory (Lofgren, 1999), life cycle assessment (Klöpffer, 1996; Ekvall, 2000; Williams et al., 2010), and linear dynamic economics (Narraway and Perkins, 1993; Kookos, 2001). The OL school would not be linked to any specific archetype, since all archetypes contain feedback whereas the OL school is a linear system. It is nonetheless important to consider the implications of fisheries restoration in this case as well.
2.3. Benefit–cost analysis
The decision-maker must take decisions as to the most beneficial use of limited resources today by examining the impact thereof in the future. They will seek the option where the benefits most exceed the costs, or the least cost option (loss minimization). For such an analysis and project appraisal, a Benefit–Cost Analysis (BCA) is most useful (Argyrous, 2017). The formula for conducting a BCA is as follows:
PV = present value.
Rt = cash inflow (benefits) or outflows (costs) during a single period t.
i = social discount rate.
n = number of time periods.
The Benefit–Cost Ratio (BCR) is calculated as the present value of the benefit stream divided by the present value of the cost stream. A BCR greater than 1 indicates that the present value of benefits exceeds the costs. From an economic efficiency perspective, any project with a BCR greater than 1 represents an efficient allocation of resources (Kee, 2004). The BCR can be useful for calculating the annual returns of a project if the timeframe of the project is known.
Static BCA (sBCA) is usually conducted using a spreadsheet and generates a single point estimate, notably Net Present Value (NPV) or related measure (Argyrous, 2017). Dynamic BCA (dBCA) is mostly conducted using a system dynamics modelling framework and a “cumulative NPV” is generated (Schade and Rothengatter, 2003). In both instances, however, time matters. Here, we combine these two concepts and use the dynamic Benefit–Cost Ratio (dBCR) as the project evaluation criteria. This metric was proposed by De Groot et al. (2013) in relation to the evaluation of ecological restoration projects.
Given that time matters, it is not surprising that arguably the single most dominant variable in the PV equation shown above is that of the social discount rate, the indicator of the time preference of money. A positive rate implies that the time preference of money in the future is less than the present, and the higher the discount rate is the less important the future financial streams become. Blignaut and Aronson (2008), however, argue that in the case of ecological restoration, when such restoration activity enhances the economic value of a resource in future value and reduces resource scarcity, a negative discount rate as an indication of the future value of restoration is appropriate. We thus utilize both positive and negative discount rates.
2.4. System dynamics model
To improve abalone biomass, at least three different interventions could be considered related to enforcement effort: (1) government could stimulate the demand for the improvement in abalone biomass through education, training and investment in enforcement efforts; (2) the focus could be on confiscations, arrests and general deterrence in the restoration sector; or (3) the government could privatize several interventions that would lead to the improvement of abalone biomass, such as by hiring private firms to patrol fishing waters.
These interventions are features of different schools of economic thought. The intervention of government is a feature of the PKI school, enforcement through prosecution of offenders represents the evolutionary school, the role of business represents the neoclassical school, and a linear specification represents the open loop school.
A system dynamics model was constructed for each of the four economic systems (neoclassical, open loop, Post Keynesian and Institutional, and evolutionary) using the Vensim DSS software (version 6.4b). This methodology is well described in Sterman (2000). A series of differential equations are constructed representing each of the schools of thought in the system (Crookes, 2022). Purnomo and Mendoza (2011) provide a recent application of this methodology to renewable resources in a developing country. The stock flow diagrams for the resulting abalone model is included in the Supplementary material, Annexure 2.
The causal loop diagram for the ABA-RESTORE model is given in Figure 2. A description of each of the loops in the system are given here (the reader is referred to the diagram for the names of the loops). Firstly, the reinforcing loops are described. Reinforcing loops lead to exponential growth or decline.
• Loop R1: An increase in employment increases population (by increasing migration into an area) which increases employment again. This is the household sub-model.
• Loop R2: An increase in government increases employment which increases population, which increases personal taxes which increases government. This is the government sub-model.
• Loop R3: An increase in business increases wages which increases population which increases employment which in turn increases business. This is the business sub-model.
• Loop R4: An increase in business increases taxes which increases government, which increases employment which increases business. This is the taxation sub-model.

Figure 2. The causal loop diagram for the ABA-RESTORE simulation model. The different loop combinations represent the different archetypes in the model. Loops B1 (government) and its archetype (PKI); loops R1 and B2 and R2 and B2 represents the “limits to success” archetype (EV); loops B3, B4, R3, and R4 represent the “tragedy of the commons” archetype (NC).
Secondly, the balancing loops are described. Balancing loops lead to goal seeking behavior or convergence on an equilibrium:
• Loop B1: An increase in government increases enforcement effort which in turn increases the marine ecosystem, which in turn increases the cost of enforcement which decreases government. This is the government sub-model
• Loop B2: An increase in government leads to an increase in employment (for example in the ecosystem restoration sector), which leads to an increase in conflict (for example poacher conflict) which leads to a decrease in government resources. This is the poaching sub-model.
• Loop B3: An increase in the business (entrepreneurship) increases rent paid, which increases land (including oceans) utilization, which increases resource constraints which decreases business (entrepreneurship). This is the capital sub-model.
• Loop B4: An increase in business results in an increase in taxes which increases government, which increases enforcement effort, which increases fishery recovery, which increases resource constraints (since demand for poaching increases), which decreases business.
2.5. Case study
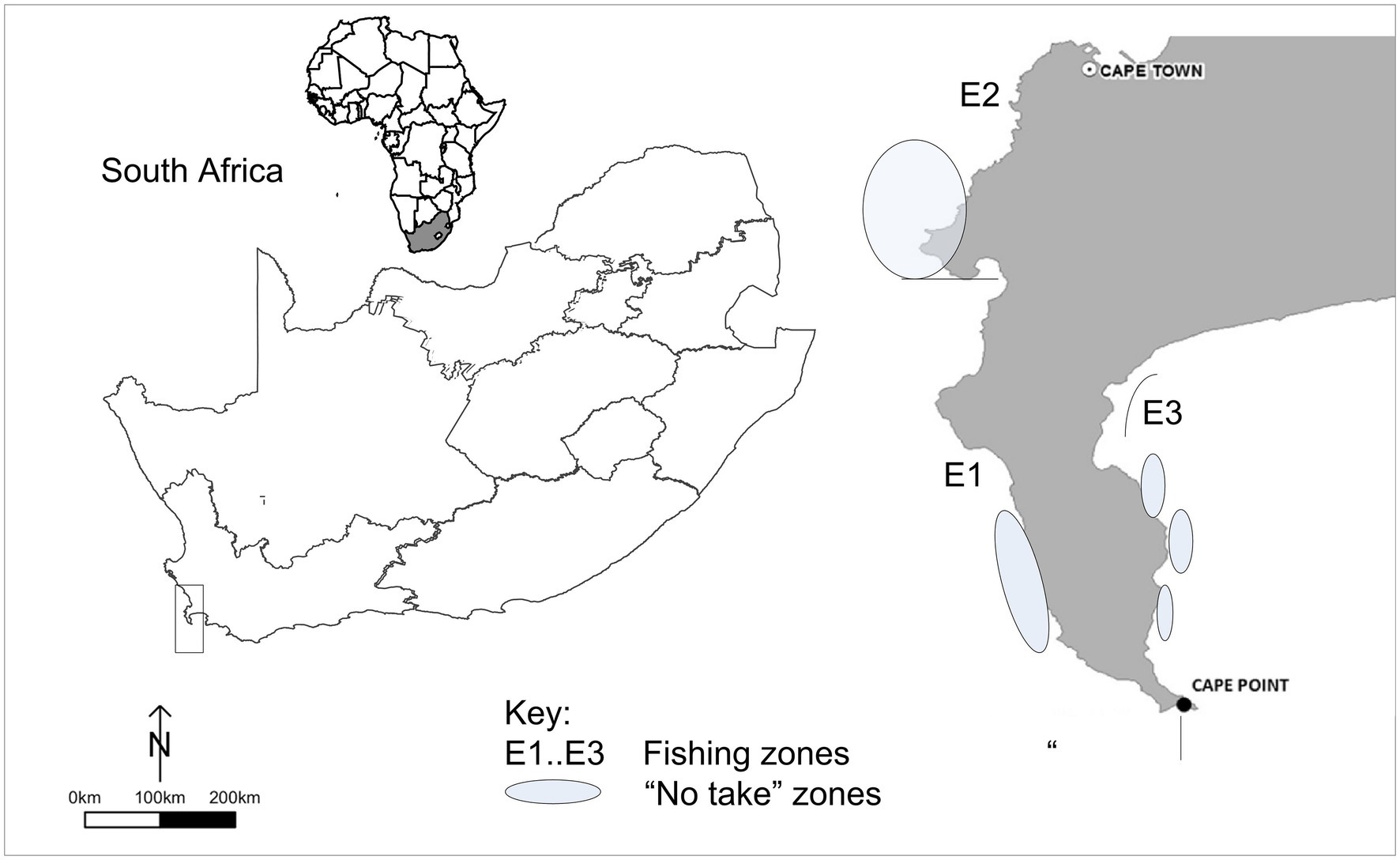
We develop a model (the ABA-RESTORE model) that presents various strategies for abalone biomass improvement based on the different schools of economic thought using a simulation model developed for the Table Mountain National Park (Crookes, 2016). The Marine Protected Area (MPA) is situated in Zone E, and includes almost 1,000 km2 of the sea and coastline around the Cape Peninsula from Moullie Point in the North to Muizenberg in the South. Fishing is allowed in the MPA, although there are five “no take” areas where no fishing or extractive use is allowed (see Figure 3).
There are two main sources of input data. The first set of input data pertains to the benefits of improving abalone biomass, or the enhancement of its in situ (existence) value, see Supplementary material, Annexure 3. As a conservative, lower-bound, proxy of the existence value the traded value of illegally harvested abalone is used. This is since it is an indicator of the willingness to pay for the resource and thus should reflect its existence value, albeit only in part.
Secondly, the costs of enforcement represent the patrolling costs that the marine authorities incur, see Supplementary material, Annexure 3. These costs would include payments to crew, as well as boat costs (Crookes, 2016). Brown et al. (2018) estimate that the cost of restoring a marine protected area from a highly depleted state to near pristine is US$29/km2 (2017 prices). Multiply this by the area of TBNP and making appropriate CPI and PPP adjustments gives a cost of improving the abalone stock in Table Mountain National Park at US$32637 per year (2019 prices).
2.6. Model validation
Model validation is essential if the model is to be used for forecasting. Crookes (2022) reviews the validation techniques proposed by eight prominent system dynamics modelers, and concludes that structure verification, parameter verification, dimensional consistency and boundary adequacy tests are sine qua non. Structure verification compares the model with structures found in the real world. Since the modelling structure is based on four systems archetypes, their relevance to the real world has already been established. Parameter verification is undertaken by comparing parameters with the real world. Many parameters used in the model are derived from the literature. Dimensional consistency is assessed by checked whether or not the units in the model are consistent across different equations. The model passed the dimensional consistency test. Boundary adequacy is usually assessed through different tests. Again, since the models are didactic models, the parameters and structure of the model are complete. The behavior of the models are also in accord with a priori expectations. Although not an exhaustive list of validation techniques were employed the model is deemed sufficiently robust for forecasting purposes.
A final validation question relates to the general applicability of the ABA-RESTORE model. The model is created for a single taxon (abalone). Is the model relevant to other fisheries restoration problems? Figure 4 indicates the boundary of the study. As one moves towards the center of the diagram, the study becomes more relevant. However, it is evident that the study is also relevant to other developing country contexts, to demersal species, specifically shellfish taxa, and cases of illegal, unregulated and unreported fishing (IUU) in developing countries, and also to demersal taxa consumption (as indicated by the interacting segments in the diagram). The data in the diagram show that these interacting segments represent a sizeable portion of the relevant interaction area. Although these interacting segments comprise the main realm of applicability of the model, the model may also be relevant to other segments, notably restoration focused on aquatic consumptive species, other demersal species, and worldwide IUU (the outer extent of the diagram).
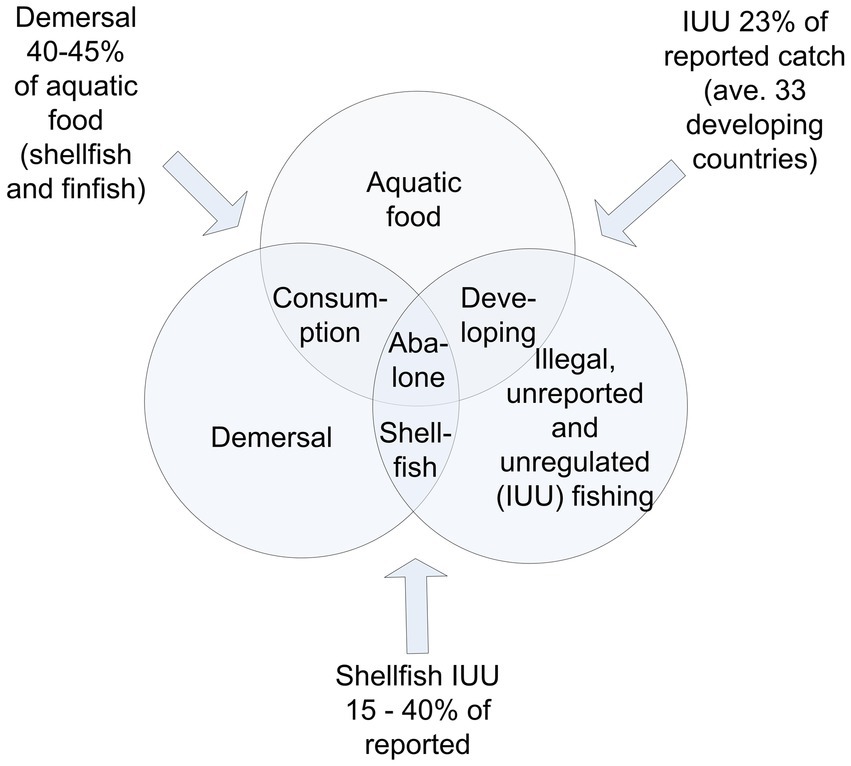
Figure 4. Boundary of the ABA-RESTORE model. How applicable is it to other fisheries? References for the data: Agnew et al. (2009), MRAG (2005), and FAO (2022).
3. Results
3.1. Classification of economic schools of thought
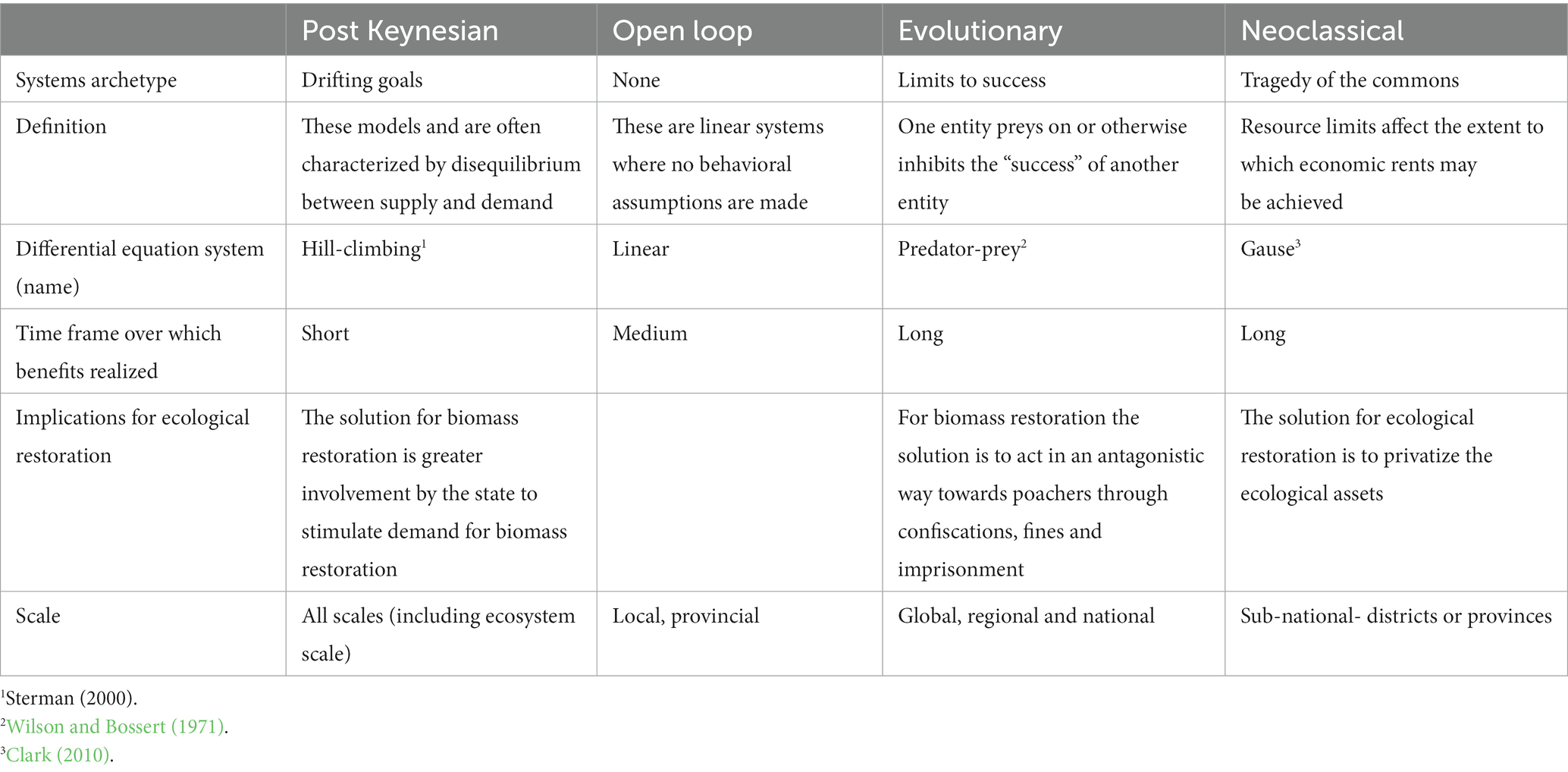
The definitive features of the different economic schools of thought under discussion are given in Table 1. The PKI School argues that government interventions are essential and necessary to stimulate the demand for the improvement of abalone biomass. Government interventions are in both the labor (supply) market as well as stimulating effective demand in the business sector. The OL model assumes no behavior and recovery is linear and exogenous. The EV school focuses on the criterion of conflict between government and poachers. The intent is for antagonism with poachers to ultimately lead to behavioral change and an improvement in abalone biomass. Finally, the NC school argues that privatizing natural capital assets, or the management thereof, is the optimal strategy to ensure the recovery of the stocks.
There are also implications of these models for the different system archetypes. As we saw previously, the PKI School is characterized by the drifting goals archetype in systems theory. The drifting goals archetype hypotheses that the gap between the goal and the current activity can be rectified through corrective action (Maani and Cavana, 2007). In this case (the case of the abalone fishery), corrective action is through the labor market reform (focusing on supply) and through stimulating demand.
The evolutionary school is characterized by the ‘limits to success” archetype. It is characterized by a reinforcing and balancing loop. The reinforcing loop represents the “success” aspect, whereas the balancing loop represents some force that is working against that success. In the case of the abalone fishery, it is potential conflicts with poachers that works against poaching behavior.
The neoclassical schools comprises the tragedy of the commons archetype. In this archetype, a desirable activity results in increasing demand, which ultimately leads to disastrous consequences (Maani and Cavana, 2007). In the case of the abalone fishery, successful restoration interventions lead to wage increases, population stimulus and ultimately (financial) resource constraints.
The open loop school has no archetype, since it is merely a linear specification. However, its implications on the abalone fishery are that there is uniform impact on stock recovery over space and time.
In the next section, we will consider the results of the ABA-RESTORE model, where the results from the different abalone biomass restoration interventions (characterized by the different schools of economic thought) are compared.
3.2. Economic modelling
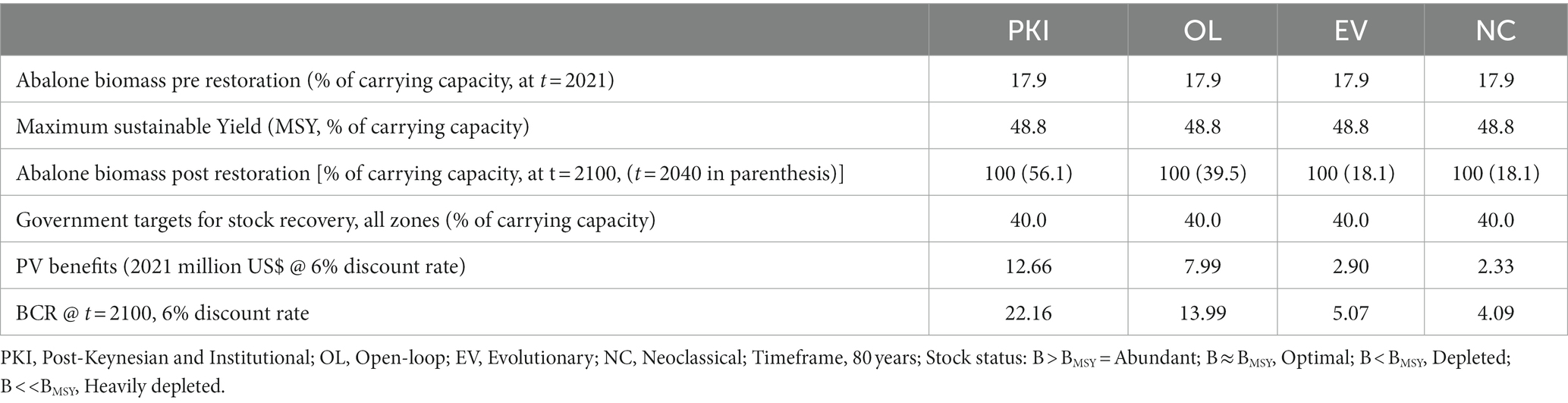
Our results show that abalone stocks in Table Mountain National park (Zone E) are heavily depleted. Stocks are currently at less than 20 percent of carrying capacity, compared with a Maximum Sustainable Yield (MSY) of around 48% of carrying capacity (Table 2). This is a crucial threshold, since the government has set as management target to prevent abalone in each zone from dropping below 20 percent of its pre-fished levels, and to promote recovery to at least 40 percent of that level [DEFF (Department of Environment, Forestry and Fisheries), 2020].
All four ABA-RESTORE models resulted in good recovery of the abalone stocks, with stocks rebounding to 100 percent of carrying capacity over the next 80 years, well in excess of government targets for stock recovery (Table 2). However, only the PKI and OL model achieve or exceed government targets of 40% stock recovery by the year 2040. All four scenarios showed positive net present values and BCRs substantially in excess of unity (the lowest was the NC model with a BCR of over four). The PKI model shows the highest net present value benefit–cost ratios (BCRs) of the four scenarios, with potential returns of almost $13 million in the value of ecosystem restored over 80 years, at a 6 % discount rate (Table 2). This was followed by the OL model (almost $8 million), the EV model (almost $3 million) and the NC model (over $2 million).
We test the sensitivity of the BCRs to different assumptions. Firstly, we model the possibility that in an imperfect world, only 75% of total economic value from abalone recovery will be realized (De Groot et al., 2013). Secondly, we investigate the sensitivity of the BCR to changes in the timeframe over which restoration is assumed to occur. Three different timeframes are investigated namely 20, 40 and 60 years. Finally, we model sensitivity to different discount rates (6% and − 2%). The results (Figure 5) show that for positive discount rates (6%), the PKI model is clearly the winner (top graphic). However, for negative discount rates the results are far more ambiguous (bottom graphic). Any one of the models could be selected and generate equivalent results.

Figure 5. Comparing the benefits of abalone biomass restoration with the costs thereof. Variation in BCRs at 75% of TEV realized, for discount rate of 6% (top graph) and − 2% (bottom graph): Timeframe for intervention: a = 20 years; b = 40 years; c = 60 years.
3.3. Implications for fisheries restoration
The policy of setting a restoration goal and pursuing it (the PKI model) is economically optimal (Figure 6). However, this is not what the South African government is currently doing. Rather, it seems to be pursuing an EV approach of maximizing revenues through enforcement confiscations (see, e.g., Nene, 2023). Naturally, these ex post seizures do not preserve the resource in the short term, as the abalone are already dead. Ex ante incentives to prevent the crime from occurring (the PKI model) not only restores the abalone population, but also maximizes societal welfare (Figure 6).
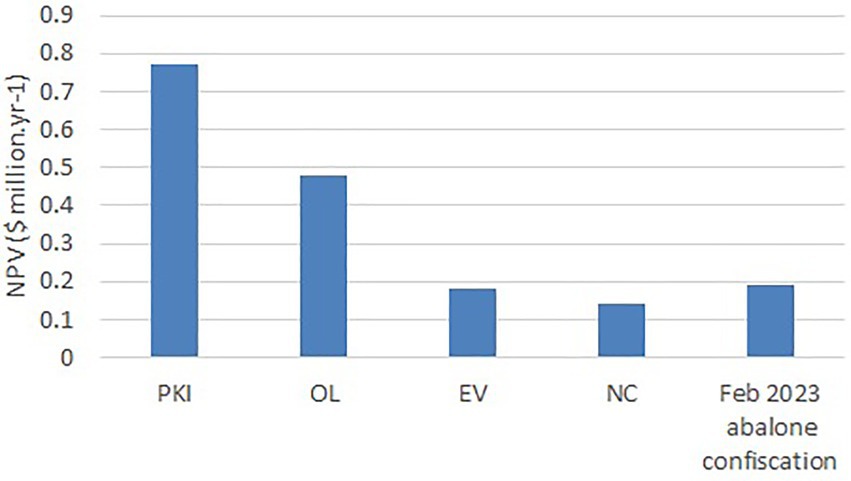
Figure 6. Annualized Net Present Values (in 2021 US$ million.yr-1) for the different schools (this study), compared with revenues from confiscations (Nene, 2023).
In one sense all of these models are co-evolutionary models. They consider how the system evolves over time. But the EV model deals explicitly with predator–prey interactions. It is “man versus man.” Evidence from the African bush shows that, when two antelope fight each other, they are more vulnerable to attacks from predators. Currently, the South African government is fighting poachers. This approach still has environmental spinoffs, but the benefits are only realized over the very long term (around 80 years). The PKI model on the other hand seeks to focus on maximizing an environmental goal (restoration of the fishery). It focusses on getting to the new equilibrium as quickly as possible. This results in greater returns as well as restored populations.
Adam Smith, the father of neoclassical economics, developed his theory of the invisible hand, where self-interested agents achieve outcomes that are societally beneficial, even though this was not their intent. Charles Darwin, in his theory of evolution, posited the same thing. That competitive behavior caused taxa to adapt and therefore become more resilient. There is merit in both of these arguments. The NC model shows that privatization of the resource may result in benefits to the resource, as private agents seek to maximize returns. The EV model indicates that antagonism towards poachers may ultimately result in them changing behavior. The present study shows however it takes time for these benefits to be realized. Furthermore, it is shown that setting and pursuing an environmental goal has greater economic welfare implications than these other two approaches. This is largely owing to the fact that the environment has a high intrinsic value compared with its use value (total economic value will always be greater than its consumptive value).
Different schools are relevant at different stages, depending on the level of compliance (Table 3). At low levels of compliance, the EV school is indicated, and at moderate levels of compliance the NC school is indicated. However, the ultimate goal is to shift towards a system of voluntary compliance (see also Hauck and Kroese, 2006; Arias, 2015).
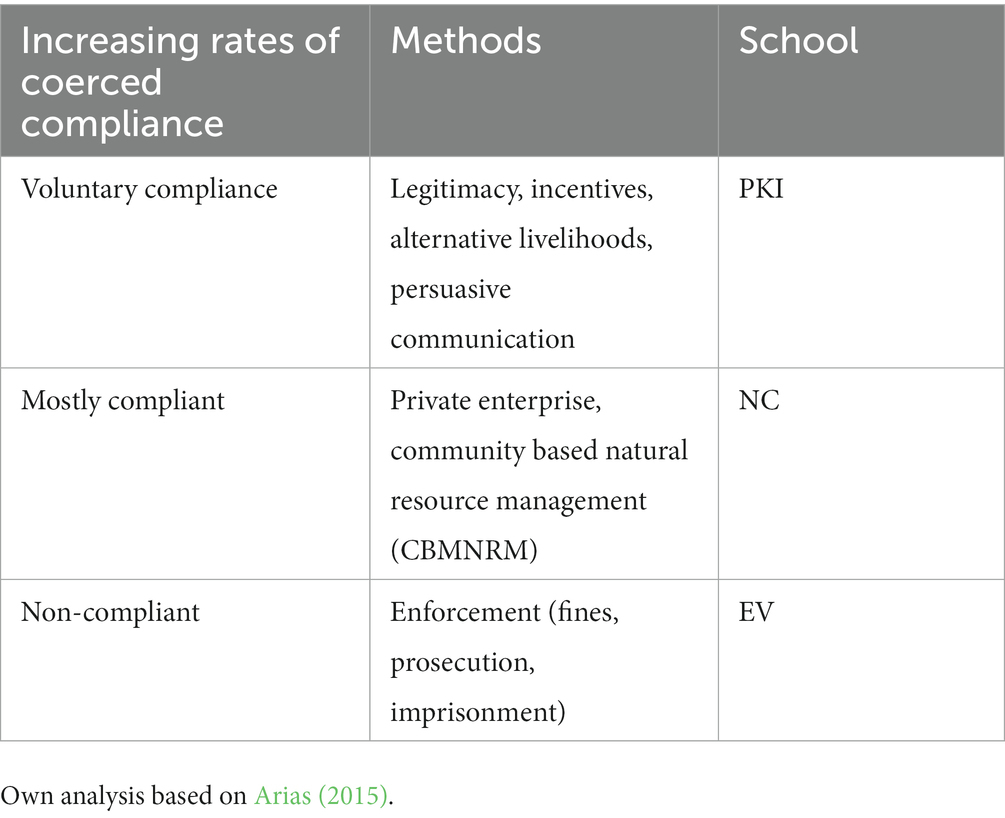
Table 3. Typology of different methods to promote fisheries restoration in the context of wildlife crime.
4. Discussion and conclusions
Non-equilibrium approaches to ecological restoration have become very important in the literature (Perring et al., 2015). We present here an approach to fisheries restoration based on the natural capital approach (Clewell and Aronson, 2012). This approach has not yet been extensively applied to fisheries restoration. The present approach incorporates a hybrid systems methodology that includes systems archetypes, economic schools of thought, system dynamics modelling, mathematics (differential equations), cost benefit analysis, and a case study, where the framework is tested.
Our findings show that the improvement of biomass can generate positive economic benefits irrespective of the behavioral model assumed. Under all simulations over the lifetime of the project (80 years), a BCR of greater than one is achieved. For both the evolutionary and neoclassical models, however, society must value the future more highly than the present (negative discount rate) for model results to be comparable to the Post Keynesian and Institutional model.
Hauck (2008) argues that: “to better understand the factors influencing (non)-compliant behavior and thus effectively respond to them, it is necessary to gain a broad understanding about the inter-relationships that exist, and the complexities that are evident in a system where people and the environment co-exist.” (p.637). One such ecological systems approach is presented here, that considers both socio-economic considerations as well as ecological imperatives.
Complex socio-economic systems require new ways of promoting compliance. Government interventions in natural resource management in developing countries should take into consideration issues such as alleviating poverty as well as intervening in ecosystem restoration (Van Wilgen et al., 1998; McConnachie et al., 2013). Government initiatives such as Working for Water, Working for Wetlands, Working for Woodlands, Working for Wetlands and Working on Fire have proved successful in achieving these goals in the past (Turpie et al., 2008). At present, these programs are confined to terrestrial ecosystems. Expanding this program to the marine environment could result in numerous positive benefits for both job creation as well as marine ecosystem health.
It is important to note that we should not draw universal conclusions from the benefit cost studies on how well the different economic schools performed in the benefit cost studies. The data are case specific and only applicable to the abalone fishery in the Table Mountain National Park. At the same time, abalone is a fairly indicative fish species. The biological attributes of abalone (Edwards and Plagányi, 2008) are similar to around 20 percent of the 170 fish species reported on in Jensen et al. (2012). We can also observe that all four schools resulted in positive net present values and the policies that they propose are applicable to fisheries restoration in general, across a wide range of fisheries and geographical contexts. A number of these policies have not been previously considered in the context of fisheries restoration in South Africa and elsewhere.
There is a growing body of literature dealing with the enforcement as it pertains to fisheries management [e.g., Sutinen and Andersen (1985), Mazany et al. (1989), Charles et al. (1999)]. Most of the economic theory of enforcement derives from the basic deterrence model first postulated by Becker (1968), with further development by Stigler (1970). Here we utilize the hybrid systems methodology (Powell and Mustafee, 2014; Eldabi et al., 2016) to model compliance, in order to promote fisheries ecological restoration. Enforcement in the context of fisheries restoration should focus on ex ante revenue maximization (i.e., through preventing fisheries crime) rather than through ex post revenue maximization (i.e., through confiscations).
In conclusion, the paper presents a toolkit that may be used to operationalize the restoration of natural capital in a marine environment, based on economic principles (including benefit cost analysis and economic schools of thought), but also systems theory (systems archetypes and system dynamics modelling) and mathematics (first order non-linear differential equations). The specific context here was fisheries restoration, but the framework may be generalized to other forms of natural capital restoration when there is a wildlife crime element.
Data availability statement
Publicly available datasets were analyzed in this study. This data can be found here: http://www.scielo.org.za/scielo.php?script=sci_abstract&pid=S0038-23532016000200019&lng=en&nrm=iso.
Ethics statement
Ethical review and approval was not required for the animal study because desktop data only was used. No sampling.
Author contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This work received funding from One Ocean Hub.
Acknowledgments
The author wishes to thank James Aronson and James Blignaut for their valuable insights and comments on an earlier version. Also, thank you to Leandri van der Elst for editing and preparing the manuscript.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2023.1067776/full#supplementary-material
Footnotes
References
Agnew, D. J., Pearce, J., Pramod, G., Peatman, T., Watson, R., Beddington, J. R., et al. (2009). Estimating the worldwide extent of illegal fishing. PLoS One 4:e4570. doi: 10.1371/journal.pone.0004570
Argyrous, G. (2017). Cost-benefit analysis as operationalized neoclassical economics: from evidence to folklore. J. Aust. Pol. Econ. 80, 201–211. doi: 10.3316/ielapa.308759724755095
Arias, A. (2015). Understanding and managing compliance in the nature conservation context. J. Environ. Manag. 153, 134–143. doi: 10.1016/j.jenvman.2015.02.013
Aronson, J., Milton, S. J., and Blignaut, J. N. (2007). “Restoring natural capital: definition and rationale” in Restoring natural capital: Science. eds. J. Aronson, S. J. Milton, and J. N. Blignaut (Washington, DC, USA: Business and Practice, Island Press)
Barbier, E. B. (2013). Valuing ecosystem services for coastal wetland protection and restoration: progress and challenges. Resource 2, 213–230. doi: 10.3390/resources2030213
Becker, G. (1968). Crime and punishment: an economic approach. J. Polit. Econ. 76, 169–217. doi: 10.1086/259394
Blignaut, J. N., and Aronson, J. (2008). Getting serious about maintaining biodiversity. Cons. Lett. 1, 12–17. doi: 10.1111/j.1755-263X.2008.00006.x
Blignaut, J. N., Mander, M., Inglesi-Lotz, R., Glavan, J., and Parr, S. (2016). The amenity value of Abu Dhabi's coastal and marine resources to its beach visitors. Ecosyst. Serv. 19, 32–41. doi: 10.1016/j.ecoser.2016.04.005
Blignaut, J. N., Mander, M., Inglesi-Lotz, R., Glavan, J., and Parr, S. (2017). “Economic value of the Abu Dhabi coastal and marine ecosystem services: estimate and management applications” in Sustainability in the Gulf: Challenges and opportunities. eds. E. Azar and M. A. Raouf (Abingdon: Routledge)
Brown, C. J., Parker, B., Ahmadia, G. N., Ardiwijaya, R., and Game, E. T. (2018). The cost of enforcing a marine protected area to achieve ecological targets for the recovery of fish biomass. Biol. Conserv. 227, 259–265. doi: 10.1016/j.biocon.2018.09.021
Charles, A. T., Mazany, R. L., and Cross, M. L. (1999). The economics of illegal fishing: a behavioral model. Mark. Res. Econ. 14, 95–110. doi: 10.1086/mre.14.2.42629256
Clark, C.W. (2010). Mathematical bioeconomics: The mathematics of conservation. New Jersey: John Wiley & Sons.
Clewell, A.F., and Aronson, J., (2012). Ecological restoration: Principles, values, and structure of an emerging profession. Washington: Island Press.
Coates, J. H., Hovel, K. A., Butler, J. L., Klimley, A. P., and Morgan, S. G. (2013). Movement and home range of pink abalone Haliotis corrugata: implications for restoration and population recovery. Mar. Ecol. Prog. Ser. 486, 189–201. doi: 10.3354/meps10365
Crookes, D. J. (2016). Trading on extinction: an open access deterrence model for the south African abalone fishery. S. Afr. J. Sci. 112, 105–113. doi: 10.17159/sajs.2016/20150237
Crookes, D. J. (2022). Mathematical models and environmental change: Case studies in long term management. Routledge: Abingdon.
Crookes, D. J., and Blignaut, J. N. (2019). Investing in natural capital and national security: a comparative review of restoration projects in South Africa. Heliyon 5:e01765. doi: 10.1016/j.heliyon.2019.e01765
De Groot, R. S., Blignaut, J. N., Van Der Ploeg, S., Aronson, J., Elmqvist, T., and Farley, J. (2013). Benefits of investing in ecosystem restoration. Conserv. Biol. 27, 1286–1293. doi: 10.1111/cobi.12158
DEFF (Department of Environment, Forestry and Fisheries) (2020). Status of the south African marine fishery resources 2020. Cape Town: DEFF.
Edwards, C. T. T., and Plagányi, É. E. (2008). Participatory assessment of the south African abalone resource and its impact on predicted population trajectories. S. Afr. J. Sci. 104, 185–191.
Ekvall, T. (2000). A market-based approach to allocation at open-loop recycling. Resour. Conserv. Recycl. 29, 91–109. doi: 10.1016/S0921-3449(99)00057-9
Eldabi, T., Balaban, M., Brailsford, S., Mustafee, N., Nance, R. E., Onggo, B. S., et al. (2016). “Hybrid simulation: historical lessons, present challenges and futures”. In Proceedings of the 2016 Winter Simulation Conference, edited by T.M. Roeder, P.I. Frazier, and R. Szechtman, et al., 1388–1403. Piscataway, New Jersey: Institute of Electrical and Electronics Engineers, Inc.
Elmqvist, T., Setälä, H., Handel, S. N., Van Der Ploeg, S., Aronson, J., Blignaut, J. N., et al. (2015). Benefits of restoring ecosystem services in urban areas. Curr. Option. Environ. Sustain. 14, 101–108. doi: 10.1016/j.cosust.2015.05.001
FAO. (2022). The state of world fisheries and aquaculture 2022. Towards blue transformation. Rome, FAO.
Fox, H. E., Mous, P. J., Pet, J. S., Muljadi, A. H., and Caldwell, R. L. (2005). Experimental assessment of coral reef rehabilitation following blast fishing. Conserv. Biol. 19, 98–107. doi: 10.1111/j.1523-1739.2005.00261.x
Francher, J. (2008). California: Restoring Bolsa Chica Wetlands. Available at: http://www.globalrestorationnetwork.org (accessed: 20 November, 2009).
Garrity, E. J. (2012). Tragedy of the commons, business growth and the fundamental sustainability problem. Sustainability 4, 2443–2471. doi: 10.3390/su4102443
Gould, D., and Cleveland, S. (2018). Evolutionary systems: applications to cybersecurity. Proceedings of the thirteenth Midwest Association for Information Systems Conference, Saint Louis, MI. Academic Press.
Hauck, M. (2008). Rethinking small-scale fisheries compliance. Mar. Policy 32, 635–642. doi: 10.1016/j.marpol.2007.11.004
Hauck, M., and Kroese, M. (2006). Fisheries compliance in South Africa: a decade of challenges and reform 1994–2004. Mar. Policy 30, 74–83. doi: 10.1016/j.marpol.2005.06.007
Higgins, R. M., Vandeperre, F., Pérez-Ruzafa, A., and Santos, R. S. (2008). Priorities for fisheries in marine protected area design and management: implications for artisanal-type fisheries as found in Southern Europe. J. Nat. Conserv. 16, 222–233. doi: 10.1016/j.jnc.2008.09.001
Hilborn, R., Hively, D. J., Jensen, O. P., and Branch, T. A. (2014). The dynamics of fish populations at low abundance and prospects for rebuilding and recovery. ICES J. Mar. Sci. 71, 2141–2151. doi: 10.1093/icesjms/fsu035
Jensen, O. P., Branch, T. A., and Hilborn, R. (2012). Marine fisheries as ecological experiments. Theor. Ecol. 5, 3–22. doi: 10.1007/s12080-011-0146-9
Kee, J. E. (2004). “Cost-effectiveness and cost-benefit analysis” in Handbook of practical program evaluation. eds. J. S. Wholey, H. P. Hatry, and K. E. Newcomer (San Francisco: Jossey-Bass), 506–542.
Keller, R. R. (1983). Keynesian and institutional economics: compatibility and complementarity? J. Econ. Issues 17, 1087–1095. doi: 10.1080/00213624.1983.11504189
Kennedy, V. S., Breitburg, D. L., Christman, M. C., Luckenbach, M. W., Paynter, K., Kramer, J., et al. (2011). Lessons learned from efforts to restore oyster populations in Maryland and Virginia, 1990 to 2007. J. Shell. Res. 30, 719–731. doi: 10.2983/035.030.0312
Klöpffer, W. (1996). Allocation rule for open-loop recycling in life cycle assessment. The International J Life Cyc Asses 1, 27–31. doi: 10.1007/BF02978629
Kookos, I.K. (2001). Control structure selection based on economics. PhD thesis, Department of Chemical Engineering and Chemical Technology, Imperial College of Science, Technology and Medicine, London.
Lavoie, M. (2006). Introduction to post-Keynesian economics. London: Palgrave Macmillan, doi: 10.1057/9780230626300.
Law, R. (1985). “Evolution in a mutualistic environment” in The biology of mutualism: Ecology and evolution. ed. D. H. Boucher (New York, USA: Oxford University Press), 145–170.
Leschen, A. (2007). Massachusetts: Boston Harbor Eelgrass Restoration. Available at: http://www.globalrestorationnetwork.org/ (accessed: 20 November, 2009).
Lewis Environmental Services (2007). Florida: Mangrove restoration at West Lake (Broward County). Available at: http://www.globalrestorationnetwork.org/ (accessed: 20 November, 2009).
Lofgren, K. G. (1999). Welfare measurement and cost-benefit analysis in Nash and Stackelberg differential fish games. Nat. Resour. Mod. 12, 291–305. doi: 10.1111/j.1939-7445.1999.tb00014.x
Magain, N., Miadlikowska, J., Goffinet, B., Sérusiaux, E., and Lutzoni, F. (2017). Macroevolution of specificity in cyanolichens of the genus Peltigera section Polydactylon (Lecanoromycetes, Ascomycota). Syst. Biol. 66, 74–99. doi: 10.1093/sysbio/syw065
Maani, K., and Cavana, R., (2007). Systems Thinking and Modelling − Managing Change and Complexity, 2nd Edn, Prentice Hall: Pearson Education.
Mazany, R. L., Charles, A. T., and Cross, M. L., (1989). Fisheries regulation and the incentives to overfish. Paper at Canadian Economic Association Meeting, June 2-4, 1989. Quebec, Canada: Laval University.
McConnachie, M. M., Cowling, R. M., Shackleton, C. M., and Knight, A. T. (2013). The challenges of alleviating poverty through ecological restoration: insights from South Africa's “working for water” program. Restor. Ecol. 21, 544–550. doi: 10.1111/rec.12038
MRAG, (2005). Review of impacts of illegal, unreported and unregulated fishing on developing countries. London: Department for International Development.
Narraway, L. T., and Perkins, J. D. (1993). Selection of process control structure based on linear dynamic economics. Ind. Eng. Chem. Res. 32, 2681–2692. doi: 10.1021/ie00023a035
Nene, N., (2023). Multi-million rand abalone bust in Cape Town. Eyewitness news 07 February 2023. Available at: https://ewn.co.za/2023/02/07/multi-million-rand-abalone-bust-in-cape-town (accessed 08 February, 2023).
Nyström, M., Norström,, Blenckner, T., de la Torre-Castro, M., Eklöf, J. S., Folke, C., et al. (2012). Confronting feedbacks of degraded marine ecosystems. Ecosystems. 15, 695–710. doi: 10.1007/s10021-012-9530-6
Palomares, M. L. D., Froese, R., Derrick, B., Meeuwig, J. J., Nöel, S. L., Tsui, G., et al. (2020). Fishery biomass trends of exploited fish populations in marine ecoregions, climatic zones and ocean basins. Estuar. Coast. Shelf Sci. 243:106896. doi: 10.1016/j.ecss.2020.106896
Panayotakis, C. (2013). Theorizing scarcity: neoclassical economics and its critics. Rev. Rad. Pol. Econ. 45, 183–200. doi: 10.1177/0486613412458649
Pauly, D. (2019). Vanishing fish: Shifting baselines and the future of global fisheries. Greystone Books, Vancouver, BC
Pauly, D., Watson, R., and Alder, J. (2005). Global trends in world fisheries: impacts on marine ecosystems and food security. Philos. Trans. R. Soc. B: Biol. Sci. 360, 5–12. doi: 10.1098/rstb.2004.1574
Perring, M. P., Standish, R. J., Price, J. N., Craig, M. D., Erickson, T. E., Ruthrof, K. X., et al. (2015). Advances in restoration ecology: rising to the challenges of the coming decades. Ecosphere 6:art131. doi: 10.1890/ES15-00121.1
Powell, J., and Mustafee, N.. (2014). “Soft OR approaches in problem formulations stage of a Hybrid M& S Study.” In Proceedings of the 2014 Winter Simulation Conference, edited by A. Tolk, S. Y. Diallo, I.O. Ryzhov, L. Yilmaz, S. Buckley, and J. A. Miller. 1664–1675. Piscataway, NJ: Institute of Electrical and Electronics Engineers, Inc.
Purnomo, H., and Mendoza, G. (2011). A system dynamics model for evaluating collaborative forest management: a case study in Indonesia. Int. J. Sust. Dev. World Ecol. 18, 164–176. doi: 10.1080/13504509.2010.549664
Retsa, A., Schelske, O., Wilke, B., Rutherford, G., and de Jong, R., (2020). Biodiversity and ecosystem services. A business case for re/insurance. Zurich: Swiss Re Institute.
Saeed, K., and Radzicki, M.J., (1993). A post Keynesian model of macroeconomic growth, instability, and income distribution. In The Role of Strategic Modelling in International Competitiveness: Proceedings of the 1993 International Conference of the System Dynamics Society (pp. 435–443). Cancún, Mexico.
Schade, W., and Rothengatter, W. (2003). Improving assessment of transport policies by dynamic cost-benefit analysis. Trans. Res. Rec. 1839, 107–114. doi: 10.3141/1839-11
Sterman, J.D. (2000). Business dynamics: Systems thinking and modeling for a complex world. Boston: Irwin McGraw-Hill.
Stewart-Sinclair, P. J., Klein, C. J., Bateman, I. J., and Lovelock, C. E. (2021). Spatial cost–benefit analysis of blue restoration and factors driving net benefits globally. Conserv. Biol. 35, 1850–1860. doi: 10.1111/cobi.13742
Stigler, G. (1970). The optimum enforcement of laws. J. Policy Econ. 78, 526–536. doi: 10.1086/259646
Sutinen, J., and Andersen, P. (1985). The economics of fisheries Law enforcement. Land Econ. 61, 387–397. doi: 10.2307/3146156
Taljaard, S., Slinger, J. H., Arabi, S., Weerts, S. P., and Vreugdenhil, H. (2021). The natural environment in port development: a ‘green handbrake’ or an equal partner? Ocean Coast. Manag. 199:105390. doi: 10.1016/j.ocecoaman.2020.105390
Tarr, R. J. Q. (1995). Growth and movement of the south African abalone Haliotis midae: a reassessment. Mar. Freshw. Res. 46, 583–590. doi: 10.1071/MF9950583
TEEB. (2011). The economics of ecosystems and biodiversity in national and international policy making. London and Washington: Earthscan.
Turpie, J. K., Marais, C., and Blignaut, J. N. (2008). The working for water programme: evolution of a payments for ecosystem services mechanism that addresses both poverty and ecosystem service delivery in South Africa. Ecol. Econ. 65, 788–798. doi: 10.1016/j.ecolecon.2007.12.024
Van den Bergh, J. C. (2007). Evolutionary thinking in environmental economics. J. Evol. Econ. 17, 521–549. doi: 10.1007/s00191-006-0054-0
Van Dover, C. L., Aronson, J., Pendleton, L., Smith, S., Arnaud-Haond, S., Moreno-Mateos, D., et al. (2014). Ecological restoration in the deep sea: desiderata. Mar. Pol. 44, 98–106. doi: 10.1016/j.marpol.2013.07.006
Van Wilgen, B. W., Le Maitre, D. C., and Cowling, R. M. (1998). Ecosystem services, efficiency, sustainability and equity: South Africa's working for water programme. Trend Ecol Evol 13:378. doi: 10.1016/S0169-5347(98)01434-7
Vergnon, R., Shin, Y. J., and Cury, P. (2008). Cultivation, Allee effect and resilience of large demersal fish populations. Aquat. Living Resour. 21, 287–295. doi: 10.1051/alr:2008042
Whalen, C. J. (2013). Post-Keynesian institutionalism after the great recession. Euro. J. Econ. Econ. Policy Intervent. 10, 12–27. doi: 10.4337/ejeep.2013.01.03
Williams, T. G., Heidrich, O., and Sallis, P. J. (2010). A case study of the open-loop recycling of mixed plastic waste for use in a sports-field drainage system. Res. Conserv. Recyc. 55, 118–128. doi: 10.1016/j.resconrec.2010.08.002
Wilson, E.O., and Bossert, W.H., (1971). A primer of population biology Sunderland, MA: Sinauer associates.
Keywords: economics, system dynamic model, schools of thought, abalone (Haliotis midae), hybrid system, restoration, wildlife crime/poaching
Citation: Crookes D (2023) Fisheries restoration: Lessons learnt from four benefit-cost models. Front. Ecol. Evol. 11:1067776. doi: 10.3389/fevo.2023.1067776
Edited by:
Jason Doll, Francis Marion University, United StatesReviewed by:
Yonvitner Yonvitner, Faculty of Fisheries and Marine Science, IndonesiaStephen Jacquemin, Wright State University, United States
Copyright © 2023 Crookes. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Douglas Crookes, ZG91Z2xhc2Nyb29rZXNAZ21haWwuY29t
†ORCID: Douglas Crookes, https://orcid.org/0000-0001-9357-5396
 Douglas Crookes
Douglas Crookes