- 1Groningen Institute for Evolutionary Life Sciences, University of Groningen, Groningen, Netherlands
- 2Department of Biosciences, Faculty of Science and Engineering, Swansea University, Swansea, United Kingdom
Moving in groups offers animals protection against predation. When under attack, grouped individuals often turn collectively to evade a predator, which sometimes makes them rapidly change their relative positions in the group. In bird flocks in particular, the quick reshuffling of flock members confuses the predator, challenging its targeting of a single individual. This confusion is considered to be greater when the internal structure of the group changes faster (i.e. the ‘diffusion’ of the group is higher). Diffusion may increase when individual birds turn collectively with equal radii (same angular velocity) but not when individuals keep their paths parallel (by adjusting their speed). However, how diffusion depends on individual behaviour is not well known. When under attack, grouping individuals change the way they interact with each other, referred to as ‘alarmed coordination’ (e.g., increase their reaction frequency or their cohesion tendency), but the effect of such changes on collective turning is unknown. Here, we aimed to gain an understanding of the dynamics of collective turning in bird flocks. First, to investigate the relation between alarmed coordination and flock diffusion, we developed an agent-based model of bird flocks. Second, to test how diffusion relates to collective turns with equal-radii and parallel-paths, we developed a metric of the deviation from these two types. Third, we studied collective turning under predation empirically, by analysing the GPS trajectories of pigeons in small flocks pursued by a RobotFalcon. As a measure of diffusion, we used the instability of neighbours: the rate with which the closest neighbours of a flock member are changing. In our simulations, we showed that this instability increases with group size, reaction frequency, topological range, and cohesion tendency and that the relation between instability of neighbours and the deviation from the two turning types depends in often counter-intuitive ways on these coordination specifics. Empirically, we showed that pigeons turn collectively with less diffusion than starlings and that their collective turns are in between those with equal-radii and parallel-paths. Overall, our work provides a framework for studying collective turning across species.
1 Introduction
The primary advantage that grouping offers to animals in nature is protection against predators (Cresswell, 1994). This advantage is rooted in the potential earlier detection of predators (many-eyes hypothesis; Lima, 1995), the decrease in the probability of a single individual to get caught instead of its group mates (selfish-herd hypothesis; Hamilton, 1971), and the decrease in the hunting success of the predator due to the confusion effect (Landeau and Terborgh, 1986). The confusion effect dictates that the predator cannot single out and catch a flock member because too many prey individuals are passing through its field of view (Ioannou et al., 2012; Olson et al., 2013; Hogan et al., 2017). It is expected that predator confusion is higher when the speed with which prey individuals move within a flock (referred to as diffusion of flock members) is faster. In bird flocks, several metrics have been used to capture this diffusion: how quickly group members change their relative position (‘mutual diffusion’), reshuffle around the centre of mass of the flock (‘global diffusion’) and change their interaction network (‘neighbour overlap’ or ‘neighbour stability’) (Cavagna et al., 2013; Hemelrijk and Hildenbrandt, 2015). These quantities have, however, only been studied in large flocks of starlings during collective turning above a roost (Cavagna et al., 2013).
Collective turns are a major method by which flocks of birds respond to predators (Papadopoulou et al., 2022b; Storms et al., 2022b). It is observed in many bird species, from small flocks of crows and homing pigeons to large flocks of jackdaws and starlings, and across many ecological contexts, during foraging and mobbing (Ling et al., 2019c), roosting (circling around roost) (Ballerini et al., 2008a; Yomosa et al., 2015), and evading predators (Papadopoulou et al., 2022a). Even though the propagation of turning among flock members has gained the attention of researchers almost 100 years ago (Selous, 1931), the complexity of collective turning has only recently been recognised (Ling et al., 2019c).
Pomeroy and Heppner (1992) were among the first to analyse collective turns in birds. By studying pigeons in small flocks, they noted that all flock members move along an arc of a similar radius and their paths cross during a collective turn (Pomeroy and Heppner, 1992). Such collective turns are referred to as ‘equal radii’ (Figure 1A) and have also been observed in starling flocks (Ballerini et al., 2008a; Attanasi et al., 2014). As a consequence, diffusion of flock members has only been studied in such turns, linking them to improved predator confusion (Cavagna et al., 2013).

Figure 1 Modes of collective turning in bird flocks. (A) Equal-radii: individuals perform a turn of identical radius and thus change their relative positions (also referred to as E-type turning by Yomosa et al., 2015). (B) Parallel-paths: individuals keep their relative positions the same by performing turns of different radii, varying their angular velocity (also referred to as P-type turning by Yomosa et al., 2015). Given that changes in individuals’ speed are needed for this mode, a turn with parallel-paths cannot emerge in a model where agents have constant speed.
In contrast to this type of collective turning, individuals may differ in their turning radii and maintain their relative positions through a turn (Figure 1B). In this case, group members turn with ‘parallel-paths’ (Pomeroy and Heppner, 1992; Yomosa et al., 2015), resulting in a flock with a stable shape and internal structure (Ballerini et al., 2008a). Even though turns with parallel-paths have been assumed to be uncommon in bird flocks (Ballerini et al., 2008a; Attanasi et al., 2014), a hybrid between the two types has been observed in pigeons flying above their roosting site (Yomosa et al., 2015). It has been proposed that, in reality, the collective turn of a flock is probably in between the two turning types (Yomosa et al., 2015). Unfortunately, there is no exact measurement for these types of collective turning to date, and our knowledge of them across species is still limited.
Properties of a group such as internal structure and global diffusion are self-organised (Camazine et al., 2003); they emerge when individuals are moving together and coordinating through simple interactions with neighbours nearby (Hemelrijk and Hildenbrandt, 2015). The specifics of local interactions during ‘coordination’ may differ across species and ecological contexts. For instance, when starlings are circling above their roost, they coordinate mostly with their 6–7 closest neighbours (referred to as ‘topological range’) (Ballerini et al., 2008b), while jackdaws, even though they interact with their mating partners and 3 other closest neighbours in foraging flights (Ling et al., 2019a), they switch to ‘metric interactions’ during mobbing (interacting with all neighbours within a given radius) (Ling et al., 2019b). Predation in particular has been shown to affect the social interactions of individuals in a group. When under threat, prey may, for instance, increase the frequency of interacting with each other (referred to as reaction or update frequency) which can lead to more frequent changes in their relative position (Bode et al., 2010; Herbert-Read et al., 2017). Prey may also increase their tendency to align with (Sankey et al., 2021) or stay close to (Herbert-Read et al., 2017) each other, which can increase the density of the group offering a high anti-predator benefit (Carere et al., 2009; King et al., 2012) or facilitate their collective escape by dodging a predator’s attack (Papadopoulou et al., 2022a; Papadopoulou et al., 2022b).
In the present work we aim to better understand the dynamics of collective turning by combining computer simulations and empirical data. We develop a biologically-inspired computational model of collective motion and simulate collective turns away from an attacking predator. We test two alternative rules that individuals may follow to collectively evade a predator: all individuals may have a tendency to turn towards a stable point in space (similar to starlings during collective escape above their roost; Ballerini et al., 2008a; Storms et al., 2019), or they may perform an escape manoeuvre (based on a tendency to turn to the left or to the right away from the predator, similar to pigeons; Sankey et al., 2021; Papadopoulou et al., 2022a). We focus our theoretical investigation on how changes in some specifics of coordination that have been linked to the presence of a predator (e.g., reaction frequency) (Carere et al., 2009; Bode et al., 2010; Ling et al., 2019b) affect the diffusion of individuals in a flock and the resemblance of a collective turn to the equal-radii and parallel-paths modes. Here, we use the instability of neighbours as our metric of flocking diffusion, since low neighbour stability is expected to have higher anti-predatory benefits (Attanasi et al., 2015). To detect the type of collective turning, we develop a metric: an estimate of the deviation of individual trajectories from turns with equal-radii and parallel-paths.
In flocks of starlings, individuals change all their nearest neighbours every few seconds (half of 10 neighbours in approximately 3.5 seconds) (Cavagna et al., 2013). The instability of neighbours is, to our knowledge, unknown for any other species, given the difficulty to collect individual trajectories during collective motion of airborne flocks. Here, we study collective turns empirically using the only existing dataset of bird flocks under predation (Sankey et al., 2021). Specifically, we analysed GPS data of homing pigeons under attack by a robotic predator. We measure neighbour instability and deviation from the two turning types in the trajectories of all the members of a flock, expecting that: (1) pigeons have lower neighbour instability than starlings (because the flocks of pigeons in our dataset are smaller and less dense than the formerly studied flocks of starlings, and because former studies have shown that pigeons may keep consistent positions in the group; Sankey et al., 2019; Sankey et al., 2022), and (2) their turns are in between equal-radii and parallel-paths (as proposed by Yomosa et al., 2015).
2 Materials and methods
2.1 A data-inspired model of collective turning
We built an agent-based model of collective motion (flocking) named ColT (Collective Turning), in which individuals perform collective turns in a large 2D space. We developed the model in 2-dimensions since collective turns in real flocks mostly lie on a plane (Cavagna et al., 2013; Yomosa et al., 2015). Our model is based on the principles of self-organisation: local interactions among neighbouring bird-agents lead to emergent patterns of flocking. Collective turns emerge from the individual tendency to turn while coordinating. We model this tendency as a steering vector with its magnitude controlled by a turning-weight parameter. Between collective turns, the flocks move forwards (straight flight). In the model, time is measured in seconds, distance in meters, and angles in degrees.
2.1.1 Collective motion
Each agent is defined in the global coordinate system by its position () and its velocity (). The unit vector of an agent’s velocity (heading vector ) defines the local coordinate system of the agent through which it senses its neighbours. Agents have a preferred speed from which they deviate to catch up or avoid collisions with their neighbours. To reduce the complexity of our model, we set the preferred speed of all individuals to be the same (u, Table 1). To reflect the inability of individuals to infinitely increase or decrease their speed, our agents are dragged back to their preferred speed based on a speed-control steering vector, similar to the drag force used in previous data-inspired models of bird flocks (Papadopoulou et al., 2022a; Papadopoulou et al., 2022b).
Agents coordinate according to the rules of alignment, attraction and avoidance with the surrounding individuals (referred to as ‘neighbours’, ) that are within their field of view (FoV). An agent aligns with the average heading of its closest neighbours and turns towards their centre of mass. The strength of this attraction depends on the distance of the individual to the centre of its neighbourhood: the further away it is, the more it is attracted towards it. To avoid collisions, an agent turns away from the position of its closest neighbour (Hemelrijk and Hildenbrandt, 2015) in a range of minimum separation (). Let be the position of neighbour j in the reference frame of a focal individual i at a given time point. Thus, the steering vector () that controls the motion of each individual is the weighted sum of these coordination rules:
where is the neighbour set of focal individual i (with cardinality ), is the heading vector of a neighbour j, is the position of i relative to its closest neighbour (), is a noise scalar sampled from a uniform distribution based on the parameter , and is the unit vector perpendicular to the heading vector of i. The w parameters (, , and ) represent the weights of alignment, centroid attraction, and separation, respectively, that control the influence of each ‘rule’ on an individual’s motion. Thus, each term in Eq.1 is the combination of a unit vector that gives the direction of the force, and the weight that sets its magnitude. Note that the cohesion term is not normalised to include the effect of an individual’s distance to its neighbourhood’s centroid. To make the social behaviour of individuals in our simulations more realistic, we model asynchronous interactions: each agent updates its information about its neighbours’ position and heading with a constant frequency () but not necessarily at the same point in time as its neighbours.
2.1.2 Collective turning
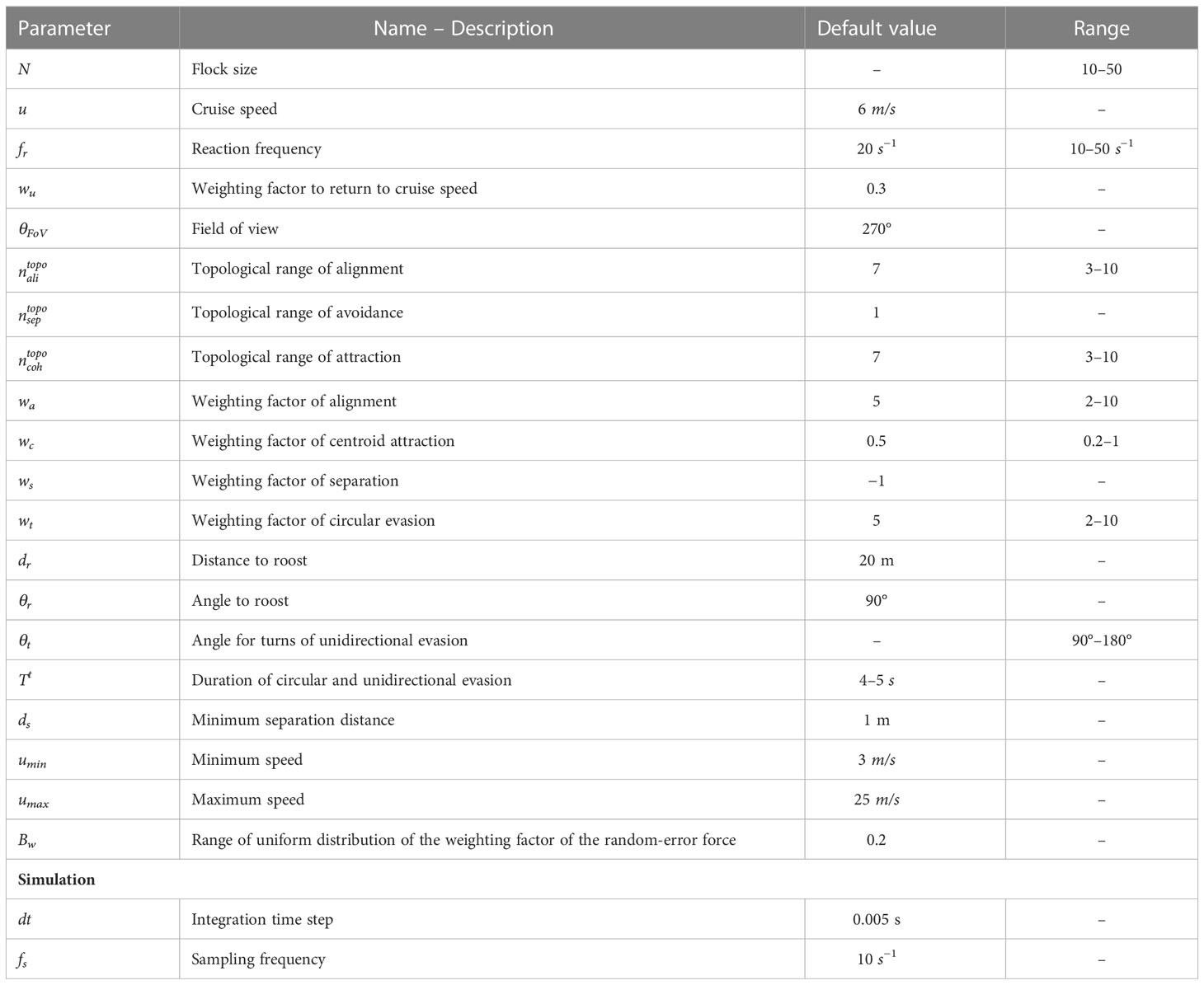
In ColT, turns are randomly initiated by one individual (or rarely a few). We label this agent as ‘the initiator’. Each agent has a probability of becoming an initiator by entering a ‘turning’ state. The neighbours of an initiator may copy its turning behaviour, resulting in the turn propagating through the flock (Figure 2A). We model two different contexts of turning when under attack by a predator: ‘circular evasion’, in which individuals are attracted towards a global point in space (inspired by starling flocks circling above their roost in the presence of a predator; Attanasi et al., 2014; Storms et al., 2019), and ‘unidirectional evasion’, in which they perform a turn of predefined angular velocity away from a predator (inspired by pigeon flocks reacting to an artificial predator, the RobotFalcon; Sankey et al., 2021; Papadopoulou et al., 2022a). While turning, individuals keep coordinating with each other as described above.
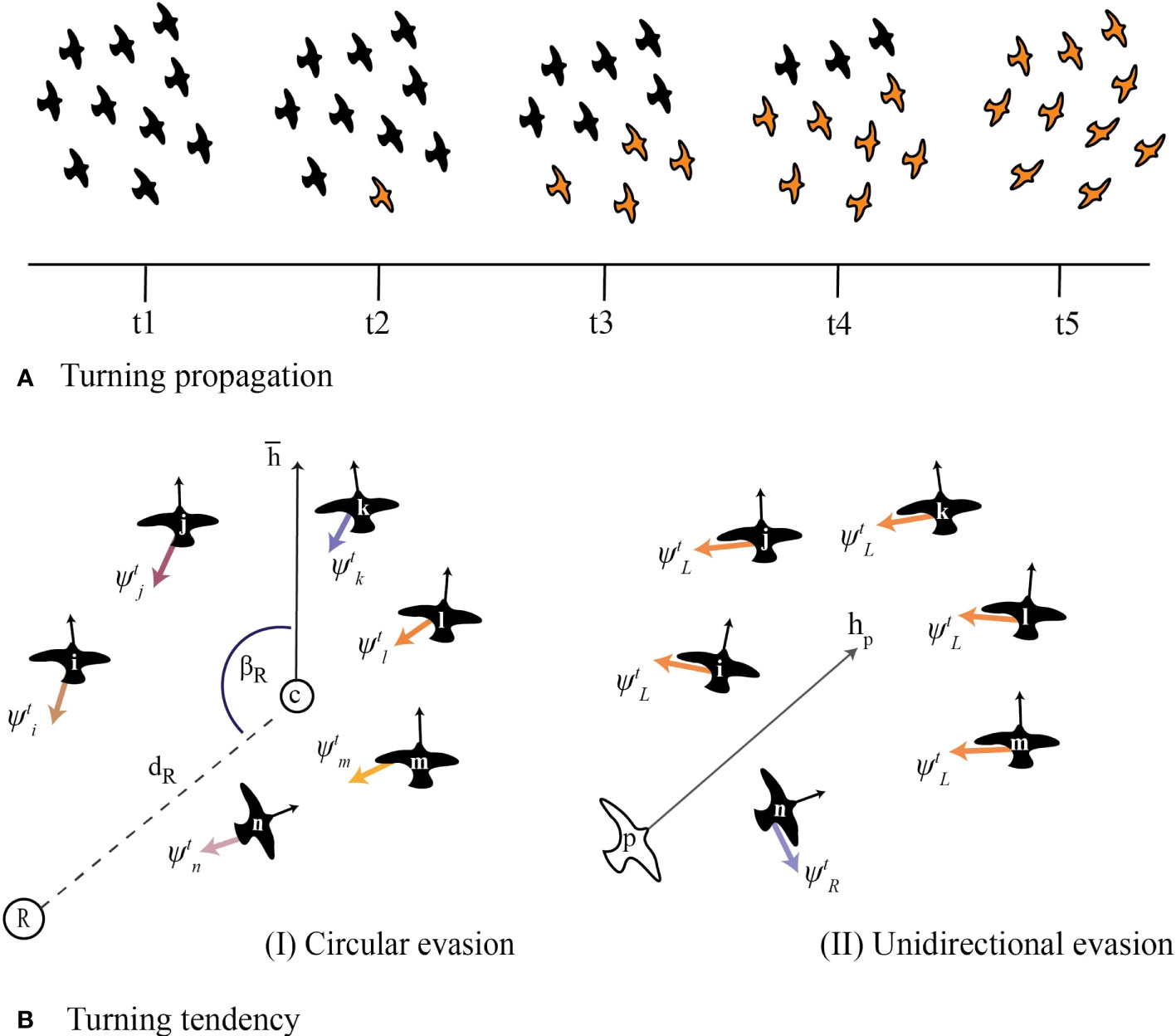
Figure 2 Individual rules of turning in the computational model ColT. (A) Schematic of how a turn propagates from a single initiator to the rest of the flock by individuals copying the behaviour of their neighbours. Light-coloured individuals represent group members that are turning. (B) The specifics of rules of turning by individuals in our model. We distinguish two scenarios: individuals may have a stable point in space that they are attracted to (resembling a roost (Yomosa et al., 2015) or home (Sankey et al., 2021)), or a global ‘escape direction’ (resembling turning manoeuvres away from a predator (Sankey et al., 2021; Papadopoulou et al., 2022a)). Coloured arrows () represent the steering vectors that make individuals turn. In circular evasion (BI), individuals are attracted to a roost (R), defined by a distance from the flock’s centre () and an angle () relative to the flock’s heading (average heading of all flock members), . Since the roost is a global point in space, each group member has a different relative position to it (different local conditions) and thus the tendency of each individual to turn differs. During unidirectional evasion (BII), individuals are turning away from the predator’s heading () from a constant steering-vector that is perpendicular to the left () or to the right () of each individual’s heading. Thus, when the flock turns collectively, all flock members have the same tendency to turn (their steering vectors to evade the predator have the same constant magnitude).The position of the predator (p) has no effect on the turning motion of the flock, according to empirical findings that pigeons respond to the heading rather than the position of a predator while escaping (Sankey et al., 2021).
We make agents turn by applying an extra steering vector () for a specific amount of time. The specifics of turning differ between the two ecological contexts that we model. For circular evasion, we add a vector with direction from the focal’s individual position towards a point in space that represents the flock’s roost. This point is calculated at the beginning of every turn at a given distance () and angle () away from the centre of the flock (Figure 2BI). The magnitude of this steering vector (and thus influence on the agent’s motion) is controlled by the parameter . For unidirectional evasion, we add a steering vector perpendicular to each individual’s heading. In this case, the vector points to the direction away from the heading of the predator (Figure 2BII). For this, we model a dummy predator-agent that follows the flock from behind (from a given distance and bearing angle, similar to previous models of bird flocks; Papadopoulou et al., 2022b). The strength of the force is such that individuals perform a turn with a predefined angular velocity (e.g. 90°, parameter , within a given turning time).
We give each flock member a unique probability to start turning. If the neighbour of a focal individual is evading, the steering vector for turning towards the roost or away from the predator, respectively, of the focal individual is activated (it ‘copies’ its neighbour’s behaviour). We give turns a predefined duration at the level of the individual (). The total steering force of every agent is thus calculated by:
We use to update the position and velocity of each agent at each time step (‘integration’ time step, dt). Since the time step is much smaller than the behavioural reaction time of an individual, we recalculate the steering vector with a given ‘reaction’ (or ‘update’) frequency (, Table 1, with ) (Hildenbrandt et al., 2010). This frequency thus reflects the time an individual needs to collect sensory information from its environment, process it and act.
2.2 Neighbour instability
To study the diffusion of different flocks in our simulations, we analysed the time-series of the position and heading of each flock-member during collective turns. The periods of free flight were discarded. We measured changes in the flocks’ interaction networks over a sliding time-window with an established measurement of diffusion: ‘neighbour stability’ (Hemelrijk and Hildenbrandt, 2015). This measurement (previously also referred to as ‘neighbour overlap’) captures the rate with which individuals change their network of interacting neighbours while changing positions in relation to the flock’s centre (‘global diffusion’) and each other (‘mutual diffusion’) (Cavagna et al., 2013; Hemelrijk and Hildenbrandt, 2015). Since here we are interested in predator confusion that is expected to increase with decreasing neighbour stability, we analyse our results looking into the instability of neighbours. In detail, instability of neighbours () is estimated by measuring how much the set of closest neighbours of a focal individual changes over time:
where N is the number of flock members, T the total length of our measuring window, the intersection of the closest neighbours of individual i at time and t. We average over all individuals in the flock and all initial time points . Based on Eq. 3, neighbour instability ranges from 0 (if all neighbours are the same) to 1 (if all neighbours have changed over the given time period). To examine how neighbour instability varies through our parameter space, we also note the ending value from each instability time-series (at the end of our sliding window ).
2.3 Measuring collective turns
To measure how close a collective turn resembles one of the two turning modes, equal-radii and parallel-paths, we created a measurement inspired by mutual diffusion (Cavagna et al., 2013). Our measurement estimates how much the flock members’ trajectories during each collective turn deviate from each type based on the expected position of neighbours if a turn with parallel-paths or equal-radii has taken place (Figure 1). Let be the position of neighbour j in the reference frame of a focal individual i at a given time point, and its position at the consecutive sampling point during which the focal individual turned by θ degrees. For equal-radii turns, we expect that:
where R is a rotation matrix, reflecting that j has moved in the opposite direction of i’s turn by . For parallel-paths, the relative position of individuals remains the same, thus we expect that:
Based on these expected positions, let be the distance between the actual relative position of each neighbour at a given time and the expected position according to parallel-paths and equal-radii such that:
capture the deviation from each turning mode, equal-radii and parallel-paths, respectively, between time points and . To test how these deviations scale with time, we use a sliding window () and estimate the increase of these deviations during collective turns (with being the duration of a turn). We calculate the average value of deviation from a parallel-paths () and an equal-radii () turn over all flock-members in a simulation, taking into account the M closest neighbours of each individual, according to:
where represents or . We then average over all collective turns in our simulations. Since neighbours’ ranks change during the turn, set M contains the M closest neighbours at the beginning of every sliding window.
2.4 Simulations, parameterisation, and experiments
We simulate flocks of 10, 30 and 50 individuals performing turns based on ‘circular evasion’ or ‘unidirectional evasion’ for 4 to 5 seconds (). The flock size, the duration and turning rate (radians per second) of each turn are set according to the empirical data of turning by flocks of pigeons and jackdaws (Yomosa et al., 2015; Ling et al., 2019c). During circular evasion, the turning rate is controlled by a ‘tendency’ to turn: the weight (, magnitude) of the steering vector for turning (Eq. 1) that is towards a stable point relative to the centre of the flock (R, Figure 2BI). During unidirectional evasion, the turning rate is set such that individuals perform a turn of a given angle () during the set duration of a turn (): we calculate the magnitude of the turning vector (, perpendicular to each individual’s heading, Figure 2BII) that is needed based on the individual’s speed. We examined low, medium, and high turning rates for each context: weighting factors of 2, 4 and 6 for circling, and turning angles of 90°, 135°, and 180° for unidirectional evading. We calculated the instability of neighbours (based on the 4 closest neighbours), and the deviation from equal-radii and parallel-paths (for up to 4 closest neighbours) using a sliding window of 3 seconds ().
Between turning events, flocks are performing straight flight for 15 seconds. During this time period, the flocks get back to a stable state. Each simulation lasts for 2.5 minutes and thus includes 8 collective turns. We sample data with a frequency of 0.1 seconds. Agents are initialised in a flock formation: positioned within a given radius with similar headings and speeds. The first 3 turns of each simulation are discarded to ensure that there is no effect of our initial conditions. We also discard turns during which a flock splits. After inspecting the time series of instability of neighbours and deviation from the two turning types for the first 4 closest neighbours, we use the average of the 4 neighbours for instability (, as described by previous studies on starling flocks; Cavagna et al., 2013; Hemelrijk and Hildenbrandt, 2015) and the average deviations based on the closest neighbour ( and ) of each flock member across all turns in each simulation.
Motivated by differences in coordination across species (Ling et al., 2019a; Ling et al., 2019b; Ballerini et al., 2008b; Evangelista et al., 2017; Sankey et al., 2021) and changes in the prey’s behaviour when under threat, namely increased reaction frequency (Domenici, 2010; Herbert-Read et al., 2017), increased cohesion (Hamilton, 1971; King et al., 2012; Sankey et al., 2021) and switch to metric interactions (Ling et al., 2019b), we examined how the coordination specifics affect the characteristics of a collective turn. We specifically studied the effects of (1) the strength of alignment and centroid-attraction, (2) the number of interacting neighbours (topological range), and (3) the reaction frequency (how often each agent updates its information concerning its neighbours’ positions). We selected the range of our parameter space after ensuring that a cohesive flock emerges. We ran 20 simulations (replicates) for each combination of parameters, ending up with 100 collective turns per parameter combination. We ran simulations varying each parameter of interest separately, using default values for the others from the middle of each range. For a list of our parameter values see Table 1.
2.5 Empirical data
We used our new measurement of deviation of a collective turn from parallel-paths and equal-radii to analyse trajectories of homing pigeons (Columba livia) using GPS data of flocks under attack by an artificial predator, the RobotFalcon (Storms et al., 2022a). During the field experiments, small (8–10 individuals) and large (30–34 individuals) flocks were released to start their homing route, with the remotely-controlled robotic predator pursuing and attacking the flock until it leaves the study site (Sankey et al., 2021). We further used the data to examine how instability of neighbour scales over time and with changes in group size and the sharpness of a collective turn.
We analysed the 2D trajectories only when the flocks were collectively turning. We defined a collective turn as a consecutive period of turning towards one direction (left or right) with average angular velocity larger than 10 degrees per second (as in Papadopoulou et al., 2022a). We included in our analysis only the collective turns that lasted at least 3 seconds (in line with previous work on flock’s diffusion; Cavagna et al., 2013; Hemelrijk and Hildenbrandt, 2015). For estimating the instability of neighbours and the deviations from parallel-paths and equal-radii we used a sliding window of 1.6 seconds. Overall, we analysed 77 turns across 26 flights with the RobotFalcon.
We tested our model prediction that larger flock sizes have higher instability of neighbours using ANOVA tests with flocks grouped into ‘small’ (N = 8 or 10) and ‘large’ (N = 30 or 32). To test the effect of turning rate in the instability of neighbours in pigeons, we further labeled each collective turn as of ‘low’ or ‘high’ turning rate, depending on whether its angular velocity was smaller or larger than the average of all turns (). We further run linear mixed effect models (LME) to test the fixed effect of flock size, accounting for the random effect of the flock id (flight date), on the average neighbour instability (), and the average deviation of nearest neighbours from equal-radii () and parallel-paths (). We also investigated the relation between the size and the density of a flock (Hemelrijk et al., 2015). We used the average nearest neighbour distance of a group as a measure of its density. We tested assumptions of normality using Shapiro-Wilk tests.
3 Results
We show examples of tracks from our simulations and empirical data in Figure 3 and Video S1.

Figure 3 Collective turns of pigeons under attack by the RobotFalcon (A–C) and of simulated birds in our computational model (D–F), with the average turning rates (ω, ) and the flock size (N) of each track. In the simulations, individuals have either a tendency to turn away from the predator (to the left or to the right) (D, E) or towards a constant point in space resembling a roost (F).
3.1 Instability of neighbours in the model
The instability of neighbours in our model increased over time (Figure 4) with individuals losing on average 30% to 50% of their initial neighbours after 3 seconds of turning (Figure 4A). This is similar to what has been found in starling flocks (Cavagna et al., 2013) and a previous computational model of collective motion of starlings (StarDisplay) (Hildenbrandt et al., 2010; Hemelrijk and Hildenbrandt, 2015). Turns with very high () and very low neighbour instability () emerged across our parameter space with no significant difference between the type of evasion tendency (ANOVA; F-value = 0.04, p-value = 0.8, ; Figure 4A).
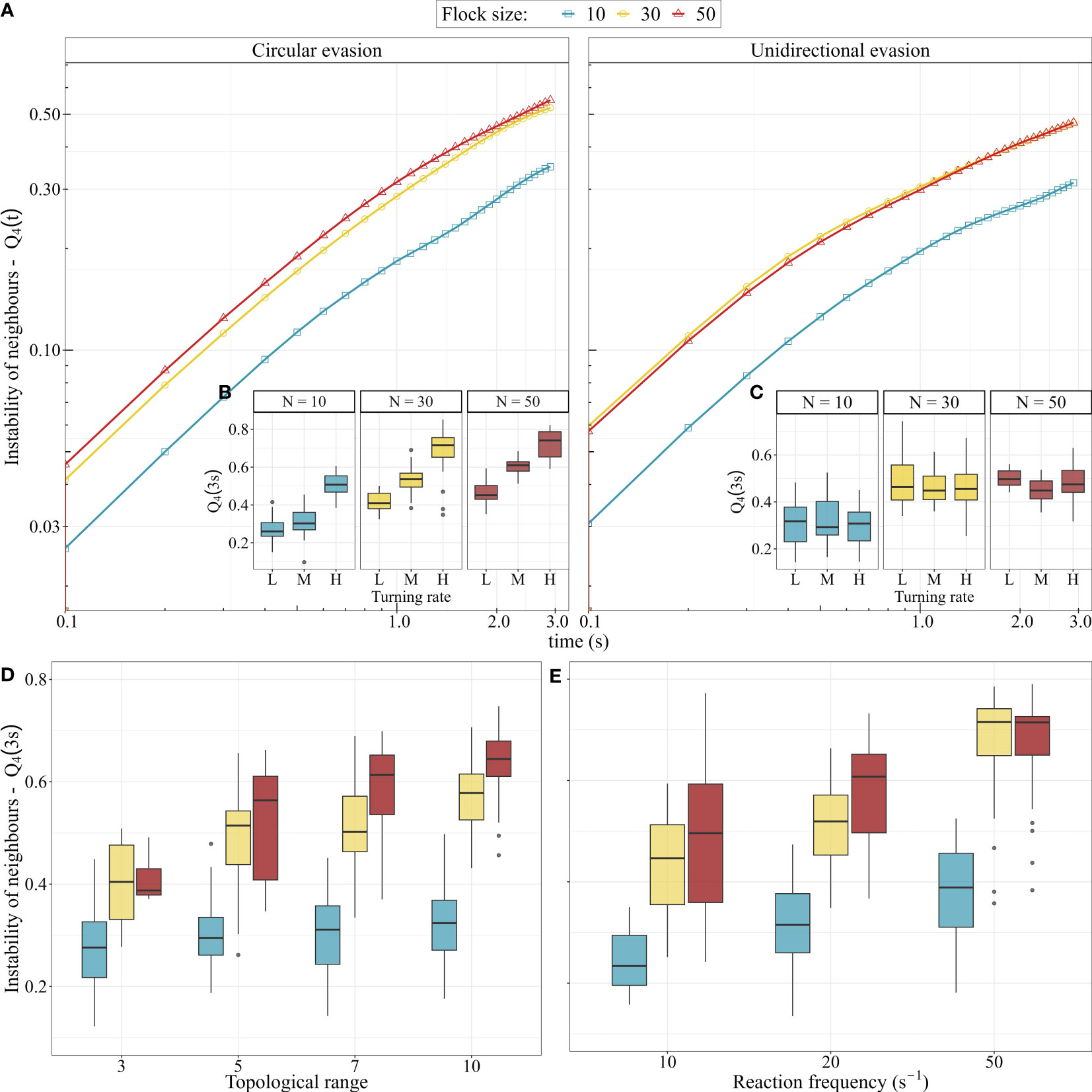
Figure 4 Instability of neighbours in the computational model. (A) Instability of 4 closest neighbours in turns based on circular and unidirectional evasion over time. The error bars that represent the standard error of each t are too small to be visible. (B, C). Instability of neighbours after 3 seconds of turning by (B) circular and (C) unidirectional evasion for low (L), medium (M) and high (H) turning rates. In circling, low, medium and high turning rates represent turning tendencies (weight ) of 2, 5, and 10, while in unidirectional evasion, turning angles of 90°, 130°, and 180°, respectively. (D, E) The effect of topological range and reaction frequency on the instability of neighbours after 3 seconds of turning in flocks of 10, 30 and 50 individuals, in both circular and unidirectional evasion.
However, higher turning rates during circular evasion (as a result of the stronger tendency to turn towards the roost) led to significantly higher instability of neighbours (ANOVA; F-value = 470.2, p-value < 0.001; Figure 4C). In circular evasion, each flock member has a different relative position to the attraction point (the roost). As a result, the tendency of each individual to turn to the roost differs from that of the other group members. This within-group variation increases with increased turning rate and thus leads to the higher instability of neighbours. In other words, at higher turning rates the effect of these small differences increases, causing individuals to reshuffle more. In unidirectional evasion, the turning rate did not affect neighbour instability (Figure 4B) because the tendencies to turn were the same among individuals (ANOVA; F-value = 0.023, p-value = 0.88).
Neighbour instability was higher in collective turns of larger flocks (30 and 50 individuals) than in smaller ones (10 individuals) (; ANOVA, 10 vs 30–50: F-value = 280.2, p-value < 0.001; 30 vs 50: F-value = 1.48, p-value = 0.22) for both unidirectional and circular evasion (Figures 4A–C) and when interacting with a larger number of nearby neighbours (increased topological range; F-value = 365.2, p-value < 0.001; Figure 4D). A higher reaction frequency (interacting more often with nearest neighbours) also leads to a higher instability of neighbours (Figure 4E). These cases of increased instability may be side-effects of the increased density of larger flocks (Hemelrijk and Hildenbrandt, 2008) and of individuals re-adjusting their positions and headings to small changes of their neighbours positions. Smaller distances among flock members and more frequent small turning motions within the flock may reinforce turns to avoid collisions and thus make individuals change their relative positions faster (increase mutual diffusion).
The higher the tendency of flock members to align, the more stable their neighbourhood remained during circular evasion (ANOVA; F-value = 29.48, p-value < 0.001). In unidirectional evasion, there was no effect of alignment tendency on the instability of neighbours (ANOVA; F-value = 0.02, p-value = 0.9). This difference may emerge from a higher occurrence of collision avoidance during circular evasion, since differences among individuals in their turning tendencies are larger. Alignment may act as an alternative mechanism for collision avoidance (individuals with parallel headings will never collide) and thus smooth out the reshuffling of individuals due to differences in their local conditions (their relative position to the roost). In line with our initial hypothesis, centroid attraction has the opposite effect of alignment: its increase led to higher instability of neighbours, for both circular (ANOVA; F-value = 20.9, p-value < 0.001) and unidirectional evasion (ANOVA; F-value = 10.15, p-value < 0.001) (Figure S1).
In sum, the highest instability of neighbours is shown by large flocks with high number of topological neighbours and strong centroid-attraction (, opposite to the lowest instability of ).
3.2 Instability and turning modes in the model
Our new metrics of deviation from equal-radii and parallel-paths are pairwise: they are calculated for each pair of individuals in the group. Thus, a deviation may differ across neighbours at different distances to the focal individual (for instance between the first and the second nearest neighbours). In our simulated trajectories, collective turns deviate less from equal-radii and parallel-paths for neighbours closer to the focal individual (increased deviation with increasing neighbour rank, Figure S2). For our analysis, we focused on how a turn deviate from the two types based on the nearest neighbour of each flock member at the end of our 3 seconds sliding window. Across our simulations, collective turns were closer to a turn with parallel-paths when the flock was small (10 individuals) and turning towards their roost with low turning rate (Dp(3s) = 0.14 m).
We expected the instability of neighbours to increase when the deviation from turns with equal-radii was smaller and the deviation from parallel-paths was larger (since during a turn with parallel-paths individuals keep their relative positions stable and neighbour instability is expected to be 0). However, the relation between neighbour instability and deviation from the two turning modes was not proportional (Figure S3). Overall, we found weak positive correlations between instability of neighbours and deviations from parallel-paths (Spearman correlation; R=0.58, p-value < 0.001, in line with our H7 hypothesis) and equal-radii (Spearman correlation; R=0.55, p-value < 0.001, in contrast to our H6 hypothesis). Unexpectedly, the deviation from equal-radii also positively correlated with that from parallel-paths (Spearman correlation; R=0.7, p-value < 0.001). However, across our parameter space, the relation between the three measurements (neighbour instability, the deviation from parallel-paths and that from equal-radii) varied according to the specific parameter that was changing (e.g. Figure S4 for topological range), with no correlation between them across smaller changes in parameter values (for example across simulations with unidirectional evasion in which only flock size changes; : , p-value = 0.64; : , p-value = 0.004).
We often saw counter-intuitive changes in deviations and neighbour instability for different changing parameters; we summarised all effects in Figure 5. For instance, during circular evasion, a higher topological range led to a lower deviation from both turns with parallel-paths (GLM; t-value = –11.8, p-value < 0.001) and equal-radii (GLM; t-value = – 21.9, p-value < 0.001), while neighbour instability slightly increased (GLM; t-value = 7.5, p-value < 0.001). Larger flocks showed larger deviation from both turns with parallel-paths (ANOVA, unidirectional evasion: F-value = 9.4, p-value = 0.003; circular evasion: F-value = 85.9, p-value < 0.001) and equal-radii (but only during circular evasion; ANOVA, unidirectional evasion: F-value = 3.58, p-value = 0.06; circular evasion: F-value = 16.3, p-value < 0.001) (Figure 5). Increasing the reaction frequency of individuals in turns towards a roost showed, as expected, that the deviation from equal-radii decreased (ANOVA, F-value = 344, p-value < 0.001) and the deviation from parallel-paths increased (ANOVA, F-value = 319, p-value < 0.001). Interestingly, in unidirectional turns we saw the reverse effect on the deviation from equal-radii (ANOVA, F-value = 31.4, p-value < 0.001). In total, measurements of unidirectional evasion seemed to be more robust than circular evasion against changes in our parameters (Figure 5); this highlights the importance of small difference in the tendency to turn (turning rate) among flock members.
Figure 5 The effect of our parameters in the computational model on the neighbour instability, the deviation from equal-radii and from parallel-paths. The tiles show the correlation coefficients (with p-value < 0.05) between a parameter and a measurement. Empty (white) tiles represent non-significant effects (p-value > 0.05). The exact p-value of each correlation is given in Figure S6.
3.3 Collective turns in pigeon flocks
We confirm that the instability of neighbours in flocks of pigeons (normally distributed, Shapiro-Wilk test: W = 0.98,p-value = 0.19), is on average lower (approx. 0.2) than in flocks of starlings (approx. 0.4, Cavagna et al., 2013). In line with our model predictions, the instability of neighbours in small flocks is lower than in large ones (LME: beta = 0.63, Std.Error = 0.03, p-value < 0.0001; Figure 6A). Specifically, after 1.6 seconds in a collective turn, pigeons in small flocks lose only 18% of their 4 closest neighbours, while in large flocks they lose on average 37%. As expected by theory (Hemelrijk et al., 2015), larger flocks in our dataset are denser than smaller ones (Figure S7). A sharper turn leads to higher instability of neighbours than a wider one in large flocks (LME: beta = 0.11, p-value = 0.017) but not in small flocks (LME: beta = −0.018, p-value = 0.43; Figure 6B).
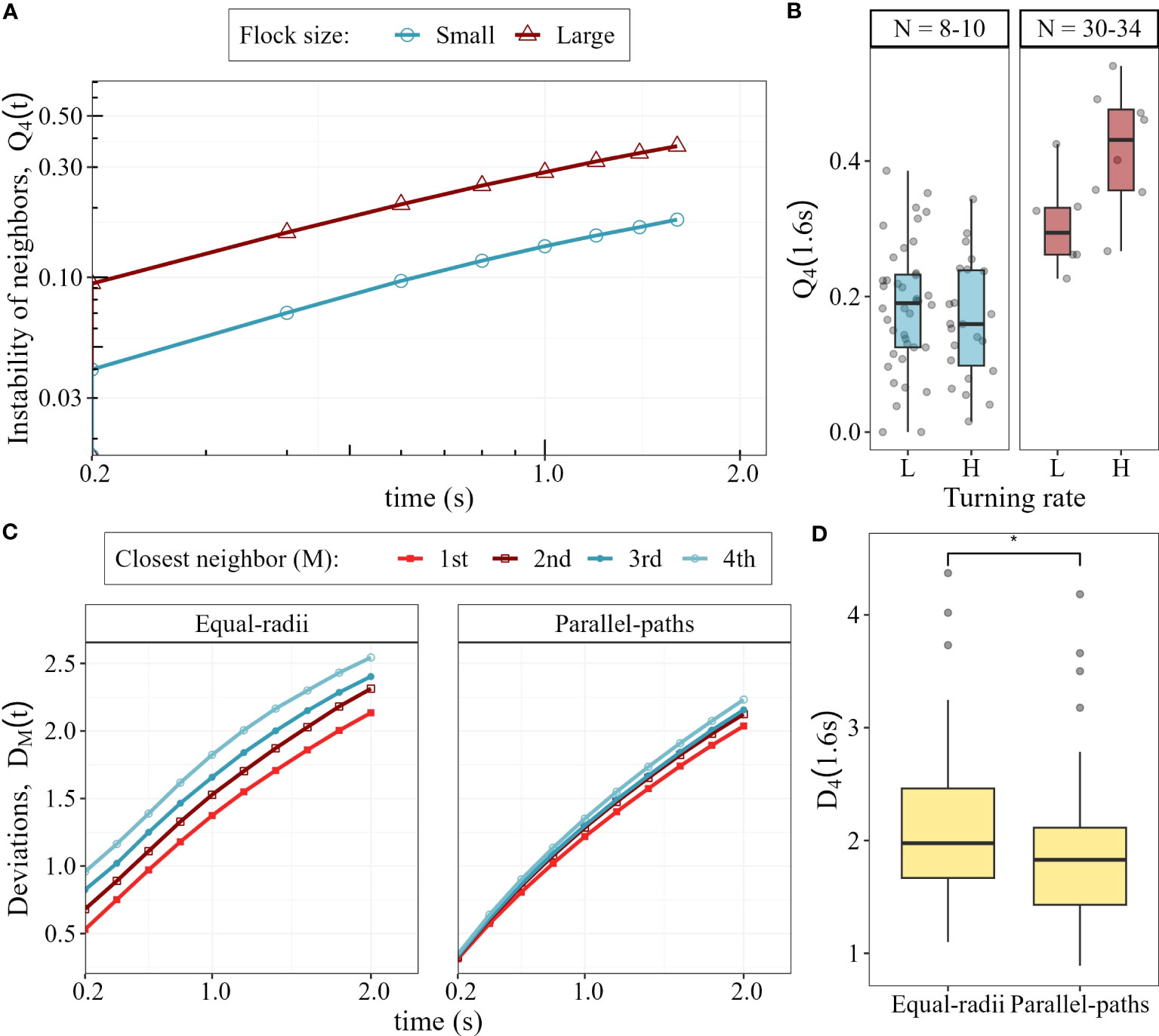
Figure 6 Neighbour instability and changes in internal structure in pigeons flocks under attack. (A) Instability of the closest 4 neighbours during collective turning. (B) Instability of neighbours after 1.6 seconds of turning in small and large flocks, for low (L) and high (H) turning rates. (C) Average deviation of the 4 closest neighbours from parallel-paths () and equal-radii () during collective turns. (D) Overall, the deviation from parallel-paths is smaller than the deviation from equal-radii (*: p-value < 0.05).
Our new metric, the deviation from turns with equal-radii and parallel-paths for a focal individual, is smaller the closer the neighbour is (increased deviation with increasing neighbour rank, p-value < 0.0001; : p-value < 0.0001; Figure 6C). The difference in deviation between neighbour rank (from 1st to 4th closest neighbour) are larger in the deviation from equal-radii than from parallel-paths. Overall, the collective turns of pigeons (N = 77) are closer to parallel-paths (average deviation 1.89 m) than to equal-radii (average deviation 2.13 m, p-value < 0.05) (Figure 6D). Flock size does not affect the deviation from either turn type ( p-value = 0.6; : p-value = 0.9), according to the prediction of our model concerning unidirectional evasion (Figure 5).
4 Discussion
We examined the link between the specifics of coordination among flock members and their instability of neighbours during collective turns, using instability as a proxy of flock diffusion. We did so in our new computational model of collective turning. In it, collective turns are initiated by one or a few flock members, like in real flocks (Ling et al., 2019c). To study the relationship between neighbour instability and the two modes of collective turning (equal-radii and parallel-paths; Pomeroy and Heppner, 1992), we developed a metric of the deviation from these modes. In our simulations, we find many counter-intuitive effects of changing parameters that are linked to increased predation pressure (e.g., increased reaction frequency of individuals; Domenici, 2010; Herbert-Read et al., 2017) and our measurements of instability of neighbours and type of collective turning. We further used our new measurements on empirical data of pigeon flocks pursued by the RobotFalcon (Sankey et al., 2021), investigating for the first time diffusion and dynamics of internal structure in small flocks under predation.
Instability of neighbours (measured after 3 seconds of collectively turning) varied across our simulations, including the range of instability measured in real flocks of starlings (Cavagna et al., 2013). Higher instability of neighbours emerged in a previous computational model from a decrease in the topological range of collision avoidance (when individuals avoid a single neighbour instead of their closest 7 neighbours) (Hemelrijk and Hildenbrandt, 2015). In our simulations, it emerges from an increase in the topological range of alignment and centroid attraction (when individuals interact with a higher number of neighbours). Thus, interacting with many neighbours may have a strong anti-predator effect, not only through increased speed of information transfer through the flock (Ling et al., 2019c), but also by increasing the predator’s confusion. However, given that such change may be cognitively demanding, future work should investigate the balance between the cost (Usherwood et al., 2011) and the anti-predatory benefits (Carere et al., 2009; Papadopoulou et al., 2022b) of predator induced changes in social interactions.
Other parameters that led to higher instability of neighbours in our simulations are larger flock sizes, stronger centroid-attraction, and higher reaction frequencies. Group density may have an important role in these effects. Neighbour instability increases less between flock sizes of 30 and 50 individuals than 10 and 30 individuals. Since this effect may depend on the local volume of the group (how dense the neighbourhoods of non-border individuals are; Cavagna et al., 2013), it remains to be studied whether there is a critical point after which further increase in flock size does not affect neighbour instability. In our empirical data of pigeons, we confirmed that larger flocks are denser (Hemelrijk et al., 2015). Increased density of the flock, a common effect of predator presence in nature (Carere et al., 2009; King et al., 2012), may be the result of stronger centroid-attraction which also led to increased neighbour instability in our simulations. In a denser flock with metric interactions among flock members, the number of interacting neighbours is expected to increase. Thus, we predict that a switch from topological to metric interactions under threat, as found in jackdaws during mobbing flights (Ling et al., 2019b), will increase diffusion and thus confuse the predator more. Similarly, instability of neighbours increases in our model when individuals increase their reaction frequency, a property that has been identified in groups under predation (Bode et al., 2010; Domenici, 2010).
In a collective turn with parallel-paths, neighbour instability is 0 (no neighbour is changing); we thus expected the parameters that led to high neighbour instability to also lead to high deviation from parallel paths. Surprisingly, many of our coordination parameters showed the opposite: circular evasion with increased topological range and stronger centroid-attraction deviated less from parallel-paths despite their higher instability of neighbours. This may be a side-effect of increased collision avoidance and coordination by averaging ones heading over the headings and positions of more neighbours: individuals may lose the neighbours that are furthest away more often (and thus increase their neighbour instability), but keep their closest neighbour in a more stable relative position (decreasing the deviation from parallel-paths). These self-organised processes cause the relationship between flocking properties (such as neighbour instability) and turning modes to be more complex than we expected.
Whether the internal structure of a flock during a turn has adaptive value is unclear. Turning with parallel paths has been ruled out as a plausible behaviour of bird flocks since it is assumed to require more energy (individuals need to adjust their speed) and to confuse the predator less than turns of equal-radii (Ballerini et al., 2008a; Attanasi et al., 2014). Turns of parallel-paths were thus assumed to be the extreme opposite of turns of equal-radii (Ballerini et al., 2008a). Our results challenge this hypothesis; the deviations from parallel-paths and equal-radii often correlated positively and both showed positive and negative correlations with instability of neighbours. In line with Yomosa et al. (2015), our new measurement of deviation showed that the collective turns of pigeons fall in between parallel-paths and equal-radii. In nature, turns closer to parallel-paths may emerge from individual variation in certain traits (e.g. speed) that leads to stable internal structure of the group (Sankey et al., 2022), and may be favourable if such structure is energetically advantageous (for instance during V-formations; Corcoran and Hedrick, 2019) or social-bonds in the group make it important for individuals to keep the same neighbours (for instance when flying with mating partners; Ling et al., 2019a).
A challenge when studying collective turns are the many emergent factors of a flock (internal structure, shape, and turning mode). Disentangling the indirect effects of parameters on the dynamics of each turn is not straightforward; a parameter may alter the shape or density of the flock, and these may affect other flock characteristics during a collective turn. To understand this interconnection, more insight is needed in the relation among shape, diffusion and turning mode of a flock. Our new model and metric of deviation from the two turning modes provide a framework with which this can be studied. Our metric is the first to quantitatively capture the resemblance of a collective turn to the two turning modes. One potential limitation of our model is its representation in 2D; it may be enhancing the effect of crossing of individual paths during a turn and this may cause the collision avoidance in our model to have a disproportionately large effect on the type of collective turn (larger than it would have in a 3D simulation).
Understanding collective turning can provide valuable theoretical insight (as discussed above) and help identify the reasons behind internal structure in real flocks (e.g., leadership; Sankey et al. 2022). Even though diffusion has been assumed to relate to predator confusion, the exact link between the two is not well studied. Our model can be extended in the future to theoretically investigate this relationship. Knowledge of the self-organised processes that underlie diffusion can also aid the development of future models (Grimm et al., 2005) and support bio-mimetic applications of collective motion such as swarm robotics (Şahin et al., 2008; Konda et al., 2020; Whiten et al., 2022).
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repositories and accession number(s) can be found below: the simulated data at https://zenodo.org/record/7790138 and the computational model at https://github.com/marinapapa/ColT-Model/.
Author contributions
MP, HH, and CKH contributed to conception and design of the study. MP and HH developed the computational model and the metrics of collective turning. MP ran the simulations, analysed the empirical and the simulated data, performed all statistical analyses and wrote the first draft of the manuscript. All authors contributed to the article and approved the submitted version.
Funding
This work has been financed by the Dutch Research Council (NWO) as part of the project ‘Preventing bird strikes: Developing RoboFalcons to deter bird flocks’ (grant no. 14723) awarded to CKH.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2023.1198248/full#supplementary-material
References
Attanasi A., Cavagna A., Del Castello L., Giardina I., Jelic A., Melillo S., et al. (2015). Emergence of collective changes in travel direction of starling flocks from individual birds’ fluctuations. J. R. Soc. Interface 12, 20150319. doi: 10.1098/rsif.2015.0319
Attanasi A., Cavagna A., Del Castello L., Giardina I., Melillo S., Parisi L., et al. (2014). Collective behaviour without collective order in wild swarms of midges. PloS Comput. Biol. 10, 1–10. doi: 10.1371/journal.pcbi.1003697
Ballerini M., Cabibbo N., Candelier R., Cavagna A., Cisbani E., Giardina I., et al. (2008a). Empirical investigation of starling flocks: a benchmark study in collective animal behaviour. Anim. Behav. 76, 201–215. doi: 10.1016/j.anbehav.2008.02.004
Ballerini M., Cabibbo N., Candelier R., Cavagna A., Cisbani E., Giardina I., et al. (2008b). Interaction ruling animal collective behavior depends on topological rather than metric distance: evidence from a field study. Proc. Natl. Acad. Sci. 105, 1232–1237. doi: 10.1073/pnas.0711437105
Bode N. W., Faria J. J., Franks D. W., Krause J., Wood A. J. (2010). How perceived threat increases synchronization in collectively moving animal groups. Proc. R. Soc. B: Biol. Sci. 277, 3065–3070. doi: 10.1098/rspb.2010.0855
Camazine S., Deneubourg J. L., Franks N. R., Sneyd J., Theraulaz G., Bonabeau E. (2003). Self-organization in biologican systems (Princeton University Press).
Carere C., Montanino S., Moreschini F., Zoratto F., Chiarotti F., Santucci D., et al. (2009). Aerial flocking patterns of wintering starlings, sturnus vulgaris, under different predation risk. Anim. Behav. 77, 101–107. doi: 10.1016/j.anbehav.2008.08.034
Cavagna A., Queiros S. M. D., Giardina I., Stefanini F., Viale M. (2013). Diffusion of individual birds in starling flocks. Proc. R. Soc. B: Biol. Sci. 280, 20122484–20122484. doi: 10.1098/rspb.2012.2484
Corcoran A. J., Hedrick T. L. (2019). Compound-V formations in shorebird flocks. eLife 8, 1–18. doi: 10.7554/eLife.45071
Cresswell W. (1994). Flocking is an effective anti-predation strategy in redshanks, tringa totanus. Anim. Behav. 47, 433—–442. doi: 10.1006/anbe.1994.1057
Domenici P. (2010). Context-dependent variability in the components of fish escape response: integrating locomotor performance and behavior. J. Exp. Zoology Part A: Ecol. Genet. Physiol. 313 A, 59–79. doi: 10.1002/jez.580
Evangelista D. J., Ray D. D., Raja S. K., Hedrick T. L. (2017). Three-dimensional trajectories and network analyses of group behaviour within chimney swift flocks during approaches to the roost. Proc. R. Soc. B: Biol. Sci. 284, 20162602. doi: 10.1098/rspb.2016.2602
Grimm V., Revilla E., Berger U., Jeltsch F., Mooij W. M., Railsback S. F., et al. (2005). Pattern-oriented modeling of agent-based complex systems: lessons from ecology. Science 310, 987–991. doi: 10.1126/science.1116681
Hamilton W. D. (1971). Geometry for the selfish herd. J. Theor. Biol. 31, 295–311. doi: 10.1016/0022-5193(71)90189-5
Hemelrijk C. K., Hildenbrandt H. (2008). Self-organized shape and frontal density of fish schools. Ethology 114, 245–254. doi: 10.1111/j.1439-0310.2007.01459.x
Hemelrijk C. K., Hildenbrandt H. (2015). Diffusion and topological neighbours in flocks of starlings: relating a model to empirical data. PloS One 10, 1–12. doi: 10.1371/journal.pone.0126913
Hemelrijk C. K., van Zuidam L., Hildenbrandt H. (2015). What underlies waves of agitation in starling flocks. Behav. Ecol. Sociobiology 69, 755–764. doi: 10.1007/s00265-015-1891-3
Herbert-Read J. E., Rosén E., Szorkovszky A., Ioannou C. C., Rogell B., Perna A., et al. (2017). How predation shapes the social interaction rules of shoaling fish. Proc. R. Soc. B: Biol. Sci. 284, 20171126. doi: 10.1098/rspb.2017.1126
Hildenbrandt H., Carere C., Hemelrijk C. K. (2010). Self-organized aerial displays of thousands of starlings: a model. Behav. Ecol. 21, 1349–1359. doi: 10.1093/beheco/arq149
Hogan B. G., Hildenbrandt H., Scott-Samuel N. E., Cuthill I. C., Hemelrijk C. K. (2017). The confusion effect when attacking simulated three-dimensional starling flocks. R. Soc. Open Sci. 4, 1–9. doi: 10.1098/rsos.160564
Ioannou C. C., Guttal V., Couzin I. D. (2012). Predatory fish select for coordinated collective motion in virtual prey. Science 337, 1212–1215. doi: 10.1126/science.1218919
King A. J., Wilson A. M., Wilshin S. D., Lowe J., Haddadi H., Hailes S., et al. (2012). Selfish-herd behaviour of sheep under threat. Curr. Biol. 22, R561–R562. doi: 10.1016/j.cub.2012.05.008
Konda R., La H. M., Zhang J. (2020). Decentralized function approximated q-learning in multi-robot systems for predator avoidance. IEEE Robot. Autom. Lett. 5, 6342–6349. doi: 10.1109/LRA.2020.3013920
Landeau L., Terborgh J. (1986). Oddity and the ‘confusion effect’ in predation. Anim. Behav. 34, 1372–1380. doi: 10.1016/S0003-3472(86)80208-1
Lima S. L. (1995). Back to the basics of anti-predatory vigilance: the group-size effect. Anim. Behav. 49, 11–20. doi: 10.1016/0003-3472(95)80149-9
Ling H., Mclvor G. E., van der Vaart K., Vaughan R. T., Thornton A. (2019a). Costs and benefits of social relationships in the collective motion of bird flocks. Nat. Ecol. Evol. 3, 943–948. doi: 10.1038/s41559-019-0891-5
Ling H., Mclvor G. E., Westley J., van der Vaart K., Vaughan R. T., Thornton A., et al. (2019b). Behavioural plasticity and the transition to order in jackdaw flocks. Nat. Commun 10, 5174. doi: 10.10.1038/s41467-019-13281-4
Ling H., Mclvor G. E., Westley J., van der Vaart K., Yin J., Vaughan R. T., et al. (2019c). Collective turns in jackdaw flocks: kinematics and information transfer. J. R. Soc. Interface 16, 20190450. doi: 10.1098/rsif.2019.0450
Olson R. S., Hintze A., Dyer F. C., Knoester D. B., Adami C. (2013). Predator confusion is sufficient to evolve swarming behaviour. J. R. Society Interface 10, 20130305. doi: 10.1098/rsif.2013.0305
Papadopoulou M., Hildenbrandt H., Sankey D. W. E., Portugal S. J. (2022b). Self-organization of collective escape in pigeon flocks. PloS Comput. Biol. 18, e1009772. doi: 10.1371/journal.pcbi.1009772
Papadopoulou M., Hildenbrandt H., Sankey D. W. E., Portugal S. J., Hemelrijk C. K. (2022a). Emergence of splits and collective turns in pigeon flocks under predation. R. Soc. Open Sci. 9, 211898. doi: 10.1098/rsos.211898
Pomeroy H., Heppner F. (1992). Structure of turning in airborne rock dove (Columba livia) flocks. Auk 109, 256–267. doi: 10.2307/4088194
Şahin E., Girgin S., Bayindir L., Turgut A. E. (2008). ‘Swarm robotics,’ in Swarm intelligence: introduction and applications. Eds. Blum C., Merkle D. (Berlin, Heidelberg: Springer), 87–100. doi: 10.1007/978-3-540-74089-6_3
Sankey D. W., Biro D., Ricketts R. L., Shepard E. L., Portugal S. J. (2022). Pigeon leadership hierarchies are not dependent on environmental contexts or individual phenotypes. Behav. Processes 198, 104629. doi: 10.1016/j.beproc.2022.104629
Sankey D. W., Shepard E. L., Biro D., Portugal S. J. (2019). Speed consensus and the ‘Goldilocks principle’ in flocking birds (Columba livia). Anim. Behav. 157, 105–119. doi: 10.1016/j.anbehav.2019.09.001
Sankey D. W., Storms R. F., Musters R. J., Russell T. W., Hemelrijk C. K., Portugal S. J. (2021). Absence of ‘selfish herd’ dynamics in bird flocks under threat. Curr. Biol. 31, 1–7. doi: 10.1016/j.cub.2021.05.009
Storms R., Carere C., Musters R. J., van Gasteren H., Verhulst S., Hemelrijk C. K. (2022a). Deterrence of birds with an artificial predator, the RobotFalcon. J. Royal Soc. Interface 19 (195), 20220497. doi: 10.1101/2022.05.18.492297
Storms R., Carere C., Verhulst S., Hemelrijk C. K. (2022b). Collective responses of aerial flocks of birds to a robotfalcon. In prep.
Storms R. F., Carere C., Zoratto F., Hemelrijk C. K. (2019). Complex collective motion: collective escape patterns of starling flocks under predation. Behav. Ecol. Sociobiology 73, 1–10. doi: 10.1007/s00265-018-2609-0
Usherwood J. R., Stavrou M., Lowe J. C., Roskilly K., Wilson A. M. (2011). Flying in a flock comes at a cost in pigeons. Nature 474, 494–497. doi: 10.1038/nature10164
Whiten A., Biro D., Bredeche N., Garland E. C., Kirby S. (2022). The emergence of collective knowledge and cumulative culture in animals, humans and machines. Philos. Trans. R. Soc. B: Biol. Sci. 377, 20200306. doi: 10.1098/rstb.2020.0306
Keywords: collective behaviour, self-organisation, bird flock, collective turn, diffusion, predation, agent-based model, homing pigeon
Citation: Papadopoulou M, Hildenbrandt H and Hemelrijk CK (2023) Diffusion during collective turns in bird flocks under predation. Front. Ecol. Evol. 11:1198248. doi: 10.3389/fevo.2023.1198248
Received: 31 March 2023; Accepted: 08 June 2023;
Published: 11 July 2023.
Edited by:
Joseph Bailey, University of Essex, United KingdomReviewed by:
Richard Bon, Université Toulouse III Paul Sabatier, FranceMonique De Jager, Netherlands Institute of Ecology (NIOO-KNAW), Netherlands
Copyright © 2023 Papadopoulou, Hildenbrandt and Hemelrijk. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Marina Papadopoulou, bS5wYXBhZG9wb3Vsb3UucnVnQGdtYWlsLmNvbQ==
 Marina Papadopoulou
Marina Papadopoulou Hanno Hildenbrandt1
Hanno Hildenbrandt1 Charlotte K. Hemelrijk
Charlotte K. Hemelrijk