- 1Forest Systems, New Zealand Forest Research Institute (Scion), Rotorua, New Zealand
- 2Center for Forest Damage and Risk Management, Forestry and Forest Products Research Institute, Tsukuba, Japan
Quantifying wind risk in planted forests is critical to ensure the provision of wood-based biomaterials and forest ecosystem services in the future. Tree sway dynamics play a major role in determining their vulnerability to wind storms. While structural engineering theory can greatly assist in predicting tree and branch motion accurately, the effects of forest aging and silvicultural treatments on motion and the likelihood of mechanical failure are still poorly understood. In this study, we simulate the growth of an individual model tree and its architecture for a managed, even-aged pure Cryptomeria japonica D. Don. stand. The dynamic behavior of the tree is predicted for a rotation period at a 5-year interval using finite element analysis. Results show that tree natural sway frequency is subject to a 5-fold decrease over the tree's lifetime. The tree is thus more susceptible to absorb turbulent kinetic energy from the wind as it grows older. The damping ratio, which measures how rapidly the tree can return to its rest position after being deflected, is predicted to increase by a factor of four. By simulating the mechanical response to a wind gust, the model predicts a quick transition from a low risk of failure in the juvenile phase to a high-risk situation in the mature phase. The transition occurs between ages 15 and 30 when canopy closure takes place, when juvenile wood formation stops in the lower stem region and when the first thinning is carried out. Wind risk plateaus after the transition period. The age-risk relationship shown by the model is consistent with post-typhoon damage patterns documented by inventories in Japanese planted forests, albeit with a sharper transition.
Introduction
Trees are the longest-living organisms on Earth. To ensure that longevity, they must withstand the forces exerted on them by the physical environment throughout their lifetime. Although tree mechanical failure is a natural disturbance process important to forest dynamics and biodiversity (Thompson et al., 2009; Mitchell, 2013), large-scale damage is mostly detrimental in forestry because of the associated economic losses (Gardiner et al., 2013) and forest health issues (Stadelmann et al., 2014). As trees grow in size and exposure, they are subject to continuously increasing mechanical forces that should eventually compromise their likelihood of survival. Studies have shown that tree allometric patterns ensures that mechanical stability is less limiting for tree development than other constraints such as hydraulic transport (Koch et al., 2004; Niklas and Spatz, 2004). Often, those studies only consider elastic instability (buckling) under self-weight and neglect other agents and processes that can cause failure.
As top-loaded, tall and slender mechanical structures, forest trees are inherently unstable. To counteract this, they have evolved adaptive growth mechanisms limiting the effects of chronic and acute mechanical loading. A large focus in the study of tree biomechanics has been posture control and gravitropism, an active reorientation process to keep the tree upright thus minimizing the effects of weight (Fourcaud et al., 2003; Coutand et al., 2007; Alméras and Fournier, 2009). Other key adaptive mechanisms are thigmomorphogenesis (Jaffe, 1973) and thigmotropism (Telewski, 2012). They involve regulatory cambial growth to increase resistance and decrease exposure to mechanical loads. Trees also display passive mechanisms such as streamlining (Harder et al., 2004; Butler et al., 2012) and branch damping (Théckès et al., 2015). They allow reducing excess drag and improving kinetic energy dissipation in the swaying tree, respectively. They also make aerial architecture, (i.e., the geometrical and topological configuration of the branch system) a significant actor in tree biomechanical function and safety. The contribution of all those mechanisms is essential to ensure long-term tree stability.
Wind is a major abiotic agent of damage in forest plantations. While mechanical stability to wind loading has been studied in relation to growth (Ancelin et al., 2004; Gardiner et al., 2008), the effects of aging on tree vibrational properties and aerial architecture are rarely included. Instead, the dynamic behavior, which is essential to quantify the risk of windthrow and windbreak, is often investigated at a fixed point of a tree's lifetime (Moore and Maguire, 2008; Sellier and Fourcaud, 2009). As a result, the effects of canopy closure, silviculture, and juvenile wood formation on tree structural dynamics are poorly understood. That knowledge is critical to evaluate the vulnerability of forest plantations to extreme storm events. Extreme storm systems are expected to become regionally more intense and more frequent in future climate projections (Ulbrich et al., 2008; Gastineau and Soden, 2009). Because those events are rare, it is difficult to expand our knowledge about the damage they cause to forests.
In this study, we investigate how tree sway properties and the dynamic response to wind loading vary with tree age on a theoretical basis. The case study is an individual Cryptomeria japonica D. Don. tree representing managed, even-aged pure stand conditions. As Japan is annually subject to several tropical cyclonic storms (typhoons) and has ~10 million hectares (30% of land area) of planted forests (MAFF, Japan, 2017), extensive information on tree growth and wind damage was available to support model development and evaluate the predicted age patterns of wind risk.
Materials and Methods
The aerial system of a C. japonica tree was reconstructed from age 5 (sapling) to age 55. The common age of harvest in Japanese forestry is 60. The model tree was assembled using distinct experimental datasets and relationships for tree stem, architecture, foliage, and wood properties. A complete dataset was unavailable, even for a single age. The dynamic behavior of the tree was evaluated under impulse loading and wind loading using finite element analysis.
Tree Stem
The shape of the stem corresponds to a measured C. japonica tree named Sugi 2 (Minato et al., 1989). The tree was planted in the Wakayama experimental forest (135.40E 33.4N, Honshu island, Japan). It was 53 years old, 26.8 m tall and had a DBH of 28.5 cm when it was felled. The stem taper (diameter variation over height) was reconstructed from the internal ring structure at a 5-years interval. Stem taper at age 55 was obtained in this study by extrapolating ring width using the last known growth rates.
Crown Structure
The branching structure was modeled using the crown patterns measured in 9, 16, and 22-year-old stands (Hashimoto, 1991). Those ages represent the main phases of crown development from a young crown covering the full length of the stem to a mature crown after canopy closure. The number of branches borne per unit length of stem was given by a random Gaussian distribution (22.5 ± 3.3 branch m−1) (Hashimoto, 1991). Branches were uniformly positioned over the growth unit as C. japonica does not form whorls. Each branch was assigned a random growth potential at formation which acts as a scaling factor for initial length and growth rate. The upper crown length was defined as the topmost 4 m of the crown (Kajihara, 1976). In the lower crown region, branches were assigned a probability p = 0.1 to die every year because of limited light availability. Overall crown length increased with age up to a maximum of 9 m (Kajihara, 1976). The azimuthal orientation of branches was predicted using a phyllotactic pattern with a divergence angle equal to 139.5°. The branch angle with the vertical is higher in older trees (Hashimoto, 1991), which was represented using θ = 71−0.5n where n is tree age at time of branch formation.
Branch primary growth was modeled using an age-dependent yearly length increment: ΔL = a nbec n + d (Hashimoto, 1991), with a = 0.06; b = 2; c = −0.5; d = 0.2. Branch basal diameter, D, was increased with branch length as D = 0.28L. The number of trees per hectare (stocking), s, ultimately limits the lateral extent of branches. For a circular crown, maximum length is equal to . A thinning event causes s to decrease, allowing branch elongation to resume to take advantage of newly available space. At the Wakayama site, thinning events took place at age 20, 27, and 47 (Minato et al., 1989). In this approach, crown size expansion can resume or accelerate after thinning occurs. Modeling thinning was essential to synchronize crown growth with stem growth. The architecture of the model tree during growth is shown in Figure 1.
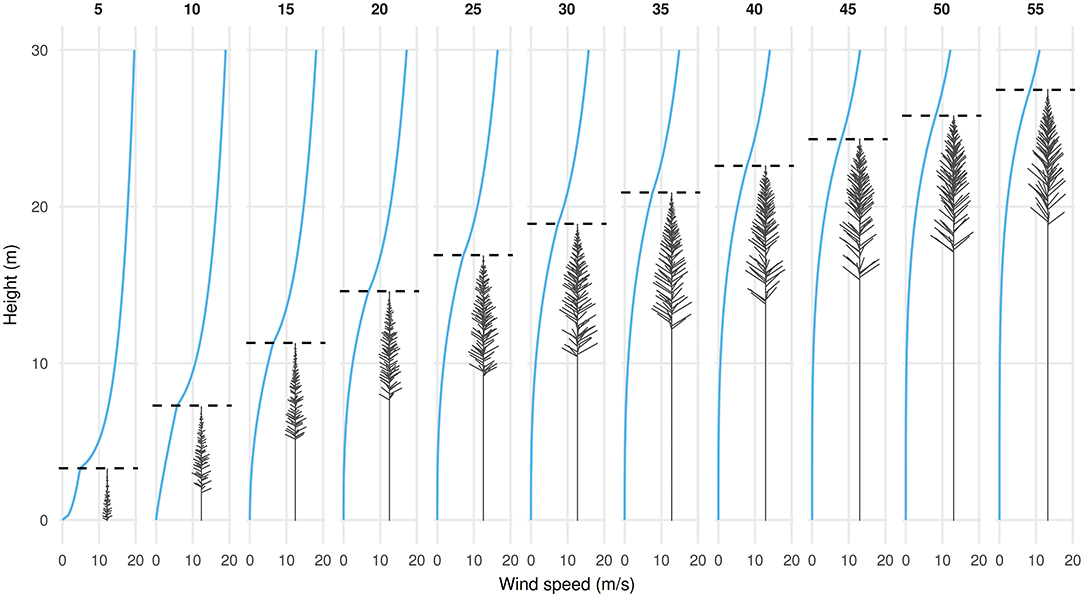
Figure 1. Tree architecture and profile of horizontal wind speed in a Cryptomeria japonica forest stand from age 5 to 55. Dashed lines show canopy height.
Foliage Properties
Tree's foliage mass, mF(n), is required to simulate tree mechanical behavior at any age n. It allows the inertia, the weight and the sail area of the crown to be calculated. In absence of repeated measurements during the growth of the tree Sugi 2, foliage mass was estimated using allometric models. Two models were considered. Both predicted foliage mass in relation to stem size or mass, which were measured (Minato et al., 1989). Only these two models provided a realistic trend of foliage biomass among considered models.
The first model relates directly foliage mass to stem diameter at breast height, D (cm). The model (Hashimoto and Gyokusen, 1995) predicts foliage mass as:
It was retained as the best model describing the functional relationship between foliage mass and shoot cross-sectional area derived from plant hydraulic principles. The second model, purely empirical, was developed to obtain the most realistic allometric for the studied species. It predicts the foliage-to-stem mass ratio as a function of age. It was obtained by fitting a power law on the biomass ratio using measurements across nine C. japonica forest sites at multiple times during the rotation. Those sites were Gunma/Ibaraki, Saitama, and Nara (Ando et al., 1968), Chiba (Negishi et al., 1988), Gifu (Watanabe and Moteki, 2007), Miyazaki, Nagasaki, Oita (Tadaki et al., 1965), and Toyama (Kato et al., 2005). They cover a broad range of silvicultural and environmental conditions, including different stocking densities and thinning schedules. The power law was fitted using Standardized Major Axis (SMA) regression as provided by the smatr R package (Warton et al., 2012). With both foliar models, the effects of thinning on total foliage mass result from the effects of thinning on stem growth (diameter or mass).
The amount of foliage borne by each branch was a fraction of the total crown foliage weighted by the basal diameter of the branch. Foliage was then distributed over the five most recent growth units of each branch to match the average lifespan of needles in C. japonica (5 years). The vertical distributions of foliage mass were in good agreement with profiles measured at ages 9, 16, and 22 (Hashimoto, 1991).
The foliage area, AF, is used for calculating the drag force applied to the crown of the tree. For an individual tree, it is approximated by , where [m2 kg−1 (green weight)] is the specific leaf area (SLA) (Tadaki, 1966).
Wood Properties
Three material properties were used to define wood mechanical behavior in the model. Those are the longitudinal Young's modulus, E (GPa), the density ρ (kg m−3), and the damping ratio, ξ0. E and ξ0 are often known for dry wood. However, their values differ for green material in trees. Green wood is typically less stiff (lower E) and more viscous (higher ξ0) than dry wood.
Most softwood species exhibit a typical radial pattern (TRP) of wood properties. The TRP consists of an increase, or a decrease depending on the property considered, followed by a plateau as the age of wood formation increases. In C. japonica, E follows the TRP (Nakatani et al., 1988; Zhu et al., 2005) and can be expressed as a function of the tree-ring number k (Zhu et al., 2005) as E(k) = cG(2.369 + 2.263ln(k)) where cG = 0.7 is the green-to-dry ratio E (arbitrary value for a 30% reduction in stiffness). Wood forming higher in the tree is stiffer than in the lower stem region (Yamashita et al., 2009). The effect of the height at which the wood is formed z was modeled by E(k, z) = E(k)(0.722 + 0.169ln(5.204z)). The cross-section of any stem or branch element is composed of several rings. The effective modulus of elasticity (MOE) of a cross-section was calculated as the sum of each ring's E value weighted by ring's moment of inertia:
where Rk is the outer radius of the kth ring. Unlike E, basic density remains relatively constant with cambial age in C. japonica (Minato et al., 1989; Yamashita et al., 2009). It was thus modeled as a homogeneous quantity. The green density value, 1,213 kg m−3, was obtained using the average basic density (ρ = 438 kg m−3) and the average moisture content (w = 1.77) of Sugi 2 (Minato et al., 1989). The density value of woody elements bearing foliage was increased by foliage mass divided by the element's volume. The damping ratio of wood depends on the ratio of Young's modulus to basic density (Ono and Norimoto, 1983; Brémaud et al., 2013). For the kth ring, it was predicted using:
where the specific density γ is equal to the ratio of basic density to water density. The factor dG = 1.27 corrects the material viscosity for the fact it is greater for saturated cell walls. The value of dG was calculated from damping experiments in relation to moisture content (Obataya et al., 1998). The effective damping ratio of a cross-section was calculated as the sum of each ring's ξ0 value weighted by ring area. Material damping was then modeled using Rayleigh's model, which linearly relates damping to mass using the coefficient where f0 is the natural sway frequency of the tree.
Numerical Model
The mechanical behavior of the tree was simulated using a finite element (FE) model developed and tested to study tree dynamics (Sellier et al., 2006, 2008). The model uses ABAQUS software with the AQUA module (SIMULIA, Dassault systèmes, France). Tree stem and primary branches are meshed using beam elements. Foliage was modeled by modifying the drag area and the density of elements bearing foliage. Dynamic analyses were carried out by direct integration of the equations of movement using an implicit solver. Unlike with a modal procedure, the geometry of the structure is updated at every time step of a simulation using non-linear analysis. This is essential to simulate large structural displacements, which may occur in response to gale force winds. Furthermore, geometrical non-linearity accounts for the streamlining phenomenon, (i.e., a reduced drag area when the crown is deformed by wind action). There is no need for ad hoc modifications of the drag equation.
Stability Criteria
Two types of simulations were carried out with the FE model. For both types, the mechanical behavior is simulated every 5 years. The first experiment was a virtual pull-and-release experiment. The tree was initially displaced by applying static wind loading on the tree's crown, then released suddenly to induce movement. A 100 tree architectures were randomly generated and tested. The crown features affected by random state were: number of branches borne by a growth unit, height of insertion, growth potential, and branch survival in the lower crown. The foliar model fitted on the experimental datasets was used to predict foliage biomass in this experiment because of its stronger empirical basis. Two important sway characteristics were calculated from the free oscillation response:
• f0, the natural sway frequency of the tree. It is the inverse of the period required by a tree to sway back-and-forth once. f0 is also referred to as the frequency of the fundamental (i.e., of lowest frequency) mode of vibration. Although the presence of modes of higher frequency has sometimes been observed in tree motion, the fundamental mode typically dominates the response.
• ξ0, the damping ratio of the fundamental mode. ξ0 measures the decrease of sway amplitude every cycle. For example, a structure would perpetually oscillate for ξ0 = 0; the amplitude of lateral movement is divided by two every sway when ξ0~0.11; sway amplitude is divided by four every cycle when ξ0 ~ 0.22; and there is no oscillation (single cycle) when damping is critical (ξ0 = 1). ξ0 was calculated by fitting the theoretical motion of a simple damped oscillator to simulated tree response using least-squares optimization.
In the second numerical experiment, the behavior under wind loading was simulated. Because of the computational cost of those simulations, only one tree architecture was tested under wind loading: that of the tree with the sway frequency and the damping ratio closest to the mean values obtained in the first experiment. Simulations were done with both foliar models (section foliage properties). Two criteria were used to characterize the tree response.
• M0, the bending moment at the base of the tree. If M0 exceeds the anchorage strength of the soil/root plate, structural failure by uprooting occurs. Anchorage strength is well-predicted by stem mass mS or, equivalently, volume (Moore and Quine, 2000; Cucchi et al., 2005; Kitagawa et al., 2010). The ratio was used to indicate the relative risk of uprooting. Other aspects not considered here, such as soil water logging or limiting rooting depth, may further reduce anchorage strength and thus increase the relative risk.
• σ(z) the longitudinal stress along the tree stem. Breakage can occur at any point on the stem where σ exceeds the Modulus of Rupture (MOR). Thus, it is max(σ) and not the mean stress that is relevant to analyze the risk of structural failure by windbreak. A single point of failure on the stem is sufficient to cause failure. MOR = 30 MPa is used as reference for green C. japonica wood. Natural variation is ~± 50% of that value (Nakatani et al., 1988). It is consistent with MOR values from bending tests on green logs from a 33-year-old plantation (mean 34.9 MPa, min. 25.8 MPa max. 49 MPa, n = 36) (Suzuki and Ito, 1994).
Wind Loading
Wind exerts a force called aerodynamic drag (Cullen, 2005) on any tree element that is function of the speed of the wind relative to the structure:
where ρ is the air density (1.25 kg m−3), cD is the drag coefficient (0.8), A is the projected area exposed to the moving fluid (m2), u(z, t) the horizontal wind speed (m s−1) and the speed of displacement (m s−1) of the tree element considered. A was calculated as the product of foliage area per unit length and element's length projected on the vertical plane normal to wind direction. The value of A was updated during simulations using the current element orientation.
u(z, t) was decomposed into a spatial component u(z) and a temporal component u(t). To derive the spatial component of wind speed inside a forest stand, one must first define the wind speed when unperturbed by the forest (at the edge). Horizontal wind speed varies with height (Peltola et al., 1999; Gardiner et al., 2008). At the edge of a forest stand, the profile of u(z) is logarithmic (Ancelin et al., 2004):
where h is the mean height of the canopy and z0 is the roughness length (z0 = 0.06h). uE(h) was calculated for each tree age using the above equation with uE(30) = 20 m s−1 for reference. At a distance more than 8–10 h away from the edge downwind, forest stand conditions apply (Dupont et al., 2011). Due to the presence of vegetation, the wind profile in the stand uS(z) is rapidly attenuated below the top of the canopy. Here the wind profile is represented by a power law:
where uS(h) was obtained with a logarithmic profile above the canopy and uE = uS at 1 km altitude (Ancelin et al., 2004). The attenuation coefficient α was chosen as:
where zC is the height at the base of the crown and the ratio u(zC)/u(h) is equal to 0.2. The resulting wind speed profiles are shown in Figure 1.
The time-dependent component of wind speed u(t) corresponds to a single gust event. In forest canopies, gusts are characterized by periodic ramp patterns of turbulent quantities with large deviation from the mean (Raupach et al., 1996). In the case of horizontal velocity, a gust is associated with air movement slowing down followed by a strong acceleration (Collineau and Brunet, 1993). In this study, corresponds to a 30-s event measured below canopy top (Collineau and Brunet, 1993). A maximum velocity equal to twice the mean is typical of wind storm conditions (Oliver and Mayhead, 1974).
Results
Above-Ground Growth Allocation
Figure 2 shows the evolution of stem biomass for 60 years in nine different C. japonica plantations. At a young age (9-year-old), allocation was prioritized toward foliage production with nearly 60% of biomass allocated to it. This was measured at two forest sites: Saitama (Nishikawa management, 4,000–4,500 trees ha−1) and Gunma/Ibaraki (National Forest management, 3,000 trees ha−1) (Ando et al., 1968). The fitted model predicted up to 75% of biomass allocated to foliage for a 5-year-old tree. The situation changed rapidly: stem biomass was three times higher than foliage biomass at age of 20. The relative stem biomass kept increasing as the forest grew older, but more slowly. At harvest age, stem biomass was ~6 times the foliage biomass.
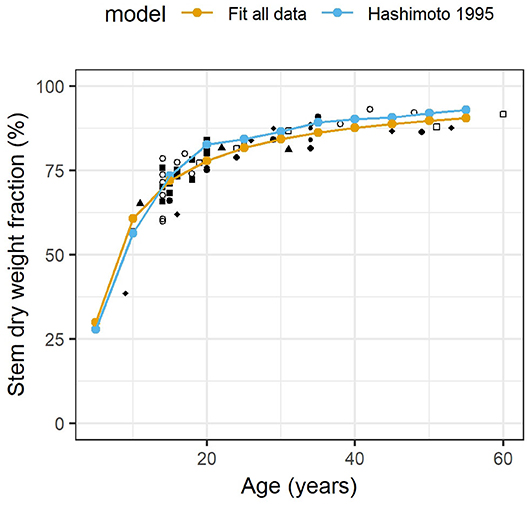
Figure 2. Fraction of stem weight in total stem and foliage dry weight in nine Cryptomeria japonica plantations with distinct silvicultural regimes. The fitted model is (r2 = 0.868; p < 0.001) with mS stem mass and mF foliage mass at age n. Hashimoto and Gyokusen (1995)'s model is with D the diameter at breast height in cm. Each site is shown with a different marker (site names not given). See materials and methods for full details.
The trend of allocation between foliage and stem was consistent for all sites despite varied initial stocking (up to 10,000 trees ha−1 at the Nara site under Yoshino management), cultivars and geographical locations (Kyushu and Honshu islands). Unlike the foliage:stem biomass ratio, the absolute foliage biomass productivity is highly variable across sites (not shown). The allometric relationship (Hashimoto and Gyokusen, 1995) predicted a evolution of allocation similar to the national trend obtained with the fitted model although it overestimated the amount of foliage at early age and underestimated it later on. It performed remarkably well for a simple relationship based on functional hydraulics without any age information. It also predicted more short-term variation in foliage biomass.
Natural Sway Frequency
The modeled tree displayed a general decrease in natural sway frequency with age (Figure 3A). The decrease was observed whether the tree was debranched, defoliated, or complete. There was an exception for the complete tree which, at age 5, was found to sway more slowly (f0 = 0.85 Hz) than at age 10 (f0 = 0.93 Hz). Afterwards, f0 decreased until it reached 0.19 Hz at age 55. Defoliation had for effect to increase f0 with respect to the intact tree. The relative increase was greatest at age 5 (52%) and less but notable (19–30%) at older ages. Branch removal caused an additional increase in f0 (i.e., the tree stem swayed faster without any crown). The increase due to debranching in addition to defoliating was smallest (12%) at age 10–15 and largest (27%) at age 35.
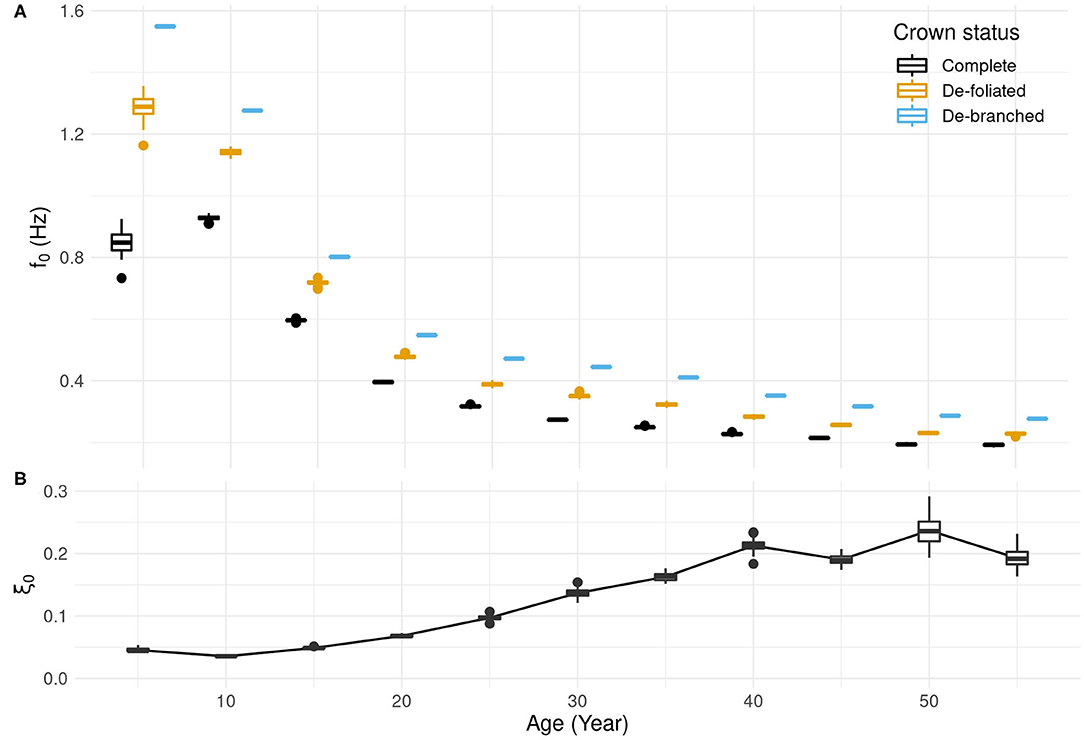
Figure 3. Evolution with age of tree's (A) natural sway frequency f0 and (B) damping ratio ξ0. Each box plot shows the median, the interquartile range and outliers for n = 100 different crowns. Box plots are displayed with a minor age shift for each crown status to avoid overlapping but apply to the same age class.
Damping Ratio
The damping ratio ξ0 increased with tree age (Figure 3B). Damping was relatively low (ξ0 = 0.05) when the tree was young (15-yo or less). It increased until the tree was 40-yo and stabilized at ξ0 ~ 0.2. The amount of variation in the damping ratio due to architectural differences increased as the tree got older. The quality of the fit used for determining ξ0 was found unsatisfying at age 5 and at ages above 35 for different reasons. At age 5, a shift in natural sway frequency occurred while the tree was oscillating. A single degree-of-freedom (1-DOF) model cannot describe that phenomenon (Figure 4). At age 50, oscillation damping exhibited a distinctive non-linear behavior. Motion was strongly damped during the first cycle, but residual oscillations persisted for a long time afterwards. As a result, the 1-DOF model with linear damping under- then over-estimated the amplitude of tree sways during free vibrations. The r2 value was high because the model performed well-quantitatively on average but less so qualitatively. This occurred from age 40 onwards. At age 20, a transient component was found in tree sway response (Figure 4). It probably resulted from the initial activation of a secondary vibration mode of higher frequency. The 1-DOF model could not represent that additional contribution and overestimated the amplitude of displacement during the first cycle. However, the quality of the fit is considered acceptable because the r2 value was high and the signal perturbation was short-lived.
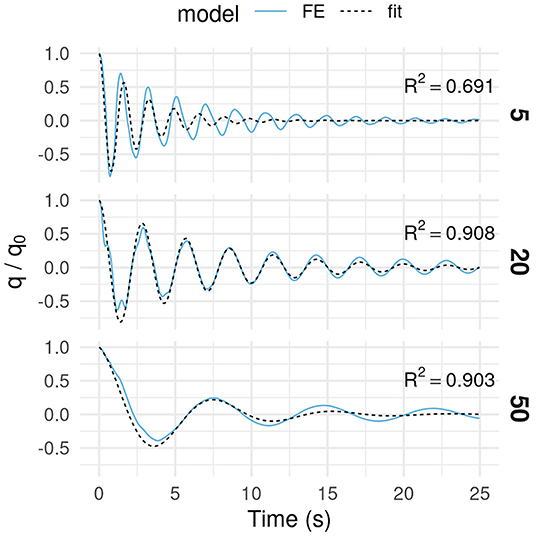
Figure 4. Relative lateral displacement of a fixed point on the tree stem during free oscillations at a young age (5), a mature age (20) and near harvest (50). Free oscillations were simulated by finite element analysis (blue line) for trees bearing individual first-order branches. A one-degree-of-freedom oscillator model (black line) was fitted to the simulated displacement time series to calculate the damping ratio. During the test, the initial deflection before release was applied to the tree crown using static wind loading.
Sway Frequency and Crown Structure
Variability in branch positions in the crown caused variation in sway frequency. At age 5, f0 ranged from 0.73 to 0.93 Hz depending on the crown arrangement, which corresponds to 22.6% of the mean. The range of variation was lower from age 10 onwards, between 2.5 and 8% of the mean. Figure 5 shows the relationship between f0 (normalized by the sway frequency of the stem alone, ) and simple crown descriptors as the crown transitioned to a mature stage (age 25). At age 5, f0 and crown mass mC were independent as f0 varied by more than 20% for the same mC value (Figure 5A). At ages 10 and 15, no clear relationship was observed. At ages 20 and 25, a linear relationship was found. At those ages, it must be noted that f0 was 30% less than for the stem alone whereas the crown represented 15% of tree mass. A better predictor of the influence of the crown on f0 was found to be the change in height of center mass, zM, associated to the presence of the crown. The relationship between f0 and zM were distinctively linear at all ages but 5 (Figure 5B). At 5, a crown of similar mass could either lower or heighten the center of mass depending on how the branches were positioned. As a result, f0 values were quite dispersed. In older trees, a heavier crown always translated to a center of mass located higher than for the stem alone.
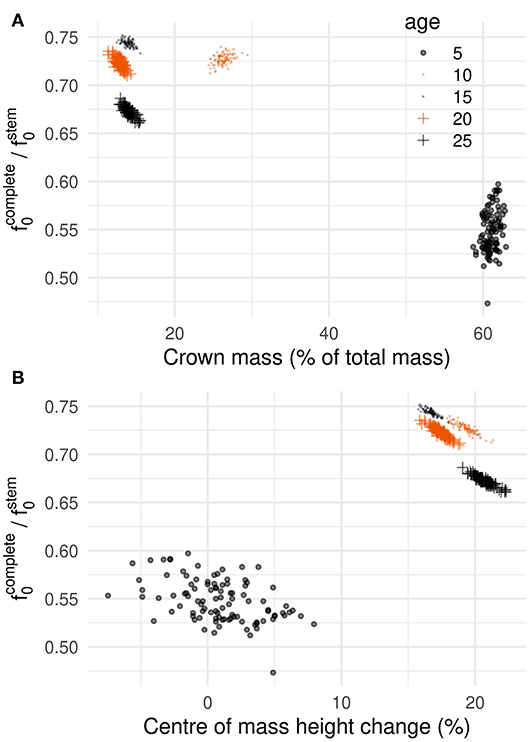
Figure 5. Predicting tree's natural frequency using aggregated crown descriptors during the transition from juvenile to mature. Ratio of sway frequency between the complete tree and the stem alone as a function of (A) crown mass (as percentage of total tree mass) and (B) center of mass displacement, given as percentage of center of mass height for the stem alone, [i.e., ].
Response to Wind Loading
The bending moment and bending stress applied to the tree during a wind gust varied with tree age and size. The basal bending moment increased throughout the rotation period (Figure 6). The overall increase was three orders of magnitude for both the mean and the maximum values. Although the increase slowed down over time, the moment reached the highest value at the oldest age.
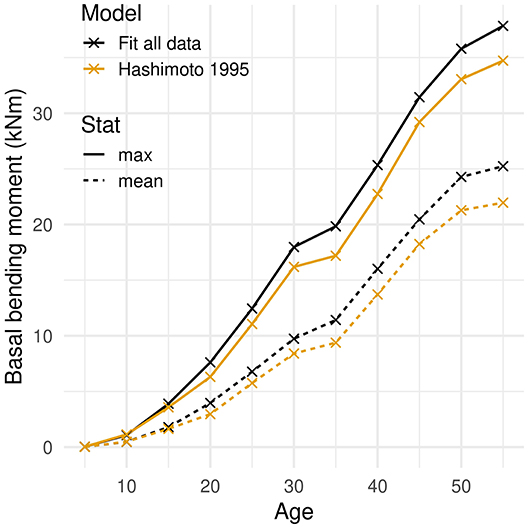
Figure 6. Bending moment at the base of the tree induced by a wind gust as a function of tree age. The mean and maximum moment values recorded during the gust are given. Two model trees with different models of foliar allometry are considered: a fit of experimental allometric ratios and an empirical power law (Hashimoto and Gyokusen, 1995).
The magnitude of bending stress increased by a factor of 3–4 during the entire rotation (Figure 7). Unlike the bending moment, the mean bending stress peaked 5 years before the oldest age. The maximum bending stress caused by the gust event peaked even earlier, at age 40. Both mean and maximum stress values transitioned from low stress levels in the early phase to high stress levels that plateau later. In the case of the maximum stress, the transition was rapid, between age 10 and 25, whereas it took longer for the mean stress.
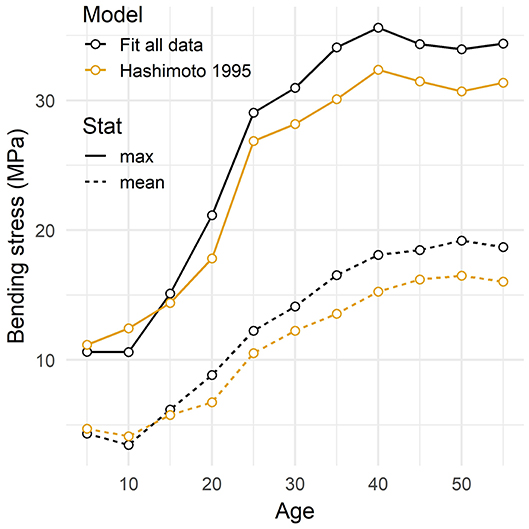
Figure 7. Bending stress induced by a wind gust in the tree stem as a function of tree age. The mean and maximum stress values recorded during the gust are given. The mean value is averaged in time and along stem length. The maximum value is the overall maximum recorded at any stem height at any time during the gust. Two model trees with different models of foliar allometry are considered: a fit of experimental allometric ratios and an empirical power law (Hashimoto and Gyokusen, 1995).
Both predicted basal bending moment and bending stress were higher when using the model describing the national trend of fractional foliage biomass. This stemed from the additional foliar biomass and crown area predicted by that model. Despite differences in load magnitude, the age dynamics of wind loading were similar for both foliar models.
Figure 8 shows peak tree deflection during a wind gust at three different tree ages. When the tree was 15- or 25-yo, the lateral displacement was moderate. However, the stress profiles were completely different. Bending stress was uniformly distributed along the length of the stem at age 15 whereas it is concentrated in the upper crown region at age 25. At age 45, the wind-induced lateral displacement became large and the curvature more pronounced. Bending stress was high over most of stem length excluding the lower region extending from tree base and the very top of the tree.

Figure 8. Tree maximum deflection during a gust event at ages 15, 25, and 45. Grayed silhouettes represent trees at rest. Color scale, from blue (low) to red (high) corresponds to the relative magnitude of longitudinal stress under wind loading.
Age-Risk Relationship
Figure 9 shows how wind risk evolved with the age of the plantation forest using the maximum loads obtained under wind loading (Figures 6, 7). Risk of structural failure is given as a ratio of load to notional resistances to windthrow and windbreak. The risk of windthrow (Figure 9A) increased up to age 30 with both foliar models considered. The likelihood of overturning remained high in older trees without increasing further. The fitted foliar model yielded a risk of windthrow that was 10.9% higher on average, all other factors being equal, which is consistent with higher foliage area.
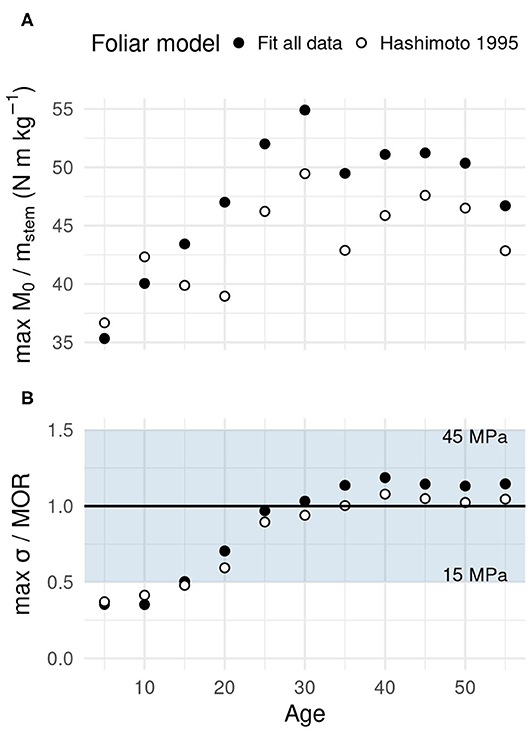
Figure 9. Simulated evolution of the relative risk of windthrow and windbreak in a growing forest. (A) The windthrow risk indicator is given as the ratio of the basal bending moment to stem mass, which predicts well tree overturning strength. (B) The relative windbreak risk is given as the ratio of maximum mechanical stress in tree stem to the wood's Modulus of Rupture (MoR). The grayed area in (B) indicates ±50% of reference MoR; it covers most of the natural range of variation for green C. japonica (Nakatani et al., 1988). Results shown for both foliar models.
The stress maximum in the stem did not reach the lower end of the MOR range in young trees (Figure 9B). Because compression strength is between 50 and 60% of the MOR value (Chiba, 2000; Zhu et al., 2005), local compression failures could happen. After the age of 20, the maximum bending stress reached a level which implies windbreak would occur in trees with weak wood. In the later growth phases (age ≥ 30), the maximum stress reached a value sufficient to induce stem failure in most trees. However, tree stems with the strongest wood and no point of weakness could theoretically resist those stress levels. Like the risk of windthrow, the risk of windbreak was found high and stable after a 10-year period of transition (age 15–25) from a low risk level. The same evolution of windbreak risk was obtained independently of the foliar model, except for an average increase in maximum stress of 10.6% associated to using the fitted model for foliage allocation.
Discussion
Evolution of Natural Sway Frequency With Age
The model predicted a 6-fold decrease of natural sway frequency over the lifetime of the studied C. japonica tree. The overall range 0.18–0.94 Hz, lies within the global 0.16–1.39 Hz range known for trees (Moore and Maguire, 2004). Albeit shifted toward higher values, the predicted natural frequency evolved with age similarly to measurements: 0.62–0.78 Hz in 4-yo Pinus pinaster Ait. (Sellier and Fourcaud, 2005), 0.65 Hz in a 6-yo C. japonica (Suzuki, 2012), 0.18–19 Hz for 36-yo P. pinaster (Sellier et al., 2008) and 0.11 Hz in a 63-yo C. japonica (Suzuki, 2020). Age is useful to define a main trend in sway frequency evolution during growth. However, frequency depends principally on size. Silviculture through thinning schedules and stocking densities will modify the age-size relationship and, therefore, the age-frequency relationship.
The decrease of f0 with age is consistent with mechanical theory which predicts that f0 varies as the square root of the stiffness to mass ratio [i.e., a specific stiffness ( for a cantilever beam)]. As the structure grows heavier and taller, mass scales faster than bending stiffness and the frequency decreases. Those effects are mostly size effects dictated by growth rates. Trees of different ages with similar dimensions will oscillate at similar natural frequencies. Age might have a direct effect on f0 through the modulus of elasticity, E. The progressive stiffening of wood with age of formation would increase f0. That effect must be minor because it is insufficient to counteract the general decrease of f0 observed in the numerical simulations.
The sway frequency helps in estimating the stability of an individual tree. Movement is amplified when the frequency of a dynamic load is similar the frequency of one mode of vibration of the structure (Wood, 1995). Trees are more sensitive to the turbulent kinetic energy of wind in the frequency range close to their natural frequency. In non-storm conditions, the peak frequency of forest canopy turbulence is less (0.02–0.05 Hz) than that of tree sways (Amiro, 1990). Higher peak frequency values equal to 0.1 Hz have been recorded during a typhoon (Yamanoi et al., 2005). Trees with the lowest f0 values, (i.e., the older and larger ones), are more at risk of experiencing large sway displacements due to dynamic amplification and resonance. The decrease of f0 with age is asymptotic (0.25 Hz at age 35 vs. 0.18 Hz at age 55). The transition to a less stable state, with respect to sway frequency, occurs rather early and rapidly.
Evolution of Damping Ratio With Age
Between ages 5 and 40, the tree structure transitioned from being lightly damped (ξ0 ≈ 0.05) to being heavily dampened (ξ0 ≥ 0.2). That transition corresponds to a positive effect of aging on tree stability to wind forces. A higher damping limits the dynamic amplification of tree sways under dynamic loading more effectively. This positive effect contrasts with the negative effect of aging on frequency and wind load magnitudes. Values predicted for ξ0 lie within the 0.03–0.25 range documented by (Moore and Maguire, 2004). However, measured ξ0 values are more commonly found between 0.05 and 0.1. Furthermore, no relationship has been documented between ξ0 and tree size and, a fortiori, age (Moore and Maguire, 2004). ξ0 can also vary substantially among trees of similar age and dimensions [e.g., 0.05–0.12 in pine saplings (Sellier and Fourcaud, 2005)]. Because of lack of data, it is not possible to assert that the simulated increase of ξ0 occurs in nature.
The predicted increase of damping with age is consistent under the hypothesis that aerodynamic drag is the main source of damping in trees. The exponential increase of foliage biomass in the early stage of tree growth would translate to a rapidly increasing aerodynamic damping. That increase would cease after canopy closure unless crown growth is released by thinning events. Once crown size and foliage mass have stabilized after release, the aerodynamic damping would plateau as it is observed in the numerical simulations. The higher ξ0 value predicted at age 50 is likely a response to thinning at age 47. Trees also dampen motion thanks to branch vibrations (Sellier et al., 2006; Spatz et al., 2007). The efficiency of branch damping does not depend on crown size but on a fine-tuning of branch natural frequencies (Scannell, 1984; Théckès et al., 2015). Viscous damping, which dissipates motion though internal friction in wood, is known to have a minor contribution to overall damping (Milne, 1991; Sellier and Fourcaud, 2005). Viscosity should decrease for wood formed later in tree lifetime declines because of the inverse relationship between viscous damping and specific modulus (Ono and Norimoto, 1983).
Two important aspects have emerged about damping in this study. Firstly, the absolute damping rate varied little with tree age. It means that the tree deflected by a wind gust remains swaying for a similar time window (20–30 s) whether it was 5, 20, or 50 years old. During that window before the tree returns to rest, it is temporarily more exposed to the arrival of another gust. Secondly, the nature of tree sways changed as the tree grew. At a young age, tree's response exhibited a frequency shift. At an intermediate age, a secondary mode of vibration was excited. That mode limited the lateral displacement during the first cycles. At an old age, damping appeared quadratic (i.e., drag-dominated) with a relatively higher dissipation of initial cycles followed by persistent small-scale vibrations. In all those cases, the notional simple oscillator model used for calculating ξ0 was insufficient to represent the aspects of damping at each age. However, ξ0 remains useful to provide a gross estimate of the structure's ability to dissipate motion.
The Role of Crown Architecture in Tree Dynamics
From the numerical experiments manipulating the crown status, we find that the presence of branches and foliage slows down tree sways. In absence of any crown, at age 5, the tree swayed twice as fast as the complete tree. A similar ratio was measured for a 4-years-old P. pinaster sapling (Sellier and Fourcaud, 2005). The frequency ratio between the debranched tree and the complete tree continuously decreased during growth until it was 1.25 at harvest age. Thus, the crown's influence on tree sway frequency is reduced with tree age. The crown slows down tree motion because it adds mass onto the stem without contributing any stiffness. Despite that, the relationship between crown mass and frequency is weak. Most of the crown must be removed to significantly increase f0 (Moore and Maguire, 2005). It is also found that the relationship between crown and sway frequency was better represented when the spatial distribution of crown mass was taken into account, for instance by using the height of the center of mass as a predictor of f0 changes. The effects of branch distribution along the stem on natural sway frequency was found to be age-related too, with the youngest trees affected most. Integrated silviculture could become a tool for wind damage risk management by influencing the sway frequency of planted trees because it can change crown structure and allocation between compartments (Ando et al., 1968).
Even the center of mass was a poor predictor of the influence of crown on f0 at age 5. At that age, the spatial distribution and the amount of crown biomass were loosely coupled. All other things being equal, a sapling with a heavy crown could have a center of mass at the same height as a sapling with a light crown. Inversely, two saplings with crowns of equal mass could have centers of mass at a different height. It is possible to accurately predict f0 in the case of saplings, but those predictions require to describe tree's aerial architecture extensively (Sellier et al., 2006). This is in extenso also the case of mature open-grown angiosperm trees, where large branches have a significant impact on the dynamics of the whole tree (Rudnicki et al., 2012; Ciftci et al., 2013). The emergence of laser scanning technology to measure tree architecture will play a major role to systematically perform complex analysis like finite element modeling (Jackson et al., 2019) and to characterize the dynamical properties of trees during their development.
Aerodynamic Behavior: Juvenile and Mature
Wind forces continuously increase as the tree grows larger and taller. The height growth translates to exposure to higher wind speed and an increased lever arm for the bending moment. Foliage growth and branch growth cause greater sail area and drag. Despite tree dimensions and exposure continually increasing because of growth, the increase in wind forces becomes gradually smaller in the late stages of the rotation. This behavior may result from the shift in carbon allocation from foliage to woody biomass due to aging. The shifted allocation translates to relatively less crown sail area and a stronger stem. If that is the case, then there is a clear need to capture precisely allocation trends and to investigate the role of forest management on those trends in future studies of wind risk. We have presented two allometric models that predict reasonably well foliage mass and crown area across a wide range of sites, even for a single individual tree. They are a practical alternative to repetitive foliage measurements for a plantation lifetime. Hashimoto and Gyokusen (1995)'s model is interesting in that it describes the functional relationship between foliage area and sapwood area promoted by the pipe model theory (Lehnebach et al., 2018). In the future, conceptual models of allometry based on the constant-stress theory (Morgan and Cannell, 1994) or source-sink relationships (White et al., 2016) could be used or tested.
In the juvenile tree, mechanical stresses are approximately uniform along the length of the stem. This agrees with the uniform stress theory that is a well-known paradigm in plant biomechanics. Stresses induced by wind loading are expected to be uniform below the crown and above the butt swell (Morgan and Cannell, 1994). The mature tree also presents a long stem section where bending stresses are uniform. This corresponds to the stem region where breakage is expected to occur (Chiba, 2000). That section extends well into the lower crown region. The modulus of rupture of wood increases with height in trees (Nakatani et al., 1988), which might be a beneficial trait to withstand higher stress levels in the stem region where branches are borne. Breakage of the top part of old trees during typhoons sometime occur in old C. japonica specimens growing in natural forests (Takashima et al., 2009). That type of windbreak could be associated to a decurrent tree form, however, and is atypical in plantations. The tree at age 25 presented a significant deviation from uniformity with very high bending stresses near tree top. The exception can be explained as a response to thinning at age 20 with crown growth in width temporarily exceeding stem radial growth.
Age-Risk Pattern and Consequences for Future Forestry
The risk of wind damage was found to strongly depend on which age class the tree belongs to. In the simulations, trees <20-years-old are submitted to low-magnitude wind loads. All the criteria considered, except for damping, indicate that juvenile trees can be considered as stable under wind loading. During an intermediate phase (age 20–30), the tree transitioned from a situation of low risk to one of high risk. Several events occurred during that period: LAI peaked, the canopy closed, wood properties plateaued, and two thinning events were applied. Any of those events would be detrimental to stability on their own. Because all those changes were concurrent, it could explain why the transition to a situation of high risk was particularly rapid and pronounced. In future studies, it would be interesting to quantify how successive thinning events interact with canopy growth and, by releasing growth, if they contribute to an artificially heightened or precocious risk of wind damage. This would allow the onset and magnitude of high wind risk to be tied with silvicultural planning and productivity curves. This and the role of planting density could be investigated using a combination of growth and yield models and theoretical allometric models.
In the second half of the rotation period (after age 30), the predicted level of wind risk remained approximately constant despite the continuously increasing wind loading on the structure. It appears that the strength of the stem and the strength of the root system increased in proportion to the applied loads. Dedicated models of stem and root plate mechanics should be employed to investigate the scaling of strength with age in more detail.
Wind damage recorded in planted forests after typhoon events has a distinctive pattern. Minimal damage is reported for trees 20-years-old or younger. Later, the amount and likelihood of damage increase to a peak value followed by a decrease. Numerous damage inventories reported this “bell-shaped” pattern (Nakao et al., 1993; Fujimori, 1995; Abe, 2005; Sato and Abe, 2006). It is observed across different regions, from Kyushu to Hokkaido, and across different planted species [C. japonica, C. obtusa, Larix kaempferi (Lamb.) Carr.]. The age of peak damage can vary significantly across sites from 35 (Nakao et al., 1993) to 80 (Sato and Abe, 2006), commonly between 50 and 60 (Fujimori, 1995; Abe, 2005). Deviation from the general pattern may happen. For example, important damage has been recorded in the sub-20 age classes at one site (Nakao et al., 1993). Damage inventories for natural forests have shown an altogether different age-risk relationship with a steadily increasing likelihood of damage over a 100 of year (Fujimori, 1995). Similarly, in the natural forests of the Pacific northwest (North America), wind becomes a significant cause of tree mortality only after age 20 and becomes the primary cause in age classes older than 100 (Franklin et al., 1987). The differences between natural forests and plantation forests indicate that the age-risk relationship shown in this study is not inherent to tree's increase in size during growth in general. Whether the influence of forest management on risk derives from the impact on tree growth (slenderness, taper, allocation) or the impact on forest structure heterogeneity remains to be investigated.
In Japan, the dominant age class in plantation forests was 50–55 in 2017. It is of paramount importance to determine whether the age of peak damage likelihood has been reached to decide if the rotation period can be extended without increasing the vulnerability of forests to wind storms nation-wide. Age 50 is approximately the mean reported age for peak damage but, because that age is variable, it is difficult to estimate if the risk associated to windstorms has already peaked. Although the present model can, to a large extent, reproduce the documented age-risk pattern, the lack of available growth data unfortunately did not allow predicting tree mechanical behavior beyond age 55. Assessing wind risk beyond the current traditional age of harvest remains difficult because experimental data on biomass spatial patterns (including architecture) is scarce past that age and because of the strong coupling between those patterns and tree aerodynamic behavior. Linking tree mechanical behavior to the age dynamics of forest above-ground biomass allocation as a function of climate and forest management is an important challenge for future research on wind-tree interactions.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
DS developed and implemented the growth model, performed the finite element analyses, analyzed the results, and wrote the manuscript. SS sourced published and unpublished experimental data sets, translated scientific literature, analyzed the results, and edited the manuscript. All authors contributed to the article and approved the submitted version.
Funding
The Japanese Society for the Promotion of Science (Grant no. S12707) provided a short-term fellowship funding to support DS 5-weeks stay at FFPRI, Tsukuba, Japan in 2012.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are grateful to all the people at FFPRI in Tsukuba and Kumamoto offices who generously contributed their time and knowledge to support this study. We thank Les Dowling and Grant Emms for reviewing an earlier version of the manuscript.
References
Abe, T. (2005). Factorial Analysis of Forest Damage Occurred in the Oji Paper Company in Tomakomai City and Hazard Map. 18th Report of Forest Wind Damage Analysis by RemoteSensing: A Damage Survey for 2004 Typhoon, 51–54.
Alméras, T., and Fournier, M. (2009). Biomechanical design and long-term stability of trees: morphological and wood traits involved in the balance between weight increase and the gravitropic reaction. J. Theor. Biol. 256, 370–381. doi: 10.1016/j.jtbi.2008.10.011
Amiro, B. D. (1990). Drag coefficients and turbulence spectra within three boreal forest canopies. Bound. Layer Meteorol. 52, 227–246. doi: 10.1007/BF00122088
Ancelin, P., Courbaud, B., and Fourcaud, T. (2004). Development of an individual tree-based mechanical model to predict wind damage within forest stands. For. Ecol. Manag. 203, 101–121. doi: 10.1016/j.foreco.2004.07.067
Ando, T., Hatiya, K., Doi, K., Kataoka, H., Kato, Y., and Sakaguchi, K. (1968). Studies on the system of density control of Sugi (Cryptomeria japonica) stand. Bull. Govt. For. Exp. Station 209, 1–76.
Brémaud, I., Ruelle, J., Thibaut, A., and Thibaut, B. (2013). Changes in viscoelastic vibrational properties between compression and normal wood: roles of microfibril angle and of lignin. Holzforschung 67, 75–85. doi: 10.1515/hf-2011-0186
Butler, D. W., Gleason, S. M., Davidson, I., Onoda, Y., and Westoby, M. (2012). Safety and streamlining of woody shoots in wind: an empirical study across 39 species in tropical Australia. New Phytol. 193, 137–149. doi: 10.1111/j.1469-8137.2011.03887.x
Chiba, Y. (2000). Modelling stem breakage caused by typhoons in plantation Cryptomeria japonica forests. For. Ecol. Manag. 135, 123–131. doi: 10.1016/S0378-1127(00)00304-2
Ciftci, C., Brena, S. F., Kane, B., and Arwade, S. R. (2013). The effect of crown architecture on dynamic amplification factor of an open-grown sugar maple (Acer saccharum L.). Trees 27, 1175–1189. doi: 10.1007/s00468-013-0867-z
Collineau, S., and Brunet, Y. (1993). Detection of turbulent coherent motions in a forest canopy part II: time-scales and conditional averages. Bound. Layer Meteorol. 66, 49–73. doi: 10.1007/BF00705459
Coutand, C., Fournier, M., and Moulia, B. (2007). The gravitropic response of poplar trunks: key roles of prestressed wood regulation and the relative kinetics of cambial growth versus wood maturation. Plant Physiol. 144:1166. doi: 10.1104/pp.106.088153
Cucchi, V., Meredieu, C., Stokes, A., De Coligny, F., Suarez, J., and Gardiner, B. A. (2005). Modelling the windthrow risk for simulated forest stands of Maritime pine (Pinus pinaster Ait.). For. Ecol. Manag. 213, 184–196. doi: 10.1016/j.foreco.2005.03.019
Cullen, S. (2005). Trees and wind: a practical consideration of the drag equation velocity exponent for urban tree risk management. J. Arboric. 31, 101–113.
Dupont, S., Bonnefond, J.-M., Irvine, M. R., Lamaud, E., and Brunet, Y. (2011). Long-distance edge effects in a pine forest with a deep and sparse trunk space: in situ and numerical experiments. Agric. For. Meteorol. 151, 328–344. doi: 10.1016/j.agrformet.2010.11.007
Fourcaud, T., Blaise, F., Lac, P., Castéra, P., and de Reffye, P. (2003). Numerical modelling of shape regulation and growth stresses in trees. Trees 17, 31–39. doi: 10.1007/s00468-002-0203-5
Franklin, J. F., Shugart, H. H., and Harnmon, M. E. (1987). Tree death as an ecological process. BioScience 37, 550–556. doi: 10.2307/1310665
Fujimori, T. (1995). Relationships between stand ages and wind resistances of stand—forest damage by typhoon 7 in the Tokyo regional forestry office, Japan. J. Jpn. For. Soc. 77, 602–605. doi: 10.11519/jjfs1953.77.6_602
Gardiner, B., Byrne, K., Hale, S., Kamimura, K., Mitchell, S. J., Peltola, H., et al. (2008). A review of mechanistic modelling of wind damage risk to forests. Forestry 81, 447–463. doi: 10.1093/forestry/cpn022
Gardiner, B., Schuck, A. R. T., Schelhaas, M.-J., Orazio, C., Blennow, K., and Nicoll, B. (2013). Living With Storm Damage to Forests. Joensuu: European Forest Institute.
Gastineau, G., and Soden, B. J. (2009). Model projected changes of extreme wind events in response to global warming. Geophys. Res. Lett. 36, 1–5. doi: 10.1029/2009GL037500
Harder, D. L., Speck, O., Hurd, C. L., and Speck, T. (2004). Reconfiguration as a prerequisite for survival in highly unstable flow-dominated habitats. J. Plant Growth Regul. 23, 98–107. doi: 10.1007/s00344-004-0043-1
Hashimoto, R. (1991). Canopy development in young Sugi (Cryptomeria japonica) stands in relation to changes with age in crown morphology and structure. Tree Physiol. 8, 129–143. doi: 10.1093/treephys/8.2.129
Hashimoto, R., and Gyokusen, K. (1995). Growth pattern of tree organs in relation to the process of canopy development in a Cryptomeria japonica stand. J. Jpn. For. Soc. 77, 153–162. doi: 10.11519/jjfs1953.77.2_153
Jackson, T., Shenkin, A., Wellpott, A., Calders, K., Origo, N., Disney, M., et al. (2019). Finite element analysis of trees in the wind based on terrestrial laser scanning data. Agric. For. Meteorol. 265, 137–144. doi: 10.1016/j.agrformet.2018.11.014
Jaffe, M. J. (1973). Thigmomorphogenesis: the response of plant growth and development to mechanical stimulation. Planta 114, 143–157. doi: 10.1007/BF00387472
Kajihara, M. (1976). Studies on the morphology and dimensions of tree crowns in even-aged stand of Sugi (II) crown morphology within a stand. J. Jpn. For. Soc. 58, 97–103. doi: 10.11519/jjfs1953.58.3_97
Kato, A., Matsuura, T., Aiura, H., and Yasuda, H. (2005). Biomass and net production of Tateyama-sugi (Cryptomeria japonica D. Don) stands planted in Toyama Prefecture. J. Toyama For. For. Prod. Res. Center 18, 5–15. doi: 10.1007/s10310-005-0145-z
Kitagawa, K., Kamimura, K., Saito, S., Uchida, T., and Mizunaga, H. (2010). Wind profiles and mechanical resistance of uprooted trees in a Japanese cypress (Chamaecyparis obtusa) plantation slightly damaged by Typhoon Melor 0918 at Kamiatago Experimental Forest, Tenryu, Japan: validity of mechanistic models for wind damage risks. Jpn. J. For. Environ. 52, 57–66. doi: 10.18922/jjfe.52.2_57
Koch, G. W., Sillett, S. C., Jennings, G. M., and Davis, S. D. (2004). The limits to tree height. Nature 428, 851–854. doi: 10.1038/nature02417
Lehnebach, R., Beyer, R., Letort, V., and Heuret, P. (2018). The pipe model theory half a century on: a review. Ann. Bot. 121, 773–795. doi: 10.1093/aob/mcx194
MAFF, Japan. (2017). Annual Report of Forest and Forestry in Japan—Fiscal Year 2017. Forestry agency, Ministry of Agriculture, Forestry and Fisheries, Japan. Available online at: https://www.maff.go.jp/e/data/publish/attach/pdf/index-95.pdf (accessed May 8, 2020).
Milne, R. (1991). Dynamics of swaying of Picea sitchensis. Tree Physiol. 9, 383–399. doi: 10.1093/treephys/9.3.383
Minato, K., Ujiie, M., and Hishihuma, Y. (1989). Growth and wood quality of Sugi and Hinoki trees in the plantations of the Wakayama experiment forest. Res. Bull. Coll. Exp. For. Hokkaido Univ. 46, 223–247.
Mitchell, S. J. (2013). Wind as a natural disturbance agent in forests: a synthesis. Forestry 86, 147–157. doi: 10.1093/forestry/cps058
Moore, J., and Quine, C. P. (2000). A comparison of the relative risk of wind damage to planted forests in Border Forest Park, Great Britain, and the Central North Island, New Zealand. For. Ecol. Manag. 135, 345–353. doi: 10.1016/S0378-1127(00)00292-9
Moore, J. R., and Maguire, D. A. (2004). Natural sway frequencies and damping ratios of trees: concepts, review and synthesis of previous studies. Trees 18, 195–203. doi: 10.1007/s00468-003-0295-6
Moore, J. R., and Maguire, D. A. (2005). Natural sway frequencies and damping ratios of trees: influence of crown structure. Trees 19, 363–373. doi: 10.1007/s00468-004-0387-y
Moore, J. R., and Maguire, D. A. (2008). Simulating the dynamic behavior of Douglas-fir trees under applied loads by the finite element method. Tree Physiol. 28, 75–83. doi: 10.1093/treephys/28.1.75
Morgan, J., and Cannell, M. G. (1994). Shape of tree stems—a re-examination of the uniform stress hypothesis. Tree Physiol. 14, 49–62. doi: 10.1093/treephys/14.1.49
Nakao, H., Kim, S., Mataki, Y., and Fujimoto, N. (1993). Factorial analysis of forest damage by T9117 and T9119. Bull. Kyusyu Univ. For. 68, 11–48.
Nakatani, H., Kato, A., Hasegawa, M., Aiura, H., and Iijima, Y. (1988). Structural mechanics study on the damage of tree stems caused by accumulating in the crown III. J. Toyama For. For. Prod. Res. Center 1, 25–33.
Negishi, K., Suzuki, M., Sakura, T., Tange, K., Suzuki, S., and Shiba, Y. (1988). Changes in aboveground biomass with age in young Cryptomeria japonica stands. Bull. Tokyo Univ. For. 78, 31–57.
Niklas, K. J., and Spatz, H.-C. (2004). Growth and hydraulic (not mechanical) constraints govern the scaling of tree height and mass. PNAS 101, 15661–15663. doi: 10.1073/pnas.0405857101
Obataya, E., Norimoto, M., and Gril, J. (1998). The effects of adsorbed water on dynamic mechanical properties of wood. Polymer 39, 3059–3064. doi: 10.1016/S0032-3861(97)10040-4
Oliver, H. R., and Mayhead, G. J. (1974). Wind measurements in a pine forest during a destructive gale. Forestry 47, 185–193. doi: 10.1093/forestry/47.2.185
Ono, T., and Norimoto, M. (1983). Study on Young's modulus and internal friction of wood in relation to the evaluation of wood for musical instruments. Jpn. J. Appl. Phys. 22, 611–614. doi: 10.1143/JJAP.22.611
Peltola, H., Kellomaki, S., Vaisanen, H., and Ikonen, V. P. (1999). A mechanistic model for assessing the risk of wind and snow damage to single trees and stands of Scots pine, Norway spruce, and birch. Can. J. For. Res. 29, 647–661. doi: 10.1139/x99-029
Raupach, M. R., Finnigan, J. J., and Brunet, Y. (1996). Coherent eddies and turbulence in vegetation canopies: the mixing layer analogy. Bound. Layer Meteorol. 78, 351–382. doi: 10.1007/BF00120941
Rudnicki, M., Murphy, K., and Campiformio, A. (2012). “Branch motion of mature decurrent crowns: experimental and theoretical analysis,” in 7th Plant Biomechanics International Conference, 20–24 August (Clermont-Ferrand, France).
Sato, H., and Abe, T. (2006). Factorial analysis of forest damage by T0418. Kosyunaikiho 143, 7–11. doi: 10.1007/s10310-006-0198-7
Scannell, B. (1984). Quantification of the interactive motions of the atmospheric surface layer and a conifer canopy (Ph.D. thesis), Cranfield Institute of Technology, Bedford, United Kingdom.
Sellier, D., Brunet, Y., and Fourcaud, T. (2008). A numerical model of tree aerodynamic response to a turbulent airflow. Forestry 81, 279–297. doi: 10.1093/forestry/cpn024
Sellier, D., and Fourcaud, T. (2005). A mechanical analysis of the relationship between free oscillations of Pinus pinaster Ait. Saplings and their aerial architecture. J. Exp. Bot. 56, 1563–1573. doi: 10.1093/jxb/eri151
Sellier, D., and Fourcaud, T. (2009). Crown structure and wood properties: influence on tree sway and response to high winds. Am. J. Bot. 96, 885–896. doi: 10.3732/ajb.0800226
Sellier, D., Fourcaud, T., and Lac, P. (2006). A finite element model for investigating effects of aerial architecture on tree oscillations. Tree Physiol. 26, 799–806. doi: 10.1093/treephys/26.6.799
Spatz, H.-C., Brüchert, F., and Pfisterer, J. (2007). Multiple resonance damping or how do trees escape dangerously large oscillations? Am. J. Bot. 94, 1603–1611. doi: 10.3732/ajb.94.10.1603
Stadelmann, G., Bugmann, H., Wermelinger, B., and Bigler, C. (2014). Spatial interactions between storm damage and subsequent infestations by the European spruce bark beetle. For. Ecol. Manag. 318, 167–174. doi: 10.1016/j.foreco.2014.01.022
Suzuki, N., and Ito, H. (1994). Bending test of large size log and drum shaped log. Bull. Miyagi Prefect. For. Exp. Stn. 9, 28–58. doi: 10.1021/acssensors.6b00145
Suzuki, S. (2020). “To know the wind damage risk from the oscillation of trees,” in Exploring the risk of Forest Damage Caused By Meteorological reason (Newberry, MI: Forestry Insurance Center), 2–5.
Tadaki, Y. (1966). Some discussions on the leaf biomass of forest stands and trees. Bull. Govt. For. Exp. Sta. Tokyo 84, 135–161.
Tadaki, Y., Ogata, N., and Nagatomo, Y. (1965). The dry matter productivity in several stands of Cryptomeria japonica in Kyusyu. Bull. For. For. Prod. Res. Inst. 173, 45–66.
Takashima, A., Kume, A., Yoshida, S., Murakami, T., Kajisa, T., and Mizoue, N. (2009). Discontinuous DBH–height relationship of Cryptomeria japonica on Yakushima Island: effect of frequent typhoons on the maximum height. Ecol. Res. 24, 1003–1011. doi: 10.1007/s11284-008-0574-1
Telewski, F. W. (2012). Is windswept tree growth negative thigmotropism? Plant Sci. 184, 20–28. doi: 10.1016/j.plantsci.2011.12.001
Théckès, B., Boutillon, X., and de Langre, E. (2015). On the efficiency and robustness of damping by branching. J. Sound Vib. 357, 35–50. doi: 10.1016/j.jsv.2015.07.018
Thompson, I., Mackey, B., McNulty, S., and Mosseler, A. (2009). Forest resilience, biodiversity, and climate change. Secr. Conv. Biol. Divers. Montr. Tech. Ser. 43, 1–67.
Ulbrich, U., Pinto, J. G., Kupfer, H., Leckebusch, G. C., Spangehl, T., and Reyers, M. (2008). Changing Northern Hemisphere storm tracks in an ensemble of IPCC climate change simulations. J. Clim. 21, 1669–1679. doi: 10.1175/2007JCLI1992.1
Warton, D. I., Duursma, R. A., Falster, D. S., and Taskinen, S. (2012). smatr 3–an R package for estimation and inference about allometric lines. Methods Ecol. Evol. 3, 257–259. doi: 10.1111/j.2041-210X.2011.00153.x
Watanabe, H., and Moteki, Y. (2007). Process of growth and biomass for 92 years old Sugi forest. Bulletin Gifu Prefectural Forest Exp. Station 36, 1–7.
White, A. C., Rogers, A., Rees, M., and Osborne, C. P. (2016). How can we make plants grow faster? A source–sink perspective on growth rate. J. Exp. Bot. 67, 31–45. doi: 10.1093/jxb/erv447
Wood, C. (1995). “Understanding wind forces on trees,” in Wind and trees (Cambridge University Press), 133–164. doi: 10.1017/CBO9780511600425.008
Yamanoi, K., Ohtani, Y., Kitamura, K., Nakai, Y., and Suzuki, S. (2005). “Strong wind analysis of Typhoon No.18 in 2004 that caused large-scale wind damage to the forest,” in Proceedings of the 116th Annual Meeting of the Japan Forest Society (Sapporo), PA004.
Yamashita, K., Hirakawa, Y., Nakatani, H., and Ikeda, M. (2009). Longitudinal shrinkage variations within trees of Sugi (Cryptomeria japonica) cultivars. J. Wood Sci. 55, 1–7. doi: 10.1007/s10086-008-0987-z
Keywords: wind risk, sway frequency, damping, tree growth, extreme events, biomechanics
Citation: Sellier D and Suzuki S (2020) Age Dynamics of Wind Risk and Tree Sway Characteristics in a Softwood Plantation. Front. For. Glob. Change 3:89. doi: 10.3389/ffgc.2020.00089
Received: 16 May 2020; Accepted: 02 July 2020;
Published: 11 August 2020.
Edited by:
Lars Lundqvist, Swedish University of Agricultural Sciences, SwedenReviewed by:
Thomas J. Dean, Louisiana State University, United StatesChristian Temperli, Swiss Federal Institute for Forest, Snow and Landscape Research (WSL), Switzerland
Copyright © 2020 Sellier and Suzuki. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Damien Sellier, ZGFtaWVuLnNlbGxpZXJAc2Npb25yZXNlYXJjaC5jb20=
 Damien Sellier
Damien Sellier Satoru Suzuki
Satoru Suzuki