Benefit-cost analysis of forest carbon for landowners: An illustration based on a southern pine plantation

Mei, Bin; Clutter, Michael L.

doi:10.3389/ffgc.2022.931504

ORIGINAL RESEARCH article

Front. For. Glob. Change, 10 August 2022

Sec. Forest Management

Volume 5 - 2022 | https://doi.org/10.3389/ffgc.2022.931504

This article is part of the Research Topic Forest Carbon Credits as a Nature-Based Solution to Climate Change? View all 10 articles

Benefit-cost analysis of forest carbon for landowners: An illustration based on a southern pine plantation

$\r\nBin Mei*$ Bin Mei^1*

Michael L. Clutter²

¹Warnell School of Forestry and Natural Resources, University of Georgia, Athens, GA, United States
²F&W Forestry, Albany, NY, United States

Using a hypothetic southern pine plantation in the state of Georgia of the United States, a benefit-cost analysis of forest carbon is conducted for landowners in the voluntary carbon market. With carbon values being defined by the marginal forest growth, it is found that the inclusion of carbon into the objective function usually leads to longer rotations and higher total profits. In our baseline analysis, the rotation age increases by four years when both timber and carbon are considered. Thus, landowners can benefit from voluntary carbon trading and additional carbon can be fixed in the forests. Landowners’ decision on forest carbon is most sensitive to the discount rate and timber and carbon prices. When the discount rate is higher, future cash flows become less valuable and the optimal rotation shortens. When timber prices exceed carbon price by a large margin, timber value dominates carbon value and the optimal carbon rotation approaches the Faustmann rotation. Therefore, with a higher discount rate and higher timber prices, voluntary carbon trading will result in less carbon additionality. Finally, when the economic uncertainty is incorporated into the decision making, the results tend to be sustained albeit carbon additionality is slightly reduced.

Introduction

Forests not only provide fiber and fuel for humans but also fix the majority of the total terrestrial carbon. In fact, covering 65% of the total land surface, forests contain 90% of the total vegetation carbon, hold 80% of the total soil carbon, and account for 67% of the total CO2 assimilated from the atmosphere by all terrestrial ecosystems (Landsberg and Gower, 1997; Hou et al., 2020). Since the preindustrial era, nevertheless, the concentration of CO2 in the atmosphere has increased by more than 30% (Pan et al., 2011; Wenzel et al., 2016). The increased concentrations of CO2 and other greenhouse gas have been widely recognized as the major cause of the global warming. As a result, a considerable public attention has been paid to forests as a carbon sink and more discussion has been initiated on how to use forest carbon effectively to combat climate change in recent years (van der Gaast et al., 2018). It has been expected that planting trees to remove atmospheric CO2 would be more cost efficient than developing and implementing technologies or carbon taxes to reduce the emissions of existing industries (Dang Phan et al., 2014; Gren and Aklilu, 2016; Lin and Ge, 2019; Li et al., 2022). Unfortunately, there is a lack of research on these topics, although it is the biome that global models associate with the largest potentials of carbon removal (Fuss et al., 2018).

The United States has abundant forest resources with forestland occupying about 766 million acres or 34% of the total land area in the country. Out of the total forestland, about 58% is privately owned and this proportion is even higher at about 90% in the US South (Oswalt et al., 2019). The southern US supplies a significant portion of wood products to the country as well as provides a wide variety of ecosystem services such as water quality and quantity, soil stabilization, wildlife habitat protection and biodiversity, to name a few. For example, in Georgia the total economic impact of the forest industry in 2018 was estimated to be $36.3 billion (Enterprise Innovation Institute, 2018), while the non-timber and non-recreation ecosystem service value of forestland was estimated to be $37.6 billion (Moore et al., 2011). Despite an active and competitive timber market in the southern US, there is only a nascent carbon market, which impedes the effective provision of forest carbon from vast private landowners as a climate mitigation tool. The goal of this study is to examine the benefit and cost of forest carbon for landowners in the voluntary carbon market. The analysis is based on a southern pine plantation for two reasons. First, southern pine is a major species in the US South (Oswalt et al., 2019). Second, pine forests are often intensively managed as plantations, which not only produce traditional industrial wood products but also contain a significant portion of forest carbon in the US (Johnsen et al., 2001).

The forest carbon literature has been rapidly snowballing in the last three decades. Gower (2003) reviewed the key components of the forest carbon cycle and inspected how global changes might influence the carbon dynamics between forests and the atmosphere. Helin et al. (2013) concluded that biomass carbon stored in the products and the timing of sinks and emissions should be taken into consideration in the life cycle analysis in order to accurately measure greenhouse gas emissions and the related climate impacts. They also recommended the use of dynamic forest models rather than carbon stock values taken from the literature. Forest modeling having gone beyond the domain of scientific discovery into the policy arena, Prisley and Mortimer (2004) synthesized the literature on the application of models for forest carbon accounting, discussed validation, verification and evaluation as applied to modeling, and concluded that forest carbon models should abide by scientifically relevant and judicially proven guidelines. Gren and Aklilu (2016) reviewed the economics literature on efficient policy design for forest carbon and associated the difficulties in policy deign with the site-specific sequestration conditions, uncertainty in sequestration, additionality, and permanence. While an exclusive synthetization of the forest carbon literature is not the emphasis here, these review papers provide us a solid background of the endeavors in forest carbon analyses.

Regarding the economics of forest carbon, many studies found that forest carbon could reduce net emission with a relatively low-cost (Vass and Elofsson, 2016; Cho et al., 2018). Newell and Stavins (2000) examined the sensitivity of carbon sequestration costs to the nature of management and deforestation regimes, silvicultural species, relative prices, and discount rates. They found higher costs of carbon sequestration for (1) periodically harvested rather than permanently established forests, (2) higher discount rates, (3) higher agricultural prices, and (4) increased forestation instead of retarded deforestation. Richards and Stokes (2004) pointed out that carbon sequestration cost studies were not directly comparable because of the inconsistent use of terms, geographic scope, assumptions, program definitions, and methods. They further claimed that market interactions need more attention when analyzing carbon sequestration programs. Using meta-analysis, van Kooten and Sohngen (2007) found a wide range of cost from $2 to $80 per ton of CO2 equivalent for creating carbon offsets using forestry in North America. Given the great uncertainty in model scenarios and the difficulty of contracting, van Kooten and Johnston (2016) claimed that caution would be needed to identify carbon offsets from forestry activities should they be traded in the emission markets.

A summarization of the forest carbon literature reveals two primary features. One is that most analyses were conducted on forest carbon markets outside the US. The other is that stand-level analyses centered around the optimal forest rotation. Thus, our study intends to examine the economic feasibility of forest carbon supply by landowners the at the stand level in the US South, given its rapid developing carbon market and its primary private timberland ownership. Because an intensively managed forest is a more effective approach in mitigating climate change (van Kooten and Sohngen, 2007; van Kooten and Johnston, 2016), and more of the assimilated carbon is allocated to aboveground pools in managed than in unmanaged forests (Noormets et al., 2015), our study focuses on benefit and cost of forest carbon for landowners using a carbon accounting model based on a hypothetical southern pine plantation. Following the recommendations of Prisley and Mortimer (2004), our model aims to be clearly defined, clearly documented, sensitized on key parameters, available for testing or evaluation, and updatable with new knowledge and data.

This study contributes to the existing literature by evaluating the potential supply of forest carbon from private landowners at the stand level in the voluntary carbon market. Such information can shed light on the aggregate supply of both timber and carbon at the regional or higher level. Our analysis explicitly examines incremental cash flows from forest carbon and contrast those with the timber production only scenario to identify changes in the optimal forest management and the resulting additional carbon storage. As the timber and carbon markets are both volatile, incorporating price volatility into the analysis under the Monte Carlo simulation or the real options framework can help us better understand landowners’ decision-making in an uncertain environment. The next section explains the materials and methods; section 3 summarizes the results; and the last section concludes the analysis.

Materials and methods

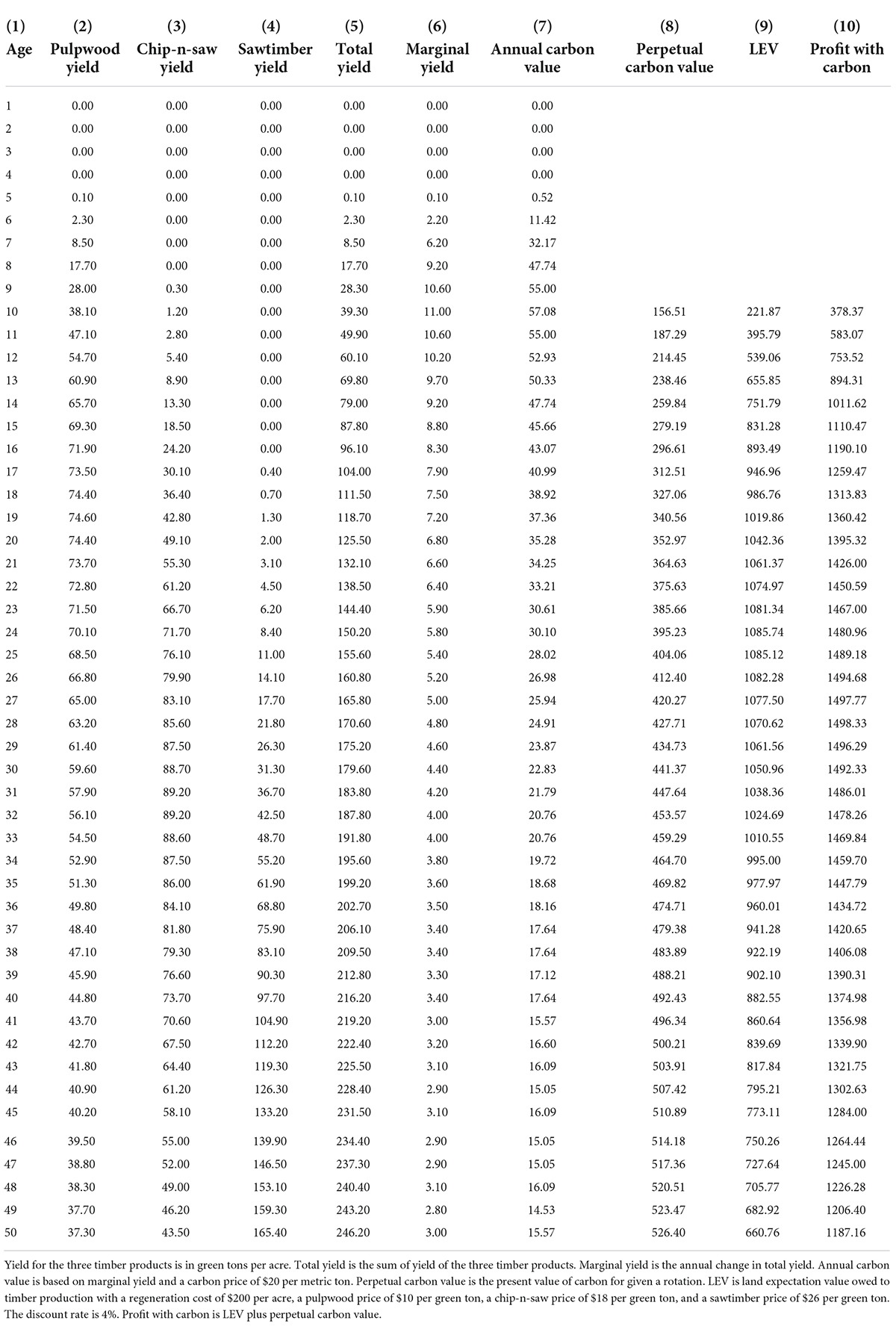
An aboveground forest carbon regime is illustrated based on a hypothetical southern pine plantation in the state of Georgia. Timber yield data are generated from the current version of the Plantation Management Research Cooperative forest growth and yield simulator with a site index of 65 (base age 25) and an initial planting density of 680 trees per acre (1 acre = 0.4047 hectares) (PMRC, 2022). Forest carbon storage at the stand level is positively related to the site quality, all else equal (Sampo et al., 2014; Gonzalez-Benecke et al., 2015; West et al., 2019). As the average site index of timberland in the US South is around 60-80 (Zhao et al., 2016a; Gopalakrishnan et al., 2019; PMRC, 2022), the hypothetical southern pine plantation is representative of the region. Yield is categorized into three product classes, by the diameter at breast height, as pulpwood 6 inches (1 inch = 2.54 cm) and up, chip-n-saw 8 to 11 inches, and sawtimber 12 inches and up (TMS, 2022).¹ Total yield is the sum of yield by product and marginal yield is the annual change in total yield.

Equation 1 is used to convert timber yield in green tons to total carbon stored in the aboveground biomass in metric tons,

A C = T Y \times B E F \times (1 - M C) \times C T (1)

where AC is aboveground carbon in metric tons, TY is total yield of merchantable timber in green tons, BEF is biomass expansion factor (the ratio of the total aboveground tree biomass to the biomass of merchantable timber), MC is moisture content, and CT is carbon content in dry wood. Base on the literature (Smith et al., 2006; Zhao et al., 2016b; PMRC, 2022), the followings parameter values are used: BEF = 1.20, MC = 0.54, and CT = 0.47.

Annual carbon value is marginal carbon stored multiplied by carbon price. A carbon price of $20 per metric ton, or $5.45 per ton of CO2 equivalent is used based on the average transacted price in the voluntary carbon market (Donofrio et al., 2021). Perpetual carbon value is the present value of carbon credits for a given rotation with a carbon release factor (δ(T) = 0.70205−0.001266T + 0.0000168T²) at harvest time T (Creedy and Wurzbacher, 2001). Based on the past research (e.g., Cascio and Clutter, 2008; Baral et al., 2020) and TimberMart-South data (TMS, 2022), our baseline land expectation value (LEV) for timber production only is calculated with a regeneration cost of $200 per acre, a pulpwood price of $10 per green ton, a chip-n-saw price of $18 per green ton, a sawtimber price of $26 per green ton, and a discount rate of 4% as in Equation 2,

L E V (T) = \frac{P_{T} Y_{T} - E {(1 + r)}^{T}}{{(1 + r)}^{T} - 1} (2)

where rotation length T is the decision variable, P_T and Y_T are the respective price and yield vectors of the three timber products, E is the regeneration cost, and r is the discount rate. Equation 2 is also known as the Faustmann model (Faustmann, 1995). The profit function π(T) for both timber and carbon provision is the net present value all future cash flows associated with timber production and carbon sequestration. The calculation is shown in Equation 3,

π (T) = L E V (T) + \frac{\sum_{t = 1}^{T} (P_{c} \cdot Δ W_{t}) {(1 + r)}^{(T - t)} - P_{c} \cdot δ (T) \cdot W_{T}}{{(1 + r)}^{T} - 1} (3)

where P_c is carbon price in dollars per metric ton, ΔW_t is the marginal weight of carbon captured in metric tons, δ(T) is the carbon release factor at harvest, and W_T is total weight of carbon at harvest. A brief summarization of all parameters and variables is presented in Table 1. Note that all costs, prices and the discount rate are in real terms as of year 2022.

TABLE 1

Table 1. A brief summarization of all parameters and variables for the forest carbon analysis.

Based on the LEV framework, two scenarios of forest carbon are analyzed. In the first scenario, a landowner contemplates whether to offer forest carbon credits starting from an afforestation. In the second scenario, a landowner has some mature trees standing on the land and decides whether to delay timber harvest for carbon credits. In the first scenario, sensitivity analysis is conducted on the key parameters, and a Monte Carlo simulation is used for the risk assessment. A Monte Carlo simulation is a computational algorithm that uses repeated random sampling to obtain numerical results. The idea is to use randomness to solve problems that might be deterministic in principle. That is, financial uncertainty is taken into account in the simulation. For timber and carbon prices, a lognormal distribution is used to guarantee that prices are positive. For the discount rate, a triangular distribution is used, which is a continuous probability distribution with a lower limit, an upper limit and a mode. This setting enables us to examine the impact of most likely discount rates on the valuation.

In addition, the option to wait for a year to make the decision about the enrollment of a 30-year carbon contract is evaluated under the real options framework. In general, an investment decision in an uncertain world is similar to a financial call option in that it incurs the initial investment cost to exercise the option and in return the investor holds a risky asset whose value is stochastic over time. In our case, the cost for entering into a carbon contract arises from the deviation from the optimal rotation; and the underlying asset value is the net present value of cash flows associated with carbon sequestration during the contract period. Other key inputs for the option pricing are the time to maturity, the volatility of the underlying asset, and the risk-free rate. Then, the call option price C can be determined by the Black-Scholes model expressed in Equation 4 (Black and Scholes, 1973),

C = N (d_{1}) S_{t} - N (d_{2}) K e^{- r t} (4)

where N(⋅) is the cumulative distribution function of the standard normal distribution, $d_{1} = \frac{\ln (S_{t} / K) + (r + .5 σ^{2}) t}{σ \sqrt{t}}$ , S_t is the spot price of an asset, K is the strike price, r is the risk-free rate, t is time to maturity, σ is the volatility of the asset, and $d_{2} = d_{1} - σ \sqrt{t}$ . Observing the uncertainty of forest carbon, risk averse landowners will value the option to wait to make the enrollment decision. The investment timing option itself can be valued as a financial call option.

In the second scenario, incremental cash flows are analyzed to help the landowner with a mature stand decide whether to enter into a short-term carbon contract. The cost arises from a reduced LEV due to a delayed harvest, whereas the benefit comes from payments for carbon credits. Whenever the net present value of the incremental cash flows is positive, the carbon contract will add value to the landowner.

Results

The growth and yield data for the hypothetical southern pine plantation together with the valuation results are reported in Table 2. Columns 2-4 are timber yield in green ton in three products (i.e., pulpwood, chip-and-saw, and sawtimber) based on the PMRC model. Column 5 is the total timber yield, i.e., the summation of the previous three columns. Column 6 is the marginal timber yield, i.e., the annual incremental gain in the total timber yield. Column 7 is the dollar value of annual carbon sequestered, calculated as the weight of marginal carbon sequestered in metric ton times carbon price in dollar per metric ton. Column 8 is the dollar value of carbon sequestered on a perpetual basis for a given rotation. According to Column 9, the optimal rotation for timber production only is 24 years, resulting in a maximum LEV of $1,085.74 per acre.² When carbon is also considered, the optimal rotation is four years longer, resulting in a maximum profit of $1,498.33 per acre at age 28. The result is consistent with previous research in that the inclusion of carbon only makes the rotation a bit longer than the Faustmann rotation (e.g., van Kooten and Binkley, 1995; Hoel et al., 2014; Ning and Sun, 2019; Dong et al., 2020). As such, it could be a win-win situation in that the landowner realizes a higher profit from the timberland by lengthen the rotation by four years, and the society has four-year additional carbon fixed in the trees.

TABLE 2

Table 2. Growth and yield of a southern pine plantation and valuation of forest carbon.

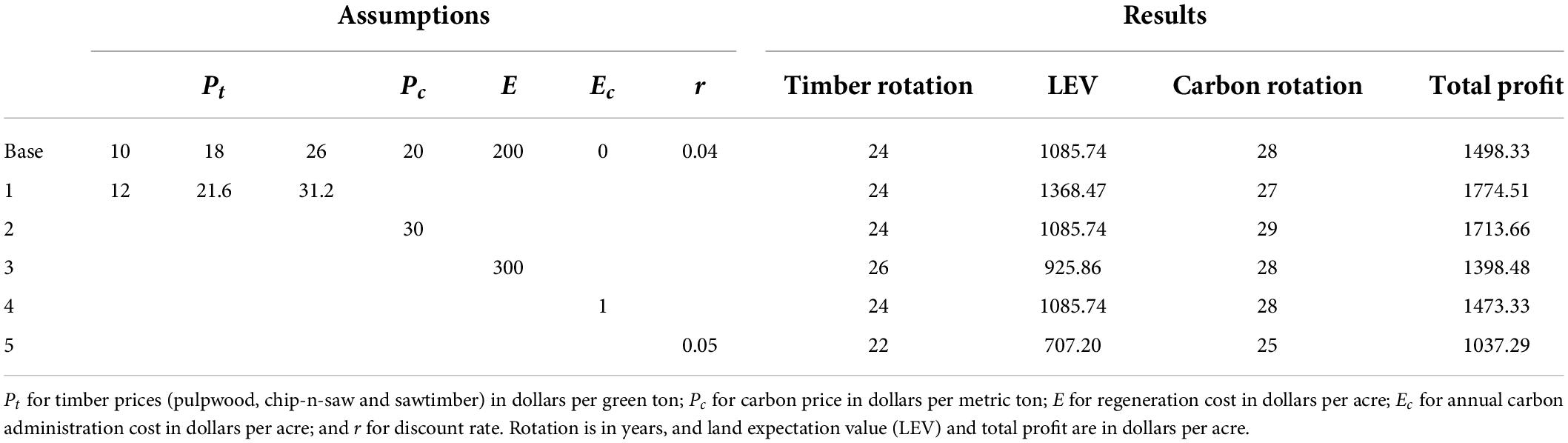
Next, the results are sensitized on the key parameters or variables (Table 3). First, all three timber prices are increased by 20%, corresponding to the price levels prior to the 2008 financial crisis. With higher timber prices, LEV increases to $1,368.47 per acre at age 24, and the maximum total profit of $1,774.51 per acre occurs at age 27. Thus, one less year of carbon is sequestered compared with the base case. Second, carbon price is increased to $30 per metric ton. Then, the total profit increases to $1,713.66 per acre at age 28. Therefore, one additional year of carbon sequestration can be achieved with a higher carbon price.

TABLE 3

Table 3. Sensitivity analysis of key variables on the forest carbon analysis.

Third, when the regeneration cost is increased to $300 per acre, LEV is reduced to $925.86 per acre with a 26-year rotation. The total profit is maximized at $1,349.09 with a 29-year rotation. The net result is 1-year carbon additionality. Fourth, a carbon administration cost of $1 per year is considered in the model.³ This has a similar impact on the total profit as a decrease in carbon price. The total profit falls to $1,473.33 per acre at age 28. Thus, carbon additionality remain the same as the base case. Lastly, when the discount rate is increased to 5%, the maximized LEV is $707.20 per acre at age 22 and the maximum total profit is $1,037.29 per acre at age 25. So a higher discount rate reduces the rotation length and the profit compared with the base case.

Given that the decision on forest carbon is most sensitive to prices and the discount rate, a Monte Carlo simulation is conducted on the base case analysis. Prices are specified to be lognormal with mean values the same as those used in the static analysis. Regarding the standard deviation, $2, $3, and $6 per green ton are used for pulpwood, chip-n-saw, and sawtimber prices (TMS, 2022), and $6 per metric ton is used for carbon price (Donofrio et al., 2021). In addition, the discount rate is assumed to follow a triangular distribution with a mean 4%, a minimum of 3% and a maximum of 5%.

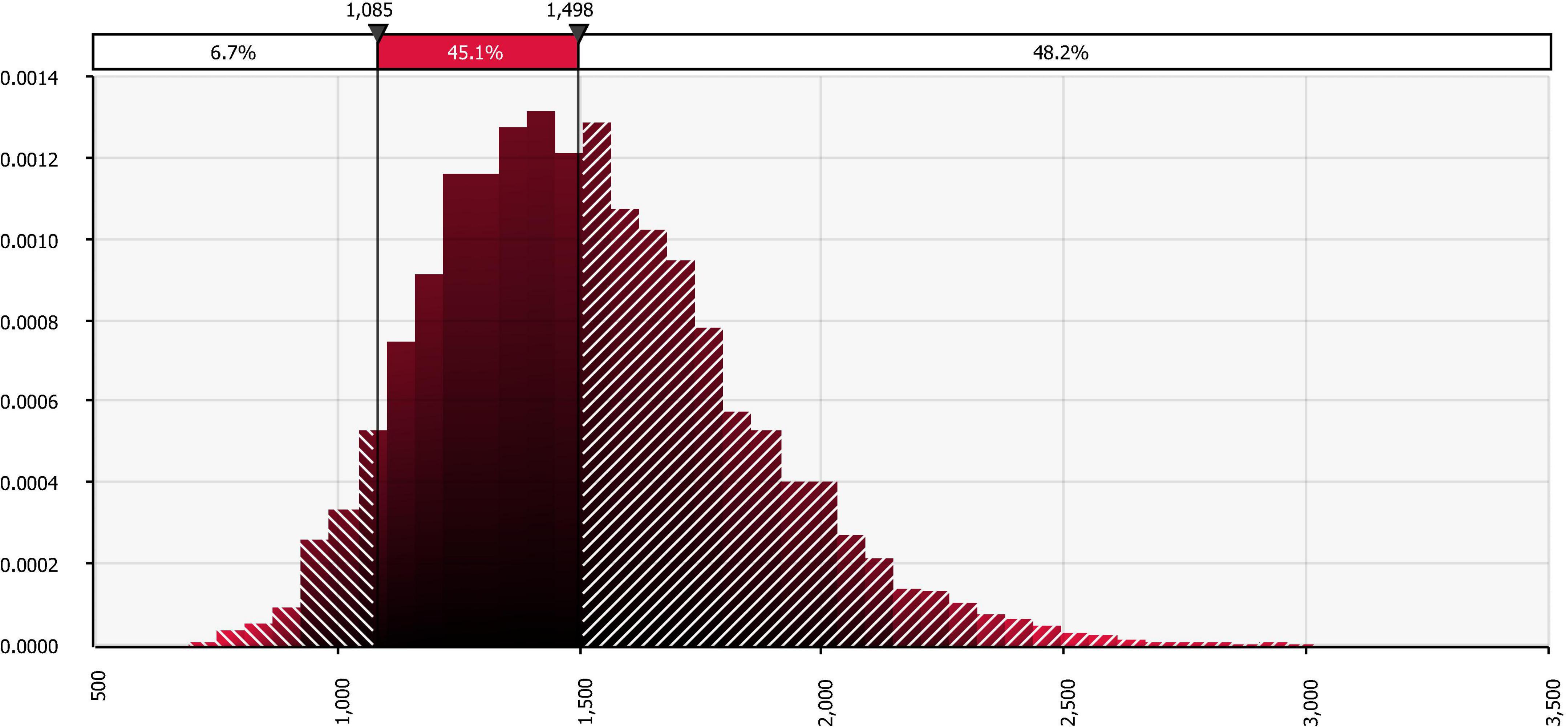
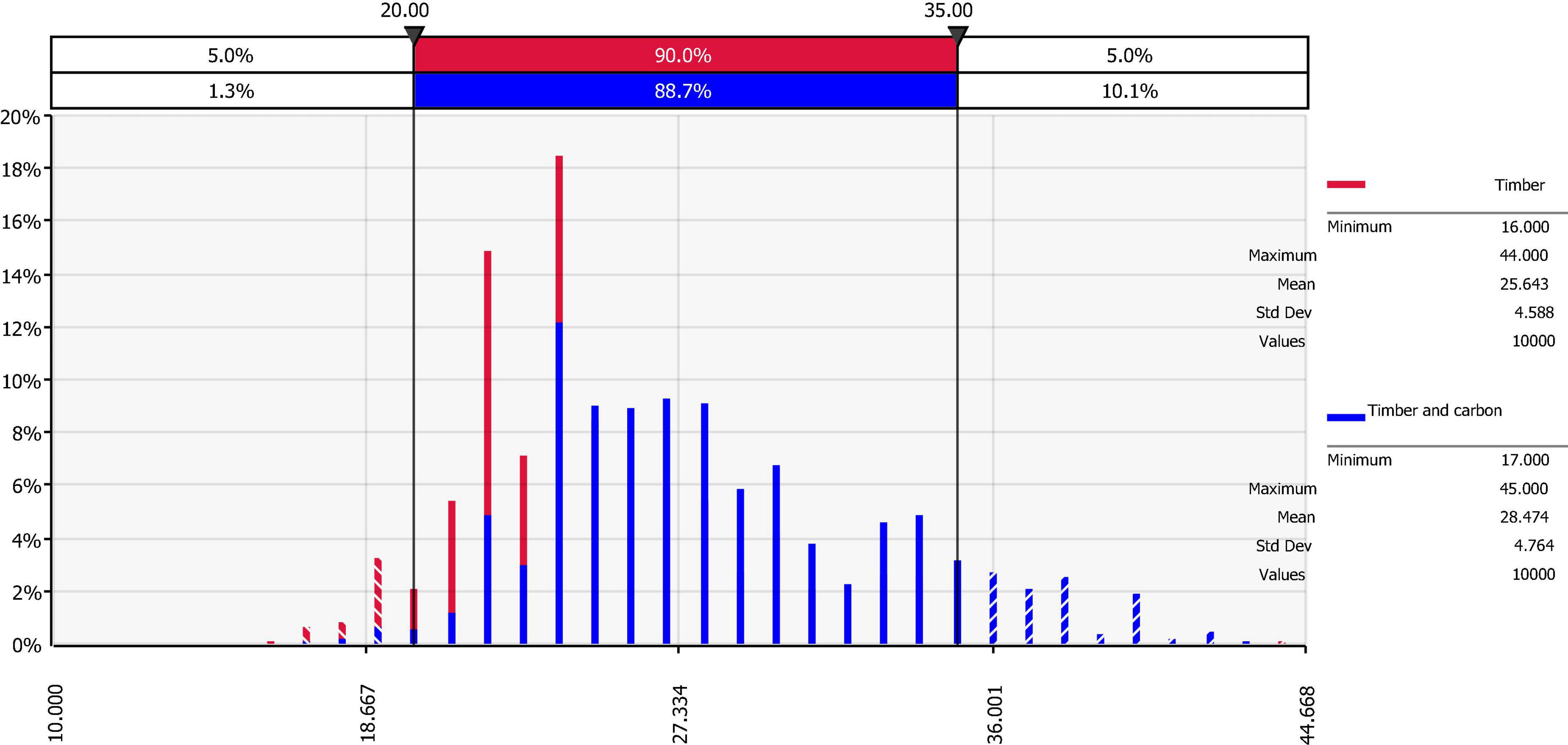
The simulated total profit for timber and carbon with a 28-year rotation is presented in Figure 1. With a 10,000 iterations, the respective mean and standard deviation are $1,524.88 and $323.63 per acre. Compared with the base case, there is a 48.2% chance that the total profit exceeds that from the static analysis on the upside; and there is a 6.7% chance that the total profit falls below the maximized LEV from the static analysis on the downside. As shown in the tornado chart (Figure 2), discount rate is the most sensitive factor on total profit, followed by chip-n-saw and carbon prices. The sensitivity of chip-n-saw price can be explained by the fact that, with a 28-year rotation, chip-n-saw is the major timber product that accounts for a significant portion of the total output.

FIGURE 1

Figure 1. Simulated total profit for timber and carbon with a 28-year rotation.

FIGURE 2

Figure 2. Sensitivity of the simulated total profit on different factors.

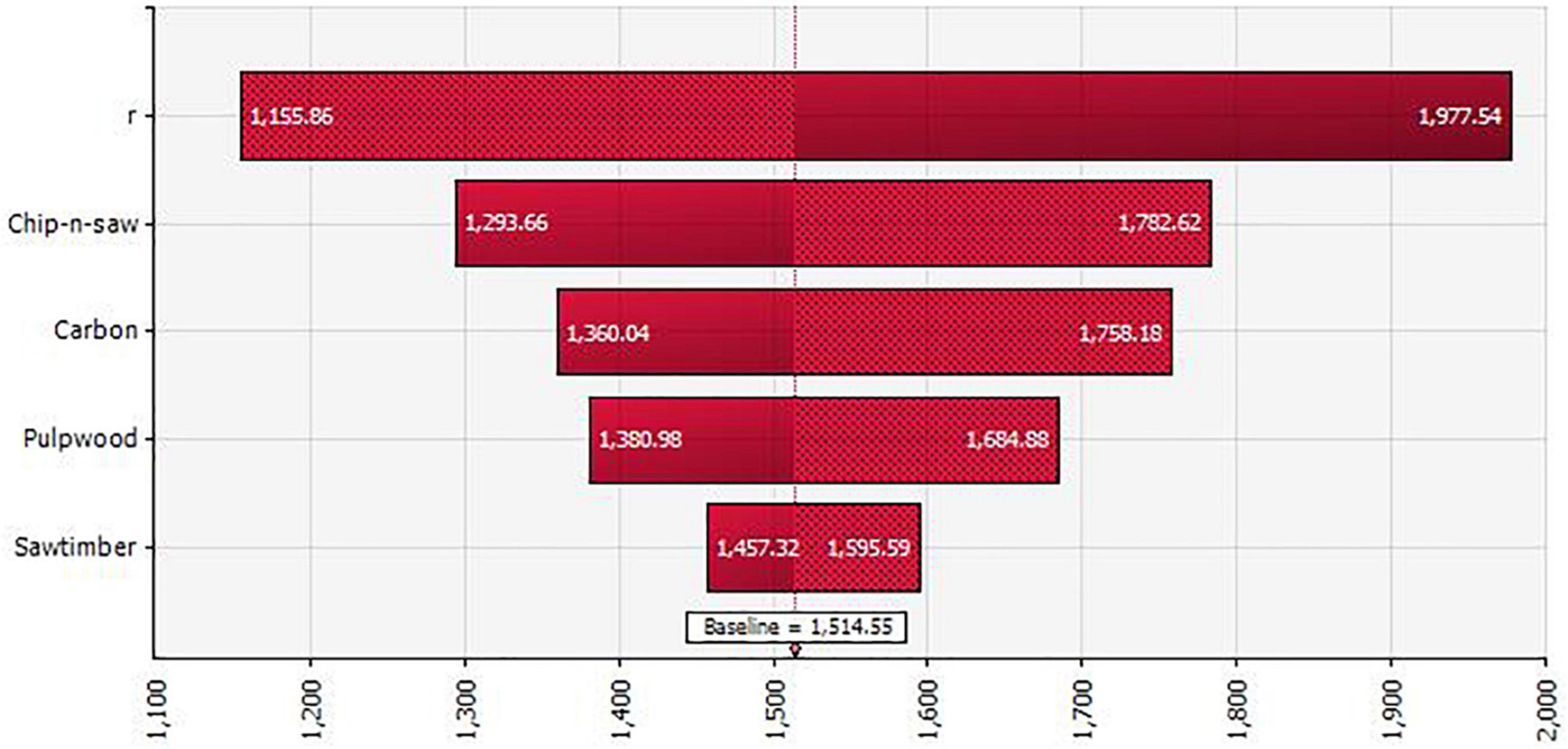
Another useful information from the simulation is the impact of the economic uncertainty on the optimal rotation age. The mean rotation age for timber production only is 25.64 with a standard deviation of 4.59; that for both timber production and carbon sequestration is higher at 28.47 with a standard deviation of 4.76 (Figure 3). Compared with the static analysis, about one less year of carbon additionality can be achieved from the voluntary carbon trading when the economic uncertainty is considered. Figure 4 shows the sensitivity of the optimal rotation on different factors under the economic uncertainty. Compared with timber prices, carbon price has a much lower impact on the optimal rotation due to its relatively small value. In short, landowners tend to be risk averse and behave more conservatively on forest carbon when facing financial risks.

FIGURE 3

Figure 3. Impact of the economic uncertainty on the optimal rotation.

FIGURE 4

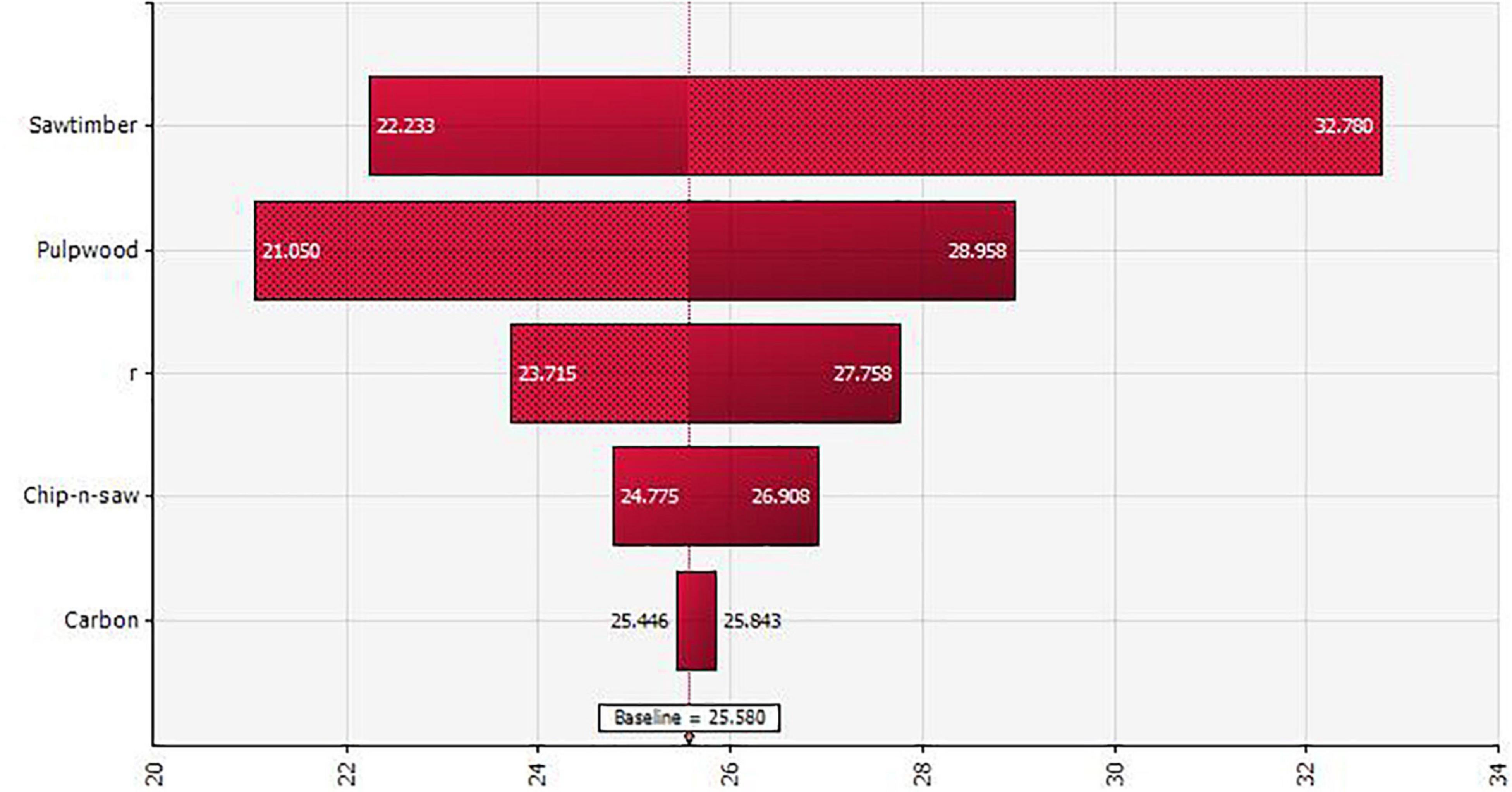
Figure 4. Sensitivity of the optimal rotation for both timber production and carbon sequestration on different factors under the economic uncertainty.

Concerning additionality, next evaluated is the benefit and cost a 5-year contract with a landowner who has a mature forest at age 24 and has been paid for forest carbon up to that age. The evaluation is based on the same values for the key variables and parameters in the baseline analysis. For the landowner to enter into a 5-year (age 25-29) contract for forest carbon, the cost is the change in total profit due to a delayed harvest, i.e., $1,085.74 – $1,061.56 = $24.18 (Column 9 of Table 1). Hence, the landowner should be compensated by at least a lump sum of $24.18 per acre at the initiation of the 5-year contract (or $5.43 per acre per year over the next five years), or this carbon additionality cannot be realized at the current carbon price without any government intervention.

If the additionality is the ultimate goal, a 30-year carbon contract from an afforestation may still be appealing to a landowner. Without the carbon contract, the landowner expects the maximum LEV of $1,085.47 per acre with a 24-year rotation (Column 9 of Table 1); with the carbon contract, the landowner expects a total profit of $1,492.33 per acre with a 30-year rotation (Column 10 of Table 1). Thus, the net gain is $1,492.33 - $1,085.47 = $406.59 per acre. Alternatively, if the cash flows of timber are separated from carbon, the cost of the 30-year carbon contract results from the change in LEV due to a delayed harvest ($1,085.47 - $1,050.96 = $34.78), the gain comes from carbon credit ($441.37), and the net present value is $406.59. The longer the term of the contract, the larger the cost of a delayed harvest and the smaller the gain from carbon credit due to the law of diminishing marginal returns of forest growth and yield.⁴

From the option pricing perspective, the 30-year carbon contract is like a financial call option. The strike price is the change in LEV due to a delayed harvest that is converted to a cost every 30 years (K = $24.06).⁵ The underlying asset price (S_t = $305.29) is the net present value of carbon-related cash flows over 30 years (Column 8 of Table 1, with carbon release at harvest incorporated). Time to maturity is the period that landowners can afford to wait and is assumed to be one year (t = 1) when there is no merchantable timber on the ground. The risk-free rate is set to 2% (r = 2%) and the volatility is assumed to be 15% (σ = 15%). With these inputs, the value of the investment timing option is calculated to be $281.71 per acre by the Black-Scholes model. As discussed before, for a longer-term carbon contract, both the strike price and the asset price increase, with the former rising at a more rapid rate. So the option value will decrease. However, this option value can offset some of the negative impact of the longer duration of a carbon contract on its static net present value. Therefore, landowners should still keep a reasonably longer-term carbon contract in mind when doing an afforestation.

Next, the decision making is examined for a landowner who has a mature forest and has not been paid for any forest carbon yet.⁶ The landowner has the option to enroll into a carbon contract in which he/she has to postpone harvest for five years, will be paid for existing carbon fixed in the forest, and will be paid for marginal carbon sequestration in the next five years. Because all previous costs are sunk, incremental cash flows are focused on. The cash flows associated with timber are a forgone harvest proceeds of $3,406.00 per acre at age 33 and an expected harvest proceeds of $4,059.00 per acre at age 38, with a net present value of -$69.80 per acre; those associated with carbon are a payment of $995.21 per acre for carbon fixed in the existing trees, a series of annual payments ($19.72, $18.68, $18.16, and $17.64 per acre, respectively) for marginal carbon sequestered between age 34 and 37, and a cash outflow of $719.60 for the net carbon release at age 38, with a net present value of $471.21. Thus, the landowner should benefit from enrolling in such a 5-year carbon contract with a total net present value of $401.41 per acre. Nevertheless, if carbon on existing trees are not paid for, the total net present value become negative, and the contract should be rejected by the landowner.

Lastly examined is the benefit and cost a 1-year carbon contract similar to what is being offered by Natural Capital Exchange (NCX, 2022). With the contract, the landowner agrees to delay harvest for a year in exchange for a payment for carbon. On an incremental basis, the cash flows associated with timber are forgone harvest proceeds of $3,406.00 per acre at age 33 and an expected harvest proceeds of $3,539.20 per acre at age 34, with a net present value of -$2.92 per acre. Thus, a payment larger than $2.92 per acre for a year would trigger a landowner’s enrollment in this carbon program.

Discussion

Given the importance of southern pine to the forestry industry in the US South, the benefit and cost of forest carbon to landowners in the voluntary carbon market is examined based on a hypothetical southern pine plantation. Carbon value being defined according to marginal growth of trees, its inclusion into the objective function usually leads to longer rotations and higher total profits. In our baseline analysis, the rotation age increases by four years when both timber and carbon are considered. Therefore, landowners benefit from extra cash flows from carbon credits and additional carbon is fixed in the forests for four years.

Landowners’ decision on forest carbon is most sensitive to the discount rate and timber and carbon prices. When the discount rate is higher, future cash flows become less valuable and the optimal rotation shortens. When timber prices exceed carbon price by a large margin, as is the current market condition, timber value dominates carbon value and the optimal rotation age does not deviate much from that defined by the Faustmann model. Therefore, with a higher discount rate and higher timber prices, voluntary carbon trading results in little additionality. When the economic uncertainty is incorporated into the decision making, results tend to be sustained albeit carbon additionality is slightly reduced.

The analysis of a 30-year carbon contract starting from the afforestation shows that landowners can benefit from such a long-term contract. If a landowner can wait for a year prior to making the enrollment decision, the benefit is even larger given the uncertainty of carbon price. That is, landowners should keep forest carbon in mind when making the afforestation decision. However, as the contractual period lengthens (e.g., to 100 years), the incremental gain from carbon is not enough to offset the cost from delayed harvest because of the law of diminishing marginal returns of forest yield. Therefore, subsidies are needed to incentivize landowners’ enrollment in longer-term carbon contracts.

For landowners who have mature forests but have not been paid for forest carbon yet, a 5-year carbon contract that pays for carbon already sequestered in the existing trees as well as marginal carbon sequestration over the next five years will benefit the landowners. However, if the 5-year carbon contract only pays for marginal carbon during the contractual period, such a contract provides additional carbon but at the cost of the landowners. In this case, government interventions are needed again to guide and regulate the provision of forest carbon. Given that delaying harvest has a lower opportunity cost on a less productive site, both the cost of conserving such a stand and the amount of carbon stored are lower. Therefore, when facing a flat payment for forest carbon (e.g., a fixed payment per acre of enrollment), landowners with lower site qualities are more willing to participate in the voluntary carbon market.

In closing, forest carbon being a crucial nature-based solution to the climate change, additionality does not always autonomously occur from voluntary carbon trading. Hence, government interventions are often needed in sustaining forest carbon. Results from this study can help landowners better understand the economics, the contractual design, and the trading mechanism of the voluntary forest carbon market. Future research can integrate silvicultural management into the forest carbon analysis, extend the current analysis to a landscape level by considering multiple tree species and geographic locations, or take into account possible land use changes.

Data availability statement

The original contributions presented in this study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

BM: conceptualization (equal); data curation (lead); methodology (equal); software (lead); writing—original draft (lead); writing—review and editing (equal). MC: conceptualization (equal); data curation (supporting); methodology (equal); software (supporting); writing—original draft (supporting); writing—review and editing (equal). Both authors contributed to the article and approved the submitted version.

Funding

This research was supported by the United States Department of Agriculture grant GEOZ-0199-MS.

Conflict of interest

MC was employed by F&W Forestry.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

^ Smaller-size timber is used to produce pulp and paper products, while larger-size timber is used to produce lumber and veneer products.
^ Annual property tax is ignored in the analysis, or it will reduce the LEV.
^ We suspect that the voluntary carbon market will be more standardized in the future and forest carbon should be third-party audited with a cost, just like that for forest certification.
^ Forests have a sigmoid growth curve. The law of diminishing marginal returns of forest growth and yield means that the marginal growth (current annual increment) declines when a forest passes the inflection point and approaches maturity.
^ K is solved by setting 34.78 = K/(1 – (1 + r)^–30), assuming K occurs at the beginning of a year every 30 years.
^ At age 33, the net present value of the single rotation is maximized. At this age, a landowner considers whether or not to enter into a carbon contract. Similar analysis can be conducted for ages around 33.

References

Baral, S., Li, Y., and Mei, B. (2020). Financial effects of the 2017 Tax Cuts and Jobs Act on nonindustrial private forest landowners: A comparative study for 10 southern States of the United States. J. For. 118, 584–597. doi: 10.1093/jofore/fvaa032