Improving the accuracy of forest aboveground biomass using Landsat 8 OLI images by quantile regression neural network for Pinus densata forests in southwestern China

1. Introduction

Forest biomass is a critical factor in the carbon recycling of forest ecosystems (Ploton et al., 2017; Qin et al., 2022). However, the field investigation of forest biomass is time-consuming and labor-intensive, and it is challenging to obtain biomass estimation in a large region (Feng et al., 2021). Using remote sensing data can help find information about forest AGB estimation quickly and efficiently (Banerjee et al., 2020; Sun et al., 2021; Wulder et al., 2022).

As the active remote sensing data, Radar and Light Detection and Ranging (LiDAR), which were commonly used to access forest AGB estimation, have intense penetration into vegetation (Foody et al., 2003; Lu, 2005; Lu et al., 2012). LiDAR was still hard to apply in large areas due to data collection being costly and non-spatially continuous (Listopad et al., 2011; Geng et al., 2021; Ehlers et al., 2022). The signal of Radar was easily limited by fluctuating landforms, leading to Radar being unsuitable in complex landform areas (Minh et al., 2013). It is still an excellent alternative to use optical images for estimating and mapping forest AGB for large areas due to the lower cost, higher temporal resolution, and spatial coverage (Zhang and Liang, 2020; Ye et al., 2021). However, the optical remote sensing detection of high-density forests is a phenomenon that leads to the underestimation of the high AGB value. Meanwhile, the mixing of light waves from another vegetation surface would lead to an overestimation of the lower AGB value (Chen and Cao, 2012; López-Serrano et al., 2016; Li et al., 2019, 2021; Simona et al., 2020; Gao and Zhang, 2021). How to improve the precision influence caused by underestimation and overestimation is still significant work for AGB evaluation by optical remote sensing in a large area (Víctor et al., 2018; Li et al., 2019; Zeng et al., 2019; Sagang et al., 2020).

More than 50% of the uncertainty is caused by the assessment models (Shettles et al., 2015); thus, it’s important to choose a high-precision model. The AGB estimation models include the parametric and non-parametric models (Huang et al., 2019; Lourenço et al., 2021). The parametric models use linear, logarithm, exponential, and other functions to describe the correlation between forest AGB and the remote sensing variables. This approach has become one of the most popular estimation models due to its ability to quantify the relationship between forest AGB and the independent variables (Ou et al., 2019a). The stepwise linear regression model (LSR) can select variables closely related to the response variables by significance testing, solving the problem of collinearity among explanatory variables (Zhu et al., 2017). However, when the models with insignificant influence on dependent variables are ignored, there would be a lower prediction accuracy when the forest AGB and the independent variables do not have a simple linear relationship (Yadav et al., 2021; Zhao et al., 2022).

Many non-parametric models have been explored for forest AGB estimation, such as random forest (RF) (Yadav et al., 2021), k-nearest neighbors (kNN) (Wan et al., 2021; Andras et al., 2022; Beaudoin et al., 2022), support vector machine (SVM) (Mountrakis et al., 2010; Christoffer et al., 2013), and maximum entropy (MaxEnt) (Wang et al., 2022; Zhao et al., 2022). Although the non-parametric models can provide an excellent fitting effect, it is still hard to improve the precision influence caused by overestimation and underestimation.

Taylor (2000) used a neural network structure and proposed a new non-parametric model named quantile regression neural network (QRNN); it includes the advantages of both artificial neural networks (ANN) and quantile regression (QR). QR was generated by Koenker and Bassett (1978). It can more accurately describe the change range of the dependent variables and variables corresponding to the independent variable (Das et al., 2019; Tian et al., 2020). QR can provide a flexible and stable value, which is not affected by data outliers and heavy-tailed distributions under the basic assumptions of conventional models (Cade and Noon, 2003; Julien, 2012). Meanwhile, the QR-based method is a better choice as it cannot only reveal the mean value (Cade and Noon, 2003; Das et al., 2019) but also show its quantiles, especially when there is a trend of the data getting close to “extreme” regimes (Scharf et al., 1998; Cade and Noon, 2003; Friederichs and Hense, 2007; Julien, 2012). Thus, it would effectively express the shape change and depict the features of distribution from low biomass value to high biomass more comprehensively through different quantiles to reduce the error caused by data dispersion and heavy-tailed distribution. ANN has a non-linear adaptive ability and solid ability to fit more complicated data (Alizadeh et al., 2021; Alquraish and Khadr, 2021; Tzanis et al., 2022; Wang et al., 2022; Zhao et al., 2022), which is widely used in forest biomass estimation. For example, Ou et al. (2019a) used the ANN model to estimate forest AGB of the Pinus densata., and it got a better performance of the AGB estimation. It cannot be more clearly reflected that with an increase in the independent variable, the data in different ranges of the dependent variables change to different degrees, and this conclusion could not be obtained through the previous regression models (RF, k-NN, and SVM) analysis. QRNN combined the advantages of QR and ANN, which means QRNN not only has a high adaptive ability but also can depict the shape change of dependent variables on each quantile. The forest AGB data were usually widely distributed and had extreme values normally. QRNN may be a suitable model to reduce the precision influence caused by overestimation and underestimation because QRNN can reveal the value from low biomass to high biomass by different quantiles. It has achieved good results in many aspects (Cao et al., 2018; Suhartono et al., 2018; Yang et al., 2021), but there are few studies on the estimation of forest AGB.

If the relationship between forest AGB and the independent variables was linear, then, LSR would have a better performance. Otherwise, a non-parametric like QRNN was a better choice if the dependent variables were scattered or heavy-tailed. QRNN was rarely used in forest biomass; hence, its estimated performance needs to be further researched in a future study. QRNN was created based on QR and ANN; the performance of those two models also needs to be compared to analyze whether QRNN can improve the precision or not. Overall, we estimated AGB by combining QRNN with optical remote sensing data to reduce the precision influence caused by overestimation and underestimation, and to improve the forest AGB estimation accuracy. We analyzed the fitting performance and residual variation for LSR, ANN, and QR. The capability of improving the precision was compared in the remote sensing estimation of AGB. The significant contributions of this work are:

(1) Four models–LSR, ANN, QR, and QRNN were used to compare AGB estimation and we determined the fitting performance for these models.

(2) We aimed to seek the optimal quantile that corresponds with the different AGB segments using QRNN and QR and explore optimal AGB estimations to improve the precision influence caused by overestimation and underestimation of AGB using QRNN and QR.

2. Study area and datasets

2.1. Study site

The study was conducted in Pinus densata forests in Shangri-La City, north-western Yunnan Province, southwest China (Figure 1). The region has a cold-temperate monsoon climate with altitudes ranging from 3,350 to 3,696 meters above sea level. Due to the high altitude, winters are cold but sunny, and the mean annual temperature is 5.4°C. The temperature in the coldest month (December) and hottest month (July) is −3.8°C and 13.3°C, respectively. The average annual precipitation in the study area is 607 mm, of which 70% occurs from June to September. Evaporation is 1,671 mm, and relative humidity is 70%. Soil types are dominated by dark brown forest soils (Lefsky et al., 2004; Zheng et al., 2007).

FIGURE 1

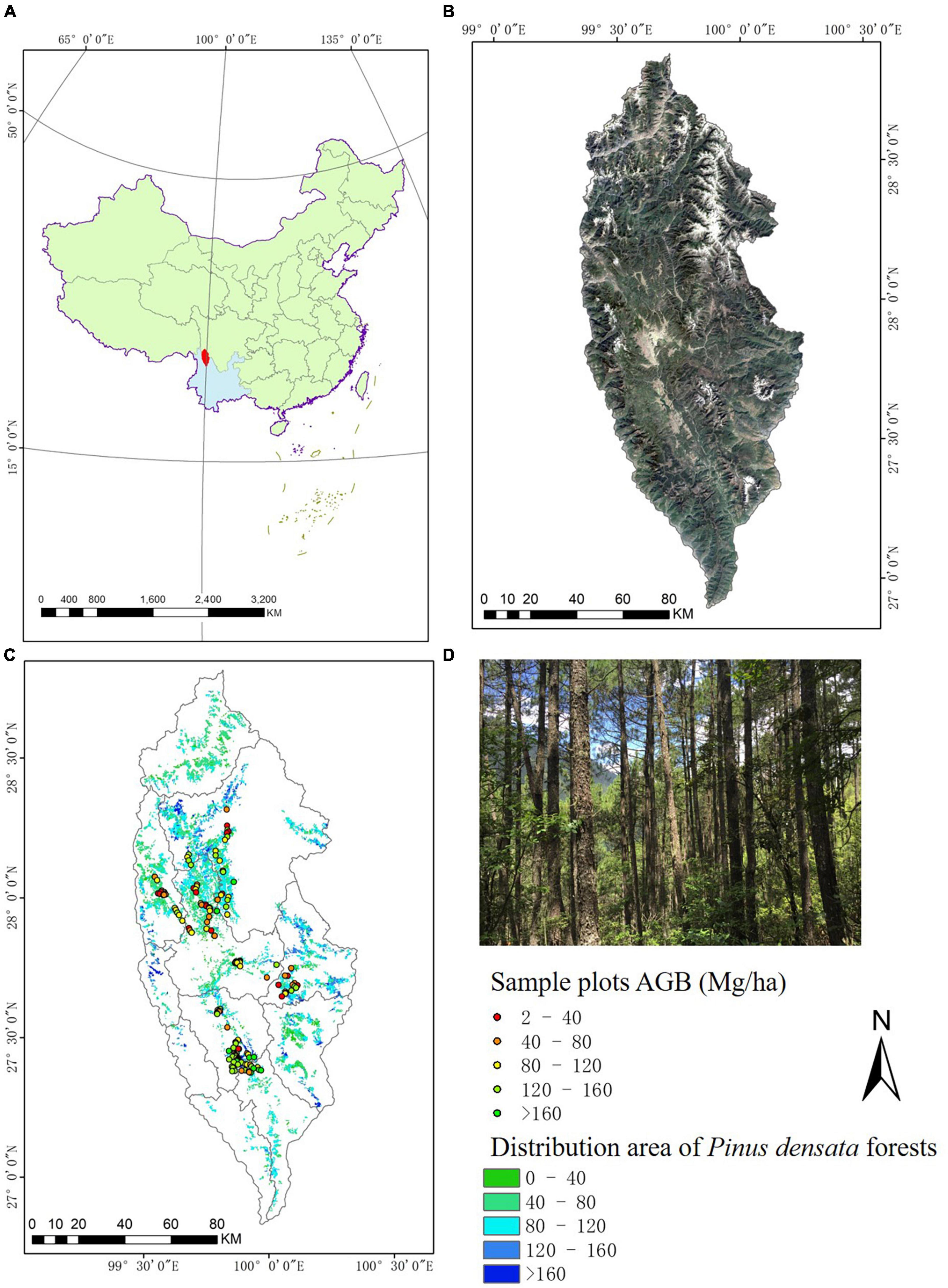
Figure 1. (A) The location of the study area; (B) Shangri-la City shown by a composite image; (C) the spatial distribution of Pinus densata forests according to the forest management inventory (FMI) data in 2016 and the sample plots investigated in 2016; (D) Pinus densata forests in the study area.

Pinus densata is a dominant tree species mainly at an altitude of approximately 2,700 to 4,200 meters in the Tibetan Plateau, and a unique and pioneer species of the Hengduan Mountains (Zheng et al., 2007; Ou et al., 2019b). Moreover, Pinus densata belongs to the evergreen tree, which has a strong natural regeneration ability, and it grows slowly within 1 to 2 years (Xie et al., 2018). It is the primary type of forest in Shangri-La City and is often distributed in the form of pure forest or mixed forest with the species of Quercus spp., Pinus armandii, Picea spp., and Betula spp. (Ou et al., 2019a).

2.2. Sample trees measurement and aboveground biomass calculation

There was a total of 146 sample plots that were surveyed and calculated in August 2016, and the sample plot size was set as 30 m × 30 m. A handheld GPS was used to locate the random plots; the coordination was recorded with UTM/WGS 84, and the mean horizontal accuracy of the coordinate was 3 to 5 m after correcting the deviation. The same project system images were downloaded and georeferenced with the ground inventory data, and a 20 m buffer was left in case the plots were outside of the research area when the images were clipped. The diameter at breast height (DBH) (1.3 m above ground) and height (H) of each tree were recorded, as well as the coordinates of the location, elevation, degree, and slope direction of the sample plot.

In all sample plots, 100 sample trees were chosen, and each sampled tree was measured for information such as its bark, branches, and foliage data. Sample trees were selected based on the DBH grades, and the range was from 6 to 76 cm by 2 cm intervals. Three trees, at least, needed to be selected for each class of DBH. Meanwhile, the tree stems, bark, branches, and needles were collected based on this method by Wang. Each tree stems were cut at 2-m intervals and a 2-cm disc was gotten in each interval (Peichl and Arain, 2007). There were three classes to be divided for the branches: top, middle, and bottom, and two samples were chosen for each component. The sample biomass was converted to calculate the biomass (Xu et al., 2014). The AGB values of single sample trees could be fitted by the following function (Ou et al., 2019b). The AGB value of trees in one plot:

$AG{B}_i=0.073\cdot DB{H}^{1.739}\cdot H^{0.880}(1)$

where DBH is the diameter at breast height greater than 5 cm, H is tree height greater than 1.3 m, and AGBi is the aboveground biomass of the sampling tree (kg).

In order to obtain the AGB of each sample plot, we used equation (2) for the calculation to get the plot AGB (Mg/ha) with an area of 30 m × 30 m; the AGB range was from 2.1 to 251.5 Mg/ha, and the statistical information is listed in Table 1.

$AG{B}_i=\frac{{\sum }_{i=1}^{n}AG{B}_i}{900}\cdot 10000/1000(2)$

TABLE 1

Table 1. The statistical parameters of sample plot datasets.

where AGBs is the AGB of a plot, AGBi is the biomass of individual trees, and n is the number of trees within the plot.

2.3. Remote sensing data and pre-processing

Cloud and snow will significantly affect the spectral bands of optical remote sensing (Xu and Yue, 2014), atmospheric corrections (Vermote et al., 2002), calculation of interference vegetation index (Zhu et al., 2015), identification of land types, etc., (Zhang et al., 2002). Therefore, the images required for the experiment were obtained from Google Earth Engine (GEE). To synthesize a completely cloudless image, Landsat 8-Operational Land Image (OLI) atmospheric correction surface reflectance data were operated with each scene image in 2016, using the bit operation cloud removal method, and then the standardization index was calculated. Finally, the average value of the annual image data set was combined through time aggregation to obtain a cloudless high-quality image, which cannot only significantly reduce the amount of time spent on calculation and make the analysis faster but also reduce the error caused by different surface reflectance, and it can produce the same accuracy as the time series data (Phan et al., 2020). The satellite images of the study area are shown in Figure 1.

There were 174 variables derived from remote sensing, including 7 spectral bands, 13 vegetation indices, 6 image transform algorithms, and 148 textural measures (Table 2). Pearson correlation analysis was used to analyze the correlation of spectral variables and AGB, and spectral variables with significant correlation with AGB were used to set the AGB estimation model.

TABLE 2

Table 2. Spectral variables derived from a total of seven bands for the Landsat 8 OLI image.

3. Materials and methods

3.1. Flow chart

In Figure 2, the methodological framework was described as (1) collecting data of the plots and tree biomass, Landsat 8 OLI images, and digital elevation model (DEM); (2) calculating the plot AGB; (3) pre-processing the Landsat 8 OLI images; (4) correlating spectral variables and AGB; (5) developing the linear stepwise regression (LSR), artificial neural network (ANN), quantile regression (QR), and quantile regression neural network (QRNN); and (6) assessing the models.

FIGURE 2

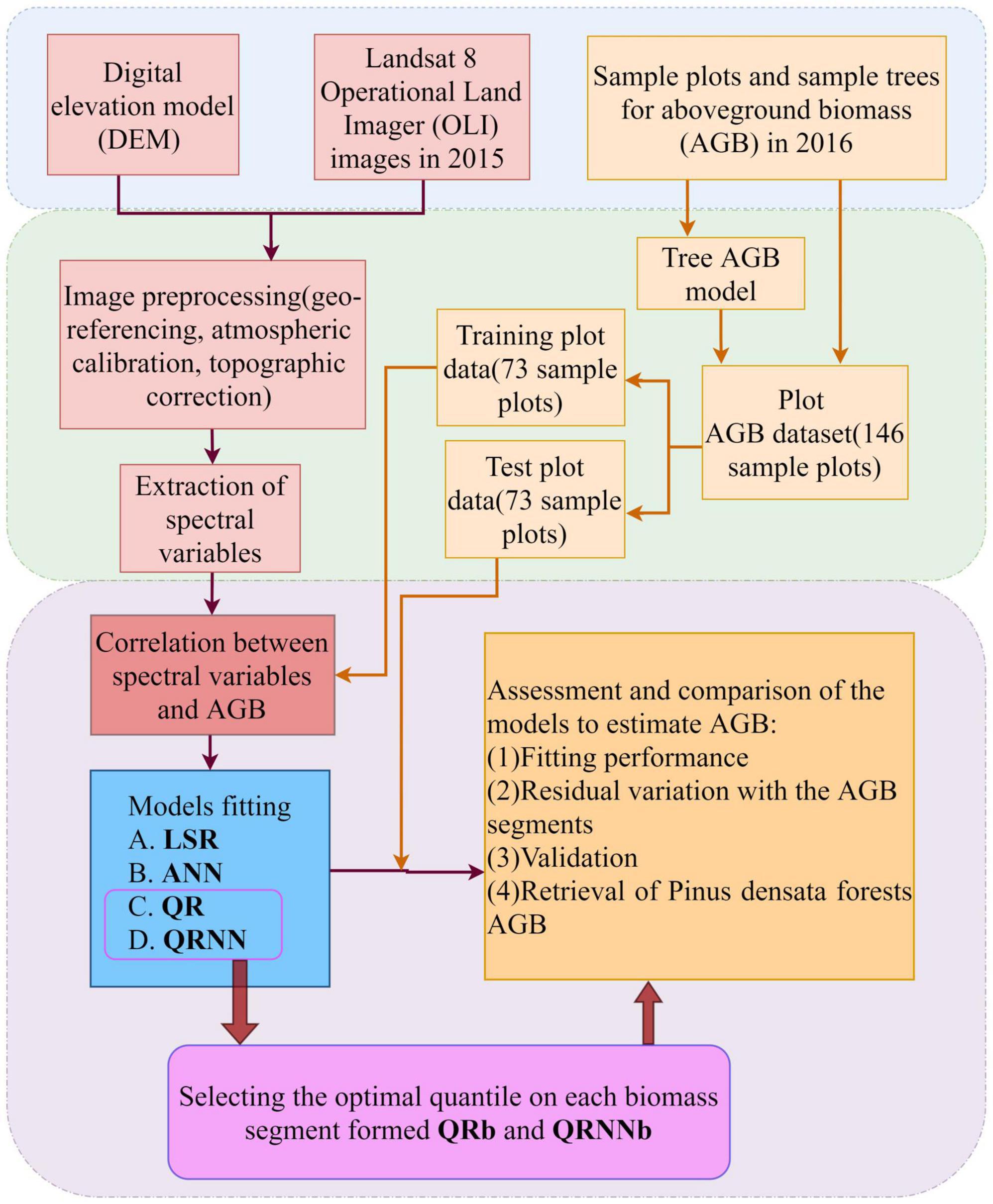
Figure 2. The methodological framework of estimating the forest aboveground biomass (AGB). LSR is linear stepwise regression, ANN is an artificial neural network, QR is quantiles regression, QRNN is quantiles regression neural network, QRb is the quantile regression with the best fitting performance in each biomass segment, and QRNNb is the quantile regression neural network with the best fitting performance in each biomass segment.

3.2. Modeling methods

3.2.1. Linear stepwise regression (LSR)

The linear stepwise regression (LSR) model could automatically select the most important variables from a large number of available variables by regression analysis (Zhu et al., 2017). Because of its feature selection technology, it can avoid the disadvantage of predicting stability in traditional linear models to some extent (Yan et al., 2009; Almeida et al., 2019). LSR can be expressed using equation 3, and it was carried out using the R software, and the MASS package was used to build the model.

$\mathrm{y}={\mathrm{b}}_0+{\mathrm{b}}_1{\mathrm{x}}_1+{\mathrm{b}}_2{\mathrm{x}}_2+\mathrm{\cdots }+{\mathrm{b}}_{\mathrm{n}}{\mathrm{x}}_{\mathrm{n}}(3)$

Where y is the dependent variable, b1, b2,…, and bn are the partial regression coefficient of the independent variables, and b0 is the constant term; x1, x2,…, xn are the independent variables.

Moreover, to avoid poor performance due to redundancy and collinearity, the variance inflation factor (VIF) was used to evaluate the LSR model. Only if the VIF value of the independent variables is lower than 10, the variables could be selected for the model (Ou et al., 2019a).

3.2.2. Artificial neural networks model (ANN)

Artificial neural networks (ANN) are an algorithmic mathematical model based on a large number of neurons interacting in a distributed manner and performing information processing, which has the characteristics of self-adaptive, self-learning, and real-time learning. It generally consists of three layers, including the input, hidden, and output layers. There are many nodes in each layer, and two layers are connected by the weights of nodes. When it receives input signals, it makes a non-linear weight operation through the activation function and passes the calculation result to the next neuron. The initial weights are randomly generated, and the output value reaches the predefined target by continuously adjusting the weights between each neuron during the training process (Alizadeh et al., 2021; Alquraish and Khadr, 2021; Tzanis et al., 2022; Wang et al., 2022; Zhao et al., 2022). Building remote sensing models of forest biomass based on artificial neural networks has the characteristics of self-adaptive, self-learning, and real-time learning. Currently, neural networks have been used in ecosystem simulation, ecological data processing, and extraction of environmental parameters from remote sensing (Luca et al., 2022).

Artificial neural networks was carried out using the R software, and the neuralnet package was utilized for building this model in this study. Neural networks usually use a three-layer structure with only one hidden layer. In addition, the input variables of this study are seven, and hidden layers’ nodes are usually around 2/3 of the input nodes (Wang et al., 2022). The number of hidden layers is four through experiments. Before modeling, we normalized the input variables to a value between −1 and 1 to eliminate the algorithm impact caused by the excessive magnitude of each number variable.

3.2.3. Quantile regression (QR)

Quantile regression (QR) is a natural extension of the linear regression model proposed by Koenker and Basset (Lin et al., 2020). The linear regression model describes the conditional mean’s change for the independent variable along with the change of covariates while QR emphasizes the change of the conditional quantile. The different quantiles will produce various fitting functions of their conditional distributions (Taylor, 2000; He and Li, 2018; Suhartono et al., 2018; Lin et al., 2020). In this study, QR was carried out using the R software, and the quantreg package was utilized to build this model. In addition, the more classic five quartiles group (τ = 0.1, 0.25, 0.5, 0.75, and 0.9) (Sun et al., 2021) was selected.

3.2.4. Quantile regression neural network (QRNN)

Quantile regression neural network (QRNN) is a method that combines QR and ANN that can be used for non-parametric non-linear calculations, which combines two advantages. On the one hand, the neural network can fit the non-linear structure of the actual problem and can achieve more accurate simulations without relying on the setting of an explicit functional form, and it has the characteristics of quantiles regression where different quantiles are selected to obtain different conditional quantile of the response variable (He and Li, 2018; Suhartono et al., 2018). On the other hand, it is characterized by quantile regression, where different quantiles are selected to obtain different conditional quantiles of the response variable. Then it can be portrayed more thoroughly and carefully, and the conditional distribution characteristics can be comprehensively described (Cao et al., 2018; Yang et al., 2021).

Quantile regression neural network was carried out using the R software, and the QRNN package was utilized for building this model in this study. Like ANN, we set QRNN as a hidden layer and four hidden nodes. In addition, the setting of the quartiles was consistent with that of the QR.

3.3. Model assessment and validation

The determination coefficient (R²) and the root of the mean square error (RMSE) were used to evaluate the AGB model and the corresponding assessment. Both indices of the QRNN and QR were listed according to the five quartiles. Then, the scatter plots (Figure 3) of the prediction values to the observed ones according to the modeling dataset were drawn. Furthermore, for both QRNN and QR, the corresponding optical quartile models with the lowest mean error at each AGB segment were combined as the best QRNN (QRNNb) and the best QR (QRb), respectively, and the AGB segments are 0 to 40 Mg/ha, 40 to 80 Mg/ha, 80 to 120 Mg/ha, 120 to 160 Mg/ha, and greater than 160 Mg/ha (Zhao et al., 2016; Yadav et al., 2021).

FIGURE 3

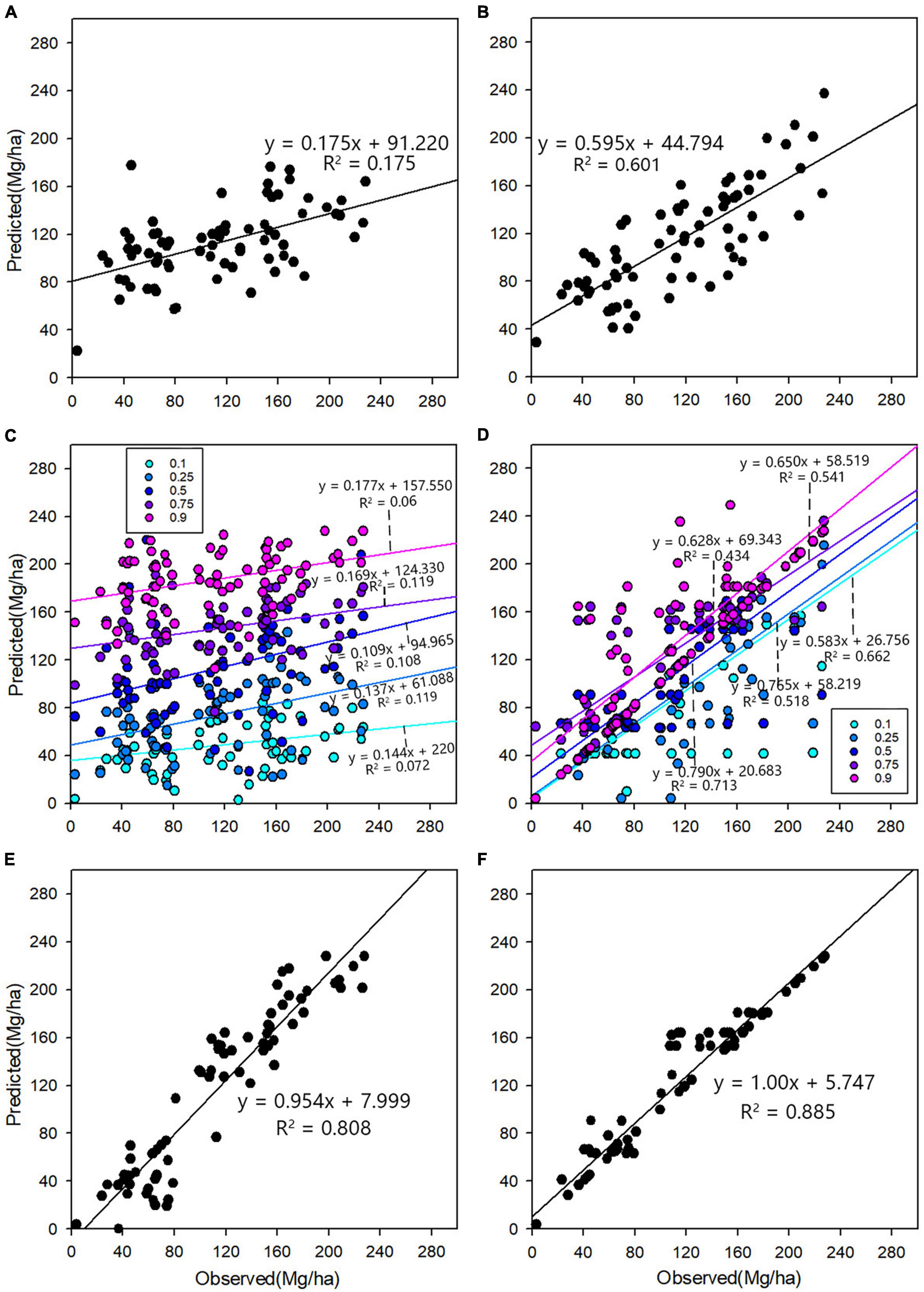
Figure 3. The scatter graphs of the predicted plot AGB values against the observed or reference values based on the modeling dataset (n = 73) (A) linear stepwise regression (LSR); (B) artificial neural network (ANN); (C) quantiles regression (QR): the quartiles groups are 0.1, 0.25, 0.5, 0.75, and 0.9, respectively; (D) quantiles regression neural network (QRNN): the quartiles groups are 0.1, 0.25, 0.5, 0.75, and 0.9, respectively; (E) the quantile regression with the best fitting performance in each biomass segment (QRb); and (F) the quantile regression neural network with the best fitting performance in each biomass segment (QRNNb).

Moreover, R², RMSE, the mean absolute error (MAE), and mean error (ME) were selected to validate each model using the test dataset according to the different AGB segments. The ME and MAE were statistically tested for their significant difference from zero at a significant level of 0.05.

4. Results

4.1. Correlation between spectral variables and AGB

Forest communities generally have different forest structures and biophysical parameter characteristics expressed as various spectral, structural, and textural features on remote sensing images. Therefore, the remote sensing feature extraction technique can be used to obtain the feature parameters, reflecting the biomass-related situation and then estimate the forest biomass over a large area. The key to using regression analysis to model forest AGB is to select variables that correlate with the AGB. Still, it is necessary to ensure that the correlation between the variables chosen is weak (Zhang et al., 2018). Therefore, we listed the remote sensing variables that significantly correlated with AGB and Pearson correlation coefficients that are more significant than 0.1 in Table 3. The 66 remote sensing factors related to the AGB of Pinus densata are extensive, ranging from 0.153 to 0.550, and the texture variable occupies the most significant number for the correlations among these variables. The second is the vegetation index. Therefore, the variables are used in AGB estimation models.

TABLE 3

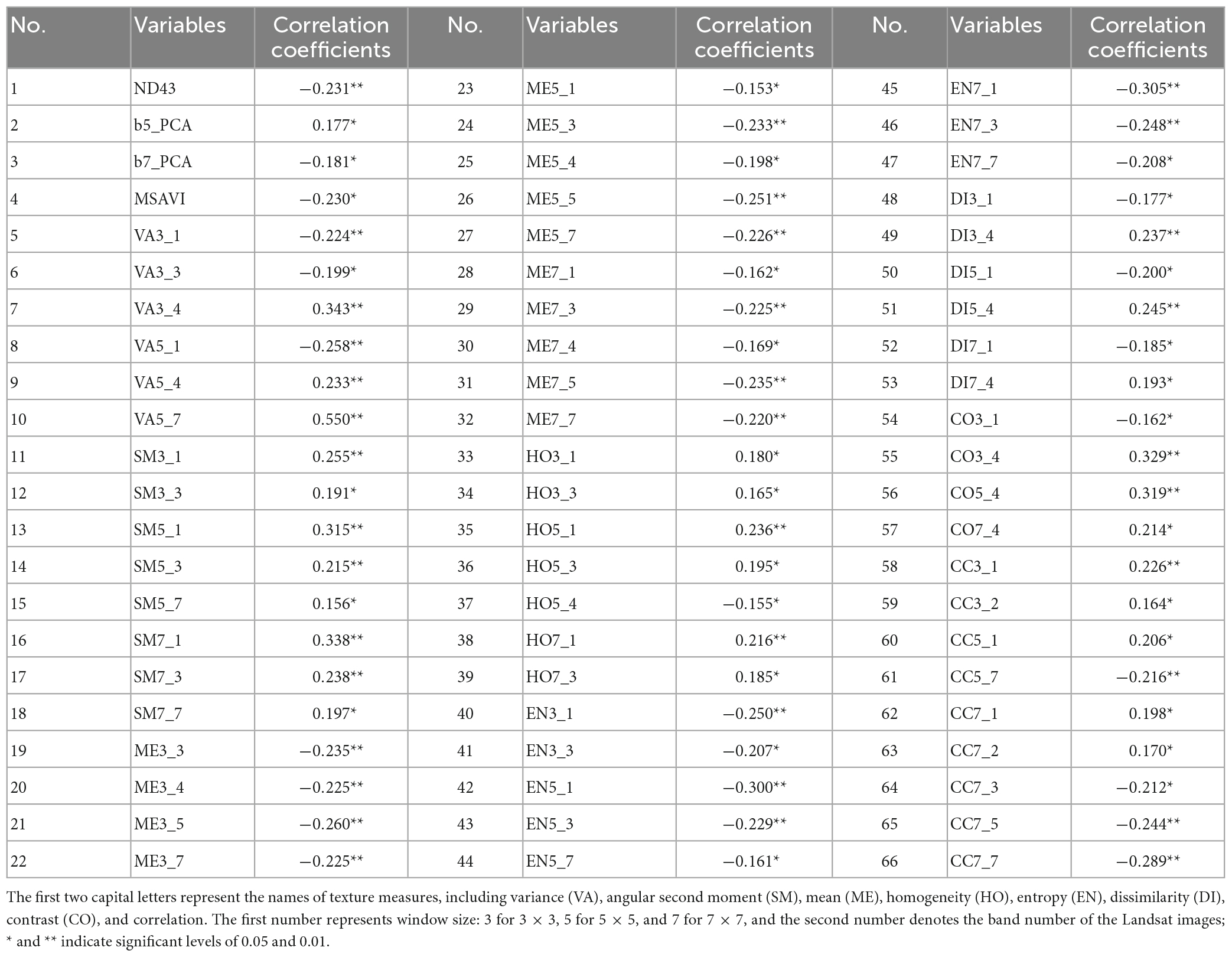
Table 3. Significant pearson correlation coefficients between remote sensing factors and AGB (ND43, normalized difference vegetation index using R and G bands; B5_PCA, the 5th component of PCA; B7_PCA, the 7th component of PCA; MSAVI, modified soil vegetation index, and all other variables are texture measures).

4.2. Model fitting

Seven independent variables related to AGB were selected, including VA3_3, VA3_1, VA5_7, VA5_1, ND43, CC5_1, and CC7_3. The largest value of VIF for these seven factors is 5.37, meeting the requirements of subsequent modeling (Zhang et al., 2018).

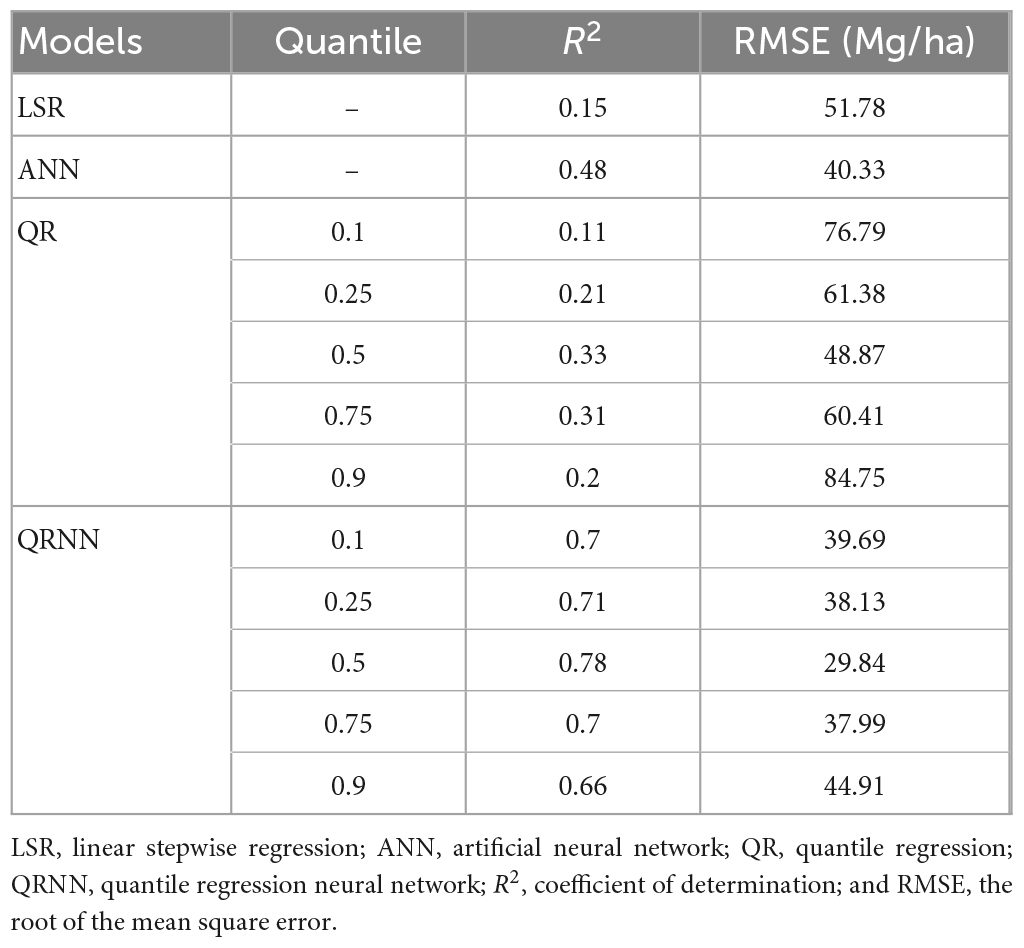
Three models–LSR, ANN, and QR were applied to compare with QRNN, and the results are shown in Table 4. In terms of the model fitting ability, LSR was the weakest fit for the AGB of Pinus densata forest in Shangri-La City. The fit results of QR are higher than LSR except for 0.1 quantile due to the extreme quantile having more significant uncertainty (Koenker and Bassett, 1978). The R² and RMSE of ANN are 0.48 and 40.33 Mg/ha, respectively, indicating that the fitting result of ANN is better than LSR and QR. In general, QRNN performs best, especially since it has the highest R² with 0.78, and the lowest RMSE is 29.84 Mg/ha at 0.5 quantile. The results showed that the fitting ability of LSR could not appropriately explain the correlation of remote sensing variables and sample plot biomass. ANN, QR, and QRNN further improve the fitting ability to explain the data compared to LSR.

TABLE 4

Table 4. The evaluation results of four models (n = 73).

By comparing QR and QRNN with the ability of quantile, we found that the AGB fit coefficient of QRNN was more than double of QR at each quantile. The RMSE also showed the same results, which demonstrated that QRNN can supply the highest accuracy for the AGB assessment. When the RMSE of the five quantiles of QR and QRNN were calculated in SPSS, the coefficients of variation of QR and QRNN were 0.386 and 0.061, respectively. It indicated that the relevant results of QRNN at different quantiles were more stable and less influenced by the quantile level.

Figure 4 shows that QR, except at the 0.25 quantile, has abnormal values during model fitting. QRNN has no abnormal value on each quantile, compared with QR; QRNN improves the situation of abnormal values during model fitting. From the aggregation of scattered distribution, the LSR is the most spread and far from the fully fitted line. In particular, LSR showed obvious overestimation when the values of the AGB plot were lower than approximately 80 Mg/ha and underestimation when the values of the AGB plot were lower than 160 Mg/ha (Figure 3A). The scatter distribution of the ANN model has improved to some extent compared with the aggregation of LSR. However, the scatter distribution of ANN still does not reach an ideal result; that is, ANN does not solve the problem of overestimation and underestimation well (Figure 3B). The scatter of the QRb (Figure 3E) model is more aggregated to the fully fitted line than ANN. The errors for an overestimation in low AGB segments and underestimation in high AGB segments are reduced, and the scatter of QRNNb (Figure 3F) is closest to the linear of y = x. It may be because QRb and QRNNb have the advantage of integrating the quantitative models corresponding to the lowest errors for each biomass segment. Compared with ANN, the scatter points of QRb and QRNNb were more aggregated toward the fully fitted line than ANN. Moreover, the overestimation error for low AGB segments and the underestimation error for high AGB segments were reduced, which significantly solved the problem of low-value overestimation and high-value underestimation of biomass. In addition, the scatter points of QRNN matched the fully fitted line, and the scatter points were most aggregated compared to the fully fitted line. So QRNN has a better fitting effect than QR.

FIGURE 4

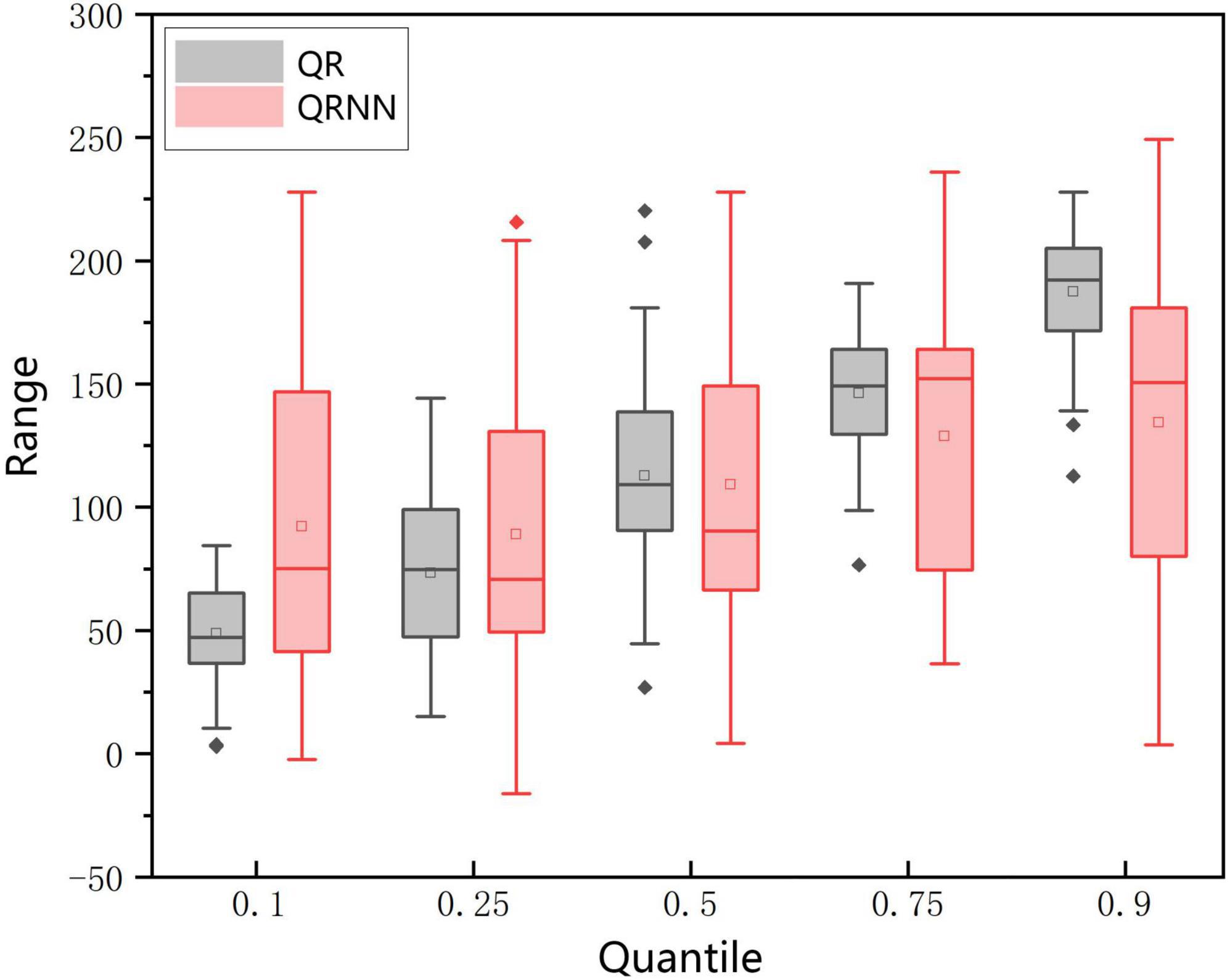
Figure 4. Boxplot of QR and QRNN fitting values on five quantiles (QR: quantiles regression; QRNN: quantiles regression neural network).

Moreover, the linear regression’s R² between predicted and observed AGB can also reflect the fitting performance difference among the four models. The order of R² is QRNNb > QRb > ANN > LSR, and the R² of LSR is lower than 0.2, but the value of QRNNb reaches 0.885. All R² of the different quantiles of the QR is approximately 0.1, and for the QRNN, the values are greater than 0.4; even the R² of the 0.5 quantile in QRNN reaches 0.713. Furthermore, the absolute intercept values of the QRNNb and QRb are lower than 10, and the value is the lowest for the QRNNb. Meanwhile, the slope value of the QRNN is 1.004 and 1.116 for QRb. But the intercept values of LSR, ANN, and five quantiles of QRNN and QR are greater than 20 Mg/ha, even reaching 80 Mg/ha. The slope values of LSR and five quantiles for QR are lower than 0.18, and the value range of ANN and five quantiles for QRNN is from 0.583 to 0.790. These indicate that the QRNN has the best fitting performance compared with LSR, ANN, and QR (Figure 3).

4.3. Model assessment

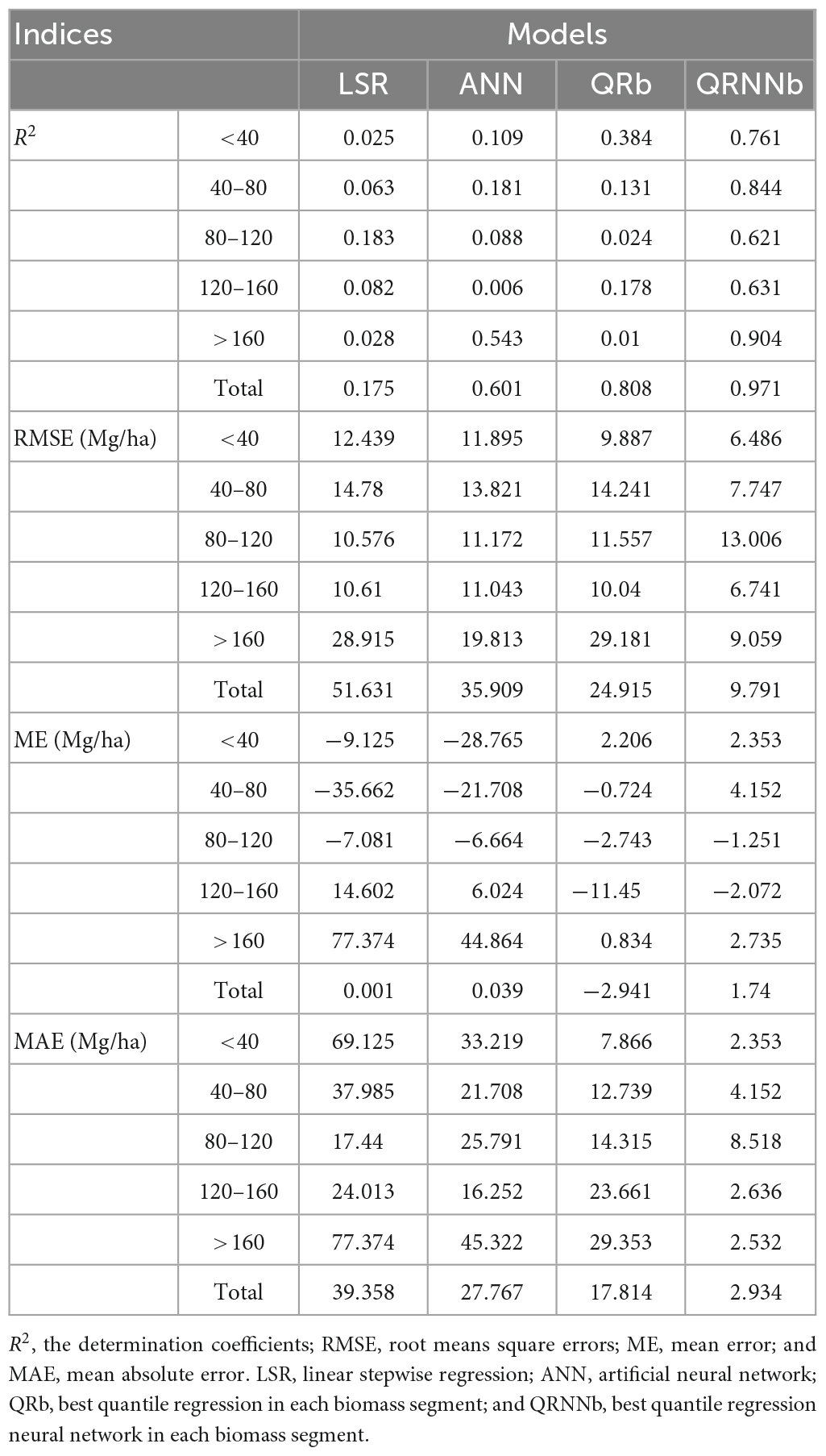
Seventy-three test plots were used to compare the coefficients of determination of these four models to further verify each model’s predictive power for each biomass segment (Table 5). The R² and RMSE as shown in Table 5 can intuitively know that the effect of model performance is QRNNb > QRb > ANN > LSR. At the stage of AGB <40 Mg/ha, the fitting results of each model were arranged in descending order as QRNN, QR, ANN, and LSR. In the 40 to 80 Mg/ha stage, the fitting performance order was LSR < QR < ANN < QRNN. The fitting results in the 80 to 120 Mg/ha stage were ranked as QR < ANN < LSR < QRNN, while in the 120 to 160 Mg/ha stage, the ranking was ANN < LSR < QR < QRNN. The fitting results at the highest stage of the AGB rank are ordered as QR < LSR < ANN < QRNN. This study has shown that the use of the QRNN model performs better and has more stability, compared to the remaining three models for AGB estimation in the low AGB segment (AGB < 80 Mg/ha) and high AGB segment (AGB >160 Mg/ha), where the forest AGB estimation is more complicated.

TABLE 5

Table 5. Model validation results using the test dataset (n = 73).

As shown in Figure 5, in both the low to medium and mid-high biomass segments, the negative mean errors (overestimations) of predictions from LSR and ANN were statistically and significantly different from zero. The positive mean errors (underestimations) from LSR and ANN were also statistically and significantly different from zero (Figure 5A). This study has shown that all models are statistically and significantly different from zero except QRNN on the low and high biomass segments (Figure 5B). Moreover, ANN has a more significant mean absolute error in the low and high biomass segments, and it indicates that LSR and ANN have more obvious disadvantages in overestimating and underestimating biomass. Comparing (Figures 5A, B), we can see that the ME and MAE of both QR and QRNN are lower than LSR and ANN, especially on the low and high biomass segments with significant improvement, which solves the problem of overestimation of low values and underestimation of high values.

FIGURE 5

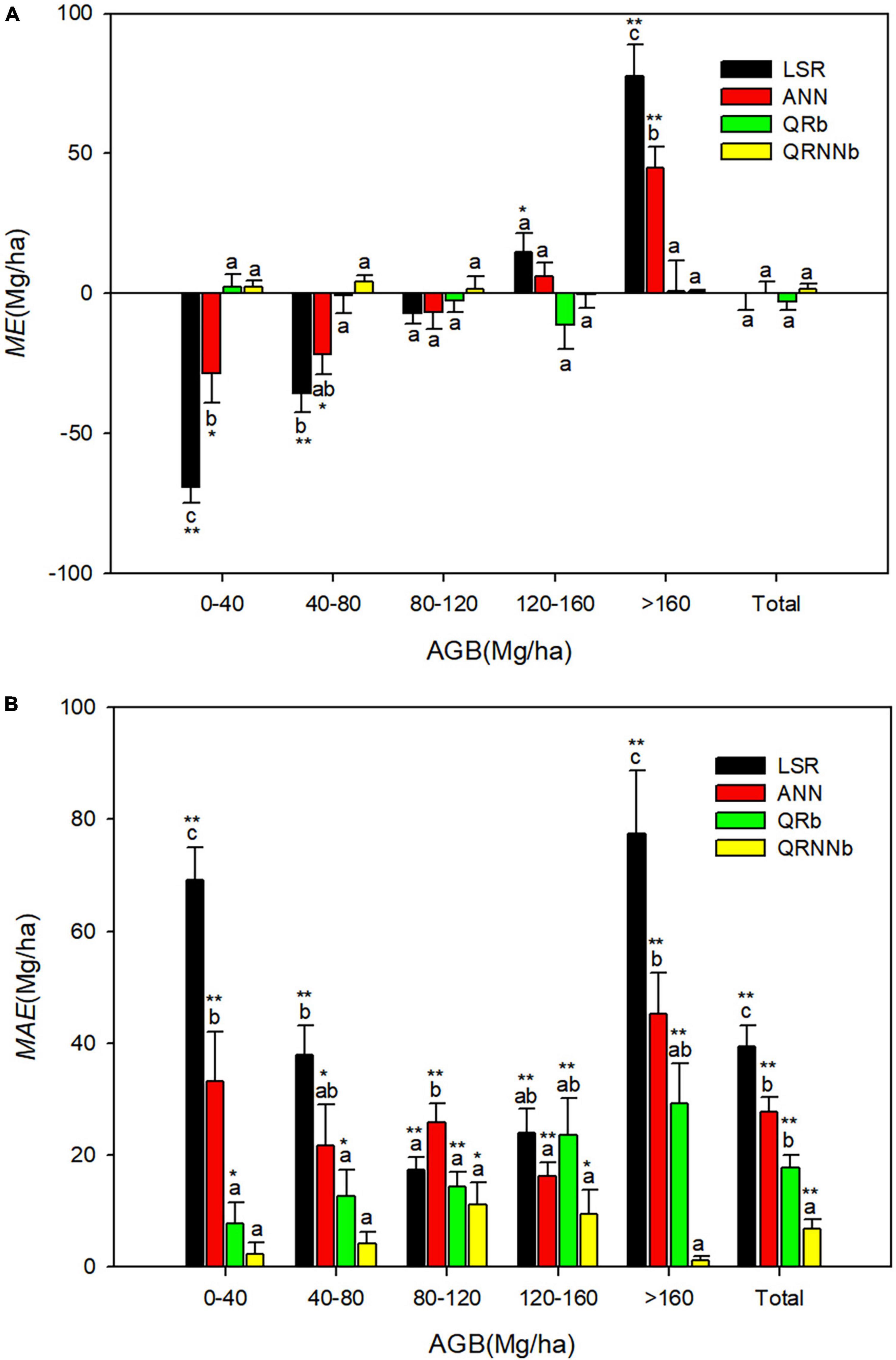
Figure 5. The statistical results of significant differences in the mean errors from zero. (A) The statistical test results of significant differences of mean errors from zero; (B) the statistical test results of significant differences of mean absolute error (LSR, linear stepwise regression; ANN, artificial neural network; QRb, best quantile regression in each biomass segment; QRNNb, best quantile regression neural network in each biomass segment; AGB, aboveground biomass; ME, mean error; MAE, mean absolute error; * and ** represent significant levels of 0.05 and 0.01, respectively).

Moreover, Figure 5 shows that QRNN performs better than QR overall. QRNN is more stable in estimating biomass, and both the low and high biomass segments are significantly better. It also improves the accuracy of the underestimation of high values.

4.4. Spatial distributions of the predicted aboveground biomass

As shown in Figure 6, the AGB maps of the Pinus densata forests were inverted using four models. The heterogeneity of the AGB distribution for both LSR and QR is lower than that of the other two models, and the proportion of the larger AGB segments is high. It is difficult to distinguish the biomass segments below 160 Mg/ha. Compared with the ANN, the AGB inversion map using the QRNN model has a higher heterogeneity. QRNN has a better performance in all segments, especially at segments <40 Mg/ha and >160 Mg/ha. On the contrary, the red and blue color is hard to recognize in the ANN figure, which means ANN neither had a good performance at low nor at high biomass segments <40 Mg/ha and >160 Mg/ha. This study has shown that QRNN can better estimate the lower and higher biomass segments, and QRNN can improve the accuracy influence caused by underestimation and overestimation.

FIGURE 6

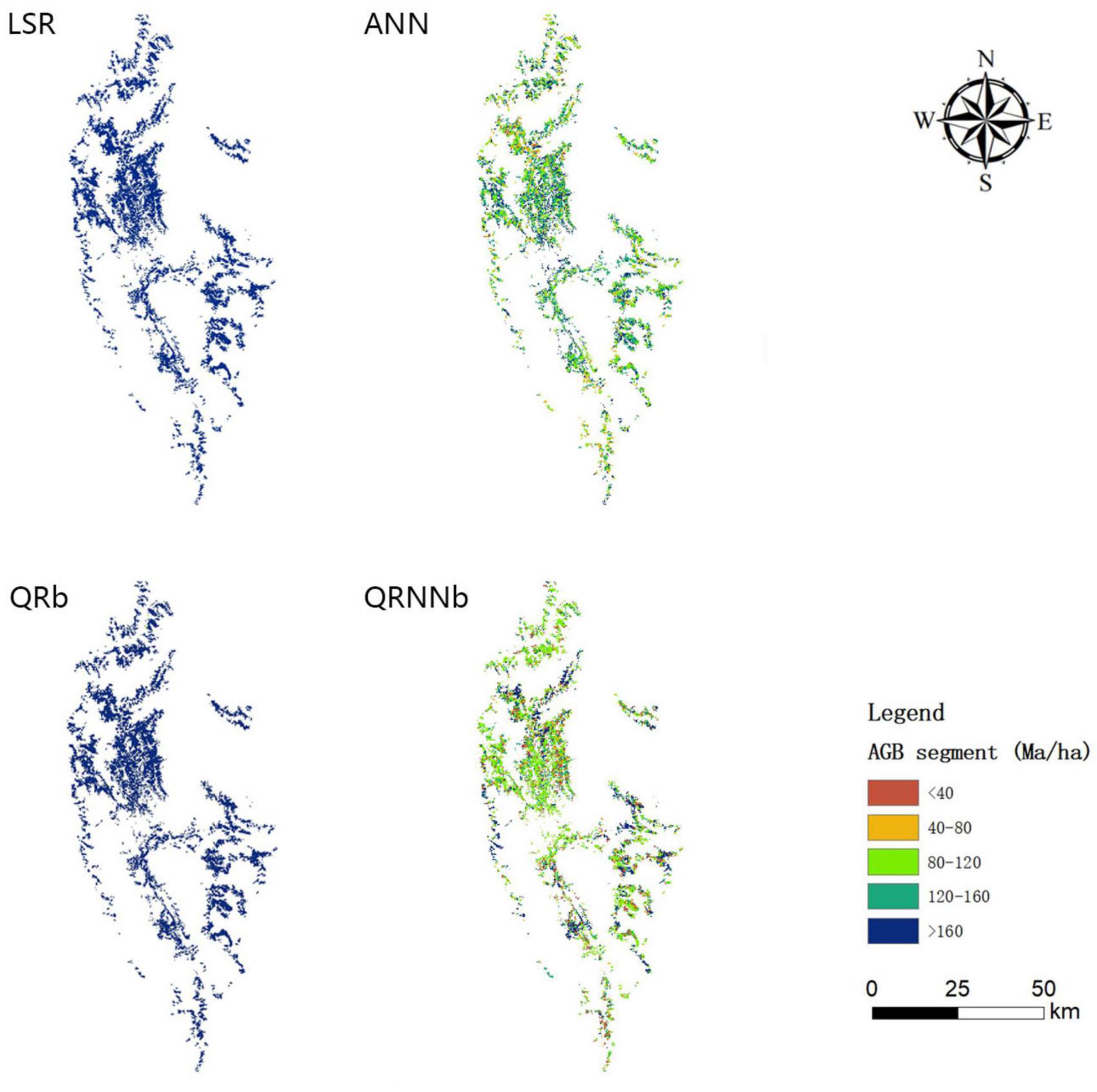
Figure 6. The spatial distributions of the predicted aboveground biomass (AGB) values of the Pinus densata forests using four models (LSR, linear stepwise regression; ANN, artificial neural network; QRb, best quantile regression in each biomass segment; QRNNb, best quantile regression neural network in each biomass segment).

5. Discussion

5.1. Reducing the uncertainties from overestimation and underestimation of forest AGB using QRNN

Variable selection is the first step of model construction. In general, most of the significant correlation variables which were extracted from remote sensing of the AGB of Pinus densata forest are texture measures in this study, and the rest are vegetation indexes. Since texture measures can describe subtropical forest canopy structure to a certain extent (Gao et al., 2018), which makes up for the shortage of using remote sensing data to describe forest stand structure, it further improves the possibility of forest AGB estimation accuracy. The vegetation index describes vegetation information by calculating spectral information between bands, which can better reflect vegetation characteristics in the region than single optical remote sensing image band information (Jiang et al., 2022). As early as Lu (2005) found that using texture information and vegetation index in Landsat Thematic Mapper (TM) data helps improve tropical forest AGB estimation accuracy. Since the vegetation indices integrate the information of infrared bands and other bands, the vegetation index is selected in addition to the texture measures in the variable selection of this study.

From the estimation and test results of the four models, it is evident that the AGB assessment of the Pinus densata forest has different degrees of overestimation and underestimation. The estimation error is significant when AGB is less than 40 Mg/ha and AGB is greater than 160 Mg/ha. The LSR shows a large estimation error in each AGB segment through the analysis. In addition, except for the segment of 120 to 160 Mg/ha, the estimation error of ANN is larger than QR and QRNN. It indicates that the QR and QRNN can estimate the entire dependent variable of conditional distribution or a specific quantile function for the pure natural forest with a wide distribution range and high complexity of AGB. Moreover, it allows the derivation of conditional estimates corresponding to each quantile, is less susceptible to extreme values, and has an excellent fitting performance.

The LSR mainly focuses on explaining the dependent variable’s mean value under each specific independent variable to describe the relationship between the independent variable and the dependent variable (Main-Knorn et al., 2011; Zhu et al., 2017). When generalizing the dependent variable under the specific value of the independent variable, LSR cannot be easily extended to the non-mean estimate. However, the non-mean estimate, such as the overestimation and underestimation in the forest AGB estimation mentioned in this paper is the most difficult in most studies. QR estimated the impact of potential changes in covariates on different quantiles in conditional distribution (Taylor, 2000) such as the five quantiles (0.1, 0.25, 0.5, 0.75, and 0.9) we selected in this paper. These five fitting regression lines of QR can capture location changes (median regression line), scale, and more complex shape changes (the other non-median regression lines). The distribution of vegetation index data has an unequal variation which is caused by complex interactions in factors affecting biomass that cannot all be loaded into the model and cannot all be measured and explained; there is no zero-change in heterogeneous distributions. The valuable information about the distribution of dependent variables will be neglected if only the concentration trend is the focus, especially when the distribution of dependent variables is asymmetrical. The right skewness of the distribution will cause the mean value to be much larger than the median, which will lead to overestimation, and a lower estimation will present on the contrary. This phenomenon of overestimation or lower estimation could be solved as the QR model can model the shape change and skewness of multi-variable in which the slopes range from minimum to maximum, and the quantile sampling changes can vary rapidly over short quantile intervals, especially when the data is close to an extreme value. Therefore, QR allows the derivation of conditional estimation corresponding to each quantile and is less susceptible to extreme values to reduce the error in biomass estimation (Lin et al., 2020; Tian et al., 2021). Moreover, the lack of both parametric models is obvious in the lower AGB fitting and prediction accuracy.

Artificial neural networks is a simplified simulation that simulates the characteristics of the intelligent structure of the human brain and abstracts problems with unique information processing and solution capabilities. Moreover, this estimation is used in ecosystem simulation, ecological data processing, and extraction of environmental parameters from remote sensing (Yadav et al., 2021; Andras et al., 2022). Combining the advantages of QR and ANN, the QRNN is not affected by the outliers in the data and does not fit the data in the regression to meet the basic assumptions of the conventional model (He and Li, 2018; Wang et al., 2022). Therefore, it is more suitable for the data fitting of Pinus densata forest with a large AGB span. This study’s results show that the error of the AGB assessment of Pinus densata forest in different AGB segments of QRNN is the lowest among all models, and QRNN can effectively reduce the underestimation and overestimation error of AGB estimation of Pinus densata forest. Furthermore, its stability is also higher than other models. So, the QRNN is an optimal choice to solve the overestimation and underestimation of the AGB estimation of the Pinus densata forest in Shangri-La City.

5.2. Comparison and implication of similar studies

To analyze the results of this study, some research on AGB estimation of Pinus densata forest in Shangri-La City was used for comparison. Ou et al. (2019b) assessed the AGB of Pinus densata forest in Shangri-La City using Landsat 8 OLI image data by the ordinary least square method and four non-parametric regression methods. The study found that the estimation model considering the spatial features of the plot data can improve the AGB fitting performance of Pinus densata forests, and the geographically weighted regression (GWR) model has the best estimation performance, with R² and RMSE of 0.665 and 34.507, respectively. The fit result is lower than the QRNN with the best-fit performance in this study, which indicates that in the AGB assessment of the natural Pinus densata forest in Shangri-La City, the model considering the data distribution features is preferred to the data model considering the geographical distribution characteristics. It is consistent with the research of Loiselle et al. (2007). Data distribution characteristics are more critical in estimation and prediction on a large scale. Ou et al. (2019b) pointed out that with an AGB <70 Mg/ha and AGB >150 Mg/ha, there will be an apparent overestimation and underestimation of AGB in the Pinus densata forest. In this study, using QRNN, the overestimation and underestimation can be controlled to AGB <40 Mg/ha and AGB >160 Mg/ha, which improves the performance of AGB estimation. It may be because QRNN can embed quantile regression into the estimation for a complex environment (Chen et al., 2021), reflecting the stress variable’s characteristics in the whole distribution condition. More accurate estimation results can be obtained in the higher and lower biomass segments than in other methods (Xu et al., 2014). Moreover, the spatial difference in the stand distribution in the forest will affect the AGB distribution of the woods (Zhang and Shi, 2004; Assal et al., 2016). Integrating the spatial distribution features of the forest into the estimation parameters of the QRNN would further improve the AGB estimation accuracy. Moreover, Zhang et al. (2018) applied continuous Landsat images and national forest inventory data from 1987 to 2007 to estimate the AGB of Pinus densata forest in Shangri-La City with the use of parametric models and non-parametric models. Their research results show that the result of the non-parametric model for Pinus densata forest AGB is better than that of the parametric model, which is consistent with that of non-parametric ANN, and QRNN is better than LSR in our paper. It is not easy to estimate forest AGB with a simple linear model (Huang et al., 2017). In Zhang et al.’s (2018) study, the R² of the gradient boosted regression tree model with the best accuracy for estimating the AGB of Pinus densata forest reached 0.94, and the RMSE was only 14.94, which was slightly lower than the QRNN of 0.971 and 9.791 in this study. The reason may be that in this study, quantile fitting was carried out with QRNN, which fully considered low and high biomass values, making the final results more accurate (Chen and Cao, 2012).

5.3. Limitations and future research

There were 174 factors responsible for building the model and gaining the relationship between the biomass and the dependent variables. The factors included 148 textural measures and 26 variables derived from remote sensing, which had 7 spectral bands, 13 vegetation indices, and 6 image transform algorithms (Table 2). In addition, we obtained a more accurate biomass value by five quantiles group modeling. We aim to conduct further research, hoping to solve the problem of low accuracy of large-scale carbon storage estimation from the perspective of the correlation between biomass and the influencing factors. The QR model can provide more values than other models and effectively avoid the loss of valid information. Unequal variation is better than a single slope (rate of change) which may lead to uncertainty among the response variable and the predictive variable in influencing factors. A bootstrap procedure can be applied to get a distribution of slope value instead of a single punctual estimate (Hao and Daniel, 2007). In this study, a quartile group (0.1, 0.25, 0.5, 0.7, and 0.9) was used to improve the models combined within the textural features and vegetation index. In the future, 19 equidistant quantiles (Cade and Noon, 2003) or more can be selected to reveal the influence which was mentioned above to compare the estimated value of QR and QRNN models for image interpretation and to measure the quantitative method for shape change, including position, scale, and skew. Suppose 19 quantiles ranging from 0.05 to 0.95 were used, it means 19 or more fitted regression lines can capture changes in position (median regression line), scale, and more complex shape changes (non-median regression line). Then, we will boldly attempt multi-factors and multi-quantiles modeling directly to solve: (1) Extreme value problem. It would be a methodology used to capture more accurate carbon storage data to obtain the stable biomass value range and provide an objective basis for global large-scale biomass calculation. (2) Uncertainty problems. The multi-scale, multi-location, and multi-skewness information can be calculated via modeling multi-factors and multi-quantiles without screening, which helps us solve the uncertainty problem that affects biomass assessment.

In addition, except LSR, the other three models are non-parametric. For the non-parametric model, it is not necessary to make any assumptions about the distribution of the samples (Mountrakis et al., 2010; Yadav et al., 2021; Andras et al., 2022), and it is possible to use the samples for analysis directly. Moreover, in this study, the minimum value of AGB of sample plots is 2.1 Mg/ha greater than zero, and the maximum value is 251.5 Mg/ha; they cover the AGB value of Pinus densata in the study area, and the AGB low value in the study area is less. Meanwhile, the study area is very typical of northwest Yunnan, and the Pinus densata forest is principally distributed there. Therefore, it is necessary to validate the model in other forest stands and regions in the future. Furthermore, the feasibility of the method also would be further confirmed by increasing the sample size in subsequent experiments.

6. Conclusion

To promote the evaluation accuracy of forest AGB of Pinus densata with Landsat 8 OLI images and reduce the precision effect from the overestimations and underestimations, four models–LSR, ANN, QR, and QRNN were compared in this study. The following conclusions were obtained: (1) the texture features extracted from the Landsat 8 OLI images had greater correlations with the Pinus densata forest AGB than the single spectral band and other variables. (2) The QRNN has the highest R² (0.971) and smallest RMSE (9.791 Mg/ha), representing an excellent first-choice model for AGB evaluation of Pinus densata forests. (3) QRNN showed a reduced estimation error and remarkably promoted assessment accuracy of Pinus densata forests AGB compared with LSR, ANN, and QR for all biomass segments and the pooled dataset by significantly decreasing the overestimations for the plots with lower AGB values and the underestimations for the plots with higher AGB values. In conclusion, this study supplies a more accurate model for the AGB evaluation of the Pinus densata forest in Shangri-La City by improving the precision effect from the overestimations and underestimations.

Data availability statement

The original contributions presented in this study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

XZ and LL participated in the field data collection, conducted the data analysis, and wrote the draft of the manuscript. YL and JT helped with the data analysis and writing of the manuscript. YL, YW, WX, and LW participated in collecting and analyzing the field data. GO supervised and coordinated the research project, designed the experiment, and revised the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This study was funded by the National Natural Science Foundation of China (grant numbers: 31770677 and 31760206) and the Ten-Thousand Talents Program of Yunnan Province, China (YNWR-QNBJ-2018-184).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alizadeh, M., Zabihi, H., Rezaie, F., Asadzadeh, A., Wolf, I. D., Langat, P. K., et al. (2021). Earthquake vulnerability assessment for urban areas using an Ann and hybrid swot-qspm model. Remote Sens. 13:4519. doi: 10.3390/rs13224519

CrossRef Full Text | Google Scholar

Almeida, C. T., Galvao, L. S., Ometto, J. P. H. B., Jacon, A. D., Souza, P. F. R., Sato, L. Y., et al. (2019). Combining LiDAR and hyperspectral data for aboveground biomass modeling in the Brazilian amazon using different regression algorithms. Remote Sens. Environ. 232:111323. doi: 10.1016/j.rse.2019.111323

CrossRef Full Text | Google Scholar

Alquraish, M. M., and Khadr, M. (2021). Remote-sensing-based streamflow forecasting using artificial neural network and support vector machine models. Remote Sens. 13:4147.

Google Scholar

Andras, B., Eero, L., Sakari, T., and Annika, K. (2022). Comparison of neural networks and k-nearest neighbors methods in forest stand variable estimation using airborne laser data. ISPRS Open J. Photogr. Remote Sens. 4:100012. doi: 10.1016/j.ophoto.2022.100012

CrossRef Full Text | Google Scholar

Assal, T. J., Anderson, P. J., and Sibold, J. (2016). Spatial and temporal trends of drought effects in a heterogeneous semi-arid forest ecosystem. For. Ecol. Manage. 365, 137–151. doi: 10.1016/j.foreco.2016.01.017

CrossRef Full Text | Google Scholar

Banerjee, B. P., Spangenberg, G., and Kant, S. (2020). Fusion of spectral and structural information from aerial images for improved biomass estimation. Remote Sens. 12, 3164–3164. doi: 10.3390/rs12193164

CrossRef Full Text | Google Scholar

Beaudoin, A., Hall, R. J., Castilla, G., Filiatrault, M., Villemaire, P., Skakun, R., et al. (2022). Improved K-Nn mapping of forest attributes in Northern Canada using spaceborne L-Band Sar, multispectral and LiDAR data. Remote Sens. 14:1181. doi: 10.3390/rs14051181

CrossRef Full Text | Google Scholar

Cade, B. S., and Noon, B. R. (2003). A gentle introduction to quantile regression for ecologists. Front. Ecol. Environ. 1:412–420. doi: 10.2307/3868138

CrossRef Full Text | Google Scholar

Cao, S., Xu, Q., Jiang, C., and He, Y. (2018). Conditional density forecast of China’s energy demand via QRNN model. Appl. Econ. Lett. 25, 867–875. doi: 10.1126/science.115545

CrossRef Full Text | Google Scholar

Chen, W., and Cao, C. (2012). Topographic correction-based retrieval of leaf area index in mountain areas. J. Mount. Sci. 9, 166–174. doi: 10.1007/s11629-012-2248-2

CrossRef Full Text | Google Scholar

Chen, Z. S., Zhu, M. Y., He, Y. L., Xu, Y., and Zhu, Q. X. (2021). Quantile regression CGAN based virtual samples generation and its applications to process modeling. CIESC J. 72, 1529–1538. doi: 10.11949/0438-1157.20201748

CrossRef Full Text | Google Scholar

Christoffer, A., Andrew, K. S., Martin, S., Anas, F., and Wouter, V. (2013). Hyperspectral analysis of mangrove foliar chemistry using plsr and support vector regression. Int. J. Remote Sens. 34, 1724–1743. doi: 10.1080/01431161.2012.725958

CrossRef Full Text | Google Scholar

Das, K., Krzywinski, M., and Altman, N. (2019). Quantile regression. Nat. Methods 16, 451–452. doi: 10.1038/s41592-019-0406-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Ehlers, D., Wang, C., Coulston, J., Zhang, Y., Pavelsky, T., Frankenberg, E., et al. (2022). Mapping forest aboveground biomass using multisource remotely sensed data. Remote Sens. 14:1115. doi: 10.3390/rs14051115

CrossRef Full Text | Google Scholar

Feng, H., Chen, Q., Hu, Y., Du, Z., Lin, G., Wang, C., et al. (2021). Estimation of forest aboveground biomass by using mixed effects model. Int. J. Remote Sens. 42, 8675–8690. doi: 10.1080/01431161.2021.1984611

CrossRef Full Text | Google Scholar

Foody, G. M., Boyd, D. S., and Cutler, M. E. J. (2003). Predictive relations of tropical forest biomass from Landsat TM data and their transferability between regions. Remote Sens. Environ. 85, 463–474. doi: 10.1016/S0034-4257(03)00039-7

CrossRef Full Text | Google Scholar

Friederichs, P., and Hense, A. (2007). Downscaling of extreme precipitation events using censored quantile regression. Monthly Weather Rev. 135, 2365–2378. doi: 10.1175/MWR3403.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, L. H., and Zhang, X. L. (2021). Aboveground biomass estimation of plantation with complex forest stand structure using multiple features from airborne laser scanning point cloud data. Forests 12, 1713–1713. doi: 10.3390/f12121713

CrossRef Full Text | Google Scholar

Gao, Y., Lu, D., Li, G., Wang, G., Chen, Q., Liu, L., et al. (2018). Comparative analysis of modeling algorithms for forest aboveground biomass estimation in a subtropical region. Remote Sens. 10:627. doi: 10.3390/rs10040627

CrossRef Full Text | Google Scholar

Geng, L., Che, T., Ma, M., Tan, J., and Wang, H. (2021). Corn biomass estimation by integrating remote sensing and Long-Term observation data based on machine learning techniques. Remote Sens. 13:2352. doi: 10.3390/rs13122352

CrossRef Full Text | Google Scholar

Hao, L. X., and Daniel, Q. N. (2007). Quantile Regression. Thousand Oaks, CA: SAGE Publications, Inc.

Google Scholar

He, Y. Y., and Li, H. Y. (2018). Probability density forecasting of wind power using quantile regression neural network and kernel density estimation. Energy Convers. Manage 164, 374–384. doi: 10.1016/j.enconman.2018.03.010

CrossRef Full Text | Google Scholar

Huang, H. B., Liu, C. X., Wang, X. Y., Zhou, X. L., and Geng, P. (2019). Integration of multi-resource remotely sensed data and allometric models for forest aboveground biomass estimation in China. Remote Sens. Environ. 221, 225–234. doi: 10.1016/j.rse.2018.11.017

CrossRef Full Text | Google Scholar

Huang, J. X., Hou, Y. Z., Su, W., and Zhu, D. H. (2017). Mapping corn and soybean cropped area with GF-1 WFV data. Trans. Chin. Soc. Agric. Eng. 33, 164–170. doi: 10.11975/j.issn.1002-6819.2017.07.021

CrossRef Full Text | Google Scholar

Jiang, H., Yao, M. L., Guo, J., Zhang, Z. M., Wu, W. T., and Mao, Z. Y. (2022). Vegetation monitoring of protected areas in rugged mountains using an improved shadow-eliminated vegetation index (SEVI). Remote Sens. 14, 882–882. doi: 10.3390/rs14040882

CrossRef Full Text | Google Scholar

Julien, L. (2012). “A quantile regression study of climate change in Chicago. 1960-2010,” in Department of mathematics, statistics and computer science, ed. J. Korbicz (Chicago: University of Illinois), doi: 10.1137/12S01174X

CrossRef Full Text | Google Scholar

Koenker, R., and Bassett, G. J. (1978). Regression quantiles. Econometrica 46, 33–50. doi: 10.2307/1913643

CrossRef Full Text | Google Scholar

Lefsky, M. A., Turner, D. P., Guzy, M., and Cohen, W. B. (2004). Combining LiDAR estimates of aboveground biomass and Landsat estimates of stand age for spatially extensive validation of modeled forest productivity. Remote Sens. Environ. 95, 549–558. doi: 10.1016/j.rse.2004.12.022

CrossRef Full Text | Google Scholar

Li, C., Li, Y. C., and Li, M. Y. (2019). Improving forest aboveground biomass (AGB) estimation by incorporating crown density and using Landsat 8 oli images of a subtropical forest in western Hunan in central China. Forests 10:104. doi: 10.3390/f10020104

CrossRef Full Text | Google Scholar

Li, X. Y., Ling, F., Cai, X. B., Ge, Y., Li, X. D., Yin, Z. X., et al. (2021). Mapping water bodies under cloud cover using remotely sensed optical images and a spatiotemporal dependence model. Int. J. Appl. Earth Observat. Geoinformat. 103:102470. doi: 10.1016/j.jag.2021.102470

CrossRef Full Text | Google Scholar

Lin, F. Z., Tang, Y. L., and Zhu, Z. Y. (2020). Weighted quantile regression in varying-coefficient model with longitudinal data. Computat. Stat. Data Anal. 145:106915. doi: 10.1016/j.csda.2020.106915

CrossRef Full Text | Google Scholar

Listopad, C. M. C. S., Drake, J. B., Masters, R. E., and Weishampel, J. F. (2011). Portable and airborne small footprint LiDAR: Forest canopy structure estimation of fire managed plots. Remote Sens. 3, 1284–1307. doi: 10.3390/rs3071284

CrossRef Full Text | Google Scholar

Loiselle, B. A., Jørgensen, P. M., Consiglio, T., Jiménez, I., Blake, J. G., Lohmann, L. G., et al. (2007). Predicting species distributions from herbarium collections: Does climate bias in collection sampling influence model outcomes? J. Biogeogr. 35, 105–116. doi: 10.1111/j.1365-2699.2007.01779.x

CrossRef Full Text | Google Scholar

López-Serrano, P. M., Corral-Rivas, J. J., Varela, R., Álvarez-González, J., and López-Sánchez, C. (2016). Evaluation of radiometric and atmospheric correction algorithms for aboveground forest biomass estimation using landsat 5 Tm data. Remote Sens. 8:369. doi: 10.3390/rs8050369

CrossRef Full Text | Google Scholar

Lourenço, P., Godinho, S., Sousa, A. C., and Gonçalves, A. C. (2021). Estimating tree aboveground biomass using multispectral satellite-based data in mediterranean agroforestry system using random forest algorithm. Remote Sens. Appl. Soc. Environ. 23:100560. doi: 10.1016/j.rsase.2021.100560

CrossRef Full Text | Google Scholar

Lu, D. (2005). Aboveground biomass estimation using Landsat TM data in the Brazilian Amazon. Int. J. Remote Sens. 26, 2509–2525. doi: 10.1080/01431160500142145

CrossRef Full Text | Google Scholar

Lu, D. S., Chen, Q., Wang, G. X., Moran, E., Batistella, M., Zhang, M. Z., et al. (2012). Aboveground forest biomass estimation with landsat and LiDAR data and uncertainty analysis of the estimates. Int. J. For. Res. 2012:436537. doi: 10.1155/2012/436537

CrossRef Full Text | Google Scholar

Luca, O., Kerstin, B., and Nicoló, N. (2022). Advances in artificial neural networks, machine learning and computational intelligence. Neurocomputing 470, 300–303. doi: 10.1016/j.neucom.2020.03.059

CrossRef Full Text | Google Scholar

Main-Knorn, M., Moisen, G. G., Healey, S. P., Keeton, W. S., Freeman, E. A., and Hostert, P. (2011). Evaluating the remote sensing and inventory-based estimation of biomass in the Western Carpathians. Remote Sens. 3, 1427–1446. doi: 10.3390/rs3071427

CrossRef Full Text | Google Scholar

Minh, D., Toan, T. L., Rocca, F., Tebaldini, S., D’Alessandro, M. M., and Villard, L. (2013). Relating p-band synthetic aperture radar tomography to tropical forest biomass. IEEE Trans. Geosci. Remote Sens. 52, 967–979. doi: 10.1109/tgrs.2013.2246170

CrossRef Full Text | Google Scholar

Mountrakis, G., Im, J., and Ogole, C. (2010). Support vector machines in remote sensing: A review. ISPRS J. Photogr. Remote Sens. 66, 247–259. doi: 10.1016/j.isprsjprs.2010.11.001

CrossRef Full Text | Google Scholar

Ou, G. L., Lu, C., Lv, Y. Y., Wei, A. C., Xiong, H. X., Xu, H., et al. (2019a). Improving aboveground biomass estimation of pinus densata forests in Yunnan using Landsat 8 imagery by incorporating age dummy variable and method comparison. Remote Sens. 11:738. doi: 10.3390/rs11070738

CrossRef Full Text | Google Scholar

Ou, G. L., Lv, Y. Y., Xu, H., and Wang, G. X. (2019b). Improving forest aboveground biomass estimation of pinus densata forest in Yunnan of Southwest China by spatial regression using Landsat 8 images. Remote Sens. 11:2750. doi: 10.3390/rs11232750

CrossRef Full Text | Google Scholar

Peichl, M., and Arain, M. A. (2007). Allometry and partitioning of above- and belowground tree biomass in an age-sequence of white pine forests. For. Ecol. Manage 253, 68–80. doi: 10.1016/j.foreco.2007.07.003

CrossRef Full Text | Google Scholar

Phan, T. N., Kuch, V., and Lehnert, L. W. (2020). Land cover classification using google earth engine and random forest classifier—the role of image composition. Remote Sens. 12:2411. doi: 10.3390/rs12152411

CrossRef Full Text | Google Scholar

Ploton, P., Barcbier, B., Couteron, P., Antin, C. M., Ayyappan, N., Balachandran, N., et al. (2017). Toward a general tropical forest biomass prediction model from very high resolution optical satellite images. Remote Sens. Environ. 200, 140–153. doi: 10.1016/j.rse.2017.08.001

CrossRef Full Text | Google Scholar

Qin, S. Z., Nie, S., Guan, Y. S., Zhang, D., Wang, C., and Zhang, X. L. (2022). Forest emissions reduction assessment using airborne LiDAR for biomass estimation. Resour. Conservat. Recycl. 181:106224. doi: 10.1016/j.resconrec.2022.106224

CrossRef Full Text | Google Scholar

Sagang, L. B. T., Ploton, P., Sonké, B., Poilvé, H., and Couteron, P. (2020). Airborne LiDAR sampling pivotal for accurate regional AGB predictions from multispectral images in forest-savanna landscapes. Remote Sens. 12:1637. doi: 10.3390/rs12101637

CrossRef Full Text | Google Scholar

Scharf, F. S., Juanes, F., and Sutherland, M. (1998). Inferring ecological relationships from the edges of scatter diagrams: Comparison of regression techniques. Ecology 79, 448–460.

Google Scholar

Shettles, M., Temesgen, H., Gray, A. N., and Hilker, T. (2015). Comparison of uncertainty in per unit area estimates of aboveground biomass for two selected model sets. For. Ecol. Manage 354, 18–25. doi: 10.1016/j.foreco.2015.07.002

CrossRef Full Text | Google Scholar

Simona, N., Boissonnat, J. B., Cédric, L., Dar, R., Jenica, H., Antoine, B., et al. (2020). Synergy of high resolution radar and optical images satellite for identification and mapping of wetland macrophytes on the Danube delta. Remote Sens. 14:2188. doi: 10.3390/rs12142188

CrossRef Full Text | Google Scholar

Suhartono, P. D., Prastyo, D. D., and Rahayu, S. P. (2018). Hybrid quantile regression neural network model for forecasting currency inflow and outflow in Indonesia. J. Phys. Conf. Ser. 1028:012213. doi: 10.1088/1742-6596/1028/1/012213

CrossRef Full Text | Google Scholar

Sun, S. B., Wang, Y. F., Song, Z. L., Chen, C., Zhang, Y. R., Chen, X., et al. (2021). Modeling aboveground biomass carbon stock of the Bohai rim coastal wetlands by integrating remote sensing, terrain, and climate data. Remote Sens. 13, 4321–4321. doi: 10.3390/rs13214321

CrossRef Full Text | Google Scholar

Taylor, J. W. (2000). A quantile regression neural network approach to estimating the conditional density of multiperiod returns. J. Forecast. 19, 299–311.

Google Scholar

Tian, D. C., Bi, H. Q., Jin, X. J., and Li, F. R. (2020). Stochastic frontiers or regression quantiles for estimating the self-thinning surface in higher dimensions. J. For. Res. 32, 1515–1533. doi: 10.46488/NEPT.2022.v21i01.019

CrossRef Full Text | Google Scholar

Tian, Y. C., Hu, H., Zhou, G. Q., Zhang, Q., Tao, J., Zhang, Y., et al. (2021). Aboveground mangrove biomass estimation in Beibu gulf using machine learning and UAV remote sensing. Sci. Total Environ. 781:146816. doi: 10.1016/j.scitotenv.2021.146816

CrossRef Full Text | Google Scholar

Tzanis, C. G., Benetatos, C., and Philippopoulos, K. (2022). Solar cycle signal in climate and artificial neural networks forecasting. Remote Sens. 14:751. doi: 10.3390/rs14030751

CrossRef Full Text | Google Scholar

Vermote, E. F., Saleous, N. Z., and Justice, C. O. (2002). Atmospheric correction of MODIS data in the visible to middle infrared: First results. Remote Sens. Environ. 83, 97–111. doi: 10.1016/S0034-4257(02)00089-5

CrossRef Full Text | Google Scholar

Víctor, G. J., Andreas, F., Jörg, Z., Jürgen, H., Jhoana, P. B., and Jörg, B. (2018). Estimation of aboveground biomass in a tropical mountain forest in southern Ecuador using airborne LiDAR data. Remote Sens. 10:660. doi: 10.3390/rs10050660

CrossRef Full Text | Google Scholar

Wan, X. X., Li, Z. Y., Chen, E. X., Zhao, L., Zhang, W. F., and Xu, K. P. (2021). Forest aboveground biomass estimation using multi-features extracted by fitting vertical backscattered power profile of tomographic Sar. Remote Sens. 13:186. doi: 10.3390/rs13020186

CrossRef Full Text | Google Scholar

Wang, S., Wang, D., and Sun, J. R. (2022). Artificial neural network-based ionospheric delay correction method for satellite-based augmentation systems. Remote Sens. 14:676. doi: 10.3390/rs14030676

CrossRef Full Text | Google Scholar

Wulder, M. A., Roy, D. P., Radeloff, V. C., Loveland, T. R., Anderson, M. C., Johnson, D. M., et al. (2022). Fifty years of Landsat science and impacts. Remote Sens. Environ. 280:113195. doi: 10.1016/J.RSE.2022.113195

CrossRef Full Text | Google Scholar

Xie, F. M., Shu, Q. T., Zi, L., Wu, R., Wu, Q. J., Wang, H., et al. (2018). Remote sensing estimation of pinus densata aboveground biomass based on k-NN nonparametric model. Acta Agric. Univ. Jiangxiensis 40, 743–750.

Google Scholar

Xu, H., and Yue, C. R. (2014). Study on forest landscape change and forest biomass estimation in shangri-la based on remote sensing technology. Kunming: Yunnan Science and Technology Press.

Google Scholar

Xu, Q., Xu, J., Jiang, C., and Liu, X. (2014). Financial risk measure of VaR based on quantile regression neural network. Nat. Sci. 37, 1518–1522. doi: 10.5194/isprs-annals-IV-3-77-2018

CrossRef Full Text | Google Scholar

Yadav, S., Padalis, H., Sinha, S. K., Srinet, R., and Chauhan, P. (2021). Above ground biomass estimation of Indian tropical forests using X band pol insar and random forest. Remote Sens. Appl. Soc. Environ. 21:100462. doi: 10.1016/j.rsase.2020.100462

CrossRef Full Text | Google Scholar

Yan, W., Zong, Z. S., Luo, Y. Q., Cao, C. J., Li, Z. W., and Lin, G. Q. (2009). Application of stepwise regression model in predicting the movement of Artemisia lordosis boring insects. J. Beijing For. Univ. 31, 140–144.

Google Scholar

Yang, C. M., Wang, W. X., Zhang, X. X., Guo, Q. H., Zhu, T. Y., and Ai, Q. (2021). A parallel electrical optimized load forecasting method based on Quasi-Recurrent neural network. IOP Conf. Ser. 696:012040. doi: 10.1088/1755-1315/696/1/012040

CrossRef Full Text | Google Scholar

Ye, Y. X., Yang, C., Zhu, B., Zhou, L., He, Y. Q., and Jia, H. R. (2021). Improving co-registration for sentinel-1 Sar and sentinel-2 optical images. Remote Sens. 13:928. doi: 10.3390/rs13050928

CrossRef Full Text | Google Scholar

Zeng, N., Ren, X. L., He, H. L., Zhang, L., Zhao, D., Ge, R., et al. (2019). Estimating grassland aboveground biomass on the Tibetan plateau using a random forest algorithm. Ecol. Indicat. 102, 479–487. doi: 10.1016/j.ecolind.2019.02.023

CrossRef Full Text | Google Scholar

Zhang, J. L., Lu, C., Xu, H., and Wang, G. X. (2018). Estimating aboveground biomass of Pinus densata-dominated forests using Landsat time series and permanent sample plot data. J. For. Res. 30, 1689–1706. doi: 10.1007/s11676-018-0713-7

CrossRef Full Text | Google Scholar

Zhang, L. J., and Shi, H. J. (2004). Local modeling of tree growth by geographically weighted regression. For. Sci. 50, 225–244. doi: 10.1093/forestscience/50.2.225

CrossRef Full Text | Google Scholar

Zhang, Y., Guindon, B., and Cihlar, J. (2002). An image transform to characterize and compensate for spatial variations in thin cloud contamination of Landsat images. Remote Sens. Environ. 82, 173–187. doi: 10.1016/S0034-4257(02)00034-2

CrossRef Full Text | Google Scholar

Zhang, Y. Z., and Liang, S. L. (2020). Fusion of multiple gridded biomass datasets for generating a global forest aboveground biomass map. Remote Sens. 12:2559. doi: 10.3390/rs12162559

CrossRef Full Text | Google Scholar

Zhao, P. X., Masoumi, Z., Kalantari, M., Aflaki, M., and Mansourian, A. (2022). A Gis-based landslide susceptibility mapping and variable importance analysis using artificial intelligent training-based methods. Remote Sens. 14, 211–211. doi: 10.3390/rs14010211

CrossRef Full Text | Google Scholar

Zhao, P., Lu, D., Wang, G., Wu, C., Huang, Y., and Yu, S. (2016). Examining spectral reflectance saturation in Landsat imagery and corresponding solutions to improve forest aboveground biomass estimation. Remote Sens. 8:469. doi: 10.3390/rs8060469

CrossRef Full Text | Google Scholar

Zheng, G., Chen, J. M., Tian, Q. J., Ju, W. M., and Xia, X. Q. (2007). Combining remote sensing imagery and forest age inventory for biomass mapping. J. Environ. Manage 85, 616–623. doi: 10.1016/j.jenvman.2006.07.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, J., Huang, Z., Sun, H., and Wang, G. X. (2017). Mapping forest ecosystem biomass density for Xiangjiang River Basin by combining plot and remote sensing data and comparing spatial extrapolation methods. Remote Sens. 9:241. doi: 10.3390/rs9030241

CrossRef Full Text | Google Scholar

Zhu, Z., Wang, S. X., and Woodcock, C. E. (2015). Improvement and expansion of the mask algorithm: Cloud, cloud shadow, and snow detection for Landsats 4–7, 8, and Sentinel 2 images. Remote Sens. Environ. 159, 269–277. doi: 10.1016/j.rse.2014.12.014

CrossRef Full Text | Google Scholar