Molecular Generation for Desired Transcriptome Changes With Adversarial Autoencoders

Gene expression profiles are useful for assessing the efficacy and side effects of drugs. In this paper, we propose a new generative model that infers drug molecules that could induce a desired change in gene expression. Our model—the Bidirectional Adversarial Autoencoder—explicitly separates cellular processes captured in gene expression changes into two feature sets: those related and unrelated to the drug incubation. The model uses related features to produce a drug hypothesis. We have validated our model on the LINCS L1000 dataset by generating molecular structures in the SMILES format for the desired transcriptional response. In the experiments, we have shown that the proposed model can generate novel molecular structures that could induce a given gene expression change or predict a gene expression difference after incubation of a given molecular structure. The code of the model is available at https://github.com/insilicomedicine/BiAAE.

Introduction

Following the recent advances in machine learning, deep generative models found many applications in biomedicine, including drug discovery, biomarker development, and drug repurposing (Mamoshina et al., 2016; Zhavoronkov, 2018). A promising approach to drug discovery is conditional generation, where a machine learning model learns a distribution p(x | y) of molecular structures x with given property y. Such models can generate molecules with a given synthetic accessibility, binding energy, or even activity against a given protein target (Kadurin et al., 2016; Polykovskiy et al., 2018a).

In this paper, we studied how conditional models scale to a more complex biological property; specifically, we have studied how drug incubation influences gene expression profiles. Using the LINCS L1000 (Duan et al., 2014) dataset, we build a joint model p(x, y) on molecular structures x and induced gene expression changes y.

In many conditional generation tasks, x completely defines y. For example, molecular structure completely defines its synthetic accessibility score. For our task, however, some transcriptome changes are unrelated to the drug effect on cells, and we cannot infer them only from an incubated drug.

We propose a new model—the Bidirectional Adversarial Autoencoder—that learns a joint distribution p(x, y) of objects and conditions. The model decomposes objects and their properties into three feature parts: shared features s common to both x and y; exclusive features z_x relevant only to x and not y; and exclusive features z_y relevant only to y and not x: p(x, y) = p(s, z_x, z_y). For the transcriptomes and drugs, shared features s may contain pharmacophore properties, target protein information, binding energy, and inhibition level; exclusive features z_x may describe the remaining structural information; and z_y may represent unrelated cellular processes. As features s are common to both x and y, the model can extract them from both x and y.

The paper is organized into sections: Related Work surveys related work; Models presents the proposed Bidirectional Adversarial Autoencoder; Experimental Evaluation compares and validates the models on two datasets: the toy Noisy MNIST dataset of hand-written digits and LINCS L1000 dataset of small molecules with corresponding gene expression changes; and Conclusion concludes the paper.

Related Work

Conditional generative models generate objects x from a conditional distribution p(x | y), with y usually being limited to class labels. The Adversarial Autoencoder (AAE) (Makhzani et al., 2015) consists of an autoencoder with a discriminator on the latent representation z that tries to make the latent space distribution indistinguishable from a prior distribution p(z); its conditional extension—Supervised AAE (Makhzani et al., 2015)—works well for simple conditions but can violate the conditions in other cases (Polykovskiy et al., 2018b). Conditional Generative Adversarial Networks (CGAN) (Mirza and Osindero, 2014) supplied the condition as an auxiliary input to both generator and discriminator. Perarnau et al. (2016) inverted CGANs, allowing us to edit images by changing the labels y. In FusedGAN (Bodla et al., 2018), a GAN generated a generic “structure prior” with no supervision, and a CGAN generated an object x from condition y and the latent representation learned by the unconditional GAN. Other papers explored applications of Conditional AAE models to the task of image modification (Antipov et al., 2017; Lample et al., 2017; Zhang et al., 2017).

CausalGAN (Kocaoglu et al., 2018) allowed components of the condition to have a dependency structure in the form of a causal model making conditions more complex. The Bayesian counterpart of AAE, the Variational Autoencoder (VAE) (Kingma and Welling, 2013), also had a conditional version (Sohn et al., 2015a), where conditions improved structured output prediction. CycleGAN (Zhu et al., 2017) examined a related task of object-to-object translation.

Multimodal learning models (Ngiam et al., 2011) and multi-view representation models (Wang et al., 2016a) explored translations between different modalities, such as image to text. Wang et al. (2016b) presented a VAE-based generative multi-view model. Our Bidirectional Adversarial Autoencoder provided explicit decoupling of latent representations and brought the multi-view approach into the AAE framework, where the basic Supervised AAE-like models (Makhzani et al., 2015) did not yield correct representations for sampling (Polykovskiy et al., 2018b).

Information decoupling ideas have been previously applied in other contexts: Yang et al. (2015) disentangled identity and pose factors of a 3D object; adversarial architecture from Mathieu et al. (2016) decoupled different factors in latent representations to transfer attributes between objects; Creswell et al. (2017) used VAE architecture with separate encoders for class label y and latent representation z, forcing z to exclude information about y; InfoVAE (Zhao et al., 2017) maximized mutual information between input and latent features; and Li et al. (2019) proposed a VAE modification that explicitly learns a “disentangled” representation s to predict the class label and a “non-interpretable” representation z that contains the rest of the information used for decoding.

InfoGAN (Chen X. et al., 2016) maximized mutual information between a subset of latent factors and the generator distribution. FusedGAN (Bodla et al., 2018) generated objects from two components, where only one component contains all object-relevant information. Hu et al. (2018) explicitly disentangles different factors in the latent representation and maps a part of the latent code to a particular external information.

Conditional Generation for Biomedicine

Machine learning has numerous applications in biomedicine and drug discovery (Gawehn et al., 2016; Mamoshina et al., 2016; Ching et al., 2018). Deep neural networks demonstrated positive results in various tasks, such as prediction of biological age (Putin et al., 2016; Mamoshina et al., 2018a; Mamoshina et al., 2019), prediction of targets and side effects Aliper et al., 2017; Mamoshina et al., 2018b; West et al., 2018), and applications in medicinal chemistry (Lusci et al., 2013; Ma et al., 2015).

Alongside large-scale studies that measure cellular processes, deep learning applications explore transcriptomics (Aliper et al., 2016b; Chen Y. et al., 2016); these works study cellular processes and their change following molecular perturbations. Deep learning has also been applied to pathway analysis (Ozerov et al., 2016), the prediction of protein functions (Liu, 2017), the discovery of RNA binding proteins (Zheng et al., 2017), the discovery of binding patterns of transcription factors (Qin and Feng, 2017), medical diagnostics based on omics data (Chaudhary et al., 2017), and the analysis of DNA and RNA sequences (Budach and Marsico, 2018).

In drug discovery, apart from predicting pharmacological properties and learning useful representations of small molecules (Duvenaud et al., 2015; Aliper et al., 2016a; Kuzminykh et al., 2018), deep learning is being widely applied to the generation of molecules (Sanchez and Aspuru-Guzik, 2018). Multiple authors have published models that generate new molecules that are similar to the training data or molecules with predefined properties (Kadurin et al., 2017a; Kadurin et al., 2017b; Segler et al., 2017 Gómez-Bombarelli et al., 2018). AI-generated molecules have also been tested in vitro (Polykovskiy et al., 2018b). Reinforcement learning and generative models further enabled the generation of complex non-differentiable objectives, such as novelty (Guimaraes et al., 2017; Putin et al., 2018a; Putin et al., 2018b). Generative models aim to eliminate the bottleneck of traditional drug development pipelines by providing promising new lead molecules for a specific target and automating the initial proposal of lead molecules with desired properties. Recently, Zhavoronkov et al. (2019) developed a model GENTRL to discover potent inhibitors of discoidin domain receptor 1 (DDR1) in 21 days.

Models

In this section, we introduce Unidirectional and a Bidirectional Adversarial Autoencoders and discuss their applications to conditional modeling. While we have focused on an example of molecular generation for transcriptome changes, in general, our model is not limited to these data types and can be used for generation in other domains.

Supervised Adversarial Autoencoder

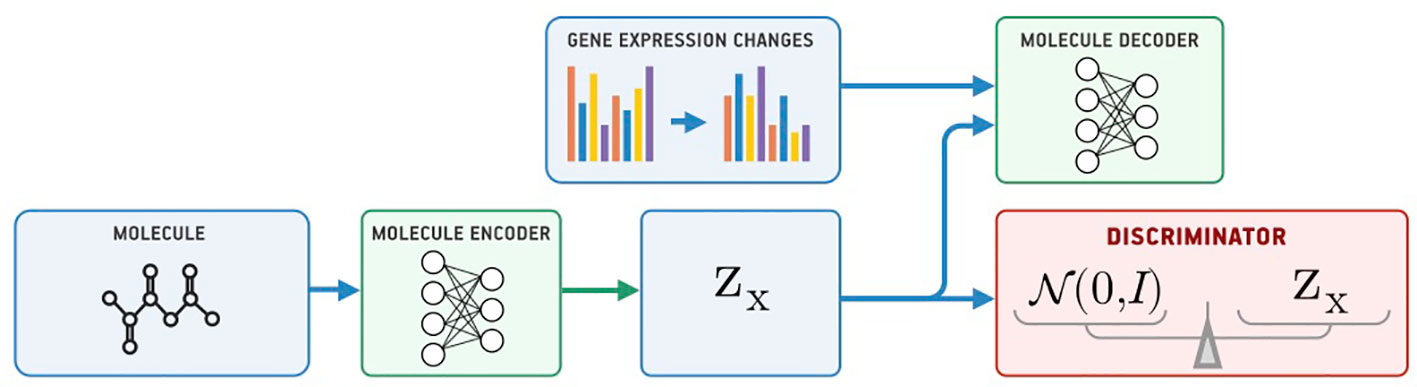
Our model for conditional generation is based on a Supervised Adversarial Autoencoder (Supervised AAE, SAAE) (Makhzani et al., 2015) shown in Figure 1. The Supervised AAE learns three neural networks—an encoder E_x, a generator (decoder) G_x, and a discriminator D. The encoder maps a molecule x onto a latent representation z = E_x(x), and a generator reconstructs the molecule back from z and gene expression changes y: G_x(z, y). We trained a discriminator D to distinguish latent codes from samples of the prior distribution p(z) and modified the encoder to make the discriminator believe that encoder’s outputs are samples from the prior distribution:

$\begin{array}{ll}\underset{E_{\mathit{x}},G_{\mathit{x}}}{\min }\underset{D}{\max }{\lambda }_1{\mathbb{E}}_{\mathit{x},\mathit{y}\sim p_{\text{d}}\left(\mathit{x},\mathit{y}\right)}{l}_{\text{rec}}^{\mathit{x}}\left(\mathit{x},G_{\mathit{x}}\left(E_{\mathit{x}}\left(\mathit{x}\right),\mathit{y}\right)\right)+{\mathbb{E}}_{z\sim p\left(\mathit{z}\right)}\log D\left(\mathit{z}\right)+{\mathbb{E}}_{\mathit{x}\sim p_{\text{d}}\left(\mathit{x}\right)}\log (1-D\left(E_{\mathit{x}}\left(\mathit{x}\right)\right)),& (1)\end{array}$

FIGURE 1

Figure 1 The Supervised Adversarial Autoencoder model (SAAE).

where $l_{\text{rec}}^x$ is a similarity measure between the original and reconstructed molecule, and p_d(x, y) is the data distribution. Hyperparameter λ₁ balances reconstruction and adversarial losses. We trained the model by alternately maximizing the loss in Equation 1 with respect to the parameters of D and minimizing it with respect to the parameters of E_x and G_x (Goodfellow et al., 2014).

Besides passing gene expression changes y directly to the generator, we could also train an autoencoder (E_y, G_y) on y and pass its latent codes to the molecular decoder G_x (Figure 2). We call this model a Latent Supervised Adversarial Autoencoder (Latent SAAE). Its optimization problem is:

$\begin{array}{ll}\underset{E_{\mathit{x}},E_{\mathit{y}},G_{\mathit{x}},G_{\mathit{y}}}{\min }\underset{D}{\max }{\lambda }_1{\mathbb{E}}_{\mathit{x},\mathit{y}\sim p_{\text{d}}\left(\mathit{x},\mathit{y}\right)}{l}_{\text{rec}}^{\mathit{x}}\left(\mathit{x},G_{\mathit{x}}\left(E_{\mathit{x}}\left(\mathit{x}\right),E_{\mathit{y}}\left(\mathit{y}\right)\right)\right)+{\lambda }_2{\mathbb{E}}_{\mathit{y}\sim p_{\text{d}}\left(\mathit{y}\right)}{l}_{\text{rec}}^{\mathit{y}}\left(\mathit{y},G_{\mathit{y}}\left(E_{\mathit{x}}\left(\mathit{y}\right)\right)\right)+{\mathbb{E}}_{\mathit{z}\sim p\left(\mathit{z}\right)}\log D\left(\mathit{z}\right)+{\mathbb{E}}_{\mathit{x}\sim p_{\text{d}}\left(\mathit{x}\right)}\log (1-D\left(E_{\mathit{x}}\left(\mathit{x}\right)\right)).& (2)\end{array}$

FIGURE 2

Figure 2 The Latent Supervised Adversarial Autoencoder model (Latent SAAE).

Hyperparameters λ₁ and λ₂ balance object and condition reconstruction losses as well as the adversarial loss.

Bidirectional Adversarial Autoencoder

Both SAAE and Latent SAAE models learn conditional distribution p(x | y) of molecules for specific transcriptome changes. In this paper, we learned a joint distribution p(x, y) instead. Our model is symmetric in that it can generate both x for a given y and y for a given x. We assume that the data are generated with a graphical model shown in Figure 3. Latent variables z_x and z_y are exclusive parts that represent features specific only to molecules or transcriptome changes. Latent variable s represents a shared part that describes features significant for both molecules and expression changes. To produce a new data point, we sampled exclusive (z_x, z_y) and shared (s) parts independently and used generative distributions G_x (x | s, z_x) and G_y (y | s, z_y) to produce x and y.

FIGURE 3

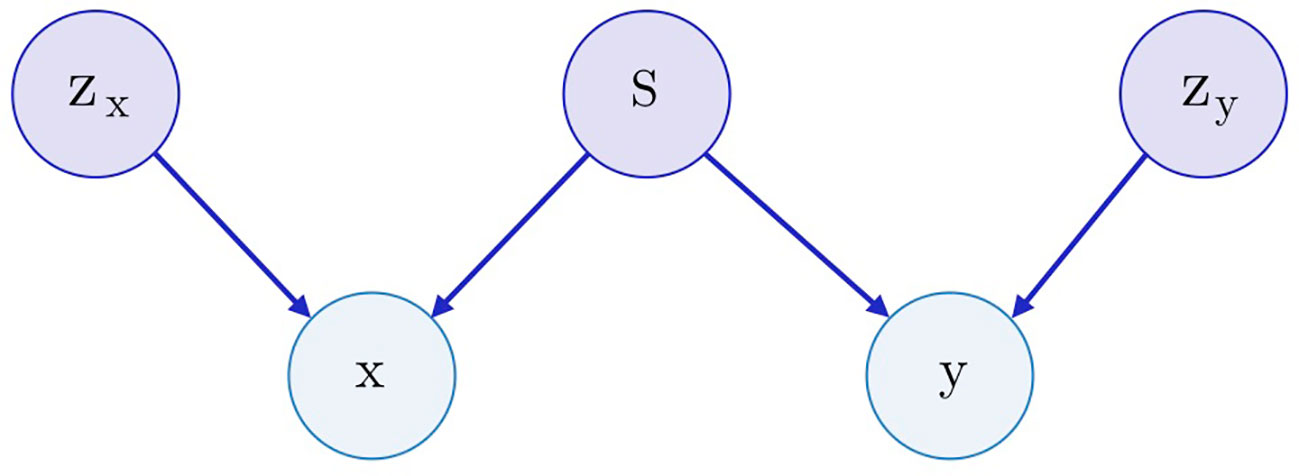
Figure 3 The underlying graphical model of the data: molecules x, gene expression changes y, three latent variables correspond to the exclusive (z_x, z_y) and shared (s) features between x and y.

To train a model, we used inference networks that predict values of s, z_x, and z_y: E_x(z_x | x), E_y(z_y | y), and E(s | x, y) = E_x(s | x) = E_y(s | y). Note that we used two separate networks for inference of s from one of x and y to perform conditional sampling (when only one of x or y is known). For example, to sample p(x | y), we would do the following steps:

$\begin{array}{ll}\mathit{s}\sim E_{\mathit{y}}(\mathit{s}|\mathit{y}),{\mathit{z}}_{\mathit{x}}\sim p\left({\mathit{z}}_x\right),\mathit{x}\sim G_{\mathit{x}}\left(\mathit{s},{\mathit{z}}_{\mathit{x}}\right).& (3)\end{array}$

For the molecule, s may describe its pharmacophore—binding points that are recognized by macromolecules. For the gene expression, s may describe affected proteins. Note that we can infer pharmacophore from a list of affected genes and vice versa. The exclusive part z_x of a molecule describes the remaining structural parts besides the pharmacophore points. The exclusive part z_y of a transcriptome describes cellular processes that influence the expression but are not caused by the drug.

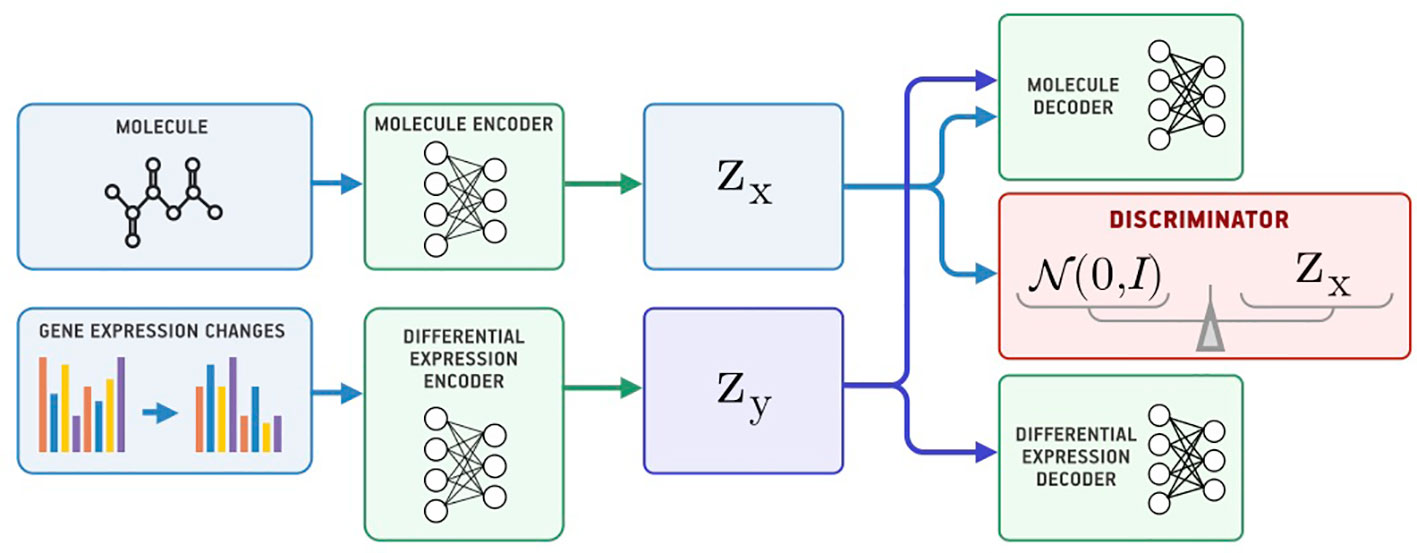
Figure 4 shows the proposed Bidirectional AAE architecture. We used two deterministic encoders E_x and E_y that infer latent codes from molecules and transcriptomes:

$\begin{array}{ll}\left({\mathit{z}}_{\mathit{x}},{\mathit{s}}_{\mathit{x}}\right)=E_{\mathit{x}}\left(\mathit{x}\right),\left({\mathit{z}}_{\mathit{y}},{\mathit{s}}_{\mathit{y}}\right)=E_{\mathit{y}}\left(\mathit{y}\right).& (4)\end{array}$

FIGURE 4

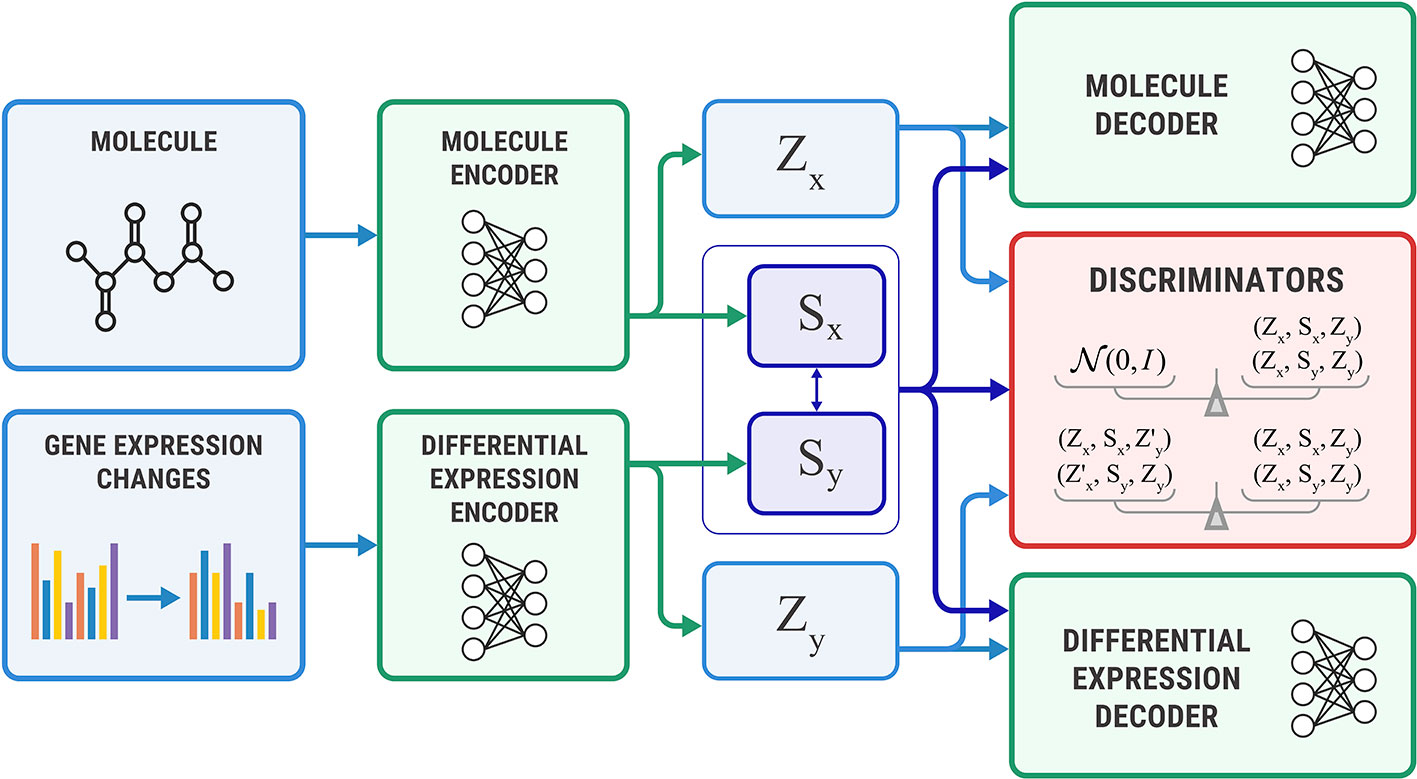
Figure 4 The Bidirectional Adversarial Autoencoders model. The discriminators ensure that three latent code components are independent and indistinguishable from the prior distribution.

Two deterministic decoders (generators) G_x and G_y reconstruct molecules x and gene expression changes y back from the latent codes:

$\begin{array}{ll}\mathit{x}=G_{\mathit{x}}\left({\mathit{z}}_{\mathit{x}},{\mathit{s}}_{\mathit{x}}\right),\mathit{y}=G_{\mathit{y}}\left({\mathit{z}}_{\mathit{y}},{\mathit{s}}_{\mathit{y}}\right)& (5)\end{array}$

The objective function consists of three parts, each capturing restrictions from the graphical model—the structure of the shared representation, reconstruction quality, and independence of shared and exclusive representations.

Shared loss ensures that shared representations extracted from the molecule s_x and gene expression s_y are close to each other, as suggested by the graphical model:

$\begin{array}{ll}\underset{E_{\mathit{x}},E_{\mathit{y}}}{\min }{\mathrm{ ℒ}}_{\text{shared}}={\mathbb{E}}_{\mathit{x},\mathit{y}\sim P\text{d}\left(\mathit{x},\mathit{y}\right)}\Vert {\mathit{s}}_{\mathit{x}}-{\mathit{s}}_{\mathit{y}}{\Vert }_2^2.& (6)\end{array}$

Reconstruction loss ensures that decoders reconstruct molecules and gene expressions back from the latent codes produced by the encoders. We also use a cross-reconstruction loss, where molecular decoder E_x uses shared part s_y from a gene expression encoder E_y for reconstruction and vice versa:

$\begin{array}{ll}\underset{E_{\mathit{x}},E_{\mathit{y}},G_{\mathit{x}}}{\min }{ℒ}_{\text{rec}}^x={\mathbb{E}}_{\mathit{x}\sim p_{\text{d}}\left(\mathit{x}\right)}{l}_{\text{rec}}^{\mathit{x}}\left(\mathit{x},G_{\mathit{x}}\left({\mathit{z}}_{\mathit{x}},{\mathit{s}}_{\mathit{x}}\right)\right)+{\mathbb{E}}_{\mathit{x},\mathit{y}\sim p_{\text{d}}\left(\mathit{x},\mathit{y}\right)}{l}_{\text{rec}}^{\mathit{x}}\left(\mathit{x},G_{\mathit{x}}\left({\mathit{z}}_{\mathit{x}},{\mathit{s}}_{\mathit{y}}\right)\right)& (7)\end{array}$

$\begin{array}{ll}\underset{E_{\mathit{x}},E_{\mathit{y}},G_{\mathit{y}}}{\min }{ℒ}_{\text{rec}}^y={\mathbb{E}}_{\mathit{y}\sim p_{\text{d}}\left(\mathit{y}\right)}{l}_{\text{rec}}^{\mathit{y}}\left(\mathit{y},G_{\mathit{x}}\left({\mathit{z}}_{\mathit{y}},{\mathit{s}}_{\mathit{y}}\right)\right)+{\mathbb{E}}_{\mathit{x},\mathit{y}\sim p_{\text{d}}\left(\mathit{x},\mathit{y}\right)}{l}_{\text{rec}}^{\mathit{y}}\left(\mathit{y},G_{\mathit{y}}\left({\mathit{z}}_{\mathit{x}},{\mathit{s}}_{\mathit{y}}\right)\right)& (8)\end{array}$

where $l_{\text{rec}}^{\mathit{x}}$ and $l_{\text{rec}}^{\mathit{y}}$ are some distance measures in the molecules and gene expression space.

Discriminator loss is an objective that encourages distributions p(s), p(z_x), and p(z_y) to be independent, which means that shared and exclusive parts must learn different features. This restriction comes from a graphical model. It also encourages p(s), p(z_x), and p(z_y) to be standard Gaussian distributions N(0, I) to perform a sampling scheme from Equation 3. We optimized the discriminator in an adversarial manner (Goodfellow et al., 2014) similar to SAAE:

$\begin{array}{ll}\underset{E_{\mathit{x}},E_{\mathit{y}},G_{\mathit{x}},G_{\mathit{y}}}{\min }\underset{D}{\max }{ℒ}_{\text{adv}}={\mathbb{E}}_{{\mathit{s}}^{\prime },{{\mathit{z}}^{\prime }}_{\mathit{x}},{{\mathit{z}}^{\prime }}_y\sim p\left(\mathit{s}\right)p\left({\mathit{z}}_{\mathit{x}}\right)p\left({\mathit{z}}_{\mathit{y}}\right)}\log D\left({{\mathit{z}}^{\mathbf{\prime }}}_{\mathit{x}},{\mathit{s}}^{\mathbf{\prime }},{{\mathit{z}}^{\mathbf{\prime }}}_{\mathit{y}}\right)+\frac{1}{2}{\mathbb{E}}_{\mathit{x},\mathit{y}\sim p_{\text{d}}\left(\mathit{x},\mathit{y}\right)}\log \left(1-D({\mathit{z}}_{\mathit{x}},{\mathit{s}}_{\mathit{x}},{\mathit{z}}_{\mathit{y}})\right)+\frac{1}{2}{\mathbb{E}}_{\mathit{x},\mathit{y}\sim p_{\text{d}}\left(\mathit{x},\mathit{y}\right)}\log \left(1-D({\mathit{z}}_{\mathit{x}},{\mathit{s}}_{\mathit{y}},{\mathit{z}}_{\mathit{y}})\right)& (9)\end{array}$

Note that since the target distribution for adversarial training is factorized, we expected that the trained model would learn independence of s, z_x, and z_y.

Additional discriminator losses We also added additional discrimination objective to explicitly encourage independence of z_x from (s_y, z_y) and z_y from (s_x, z_x):

$\begin{array}{ll}\underset{E_{\mathit{x}},E_{\mathit{y}},G_{\mathit{x}},G_{\mathit{y}}}{\min }\underset{D}{\max }{ℒ}_{\text{info}}={\mathbb{E}}_{\mathit{x},\mathit{y}\sim p_{\text{d}}\left(\mathit{x},\mathit{y}\right)}{\mathbb{E}}_{{\mathit{y}}^{\prime }\sim p_{\text{d}}\left(\mathit{y}\right)}\left[\log D\left({\mathit{z}}_{\mathit{x}},{\mathit{s}}_{\mathit{x}},{\mathit{z}}_{\mathit{y}}\right)+\log \left(1-D({\mathit{z}}_{\mathit{x}},{\mathit{s}}_{\mathit{x}},{{\mathit{z}}^{\prime }}_{\mathit{y}})\right)\right]+{\mathbb{E}}_{\mathit{x},\mathit{y}\sim p_{\text{d}}\left(\mathit{x},\mathit{y}\right)}{\mathbb{E}}_{{\mathit{x}}^{\prime }\sim p_{\text{d}}\left(\mathit{x}\right)}\left[\log D\left({\mathit{z}}_{\mathit{x}},{\mathit{s}}_{\mathit{y}},{\mathit{z}}_{\mathit{y}}\right)+\log \left(1-D({{\mathit{z}}^{\mathbf{\prime }}}_{\mathit{x}},{\mathit{s}}_{\mathit{y}},{\mathit{z}}_{\mathit{y}})\right)\right],& (10)\end{array}$

where ${z^{\prime }}_x$ is an exclusive latent code of x′, and ${z^{\prime }}_y$ is an exclusive latent code of y′. In practice, we obtain z_x′ and z_y′ by shuffling z_x and z_y in each batch.

Combining these objectives, the final optimization problem becomes a minimax problem that can be solved by alternating gradient descent with respect to encoder and decoder parameters, and gradient ascent with respect to the discriminator parameters:

$\begin{array}{ll}\underset{E_{\mathit{x}},E_{\mathit{y}},G_{\mathit{x}},G_{\mathit{y}}}{\min }\underset{D}{\max }{\lambda }_1{ℒ}_{\text{shared}}+{\lambda }_2{ℒ}_{\text{rec}}^x+{\lambda }_3{ℒ}_{\text{rec}}^y+{ℒ}_{\text{adv}}+{ℒ}_{\text{info}}.& (11)\end{array}$

The hyperparameters λ₁, λ₂, and λ₃ balance different objectives. In general, we optimize lambdas based on the performance of BiAAE on the holdout set in terms of the target metrics, such as estimated negative conditional log-likelihood. In practice, we found that optimal values of lambdas yielded the gradients of loss components on a similar scale.

Unidirectional Adversarial Autoencoder

The Bidirectional AAE can generate molecules that cause given transcriptome changes and transcriptome changes caused by a given molecule. However, if we only need conditional generation of molecules p(x | y), we simplify the model by removing the encoder of s_x. The encoder E_x returns only an exclusive part: z_x = E_x(x). For this model, we derived the objective from Equation 11 by setting s_x equal to s_y (Figure 5).

FIGURE 5

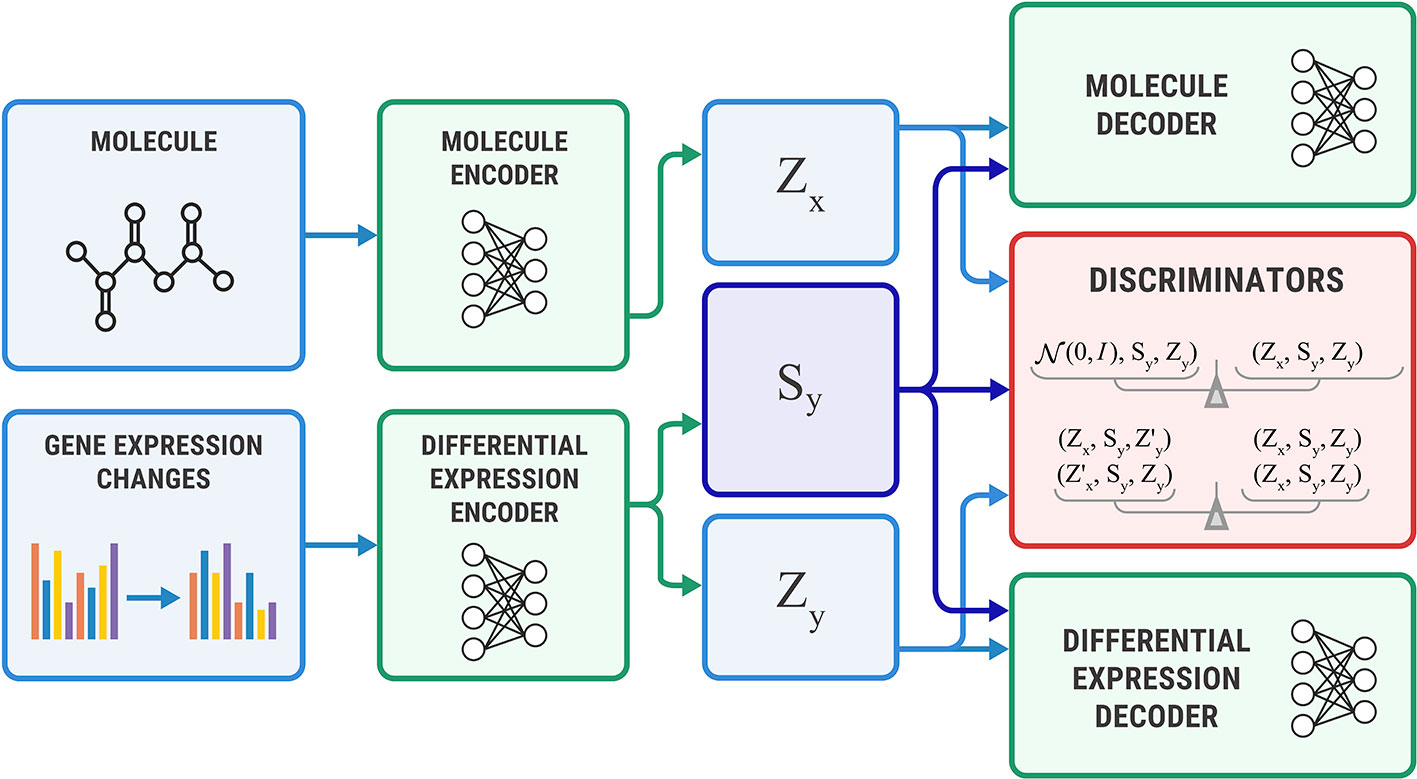
Figure 5 The Unidirectional Adversarial Autoencoder: a simplified version of a Bidirectional Adversarial Autoencoder for generating from p(x|y). The discriminator part ensures that the three latent code components are independent, and the object’s exclusive latent code is indistinguishable from the prior distribution.

Experimental Evaluation

In this section, we have described the experimental setup and presented numerical results on the toy Noisy MNIST dataset and a LINCS L1000 dataset (Duan et al., 2014) of gene expression data.

Noisy MNIST

We start by validating our models on the Noisy MNIST (Wang et al., 2015) dataset of image pairs (x, y), for which we know the correct features in the shared representation s. The image x is a handwritten digit randomly rotated by an angle in [−π/4,π/4]. The image y is also a randomly rotated version of another image containing the same digit as x but with strong additive Gaussian noise. As a result, the only common feature between x and y is the digit. Bidirectional and Unidirectional AAEs should learn to store only the information about the digit in s.

The train-validation-test splits contain 50,000, 10,000, and 10,000 samples respectively. We set the batch size to 128 and the learning rate to 0.0003, and we used the Adam (Kingma and Ba, 2015) optimizer with β₁ = 0.5, β₂ = 0.9 for models with adversarial training and β₁ = 0.99 and β₁ = 0.999 for others with a single update of autoencoders per a single update of the discriminator. Encoder and decoder architectures were the same for all models, with 12-dimensional z_x, z_y and 4-dimensional s. The encoder had 2 convolutional layers with a number of channels 1 → 32 → 16 with 2D dropout rate 0.2 followed by three fully-connected layers of size 64 → 128 → 128 → 16 with batch normalization. The decoder consisted of 2 fully connected layers followed by 3 transposed convolution layers; the discriminators have two hidden layers with 1024 → 512 units. We set the weights for ℒ_rec to 10 and 0.1 for ℒ_shared. Other λ were set to 1. For Unidirectional AAE, we increased weight for ℒ_info to 100. For baseline models we used similar architectures. Please refer to the Supplementary Material for additional hyperparameters.

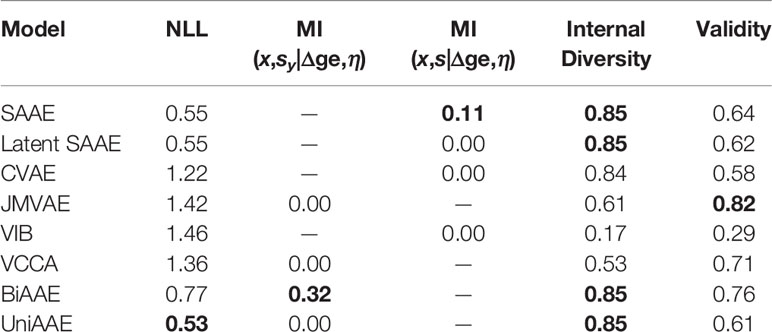
Conditional generative model p(x | y) should produce images with the same digit as image y, which we evaluate by training a separate convolutional neural network to predict the digit from x and comparing the most probable digit to the actual digit of y known from the dataset. We also estimated a conditional mutual information ℳℐ(x,s_y|y) using a Mutual Information Neural Estimation (MINE) (Belghazi et al., 2018) algorithm for BiAAE, UniAAE, JMVAE, and VCCA models. For SAAE, LatentSAAE, CVAE, and VIB we estimated ℳℐ(x,s|y) since these models do not separate embeddings into shared and exclusive parts explicitly. Models with high mutual information extract relevant information from y. A neural network for MINE consisted of a convolutional encoder for x and fully-connected encoder for s_y. We then passed a concatenated embedding through a fully-connected neural network to get a final estimate of mutual information. Results in Table 1 suggest that the BiAAE model extracted relevant mutual information which, besides all, contained information about the digit of y. In Figure 6, we show example samples from the model.

TABLE 1

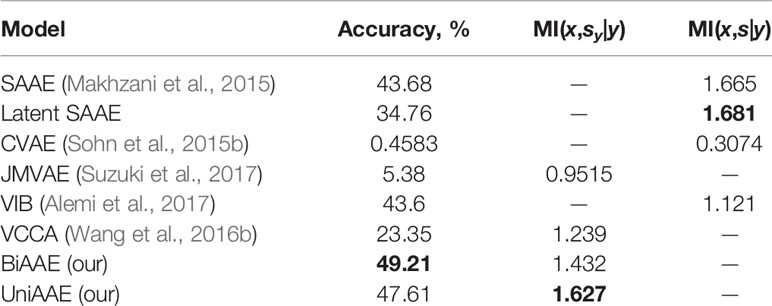
Table 1 Quantitative results for a Noisy MNIST experiment. Conditional Generation section evaluates how often the model produced a correct digit. Latent Codes section estimates the Mutual Information between z_x and s (y for SAAE).

FIGURE 6

Figure 6 Qualitative results on a Noisy MNIST dataset. The figure shows generated images x for a noisy image y (left column) as a condition. Generated images must have the same digit as y.

Differential Gene Expression

In this section, we have validated Bidirectional AAE on a gene expression profiles dataset with 978 genes. We use a dataset of transcriptomes from the Library of Integrated Network-based Cellular Signatures (LINCS) L1000 project (Duan et al., 2014). The database contains measurements of gene expressions before and after cells react with a molecule at a given concentration.

For each cell line, the training set contains experiments characterized by the control (ge_b∈ℝ⁹⁷⁸) and perturbation-induced (ge_a∈ℝ⁹⁷⁸) gene expression profiles. We represented molecular structures in the SMILES format (Weininger, 1988; Weininger et al., 1989). We augmented the dataset by randomly matching control and perturbation-induced measurements from the same plate.

We preprocessed the training dataset by removing molecules with a molecular weight less than 250 and more than 550 Da. We then removed molecules that did not contain any oxygen or nitrogen atoms or contained atoms besides C, N, S, O, F, Cl, Br, and H. Finally, we removed molecules that contained rings with more than eight atoms or tetracyclines. The resulting dataset contained 5,216 unique SMILES. Since the dataset is small, we pretrained an autoencoder on the MOSES (Polykovskiy et al., 2018a) dataset and used its encoder and decoder as initial weights in all models.

For all baseline models on differential gene expressions, we used similar hyperparameters shown in Table 2 (please refer to the Supplementary Material for the exact hyperparameters). In all experiments, we split our dataset into train, validation, and test sets, all containing different drugs. To construct a training example, we sampled a drug-dose pair, a perturbation for this drug and dose, and a control expression from the same plate as the perturbed expression.

TABLE 2

Table 2 Hyperparameters for neural networks training on gene expression data. All neural networks are fully connected, and decoders have an architecture symmetric to the encoders.

We used a two-step encoder for y = (η, Δge) shown in Figure 7, where Δge=ge_a−ge_b. We first embedded Δge with a fully-connected neural network, and then concatenated the obtained representation with a logarithm of concentration η. We passed the resulting vector through a final encoder. The decoder has a symmetric architecture.

FIGURE 7

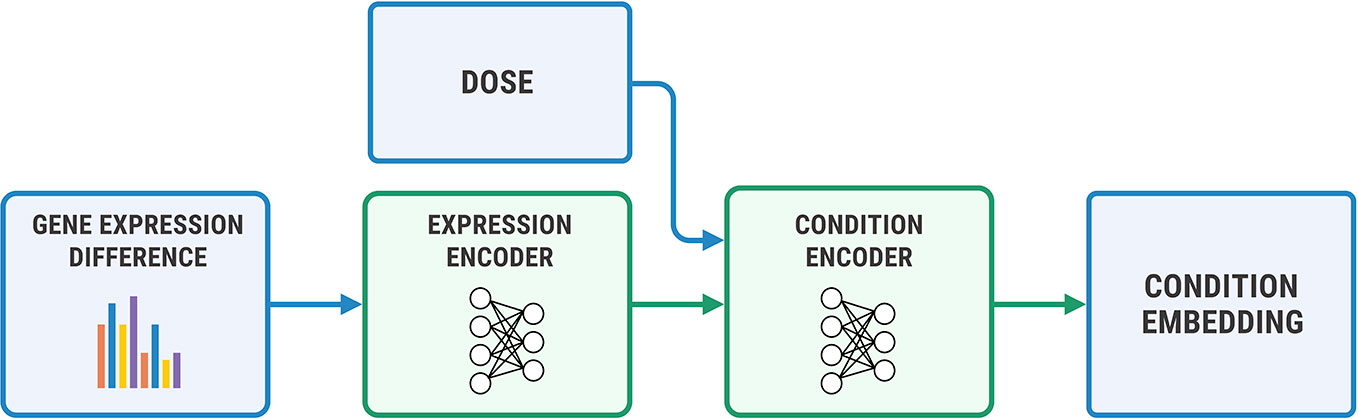
Figure 7 The architecture of the condition encoder for changes in the transcriptome. The input to the expression encoder is the difference between the control and perturbed expressions. We passed the dose to the last layers of the encoder.

Generating Molecular Structures for Gene Expression Profiles

The proposed BiAAE model can generate molecules for given gene expression changes and vice versa. We started by experimenting with the molecular generation (Table 3). In the experiment, we reported a negative log-probability of generating the exact incubated drug x given the dose and gene expression change averaged over tokens log p(x|Δge,η). We also estimated a Mutual Information ℳℐ(x,s_y|Δge,η) similar to the MNIST experiment described above. For each η and Δge, we generated a set of molecules G and estimated a fraction of valid molecules and internal diversity of G:

$\begin{array}{ll}\text{IntDiv}\left(G\right)=1-\frac{1}{\left|G\right|\left(\left|G\right|-1\right)}{\displaystyle \sum _{\begin{array}{c}{m}_1,m_2\in G\\ m_1\ne m_2\end{array}}}T\left(m_1,m_2\right),& (12)\end{array}$

TABLE 3

Table 3 Validation results of conditional generation p(x|Δge,η).

where T is a Tanimoto similarity on Morgan fingerprints. This metric shows whether a model can produce multiple candidates for a given gene expression or collapses to a single molecule.

The proposed BiAAE and UniAAE architectures show the ability to capture the dependencies in the training set and generalize to new objects from the validation set. The BiAAE model provides better mutual information while preserving valid diverse molecules.

Comparing Generated Molecular Structures to Known Active Molecules

In this experiment, we show that the proposed generative model (BiAAE) can produce biologically meaningful results. We used a manually curated database of bioactive molecules ChEMBL 24.1 (Gaulton et al., 2016) and additional profiles of gene expression knockdown from LINCS L1000 (Duan et al., 2014).

The first experiment evaluates molecular generation given a transcriptome change of a small molecule inhibitor of a specific protein. The ChEMBL dataset has experimental data on molecules that inhibit a certain human protein. We chose template molecules that are present in both LINCS molecule perturbation dataset and ChEMBL dataset. We used molecules that had inhibition concentration less than 10 μM IC50 for only one protein.

The condition for molecular generation is a transcriptome change and a dose of a template molecule. Specifically, the condition is a shared part s_y of the gene expression and dose embedding. The model is expected to generate molecules that are similar to known drugs. In Figure 8, for several protein targets, we show a known inhibitor and generated molecules that could induce similar transcriptome profile changes.

FIGURE 8

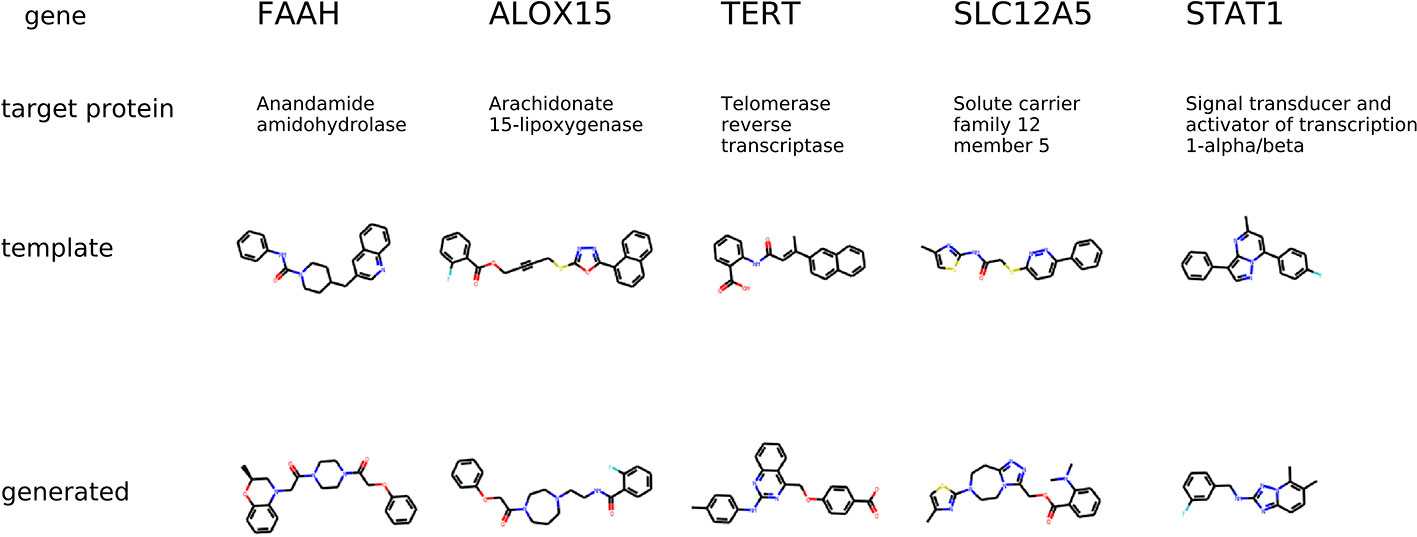
Figure 8 The examples of generated molecules conditioned on gene expression changes from a protein inhibitor; Real most similar inhibitors from ChEMBL are provided for comparison.

The second experiment evaluates molecular generation given a transcriptome change of a specific gene knockdown. The LINCS dataset contains gene knockdown transcriptomes that the model was not trained on. For each gene knockdown, we found a corresponding human protein in the ChEMBL dataset. We chose template molecules that had a proven IC50 less than 10μM for only one protein. The condition for molecular generation is a transcriptome change of a gene knockdown and the most common dose 10 μM in LINCS. The model is expected to generate molecules that produce the same transcriptome change of gene knockdowns.

The condition is different compared to the previous experiment in a way that the gene knockdown expression profile is not induced by a small molecule but rather shows the desired behavior of the potential drug. In Figure 9, we show generated molecules and compare them to known inhibitors of a protein corresponding to a knocked down gene. We expect these molecules to produce similar effects in gene expression to gene knockdown.

FIGURE 9

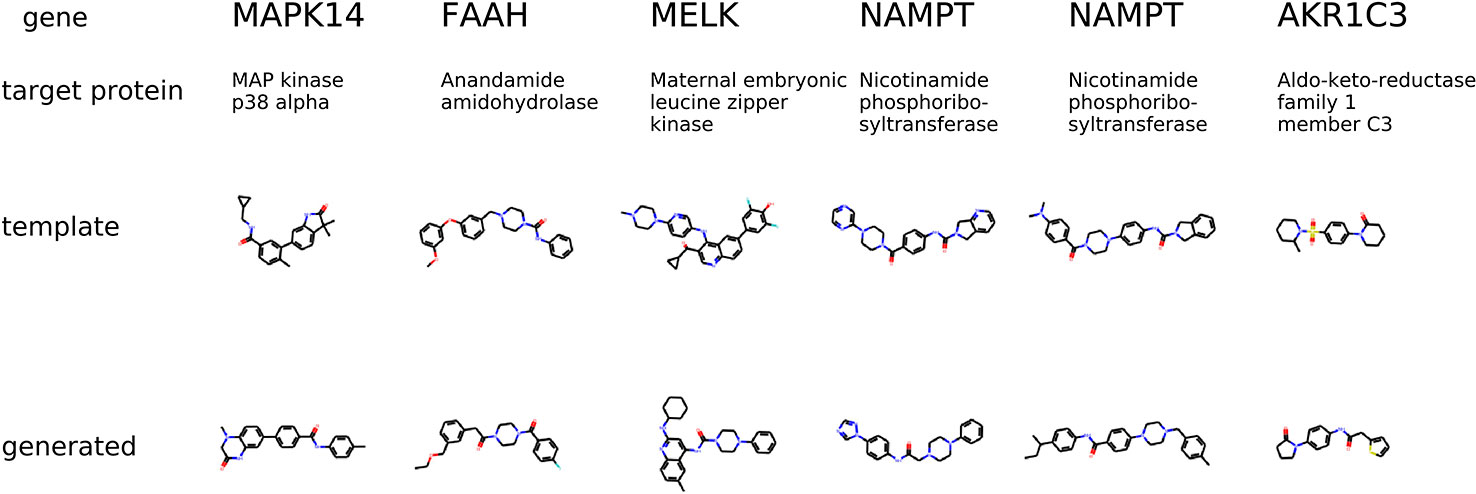
Figure 9 The examples of generated molecules conditioned on gene expression changes from a gene knockdown; Real most similar inhibitors of a knocked down gene are provided for comparison.

Predicting Gene Expression Profiles for an Incubated Drug

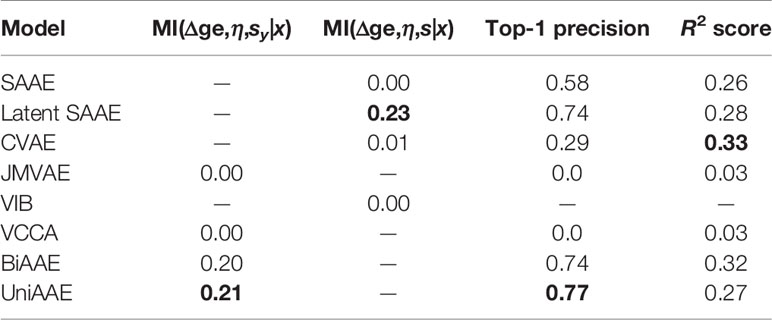
We experimented with predicting gene expression changes after drug incubation (Table 4). First, we report estimated mutual information ℳℐ(Δge,η,s_x|x) similar to the previous experiments. We also report the R² metric, which measures the determination coefficient between the real and predicted (Δge, η) for a given molecule. Finally, we report a top-1 precision metric, which shows the fraction of samples for which the largest absolute change in real and predicted Δge matched.

TABLE 4

Table 4 Validation results of conditional generation p(Δge,η|x).

To compute R² and top-1 precision, we only used drugs that were administered at η = 10 μM concentration. Since we are only interested in a certain concentration, we discarded generated (Δge, η) tuples if η was far from 10 μM (outside the range [−6.5,−5.5] in log₁₀ scale). Note that VIB was not able to generate any gene expression changes near 10 μM.

The experiment demonstrates that proposed UniAAE, BiAAE, and LatentSAAE models generalize well the symmetric task and show good metrics on predicting gene expression changes.

Discussion

The key advantage of the proposed model compared to the previous works is the joint adversarial learning of latent representations of paired objects. This representation improves conditional generation metrics and shows promising results in molecular generation for desired transcriptome changes.

Three discriminator neural networks ensure that the latent representations divided into shared and exclusive parts are more meaningful and useful for the conditional generation. Two additional discriminator losses help the model learn a more expressive shared part and make sure that all three parts are mutually independent.

However, adversarial training slightly complicates the training procedure for the BiAAE model. In comparison with other baseline models, the training loss contains more terms, each with a coefficient to tune. In general, we tune these coefficients using grid search, and we select the best coefficients according to the generative metrics on the validation set. In practice, we simplify the grid search and use the same coefficient for the adversarial terms λ₁=λ₄=λ₅ since the corresponding losses have values on the same scale. We choose the search space for coefficients λ₂,λ₃ in a way that the second and third terms provide the gradient in the same scale as the other terms.

Another problem that arises when we use the adversarial approach is the instability of training. The instability is the consequence of the minimax nature of adversarial training (Goodfellow et al., 2014). To overcome the instability, we use approaches described in (Bang and Shim, 2018), i.e., we use shallow discriminators and Adam optimizer with parameters β₁=0.5,β₂=0.9.

Conclusion

In this work, we proposed a Bidirectional Adversarial Autoencoder model for the generation of molecular structures for given gene expression changes. Our AAE-based architecture extracts shared information between molecule and gene expression changes and separates it from the remaining exclusive information. We showed that our model outperforms baseline conditional generative models on the Noisy MNIST dataset and the generation of molecular structures for the desired transcriptome changes.

Data Availability Statement

The code and datasets for this study are available at https://github.com/insilicomedicine/BiAAE.

Author Contributions

RS and MK implemented the BiAAE and baseline models and conducted the experiments. RS, AK, and AA prepared the datasets. RS, MK, AK, and DP derived the BiAAE and UniAAE models. RS, AZ, AK, SN, and DP wrote the manuscript. AK and DP supervised the project.

Conflict of Interest

RS, MK, AZ, AK, AA, and DP work for Insilico Medicine, a commercial artificial intelligence company. SN works for Neuromation OU, a company engaged in AI development through synthetic data and generative models.

Acknowledgments

The original idea for molecular generation for a specific transcriptional or proteomic profile, a technology used broadly at Insilico Medicine, was proposed in 2016 by Dr. Alex Zhavoronkov, who is the co-author of the patent covering this technology.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphar.2020.00269/full#supplementary-material.

References

Alemi, A. A., Fischer, I., Dillon, J. V., Murphy, K. (2017). Deep Variational Information Bottleneck. Int. Conf. Learn. Representations.

Google Scholar

Aliper, A., Plis, S., Artemov, A., Ulloa, A., Mamoshina, P., Zhavoronkov, A. (2016a). Deep Learning Applications for Predicting Pharmacological Properties of Drugs and Drug Repurposing Using Transcriptomic Data. Mol. Pharm. 13, 2524–2530. doi: 10.1021/acs.molpharmaceut.6b00248

PubMed Abstract | CrossRef Full Text | Google Scholar

Aliper, A. M., Plis, S. M., Artemov, A. V., Ulloa, A., Mamoshina, P., Zhavoronkov, A. (2016b). Deep learning applications for predicting pharmacological properties of drugs and drug repurposing using transcriptomic data. Mol. Pharm. 13 7, 2524–2530. doi: 10.1021/acs.molpharmaceut.6b00248

CrossRef Full Text | Google Scholar

Aliper, A., Jellen, L., Cortese, F., Artemov, A., Karpinsky-Semper, D., Moskalev, A., et al. (2017). Towards Natural Mimetics of Metformin and Rapamycin. Aging (Albany NY) 9, 2245–2268. doi: 10.18632/aging.101319

PubMed Abstract | CrossRef Full Text | Google Scholar

Antipov, G., Baccouche, M., Dugelay, J. (2017). Face aging with conditional generative adversarial networks. In. 2017 IEEE Int. Conf. Image Process. (ICIP)., 2089–2093. doi: 10.1109/ICIP.2017.8296650

CrossRef Full Text | Google Scholar

Bang, D., Shim, H. (2018). “Improved training of generative adversarial networks using representative features,” in Proceedings of the 35th International Conference on Machine Learning, vol. 80. Eds. Dy, J., Krause, A. (Stockholmsmässan, Stockholm Sweden: PMLR), 433–442.

Google Scholar

Belghazi, M. I., Baratin, A., Rajeshwar, S., Ozair, S., Bengio, Y., Hjelm, D., et al. (2018). “Mutual information neural estimation,” in Proceedings of the 35^th International Conference on Machine Learning, JMLR.org vol. 80. Eds. Dy, J., Krause, A.(Stockholmsmässan, Stockholm Sweden: PMLR)), 531–540.

Google Scholar

Bodla, N., Hua, G., Chellappa, R. (2018). “Semi-supervised FusedGAN for conditional image generation,” in Proceedings of the European Conference on Computer Vision (ECCV), Springer, Cham 669–683.

Google Scholar

Budach, S., Marsico, A. (2018). pysster: Learning Sequence and Structure Motifs in DNA and RNA Sequences using Convolutional Neural Networks. bioRxiv. 34, 3035–3037 doi: 10.1093/bioinformatics/bty222

CrossRef Full Text | Google Scholar

Chaudhary, K., Poirion, O. B., Lu, L., Garmire, L. X. (2017). Deep learning–based multi-omics integration robustly predicts survival in liver cancer. Clin. Cancer Res. 24, 1248–1259. doi: 10.1158/1078-0432.ccr-17-0853

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., Duan, Y., Houthooft, R., Schulman, J., Sutskever, I., Abbeel, P. (2016). “Infogan: Interpretable representation learning by information maximizing generative adversarial nets,” in Advances in Neural Information Processing Systems, vol. 29 . Eds. Lee, D. D., Sugiyama, M., Luxburg, U. V., Guyon, I., Garnett, R. (Curran Associates, Inc. in Red Hook, NY) 2172–2180.

Google Scholar

Chen, Y., Li, Y., Narayan, R., Subramanian, A., Xie, X. (2016). Gene expression inference with deep learning. Bioinformatics 32, 1832–1839. doi: 10.1093/bioinformatics/btw074

PubMed Abstract | CrossRef Full Text | Google Scholar

Ching, T., Himmelstein, D. S., Beaulieu-Jones, B. K., Kalinin, A. A., Do, B. T., Way, G. P., et al. (2018). Opportunities and Obstacles for Deep Learning in Biology and Medicine. J. R Soc. Interface 15, 141, 1–47. doi: 10.1098/rsif.2017.0387

CrossRef Full Text | Google Scholar

Creswell, A., Bharath, A. A., Sengupta, B. (2017). Conditional autoencoders with adversarial information factorization. CoRR. abs/1711.05175.

Google Scholar

Duan, Q., Flynn, C., Niepel, M., Hafner, M., Muhlich, J. L., Fernandez, N. F., et al. (2014). LINCS canvas browser: Interactive web app to query, browse and interrogate LINCS L1000 gene expression signatures. Nucleic Acids Res. 42, W449–W460. doi: 10.1093/nar/gku476

PubMed Abstract | CrossRef Full Text | Google Scholar

Duvenaud, D. K., Maclaurin, D., Iparraguirre, J., Bombarell, R., Hirzel, T., Aspuru-Guzik, A., et al. (2015). “Convolutional networks on graphs for learning molecular fingerprints,” in Advances in Neural Information Processing Systems, vol. 28. Eds. Cortes, C., Lawrence, N. D., Lee, D. D., Sugiyama, M., Garnett, R. (Curran Associates, Inc. in Red Hook, NY) 2224–2232.

Google Scholar

Gaulton, A., Hersey, A., Nowotka, M., Bento, A. P., Chambers, J., Mendez, D., et al. (2016). The ChEMBL database in 2017. Nucleic Acids Res. 45, D945–D954. doi: 10.1093/nar/gkw1074

PubMed Abstract | CrossRef Full Text | Google Scholar

Gawehn, E., Hiss, J. A., Schneider, G. (2016). Deep learning in drug discovery. Mol. Inf. 35, 3–14. doi: 10.1002/minf.201501008

CrossRef Full Text | Google Scholar

Gómez-Bombarelli, R., Wei, J. N., Duvenaud, D., Hernández-Lobato, J. M., Sánchez-Lengeling, B., Sheberla, D., et al. (2018). Automatic chemical design using a data-driven continuous representation of molecules. ACS Cent. Sci. 4, 268–276. doi: 10.1021/acscentsci.7b00572

PubMed Abstract | CrossRef Full Text | Google Scholar

Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., et al. (2014). “Generative adversarial nets,” in Advances in Neural Information Processing Systems, Curran Associates, Inc. vol. 27. , 2672–2680.

Google Scholar

Guimaraes, G. L., Sanchez-Lengeling, B., Farias, P. L. C., Aspuru-Guzik, A. (2017). Objective-reinforced generative adversarial networks (ORGAN) for sequence generation models. CoRR. abs/1705.10843.

Google Scholar

Hu, Q., SzabÃ, A., Portenier, T., Favaro, P., Zwicker, M. (2018). “Disentangling factors of variation by mixing them,” in The IEEE Conference on Computer Vision and Pattern Recognition, vol. 2797. (CVPR).

Google Scholar

Kadurin, A., Aliper, A., Kazennov, A., Mamoshina, P., Vanhaelen, Q., Khrabrov, K., et al. (2016). The cornucopia of meaningful leads: Applying deep adversarial autoencoders for new molecule development in oncology. Oncotarget 8, 10883–10890. doi: 10.18632/oncotarget.14073

CrossRef Full Text | Google Scholar

Kadurin, A., Aliper, A., Kazennov, A., Mamoshina, P., Vanhaelen, Q., Khrabrov, K., et al. (2017a). The Cornucopia of Meaningful Leads: Applying Deep Adversarial Autoencoders for New Molecule Development in Oncology. Oncotarget 8, 10883–10890. doi: 10.18632/oncotarget.14073

PubMed Abstract | CrossRef Full Text | Google Scholar

Kadurin, A., Nikolenko, S., Khrabrov, K., Aliper, A., Zhavoronkov, A. (2017b). druGAN: An advanced generative adversarial autoencoder model for de novo generation of new molecules with desired molecular properties in silico. Mol. Pharm. 14, 3098–3104. doi: 10.1021/acs.molpharmaceut.7b00346

PubMed Abstract | CrossRef Full Text | Google Scholar

Kingma, D. P., Ba, J. (2015). Adam: A Method for Stochastic Optimization. Int. Conf. Learn. Representations.

Google Scholar

Kingma, D. P., Welling, M. (2013). Auto-encoding variational bayes. CoRR. abs/1312.6114.

Google Scholar

Kocaoglu, M., Snyder, C., Dimakis, A. G., Vishwanath, S. (2018). CausalGAN: Learning causal implicit generative models with adversarial training. Int. Conf. Learn. Representations.

Google Scholar

Kuzminykh, D., Polykovskiy, D., Kadurin, A., Zhebrak, A., Baskov, I., Nikolenko, S., et al. (2018). 3D Molecular Representations Based on the Wave Transform for Convolutional Neural Networks. Mol. Pharm. 15, 4378–4385. doi: 10.1021/acs.molpharmaceut.7b01134

PubMed Abstract | CrossRef Full Text | Google Scholar

Lample, G., Zeghidour, N., Usunier, N., Bordes, A., Denoyer, L., Ranzato, M. A. (2017). “Fader networks: Manipulating images by sliding attributes,” in Advances in Neural Information Processing Systems 30. Eds. Guyon, I., Luxburg, U. V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R. (Curran Associates, Inc.), 5967–5976.

Google Scholar

Li, Y., Pan, Q., Wang, S., Peng, H., Yang, T., Cambria, E. (2019). Disentangled variational auto-encoder for semi-supervised learning. Inf. Sci. 482, 73–85. doi: 10.1016/j.ins.2018.12.057

CrossRef Full Text | Google Scholar

Liu, X. L. (2017). Deep recurrent neural network for protein function prediction from sequence. bioRxiv. doi: 10.1101/103994

CrossRef Full Text | Google Scholar

Lusci, A., Pollastri, G., Baldi, P. (2013). Deep Architectures and Deep Learning in Chemoinformatics: the Prediction of Aqueous Solubility for Drug-like Molecules. J. Chem. Inf. Model 53, 1563–1575. doi: 10.1021/ci400187y

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, J., Sheridan, R. P., Liaw, A., Dahl, G. E., Svetnik, V. (2015). Deep neural nets as a method for quantitative structure-activity relationships. J. Chem. Inf. Model. 55, 263–274. doi: 10.1021/ci500747n. PMID: 25635324.

PubMed Abstract | CrossRef Full Text | Google Scholar

Makhzani, A., Shlens, J., Jaitly, N., Goodfellow, I. J. (2015). Adversarial Autoencoders. CoRR. abs/1511.05644. 73, 1482–1490.

Google Scholar

Mamoshina, P., Vieira, A., Putin, E., Zhavoronkov, A. (2016). Applications of deep learning in biomedicine. Mol. Pharma. 13, 1445–1454. doi: 10.1021/acs.molpharmaceut.5b00982

CrossRef Full Text | Google Scholar

Mamoshina, P., Kochetov, K., Putin, E., Cortese, F., Aliper, A., Lee, W.-S., et al. (2018a). Population specific biomarkers of human aging: A big data study using south korean, canadian, and eastern european patient populations. Journals Gerontology: Ser. A. 73, 1482–1490. doi: 10.1093/gerona/gly005

CrossRef Full Text | Google Scholar

Mamoshina, P., Volosnikova, M., Ozerov, I. V., Putin, E., Skibina, E., Cortese, F., et al. (2018b). Machine learning on human muscle transcriptomic data for biomarker discovery and tissue-specific drug target identification. Front. Genet. 9, 242. doi: 10.3389/fgene.2018.00242

PubMed Abstract | CrossRef Full Text | Google Scholar

Mamoshina, P., Kochetov, K., Cortese, F., Kovalchuk, A., Aliper, A., Putin, E., et al. (2019). Blood biochemistry analysis to detect smoking status and quantify accelerated aging in smokers. Sci. Rep. 9, 142. doi: 10.1038/s41598-018-35704-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Mathieu, M. F., Zhao, J. J., Zhao, J., Ramesh, A., Sprechmann, P., LeCun, Y. (2016). “Disentangling factors of variation in deep representation using adversarial training,” in Advances in Neural Information Processing Systems, vol. 29. Eds. Lee, D. D., Sugiyama, M., Luxburg, U. V., Guyon, I., Garnett, R. (Curran Associates, Inc. in Red Hook, NY) 5040–5048.

Google Scholar

Mirza, M., Osindero, S. (2014). Conditional generative adversarial nets. CoRR. abs/1411.1784.

Google Scholar

Ngiam, J., Khosla, A., Kim, M., Nam, J., Lee, H., Ng, A. Y. (2011). “Multimodal deep learning,” in Proceedings of the 28th International Conference on International Conference on Machine Learning, vol. 11. (Omnipress, ICML: 2600 Anderson St, Madison, WI, United States), 689–696.

Google Scholar

Ozerov, I. V., Lezhnina, K. V., Izumchenko, E., Artemov, A. V., Medintsev, S., Vanhaelen, Q., et al. (2016). In Silico Pathway Activation Network Decomposition Analysis (iPANDA) as a Method for Biomarker Development. Nat. Commun. 7, 13427. doi: 10.1038/ncomms13427

PubMed Abstract | CrossRef Full Text | Google Scholar

Perarnau, G., van de Weijer, J., Raducanu, B., Álvarez, J. M. (2016). Invertible conditional gans for image editing. Neural Inf. Process. Syst. Workshop Adversarial Training.

Google Scholar

Polykovskiy, D., Zhebrak, A., Sanchez-Lengeling, B., Golovanov, S., Tatanov, O., Belyaev, S., et al. (2018a). Molecular Sets (MOSES): A Benchmarking Platform for Molecular Generation Models. arXiv preprint arXiv:1811.12823.

Google Scholar

Polykovskiy, D., Zhebrak, A., Vetrov, D., Ivanenkov, Y., Aladinskiy, V., Bozdaganyan, M., et al. (2018b). Entangled conditional adversarial autoencoder for de-novo drug discovery. Mol. Pharm. 15, 4398–4405. doi: 10.1021/acs.molpharmaceut.8b00839

PubMed Abstract | CrossRef Full Text | Google Scholar

Putin, E., Mamoshina, P., Aliper, A., Korzinkin, M., Moskalev, A., Kolosov, A., et al. (2016). Deep Biomarkers of Human Aging: Application of Deep Neural Networks to Biomarker Development. Aging (Albany NY) 8, 1021–1033. doi: 10.18632/aging.100968

PubMed Abstract | CrossRef Full Text | Google Scholar

Putin, E., Asadulaev, A., Ivanenkov, Y., Aladinskiy, V., Sanchez-Lengeling, B., Aspuru-Guzik, A., et al. (2018a). Reinforced Adversarial Neural Computer for de Novo Molecular Design. J. Chem. Inf. Model 58, 1194–1204. doi: 10.1021/acs.jcim.7b00690

PubMed Abstract | CrossRef Full Text | Google Scholar

Putin, E., Asadulaev, A., Vanhaelen, Q., Ivanenkov, Y., Aladinskaya, A. V., Aliper, A., et al. (2018b). Adversarial Threshold Neural Computer for Molecular de Novo Design. Mol. Pharm. 15, 4386–4397. doi: 10.1021/acs.molpharmaceut.7b01137

PubMed Abstract | CrossRef Full Text | Google Scholar

Qin, Q., Feng, J. (2017). Imputation for transcription factor binding predictions based on deep learning. PloS Comput. Biol. 13, e1005403+. doi: 10.1371/journal.pcbi.1005403

PubMed Abstract | CrossRef Full Text | Google Scholar

Sanchez, B., Aspuru-Guzik, A. (2018). Inverse molecular design using machine learning: Generative models for matter engineering. Science 361, 360–365. doi: 10.1126/science.aat2663

PubMed Abstract | CrossRef Full Text | Google Scholar

Segler, M. H. S., Kogej, T., Tyrchan, C., Waller, M. P. (2017). Generating focused molecule libraries for drug discovery with recurrent neural networks. ACS Cent. Sci. 4, 120–131. doi: 10.1021/acscentsci.7b00512

PubMed Abstract | CrossRef Full Text | Google Scholar

Sohn, K., Lee, H., Yan, X. (2015a). “Learning structured output representation using deep conditional generative models,” in Advances in Neural Information Processing Systems , vol. 28 . Eds. Cortes, C., Lawrence, N. D., Lee, D. D., Sugiyama, M., Garnett, R. (Curran Associates, Inc. in Red Hook, NY) 3483–3491.

Google Scholar

Sohn, K., Lee, H., Yan, X. (2015b). “Learning structured output representation using deep conditional generative models,” in Advances in Neural Information Processing Systems, vol. 28 . Eds. Cortes, C., Lawrence, N. D., Lee, D. D., Sugiyama, M., Garnett, R. (Curran Associates, Inc.), 3483–3491.

Google Scholar

Suzuki, M., Nakayama, K., Matsuo, Y. (2017). “Joint Multimodal Learning with Deep Generative Models,” in International Conference on Learning Representations Workshop.

Google Scholar

Wang, W., Arora, R., Livescu, K., Bilmes, J. (2015). “On deep multi-view representation learning,” in Proceedings of the 32Nd International Conference on International Conference on Machine Learning - Volume 37. (JMLR.org), ICML’15. 1083–1092.

Google Scholar

Wang, W., Arora, R., Livescu, K., Bilmes, J. A. (2016a). On deep multi-view representation learning: Objectives and optimization. CoRR. abs/1602.01024.

Google Scholar

Wang, W., Lee, H., Livescu, K. (2016b). Deep variational canonical correlation analysis. CoRR. abs/1610.03454.

Google Scholar

Weininger, D., Weininger, A., Weininger, J. L. (1989). SMILES. 2. algorithm for generation of unique SMILES notation. J. Chem. Inf. Comput. Sci. 29, 97–101. doi: 10.1021/ci00062a008

CrossRef Full Text | Google Scholar

Weininger, D. (1988). SMILES, a chemical language and information system. 1. introduction to methodology and encoding rules. J. Chem. Inf. Comput. Sci. 28, 31–36. doi: 10.1021/ci00057a005

CrossRef Full Text | Google Scholar

West, M. D., Labat, I., Sternberg, H., Larocca, D., Nasonkin, I., Chapman, K. B., et al. (2018). Use of Deep Neural Network Ensembles to Identify Embryonic-fetal Transition Markers: Repression of COX7A1 in Embryonic and Cancer Cells. Oncotarget 9, 7796–7811. doi: 10.18632/oncotarget.23748

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, J., Reed, S., Yang, M.-H., Lee, H. (2015). “Weakly-supervised disentangling with recurrent transformations for 3D view synthesis,” in Proceedings of the 28th International Conference on Neural Information Processing Systems, vol. 1. (Cambridge, MA, USA: MIT Press), 1099–1107. NIPS’15.

Google Scholar

Zhang, Z., Song, Y., Qi, H. (2017). Age progression/regression by conditional adversarial autoencoder. IEEE Conf. Comput. Vision Pattern Recogn. (CVPR). 4352–4360. doi: 10.1109/CVPR.2017.463

CrossRef Full Text | Google Scholar

Zhao, S., Song, J., Ermon, S. (2017). InfoVAE: Information maximizing variational autoencoders. CoRR. abs/1706.02262. doi: 10.1609/aaai.v33i01.33015885

CrossRef Full Text | Google Scholar

Zhavoronkov, A., Ivanenkov, Y. A., Aliper, A., Veselov, M. S., Aladinskiy, V. A., Aladinskaya, A. V., et al. (2019). Deep learning enables rapid identification of potent ddr1 kinase inhibitors. Nat. Biotechnol., 1–4. doi: 10.1038/s41587-019-0224-x

CrossRef Full Text | Google Scholar

Zhavoronkov, A. (2018). Artificial intelligence for drug discovery, biomarker development, and generation of novel chemistry. Mol. Pharm. 15, 4311–4313. doi: 10.1021/acs.molpharmaceut.8b00930

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, J., Zhang, X., Zhao, X., Tong, X., Hong, X., Xie, J., et al. (2017). Deep-RBPPred: Predicting RNA binding proteins in the proteome scale based on deep learning. bioRxiv. 8, 15264 doi: 10.1101/210153

CrossRef Full Text | Google Scholar

Zhu, J.-Y., Park, T., Isola, P., Efros, A. A. (2017). Unpaired image-to-image \ translation using cycle-consistent adversarial networks. 2017 IEEE Int. Conf. Comput. Vision (ICCV), 2242–2251. doi: 10.1109/ICCV.2017.244

CrossRef Full Text | Google Scholar