- 1Department of Physics and Astronomy, University of California Davis, Davis, CA, United States
- 2Geballe Laboratory for Advanced Materials and Department of Applied Physics, Stanford University, Stanford, CA, United States
- 3Geballe Laboratory for Advanced Materials, Stanford University, Stanford, CA, United States
- 4Department of Physics, Stanford University, Stanford, CA, United States
The suppression of ferroquadrupolar order in TmVO4 in a magnetic field is well-described by the transverse field Ising model, enabling detailed studies of critical dynamics near the quantum phase transition. We describe nuclear magnetic resonance measurements in pure and Y-doped single crystals. The non-Kramers nature of the ground state doublet leads to a unique form of the hyperfine coupling that exclusively probes the transverse field susceptibility. Our results show that this quantity diverges at the critical field, in contrast to the mean-field prediction. Furthermore, we find evidence for quantum critical fluctuations present near Tm-rich regions in Y-doped crystals at levels beyond which long-range order is suppressed, suggesting the presence of quantum Griffiths phases.
1 Introduction
Unconventional superconductivity tends to emerge in the vicinity of a quantum critical point (QCP), where some form of long-range ordered state is continually suppressed to T = 0 [1–9]. This observation suggests that there may be an important relationship between the superconducting pairing mechanism and the strong quantum fluctuations associated with the QCP, however there are major challenges to understanding the fundamental physics at play in these systems. In practice various approaches can be utilized to tune the ordered state to the QCP. Hydrostatic pressure or magnetic field are thermodynamic variables that are homogeneous throughout the material and can be varied continuously. Doping, on the other hand, offers a convenient method to apply “chemical pressure” or introduce charge carriers, but can introduce electronic heterogeneity at the nanoscale which can complicate interpretation [10, 11]. In such cases it can be difficult to disentangle what experimental observations to ascribe to fundamental properties of a quantum phase transition versus extrinsic effects arising from the long-range effects of the dopants.
In order to better understand the influence of doping in strongly interacting system near a quantum phase transition, it is valuable to study a model system in the absence of superconductivity. TmVO4 is as material that has attracted interest recently because its low temperature properties are well-described by the transverse field Ising model (TFIM), an archetype of quantum criticality [12, 13]. TmVO4 exhibits long-range ferroquadrupolar order in which the Tm 4f orbitals spontaneously align in the same direction, as illustrated in Figure 1. The Tm3+ ions (4f 12 with L = 5, S = 1, J = 6) experience a tetragonal crystal field interaction, and the ground state is well separated by a gap of
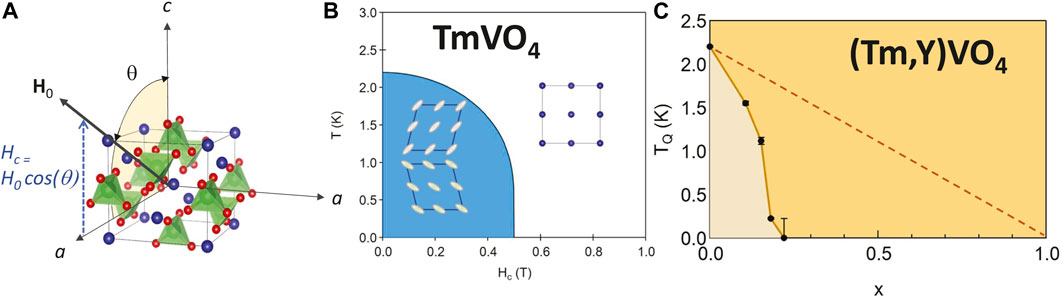
Figure 1. (A) Crystal structure of TmVO4 (I41/amd) with Tm atoms in blue, V atoms lie at the center of green tetrahedra, and oxygen atoms in red. For the studies discussed here, the magnetic field, H0, was rotated in the ac-plane, with an angle θ between H0 and the c axis. The projection of the field along the c-axis is H0 cos θ. (B) Schematic phase diagram of TmVO4 as a function of magnetic field Hc along the c-axis, illustrating the B2g orthorhombic distortion in the ferroquadrupolar state. (C) Phase diagram for Tm1−xYxVO4, reproduced from [14]. The dashed line represents the mean-field result expected purely from dilution.
LiHoF4 is another important material whose physics is well described by the TFIM [21]. There are important differences, however, between LiHoF4 and TmVO4. Although the physics of both systems derives from non-Kramers doublets, the former is a ferromagnet with Ho moments ordering along the c-axis, whereas the latter has ferroquadrupolar order with quadrupolar moments ordering in the plane. As a result, the transverse field direction for LiHoF4 is perpendicular to the c-axis, whereas in TmVO4 the transverse field direction is parallel to c. This fact is crucial for TmVO4 because it also has profound consequences for the hyperfine coupling to neighboring nuclear spins and enables unique measurements of the quantum fluctuations directly. Moreover, since the quadrupolar moments couple to strain fields, long-range order in TmVO4 is particularly sensitive to dopants. Therefore substituting with Y in TmVO4 offers a unique opportunity to investigate how the quantum phase transition changes in response to the disorder and random fields introduced by the dopant atoms.
2 Couplings to non-Kramers doublet
2.1 Lattice interaction
2.1.1 Ground state wavefunctions
The ground state wavefunctions of the Tm in the D4h point group symmetry of the TmVO4 lattice are given by:
in the |Jz⟩ basis, where the αi coefficients are determined by the details of the crystal field Hamiltonian [16, 19]. Is is straightforward to show that Jx,y operators vanish in the subspace spanned by these states. On the other hand, there are three other operators that do not vanish:
where the σα are the Pauli matrices. Physically, the first two operators represent quadrupolar moments with B1g and B2g symmetries, respectively, and the third represents a magnetic moment along the z direction. The conjugate fields to these moments are strain ϵB1g = ϵxx − ϵyy, ϵB2g = ϵxy, and magnetic field Hz, respectively. Here the strain tensor is defined as ϵij = (∂ui/∂xj − ∂uj/∂xi)/2, where u(x) is the displacement from the equilibrium lattice positions.
2.1.2 Cooperative Jahn-Teller effect
Because the quadrupolar moments have non-uniform charge distributions, they can interact with a strained lattice via a bilinear coupling of the form −ηiɛiσi, where ηi is an electron-lattice coupling constant. This coupling renormalizes the elastic constant, leading to a softening in both the B1g and B2g channels, but is strongest for the B2g channel for TmVO4. It can be shown that this leads to an effective coupling between the quadrupolar moments:
where the sum is over the lattice sites, and J(l − l′) is an Ising interaction between the Tm quadrupolar moments [17, 18]. The coupling depends on the details of the lattice, and because it is mediated by strain fields, it can extend well beyond just nearest neighbor sites. This interaction leads to long-range order in the three-dimensional TmVO4 lattice below a temperature TQ = 2.15 K, with finite expectation values of ±⟨σy⟩. This ferroquadrupolar order is accompanied by a B2g lattice distortion as illustrated in Figure 1B [22].
2.2 Zeeman interaction
The interaction between a non-Kramers doublet in a tetragonal environment and a magnetic field is given by:
where Hx,y is a magnetic field along the (x, y) direction, gJ = 7/6 for Tm3+ and gc and b depend on the crystal field Hamiltonian [23]. These parameters have been measured for TmVO4 to be gc = 10.21 and b/kB = 0.082 K−1 [16]. Note that H couples quadratically in the x and y directions, rather than linearly for a Kramers doublet. A field in the z direction splits the doublet linearly, and acts as a transverse field for the Ising interaction in Eq. 1.
2.2.1 Induced moments for perpendicular fields
The Zeeman interaction can also be written as
For sufficiently low perpendicular fields, Hx,y ≤ 3 T, the second order Zeeman interaction in the perpendicular direction will be less than 0.1kBTQ, and can be safely ignored. At higher fields, Hx and Hy can also act as either longitudinal or transverse fields for the Ising order, and can in fact be used to detwin the ferroquadrupolar order [24].
2.3 Transverse field Ising model for ferroquadrupolar order
The low temperature degrees of the Tm electronic degrees of freedom are thus captured by the sum
where the sum is over the Tm lattice sites. Here we have ignored the small contribution from the perpendicular component of the magnetic field. Mean field theory predicts a QCP for a c-axis field of TQ/gcμB ≈ 0.3 T, which is close to the experimental value of
2.4 Coupling to nuclear spins
2.4.1 Hyperfine coupling to 51V
In most insulators the hyperfine coupling between a localized electron spin and a nearby nucleus arises due to the direct dipolar interaction and can be described as
where Azz and C are constants [23]. In the absence of magnetic field, there is only a coupling along the z direction, corresponding to the transverse field direction. To determine the values of the coupling C, note that Eq. 4 can be re-written in terms of the effective magnetic moments:
where hα are the hyperfine fields at the nucleus created by the Tm moments. Using the measured values of hx/μx = −0.0336 T/μB and hz/μz = 0.0671 T/μB obtained by comparing the Knight shift versus susceptibility, we can then identify:
these values of the hyperfine fields were obtained via direct Knight shift measurements, but agree well with the calculated direct dipolar fields in the TmVO4 lattice [25].
2.4.2 Quadrupolar coupling to 51V
51V has spin I = 7/2 and a nuclear quadrupolar moment Q = 0.052 barns. Note that this moment is several orders of magnitude smaller than the electronic quadrupolar moment of the Tm 4f orbitals that undergo the ferroquadrupolar ordering at TQ. Nevertheless, the extended charge distribution of the latter can contribute to the electric field gradient (EFG) tensor at the V nuclear site, which in turn couples to Q. As a result, the nuclear spins can couple to the pseudospin via the nuclear quadrupolar interaction [23]:
Note that B2 = B1, and corresponds to a 45° rotation of the principal axes of the EFG. The last term, P, is determined by the local charge distribution in the VO4 tetrahedra, and is independent of the 4f orbitals. The EFG asymmetry parameter is given by B1⟨σx⟩/P, and can be measured through detailed spectral measurements as a function of angle in the ordered state. We estimate P ≈ 15 μK and B1 = B2 ≈ 0.22 μK [24].
Of all the terms in
2.4.3 Hyperfine coupling to 169Tm
169Tm has a spin of I = 1/2, and experiences a hyperfine coupling but no quadrupolar interaction. By symmetry, the form of the hyperfine coupling must also be described by Eq. 5. In this case, however, the coupling Azz ≈ 160 mK is nearly three orders of magnitude larger than that for the 51V due to the on-site coupling [26]. As a result, the spin lattice relaxation rate in the paramagnetic state is so fast that the 169Tm resonance has not been observed. On the other hand, Bleaney and Wells reported 169Tm in the ferroquadrupolar state, where they found a large shift of the resonance frequency for fields applied in the perpendicular direction [16]. In this case, the shift is due to the induced moments from the ordered Tm quadrupoles. The shift exhibited a two-fold rotation symmetry as the field was rotated in the perpendicular direction, which they attributed to the second order Zeeman interaction and the induced magnetization. The two-fold rotation reflects the orthorhombic crystal structure in the ferroquadrupolar state.
3 Nuclear magnetic resonance studies
Recently several studies have been conducted of the 51V NMR in TmVO4 in order to better understand the nature of the quantum phase transition [19, 24, 25]. In principle, one could perform zero-field NMR (or nuclear quadrupolar resonance, NQR) and gradually apply a c-axis field to investigate the behavior as the field is tuned to the QCP. In this case, the NMR resonance frequency is given by |γH + nνzz|, where γ = 11.193 MHz/T is the gyromagnetic ratio, νzz = 0.33 MHz, and n = −3, … , + 3. Thus the highest transition frequency at H = 0 is only 1 MHz, but experiments below 1 MHz are difficult because the signal-to-noise ratio varies as f 3/2, where f is frequency [27]. To overcome this challenge, a perpendicular field of 3.3 T was applied along the [100] direction of the crystal (corresponding to the x or y directions in Eq. 2), and the crystal was rotated to project a small component along the c-axis, as illustrated in Figure 1A.
Spectra for several different values of Hc are shown in Figure 2A. For Hc = 0, the spectra consist of seven transitions separated by a quadrupolar interaction P ∼ 300 kHz, as seen in Figure 2A. As Hc increases, the anisotropic Knight shift and EFG tensors alter the frequencies of the various quadrupolar satellites in a well-controlled fashion, shown in Figure 2B. The separation between the seven peaks gradually reduces and vanishes at the magic angle (where
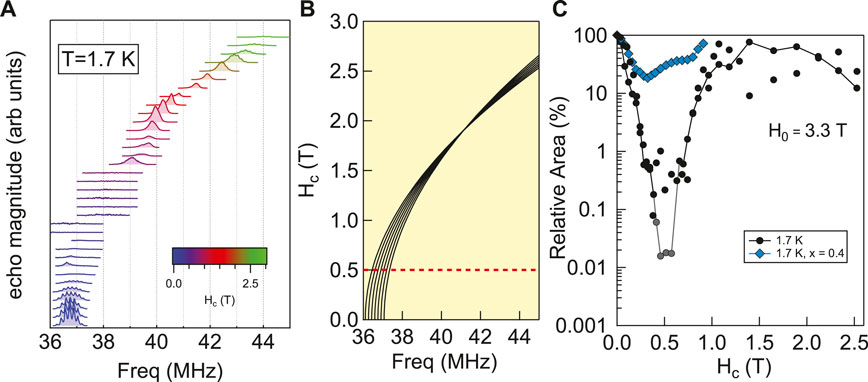
Figure 2. (A) Spectra of 51V for several different values of Hc as the crystal is rotated (see Figure 1A). (B) Calculated frequencies of the seven transitions as a function of Hc. The transitions merge at the magic angle, and then separate at higher values of Hc. The dashed red line corresponds to the critical field,
3.1 Transverse field susceptibility
The decoherence of an NMR signal can often be extended by applying refocusing pulses [28]. The simplest such pulse sequence consists of a spin echo, in which a single π pulse at time t/2 reverses the direction of precession and refocuses static field inhomogeneities. Noise fluctuations at time scales shorter than t/2, however, will lead to decoherence and loss of signal. In general, the decay envelope, L(t), of a spin-echo can be related to the noise fluctuations of the environment. In TmVO4, this quantity can be written as:
where Szz is the dynamical structure factor for the transverse field fluctuations:
and F(x) = 8 sin4(x/4) is a filter function for the spin echo pulse sequence, which takes into account the refocusing nature of the spin echo π pulse [29, 30]. The spectral area, shown in Figure 2C, is proportional to L(t) at fixed t corresponding to the pulse spacing in the spin echo experiment. Because the hyperfine coupling in TmVO4 is solely along the transverse field direction, the nuclei are invisible to the longitudinal degrees of freedom. Only Szz(ω), the noise spectrum in the transverse direction, contributes to the decoherence of the nuclear spins. This anisotropic coupling is highly unusual, but it enables us to probe the transverse fluctuations without any contamination from the longitudinal fluctuations, which diverge strongly at the QCP. The filter function acts to remove the static or low frequency (ω ≤ 105 Hz) components of the fluctuations, which are dominated by thermal fluctuations [19, 31]. The remaining contributions to Szz(ω), and hence to the decay of L(t), is from quantum fluctuations, which exist at finite frequency. This is because they arise from the intrinsic time evolution due to the many-body Hamiltonian, which has a finite gap except at the QCP. The fact that L(t) reaches a minimum at the QCP indicates that these quantum fluctuations are largest here. Importantly, these extend to finite temperature, even exceeding TQ. These results thus imply that there is a broad region of phase space, a “quantum critical fan,” where quantum fluctuations are present.
An open question is how does the transverse susceptibility behave in the vicinity of the quantum phase transition? In mean-field theory at T = 0, χzz remains constant in the ordered state, and vanishes for
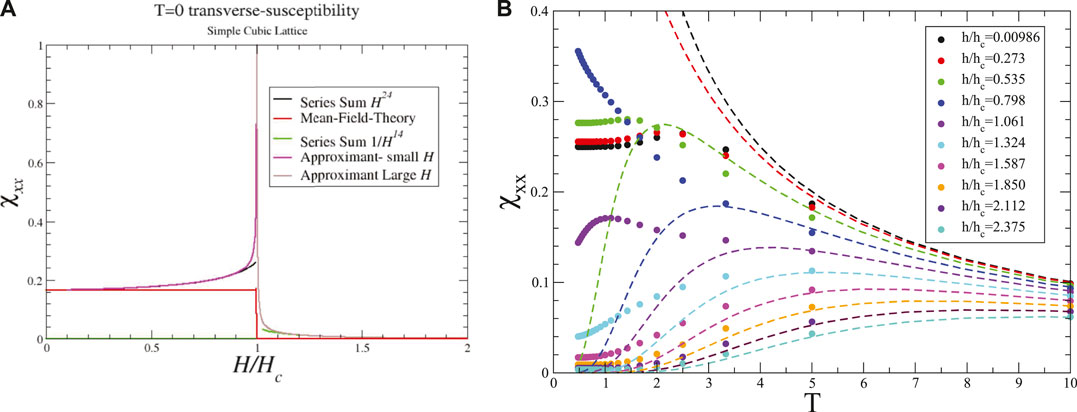
Figure 3. (A) Transverse susceptibility as a function of field for a simple cubic lattice at T = 0 in mean-field theory and in 3D short-range models. (B) Temperature dependence of the transverse field susceptibility at several different values of the transverse field calculated numerically for small periodic clusters of the square-lattice. The dashed lines are the mean field result, and the solid points of the same color are the results of numerical calculations.
3.2 Fidelity susceptibility
Understanding the mechanisms of decoherence is a key problem for quantum computing, and the behavior of a central spin coupled to a well-controlled environment is an important theoretical model that has been studied extensively [31, 33]. In the case where the central spin (or qubit) is coupled to a 1D TFIM via a hyperfine coupling along the transverse field direction, the decoherence of the qubit can be elegantly expressed in terms of the overlap of the wavefunction of the environment at different times and values of the transverse field. In fact, the 51V spins coupled to the ferroquadrupolar ordering in TmVO4 maps well to this model, but with a 3D lattice for the environment. Although the central spin model was originally developed for a single spin coupled to an environment, it is straightforward to generalize to an ensemble of nuclear spins in a lattice, each with its own identical coupling [20]. Thus, TmVO4 offers a unique opportunity to experimentally study this model.
Importantly, this connection offers a new approach to understanding NMR decoherence in terms of the quantum fidelity of the environment, which is defined as the modulus of the overlap between two states: F = |⟨Ψ′|Ψ⟩|. In the case of the central spin model, the two states are
On the surface, this picture differs from the conventional NMR picture in which decoherence arises due to the presence of stochastic fluctuations of the hyperfine field, which can be quantitatively measured via Bloch-Wangsness-Redfield theory:
4 NMR studies of Y substitution
Replacing Tm with Y suppresses the long range ferroquadrupolar order in Tm1−xYxVO4 to zero at xc ≈ 0.22, as illustrated in Figure 1C [14]. Y has no 4f electrons and thus lacks any magnetic or quadrupolar moments, so it acts to dilute the interactions between the Tm quadrupolar moments. The rapid suppression with doping is surprising because mean-field theory predicts a much weaker doping dependence: TQ ∼ 1 − x. Y doping also suppresses ferromagnetic order in LiHoF4, however in this case long-range order persists until x = 0.95 [45]. The reason for the difference between the TmVO4 and LiHoF4 is that the Y creates strain fields that couple to the ferroquadrupolar order in the former. Y is slightly larger than Tm, thus it creates local distortions in the lattice that couple to the Tm quadrupolar moments [14]. This behavior is similar to that of a random field Ising model (RFIM), and causes TQ to be suppressed much faster with Y doping [46]. The local strain fields may have components with B1g symmetry, which couples to σx and is a transverse field, as well as fields with B2g symmetry, which couples to σy and is a longitudinal field.
Y substitution offers an opportunity to test whether the decoherence observed in the pure TmVO4 is due to quantum critical fluctuations. Figure 2C shows that for x = 0.40, which has no long-range ferroquadruplar order, the relative spectral area does not change significantly at
4.1 NMR spectra
NMR spectra in doped systems are generally broader than in undoped materials because the dopants often give rise to inhomogeneity. As seen in Figure 4A, the spectra of the pure TmVO4 and YVO4 consist of seven clear resonances with small linewidths, but these resonances grow progressively broader with doping. Each of the seven resonances broadens equally between 0 ≤ x ≤ 0.1. This behavior indicates that the broadening mechanism is not quadrupolar inhomogeneity, but rather a Knight shift inhomogeneity. The red dotted lines in Figure 4A are fits to the spectra, and the data in panel (e) show how the Gaussian width, σ, varies with doping for the spectra that can be clearly fit. It is surprising that even though random strain fields are clearly present and rapidly suppressing TQ, they apparently do not significantly alter the local EFG at the V sites. In many other strongly-correlated systems, doping usually causes significant quadrupolar broadening [47–50]. In Tm1−xYxVO4, the larger Y atoms slightly displace the O and V in their vicinity [14]. On the other hand, it is possible that the VO4 tetrahedra may not be significantly distorted upon Y substitution. Also, there are two main contributions to the EFG: a lattice term arising from the arrangement of charges, and an on-site term that is determined by the electronic configuration of the local electronic orbitals [28]. It is reasonable that the latter term dominates the EFG at the V, and that the electronic configuration of the V and O orbitals remain relatively unperturbed by Y doping.
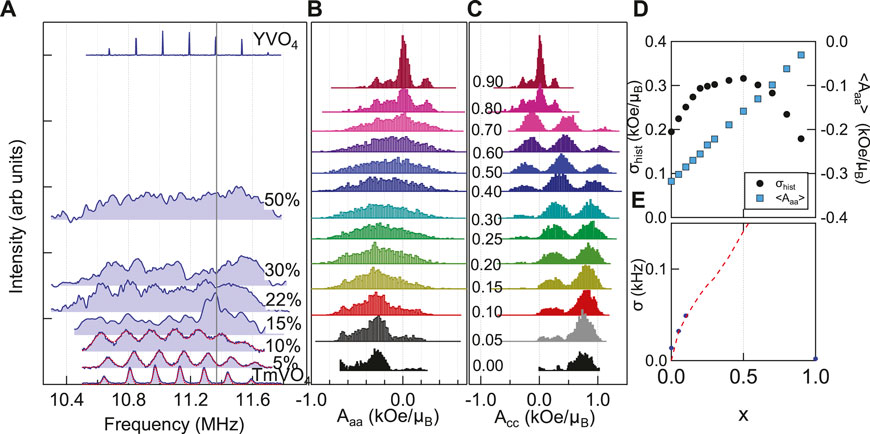
Figure 4. (A) Spectra for several values of x measured in an external field H0 = 1 T oriented perpendicular to the c-axis at 1.8 K for all but the x = 1 case. For YVO4 the spectrum was measured at 4.5 T and 10 K, but has been shifted to lower frequency by γΔH (ΔH = 3.9 T) to coincide with the other spectra. The red dotted lines are fits as described in the text. (B,C) Histograms of the hyperfine coupling constants, Aaa and Acc, respectively, for a series of Y dopings for simulations as described in the text. (D) Average ⟨Aaa⟩ and standard deviation, σ, of the distributions shown in (B) as a function of Y doping, x. (E) The measured Gaussian linewidth of the spectra shown in (A) as a function of Y doping. The dashed red line was calculated using the computed standard deviation, as discussed in the text.
4.1.1 Numerical simulations
To investigate the inhomogeneity of the magnetic environments, we computed the direct dipolar hyperfine couplings, Aaa and Acc, to the V sites in a 9 × 9 × 9 superlattice in which a fraction of the Tm sites are randomly removed. Histograms of these couplings are shown in Figures 4B, C for different Y concentrations. The sum is dominated by the two nearest neighbor Tm sites along the c-axis direction (see Figure 1A). The distribution for the perpendicular direction (Aaa) broadens with doping, but does not exhibit any structure. Figure 4D shows how the mean, ⟨Aaa⟩, and standard deviation, σhist, of the histograms vary with Y concentration. The standard deviation increases linearly with doping, which agrees with the experimental observation of the linewidth. The dashed red line in Figure 4E represents the expected magnetic linewidth in a field of H0 = 1 T, as in the experiment. This quantity is given by σ(x)|K|γH0/⟨Aaa⟩, where K = −0.66%. Here we have subtracted (in quadrature) the standard deviation of the histogram of the pure TmVO4 case, which includes boundary effects:
4.1.2 Effect of c-axis field
Figure 5A shows how the spectra for the x = 0.40 sample vary as the crystal is rotated in a fixed field, similar to the data shown in Figure 2A for the x = 0 case. As Hc increases, there is no significant wipeout at
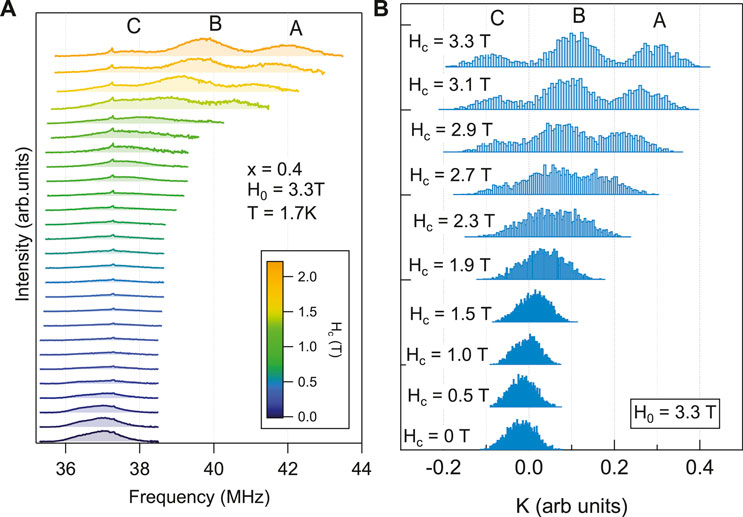
Figure 5. (A) Spectra of Tm1−xYxVO4 with x = 0.40 for several different values of Hc. For Hc ≳ 1.5 T, three peaks are discernable, A, B, and C. (B) Computed spectra based on the histograms of hyperfine couplings shown in Figures 4B, C for several different values of Hc for x = 0.40.
As seen in Figure 4B these different V sites should not be discernible for a field H0 ⊥ c. On the other hand, as H0 rotates towards the c-axis, three distinct peaks should emerge. This behavior is demonstrated in Figure 5B, which displays the histograms of the Knight shift, K(θ) = Aaaχaa sin2θ + Accχcc cos2θ, for several different values of Hc = H0 cos θ. Here χαα is the static susceptibility, and we assume χcc/χaa = 3 for concreteness. The three sites are indeed discernible for sufficiently large Hc, which agrees well with the observations shown in panel (a). Moreover, the relative intensity of the peaks (A: B: C = 0.32 : 0.49: 0.18) also agrees well with the observed spectra (0.33 ± 0.01 : 0.51 ± 0.01 : 0.16 ± 0.01). We therefore conclude that site A corresponds to V with 2 n.n. Tm, site B with 1 n.n. Tm, and site C with 0 n.n. Tm. This property enables us to learn about the electronic inhomogeneity by measuring the relaxation at the different sites.
4.2 Spin lattice relaxation rate
Figure 6A displays
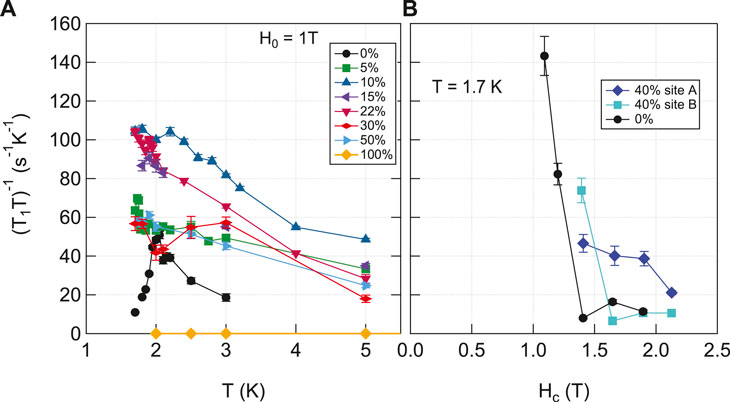
Figure 6. (A)
Sites A, B and C can be discerned when there is a finite Hc component present. Figure 6B compares
Inhomogeneous dynamics in the disordered lattice may also explain the fact that the spectra in Figure 5A appear to exhibit an increasing intensity for Hc ≳ 1.5 T once the A and B peaks emerge. If local clusters of Tm continue to exhibit quantum critical fluctuations at these sites, then
5 Conclusion
TmVO4 offers a unique new experimental platform to investigate quantum critical phenomena and the effects of doping. The unique properties of the non-Kramers doublet in this system not only gives rise to the unusual Ising ferroquadrupolar order, but also ensures that the nuclear spins in this system only couple to the transverse field degrees of freedom. Studies of the Tm1−xYxVO4 uncovered several unexpected results. First, despite the presence of random strain fields, the EFG at the V sites remains unperturbed, at least for low doping concentrations. As the doping level increases and the long range ferroquadrupolar order vanishes, the spin lattice relaxation rate for the V sites is enhanced, before decreasing for doping levels that exceed the critical concentration. However, we find evidence that quantum critical fluctuations remain present for V sites that belong to Tm-rich clusters, even beyond the critical doping level, suggesting the presence of quantum Griffiths phases in the Y-doped system. It is unclear whether such isolated Tm clusters also experience random transverse or longitudinal strain fields. Further studies of this doped system will shed important light on how quantum fluctuations are destroyed by disorder.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
Y-HN: Data curation, Investigation, Writing–review and editing. IV: Data curation, Investigation, Writing–review and editing. CC: Investigation, Writing–review and editing. YL: Resources, Writing–review and editing. MZ: Resources, Writing–review and editing. PM: Resources, Writing–review and editing. RS: Conceptualization, Formal Analysis, Investigation, Writing–review and editing. IF: Conceptualization, Resources, Writing–review and editing. NC: Conceptualization, Writing–original draft, Writing–review and editing.
Funding
The authors declare financial support was received for the research, authorship, and/or publication of this article. Work at UC Davis was supported by the NSF under Grants No. DMR-1807889 and DMR-2210613, as well as the UC Laboratory Fees Research Program ID LFR-20-653926. Crystal growth performed at Stanford University was supported by the Air Force Office of Scientific Research under award number FA9550-20-1-0252.
Acknowledgments
We thank P. Klavins for support with cryogenic operations at UC Davis, and A. Albrecht and R. Fernandes for enlightening discussions.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Balakirev FF, Betts JB, Migliori A, Ono S, Ando Y, Boebinger GS. Signature of optimal doping in Hall-effect measurements on a high-temperature superconductor. Nature (2003) 424:912–5. doi:10.1038/nature01890
3. Park T, Ronning F, Yuan HQ, Salamon MB, Movshovich R, Sarrao JL, et al. Hidden magnetism and quantum criticality in the heavy fermion superconductor CeRhIn5. Nature (2006) 440:65–8. doi:10.1038/nature04571
4. Park T, Sidorov VA, Ronning F, Zhu JX, Tokiwa Y, Lee H, et al. Isotropic quantum scattering and unconventional superconductivity. Nature (2008) 456:366–8. doi:10.1038/nature07431
5. Shibauchi T, Carrington A, Matsuda Y. A quantum critical point lying beneath the superconducting dome in iron pnictides. Annu Rev Condens Matter Phys (2014) 5:113–35. doi:10.1146/annurev-conmatphys-031113-133921
6. Kuo HH, Chu JH, Palmstrom JC, Kivelson SA, Fisher IR. Ubiquitous signatures of nematic quantum criticality in optimally doped Fe-based superconductors. Science (2016) 352:958–62. doi:10.1126/science.aab0103
7. Lederer S, Schattner Y, Berg E, Kivelson SA. Enhancement of superconductivity near a nematic quantum critical point. Phys Rev Lett (2015) 114:097001. doi:10.1103/PhysRevLett.114.097001
8. Schuberth E, Tippmann M, Steinke L, Lausberg S, Steppke A, Brando M, et al. Emergence of superconductivity in the canonical heavy-electron metal YbRh2Si2. Science (2016) 351:485–8. doi:10.1126/science.aaa9733
9. Paschen S, Si Q. Quantum phases driven by strong correlations. Nat Rev Phys (2020) 3:9–26. doi:10.1038/s42254-020-00262-6
10. Alloul H, Bobroff J, Gabay M, Hirschfeld PJ. Defects in correlated metals and superconductors. Rev Mod Phys (2009) 81:45–108. doi:10.1103/RevModPhys.81.45
11. Seo S, Lu X, Zhu JX, Urbano RR, Curro N, Bauer ED, et al. Disorder in quantum critical superconductors. Nat Phys (2014) 10:120–5. doi:10.1038/nphys2820
12. Massat P, Wen J, Jiang JM, Hristov AT, Liu Y, Smaha RW, et al. Field-tuned ferroquadrupolar quantum phase transition in the insulator TmVO4. Proc Natl Acad Sci (2022) 119:e2119942119. doi:10.1073/pnas.2119942119
14. Li Y, Zic MP, Ye L, Meese WJ, Massat P, Zhu Y, et al. Disorder-induced local strain distribution in Y-doped TmVO4 (2024). doi:10.48550/ARXIV.2402.17049
15. Knoll KD. Absorption and fluorescence spectra of Tm3+ in YVO4 and YPO4. Physica Status Solidi (B) (1971) 45:553–9. doi:10.1002/pssb.2220450218
16. Bleaney B, Wells MR. Radiofrequency studies of TmVO4. Proc R Soc Lond Ser A, Math Phys Sci (1980) 370:131–53.
17. Melcher RL The anomalous elastic properties of materials undergoing cooperative Jahn Teller phase transisions (Elsevier), chap. The anomalous elastic properties of materials undergoing cooperative Jahn Teller phase transisions (1976). p. 1–77. doi:10.1016/B978-0-12-477912-9.50006-0
18. Gehring GA, Gehring KA. Co-operative Jahn-Teller effects. Rep Prog Phys (1975) 38:1–89. doi:10.1088/0034-4885/38/1/001
19. Maharaj AV, Rosenberg EW, Hristov AT, Berg E, Fernandes RM, Fisher IR, et al. Transverse fields to tune an Ising-nematic quantum phase transition. Proc Natl Acad Sci (2017) 114:13430–4. doi:10.1073/pnas.1712533114
20. Nian YH, Vinograd I, Green T, Chaffey C, Massat P, Singh RRP, et al. Spin-echo and quantum versus classical critical fluctuations in TmVO4. Phys. Rev. Lett (2024) 132:216502. doi:10.1103/PhysRevLett.132.216502
21. Bitko D, Rosenbaum TF, Aeppli G. Quantum critical behavior for a model magnet. Phys Rev Lett (1996) 77:940–3. doi:10.1103/PhysRevLett.77.940
22. Melcher RL, Pytte E, Scott BA. Phonon instabilities in TmVO4. Phys Rev Lett (1973) 31:307–10. doi:10.1103/PhysRevLett.31.307
23. Washimiya S, Shinagawa K, Sugano S. Effective Hamiltonian for non-Kramers doublets. Phys Rev B (1970) 1:2976–85. doi:10.1103/physrevb.1.2976
24. Vinograd I, Shirer KR, Massat P, Wang Z, Kissikov T, Garcia D, et al. Second order Zeeman interaction and ferroquadrupolar order in TmVO4. npj Quan Mater (2022) 7:68. doi:10.1038/s41535-022-00475-1
25. Wang Z, Vinograd I, Mei Z, Menegasso P, Garcia D, Massat P, et al. Anisotropic nematic fluctuations above the ferroquadrupolar transition in TmVO4. Phys Rev B (2021) 104:205137. doi:10.1103/PhysRevB.104.205137
26. Schwab G, Hillmer W. Epr of non-kramers rare-earth ions in tetragonal crystals. physica status solidi (b) (1975) 70:237–44. doi:10.1002/pssb.2220700122
27. Hoult D, Richards R. The signal-to-noise ratio of the nuclear magnetic resonance experiment. J Magn Reson (1969) (1976) 24:71–85. doi:10.1016/0022-2364(76)90233-x
29. Cywiński Ł, Lutchyn RM, Nave CP, Sarma SD. How to enhance dephasing time in superconducting qubits. Phys Rev B (2008) 77:174509. doi:10.1103/physrevb.77.174509
30. Yang W, Ma WL, Liu RB. Quantum many-body theory for electron spin decoherence in nanoscale nuclear spin baths. Rep Prog Phys (2016) 80:016001. doi:10.1088/0034-4885/80/1/016001
31. Chen SW, Jiang ZF, Liu RB. Quantum criticality at high temperature revealed by spin echo. New J Phys (2013) 15:043032. doi:10.1088/1367-2630/15/4/043032
32. Weihong Z, Oitmaa J, Hamer CJ. Series expansions for the 3D transverse Ising model at T=0. J Phys A: Math Gen (1994) 27:5425–44. doi:10.1088/0305-4470/27/16/010
33. Quan HT, Song Z, Liu XF, Zanardi P, Sun CP. Decay of Loschmidt echo enhanced by quantum criticality. Phys Rev Lett (2006) 96:140604. doi:10.1103/physrevlett.96.140604
34. Hauke P, Heyl M, Tagliacozzo L, Zoller P. Measuring multipartite entanglement through dynamic susceptibilities. Nat Phys (2016) 12:778–82. doi:10.1038/nphys3700
35. König EJ, Levchenko A, Sedlmayr N. Universal fidelity near quantum and topological phase transitions in finite one-dimensional systems. Phys Rev B (2016) 93:235160. doi:10.1103/PhysRevB.93.235160
36. Tang HK, Marashli MA, Yu WC. Unveiling quantum phase transitions by fidelity mapping. Phys Rev B (2021) 104:075142. doi:10.1103/PhysRevB.104.075142
37. Wangsness RK, Bloch F. The dynamical theory of nuclear induction. Phys Rev (1953) 89:728–39. doi:10.1103/PhysRev.89.728
38. Redfield AG. On the theory of relaxation processes. IBM J Res Dev (1957) 1:19–31. doi:10.1147/rd.11.0019
39. Gu SJ. Fidelity approach to quantum phase transitions. Int J Mod Phys B (2010) 24:4371–458. doi:10.1142/S0217979210056335
40. Curro N, Hammel P. The Cu NMR echo decay in stripe ordered La1.65Eu0.2Sr0.15CuO4. Phys C (2000) 341:1797–8. doi:10.1016/S0921-4534(00)01084-4
41. Curro N, Hammel P, Suh B, Hücker M, Büchner B, Ammerahl U, et al. Inhomogeneous low frequency spin dynamics in La1.65Eu0.2Sr0.15CuO4. Phys Rev Lett (2000) 85:642–5. doi:10.1103/PhysRevLett.85.642
42. Hunt A, Singer P, Thurber K, Imai T. 63Cu NQR measurement of stripe order parameter in La2−xSrxCuO4. Phys Rev Lett (1999) 82:4300–3. doi:10.1103/PhysRevLett.82.4300
43. Julien MH, Campana A, Rigamonti A, Carretta P, Borsa F, Kuhns P, et al. Glassy spin freezing and NMR wipeout effect in the high-Tc superconductor La1.90Sr0.10CuO4 critical discussion of the role of stripes. Phys Rev B (2001) 63:144508. doi:10.1103/PhysRevB.63.144508
44. Dioguardi AP, Crocker J, Shockley AC, Lin CH, Shirer KR, Nisson DM, et al. Coexistence of cluster spin glass and superconductivity in Ba(Fe1−xCox)2As2 for 0.060 ≤ x ≤ 0.071. Phys Rev Lett (2013) 111:207201. doi:10.1103/PhysRevLett.111.207201
45. Babkevich P, Nikseresht N, Kovacevic I, Piatek JO, Dalla Piazza B, Kraemer C, et al. Phase diagram of diluted Ising ferromagnet LiHoxy1−xf4. Phys Rev B (2016) 94:174443. doi:10.1103/PhysRevB.94.174443
46. Nattermann T Theory of the random field ising model (world scientific) (1997). p. 277–98. doi:10.1142/9789812819437_0009
47. Imai T, Slichter CP, Yoshimura K, Kosuge K. Low frequency spin dynamics in undoped and Sr-doped La2CuO4. Phys Rev Lett (1993) 70:1002–5. doi:10.1103/PhysRevLett.70.1002
48. Lang G, Grafe HJ, Paar D, Hammerath F, Manthey K, Behr G, et al. Nanoscale electronic order in iron pnictides. Phys Rev Lett (2010) 104:097001. doi:10.1103/PhysRevLett.104.097001
49. Kissikov T, Dioguardi AP, Timmons EI, Tanatar MA, Prozorov R, Bud’ko SL, et al. NMR study of nematic spin fluctuations in a detwinned single crystal of underdoped Ba(Fe2−xCox)2As2. Phys Rev B (2016) 94:165123. doi:10.1103/PhysRevB.94.165123
50. Menegasso P, Souza JC, Vinograd I, Wang Z, Edwards SP, Pagliuso PG, et al. Hyperfine couplings as a probe of orbital anisotropy in heavy-fermion materials. Phys Rev B (2021) 104:035154. doi:10.1103/physrevb.104.035154
51. Vinograd I, Edwards SP, Wang Z, Kissikov T, Byland JK, Badger JR, et al. Inhomogeneous Knight shift in vortex cores of superconducting FeSe. Phys Rev B (2021) 104:014502. doi:10.1103/physrevb.104.014502
Keywords: nuclear magnetic resonance, quantum criticality, transverse field Ising model, Griffiths phases, hyperfine coupling, quantum fidelity
Citation: Nian Y-H, Vinograd I, Chaffey C, Li Y, Zic MP, Massat P, Singh RRP, Fisher IR and Curro NJ (2024) Nuclear magnetic resonance studies in a model transverse field Ising system. Front. Phys. 12:1393229. doi: 10.3389/fphy.2024.1393229
Received: 28 February 2024; Accepted: 13 May 2024;
Published: 04 June 2024.
Edited by:
James Avery Sauls, Louisiana State University, United StatesReviewed by:
William Paul Halperin, Northwestern University, United StatesVesna Mitrovic, Brown University, United States
Copyright © 2024 Nian, Vinograd, Chaffey, Li, Zic, Massat, Singh, Fisher and Curro. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: N. J. Curro, njcurro@ucdavis.edu
 Y.-H. Nian
Y.-H. Nian I. Vinograd1
I. Vinograd1 C. Chaffey
C. Chaffey Y. Li
Y. Li N. J. Curro
N. J. Curro