- 1Department of Computer Science, Shantou University, Shantou, China
- 2Yangtze Delta Region Institute (Quzhou), University of Electronic Science and Technology of China, Quzhou, Zhejiang, China
- 3Quzhou People’s Hospital, Quzhou Affiliated Hospital of Wenzhou Medical University, Quzhou, Zhejiang, China
- 4Department of Automation, School of Electrical Engineering, Yancheng Institute of Technology, Yancheng, China
- 5Environment Design Department, Chengdu University, Chengdu, China
The outbreak of an epidemic often stimulates the generation of public awareness about epidemic prevention. This heightened awareness encourages individuals to take proactive protective measures, thereby curbing the transmission of the epidemic. Previous research commonly adopts an assumption that each individual has the same probability of awakening self-protection awareness after infection. However, in the real-world process, different individuals may generate varying awareness responses due to the differences in the amount of information received. Therefore, in this study, we first propose a coupled awareness-epidemic spreading model, where the self-initiated awareness of each individual can be influenced by the number of aware neighbors. Subsequently, we develop a Micro Markov Chain Approach to analyze the proposed model and explore the effects of different dynamic and structural parameters on the coupled dynamics. Findings indicate that individual awareness awakening can effectively promote awareness diffusion within the proposed coupled dynamics and inhibit epidemic transmission. Moreover, the influence of awareness diffusion on epidemic transmission exhibits a metacritical point, from which the epidemic threshold increases with the increase in the awareness diffusion probability. The research findings also suggest that the increase in the average degree of virtual-contact networks can reduce the value of the metacritical point, while the change in the average degree of the physical-contact networks does not affect the metacritical point. Finally, we conduct extensive experiments on four real networks and obtain results consistent with the above conclusions. The systematic research findings of this study provide new insights for exploring the interaction between individual awareness and epidemic transmission in the real world.
1 Introduction
The spread of infectious diseases poses a significant threat to human health and can lead to substantial economic losses [1]. Throughout history, human society has repeatedly suffered devastating impacts from infectious diseases. For example, in the 16th and 17th centuries, the rampant smallpox virus led to a sharp decline in the population of indigenous peoples in the Americas. The outbreak of novel coronavirus pneumonia (COVID-19) in 2019 has caused nearly seven million deaths worldwide [2–4]. It is worth noting that the large-scale outbreak of an epidemic often effectively stimulates individuals to develop self-initiated awareness, which can effectively curb the spread of the epidemic [5–9]. For example, after the outbreak of the COVID-19 pandemic, information related to it started diffusing on social networks or community networks, thereby sparking the development of individual awareness about epidemic prevention [10, 11]. After developing self-initiated awareness, individuals will actively take a series of self-protective measures to reduce the risk of infection, such as wearing masks, frequent hand-washing, reducing outdoor activities, maintaining social distancing, and more [12]. These self-protective measures can effectively interrupt the transmission pathways of the virus, thereby suppressing further transmission of the disease [13–17]. Therefore, how to model and analyze the coupled awareness-epidemic dynamics has long been a subject of significant interest among scholars from various fields.
In real life, individuals can not only have physical contact with others, such as shaking hands and sharing meals, which promote the spread of diseases but also communicate with others to receive disease-related information and generate awareness of self-protection [18–22]. Therefore, in recent years, scholars typically adopt a two-layer multiplex network structure to establish the coupled awareness-epidemic dynamics in their research, aiming to explore the interaction between awareness diffusion and epidemic transmission in the real world [23–27]. In the two-layer multiplex network structure, the first layer is the physical-contact network, where nodes represent individuals in the real world, and edges represent physical contact relationships between individuals; the second layer (virtual contact) is the network with the same nodes as the physical-contact network, while edges represent information interaction between individuals [28–31]. In 2013, Granell et al. proposed a coupled awareness-epidemic dynamics model with the multiplex network structure to investigate the real-world coupled awareness-epidemic dynamics. They identified the presence of a metacritical point for awareness diffusion rate, and when the awareness diffusion rate is larger than this point, the epidemic threshold will increase with it [32]. Subsequently, scholars have proposed several improved models from different perspectives to consider the effects of various real-world factors on the coupled awareness-epidemic dynamics. For instance, Granell et al. further integrates mass media into the awareness diffusion process, elucidating that the metacritical point for epidemic outbreaks vanishes under the influence of mass media [33]. Chen et al. introduced a resource-epidemic coevolution model on a multiplex network and discovered an optimal heterogeneity of self-awareness at which the disease can be suppressed to the greatest extent [34]. Wu et al. introduce a two-layer network where the inter-layer coupling is induced by the movement of traveler individuals between layers, and they find that travelers’ hopping preference for different layers can lead to non-monotonic changes in the epidemic threshold and spreading coverage [35]. Furthermore, many scholars have delved into the effects of the spatio-temporal characteristics of networks on epidemic spreading. Liu et al. proposed a spatio-temporal network model based on co-location interactions using massive cellphone data. They reveals that universal laws underlying spatio-temporal contact patterns among residents is essential for epidemic spreading [36]. Furthermore, Li et al. introduced a temporal multiplex network consisting of a static information spreading network and a temporal physical contact network with a layer-preference walk. They found that the epidemic threshold decreases with the decrease of the effective information spreading rate and the increase of the layer [37].
As mentioned above, scholars have made significant progress in the study of coupled awareness-epidemic dynamics. However, there is limited research that incorporates individualized self-initiated awareness into the coupled awareness-epidemic dynamics. In the real world coupled awareness-epidemic spreading, different individuals generate varying awareness responses due to the differences in the amount of information received from their neighbors. Hence, research on the coupled awareness-epidemic dynamics that takes into account individualized self-initiated awareness holds significant importance. In light of this, this study first proposes a coupled awareness-epidemic dynamics model that incorporates individualized self-initiated awareness, where the probability of infected individuals developing self-initiated awareness is influenced by the number of their aware neighbors. Subsequently, we develop the Microscopic Markov Chains Approach to theoretically analyze the aforementioned model and investigate the effects of crucial dynamics and structural parameters on the coupled awareness-epidemic dynamics.
The paper is structured as follows: Section 2 provides a detailed description of the coupled awareness-epidemic dynamics with individualized self-initiated awareness. In Section 3, we introduce the Micro Markov Chain Approach to analyze the previous model, and derive the stationary spread range and transmission threshold of the epidemic. In Section 4, we explore the effects of different dynamics and structural parameters on the coupled awareness-epidemic dynamics. Finally, Section 5 summarizes the entire work and outlines potential avenues for further study.
2 Model description
In the study, we consider the coupled awareness-epidemic dynamics on top of a two-layer multiplex networks as shown in Figure 1. The nodes of the two network layers are one-to-one correspondence, but the connectivity between them is different. Awareness of the epidemic diffuses on the second layer of the multiplex network (namely, the virtual-contact layer), and the epidemic takes place on the first layer (namely, the physical-contact network).
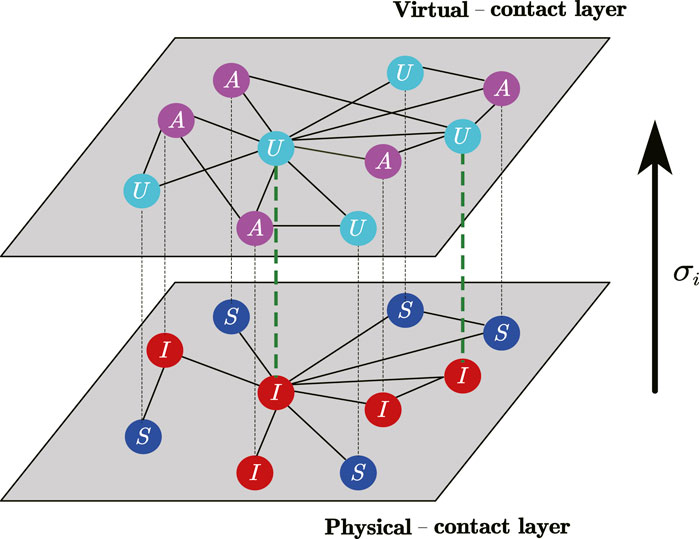
Figure 1. (Color online) A schematic illustration showcasing the coupled awareness-epidemic dynamics with individualized self-initiated awareness in multiplex networks. The first layer (physical-contact network) employs a susceptible-infected-susceptible (SIS) model to delineate the transmission of the epidemic. Within this layer, susceptible (S) nodes can be infected by their infected (I) neighbors. The second layer corresponds to the virtual-contact network, sharing identical nodes with the physical-contact network. In this layer, an unaware-aware-unaware (UAU) model captures the diffusion of epidemic awareness. Nodes in the unaware (U) state lack epidemic awareness and consequently take no preventive measures. Conversely, the aware (A) nodes possess knowledge about the epidemic and implement specific precautionary measures. Additionally, when a node in the unaware state becomes infected, it has a probability of
In the virtual-contact layer, an unaware-aware-unaware (UAU) model is adopted to depict the diffusion of epidemic awareness. Unaware (U) nodes have no epidemic awareness and will take no precautions against the epidemic, while aware (A) nodes know about the epidemic and will take certain preventive measures. The diffusion of epidemic awareness occurs from the A-state node to the U-state node with a probability of
where
In physical-contact layer, a susceptible-infected-susceptible (SIS) model is adopted to describe the epidemic-transmitting process. The susceptible (S) node, both with and without epidemic awareness, can become infected by its infected (I) neighbor with the certain probability of
3 Theoretical analysis
3.1 Microscopic markov chain approach
We will provide an analytical derivation based on the Microscopic Markov Chain Approach (MMCA) for our model in this section. Denote
The probabilities of node
Figure 2 shows the transition probability trees for the four possible states of nodes in our model. The dynamics governing
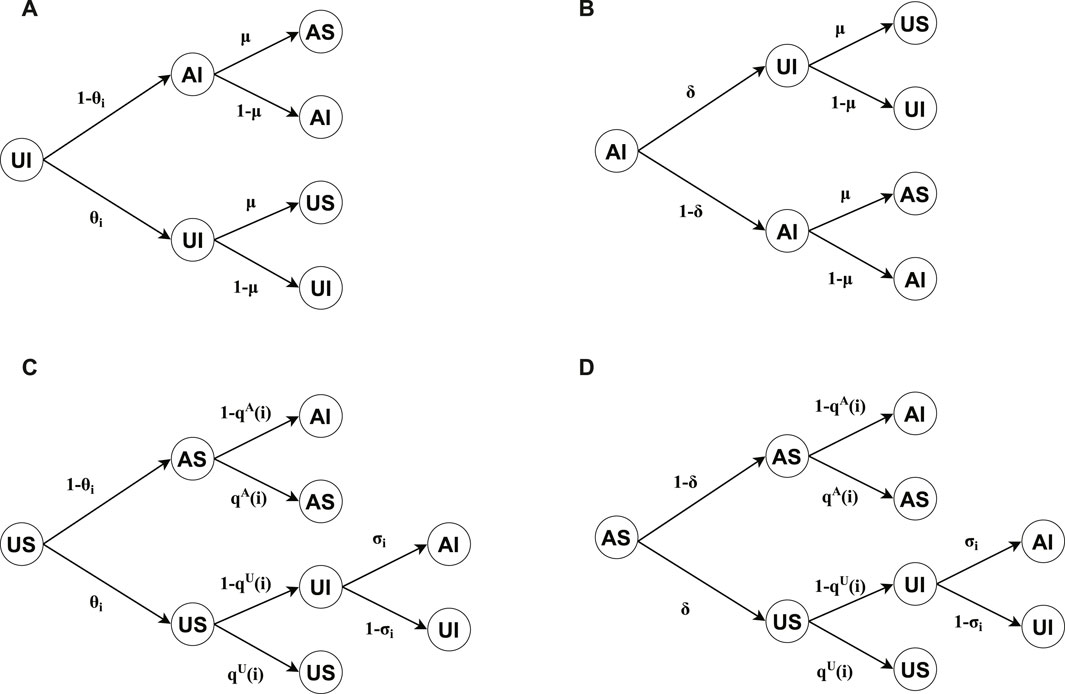
Figure 2. Transition probability trees are illustrated for four distinct node states: (A) unaware-infected (UI), (B) aware-infected (AI), (C) unaware-susceptible (US), and (D) aware-susceptible (AS). The tree roots denote the state of each node at time
3.2 Threshold analysis
The epidemic threshold is given by the parameter
In the steady state, by summing Eqs 5, 8, we acquire
Near the epidemic threshold, the fraction of I-state nodes is close to zero, i.e.,
and
respectively, where
Substituting Eqs 11, 12 into Eq. 10 leads to
Since
and
Then, substituting Eqs 15, 16 into Eq. 14 leads to Eq. 17:
which can be written as
where
the nontrivial solutions of Eq. 18 are eigenvectors of
Equation 20 provides a quantitative representation indicating that the epidemic threshold is dependent on the spreading dynamics on both network layers.
4 Simulation results
In this section, we explore the effects of various dynamics and structural parameters on the proposed coupled awareness-epidemic dynamics. In reality, the behavior of the same individual on the virtual-contact network and the physical-contact network may not be consistent. For example, individuals who appear active on the virtual-contact networks may have rare physical contact with others. To imitate the variability in individual behavior between the virtual-contact layer and the physical-contact layer, we employ three multiplex networks with varying inter-layer degree correlation
Firstly, we assess the efficacy of the MMCA method in describing the coupled awareness-epidemic dynamics proposed in this study on a group of multiplex networks. Figure 3 compares the dynamicsal results of the MMCA method and Monte Carlo (MC) simulation regarding
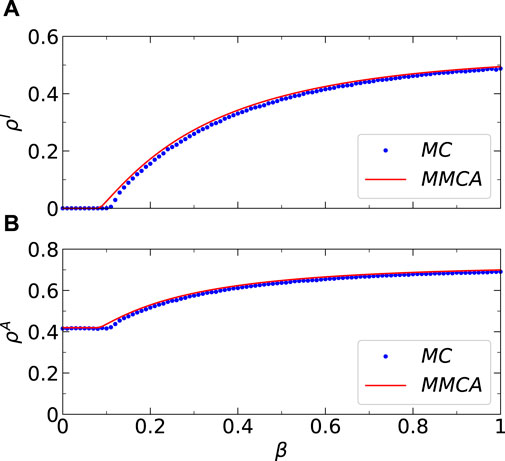
Figure 3. (Color online) Results comparisons between the Microscopic Markov Chains Approach (MMCA) and Monte Carlo (MC) simulations regarding the stationary fractions. (A) Comparisons between the stationary I-state individuals’ fraction
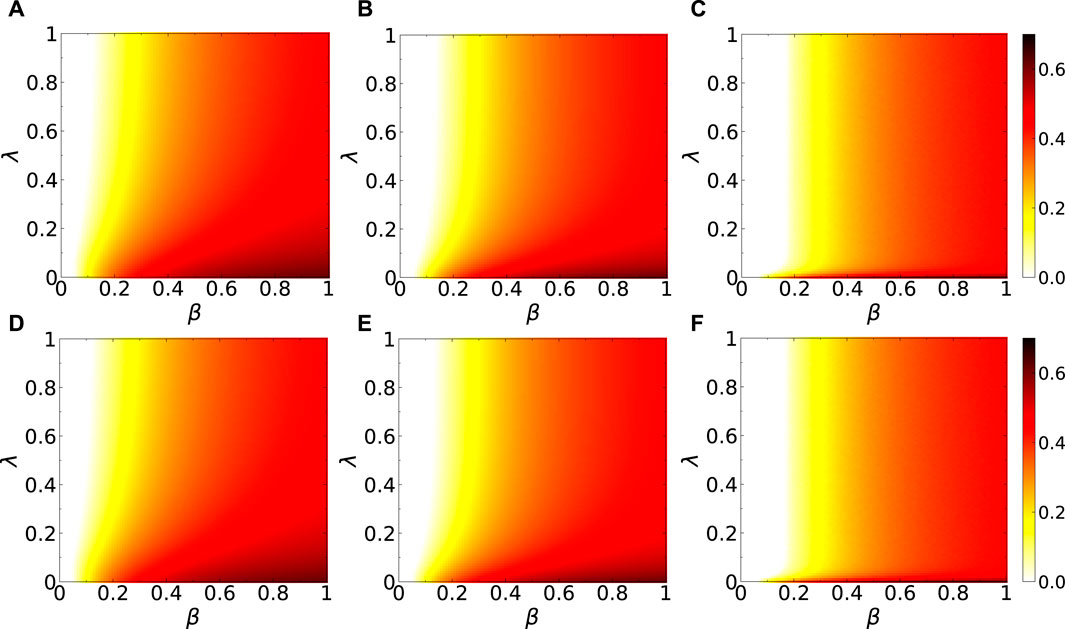
Figure 4. (Color online) Results comparisons of the full phase diagrams (
Secondly, we conducted an analysis of how two significant dynamics parameters influence the stationary states of the proposedawareness-epidemic dynamics, namely, the basic self-initiated awareness probability
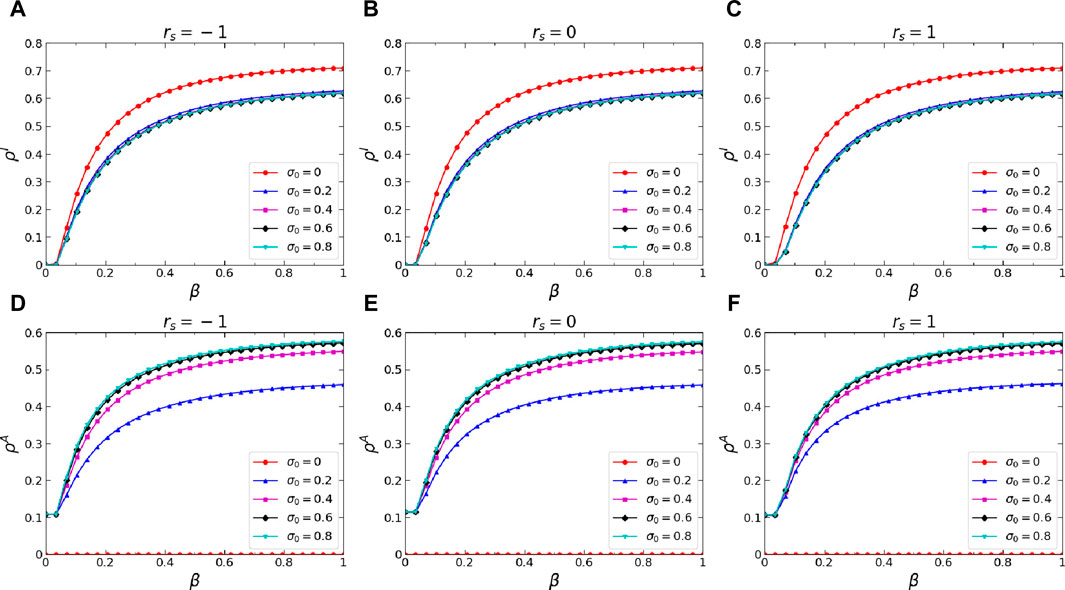
Figure 5. (Color online) Effects of the basic self-initiated awareness probability
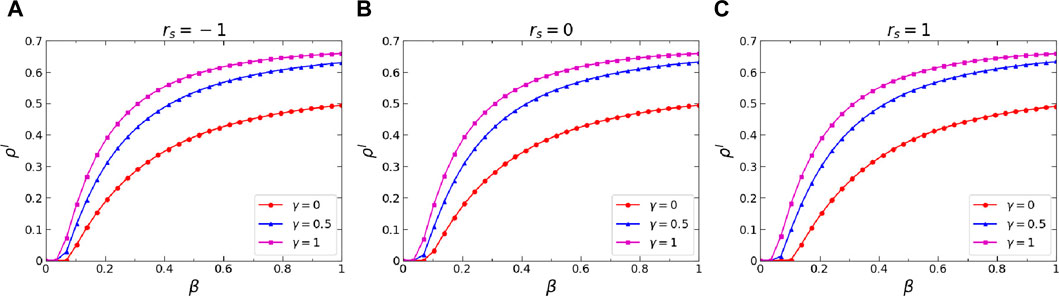
Figure 6. (Color online) Effects of the infection attenuation factor
Thirdly, we further analyzed the effects of three critical dynamics parameters on the epidemic threshold, namely, the infection attenuation factor
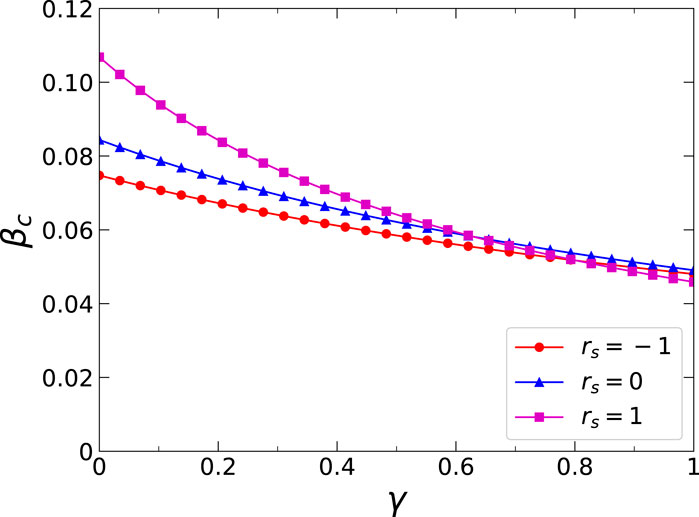
Figure 7. (Color online) Effects of the inter-layer degree correlations
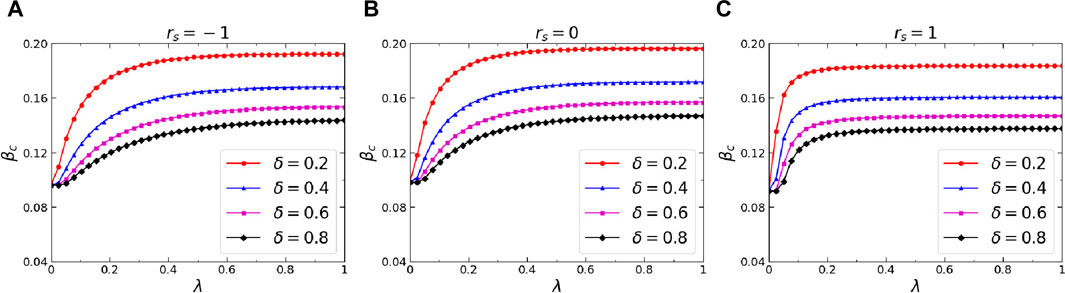
Figure 8. (Color online) Effects of the awareness forgetting probability
Finally, we investigate the effects of the average degree
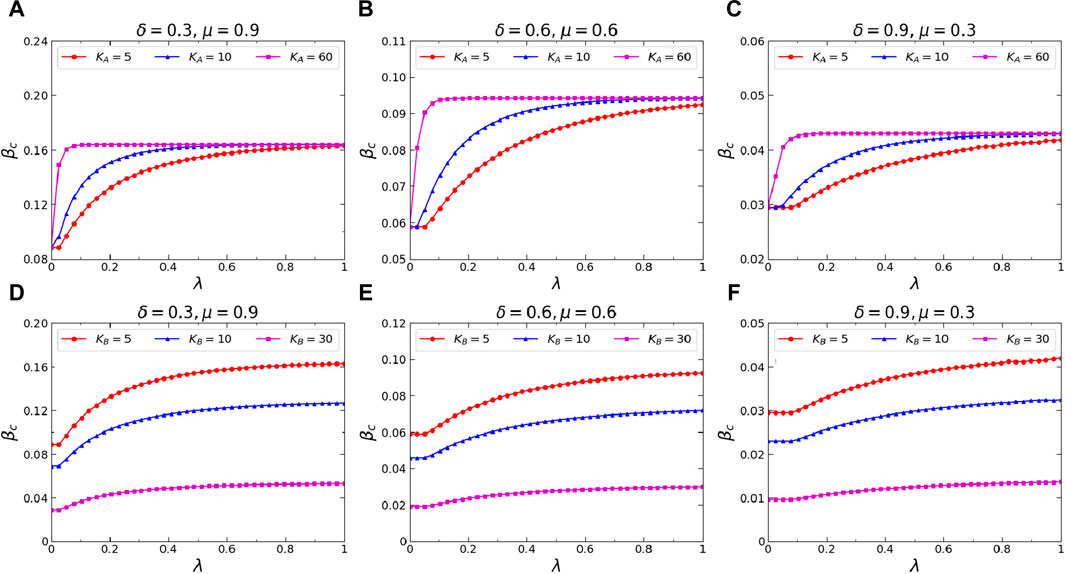
Figure 9. (Color online) Effects of the average degrees
It should be noted that all the aforementioned results are based on the configured multiplex networks. To closely align with real-world scenarios, we conduct extensive experiments on a large number of real networks. The conclusions drawn from these experiments align with those from the configured multiplex networks. For a comprehensive overview of the detailed results, please refer to the Supplementary Material.
5 Conclusion
The outbreak of an epidemic often stimulates the development of public awareness about disease prevention, which can effectively curb the process of epidemic transmission. Individuals generate different awareness responses due to varying amounts of information received from their neighbors. Therefore, considering the diversity in individual awareness responses is of significant research importance in the coupled awareness-epidemic dynamics. In this study, we first introduce a coupled awareness-epidemic dynamics model that incorporates the differences in individual awareness responses, where the self-initiated awareness probability of individuals is influenced by the number of their aware neighbors. Subsequently, we develop MMCA method for the analysis of the aforementioned model and validate the accuracy of the MMCA method in solving the coupled spreading model through MC numerical simulations. Next, we analyze the impact of crucial dynamics and structural parameters on the proposed coupled awareness-epidemic dynamics. Through abundant simulations and meticulous theoretical analyses, it has been demonstrated that individual awareness awakening can elevate the steady-state proportion of aware individuals on the networks, consequently mitigating epidemic transmission. Simultaneously, the impact of awareness diffusion on epidemic transmission exhibits a metacritical point
Data availability statement
The datasets presented in this study are available upon request in the following online repository: https://github.com/20zyli3/zzz.
Author contributions
WZ: Methodology, Validation, Writing–original draft. YY: Methodology, Validation, Writing–original draft. ZL: Methodology, Validation, Writing–original draft. JX: Conceptualization, Funding acquisition, Methodology, Project administration, Software, Validation, Writing–original draft. TW: Methodology, Supervision, Validation, Writing–review and editing. DL: Supervision, Writing–review and editing. DH: Methodology, Validation, Writing–original draft. ML: Methodology, Funding acquisition, Supervision, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by Shantou University under grants NTF20026 and NTF21041, the National Key Research and Development Program under Grant 2022YFB3104600, the China Postdoctoral Science Foundation Funded Project (2023M740519), Medico-Engineering Cooperation Funds from University of Electronic Science and Technology of China (Nos ZYGX2021YGLH213, ZYGX2022YGRH016), Interdisciplinary Crossing and Integration of Medicine and Engineering for Talent Training Fund, West China Hospital, Sichuan University under Grant No. HXDZ22010, the Municipal Government of Quzhou (Grant 2022D018, Grant 2022D029, Grant 2023D007, Grant 2023D015, Grant 2023D033, Grant 2023D034, Grant 2023D035), Zhejiang Provincial Natural Science Foundation of China under Grant No. LGF22G010009, and Guiding project of Quzhou Science and Technology Bureau (subject No 2022005, 2022K50, 2023K013, 2023K016).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1437341/full#supplementary-material
References
1. Morens DM, Folkers GK, Fauci AS. The challenge of emerging and re-merging infectious diseases. Nature (2004) 430:242–9. doi:10.1038/nature02759
2. Shereen MA, Khan S, Kazmi A, Bashir N, Siddique R. Covid-19 infection: emergence, transmission, and characteristics of human coronaviruses. J Adv Res (2020) 24:91–8. doi:10.1016/j.jare.2020.03.005
3. Tangcharoensathien V, Calleja N, Nguyen T, Purnat T, D’Agostino M, Garcia-Saiso S, et al. Framework for managing the covid-19 infodemic: methods and results of an online, crowdsourced who technical consultation. J Med Internet Res (2020) 22:e19659. doi:10.2196/19659
4. Cirrincione L, Plescia F, Ledda C, Rapisarda V, Martorana D, Lacca G, et al. Covid-19 pandemic: new prevention and protection measures. Sustainability (2022) 14:4766. doi:10.3390/su14084766
5. Wu J, Zuo R, He C, Xiong H, Zhao K, Hu Z. The effect of information literacy heterogeneity on epidemic spreading in information and epidemic coupled multiplex networks. Physica A: Stat Mech its Appl (2022) 596:127119. doi:10.1016/j.physa.2022.127119
6. W X, C Z. Epidemic spreading with an awareness-based adaptive mechanism in temporal multiplex networks. Front Phys (2023) 11:1285480. doi:10.3389/fphy.2023.1285480
7. Ma W, Zhang P, Zhao X, Xue L. The coupled dynamics of information dissemination and seir-based epidemic spreading in multiplex networks. Physica A: Stat Mech its Appl (2022) 588:126558. doi:10.1016/j.physa.2021.126558
8. Liang GCX, Cui X, Zhu P. An effective method for epidemic suppression by edge removing in complex network. Front Phys (2023) 11:1164847. doi:10.3389/fphy.2023.1164847
9. Wang JW, Zhang HF, Ma XJ, Wang J, Ma C, Zhu PC. Privacy-preserving identification of the influential nodes in networks. Int J Mod Phys C (2023) 34. doi:10.1142/S0129183123501280
10. Shi D, Shang F, Chen B, Expert P, Lü L, Stanley HE, et al. Local dominance unveils clusters in networks. Commun Phys (2024) 7:170. doi:10.1038/s42005-024-01635-4
11. Ji P, Ye J, Mu Y, Lin W, Tian Y, Hens C, et al. Signal propagation in complex networks. Phys Rep (2023) 1017:1–96. doi:10.1016/j.physrep.2023.03.005
12. Li R, Wang W, Di Z. Effects of human dynamics on epidemic spreading in côte d’ivoire. Physica A: Stat Mech its Appl (2017) 467:30–40. doi:10.1016/j.physa.2016.09.059
13. Xiong X, Zeng Z, Feng M, Szolnoki A. Coevolution of relationship and interaction in cooperative dynamical multiplex networks. Chaos: An Interdiscip J Nonlinear Sci (2024) 34:023118. doi:10.1063/5.0188168
14. Lima CMAO. Information about the new coronavirus disease (covid-19). Radiologia Brasileira (2020) 53(2). doi:10.1590/0100-3984.2020.53.2e1
15. Deng G, Peng Y, Tian Y, Zhu X. Analysis of influence of behavioral adoption threshold diversity on multi-layer network. Entropy (2023) 25:458. doi:10.3390/e25030458
16. Tian Y, Tian H, Cui Q, Zhu X. Phase transition phenomena in social propagation with dynamic fashion tendency and individual contact. Chaos: Solitons Fractals (2024) 178:114366. doi:10.1016/j.chaos.2023.114366
17. Chen J, Liu Y, Yue J, Duan X, Tang M. Coevolving spreading dynamics of negative information and epidemic on multiplex networks. Nonlinear Dyn (2022) 110:3881–91. doi:10.1007/s11071-022-07776-x
18. Zhu X, Zhang J, Liu S, Tian Y, Cui Y, Li Y, et al. Behavioral propagation influenced by fluctuating personality on single-layer limited-contact network. Physica Scripta (2024) 99:025252. doi:10.1088/1402-4896/ad1960
19. Wang J, Cai S, Wang W, Zhou T. Link cooperation effect of cooperative epidemics on complex networks. Appl Mathematics Comput (2023) 437:127537. doi:10.1016/j.amc.2022.127537
20. Chen J, Liu Y, Tang M, Yue J. Asymmetrically interacting dynamics with mutual confirmation from multi-source on multiplex networks. Inf Sci (2022) 619:478–90. doi:10.1016/j.ins.2022.11.033
21. Chen Y, Liu Y, Tang M, Lai YC. Epidemic dynamics with non-markovian travel in multilayer networks. Commun Phys (2023) 6:263. doi:10.1038/s42005-023-01369-9
22. Cai SM, Chen XH, Ye XJ, Tang M. Precisely identifying the epidemic thresholds in real networks via asynchronous updating. Appl Mathematics Comput (2019) 361:377–88. doi:10.1016/j.amc.2019.05.039
23. Liu Y, Zeng Q, Pan L, Tang M. Identify influential spreaders in asymmetrically interacting multiplex networks. IEEE Trans Netw Sci Eng (2023) 10:2201–11. doi:10.1109/TNSE.2023.3243560
24. Wang J, Yang C, Chen B. The interplay between disease spreading and awareness diffusion in multiplex networks with activity-driven structure. Chaos: An Interdiscip J Nonlinear Sci (2022) 32:073104. doi:10.1063/5.0087404
25. Tian Y, Tian H, Cui Y, Zhu X, Cui Q. Influence of behavioral adoption preference based on heterogeneous population on multiple weighted networks. Appl Mathematics Comput (2023) 446:127880. doi:10.1016/j.amc.2023.127880
26. Wang J, Xiong W, Wang R, Cai S, Wu D, Wang W, et al. Effects of the information-driven awareness on epidemic spreading on multiplex networks. Chaos: An Interdiscip J Nonlinear Sci (2022) 32:073123. doi:10.1063/5.0092031
27. Wang R, Zhang X, Wang M. A two-layer model with partial mapping: unveiling the interplay between information dissemination and disease diffusion. Appl Mathematics Comput (2024) 468:128507. doi:10.1016/j.amc.2023.128507
28. Zhu P, Zhi Q, Guo Y, Wang Z. Analysis of epidemic spreading process in adaptive networks. IEEE Trans Circuits Syst Express Briefs (2018): 1252–6. doi:10.1109/TCSII.2018.2877406
29. Cao LWX, Zhao H, X A, An X. Competitive information propagation considering local-global prevalence on multi-layer interconnected networks. Front Phys (2023) 11:1293177. doi:10.3389/fphy.2023.1293177
30. Zhu P, Wang X, Li S, Guo Y, Wang Z. Investigation of epidemic spreading process on multiplex networks by incorporating fatal properties. Appl Mathematics Comput (2019) 359:512–24. doi:10.1016/j.amc.2019.02.049
31. Wang Z, Guo Q, Sun S, Xia C. The impact of awareness diffusion on sir-like epidemics in multiplex networks. Appl Mathematics Comput (2019) 349:134–47. doi:10.1016/j.amc.2018.12.045
32. Granell C, Gómez S, Arenas A. Dynamical interplay between awareness and epidemic spreading in multiplex networks. Phys Rev Lett (2013) 111:128701. doi:10.1103/PhysRevLett.111.128701
33. Granell C, G´omez S, Arenas A. Competing spreading processes on multiplex networks: awareness and epidemics. Phys Rev E (2014) 90:012808. doi:10.1103/PhysRevE.90.012808
34. Chen X, Gong K, Wang R, Cai S, Wang W. Effects of heterogeneous self-protection awareness on resource-epidemic coevolution dynamics. Appl Mathematics Comput (2020) 385:125428. doi:10.1016/j.amc.2020.125428
35. Wu D, Liu Y, Tang M, Xu XK, Guan S. Impact of hopping characteristics of inter-layer commuters on epidemic spreading in multilayer networks. Chaos: Solitons and Fractals (2022) 159:112100. doi:10.1016/j.chaos.2022.112100
36. Liu C, Yang Y, Chen B, Cui T, Shang F, Fan J, et al. Revealing spatiotemporal interaction patterns behind complex cities. Chaos: An Interdiscip J Nonlinear Sci (2022) 32:081105. doi:10.1063/5.0098132
Keywords: multiplex networks, coupled awareness-epidemic dynamics, self-initiated awareness, metacritical point, complex networks
Citation: Zhang W, Ye Y, Li Z, Xian J, Wang T, Liu D, Hu D and Liu M (2024) The coupled awareness-epidemic dynamics with individualized self-initiated awareness in multiplex networks. Front. Phys. 12:1437341. doi: 10.3389/fphy.2024.1437341
Received: 23 May 2024; Accepted: 02 July 2024;
Published: 02 August 2024.
Edited by:
Xuzhen Zhu, Beijing University of Posts and Telecommunications (BUPT), ChinaReviewed by:
Ruiqi Li, Beijing University of Chemical Technology, ChinaPeican Zhu, Northwestern Polytechnical University, China
Copyright © 2024 Zhang, Ye, Li, Xian, Wang, Liu, Hu and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jiajun Xian, eGlhbmppYWp1bjIyQGdtYWlsLmNvbQ==
 Wei Zhang1
Wei Zhang1 Jiajun Xian
Jiajun Xian Ming Liu
Ming Liu