The meaning of additive reaction-time effects: some misconceptions
- Department of Psychology, University of Sheffield, Sheffield, UK
Previously, it has been shown experimentally that the psychophysical law known as Piéron’s Law holds for color intensity and that the size of the effect is additive with that of Stroop condition (Stafford et al., 2011). According to the additive factors method (Donders, 1868–1869/1969; Sternberg, 1998), additivity is assumed to indicate independent and discrete processing stages. We present computational modeling work, using an existing Parallel Distributed Processing model of the Stroop task (Cohen et al., 1990) and a standard model of decision making (Ratcliff, 1978). This demonstrates that additive factors can be successfully accounted for by existing single stage models of the Stroop effect. Consequently, it is not valid to infer either discrete stages or separate loci of effects from additive factors. Further, our modeling work suggests that information binding may be a more important architectural property for producing additive factors than discrete stages.
Introduction
Recently, much progress has been made on the neurological and theoretical foundations of simple perceptual decisions (Gold and Shadlen, 2001; Platt, 2002; Opris and Bruce, 2005). Key to debates about the nature of decision making is the underlying architecture of the neural and cognitive processes which implement decision making (see, as an example disagreement Carpenter and Reddi, 2001; Ratcliff, 2001). The investigation of response times has been key to progress in this area. A venerable tool of cognitive scientists when interpreting response times, both in the study of decision making and beyond, is the Additive Factors Method (Donders, 1868–1869/1969; Sternberg, 1998). In the current paper we show that the assumptions of the Additive Factors Method are untenable, using as a worked example decision making in a specific cognitive task. This work throws into contrast both models of optimal decision making and a longer tradition of experiments informed by the Additive Factors Method.
The particular task we focus on here is the Stroop task (Stroop, 1935) which affords a thoroughly investigated experimental paradigm, with established computational models of processing within the task. Importantly for our current purposes, the Stroop task is one in which both the directly perceptual and non-directly perceptual (“cognitive”) elements of the stimulus must be reconciled to produce a correct response. By manipulating the perceptual and cognitive elements of the task independently we hope, in tandem with the use of computational models and formal analysis, to shed light on the issue of “detection” versus “decision” processing (Reddi, 2001).
Reaction Times and Architectures of Decision Making
It is axiomatic to cognitive science that response or reaction times (RTs) can reveal something about the underlying mechanism of perception and choice (Luce, 1986). An example is Piéron’s Law, which describes a consistent relationship between stimulus intensity and simple reaction time (Piéron, 1952). Interestingly this relationship has been shown to hold across different sensory modalities and even for choice reaction times (Luce, 1986; Pins and Bonnet, 1996). Previously, we have suggested that Piéron’s Law emerges inevitability from rise-to-threshold decision processes (Stafford and Gurney, 2004).
The Stroop effect is a paradigmatic response conflict task (Stroop, 1935; MacLeod, 1991; MacLeod and MacDonald, 2000), in which participants are asked to name the color of words, words which may themselves spell out the names of colors. Thus, the (distracting) word-aspect of a stimulus can be conflicting, congruent, or neutral with respect to the (attended-to) color-aspect. For example, when green ink spells out the word “RED” there is heightened response conflict, which is reflected in slowed reaction times and a raised error rate. We have used a Stroop task with colors of varying saturation levels to show that Piéron’s Law holds under conditions of response conflict, and that this effect does not interact with the Stroop conflict condition (Stafford et al., 2011). This is shown in Figure 1.
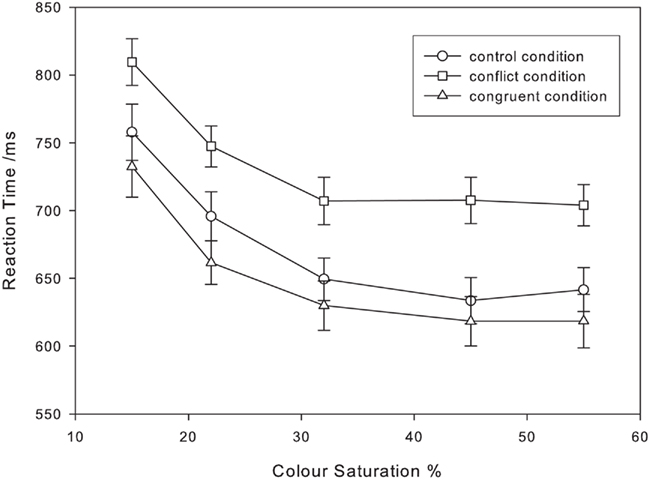
Figure 1. Mean reaction times for different stimulus color saturations in all three Stroop conditions. SE bars shown (n = 20). Data from experiment 1 of Stafford et al. (2011).
The Additive Factors Method
The results shown in Figure 1 have an obvious interpretation under what is known as the Additive Factors Method (AFM;Sternberg, 1969, 1998). According to the assumptions of the AFM, independent components – “stages” – of decision making are revealed by the analysis of how different factors affect reaction times. The analysis of reaction times to inform consideration of the stages involved in decision making is not new to psychological theory (Donders, 1868–1869/1969). By this analysis, if manipulation of one factor affects RTs independently of the manipulation of another factor, that is if their effects are additive, then it is concluded that the two factors affect different stages of decision making. Thus the AFM provides a way of both uncovering whether different factors have the same locus of influence and of inferring a minimum number of independent loci that must be involved during during decision making. The application of this method has produced consistent support for the existence of separate stages in decision making, particularly the independence of stimulus processing and response selection (Stoffels, 1996; van den Wildenberg and van der Molen, 2004). Indeed, one reviewer felt able to comment “Most research on AFM shows consistent and robust evidence in favor of seven successive processing stages in traditional choice reactions” (Sanders, 1990, p.123). Although this quotation may mark a high water mark of the AFM, it is still possible to see this inference from additive factors to discrete processing stages being made in more recent papers on decision making (e.g., Pins and Bonnet, 1996; Woodman et al., 2008). The findings of research in the AFM tradition stand in contrast to strong theoretical arguments that an informationally optimal decision making process must combine all the evidence pertaining to a decision into a single term (Gold and Shadlen, 2002; Bogacz et al., 2006).
It is important to be aware, however, that the AFM method can only point to the functional architecture of choice reactions not the implementational architecture (Marr, 1982). The correspondence between these two levels of description is by no means clear (e.g., Rumelhart and McClelland, 1985). For example, a decision making process which occurred over multiple architectural stages, optimally combining the evidence for all aspects of a decision could be modeled by a decision process with a single “weight of evidence” term (and hence would have no additive factors, and so would be – in terms of the additive factors method – a “single stage” processing model).
The AFM assumes discrete, serially connected, modules. Detailed modeling of how choice processes might produce decision times casts doubt on the validity of both this assumption and the inference from additivity of factors to discrete processing stages. Thomas (2006) shows that “additive factors” models can predict interaction of factors once reasonable assumptions about the representation of stimuli within standard decision models are included. In counter-point to this the Parallel Distributed Processing (PDP) framework for understanding cognition is founded on an explicit rejection of stage models of processing, with information being continuously available and interactively processed across multiple locations (Rumelhart et al., 1986a). McClelland (1979) showed that such a PDP “continuous processing” model could produce results which were consistent with the AFM, despite the lack of the discrete serial modules that the AFM is usually assumed to imply.
As well as these difficulties in making strong inferences from additive factors to underlying processing architectures (and vice versa), the distinction between continuous and discrete architectures is far from absolute. In two important reviews Miller (1990) and Sanders (1990) both note that further assumptions are required to constrain the models; assumptions on such issues as whether the internal codes used by any putative stages are continuous or discrete, whether the transformation between codes is continuous or discrete and whether the transmission of these codes between stages is continuous (ongoing) or discrete (instantaneous).
In light of these distinctions it is clear that neither analysis nor experiments alone will resolve the controversy over the number of stages of processes required in models of simple decision making (Carpenter and Reddi, 2001; Ratcliff, 2001). Our approach here is to use both the analytic approach of the AFM and the synthetic approach of model building within a PDP framework to inform an interpretation of new experimental data. This accords well with a review which concluded that because both discrete stage and continuous processing models can, with the right parameterization, mimic the results associated with the other it is vital to link theory and experiment using an explicit model of the particular task (Townsend and Wenger, 2004). Our investigation begins with the empirical data previously discovered and investigates how an existing model of the Stroop might account for our results involving manipulation of color intensity.
Modeling Additive Factors in the Stroop Task with Variable Color Intensity
Although a pattern of additive factors in the experimental data suggests discrete processing stages, it is appropriate to ask if existing, continuous processing – i.e. “single stage” – models of the Stroop task can fit the data. We show that they can.
Model Outline
Our starting point is the Cohen et al. (1990) model of the Stroop task. This is a model in the Parallel Distributed Processing tradition, in that it primarily consists of a number of identical units, which represent different concepts (Rumelhart et al., 1986b). Each unit has an associated activity, which influences the activity of those other units it is connected to. In Cohen et al.’s (1990) paper the model is trained to perform word and color reading using back propagation (Rumelhart et al., 1986a). Here, however, we do not consider learning and the impact of different training regimes. The essence of the model is that it performs stimulus-response translation, reconciling the word and color information in the stimulus, according to the attentional demands of the task instructions (“Respond based on the ink color, ignore the word"). The weighting of these factors and their combination, drives inputs into the response mechanism, which is that component of the model which signals the selected response. It does this after a certain amount of evidence, in terms of combined activity from upstream units in the model, has been accumulated. The mechanism of evidence accumulation is based on the drift diffusion model (Ratcliff, 1978; Ratcliff and McKoon, 2008). For a detailed discussion of this model of the Stroop task and the response mechanism see Stafford and Gurney(2004, 2007).
We take it as the starting point for our present investigation because it performs stimulus-response translation in arguably the simplest generic way within a parallel distributed processing framework. Although there are a number of other models of Stroop processing, it is beyond the scope of the current work to comprehensively investigate them and contrast them under the same manipulations as we present here.
This model is a continuous processing model. Activity in all parts of the model is continuously updated as the effect of the change in inputs (representing stimulus presentation) propagates through. In this respect, then, it is considered a “single stage” model; although it may have many architectural stages, they are a functional unit, with all components running simultaneously and passing information simultaneously and without delay to each other.
In the following sections we describe how the bare minimum of adjustments are made to this basic model to accommodate (a) the manipulation of stimulus intensity (as done experimentally in Stafford et al., 2011), and (b) the investigation of issues of stimulus binding and continuous vs. discrete stage models. For full details of the function of the model in all simulations reported here the reader is encouraged to inspect the source code which is provided in the supplementary material.
Extending Continuous Processing Models of the Stroop Task
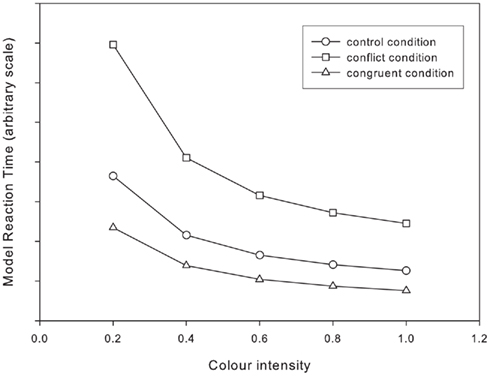
In the original model the word and color information is represented by 0 or 1 values on the input layer (so that the if the stimulus color, say, was red, the input unit for “red” would be clamped at 1 and the input unit for “green” would be clamped at 0). To simulate the present experiment intermediate intensity values between 0 and 1 were used for this input encoding, with both the color and the word inputs values clamped at the same intermediate values, namely 0.2, 0.4, 0.6, 0.8, or 1.0. This reflects the corresponding variation in the strength of the input representation with varying color saturation. Because both the word and color inputs to the model begin at the same time and have identical values we denote this the “single stage model with locked inputs.” The information flow for this simulation, and the one immediately following, is show in Figure 2.
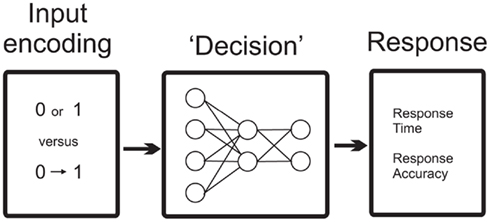
Figure 2. Information flow in the basic model. The Decision stage consists of the Cohen et al. (1990) model of Stroop processing. The continuous stage simulations reported here use this architecture, merely with modifications to the input encoding.
Figure 3 shows the results of the model. The match to the pattern of the experimental data is close. Piéron’s Law holds for all Stroop conditions and the interference and facilitation effects are constant across saturation conditions (see Table 1). In the original Cohen model, model reaction times are converted from model time-steps to simulated milliseconds using linear regression from the model reaction times to the empirical reaction times (Cohen et al., 1990, p.340).Obviously this approach is useful if we wish to compare model results with empirical data. In the current paper we are concerned with comparing between models. The linear regression, whilst producing plausible reaction times in terms of simulated milliseconds would not change the “shape” of the model results (in graphical terms, merely “distorting” the scale). Because of this we present here the model reaction times untransformed and leave the axis without value labels (the absolute values, in model time-steps are essentially arbitrary). The simulations should be judged according to the relative values of the reaction times – i.e. on whether the factors interact or not – and this judgment can be made without transforming the model reaction times into simulated milliseconds.
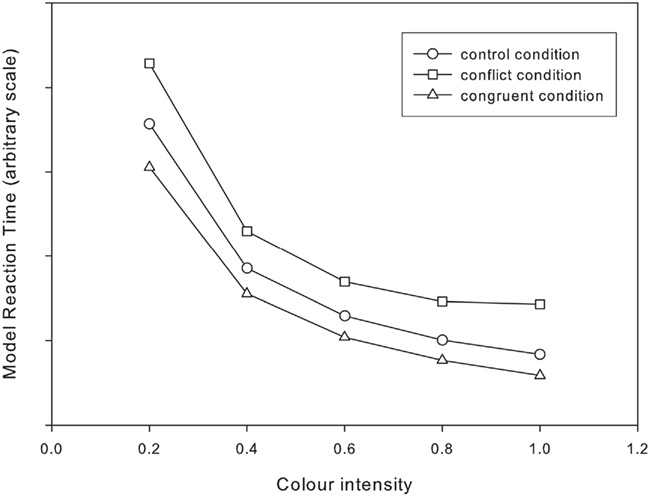
Figure 3. Single stage model with locked inputs: simulated reaction times for the standard Stroop task across a range of color intensities.
The complementary simulation to this one is to use the same “single stage” architecture but to vary the color and word intensity values independently (i.e. they are “unlocked”). Namely, the word intensity value is held at 1 (as in the original Cohen et al., 1990 simulation) and the color intensity value only is varied. The results of this simulation are shown in Figure 4.
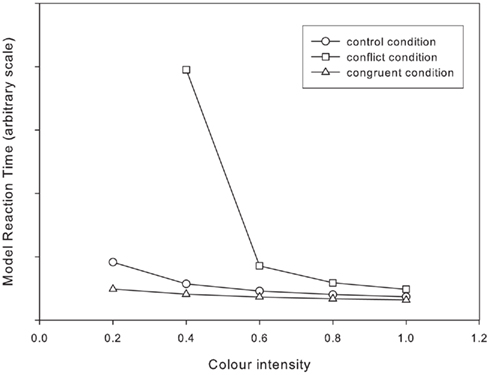
Figure 4. Single stage model with unlocked inputs: simulated reaction times for the standard Stroop task across a range of color intensities. Data point omitted where model provides the incorrect response (see text).
Note that for the single stage model with unlocked inputs the result for the conflict condition at the lowest color intensity is not shown. This is because at this point the model stops predicting the correct response, and hence, although the model does produce a reaction time it is not comparable with the other results since it is for the wrong response. This single data point was also omitted from the analysis presented in Table 2.
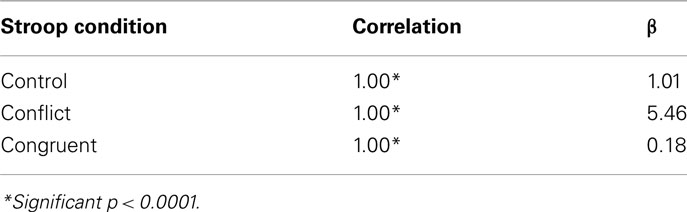
As can be seen from the graph, and confirmed by the fits to Piéron’s Law functions shown in Table 2, this simulation manifests multiplicative rather than additive factors. Although it is possible to fit a Pièron’s Law function to the data from each of the Stroop conditions, the β values of these functions are very different. This is indicative of the difference in slopes of the functions. This pattern of reaction times would be interpreted under the AFM as interactive rather than additive factors.
Prima facie these results are unsatisfactory, since the locking of inputs values would appear to be an ad hoc assumption. However, our simulation results with discrete two stage models, introduced below, call into question the unreasonableness of assuming locked input encodings. Before we move on to consider these additional simulations, note that the locked or unlocked nature of word and color inputs changes the outputs of this single stage model from appearing additive to appearing interactive. The logic of the AFM asks us to infer discrete stages from additive factors, yet these simulation results demonstrate that the manifestation of additive factors can depend entirely on changes to the input encoding, not upon the nature of the underlying processing architecture.
Discrete Stage Models of Stroop Processing
Results from simulations involving the single stage (i.e. continuous processing) Cohen model of Stroop processing are ambiguous, so it behooves us to investigate how a model with two, discrete, stages behaves under the same manipulation of inputs.
A two stage, discrete processing, variant of the standard Cohen model is constructed by adding a preliminary “detection” stage. This stage delays inputs to the second stage, the original Cohen model as described above, until a critical amount of stimulus information has accumulated. Once this detection stage is completed the original inputs – i.e., either 1 (“present”) or 0 (“absent”) – are activated and processing continues in the Cohen model as normal. The information flow in this new architecture is shown in Figure 5. The influence of color saturation is incorporated by providing continuously valued inputs to the detection stage only. The detection stage is a rise-to-threshold process where the time-to-completion is defined by thresh/intensity where, in this case, thresh = 10 and intensity reflects the stimulus intensity (i.e. color saturation here) and is taken as the values 0.2, 0.4, 0.6, 0.8, or 1.0. This stage is based on evidence accumulation models of perceptual decision making (Ratcliff, 1978; Usher and McClelland, 2001; Bogacz et al., 2006). Because the detection stage delays the activation of both word and color inputs to the Stroop processing component of the model (the Cohen model) we denote that this model has “locked inputs.”
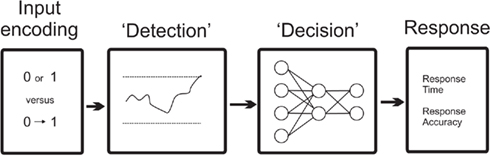
Figure 5. Information flow in the two stage models. The Detection stage consists of rise-to-threshold evidence accumulator, based on Ratcliff (1978).
The results of the simulation are shown in Figure 6. As expected, it is possible to generate simulated reaction time data which qualitatively matches the experimental data by adding an discrete detection stage to the existing Cohen model of Stroop processing.
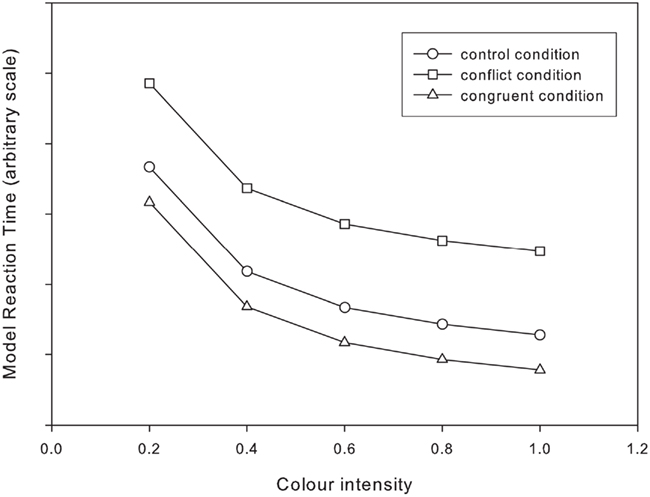
Figure 6. Two stage model with locked inputs: simulated reaction times for the standard Stroop task across a range of color intensities.
Note that, as in the experimental data, the interference effect is larger than the facilitation effect across all stimulus intensity values, and that both effects are consistent across all stimulus intensity values. Fits of the curves to Piéron’s Law (Table 3) show both strong matches and similar exponents (β) across conditions, as in the experimental data.
This is not a surprising result, since the simulation is an implementation of the architecture which inspired the logic of the AFM. The AFM infers discrete stages from additive factors, and this is based on the (correct) belief that if two experimental factors independently affect two separate processing stages then they will generate a pattern of additive factors in the response times. Note, however, that this correct belief is not logically sufficient to justify the inference of discrete stages from additive factors in the response times.
The final simulation of this paper asks if models with discrete processing stages necessarily produce additive factors. Recall that in the single stage models the input encoding could be “locked” or “unlocked,” these terms indicating whether inputs signifying word and color information had the same strength and onset timings. For the two stage model it is also possible have the input encoding as locked or unlocked. For locked inputs (i.e. as shown in the simulation immediately preceding), the inputs to the Cohen model are delayed until a preceding “sensory detection” stage is completed. To perform the final, complement, simulation – the two stage model with unlocked inputs – this means that both the word and color inputs to the Stroop processing component of the model are separately controlled by independent rise-to-threshold based “detection” processes, as described above. The color inputs vary, as before, and the word input is always 1. Because of this arrangement, in the unlocked input encoding conditions it is possible for the second stage to begin computing a response before it has received information about both aspects of the stimulus. Note that in accord with the assumptions of the AFM, the stimulus intensity only affects processing in the first stage, and the Stroop condition only affects processing in the second stage. The results are shown in Figure 7. Correlations and the β values from fitting Pièron’s curves to these simulated reaction times are shown in Table 4.
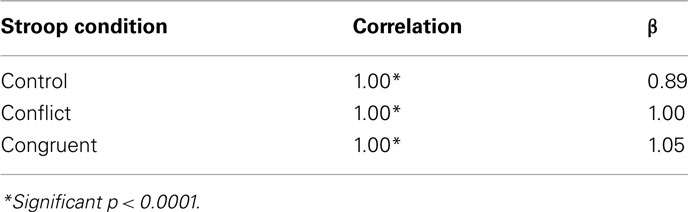
Table 4. Fit of Piéron’s law against simulation data for both two stage and one stage models with unlocked inputs.
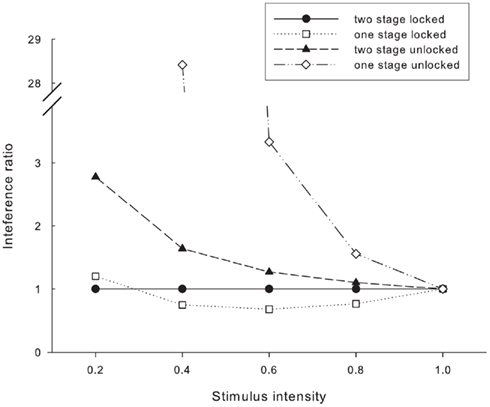
It is not clear that the exponents of the curves from fitting Pièron’s Law to the simulation results are consistent. In order to more clearly inspect this issue we calculated the ratio of the interference effect at each saturation level against the interference effect at the highest saturation level (i.e. the interference effect in the normal Stroop condition). This is shown in Figure 8 with the ratios for the one and two stage models with locked inputs also shown for comparison. This analysis should make it clear that although both the one and two stage models with locked inputs have consistent interference effects (indicative of additivity of factors), the models with unlocked inputs, both one and two stage, have variable interference effects, which is indicative of an interaction of factors. The same conclusions can be reached by analyzing facilitation effects (not shown here).
Discussion of Modeling
The present results provide a specific instance (the first simulation) of the claim that continuous processing models can mimic discrete processing models (McClelland, 1979). This weakens our confidence that inference about the underlying architecture can be made from data patterns consistent with factor additivity. The second simulation behaves in-line with the assumptions of the AFM – it is a single stage model and generates outputs consistent with having only a single stage, i.e. multiplicative factors. Note, however, that the architecture of both the first and second simulations is identical, the only change is to the independence of the input encoding. Simulations involving architectures with two clearly discrete stages of processing show that such architectures can produce additive factors, as has been traditionally assumed, but that this is not necessarily so (the fourth simulation). These results show that no simple inference from factor additivity, or its absence, to underlying architecture is possible.
Overall, the binding of color and word information during processing – which we have called locking of inputs – determines the manifestation of additive factors irrespective of processing architecture. This suggests that, vis-à-vis the experimental data (Stafford et al., 2011), the intensity at which word information is represented is affected by the intensity of color saturation. In other words, although it might at first appear unreasonable to assume that extent of color saturation affects how word information is represented by participants, modeling of the task with both established and modified models of Stroop processing suggests that this may indeed be occurring. Obviously further, direct, experimental tests are required to confirm this. For the moment we may regard this locking of inputs as a prediction from the modeling work which may, at some future point, be verified or falsified (rather than, say, as an assumption of the models that needs to be justified). For the current work the “locking” of inputs has a precise meaning - that the intensity values representing the word and color information are the same and, in the case of the discrete stage model, arrive at the “decision” stage of the model at the same time. We are aware that there is a wider debate regarding the “binding problem,” its exact nature and possible solutions, but do not wish to make strong claims about this issue here. In our models binding is declare to occur – there is no explicit mechanism within the models responsible for making this happen. Any mechanism that could bind together the representations of word and color intensity would be part of the wider operation of those phenomena known as “attention.” To postulate the binding of inputs together in this sense does not seem such an unreasonable assumption given the important role attention plays in the generating the Stroop Effect (Besner et al., 1997; MacLeod and MacDonald, 2000).
General Discussion
Consequences for Models of Decision Making
We have argued elsewhere (Stafford et al., 2011) that the empirical results treated here cannot be accounted for by a simple (one stage) response mechanism using a common metric. These models extend and qualify this conclusion by showing that a single stage model, in the sense of “single stage” used throughout this paper, can account for the additive factors in the empirical results. The Cohen model replicates the empirical data because the stimulus processing “front-end” transforms the stimulus information so that the inputs to the response mechanism produce consistent interference and facilitation at each level of color saturation, even though the absolute reaction times vary according to Piéron’s Law.
This model of Stroop processing (the first simulation) matches the pattern of empirical data, just as the two stage model with discrete processing of detection and decision stages does (the fourth simulation). This is an illustration of the phenomenon of model-mimicry (Townsend and Wenger, 2004) and more generally of the dangers of judging models solely by the goodness of fit to data (Roberts and Pashler, 2000). The strong implication, discussed further below, is that it is not possible to infer discrete processing stages from the appearance of additive factors in reaction time data.
Does it matter that the empirical data can be fitted with two fundamentally different kinds of model? It is a legitimate strategy of model development to restrict oneself to data modeling, in the sense of trying to fit outcome characteristics such as reaction time and error rates without reference to the plausibility of the internal structure of the models. From this perspective, both the single and two stage models are as good as each other. However data fitting is not the sole criterion for model development (Roberts and Pashler, 2000; Pitt and Myung, 2002). Indeed debates about internal structure seem unavoidable once an abstract model developed using data fitting is applied to biological data (as inRatcliff et al., 2003) or, conversely, biological data or arguments are recruited to help discriminate between such models (Reddi, 2001). To guide this debate, it is important to address explicitly which level(s) a model is designed to work at. A data-descriptive model should be judged differently from one that is supposed to represent the neural machinery which implements decision making. This “abstract mechanistic” level of description (Gurney, 2007) is the one at which, implicitly, the PDP models of Stroop processing, including the current models, are couched. Multiple-loci models of decision making such as these represent a problem for optimality analysis, because optimal decision making requires that all factors affecting the decision be weighed against each other, for if they are not then how can an optimal response be calculated? This requirement means that single stage models of decision making will be useful at the data-descriptive level of analysis for defining optimality, but multi-stage models will be required to account for experimental situations where decision making departs from optimality.
The models presented here suggest that the simple decision making models developed to account for simple perceptual decisions (e.g., the Diffusion Model of Ratcliff, 1978), and as refined by the optimality analysis of Bogacz et al. (2006), cannot alone be a complete model of decision making. Without assumptions about other elements of perception and action selection, such as included in these models, simple response mechanisms are insufficient to account for empirical data once the scope of decision making moves beyond the “simple perceptual” and onto even marginally more complex cases. Elsewhere we have argued that such models are also inadequate for performing adaptive action selection (Stafford and Gurney, 2007).
Consequences for the Additive Factors Model
It has been shown theoretically that models with discrete stages can mimic an interaction of factors (Thomas, 2006), and that continuous processing models can also mimic additive factors (McClelland, 1979). Here we show this with a concrete example from an existing domain of active research. These results show that without detailed additional assumptions any inference from RTs to underlying processing architecture is untenable (as suggested by Townsend and Wenger, 2004). Miller (1990) and Sanders (1990) both attempt to outline those specific additional assumptions which would define the senses in which models have discrete stages – the code used can be continuous (as in our case, values between 0 and 1) or discrete, as can the transformation of the code in any particular stage between the input and output, and the transmission of that code to the next stage. Specification of these additional constraints is necessary, they argue, in order to make firm predictions from models. We would go further and argue that numerous and additional specifications may be needed. In our case the difference between locked and unlocked input representations turns out to be crucial. It is unclear which model elements may make a prima facie discrete stage architecture behave as a continuous processing architecture, or vice versa, with respect to additive factors. This does not just complicate the distinction but makes it, we argue, irrelevant as far as the presence or absence of additive factors goes. It is not, contra the AFM, possible to infer discrete processing stages from the appearance of additive factors. Nor is it possible to infer separate loci of effects for the different factors. The first simulation presented here shows additive effects for the color intensity and Stroop condition factors, but the computation of both of these factors happened simultaneously and in parallel within the same model.
The current work also shows how data and models from a specific decision making task can be co-opted to inform our understanding. Although we have confirmed, in a specific domain, previous claims that no strong inference from RTs to architecture is possible, we have also shown that the idea of processing stages and common metrics can inform modeling investigations so as to reveal surprising new results, in this case the finding that replicating the empirical data requires that the information from the separate Stroop dimensions be tethered in intensity.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Useful reviews and discussion of an earlier incarnation of this work were provided by Marius Usher, Eddy Davelaar, W. Trammell Neill, Max Coltheart, Andrew Heathcote, Leendert van Maanen, and Ion Juvina.
References
Besner, D., Stolz, J. A., and Boutilier, C. (1997). The Stroop effect and the myth of automaticity. Psychon. Bull. Rev. 4, 221–225.
Bogacz, R., Brown, E., Moehlis, J., Holmes, P., and Cohen, J. D. (2006). The physics of optimal decision making: a formal analysis of models of performance in two-alternative forced-choice tasks. Psychol. Rev. 113, 700–765.
Carpenter, R. H. S., and Reddi, B. A. J. (2001). Putting noise into neurophysiological models of simple decision making. Nat. Neurosci. 4, 337–337.
Cohen, J. D., Dunbar, K., and McClelland, J. L. (1990). On the control of automatic processes – a parallel distributed-processing account of the Stroop effect. Psychol. Rev. 97, 332–361.
Donders, F. (1868–1869/1969). “Over de snelheid van psychische processen. onderzoekingen gedann in het physiologish laboratorium der utrechtsche hoogeshool,” in Attention and Performance, Vol. II, ed. W. G. Koster (Amsterdam: North-Holland).
Gold, J. I., and Shadlen, M. N. (2001). Neural computations that underlie decisions about sensory stimuli. Trends Cogn. Sci. (Regul. Ed.) 5, 10–16.
Gold, J. I., and Shadlen, M. N. (2002). Banburismus and the brain: decoding the relationship between sensory stimuli, decisions, and reward. Neuron 36, 299–308.
Gurney, K. N. (2007). Neural networks for perceptual processing: from simulation tools to theories. Philos. Trans. R. Soc. B Biol. Sci. 362, 339–353.
Luce, R. (1986). Response Times: Their Role in Inferring Elementary Mental Organisation. Oxford Psychology Series. New York: Clarendon Press.
MacLeod, C. (1991). Half a century of research on the Stroop effect – an integrative review. Psychol. Bull. 109, 163–203.
MacLeod, C., and MacDonald, P. (2000). Interdimensional interference in the Stroop effect: uncovering the cognitive and neural anatomy of attention. Trends Cogn. Sci. (Regul. Ed.) 4, 383–391.
Marr, D. (1982). Vision: A Computational Investigation into the Human Representation and Processing of Visual Information. New York, NY: Henry Holt and Co., Inc.
McClelland, J. (1979). On the time-relations of mental processes: an examination of systems of processes in cascade. Psychol. Rev. 86, 287–330.
Miller, J. (1990). Discreteness and continuity in models of human information-processing. Acta Psychol. (Amst.) 74, 297–318.
Opris, I., and Bruce, C. J. (2005). Neural circuitry of judgment and decision mechanisms. Brain Res. Brain Res. Rev. 48, 509–526.
Piéron, H. (1952). The Sensations: Their Functions, Processes and Mechanisms. London: Frederick Muller Ltd.
Pins, D., and Bonnet, C. (1996). On the relation between stimulus intensity and processing time: Piéron’s law and choice reaction time. Percept. Psychophys. 58, 390–400.
Pitt, M. A., and Myung, I. J. (2002). When a good fit can be bad. Trends Cogn. Sci. (Regul. Ed.) 6, 421–425.
Ratcliff, R. (2001). Putting noise into neurophysiological models of simple decision making. Nat. Neurosci. 4, 336–336.
Ratcliff, R., Cherian, A., and Segraves, M. (2003). A comparison of macaque behavior and superior colliculus neuronal activity to predictions from models of two-choice decisions. J. Neurophysiol. 90, 1392–1407.
Ratcliff, R., and McKoon, G. (2008). The diffusion decision model: theory and data for two-choice decision tasks. Neural Comput. 20, 873–922.
Roberts, S., and Pashler, H. (2000). How persuasive is a good fit? A comment on theory testing. Psychol. Rev. 107, 358–367.
Rumelhart, D., Hinton, G., and Williams, R. (1986a). “Learning internal representations by error propagation,” in Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Vol. 1, eds D. Rumelhart, J. McClelland, and the PDP Research Group (Cambridge, MA: MIT Press), 318–362.
Rumelhart, D., McClelland, J., and the PDP Research Group. (1986b). Parallel Distributed Processing: Explorations in the Microstructure of Cognition. Cambridge, MA: The MIT Press.
Rumelhart, D., and McClelland, J. (1985). Levels indeed! a response to broadbent. J. Exp. Psychol. Gen. 114, 193–197.
Sanders, A. F. (1990). Issues and trends in the debate on discrete vs. continuous processing of information. Acta Psychol. (Amst.) 74, 123–167.
Stafford, T., and Gurney, K. (2004). The role of response mechanisms in determining reaction time performance: Piéron’s law revisited. Psychon. Bull. Rev. 11, 975–987.
Stafford, T., and Gurney, K. (2007). Biologically constrained action selection improves cognitive control in a model of the Stroop task. Philos. Trans. R. Soc. Lond. B Biol. Sci. 362, 1671–1684.
Stafford, T., Ingram, L., and Gurney, K. N. (2011). Piéron’s law holds during Stroop conflict: insights into the architecture of decision making. Cogn. Sci. doi: 10.1111/j.1551-6709.2011.01195.x. [Epub ahead of print].
Sternberg, S. (1969). The discovery of processing stages: extensions of donders’ method. Acta Psychol. (Amst.) 30, 276–315.
Sternberg, S. (1998). “Discovering mental processing stages: the method of additive factors,” in An Invitation to Cognitive Science: Methods, Models, and Conceptual Issues, 2nd Edn, eds D. Scarborough, and S. Sternberg (Cambridge, MA: MIT Press), 702–863.
Stoffels, E. J. (1996). On stage robustness and response selection routes: further evidence. Acta Psychol. (Amst.) 91, 67–88.
Stroop, J. (1935). Studies of interference in serial verbal reactions. J. Exp. Psychol. 18, 643–662.
Thomas, R. D. (2006). Processing time predictions of current models of perception in the classic additive factors paradigm. J. Math. Psychol. 50, 441–455.
Townsend, J. T., and Wenger, M. J. (2004). The serial-parallel dilemma: a case study in a linkage of theory and method. Psychon. Bull. Rev. 11, 391–418.
Usher, M., and McClelland, J. L. (2001). The time course of perceptual choice: the leaky, competing accumulator model. Psychol. Rev. 108, 550–592.
van den Wildenberg, W. P., and van der Molen, M. W. (2004). Additive factors analysis of inhibitory processing in the stop-signal paradigm. Brain Cogn. 56, 253–266.
Keywords: decision making, Stroop, Piéron’s law, additive factors method
Citation: Stafford T and Gurney KN (2011) Additive factors do not imply discrete processing stages: a worked example using models of the Stroop task. Front. Psychology 2:287. doi: 10.3389/fpsyg.2011.00287
Received: 17 May 2011; Accepted: 10 October 2011;
Published online: 14 November 2011.
Edited by:
Dietmar Heinke, University of Birmingham, UKReviewed by:
Christoph T. Weidemann, Swansea University, UKEric Postma, Tilburg University, Netherlands
Copyright: © 2011 Stafford and Gurney. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Tom Stafford, Department of Psychology, University of Sheffield, Sheffield S10 2TP, UK. e-mail: t.stafford@shef.ac.uk