- 1Centre de recherche du centre hospitalier de l’Université de Montréal (CRCHUM), Université de Montréal, Montréal, QC, Canada
- 2Department of Mathematics, University of Toronto, Toronto, ON, Canada
- 3Mathematics Division, National Center for Theoretical Sciences, Taipei, Taiwan
- 4Département d’Informatique, UQAM, Montréal, QC, Canada
Background: Life stages are not clearly defined and significant determinants for the identification of stages are not discussed. This study aims to test a data-driven approach to define stages and to identify the major determinants.
Methods: This study analyzed the data on the Medical Expenditure Panel Survey interviewees from 1996 to 2011 in the United States. This study first selected features with the Spearman’s correlation to remove redundant variables and to increase computational feasibility. The retained 430 variables were log transformed, if applicable. Sixty-four nominal variables were replaced with 164 binominal variables. This led to 525 variables that were available for principal component analysis (PCA). Life stages were proposed to be periods of ages with significantly different values of principal components (PCs).
Results: After retaining subjects followed throughout the panels, 244,089 were eligible for PCA, and the number of civilians was estimated to be 4.6 billion. The age ranged from 0 to 90 years old (mean = 35.88, 95% CI = 35.67–36.09). The values of the first PC were not significant from age of 6 to 13, 30 to 41, 46 to 60, and 76 to 90 years (adjusted p > 0.5), and the major determinants were related to functional status, employment, and poverty.
Conclusion: Important stages and their major determinants, including the status of functionality and cognition, income, and marital status, can be identified. Identifying stages of stability or transition will be important for research that relies on a research population with similar characteristics to draw samples for observation or intervention.
Contribution: This study sets an example of defining stages of transition and stability across ages with social and health data. Among all available variables, cognitive limitations, income, and poverty are important determinants of these stages.
Introduction
Life course perspective links exposures in early life to incidence in later life and has been proven useful to understand distant courses of particular events, such as cardiovascular diseases and diabetes (1, 2). For example, life course epidemiology attempts to find the associations between childhood trajectories and the outcomes in later life (2, 3). Although similar ideas have been widely applied and embedded in terms like adolescence (4) and adulthood (1), it is still unclear how stages that consist of a life course could be clearly defined (1). There are theories on the transitions or trajectories of life (5), some of which are supported by evidence, to show that physiological functions evolve with different developmental stages (6, 7) and health trajectories differ at the end of life (8–10). However, these definitions might not be suitable for general questions, such as what is the beginning of aging (11) and what characteristics can be used to define healthy aging and trajectories? These questions are usually complicated by socioeconomical activities. Therefore, a population perspective is inevitable, and explicit criteria to extract information from population data should be established, if we would like to study the diverse nature of life course.
To address the need to have a better understanding of life course from a population perspective and to establish criteria for data extraction, we consider the Medical Expenditure Panel Survey (MEPS) database that documents several distinctive dimensions of life course, especially socioeconomic status, functionality, and health status. The MEPS is a source of information with important characteristics, especially national representativeness and age coverage from 0 to 90 years (12). The main theme of the MEPS includes health insurance coverage, health-care consumption, and incurred expenditures (12). It also contains a wide range of individual information on demographics, income and tax filing, health status, disability, access to care, employment, health insurance and health utilization with information on expenditure and source of payment (12). For health status, detailed information is collected on activities of daily living, instrumental activities of daily living, vision, hearing, changes in limitations, child health and preventive care, and other dimensions measured by SF-12, smoking status, Kessler Index (K6), Patient Health Questionnaire, and attitudes about health (12). Due to its rich set of variables on individual status, national coverage, and longitudinal components, the MEPS data are not only used in the health expenditure estimation but also in other social research topics, such as income tax simulations (13, 14), employment, social determinants of health (15), and longitudinal research on individual or family behaviors (12). The inclusion and balance of social and health dimensions in the MEPS database is one of the best resources available for us to establish explicit criteria to understand population data from a life course perspective.
This study aims to test the feasibility of a data-driven approach to classify potential life stages and search for determinants of the components with data on health and health-care utilization. First, we attempt to identify representative components of the population data based on applying a commonly used data summary method, linear or ordinary principal component analysis (PCA). Second, we search for life stages within the principal components (PCs) of the database. Finally, we interpret the identified life stages with the variables that are highly associated with them.
Data and Methods
The data were explored by PCA and represented by PCs. In this work, the PCs were taken as representative components or leading trajectories in a life course perspective in this exploratory project. The leading PCs might represent distinctive dimensions of life course, since they were found to be composed of distinctive input variables. A life stage is defined to be a period of consecutive ages, during which the chosen leading trajectories has a small variation. The chronological ages between life stages were stages of transition. The entire analytical process is shown step by step below.
Data Sets
This study analyzed the 16 longitudinal panels released from the MEPS that were conducted annually among the civilian non-institutionalized population to produce nationally representative statistics since 1996 in the United States (16). Each panel lasted for 2 years and consisted of five rounds of data collection (17).
Data Linkage and Processing
The 16 longitudinal panels of the MEPS were pooled and merged by variable names common to all panels. There were 1,989 common variables across 16 panels (for panels beginning throughout 1996 and 2011, see Datasheet 1 in Supplementary Material for the list of variables and their characteristics). Only subjects participating throughout the 2-year panels were retained in the data set, in addition to those deceased after a 1-year follow-up and before the end of the 2-year panels. Administrative variables and the variables that were used to flag certain circumstances in the process of data gathering were not used for analysis. The result was that only the 789 variables containing individual information in the first years of the 2-year panels were eligible for analysis.
Reserved values that identified specific responses across all variables were recoded according to the MEPS codebooks: −2 recoded to the same answers in previous rounds, −1 to inapplicability and others to missing values (−3, −7, −8, and −9 for “no data in round,” “refused,” “do not know,” and “not ascertained,” respectively; see Datasheet 1 in Supplementary Material for the proportions of these categories in the variable list). The proportions of missingness ranged from 0 to 23.62% (median 0.01% among 644 variables with any missing values, see Datasheet 1 in Supplementary Material for the proportions of missingness). Missing values in all variables were imputed with the multivariate imputation by chained equations (18). The skewness of each continuous variable was evaluated from the raw data, without adjusting the survey design. Log transformation was applied, if the skewness of a log-transformed variable was less than that of the original variable (19).
Feature Selection with Spearman’s Rank-Order Correlation
This study first selected features with a correlation-based method proposed for the purpose of removing redundant variables and increasing computational feasibility (20, 21). The data redundancy might be created for the ease of survey implementation or data labeling. For example, different sources of income were asked about separately, and total income was the sum of incomes from all sources (22). The levels of education might be presented as years spent in school or types of highest grades completed (22) (see Datasheet 1 in Supplementary Material for details on variable names and labels).
First, sex and race/ethnicity were excluded, since they do not provide dynamical information. Age is also excluded, so that we could examine the life stage without the influence of the physical status. Spearman’s rank-order correlation was used to create a correlation matrix of all variables, categorical, or continuous (20, 21). The threshold for redundancy was Spearman’s rank correlation coefficient greater than 0.9 (23). There were 430 variables left for further analysis (see Figure 1 for the flowchart).
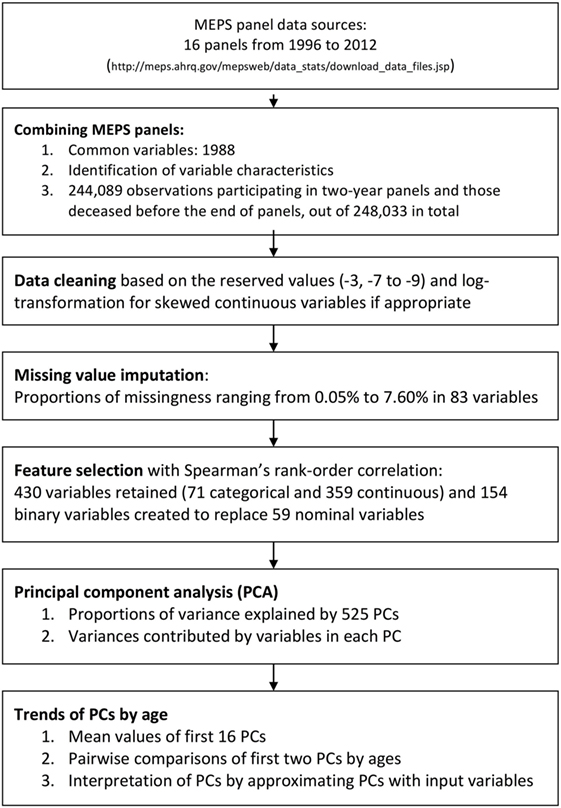
Figure 1. Flowchart of data linkage, data processing, and feature selection with the Medical Expenditure Panel Survey (MEPS) 1996–2011.
Of the 71 categorical variables, 12 ordinal variables that ranked poverty categories, difficulty in using fingers to grasp, self-rated health status, and self-rated mental health status and a summary measure of vision impairment were not transformed to dummy variables. Another 59 nominal variables were replaced with 154 multiple binominal variables. This results in 525 variables that were available for PCA. There were an additional 15 variables that were used for personal identification and control for survey design.
Principal Component Analysis
Principal component analysis was proven to be useful for dimension reduction or data preprocessing (24). We considered linear or ordinary PCA as the optimal and most feasible option in consideration of complex survey design (25). Although there are different variations of PCA (24, 26, 27) or similar data techniques (28, 29), there were limited choices of dimension reduction methods under the complex survey design (30). Before PCA, each variable was centered to 0 and scaled to unit variance. The PC comes from projecting input variables to the determined principal vector. The leading PCs had the largest variances and explained the largest proportions of total variances in a database. In this study, PCA was conducted with the 525 variables, while adjusting for complex survey design (30).
The contributions of variable variance to each PC were calculated in two steps. First, for each PC, the associated squared loadings of all input variables were obtained. These squared loadings ranged from 0 to 1. The contribution of the ith input variable in each PC is then defined as the variance of each PC was multiplied by the ith squared values.
Proposed Life Stages
The proposed life stage is evaluated from the first or second PC. We partition the dataset into subsets according to age, ranging from 0 to 90 years old. The age is determined on December 31 of each year. Each age subset consists of subjects with the same age, and there are a total of 91 age subsets. We view the p value < 0.05 as statistical significant, and the p values were adjusted for multiple comparisons with the Benjamini–Hochberg method (31). We call a group of consecutive age subsets stable, if less than 5% of all pairs of age subsets are different with statistical significance. In practice, the life stages were searched in the following greedy manner. We began with the age 0 subset and tested whether the PC value at that age subset was significantly different from the age one subset. If there was no significant difference, we found a stable group consisting of age 0 and 1 subset. We continued the iteration, and supposed that we find a stable group consisting of age 0 to age i subsets, where i > 1. We then determined if the group that consisted of age 0 to age i + 1 subsets is a stable group. This search stops when the age j, where j > i, does not belong to the stable group consisting of age 0 to age j − 1 subsets. We then restart the greedy iteration from the age j subset and view the stable group consisting of age 0 to age j − 1 subsets as an isolated group. This greedy algorithm ends when the 91 age subsets are exhausted. We call the period of consecutive ages in a stable group longer than 5 years a life stage. The ages between any two life stages were considered stages of transition.
PC Approximation and Interpretation
For the purpose of interpretation, the PCs were approximated with input variables using a linear regression model. The approximation method assessed the relative importance of all input variables in terms of R2 regarding each PC. We applied the forward selection to include input variables in the linear regression model. There were no limits on the number of input variables that could be used to approximate each PC. The PCs were interpreted according to the regression coefficients of the input variables.
This study adopted R (v. 3.20 released in April 2015) and R Studio (v. 0.99.441 released in May 2015) for data analysis. The complex survey design of the MEPS was accounted for with the survey package (30), except for Spearman’s rank-order correlation and multiple imputations that required more computational capacity than what we could afford. The R2 used to select the input variables for PC interpretation was assessed with the relaimpo package (32).
Results
Population Characteristics
There were 248,033 subjects available in panels 1–16 of the MEPS between 1996 and 2011 in the United States. After retaining those participating throughout 2-year panels and those deceased during the panels, a total of 244,089 were used for PCA. Adjusting for survey design, the populations and the demographic characteristics were tabulated for the survey years in Table 1. With a weighting, the numbers of civilians were estimated to be 270 million in 1996 to 312 million in 2011, totaling 4.6 billion. The proportion of females (51.06% of the total) did not change significantly (p = 1). The mean ages increased from 34.69 to 37.20 (p < 0.001), while the proportion of whites (from 81.70 to 79.89%, p = 0.21) did not change significantly in the study period. The population by gender and age were plotted with the variances of the 525 PCs in Figure 2. Despite the decline of population numbers with the advanced age, the sum of variances of all PCs continued to increase after 45 years of age. In Figure 3, the proportions of explained variance by the first 20 PCs were shown. Most PCs did not explain more than 1% of total variances. The proportions explained by the first five PCs were as following: 48.24, 3.28, 2.72, 1.41, and 1.26%, respectively.
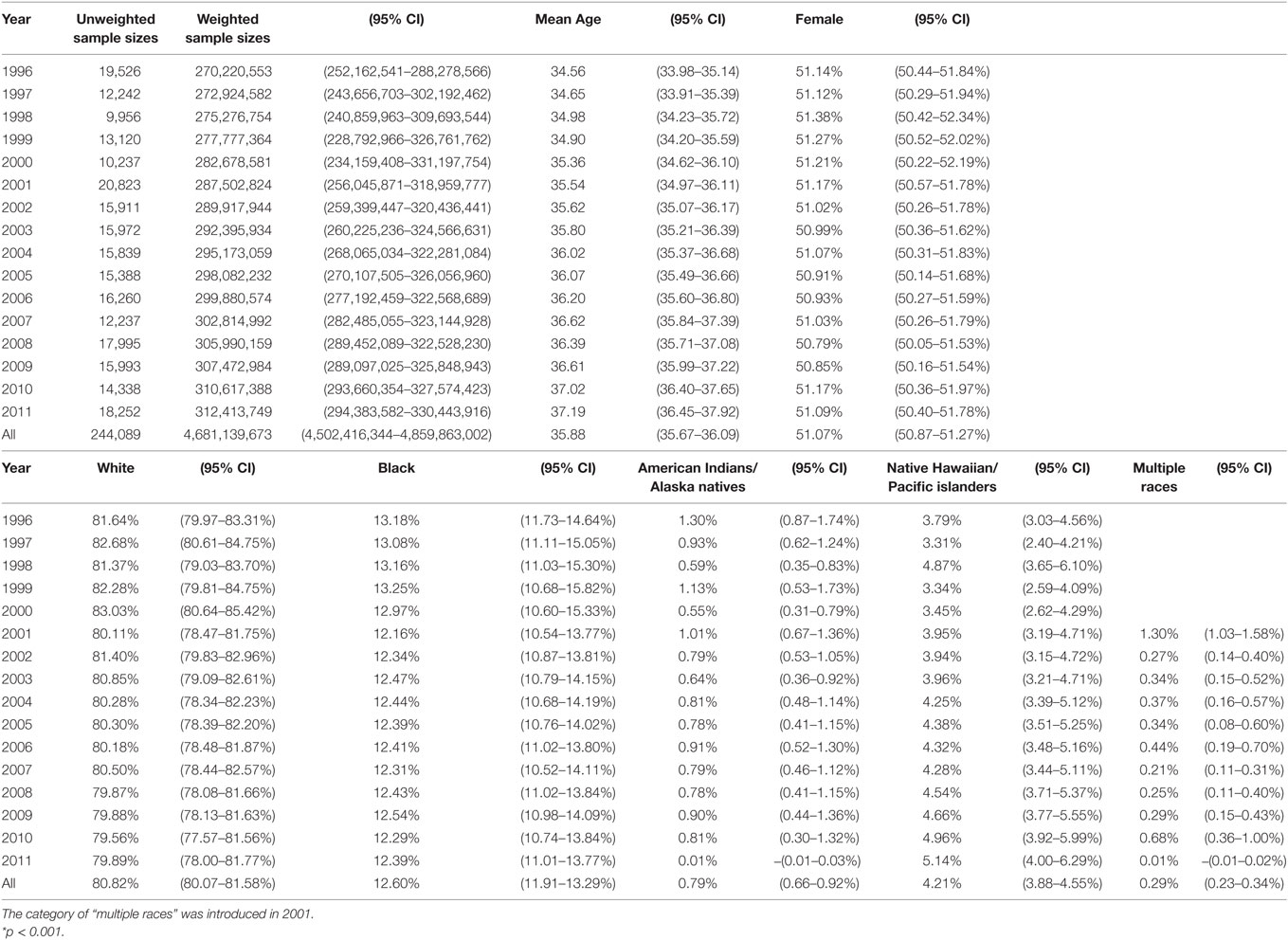
Table 1. Demographic characteristics of the populations in the Medical Expenditure Panel Surveys from 1996 to 2011.
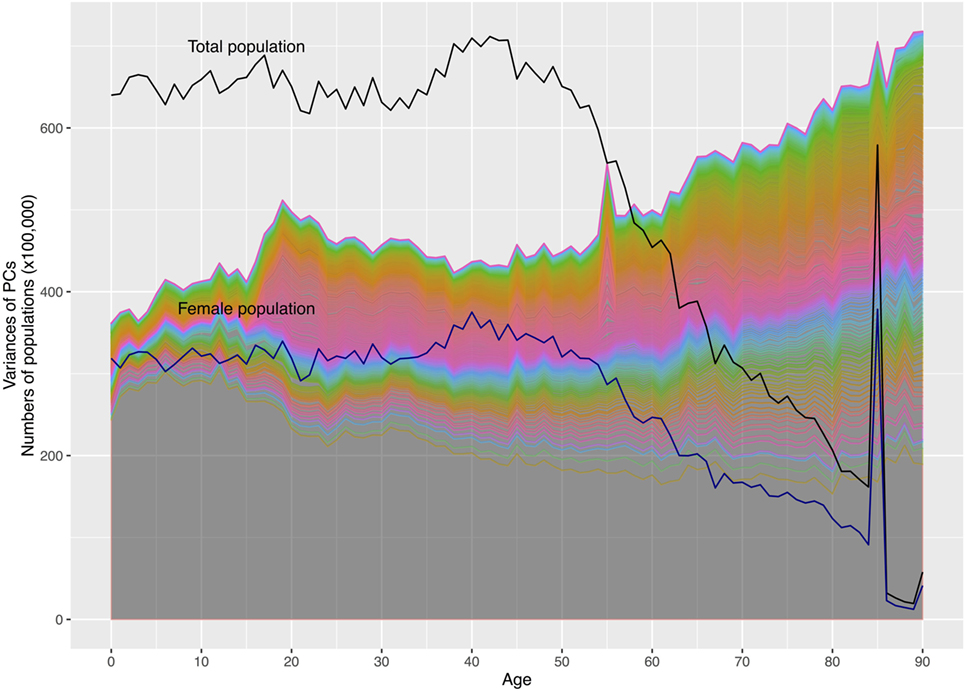
Figure 2. The numbers of population and variances of principal components (PCs) by age. Note: the area under the first lowest curve represents the variance of the first principal component (PC1); the area between the first and second lowest curves represents the variance of the second PC (PC2); this principle applies to other areas under curves. There are 525 PCs in the graph. The upper black solid line represents the numbers of total populations by age; the lower represents the numbers of female populations. The spikes of population numbers at age 85 are due to the top censoring of age beginning in 2000.
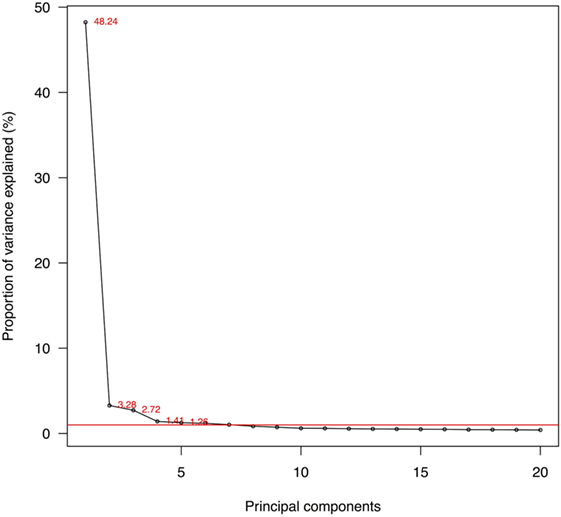
Figure 3. Proportions of variances explained by the first 20 principal components (PCs). Note: red line: 1% of total variance; 525 PCs in total.
Variables Contributing to the Variability of First PCs
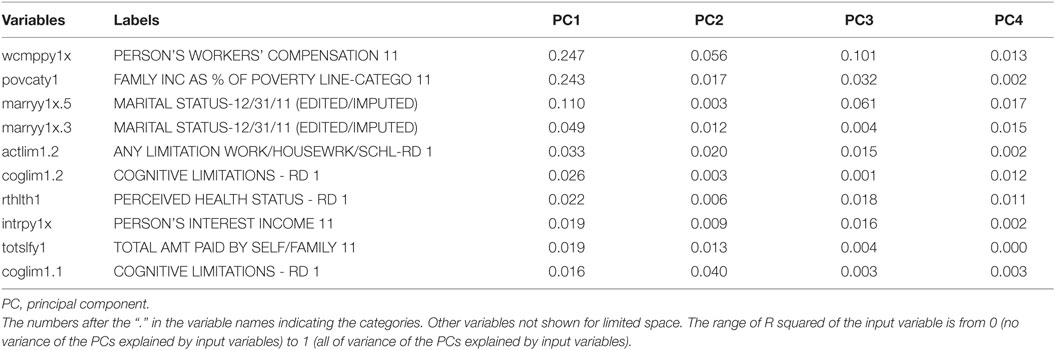
In Tables 2–4, the variables were sorted by the contributed variance of the 40 leading variables for PC1 (first PC), PC2 (second PC), and PC3 (third PC). The leading variable, in terms of the variance contributed to PC1, was the amount spent on home health non-agency workers (hhnwcpy1, 99.3% variance contributed), followed by other measures on healthcare utilization (dvowcpy1, zidosry1, and many others) that included home care, dental care, emergency room use, prescriptions, and clinical visits (Table 2). There were 125 variables whose contributions to PC1 are >0.9 and 177 variables whose contributions are >0.8.
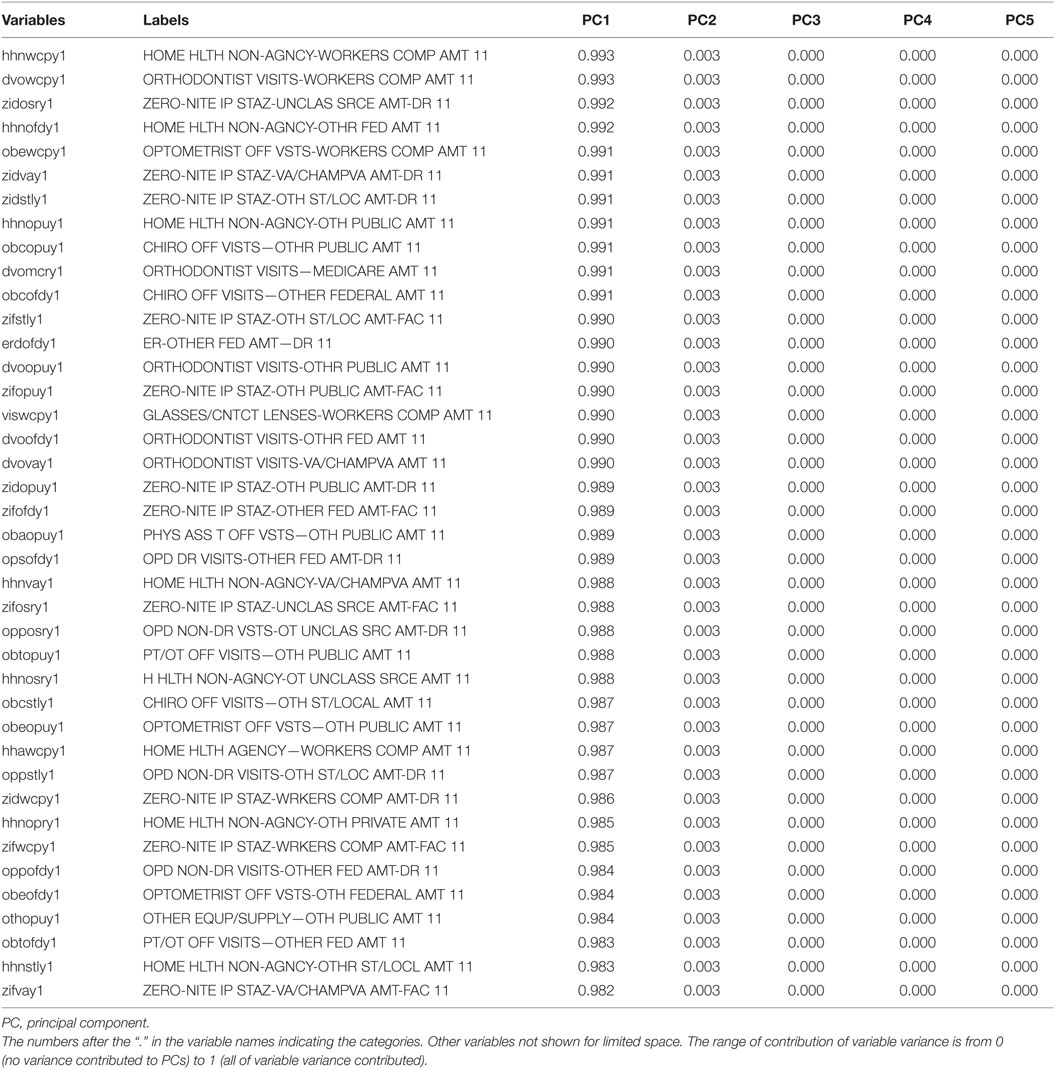
Table 2. The contribution of variance of each variable to PCs, sorted by the values in the first five PCs.
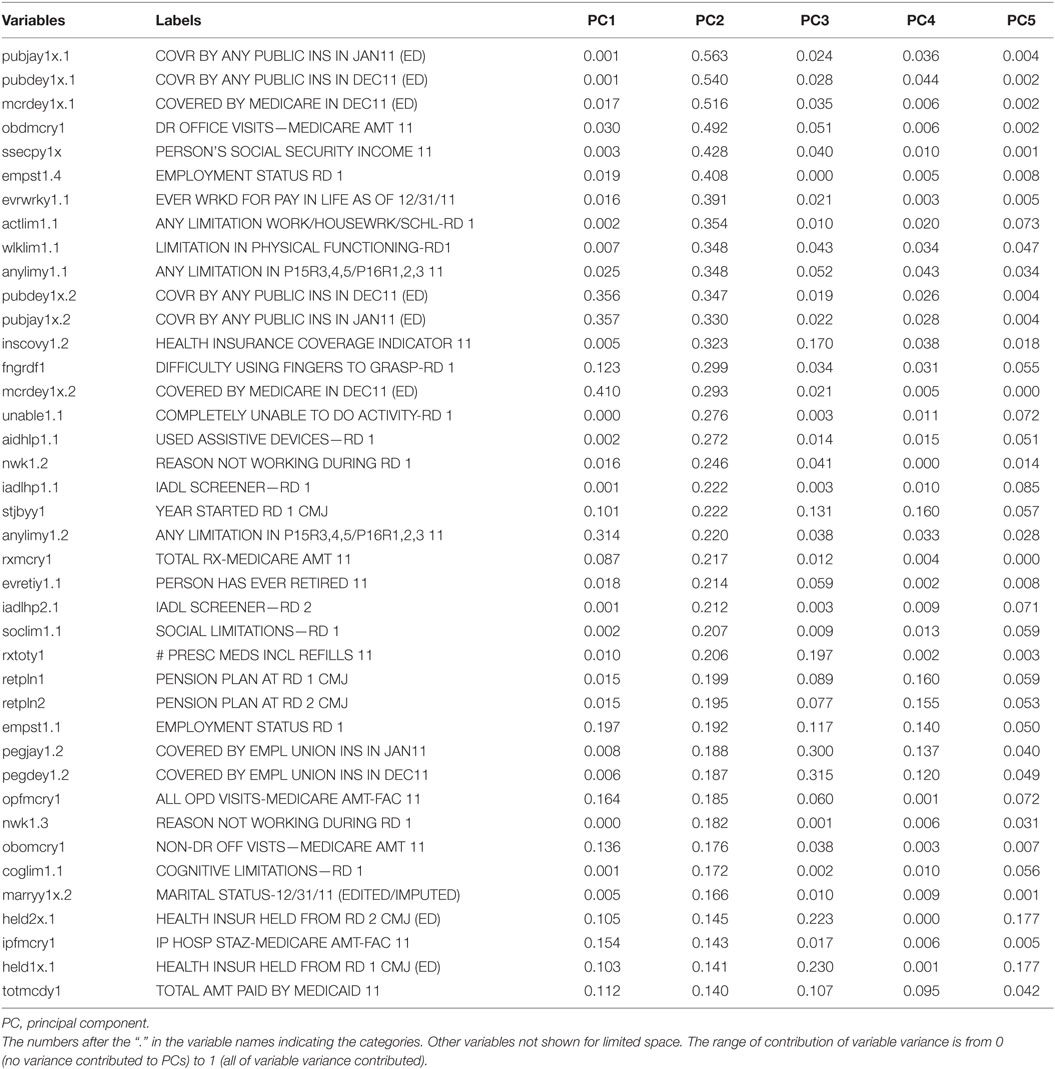
Table 3. The contribution of variance of each variable to the second principal component, sorted by the contributed variance of variables in the second principal component.
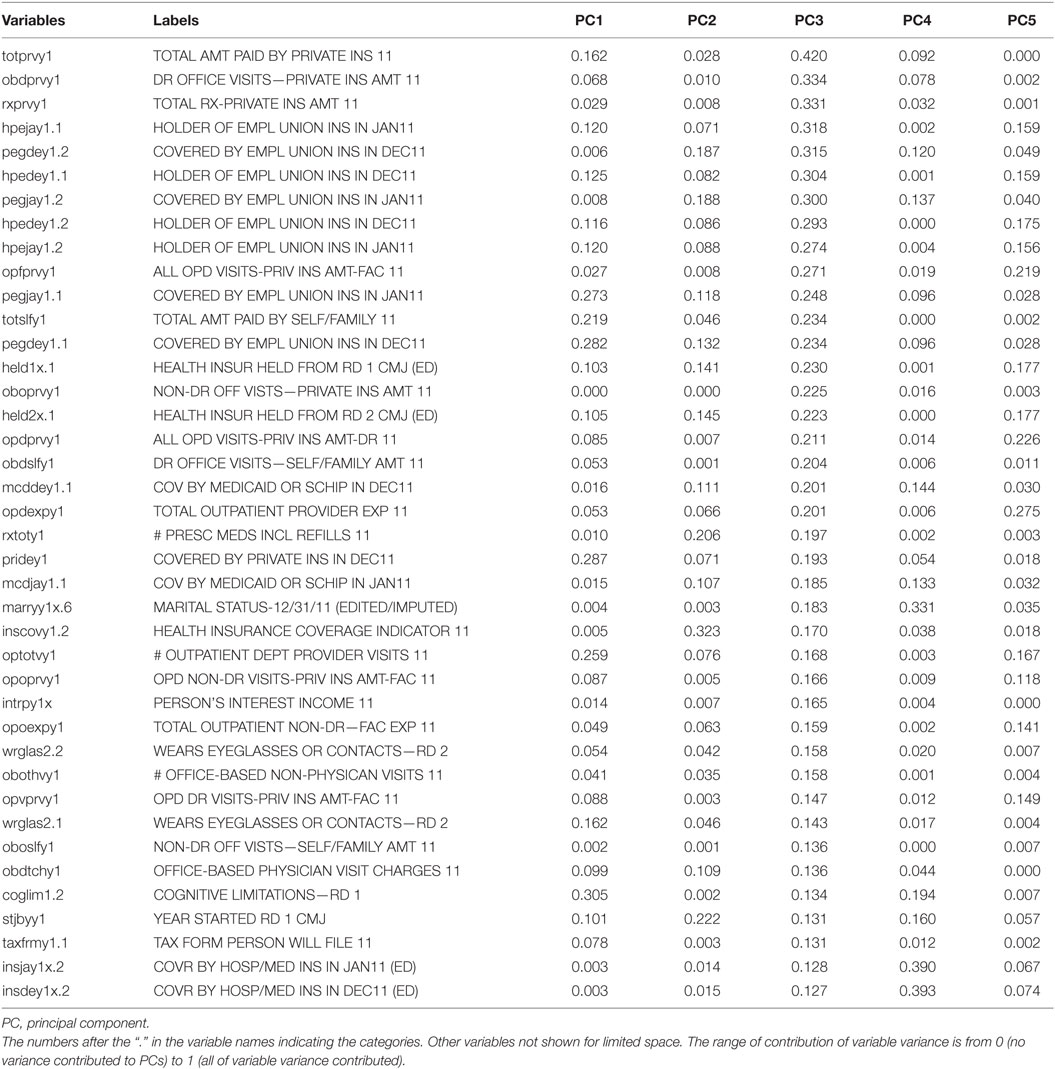
Table 4. The contribution of variance of each variable to the third principal component, sorted by the contributed variance of variables in the third principal component.
The leading variables, in terms of the contributed variances to PC2, were public insurance coverage (pubjay1x.1, pubdey1x.1, and inscovy1.2), employment-related variables (empst1.4), and functional limitations (actlim1.1, wlklim1.1, anylimy1.1, Table 3). However, there were only three variables contributing more than 0.5 to PC2. In Table 4, there were no variables contributing more than 50% of their own variances to PC3. The leading variables for PC3 were related to the amount of health-care expenditures paid by private insurance and coverage of employment-related insurance. For the other PCs, the contribution of the leading variable decreased.
Life Stages
The mean values of the first 16 PCs were plotted in Figures 4 and 5. The first eight PCs had changes of greater magnitude than the 9–16th PCs between age of 0 and 90 years. To test the significance of the changes in PC values, Figures 6 and 7 present the pairwise comparisons of the PC1 and PC2 by age, respectively. By setting the insignificant values to blank in the matrix of differences, there were clusters of blank cells along with the diagonal axis that labeled years of age. In the gray rectangles, the covered areas had less than 5% of significant differences of all cells in the areas. Therefore, the age ranges covered by gray rectangles were stages with populations of similar PC values. The values of PC1 were not different from 6 to 13, 30 to 41, 46 to 60, and 71 to 90 (adjusted p values > 0.05 for more than 95% of all pairwise comparisons). The values of PC2 were not different from 12 to 18, 29 to 38, and 41 to 45 years.
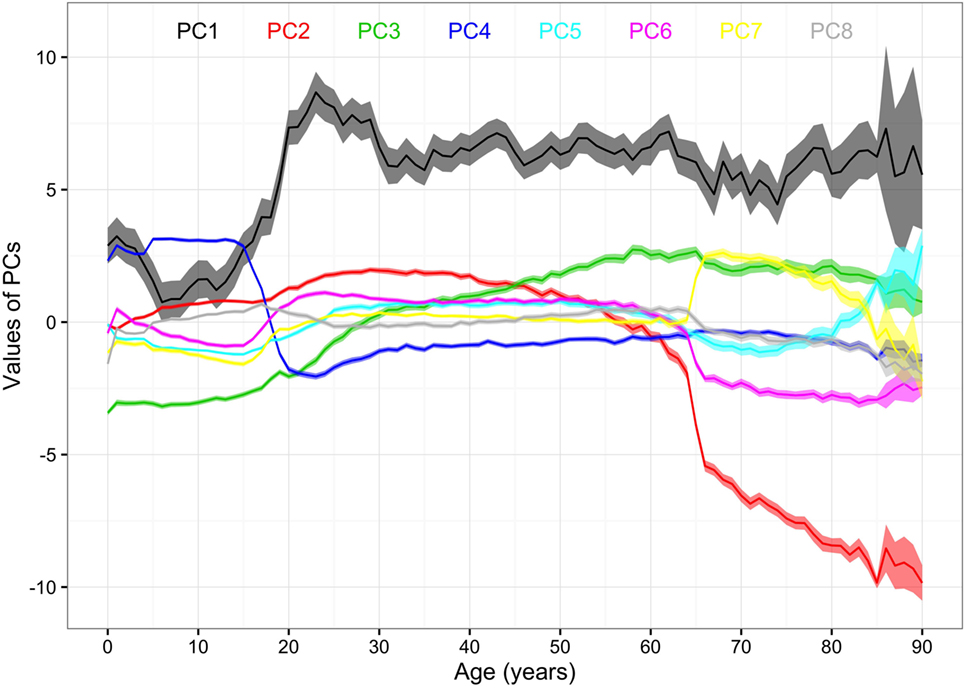
Figure 4. Mean values of the first to the eighth principal components (PCs) by age. Note: 95% CIs of the PCs are the ranges of the same colors as the PCs. The colors and corresponding numbers of PCs are labeled on the graph.
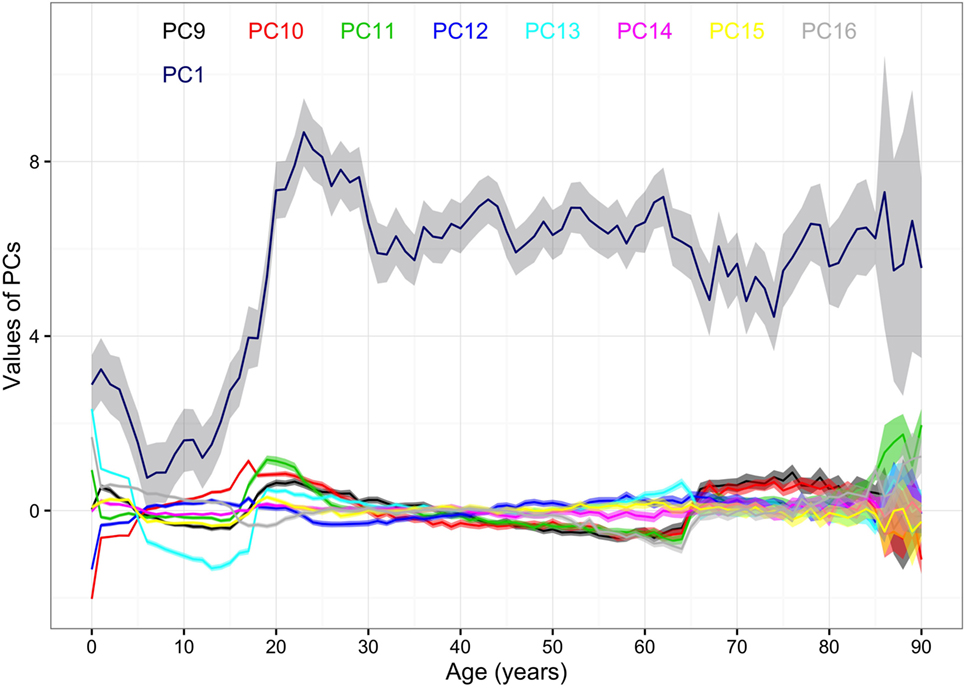
Figure 5. Mean values of the 1st and the 9th–16th principal components (PCs) by age. Note: 95% CIs of the PCs are the ranges of the same colors as the PCs. The color of first PC is navy blue. The colors and corresponding numbers of PCs are labeled on the graph.
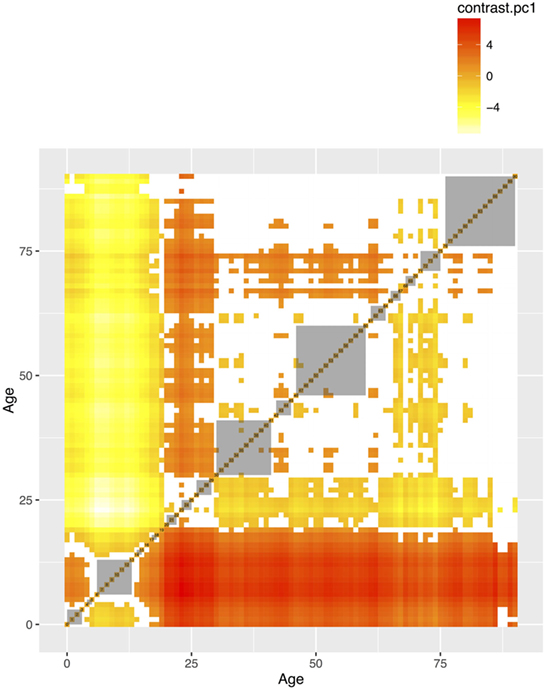
Figure 6. The pairwise comparisons of the first principal component by age groups. The value in each cell is the difference of PC1 between two age groups. The differences that are not statistically significant (p values adjusted for multiple comparisons based on the Benjamini–Hochberg method at 0.05) were left blank. The gray areas are the groups of consecutive ages with less than 5% significant differences in pairwise comparisons.
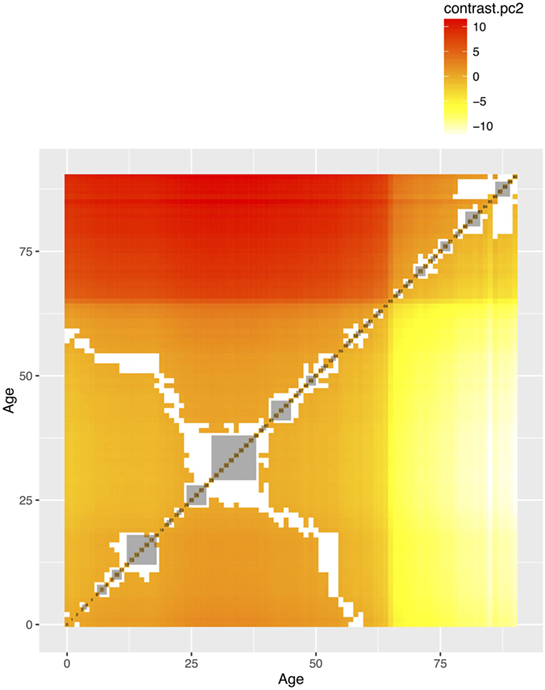
Figure 7. The pairwise comparisons of the second principal component (PCs) by age groups. The value in each cell is the difference of PC1 between two age groups. The differences that are not statistically significant (p values adjusted for multiple comparisons based on the Benjamini–Hochberg method at 0.05) were left blank. The gray areas are the groups of consecutive ages with less than 5% significant differences in pairwise comparisons.
Major Determinants of PCs
To have a good approximation of PC1 and PC2 (R2 > 0.8), it required 13 and 41 variables (see Table 5 for a partial list). The leading variables that explained the most of the PC1 variance were income and poverty status, functional and cognitive limitations, marital status, and perceived health status. In addition to marital status, cognitive limitations and income, social security income, clinical visits and healthcare expenditures covered by Medicare, and employment status were the leading variables explaining PC2. The life stages identified with the first two PCs, especially PC1, were associated with the statuses of marital status, income and cognitive limitations.
Discussion
Research Implications
This study showed that a complex dataset like the MEPS could be summarized and life stages could be adaptively identified from the data, based on the explicit criteria and statistical tests. There are several research implications. First, this is the first attempt to systematically assess the data from all age groups to better define and identify stages of stability or transition. This method can be applied to other data sets to construct a systematic process and to obtain an insight from the stages of stability and transition.
Second, the identification of life stages is important for research that relies on a research population with similar characteristics to draw samples for follow-up or intervention (33, 34). The gray rectangles in Figures 6 and 7 show that: civilians from the same stable life stages could be more comparable than those in transition stages, in terms of the PC values. Third, these life stages are also important for epidemiological investigation that sometimes a population stratification is needed to augment sample sizes in each age category (35). The beginning and the end ages of life stages could serve as references for the age stratification, if there is no empirical evidence or prior knowledge about the population under investigation. Our results provide an alternative choice of selecting age cutoffs, especially for those who lack empirical evidence to stratify age groups or information on the stages of life in social and health data.
Fourth, the application of life staging might be an important method to understand the sources of variability in the dataset, while PCA is recommended as the first step to explore the information observed, especially for complex data (36). This is increasingly important while we observe that there are many variables contributing high proportions of their own variances to PC1, but might not be frequently used for empirical research (see Tables 2–5 for the leading variables). This highlights a potential problem of information underuse and a lack of comprehensive understanding of the life course in aging and social data. This problem is particularly acute when many researchers adopt a uni-dimensional view of trajectories across certain stages of life (3, 6, 37) or propose multiple trajectories without summarizing them (38). This study aims to be the first to call attention to the potential of underused measurements in existing surveys.
Fifth, this data-driven approach also identified that the first PC seem to be related to and can be approximated with similar input variables, such as health insurance categories. This is useful for epidemiologists or data scientists, who aim to construct indexes that explain a large portion of the overall variance in the data set. We showed that this line of research may be feasible with major national surveys. We are developing this method as a strategy to systematically understand large datasets. Sixth, certain life stages might be important for the future research to understand the cause of decline or incline across a life course, such as the stages of transition identified with PC1 and PC2 values. We will focus on the life stages with significant transitions and search for a possible mechanism of these fluctuations.
Limitations
There are several limitations to this study. First, the MEPS dataset is implemented in the US with a focus on the health coverage and related issues (16). Other datasets or surveys may focus on other topics, concentrate on certain age groups or are created in distinctive manners, such as in other jurisdictions or under different policies. Individual health coverage and health-care utilization could also be influenced by public policies. For example, the Affordable Care Act sought to increase health coverage and improve access to health care (39). Therefore, the PCA analysis results with the MEPS dataset may not be able to be extrapolated.
The second limitation is also related to the contexts. The detailed data on life stages help us to have a better understanding of the ages of transitions across life course. However, the PCA results are influenced by how and what data are collected in different age groups. The sum of all variances between individuals depends on the variable variances that are directly influenced by the numbers of measures on similar characteristics and measurement scales (continuous or categorical). For example, the questionnaire of the Children with Special Health Care Needs in the MEPS is applicable to those ages of 0–17 years, although not selected for this study (22). In addition, the MEPS only surveys non-institutionalized civilians and it is unclear how this may affect the results. By recognizing these limitations, caution would be necessary for those life stages identified due to questionnaire changes, rather than transitions in the life course.
Third, there might be some questionnaire modifications introduced between 1996 and 2011 that we are not aware of. We have read through various documentation to accommodate modifications in racial categories and other variable definitions (22). However, we cannot guarantee that all questionnaire revisions are reflected in the data processing. Fourth, the cross-sectional nature of the MEPS makes it possible to have data on individuals from the whole age spectrum and illustrate trajectories across life course. However, individual trajectories are followed-up for only 2 years. It remains uncertain whether the population trajectories of mean PC values can reflect individual ones.
Fifth, the trajectories might be partly caused by the social or health policies that aim to improve population literacy or income security, such as compulsory education for children and retirement arrangements before 65 years of age. This confounding factor needs a separate study. Sixth, adjusting the complex survey design is important for maintaining national representativeness, but this leaves fewer choices of analytical tools. For example, to the best of our knowledge, there is only linear PCA available for datasets with complex survey design and no tool to implement the correlation-based feature selection process after taking the survey design into account (25). Non-linear or other types of PCA that some researchers propose for categorical variables are also not applicable for data with survey design (27, 40). Finally, there remains room for debate on what measures should or could be used to determine life stages. The use of PCs to determine life stages with the social and health data may not be optimal for researchers who need biological or epigenetic measures (41–43).
Future Work
The abovementioned limitations also suggest more research opportunities that we will explore later. The first of our future research directions will be to demonstrate the use of each PC to other datasets and produce components that can be generalized to future panels of MEPS data and other data sources. The second research opportunity will be to demonstrate the usefulness of the concept of life stages. The priority is to apply this research framework on other longitudinal data sets as the benchmark, such as the Health and Retirement Study (44) that has been widely used in the research community. Third, we will use biomarker database to demonstrate the life stages based on PCs. The fourth opportunity will be the selection of the information sources in specific life stages with different age groups. This aims to partly solve the issues related to questionnaire changes for specific age groups. Fifth, the life stages based on chronological ages may not be optimal, since the biological clock or DNA methylation age may differ to some extent (41). It may be more useful to link the biological ages with the observed life stages.
Conclusion
This study showed that complex datasets like MEPS could be summarized to identify life stages and their major determinants, including the statuses of functionality and cognition, income, and marital status. The identification of stable and transition life stages is important for research that relies on a research population with similar characteristics to draw samples for observation or intervention. There are research opportunities regarding the periods of transitions and the causes of different trajectories.
Patient Consent
The MEPS data are publicly available, and there is no patient consent form available for download.
Availability of Data and Materials
All data sets can be freely assessed via the Agency for Healthcare Research and Quality website (https://meps.ahrq.gov/data_stats/download_data_files.jsp).
Ethics Statement
This secondary data analysis study was approved by the ethics committee of the Centre hospitalier de l’Université de Montréal (number: 2016-6095).
Author Contributions
Y-SC conceptualized the research project, restructured the data, conducted the statistical analyses, and drafted the manuscripts. H-TW provided suggestions from different aspects and revised the manuscript. C-JW reviewed the manuscript and provided constructive comments.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Y-SC was financed by the Fonds de recherche du Québec – Santé (FRQS) fellowship. The granting agencies had no role in this study. The authors would like to thank Edward Ng for his useful comments.
Supplementary Material
The Supplementary Material for this article can be found online at http://journal.frontiersin.org/article/10.3389/fpubh.2017.00247/full#supplementary-material.
Abbreviations
MEPS, Medical Expenditure Panel Survey; PCA, principal component analysis; ADL, activities of daily living; IADL, instrumental activities of daily living; PHQ-2, Patient Health Questionnaire; PC, principal component; PC1, the principal component explaining the most portion of total variance; PC2, the principal component explaining the second most portion of total variance.
References
1. Ben-Shlomo Y, Kuh D. A life course approach to chronic disease epidemiology: conceptual models, empirical challenges and interdisciplinary perspectives. Int J Epidemiol (2002) 31(2):285–93. doi:10.1093/ije/31.2.285
2. Kuh D, Ben-Shlomo Y, Lynch J, Hallqvist J, Power C. Life course epidemiology. J Epidemiol Community Health (2003) 57(10):778–83. doi:10.1136/jech.57.10.778
3. Barker DJ, Osmond C, Forsén TJ, Kajantie E, Eriksson JG. Trajectories of growth among children who have coronary events as adults. N Engl J Med (2005) 353(17):1802–9. doi:10.1056/NEJMoa044160
4. Tirosh A, Shai I, Afek A, Dubnov-Raz G, Ayalon N, Gordon B, et al. Adolescent BMI trajectory and risk of diabetes versus coronary disease. N Engl J Med (2011) 364(14):1315–25. doi:10.1056/NEJMoa1006992
5. Lynn J, Adamson DM. Living well at the end of life. Adapting Health Care to Serious Chronic Illness in Old Age. Santa Monica, CA: RAND Health (2003).
6. Carlson NE, Moore MM, Dame A, Howieson D, Silbert LC, Quinn JF, et al. Trajectories of brain loss in aging and the development of cognitive impairment. Neurology (2008) 70(11):828–33. doi:10.1212/01.wnl.0000280577.43413.d9
8. Gill TM, Gahbauer EA, Han L, Allore HG. Trajectories of disability in the last year of life. N Engl J Med (2010) 362(13):1173–80. doi:10.1056/NEJMoa0909087
9. Murray SA, Kendall M, Boyd K, Sheikh A. Illness trajectories and palliative care. BMJ (2005) 330(7498):1007–11. doi:10.1136/bmj.330.7492.611
10. Covinsky KE, Eng C, Lui LY, Sands LP, Yaffe K. The last 2 years of life: functional trajectories of frail older people. J Am Geriatr Soc (2003) 51(4):492–8. doi:10.1046/j.1532-5415.2003.51157.x
11. Rosset E. Old age and the frequency of surviving to this age. Aging Process of Population. Amsterdam, Netherlands: Elsevier Science (2013).
12. Cohen SB, Cohen JW. The capacity of the Medical Expenditure Panel Survey to inform the Affordable Care Act. Inquiry (2013) 50(2):124–34. doi:10.1177/0046958013513678
13. Bernard D, Selden T. Employer offers, private coverage, and the tax subsidy for health insurance: 1987 and 1996. Int J Health Care Finance Econ (2002) 2(4):297–318. doi:10.1023/A:1022360202017
14. Selden TM, Bernard DM. Tax incidence and net benefits in the market for employment-related health insurance: sensitivity of estimates to the incidence of employer costs. Int J Health Care Finance Econ (2004) 4(2):167–92. doi:10.1023/B:IHFE.0000032422.90886.86
15. Guner N, Kulikova Y, Llull J. Does marriage make you healthier? (2014). CEPR Discussion Paper No. DP10245. Available from: https://ssrn.com/abstract=2526358
16. Cohen JW, Monheit AC, Beauregard KM, Cohen SB, Lefkowitz DC, Potter DE, et al. The Medical Expenditure Panel survey: a national health information resource. Inquiry (1996) 33(4):373–89.
17. Agency for Healthcare Research and Quality. MEPS-HC Sample Design and Collection Process (2015). Available from: http://www.meps.ahrq.gov/survey_comp/hc_data_collection.jsp
18. Buuren S, Groothuis-Oudshoorn K. mice: multivariate imputation by chained equations in R. J Stat Software (2011) 45(3):1–67. doi:10.18637/jss.v045.i03
19. Duffy ME, Jacobsen BS. Univariate descriptive statistics. In: Munro BH, editor. Statistical Methods for Health Care Research. Philadelphia, PA: Lippincott Williams & Wilkins (2005). p. 33–72.
20. Hall MA, Smith LA, editors. Feature subset selection: a correlation based filter approach. 1997 International Conference on Neural Information Processing and Intelligent Information Systems. Berlin: Springer (1997).
21. Saeys Y, Inza I, Larranaga P. A review of feature selection techniques in bioinformatics. Bioinformatics (2007) 23(19):2507–17. doi:10.1093/bioinformatics/btm344
22. Agency for Healthcare Research and Quality, editor. MEPS HC-147 2011 Full Year Consolidated Data File. Rockville, MD: Agency for Healthcare Research and Quality (2013). p. C–29.
23. Kuhn M. Building predictive models in R using the caret package. J Stat Softw (2008) 28(5):1–26. doi:10.18637/jss.v028.i05
24. Everitt BS, Hothorn T. Principal component analysis. A Handbook of Statistical Analyses Using R. London: Chapman and Hall/CRC (2006). p. 215–26.
25. Lumley T. Analysis of complex survey samples. J Stat Software (2004) 9(8):19. doi:10.18637/jss.v009.i08
26. He R, Hu B, Yuan X, Zheng W-S. Principal component analysis based on non-parametric maximum entropy. Neurocomput (2010) 73(10–12):1840–52. doi:10.1016/j.neucom.2009.12.032
28. Oja H. Multivariate Nonparametric Methods with R: An approach Based on Spatial Signs and Ranks. New York: Springer (2010).
29. Hastie T, Tibshirani R, Friedman JH. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. New York, NY: Springer (2001).
31. Krzywinski M, Altman N. Points of significance: comparing samples – part II. Nat Meth (2014) 11(4):355–6. doi:10.1038/nmeth.2858
32. Grömping U. Relative importance for linear regression in R: the package relaimpo. J Stat Software (2006) 17(1):1–27. doi:10.18637/jss.v017.i01
33. Greenland S, Rothman KJ. Introduction to categorical statistics. In: Rothman KJ, Greenland S, Lash TL, editors. Modern Epidemiology. Philadelphia, PA: Wolters Kluwer Health/Lippincott Williams & Wilkins (2008). p. 239–58.
35. Patten S. Epidemiology for Canadian Students: Principles, Methods and Critical Appraisal. Edmonton, Alberta: Brush Education (2015).
36. Ringner M. What is principal component analysis? Nat Biotech (2008) 26(3):303–4. doi:10.1038/nbt0308-303
37. Saczynski JS, Marcantonio ER, Quach L, Fong TG, Gross A, Inouye SK, et al. Cognitive trajectories after postoperative delirium. N Engl J Med (2012) 367(1):30–9. doi:10.1056/NEJMoa1112923
38. Hsu HC, Jones BL. Multiple trajectories of successful aging of older and younger cohorts. Gerontologist (2012) 52(6):843–56. doi:10.1093/geront/gns005
39. Oberlander J. The future of Obamacare. N Engl J Med (2012) 367(23):2165–7. doi:10.1056/NEJMp1213674
40. Scholz M, Kaplan F, Guy CL, Kopka J, Selbig J. Non-linear PCA: a missing data approach. Bioinformatics (2005) 21(20):3887–95. doi:10.1093/bioinformatics/bti634
41. Horvath S. DNA methylation age of human tissues and cell types. Genome Biol (2013) 14(10):R115. doi:10.1186/gb-2013-14-10-r115
42. Vallejo AN. Immune aging and challenges for immune protection of the graying population. Aging Dis (2011) 2(5):339–45.
43. Quanjer PH, Stanojevic S, Cole TJ, Baur X, Hall GL, Culver BH, et al. Multi-ethnic reference values for spirometry for the 3-95-yr age range: the global lung function 2012 equations. Eur Respir J (2012) 40(6):1324–43. doi:10.1183/09031936.00080312
Keywords: life stages, principal components, principal component analysis, medical expenditure panel survey, stages of transition, stable stages
Citation: CHAO Y-S, Wu H-t and Wu C-J (2017) Feasibility of Classifying Life Stages and Searching for the Determinants: Results from the Medical Expenditure Panel Survey 1996–2011. Front. Public Health 5:247. doi: 10.3389/fpubh.2017.00247
Received: 09 June 2017; Accepted: 31 August 2017;
Published: 27 October 2017
Edited by:
Richard Eugene Frye, Arkansas Children’s Hospital Research Institute, United StatesReviewed by:
Piotr Romaniuk, Medical University of Silesia, PolandAlbert Okunade, University of Memphis, United States
Copyright: © 2017 CHAO, Wu and Wu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yi-Sheng CHAO, Y2hhb3lpc2hlbmdAcG9zdC5oYXJ2YXJkLmVkdQ==
 Yi-Sheng CHAO
Yi-Sheng CHAO Hau-tieng Wu
Hau-tieng Wu Chao-Jung Wu
Chao-Jung Wu