- School of Mathematics and Statistics, Victoria University Wellington, Wellington, New Zealand
Deep learning is currently the subject of intensive study. However, fundamental concepts such as representations are not formally defined – researchers “know them when they see them” – and there is no common language for describing and analyzing algorithms. This essay proposes an abstract framework that identifies the essential features of current practice and may provide a foundation for future developments. The backbone of almost all deep learning algorithms is backpropagation, which is simply a gradient computation distributed over a neural network. The main ingredients of the framework are, thus, unsurprisingly: (i) game theory, to formalize distributed optimization; and (ii) communication protocols, to track the flow of zeroth and first-order information. The framework allows natural definitions of semantics (as the meaning encoded in functions), representations (as functions whose semantics is chosen to optimized a criterion), and grammars (as communication protocols equipped with first-order convergence guarantees). Much of the essay is spent discussing examples taken from the literature. The ultimate aim is to develop a graphical language for describing the structure of deep learning algorithms that backgrounds the details of the optimization procedure and foregrounds how the components interact. Inspiration is taken from probabilistic graphical models and factor graphs, which capture the essential structural features of multivariate distributions.
1. Introduction
Deep learning has achieved remarkable successes in object and voice recognition, machine translation, reinforcement learning, and other tasks (Hinton et al., 2012; Krizhevsky et al., 2012; Sutskever et al., 2014; LeCun et al., 2015; Mnih et al., 2015). From a practical standpoint, the problem of supervised learning is well-understood and has largely been solved – at least in the regime where both labeled data and computational power are abundant. The workhorse underlying most deep learning algorithms is error backpropagation (Werbos, 1974; Rumelhart et al., 1986a,b; Schmidhuber, 2015), which is simply gradient descent distributed across a neural network via the chain rule.
Gradient descent and its variants are well-understood when applied to convex or nearly convex objectives (Robbins and Monro, 1951; Nemirovski and Yudin, 1978; Nemirovski, 1979; Nemirovski et al., 2009). In particular, they have strong performance guarantees in the stochastic and adversarial settings (Zinkevich, 2003; Cesa-Bianchi and Lugosi, 2006; Bousquet and Bottou, 2008; Shalev-Shwartz, 2011). The reasons for the success of gradient descent in non-convex settings are less clear, although recent work has provided evidence that most local minima are good enough (Choromanska et al., 2015a,b); that modern convolutional networks are close enough to convex for many results on rates of convergence apply (Balduzzi, 2015); and that the rate of convergence of gradient descent can control generalization performance, even in non-convex settings (Hardt et al., 2015).
Taking a step back, gradient-based optimization provides a well-established set of computational primitives (Gordon, 2007), with theoretical backing in simple cases and empirical backing in others. First-order optimization, thus, falls in broadly the same category as computing an eigenvector or inverting a matrix: given sufficient data and computational resources, we have algorithms that reliably find good enough solutions for a wide range of problems.
This essay proposes to abstract out the optimization algorithms used for weight updates and focus on how the components of deep learning algorithms interact. Treating optimization as a computational primitive encourages a shift from low-level algorithm design to higher-level mechanism design: we can shift attention to designing architectures that are guaranteed to learn distributed representations suited to specific objectives. The goal is to introduce a language at a level of abstraction where designers can focus on formal specifications (grammars) that specify how plug-and-play optimization modules combine into larger learning systems.
1.1. What Is a Representation?
Let us recall how representation learning is commonly understood. Bengio et al. (2013) describe representation learning as “learning transformations of the data that make it easier to extract useful information when building classifiers or other predictors.” More specifically, “a deep learning algorithm is a particular kind of representation learning procedure that discovers multiple levels of representation, with higher-level features representing more abstract aspects of the data” (Bengio, 2013). Finally, LeCun et al. (2015) state that multiple levels of representations are obtained “by composing simple but non-linear modules that each transform the representation at one level (starting with the raw input) into a representation at a higher, slightly more abstract level. With the composition of enough such transformations, very complex functions can be learned. For classification tasks, higher layers of representation amplify aspects of the input that are important for discrimination and suppress irrelevant variations.”
The quotes describe the operation of a successful deep learning algorithm. What is lacking is a characterization of what makes a deep learning algorithm work in the first place. What properties must an algorithm have to learn layered representations? What does it mean for the representation learned by one layer to be useful to another? What, exactly, is a representation?
In practice, almost all deep learning algorithms rely on error backpropagation to “align” the representations learned by different layers of a network. This suggests that the answers to the above questions are tightly bound up in first-order (that is, gradient-based) optimization methods. It is, therefore, unsurprisingly that the bulk of the paper is concerned with tracking the flow of first-order information. The framework is intended to facilitate the design of more general first-order algorithms than backpropagation.
1.1.1. Semantics
To get started, we need a theory of the meaning or semantics encoded in neural networks. Since there is nothing special about neural networks, the approach taken is inclusive and minimalistic. Definition 1 states that the meaning of any function is how it implicitly categorizes inputs by assigning them to outputs. The next step is to characterize those functions whose semantics encode knowledge, and for this we turn to optimization (Sra et al., 2012).
1.1.2. Representations from Optimizations
Nemirovski and Yudin (1983) developed the black-box computational model to analyze the computational complexity of first-order optimization methods (Agarwal et al., 2009; Raginsky and Rakhlin, 2011; Arjevani et al., 2016). The black-box model is a more abstract view on optimization than the Turing machine model: it specifies a communication protocol that tracks how often an algorithm makes queries about the objective. It is useful to refine Nemirovski and Yudin’s terminology by distinguishing between black-boxes, which respond with zeroth-order information (the value of a function at the query-point), and gray-boxes,1 which respond with zeroth- and first-order information (the gradient or subgradient).
With these preliminaries in hand, Definition 4 proposes that a representation is a function that is a local solution to an optimization problem. Since we do not restrict to convex problems, finding global solutions is not feasible. Indeed, recent experience shows that global solutions are often not necessary practice (Hinton et al., 2012; Krizhevsky et al., 2012; Sutskever et al., 2014; LeCun et al., 2015; Mnih et al., 2015). The local solution has similar semantics to – that is, it represents – the ideal solution. The ideal solution usually cannot be found: due to computational limitations, since the problem is non-convex, because we only have access to a finite sample from an unknown distribution, etc.
To see how Definition 4 connects with representation learning as commonly understood, it is necessary to take a detour through distributed optimization and game theory.
1.2. Distributed Representations
Game theory provides tools for analyzing distributed optimization problems where a set of players aim to minimizes losses that depend not only on their actions but also the actions of all other players in the game (von Neumann and Morgenstern, 1944; Nisan et al., 2007). Game theory has traditionally focused on convex losses since they are more theoretically amenable. Here, the only restriction imposed on losses is that they are differentiable almost everywhere.
Allowing non-convex losses means that error backpropagation can be reformulated as a game. Interestingly, there is enormous freedom in choosing the players. They can correspond to individual units, layers, entire neural networks, and a variety of other, intermediate choices. An advantage of the game-theoretic formulation is, thus, that it applies at many different scales.
Non-convex losses and local optima are essential to developing a scale-free formalism. Even when it turns out that particular units or a particular layer of a neural network are solving a convex problem, convexity is destroyed as soon as those units or layers are combined to form larger learning systems. Convexity is not a property that is preserved in general when units are combined into layers or layers into networks. It is, therefore, convenient to introduce the computational primitive arglocopt to denote the output of a first-order optimization procedure, see Definition 4.
1.2.1. A Concern about Excessive Generality
A potential criticism is that the formulation is too broad. Very little can be said about non-convex optimization in general; introducing games where many players jointly optimize a set of arbitrary non-convex functions only compounds the problem.
Additional structure is required. A successful case study can be found in Balduzzi (2015), which presents a detailed game-theoretic analysis of rectifier neural networks. The key to the analysis is that rectifier units are almost convex. The main result is that the rate of convergence of a neural network to a local optimum is controlled by the (waking-)regret of the algorithms applied to compute weight updates in the network.
Whereas Balduzzi (2015) relied heavily on specific properties of rectifier non-linearities, this paper considers a wide-range of deep learning architectures. Nevertheless, it is possible to carve out an interesting subclass of non-convex games by identifying the composition of simple functions as an essential feature common to deep learning architectures. Compositionality is formalized via distributed communication protocols and grammars.
1.2.2. Grammars for Games
Neural networks are constructed by composing a series of elementary operations. The resulting feedforward computation is captured via as a computation graph (Griewank and Walther, 2008; Bergstra et al., 2010; Bastien et al., 2012; Baydin and Pearlmutter, 2014; Schulman et al., 2015; van Merriënboer et al., 2015). Backpropagation traverses the graph in reverse and recursively computes the gradient with respect to the parameters at each node.
Section 3 maps the feedforward and feedback computations onto the queries and responses that arise in Nemirovski and Yudin’s model of optimization. However, queries and responses are now highly structured. In the query phase, players feed parameters into a computation graph (the Query graph Q) that performs the feedforward sweep. In the response phase, oracles reveal first-order information that is fed into a second computation graph (the Response graph R).
In most cases, the Response graph simply implements backpropagation. However, there are examples where it does not. Three are highlighted here, see Section 3.5, and especially Sections 3.6 and 3.7. Other algorithms where the Response graphs do not simply implement backprop include difference target propagation (Lee et al., 2015) and feedback alignment (Lillicrap et al., 2014) [both discussed briefly in Section 3.7] and truncated backpropagation through time (Elman, 1990; Williams and Peng, 1990; Williams and Zipser, 1995), where a choice is made about where to cut backprop short. Examples where the query and response graph differ are of particular interest, since they point toward more general classes of deep learning algorithms.
A distributed communication protocol is a game with additional structure: the Query and Response graphs, see Definition 7. The graphs capture the compositional structure of the functions learned by a neural network and the compositional structure of the learning procedure, respectively. It is important for our purposes that (i) the feedforward and feedback sweeps correspond to two distinct graphs and (ii) the communication protocol is kept distinct from the optimization procedure. That is, the communication protocol specifies how information flows through the networks without specifying how players make use of it. Players can be treated as plug-and-play rational agents that are provided with carefully constructed and coordinated first-order information to optimize as they see fit (Russell and Norvig, 2009; Gershman et al., 2015).
Finally, a grammar is a distributed communication protocol equipped with a guarantee that the response graph encodes sufficient information for the players to jointly find a local optimum of an objective function. The paradigmatic example of a grammar is backpropagation. A grammar is a, thus, a game designed to perform a task. A representation learned by one (p)layer is useful to another if the game is guaranteed to converge on a local solution to an objective – that is, if the players interact though a grammar. It follows that the players build representations that jointly encode knowledge about the task.
1.3. Contribution
The content of the paper is sketched above. In summary, the main contributions are as follows:
1. A characterization of representations as local solutions to functional optimization problems, see Definition 4.
2. An extension of Nemirovski and Yudin’s first-order (Query– Response) protocol to deep learning, see Definition 7.
3. Grammars, Definition 8, which generalize the first-order guarantees provided by the error backpropagation to Response graphs that do not implement the chain rule.
4. Examples of grammars that do not reduce to the chain rule, see Sections 3.5, 3.6, and 3.7.
The essay presents a provisional framework; see Balduzzi (2015), Balduzzi and Ghifary (2015), Balduzzi et al. (2015) for applications of the ideas presented here. The essay is not intended to be comprehensive. Many details are left out and many important aspects are not covered: most notably, probabilistic and Bayesian formulations, and various methods for unsupervised pre-training.
1.3.1. A Series of Worked Examples
In line with its provisional nature, much of the essay is spent applying the framework to worked examples: error backpropagation as a supervised model (Rumelhart et al., 1986a); variational autoencoders (Kingma and Welling, 2014) and generative adversarial networks (Goodfellow et al., 2014) for unsupervised learning; the deviator-actor-critic (DAC) model for deep reinforcement learning (Balduzzi and Ghifary, 2015); and kickback, a biologically plausible variant of backpropagation (Balduzzi et al., 2015). The examples were chosen, in part, to maximize variety and, in part, based on familiarity. The discussions are short; the interested reader is encouraged to consult the original papers to fill in the gaps.
The last two examples are particularly interesting since their Response graphs differ substantially from backpropagation. The DAC model constructs a zeroth-order black-box to estimate gradients rather than querying a first-order gray-box. Kickback prunes backprop’s Response graph by replacing most of its gray-boxes with black-boxes and approximating the chain rule with (primarily) local computations.
1.3.2. Related Work
Bottou and Gallinari (1991) proposed to decompose neural networks into cooperating modules (Bottou, 2014). Decomposing more general algorithms or models into collections of interacting agents dates back to the shrieking demons that comprised of Selfridge’s Pandemonium (Selfridge, 1958) and a long line of related work (Klopf, 1982; Barto, 1985; Minsky, 1986; Baum, 1999; Kwee et al., 2001; von Bartheld et al., 2001; Seung, 2003; Lewis and Harris, 2014). The focus on components of neural networks as players, or rational agents, in their own right developed here derives from work aimed at modeling biological neurons game-theoretically, see Balduzzi and Besserve (2012), Balduzzi (2013, 2014), Balduzzi and Tononi (2013), and Balduzzi et al. (2013).
A related approach to semantics based on general value functions can be found in Sutton et al. (2011), see Remark 1. Computation graphs applied to backprop are the basis of the deep learning library Theano (Bergstra et al., 2010; Bastien et al., 2012; van Merriënboer et al., 2015) among others and provide the backbone for algorithmic differentiation (Griewank and Walther, 2008; Baydin and Pearlmutter, 2014).
Grammars are a technical term in the theory of formal languages relating to the Chomsky hierarchy (Hopcroft and Ullman, 1979). There is no apparent relation between that notion of grammar and the one presented here, aside from both relating to structural rules governing composition. Formal languages and deep learning are sufficiently disparate fields that there is little risk of terminological confusion. Similarly, the notion of semantics introduced here is distinct from semantics in the theory of programing languages.
Although game theory was developed to model human interactions (von Neumann and Morgenstern, 1944), it has been pointed out that it may be more directly applicable to interacting populations of algorithms, the so-called machina economicus (Lay and Barbu, 2010; Abernethy and Frongillo, 2011; Storkey, 2011; Frongillo and Reid, 2015; Parkes and Wellman, 2015; Syrgkanis et al., 2015). This paper goes one step further to propose that games played over first-order communication protocols are a key component of the foundations of deep learning.
A source of inspiration for the essay is Bayesian networks and Markov random fields. Probabilistic graphical models and factor graphs provide simple, powerful ways to encode a multivariate distribution’s independencies into a diagram (Pearl, 1988; Kschischang et al., 2001; Wainwright and Jordan, 2008). They have greatly facilitated the design and analysis of algorithms for probabilistic inference. However, there is no comparable framework for distributed optimization and deep learning. The essay is intended as a first step in this direction.
2. Semantics and Representations
This section defines semantics and representations. In short, the semantics of a function is how it categorizes its inputs; a function is a representation if it is selected to optimize an objective. The connection between the definition of representation below and “representation learning” is clarified in Section 3.3.
Possible world semantics was introduced by Lewis (1986) to formalize the meaning of sentences in terms of counterfactuals. Let 𝒫 be a proposition about the world. Its truth depends on its content and the state of the world. Rather than allowing the state of the world to vary, it is convenient to introduce the set W of all possible worlds.
Let us denote proposition 𝒫 applied in world w ∈ W by 𝒫(w). The meaning of 𝒫 is then the mapping v𝒫: W → {0,1} which assigns 1 or 0 to each w ∈ W according to whether or not proposition 𝒫(w) is true. Equivalently, the meaning of the proposition is the ordered pair consisting of: all worlds, and the subset of worlds where it is true:
For example, the meaning of 𝒫blue (that) = “that is blue” is the subset of possible worlds where I am pointing at a blue object. The concept of blue is rendered explicit in an exhaustive list of possible examples.
A simple extension of possible world semantics from propositions to arbitrary functions is as follows (Balduzzi, 2011):
Definition 1 (semantics).
Given function f: X → Y, the semantics or meaning of output y ∈ Y is the ordered pair of sets:
Functions implicitly categorize inputs by assigning outputs to them; the meaning of an output is the category.
Whereas propositions are true or false, the output of a function is neither. However, if two functions both optimize a criterion, then one can refer to how accurately one function represents the other. Before we can define representations, we therefore need to take a quick detour through optimization:
Definition 2 (optimization problem).
An optimization problem is a pair (Θ, R) consisting of parameter-space Θ ⊂ ℝd and objective R: Θ → ℝ that is differentiable almost everywhere.
The solution to the global optimization problem is:
which is either a maximum or minimum according to the nature of the objective.
The solution may not be unique; it also may not exist unless further restrictions are imposed. Such details are ignored here.
Next recall the black-box optimization framework introduced by Nemirovski and Yudin (1983) (Agarwal et al., 2009; Raginsky and Rakhlin, 2011; Arjevani et al., 2016).
Definition 3 (communication protocol).
A communication protocol for optimizing an unknown objective R: Θ → ℝ consists in a User (or Player) and an Oracle. On each round, User presents a query θ ∈ Θ. Oracle can respond in one of two ways, depending on the nature of the protocol:
• Black-box (zeroth-order) protocol. Oracle responds with the value R(θ).

• Gray-box (first-order) protocol. Oracle responds with either the gradient ▽R (θ) or with the gradient together with the value.

The protocol specifies how Player and Oracle interact without specifying the algorithm used by Player to decide which points to query. The next section introduces distributed communication protocols as a general framework that includes a variety of deep learning architectures as special cases – again without specifying the precise algorithms used to perform weight updates.
Unlike Nemirovski and Yudin (1983), Raginsky and Rakhlin (2011), we do not restrict to convex problems. Finding a global optimum is not always feasible, and in practice often unnecessary.
Definition 4 (representation).
Let ℱ ⊂ {f : X → Y} be a function space and:
be a map from parameter space to functions. Further suppose that objective function R:ℱ → ℝ is given.
A representation is a local solution to the optimization problem:
corresponding to a local maximum or minimum according to whether the objective is minimized or maximized.
Intuitively, the objective quantifies the extent to which functions in ℱ categorize their inputs similarly. The operation arglocopt applies a first-order method to find a function whose semantics resembles the optimal solution fθ* where θ* = argopt θ∈ Θ R( f θ).
In short, representations are functions with useful semantics, where usefulness is quantified using a specific objective: the lower the loss or higher the reward associated with a function, the more useful it is. The relation between Definition 4 and representations as commonly understood in the deep learning literature is discussed in Section 3.3 below.
Remark 1 (value function semantics).
In related work, Sutton et al. (2011) proposed that semantics – i.e., knowledge about the world – can be encoded in general value functions that provide answers to specific questions about expected rewards. Definition 1 is more general than their approach since it associates a semantics to any function. However, the function must arise from optimizing an objective for its semantics to accurately represent a phenomenon of interest.
2.1. Supervised Learning
The main example of a representation arises under supervised learning.
Representation 1 (supervised learning).
Let X and Y be an input space and a set of labels and ℓ: Y × Y → ℝ be a loss function. Suppose that {f θ: X → Y |θ ∈ Θ} is a parameterized family of functions.
• Nature which samples labeled pairs (x,y) i.i.d. from distribution ℙXY, singly or in batches.
• Predictor chooses parameters θ ∈ Θ.
• Objective is
The query and responses phases can be depicted graphically as

The predictor = arglocminθ∈Θ R(θ) is then a representation of the optimal predictor f θ* = argminθ∈Θ R(θ).
A commonly used mapping from parameters to functions is
where a feature map ϕ: X → ℝd is fixed.
The setup admits a variety of complications in practice. First, it is typically infeasible even to find a local optimum. Instead, a solution that is within some small ϵ > 0 of the local optimum suffices. Second, the distribution ℙXY is unknown, so the expectation is replaced by a sum over a finite sample. The quality of the resulting representation has been extensively studied in statistical learning theory (Vapnik, 1995). Finally, it is often convenient to modify the objective, for example, by incorporating a regularizer. Thus, a more detailed presentation would conclude that
yields a representation of the solution to . To keep the discussion and notation simple, we do not consider any of these important details.
It is instructive to unpack the protocol, by observing that the objective R is a composite function involving f (θ, x), ℓ( f,y), and E[•]:

The notation δθ is borrowed from backpropagation. It is shorthand for the derivative of the objective with respect to parameters θ.
Nature is not a deterministic black-box since it is not queried directly: nature produces (x,y) pairs stochastically, rather than in response to specific inputs. Our notion of black-box can be extended to stochastic black-boxes, see Schulman et al. (2015). However, once again we prefer to keep the exposition as simple as possible.
2.2. Unsupervised Learning
The second example concerns fitting a probabilistic or generative model to data. A natural approach is to find the distribution under which the observed data is most likely:
Representation 2 (maximum likelihood estimation).
Let X be a data space.
• Nature samples points from distribution ℙX.
• Estimator chooses parameters θ ∈ Θ.
• Operator ℚ(x; θ) = ℚθ(x) computes a probability density on X that depends on parameter θ.
• Operator −log(⋅) acts as a loss. The objective is to minimize

The estimate , where , is a representation of the optimal solution, and can also be considered a representation of ℙX. The setup extends easily to maximum a posteriori estimation.
As for supervised learning, the protocol can be unpacked by observing that the objective has a compositional structure:

2.3. Reinforcement Learning
The third example is taken from reinforcement learning (Sutton and Barto, 1998). We will return to reinforcement learning in Section 3.6, so the example is presented in some detail. In reinforcement learning, an agent interacts with its environment, which is often modeled as a Markov decision process consisting of state space 𝒮 ⊂ ℝm, action space 𝒜 ⊂ ℝd, initial distribution ℙ1(s) on states, stationary transition distribution ℙ(s t+1|s t,a t) and reward function r: 𝒮 × 𝒜 → ℝ. The agent chooses actions based on a policy: a function μθ : 𝒮 → 𝒜 from states to actions. The goal is to find the optimal policy.
Actor-critic methods break up the problem into two pieces (Barto et al., 1983). The critic estimates the expected value of state-action pairs given the current policy, and the actor attempts to find the optimal policy using the estimates provided by the critic. The critic is typically trained via temporal difference methods (Sutton, 1988; Dann et al., 2014).
Let ℙt (s → s′, μ) denote the distribution on states s′ at time t given policy μ and initial state s at t = 0 and let . Let be the discounted future reward. Define the value of a state-action pair as
Unfortunately, the value–function Qμ(s,a) cannot be queried. Instead, temporal difference methods take a bootstrapped approach by minimizing the Bellman error:
where s′ is the state subsequent to s.
Representation 3 (temporal difference learning).
Critic interacts with black-boxes Actor and Nature.2
• Critic plays parameters v.
• Operator Q and ℓ BE estimates the value function and compute the Bellman error. In practice, it turns out to clone the value-estimate periodically and compute a slightly modified Bellman error:
where is the cloned estimate. Cloning improves the stability of TD-learning (Mnih et al., 2015). A nice conceptual side-effect of cloning is that TD-learning reduces to gradient descent.

The estimate is a representation of the true value function.
Remark 2 (on temporal difference learning as first-order method).
Temporal difference learning is not strictly speaking a gradient-based method (Dann et al., 2014). The residual gradient method performs gradient descent on the Bellman error, but suffers from double sampling (Baird, 1995). Projected fix point methods minimize the projected Bellman error via gradient descent and have nice convergence properties (Sutton et al., 2009a,b; Maei et al., 2010). An interesting recent proposal is implicit TD-learning (Tamar et al., 2014), which is based on implicit gradient descent (Toulis et al., 2014).
Section 3.6 presents the Deviator-Actor-Critic model, which simultaneously learns a value–function estimate and a locally optimal policy.
3. Protocols and Grammars
It is often useful to decompose complex problems into simpler subtasks that can handled by specialized modules. Examples include variational autoencoders, generative adversarial networks, and actor-critic models. Neural networks are particularly well-adapted to modular designs, since units, layers, and even entire networks can easily be combined analogously to bricks of lego (Bottou and Gallinari, 1991).
However, not all configurations are viable models. A methodology is required to distinguish good designs from bad. This section provides a basic language to describe how bricks are glued together that may be a useful design tool. The idea is to extend the definitions of optimization problems, protocols, and representations from Section 2 from single to multi-player optimization problems.
Definition 5 (game).
A distributed optimization problem or game ([N], Θ, ℓ) is a set [N] = {1, … N} of players, a parameter space , and loss vector ℓ = (ℓ1, …, ℓN): Θ → ℝN. Player i picks moves from and incurs loss determined by ℓi: Θ → ℝ. The goal of each player is to minimize its loss, which depends on the moves of the other players.
The classic example is a finite game (von Neumann and Morgenstern, 1944), where player i has a menu of di-actions and chooses a distribution over actions, on each round. Losses are specified for individual actions, and extended linearly to distributions over actions. A natural generalization of finite games is convex games where the parameter spaces are compact convex sets and each loss ℓi is a convex function in its ith-argument (Stoltz and Lugosi, 2007). It has been shown that players implementing no-regret algorithms are guaranteed to converge to a correlated equilibrium in convex games (Foster and Vohra, 1997; Blum and Mansour, 2007; Stoltz and Lugosi, 2007).
The notion of game in Definition 5 is too general for our purposes. Additional structure is required.
Definition 6 (computation graph).
A computation graph is a directed acyclic graph with two kinds of nodes:
• Inputs are set externally (in practice by Players or Oracles).
• Operators produce outputs that are a fixed function of their parents’ outputs.
Computation graphs are a useful tool for calculating derivatives (Griewank and Walther, 2008; Bergstra et al., 2010; Bastien et al., 2012; Baydin and Pearlmutter, 2014; van Merriënboer et al., 2015). For simplicity, we restrict to deterministic computation graphs. More general stochastic computation graphs are studied in Schulman et al. (2015).
A distributed communication protocol extends the communication protocol in Definition 3 to multiplayer games using two computation graphs.
Definition 7 (distributed communication protocol).
A distributed communication protocol is a game where each round has two phases, determined by two computation graphs:
• Query phase. Players provide inputs to the Query graph (Q) that Operators transform into outputs.
• Response phase. Operators in Q act as Oracles in the Response graph (R): they input subgradients that are transformed and communicated to the Players.
The moves chosen by Players depend only on their prior moves and the information communicated to them by the Response graph.
The protocol specifies how Players and Oracles communicate without specifying the optimization algorithms used by the Players. The addition of a Response graph allows more general computations than simply backpropagating the gradients of the Query phase. The additional flexibility allows the design of new algorithms, see Sections 3.6 and 3.7 below. It is also sometimes necessary for computational reasons. For example, backpropagation through time on recurrent networks typically runs over a truncated Response graph (Elman, 1990; Williams and Peng, 1990; Williams and Zipser, 1995).
Suppose that we wish to optimize an objective function R: Θ → ℝ that depends on all the moves of all the players. Finding a global optimum is clearly not feasible. However, we may be able to construct a protocol such that the players are jointly able to find local optima of the objective. In such cases, we refer to the protocol as a grammar:
Definition 8 (grammar).
A grammar for objective R: Θ → ℝ is a distributed communication protocol where the Response graph provides sufficient first-order information to find a local optimum of (R, Θ).
The guarantee ensures that the representations constructed by Players in a grammar can be combined into a coherent distributed representation. That is, it ensures that the representations constructed by the Players transform data in a way that is useful for optimizing the shared objective R.
The Players’ losses need not be explicitly computed. All that is necessary is that the Response phase communicates the gradient information needed for Players to locally minimize their losses – and that doing so yields a local optimum of the objective.
3.1. Basic Building Blocks: Function Composition (Q) and the Chain Rule (R)
Functions can be inserted into grammars as lego-like building blocks via function composition during queries and the chain rule during responses. Let G(θ, F) be a function that takes inputs θ and F, provided by a Player and by upstream computations, respectively. The output of G is communicated downstream in the Query phase:
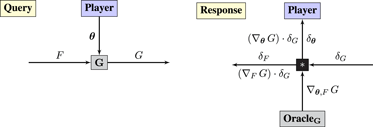
The chain rule is implemented in the Response phase as follows. OracleG reports the gradient ∇θ,F G: = (∇ θ G, ∇F G) in the Response phase. Operator “*” computes the products (∇ θ G ⋅ δG, ∇F G ⋅ δG) via matrix multiplication. The projection of the product onto the first and second components3 is reported to Player and upstream, respectively.
3.2. Summary of Guarantees
A selection of examples is presented below. Guarantees fall under the following broad categories:
1. Exact gradients: under error backpropagation the Response graph implements the chain rule, which guarantees that Players receive the gradients of their loss functions; see Section 3.3.
2. Surrogate objectives: the variational autoencoder uses a surrogate objective: the variational lower bound. Maximizing the surrogate is guaranteed to also maximize the true objective, which is computational intractable; see Section 3.4.
3. Learned objectives: in the case of generative adversarial network and the DAC-model, some of the players learn a loss that is guaranteed to align with the true objective, which is unknown; see Sections 3.5 and 3.6.
4. Estimated gradient: in the DAC-model and kickback, gradient estimates are substituted for the true gradient; see Sections 3.5 and 3.6. Guarantees are provided on the estimates.
Remark 3 (fine- and coarse-graining).
There is considerable freedom regarding the choice of players. In the examples below, players are typically chosen to be layers or entire neural networks to keep the diagrams simple. It is worth noting that zooming in, such that players correspond to individual units, has proven to be a useful tool when analyzing neural networks (Balduzzi, 2015; Balduzzi and Ghifary, 2015; Balduzzi et al., 2015).
The game-theoretic formulation is thus scale-free and can be coarse or fine grained as required. A mathematical language for tracking the structure of hierarchical systems at different scales is provided by operads, see Spivak (2013) and the references therein, which are the natural setting to study the composition of operators that receive multiple inputs.
3.3. Error Backpropagation
The main example of a grammar is a neural network using error backpropagation to perform supervised learning. Layers in the network can be modeled as players in a game. Setting each (p)layer’s objective as the network’s loss, which it minimizes using gradient ascent, yields backpropagation.
Syzygy 1 (backpropagation).
An L-layer neural network can be reformulated as a game played between L + 1 players, corresponding to Nature and the Layers of the network. The query graph for a 3-layer network is:

• Nature plays samples data points (x, y) i.i.d. from ℙX× Y and acts as the zeroth player.
• Layeri plays weight matrices θ i.
• Operators compute Si(θi, Si−1): = Si(θ i ⋅ Si−1) for each layer, along with loss ℓ(SL, y).
The response graph performs error backpropagation:
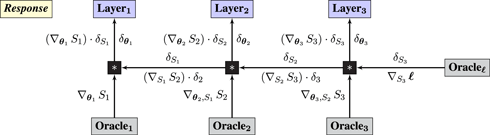
The protocol can be extended to convolutional networks by replacing the matrix multiplications performed by each operator, Si(θ i⋅Si−1), with convolutions and adding parameterless max-pooling operators (LeCun et al., 1998).
Guarantee. The loss of every (p)layer is
It follows by the chain rule that R communicates to player i. □
3.3.1. Representation Learning
We are now in a position to relate the notion of representation in Definition 4 with the standard notion of representation learning in neural networks. In the terminology of Section 2, each player learns a representation. The representations learned by the different players form a coherent distributed representation because they jointly optimize a single objective function.
Abstractly, the objective can be written as
where . The goal is to minimize the composite objective.
If we set then the function fits the definition of representation above. Moreover, the compositional structure of the network implies that is composed of subrepresentations corresponding to the optimizations performed by the different players in the grammar: each function is a local optimum – where is optimized to transform its inputs into a form that is useful to network as a whole.
3.3.2. Detailed Analysis of Convergence Rates
Little can be said in general about the rate of converge of the layers in a neural network since the loss is not convex. However, neural networks can be decomposed further by treating the individual units as players. When the units are linear or rectilinear, it turns out that the network is a circadian game. The circadian structure provides a way to convert results about the convergence of convex optimization methods into results about the global convergence a rectifier network to a local optimum, see Balduzzi (2015).
3.4. Variational Autoencoders
The next example extends the unsupervised setting described in Section 2.2. Suppose that observations are sampled i.i.d. from a two-step stochastic process: a latent value z(i) is sampled from ℙ(z), after which x(i) is sampled from ℙ(x|z(i)).
The goal is to (i) find the maximum likelihood estimator for the observed data and (ii) estimate the posterior distribution on z conditioned on an observation x. A straightforward approach is to maximize the marginal likelihood
and then compute the posterior
However, the integral in equation (1) is typically untractable, so a more roundabout tactic is required. The approach proposed in Kingma and Welling (2014) is to construct two neural networks, a decoder ⅅθ (x|z) that learns a generative model approximating ℙ(x|z), and an encoder 𝔼ϕ(z|x) that learns a recognition model or posterior approximating ℙ(z|x).
It turns out to be useful to replace the encoder with a deterministic function, Gϕ(ϵ,x), and a noise source, ℙnoise(ϵ) that are compatible. Here, compatible means that sampling is equivalent to sampling ϵ ~ ℙnoise(ϵ) and computing .
Syzygy 2 (variational autoencoder).
A variational autoencoder is a game played between Encoder, Decoder, Noise, and Environment. The query graph is
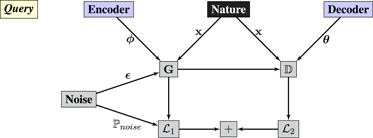
• Environment plays i.i.d. samples from ℙ(x).
• Noise plays i.i.d. samples from ℙnoise(ϵ). It also communicates its density function 𝒫noise(ϵ), which is analogous to a gradient – and the reason that Noise is gray rather than black-box.
• Encoder and Decoder play parameters ϕ and θ, respectively.
• Operator z = Gϕ(ϵ, x) is a neural network that encodes samples into latent variables.
• Operatorⅅθ(z,x) is a neural network that estimates the probability of x conditioned on z.
• The remaining operators compute the (negative) variational lower bound
The response graph implements backpropagation:
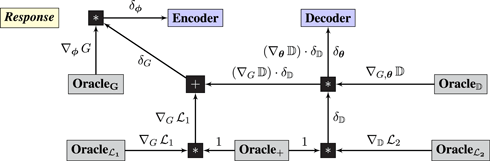
Guarantee. The guarantee has two components:
1. Maximizing the variational lower bound yields (i) a maximum likelihood estimator and (ii) an estimate of the posterior on the latent variable (Kingma and Welling, 2014).
2. The chain rule ensures that the correct gradients are communicated to Encoder and Decoder.
The first guarantee is that the surrogate objective computed by the query graph yields good solutions. The second guarantee is that the response graph communicates the correct gradients. □
3.5. Generative-Adversarial Networks
A recent approach to designing generative models is to construct an adversarial game between Forger and Curator (Goodfellow et al., 2014). Forger generates samples; Curator aims to discriminate the samples produced by Forger from those produced by Nature. Forger aims to create samples realistic enough to fool Curator.
If Forger plays parameters θ and Curator plays ϕ then the game is described succinctly via
where G θ(ϵ) is a neural network that converts noise in samples and Dϕ(x) classifies samples as fake or not.
Syzygy 3 (generative adversarial networks).
Construct a game played between Forger and Curator, with ancillary players Noise and Environment:
• Environment samples images i.i.d. from ℙ(x).
• Noise samples i.i.d. from ℙ(ϵ).
• Forger and Curator play parameters θ and ϕ, respectively.
• Operator Gθ(ϵ) is a neural network that produces fake image .
• Operator is a neural network that estimates the probability that an image is fake.
• The remaining operators compute a loss that Curator minimizes and Forger maximizes
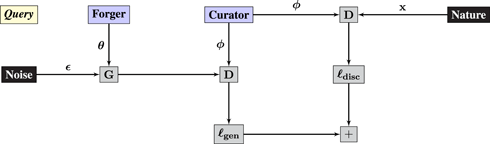
Note there are two copies of Operator D in the Query graph. The response graph implements the chain rule, with a tweak that multiplies the gradient communicated to Forger by (−1) to ensure that Forger maximizes the loss that Curator is minimizing.
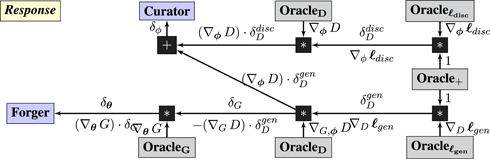
Guarantee. For a fixed Forger that produces images with probability 𝒫Forger(x), the optimal Curator would assign
The guarantee has two components:
1. For fixed Forger, the Curator in equation (2) is the global optimum for ℒ.
2. The chain rule ensures the correct gradients are communicated to Curator and Forger.
It follows that the network converges to a local optimum where Curator represents [equation (2)] and Forger represents the “ideal Forger” that would best fool Curator. □
The generative-adversarial network is the first example where the Response graph does not simply backpropagate gradients: the arrow labeled δG is computed as −(∇G D) ⋅ δD, whereas backpropagation would use (∇G D) ⋅ δD. The minus sign arises due to the adversarial relationship between Forger and Curator – they do not optimize the same objective.
3.6. Deviator-Actor-Critic (DAC) Model
As discussed in Section 2.3, actor-critic algorithms decompose the reinforcement learning problem into two components: the critic, which learns an approximate value function that predicts the total discounted future reward associated with state-action pairs, and the actor, which searches for a policy that maximizes the value approximation provided by the critic. When the action-space is continuous, a natural approach is to follow the gradient (Sutton et al., 2000; Deisenroth et al., 2013; Silver et al., 2014). In Sutton et al. (2000), it was shown how to compute the policy gradient given the true value function. Furthermore, sufficient conditions were provided for an approximate value function learned by the critic to yield an unbiased estimator of the policy gradient. More recently, Silver et al. (2014) provided analogous results for deterministic policies.
The next example of a grammar is taken from Balduzzi and Ghifary (2015), which builds on the above work by introducing a third algorithm, Deviator, that directly estimates the gradient of the value function estimated by Critic.
Syzygy 4 (DAC model).
Construct a game played by Actor, Critic, Deviator, Noise, and Environment:
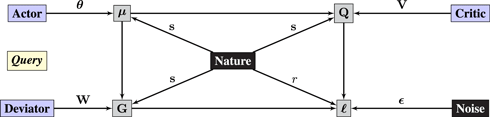
• Nature samples states from ℙ(s t+1|s t,at) and announces rewards r(s t,a t) that are a function of the prior state and action; Noise samples ϵ ~ N(0, σ2 ⋅ Id).
• Actor, Critic, and Deviator play parameters θ, V, and W, respectively.
• Operator μ is a neural network that computes actions a = μθ(s).
• Operator Qv(s, μ θ(s)) is a neural network that estimates the value of state-action pairs.
• Operator GW(s, μ θ(s)) is a neural network that estimates the gradient of the value function.
• The remaining Operator computes the Bellman gradient error (BGE) which Critic and Deviator minimize
The response graph backpropagates the gradient of ℓ BGE to Critic and Deviator, and communicates the output of Operator G, which is a gradient estimate, to Actor:
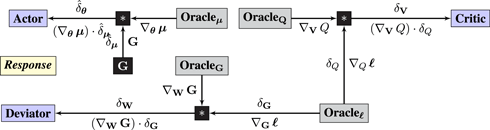
Note that instead of backpropagating first-order information in the form of gradient ∇μ G, the Response graph instead backpropagates zeroth-order information in the form of gradient-estimate G, which is computed by the Query graph during the feedforward sweep. We therefore write and (instead of δμ and δθ) to emphasize that the gradients communicated to Actor are estimates.
As in Section 2.3, an arrow from Actor to Nature is omitted from the Query graph for simplicity.
Guarantee. The guarantee has the following components:
1. Critic estimates the value function via TD-learning (Sutton and Barto, 1998) with cloning for improved stability (Mnih et al., 2015).
2. Deviator estimates the value gradient via TD-learning and the gradient perturbation trick (Balduzzi and Ghifary, 2015).
3. Actor follows the correct gradient by the policy gradient theorem (Sutton et al., 2000; Silver et al., 2014).
4. The internal workings of each neural network are guaranteed correct by the chain rule.
It follows that Critic and Deviator represent the value function and its gradient; and that Actor represents the optimal policy. □
Two appealing features of the algorithm are that (i) Actor is insulated from Critic, and only interacts with Deviator and (ii) Critic and Deviator learn different features adapted to representing the value function and its gradient, respectively. Previous work used the derivative of the value–function estimate, which is not guaranteed to have compatible function approximation, and can lead to problems when the value-function is estimated using functions such as rectifiers that are not smooth (Prokhorov and Wunsch, 1997; Hafner and Riedmiller, 2011; Heess et al., 2015; Lillicrap et al., 2015).
3.7. Kickback (Truncated Backpropagation)
Finally, we consider Kickback, a biologically motivated variant of Backprop with reduced communication requirements (Balduzzi et al., 2015). The problem that kickback solves is that backprop requires two distinct kinds of signals to be communicated between units – feedforward and feedback – whereas only one signal type – spikes – are produced by cortical neurons. Kickback computes an estimate of the backpropagated gradient using the signals generated during the feedforward sweep. Kickback also requires the gradient of the loss with respect to the (one-dimensional) output to be broadcast to all units, which is analogous to the role played by diffuse chemical neuromodulators (Schultz et al., 1997; Pawlak et al., 2010; Dayan, 2012).
Syzygy 5 (kickback).
The query graph is the same as for backpropagation, except that the Operator for each layer produces the additional output :

• Nature samples labeled data (x, y) from ℙX× Y.
• Layers by weight matrices θi. The output of the neural network is required to be one-dimensional.
• Operators for each layer compute two outputs: Si = max(0, θ i ⋅ Si−1) and where 𝟙a = 1 if a ≥ 0 and 0 otherwise.
• The task is regression or binary classification with loss given by the mean-squared or logistic error. It follows that the derivative of the loss with respect to the network’s output is a scalar.
The response graph contains a single Oracle that broadcasts the gradient of the loss with respect to the network’s output (which is a scalar). Gradient estimates for each Layer are computed using a mixture of Oracle and local zeroth-order information referred to as Kicks:
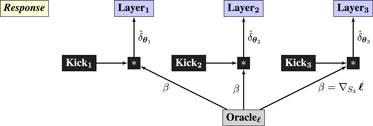
Kicki is computed using locally available zeroth-order information as follows
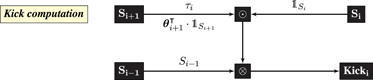
where ⊙ is coordinatewise multiplication and ⊗ is the outer product. If i = 1 then Nature is substituted for Si–1. If i = L then Si+1 is replaced with the scalar value 1.
The loss functions for the layers are not computed in the query graph. Nevertheless, the gradients communicated to the layers by the response graph are exact with respect to the layers’ losses, see Balduzzi et al. (2015). For our purposes, it is more convenient to focus on the global objective of the neural network and treat the gradients communicated to the layers as estimates of the gradient of the global objective with respect to the layers’ weights.
Guarantee. Define unit j to be coherent if τj > 0. A network is coherent if all its units are coherent. A sufficient condition for a rectifier to be coherent is that its weights are positive.
The guarantee for Kickback is that, if the network is coherent, then the gradient estimate computed using the zeroth-order Kicks has the same sign as the backpropagated error computed using gradients, see Balduzzi et al. (2015) for details. As a result, small steps in the direction of the gradient estimates are guaranteed to decrease the network’s loss. □
Remark 4 (biological plausibility of kickback).
Kickback uses a single oracle, analogous to a neuromodulatory signal, in contrast to Backprop which requires an oracle per layer. The rest of the oracles are replaced by kicks – zeroth-order information from which gradient estimates are constructed. Importantly, the kick computation for layer i only requires locally available information produced by its neighboring layers i − 1 and i + 1 during the feedforward sweep. The feedback signals τi are analogous to the signals transmitted by NMDA synapses.
Finally, rectifier units with non-negative weights (for which coherence holds) can be considered a simple model of excitatory neurons (Glorot et al., 2011; Balduzzi and Besserve, 2012; Balduzzi, 2014).
Two recent alternatives to backprop that also do not rely on backpropagating exact gradients are target propagation (Lee et al., 2015) and feedback alignment (Lillicrap et al., 2014). Target propagation makes do without gradients by implementing
autoencoders at each layer. Unfortunately, optimization problems force the authors to introduce a correction term involving differences of targets. As a consequence, and in contrast to Kickback, the information required by layers in difference target propagation cannot be computed locally but instead requires recursively backpropagating differences from the output layer.
Feedback alignment solves a different problem: that feedback and forward weights are required to be equal in backprop (and also in kickback). The authors observe that using random feedback weights can suffice. Unfortunately, as for difference target propagation, feedback alignment still requires separate feedforward and recursively backpropagated training signals, so weight updates are not local.
Unfortunately, at a conceptual level kickback, target propagation and feedback alignment all tackle the wrong problem. The cortex performs reinforcement learning: mammals are not provided with labels, and there is no clearly defined output layer from which signals could backpropagate. A biologically plausible deep learning algorithm should take advantage of the particularities of the reinforcement learning setting.
4. Conclusion
Backpropagation was proposed by Rumelhart et al. (1986a) as a method for learning representations in neural networks. Grammars are a framework for distributed optimization that includes backprop as a special case. Grammars abstract two essential features of backprop:
• distributing first-order information about the objective to nodes in a graph (generalizing the backpropagation algorithm itself) such that,
• the first-order information is sufficient to find a local optimum of the objective (generalizing the guarantee that follows from the chain-rule).
Generative-adversarial networks, the deviator-actor-critic model, and kickback are examples of grammars that do not straightforwardly implement backprop, but nevertheless perform well since they communicate the necessary gradient information.
Grammars enlarge the design space for deep learning. A potential application of the framework is to connect deep learning with cortical learning. Thirty years after backpropagation’s discovery, no evidence for backpropagated error signals has been found in cortex (Crick, 1989; Lamme and Roelfsema, 2000; Roelfsema and van Ooyen, 2005). Nevertheless, backpropagation is an essential ingredient in essentially all state-of-the-art algorithms for supervised, unsupervised, and reinforcement learning. This suggests investigating algorithms with similar guarantees to backprop that do not directly implement the chain rule.
Author Contributions
DB wrote the article.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I am grateful to Marcus Frean, J. P. Lewis, and Brian McWilliams for useful comments and discussions.
Funding
Research funding in part by VUW Research Establishment Grant.
Footnotes
References
Abernethy, J. D., and Frongillo, R. M. (2011). “A collaborative mechanism for crowdsourcing prediction problems,” in Advances in Neural Information Processing Systems 24, eds J. Shawe-Taylor, R. S. Zemel, P. L. Bartlett, F. Pereira, and K. Q. Weinberger (Curran Associates, Inc.), 2600–2608.
Agarwal, A., Bartlett, P. L., Ravikumar, P. K., and Wainwright, M. J. (2009). “Information-theoretic lower bounds on the oracle complexity of convex optimization,” in Advances in Neural Information Processing Systems 22, eds Y. Bengio, D. Schuurmans, J. D. Lafferty, C. K. I. Williams, and A. Culotta (Curran Associates, Inc.), 1–9.
Arjevani, Y., Shalev-Shwartz, S., and Shamir, O. (2016). On Lower and Upper Bounds for Smooth and Strongly Convex Optimization Problems. J. Mach. Learn. Res. arXiv:1503.06833.
Baird, L. C. III. (1995). “Residual algorithms: reinforcement learning with function approximation,” in Machine Learning, Proceedings of the Twelfth International Conference on Machine Learning, Tahoe City, California, USA, July 9–12, 1995, 30–37.
Balduzzi, D. (2011). “Falsification and future performance,” in Algorithmic Probability and Friends. Bayesian Prediction and Artificial Intelligence – Papers from the Ray Solomonoff 85th Memorial Conference, Melbourne, VIC, Australia, November 30 – December 2, 2011, Vol. 7070, ed. D. Dowe (Springer), 65–78. doi: 10.1007/978-3-642-44958-1_5
Balduzzi, D. (2013). “Randomized co-training: from cortical neurons to machine learning and back again,” in Randomized Methods for Machine Learning Workshop, Neural Inf Proc Systems (NIPS).
Balduzzi, D. (2014). “Cortical prediction markets,” in International conference on Autonomous Agents and Multi-Agent Systems, AAMAS ’14, Paris, France, May 5–9, 2014, 1265–1272.
Balduzzi, D. (2015). Deep Online Convex Optimization by Putting Forecaster to Sleep. arXiv:1509.01851.
Balduzzi, D., and Besserve, M. (2012). “Towards a learning-theoretic analysis of spike-timing dependent plasticity,” in Advances in Neural Information Processing Systems 25, eds F. Pereira, C. J. C. Burges, L. Bottou, and K. Q. Weinberger (Curran Associates, Inc.), 2456–2464.
Balduzzi, D., and Ghifary, M. (2015). Compatible Value Gradients for Reinforcement Learning of Continuous Deep Policies. arXiv:1509.03005.
Balduzzi, D., Ortega, P. A., and Besserve, M. (2013). Metabolic cost as an organizing principle for cooperative learning. Adv. Complex Syst. 16, 1350012. doi:10.1142/S0219525913500124
Balduzzi, D., and Tononi, G. (2013). What can neurons do for their brain? Communicate selectivity with spikes. Theory Biosci. 132, 27–39. doi:10.1007/s12064-012-0165-0
Balduzzi, D., Vanchinathan, H., and Buhmann, J. M. (2015). “Kickback cuts Backprop’s red-tape: biologically plausible credit assignment in neural networks,” in Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, January 25–30, 2015, Austin, Texas, USA, 485–491.
Barto, A. G. (1985). Learning by statistical cooperation of self-interested neuron-like computing elements. Hum. Neurobiol. 4, 229–256.
Barto, A. G., Sutton, R. S., and Anderson, C. W. (1983). Neuronlike adapative elements that can solve difficult learning control problems. IEEE Trans. Syst. Man. Cybern. 13, 834–846. doi:10.1109/TSMC.1983.6313077
Bastien, F., Lamblin, P., Pascanu, R., Bergstra, J., Goodfellow, I. J., Bergeron, A., et al. (2012). Theano: new features and speed improvements. CoRR.
Baum, E. B. (1999). Toward a model of intelligence as an economy of agents. Mach. Learn. 35, 155–185. doi:10.1023/A:1007593124513
Baydin, A. G., and Pearlmutter, B. A. (2014). “Automatic differentiation of algorithms for machine learning,” in Journal of Machine Learning Research: Workshop and Conference Proceedings, 1–7.
Bengio, Y. (2013). “Deep learning of representations: looking forward,” in Statistical Language and Speech Processing – First International Conference, SLSP 2013, Tarragona, Spain, July 29–31, 2013. Proceedings, eds A.-H. Dediu, C. Martín-Vide, R. Mitkov, and B. Truthe (Springer) 1–37. doi:10.1007/978-3-642-39593-2_1
Bengio, Y., Courville, A., and Vincent, P. (2013). Representation learning: a review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 35, 1798–1828. doi:10.1109/TPAMI.2013.50
Bergstra, J., Breuleux, O., Bastien, F., Lamblin, P., Pascanu, R., Desjardins, G., et al. (2010). “Theano: a CPU and GPU math expression compiler,” in Proceedings of the Python for Scientific Computing Conference (SciPy), Austin.
Blum, A., and Mansour, Y. (2007). From external to internal regret. J. Mach. Learn. Res. 8, 1307–1324.
Bottou, L. (2014). From machine learning to machine reasoning: an essay. Mach. Learn. 94, 133–149. doi:10.1007/s10994-013-5335-x
Bousquet, O., and Bottou, L. (2008). “The tradeoffs of large scale learning,” in Advances in Neural Information Processing Systems 20, eds J. C. Platt, D. Koller, Y. Singer, and S. T. Roweis (Curran Associates, Inc.) 161–168.
Bottou, L., and Gallinari, P. (1991). “A framework for the cooperation of learning algorithms,” in Advances in Neural Information Processing Systems 3, eds R. P. Lippmann, J. E. Moody, and D. S. Touretzky (Morgan-Kaufmann) 781–788.
Cesa-Bianchi, N., and Lugosi, G. (2006). Prediction, Learning and Games. Cambridge, UK: Cambridge University Press.
Choromanska, A., Henaff, M., Mathieu, M., Arous, G. B., and LeCun, Y. (2015a). “The loss surface of multilayer networks,” in Proceedings of the Eighteenth International Conference on Artificial Intelligence and Statistics, AISTATS 2015, San Diego, California, USA, May 9–12, 2015.
Choromanska, A., LeCun, Y., and Arous, G. B. (2015b). “Open problem: the landscape of the loss surfaces of multilayer networks,” in Proceedings of The 28th Conference on Learning Theory, COLT 2015, Paris, France, July 3–6, 2015, 1756–1760.
Crick, F. (1989). The recent excitement about neural networks. Nature 337, 129–132. doi:10.1038/337129a0
Dann, C., Neumann, G., and Peters, J. (2014). Policy evaluation with temporal differences: a survey and comparison. J. Mach. Learn. Res. 15, 809–883.
Dayan, P. (2012). Twenty-five lessons from computational neuromodulation. Neuron 76, 240–256. doi:10.1016/j.neuron.2012.09.027
Deisenroth, M. P., Neumann, G., and Peters, J. (2013). A survey on policy search for robotics. Found. Trends in Robotics 2, 1–142. doi:10.1561/2300000021
Foster, D. P., and Vohra, R. V. (1997). Calibrated learning and correlated equilibrium. Games Econ. Behav. 21, 40–55. doi:10.1006/game.1997.0595
Frongillo, R., and Reid, M. (2015). “Convergence analysis of prediction markets via randomized subspace descent,” in NIPS.
Gershman, S. J., Horvitz, E. J., and Tenenbaum, J. (2015). Computational rationality: a converging paradigm for intelligence in brains, minds, and machines. Science 349, 273–278. doi:10.1126/science.aac6076
Glorot, X., Bordes, A., and Bengio, Y. (2011). “Deep sparse rectifier neural networks,” in Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, AISTATS 2011, Fort Lauderdale, USA, April 11–13, 2011, 315–323.
Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., et al. (2014). “Generative adversarial nets,” in Advances in Neural Information Processing Systems 27, eds Z. Ghahramani, M. Welling, C. Cortes, N. D. Lawrence, and K. Q. Weinberger (Curran Associates, Inc.), 2672–2680.
Gordon, G. J. (2007). “No-regret algorithms for online convex programs,” in Advances in Neural Information Processing Systems 19, eds B. Schölkopf, J. C. Platt and T. Hoffman (MIT Press), 489–496.
Griewank, A., and Walther, A. (2008). “Society for industrial and applied mathematics,” in Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation. Philadelphia: SIAM.
Hafner, R., and Riedmiller, M. (2011). Reinforcement learning in feedback control: challenges and benchmarks from technical process control. Mach. Learn. 84, 137–169. doi:10.1007/s10994-011-5235-x
Hardt, M., Recht, B., and Singer, Y. (2015). Train Faster, Generalize Better: Stability of Stochastic Gradient Descent. arXiv:1509.01240.
Heess, N., Wayne, G., Silver, D, Lillicrap, T, Tassa, Y., and Erez, T. (2015). “Learning continuous control policies by stochastic value gradients,” in Advances in Neural Information Processing Systems 28, eds A. Cortes, N. D. Lawrence, D. D. Lee, M. Sugiyama, and R. Garnett (Curran Associates, Inc.), 2926–2934.
Hinton, G., Deng, L., Yu, D., Dahl, G. E., Mohamed, A., Jaitly, N., et al. (2012). Deep neural networks for acoustic modeling in speech recognition. IEEE Signal Process. Mag. 29, 82–97. doi:10.1109/MSP.2012.2205597
Hopcroft, J. E., and Ullman, J. D. (1979). Introduction to Automata Theory, Languages, and Computation. Reading, MA: Addison-Wesley.
Klopf, A. H. (1982). The Hedonistic Neuron: A Theory of Memory, Learning and Intelligence. Washington, DC: Hemisphere Pub. Corp.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). “Imagenet classification with deep convolutional neural networks,” in Advances in Neural Information Processing Systems 25, eds F. Pereira, C. J. C. Burges, L. Bottou, and K. Q. Weinberger (Curran Associates, Inc.), 1097–1105.
Kschischang, F., Frey, B. J., and Loeliger, H.-A. (2001). Factor graphs and the sum-product algorithm. IEEE Trans. Inf. Theory 47, 498–519. doi:10.1109/18.910572
Kwee, I., Hutter, M., and Schmidhuber, J. (2001). “Market-based reinforcement learning in partially observable worlds,” in Artificial Neural Networks – ICANN 2001, International Conference Vienna, Austria, August 21–25, 2001 Proceedings, 865–873. doi:10.1007/3-540-44668-0_120
Lamme, V., and Roelfsema, P. (2000). The distinct modes of vision offered by feedforward and recurrent processing. Trends Neurosci. 23, 571–579. doi:10.1016/S0166-2236(00)01657-X
Lay, N., and Barbu, A. (2010). “Supervised aggregation of classifiers using artificial prediction markets,” in Proceedings of the 27th International Conference on Machine Learning (ICML-10), June 21–24, 2010, Haifa, Israel, 591–598.
LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learning. Nature 521, 436–444. doi:10.1038/nature14539
LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998). Gradient-based learning applied to document recognition. Proc. IEEE 86, 2278–2324. doi:10.1109/5.726791
Lee, D.-H., Zhang, S., Fischer, A., and Bengio, Y. (2015). “Difference Target Propagation,” in European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases (ECML PKDD).
Lewis, S. N., and Harris, K. D. (2014). The Neural Market Place: I. General Formalism and Linear Theory. bioRxiv.
Lillicrap, T. P., Cownden, D., Tweed, D. B., and Ackerman, C. J. (2014). Random Feedback Weights Support Learning in Deep Neural Networks. arXiv:1411.0247.
Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T., Tassa, Y., et al. (2015). Continuous control with deep reinforcement learning. CoRR.
Maei, H. R., Szepesvári, C., Bhatnagar, S., and Sutton, R. S. (2010). “Toward off-policy learning control with function approximation,” in Proceedings of the 27th International Conference on Machine Learning (ICML-10), June 21–24, 2010, Haifa, Israel, 719–726.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., et al. (2015). Human-level control through deep reinforcement learning. Nature 518, 529–533. doi:10.1038/nature14236
Nemirovski, A. (1979). “Efficient methods for large-scale convex optimization problems,” in Ekonomika i Matematicheskie Metody, 15.
Nemirovski, A., Juditsky, A., Lan, G., and Shapiro, A. (2009). Robust stochastic approximation approach to stochastic programming. SIAM J. Optim. 19, 1574–1609. doi:10.1137/070704277
Nemirovski, A., and Yudin, D. B. (1978). On Cezari’s convergence of the steepest descent method for approximating saddle point of convex-concave functions. Sov. Math. Dokl. 19.
Nemirovski, A. S., and Yudin, D. B. (1983). Problem Complexity and Method Efficiency in Optimization. New York, NY: Wiley-Interscience.
Nisan, N., Roughgarden, T., Tardos, É, and Vazirani, V. (eds) (2007). Algorithmic Game Theory. Cambridge: Cambridge University Press.
Parkes, D. C., and Wellman, M. P. (2015). Economic reasoning and artificial intelligence. Science 349, 267–272. doi:10.1126/science.aaa8403
Pawlak, V., Wickens, J. R., Kirkwood, A., and Kerr, J. N. D. (2010). Timing is not everything: neuromodulation opens the STDP gate. Front. Syn. Neurosci. 2:146. doi:10.3389/fnsyn.2010.00146
Pearl, J. (1988). Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Morgan Kaufmann.
Prokhorov, D. V., and Wunsch, D. C. (1997). Adaptive critic designs. IEEE Trans. Neural. Netw. 8, 997–1007. doi:10.1109/TNN.1997.641481
Raginsky, M., and Rakhlin, A. (2011). Information-based complexity, feedback and dynamics in convex programming. IEEE Trans. Inf. Theory 57, 7036–7056. doi:10.1109/TIT.2011.2154375
Robbins, H., and Monro, S. (1951). A stochastic approximation method. Ann. Math. Stat. 22, 400–407. doi:10.1214/aoms/1177729586
Roelfsema, P. R., and van Ooyen, A. (2005). Attention-gated reinforcement learning of internal representations for classification. Neural Comput. 17, 2176–2214. doi:10.1162/0899766054615699
Rumelhart, D., Hinton, G., and Williams, R. (1986a). Parallel Distributed Processing. Vol I: Foundations. Cambridge, MA: MIT Press.
Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986b). Learning representations by back-propagating errors. Nature 323, 533–536. doi:10.1038/323533a0
Russell, S., and Norvig, P. (2009). Artificial Intelligence: A Modern Approach, 3rd Edn. Upper Saddle River, NJ: Prentice Hall.
Schmidhuber, J. (2015). Deep learning in neural networks: an overview. Neural Netw. 61, 85–117. doi:10.1016/j.neunet.2014.09.003
Schulman, J., Heess, N., Weber, T., and Abbeel, P. (2015). “Gradient estimation using stochastic computation graphs,” in Advances in Neural Information Processing Systems 28, eds C. Cortes, N. D. Lawrence, D. D. Lee, M. Sugiyama, R. Garnett, and R. Garnett (Curran Associates, Inc.), 3510–3522.
Schultz, W., Dayan, P., and Montague, P. (1997). A neural substrate of prediction and reward. Science 275, 1593–1599. doi:10.1126/science.275.5306.1593
Selfridge, O. G. (1958). “Pandemonium: a paradigm for learning,” in Mechanisation of Thought Processes: Proc Symposium Held at the National Physics Laboratory.
Seung, H. S. (2003). Learning in spiking neural networks by reinforcement of stochastic synaptic transmission. Neuron 40, 1063–1073. doi:10.1016/S0896-6273(03)00761-X
Shalev-Shwartz, S. (2011). Online learning and online convex optimization. Found. Trends Mach. Learn. 4, 107–194. doi:10.1561/2200000018
Silver, D., Lever, G., Heess, N., Degris, T., Wierstra, D., and Riedmiller, M. A. (2014). “Deterministic policy gradient algorithms,” in Proceedings of the 31th International Conference on Machine Learning, ICML 2014, Beijing, China, 21–26 June 2014, 387–395.
Spivak, D. I. (2013). The Operad of Wiring Diagrams: Formalizing a Graphical Language for Databases, Recursion, and Plug-and-Play Circuits. arXiv:1305.0297.
Sra, S., Nowozin, S., and Wright, S. J. (2012). Optimization for Machine Learning. Cambridge, MA: MIT Press.
Stoltz, G., and Lugosi, G. (2007). Learning correlated equilibria in games with compact sets of strategies. Games Econ. Behav. 59, 187–208. doi:10.1016/j.geb.2006.04.007
Storkey, A. J. (2011). “Machine learning markets,” in Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, AISTATS 2011, Fort Lauderdale, USA, April 11–13, 2011, 716–724.
Sutskever, I., Vinyals, O., and Le, Q. V. (2014). “Sequence to sequence learning with neural networks,” in Advances in Neural Information Processing Systems 27, eds Z. Ghahramani, M. Welling, C. Cortes, N. D. Lawrence, and K. Q. Weinberger (Curran Associates, Inc.), 3104–3112.
Sutton, R. (1988). Learning to predict by the method of temporal differences. Mach. Learn. 3, 9–44. doi:10.1007/BF00115009
Sutton, R. S., Maei, H. R., Precup, D., Bhatnagar, S., Silver, D., Szepesvári, C., et al. (2009a). “Fast gradient-descent methods for temporal-difference learning with linear function approximation,” in Proceedings of the 26th Annual International Conference on Machine Learning, (ICML) 2009, Montreal, Quebec, Canada, June 14–18, 2009, 993–1000. doi:10.1145/1553374.1553501
Sutton, R. S., Szepesvári, C., and Maei, H. R. (2009b). “A convergent O(n) temporal-difference algorithm for off-policy learning with linear function approximation,” in Advances in Neural Information Processing Systems 21, eds D. Koller, D. Schuurmans, Y. Bengio, and L. Bottou (Curran Associates, Inc.), 1609–1616.
Sutton, R. S., McAllester, D. A., Singh, S. P., and Mansour, Y. (2000). “Policy gradient methods for reinforcement learning with function approximation,” in Advances in Neural Information Processing Systems 12, eds S. A. Solla, T. K. Leen, and K. Müller (MIT Press), 1057–1063.
Sutton, R. S., Modayil, J., Delp, M., Degris, T., Pilarski, P. M., White, A., et al. (2011). “Horde: a scalable real-time architecture for learning knowledge from unsupervised sensorimotor interaction,” in The 10th International Conference on Autonomous Agents and Multiagent Systems – Volume 2 AAMAS ’11, (Taipei: International Foundation for Autonomous Agents and Multiagent Systems), 761–768.
Sutton, R. S., and Barto, A. G. (1998). Reinforcement Learning: An Introduction. Cambridge, MA: MIT Press.
Syrgkanis, V., Agarwal, A., Luo, H., and Schapire, R. E. (2015). “Fast convergence of regularized learning in games,” in Advances in Neural Information Processing Systems 28, eds C. Cortes, N. D. Lawrence, D. D. Lee, M. Sugiyama, R. Garnett, and R. Garnett (Curran Associates, Inc.), 2971–2979.
Tamar, A., Toulis, P., Mannor, S., and Airoldi, E. M. (2014). “Implicit temporal differences,” in NIPS Workshop on Large-Scale Reinforcement Learning and Markov Decision Problems.
Toulis, P., Airoldi, E. M., and Rennie, J. (2014). “Statistical analysis of stochastic gradient methods for generalized linear models,” in Proceedings of the 31th International Conference on Machine Learning, ICML 2014, Beijing, China, 21–26 June 2014, 667–675.
van Merriënboer, B., Bahdanau, D., Dumoulin, V., Serdyuk, D., Warde-Farley, D., Chorowski, J., et al. (2015). Blocks and Fuel: Frameworks for Deep Learning. arXiv:1506.00619.
von Bartheld, C. S., Wang, X., and Butowt, R. (2001). Anterograde axonal transport, transcytosis, and recycling of neurotrophic factors: the concept of trophic currencies in neural networks. Mol. Neurobiol. 24, 1–28. doi:10.1385/MN:24:1-3:001
von Neumann, J., and Morgenstern, O. (1944). Theory of Games and Economic Behavior. Princeton, NJ: Princeton University Press.
Wainwright, M. J., and Jordan, M. I. (2008). Graphical models, exponential families, and variational inference. Found. Trends Mach. Learn. 1, 1–305. doi:10.1561/2200000001
Werbos, P. J. (1974). Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Ph.D. thesis, Cambridge, MA: Harvard.
Williams, R. J., and Peng, J. (1990). An efficient gradient-based algorithm for on-line training of recurrent network trajectories. Neural Comput. 2, 490–501. doi:10.1162/neco.1990.2.4.490
Williams, R. J., and Zipser, D. (1995). “Gradient-based learning algorithms for recurrent networks and their computational complexity,” in Backpropagation: Theory, Architectures, and Applications, eds Y. Chauvin and D. Rumelhart (Lawrence Erlbaum Associates).
Keywords: deep learning, representation learning, optimization, game theory, neural networks
Citation: Balduzzi D (2016) Grammars for Games: A Gradient-Based, Game-Theoretic Framework for Optimization in Deep Learning. Front. Robot. AI 2:39. doi: 10.3389/frobt.2015.00039
Received: 30 September 2015; Accepted: 21 December 2015;
Published: 18 January 2016
Edited by:
Fabrizio Riguzzi, Università degli Studi di Ferrara, ItalyReviewed by:
Raul Vicente, Max-Planck Institute for Brain Research, GermanyKate Cerqueira Revoredo, Federal University of the State of Rio de Janeiro, Brazil
Copyright: © 2016 Balduzzi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: David Balduzzi, ZGF2aWQuYmFsZHV6emlAdnV3LmFjLm56
 David Balduzzi
David Balduzzi