- 1Department of Aeronautics and Astronautics, Graduate School of Engineering, Kyoto University, Kyoto, Japan
- 2Department of Physiology, School of Medicine, Dokkyo Medical University, Tochigi, Japan
Interlimb coordination plays an important role in adaptive locomotion of humans and animals. This has been investigated using a split-belt treadmill, which imposes different speeds on the two sides of the body. Two types of adaptation have been identified, namely fast and slow adaptations. Fast adaptation induces asymmetric interlimb coordination soon after a change of the treadmill speed condition from same speed for both belts to different speeds. In contrast, slow adaptation slowly reduces the asymmetry after fast adaptation. It has been suggested that these adaptations are primarily achieved by the spinal reflex and cerebellar learning. However, these adaptation mechanisms remain unclear due to the complicated dynamics of locomotion. In our previous work, we developed a locomotion control system for a biped robot based on the spinal reflex and cerebellar learning. We reproduced the fast and slow adaptations observed in humans during split-belt treadmill walking of the biped robot and clarified the adaptation mechanisms from a dynamic viewpoint by focusing on the changes in the relative positions between the center of mass and foot stance induced by reflex and learning. In this study, we modified the control system for application to a quadruped robot. We demonstrate that even though the basic gait pattern of our robot is different from that of general quadrupeds (due to limitations of the robot experiment), fast and slow adaptations that are similar to those of quadrupeds appear during split-belt treadmill walking of the quadruped robot. Furthermore, we clarify these adaptation mechanisms from a dynamic viewpoint, as done in our previous work. These results will increase the understanding of how fast and slow adaptations are generated in quadrupedal locomotion on a split-belt treadmill through body dynamics and sensorimotor integration via the spinal reflex and cerebellar learning and help the development of control strategies for adaptive locomotion of quadruped robots.
1 Introduction
Humans and animals change their locomotor behaviors depending on the environment and situation. Interlimb coordination plays an important role in such adaptive locomotion. For example, to walk along a curved path, the outer legs have a longer stride and higher speed than those of the inner legs (Courtine and Schieppati, 2003; Gruntman et al., 2007). Split-belt treadmills, which impose different speeds on the two sides of the body (Yanagihara and Udo, 1994; Prokop et al., 1995; Reisman et al., 2005; Morton and Bastian, 2006; Choi and Bastian, 2007; Frigon et al., 2013), have been used to investigate the mechanisms that control interlimb coordination. Adaptive behaviors induced by changes in the treadmill speed condition have been investigated. During the split-belt treadmill walking of humans, when the treadmill speed condition is changed from the tied configuration (belts move at the same speed) to the split-belt configuration (belts move at different speeds), the relative phase between the leg movements rapidly changes to break the antiphase relationship (i.e., asymmetric interlimb coordination appears) and the stride length and duty factor differ between the two legs (Reisman et al., 2005). However, the relative phase slowly returns to regain the antiphase relationship and to reduce the asymmetric interlimb coordination in the split-belt configuration. The stride length and duty factor remain almost unchanged and different between the two legs. Furthermore, when the treadmill speed condition is returned to the tied configuration, the stride length and duty factor quickly return, whereas the relative phase rapidly diverges from antiphase (i.e., asymmetric interlimb coordination appears even in the tied configuration) and then slowly returns to antiphase to reduce the asymmetry. Because the spinal cord and reflex contribute to rapid changes in locomotor behavior due to environmental changes (Grillner, 1975), it has been suggested that the fast adaptations in split-belt treadmill walking are induced by sensorimotor integration in the spinal cord. The slow changes in the relative phase and the quick divergence of the relative phase from antiphase upon return to the tied configuration do not appear during split-belt treadmill walking of subjects with cerebellar damage (Morton and Bastian, 2006), which suggests that these changes are induced by learning in the cerebellum. In particular, the quick divergence of the relative phase upon return to the tied configuration has been suggested to be the after-effect of learning.
Although these adaptive behaviors are observed in walking on a split-belt treadmill, locomotion is a complicated dynamical phenomenon generated through interactions between the central nervous system, the body’s musculoskeletal system, and the environment, and thus it is difficult to fully understand the locomotion mechanism based on only observations and measurements of the locomotor system. To overcome this limitation, mathematical models and legged robots have been applied to study locomotion (Aoi et al., 2011, 2017; Fukui et al., 2019; Fukuoka et al., 2015; Ijspeert, 2014; Masuda et al., 2021; Otoda et al., 2009; Owaki et al., 2013; Owaki and Ishiguro, 2017; Spröwitz et al., 2013). In our previous works (Fujiki et al., 2013, 2015), we developed a locomotion control system for a biped robot based on the spinal reflex and cerebellar learning. We reproduced the fast and slow adaptive behaviors observed in humans during split-belt treadmill walking of the robot. These behaviors were not the result of specifically designed features in our control system, but emerged through the body dynamics and sensorimotor integration via the spinal reflex and cerebellar learning. We clarified these adaptation mechanisms from a dynamic viewpoint by focusing on the changes in the relative positions between the center of mass and foot stance induced by reflex and learning.
Quadrupeds such as cats and mice also exhibit fast and slow changes in interlimb coordination during split-belt treadmill walking (D’Angelo et al., 2014; Darmohray et al., 2019; Frigon et al., 2013; Yanagihara and Udo, 1994). Interlimb coordination in quadrupedal locomotion is more complicated than that in human locomotion due to the increased number of legs. Rapid changes have been observed in spinal cats (Forssberg et al., 1980; Frigon et al., 2013) and slow changes and the after-effect do not appear in mice with cerebellar dysfunction (Darmohray et al., 2019), which suggest that the spinal reflex and cerebellar learning contribute to fast and slow adaptations, respectively, during split-belt treadmill walking of quadrupeds, as is the case for humans. Although previous works (Ito et al., 1998; Kodono and Kimura, 2020; Latash et al., 2020) have investigated adaptive quadrupedal locomotion on a split-belt treadmill using mathematical models and legged robots, they considered specific conditions [e.g., only one of the four legs moved at a different speed (Ito et al., 1998; Kodono and Kimura, 2020) and only the center of mass dynamics in the frontal plane were considered (Latash et al., 2020)]. The gait adaptation mechanism in quadrupedal locomotion through whole-body dynamics and sensorimotor integration for different left- and right-side speeds remains unclear.
In this study, we improve our locomotion control system for a biped robot and apply it to a quadruped robot. We demonstrate that although the basic gait pattern of our robot is different from that of general quadrupeds (due to limitations of the robot experiment), fast and slow adaptations similar to those of quadrupeds appear during split-belt treadmill walking of the quadruped robot. Furthermore, we clarify the adaptation mechanisms from a dynamic viewpoint, as done in our previous work (Fujiki et al., 2015). These results will increase the understanding of how fast and slow adaptations are generated in quadrupedal locomotion on a split-belt treadmill through body dynamics and sensorimotor integration via the spinal reflex and cerebellar learning and help the development of control strategies for adaptive locomotion of quadruped robots.
2 Materials and Methods
2.1 Quadruped Robot
In this study, we used the quadruped robot (Figure 1) developed in our previous work (Aoi et al., 2013a). It consists of a body and four legs (Legs 1–4). Each leg consists of two links connected by pitch joints (Joints 1 and 2), with each joint manipulated by a motor. A touch sensor is attached to the tip of each leg.
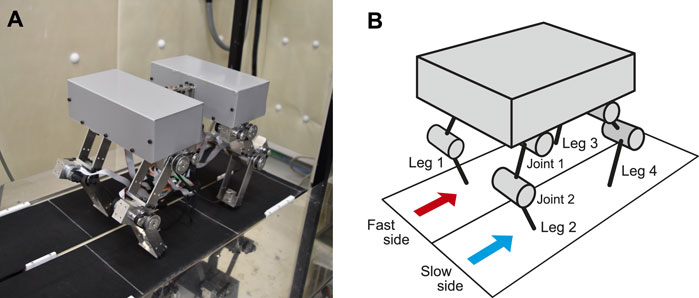
FIGURE 1. Experimental setup. (A) Photograph of quadrupedal robot on split-belt treadmill. The robot body consists of two sections that are mechanically attached to each other. (B) Schematic model of quadrupedal robot.
Electric power is externally supplied and the robot is controlled by an external host computer (Intel Pentium 4 2.8 GHz, RT-Linux), which calculates the desired joint motions and solves the oscillator phase dynamics in the control system (see Section 2.3). The robot receives command signals at intervals of 1 ms. It is connected to the electric power unit and the host computer by cables, which are slack and suspended during the experiment to avoid influencing the robot’s locomotor behavior.
2.2 Split-Belt Treadmill
The robot walked on the split-belt treadmill (Figure 1) developed in our previous works (Fujiki et al., 2013, 2015). The treadmill has two parallel belts, each of which is equipped with a motor and an encoder to control the individual belt speed. The width of each belt is 15 cm and the distance between rotation axes is 64 cm.
2.3 Locomotion Control System
In our previous work (Fujiki et al., 2015), we developed a locomotion control system for a biped robot based on the spinal and cerebellum functions. In this study, we improved the control system and applied it to the quadruped robot (Figure 2). The control system consists of spinal and cerebellum models. The spinal model produces motor commands to manipulate the robot based on a central pattern generator (CPG) and the sensory reflex, and the cerebellum model modulates motor commands through learning.
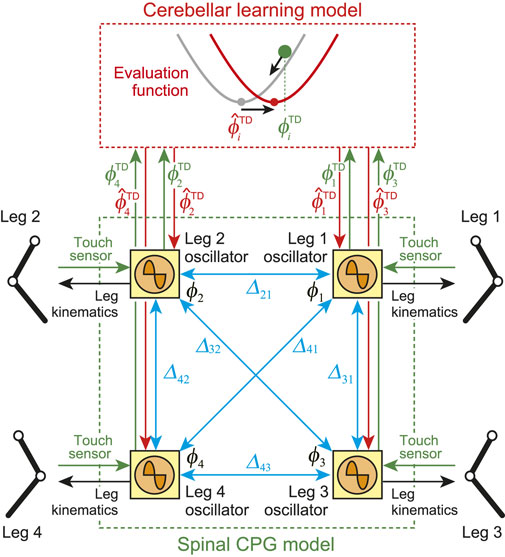
FIGURE 2. Locomotion control model composed of spinal CPG and cerebellar learning models. Spinal model consists of four phase oscillators (Leg 1–4 oscillators). Blue arrows indicate relative phase
2.3.1 Spinal CPG Model
Our spinal CPG model is based on a physiological two-layer network model composed of rhythm generator (RG) and pattern formation (PF) networks (Burke et al., 2001; Rybak et al., 2006). The RG network creates the basic rhythm. It alters the rhythm by producing phase shifts and by performing rhythm resetting in response to sensory feedback (phase resetting). The PF network shapes the rhythm into spatiotemporal motor command patterns. Based on this physiological finding, we developed the spinal CPG model using the following RG and PF models.
For the RG model, we used four simple phase oscillators (Leg 1–4 oscillators), whose phases are denoted by
where ω is the basic oscillator frequency,
For the PF model, taking inspiration from the physiological finding that spinocerebellar neurons encode the global information of limb kinematics, such as the length and orientation of the limb axis (Bosco and Poppele, 2001; Poppele et al., 2002; Poppele and Bosco, 2003), we produced the motor commands to achieve the desired leg kinematics of the robot based on the oscillator phases obtained from the RG model. We use simple leg kinematics, which consist of the swing and stance phases (Figure 3), in reference to the length and orientation of the limb axis in the pitch plane. The swing phase uses a simple closed curve for the leg tip that includes the anterior extreme position (AEP) and the posterior extreme position (PEP). It starts from the PEP and continues until touchdown. The AEP corresponds to the desired position of touchdown. The stance phase uses a straight line from the touchdown position (TDP) to the PEP. The trajectories for the swing and stance phases are given as functions of the corresponding oscillator phase, where
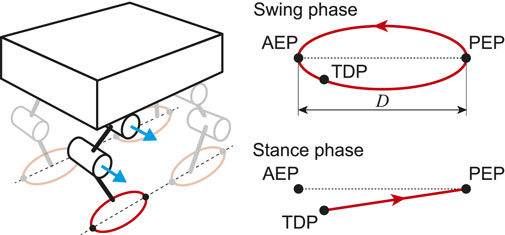
FIGURE 3. Desired leg kinematics composed of swing and stance phases. At touchdown position (TDP), trajectory changes from swing to stance phase. When leg tip reaches posterior extreme position (PEP), trajectory moves into swing phase. Anterior extreme position (AEP) is desired position of touchdown.
To generate the desired kinematics, the desired joint trajectories are calculated based on the inverse kinematics and each joint is controlled by the joint torque based on proportional-derivative feedback control.
2.3.2 Cerebellar Learning Model
The cerebellum predicts the sensory consequences of movement based on the efference copy, and modifies motor commands to reduce errors between the predicted and actual sensory information through learning. Furthermore, it predicts the timing of sensory events (Nixon and Passingham 2001; O’Reilly et al. 2008) and contributes to achieving tasks that require accurate temporal control (Ivry et al., 2012; Ivry and Keele, 1989; Spencer et al., 2005). During walking on a surface with an unexpected hole, the absence of touchdown sensory feedback at the predicted timing triggers reflex-like reaction behavior (Hiebert et al., 1994; van der Linden et al., 2007), which suggests that the prediction of touchdown timing is important for motor learning in walking.
We focused on touchdown timing for the cerebellar model. In particular, we modulate the desired (predicted) touchdown timing
Based on this evaluation function, we predict the next touchdown timing. Specifically, from the gradient direction of the evaluation function,
where α is the learning rate. Because
2.4 Robot Experiment
To clarify the functional roles of the spinal and cerebellar models in gait adaptation during split-belt treadmill walking of the quadruped robot, we considered the following two cases in the robot experiment: 1) with the spinal model but without the cerebellar model, that is, the desired (predicted) touchdown timing
For the quadruped robot, we used the following control parameters:
For the split-belt treadmill, we used the tied configuration at the beginning of the robot walk with
We performed these robot trials five times for each speed condition and investigated the robot’s behavior from the averages of the results for six steps in each configuration period. When we incorporated the cerebellar model, we separated the periods of the split-belt configuration and the second tied configuration into two halves to clarify early and late stages of adaptation in each period. We used one-way repeated-measures analysis of variance (ANOVA) to compare the differences between the periods and to clarify the significance of the locomotor behavior changes. When the ANOVA results showed a significant difference, we conducted post hoc analysis using Tukey’s honestly significant difference test, where we considered that
3 Results
3.1 Fast Adaptation by Reflex
We first used only the spinal model for the robot experiment. At the beginning, the robot walked on the treadmill in the tied configuration with the fore and hind legs in contact with the ipsilateral belt. It continued walking after the treadmill speed condition changed to the 3x, 4x, and 5x conditions of the split-belt configuration. Note that when we did not use phase resetting in Eq. 1, the robot could not walk on the treadmill even in the tied configuration.
Figure 4A shows the relative phases
FIGURE 4. Relative phases between leg oscillators with use of only spinal model. (A)
Figure 5A shows the duty factors of Legs 1–4 for one representative trial of the 5x condition. The duty factors of Legs 1 and 2 were around 0.6 in the tied configuration. That of Leg 1 decreased and that of Leg 2 increased in the split-belt configuration. In contrast, those of Legs 3 and 4 slightly fluctuated around 0.6 and did not show clear trends. Figure 5B shows their averages in the tied configuration and the split-belt configuration in the 5x condition for five trials. The duty factors of Legs 1 and 2 showed significant differences between the belt speed conditions (both
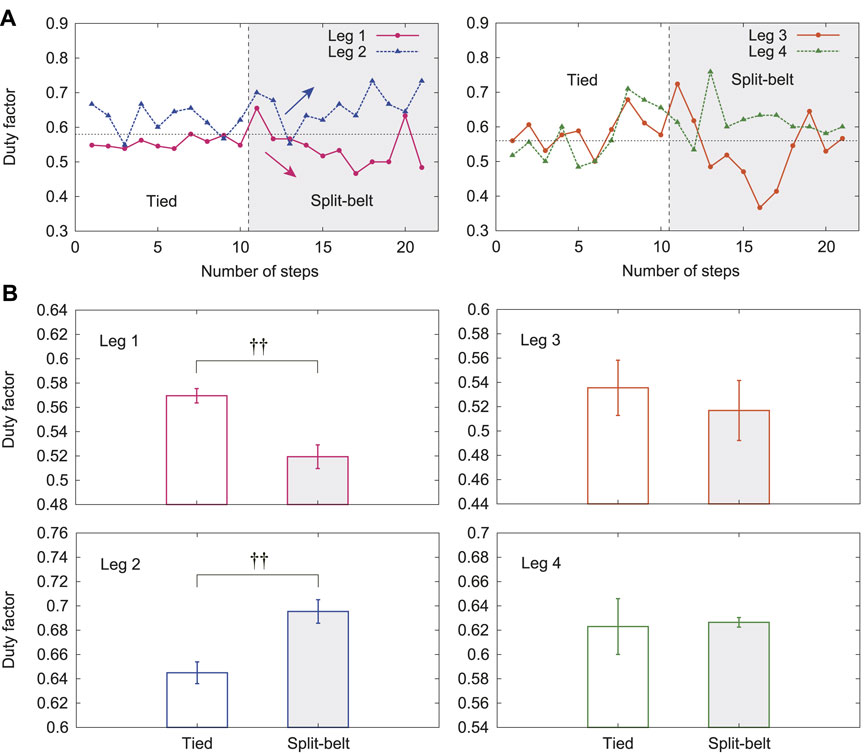
FIGURE 5. Duty factors with use of only spinal model. (A) Duty factors for Legs 1–4 for one representative trial of 5x condition. (B) Their averages for tied and split-belt configurations. Data points and error bars are the mean and standard error results of five experiments, respectively.
Figures 6A, B show the changes in the average relative phases and duty factors, respectively, between the tied configuration and the split-belt configuration for three speed conditions (3x, 4x, and 5x). The changes in the relative phases
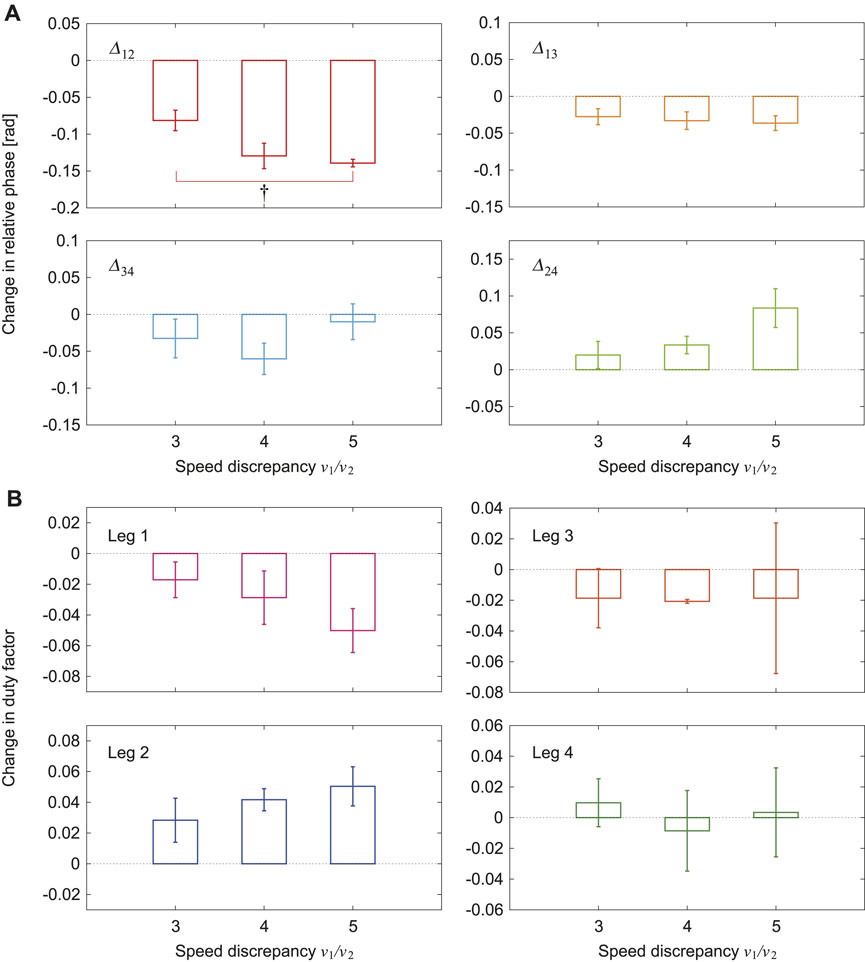
FIGURE 6. Changes in average (A) relative phases and (B) duty factors between tied and split-belt configurations for 3x, 4x, and 5x conditions (
3.2 Slow Adaptation by Learning
We next used both the spinal and cerebellar models for the robot experiment. At the beginning, the robot walked on the treadmill in the tied configuration. It continued walking when the treadmill speed condition changed to the 5x condition of the split-belt configuration. Furthermore, the robot continued walking after the treadmill speed condition returned to the tied configuration.
The relative phase
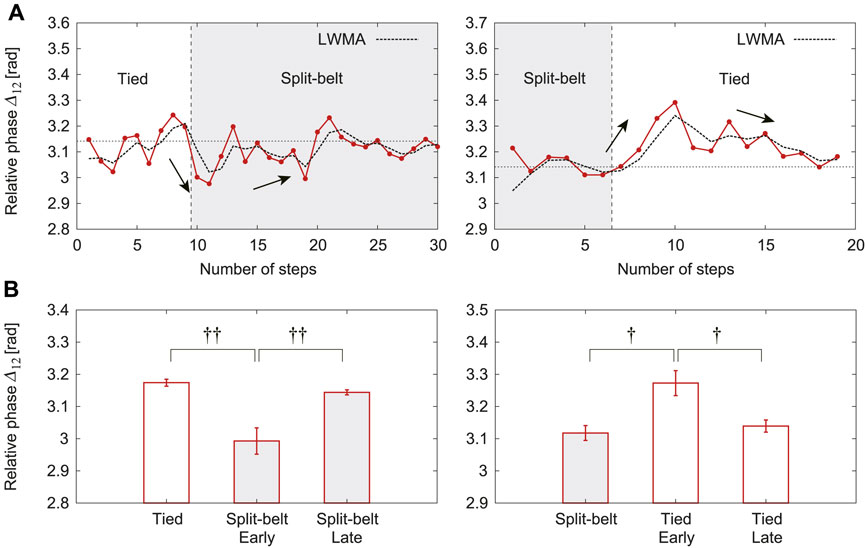
FIGURE 7. Relative phase
In this experiment, the duty factors for Legs 1 and 2 clearly changed depending on the treadmill speed condition, whereas the other duty factors did not, similar to previous results. Figure 8A shows the duty factors for Legs 1 and 2 for one representative trial, where the left and right figures show the results from the first tied configuration to the split-belt configuration and from the split-belt configuration to the second tied configuration, respectively. The duty factors for Legs 1 and 2 were almost 0.6 in the first tied configuration. The duty factor for Leg 1 quickly decreased and that for Leg 2 increased at the early stage of the split-belt configuration. However, they had almost no change at the late stage, unlike the relative phases (Figure 7). They quickly returned to almost 0.6 at the early stage of the second tied configuration and did not change at the late stage. Figure 8B shows their averages for the first tied configuration and the early and late stages for the split-belt and second tied configurations. The duty factor for Leg 1 showed significant differences between the first tied configuration and early stage of the split-belt configuration (
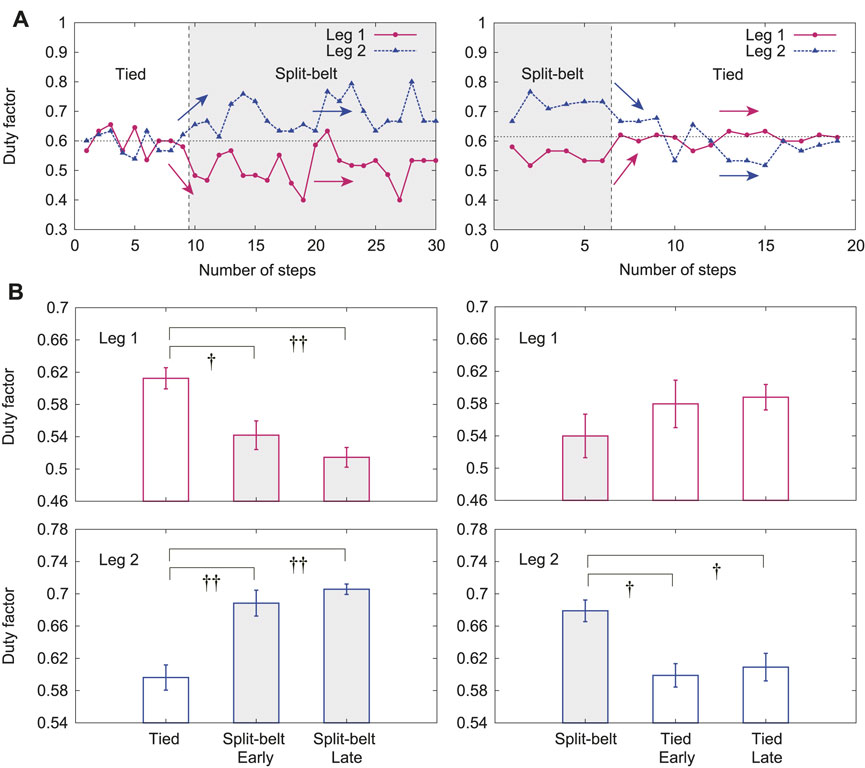
FIGURE 8. Duty factors for Legs 1 and 2 with use of both spinal and cerebellar models. (A) One representative trial. (B) Averages for each period. Data points and error bars are the mean and standard error results of five experiments, respectively.
4 Discussion
4.1 Fast Adaptation Mechanism Upon Change to Split-Belt Configuration
When we used only the spinal model, the relative phase
In the tied configuration, the stance legs on both the fast and slow sides are pulled at the same speed. The fore and hind legs on the ipsilateral side contact the belt simultaneously (Figure 9A). In contrast, the stance legs on the fast side (Legs 1 and 3) are strongly pulled in the split-belt configuration, which accelerates the body and tilts it forward (Figure 9B). As a result, the fore leg on the slow side (Leg 2) touches the belt earlier than in the tied configuration. However, the foot contact timing of the hind leg on the slow side (Leg 4) shows almost no change because the swing leg trajectory moves upward due to the body tilt while the anterior part of the trajectory moves downward due the trajectory tilt. The stance legs on the slow side (Legs 2 and 4) are weakly pulled in the split-belt configuration, which decelerates the body and tilts it backward. As a result, the fore leg on the fast side (Leg 1) touches the belt later than in the tied configuration. However, the foot contact timing of the hind leg on the fast side (Leg 3) shows almost no change because the swing leg trajectory moves downward due to the body tilt while the anterior part of the trajectory moves upward due the trajectory tilt. These changes in the foot contact timings change the relative phases
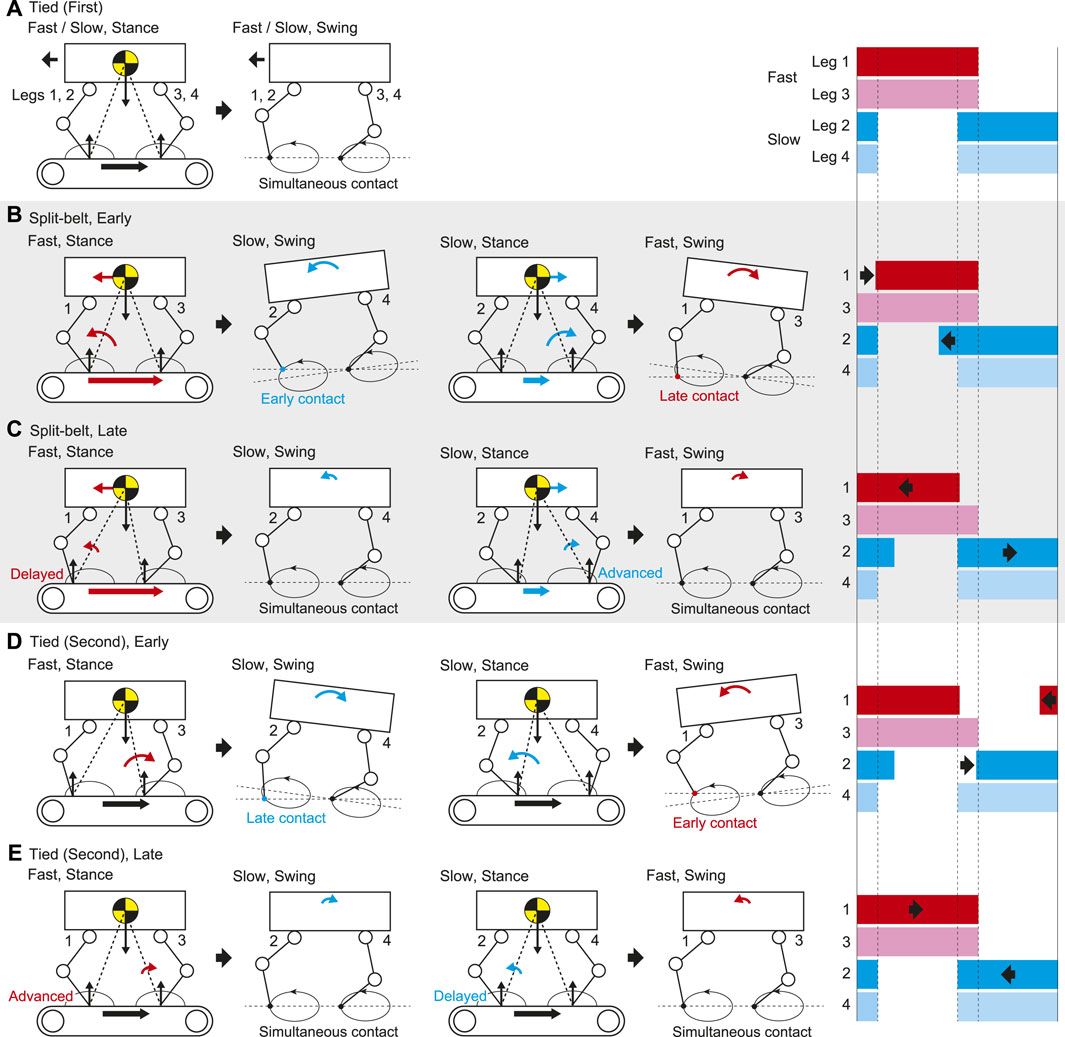
FIGURE 9. Gait adaptation mechanism through reflex and learning based on foot contact timing in (A) first tied, (B) early stage of split-belt, (C) late stage of split-belt, (D) early stage of second tied, and (E) late stage of second tied configurations. Right figures show foot diagrams.
4.2 Slow Adaptation Mechanism in Split-Belt Configuration
When we incorporated the cerebellar model as well as the spinal model, adaptive changes in locomotor behaviors similar to those observed with the use of only the spinal model appeared at the early stage of the split-belt configuration. However, different adaptive behavior appeared in the late stage of the split-belt configuration due to the learning by the cerebellar model. In particular, after the relative phase
Because the touchdown of the fore leg on the slow side (Leg 2) is advanced at the early stage (Figure 9B), the swing leg speed slowly increases due to learning. As a result, the stance legs on the fast side (Legs 1 and 3) are delayed relative to the slow side at the late stage, which reduces the pitching moment to tilt the body forward and induces simultaneous foot contact between the fore and hind legs on the slow side (Legs 2 and 4), as shown in Figure 9C. Similarly, because the touchdown of the fore leg on the fast side (Leg 1) is delayed at the early stage (Figure 9B), the swing leg speed slowly decreases due to learning. As a result, the stance legs on the slow side (Legs 2 and 4) are advanced relative to the fast side at the late stage, which reduces the pitching moment to tilt the body backward and induces simultaneous foot contact between the fore and hind legs on the fast side (Legs one and 3), as shown in Figure 9C. These slow changes in the foot contact timings change the relative phase
4.3 After-Effect Mechanism due to Fast and Slow Adaptations Upon Return to Tied Configuration
When the treadmill speed condition was returned to the tied configuration, locomotor behaviors different from those in the first tied configuration appeared. In particular, the relative phase
In the late stage of the split-belt configuration, the stance legs on the fast side (Legs 1 and 3) are delayed relative to the slow side due to the learning effect, which reduces the pitching moment to tilt the body forward by the strong pulling (Figure 9C). When the treadmill speed condition is returned to the tied configuration, the strong pulling also returns, which induces the pitching moment to tilt the body backward (Figure 9D). As a result, the fore leg on the slow side (Leg 2) touches the belt later than in the late stage of the split-belt configuration. The foot contact timing of the hind leg on the slow side (Leg 4) shows almost no change for the same reason as that for the foot contact timing of the hind leg on the fast side (Leg 3) in the early stage of the split-belt configuration (Figure 9B). Similarly, in the late stage of the split-belt configuration, the stance legs of the slow side (Legs 2 and 4) are advanced relative to the fast side due to the learning effect, which reduces the pitching moment to tilt the body backward by the weak pulling (Figure 9C). When the treadmill speed condition is returned to the tied configuration, the weak pulling also returns, which induces the pitching moment to tilt the body forward (Figure 9D). As a result, the fore leg on the fast side (Leg 1) touches the belt earlier than in the late stage of the split-belt configuration. The foot contact timing of the hind leg on the fast side (Leg 3) shows almost no change for the same reason as that for the foot contact timing of the hind leg on the slow side (Leg 4) in the early stage of the split-belt configuration (Figure 9B). These changes in the foot contact timings induce a different behavior of
4.4 Slow Adaptation Mechanism After Return to Tied Configuration
Although the relative phase
Because the touchdown of the fore leg on the slow side (Leg 2) is delayed at the early stage (Figure 9D), the swing leg speed slowly decreases due to learning. As a result, the stance legs on the fast side (Legs 1 and 3) are advanced relative to the slow side at the late stage, which reduces the pitching moment to tilt the body backward and induces simultaneous foot contact between the fore and hind legs on the slow side (Legs 2 and 4), as shown in Figure 9E. Similarly, because the touchdown of the fore leg on the fast side (Leg 1) is advanced at the early stage (Figure 9D), the swing leg speed slowly increases due to learning. As a result, the stance legs on the slow side (Legs 2 and 4) are delayed relative to the fast side at the late stage, which reduces the pitching moment to tilt the body forward and induces simultaneous foot contact between the fore and hind legs on the fast side (Legs 1 and 3), as shown in Figure 9E. These slow changes in the foot contact timings change the relative phase
4.5 Contributions of Spinal Cord and Cerebellum to Locomotor Adaptation
A split-belt treadmill imposes different speeds on the two sides of the body and highlights the functional role of interlimb coordination in adaptive locomotion. In particular, the adaptive behavior in interlimb coordination can be classified into two types, namely fast and slow adaptations. That is, the locomotion control system has two different time scales. These adaptations are primarily achieved by the contributions of different layers in the neural system, namely the spinal cord and cerebellum. The spinal cord provides motor commands through the RG and PF networks (Burke et al., 2001; Rybak et al., 2006) and modulates the commands immediately responding to sensory feedback (Grillner, 1975). This immediate modulation contributes to fast adaptation, as suggested by the fact that spinal cats walking on a split-belt treadmill show rapid adaptive behavior (Forssberg et al., 1980; Frigon et al., 2013). The cerebellum receives the efference copy from the spinal cord via the ventral spinocerebellar tract and sensory information via the dorsal spinocerebellar tract (Arshavsky et al., 1983; Fedirchuk et al., 2013). Purkinje cells provide the output from the cerebellar cortex to modulate motor commands based on error information between the sensory information predicted via the efference copy and the actual sensory information. This modification contributes to slow adaptation, as suggested from the fact that mice with Purkinje cell degeneration walking on a split-belt treadmill do not exhibit slow adaptive behavior and after-effect (Darmohray et al., 2019). The reflexive response in the spinal cord secures the ability to continue walking as the environment changes, which quickly induces asymmetric interlimb coordination. The cerebellum slowly modulates the movements under the secured condition to make walking smoother and more efficient, which slowly reduces asymmetric interlimb coordination.
Animals make predictions by evaluating various parameters to enhance their movements through learning in motor control. The cerebellum contributes to this prediction and learning. However, because it remains unclear what is predicted and how to use it in learning, modeling studies have attracted attention. In particular, learning models of human arm movements have been proposed to minimize jerk and torque change (Flash and Hogan, 1985; Uno et al., 1989). Although learning techniques, such as deep reinforcement learning, have been used to control legged robots (Hwangbo et al., 2019; Lee et al., 2020; Lillicrap et al., 2016), cerebellar learning models for locomotion remain largely unestablished. This is partly because locomotion is a whole-body movement through leg movement and posture controls and is governed by complicated dynamics, including foot contact and lift off, which change the physical constraints. In this study, we focused on the foot contact timing for prediction and learning in the cerebellar model. This is because phase modulation in response to the stimulation of nerves in the legs (Conway et al., 1987; Duysens, 1977; Frigon et al., 2010; Fujiki et al., 2019; Schomburg et al., 1998) and reflexive reaction in the absence of foot contact sensory information (Hiebert et al., 1994; van der Linden et al., 2007) suggest that sensory information related to foot contact timing play important roles in modulating locomotor behavior. In addition, ankle stiffness is predictively modulated at foot contact in split-belt treadmill walking (Ogawa et al., 2014). Moreover, climbing fiber responses of Purkinje cells, which provide error information for motor control, increase around foot contact (Yanagihara and Udo, 1994). However, the prediction and learning of foot contact timing do not necessarily lead to the adaptations observed during split-belt treadmill walking of animals. Our previous works (Fujiki et al., 2013, 2015) showed that a biped robot with our control system exhibits the fast and slow adaptations observed in humans. Furthermore, this study showed that a quadruped robot with our control system exhibits fast and slow adaptations similar to those of quadrupeds. Our results clarify the importance of foot contact timing modification through sensorimotor integration for adaptive locomotion in animals.
4.6 Limitations of Our Study and Future Work
In this study, we used a robotic platform to investigate the gait adaptation mechanism during quadrupedal locomotion on a split-belt treadmill. The robot mechanical system is much simpler than an animal musculoskeletal system. Furthermore, the robot body is rigid and the joints are strictly controlled by motors, whereas an animal body and joints are flexible due to control by muscles. In addition, we used a much simpler locomotion control system than the neural system used by animals. These simplifications in the robot mechanical and locomotion control systems facilitated the capture of the essential aspects of adaptive locomotion. However, they caused quantitative differences in locomotor behavior. In particular, these simplifications forced our robot to use a pace pattern, unlike the walk and trot patterns of general quadrupeds. For intact cats walking on a split-belt treadmill using a walk pattern, when the left and right belt speeds are changed, the relative phases are altered on both the contralateral and ipsilateral sides to induce asymmetric interlimb coordination, where the contralateral sides for the fore and hind legs change most significantly (D’Angelo et al., 2014). These results are not necessarily the same as our results, where the contralateral side for the fore legs showed significant changes whereas that for the hind legs showed no significant changes (Figure 4). Although some quadrupeds such as giraffes and camels use a pace pattern (Muybridge, 1957), there are no experimental data regarding how their interlimb coordination changes when they walk on a split-belt treadmill, which prevents us from verifying our results from a biological viewpoint and requires further biological studies. To overcome these limitations, musculoskeletal models, which can use similar walk and trot patterns to those used by general quadrupeds, would be useful (Fujiki et al., 2018; Toeda et al., 2020) in future studies.
Although this study focused on split-belt treadmill walking to investigate the contribution of interlimb coordination to adaptive quadrupedal locomotion, interlimb coordination plays an important role in numerous other locomotor tasks. For example, the gait transition between walk, trot, and gallop changes the phase relationship between the movements of four legs while creating and breaking the synchronization between the leg movements (Aoi et al., 2013a; Aoi et al., 2011; Fukui et al., 2019; Fukuoka et al., 2015; Masuda et al., 2021; Owaki et al., 2013; Owaki and Ishiguro, 2017). When crossing an obstacle during walking, the leading limb, which steps over the obstacle first, and the trailing limb, which steps over the obstacle after the leading limb, have different distances from the obstacle and these leg movements differ (Aoi et al., 2013b; Aoki et al., 2013). During walking along a curved path, the inner and outer limbs show different speeds (Gruntman et al., 2007). We would like to investigate the contributions of interlimb coordination to these locomotor tasks using our legged robots and mathematical models in the future.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
SA developed the study design. TA performed the robot experiment. SA, TA, and SF analyzed the data in consultation with KS and KT. SA wrote the manuscript and all the authors reviewed and approved it.
Funding
This study was supported in part by JSPS KAKENHI Grant Numbers JP19KK0377 and JP20H00229, JST FOREST Program Grant Number JPMJFR2021, and Kyoto Technoscience Center, Japan.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frobt.2021.697612/full#supplementary-material
Supplementary Movie | Quadruped robot walking on a split-belt treadmill from the tied configuration to the split-belt configuration in the 5x condition.
References
Aoi, S., Yamashita, T., and Tsuchiya, K. (2011). Hysteresis in the Gait Transition of a Quadruped Investigated Using Simple Body Mechanical and Oscillator Network Models. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 83 (6), 061909. doi:10.1103/PhysRevE.83.061909
Aoi, S., Katayama, D., Fujiki, S., Tomita, N., Funato, T., Yamashita, T., et al. (2013a). A Stability-Based Mechanism for Hysteresis in the Walk-Trot Transition in Quadruped Locomotion. J. R. Soc. Interf. 10 (81), 20120908. doi:10.1098/rsif.2012.0908
Aoi, S., Kondo, T., Hayashi, N., Yanagihara, D., Aoki, S., Yamaura, H., et al. (2013b). Contributions of Phase Resetting and Interlimb Coordination to the Adaptive Control of Hindlimb Obstacle Avoidance during Locomotion in Rats: a Simulation Study. Biol. Cybern. 107 (2), 201–216. doi:10.1007/s00422-013-0546-6
Aoi, S., Manoonpong, P., Ambe, Y., Matsuno, F., and Wörgötter, F. (2017). Adaptive Control Strategies for Interlimb Coordination in Legged Robots: A Review. Front. Neurorobot. 11, 39. doi:10.3389/fnbot.2017.00039
Aoki, S., Sato, Y., and Yanagihara, D. (2013). Lesion in the Lateral Cerebellum Specifically Produces Overshooting of the Toe Trajectory in Leading Forelimb during Obstacle Avoidance in the Rat. J. Neurophysiol. 110, 1511–1524. doi:10.1152/jn.01048.2012
Arshavsky, Y. I., Gelfand, I. M., and Orlovsky, G. N. (1983). The Cerebellum and Control of Rhythmical Movements. Trends Neurosciences 6, 417–422. doi:10.1016/0166-2236(83)90191-1
Bosco, G., and Poppele, R. E. (2001). Proprioception from a Spinocerebellar Perspective. Physiol. Rev. 81, 539–568. doi:10.1152/physrev.2001.81.2.539
Burke, R. E., Degtyarenko, A. M., and Simon, E. S. (2001). Patterns of Locomotor Drive to Motoneurons and Last-Order Interneurons: Clues to the Structure of the CPG. J. Neurophysiol. 86, 447–462. doi:10.1152/jn.2001.86.1.447
Choi, J. T., and Bastian, A. J. (2007). Adaptation Reveals Independent Control Networks for Human Walking. Nat. Neurosci. 10 (8), 1055–1062. doi:10.1038/nn1930
Conway, B. A., Hultborn, H., and Kiehn, O. (1987). Proprioceptive Input Resets Central Locomotor Rhythm in the Spinal Cat. Exp. Brain Res. 68, 643–656. doi:10.1007/BF00249807
Courtine, G., and Schieppati, M. (2003). Human Walking along a Curved Path. II. Gait Features and EMG Patterns. Eur. J. Neurosci. 18, 191–205. doi:10.1046/j.1460-9568.2003.02737.x
D'Angelo, G., Thibaudier, Y., Telonio, A., Hurteau, M. F., Kuczynski, V., Dambreville, C., et al. (2014). Modulation of Phase Durations, Phase Variations, and Temporal Coordination of the Four Limbs during Quadrupedal Split-Belt Locomotion in Intact Adult Cats. J. Neurophysiol. 112, 1825–1837. doi:10.1152/jn.00160.2014
Darmohray, D. M., Jacobs, J. R., Marques, H. G., and Carey, M. R. (2019). Spatial and Temporal Locomotor Learning in Mouse Cerebellum. Neuron. 102, 217–231. doi:10.1016/j.neuron.2019.01.038
Duysens, J., Clarac, F., and Cruse, H. (2000). Load-Regulating Mechanisms in Gait and Posture: Comparative Aspects. Physiol. Rev. 80, 83–133. doi:10.1152/physrev.2000.80.1.83
Duysens, J. (1977). Fluctuations in Sensitivity to Rhythm Resetting Effects during the Cat's Step Cycle. Brain Res. 133 (1), 190–195. doi:10.1016/0006-8993(77)90063-4
Fedirchuk, B., Stecina, K., Kristensen, K. K., Zhang, M., Meehan, C. F., Bennett, D. J., et al. (2013). Rhythmic Activity of Feline Dorsal and Ventral Spinocerebellar Tract Neurons during Fictive Motor Actions. J. Neurophysiol. 109 (2), 375–388. doi:10.1152/jn.00649.2012
Flash, T., and Hogan, N. (1985). The Coordination of Arm Movements: An Experimentally Confirmed Mathematical Model. J. Neurosci. 5, 1688–1703. doi:10.1523/jneurosci.05-07-01688.1985
Forssberg, H., Grillner, S., Halbertsma, J., and Rossignol, S. (1980). The Locomotion of the Low Spinal Cat. II. Interlimb Coordination. Acta Physiol. Scand. 108, 283–295. doi:10.1111/j.1748-1716.1980.tb06534.x
Frigon, A., Hurteau, M.-F., Thibaudier, Y., Leblond, H., Telonio, A., and D'Angelo, G. (2013). Split-Belt Walking Alters the Relationship between Locomotor Phases and Cycle Duration across Speeds in Intact and Chronic Spinalized Adult Cats. J. Neurosci. 33 (19), 8559–8566. doi:10.1523/jneurosci.3931-12.2013
Frigon, A., Sirois, J., and Gossard, J.-P. (2010). Effects of Ankle and Hip Muscle Afferent Inputs on Rhythm Generation during Fictive Locomotion. J. Neurophysiol. 103 (3), 1591–1605. doi:10.1152/jn.01028.2009
Fujiki, S., Aoi, S., Funato, T., Sato, Y., Tsuchiya, K., and Yanagihara, D. (2018). Adaptive Hindlimb Split-Belt Treadmill Walking in Rats by Controlling Basic Muscle Activation Patterns via Phase Resetting. Sci. Rep. 8, 17341. doi:10.1038/s41598-018-35714-8
Fujiki, S., Aoi, S., Funato, T., Tomita, N., Senda, K., and Tsuchiya, K. (2015). Adaptation Mechanism of Interlimb Coordination in Human Split-Belt Treadmill Walking through Learning of Foot Contact Timing: a Robotics Study. J. R. Soc. Interf. 12 (110), 20150542. doi:10.1098/rsif.2015.0542
Fujiki, S., Aoi, S., Tsuchiya, K., Danner, S. M., Rybak, I. A., and Yanagihara, D. (2019). Phase-dependent Response to Afferent Stimulation during Fictive Locomotion: a Computational Modeling Study. Front. Neurosci. 13, 1288. doi:10.3389/fnins.2019.01288
Fujiki, S., Aoi, S., Yamashita, T., Funato, T., Tomita, N., Senda, K., et al. (2013). Adaptive Splitbelt Treadmill Walking of a Biped Robot Using Nonlinear Oscillators with Phase Resetting. Auton. Robot. 35 (1), 15–26. doi:10.1007/s10514-013-9331-6
Fukui, T., Fujisawa, H., Otaka, K., and Fukuoka, Y. (2019). Autonomous Gait Transition and Galloping over Unperceived Obstacles of a Quadruped Robot with CPG Modulated by Vestibular Feedback. Robotics Autonomous Syst. 111, 1–19. doi:10.1016/j.robot.2018.10.002
Fukuoka, Y., Habu, Y., and Fukui, T. (2015). A Simple Rule for Quadrupedal Gait Generation Determined by Leg Loading Feedback: a Modeling Study. Sci. Rep. 5, 8169. doi:10.1038/srep08169
Grillner, S. (1975). Locomotion in Vertebrates: Central Mechanisms and Reflex Interaction. Physiol. Rev. 55 (2), 247–304. doi:10.1152/physrev.1975.55.2.247
Gruntman, E., Benjamini, Y., and Golani, I. (2007). Coordination of Steering in a Free-Trotting Quadruped. J. Comp. Physiol. A. 193, 331–345. doi:10.1007/s00359-006-0187-5
Hiebert, G. W., Gorassini, M. A., Jiang, W., Prochazka, A., and Pearson, K. G. (1994). Corrective Responses to Loss of Ground Support during Walking. II. Comparison of Intact and Chronic Spinal Cats. J. Neurophysiol. 71 (2), 611–622. doi:10.1152/jn.1994.71.2.611
Hwangbo, J., Lee, J., Dosovitskiy, A., Bellicoso, D., Tsounis, V., Koltun, V., et al. (2019). Learning Agile and Dynamic Motor Skills for Legged Robots. Sci. Robot. 4, eaau5872. doi:10.1126/scirobotics.aau5872
Ijspeert, A. J. (2014). Biorobotics: Using Robots to Emulate and Investigate Agile Locomotion. Science 346, 196–203. doi:10.1126/science.1254486
Ito, S., Yuasa, H., Luo, Z.-w., Yanagihara, D., and Ito, M. (1998). A Mathematical Model of Adaptive Behavior in Quadruped Locomotion. Biol. Cybern. 78, 337–347. doi:10.1007/s004220050438
Ivry, R. B., Spencer, R. M., Zelaznik, H. N., and Diedrichsen, J. (2012). The Cerebellum and Event Timing. Ann. N. Y Acad. Sci. 978, 302–317. doi:10.1111/j.1749-6632.2002.tb07576.x
Ivry, R. B., and Keele, S. W. (1989). Timing Functions of the Cerebellum. J. Cogn. Neurosci. 1 (2), 136–152. doi:10.1162/jocn.1989.1.2.136
Kodono, K., and Kimura, H. (2020). Split-Belt Adaptation Model of a Decerebrate Cat Using a Quadruped Robot with Learning. In Living Machines 2020, V. Vouloutsi, A. Mura, F. Tauber, T. Speck, T. J. Prescott, and P. F. M. J. Verschure (Eds.), pp. 217–229. doi:10.1007/978-3-030-64313-3_21
Latash, E. M., Barnett, W. H., Park, H., Rider, J. M., Klishko, A. N., Prilutsky, B. I., et al. (2020). Frontal Plane Dynamics of the Centre of Mass during Quadrupedal Locomotion on a Split-Belt Treadmill. J. R. Soc. Interf. 17, 20200547. doi:10.1098/rsif.2020.0547
Lee, J., Hwangbo, J., Wellhausen, L., Koltun, V., and Hutter, M. (2020). Learning Quadrupedal Locomotion over Challenging Terrain. Sci. Robot. 5, eabc5986. doi:10.1126/scirobotics.abc5986
Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T., Tassa, Y., et al. (2016). Continuous Control with Deep Reinforcement Learning. Proc. Int. Conf. Learn. Represent., 1–14.
Masuda, Y., Naniwa, K., Ishikawa, M., and Osuka, K. (2021). Brainless Walking: Animal Gaits Emerge from an Actuator Characteristic. Front. Robot. AI 8, 629679. doi:10.3389/frobt.2021.629679
Morton, S. M., and Bastian, A. J. (2006). Cerebellar Contributions to Locomotor Adaptations during Splitbelt Treadmill Walking. J. Neurosci. 26 (36), 9107–9116. doi:10.1523/jneurosci.2622-06.2006
Nixon, P., and Passingham, R. (2001). Predicting Sensory Events. Exp. Brain Res. 138, 251–257. doi:10.1007/s002210100702
Ogawa, T., Kawashima, N., Ogata, T., and Nakazawa, K. (2014). Predictive Control of Ankle Stiffness at Heel Contact Is a Key Element of Locomotor Adaptation during Split-Belt Treadmill Walking in Humans. J. Neurophysiol. 111, 722–732. doi:10.1152/jn.00497.2012
O’Reilly, J. X., Mesulam, M. M., and Nobre, A. C. (2008). The Cerebellum Predicts the Timing of Perceptual Events. J. Neurosci. 28 (9), 2252–2260. doi:10.1523/JNEUROSCI.2742-07.2008
Otoda, Y., Kimura, H., and Takase, K. (2009). Construction of a Gait Adaptation Model in Human Split-Belt Treadmill Walking Using a Two-Dimensional Biped Robot. Adv. Robotics 23 (5), 535–561. doi:10.1163/156855309x420057
Owaki, D., and Ishiguro, A. (2017). A Quadruped Robot Exhibiting Spontaneous Gait Transitions from Walking to Trotting to Galloping. Sci. Rep. 7, 277. doi:10.1038/s41598-017-00348-9
Owaki, D., Kano, T., Nagasawa, K., Tero, A., and Ishiguro, A. (2013). Simple Robot Suggests Physical Interlimb Communication Is Essential for Quadruped Walking. J. R. Soc. Interf. 10, 20120669. doi:10.1098/rsif.2012.0669
Poppele, R., and Bosco, G. (2003). Sophisticated Spinal Contributions to Motor Control. Trends Neurosciences 26, 269–276. doi:10.1016/s0166-2236(03)00073-0
Poppele, R. E., Bosco, G., and Rankin, A. M. (2002). Independent Representations of Limb Axis Length and Orientation in Spinocerebellar Response Components. J. Neurophysiol. 87, 409–422. doi:10.1152/jn.00022.2001
Prokop, T., Berger, W., Zijlstra, W., and Dietz, V. (1995). Adaptational and Learning Processes during Human Split-Belt Locomotion: Interaction between Central Mechanisms and Afferent Input. Exp. Brain Res. 106, 449–456. doi:10.1007/BF00231067
Reisman, D. S., Block, H. J., and Bastian, A. J. (2005). Interlimb Coordination during Locomotion: What Can Be Adapted and Stored? J. Neurophysiol. 94, 2403–2415. doi:10.1152/jn.00089.2005
Rybak, I. A., Shevtsova, N. A., Lafreniere-Roula, M., and McCrea, D. A. (2006). Modelling Spinal Circuitry Involved in Locomotor Pattern Generation: Insights from Deletions during Fictive Locomotion. J. Physiol. 577 (2), 617–639. doi:10.1113/jphysiol.2006.118703
Schomburg, E. D., Petersen, N., Barajon, I., and Hultborn, H. (1998). Flexor Reflex Afferents Reset the Step Cycle during Fictive Locomotion in the Cat. Exp. Brain Res. 122 (3), 339–350. doi:10.1007/s002210050522
Spencer, R. M. C., Ivry, R. B., and Zelaznik, H. N. (2005). Role of the Cerebellum in Movements: Control of Timing or Movement Transitions? Exp. Brain Res. 161 (3), 383–396. doi:10.1007/s00221-004-2088-6
Spröwitz, A., Tuleu, A., Vespignani, M., Ajallooeian, M., Badri, E., and Ijspeert, A. J. (2013). Towards Dynamic Trot Gait Locomotion: Design, Control, and Experiments with Cheetah-Cub, a Compliant Quadruped Robot. Int. J. Robotics Res. 32 (8), 932–950. doi:10.1177/0278364913489205
Toeda, M., Aoi, S., Fujiki, S., Funato, T., Tsuchiya, K., and Yanagihara, D. (2020). Gait Generation and its Energy Efficiency Based on Rat Neuromusculoskeletal Model. Front. Neurosci. 13, 1337. doi:10.3389/fnins.2019.01337
Uno, Y., Kawato, M., and Suzuki, R. (1989). Formation and Control of Optimal Trajectory in Human Multijoint Arm Movement. Minimum Torque-Change Model. Biol. Cybern. 61, 89–101. doi:10.1007/BF00204593
van der Linden, M. H., Marigold, D. S., Gabreëls, F. J. M., and Duysens, J. (2007). Muscle Reflexes and Synergies Triggered by an Unexpected Support Surface Height during Walking. J. Neurophysiol. 97 (5), 3639–3650. doi:10.1152/jn.01272.2006
Keywords: split-belt treadmill walking, quadruped robot, interlimb coordination, spinal reflex, cerebellar learning, central pattern generator
Citation: Aoi S, Amano T, Fujiki S, Senda K and Tsuchiya K (2021) Fast and Slow Adaptations of Interlimb Coordination via Reflex and Learning During Split-Belt Treadmill Walking of a Quadruped Robot. Front. Robot. AI 8:697612. doi: 10.3389/frobt.2021.697612
Received: 19 April 2021; Accepted: 12 July 2021;
Published: 06 August 2021.
Edited by:
Dai Owaki, Tohoku University, JapanCopyright © 2021 Aoi, Amano, Fujiki, Senda and Tsuchiya. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shinya Aoi, c2hpbnlhX2FvaUBrdWFlcm8ua3lvdG8tdS5hYy5qcA==
 Shinya Aoi
Shinya Aoi Takashi Amano1
Takashi Amano1 Kei Senda
Kei Senda