Intraparticle entanglement in noisy quantum channels: degradation and revival through amplitude damping

Quantum correlations between two or more different degrees of freedom of the same particle are sometimes referred to as intraparticle entanglement. In this work, we study these intraparticle correlations between two different degrees of freedom under various decoherence channels, viz. amplitude damping, depolarizing, and phase damping channels. We mainly focus on the amplitude-damping channel for which we obtain an exact analytical expression for the concurrence of an arbitrary initial pure state. In this channel, we observe the unique feature of entanglement arising from a separable initial state. We show that this channel allows for a revival of entanglement with an increasing damping parameter, including from a zero value of the concurrence. We also consider the amplitude-damping channel for interparticle entanglement and show that it does not display any of the above-mentioned interesting features. Further, for comparable parameters, the decay of entanglement in the interparticle system is much greater than in the intraparticle system, which we also find to be true for the phase damping and depolarizing channels. Thus, intraparticle entanglement subjected to damping is much more robust than interparticle entanglement.

1 Introduction

Entanglement can arise between two spatially separated particles or two different degrees of freedom of the same particle due to the nonseparability of the states in the Hilbert space. Interparticle entanglement refers to quantum correlations between two or more spatially separated particles in a single degree of freedom (Horodecki et al., 2009), while intraparticle entanglement refers to quantum correlations between two or more degrees of freedom of the same particle (Azzini et al., 2020; Basu et al., 2001). Intraparticle entanglement has been experimentally verified for various quantum systems (Michler et al., 2000; Gadway et al., 2008; Barreiro et al., 2005; Hasegawa et al., 2003; Shen et al., 2020). It is an important property for the testing of quantum contextuality and other various applications, such as quantum key distribution protocols (Sun et al., 2011; Adhikari et al., 2015), quantum teleportation protocols (Heo et al., 2015a; Pramanik et al., 2010; Heo et al., 2015b), entanglement swapping protocols (Adhikari et al., 2010), etc.

Any real-life applications of entanglement would suffer from interactions with a noisy environment. Thus, for realistic applications, it is imperative to investigate the nature of intraparticle entanglement in noisy channels. Furthermore, to find its efficacy, the same should be contrasted and compared with the decohering effects of noisy channels on interparticle entanglement, which have been systematically studied (Yu and Eberly, 2009; Almeida et al., 2007; Salles et al., 2008). Investigating intraparticle entanglement in noisy channels and comparing it with interparticle entanglement will help researchers in developing more robust quantum protocols and systems. This research is crucial for advancing applications like quantum key distribution, teleportation, and entanglement swapping, ensuring they can function effectively in real-world scenarios.

Previous studies of entanglement dynamics under decoherence have focused on interparticle systems. The main characteristic features observed in the dynamics of an interparticle system include entanglement sudden death (ESD) (Yu and Eberly, 2004; Yu and Eberly, 2005, Yu and Eberly, 2009; Almeida et al., 2007) followed by its revival and creation of entanglement, etc., that are rigorously (systematically) studied in the literature. The basic interpretation of entanglement revival in an interparticle system is based on the information backflow between the system and environment, that is, when the system is coupled to a non-Markovian environment. For such systems, the dynamics show entanglement revival even if the subsystems are noninteracting and independently coupled to local environments (Bellomo et al., 2007; D’Arrigo et al., 2014; Bellomo et al., 2008; Tong et al., 2010; Xu et al., 2010). However, the Markovian evolution of the system also shows entanglement revival for an interacting subsystem coupled to a common bath (Ficek and Tanaś, 2006; Ficek, 2010; Aolita et al., 2015). Similarly, the entanglement between two noninteracting qubits can be created by interaction with a common bath (Benatti et al., 2003; Mazzola et al., 2009; Braun, 2002; Benatti et al., 2010).

Intraparticle entanglement between different degrees of freedom (e.g., spin-path in neutrons) was experimentally demonstrated by Hasegawa et al. (2003), but its decoherence properties remained unexplored theoretically. Recent work by Shen et al. (2020) showed the robustness of neutron intraparticle entanglement between spin, path, and energy to experimentally verify quantum contextuality by violating Clauser–Horne–Shimony–Holt (CHSH) and Mermin inequalities but did not address the effect of any damping channels. Another recent work by De Moraes et al. (2020) shows that spin and pseudospin of electrons in graphene become strongly and dynamically entangled due to Rashba spin-orbit coupling, leading to a time-dependent violation of Bell inequalities. Here also, the effect of noise is not addressed. Our work provides a detailed theoretical analysis of noise by revealing that intraparticle entanglement exhibits ESD, followed by revival and creation of entanglement under an amplitude-damping channel.

In this work, the effects of noisy channels, namely amplitude damping, phase damping, and depolarizing channels, on the intraparticle correlations shared between degrees of freedom of a single particle are studied. The entanglement between two degrees of freedom is examined by calculating the concurrence as a function of the channel and input parameters. This study mainly focuses on the amplitude-damping channel, for which an exact analytical expression for the concurrence is obtained, revealing the very interesting phenomenon of the rebirth of entanglement as a function of the channel parameter. This result demonstrates that increasing noise, as quantified by the channel parameter, can counter-intuitively be beneficial for the generation of entanglement. This finding represents the central result of the work and offers a clear distinction between the effect of damping on intraparticle entanglement and the more conventional case of interparticle entanglement with non-Markovian noise (Bellomo et al., 2007). The behavior of intraparticle entanglement is explained through an extensive analysis of the concurrence in terms of the channel and input state parameters. Finally, the decoherence of intraparticle entanglement in the phase damping and depolarizing channels is investigated, and the results are contrasted with the interparticle entanglement scenario to demonstrate the robustness of intraparticle entanglement.

The damping is modeled using the Kraus operator formalism (Kraus et al., 1983), where the evolution of an initial state $\rho$ is described by a trace-preserving map $\rho \to {\rho }^{\prime }={\sum }_i{M}_i\rho M_i^{†}$. The operators $M_i$ are the Kraus operators satisfying the completeness relation ${\sum }_i{M}_i^{†}{M}_i=\mathcal{I}$.

This study considers a pure state of a single quantum system $S$ with two different degrees of freedom, $A$ and $B$, whose states belong to two-dimensional Hilbert spaces ${\mathcal{H}}_A$ and ${\mathcal{H}}_B$ with orthonormal bases $\left\{|a_1\rangle ,|a_2\rangle \right\}$ and $\left\{|b_1\rangle ,|b_2\rangle \right\}$, respectively:

$|{\psi \rangle }_{in}=a|a_1{b}_1\rangle +b|a_1{b}_2\rangle +c|a_2{b}_1\rangle +d|a_2{b}_2\rangle (1)$

with complex coefficients $a$, $b$, $c$ and $d$ with $|a{|}^2+|b{|}^2+|c{|}^2+|d{|}^2=1$.

Note that this structure is identical to the form of a pure state of two spatially separated particles, each with states in separate two-dimensional Hilbert spaces. Consequently, the formalism developed for calculating the concurrence of such systems can be applied to the present setup as well (Wootters, 1998). For an arbitrary bipartite quantum state $\rho$, the concurrence is defined as

$C\left(\rho \right)=max\left\{0,\sqrt{{\lambda }_1}-\sqrt{{\lambda }_2}-\sqrt{{\lambda }_3}-\sqrt{{\lambda }_4}\right\}(2)$

where the quantities ${\lambda }_i$ are the eigenvalues in decreasing order of the matrix:

$R=\rho \left({\sigma }_y\otimes {\sigma }_y\right){\rho }^{*}\left({\sigma }_y\otimes {\sigma }_y\right).(3)$

Here, ${\rho }^{*}$ is the complex conjugate of the matrix representing the input state $\rho$ and ${\sigma }_y$ is the Pauli matrix,

${\sigma }_y=\left(\begin{array}{cc}\hfill 0\hfill & \hfill -i\hfill \\ \hfill i\hfill & \hfill 0\hfill \end{array}\right)$

The intraparticle entanglement between two degrees of freedom for the pure state in Equation 1 is $C=2|ad-bc|$.

When studying decoherence in systems with interparticle entanglement, environmental noise can either act locally on each particle’s state (Bellomo et al., 2007; D’Arrigo et al., 2014; Bellomo et al., 2008; Tong et al., 2010; Xu et al., 2010) or globally on their joint state (Ficek and Tanaś, 2006; Ficek, 2010; Aolita et al., 2015; Rao et al., 2008; D’Arrigo et al., 2013; Yeo and Skeen, 2003). Similarly, in the case of intraparticle entanglement—where different degrees of freedom within a single particle are entangled—the environment can influence each degree of freedom independently or act globally on their combined state.

In the present study, we focus on the latter scenario: a global noise channel that acts jointly on both degrees of freedom. This choice is motivated by the fact that both degrees of freedom originate from the same particle, making global interactions physically plausible. To the best of our knowledge, this global noise model for intraparticle entanglement remains largely unexplored in the literature. Nonetheless, it is important to acknowledge that in some situations, noise can affect individual degrees of freedom independently. For instance, in neutron interferometry, magnetic fields can induce spin decoherence without disturbing the path degree of freedom (Hasegawa et al., 2003). Such independent noise models could be explored in future work. In the case of intraparticle entanglement, we consider a noise model where noise treats the particle as a single entity and acts on the state of the particle as the quantum state of that single entity. Because the state of this single entity belongs to a higher four-dimensional system, that is, a qudit (d = 4), the noise also acts on the qudit.

2 Amplitude-damping channel

The amplitude-damping channel is a fundamental model of energy dissipation in a quantum system, typically describing spontaneous emission where a quantum system loses energy to its environment. In the context of intraparticle entanglement, this channel represents a process where the two internal degrees of freedom of a single particle collectively interact with the environment, causing transitions from excited states to a common ground state.

To model this process, the Kraus operator formalism is employed. Here, the evolution of an initial pure state $|{\psi \rangle }_{in}$—comprising two internal degrees of freedom $A$ and $B$ is governed by trace-preserving quantum operations represented by a set of Kraus operators $\{{\mathcal{M}}_i\}$. For the amplitude-damping channel affecting a single particle’s two degrees of freedom jointly, the Kraus operators take the form Dutta et al. (2016); Fonseca (2019):

$\begin{array}{ll}\hfill M_0& =|0\rangle \langle 0|+\sqrt{1-P}{\displaystyle \sum _{j=1}^3}|j\rangle \langle j|,\hfill \\ \hfill M_i& =\sqrt{P}|0\rangle \langle i|\left(i=\mathrm{1,2,3}\right)\hfill \end{array}(4)$

where $P$ is the channel parameter, and the states $|0\rangle =|a_1{b}_1\rangle$, $|1\rangle =|a_1{b}_2\rangle$, $|2\rangle =|a_2{b}_1\rangle$, and $|3\rangle =|a_2{b}_2\rangle$ for brevity. The state $|0\rangle$ corresponds to the ground state of the system, and because the damping affects both degrees of freedom simultaneously, we assume that it causes transitions from all excited states to the ground state in an equivalent manner. After the evolution of $|{\psi \rangle }_{in}$ through the amplitude-damping channel, the final state becomes (Supplementary Material)

$\begin{array}{ll}\hfill & {\rho }_{\mathit{out}}=\left[P+\left(1-P\right)|a{|}^2\right]|a_1{b}_1\rangle \langle a_1{b}_1|\hfill \\ \hfill & +\sqrt{1-P}\times \sqrt{1-|a{|}^2}\left(a|a_1{b}_1\rangle \langle \varphi |\right.\hfill \\ \hfill & \left.+a^{*}|\varphi \rangle \langle a_1{b}_1|\right)+\left(1-P\right)\left(1-|a{|}^2\right)|\varphi \rangle \langle \varphi |\hfill \end{array}(5)$

where $a^{*}$ is the complex conjugate of the state parameter $a$ and

$|\varphi \rangle =\frac{1}{\sqrt{1-|a{|}^2}}\left(b|a_1{b}_2\rangle +c|a_2{b}_1\rangle +d|a_2{b}_2\rangle \right)(6)$

Because ${\rho }_{\mathit{out}}$ can be written in terms of two orthogonal states, $|a_1{b}_1\rangle$ and $|\varphi \rangle$, it has two nonzero eigenvalues. As a result, the matrix $R$ [Equation 3] also has two nonzero eigenvalues, which are

${\lambda }_{\pm }=\frac{1}{2}\left(S\pm \sqrt{S^2-T^2}\right)(7)$

where (Supplementary Material)

$\begin{array}{ll}\hfill S& =4|b{|}^2|c{|}^2{\left(1-P\right)}^2-4{\left(1-P\right)}^{3/2}\left[ad{b}^{*}{c}^{*}\right.\hfill \\ \hfill & \left.+bc{a}^{*}{d}^{*}\right]+2|d{|}^2\left(1-P\right)\left[P+\left(1-P\right)|a{|}^2\right],\hfill \end{array}(8)$

and

$T=2P\left(1-P\right)\left(1-|a{|}^2\right)|d{|}^2(9)$

After substituting the expressions for $S$ and $T$ into ${\lambda }_{\pm }$ and doing some algebra, we get the concurrence of the output state as (Supplementary Material)

$C=2|bc\sqrt{\left(1-P\right)}-ad|\sqrt{1-P}(10)$

The above expression is a key result of this paper. If there is no noise (i.e., $P=0$), $C=2|bc-ad|$, as expected for the initial pure state. The concurrence for $P\ne 0$ is equivalent to the substitution $\{a,b,c,d\}\to \{a,b\sqrt{1-P},c\sqrt{1-P},d\sqrt{1-P}\}$, reflecting the fact that amplitude damping causes the particle to remain in the excited states $|1\rangle$, $|2\rangle$, and $|3\rangle$ with probability $1-P$. To better understand the behavior of the concurrence, we write

$\begin{array}{ll}\hfill C& =2\left[|b{|}^2|c{|}^2\left(1-P\right)+|a{|}^2|d{|}^2\right.\hfill \\ \hfill & {\left.-2|a\Vert b\Vert c\Vert d|\sqrt{1-P}\cos \left(\mathrm{\Delta }\theta \right)\right]}^{1/2}\sqrt{1-P}\hfill \end{array}(11)$

in terms of the amplitudes and phases of the coefficients $a$, $b$, $c$, and $d$, where $\mathrm{\Delta }\theta ={\theta }_b+{\theta }_c-{\theta }_a-{\theta }_d$. The concurrence can thus also be geometrically interpreted as $2\sqrt{1-P}$ times the length of the difference between two vectors ${\vec{V}}_1$ and ${\vec{V}}_2$ of lengths $|b\Vert c|\sqrt{1-P}$ and $|a\Vert d|$, respectively, with angle $\mathrm{\Delta }\theta$ between them, as shown in Figure 1.

Figure 1

Figure 1. In this figure, ${\vec{V}}_1$, ${\vec{V}}_2$, $\vec{V}={\vec{V}}_1-{\vec{V}}_2$, and $\mathrm{\Delta }\theta$ are shown.

It can be seen that the concurrence is 0 when $P=1$ or

$P=1-{\left(\frac{|a\Vert d|}{|b\Vert c|}\right)}^2\text{\hspace{0.17em}\hspace{0.17em}and\hspace{0.17em}\hspace{0.17em}}\mathrm{\Delta }\theta =0,\pm 2\pi .(12)$

The condition $\mathrm{\Delta }\theta =0,\pm 2\pi$ arises because the individual angles (${\theta }_a$, ${\theta }_b$, ${\theta }_c$, ${\theta }_d$) $\in [\mathrm{0,2}\pi ]$. It is important that for fixed values of the coefficients $a$, $b$, $c$, and $d$, the concurrence can go to zero only at a particular value of $P$ as opposed to a range of values. This is a consequence of the fact that two of the eigenvalues of the final state density matrix ${\rho }_{\mathit{out}}$ are equal to zero, and hence so are two of the eigenvalues of the matrix $R$ defined in Equation 3 used to calculate the concurrence. A zero value of concurrence results when the remaining two nonzero eigenvalues of $R$ become degenerate. This corresponds to a level crossing, which can occur only at isolated points in parameter space, and thus, the concurrence cannot be zero over a range of values of $P$. This behavior is unique to the intraparticle amplitude-damping channel and is in sharp contrast to that observed in the other channels, as shown later. For the other channels, all four eigenvalues of $R$ are, in general, nonzero, and thus, the concurrence can remain zero over a range of values of $P$ without exhibiting a revival.

The concurrence can go to 0 only when the condition in Equation 12 is satisfied. In Figure 2, one can observe three distinct evolutions of the concurrence represented by the blue, yellow, and green plots. These evolutions correspond to three different input states with state parameters that satisfy Equation 12. For other combinations of parameters, it can still have a minimum at a value $P\ne 1$. This is also a type of revival, although not from the value of 0. The condition for such a minimum to exist is $\cos \mathrm{\Delta }\theta \ge 0$ and $|\sin \mathrm{\Delta }\theta |\le 1/3$. Because the concurrence must go to zero at $P=1$ and is a smooth function of $P$, it must go through a maximum as well. The values of $P$ at which the minima and maxima occur ($P_{-}$ and $P_{+}$, respectively) are (Supplementary Material).

$\begin{array}{ll}\hfill P_{\pm }& =1-\frac{|a{|}^2|d{|}^2}{16|b{|}^2|c{|}^2}\left[3\cos \mathrm{\Delta }\theta \right.{\left.\mp \sqrt{{\left(3\cos \mathrm{\Delta }\theta \right)}^2-8}\right]}^2\hfill \end{array}(13)$

Figure 2

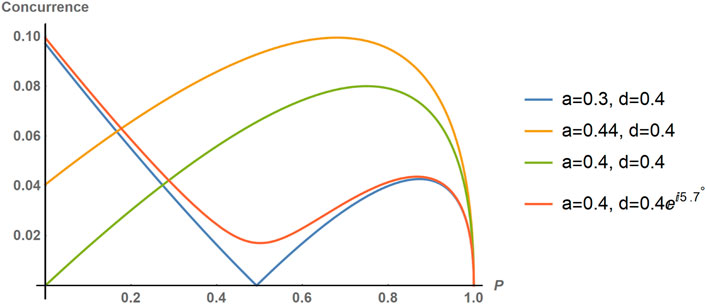
Figure 2. The variation of the concurrence with $P$ for three different input states with state parameters $|a|=0.3$, 0.44, and 0.4 are represented by the blue, yellow, and green plots, respectively. Other state parameters for these three input states are $|c|=0.2$, $|d|=0.4$, and $\mathrm{\Delta }\theta =0$. The variation of the concurrence with channel parameter $P$ for an input state with state parameters $|a|=0.3$, $|b|=0.84$, $|c|=0.2$, $d=0.4$, ${\theta }_a={\theta }_b={\theta }_c=0$, and ${\theta }_d=5.7°$ is represented by the red plot. The state representing the blue plot satisfies the condition (i) $|a\Vert d|<|b\Vert c|$, which first shows entanglement sudden death and then a rebirth of entanglement and finally asymptotically decays to 0. The value of $P$ where we observe the entanglement sudden death is given by Equation 12. The state representing the yellow plot satisfies the condition (ii) $|a\Vert d|>|b\Vert c|$, which first shows the creation of entanglement and finally asymptotically decays to 0. The state representing the green plot is initially a separable state satisfying the condition (iii) $|a\Vert d|=|b\Vert c|$, and with the increase of $P$, the concurrence first becomes nonzero and gradually increases and finally asymptotically decreases to 0. In the cases (i), (ii), and (iii), $\mathrm{\Delta }\theta =0$. If we make ${\theta }_d=5.7°$ while ${\theta }_a={\theta }_b={\theta }_c=0$, that is, $\mathrm{\Delta }\theta \ne 0\pm 2\pi$, then we observe that the concurrence reaches its minimum nonzero value $C_{-}$ and then a maximum values $C_{+}$ and finally asymptotically decays to 0.

With $P_{+}>P_{-}$ as expected. The corresponding minimum and maximum values ($C_{-}$ and $C_{+}$, respectively) of the concurrence are (Supplementary Material)

$\begin{array}{ll}\hfill C_{\pm }& =\frac{|a{|}^2|d{|}^2}{2\sqrt{3}|b\Vert c|}\left[1-\frac{1}{16}\left\{3\cos \mathrm{\Delta }\theta \right.\right.\hfill \\ \hfill & {\left.{\left.\mp \sqrt{{\left(3\cos \mathrm{\Delta }\theta \right)}^2-8}\right\}}^2\right]}^{1/2}\times \left[3\cos \mathrm{\Delta }\theta \mp \sqrt{{\left(3\cos \mathrm{\Delta }\theta \right)}^2-8}\right]\hfill \end{array}(14)$

In Figure 2, the red plot illustrates the evolution of the concurrence for an intraparticle entangled state with state parameters that do not conform to Equation 12, that is, $\mathrm{\Delta }\theta \ne 0,\pm 2\pi$. The non-monotonic behavior of the concurrence as a function of $P$ is special to the amplitude-damping channel and can be quantified by $\tilde{C}=\frac{C_{+}-C_{-}}{C_{+}+C_{-}}$. This can be taken to be a measure of the effectiveness of the channel in terms of reviving the concurrence. $\tilde{C}$ is a maximum when $\mathrm{\Delta }\theta =0,\pm 2\pi$. The behavior of $\tilde{C}$ with $\mathrm{\Delta }\theta$ is shown in Figure 3. The Figure 3 shows that $\tilde{C}$ is maximum at $\mathrm{\Delta }\theta =0$ and decreases with the increase of $\mathrm{\Delta }\theta$. $\tilde{C}=0$ at $\mathrm{\Delta }\theta ={\cos }^{-1}\frac{2\sqrt{2}}{3}=19.47°$.

Figure 3

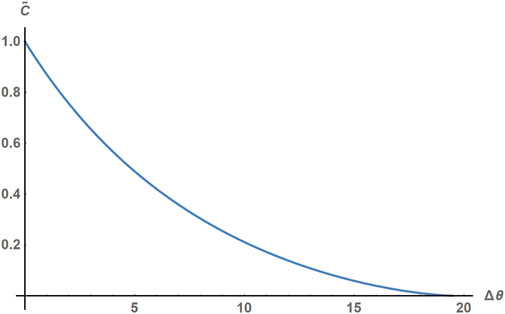
Figure 3. Variation of $\tilde{C}$ with $\mathrm{\Delta }\theta$ under the effect of the amplitude-damping channel. Here $\tilde{C}$ is maximum at $\mathrm{\Delta }\theta =0$. With the increase of $\mathrm{\Delta }\theta$, $\tilde{C}$ gradually decreases and becomes zero at $\mathrm{\Delta }\theta =19.47°$.

Interparticle entanglement: Next, for the sake of comparison, we consider the decoherence of an interparticle entangled state $|{\psi \rangle }_{in}$ due to the amplitude-damping channel. The two particles $A$ and $B$ are assumed to have individual two-dimensional Hilbert spaces and are spatially well separated. The environment is assumed to act on each particle locally and identically. Each of the Kraus operators for the system is thus a tensor product of the local Kraus operators for each particle. The local Kraus operators are (Salles et al., 2008).

$M_0=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \sqrt{1-P}\hfill \end{array}\right),M_1=\left(\begin{array}{cc}\hfill 0\hfill & \hfill \sqrt{P}\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)(15)$

We consider a pure input state that has the same form as in Equation 1. The concurrence of the output state is

$\begin{array}{l}C=max\left[0,\sqrt{\alpha +\beta }-\sqrt{\alpha -\beta }-2d^{2}P\left(1-P\right)\right]\hfill \end{array}(16)$

where

$\begin{array}{ll}\hfill \alpha & =2{\left(ad-bc\right)}^2{\left(1-P\right)}^2+d^4{P}^2{\left(1-P\right)}^2,\hfill \\ \hfill \beta & =2{\left(ad-bc\right)}^2{\left(1-P\right)}^2\sqrt{1-\frac{d^4}{{\left(ad-bc\right)}^2}{P}^2}\hfill \end{array}(17)$

where $P$ is the channel parameter. The effect of interparticle amplitude damping is quite distinct from that of intraparticle damping. Because no local operator can create entanglement (Bennett et al., 1996; Vidal, 2000), an initially unentangled state continues to remain unentangled under the effect of an interparticle amplitude-damping channel. Furthermore, as shown in Figure 4, if the concurrence goes to zero at $P<1$, it does not exhibit a revival. Mathematically, this is related to all four eigenvalues of the matrix $R$ generically being nonzero, as remarked earlier. Furthermore, the concurrence does not appear to exhibit a minimum and always decreases monotonically, showing that increasing the level of damping has a deleterious effect on the concurrence.

Figure 4

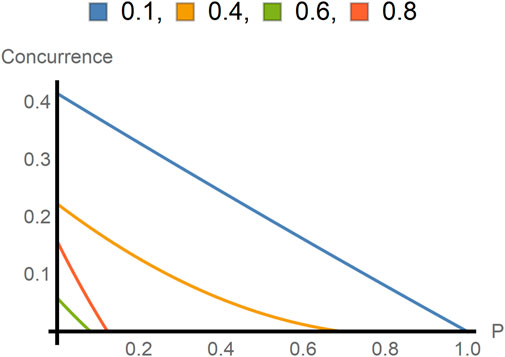
Figure 4. In this figure, the concurrence is plotted as a function of $P$ for four different interparticle entangled states with input state parameter $d=0.1,0.4,0.6$, and 0.8. For these four states, other input state parameters are $a=c=\frac{1}{4}$.

Next, we compare the concurrence of intraparticle and interparticle entangled states with the same coefficients $a$, $b$, $c$, and $d$. The results for representative values are shown in Figure 5. The intraparticle case displays a rebirth of entanglement, while the interparticle case does not, as remarked earlier. Lastly, it can be seen that the concurrence in the interparticle case is lower than in the interparticle case for the same channel strength, demonstrating that the former has suppressed quantum correlations more strongly than the latter.

Figure 5

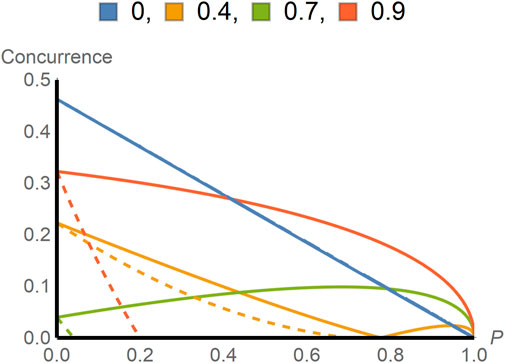
Figure 5. In this figure, the concurrences for intraparticle entangled states and interparticle entangled states are plotted as a function of $P$ for four different values of $d=0$, 0.4, $0.7$, and $0.9$. For these four states, other input state parameters are $a=c=\frac{1}{4}$. In the figure, solid curves represent the concurrence for intraparticle entangled states, while dashed curves represent the concurrence for interparticle entangled states. From the curve, it is clear that only intraparticle entanglement demonstrates rebirth and creation of entanglement.

Revival of interparticle entanglement is possible under special circumstances. Bellomo et al. (2007) showed a revival of interparticle entanglement under the non-Markovian dissipative amplitude-damping channel where the channel parameter takes a special form:

$P=e^{-\mathrm{\Gamma }t}{\left(\cos \left(\frac{dt}{2}\right)+\frac{\mathrm{\Gamma }}{d}\sin \left(\frac{dt}{2}\right)\right)}^2(18)$

where $d=\sqrt{2\gamma \mathrm{\Gamma }-{\mathrm{\Gamma }}^2}$ and $t$ is the time parameter. However, unlike the intraparticle case we consider, an initially unentangled state remains unentangled. The specific model of the channel parameter is required to get a revival of interparticle entanglement, while intraparticle entanglement can be revived without considering any specific model of the channel parameter. Thus, the revival of intraparticle entanglement under the amplitude-damping channel is model-independent, whereas the revival of interparticle entanglement can be observed only under specific model-dependent forms for the amplitude-damping channel.

There are interesting works in the literature (Braun, 2002; Hamdouni et al., 2006; Ficek and Tanaś, 2006; Sun et al., 2007) on the revival of interparticle entanglement under decoherence. If we look carefully, we notice that in those works, the environment is a very large dimensional quantum system. These cases are markedly different from our cases, where the dimension of the Hilbert space of the environment is comparable to the Hilbert space dimension of the system. In our case, the environment’s dimension is not large; it matches the system’s dimension, which is 4. Interestingly, with this 4-dimensional environment, we observe the rebirth of intraparticle entanglement after ESD and the initial creation of entanglement from a separable initial state.

3 Other damping channels

We have investigated the effect of the phase damping and the depolarizing channels separately on a pure intraparticle entangled state $|{\psi \rangle }_{in}$ described by Equation 1. A detailed investigation is given in the supplementary material. We do not observe any rebirth of intraparticle entanglement after entanglement sudden death or creation of intraparticle entanglement under these two damping channels. We have also calculated the decay of concurrence of a pure interparticle entangled state under the phase damping and depolarizing channels and have compared this result to the decay for an intraparticle entangled state. We find that the decay of interparticle entanglement is much faster than the decay of intraparticle entanglement for these channels, which is similar to the case of the amplitude-damping channel.

4 Future scope

In this study, we have conducted a theoretical examination of the decoherence behavior of a pure, generic intraparticle entangled state. Specifically, we analyzed how this state is affected by three different types of quantum noise channels: amplitude damping, phase damping, and depolarizing channels. It is important to note that our analysis is not tied to any particular physical implementation of an intraparticle entangled system. Instead, our findings are broadly applicable to any such system, regardless of the specific physical system details.

The focus of our theoretical analysis is to provide a general understanding of the decoherence mechanisms without being constrained by the peculiarities of a specific system. This generality allows our results to be versatile and widely applicable.

As a future scope, we can consider any physical system in which intraparticle states undergo decoherence and verify the results obtained for different damping channels. Our study aids in understanding the state parameters and in modeling experiments with reduced decoherence effects. This helps achieve intraparticle entangled states as an efficient resource, enabling researchers to design quantum systems more effectively, with minimal information loss, thereby ensuring the successful completion of quantum information tasks.

5 Concluding remarks

To conclude, we have studied the generation and decay of intraparticle entanglement under the amplitude-damping channel by calculating the concurrence. We obtain an exact analytical expression for the concurrence for an arbitrary initial pure state. The concurrence exhibits the interesting phenomenon of entanglement revival as a function of the damping parameter. We also calculate the concurrence as a function of the channel parameter for the more conventional case of interparticle entanglement and show that there is no revival of entanglement or, indeed, any non-monotonic dependence on the channel parameter. Thus, the intraparticle system displays the counterintuitive phenomenon of the growth of entanglement with increasing damping strength. We explain this in terms of the number of nonzero eigenvalues of the output density matrix. Furthermore, the entanglement decay is much greater for the interparticle than the intraparticle case for the same input state and channel parameter. We also study the effects of phase damping and the depolarizing channel for both the intraparticle and interparticle cases and find no evidence of entanglement revival in either. However, the decay of entanglement for comparable parameters is always greater for the interparticle case than the intraparticle case, consistent with our observations for the amplitude-damping channel. Thus, intraparticle entanglement is, in general, more robust than interparticle entanglement. While ESD and revival of entanglement after that are typically observed in systems coupled to very large environments, such as a common bath, our case is particularly interesting because the environment is a much smaller, four-dimensional system. Remarkably, even with this small environment, ESD and revival of intraparticle entanglement can still occur under the amplitude-damping channel. However, these phenomena are not observed for the phase damping and depolarizing channels.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

ASR: Validation, Formal analysis, Methodology, Investigation, Writing – review and editing, Writing – original draft. NC: Writing – review and editing, Methodology, Writing – original draft, Investigation. SM: Writing – original draft, Methodology, Validation. PP: methodology, Writing – original draft, Conceptualization. US: Funding acquisition, Writing – review and editing, Project administration, Writing – original draft, Supervision, Conceptualization, Validation, Investigation.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. US and ASR acknowledge partial support from the National Quantum Mission of DST. US and PKP acknowledge partial support from the DST-ITPAR grant IMT/Italy/ITPAR-IV/QP/2018/G. US acknowledges partial support provided by the Ministry of Electronics and Information Technology (MeitY), Government of India, under a grant for Centre for Excellence in Quantum Technologies with Ref. No. 4(7)/2020 – ITEA and QuEST-DST project Q-97 of the Government of India. SM acknowledges support from the QuEST-DST project Q-34 of the Govt. of India.

Acknowledgments

US and PKP acknowledge Dipankar Home, and PKP acknowledges Abhinash K Roy for many useful discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frqst.2025.1592872/full#supplementary-material

References

Adhikari, S., Home, D., Majumdar, A. S., Pan, A. K., Shenoy, H. A., and Srikanth, R. (2015). Toward secure communication using intra-particle entanglement. Quantum Inf. Process. 14, 1451–1468. doi:10.1007/s11128-015-0941-0

CrossRef Full Text | Google Scholar

Adhikari, S., Majumdar, A., Home, D., and Pan, A. (2010). Swapping path-spin intraparticle entanglement onto spin-spin interparticle entanglement. Europhys. Lett. 89, 10005. doi:10.1209/0295-5075/89/10005

CrossRef Full Text | Google Scholar

Almeida, M. P., de Melo, F., Hor-Meyll, M., Salles, A., Walborn, S., Ribeiro, P. S., et al. (2007). Environment-induced sudden death of entanglement. Science 316, 579–582. doi:10.1126/science.1139892

PubMed Abstract | CrossRef Full Text | Google Scholar

Aolita, L., De Melo, F., and Davidovich, L. (2015). Open-system dynamics of entanglement: a key issues review. Rep. Prog. Phys. 78, 042001. doi:10.1088/0034-4885/78/4/042001

PubMed Abstract | CrossRef Full Text | Google Scholar

Azzini, S., Mazzucchi, S., Moretti, V., Pastorello, D., and Pavesi, L. (2020). Single-particle entanglement. Adv. Quantum Technol. 3, 2000014. doi:10.1002/qute.202000014

CrossRef Full Text | Google Scholar

Barreiro, J. T., Langford, N. K., Peters, N. A., and Kwiat, P. G. (2005). Generation of hyperentangled photon pairs. Phys. Rev. Lett. 95, 260501. doi:10.1103/PhysRevLett.95.260501

PubMed Abstract | CrossRef Full Text | Google Scholar

Basu, S., Bandyopadhyay, S., Kar, G., and Home, D. (2001). Bell’s inequality for a single spin-1/2 particle and quantum contextuality. Phys. Lett. A 279, 281–286. doi:10.1016/S0375-9601(00)00747-7

CrossRef Full Text | Google Scholar

Bellomo, B., Lo Franco, R., and Compagno, G. (2007). Non-markovian effects on the dynamics of entanglement. Phys. Rev. Lett. 99, 160502. doi:10.1103/PhysRevLett.99.160502

PubMed Abstract | CrossRef Full Text | Google Scholar

Bellomo, B., Lo Franco, R., and Compagno, G. (2008). Entanglement dynamics of two independent qubits in environments with and without memory. Phys. Rev. A—Atomic, Mol. Opt. Phys. 77, 032342. doi:10.1103/PhysRevA.77.032342

CrossRef Full Text | Google Scholar

Benatti, F., Floreanini, R., and Marzolino, U. (2010). Entangling two unequal atoms through a common bath. Phys. Rev. A—Atomic, Mol. Opt. Phys. 81, 012105. doi:10.1103/PhysRevA.81.012105

CrossRef Full Text | Google Scholar

Benatti, F., Floreanini, R., and Piani, M. (2003). Environment induced entanglement in markovian dissipative dynamics. Phys. Rev. Lett. 91, 070402. doi:10.1103/PhysRevLett.91.070402

PubMed Abstract | CrossRef Full Text | Google Scholar

Bennett, C. H., DiVincenzo, D. P., Smolin, J. A., and Wootters, W. K. (1996). Mixed-state entanglement and quantum error correction. Phys. Rev. A 54, 3824–3851. doi:10.1103/PhysRevA.54.3824

PubMed Abstract | CrossRef Full Text | Google Scholar

Braun, D. (2002). Creation of entanglement by interaction with a common heat bath. Phys. Rev. Lett. 89, 277901. doi:10.1103/PhysRevLett.89.277901

PubMed Abstract | CrossRef Full Text | Google Scholar

D’Arrigo, A., Benenti, G., Falci, G., and Macchiavello, C. (2013). Classical and quantum capacities of a fully correlated amplitude damping channel. Phys. Rev. A—Atomic, Mol. Opt. Phys. 88, 042337. doi:10.1103/PhysRevA.88.042337

CrossRef Full Text | Google Scholar

D’Arrigo, A., Franco, R. L., Benenti, G., Paladino, E., and Falci, G. (2014). Recovering entanglement by local operations. Ann. Phys. 350, 211–224. doi:10.1016/j.aop.2014.07.021

CrossRef Full Text | Google Scholar

De Moraes, B. G., Cummings, A. W., and Roche, S. (2020). Emergence of intraparticle entanglement and time-varying violation of bell’s inequality in Dirac matter. Phys. Rev. B 102, 041403. doi:10.1103/PhysRevB.102.041403

CrossRef Full Text | Google Scholar

Dutta, A., Ryu, J., Laskowski, W., and Żukowski, M. (2016). Entanglement criteria for noise resistance of two-qudit states. Phys. Lett. A 380, 2191–2199. doi:10.1016/j.physleta.2016.04.043

CrossRef Full Text | Google Scholar

Ficek, Z. (2010). Quantum entanglement and disentanglement of multi-atom systems. Front. Phys. China 5, 26–81. doi:10.1007/s11467-009-0078-7

CrossRef Full Text | Google Scholar

Ficek, Z., and Tanaś, R. (2006). Dark periods and revivals of entanglement in a two-qubit system. Phys. Rev. A—Atomic, Mol. Opt. Phys. 74, 024304. doi:10.1103/PhysRevA.74.024304

CrossRef Full Text | Google Scholar

Fonseca, A. (2019). High-dimensional quantum teleportation under noisy environments. Phys. Rev. A 100, 062311. doi:10.1103/PhysRevA.100.062311

CrossRef Full Text | Google Scholar

Gadway, B., Galvez, E., and De Zela, F. (2008). Bell-inequality violations with single photons entangled in momentum and polarization. J. Phys. B Atomic, Mol. Opt. Phys. 42, 015503. doi:10.1088/0953-4075/42/1/015503

CrossRef Full Text | Google Scholar

Hamdouni, Y., Fannes, M., and Petruccione, F. (2006). Exact dynamics of a two-qubit system in a spin star environment. Phys. Rev. B—Condensed Matter Mater. Phys. 73, 245323. doi:10.1103/PhysRevB.73.245323

CrossRef Full Text | Google Scholar

Hasegawa, Y., Loidl, R., Badurek, G., Baron, M., and Rauch, H. (2003). Violation of a bell-like inequality in single-neutron interferometry. Nature 425, 45–48. doi:10.1038/nature01881

PubMed Abstract | CrossRef Full Text | Google Scholar

Heo, J., Hong, C.-H., Lim, J.-I., and Yang, H.-J. (2015a). Bidirectional quantum teleportation of unknown photons using path-polarization intra-particle hybrid entanglement and controlled-unitary gates via cross-kerr nonlinearity. Chin. Phys. B 24, 050304. doi:10.1088/1674-1056/24/5/050304

CrossRef Full Text | Google Scholar

Heo, J., Hong, C.-H., Lim, J.-I., and Yang, H.-J. (2015b). Simultaneous quantum transmission and teleportation of unknown photons using intra-and inter-particle entanglement controlled-not gates via cross-kerr nonlinearity and p-homodyne measurements. Int. J. Theor. Phys. 54, 2261–2277. doi:10.1007/s10773-014-2448-3

CrossRef Full Text | Google Scholar

Horodecki, R., Horodecki, P., Horodecki, M., and Horodecki, K. (2009). Quantum entanglement. Rev. Mod. Phys. 81, 865–942. doi:10.1103/RevModPhys.81.865

CrossRef Full Text | Google Scholar

Kraus, K., Böhm, A., Dollard, J. D., and Wootters, W. (1983). States, effects, and operations fundamental notions of quantum theory: lectures in mathematical physics at the university of Texas at austin. Springer. doi:10.1007/3-540-12732-1

CrossRef Full Text | Google Scholar

Mazzola, L., Maniscalco, S., Piilo, J., Suominen, K.-A., and Garraway, B. M. (2009). Sudden death and sudden birth of entanglement in common structured reservoirs. Phys. Rev. A—Atomic, Mol. Opt. Phys. 79, 042302. doi:10.1103/PhysRevA.79.042302

CrossRef Full Text | Google Scholar

Michler, M., Weinfurter, H., and Żukowski, M. (2000). Experiments towards falsification of noncontextual hidden variable theories. Phys. Rev. Lett. 84, 5457–5461. doi:10.1103/PhysRevLett.84.5457

PubMed Abstract | CrossRef Full Text | Google Scholar

Pramanik, T., Adhikari, S., Majumdar, A., Home, D., and Pan, A. K. (2010). Information transfer using a single particle path-spin hybrid entangled state. Phys. Lett. A 374, 1121–1125. doi:10.1016/j.physleta.2009.12.070

CrossRef Full Text | Google Scholar

Rao, D. B., Panigrahi, P., and Mitra, C. (2008). Teleportation in the presence of common bath decoherence at the transmitting station. Phys. Rev. A—Atomic, Mol. Opt. Phys. 78, 022336. doi:10.1103/PhysRevA.78.022336

CrossRef Full Text | Google Scholar

Salles, A., de Melo, F., Almeida, M., Hor-Meyll, M., Walborn, S., Souto Ribeiro, P., et al. (2008). Experimental investigation of the dynamics of entanglement: sudden death, complementarity, and continuous monitoring of the environment. Phys. Rev. A—Atomic, Mol. Opt. Phys. 78, 022322. doi:10.1103/PhysRevA.78.022322

CrossRef Full Text | Google Scholar

Shen, J., Kuhn, S. J., Dalgliesh, R. M., de Haan, V., Geerits, N., Irfan, A. A., et al. (2020). Unveiling contextual realities by microscopically entangling a neutron. Nat. Commun. 11, 930. s41467-020-14741-y. doi:10.1038/s41467-020-14741-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, Y., Wen, Q.-Y., and Yuan, Z. (2011). High-efficient quantum key distribution based on hybrid entanglement. Opt. Commun. 284, 527–530. doi:10.1016/j.optcom.2010.08.061

CrossRef Full Text | Google Scholar

Sun, Z., Wang, X., and Sun, C. (2007). Disentanglement in a quantum-critical environment. Phys. Rev. A—Atomic, Mol. Opt. Phys. 75, 062312. doi:10.1103/PhysRevA.75.062312

CrossRef Full Text | Google Scholar

Tong, Q.-J., An, J.-H., Luo, H.-G., and Oh, C. (2010). Mechanism of entanglement preservation. Phys. Rev. A—Atomic, Mol. Opt. Phys. 81, 052330. doi:10.1103/PhysRevA.81.052330

CrossRef Full Text | Google Scholar

Vidal, G. (2000). Entanglement monotones. J. Mod. Opt. 47, 355–376. doi:10.1080/09500340008244048

CrossRef Full Text | Google Scholar

Wootters, W. K. (1998). Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245–2248. doi:10.1103/PhysRevLett.80.2245

CrossRef Full Text | Google Scholar

Xu, J.-S., Li, C.-F., Gong, M., Zou, X.-B., Shi, C.-H., Chen, G., et al. (2010). Experimental demonstration of photonic entanglement collapse and revival. Phys. Rev. Lett. 104, 100502. doi:10.1103/PhysRevLett.104.100502

PubMed Abstract | CrossRef Full Text | Google Scholar

Yeo, Y., and Skeen, A. (2003). Time-correlated quantum amplitude-damping channel. Phys. Rev. A 67, 064301. doi:10.1103/PhysRevA.67.064301

CrossRef Full Text | Google Scholar

Yu, T., and Eberly, J. (2004). Finite-time disentanglement via spontaneous emission. Phys. Rev. Lett. 93, 140404. doi:10.1103/PhysRevLett.93.140404

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, T., and Eberly, J. (2009). Sudden death of entanglement. Science 323, 598–601. doi:10.1126/science.1167343

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, T., and Eberly, J. H. (2005). Evolution from entanglement to decoherence of bipartite mixed “x” states. arXiv preprint quant-ph/0503089

Google Scholar