Single-qubit multi-party transmission using universal symmetric quantum cloning

This study considers the hypothetical quantum network case where Alice wishes to transmit one qubit of information (specifically a pure quantum state) to $M$ parties, where $M$ is some large number. The remote receivers locally perform single-qubit quantum state tomography on the transmitted qubits in order to compute the quantum state within some error rate (dependent on the tomography technique and the number of transmitted qubits). We show that with the use of an intermediate optimal symmetric universal quantum cloning machine (between Alice and the remote receivers) as a repeater-type node in a hypothetical quantum network, Alice can send significantly fewer qubits compared to direct transmission of the message qubits to each of the $M$ remote receivers. This is possible due to two properties of quantum cloning. The first is that single qubit quantum clones retain the same Bloch angle as the initial quantum state. This means that if the mixed state of the quantum clone can be computed to high enough accuracy, the original pure quantum state can be inferred by extrapolating that vector to the surface of the Bloch sphere. The second property is that the state overlap of approximate quantum clones, with respect to the original pure quantum state, quickly converges (specifically for $1\to M$, the limit of the fidelity as M goes to infinity is $\frac{2}{3}$). This means that Alice can prepare a constant number of qubits (which are then passed through the quantum cloning machine) in order to achieve a desired error rate if $M$ is large enough. Combined, these two properties mean that for a large $M$, Alice can prepare many orders of magnitude fewer qubits in order to achieve the same single qubit transmission accuracy compared to the naive direct qubit transmission approach.

1 Introduction

Unknown quantum information cannot, in general, be cloned; this is a fundamental property of quantum mechanics (Wootters and Zurek, 1982; DGBJ, 1982). However, approximate quantum cloning is possible (Buž ek and Hillery, 1996). This study proposes that universal, symmetric, optimal quantum cloning machines can be used in a repeater-type quantum network in order to transmit single qubits to a large number ($M$) of remote receivers, where each remote receiver applies single-qubit quantum state tomography on the received qubits in order to compute what the mixed-density matrix state of the received quantum clones are, and then extrapolates what the original intended pure quantum state is (with some error rate). The proposed protocol is conceptually outlined in Figure 1. The use of qubits as the unit of transmitted information in this hypothetical protocol is motivated by the security given by the no-cloning theorem itself and thus is used in a standard single qubit quantum key distribution (Wootters and Zurek, 1982; DGBJ, 1982; Bennett and Brassard, 2014; Shor and Preskill, 2000; Renner et al., 2005; Christandl et al., 2004)—in this case, that measuring individual qubits that are being transmitted does not give sufficient information to fully reconstruct the original quantum state. Therefore in this hypothetical scenario, we also imagine that we wish to keep the information contained in the qubits used in this protocol secure as well. These single qubits transmitted in the proposed protocol have the same security inherent in quantum key distribution.

Figure 1

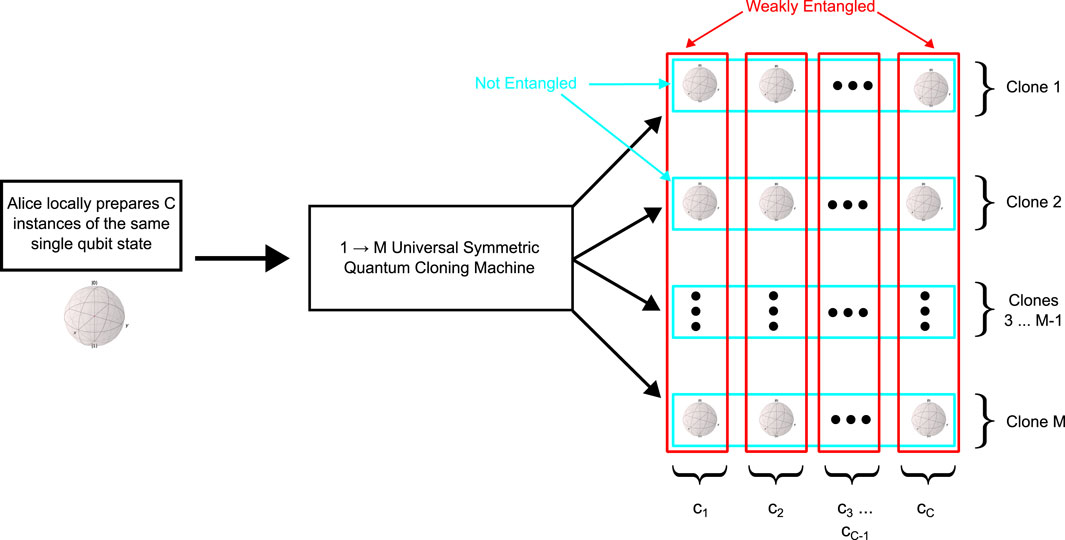
Figure 1. Qubit cloning network diagram, where the $1\to M$ universal symmetric quantum cloning machine acts like a repeater for producing multiple approximate quantum clones. Each qubit that is fed into the quantum cloning machine results in $M$ approximate quantum clones that are weakly entangled (denoted in red). Alice can send $C$ independent instances of the same qubit through this cloning process, resulting in $C$ approximate clones (that are not entangled) being produced for each of the $M$ hypothetical receivers. To simplify the protocol, we assume that there are $M$ remote receivers and that the symmetric universal quantum cloning machine produces $M$ quantum clones from a single input qubit. Only the group of clone qubits produced by each execution of the symmetric universal quantum cloning machine will produce qubits which are weakly entangled. This hypothetical protocol is also assumed to be noiseless, in the sense that this assumes no decoherence and no loss of qubits during transmission.

Since the initial $1\to 2$ quantum cloning was proposed (Buž ek and Hillery, 1996), it has been generalized to $N\to M$ quantum cloning (Gisin and Massar, 1997). There are many variants of approximate quantum cloning (Scarani et al., 2005; Fan et al., 2014; Murao et al., 1999; Fiurasek et al., 2005; Fan et al., 2003; Bruß et al., 2000; Durt et al., 2005; Fiurášek, 2001; Hardy and Song, 1999; Buzek and Hillery, 1998; Fan et al., 2001; Karimipour et al., 2002; van Loock and Braunstein, 2001; Iblis et al., 2005; Chefles and Barnett, 1999), and there have been numerous experimental demonstrations of variants of quantum cloning (Cummins et al., 2002; Liu et al., 2021; Chen et al., 2011; Nagali et al., 2010; Bouchard et al., 2017; Du et al., 2005; Pelofske, 2024; Pelofske, 2022; Pelofske et al., 2022). The primary characteristics that differentiate quantum cloning variants are as follows. Universal means that the cloning process is input-state-independent, and non-universal means that the cloning process is state-dependent. Symmetric means that all generated clones have the same quality, whereas non-symmetric means that the generated clones can be of different quality (e.g., distinguishable). Optimal quantum cloning means that the process produces clones which are of the highest quality possible within the laws of quantum mechanics; this bound in terms of quantum fidelity is given by Equation 1:

$F_{N\to M}=\frac{MN+M+N}{M\left(N+2\right)}.(1)$

Whereas typically in quantum networks, one of the central goals is to share entanglement using entanglement swapping (Shchukin and van Loock, 2022; Xu et al., 2017; Goebel et al., 2008; Bruschi et al., 2014; Zhao et al., 2010; Sangouard et al., 2008), there are a number of proposed algorithms that encode information into individual qubits, usually in the context of quantum machine learning (Pérez-Salinas, 2020; Thumwanit, 2021; Ambainis, 2009; Tapia et al., 2023). Therefore, it is conceivable that in a hypothetical future large-scale quantum network, one may wish to transmit a single qubit state to a large number of remote parties. We can imagine two potential cases where the proposed method could be used. The first is where the preparation of the single qubit state requires a non-insignificant amount of computing time, and therefore Alice wishes to reduce the total number of preparations (particularly to offload the computing time onto the quantum cloning process). The second is where a quantum cloning machine already has a direct networked connection to the intended recipients, and therefore it is easier for Alice to send qubits through the quantum cloning node in order to distribute the quantum information.

Accurately measuring which quantum state has been prepared, particularly on hardware experiments, is of considerable interest for quantum information processing. In particular, quantum state tomography of a single qubit (Roman, 2016) is the simplest of these types of tasks since there is not an exponential overhead that comes with larger system sizes. Therefore, this study strictly considers the case in which recipients measure the state of single qubits using quantum-state tomography. There are many methods for performing full quantum-state tomography, but in this case we use Pauli basis state tomography in all simulations. Geometrically, the factor by which the Bloch vector of an input message state in the Bloch sphere representation is shrunk when copied by an optimal universal symmetric quantum cloning process is given by

$\eta \left(N,M\right)=\frac{N}{M}\frac{M+2}{N+2},(2)$

(Scarani et al., 2005; Bruss et al., 1998; Bruß et al., 1998) (for a qubit, e.g., $d=2$).

For universal symmetric quantum cloning machines, there is a known optimal bound on the best quantum state fidelity that can be achieved for single-qubit clones. This bound is shown in Equation 1. The primary motivation of this proposed single-qubit distribution methodology is that ${\lim }_{M\to \infty }{F}_{1\to M}=\frac{2}{3}$. This fidelity convergence is plotted in Figure 2. Thus, the single-qubit clone quality is asymptotic, which means in particular that there are not diminishing returns as $M$ gets extremely large, in terms of error measures such as the state overlap between any one of the approximate quantum clones and the original message qubit. In this context, the property of quantum cloning machines that gives this asymptotic fidelity quality is that asymptotic quantum cloning (where the number of clones tends to infinity) is the same as direct quantum-state estimation (Bae and Acín, 2006; Yang and Chiribella, 2013). Quantum state estimation is the general task of learning information about a quantum state using measurements (Paris and Rehacek, 2004), and quantum state tomography is a specific type of quantum state estimation.

Figure 2

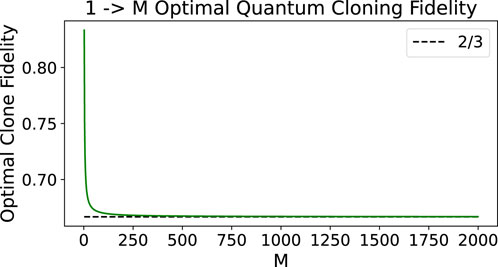
Figure 2. Ideal quantum clone fidelity (Equation 1) for $1\to M$ universal cloning as a function of $M$ for $M=2\dots 2000$.

Iqbal (2022) and Iqbal et al. (2023) studied similar concepts of using quantum cloning for qubit transmission but limited the number of clones to four; they did not use single-qubit quantum state tomography (QST) or geometric extrapolation to determine the intended pure quantum state. Wang and Cai (2018); Wang and Cai (2019) similarly studied using many qubit copies to transmit information but only examined making repeated quantum copies of classical bits; they did not extend the number of clones to large $M$.

2 Methods

In order to quantify how close the post-processed quantum clones are to the original pure quantum state, we measure the distance along the surface of the Bloch sphere between the extrapolated single qubit clone vector (since universal quantum cloning only shrinks the Bloch vector by a factor given in Equation 2, and does not change the angle of the vector) and the pure quantum state vector at the point at which they intersect the surface of the Bloch sphere. This error measure thus quantifies the geodesic distance along the Bloch sphere between two Bloch vectors. This measure is 0 when the two states are exactly the same and is a maximum of $\pi$ when the vectors point in opposite directions. The distance between the two points along the surface of the Bloch sphere is computed by $\arccos ({\rho }_x\cdot {\rho }_{{\text{clone}}_x}+{\rho }_y\cdot {\rho }_{{\text{clone}}_y}+{\rho }_z\cdot {\rho }_{{\text{clone}}_z})$, where ${\rho }_x,{\rho }_y,{\rho }_z$ are the x, y, z coordinates for the intersection point on the surface of the Bloch sphere for the pure quantum state, and ${\rho }_{{\text{clone}}_x},{\rho }_{{\text{clone}}_y},{\rho }_{{\text{clone}}_z}$ are the x, y, z coordinates for the intersection point of the extrapolated vector of the single-qubit clone density matrix. Due to numerical precision error, this term will occasionally be outside of $[-\mathrm{1,1}]$ making it undefined for $\arccos$, in which case the computed value is set to $-1$ or 1, respectively. The implementation of the numerical simulation protocol is specified with the goal of showing how relatively easy this protocol can be implemented conceptually. The difficulty of the proposed protocol is strictly due to the quantum information processing and quantum networking that would be required to actually physically implement it.

The extrapolation procedure we employ is to compute the coordinates of the mixed-state density matrix within the Bloch sphere and then compute the intersection of that Bloch vector with the surface of the Bloch sphere. The extrapolated Bloch vector intersection point with the Bloch sphere can be computed by solving the positive value of $t$ in ${(t\cdot x)}^2+{(t\cdot y)}^2+{(t\cdot z)}^2-1=0$, where $x$, $y$, and $z$ are the coordinates of the mixed state Bloch vector. The extrapolated $x,y,z$ coordinates are then given by $x\cdot t$, $y\cdot t$ and $z\cdot t$. This is easily computed over many numerical simulations using “sympy” (Meurer et al., 2017). The error of the extrapolated point can then be measured by the distance along the surface of the Bloch sphere, as described above, or can be measured by converting the coordinates into a density matrix form, and the state overlap with the message state can be measured. The second metric we will use to quantify the error rate of the single-qubit state tomography (both for the standard approach and the proposed quantum cloning approach) is the well-established quantum fidelity (Jozsa, 1994; Müller, 2023) metric, which measures the state overlap between two density matrices (Equation 3). A fidelity of 0 means there is no state overlap, and a fidelity of 1 means that the two states exactly overlap. The error rate will be reported as 1 minus the fidelity—for example, infidelity. The quantum fidelity measure, which is an overlap measure between two density matrices, is given as

$F\left({\rho }_1,{\rho }_2\right)=Tr{\left[\sqrt{\sqrt{{\rho }_1}{\rho }_2\sqrt{{\rho }_1}}\right]}^2.(3)$

The density matrix reconstruction was performed using a slightly modified version of Qiskit Ignis (Contributors, 2023), with the least squares parameter optimization performed using the Python 3 package “cvxopt” (Diamond and Boyd, 2016; Agra et al., 2018) which uses convex optimization (Agrawal et al., 2019; Agrawal and Boyd, 2020a; Agrawal, 2019; Agrawal and Boyd, 2020b) to perform maximum likelihood estimation (Smolin et al., 2012). Conversion formulas between density matrix representations and Bloch sphere coordinates are given in Supplementary Appendix S1. All simulations in this study assume no de-coherence of any of the quantum states during transmission (or any other part of the protocol) and assume in general ideal conditions—for example, we assume no qubit loss during transmission either. The only noise considered is shot noise (e.g., finite sampling effect).

Quantum fidelity is a standard quantum state overlap measure and therefore is most likely to be interpretable. However, the distance along the surface of the Bloch sphere provides a geometrical intuition which is very compatible with the notion of single-qubit quantum cloning, and therefore we report both error measures in this study.

2.1 Clone emulation

Single qubit clones of universal, symmetric, quantum cloning machines have well defined properties—namely, that the clones of quantum state correspond geometrically to the vector of the original state being shrunk by factor $\eta$ (Equation 2).

This means that for the purposes of analyzing unentangled sequences of single-qubit clones (e.g., the unentangled sequences described in Figure 1), the relevant quantum cloning procedure can be emulated by constructing a density matrix that describes the mixed state of the original pure quantum state, shrunk by $\eta$. Importantly, this involves only a single qubit, and thus classical simulations of the state are extremely rapid and can be executed for any $M$. This procedure is referred to as clone emulation in order to clarify that it does not produce a full set of $M$ quantum clones (which themselves form an entangled system) and is a limited but extremely useful tool for analyzing single-qubit quantum cloning in this proposed protocol. It should emphasized, however, that this cloning emulation is only a numerical simulation method that allows us to examine the expected error rates and overhead of this hypothetical networking protocol. If one were to implement this protocol, the full universal quantum cloning machine would need to implement a very large and complex unitary, thus generating $M$ weakly entangled clones. Exact statevector simulation of such a quantum cloning unitary for very a large $M$ is not feasible because of the exponentially growing computing time and memory cost of a full statevector simulation of quantum states.

In this study, $M$ is denoted simultaneously as the number of approximate quantum clones generated by the $1\to M$ cloning process and the number of remote clone receivers illustrated in Figure 1. Each of the $M$ clones that is produced given an input of a single original pure quantum single-qubit state is thus sent to exactly one (independent) remote receiver which then performs local operations and measurements. Additionally in all simulations, the same original message qubit is repeatedly transmitted to all $M$ parties so that a baseline of error rate metrics can be measured as other parameters are changed.

For all numerical simulations, a single qubit state is used since the cloning process is universal (state-independent). For the clone emulation procedure, 10,000 instances (for each number of shots) are executed instead of all $M$ instances. This only works because the cloning is symmetric (i.e., all quantum clones are identical) and because the remote receiver measurements are always from separate groups of clones (cyan boxes in Figure 1) and are therefore not entangled. Note that if we were interested in computing the full quantum state of a group of clones (e.g., the red boxes in Figure 1), the computational cost would be immense for a large $M$—in particular, this would require at least $M$ qubits with no or very few errors and for a significant number of quantum gates to be executed; see Pelofske (2024), Pelofske (2022), and Pelofske et al. (2022) for detailed circuit descriptions of quantum telecloning circuits, as an example. Alternatively, if the form of the cloning state density matrix was known, then it could be computed and sampled; however, this would require a matrix that has dimensions $2^M$ by $2^M$. For the scenario in Figure 1, it is not necessary that these full state simulations be performed in order to assess the transmission error rates that each remote receiver would experience. In particular, for universal and symmetric quantum cloning, the clone quality is significantly simplified, as single-qubit state tomography on approximate quantum clones can show what the resulting transmission accuracy would be (after single-qubit quantum state tomography and state reconstruction).

In order to verify that the clone emulation worked as expected, we performed simulations that compared classical simulations of quantum cloning circuits with the single qubit emulation. This comparison was made using parallel single-qubit quantum state tomography run using full statevector simulations of quantum cloning circuits in order to compute (ground-truth) clone quality. The quantum cloning circuits used to simulate this protocol are a variant of quantum cloning known as “quantum telecloning”; they are universal, symmetric, and optimal. The construction of these telecloning circuits is described in Pelofske (2024), Pelofske (2022), and Pelofske et al. (2022). Supplementary Appendix S1 shows an example of one of these circuits, described in the form of an explicit compiled quantum circuit diagram.

3 Results

Figure 3 verifies that the clone emulation procedure produces identical results, up to shot noise, compared with the full parallel single-qubit state tomography procedure. The full parallel single-qubit state tomography procedure was performed using the quantum telecloning circuits from Pelofske (2024), Pelofske (2022), and Pelofske et al. (2022).

Figure 3

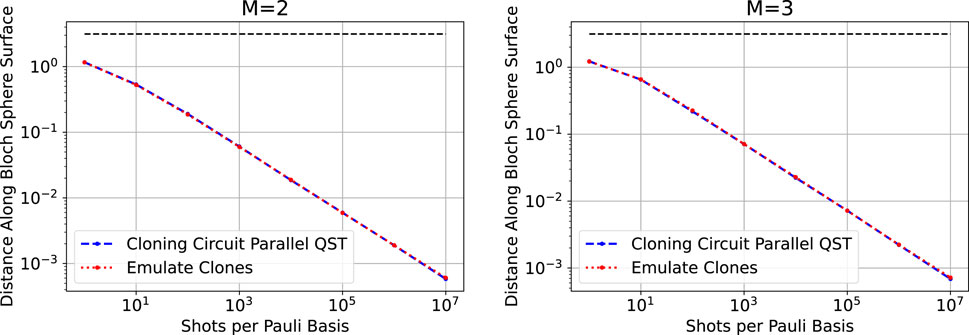
Figure 3. Comparison of single-qubit clone emulation against full quantum circuit parallel single-qubit state tomography for $M=2$ and $M=3$. For each point, the mean geodesic distance from the intended point on the Bloch sphere is plotted, averaged over 1,000 separate simulations ($3\cdot M\cdot 1000$ measurements were taken for both procedures for each point, although because the cloning is symmetric, these properties hold for any of the $M$ clones). The high agreement shown in these plots demonstrates that the clone emulation trick matches full (parallel measured) quantum state tomography of a small (example) universal quantum-cloning machine unitary, implemented as a quantum circuit. Data are plotted on a log–log scale axis.

Figure 4 compares direct single-qubit state tomography and extrapolated quantum state reconstruction from the approximate quantum clones. “Direct QST” refers to the procedure where Alice transmits the qubit to each of the $M$ recipients, repeated many times (plotted on the x-axis of Figure 4). The metrics used for this comparison are i) distance along the surface of the Bloch sphere (closer to 0 means lower error rate) and ii) $1-F$ (closer to 0 means lower error rate). As expected, because ${\lim }_{M\to \infty }{F}_{1\to M}=\frac{2}{3}$, there is an asymptote of the error rate of the reconstructed quantum states as $M$ gets large; $M=100$ and $M=10^6$ are effectively visually indistinguishable, which makes sense because all of the generated clones at this scale are approaching the same state overlap with the pure quantum state. The data in Figure 4 represent the mean error rate from 1,000 separate executions of quantum state tomography for each point on the x-axis. The emulated quantum clones are generated in batched simulations of 10,000 per parameter.

Figure 4

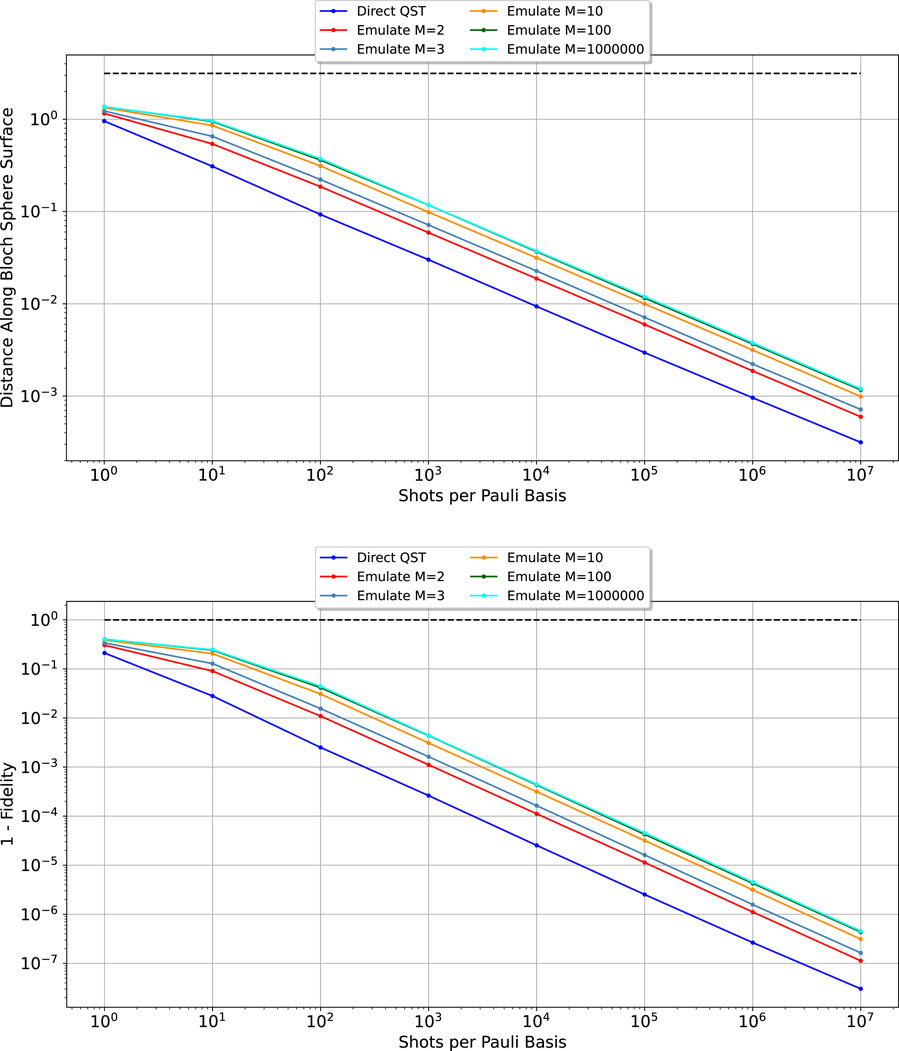
Figure 4. Comparison of direct quantum state tomography and quantum state tomography on single-qubit emulated clones, using the metric of mean distance along the Bloch sphere surface (top) and mean infidelity, which is 1 minus the standard-state overlap quantum fidelity measure (bottom). Both metrics quantify the error of the transmission protocol, when recipients measure using quantum state tomography; therefore, both error rate measures closer to 0 correspond to a lower error rate. Due to the convergence of the state overlap between the single qubit clones and the original state (Equation 1), for example, the error rates of $M=100$ and $M=10^6$ have converged to nearly identical values, resulting in those lines being visually nearly identical. This figure shows that as expected when transmitting single qubits, the direct qubit transmission (labeled “Direct QST”) gives the lowest error rate. The maximum error rates for both metrics are plotted as black horizontal dashed lines. Data are plotted on a log–log scale axis.

Figure 4 shows that the proposed protocol (Figure 1) provides a significant improvement over direct single-qubit transmission when $M$ is large (but when considering only single qubits, and particularly single clones of the original qubit, as expected, direct QST gives the lowest error rate). The tradeoff that this protocol proposes is to sacrifice some error rate in the small $M$ regime in order to make the total number of transmitted copies of that original qubit very large, and at very large $M$ we obtain a constant error rate (Figure 5). Note that because of the asymptotic clone quality, $M$ can be any large finite number. Figure 5 shows this asymptotic clone quality as $M$ becomes extremely large for both error metrics for a fixed number of shots. This shows that, for sufficiently large $M$, Alice can use a constant number of qubits (for a desired error rate) in order to transmit those qubits, via a symmetric universal quantum cloning machine, to $M$ remote receivers. Figure 4 shows that there is approximately an order of magnitude separation between the limiting behavior of the quantum cloning and the direct qubit transmission. In order to quantify this, we can measure the breakeven point between these two transmission methods.

Figure 5

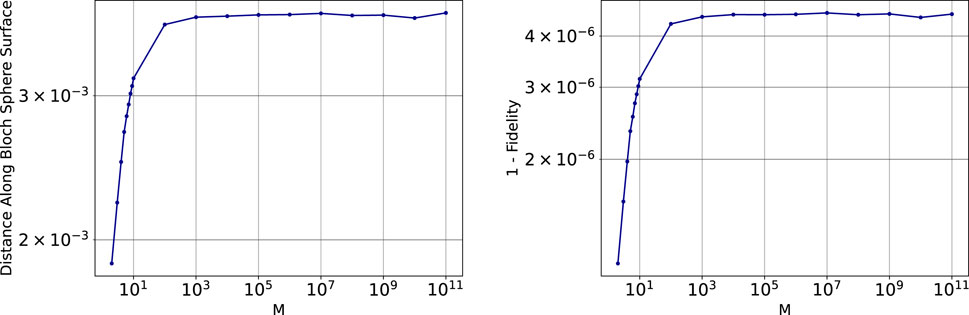
Figure 5. Average error rate (y-axis) as a function of $M$ when using $1\to M$ quantum cloning. Both the error rate metrics of quantum infidelity (right) and geodesic distance along the surface of the Bloch sphere between the two vectors (left) are shown. A fixed number of shots, $10^6$ (per Pauli basis, meaning $3\cdot 10^6$ in total), is used to estimate these error rates. These plots show a clear convergence of error rates while $M$ is increasing. Log–log scale axis.

The breakeven point is defined as the point where the two methods (the direct single qubit transmission and the proposed quantum cloning protocol) require the same number of message qubits to be prepared by Alice in order for the receiver error rate (for all $M$ receivers) to be the same. Figure 6 plots this breakeven point as a function of the error rate. The breakeven point for this range of error rates was computed using an interpolation between the datapoints in Figure 4.

Figure 6

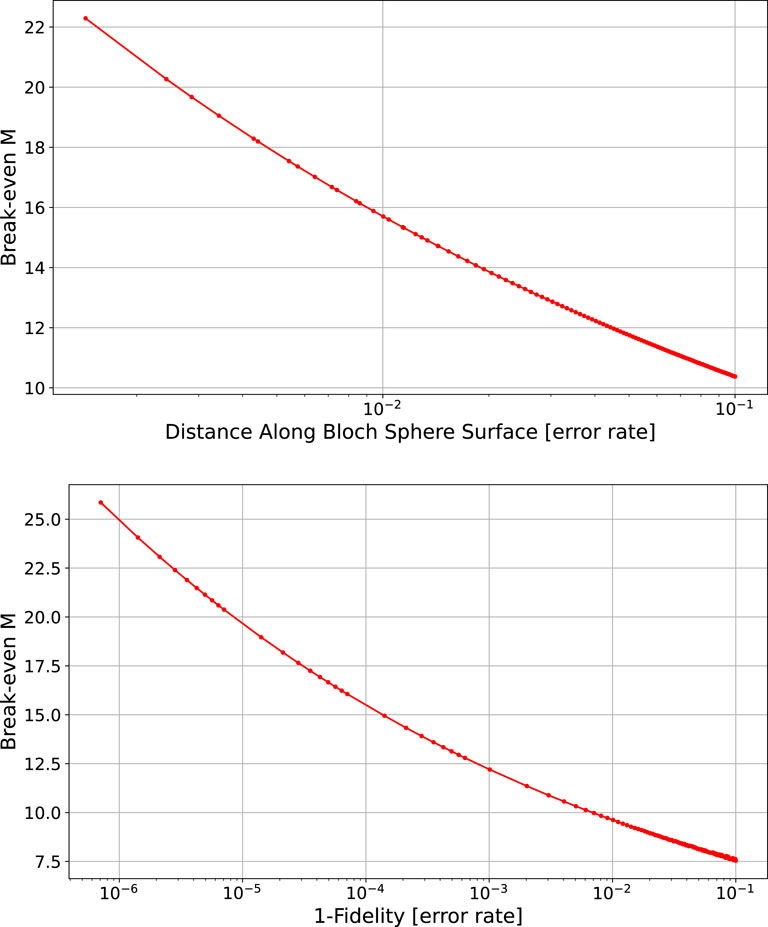
Figure 6. Average breakeven point in terms of $M$ (y-axis), as a function of the two error rate metrics (x-axis); distance along the surface of the Bloch sphere (top) and quantum infidelity (bottom). The breakeven point we define as the point where the two single qubit transmission methods require Alice to prepare the same number of message qubits in order for the transmission error rate to be equivalent (for all $M$ remote receivers) when the single qubit states are being measured using Pauli basis quantum-state tomography. X-axis is log scale.

For a desired error rate, if $M$ is greater than the break-even point in Figure 6, Alice must produce a constant number of message qubits (given by the error-dependent curve, approximated to high accuracy by the $M=100000$ curve in Figure 4) to be passed through the quantum cloning machine (Figure 1). In order for the direct single qubit transmission, without quantum cloning, to achieve the same error rate and throughput (e.g., sending the qubits to each of the $M$ remote receivers), Alice would need to prepare $M$ qubits per Pauli basis (in this case, three) for each sample shown by the x-axis of the blue Direct QST curve in Figure 4. This shows a clear and significant scaling advantage when using quantum cloning to perform this type of single-qubit transmission compared to direct qubit transmission without cloning.

Figure 6 contains three key observations. The first is that the scaling of the breakeven point as a function of $M$ is increasing—as the transmission error rate decreases, $M$ increases. This increase of $M$ is not significant (it reaches 25 in Figure 6), but a thorough analysis of this scaling for substantially smaller error rates is an interesting question for the future. Second, the breakeven point is similar but not identical for the two error metrics. Third, the breakeven point scaling, at least for the tested error rate range, is incredibly favorable to the proposed quantum cloning protocol. Thus, in order for Alice to see a reduction in the number of local qubit preparations, $M$ (the number of remote receivers) must be greater than 25. Importantly, as shown by the convergence of the transmission error rates for large $M$ in Figure 5, the number of qubits that Alice must prepare locally for any desired error rate (or better) is then constant for any larger value of $M$.

4 Discussion and conclusion

This study proposes a hypothetical use for a large scale universal symmetric quantum cloning machine in the context of transmitting a single qubit from a local sender Alice to a large number of remote receivers $M$ which receive multiple transmitted qubits and perform single qubit quantum state tomography in order to reconstruct the intended quantum state. We have shown that the use of a large-scale quantum cloning node in a hypothetical quantum network can significantly reduce the total number of qubits that Alice must prepare locally. This occurs when the transmitted qubits can be sent through a universal symmetric quantum cloning machine and when $M$ is sufficiently large (Figure 6). This method works due to two properties of optimal symmetric universal quantum cloning.

1. Single-qubit clones retain the same Bloch angle as the parent clone in the Bloch sphere representation; the loss of fidelity corresponds to a shrinking of the Bloch vector, making the clone a mixed quantum state when the original quantum state was pure. This means that given a sufficient number of samples of an approximate quantum clone generated from the same input quantum state, the original quantum state can be extrapolated by extending the computed mixed state Bloch vector to the surface of the Bloch sphere.

2. The state overlap (e.g., fidelity) of the clones generated by $1\to M$ quantum cloning quickly converges to $\frac{2}{3}$ in the limit as $M$ goes to infinity. There is thus a limit on the reduction of clone quality as $M$ becomes large.

The primary logical next question is the extent to which more general (universal, symmetric) $N\to M$ quantum cloning processes could be used in this type of quantum information distribution protocol since typically entangled states contain more interesting algorithmic information that one may wish to distribute over a quantum network. Specifically, the most important question is how the extrapolation procedure can be extended to entangled multi-qubit systems. It would be of interest to determine the extent to which entangled quantum states can be accounted for in this type of quantum cloning extrapolation protocol. This certainly should be possible, although the clear Bloch sphere geometric argument used in this paper would not easily extend to $N\ge 2$; most likely, an extrapolation method based purely on the density matrices would be necessary.

The emphasis of this study is to show proof-of-principle for a specific type of quantum networking protocol. Importantly, this type of protocol is far from currently feasible on real quantum computers or quantum networks; this study does not examine real world aspects that would certainly be relevant, such as timing. Quantifying how real world decoherence error rates, both for the transmission and for the preparation of the quantum cloning circuit, impact the reconstruction error is another important future question. Noise, particularly de-coherence, could both shrink the length of the Bloch vector as well as bias its angle. Nevertheless, the implementation shown here uses the real-world characterization protocol of quantum state tomography, thus showing that this could be algorithmically implemented if there was hardware that could perform these operations. It would need to be possible to obtain good low error rate state reconstruction despite very large numbers of clones being generated in total.

Although not investigated here, this proposed protocol could certainly also be applied to message qubits which are mixed states. However, this would cause the cloning fidelity to be even lower than it is when the message qubit is a pure quantum state, thus necessitating more copies to passed through the quantum cloning machine in order to achieve reasonably low error rate single-qubit state tomography for the receivers.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

EP: Methodology, Funding acquisition, Formal Analysis, Visualization, Software, Writing – review and editing, Data curation, Project administration, Validation, Conceptualization, Writing – original draft, Resources, Supervision, Investigation.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the U.S. Department of Energy through the Los Alamos National Laboratory. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (Contract No. 89233218CNA000001). Research presented in this article was supported by the NNSA’s Advanced Simulation and Computing Beyond Moore’s Law Program at Los Alamos National Laboratory.

Acknowledgments

This research used resources provided by the Darwin testbed at Los Alamos National Laboratory (LANL) which is funded by the Computational Systems and Software Environments subprogram of LANL’s Advanced Simulation and Computing program (NNSA/DOE). LANL report number LA-UR-23-31,425.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frqst.2025.1598893/full#supplementary-material

References

Agrawal, A. (2019). “Differentiable convex optimization layers,” in Advances in neural information processing systems, 9558–9570.

Google Scholar

Agrawal, A., and Boyd, S. (2020a). “Disciplined quasiconvex programming,” in Optimization letters.

Google Scholar

Agrawal, A., and Boyd, S. (2020b). Differentiating through log-log convex programs. arXiv, 12553. Available online at: https://arxiv.org/abs/2004.12553

Google Scholar

Agrawal, A., Diamond, S., and Boyd, S. (2019). Disciplined geometric programming. Optim. Lett. 13.5, 961–976. doi:10.1007/s11590-019-01422-z

CrossRef Full Text | Google Scholar

Agrawal, A., Verschueren, R., Diamond, S., and Boyd, S. (2018). A rewriting system for convex optimization problems. J. Control Decis. 5.1, 42–60. doi:10.1080/23307706.2017.1397554

CrossRef Full Text | Google Scholar

Ambainis, A. (2009). Quantum random access codes with shared randomness, 2937.

Google Scholar

Bae, J., and Acín, A. (2006). Asymptotic quantum cloning is state estimation. Phys. Rev. Lett. 97 (3), 030402. doi:10.1103/PhysRevLett.97.030402

PubMed Abstract | CrossRef Full Text | Google Scholar

Bennett, C. H., and Brassard, G. (2014). Quantum cryptography: public key distribution and coin tossing. Theor. Comput. Sci. 560, 7–11. doi:10.1016/j.tcs.2014.05.025

CrossRef Full Text | Google Scholar

Bouchard, F., Fickler, R., Boyd, R. W., and Karimi, E. (2017). High-dimensional quantum cloning and applications to quantum hacking. Sci. Adv. 3.2, e1601915. doi:10.1126/sciadv.1601915

PubMed Abstract | CrossRef Full Text | Google Scholar

Bruschi, D. E., Barlow, T. M., Razavi, M., and Beige, A. (2014). Repeat-until-success quantum repeaters. Phys. Rev. A 90 (3), 032306. doi:10.1103/PhysRevA.90.032306

CrossRef Full Text | Google Scholar

Bruss, D., Ekert, A., and Macchiavello, C. (1998). Optimal universal quantum cloning and state estimation. Phys. Rev. Lett. 81 (12 1998), 2598–2601. doi:10.1103/PhysRevLett.81.2598

CrossRef Full Text | Google Scholar

Bruß, D., Cinchetti, M., Mauro D’Ariano, G., and Macchiavello, C. (2000). Phase-covariant quantum cloning. Phys. Rev. A 62 (1), 012302. doi:10.1103/PhysRevA.62.012302

CrossRef Full Text | Google Scholar

Bruß, D., DiVincenzo, D. P., Ekert, A., Fuchs, C. A., Macchiavello, C., and Smolin, J. A. (1998). Optimal universal and state-dependent quantum cloning. Phys. Rev. A 57 (4), 2368–2378. doi:10.1103/PhysRevA.57.2368

CrossRef Full Text | Google Scholar

Buž ek, V., and Hillery, M. (1996). Quantum copying: beyond the no-cloning theorem. Phys. Rev. A 54 (3), 1844–1852. doi:10.1103/physreva.54.1844

PubMed Abstract | CrossRef Full Text | Google Scholar

Buzek, V., and Hillery, M. (1998). Universal optimal cloning of qubits and quantum registers. doi:10.1103/PhysRevLett.81.5003

CrossRef Full Text | Google Scholar

Chefles, A., and Barnett, S. M. (1999). Strategies and networks for state-dependent quantum cloning. Phys. Rev. A 60 (1), 136–144. doi:10.1103/PhysRevA.60.136

CrossRef Full Text | Google Scholar

Chen, H., Lu, D., Chong, B., Qin, G., Zhou, X., Peng, X., et al. (2011). Experimental demonstration of probabilistic quantum cloning. Phys. Rev. Lett. 106 (18), 180404. doi:10.1103/PhysRevLett.106.180404

PubMed Abstract | CrossRef Full Text | Google Scholar

Christandl, M., Renner, R., and Ekert, A. (2004). A generic security proof for quantum key distribution. Available online at: https://arxiv.org/abs/quant-ph/0402131.

Google Scholar

Contributors, Q. (2023). Qiskit: an open-source framework for quantum computing. doi:10.5281/zenodo.2573505

CrossRef Full Text | Google Scholar

Cummins, H. K., Jones, C., Furze, A., Soffe, N. F., Mosca, M., Peach, J. M., et al. (2002). Approximate quantum cloning with nuclear magnetic resonance. Phys. Rev. Lett. 88 (18), 187901. doi:10.1103/PhysRevLett.88.187901

PubMed Abstract | CrossRef Full Text | Google Scholar

Dgbj, D. (1982). Communication by EPR devices. Phys. Lett. A 92 (6), 271–272. doi:10.1016/0375-9601(82)90084-6

CrossRef Full Text | Google Scholar

Diamond, S., and Boyd, S. (2016). CVXPY: a Python-embedded modeling language for convex optimization. J. Mach. Learn. Res. 17.83, 83–85.

PubMed Abstract | Google Scholar

Du, J., Durt, T., Zou, P., Li, H., Kwek, L. C., Lai, C. H., et al. (2005). Experimental quantum cloning with prior partial information. Phys. Rev. Lett. 94 (4), 040505. doi:10.1103/PhysRevLett.94.040505

PubMed Abstract | CrossRef Full Text | Google Scholar

Durt, T., Fiurášek, J. r, and Cerf, N. J. (2005). Economical quantum cloning in any dimension. Phys. Rev. A 72, 5. doi:10.1103/physreva.72.052322

CrossRef Full Text | Google Scholar

Fan, H., Imai, H., Matsumoto, K., and Wang, X. B. (2003). Phase-covariant quantum cloning of qudits. Phys. Rev. A 67 (2), 022317. doi:10.1103/PhysRevA.67.022317

CrossRef Full Text | Google Scholar

Fan, H., Matsumoto, K., Wang, X. B., and Wadati, M. (2001). Quantum cloning machines for equatorial qubits. Phys. Rev. A 65 (1), 012304. doi:10.1103/PhysRevA.65.012304

CrossRef Full Text | Google Scholar

Fan, H., Wang, Y. N., Jing, L., Yue, J. D., Shi, H. D., Zhang, Y. L., et al. (2014). Quantum cloning machines and the applications. Phys. Rep. 544.3, 241–322. doi:10.1016/j.physrep.2014.06.004

CrossRef Full Text | Google Scholar

Fiurasek, J., Filip, R., and Cerf, N. J. (2005). Highly asymmetric quantum cloning in arbitrary dimension.

Google Scholar

Fiurášek, J. R (2001). Optical implementation of continuous-variable quantum cloning machines. Phys. Rev. Lett. 86 (21), 4942–4945. doi:10.1103/physrevlett.86.4942

PubMed Abstract | CrossRef Full Text | Google Scholar

Gisin, N., and Massar, S. (1997). Optimal quantum cloning machines. Phys. Rev. Lett. 79 (11 1997), 2153–2156. doi:10.1103/PhysRevLett.79.2153

CrossRef Full Text | Google Scholar

Goebel, A. M., Wagenknecht, C., Zhang, Q., Chen, Y. A., Chen, K., Schmiedmayer, J., et al. (2008). Multistage entanglement swapping. Phys. Rev. Lett. 101 (8), 080403. doi:10.1103/PhysRevLett.101.080403

PubMed Abstract | CrossRef Full Text | Google Scholar

Hardy, L., and Song, D. D. (1999). No signalling and probabilistic quantum cloning. Phys. Lett. A 259 (5), 331–333. doi:10.1016/s0375-9601(99)00448-x

CrossRef Full Text | Google Scholar

Iblisdir, S., Acín, A., Cerf, N. J., Filip, R., Fiurášek, J., and Gisin, N. (2005). Multipartite asymmetric quantum cloning. Phys. Rev. A 72 (4), 042328. doi:10.1103/PhysRevA.72.042328

CrossRef Full Text | Google Scholar

Iqbal, M. (2022). “Quantum bit retransmission using universal quantum copying machine,” in 2022 international conference on optical network design and modeling (ONDM), 1–3. doi:10.23919/ONDM54585.2022.9782866

CrossRef Full Text | Google Scholar

Iqbal, M., Velasco, L., Costa, N., Napoli, A., Pedro, J., and Ruiz, M. (2023). Investigating imperfect cloning for extending quantum communication capabilities. Sensors 23, 7891. doi:10.3390/s23187891

PubMed Abstract | CrossRef Full Text | Google Scholar

Jozsa, R. (1994). Fidelity for mixed quantum states. J. Mod. Opt. 41.12, 2315–2323. doi:10.1080/09500349414552171

CrossRef Full Text | Google Scholar

Karimipour, V., and Rezakhani, A. T. (2002). Generation of phase-covariant quantum cloning. Phys. Rev. A 66 (5), 052111. doi:10.1103/PhysRevA.66.052111

CrossRef Full Text | Google Scholar

Liu, S., Lou, Y., Chen, Y., and Jing, J. (2021). All-optical optimal N-to-M quantum cloning of coherent states. Phys. Rev. Lett. 126 (6), 060503. doi:10.1103/PhysRevLett.126.060503

PubMed Abstract | CrossRef Full Text | Google Scholar

Meurer, A., Smith, C. P., Paprocki, M., Čertík, O., Kirpichev, S. B., Rocklin, M., et al. (2017). SymPy: symbolic computing in Python. PeerJ Comput. Sci. 3, e103–e5992. doi:10.7717/peerj-cs.103

CrossRef Full Text | Google Scholar

Müller, A. (2023). A simplified expression for quantum fidelity.

Google Scholar

Murao, M., Jonathan, D., Plenio, M. B., and Vedral, V. (1999). Quantum telecloning and multiparticle entanglement. Phys. Rev. A 59 (1), 156–161. doi:10.1103/PhysRevA.59.156

CrossRef Full Text | Google Scholar

Nagali, E., Giovannini, D., Marrucci, L., Slussarenko, S., Santamato, E., and Sciarrino, F. (2010). Experimental optimal cloning of four-dimensional quantum states of photons. Phys. Rev. Lett. 105 (7), 073602. doi:10.1103/PhysRevLett.105.073602

PubMed Abstract | CrossRef Full Text | Google Scholar

Paris, M., and Rehacek, J. (2004). “Quantum state estimation,”, 649. Springer Science and Business Media.

Google Scholar

Pelofske, E. (2022). “Quantum telecloning on NISQ computers,” in 2022 IEEE international conference on quantum computing and engineering (QCE) (IEEE). doi:10.1109/qce53715.2022.00083

CrossRef Full Text | Google Scholar

Pelofske, E. (2024). Probing quantum telecloning on superconducting quantum processors. IEEE Trans. Quantum Eng. 5, 1–19. doi:10.1109/tqe.2024.3391654

CrossRef Full Text | Google Scholar

Pelofske, E., Bärtschi, A., and Eidenbenz, S. (2022). “Optimized telecloning circuits: theory and practice of nine NISQ clones,” in 2022 IEEE international conference on rebooting computing (ICRC) (IEEE). doi:10.1109/icrc57508.2022.00009

CrossRef Full Text | Google Scholar

Pérez-Salinas, A. (2020). “Data re-uploading for a universal quantum classifier,” in Quantum 4 (issn), 226, 2521–327X. doi:10.22331/q-2020-02-06-226

CrossRef Full Text | Google Scholar

Renner, R., Gisin, N., and Kraus, B. (2005). Information-theoretic security proof for quantum-key-distribution protocols. Phys. Rev. A 72 (1), 012332. doi:10.1103/PhysRevA.72.012332

CrossRef Full Text | Google Scholar

Roman, S. (2016). Quantum state tomography of a single qubit: comparison of methods. J. Mod. Opt. 63 (18), 1744–1758. doi:10.1080/09500340.2016.1142018

CrossRef Full Text | Google Scholar

Sangouard, N., Simon, C., Zhao, B., Chen, Y. A., de Riedmatten, H., Pan, J. W., et al. (2008). Robust and efficient quantum repeaters with atomic ensembles and linear optics. Phys. Rev. A 77 (6), 062301. doi:10.1103/PhysRevA.77.062301

CrossRef Full Text | Google Scholar

Scarani, V., Iblisdir, S., Gisin, N., and Acín, A. (2005). Quantum cloning. Rev. Mod. Phys. 77 (4), 1225–1256. doi:10.1103/revmodphys.77.1225

CrossRef Full Text | Google Scholar

Shchukin, E., and van Loock, P. (2022). Optimal entanglement swapping in quantum repeaters. Phys. Rev. Lett. 128 (15), 150502. doi:10.1103/PhysRevLett.128.150502

PubMed Abstract | CrossRef Full Text | Google Scholar

Shor, P. W., and Preskill, J. (2000). Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 85 (2), 441–444. doi:10.1103/physrevlett.85.441

PubMed Abstract | CrossRef Full Text | Google Scholar

Smolin, J. A., Gambetta, J. M., and Smith, G. (2012). Efficient method for computing the maximum-likelihood quantum state from measurements with additive Gaussian noise. Phys. Rev. Lett. 108, 070502. doi:10.1103/physrevlett.108.070502

PubMed Abstract | CrossRef Full Text | Google Scholar

Tapia, E. P. A, Scarpa, G., and Pozas-Kerstjens, A. (2023). A didactic approach to quantum machine learning with a single qubit. Phys. Scr. 98 (5), 054001. doi:10.1088/1402-4896/acc5b8

CrossRef Full Text | Google Scholar

Thumwanit, N. (2021). Trainable discrete feature embeddings for variational quantum classifier.

Google Scholar

van Loock, P., and Braunstein, S. L. (2001). Telecloning of continuous quantum variables. Phys. Rev. Lett. 87 (24 2001), 247901. doi:10.1103/PhysRevLett.87.247901

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, M., and Cai, Q. (2018). Filling the gap between quantum no-cloning and classical duplication. arXiv 1803.05602.

Google Scholar

Wang, M. H., and Cai, Q. (2019). Duplicating classical bits with universal quantum cloning machine. Sci. China Phys. Mech. and Astronomy 62, 30312–30315. doi:10.1007/s11433-018-9296-3

CrossRef Full Text | Google Scholar

Wootters, W. K., and Zurek, W. H. (1982). A single quantum cannot be cloned. Nature 299, 802–803. doi:10.1038/299802a0

CrossRef Full Text | Google Scholar

Xu, P., Yong, H. L., Chen, L. K., Liu, C., Xiang, T., Yao, X. C., et al. (2017). Two-hierarchy entanglement swapping for a linear optical quantum repeater. Phys. Rev. Lett. 119 (17), 170502. doi:10.1103/PhysRevLett.119.170502

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Y., and Chiribella, G. (2013). ““Is Global Asymptotic Cloning State Estimation?” en,” in Schloss Dagstuhl – Leibniz-Zentrum für Informatik. doi:10.4230/LIPICS.TQC.2013.220

CrossRef Full Text | Google Scholar

Zhao, Bo, Müller, M., Hammerer, K., and Zoller, P. (2010). Efficient quantum repeater based on deterministic Rydberg gates. Phys. Rev. A 81 (5), 052329. doi:10.1103/PhysRevA.81.052329

CrossRef Full Text | Google Scholar