- 1Department of Mathematics and Industrial Engineering, Polytechnique Montreal, Montreal, QC, Canada
- 2Department of Civil and Systems Engineering, Johns Hopkins University, Baltimore, MD, United States
- 3Energy Research Group, University of California, Berkeley, Berkeley, CA, United States
- 4College of Business Strayer University, Alexandria, VA, United States
- 5College of Development Studies Addis Ababa University, Addis Ababa, Ethiopia
- 6Department of Earth and Planetary Sciences, Johns Hopkins University, Baltimore, MD, United States
In response to global food price volatility and trends toward increased global food demand, Ethiopian policy makers were forced to adopt strategies such as restricting food exports in order to protect domestic food security. However, these policies can have a disproportionate regional impact on domestic markets and can result in lost revenue from exports. For this reason, they have been criticized as inefficient from the perspective of economic development. Here, we examine the sub-national dynamics of a ban on food exports. We do this for the case of Ethiopia's ban on exports of teff, a staple grain in the country that has increasing global demand. We assess the impact of the ban and of proposed policies to relax the ban, across regions within the country and for various market actors along the teff value chain. Using a partial-equilibrium model developed with a detailed modeling of the agro-economic features of the country, we analyze the direct impacts on export revenue, producers' profits, transport patterns, and consumption across the disaggregated regions in Ethiopia due to changes to its teff export policy. In particular, we show that the immediate benefit due to significant increase in international revenue due to large teff export would be enjoyed primarily by food distributors and storage operators while the crop producers' profits increase only negligibly. Simulations also indicate that lifting the export ban would be expected to have significant impacts on domestic transportation of teff between regions (for example from Mekelle to Werder), and to reduce consumption of teff significantly in some regions (for example, Semera, Jijiga), an effect due to the lack of competition in the transportation sector. The granularity of the model helps us capture the possibility of such lopsided benefits which were not captured in earlier studies.
Introduction
Ethiopia is an East African country with a population of about 105 million (Central Intelligence Agency, 2015; Central Statistical Agency of Ethiopia, 2016) and a GDP of 72 billion US dollars (Central Intelligence Agency, 2015). Over 70% of the labor force depends on agriculture for their livelihood (Central Intelligence Agency, 2015) and agriculture contributes to about 40% of the GDP of the country (Central Intelligence Agency, 2015). Moreover, about 60% of all Ethiopia's exports are generated from the agricultural sector (MIT, 2018). However, agriculture in Ethiopia is characterized by smallholder forming and is extremely sensitive to weather and climate variation. The recent 2015 and 2017 El Nino event, for example, led to drought across much of the country. Resulting crop and livestock losses led the government of Ethiopia to call for emergency assistance to over 18 million people, via a combination of domestic and international relief efforts (USAID, 2016). These impacts are consistent with Ethiopia's past sensitivity to climate shocks, which has motivated a number of studies on the agricultural impacts of climate variability in Ethiopia (Mccornick et al., 2008; Di Falco and Veronesi, 2012; Iizumi et al., 2014; Bakker et al., 2018) and other detailed strategies to combat food shortage (Wossen et al., 2016; Di Falco and Zoupanidou, 2017).
In addition to climatic shocks, the country's agriculture and food supply chain is not immune to other exogenous shocks. The 2008 global financial crises, which caused a worldwide food price hike, brought Ethiopian agricultural commodities into deep distress. Researchers deployed surveys to quantify the impact of the price hike in terms of changes in food consumption patterns and changes in nutrient intake (Alem and Söderbom, 2012; Kumar and Quisumbing, 2013). The adverse effect of such a global event motivated the Ethiopian government to implement an export ban on food grains, including teff, indefinitely.
Teff is a critical grain for Ethiopia. It is central to Ethiopian diets as it is the primary and preferred ingredient in Ethiopian bread (injera), and it has also shown significant potential since it is unique, has high nutrient content and is gluten free (Minten et al., 2018). The main goal of the export ban policy was to limit the upward pressure on domestic grain prices. A study analyzed the impacts of the ban on the country's macroeconomy under export ban policy scenarios (Woldie and Siddig, 2009). While predicting that the policy will indeed fulfill its goal of reducing domestic food prices, the study found that it comes at a cost of social welfare, quantified post facto at about $148 million. The government export ban policy was also studied extensively in Sharma (2011). In this study, the government's export ban policy was compared to similar policies in other countries and was criticized as a poorly designed restrictive measure. As a result, the authors suggest an alternative policy package for the government, including various tax regimes, price floors for exports, and government to government sales, among others. The study did not, however, perform an analysis of the welfare impacts of potential alternative policies.
While the existing literature quantifies the effects of global food prices and governmental policies on agricultural food commodities, to the best of our knowledge, there are few models that can analyze the distributed impacts of future policy changes across disaggregated regions under different policy scenarios. There are some mature partial-equilibrium models that can be used to understand the impact of agricultural policies at country scale, including the International Model for Policy Analysis for Agricultural Commodities and Trade (IMPACT) (Rosegrant et al., 2008; Robinson et al., 2015), rice outlook model (Wailes and Chavez, 2011) and world food model of agriculture (FAO, 1998), but these tools do not provide sub-national analysis in Ethiopia and most other small to mid-size countries. Further, a detailed analysis of the upstream, midstream and downstream domestic supply chain of teff, including historic variation in production, sensitivity of production, transportation and consumption and welfare effects is available from IFPRI (Minten et al., 2018).
In this paper, we address the direct impacts in regional teff markets, transport patterns, and market actors' profits across disaggregated regions in Ethiopia due to changes in the teff export ban policy. The specific focus on teff is motivated by the fact that teff has been predicted by researchers to become a new super-crop (Provost and Jobson, 2014; Crymes, 2015), with dramatically increased international demand. Our analysis complements the existing macroeconomic analyses (Woldie and Siddig, 2009; Sharma, 2011) in providing a detailed understanding of the regional effects of such policy changes within Ethiopia, along with comparing the effects of the policy change under potential shifts in the global demand curve.
Specifically, we address the following questions regarding potential relaxation or removal of teff export restrictions:
1. How do regional microeconomic market indicators change under different teff trade policy scenarios?
2. Which regions in the country are affected the most by a change in the teff export ban policy?
3. Which regional market actors are affected the most by a change in the teff export ban policy?
To answer these questions, we present an advanced integrated partial-equilibrium model, called the Distributed Extendible COmplementarity model (DECO). The model is an extension of the original DECO model introduced in Bakker et al. (2018) to model food systems. The model is a partial equilibrium model that represents the decision of multiple market actors, non-cooperatively maximizing their objective (typically profit or utility) with a detailed representation of the agro-economic properties of the regions in the country and the food markets therein. This detailed modeling enables us to present the regionalized effects of policy changes to the country's food markets. To distinguish this version of the model from that in Bakker et al. (2018), we refer to it as DECO2. In particular, the specific contributions of this paper in terms of modeling are:
1) Updating the production regions to coincide with government defined agro-climatic “adaptation zones” (Figure 1), as opposed to administrative regions in the original model. This allows us to represent production activities integrated with climate and soil characteristics, rather than arbitrary administrative regions.
2) Endogenously modeling transportation in the country by splitting the country into Thiessen polygons to account for both inter-regional and intra-regional trade
3) Incorporating more detailed water activities to integrate with climate variability, crop yield, and hydrological conditions.
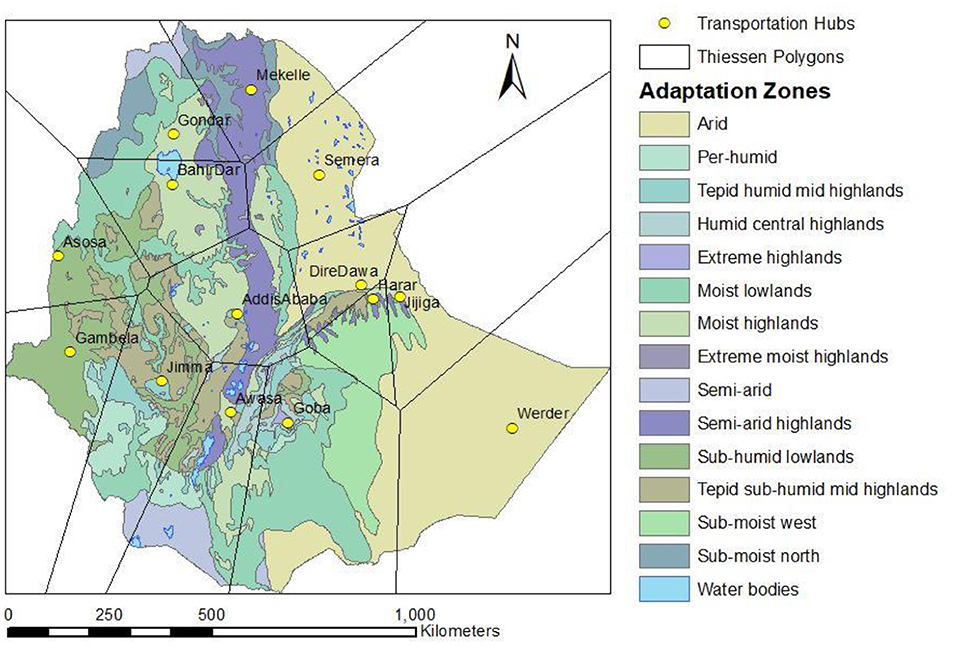
Figure 1. Adaptation zones of Ethiopia and regions centered around transportation hubs or food markets. Based on Deribew et al. (2015).
We apply the updated model to simulate several scenarios of teff export policies that potentially affect teff market dynamics within the country, and we compare the performance of different market actors under each of the scenarios. Such an analysis helps compare policy under various stimuli and identify quantifiable differences in regionalized benefits for different market actors such as producers as well as consumers. The rest of the paper is divided as follows. Section Model Description describes the features and the enhancements in the DECO2 model. Section Base Case Calibration and Scenarios presents the scenarios we analyze in detail and explains the methods employed in implementing these scenarios. Section Results contains results and analysis, and section Conclusions and Discussions includes conclusions and an assessment of limitations.
Model Description
Partial equilibrium models are useful tools for studying the effect of a policy change or other intervention on certain parts of the market. This approach allows one to understand the effect of policy changes at a disaggregated micro level, which is a feature of particular interest when studying food systems. DECO2 accordingly is an integrated partial-equilibrium model that is designed to simulate supply chains in the food market in Ethiopia. Since our model is a partial equilibrium model, we assume that most of the macroeconomic variables (i.e., population, GDP) are constant. Modelers follow this approach typically to capture more granular detail than general equilibrium models, which factor all macroeconomic variables but do not explicitly model regional markets and infrastructure. Partial-equilibrium models are more suited for analyzing localized changes under isolated shocks or scenarios, and not for projecting future macroeconomic trends. In DECO2, we compute the equilibrium resulting from the interaction of five types of aggregated market actors in the model, namely:
(i) Crop producers
(ii) Livestock raisers
(iii) Food distribution operators
(iv) Food storage operators or warehouses
(v) Consumers
Each market actor competitively maximizes their own objective under the assumption of perfect competition market structure. In the rest of the section, we formally describe the spatial disaggregation and time steps used in the model. Then we sequentially describe the role of each market actor in the model.
Spatial Disaggregation
We use two types of spatial disaggregation in the model, namely disaggregation by adaptation zone to represent production and consumption, and disaggregation by regions centered with selected transportation hubs to model regional food markets and transportation. From a modeling perspective, however, it is inappropriate to use politically delineated areas (for example, the administrative regions) that might not account for crop suitability, productivity, and the diverse Ethiopian climate zones with steep pluvial gradients. However, in Ethiopia, 14 adaptation zones divide the country into regions of similar climate patterns and soil fertility patterns, so that in our model, any crop will have a representative yield across a single adaptation zone. These zones have been defined by the government of Ethiopia as a framework for climate resilience efforts to boost production by allowing officials to design climatically-relevant adaptation strategies at scale, and to identify populations that might face elevated risk under climate change (Deribew et al., 2015), but given the dominance of smallholder subsistence agriculture in Ethiopia, and the idea that consumption preferences are dictated by what is grown in a particular region, we use the adaptation zones as the unit for modeling consumption as well.
However, the adaptation zones are not necessarily a contiguous stretch of land, and they can spread over long distances geographically. For this reason, we cannot use adaptation zones to model food transport. Therefore, we divide the country into regions surrounding 15 transportation hubs or food markets and assume that all transport occurs between pairs of these markets. The markets were chosen to ensure that they were both reasonably spread across the country and correspond to highly populated cities in the country. We use the markets as seeds to a Voronoi tessellation (Voronoi, 1908), such that the country is partitioned into Thiessen polygons, each which contains exactly one market (Figure 1). The Thiessen polygons have the property that the market contained in the polygon is the closest market to every point within the polygon (Voronoi, 1908). We assume that the aggregated crop producer in any adaptation zone sells in one or more markets proportionally based on the overlap between the adaptation zone and each market's Thiessen polygon. This indicates that the crop producers sell in the markets closest to them geographically.
Exports from Ethiopia are modeled by adding an external node to the collection of transportation hubs. The prices in the external node are set by global demand and supply for a food commodity. For teff, we draw the international price from (USDA Foreign Agricultural Service, 2013). We do not simulate demand-supply dynamics external to Ethiopia, and we also do not consider production outside of Ethiopia, which is a small but growing phenomenon. Any export from Ethiopia is sent to the external node and any import to Ethiopia comes in through the external node, which is connected to other nodes via the national capital, Addis Ababa.
Time Steps
DECO2 solves for equilibrium in semi-annual time steps, each step corresponding to a cropping season. We solve the model on a year-by-year basis to simulate the responses due to policy changes, without information about future years. Two additional years are solved in each iteration and then dropped to remove excessive model short-sight. We call this the rolling-horizon process and refer readers to Sethi and Sorger (1991) for a rigorous analysis of the approach.
Within each year, we explicitly model the two cropping seasons of Ethiopia. The meher season, which relies on the summertime kremt rains (primarily June-September), and the springtime belg season, which relies primarily on March-April rains. The meher season is the primary cropping season, in which more than 70% of all food is produced.
We now discuss the six market actors we model in DECO2. They are all profit maximizing market actors, aside from the consumer who maximizes utility. The model assumes a non-cooperative game played between the market actors under an assumption of perfect competition.
Crop Producers
We assume that the agricultural land in Ethiopia is used to produce either primary food crops or secondary food crops or cash crops. The primary food crops are teff, sorghum, barley, maize and wheat, the secondary food crops are pulses, vegetables and fruits, and the cash crops are coffee and oil seeds. The primary crops are grown in about 70% of the total cropping area while the secondary and cash crops are grown in roughly 20 and 10% of the total cropping area, respectively (Central Statistical Agency of Ethiopia, 2015). We assume that there is a representative aggregate crop producer in each adaptation zone who always makes a production decision subject to the limited farm land available. Factor inputs other than farm land in this model are assumed to be invariant over the period of analysis. Accordingly, the aggregate crop producer decides on the size of farm land allotted to each crop with the objective of maximizing profits. In the zone z, for the crop c, during the cropping season s of year y, the problem of the food producer can be written as:
subject to:
In this formulation, refers to the total quantity of crop c produced in the region z. The crop producer in this region sells to a distributor in node n which fetches a price of . refers to the cost of production per unit area.
The decision variables are the area that the crop producers allot for each crop in the adaptation zone. The crop producers make these decisions to maximize their profit, which is the difference between the revenue obtained by selling crops to distributors in different cities or nodes n, and the cost of production. We also include a penalty term which penalizes substantial changes in cropping patterns in consecutive years. This happens by subtracting a large value proportional to the difference in cropping patterns between consecutive years, from the objective (which the crop producer wants to maximize). For brevity, we have not detailed the precise form of the penalty term, but information can be found in the more formal set of equations in the Appendices. This approach mimics the real-life behavior of crop producers, who are reluctant to change cropping patterns drastically in response to single year fluctuations in climate.
The constraint in (2.1) ensures that the sum of areas allotted for each crop equals the total cropping area in each adaptation zone. The constraint in (2.2) connects the cropped area with the yield of the crop to get the crop producer's total production. The yield of a crop, 𝕐zcsy, is calculated using a crop yield model based on a Food and Agriculture Organization (FAO) approach described in Doorenbos and Kassam (1979) and Allen et al. (1998). In summary, using historical data, the model helps us predict the yield of crops (quintals per hectare) under various conditions affected by meteorology, irrigation patterns, soil properties, and crop characteristics. The meteorological inputs include daily maximum and minimum temperature, precipitation, humidity, wind, solar radiation, and cloud cover. For each growing season, this model outputs a yield factor. The yield factor ranges from 0 to 1, with 0 indicating total crop failure and 1 indicating no water stress.
The constraint (2.3) limits the proportion of the aggregated crop producer's production that goes to each transportation hub or node n from the adaptation zone z. Keep in mind that, given that the adaptation zones are just regions of similar agro-climatic features, these can be quite disconnected. Regions in different adaptation zones can be geographically clustered together while regions in the same adaptation zone can be scattered across the country. Hence the proportion Ψzn is decided by the percentage of area in the adaptation zone that is geographically closest to the node n. The price that the crop producer gets is the price a food distributor at node n is ready to pay for the crop c. We note that there is a single price, that arises as the shadow price for the market clearing constraint, for any crop at any node at any given time. By this principle, the price, , is called the market clearing price or the equilibrium price of the crop in the food market.
To avoid price discrimination and to align with the principles of perfect market competition, we assume that every producer produces an undifferentiated product, and both market actors (crop producers and distributors) have perfect information about the market structure. Finally, the quantities in parentheses at the end of each constraint are the dual variables corresponding to the constraints. They quantify the impact of the constraint to the optimization problem. In other words, this value is the proportional increase in the objective value for a marginal relaxation of the constraint.
Livestock Raisers
The livestock raiser is also a food producer like the aggregated crop producer. Livestock raisers produce beef and milk in quantities proportional to the number of cattle they raise. We do not attempt to model the climate sensitivity of livestock growth or survival rates in the current version of the model. However, if adverse climate conditions lead to a small crop yield and hence food scarcity, the livestock raiser might slaughter more cattle to raise beef production in a certain year to provide for the food demand. Livestock holdings are thus sensitive to climate via climate's impact on crops. Their optimization problem is shown below,
subject to:
In this formulation, refers to the quantity of cattle raised in a year and refers to the quantity of cattle slaughtered in the year. ξ refers to both beef and milk, the products obtained from cattle. The objective of the market actor is to maximize the difference between the revenue from selling milk and beef in various food markets indexed by n and the cost of raising cattle.
The constraint in (2.4) connects the number of cattle from 1 year to the next. The count varies due to both fertility and mortality of cattle, and due to slaughtering. The mortality rate is typically zero or a small number as the market actor generally slaughters the animal before it dies.
The constraint in (2.5) ensures that the market actor slaughters at least a certain number of cattle each year, without which they might die of natural causes. In contrast, the constraint in (2.6) ensures that the market actor does not slaughter too many animals, thus not being able to maintain the herd size they desire to have.
The next constraints (in 2.7 and 2.8) connect the quantity of milk with the number of animals alive and the quantity of beef with the number of animals slaughtered. Like the crop producer, the livestock raiser is also expected to sell the milk and beef they produce to various food markets in fixed proportion, based on geographical proximity. This is addressed by the constraint in (2.9). The prices in the formulation are the clearing prices obtained in the market. This is again similar to the food crops. We assume that the distributors and the storage operators do not differentiate between the food crops and the animal products in the model. We also assume that the quantity of agricultural and animal products produced is capable of meeting a market demand for food or a food consumption need. This simplification could be modified in future versions of the model.
Distributors and Warehouses
The distributor buys agricultural and animal products from crop producers and livestock raisers in the cities across the country. Each food market has a unique market clearing price for each crop and animal product that establishes the equilibrium quantity demand and supply between producers and distributors. There is always a possibility of excess stock in the distributors' store. Since we assumed a two-level price transmission, and to abide with the rule of perfect market competition, distributors transport any excess output (animal and crop) to other markets by bearing the costs of transportation, so that there is also a unique market clearing price that clears demand and supply between distributors and warehouses. Keeping in mind that there are different regions which preferentially grow different crops, and animals and that the consumption preference might not coincide with production, the distributors move the agricultural and animal products between the food markets in different cities. As a result, distributors transport from low demand area to high demand area taking advantage of the price differential between any two food markets while incurring the cost of transporting the goods. We fix the cost of transport as a function of time taken to travel in between cities and the distance between them. The warehouses in each city store agricultural and animal products from the distributor and store them, potentially across seasons, for sale to consumers. The warehouses incur a cost to store the food items through the period of storage.
Consumers
We assume homogeneous food consumption in each adaptation zone, since the large presence of subsistence-farming-type demand in the model means that consumer preferences are determined by what grows in a particular area. More precisely, we assume that preference for choice of food changes based on the regional production due to subsistence farming practices (Central Statistical Agency of Ethiopia, 2015), and hence assume a similar utility function of food for people in the same adaptation zone.
The utility function is constructed using the price elasticity (Tafere et al., 2010) of various crops across the country. People from the given adaptation zone, who exhibit similar preferences, might be forced to purchase food from different markets in different cities at different prices. Thus, the problem is modeled as follows.
subject to
Here Uzfsy(·) is the utility function of the consumers in the adaptation zone z given the consumed food f including both agricultural and animal products. is the actual quantity consumed in zone z while is the quantity consumed in zone z that is purchased from a warehouse in node n. The objective of a consumer is to maximize subjective utility under a budget constraint. The constraint shown there connects the total quantity consumed with the quantity purchased from each warehouse. Note that is not dependent on z, implying a single price for a crop in warehouses irrespective of the consumer. Again, these prices are shadow prices from market clearing equations between warehouses and consumers. Finally, for computational tractability, the utility functions have been assumed to be a concave quadratic function, a standard practice used in previous studies (Gabriel et al., 2012; Feijoo et al., 2016, 2019; Sankaranarayanan et al., 2018).
Market Clearing Conditions
Besides each market actor's optimization problem, we have the so-called market clearing conditions that are not a part of any market actor's optimization problem but connect the optimization problems of different market actors. They also have dual variables associated with them and they represent the equilibrium price of the corresponding food item in the market.
The price linkage is from Farmer (i.e., crop producer and livestock raiser)—Distributor—Warehouses—Consumer. Trade between a farmer and distributor is cleared at a price, . Trade between the distributor and warehouses is cleared at price . Trade between the warehouses and the consumers is cleared at price . These are the shadow prices for the market clearing constraints between each buyer-seller pair in the markets.
We have three sets of market clearing equations in DECO2.
The first conditions (2.11) ensures that the total quantity supplied by farmers (crop and animal products) in each market n equals the quantity demanded by distributors. The second condition (2.12) ensures that the quantity supplied by the distributor is equal to the quantity demanded by the storage operator in market n, and the third condition (2.13) ensures that the quantity supplied by the storage operator in market n is equal to the total quantity demanded by consumers in that market.
It is common to model spatial prices in Ethiopia assuming the central market hypothesis for Addis, given its large size and central role (Negassa and Jayne, 1997; Getnet et al., 2005; Tamru, 2013). The shadow prices resulting from the duals to equations (2.11)–(2.13) adhere well with this hypothesis as the food prices elsewhere in the country move up or down with the prices in Addis Ababa after accounting for transportation costs, a crucial factor for spatial price integration (Jaleta and Gebremedhin, 2012). This follows from the perfect competition assumption and the fact that the markets are all connected to Addis Ababa, the market with the highest volume.
The External Sector
In DECO2, food exports are represented by an external node that is connected to the national capital, Addis Ababa. The food distributor, under this setting, does not only transport food between the chosen set of cities in Ethiopia, but also to the external node. The external node allows us to account for global demand using a global demand curve, which can be informed by global price for a commodity and its elasticity. To model specific policy scenarios of export limits, this node also can have a consumption limit, which enables us to model caps on exports. The external node is export-only and does not allow for the possibility that teff produced elsewhere might be imported to Ethiopia. This is an accurate assumption under the current conditions.
Base Case Calibration And Scenarios
In this section we present the sources of data for our model and describe the simulation scenarios.
Crop Area and Yield
The area allotted for individual crops in both the meher and belg seasons in 2015 is available at the level of the administrative zone in the Ethiopian Central Statistics Agency's report on Area and Production of Major Crops (Central Statistical Agency of Ethiopia, 2015). There were 64 administrative zones in the country in 2015. The production data is aggregated at adaptation zone level. If an administrative zone is completely contained in an adaptation zone, all production in the zone is counted within the adaptation zone. However, if the boundary of an administrative zone cuts a zone into two (or more) parts, then the production is split into the two (or more) adaptation zones proportional to the area contained in each adaptation zone. Using the administrative zone-level data helps capture heterogeneity of cropping patterns and yield within a given administrative region, and attribute appropriate proportion of the yield to the right adaptation zone. As an example, let a region produce 100 units of a crop, and let the region be 30% highland and 70% lowlands. We do not attribute 30 and 70% of the production to the high and lowlands, respectively. Instead, suppose when we look at the more granular administrative zones, we observe that the 3 zones in the highland contribute to 60% of the production, the 3 zones in the lowland contribute to 30% of the production, and one zone which is partly in both the region contributes to 10% of the production. In that case we attribute 65% of the total production to the highlands and 35% of the total production to the lowlands.
Consumption
In the DECO2 model, the quantity demanded I assumed to be proportional to the population in each region. The data for population is obtained from the MIT atlas of Ethiopia (MIT, 2018). Further, the demand curve for each adaptation zone is derived as follows. Price elasticity of demand (e), which is defined as the percentage change in quantity consumption for a unit percentage change in price, is obtained from Tafere et al. (2010). The utility function mentioned in section Consumers is assumed to be a concave quadratic function of the form for some a and b. Thus, we obtain an inverse demand curve of the form π = a − bQ. This, along with the equation for price elasticity, , gives the parameters of the utility function as and . The national average price for each crop is obtained from Tafere et al. (2010) and assume the same price in each market for calibration purposes.
Transportation
Transportation is modeled between pairs of markets in Ethiopia and the markets are located in a chosen set of 15 market cities mentioned earlier. The distance between any pair of cities through roads is obtained from Google Inc (2018). The per-unit cost of transportation is proportional to the distance between markets and the travel time between markets, a standard practice in literature (Bakker et al., 2018). Given the transportation costs, supply, and demand, the transport between markets is endogenously determined by the model.
Scenarios
We are interested in comparing the regional changes in market indicators—namely, regional food transport, crop producers' profit, regional consumption, and prices within Ethiopia—due to teff-related governmental policies under typical as well as high future global demand. This requires an adequate granularity in the representation of the teff supply-chain infrastructure. To do this, we include detailed modeling of agricultural production area, yield, transport, markets, storage, and consumption for teff and major crops.
With respect to the cereal export ban policy, we are interested in how potential relaxation or removal of teff export restrictions would affect the regional microeconomic market indicators and which regions/market actors would be affected the most, given the following policy change scenarios:
1. When the government allows up to 200,000 quintals of teff export per year (or 100,000 quintals of teff export per season).
2. Same as 1, but with an upward shift in the global demand curve for teff (modeled as a 10% increase in the intercept of the demand curve).
3. When the government allows up to 2 million quintals of teff export each year (or 1 million quintals of teff export per season).
4. Same as 3, but with an upward shift in the global demand curve for teff (modeled as a 10% increase in the intercept of the global demand curve for teff).
5. When the government allows a fully free market for teff export.
Results
In this section, we will compare the regional outcomes within Ethiopia associated with different market actors under different scenarios of governmental policies and changes in global demand. First, we analyze how the change in the teff export policy changes the revenue of crop producers. We then compare the changes in domestic price of teff, followed by the changes in teff transport and domestic consumption pattern under each of these scenarios.
Changes in Crop Producers' Profit
Scholars who advocate for the removal of the teff export ban do so primarily on account of the lost international revenue from teff export (Bigman, 1985; Gilbert, 2012). The author in Crymes (2015), for example, assumes a direct increase in the revenue and hence the welfare of the crop producers due to increased international revenue.
While we do note that significant international revenue is lost due to the ban, we analyze the fraction of that revenue that would actually be expected to be enjoyed by the crop producers if the ban is lifted.
In our model the revenues generated from teff export range from 0 USD under a complete ban to 15 million USD and 160 million USD under 200,000 quintal per annum export case and 2 million quintal per annum export case, respectively. To put these figures in context, these revenues represent approximately 1 and 5% of total domestic teff sales in Ethiopia, respectively. They are also significant relative to current agricultural exports from Ethiopia, as non-coffee agricultural products currently amount to $675 million per annum (MIT, 2018); that is, for the 2 million quintal export case, teff exports would add nearly 24% to total non-coffee export revenue [For further context, Ethiopia's coffee export revenue is $712 million per annum (MIT, 2018), and its total annual export revenue for all products is $2.2 billion (MIT, 2018)].
In our simulations, however, hardly any benefit from these revenues actually reaches the crop producer. We notice, as shown in Figure 2A, that the increase in crop producers' profit remains relatively small (not more than 10 million USD) compared to the added total export revenue due to release of the export ban under any of these scenarios. We also observe that the primary effect is for producers in the adaptation zone of moist highlands (M3), where teff is primarily grown as shown in Figure 2B. Geographically, this corresponds to the regions of Amhara and Oromia primarily where a more evident increase in the revenue is observed as shown in Figure 2C. The additional inflow of money from the export is enjoyed almost exclusively by the distributors and storage operators. So, unless a crop producer is a large-scale market actor who can afford to do their own distribution of production across the country or outside, the increase in their profit is marginal. We observe this effect because any increase in domestic price due to increased foreign demand does not filter through the teff distribution chain to affect the price paid to crop producers. This is again observed in Figure 2D where the consumer price and export price of teff fluctuates over different scenarios, but the producer price, i.e., the price paid by the distributor to the producer, does not vary too much. We emphasize that this is not an inherent outcome of a policy to increase exports. It is, rather, a product of poor transportation infrastructure and immature distribution markets—represented in the model by the lack of competition in distributors—that allow the aggregated distributor to accrue profits associated with higher market prices, without sharing these benefits with the producers. This highlights the critical role of distribution markets, and the infrastructure required to support distribution, in the efficacy of any policy intended to benefit rural food producers through increased demand. In particular, this is seen when surplus is diverted to export if demand regions are distant from supply regions. The result is consistent with Chapter 6 of Minten et al. (2018), which shows extensive evidence that inefficiencies in transportation significantly impact the spatial price of teff.
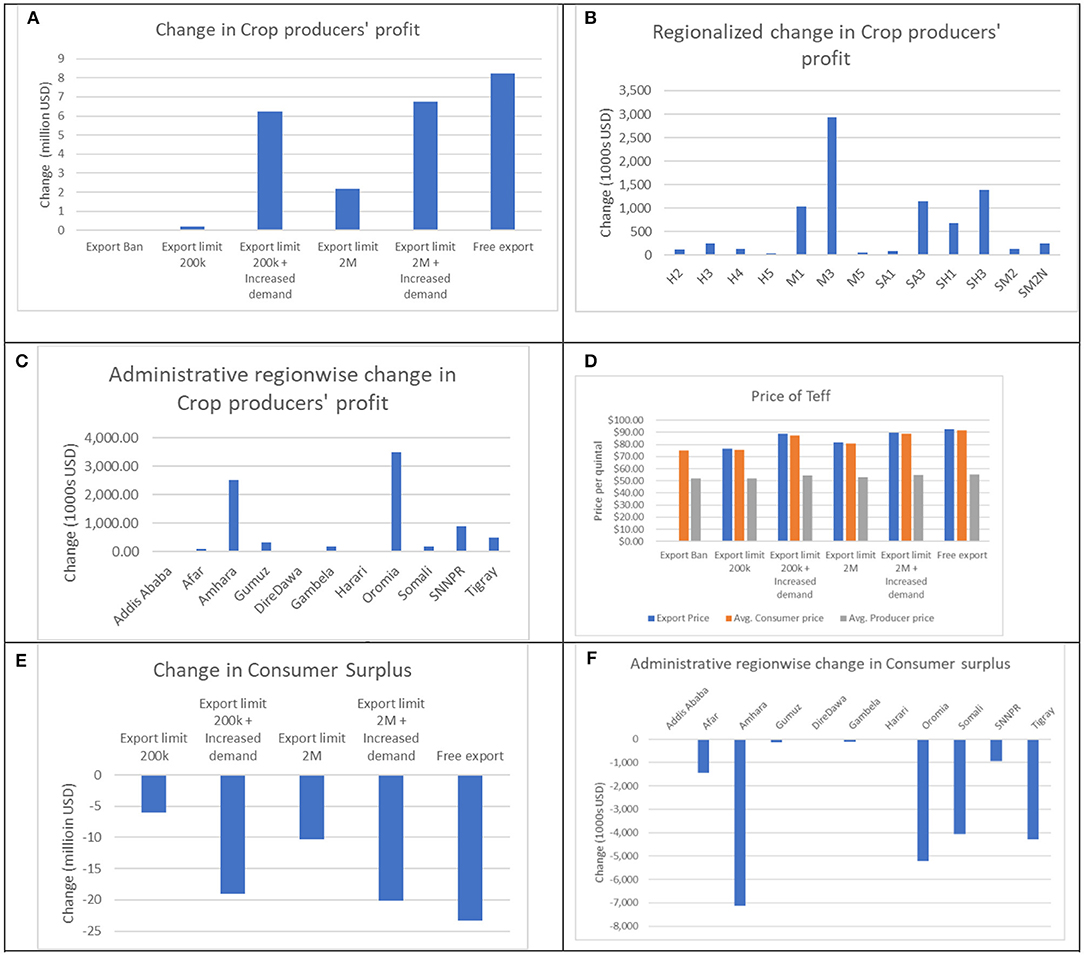
Figure 2. Crop producers' profits, consumer surplus and consumer prices under different scenarios. (A) Change in aggregated crop producers' profit under different scenarios with reference to the teff export-ban scenario. (B) Regionalized change in aggregated crop producers' profit under the free export scenario—adaptation zone wise. (C) Change in aggregated crop producers' profit under the free export scenario—administrative region wise. (D) Changes in aggregated producer, consumer, and export price of teff under different scenarios. (E) Change in aggregated consumers' surplus under different scenarios with reference to the teff export-ban scenario. (F) Change in aggregated consumers' surplus—administrative region wise for free export scenario.
Consumer Price of Teff and Revenue From Teff Export
We now evaluate the fluctuations in prices due to changes in export policy, as one of the primary reasons to implement a ban on teff export is to curtail increase in the domestic price of teff. We interpret these fluctuations as a direct, first order response to a change in policy, since our model does not include macroeconomic adjustments that might occur in the wake of a change in teff export policy. Currently, the domestic price of teff averages about 74 United States dollars (USD) per quintal (Tafere et al., 2010), which is the price assumed for the base case in simulations. We note that under no restrictions for teff export, our simulations indicate that the price can rise to as high as 91 USD per quintal. This amounts to over a 22% increase in the price of teff. In the model, this has the ability to wipe out teff consumption in certain regions of the country (for example the moist lowlands, adaptation zone M1). This happens because these regions then have an alternative crop like wheat, barley, or sorghum, which contributes to the utility of the consumer without forcing them to pay significantly higher prices. This substitution has no meaningful impact on the prices of these other grains in our simulations; the change in price of other grains is on the order of 0.05%. Under no taxation for export, the export price is commensurate with the average domestic price. We also note that under the considered milder restrictions on export as opposed to a complete ban, namely a cap of 200,000 quintals or two million quintals of teff export per year, the price-increase is relatively smaller at 0.58 and 7.5%. However, if there is an increase in the global demand for teff, even under these milder restrictions on export, increase in domestic prices can be as high as 17 and 18%, respectively. In other words, we observe that the domestic prices of teff could be quite sensitive to global fluctuations of teff demand compared to governmental policies on teff export. The details of these results are shown in Figure 2D. We note that in each scenario, the decrease in consumer surplus is always exceeded by the increase in producer surplus, by a comparison of Figures 2A,E. Further, we also see a drop in the consumer surplus for each scenario, and observe that apart from Oromia and Amhara, the desert regions of Somali are significantly affected by the policy change, as shown in Figures 2E,F. The simultaneous increase in producer surplus and decrease in consumer surplus in the Oromia and Amhara is explained by the fact that a fraction of self-consumed crops are now exported due to better prices for more profits, but the decrease in consumer surplus in Somali without an appropriate increase in the producer surplus there shows the harmful impact of the policy on the desert region.
Changes in Teff Transport Pattern and Domestic Consumption
Now we analyze the regions that primarily contribute to teff export and the changes in domestic consumption patterns. Teff from the fertile regions in Amhara and Tigray regions contribute the majority of the teff exported from the country. This is observable in the significant changes in transportation patterns of teff in Figure 3. We note that the teff that would have otherwise gone to Dire Dawa and thereon to Jijiga and Werder is diverted to Addis Ababa, from where export occurs. We also note that relatively small quantities of teff from the Oromia and SNNPR regions of Ethiopia are sent for export.
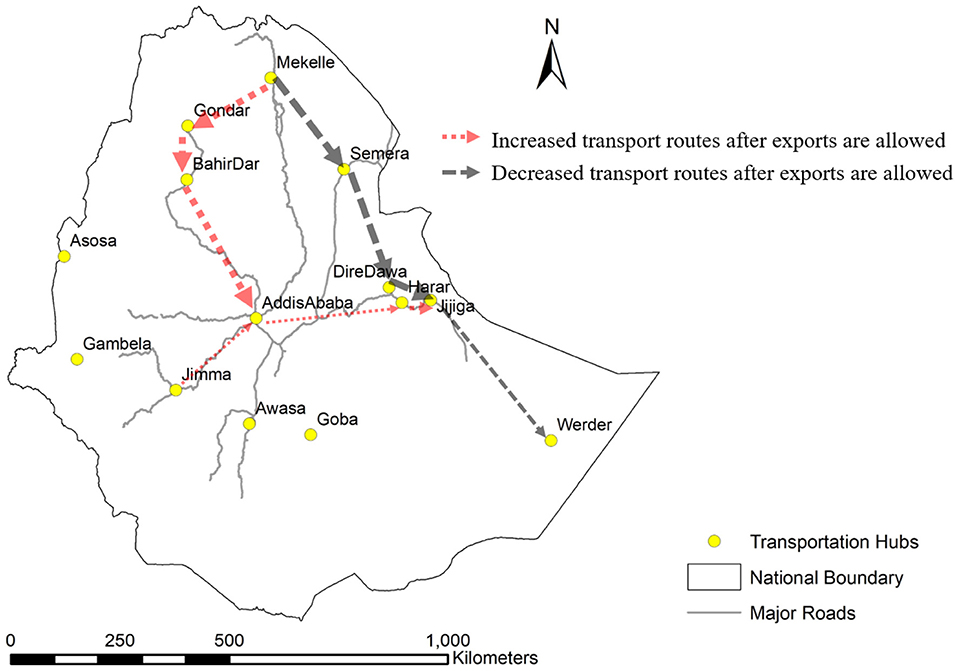
Figure 3. Changes in teff transport pattern: The black lines correspond to the connections whose usage decreases after the ban is lifted. The red lines correspond to the connections whose usage increases after the ban is lifted. Thickness is proportional to magnitude of change.
Due to this effect, some markets sell significantly less teff under the free export scenario than under the baseline case with the ban in place (Figure 4; note that the pins are scaled to the percentage decrease in quantity sold in the markets). This includes markets in Gondar, Mekelle, Harar and Semera, which are all located in the northern and eastern part of the country. These disruptions are significantly smaller for a scenario of capped exports (Figure 4). This result suggests that the government's proposal to allow regulated quantities of teff export (Abdu, 2015) is less harmful to the local markets and hence consumers than an unregulated teff export market. However, this still comes at a vulnerability to increase in domestic food prices should there be an upward shift in the global demand curve (e.g., the export + increased demand scenario, Figure 2D).
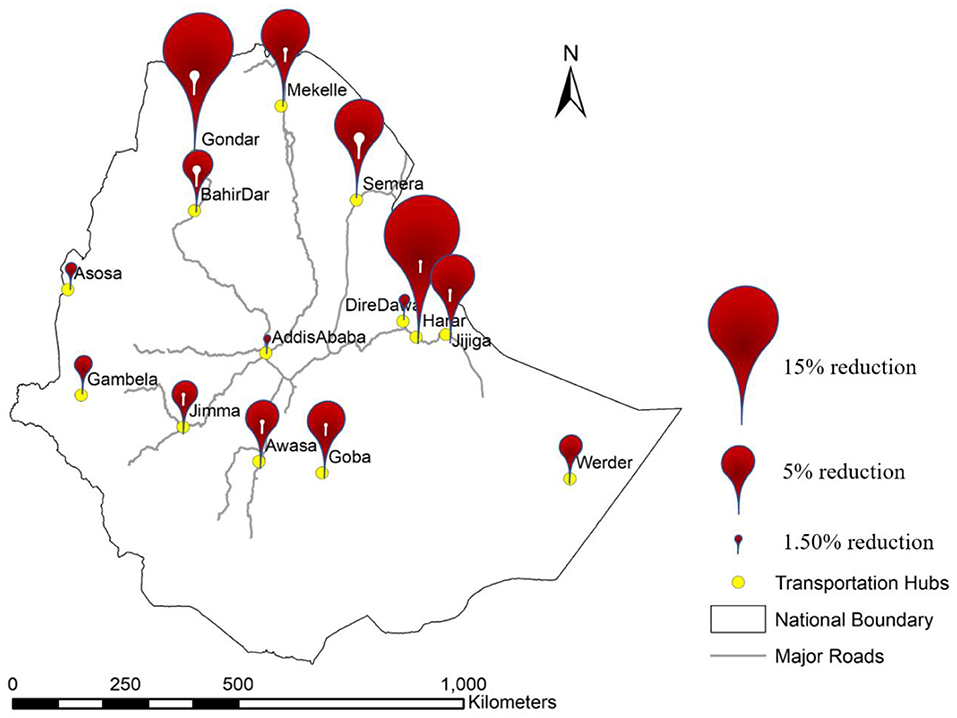
Figure 4. Reduction in quantities sold in domestic markets relative to amount sold under an export ban. Red pin heads correspond to the free export scenario. White pinheads correspond to the scenario with an export cap of 200 thousand quintals per year.
Somali, a low fertility arid region of Ethiopia, is the region that is affected the most by the teff export. It is costlier and unattractive for any producer to transport teff to Jijiga or Werder than to export. Thus, these locations suffer a price higher than the export price of teff. Further, this leads to decreased consumption of teff in these regions. We do note that teff is a smaller portion of local diets in this region compared to many other regions in Ethiopia, so though the impact on teff is substantial the impact on overall diets might not be overly severe. At present DECO2 does not account for these sub-national differences in food preference.
Conclusions and Discussions
In this paper,
i. We present the DECO2 model with its more detailed modeling of disaggregation of the food-production regions of Ethiopia and,
ii. We apply the model to simulate shifts in Ethiopian food markets at regionalized scale in response to changes in teff export policy.
Compared to the partial equilibrium model presented in Bakker et al. (2018), DECO2 includes a more detailed representation of food production, using adaptation zones that group regions with similar agro-climatic properties together. DECO2 also has a more sophisticated representation of food markets across the country and transport between them, which helps in assessing the distribution of benefits as well as quantifying increase in domestic food prices under a range of government policies for teff export. DECO2 is also calibrated based on a more inclusive observational data set from reliable sources.
Discussion of Model Results
We use the status of a complete ban on teff export as the base case. We then use the DECO2 model to identify shifts in equilibrium under scenarios of a completely free international export market for teff, and limited export quantities of 200,000 quintals per year and two million quintals per year. We also run these scenarios under a constant and then a higher global demand for teff.
We observe that a lion's share of the additional international revenue is enjoyed by the distribution and operating warehouse activities as opposed to the initial production activity, unless the crop producers are large market actors themselves who also afford distribution or storage of their produce. Though there is a minor increase in national revenue during a typical year, a surge in the global demand for teff could cause significant harm to consumers across the country, especially to those in the northern and eastern parts of the country. This also comes with a general decrease in domestic food consumption under the release of a teff export ban. While these results suggest the lopsided benefits due to removal of teff export ban, we caution against interpreting these results as policy prescriptive. A more comprehensive analysis is required to decide if the loss in the welfare of some market actor in some region is outweighed by the benefit for the other. Such analysis might require a study based on demographics of the region, potential for intra-country migration, potential for the government to provide alternative benefits and others. Nevertheless, our results are relevant in that they quantitatively as well as qualitatively capture the impacts of the removal of the ban and can inform discussion of modifications to the ban and relevant complementary policies.
It is likely that there are additional policies that may be able to control for the lopsided effects, such as by allowing crop producers to expand into forest and barren lands, improving the usage of irrigation, fertilizers and encouraging better farm management practices, collecting international export taxes, or subsidizing crop producers given the additional revenue from teff export. These mentioned policies can be modeled by DECO2 with simple modifications, providing ex ante evaluations for the policymakers.
Limitations
While DECO2 has a detailed modeling of spatially explicit food production, transport, and consumption under a partial-equilibrium framework, it has its own set of limitations and simplifying assumptions. Being a partial-equilibrium model, DECO2 assumes invariability of macroeconomic parameters that have significant impacts on the variables that are considered in the model. For example, we do not consider endogenous changes in GDP of the country throughout the time-horizon over which the model is solved. This contrasts with the fact that the GDP of Ethiopia has been growing at about 8–10% per annum over the last decade and might change if the country starts exporting teff. Similarly, Ethiopia has also imported about 15 million quintals of wheat per annum in recent years. We again assume that these imports stay constant throughout the time horizon. This assumption of constant imports simplifies interpretation of results, and there is some reason to expect that any large-scale adjustments in grain imports will be slow relative to the time horizon of our simulations, but making this assumption limits the range of market and policy dynamics at play in our scenarios. The lack of these kinds of adjustments in our model means that results are best interpreted as an estimate of the expected direct impacts of a policy change propagating through the Ethiopian food system, rather than as a projection of a new equilibrium after macroeconomic adjustment. It is possible that the direct impacts of a policy change, as estimated in our simulations, would in fact trigger economic or policy responses that modify the long-term outcomes of the policy.
One can also find differences or changes in preferences of consumers over the course of the simulation period. Changes in social and environmental systems have great implications for the consumption preferences of consumers. However, to avoid aggregation problems and for ease of calibration we assumed that preferences of consumers remained the same over the period of analysis. Such an assumption might prevent us from capturing long-term substitution effects in food consumption, but our analysis is over a short time period over which such dynamics are unlikely to be significant. In addition to the above listed variables, our model also neglects the presence of any food aid dependent community, and assumes a constant foreign-exchange rate, fixed interest rate, and a stable political environment (which has implications for transportation).
These assumptions on the macroeconomic variables could be unrealistic if we are interested in future macroeconomic trends. However, we observe that the macroeconomic variables affect all the scenarios in a similar way. These macroeconomic variables include imports and exports of all grains. So, for researchers and policy-makers who are interested in analyzing the direct impacts of policy changes, and evaluating the differences in microeconomic parameters, DECO2 serves as a useful tool to compare policies on a “what-if” basis. If, instead, long-term effects of a policy are of interest, it would be important to capture macroeconomic changes and their sensitivity to simulated policies. This can be achieved by coupling DECO2 with a computable general equilibrium model (CGE) or a model that informs DECO2 about macro-economic changes. In fact, such a coupling between a partial equilibrium model (NANGAM) and a macroeconomic model (GCAM) has been done for energy markets (Feijoo et al., 2018) and is currently under development for DECO2.
Another caveat of the model is that we do not consider dual responsibility of any market actor. In reality, it is customary in Ethiopia to find individuals that act as both a distributer and owner of a warehouse, or as a producer and a distributer. It is also difficult to disentangle a crop producer from a livestock raiser in some cases, although a sizeable proportion of livestock raisers whose livelihood depends on livestock can be viewed as separate from crop producers, particularly in drier adaptation zones. That is why our analysis should be studied through the lens of regional activities, rather than individuals making decisions. Finally, cattle are traded in Ethiopia as opposed to beef. However, since our analysis does not depend upon the supply chain of beef, we assume that the livestock raisers slaughter the cattle and sell the final consumable—beef.
The strengths and limitations noted above have to do with the structure of the DECO2 model. In addition, there are caveats associated with the present study due to data limitations or scenario simplifications that could be addressed in future work without major changes to DECO2. (1) We assumed a constant marginal cost of farming per area of farmland. However, one can model a variable cost through incorporating farm investment and management practices, given available data. (2) We assumed the same price elasticity for a crop across the country; however, in the eastern part of the country teff is not as central to diets, such that cultural preferences could affect regional elasticities. Reliable data about regional differences in price elasticity can be readily incorporated into DECO2. (3) We did not consider any cross-price elasticity among the different food items. Market interaction is modeled exclusively by the consumer's objective, in which the market actor maximizes the sum of utility obtained from all food items. Cross price elasticity-based market interaction can be incorporated with the availability of relevant reliable data. (4) We do not account for informal teff export, which is known to occur across some land borders notwithstanding the official ban on teff export, and we do not consider the legal flow of teff as finished product (i.e., direct export of injera bread). (5) We assume no natural or social barrier that can hinder the crop producers from going to the closest market as determined by Thiessen polygon overlap with adaptation zone. Consistent data on market preference can be used easily to update the proportion of crop producers going to different markets. (6) We do not validate the flows in the base case of the model. This is due to lack of reliable data on the quantity of grains transported from one region to another. In the base case, we ensure that the production and consumption at various locations match the data from the central statistical agency and let the model decide the flows. These data are thus synthetically generated, and the best we can do with the current science and information available to us.
Despite the above caveats and limitations, DECO2 serves as a valuable tool to analyze food-related policies based on their impacts at sub-national scale and on diverse groups of market actors in the economy. The model has a regional representation of food production, trade, transport, consumption, and export. In this application we have used the model to analyze the regional effects of changes to the teff export policy on different market actors. The resulting scenario analysis can help to identify potential risks and benefits of different approaches to teff export policy, considering both the potential to increase revenue and possible impacts on domestic food grain price and consumption across the country.
Data Availability Statement
All datasets generated for this study are included in the article/Supplementary Material.
Author Contributions
SSa, YZ, and SSi developed the model equations. SSa programmed the model. YZ programmed and computed the spatial conversion factors and simulated the crop yield model. BE, BS, and BZ provided the relevant food production data for the model. JC analyzed and interpreted the data and helped develop output analysis tools. SSa, YZ, BZ, and SSi designed the sets of scenarios for analysis. SSa, YZ, YN, BZ, and SSi analyzed the results and critically edited the manuscript.
Funding
This work was supported by NSF Grant #1639214 for INFEWS/T1: Understanding multi-scale resilience options for vulnerable regions.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Molly Brown, University of Maryland, College Park; Kathryn Grace, University of Minnesota and Jeremy Foltz, University of Wisconsin, Madison for their valuable inputs during the study and preparation of this manuscript.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fsufs.2020.00004/full#supplementary-material
References
Abdu, B. (2015). Government to Resume Teff Exports With 180,000 Quintal by Next Fiscal Year [WWW Document]. Addis Fortune. Available online at: https://addisfortune.net/articles/government-to-resume-teff-exports-with-180000ql-by-next-fiscal-year/ (accessed May 22, 2019).
Alem, Y., and Söderbom, M. (2012). Household-level consumption in Urban Ethiopia: the effects of a large food price shock. World Dev. 40, 146–162. doi: 10.1016/j.worlddev.2011.04.020
Allen, R. G., Pereira, L. S., Raes, D., and Smith, M. (1998). Crop evapotranspiration-Guidelines for computing crop water requirements. FAO 300:D05109.
Bakker, C., Zaitchik, B. F., Siddiqui, S., Hobbs, B. F., Broaddus, E., Neff, R. A., et al. (2018). Shocks, seasonality, and disaggregation: modelling food security through the integration of agricultural, transportation, and economic systems. Agric. Syst. 164, 165–184. doi: 10.1016/j.agsy.2018.04.005
Bigman, D. (1985). Food Policies and Food Security Under Instability: Modeling and Analysis. Lexington, MA: Lexington Books D.C. Heath and Company.
Central Intelligence Agency (2015). The World Fact Book [WWW Document]. Available online at: https://www.cia.gov/library/publications/the-world-factbook/geos/et.html (accessed November 23, 2017).
Central Statistical Agency of Ethiopia (2016). Ethiopia - Demographic and Health Survey. Technical Report, The Federal Democratic Republic of Ethiopia Central Statistical Agency, Addis Ababa.
Central Statistical Agency of Ethiopia (2015). Area and Production of Major Crops. Technical Report, The Federal Democratic Republic of Ethiopia Central Statistical Agency, Addis Ababa.
Crymes, A. R. (2015). The International Footprint of Teff: Resurgence of an Ancient Ethiopian Grain. St. Louis, MQ: Washington University.
Deribew, T., Tafere, B., and Gebre-Ab, N. (2015). Ethiopia's Climate Resilient Green Economy: Climate resilience Strategy -Agriculture and Forestry. Addis Ababa: Global Green Growth Institute. Available online at: https://www.greengrowthknowledge.org/national-documents/ethiopia's-climate-resilient-green-economy-climate-resilience-strategy (accessed May 22, 2019).
Di Falco, S., and Veronesi, M. (2012). How african agriculture can adapt to climate change? - A counterfactual analysis from Ethiopia. SSRN Electron. J. 89, 743–766. doi: 10.2139/ssrn.2030220
Di Falco, S., and Zoupanidou, E. (2017). Soil fertility, crop biodiversity, and farmers' revenues: evidence from Italy. Ambio 46, 162–172. doi: 10.1007/s13280-016-0812-7
Doorenbos, J., and Kassam, A. H. (1979). Yield response to water. Irrig. Drain. Pap. 33, 257–280. doi: 10.1016/B978-0-08-025675-7.50021-2
Feijoo, F., Huppmann, D., Sakiyama, L., and Siddiqui, S. (2016). North American natural gas model: Impact of cross-border trade with Mexico. Energy 112, 1084–1095. doi: 10.1016/j.energy.2016.06.133
Feijoo, F., Iyer, G. C., Avraam, C., Siddiqui, S. A., Clarke, L. E., Sankaranarayanan, S., et al. (2018). The future of natural gas infrastructure development in the United states. Appl. Energy 228, 149–166. doi: 10.1016/j.apenergy.2018.06.037
Feijoo, F., Sankaranarayanan, S., Avraam, C., and Siddiqui, S. (2019). Mathematical Models for Evolving Natural Gas Markets. Springer
Gabriel, S. A., Conejo, A. J., Fuller, J. D., Hobbs, B. F., and Ruiz, C. (2012). Complementarity Modeling in Energy Markets, Springer Science and Business Media. New York, NY: Springer Science & Business Media.
Getnet, K., Verbeke, W., and Viaene, J. (2005). Modeling spatial price transmission in the grain markets of Ethiopia with an application of ARDL approach to white teff. Agric. Econ. 33, 491–502. doi: 10.1111/j.1574-0864.2005.00469.x
Gilbert, C. L. (2012). International agreements to manage food price volatility. Glob. Food Sec. 1, 134–142. doi: 10.1016/j.gfs.2012.10.001
Google Inc. (2018). Google Maps [WWW Document]. Available online at: https://maps.google.com (accessed May 22, 2019).
Iizumi, T., Luo, J.-J., Challinor, A. J., Sakurai, G., Yokozawa, M., Sakuma, H., et al. (2014). Impacts of El Niño Southern Oscillation on the global yields of major crops. Nat. Commun. 5:ncomms4712. doi: 10.1038/ncomms4712
Jaleta, M., and Gebremedhin, B. (2012). Price co-integration analyses of food crop markets: the case of wheat and teff commodities in Northern Ethiopia. African J. Agric. Res. 7, 3643–3652. doi: 10.5897/AJAR11.827
Kumar, N., and Quisumbing, A. R. (2013). Gendered impacts of the 2007–2008 food price crisis: evidence using panel data from rural Ethiopia. Food Policy 38, 11–22. doi: 10.1016/j.foodpol.2012.10.002
Mccornick, P. G., Awulachew, S. B., and Abebe, M. (2008). Water –food –energy –environment synergies and tradeoffs: major issues and case studies. Water Policy 1, 23–26. doi: 10.2166/wp.2008.050
Minten, B., Taffesse, A. S., and Brown, P. (2018). The Economics of Teff: Exploring Ethiopia's Biggest Cash Crop. Washington, DC: International Food Policy Research Institute (IFPRI).
MIT (2018). MIT Atlas Ethiopia [WWW Document]. MIT Atlas. Available online at: https://atlas.media.mit.edu/en/profile/country/eth/ (accessed June 23, 2018).
Negassa, A., and Jayne, T. S. (1997). “The response of ethiopian grain markets to liberalization,” Working Paper No. 6 (Addis Ababa: Grain Market Research Project).
Provost, C., and Jobson, E. (2014). Move over Quinoa, Ethiopia's Teff poised to be next big super grain. Guardian.
Robinson, S., Mason-D'Croz, D., Sulser, T., Islam, S., Robertson, R., Zhu, T., et al. (2015). The International Model for Policy Analysis of Agricultural Commodities and Trade (IMPACT): model description for Version 3. SSRN Electron. J. doi: 10.2139/ssrn.2741234
Rosegrant, M. W., Msangi, S., Ringler, C., Sulser, T. B., Zhu, T., and Cline, S. A. (2008). International Model for Policy Analysis of Agricultural Commodities and Trade (IMPACT): Model description. Washington, DC: International Food Policy Research Institute.
Sankaranarayanan, S., Feijoo, F., and Siddiqui, S. (2018). Sensitivity and covariance in stochastic complementarity problems with an application to North American natural gas markets. Eur. J. Oper. Res. 268, 25–36. doi: 10.1016/j.ejor.2017.11.003
Sethi, S., and Sorger, G. (1991). A theory of rolling horizon decision making. Ann. Oper. Res. 29, 387–415. doi: 10.1007/BF02283607
Sharma, R. (2011). “Food export restrictions: review of the 2007-2010 experience and considerations for disciplining restrictive measures,” Working Paper No. 32 (Rome: FAO Commodity and Trade Policy).
Tafere, K., Taffesse, A. S., Tamru, S., Tamiru, S., Tefera, N., and Paulos, Z. (2010). “Food demand elasticities in Ethiopia: estimates using Household Income Consumption Expenditure (HICE) survey data,” ESSP Working Papers 11 (Washington, DC: International Food Policy Research Institute (IFPRI)).
Tamru, S. (2013). “Spatial integration of cereal markets in Ethiopia,” in Ethiopia Strategy Support Program-Ethiopian Development Research Institute (Washington, DC).
USAID (2016). El Niño in Ethiopia, 2015-2016: A Real-Time Review of Impacts and Responses. Washington, DC: USAID. Available online at: https://www.agri-learning-ethiopia.org/wp-content/uploads/2016/06/AKLDP-El-Nino-Review-March-2016.pdf (accessed May 22, 2019).
Voronoi, G. M. (1908). Nouvelles applications des param‘etres continus ‘a la th'eorie des formes quadratiques. deuxi‘eme M'emoire: Recherches sur les parall'ello‘edres primitifs. J. Reine Angew. Math. 134, 198–287. doi: 10.1515/crll.1908.134.198
Wailes, E. J., and Chavez, E. C. (2011). “2011 Updated Arkansas Global Rice Model,” in Staff Paper 1. Fayetteville, AR: University of Arkansas, Department of Agricultural Economics & Agribusiness, Division of Agriculture.
Woldie, G. A., and Siddig, K. (2009). The Impact of Banning Export of Cecreals in Response to Soaring Food Prices: Evidence From Ethiopia Using the New GTAP African Database. Giessen: Munich Papers. RePEc Arch.
Keywords: food policy, food exports, ethiopia, food supply chain, policy analyses
Citation: Sankaranarayanan S, Zhang Y, Carney J, Nigussie Y, Esayas B, Simane B, Zaitchik B and Siddiqui S (2020) What Are the Domestic and Regional Impacts From Ethiopia's Policy on the Export Ban of Teff? Front. Sustain. Food Syst. 4:4. doi: 10.3389/fsufs.2020.00004
Received: 22 May 2019; Accepted: 06 January 2020;
Published: 24 January 2020.
Edited by:
Patrick Meyfroidt, Catholic University of Louvain, BelgiumReviewed by:
Getaw Tadesse, International Food Policy Research Institute, United StatesRuerd Ruben, Wageningen University and Research, Netherlands
Copyright © 2020 Sankaranarayanan, Zhang, Carney, Nigussie, Esayas, Simane, Zaitchik and Siddiqui. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sriram Sankaranarayanan, c3JpcmFtLnNhbmthcmFuYXJheWFuYW5AcG9seW10bC5jYQ==
 Sriram Sankaranarayanan
Sriram Sankaranarayanan Ying Zhang
Ying Zhang Jess Carney3
Jess Carney3 Befikadu Esayas
Befikadu Esayas Belay Simane
Belay Simane Benjamin Zaitchik
Benjamin Zaitchik Sauleh Siddiqui
Sauleh Siddiqui