- Department of Mathematic, Faculty of Science, King Mongkut’s University of Technology Thonburi, Bangkok, Thailand
The purpose of this article is to explore a new method for solving one of the nonlinear partial differential equations (NPDE) which is difficult to solve. The dispersive modified Benjamin-Bona-Mahony (DMBBM) equation and the solutions of space-time fractional Bateman-Burgers equation is solved by a travelling wave analysis method as the Riccati sub-equation. The solutions of space-time fractional DMBBM equation and the solutions of space-time fractional Bateman-Burgers equation can be expressed in the forms of exponential functions, trigonometric functions, rational functions, and hyperbolic functions. The singular wave, singular kink wave, and periodic wave are the representations of the solution graphs.
1 Introduction
The nonlinear partial differential equations (NPDE) are the partial differential equation (PDE) which have nonlinear terms. The NPDEs are well known for their application of mathematics and physics. Investigating the analytical solutions of NPDEs plays important role in nonlinear science. In fact, NPDEs of physical problems are difficult to solve analytically.
At present, there are many alternative methods could obtain exact travelling wave solutions of NPDEs such as Riccati sub-equation (1, 15–17, 19), Kudryashov method (2, 18, 20), -expansion method (3), -expansion method (4–6) and hyperbolic tangent method.
One of interested NPDEs is the nonlinear dispersive modified Benjamin-Bona-Mahony (DMBBM) equation (7, 8) which was proposed by Benjamin, Bona and Mahony in 1972. It describes the role of nonlinear dispersion. The DMBBM equation is presented as
where is a nonzero positive constant and . However, this method has complicated solutions and still difficult to solve even though the analytical solutions of DMBBM equation are established by using the direct reduction methods and some transformations. The article aims to investigate the travelling wave analysis methods to solve the analytical solutions of the DMBBM (Equation 1) and the Bateman-Burgers (Equation 2) in other ways.
In 1915, Harry Bateman presented the Bateman-Burgers equation which is illustrious in the field of applied mathematics such as fluid mechanics, traffic flow and gas dynamics. Bateman-Burgers equation is presented as
where is a function of variables and , is the viscosity of a fluid (1).
1.1 Jumarie’s Riemann-Liouville derivative
The Jumatie’s Riemann-Liouville derivative of order respect to is defined as follows (9),
The important properties of fractional Riemann-Liouville derivatives are following (10),
By combining the fractional Jumatie’s Riemann-Liouville derivative (Equations 3–6) with the algorithm of the Riccati sub-equation method, we have found numerous new exact travelling wave solutions of the fractional nonlinear space–time DMBBM equation and the fractional nonlinear space–time Bateman-Burgers equation. Wave behavior graphs in contour, two-dimensional, and three-dimensional plots are demonstrated. Additionally, compared to results from previous approaches, the acquired results showed greater variability.
The researcher intends to use the Riccati sub-equation method to determine the exact solutions and analyse the behavior of the fractional nonlinear space–time DMBBM equation and the fractional nonlinear space–time Bateman-Burger equation. This method will provide the exact solution in three different forms: rational functions, generalised hyperbolic functions, and generalised triangular functions. There are a total of 15 distinct solutions. The researcher analysed the behavior of the solution by examining the graph of the solutions in three different formats: contour, two-dimensional graph, and three-dimensional graph. Using Jumarie’s Riemann-Liouville Derivative and its properties, the above procedure must convert nonlinear fractional PDE to nonlinear PDE. Then, it must use the wave transform to convert nonlinear PDE to nonlinear ODE, and finally, the Riccati sub-equation technique to solve the problem further.
2 Methodology
The simple equation method with the Riccati sub-equation for solving the DMBBM equation and Bateman-Burgers equation are illustrated as the following procedures. To begin with, the general form of (1 + 1) dimensional NPDEs.
where is the functional of and . Considering two independent variables and , the nonlinear conformable fractional partial differential equation is as follows:
where and is a polynomial expression that contains both greatest order and nonlinear factors in , along with fractional derivatives.
2.1 Step 1. Wave transformation
Setting the wave variable where and are nonzero with positive direction of travelling wave when and a negative direction of the travelling wave when , and (11). Nonlinear Equation 8 can be transformed into an ODE
where Φ is a polynomial that contains its derivatives for both largest order and nonlinear factors in
2.2 Step 2. Solution supposition
2.2.1 Riccati sub-equation method
Recall that the solution of the simple equation (SE) method may be expressed in the form (11).
where are the real constants with is nonzero. The Riccati sub-equation method is used to find defined as (12, 13):
Where is an arbitrary constant. There are general three cases solutions of Equation 11 shown as follows:
Case I: when
where are nonzero constants with .
Case II: when ,
where are nonzero constants with
Case III: when ,
where is a constant.
The generalised hyperbolic functions in Equations 12–18, with and are arbitrary constants and , are defined as follow,
where is an independent variable.
The generalised triangular functions in Equations 19–25, with and are arbitrary constants and , are defined as follow,
where is an independent variable. Substituting the appropriate solutions for case I, II, or III in Equations 12–38 leads to the general three-case solutions of Equation 11. Step 3 Finding the integer.
2.3 Step 3. Finding the integer
The integer (11) in Equation 10 of this method can be obtained by balancing the highest order derivative and nonlinear terms, which are appeared in Equation 9.
2.4 Step 4. Solution obtaining
Collect all the coefficient terms with the same order of , . Set them to zero (11). The parameters and are obtained. Thus, the analytical solutions of Equation 7 are composed.
3 Application
The travelling wave behaviors were investigated by the fractional nonlinear space–time DMBBM equation and the fractional nonlinear space–time Bateman-Burgers equation shown here.
3.1 The fractional nonlinear space–time DMBBM equation
In this chapter, we apply some travelling wave analysis methods in the previous chapter to solve the analytical solutions of the DMBBM equation with the following methods using simple equation. The nonlinear space–time fractional DMBBM equation,
where is a nonzero positive constant. Equation 39 is transformed into Equation 40 as the following (14):
Integrating concerning choosing of integration as zero, we obtain the following ODE,
Balance the highest order derivative and the nonlinear term. So, we have N = 1. The solution is expressed as
Differentiating Equation 42 yields,
and
Substitute Equations 42, 44–46 into Equation 41,
Setting the coefficients of to zero, we obtain
Solving the system of Equations 47–50, we get
and where . The exact solutions of the fractional DMBBM equation are:
Type I: when
where are nonzero constants with .
Type II: when ,
where are nonzero constants with
Type III: when ,
where is a constant, . The analytical solutions of the fractional DMBBM equation are shown in Equations 51–66. Replacing Equations 59, 60, and 66 by setting the parameters and , the wave of the solutions of the space–time fractional DMBBM equation by Riccati sub-equation can be demonstrated as the following Figures 1–3.
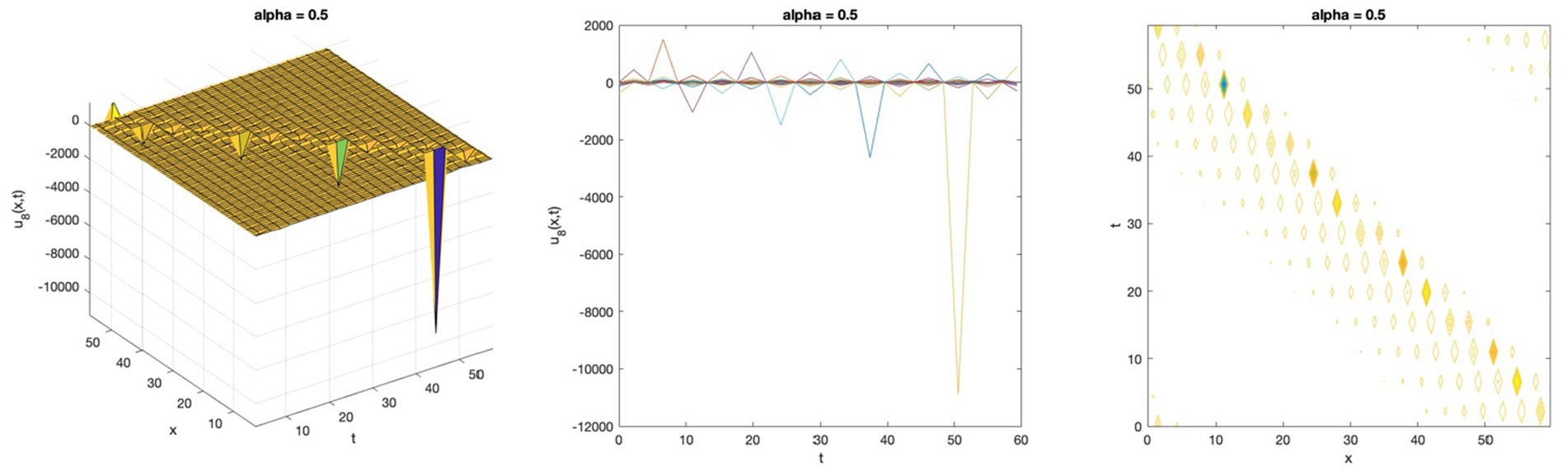
Figure 1. Periodic wave solution profile of the space–time fractional DMBBM equation by Riccati sub-equation for Equation 59.
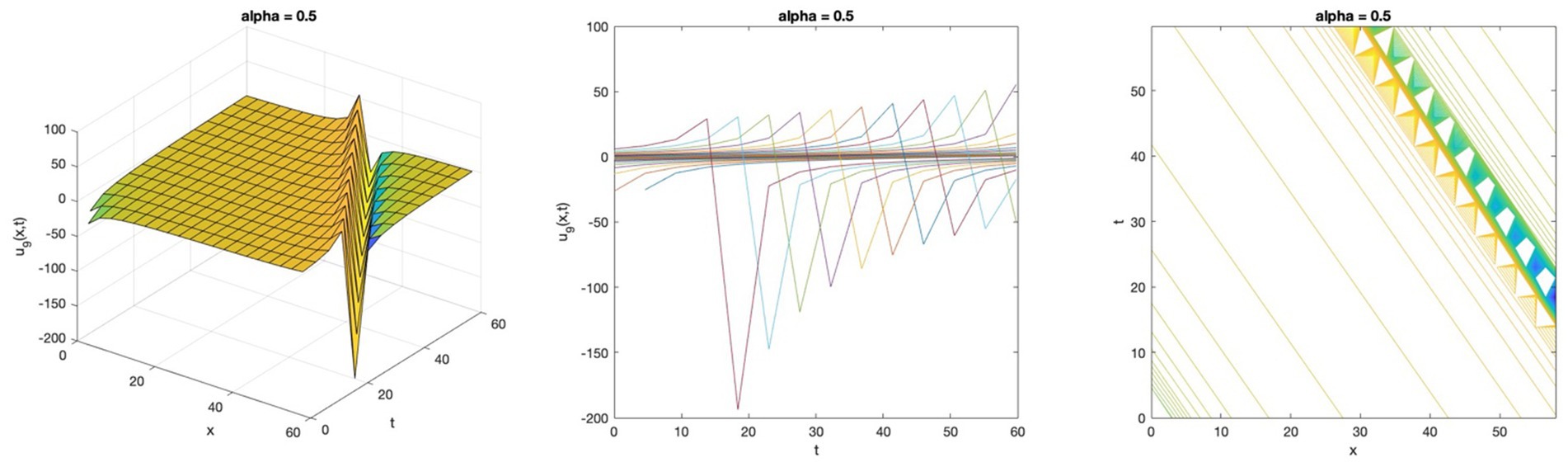
Figure 2. Singular solution profile of the space–time fractional DMBBM equation by Riccati sub-equation for Equation 60.
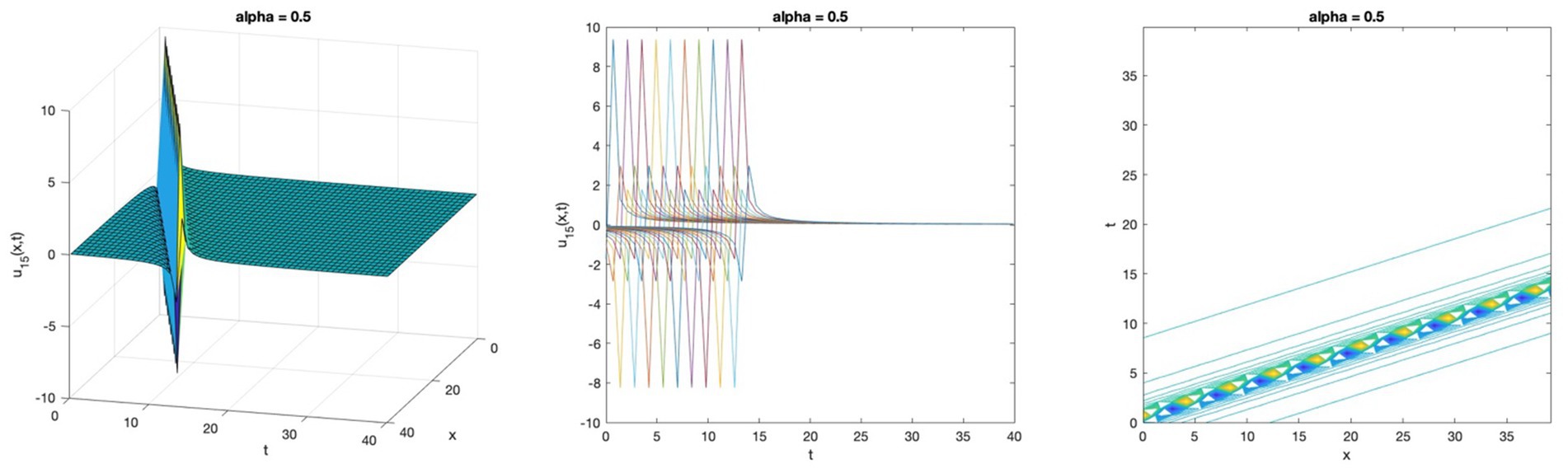
Figure 3. Singular Kink wave solution profile of the space–time fractional DMBBM equation by Riccati sub-equation for Equation 66.
3.2 The fractional nonlinear space–time Bateman-Burgers equation
Given,
where is the viscosity of a fluid. Transform Equation 67 into the differential equation, setting the wave variable and yields,
Balance the highest order derivative and the nonlinear term. So, we have N = 1. The solution is expressed as
Substitute Equations 69, 43, and 44 into Equation 68, we get
Setting coefficients of to zero, we obtain
Solving the system of Equations 70–73, we get
The exact solutions of the fractional Bateman-Burgers equation are:
Type I: when
where are nonzero constants with .
Type II: when ,
where are nonzero constants with
Type III: when ,
where is a constant, . The analytical solutions of the fractional Bateman-Burgers equation are shown in Equations 74–89.
Replacing Equations 82, 83, and 89 by setting the parameters and , the wave of the solutions of the space–time fractional Bateman-Burgers equation by Riccati sub-equation can be demonstrated as the following Figures 4–6.
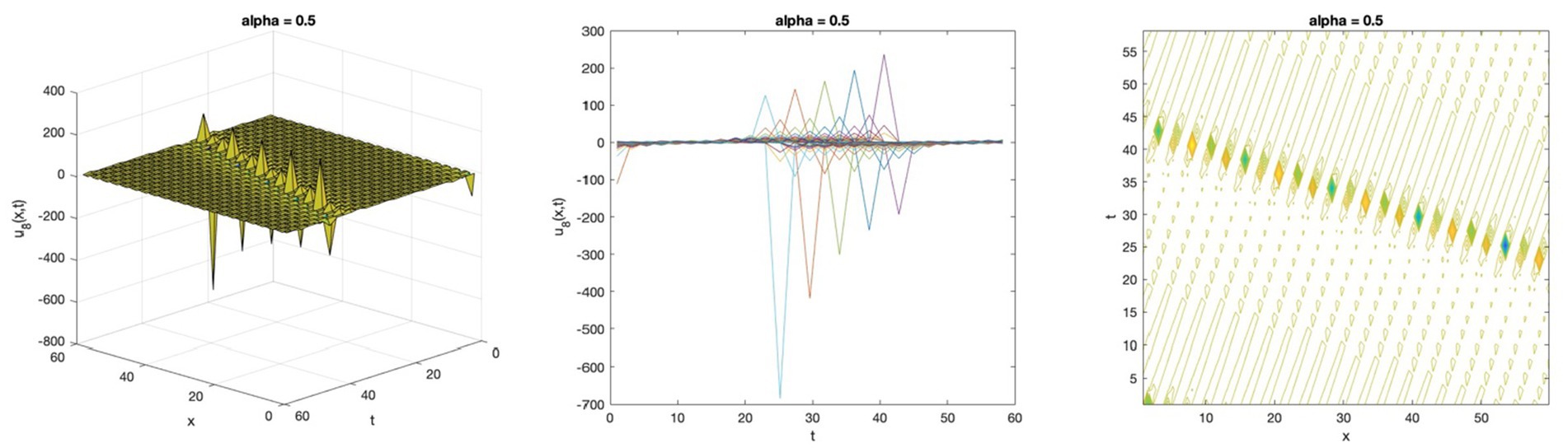
Figure 4. Periodic wave solution profile of the space–time fractional Bateman-Burgers equation by Riccati sub-equation for Equation 82.
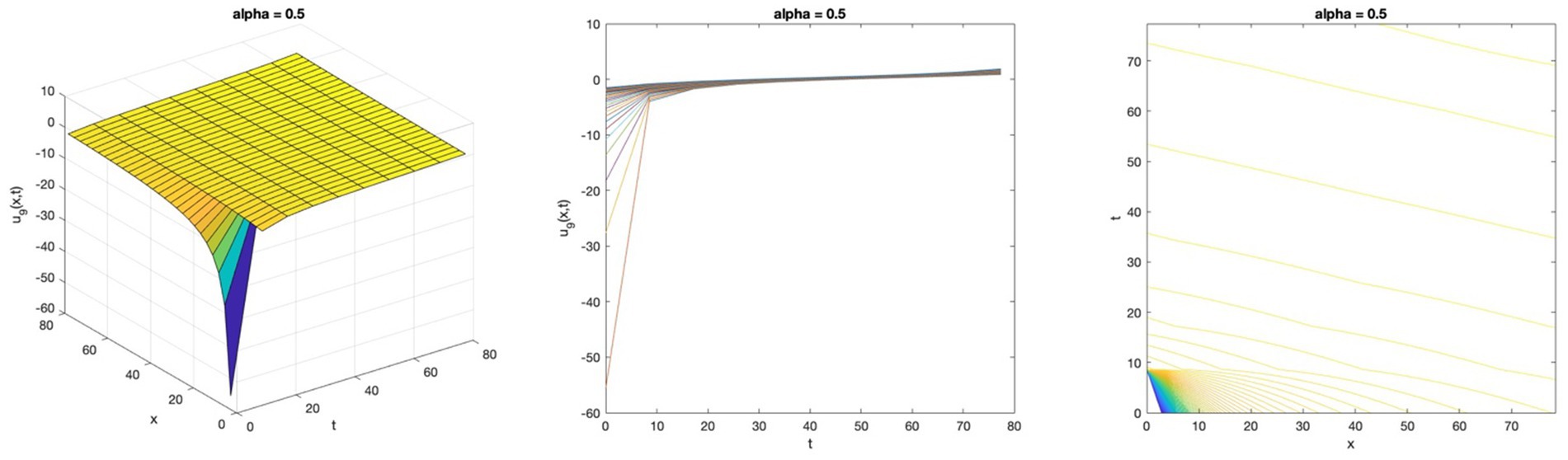
Figure 5. Singular wave solution profile of the space–time fractional Bateman-Burgers equation by Riccati sub-equation for Equation 83.
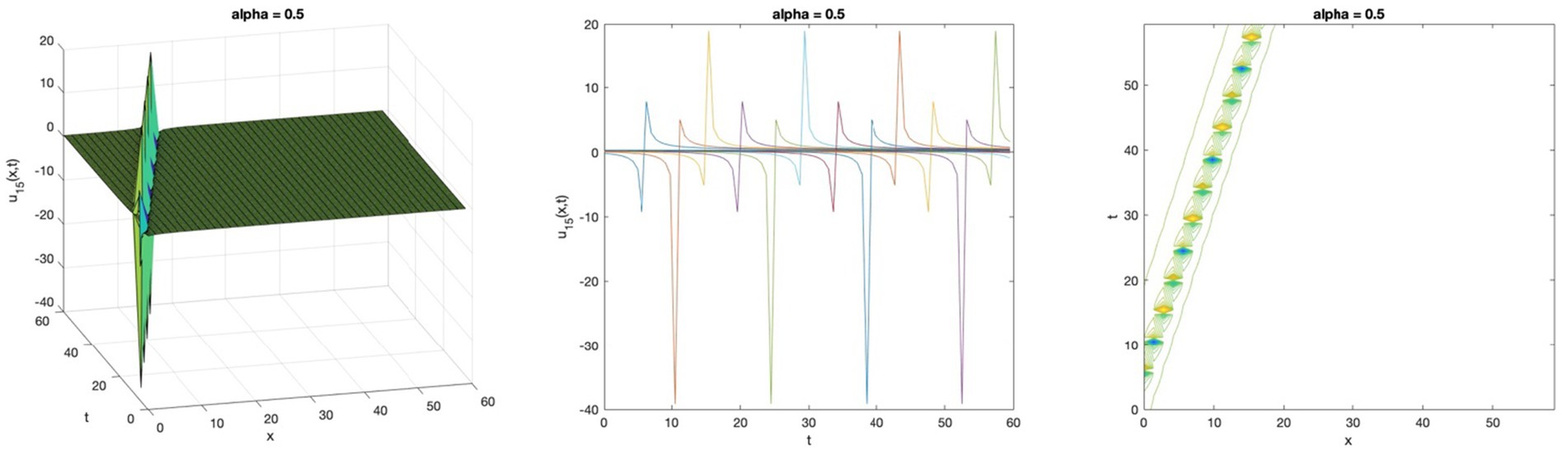
Figure 6. Singular Kink wave solution profile of the space–time fractional Bateman-Burgers equation by Riccati sub-equation for Equation 89.
4 Discussion and results
The fifteen novel solutions found using the Riccati sub-equation method for the two equations are as follows: seven generalised hyperbolic functions, seven generalised triangular functions, and one rational function. The new solutions are more varied than the ones that were previously available: the space–time fractional modified Benjamin-Bona-Mahony (mBBM) equation, which was solved using the modified Kudryashov method, has four solutions (15), while the (1 + 1)-dimensional nonlinear dispersive modified Benjamin-Bona-Mahony (DMBBM) equation, which was solved using the Bernoulli equations, has four solutions (8). In addition, the solution graphs of the equation display periodic waves which are solutions to travelling waves that are periodic, in Figures 1, 4. Singular waves, as seen in Figures 2, 5, and kink waves, as depicted in Figures 3, 6.
5 Conclusion
In this article, the simple equation method has been successfully implemented. The wave solutions for the space–time fractional DMBBM equation and the space–time fractional Bateman-Burgers equation are found using the Riccati sub-equation. This method releases fifteen solutions with independent parameters in the form of generalised triangular functions and generalised hyperbolic functions which are considered to describe some intricate physical phenomena. This research shows some physical wave behavior graphs in three-dimensional plots. Both Figures 1, 4 are exhibit periodic wave solutions which increase and decrease, Figures 2, 5 show singular solutions and singular kink wave solutions were presented in Figures 3, 6. Based on the results, the Riccati sub-equation methodology is an effective, dependable, and efficient method that provides new solutions to these equations and shows the wave impacts of those solutions in different ways.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
NS-I: Formal analysis, Investigation, Methodology, Writing – original draft. SC: Conceptualization, Formal analysis, Methodology, Validation, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The authors declare that no Gen AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Bateman, H. Some recent researches on the motion of fluids. Monthly Weather Rev. (1915) 43:163–70. doi: 10.1175/1520-0493(1915)43<163:SRROTM>2.0.CO;2
2. Neirameh, A. Exact analytical solutions for 3D-gross-Pitaevskii equation with periodic potential by using the Kudryashov method. J Egypt Math Soc. (2016) 24:49–53. doi: 10.1016/j.joems.2014.11.004
3. Abdel-Razek, MA, Seddeek, AK, and Abdel, NH. New exact Jacobi elliptic function solution for nonlinear equations using F-expansion method. Stud Math Sci. (2011) 2:88–95. doi: 10.3968/j.sms.1923845220120201.014
4. Wang, M, Li, X, and Zhang, J. The G′/G -expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys Lett A. (2008) 372:417–23. doi: 10.1016/j.physleta.2007.07.051
5. Ebadi, G, and Biswas, A. Application of the G′/G-expansion method for nonlinear diffusion equations with nonlinear source. J Franklin Inst. (2010) 347:1391–8. doi: 10.1016/j.jfranklin.2010.05.013
6. Naher, H. New approach of (G′/G)-expansion method and new approach of generalized (G’/G)-expansion method for ZKBBM equation. J Egypt Math Soc. (2015) 23:42–8. doi: 10.1016/j.joems.2014.03.005
7. Khan, K, Akbar, MA, and Islam, SMR. Exact solutions for (1 + 1)-dimensional nonlinear dispersive modified Benjamin-Bona-Mahony equation and coupled Klein-Gordon equations. SpringerPlus. (2014) 3:724. doi: 10.1186/2193-1801-3-724
8. Sanjun, J, and Chankaew, A. Wave solutions of the DMBBM equation and the cKG equation using the simple equation method. Front Appl Math Stat. (2022) 8:952668. doi: 10.3389/fams.2022.952668
9. Jumarie, G. Modified Riemann-Liouville derivative and fractional Taylor series of non-differentiable functions further results. Comput Math Appl. (2006) 51:1367–76. doi: 10.1016/j.camwa.2006.02.001
10. Jumarie, G. Table of some basic fractional calculus formulae derived from a modified Riemann-Liouville derivative for non-differentiable functions. Appl Math Lett. (2009) 22:378–85. doi: 10.1016/j.aml.2008.06.003
11. Fan, E. Extended tanh-function method and its applications to nonlinear equations. Phys Lett A. (2000) 277:212–8. doi: 10.1016/S0375-9601(00)00725-8
12. Khodadad, FS, Nazari, F, Eslami, M, and Rezazadeh, H. Soliton solutions of the conformable fractional Zakharov-Kuznetsov equation with dual-power law nonlinearity. Opt Quant Electron. (2017) 49:384. doi: 10.1007/s11082-1225-y
13. Thadee, W, Phookwanthong, J, Jitphusa, P, and Phoosree, S2023. Wave solution behaviors for fractional nonlinear fluid dynamic equation and shallow water equation. Songklanakarin J Sci Technol. (2023) 45:627–37.
14. Ali, HMS, Habib, MA, Miah, MM, and Akbar, MA. Solitary wave solutions to some nonlinear fractional evolution equations in mathematical physics. Heliyon. (2020) 6:e03727–12. doi: 10.1016/j.heliyon.2020.e03727
15. Ege, SM, and Misirli, E. The modified Kudryashov method for solving some fractional-order nonlinear equations. Adv Differ Equations. (2014) 2014:135. doi: 10.1186/1687-1847-2014-135
16. Zill, D.G., and Wright, W.S., 2013, Differential equations with boundary-value problems, international edition, Brooks Cole, Pacific Grove, CA, pp. 1–5.
17. Griffiths, G.W., and Schiesser, W.E., 2011, Traveling wave analysis of partial differential equations: Numerical and analytical methods with Matlab and maple, Cambridge, MA, Academic Press, pp. 1–2
18. Zayed, EME, and Alurrfi, KAE. The modified Kudryashov method for solving some seventh order nonlinear PDEs in mathematical physics. World J Modell Simul. (2015) 11:308–19.
19. Phoosree, S, Khongnual, N, Sanjun, J, and Kammanee, A. 2024, “Riccati sub-equation method for solving fractional flood wave equation and fractional plasma physics equation”. Partial Differ Equations Appl Math. (2024) 10:100672. doi: 10.1016/j.padiff.2024.100672
Keywords: dispersive modified Benjamin-Bona-Mahony (DMBBM) equation, Bateman-Burgers equation, nonlinear partial differential equation, travelling wave analysis method, Riccati sub-equation
Citation: Sribua-Iam N and Chinviriyasit S (2025) New analytical wave solutions of fractional order DMBBM and Bateman-Burgers equations. Front. Appl. Math. Stat. 11:1568834. doi: 10.3389/fams.2025.1568834
Edited by:
Christos Xenophontos, University of Cyprus, CyprusReviewed by:
Diptiranjan Behera, University of the West Indies, JamaicaDanyal Soybaş, Erciyes University, Türkiye
Copyright © 2025 Sribua-Iam and Chinviriyasit. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Settapat Chinviriyasit, c2V0dGFwYXQuY2hpQGttdXR0LmFjLnRo
 Nathanon Sribua-Iam
Nathanon Sribua-Iam Settapat Chinviriyasit
Settapat Chinviriyasit