On Destruction of a Thermally Stable Layer by Compositional Convection in the Earth's Outer Core

We discuss destruction of a thermally stable layer in the upper part of the Earth's outer core by compositional convection excited at the inner core boundary. We propose to use the radial distribution of power induced by thermal and compositional buoyancy (rate of kinetic energy production) as a measure of occurrence of thermal and compositional convection. The power consists of the terms proportional to convective entropy flux and convective compositional flux. In the region with positive power, convection is active because kinetic energy can be produced by buoyancy force, and a stably stratified layer could not be formed there. On the other hand, in the region with negative power, convection is suppressed and a stably stratified layer may be produced. Considering penetration effect of convection, we discuss possible maximum and minimum thicknesses of the stable layer based on the radial distribution of power and its radial integral, respectively. We construct a 1-dimensional thermal and compositional balance model of the Earth's core with a larger value of thermal conductivity recently suggested by high-pressure experiments and first principle calculations, and estimate radial distributions of power for various values of core mantle boundary (CMB) heat flux Q_CMB. When Q_CMB > Q_sCMB no thermally stable layer can exist, where Q_sCMB is the conductive heat flux along the adiabat at the CMB. On the other hand, when Q_CMB < Q_sCMB, formation of an upper thermally stable layer becomes possible, depending on the extent of penetration of compositional convection excited below. When Q_CMB is sufficiently lower than Q_sCMB, a thermally stable layer survives the maximum penetration of compositional convection. The results show that a thermally stable layer becomes effectively thinner when the effect of compositional convection is considered compared with the results of previous studies where the existence of a stable layer is evaluated based on the convective flux only.

1. Introduction

It is widely thought that fluid motion driven in the Earth's outer core by cooling due to mantle convection generates and maintains the geomagnetic field through dynamo action. Although thermal convection would occur as a direct effect of cooling from the core mantle boundary (CMB) and as a result of the latent heat release at the inner core boundary (ICB) associated with growth of the inner core through solidification of Fe and Ni, the main energy source for geomagnetic field generation is considered to be supplied by compositional convection induced by the release of light elements at the ICB (e.g., Lister and Buffett, 1995). Estimation of the power available for magnetic energy as well as evolution of the structure of the Earth's core has been studied extensively using 1-dimensional thermal and compositional budget models (e.g., Loper, 1978; Gubbins et al., 1979; Stevenson, 1983).

Most of the models assumed vigorous convection mixes completely the whole fluid core, and entropy and composition are homogeneous. Alternative models considering formation of a stably stratified layer below the CMB were proposed (Labrosse et al., 1997; Lister and Buffett, 1998). They assumed that, when heat flow at the CMB Q_CMB determined by strength of mantle convection becomes smaller than upward conductive heat flow along the adiabatic temperature profile Q_s, heat accumulates below the CMB, and a thermally stable layer starts to develop by conduction. Labrosse et al. (1997) assumed that erosion of the stable layer by mixing due to compositional convection generated from the deeper region does not occur, whereas Lister and Buffett (1998) considered accumulation of light elements due to inner core growth explicitly. They discussed the competition between light elements accumulating in the convecting region of the core and heat accumulating in the stratified layer due to a subadiabatic heat flux at the CMB.

Recently, it was suggested from high-pressure experiments and first principle calculations that the values of thermal conductivity under conditions of planetary cores are larger than those considered so far (Gomi et al., 2013; Pozzo et al., 2014). By using 1-dimensional thermal balance models with the updated values of thermal conductivity, generation and existence of a stably stratified layer in the Earth's outer core was discussed (Gomi et al., 2013; Labrosse, 2015). Their results showed that a stable layer with a thickness of O(1,000 km) could be produced when the heat flux across the CMB is small. They assumed that the region with negative convective heat flux is stably stratified. This assumption seems to be appropriate when convection is driven only by thermal effects, however, it is not correct when compositional convection occurs simultaneously. When compositional convection is sufficiently vigorous to overcome thermally stable stratification, it would mix up the stable layer and make it neutral.

Whether the stably stratified layer is formed and maintained below the CMB or it is destroyed by compositional convection from the deeper region is a significant issue for the evolution of the Earth's core structure. Formation of the stable layer affects the thermal history of the core, such as the age of the inner core and field intensity (e.g., Labrosse et al., 1997; Lister and Buffett, 1998). It is also related to geomagnetic secular variation observed at the surface of the Earth, since it could originate from the fluid motions in the stable layer if it exists (e.g., Braginsky, 1984, 1993; Buffett, 2014).

In the present study, we propose to use radial distribution of power induced by thermal and compositional buoyancy (rate of kinetic energy production) as a measure of occurrence of thermal and compositional convection. The power consists of the terms proportional to heat flux and compositional flux. In the region with positive power convection is active because kinetic energy can be produced by buoyancy force. On the other hand, in the region with negative power, convection is suppressed and the stably stratified layer may be produced.

In the following, formulation of a 1-dimensional thermal and compositional budget model is recalled, and a criterion for formation and destruction of the stable layer is proposed in section 2. Then we apply the model and the criterion to a simple core model, and illustrate formation of a stable layer and its thickness depending on the CMB heat flux in section 3. Summary and discussion are in the final section.

2. Model and Method

2.1. Estimation of Stratified Layer

The procedure for calculation of the power induced by thermal and compositional buoyancy (rate of kinetic energy production) in 1-dimensional thermal and compositional budget models was proposed by Lister and Buffett (1995). They did not apply it to the stable layer formation problem but estimated available energy for magnetic field generation using the integral value of the power in the whole domain. We propose to use the radial distribution of power as a criterion for the formation and destruction of the stable layer. The rationale for this criterion is as follows.

We assume that the whole outer core is well mixed by convection, so that concentrations of light elements and entropy are homogeneous in the radial direction. Temperature follows an adiabatic profile. Then the radial distribution of power by buoyancy force (kinetic energy production) w_b(r) can be calculated from distributions of convective entropy flux and convective compositional flux, which are diagnostically obtained by thermal and compositional budgets as explained below.

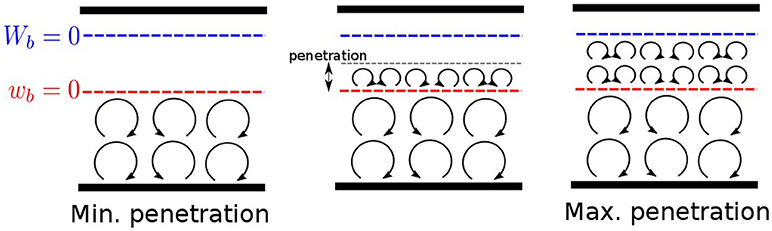
The regions where kinetic energy production is positive (w_b(r) > 0) can be mixed up by convection since it can emerge there, which is consistent with the assumption. Therefore, a stable layer is not formed there. On the other hand, in the regions where kinetic energy production is negative (w_b(r) < 0) convection cannot be driven locally, and mixing may not occur there. However, the region would be mixed up even when w_b(r) < 0 if convection driven in the lower part penetrates into there. Penetration could occur when total kinetic energy production in the convecting and penetrating regions is still positive. Then, possible penetration of convection can be evaluated by the radial integral of power $W_b(r)={\displaystyle {\int }_c^{r}4}\pi {r^{\prime }}^2{w}_b(r^{\prime })d{r}^{\prime },$, where c is the radius of ICB. We estimate the region with W_b(r)>0 which could be mixed up by penetrative convection (Figure 1).

FIGURE 1

Figure 1. The thickness of a stable layer depending on the extent of penetration of convection.

Therefore, the maximum and minimum thicknesses of the stable layer are determined with w_b(r) < 0 and W_b(r) < 0, respectively.

2.2. 1-dimensional Thermal and Compositional Balance Model

1-dimensional thermal and compositional budget model of the Earth's core used in this study basically follows that developed by Lister and Buffett (1995), Gomi et al. (2013), and Labrosse (2015).

The equation for compositional budget is

$\begin{array}{rcl}{X}_C+F_C=S_C,& (1)& (1)\end{array}$

where X_C is averaged concentration increase of light elements, F_C is convective compositional flux, and S_C is light elements release at the ICB.

$\begin{array}{cc}{X}_C(r)=\frac{d\overline{C}}{dt}{\displaystyle {\int }_c^{r}4}\pi r^2{\rho }_{a}dr,& (2)\end{array}$

$\begin{array}{cc}{F}_C(r)=4\pi r^2{\rho }_a\overline{C^{\prime }{u}_r},& (3)\end{array}$

$\begin{array}{cc}{S}_C=4\pi c^2{\rho }_c\overline{C}\frac{dc}{dt},& (4)\end{array}$

where r is radius, b and c are radii of the CMB and ICB, respectively, $\overline{C}$ is the homogeneous concentration of light elements in the outer core, C′ is the concentration fluctuation from $\overline{C}$, u_r the radial component of velocity, $\overline{C^{\prime }{u}_r}$ the convective compositional flux, ρ_a and ρ_c are the horizontally averaged density in the outer core and at the ICB, respectively. Here, the light elements are assumed to be perfectly incompatible in the inner core for simplicity. Total compositional budget is expressed by X_C(b) = S_C. Using (1) and the boundary condition F_C(b) = 0, F_C can be described alternatively as follows:

$\begin{array}{cc}{F}_C(r)=4\pi c^2{\rho }_c\overline{C}\frac{dc}{dt}\frac{M(b)-M(r)}{M(b)-M(c)},& (5)\end{array}$

$\begin{array}{cc}M(r)={\displaystyle {\int }_c^{r}4}\pi r^2{\rho }_{a}dr.& (6)\end{array}$

The equation for the thermal budget is

$\begin{array}{rc}{Q}_{conv}(r)=Q_{cooling}+E_{comp}+Q_{latent}-Q_s+Q_{visc}+Q_J+Q_{ICB},& (7)\end{array}$

where Q_conv, Q_cooling, E_comp, Q_latent and Q_s are the convective heat flux, and its contributions by secular cooling, compositional energy, latent heat release, and thermal conduction, respectively, which are described as follows:

$\begin{array}{rc}{Q}_{conv}(r)=4\pi r^2\left[{\mu }^{\prime }(r){\rho }_a\overline{C^{\prime }{u}_r}+{\rho }_a{T}_a\overline{S^{\prime }{u}_r}\right],& (8)\end{array}$

$\begin{array}{cc}{Q}_{cooling}(r)=-{\displaystyle {\int }_0^{r}4}\pi r^2{\rho }_a{T}_a\frac{\partial S_a}{\partial t}dr,& (9)\end{array}$

$\begin{array}{cc}{E}_{comp}(r)=-{\displaystyle {\int }_c^{r}4}\pi r^2{\mu }^{\prime }(r){\rho }_a\frac{d\overline{C}}{dt}dr,& (10)\end{array}$

$\begin{array}{cc}{Q}_{latent}=T_l\Delta S{\rho }_{c}4\pi c^2\frac{dc}{dt},& (11)\end{array}$

$\begin{array}{rc}{Q}_s(r)=-4\pi r^{2}k(r)\frac{\partial T_a}{\partial r},& (12)\end{array}$

where T_a(r) is the adiabatic temperature profile in the outer core, S_a is entropy, which is assumed to be uniform, S′ is the entropy fluctuation from S_a, $\overline{S^{\prime }{u}_r}$ is the convective entropy flux, ΔS is the entropy jump associated with the crystallization of the inner core, T_L is liquidus temperature, k(r) is thermal conductivity and μ′(r) is the chemical potential based on the value at the ICB. Following the discussion by Lister and Buffett (1995), we assume that Joule heating Q_J, viscous dissipation Q_visc and the heat flow coming from the inner core Q_ICB can be neglected in the thermal budget (7). From the total thermal budget in the whole core, we obtain

$\begin{array}{rc}{Q}_{CMB}=Q_{cooling}(b)+E_{comp}(b)+Q_{latent}.& (13)\end{array}$

Previous studies showed that all the terms on the right hand side of (13) are proportional to dc/dt, and then, the radial distributions of all the terms are obtained for given CMB heat flow Q_CMB.

The convective entropy flux F_S is expressed as

$\begin{array}{rc}{F}_S(r)\equiv 4\pi r^2{\rho }_a\overline{S^{\prime }{u}_r}=\frac{Q_{conv}(r)-{\mu }^{\prime }(r)F_C(r)}{T_a(r)}.& (14)\end{array}$

The power by buoyancy forces w_b(r) is calculated with the convective fluxes as follows:

$\begin{array}{cc}{w}_b(r)\equiv 4\pi r^{2}g\left[\frac{\alpha T_a}{C_p}{\rho }_a\overline{S^{\prime }{u}_r}-{\rho }_a\beta \overline{C^{\prime }{u}_r}\right]=\frac{\alpha g{T}_a}{C_p}{F}_S-\beta g{F}_C& (15)\end{array}$

where $\alpha =-\frac{1}{\rho }{\left(\frac{\partial \rho }{\partial T}\right)}_{P,C}$ and $\beta =\frac{1}{\rho }{\left(\frac{\partial \rho }{\partial C}\right)}_{P,S}$ are thermal and compositional expansion coefficients, respectively.

2.3. Analytical Expressions of the Fluxes in a Simple Model

Here, we illustrate the result of a diagnosis on the formation of a stable layer in the present Earth's core with a simple setup similar to that used in Lister and Buffett (1995).

Density in the outer core is assumed to be constant. Gravity is given in the form of g(r) = g_o(r/b), where g₀ is the gravitational acceleration at the CMB. Then adiabatic temperature T_a(r, t) and its radial gradient can be described as

$\begin{array}{cc}{T}_a(r,t)=T_i(t)f_a(r),\frac{d{T}_a}{dr}=-\frac{\alpha g(r)T_a(r)}{C_p}=-A{T}_a(r)r,& (16)\end{array}$

where T_i(t) is temperature at the ICB and

$\begin{array}{rc}{f}_a(r)=e^{-A(r^2-c^2)/2},A=\frac{\alpha g_o}{C_{p}b}.& (17)\end{array}$

Since $A{b}^2=\alpha g_{o}b/C_p~0.44<1$ for the values of the Earth's core, we approximate f_a(r) as $f_a(r)~\frac{1-(A/2)r^2}{1-(A/2)c^2}$, and get

$\begin{array}{rcl}{T}_a(r,t)& =& T_i(t)\frac{1-(A/2)r^2}{1-(A/2)c^2},\\ \frac{d{T}_a}{dr}& =& -\frac{\alpha g(r)T_a(r)}{C_p}=-A{T}_a(r)r,& (18)\end{array}$

Accordingly, Q_s(r) becomes

$\begin{array}{rc}{Q}_s(r)=-4\pi r^{2}k(r)\frac{d{T}_a}{dr}=4\pi r^{3}k(r)A{T}_a(r),& (19)\end{array}$

The present value of T_i is determined by setting the conductive heat flow along the adiabat at the CMB Q_sCMB = Q_s(b).

On the other hand, the time derivative of T_i(t) should be evaluated to calculate Q_cooling. From entropy variation with respect to temperature, pressure and composition variations

$\begin{array}{l}{T}_a\frac{\partial S_a}{\partial t}=C_p\frac{\partial T_a}{\partial t}-\frac{\alpha T}{\rho }\frac{\partial P_a}{\partial t}+Q_H\frac{\partial \overline{C}}{\partial t}~C_p\frac{d{T}_i}{dt}{f}_a(r)\\ =-C_p{\rho }_{a}g\frac{d{T}_L}{dp}\frac{dc}{dt}{f}_a,& (20)\end{array}$

where T_i is temperature at the ICB, $Q_H=T{\left(\frac{\partial S}{\partial C}\right)}_{T,P}$ is heat of reaction, which is neglected for simplicity as well as contribution of pressure variation. Then, we have

$\begin{array}{cc}{Q}_{ccoling}(r)=C_p{\rho }_0^{2}g\frac{d{T}_L}{dp}\frac{4\pi }{1-(A/2)c^2}\left(\frac{1}{3}{r}^3-\frac{A}{10}{r}^5\right)\frac{dc}{dt}.& (21)\end{array}$

Since the chemical potential is calculated as

$\begin{array}{cc}{\mu }^{\prime }(r)={\displaystyle {\int }_c^r\beta }g(r)dr={\displaystyle {\int }_c^r\frac{\beta g_o}{b}}rdr=\frac{\beta g_o}{2b}(r^2-c^2),& (22)\end{array}$

its radial integral becomes

$\begin{array}{cc}{\displaystyle {\int }_c^{r}4}\pi r^2{\mu }^{\prime }(r){\rho }_{a}dr=\frac{2}{15}\pi \frac{{\rho }_0\beta g_o}{b}{\left(r-c\right)}^2(3r^3+6r^{2}c+4r{c}^2+2c^3).& (23)\end{array}$

Then we obtain, from equation (10):

$\begin{array}{l}{E}_{comp}(r)=-\frac{1}{10}\frac{\beta g_o}{b(b^3-c^3)}{\left(r-c\right)}^2(3r^3+6r^{2}c+4r{c}^2+2c^3)\\ \times 4\pi c^2{\rho }_c\overline{C}\frac{dc}{dt}.& (24)\end{array}$

Here, we used the relation

$\begin{array}{cc}\frac{d\overline{C}}{dt}\frac{4\pi }{3}{\rho }_0(b^3-c^3)=4\pi c^2{\rho }_c\overline{C}\frac{dc}{dt}& (25)\end{array}$

derived by the total compositional budget X_C(b) = S_C.

The growth rate of the inner core dc/dt is determined by the global thermal budget Equation (13). By using the value of dc/dt, the convective compositional flux is calculated by (5), while the convective thermal flux is determined by

$\begin{array}{rc}{Q}_{conv}(r)=Q_{cooling}(r)+E_{comp}(r)+Q_{latent}-Q_s(r),& (26)\end{array}$

Finally, the convective entropy flux is estimated by (14), and the power by buoyancy forces is determined by (15).

The radial profile of thermal conductivity is approximated to a recent large estimated value (Gomi et al., 2013) with a quadratic function as $k(r)=(k_b-k_0){(r/b)}^2+k_0$, where k_b, k₀ are the values at the CMB and the center of the core, respectively. The adiabatic temperature at CMB is given so that Q_s(b) = Q_sCMB = 9.3TW. The parameters used in the calculation are listed in Table 1.

TABLE 1

Table 1. The parameters used in the calculation.

3. Results

Figure 2 shows the results in the case with Q_CMB = 12TW. The radial distributions of contributions to the thermal budget in the left panel of Figure 2 are qualitatively consistent with previous studies (e.g., Figure 9 in Gomi et al., 2013) although there are several differences. In this case, no stable layer is formed since Q_conv is positive in the whole outer core. Kinetic energy production w_b(r) shown in the center panel of Figure 2 is positive in the whole outer core. Note that both compositional and thermal contribution to w_b(r) is positive in the whole outer core, indicating that thermal and compositional convection emerges there.

FIGURE 2

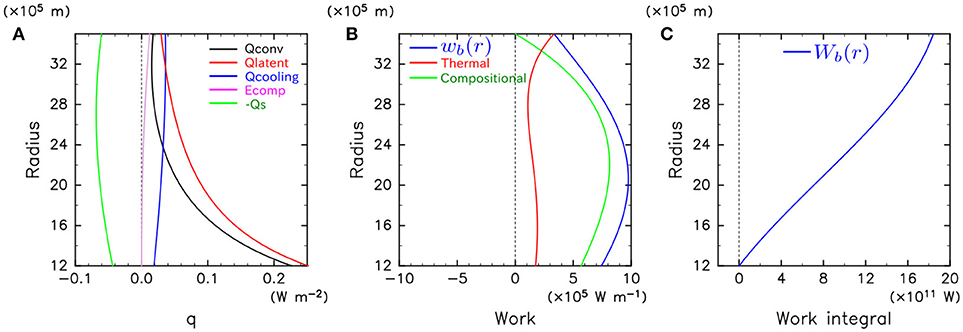
Figure 2. Result of 1-dimensional thermal and compositional budget model for Q_CMB = 12TW. (A) Radial distributions of heat flows. Black, blue, purple, red and green lines indicate Q_conv, Q_cooling, E_comp, Q_latent, and Q_s, respectively. (B) Radial distributions of work by buoyancy forces w_b(r). Green and red lines indicate contributions from compositional and thermal buoyancies. Blue line shows total work. (C) Radially integrated work by buoyancy forces W_b(r).

Figure 3 shows the results in the case with Q_CMB = 8TW. In this case, a stable layer is possible since Q_conv becomes negative. The region with w_b(r) < 0 below the CMB appears in the center panel of Figure 3. The middle panel of Figure 3 shows the compositional contribution to w_b(r) is positive in the whole outer core while the thermal contribution is negative at r≳2, 200 km, meaning that compositional convection is possible to emerge in the upper part of the outer core although thermal and compositional convection can be excited in the lower part. On the other hand, W_b(r) is positive in the whole outer core as shown in the right panel of Figure 3. This means that formation of a stable layer depends on the extent of penetration of compositional convection from below. A stable layer survives below the CMB when penetration is weak, whereas a stable layer is completely destroyed by compositional convection when its penetration is strong. Note that the stable layer is thinner than that estimated by the criterion with thermal convective heat flux only (Q_conv < 0) used in the previous studies.

FIGURE 3

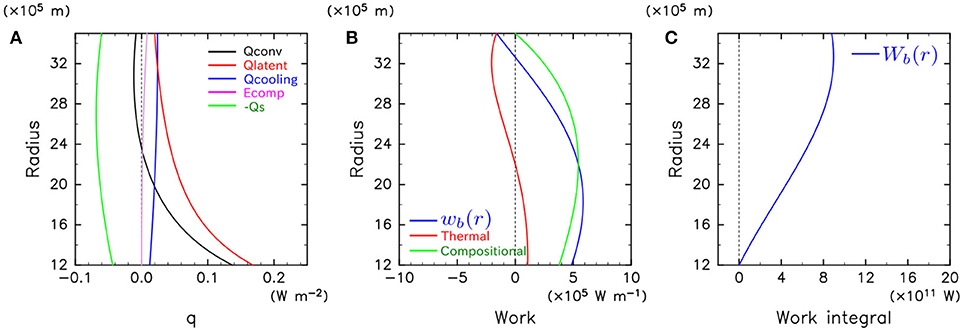
Figure 3. As in Figure 2 but for Q_CMB = 8TW.

Figure 4 shows the result in the case with Q_CMB = 4TW. In the right panel of Figure 4, there appears the region with W_b(r) < 0 below CMB, meaning that a stable layer is formed even when the extent of penetration of convection is maximum in this case. Note that the thermal contribution is negative in the almost whole outer core in this case.

FIGURE 4

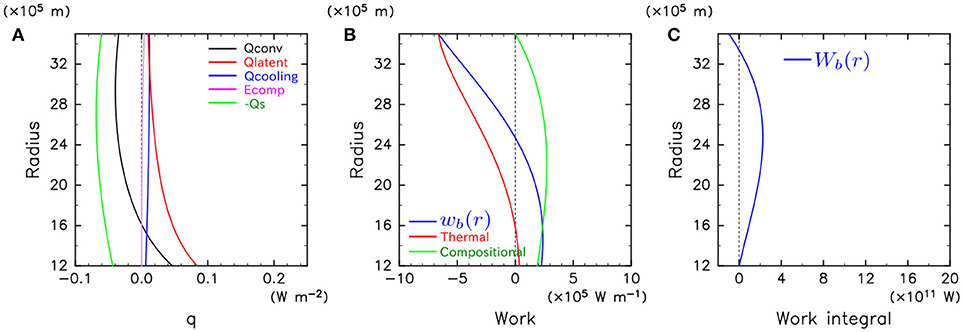
Figure 4. As in Figure 2 but for Q_CMB = 4TW.

Figure 5 shows the summary of stable layer formation as a function of Q_CMB. The red and blue lines indicate the thickness of a stable layer in the case of minimum and maximum penetration, respectively. It is found that no stable layer is formed when Q_CMB>Q_sCMB = 9.3TW, whereas a stable layer is absolutely formed when Q_CMB < 4.4TW. We also show the bottom of a stable layer estimated by the criterion with thermal convective flux only by the black line for comparison. It is clear that destruction by compositional convection cannot be ignored in order to estimate the thickness of the stable layer.

FIGURE 5

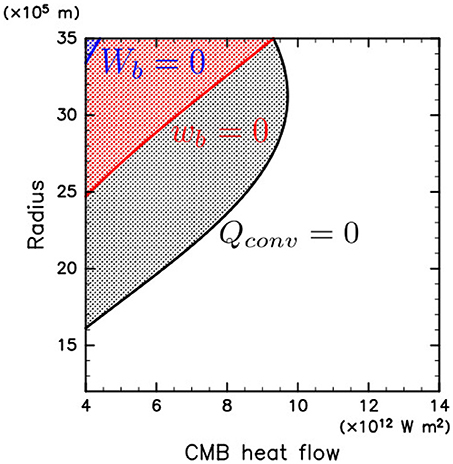
Figure 5. Possible stable layer thickness as a function of CMB heat flow. The blue and red lines indicate the thickness of the minimum and maximum stable layers, respectively. The black line shows the thickness of a stable layer estimated by thermal convective flux only.

4. Conclusions and Discussion

We proposed to use radial distribution of power by thermal and compositional buoyancy (rate of kinetic energy production) as a new criterion for estimating formation and destruction of a stably stratified layer by thermal and compositional convection. The method for calculating power by buoyancy forces in a 1-dimensional thermal and compositional budget model was presented, and was applied to a simple 1-dimensional model for the Earth's core. The thickness of the stable layer formed below the CMB is estimated for various values of the CMB heat flow considering the effect of mixing by compositional convection in the deeper region. When Q_CMB>Q_sCMB(= 9.3TW), no stable layer is formed due to occurrence of compositional and thermal convection in the whole outer core. When Q_CMB<Q_sCMB(= 9.3TW), formation of an upper thermally stable layer becomes possible, depending on the extent of penetration of compositional convection excited at ICB. When Q_CMB < 4.4TW, a stable layer can be formed even when penetration of compositional convection is maximal. Note that this critical value of Q_CMB varies depending on the value of Q_sCMB and model configuration for Earth's core. For example, constant density distribution and degree 2 polynomial isentropic temperature used in this study would not be precise enough for estimation of stable layer formation, since some discrepancies between previous studies were found to originate from different levels of approximation in the isentropic temperature profile (e.g., Labrosse, 2015). It is necessary to use more precise Earth models with more realistic distributions of density, isentropic temperature and other physical properties for definitive conclusions about the Earth's core.

Since the present CMB heat flow is expected in the range 5–15 TW (e.g., Lay et al., 2008), our results also support possibility of a stable layer formation below the CMB as the previous studies. However our estimations show the thickness of the stable layer is significantly thinner than that estimated with the criterion only by thermal convective flux used in the previous studies due to mixing by compositional convection. For example, when Q_CMB = 8TW, the thickness of the stable layer can be 250 km at most, which is about 1,000 km thinner than the estimation by convective heat flux criterion (see Figure 5).

The present paper significantly contributes to thermal and compositional evolution problems in planetary cores by giving dynamically consistent estimation of stable layer formation. All the previous studies did not consider whether kinetic energy is adequately supplied to the convecting part or not, which should be checked by calculating kinetic energy production distribution.

We estimate emergence of a stable layer by assuming that the whole outer core is convecting. This procedure seems to be contradictory since existence of a stable layer breaks the assumption of the whole outer core convection. As a matter of fact, the solutions obtained by our method are first order approximations of quasi-steady states where concentrations of ight elements and temperature averaged in the whole outer core vary in time while their radial distributions are stationary. Spherically averaged conservation equation of light elements without assuming a homogeneous mixed state is described as follows:

$\begin{array}{rc}\frac{\partial }{\partial t}(4\pi {\rho }_{a}C)+\frac{1}{r^2}\frac{\partial }{\partial r}(F_C+F_D)=0,& (27)\end{array}$

where C(r, t) is concentration of light elements, F_C(r, t) and F_D(r, t) are convective and non-convective fluxes such as diffusion, respectively. Assuming quasi-steady state, $C(r,t)=\overline{C}(t)+C^{\prime }(r)$, and integrating from r = c with the boundary condition F_C(c)+F_D(c) = S_C, Equation (1) is modified as

$\begin{array}{rc}{X}_C+F_C+F_D=S_C.& (28)\end{array}$

This equation means that we can construct new solutions by replacing F_C obtained with the assumption of whole outer core convection by F_C+F_D. For example, the flux distributions with F_D = 0 (r<r_t) and F_C = 0 (r>r_t) provide a quasi-steady solution for a given boundary r = r_t. The upper part of C′(r) can be constructed from F_D(r). This solution expresses the state where convection is active and mixes up the lower part r<r_t, while convection is suppressed and diffusion is dominant in the upper part r>r_t, forming stable stratification. Similar argument is possible for temperature by assuming T(r, t) = T_i(t)f(r), however, the thermal fluxes would be varied due to the difference of the temperature structure between the solutions with and without a stable layer. Then, in order to estimate thickness of a stable layer more precisely, after determining its bottom boundary with the criterion of kinetic energy production, we should give a certain temperature distribution in a stable layer and calculate distribution of kinetic energy production again. By repeating this procedure we can obtain more precise estimation of a thickness of a stable layer. For example, given a thermally diffusive temperature profile stable layer, re-calculations of w_b lead to 0.07% and 1% differences of a stable layer thickness for Q_CMB = 8TW and 4TW (examples of Figures 3, 4), respectively.

Quasi-steady stable layer thickness obtained in this study does not consider time scale for its formation, which would be governed by thermal diffusion. In order to discuss stable layer formation in the Earth's core more precisely, we should compare the diffusion time of possible thickness of the stable layer with a possible age of the inner core. When the diffusion time is sufficiently short, estimation with our method would be effective. In contrast, when the diffusion time is longer, we should solve thermal and chemical evolution of the core as a time-dependent problem in order to estimate formation of the stable layer, for example, as performed by Lister and Buffett (1998). For example, when the thickness of the stable layer is 100km, and thermal diffusivity is 10⁻⁵ m²/s, the thermal diffusive time becomes 30Myr. This is presumably much less than the age of the inner core, since it was estimated as O(Gyr) by the previous studies without the effects of the stable layer and the stable layer would be so thin that it would not largely affect the age of the inner core. In contrast, when the thickness is 1000km, the thermal diffusive time becomes 3Gyr, which is probably larger than the age of the inner core if it is not affected by the presence of the stable layer. Note that in the case of destruction of a pre-existing stable layer due to thermal and compositional convection excited at the ICB, we should examine time scale for destruction (erosion rate), which would be determined not only by thermal diffusion but also by other physical properties, such as convective velocity, strength of stratification and rotation, and so on.

Our model assumes that thermal and/or compositional convection mixes entropy and composition uniformly because thermal and/or compositional Rayleigh numbers become so large that convective motion is turbulent due to the smallness of the molecular diffusivities of the outer core. However, there are possibilities that convection with coherent structures emerges. For example, large scale columnar convection affected by the Earth's rotation may coexist with small scale turbulent convective motion due to larger values of eddy diffusivities which may contribute to decrease the effective Rossby number for large scale fluid motions. The extent of penetration of columnar convection into the upper stable layer depends on the ratio between the Brunt-Väisälä frequency and the rotation frequency, and on the typical width scale of the convective columns in the linear theory (Takehiro and Lister, 2001). However, it is not known whether the penetration of columnar convection would be an effective mechanism to erode the stable layer. Furthermore, it has been proposed that the light elements released at the ICB may form chemical plumes and/or blobs rising through the outer core without mixing, which could create a chemically stratified layer at the top of the core (e.g., Braginsky, 1993; Shimizu and Loper, 1997). Recent numerical calculations by Manglik et al. (2010) show that chemical plumes can penetrate into the thermally stratified layer and keep rising to some extent. In order to clarify these possibilities, 3-dimensional numerical simulations are needed although it may be difficult to resolve fluid motions with wide spatial spectral ranges.

In the present paper, we illustrate formation of thermally stable layer below the CMB when the heat flow is drawn by mantle convection and its destruction by compositional convection excited at the ICB. The method presented here can also be applied to compositionally stable layer and its destruction by thermal convection. It has been proposed that a stable layer would be formed below the CMB by accumulation of light elements released at the ICB (e.g., Loper and Roberts, 1983) or by diffusion of light elements from the mantle (e.g., Buffett and Seagle, 2010, 2011). By introducing contribution terms of barodiffusion and injection of light elements from the CMB, we can model stable layer formation including the effects of mixing by convection in a similar way with radial distribution of power by buoyancy forces.

In the layer diagnosed as thermally stable stratification, radial temperature gradient contributes to stabilize but that of concentration to destabilize. This configuration permits emergence of finger-type double diffusive convection. However, since finger-type convection mainly transports light elements (Turner, 1967) and increase stability through weakening radial concentration gradient, the stable layer would not be destroyed by this effect. In the case of a compositional stable layer, diffusive-type convection may emerge which mainly transports heat (Turner, 1965). Therefore, the stable layer would be maintained even when double diffusive convection occurs, although double diffusive convection may break up into a series of alternating convecting layers in some specific conditions.

Note that our method can apply not only to planetary cores but also to other general situations where convective and stable layers coexist. In general, the stable layer thickness, which is expected to be between the maximum and minimum estimates evaluated by W_b(r) = 0 and w_b(r) = 0, would be determined through complicated combined effects tied to the dynamics of chemical plumes and their possible interaction with the thermally stable layer, which are poorly understood. Nevertheless, in some extreme cases, the maximum or minimum estimates would give good stable layer thicknesses. For example, in planetary atmospheres where the effect of inertia is strong and advection of kinetic energy dominates local kinetic energy dissipation, the radially integrated kinetic energy production rate W_b(r) presumably gives a good estimation of stable layer thickness. In contrast, in the Earth's outer core, it is expected that the inertia terms in the equation of fluid motion can be neglected since the value of compositional diffusivity is significantly smaller than that of kinetic viscosity and the work done by convection is converted into magnetic energy. This means that advection of kinetic energy can be ignored and penetration of compositional convection scarcely occurs. Therefore, we can estimate thickness of a stable layer with local kinetic energy production rate w_b(r) only. For example, the red line in Figure 5 shows that a stable layer with a thickness of 250 km is formed when Q_CMB = 8TW in the simple model presented in the previous section. We should verify our new criterion by performing numerical experiments of 2- or 3-dimensional hydrodynamic models, and check the expectation mentioned above. Effects of double diffusive convection possibly emerging in the stable layer should be examined as well. Moreover, by investigating parameter dependence of extent of penetration of convection, more precise estimation of stable layer formation will be possible.

Author Contributions

ST did most of the theoretical formulation of this work. YS significantly contributed to 1D model development and figure generation.

Funding

This work was supported by JSPS (Japan Society for Promotion Science) KAKENHI Grant Numbers 16H01117 and 15H05834.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank three reviewers and the editor for their valuable comments, which were very helpful for improving the manuscript. This work was supported by the Research Institute for Mathematical Sciences, a Joint Usage/Research Center located in Kyoto University.

References

Braginsky, S. I. (1984). Short-period geomagnetic secular variation. Geophys. Astrophys. Fluid Dyn. 30, 1–78. doi: 10.1080/03091928408210077

CrossRef Full Text | Google Scholar

Braginsky, S. I. (1993). Mac-oscillations of the hidden ocean of the core. J. Geomag. Geoelectr. 45, 1517–1538. doi: 10.5636/jgg.45.1517

CrossRef Full Text | Google Scholar

Buffett, B. A. (2014). Geomagnetic fluctuations reveal stable stratification at the top of the earth's core. Nature 507, 484–487. doi: 10.1038/nature13122

PubMed Abstract | CrossRef Full Text | Google Scholar

Buffett, B. A., and Seagle, C. T. (2010). Stratification of the top of the core due to chemical interactions with the mantle. J. Geophys. Res. 115:B04407. doi: 10.1029/2009JB006751

CrossRef Full Text | Google Scholar

Buffett, B. A., and Seagle, C. T. (2011). Correction to 'stratification of the top of the core due to chemical interactions with the mantle'. J. Geophys. Res. 116:B07405. doi: 10.1029/2011JB008376

CrossRef Full Text | Google Scholar

Gomi, H., Ohta, K., Hirose, K., Labrosse, S., Caracas, R., Verstraete, M. J., et al. (2013). The high conductivity of iron and thermal evolution of the earth's core. Phys. Earth Planet. Inter. 224, 88–103. doi: 10.1016/j.pepi.2013.07.010

CrossRef Full Text | Google Scholar

Gubbins, D., Masters, T. G., and Jacobs, A. (1979). Thermal evolution of the earth's core. Geophys. J. Roy. astr. Soc. 59, 57–99. doi: 10.1111/j.1365-246X.1979.tb02553.x

CrossRef Full Text | Google Scholar

Labrosse, S. (2015). Thermal evolution of the core with a high thermal conductivity. Phys. Earth Planet. Inter. 247, 36–55. doi: 10.1016/j.pepi.2015.02.002

CrossRef Full Text | Google Scholar

Labrosse, S., Poirier, J. P., and le Mouel, J. L. (1997). On cooling of the earth's core. Phys. Earth Planet. Inter. 99, 1–17. doi: 10.1016/S0031-9201(96)03207-4

CrossRef Full Text | Google Scholar

Lay, T., Hernlund, J., and Buffett, B. A. (2008). Core-mantle boundary heat flow. Nat. Geosci. 1, 25–32. doi: 10.1038/ngeo.2007.44

CrossRef Full Text | Google Scholar

Lister, J. R., and Buffett, B. A. (1995). The strength and efficiency of thermal and compositional convection in the geodynamo. Phys. Earth Planet. Inter. 91, 17–30. doi: 10.1016/0031-9201(95)03042-U

CrossRef Full Text | Google Scholar

Lister, J. R., and Buffett, B. A. (1998). Stratification of the outer core at the core-mantle boundary. Phys. Earth Planet. Inter. 105, 5–19. doi: 10.1016/S0031-9201(97)00082-4

CrossRef Full Text | Google Scholar

Loper, D. E. (1978). The gravitationally powered dynamo. Geophys. J. Roy. Astr. Soc. 54, 389–404. doi: 10.1111/j.1365-246X.1978.tb04265.x

CrossRef Full Text | Google Scholar

Loper, D. E., and Roberts, P. H. (1983). “Compositional convection and the gravitationally powered dynamo,” in Stellar and Planetary Magnetism, ed A. M. Soward (New York, NY: Gordon Bearch Science Publlication), 297–327.

Google Scholar

Manglik, A., Wicht, J., and Christensen, U. R. (2010). A dynamo model with double diffusive convection for mercury's core. Earth Planet. Sci. Lett. 289, 619–628. doi: 10.1016/j.epsl.2009.12.007

CrossRef Full Text | Google Scholar

Pozzo, M., Davies, C., Gubbins, D., and Alfe, D. (2014). Thermal and electrical conductivity of solid iron and iron-silicon mixtures at earth's core conditions. Earth Planet. Sci. Lett. 393, 159–164. doi: 10.1016/j.epsl.2014.02.047

CrossRef Full Text | Google Scholar

Shimizu, H., and Loper, D. E. (1997). Time and length scales of buoyancy-driven flow structures in a rotating hydromagnetic fluid. Phys. Earth Planet. Inter. 104, 307–329. doi: 10.1016/S0031-9201(97)00035-6

CrossRef Full Text | Google Scholar

Stacey, F. D., and Davis, P. M. (2008). Physics of the Earth, 4th Edn. New York, NY: Cambridge University Press.

Google Scholar

Stevenson, D. J. (1983). Planetary magnetic fields. Rep. Prog. Phys. 46, 555–620. doi: 10.1088/0034-4885/46/5/001

CrossRef Full Text | Google Scholar

Takehiro, S., and Lister, J. R. (2001). Penetration of columnar convection into an outer stably stratified layer in rapidly rotating spherical fluid shells. Earth Planet. Sci. Lett. 187, 357–366. doi: 10.1016/S0012-821X(01)00283-7

CrossRef Full Text | Google Scholar

Turner, J. S. (1965). The coupled turbulent transports of salt and heat across a sharp density interface. Int. J. Heat Mass Trans. 8, 759–767. doi: 10.1016/0017-9310(65)90022-0

CrossRef Full Text | Google Scholar

Turner, J. S. (1967). Salt fingers across a density interface. Deep Sea Res. 14, 599–611. doi: 10.1016/0011-7471(67)90066-6

CrossRef Full Text | Google Scholar