- 1Department of Earth Sciences, University of Oregon, Eugene, OR, United States
- 2Department of Earth and Environmental Sciences, University of Michigan, Ann Arbor, MI, United States
- 3Department of Geosciences, University of Arizona, Tucson, AZ, United States
Flood basalt volcanism involves large volumes of magma emplaced into the crust and surface environment on geologically short timescales. The mechanics of flood basalt emplacement, including dynamics of the crustal magma transport system and the tempo of individual eruptions, are not well-constrained. Here we study two exhumed dikes from the Columbia River Flood Basalt province in northeast Oregon, USA, using apatite and zircon (U-Th)/He thermochronology to constrain dike emplacement histories. Sample transects perpendicular to the dike margins document transient heating of granitic host rocks. We model heating as due to dike emplacement, considering a thermal model with distinct melt-fraction temperature relationships for basaltic magma and granitic wallrock, and a parameterization of unsteady flow within the dike. We model partial resetting of thermochronometers by considering He diffusion in spherical grains as a response to dike heating. A Bayesian Markov-Chain Monte Carlo framework is used to jointly invert for six parameters related to dike emplacement and grain-scale He diffusion. We find that the two dikes, despite similar dimensions on an outcrop scale, exhibit different spatial patterns of thermochronometer partial resetting away from the dike. These patterns predict distinct emplacement histories. We extend previous modeling of a presumed feeder dike at Maxwell Lake in the Wallowa Mountains of northeastern Oregon, finding posterior probability distribution functions (PDFs) that predict steady heating from sustained magma flow over 1–6 years and elevated farfield host rock temperatures. This suggests regional-scale heating in the vicinity of Maxwell Lake, which might arise from nearby intrusions. The other dike, within the Cornucopia subswarm, is predicted to have a 1–4 year thermally active lifespan with an unsteady heating rate suggestive of low magma flow rate compared to Maxwell Lake, in a cool near-surface thermal environment. In both cases, misfit of near-dike partial resetting of thermochronometers by models suggests either heat transfer via fluid advection in host rocks or pulsed magma flow in the dikes. Our results highlight the diversity of dike emplacement histories within the Columbia River Flood Basalt province and the power of Bayesian inversion methods for quantifying parameter trade-offs and uncertainty in thermal models.
1. Introduction
The emplacement of flood basalt provinces involves a massive flux of magma into the crust from the mantle over 1–10 Myr timescales. Magmas that make it to the surface erupt to produce deposits with volumes of up to 103−104 km3 that are the largest known effusive eruptive events. Large volumes of intrusive magmatism accompany surface eruptions, as constrained by exhumed networks of large dikes and sills (e.g., Burgess et al., 2017), geophysical observations (e.g., Davenport et al., 2017), and petrologic mass balance (e.g., White et al., 2006). The extreme nature of these events, which are often associated with mass extinctions of life and oceanic anoxia (Courtillot and Renne, 2003), suggests that individual flood basalt eruptions are also anomalous within the spectrum of volcanic activity.
Eruptive rates estimated based on radioisotopic dating of flow sequences suggests average eruption rates between ~ 10−2 and ~ 101 km3/yr (e.g., Burgess and Bowring, 2015; Kasbohm and Schoene, 2018). Field observations of lava flows along with paleo-environmental proxies for flow advance (e.g., Thordarson and Self, 1998; Keszthelyi et al., 2006) suggest larger rates of ~ 102 − 104 km3/yr. Differences in these two estimates are not surprising, given that the geochronology considers an average over many flows and may include eruptive hiatuses. Such differences are an indication that eruptive tempo is highly unsteady over the duration of a typical flood basalt province.
Here we examine the problem of flood basalt eruption longevity and tempo through the lens of an exposed crustal transport network. We focus on two 8–10 m wide dikes exposed within the Chief Joseph Dike Swarm of the Columbia River Flood Basalts (CRFB) in northeastern Oregon, USA (Figure 1), integrating new thermochronologic measurements with modeling to constrain the thermal field around dikes produced as magma intruded then cooled and crystallized within the crust. We re-examine the Maxwell Lake dike, where previous modeling of geothermometry from high-temperature phase equilibria in partially melted granitoid host rocks near the dike margin (Petcovic and Grunder, 2003), has generated widely cited constraints on flood basalt eruption longevity. A new thermochronologic transect extends time-temperature constraints at Maxwell Lake to lower temperatures, providing constraints on the thermal history of host rocks as well as the duration of dike emplacement. We compare these results with a dike exposed in the Cornucupia region south of Maxwell Lake that we will refer to as the Lee dike, with similar outcrop scale geometry and a complementary low-temperature thermochronologic transect in granitic host rocks (Reiners, 2005).
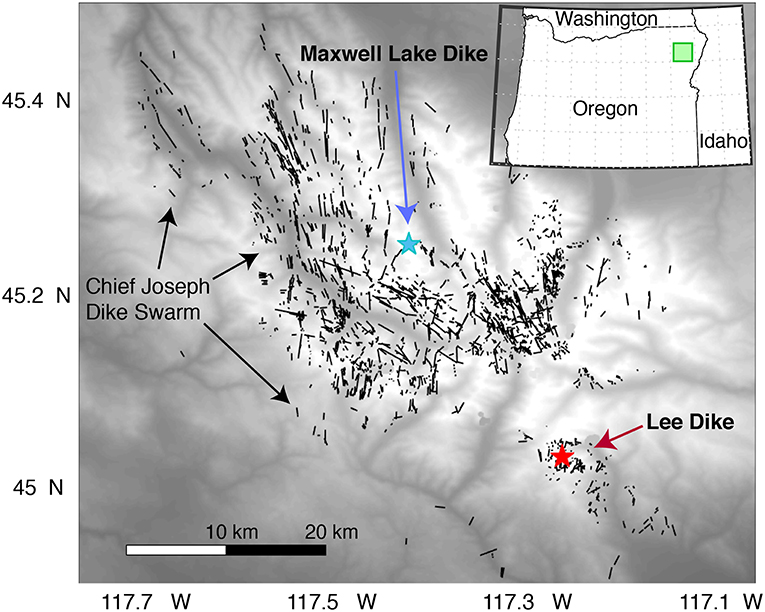
Figure 1. Map showing locations of the Maxwell Lake and Lee dikes, along with distribution of Columbia River Flood Basalt Chief Joseph Dike Swarm segments (green square on inset map).
To invert thermochronometric data for dike emplacement involves forward modeling of heat transport away from the dike and resetting of thermochronometers, both of which involve substantial uncertainties. We implement a Bayesian Markov-Chain Monte Carlo (MCMC) inversion as an objective information-gathering approach, in which many forward models with parameters stochastically sampled from prior constraints generate a posterior probability distribution function (PDF) representing the extent to which the data constrain unknowns of interest. In our case, these unknowns include dike longevity and time variation in magma flow, background temperature of the crust, thermal conductivity of wall rock, and parameters associated with diffusion of He in apatite and zircon grains.
MCMC inversion predicts that the two dikes have well-resolved but distinct thermal histories. The Maxwell Lake dike shows evidence for steady heating by magma over 1–6 years, within a warmed background environment at temperatures higher than a normal geotherm at paleodepth of ~ 2 km. The Lee dike, slightly thicker than Maxwell Lake, heated host rocks for a similar total duration of 1–4 years but at a highly unsteady rate that implies lower overall magma flux, in a normal geotherm at exposed paleodepth of < 1 km.
In what follows, we first introduce the regional geological context and prior work on the Maxwell Lake and Lee dikes. Sections 3–5 develop the methods for data analysis, forward modeling, and inversion. We then present the MCMC results in section 6, ending in section 7 with a discussion of implications for CRFB eruptive phenomenology and the general merits of the MCMC inversion approach for volcanologic data.
2. Field Sites
The CRFB are the youngest Large Igneous Province (LIP) on Earth, encompassing ~ 210,000 km3 basalt erupted in eastern Oregon, Washington and western Idaho, USA, in the interval between ~ 17 and 5 Ma. Although total volumes erupted are the smallest of known continental LIPs globally, the degree to which primary structures are well-exposed and a rich history of study (Reidel et al., 2013; Camp et al., 2017) make the CRFB a model for LIP phenomenology.
CRFB dikes are variably exposed throughout the province, although the fraction of these dikes that fed surface flows is unknown. Dikes are particularly well-exposed in northeastern Oregon, where exhumation of the Wallowa mountains (Zak et al., 2015) and granitic bodies to the south provide a cross-sectional view of the shallow CRFB plumbing system. Thousands of dike segments exposed in this region define the Chief Joseph Dike Swarm (Taubeneck, 1970). Dike compositions and ages are similar to lavas from the Imnaha, Grande Ronde, and Wanapum formations, which make up ~ 84% of the total CRFB volume and may have been erupted in only 300–400 ka (Barry et al., 2013; Ladderud et al., 2015) and perhaps < 100 ka for most of the Grande Ronde (Kasbohm and Schoene, 2018).
We focus on two CJDS segments here, at Maxwell Lake in the Wallowa Mountains and in the Cornucopia region to the south of the Wallowas (Figure 1). The Maxwell Lake dike outcrops in tonalite of the ~ 125.6 Ma Craig Mountain pluton of the Wallowa batholith (Zak et al., 2015), at a paleo depth of ~ 2.5 km based on structure contouring the base of Imnaha flows regionally (Petcovic and Grunder, 2003). It strikes N20°E, similar to the average strike of CJDS segments regionally (Taubeneck, 1970). The average dip is near vertical at 75° W, although small amplitude variability on 10s of meter scale along strike is common. Dike width in our study area is ~ 8 m, however width undulations over the ~ 1 km exposed length of the dike is suggestive of an intrusive structure that is planar only on larger scales. The dike composition is correlative to the Wapshalla Ridge member of the Grande Ronde basalt (Petcovic and Dufek, 2005), one of the largest flow packages in the CRBG with total volume of 5 × 104 km3.
Previous work on the Maxwell Lake dike has focused on partial melt observed in wall rocks near the dike margin, which constrains the amount and duration of heat conducted away from the dike during active magma flow and subsequent cooling. Petcovic and Grunder (2003) mapped four zones of distinct mineralogic assemblages containing progressively decreasing partial melt as a function of distance from the dike margin. Although these zones of partial melt vary somewhat in their spatial extent along strike of the dike, on average the zone of partial melt extends 2–4 m from the dike margin. Thermal modeling of this partial melt zone (Petcovic and Grunder, 2003; Petcovic and Dufek, 2005) suggested that active flow of magma occurred for 3–4 years at Maxwell Lake. We collected a 100-m transect of wall rock samples perpendicular to the dike margin exposed at Jackson Lake, ~ 0.8 km southwest of where (Petcovic and Grunder, 2003) conducted their sampling and mapping.
The Lee dike segment is ~ 10 m wide and ~ 1 km long, in the Pine Lakes region of the Cornucopia stock in northeastern Oregon (45.0305°N, 117.250°W), dated to 120–123 Ma from biotite Ar-Ar and Zr U-Pb geochronology (unpublished data from Peter Zeitler and George Gehrels, Figure 2). Petcovic (2004) suggested that this dike is Wanapum composition, and described the petrography and textural variations across the exposure of the dike directly adjacent to which we collected a transect of wallrock samples. The strike and dip of the dike in this location is N2°E, 75°W, and the margins are strongly quenched within about 10–20 cm of the wallrock. Principal phases of the dike are plagioclase, clinopyroxene, minor orthopyroxene, and Fe-Ti oxides. Johnson et al. (1997) dated the Cornucopia stock at 116.8 ± 1.2 Ma, though ICP-MS and biotite 40Ar/39Ar dates on the most distal sample we collected were 123 and 122 Ma, respectively. The stock is dominantly two-mica trondhjemite (Taubeneck, 1964), containing plagioclase + quartz + biotite + muscovite + cordierite + Fe-Ti oxides +/– alkali feldspar + trace apatite, zircon titanite, and rare allanite (Johnson et al., 1997). In the vicinity of the Lee dike, wallrock shows some sericitization and possible poikiolitic recrystallization textures within about 5 m of the dike, possible small melt pockets and veinlets in samples 7.3 and 9.5 m away, and chloritization/sericitization around 12–14 m.
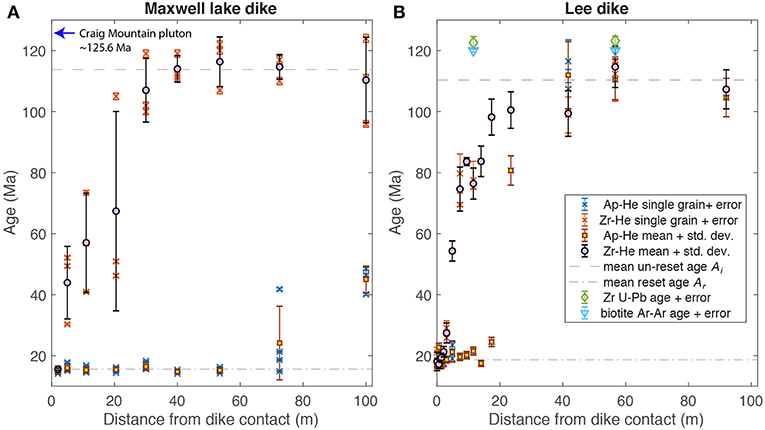
Figure 2. (A,B) Transect of apatite and zircon He thermochronometric ages as a function of distance from Maxwell Lake and Lee dike contacts. Constraints on unrest age of Maxwell Lake comes from Zak et al. (2015), while U-Pb and K-Ar ages constrain host rock ages at Lee dike. Dashed lines are mean of thermochronometric ages used for Ar and Ai in Equation (7).
2.1. Sample Collection and Analysis
At the Maxwell Lake dike, we collected ~ 2 kg samples at approximately 2, 5, 11, 20.5, 30, 40, 53.5, 72.5, and 100 m distance from the dike margin. Samples were processed using crushing, sieving, magnetic, and density separation methods at Zirchron, LLC in order to concentrate zircon and apatite crystals. At the University of Michigan HeliUM lab, we selected apatite and zircon grains for (U-Th-Sm)/He and (U-Th)/He analyses, respectively, based on size, clarity, morphology, and the lack of visible inclusions under 120–160x stereo zoom with a Leica M165C microscope. We analyzed three or four apatite and zircon grains per sample. Grain dimensions were digitally measured under the microscope prior to packing each grain in Nb foil. An Alphachron Helium Instrument was used for He extraction. Using a diode laser, apatite grains were heated to ~ 900 °C for 3 min and zircon grains were heated to ~ 1200 °C for 10 min. The extracted He was spiked with 3He, purified using gettering methods, and analyzed on a quadrupole mass spectrometer. A known quantity of 4He was analyzed at regular intervals. We sent degassed grains to the University of Arizona for dissolution and U, Th, and Sm analysis using isotope dilution and solution HR-ICP-MS methods (Guenthner et al., 2016).
Samples from the Lee Dike region were collected in a dike-perpendicular transect at distances ranging from 2 cm to 92 m from the dike margin. Apatite and zircon separates were prepared from 2-kg samples using standard separation procedures similar to those used for the Maxwell Lake samples, and (U-Th)/He measurements were made at Yale University using procedures described in Reiners et al. (2004). Raw (U-Th)/He data for the Maxwell Lake and Lee dikes along with distances from the dike margin are presented in Supplementary Data. Slight differences in processing and resultant data arise from the 15 years difference between analysis of Maxwell Lake dike samples (2017) and Lee dike samples (2002).
3. Low-Temperature (U-Th)/He Thermochronology and Age Interpretation
Thermochronometric ages from transects around the Maxwell and Lee dikes are shown in Figure 2. Although both dikes are of similar width, the pattern of Zr-He and Ap-He partial resetting perpendicular to the contacts are quite different. Apatite is partially reset out to 100 m from the dike at Maxwell Lake, whereas it reaches unreset background values 40–50 m away from the Lee dike contact. Zircon exhibits a qualitatively similar pattern between dikes, partially reset to smaller distances from the dike contact than apatite.
The low-temperature thermochronologic record of geologically short-duration (days to thousands of years) heating events such as dike emplacement reflects a competition between the rapid rate of the thermal diffusion of heat through rocks and the comparably slow rate of the chemical diffusion of radiogenic daughter products (in the case of (U-Th)/He chronometers, 4He nuclides) in individual apatite and zircon crystals. Both thermal and chemical diffusion depend on large-scale temperature gradients in the domain, although at different scales: thermal diffusion proceeds according to bulk (outcrop-scale) heat capacity and thermal diffusivity, while chemical diffusion is a function of diffusion domain (crystal-scale) size as well as experimentally determined activation energy and diffusivity of the daughter nuclides in the mineral of interest. The patterns of partial resetting around Maxwell Lake and Lee dikes suggest that granitic wallrocks at each location experienced different thermal histories, with a longer or hotter magmatic heat pulse at the Maxwell Lake vs. Lee.
The He content of apatite and zircon crystals is controlled by two processes: the time-dependent radiogenic production of 4He during the alpha-decay of U and Th nuclides and the temperature-dependent diffusive loss of 4He. Assuming a spherical diffusion geometry and uniform distribution of parent nuclides, the He concentration as a function of time t and dimensionless radial position r* (scaled by radius a of a spherical grain, as in Wolf et al., 1998) is
D(t) is a chemical diffusivity, which is a function of time-temperature history and activation energy Ea and follows an Arrhenius relationship
where R is the gas constant, D0 is He diffusivity at infinite temperature (also called the frequency factor), and T(t) is a thermal history. Pr(t) is the He production rate
with U(t), Th(t), and Sm(t) the abundance of specific parent nuclides at time t (note that Sm is only measured in apatite) and the λ parameters are decay constants.
The general analytical solution for production-diffusion in a sphere (Equation 1), assuming a constant production rate Pr of He (Wolf et al., 1998), is
defining a helium age He/Pr as a function of time, the parameters that control D(t)/a2 (Equation 2), and an initial He age *He/Pr.
Temperature sensitivities of the apatite He and zircon He thermochronometers are commonly described using the closure-temperature concept (Dodson, 1973), because these systems are most commonly used to constrain the rock cooling over millions-of-year timescales that results from rock exhumation (Ehlers and Farley, 2003; Reiners and Brandon, 2006). The closure-temperature concept assumes an initial He age of zero, a monotonic cooling history, and a specific cooling rate (Dodson, 1973). For a 10°C/Myr cooling rate, the closure temperature for typical apatite and zircon crystals is 67 and 183°C, respectively (Farley, 2000; Reiners et al., 2004). Here, we are interested in the resetting of these He thermochronometers over much shorter (yr to kyr) timescales that characterize the emplacement, conduit activity, and thermal relaxation of a magmatic dike.
We calculate the expected fractional loss of He, Fd, that an apatite or zircon crystal would experience given a thermal history predicted for a particular location by the thermal forward model described below. We do not use approximate solutions to diffusive He loss (Watson and Cherniak, 2013), as we can accurately numerically evaluate the exact solution for fractional loss from a spherical diffusion domain with an initially uniform distribution of He (Fechtig and Kalbitzer, 1966; McDougall and Harrison, 1999; Reiners, 2009)
where σT is
We evaluate Equation (5) numerically using 1,000 terms. We calculate the approximate observed fractional resetting from the thermochronologic ages measured along each transect (Reiners, 2009; Cassata et al., 2010):
where A is the observed He age, Ar is the time elapsed since the heating event (emplacement of CRFB dikes), and Ai is the unreset age (crystallization age of the host pluton).
The kinetic parameters, activation energy Ea and frequency factor D0, vary for different minerals and are derived from diffusion experiments on apatite and zircon standards. For a single mineral system, Ea and D0 are also known to vary from crystal to crystal, most significantly as a function of self-irradiation dose (Shuster et al., 2006; Flowers et al., 2009; Gautheron et al., 2009; Guenthner et al., 2013). For our fractional resetting calculation, we explore a range of Ea and D0 values for both apatite and zircon observed in natural crystals of low to moderate self-irradiation dose, as is appropriate for the U-Th compositions and ca. 120 Ma formation age of the crystals dated here.
There is an apparent positive correlation between available Ea and D0 values (Figure 3) for the diffusivity of He in both apatite and zircon. To simplify data inversion, we make use of this relationship to reduce the total number of free parameters in the problem. We find as a function of Ea as
where (dimensional) p1 and p2 define a power regression to the data in Figure 3. In the MCMC model we explore a range of apatite Ea,Ap of 120–145 kJ/mol with a standard error of 1.414, and p2 = 5.074 in Equation (8). For zircon we explore a range Ea,Zr of 160–175 kJ/mol with a standard error of 1.288, with and p2 = 2.083 in Equation (8). Standard errors calculated from the Ea in Figure 3. We emphasize that this functional relationship is utilized to simplify grain scale complexity in the face of multi-parameter and multi-physics inversion, rather than to make inferences about the mechanics of He loss in zircon or apatite.
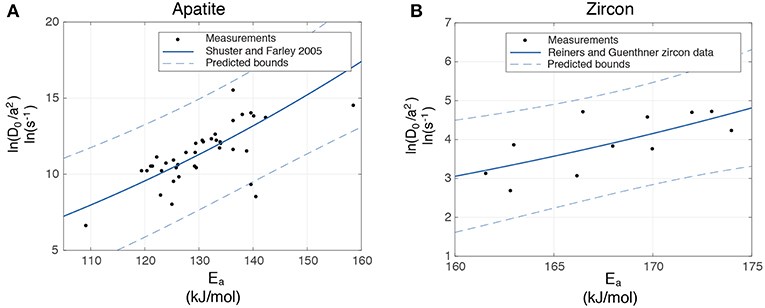
Figure 3. Observed variability in activation energy and frequency factor for the diffusion of He in (A) apatite and (B) zircon crystals (Reiners et al., 2004; Shuster et al., 2006; Guenthner et al., 2013). In each panel, the black dots are the Ea and calculated from diffusion experiments on single crystals or sample aliquot. Solid blue line is power regression fit to this relation, parameter values given in text. Dotted lines are 95% confidence bounds. Apatite data include diffusivity of both 4He (natural) and 3He (doped). Zircon data include the post-high-T results from Reiners et al. (2004) and samples RB140, BR231, M127 from Guenthner et al. (2013).
Ideally we would use the emplacement age of the basalt to constrain Ar, and Ai would correspond to the crystallization age of the plutonic host constrained from other methods. However, examination of Figure 2 suggests that neither the near-dike ages nor the far-field ages correspond precisely to inferred CRFB emplacement times or pluton crystallization ages determined by radiogenic isotopic methods. We do not focus on resolving this apparent discrepancy here, but rather use the consistency in near-dike and far-field thermochonologically determined ages to define apparent reset and unreset ages Ar and Ai (dashed lines in Figure 2). These may overestimate the intrusion ages and underestimate the crystallization ages by up to 1–2 Myr. Determining Ar and Ai from the transects allows us to focus on the pattern of partial resetting, which encodes relative differences in dike-induced wall rock heating.
4. Thermal Model
Emplacement of magmatic dikes induces a transient heating of host rocks such as recorded by the geothermometers described in section 3. Heat transport in host rocks is often assumed to be dominantly conductive, although advection of heated host pore fluid (or magmatic volatiles) also probably contributes. Coupled advection-diffusion of heat may also contribute mechanical impacts. For example, thermal pressurization of host pore fluid has been called upon to explain fracture patterns around some shallow dikes (Delaney, 1982).
The Maxwell Lake dike was previously modeled assuming conductive host rock heating in 1D, with either an analytic parameterization of magma emplacement (Petcovic and Grunder, 2003) or with a numerical 2D advection-diffusion unidirectional flow model of magma transport through a slot (Petcovic and Dufek, 2005). Both methods resulted in similar predictions of dike longevity (3–4 years) that matched near-dike high temperature constraints from petrography. Here we develop a conductive heat transfer model that accounts for distinct non-linear melt-fraction temperature relation in tonalitic host rock and basaltic dike, parameterizes magma flow within the dike, and neglects advective heat transport in wall rocks.
We assume that temperature varies in the dike-perpendicular dimension only. Small deviations from planar dike geometry are often observed and could contribute to complexities in the thermal field, but are excluded here. We model temperature evolution in a multicomponent 1D system consisting of dike material and host rock, following
where the index i is equal to 1 for assumed tonalitic host rock and 2 for basaltic dike material, T is temperature (a function of spatial location x—distinct from r in the chemical model of section 3—and time t), ρi is the density of material i, cp the specific heat capacity, k thermal conductivity, L is the latent heat of fusion, and Fi(x, t) is the melt fraction (Figure 4). It is well-known that material thermal properties vary with temperature in the presence of partial melt [non-zero Fi(x, t), Whittington et al., 2009] as well as with composition (Jaupart and Provost, 1985). For reasons discussed in the next section, we do not consider mixture models for thermal parameters or temperature-dependent thermal properties, taking constant cp and k. We also do not consider differences in density between solid and liquid phases.
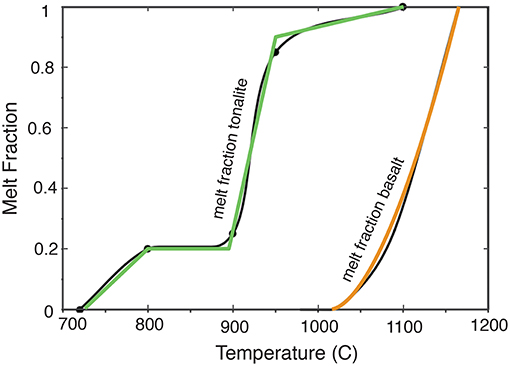
Figure 4. Melt fraction vs. temperature curves for basalt and tonalitic rocks. Black curves are reproduced from Petcovic and Dufek (2005), while colored curves are fits used for thermal modeling in this study.
Equation (9) is solved on a spatial domain of length R with left end point at the center of a dike with half-width H/2. We assume an initially constant temperature domain and sudden dike emplacement, such that initial conditions are piecewise constant
where Tl, 1 is the dike interior temperature (taken to be the magma liquidus) and TBG is the background temperature of the crust at the paleo depth of the dike. At one end of the domain, a Dirichlet boundary condition T(x = R, t) = TBG for all time mimics a background geotherm. We choose a large domain size (R at least 5 times the farthest sample ~ 100 m from the contact) to minimize boundary influence on transient temperature field near the dike.
At the other end of the domain, we assume that the dike is actively transporting magma for a certain length of time Tf, during which temperature in x ≤ H/2 is specified by a function that parameterizes the effects of monotonically decreasing flow rates within the dike as advection of magma competes with cooling. This function provides the forcing for thermal diffusion within host rocks, given by
and imposed only when Td ≥ Tbdy(t), with τc and τw as parameters that control the time variation of temperature within the dike. Parameter τc scales the dike's overall longevity; for example, if dike flow is modeled as a step function (as in Petcovic and Grunder, 2003), τc is the total duration of flow. Such a model likely oversimplifies many dike emplacement scenarios, because finite magma supply implies pressure gradients that decline over time, which leads to growing thermal boundary layers and decreasing temperature at the dike-host rock contact (Bruce and Huppert, 1989). The parameter τw controls how rapidly the dike temperature decreases around τc, as a model for such flow steadiness.
Equation 11 states that temperatures within the dike x ≤ H/2 are set to a spatially uniform but time-varying value. Total longevity of active magma flow modeled by Equation (11) is τf, the time at which point the tanh function is within a small threshold δ of unity (we take δ = 0.01). At this time, we assume that the dike has stopped transporting magma and switch to a Neumann boundary condition at the dike center for all subsequent time ∂T(x = 0, t ≥ τf)/∂x = 0. Note that Equation (11) needs not provide a boundary condition for all time less than τf. Because Tl,1 > TBG, initially dike emplacement drives diffusion of heat away from the dike. However, if at any time prior to τf the specified dike temperatures imply Td(t) < Tbdy(t), for example if the dike heats up host rocks then shuts off suddenly, host rocks buffer the dike temperature and (Equation 11) no longer forces dike temperatures (although magma is still assumed to be flowing until time exceeds τf).
Figure 5 plots Equation (11), normalized by the contact temperature difference, to illustrate how different flow scenarios translate to boundary heating and how τc, τw relate to τf. Larger values of τw result in dike temperatures that more gradually transition from the initial dike temperature (the liquidus Tl,1) to a time-evolving host rock temperature at the dike boundary τbdy(t). Although we are not modeling dike-interior temperatures explicitly, this mimics a monotonic growth of thermal boundary layers as flow rate within the dike goes down (Bruce and Huppert, 1989) to explore a range of emplacement scenarios.
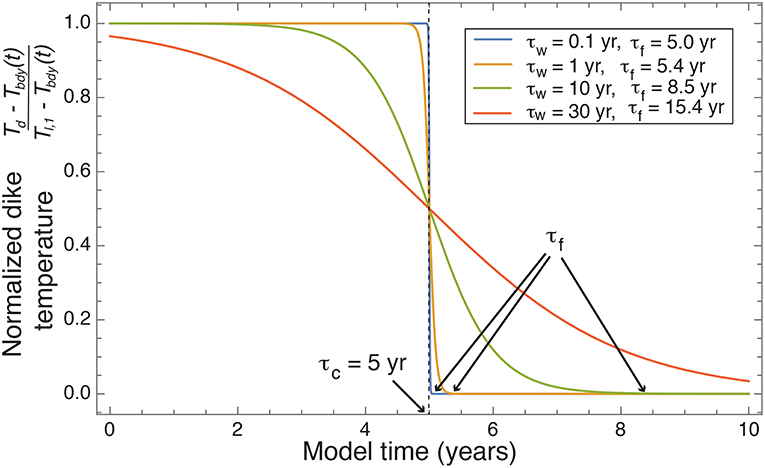
Figure 5. Normalized dike temperature from Equation (11), illustrating trade-offs between the scale for dike active flow τc and the scale for flow unsteadiness τw. τf is the total duration of temperatures elevated over background, and may be similar to τc for small τw. Equation (11) is enforced in our model for dike contact temperatures Td > Tbdy(t) and times t < τf.
For granitic wall rocks we assume a melt fraction law F2(x, t) parameterized from Petcovic and Dufek (2005), shown in Figure 4. We use a piece-wise linear fit similar to Karlstrom et al. (2010) to capture impacts of variable mineral assemblage on melting regime. For basalt we model the melt fraction temperature relation as
where Ts,1 and Tl,1 are the basalt solidus and liquidus temperatures and b is an exponent that parametrizes the effects of mineral phase assemblage. b close to 1 is appropriate for mafic compositions (e.g., Huber et al., 2009).
To solve Equation (9) we rewrite in terms of an effective heat capacity , for which i is specified by the composition (basalt or granite), in a scaled spatial domain defined by the invertible coordinate transform
ξ ∈ [0, 1] is the new spatial coordinate and λ is a stretching factor (Erickson et al., 2017). With these modifications, Equation (9) becomes
The choice of coordinate transform (Equation 13) is motivated by a need for implementing an efficient numerical solution to Equation (14) that retains high resolution near the dike for accurate prediction of partial melt, described in the next section. When discretized in space, a grid of evaluation points with uniform spacing becomes a staggered grid that concentrates points near the dike where more numerical accuracy is desired. Equation (14) is discretized using 2nd order centered finite differences and an adaptive 4th order Runge Kutta method in time. We have tested this code against a benchmarked numerical solution with equally spaced grid points (Karlstrom et al., 2017).
Typical model output is shown in Figure 6. Wall rock time-temperature histories depend on distance from the dike contact, duration and form of the heating event specified by the dike contact boundary condition (τc = 3 years, τw = 0.1 years in Figure 6, with k = 3 W/mC), and background temperature enforced by the far-field boundary condition as illustrated by two representative values of TBG. Resetting of thermochronometers is predicted by applying these time-temperature histories to Equations (5) and (7), which result in time dependent partial resetting as plotted in Figure 7. This time dependence implies that we must run our thermal models for long enough that near-equilibrium He concentrations are achieved. We find that >95% of equilibrium thermochrometer partial resetting is achieved in apatite and zircon for the range of parameters considered here if simulations are run for at least five thermal conduction timescales over the sampled region (100 m, illustrated by the vertical lines in Figure 7).
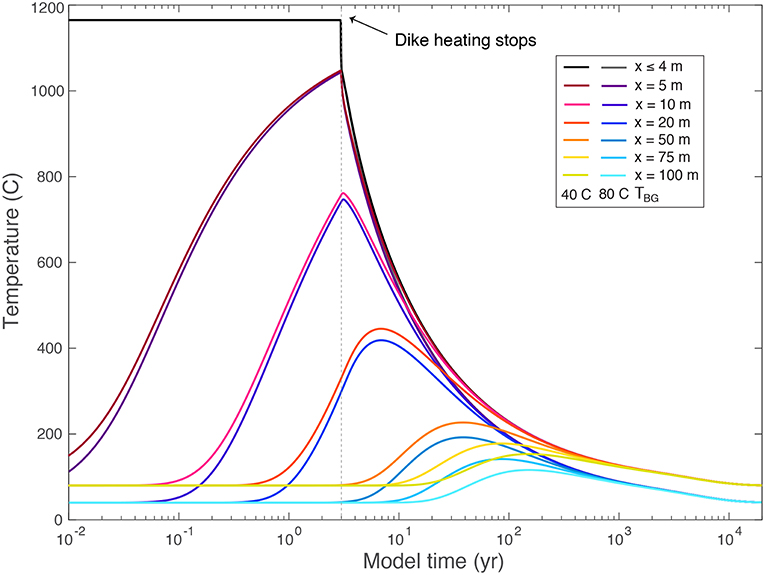
Figure 6. Temperature as a function of distance from dike center x and time for an example H/2 = 4 m thick dike emplacement scenario and two background temperatures TBG (red and blue colors). Dike interior temperature evolution is given by the black curve. Forced heating by magma flow is close to a step function in time (τc = 3 yr, τw = 0.1 yr, giving τf = 3.04 yr, k = 3 W/mC ), and stops at the time indicated by vertical dashed line.
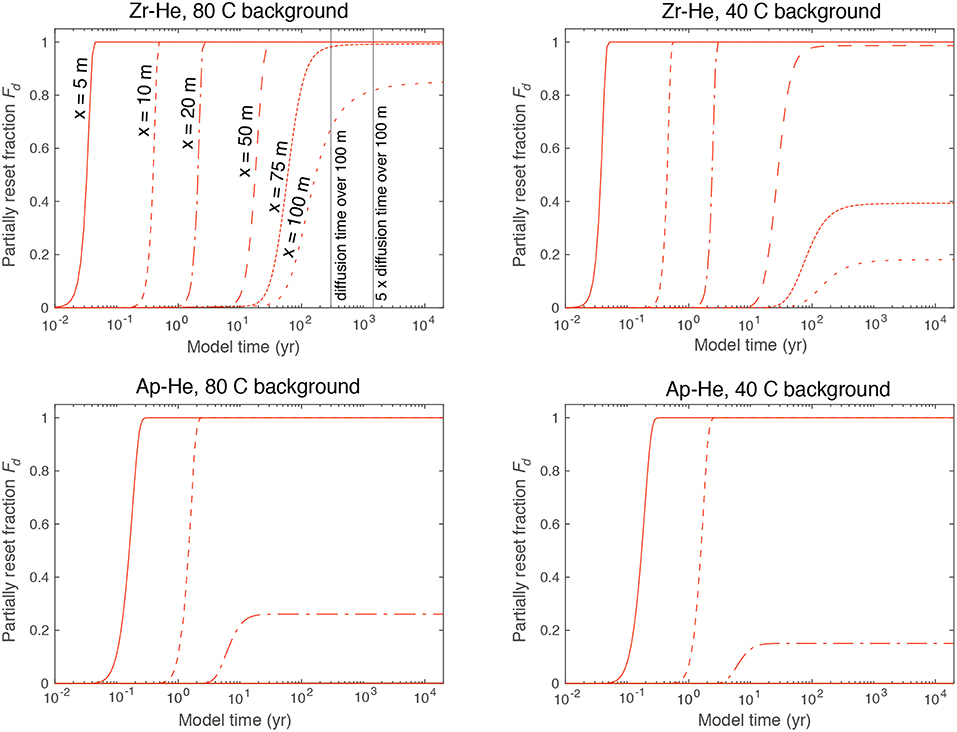
Figure 7. Relationship between partial resetting of apatite and zircon He thermochronometers as a function of heating and hold time (kinetics of thermal vs. chemical diffusion), with the same parameters as Figure 6 and two background temperatures TBG. Curves on each panel represent listed distances x from the dike center, as in Figure 6. Vertical lines in upper left panel correspond to multiples of a thermal diffusion time over 100 m ().
5. Bayesian Inverse Modeling Framework
Epistemic and aleatoric uncertainties limit our ability to accurately invert for the longevity and steadiness of magma flow through CRFB dikes or the pre-intrusion temperature of host rocks. Aleatoric uncertainties in material parameters such as thermal conductivity, activation energy for Helium diffusion in zircon or apatite may trade off with uncertainties in the precise location of samples in relation to the dike. Such uncertainties are minimizable given sufficiently accurate sampling, calibration of fractional resetting models and experimental petrology, and sufficient resources to carry out the needed experiments. However, for the models described in sections 3–4, additional epistemic uncertainties such as the precise 3D geometry of the dike margin, the functional form of the dike temperature through time that parameterizes magma flow, or the presence of advective heat transport (essentially, whether our model describes the relevant physical problem), are convolved with aleatoric uncertainties.
We therefore approach inverse modeling as an information-gathering exercise specific to our hypotheses. We pose a forward model and then systemically vary unknown parameters to assess trade-offs and find a best fit. A generic data vector containing M independent datasets , may be predicted by a possibly non-linear forward model G(m) with m model parameters such as described in section 4, d = G(m) + ϵ, where ϵ is a vector of measurement errors. Inversion consists of estimating the m that minimize the residual rk = dk − Gk(m), accounting for measurement error.
We implement a Bayesian inversion utilizing MCMC sampling of the parameter space. An introduction to Bayesian inversion can be found in Mosegaard and Tarantola (2002), and applications of similar methods to geophysical problems in (e.g., Fukada and Johnson, 2008; Bursik et al., 2012; Anderson and Segall, 2013). We briefly summarize the method here.
Our goal is to derive a multidimensional posterior PDF that represents the inversion solution in accordance with Bayes' Theorem
Equation (15) states that the posterior PDF P(m|d), defined as the probability of a model prediction vector m given a data vector d, is proportional to the product of an assumed known prior PDF P(m) with a Likelihood function P(d|m) that measures the misfit of data with model predictions accounting for data uncertainties.
It is worth emphasizing that in the framework of Bayesian statistics, the inverted parameters are given by distributions specified in the posterior PDFs rather than by single best-fitting values. Posterior PDFs reflect both our ability to predict the data with a model and our prior state of knowledge, for which we know some parameters very well and some very poorly. For all parameters in this study we assume a uniform prior distribution with upper and lower bounds. We assume that errors ϵ are uncorrelated, such that their covariance matrix Σk = diag(σk), with σk the variance associated with the error ϵ of each dataset. If each dataset is normally distributed, the appropriate likelihood function is then
where rk = dk − Gk(m) is the residual vector and |Σk| is the determinant of the covariance matrix. In our application, the number of datasets M is two for the Maxwell Lake and Lee dikes (Ap-He, Zr-He).
We derive posterior PDFs for model parameters that minimize residuals through MCMC sampling. We implement the Metropolis-Hastings algorithm (Metropolis et al., 1953) where parameters are randomly perturbed many times, and accepted if the posterior probability calculated from Equation (15) is higher than the previous iteration. Multiple Markov Chains are run with randomized initial values, to help ensure that we are exploring the enture parameter space. We follow (Anderson and Segall, 2013; Anderson and Poland, 2016) in using the log of Equation (16) to calculate acceptance of a particular iteration. A random subset of higher probability iterations is also discarded, which helps the minimization procedure escape local minima. Parameters are assumed uniformly distributed between upper and lower prior bounds given in Table 1.
5.1. The Challenge of Model Efficiency
For the 1D model and data presented in sections 3 and 4, there are a minimum of 26 parameters that must be constrained at each dike: for both host rock and intruded basalt, we need solidus and liquidus temperatures, melt fraction exponent (if using Equation 12 as a model for compositional dependence of partial melting), mixture density, latent heat of fusion, and two thermal parameters (conductivity and heat capacity). For the fractional resetting calculation to match thermochronometric ages, we further need the activation energies, diffusivities, and mean grain sizes for He diffusion in both apatite and zircon, as well as un-reset ages (crystallization age of pluton) and reset ages (exact timing of dike emplacement). Finally, we have two parameters associated with the dike flow model, mean dike thickness, and the background temperature TBG of the domain.
Our use of solely thermochronologic and structural constraints for models is insufficient to resolve this number of parameters, so we reduce the parameter space dimensionality to focus on particular sensitivities of the inversion. We use experimental values for thermal and Arrhenius parameters in the thermochronologic fractional resetting calculation, then assume known un-reset and reset ages as dictated by the data, approximately the crystallization age and Grande Ronde emplacement age respectively. However, Ar and Ai are determined by the thermochronologic transects described in section 3 in order to focus model inversion on the partial resetting pattern. We assume a uniform dike width approximately equal to field measurements.
We can assess much of the inherent trade-offs in thermal models by considering only one unknown thermal parameter—a thermal conductivity k—assuming phase equilibria and melt fraction relations for host rock and dike are known, but that background temperature is unknown. We simplify fractional resetting by parameterizing the ratio in terms of activation energy Ea (Figure 3), reducing the number of unknown parameters to one each for apatite and zircon. This results in six unknown parameters (Ea,Ap, Ea,Zr, Tbg, Tw, Tc, k) at each dike that must be inverted for.
The MCMC method is guaranteed to converge given infinite time (e.g., Mosegaard and Tarantola, 2002), and a sufficiently large number of iterations generates a PDF that closely approximates the true posterior PDF. Unfortunately, there is no way to predict the amount of time required for convergence, and many iterations (perhaps 104 − 106, e.g., Anderson and Segall, 2013) may be required to resolve a high dimensional posterior PDF. A certain amount of trial and error is also involved in picking step size for parameter perturbations during an inversion. Thus, MCMC methods require efficient forward models to be practical.
The forward model described in section 4 is only marginally well-suited to this procedure. In each iteration, we must solve a partial differential equation for long enough time that the transient heat pulse from the dike propagates past our farthest-out partially reset samples ~ 100 m from the dike contact. As Figure 7 demonstrates, the trade-off between heating and holding time inherent to thermochronometers implies that simulations running for less than ~ 5 conductive cooling timescales over the sampled extent (as plotted in Figure 6) may significantly underpredict partial resetting of apatite. We run each simulation for a total time equal to , which ranges from ~ 500-5000 years for the range of thermal parameters considered.
In addition to time stepping, we must use sufficient spatial resolution near to the dike that partial melting of host rocks can be accurately predicted. We find ~ 1 m spatial resolution near the dike to be sufficient. As a final complication, a Dirichlet temperature condition far from the dike is used to enforce a background geotherm in 1D, and we must have a large enough spatial domain that this does not affect the transient heating near to the dike. We find through numerical experimentation that ~ 500 m total domain length is sufficient.
To accomplish the required number of simulations in a reasonable amount of time, we have minimized inversion complexity in two ways. First, we use a parallelized MCMC code package (MCMC Hammer, Anderson and Poland, 2016) to run simultaneous Markov Chains on multiple cores. Second, we simplify our forward model for efficiency. We assume constant material properties, such that our predicted values will average any variation with temperature or melt fraction. We discretize the heat (Equation 14) on a transformed domain (via Equation 13 with λ = R/7) to reduce the number of spatial points required to achieve both a large domain and high resolution near the dike. We utilize a 4th order adaptive Runge Kutta method for non-uniform time stepping in Matlab. A single forward model required to evaluate Equation (16) takes on the order of 5–10 s with this method.
We run 70–75 Markov chains in parallel with randomized initial guesses until 2−4 × 104 kept MCMC steps per chain are achieved. In total 2.4 × 106 kept samples from all chains are incorporated into a posterior PDFs for Maxwell Lake, with a mean accepted fraction of 0.55 across all chains (meaning that roughly twice as many simulations were performed as kept). For the Lee dike, 3.0 × 106 kept samples are incorporated into a posterior PDF and the MCMC algorithm exhibited a mean accepted fraction of 0.23. Three diagnostics of MCMC convergence are discussed in Appendix A. Although non-normality in estimated parameters complicates a robust assessment, we are confident that convergence to the posterior PDF has been achieved at least for the thermal parameters.
6. Results
Marginal posterior PDFs for the Maxwell Lake and Lee dikes are shown in Figure 8, along with bivariate covariance plots for each of six parameters (as well as one derived parameter Tf) that were sampled during MCMC inversion in Figures 9, 10. For each dike, these plots provide an assessment of the degree to which each parameter is constrained by the inversion, and how parameters trade off in pair-wise fashion to optimize fitting the data. We can also compare the posterior PDFs of the Maxwell and Lee dikes to each other.
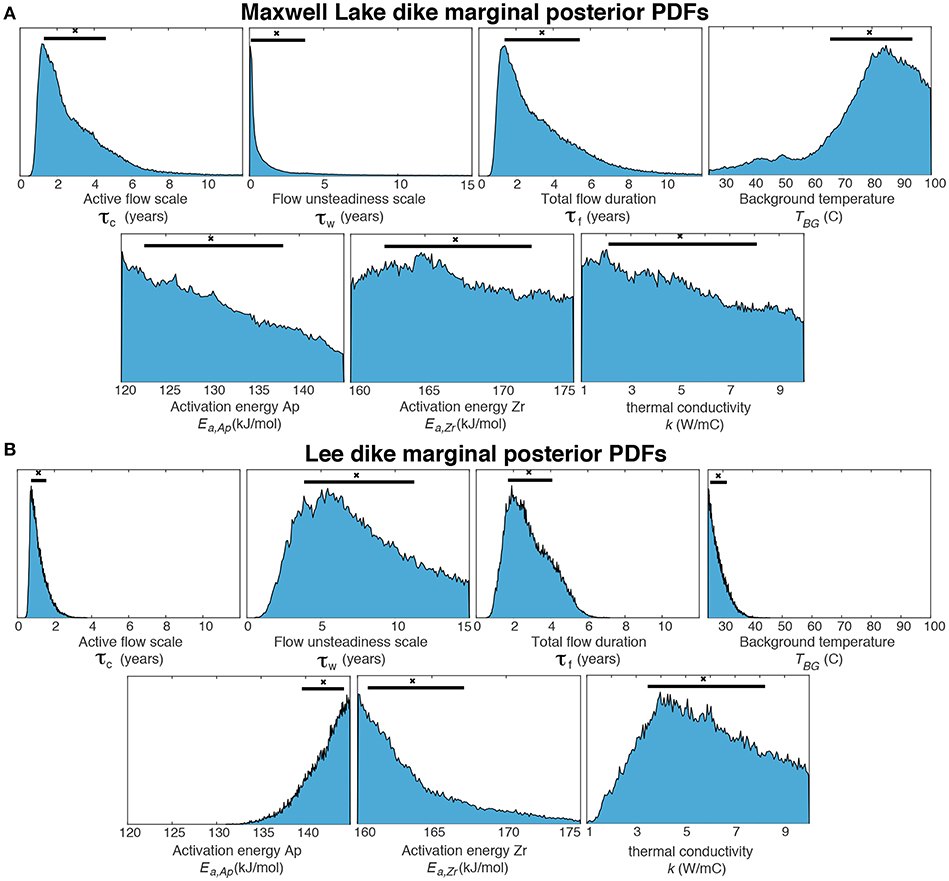
Figure 8. Marginal posterior PDFs for (A) Maxwell Lake and (B) Lee dike parameters estimated from MCMC inversion (τf is derived using Equation 11). Black horizontal bars correspond to 68% confidence intervals associated with expectation values from the posterior PDF, while black symbols are the median of the distribution (Table 1).
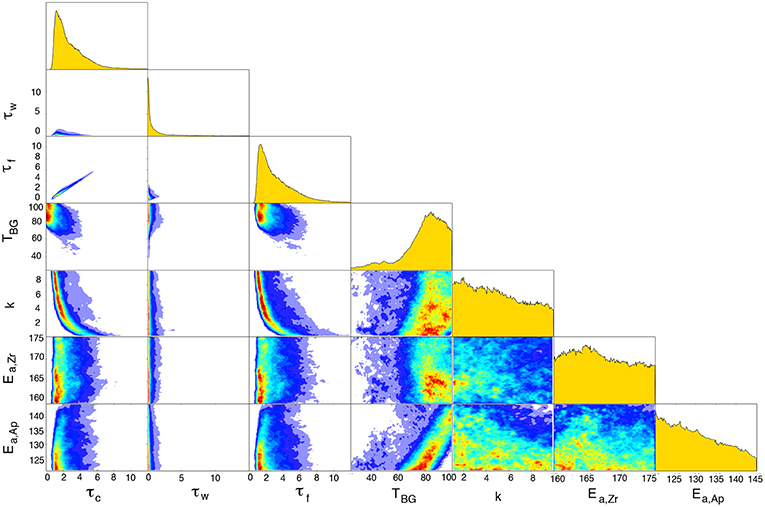
Figure 9. MCMC marginal posterior PDFs as in Figure 8 and bivariate covariance plots for the Maxwell Lake dike. TBG, τc, τw, k, Ea,Ap, Ea,Zr are estimated parameters, while total flow duration τf is derived using Equation (11). Covariance plots show how parameters trade off with one another within the posterior PDF, warmer colors indicate higher probability.
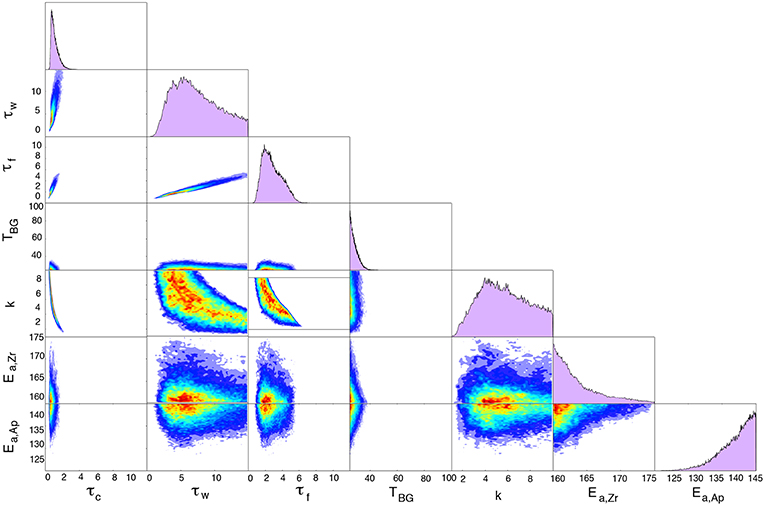
Figure 10. MCMC marginal posterior PDFs as in Figure 8 and bivariate covariance plots for the Lee dike. Warmer colors in covariance plots indicate higher probability. TBG, τc, τw, k, Ea,Ap, Ea,Zr are estimated parameters, while total flow duration τf is derived using Equation (11).
In general, we find that the overall pattern of partial resetting is well-fit by our model. Although total residual errors for the Maxwell Lake dike are lower than for the Lee dike (Table 1), this can largely be attributed to relatively greater noise in the Lee dataset. Posterior PDFs are either monotonically sloped or unimodal and peaked, implying reasonably simple and consistent forward model behavior for best fitting parameters. Best fitting parameters and residual error, as well as 68 and 95% confidence intervals that represent ranges of well-fit parameters for each dike, are reported in Table 1. Example solutions, using parameters associated with the median best fitting models for each dike, are plotted against thermochronmetric ages in Figures 11A–C. Within error we can fit the overall resetting pattern of partial resetting around both Maxwell and Lee dikes well enough to justify the relative simplicity of our thermal model. The largest errors in both cases are near to the dike, for which our best fitting models systematically predict a sharper partial resetting transition in rocks near the dike contact.
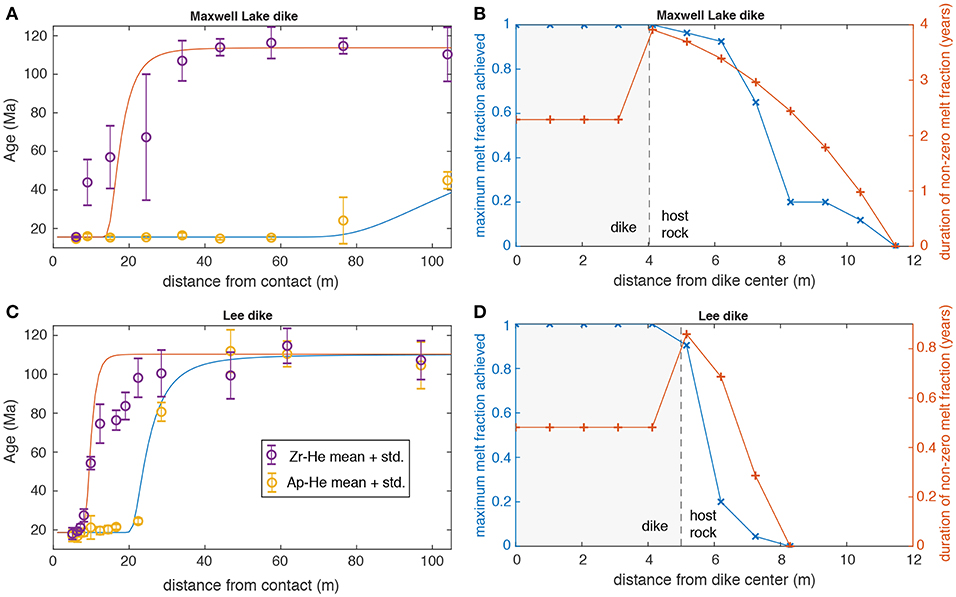
Figure 11. Example fits of Maxwell Lake and Lee dike thermochronology data, plotting curves associated with the median of MCMC-derived PDFs (Table 1) for both zircon (red curves) and apatite (blue curves) ages. (A,C) show the predicted thermochronometric ages for each dike, using average ages plotted in Figure 2. (B,D) plot the predicted maximum melt fraction and duration of non-zero melt fraction as a function of distance from the dike center associated with these model runs (dike material is shaded gray, while symbols indicate non-uniformly spaced grid nodes). Duration of partial melt in host rock can exceed the active lifetime of the dikes due to lower solidus of tonalite relative to basalt.
Posterior PDFs for each dike exhibit the well-known trade-offs between parameters in a heat conduction model (Figures 9, 10). For example, similar time-temperature histories can be obtained by increasing the longevity of active dike heating or increasing the wall rock thermal conductivity. Similarly, background temperature trades off weakly and inversely with dike longevity. But the distinct pattern of thermochronometer partial resetting at the Maxwell and Lee dike imply resolvable, distinct thermal histories.
The Maxwell dike is best explained by an emplacement scenario in which sustained dike heating (and thus magma flow) occurred over τf ~ 1.4–5.4 years, based on the 68% confidence intervals for the posterior PDF (Table 1). Small τw in the range of 0.1−3.8 years implies that unsteady flow is not likely, so τf as derived through Equation (11) is largely a function of the timescale for active flow τc. Background temperature is constrained to be between 65.8−93.7°C, and is relatively sharply peaked. On the other hand thermal conductivity is predicted to be between 2.1 and 8.1 W/mC, but is not sharply peaked implying poor constraint overall. Activation energies for apatite and zircon are even more poorly constrained. Good fits to thermochronometric ages can be attained for any value of EaAp and Ea,Zr, and the Gelman-Rubin diagnostic —although flawed, as discussed in Appendix A—suggests these parameters may have not converged in our inversion. For the Maxwell dike, we consider flow parameters and background temperature to be constrained by Bayesian MCMC inversion.
Further refinements might be made if we assume particular parameter values, due to covariance between some parameters. For example, Ea,Ap is seen to be well-correlated to TBG, with higher background temperatures implies higher activation energy parameters. Likewise, a longer lived dike (larger Tf) implies lower background temperature Tbg and lower wallrock conductivity. Tonalite rock conductivity of 3 W/mC as assumed by Petcovic and Dufek (2005) implies total flow duration in the range of 2–4 years, in agreement with their predictions based on modeling of high-temperature geothermometry.
For the Lee dike, predicted total heating duration is similar to Maxwell Lake with τf ~ 1.7–4.1 years. However, in contrast to Maxwell Lake significant time variation in heating is predicted, with large flow unsteadiness scale τw ~ 3.9–11.3 years implying an immediate and extended decrease in boundary temperature over the active duration τf. This is illustrated in Figure 12, using best fitting τc and τw for each dike. Thermal conductivity is predicted to be in the range of k~ 3.5–8.2 W/mC, similar although somewhat larger in magnitude and more peaked than Maxwell Lake. Background temperature is uniformly small, indistiguishable from near-surface temperatures TBG ~ 25.7–31.5 C. The Lee dike inversion appears to place somewhat better constraints on activation energies, predicting Ea,Zr ~ 160.7−167.2 kJ/mol and Ea,Ap ~ 139.6−144.3 kJ/mol. However, MCMC convergence is questionable for these parameters (Appendix A), and it is worth noting that the 95% confidence intervals overlap for estimates of the activation energies for the Lee and Maxwell Lake dikes.
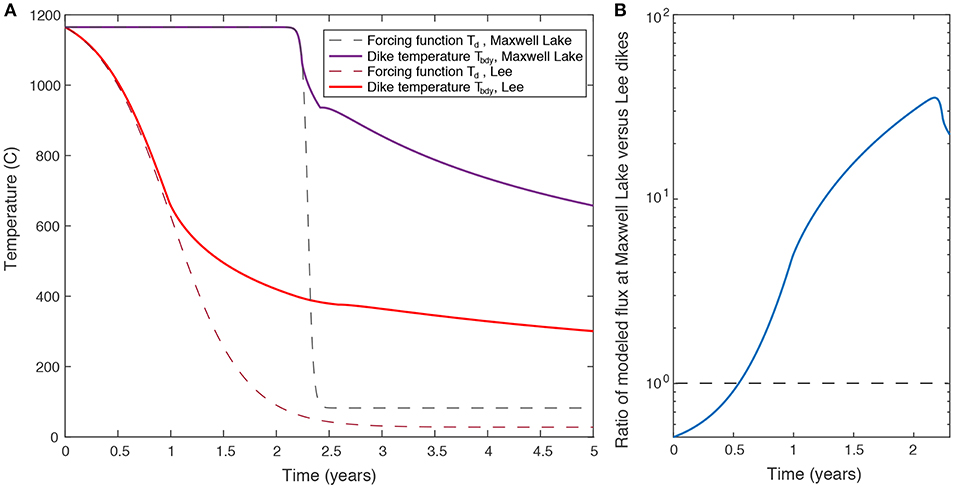
Figure 12. (A) Time variation of predicted Maxwell Lake and Lee dike contact temperatures Tbdy taking parameters τc, τw, k, and TBG from the median of MCMC posterior distributions (Table 1). Dashed line is the forcing function Td from Equation (11). Tbdy diverges from Td in time due to thermal buffering from heated wall rocks. (B) Predicted ratio of flux between Maxwell Lake and Lee dikes from Equation (18). Dashed line is equal flux, values greater than unity indicate larger flux from Maxwell Lake dike.
Our forward models predict not only the temperature distribution but also the extent and degree of partial melt in the dike and tonalitic host rock (Figure 4). Figures 11B–D shows the distribution of partial melt predicted at the Lee and Maxwell lake dikes for median fitting models (parameters in Table 1), as well as the duration of non-zero melt fraction predicted as a function of distance from the dike center. At Maxwell Lake, partial melt is predicted up to 8 m away from the dike, with significant melt lasting 3–4 years at distances up to 4 m away. At the Lee dike, despite the larger assumed half-width (5 vs. 4 m), the strongly decreasing heating predicted by the thermochronology results in significant melt only in the ~ 1 m nearest to the dike contact, lasting only 0.6–0.8 years. At both dikes, the duration of melt in the dike itself is predicted to be much shorter than in the host rocks, because higher solidus temperature of basalt vs. tonalite results in crystallization of the dike soon after flow stops, while conduction-buffered temperatures in the host rocks remain above the solidus.
At Maxwell Lake, partial melt is readily observed both in handsample and thin section, and was mapped petrographically by Petcovic and Grunder (2003). Although the location of that mapping is ~ 0.8 km along strike of the Maxwell Lake dike from our transet location, melt was observed by those authors out to 4–6 m from the dike margin, in qualitative agreement with our predictions. In contrast, the Lee dike exhibits much more subtle signs of partial melt, although a similarly detailed petrographic analysis has not yet been carried out. Our best fitting thermal models predict a much narrower zone of partial melt around the Lee dike.
7. Discussion
Large Igneous Provinces such as the Columbia River Flood Basalt Group represent an end member of volcanic activity in which large volumes of magma are rapidly emplaced into the Earth's crust and surface environment, with consequences for tectonics, climate, and life. Constraints on the tempo of these events are diverse but always indirect as there are no historical examples of similar magnitude eruptions. This study introduces new constraints on emplacement histories of two 8–10 m wide CRFB dikes from low-temperature thermochronology, using a Bayesian inversion framework that provides estimation of parameters governing heat transport into wall rocks. Previous work by Petcovic and Grunder (2003) and Petcovic and Dufek (2005) focused solely on high temperature, near-dike data at one of our study sites (the Maxwell Lake dike). The low-temperature (~60−180 C closure temperature) thermochronology here provides complimentary constraints on magma flow, as well as far-field host rock temperatures at the time of dike emplacement.
There is considerable uncertainty in physical parameters—and to some extent the physical processes themselves—involved in dike emplacement. We utilize a forward model that is relatively simple in the spectrum of magma transport modeling: a parameterization of unsteady but monotonically varying magma advection within a dike that governs 1D heat conduction in host rocks. We also simplify the description of He atomic diffusion in modeling partial resetting of thermochronometric ages, by parameterizing the role of grain size as a function of activation energy in zircon and apatite. Such simplifications permit a Bayesian Markov Chain Monte Carlo inversion approach for exploring a six dimensional parameter space with ~ 106 forward calculations to resolve posterior PDFs that outline the most likely parameter values.
Conductive heating models fit the apatite and zircon partial resetting patterns in granitic host rocks well, except for regions near to the dike contact. The manner of this misfit (overpredicted ages near to the dike and thus underprediction of heat pulse propagation) is likely evidence for either pulsed non-monotonic flow, or advection of heat by fluids. Petcovic (2004) modeled pulsed heating to explain high temperature thermometry, although did not present a systemic study of such models. Distinguishing between transport-limited vs. diffusion-limit thermal regimes (e.g., Petford and Gallagher, 2001; Karlstrom et al., 2017) or the specific time-variations in magma flow that is allowable by the data is beyond the scope of our study. Such work would also benefit from high temperature near-dike (1–5 m from the margin) constraints in addition to low temperature thermochronology that constrain 10–100 m partial resetting patterns. Here, we focus on the predicted differences in emplacement histories between two otherwise similar dikes, and the physical implications of parameter trade offs. Such uncertainty analysis is a critical aspect of inversion: we can demonstrate that the two dikes have resolvably different emplacement histories but can also identify poorly constrained parameters that will help future model development and data collection efforts.
The Maxwell Lake dike has been geochemically linked to the Wapshilla Ridge member of the Grande Ronde formation (Petcovic and Dufek, 2005), the single most voluminous eruptive unit preserved in the CRFB (5−10 × 103 km3 erupted in multiple events contained within Wapshilla Ridge). However, macroscale structural characteristics of the Maxwell Lake dike are similar to thousands of other Chief Joseph Dike Swarm segments in the region as illustrated in Figure 1 (Taubeneck, 1970; Morriss and Karlstrom, 2018). Without petrographic and textural indicators of partial melt in the granitic host rocks that indicate prolonged magma flow and careful geochemical fingerprinting, it would be challenging to identify this segment as a prominant feeder of CRFB flows. Our results show that the Lee dike, located south of the Maxwell Lake dike in a region of high dike segment spatial density and exhibiting similar (slightly larger) width and orientation, has a resolvably different emplacement history recorded by low temperature thermochronetry.
Although the total duration of active heating (and thus magma advection) from the Lee dike is not predicted to be significantly different than the Maxwell Lake dike by our inversion, the time variation of dike-host contact temperature and thus magma flux rate is resolvably different. Our model for unsteady heating at the dike/host rock contact (Equation 11) parameterizes the growth of thermal boundary layers separating flowing magma initially at its liquidus temperature from host rocks with parameters τc and τw (Figure 5). Such decreases could arise from solification or decreases in driving pressure gradient that reduce the effective width of active flow within the dike (Bruce and Huppert, 1990; Petcovic and Dufek, 2005), from along-strike flow localization (Bruce and Huppert, 1989; Wylie et al., 1999), or variations in viscous dissipation (Fialko and Rubin, 1999). Equation (11) also parameterizes unsteady flow as long as pulses are close enough spaced in time that heat transport in wall rocks is diffusion-limited.
We leave explicit consideration of flow mechanics, and thus the assessment of dike-transported flow volumes, for a future study. However, a simple model illustrates some of the expected implications of our results for relative flux between the two dikes. Volumetric flux of unidirectional viscous flow through a slot of length ℓ and halfwidth H/2 is
where dP/dz is the non-hydrostatic pressure gradient driving flow and μ is the magma viscosity. Let us assume that the dike-host rock contact temperature Tbdy(t) is proportional to effective dike width H and separately to pressure gradient dP/dz, as might occur if growing thermal boundary layers are gradually truncating flow in the dike. If we then assume that all but measured width is equal between dikes, the ratio of flux from Equation (17) between Maxwell Lake and Lee dikes is then related to the different dike widths HM, HL cubed. Due to the assumption that boundary temperature is proportional both to vertical pressure gradient and dike thickness, the flux ratio is proportional to boundary temperatures Tbdy,M, Tbdy,L raised to the fourth power, giving
Equation (18) is plotted in Figure 12B for representative model fit parameters (MCMC median values listed in Table 1). We see that, initially, the thicker Lee dike has a higher flux due to the strong dependence on width in Equation (17). However, declining pressure gradients and growth of boundary layers as implied by the predicted dike contact temperature Tbdy,L(t) quickly dominate and Maxwell Lake has sustained flow rates more than an order of magnitude larger than Lee for most of its active lifetime. This is consistent with an interpretation that Maxwell Lake was a feeder dike to a significant surface eruption (known to be the case from its chemical composition) whereas the Lee dike might not have generated much if any surface eruptive flux.
MCMC inversion predicts a cooler background temperature (by some 50–70 degrees) for the Lee dike relative to Maxwell. Distinct background temperatures would be expected based on the paleodepth differences between Maxwell and Lee dikes. But partial resetting of apatites out to >100 m away from the Maxwell dike contact indicate temperatures that are hotter than any reasonable geotherm at ~ 2 km depths. We speculate that CRFB magmatism transiently increased the regional geothermal gradient (e.g., Murray et al., 2018), sufficiently raising the background temperatures to produce the observed apatite He age pattern next to the Maxwell Lake dike without resetting apatite He ages across the Wallowa Mountains region (Crowley and Reiners, 2001). Maxwell Lake lies within a region containing a large spatial density of CRFB dike segments exposed at the surface, with ~ 5 segments per km2 (Morriss and Karlstrom, 2018). If most segments are Grande Ronde age, recent dating (Kasbohm and Schoene, 2018) implies an eruptive flux of ~ 1 km3/yr. Crustal magma transport of this magnitude is likely sufficient not only to induce regional heating but also to modulate the bulk rheology of the crustal column participating in magmatism (Karlstrom et al., 2017; Perry-Houts and Karlstrom, 2018).
Marginal posterior PDFs for thermal conductivity of wall rocks are somewhat similar for each dike, in both cases suggesting conductivities larger than typical for intact granitic rocks. We view this result as an indication that our physical model is incomplete. Near-surface advection of hydrothermal fluids are an obvious missing ingredient, as this would result in more efficient heat transport away from the dike contact and a larger apparant thermal conductivity. Such results might also be consistent with the lesser degree of partial melt in the vicinity of Maxwell Lake and Lee dikes than predicted by our model (Figure 11), although we expect low permeability of granite would limit the efficiency of fluid movement. We do not attempt to quantify this scenario further here.
Our inversions do not constrain activation energies for the He diffusion model at either Maxwell Lake or Lee dikes, as indicated by the shapes of the PDFs (95% confidence intervals for Ea,Zr, Ea,Ap overlap for both dikes) and our metrics of inversion convergence (the Gelmin-Rubin diagnostic in Table 1). Another thermochronology transect at both dikes to constrain chemical kinetics or petrographic analysis that resolve near-dike temperatures could help better define these parameters. More detailed kinetic models that explicitly invert for grain size and diffusivity along with activation energy may also be required.
8. Conclusions and Future Directions
Bayesian Markov-Chain Monte Carlo inversion of low temperature thermochronology around two CRFB dikes near the spatial locus of the Chief Joseph Dike Swarm in NE Oregon suggests distinct emplacement histories. By combining physics-based forward models with a probabilistic approach to inversion, we can identify differences in likely patterns of magma flow and in the background temperatures far from the dike contact at the time of emplacement. Although both dikes are of similar spatial dimensions, the Maxwell Lake dike likely transported a larger volume of magma for a longer time than the Lee dike, consistent with near-dike host rock petrography and the correlation of Maxwell Lake dike to Wapshilla Ridge flows. The Lee dike has composition similar to Wanapum lavas but is not yet linked to any particular surface expression. Our inversion suggests that application of thermochronology to other CRFB dikes in granitic host rocks that are common in the Wallowa Mountains region could resolve feeder vs. non-feeder dikes and magma transport mechanics on a LIP scale.
More broadly, this study suggests that Bayesian inversion methods have utility in inverting volcanologic data. We have focused on thermochronology, jointly inverting for partial resetting of two different chronometers by combining models for dike-scale heat conduction with grain-scale models for Helium diffusion in zircon and apatite. Other data, for example from high temperature geothermometry or paleomagnetic partial resetting, could easily be incorporated into this framework and might contribute to a more well-constrained posterior PDF. Model complexity does represent a significant challenge, due to the requirement that many thousands of forward models are needed for the MCMC inversion to converge. More effort is needed to develop reduced-order models for magma transport processes that are faithful parameterizations of computationally intensive multiphysics simulations. The payoff is a more robust predictive understanding of magmatic processes at a level commensurate with data granularity, which is a needed step toward connecting observations of active processes with the geologic record of magmatism.
Author Contributions
LK performed MCMC inversions, wrote the forward modeling codes, and the manuscript. KM performed Maxwell Lake dike measurements. PR performed Lee dike measurements. LK and KM devised the study. All authors contributed to manuscript editing.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Matthew Morriss for field assistance during sampling of the Maxwell Lake dike and for discussions surrounding the Chief Joseph Dike Swarm, Heather Petcovic for helpful information about prior work at Maxwell Lake, and Victoria E. Lee for assistance during sampling of the Lee dike. LK acknowledges field work support from the National Science Foundation EAR 1547594. Peter Zeitler and George Gehrels are acknowledged for providing dates on the Cornucopia pluton at the Lee Dike. We thank Kyle Anderson for developing the MCMC Hammer code used for data inversion, Stefan Nicolescu for analytical assistance with the Lee dike samples, and Amanda Maslyn for analytical support at the University of Michigan HeliUM lab. Two reviewers and editor Mattia Pistone provided constructive comments that improved the manuscript.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2019.00090/full#supplementary-material
Supplementary Data. Table S1 contains thermochronology data for each grain analyzed, sample locations, ages, and errors for Maxwell Lake and Lee dikes.
References
Anderson, K., and Segall, P. (2013). Bayesian inversion of data from effusive volcanic eruptions using physics-based models: application to Mount St Helens 2004-2008. J. Geophys. Res. 118, 2017–2037. doi: 10.1002/jgrb.50169
Anderson, K. R., and Poland, M. P. (2016). Bayesian estimation of magma supply, storage, and eruption rates using a multiphysical volcano model: Kilauea volcano, 2000-2012. Earth Planet. Sci. Lett. 447, 161–171. doi: 10.1016/j.epsl.2016.04.029
Barry, T., Kelley, S., Reidel, S., Camp, V., Self, S., Jarboe, N., et al. (2013). Eruption chronology of the Columbia River Basalt Group. Geol. Soc. Am. Spec. Pap. 497, 45–66. doi: 10.1130/2013.2497(02)
Bruce, P. M., and Huppert, H. E. (1989). Thermal control of basaltic fissure eruptions. Nature 342, 665–667.
Bruce, P. M., and Huppert, H. E. (1990). “Solidification and melting along dykes by the laminar flow of basaltic magmam” in Magma Transport and Storage, ed M. P. Ryan (Chichester, UK: John Wiley and Sons).
Burgess, S. D., and Bowring, S. A. (2015). High-precision geochronology confirms voluminous magmatism before, during, and after Earth's most severe extinction. Sci. Adv. 1:e1500470. doi: 10.1126/sciadv.1500470
Burgess, S. D., Muirhead, J. D., and Bowring, S. A. (2017). Initial pulse of Siberian Traps sills as the trigger of the end-Permian mass extinction. Nat. Commun. 8:164. doi: 10.1038/s41467-017-00083-9
Bursik, M., Jones, M., Carn, S., Dean, K., Patra, A., Pavolonis, M., et al. (2012). Estimation and propagation of volcanic source parameter uncertainty in an ash transport and dispersal model: application to the Eyjafljallajokull plume of 14-16 April 2010. Bull. Volcanol. 74, 2321–2338. doi: 10.1007/s00445-012-0665-2
Camp, V. E., Reidel, S. P., Ross, M. E., Brown, R. J., and Self, S. (2017). Field-trip guide to the vents, dikes, stratigraphy, and structure of the Columbia River Basalt Group, Eastern Oregon and Southeastern Washington. Sci. Invest. Rep. 5022, 1–88. doi: 10.3133/sir20175022N
Cassata, W. S., Shuster, D. L., Renne, P. R., and Weiss, B. P. (2010). Evidence for shock heating and constraints on Martian surface temperatures revealed by 40Ar/39Ar thermochronometry of Martian meteorites. Geochim. Cosmochim. Acta 74, 6900–6920. doi: 10.1016/j.gca.2010.08.027
Courtillot, V. E., and Renne, P. R. (2003). On the ages of flood basalt events. C. R. Geosci. 335, 113–140. doi: 10.1016/S1631-0713(03)00006-3
Crowley, P. D., and Reiners, P. W. (2001). “Timing of exhumation of the Wallowa Mountains, ne Oregon: a U-Th/He thermochronologic study,” in GSA Annual Meeting Abstracts (Boston, MA) (108-0).
Davenport, K. K., Hole, J. A., Tikoff, B., Russo, R. M., and Harder, S. H. (2017). A strong contrast in crustal architecture from accreted terranes to craton, constrained by controlled-source seismic data in Idaho and eastern Oregon. Lithosphere 9, 325–340. doi: 10.1130/L553.1
Delaney, P. T. (1982). Rapid intrusion of magma into wet rock: Groundwater flow due to pore pressure increases. J. Geophys. Res. 87, 7739–7756.
Dodson, M. (1973). Closure temperature in cooling geochronological and petrological systems. Contrib. Mineral. Petrol. 40, 259–274.
Ehlers, T., and Farley, K. A. (2003). Apatite (U-Th)/He thermochronometry: methods and applications to problems in tectonic and surface processes. Earth Planet. Sci. Lett. 206, 1–14. doi: 10.1016/S0012-821X(02)01069-5
Erickson, B. A., Dunham, E. M., and Khosravifar, A. (2017). A finite difference method for off-fault plasticity throughout the earthquake cycle. J. Mech. Phys. Solids 109, 50–77. doi: 10.1016/j.jmps.2017.08.002
Farley, K. A. (2000). Helium diffusion from apatite: general behavior as illustrated by Durango fluorapatite. J. Geophys. Res. 105, 2903–2914. doi: 10.1029/1999JB900348
Fechtig, H., and Kalbitzer, S. (1966). The diffusion of Argon in Potassium-bearing solids. in Potassium Argon Dating, eds O. A. Schaeffer and J. Zahringer (Berlin: Springer-Verlag), 68–107.
Fialko, Y. A., and Rubin, A. M. (1999). Thermal and mechanical aspects of magma emplacement in giant dike swarms. J. Geophys. Res. 104, 23033–23049.
Flowers, R. M., Ketcham, R. A., Shuster, D. L., and Farley, K. A. (2009). Apatite (U–Th)/He thermochronometry using a radiation damage accumulation and annealing model. Geochim. Cosmochim. Acta 73, 2347–2365. doi: 10.1016/j.gca.2009.01.015
Fukada, J., and Johnson, K. (2008). A fully Bayesian inversion for spatial distribution of fault slip with objective smoothing. Bull. Seismol. Soc. Am. 98, 1128–1146. doi: 10.1785/0120070194
Gautheron, C., Tassan-Got, L., Barbarand, J., and Pagel, M. (2009). Effect of alpha-damage annealing on apatite (U–Th)/He thermochronology. Chem. Geol. 266, 157–170. doi: 10.1016/j.chemgeo.2009.06.001
Gelman, A., and Rubin, D. B. (1992). Inference from iterative simulation using multiple sequences. Stat. Sci. 7, 457–511.
Guenthner, W. R., Reiners, P. W., and Chowdhury, U. (2016). Isotope dilution analysis of Ca and Zr in apatite and zircon (U-Th)/He chronometry. Geochem. Geophys. Geosyst. 17, 1623–1640. doi: 10.1002/2016GC006311
Guenthner, W. R., Reiners, P. W., Ketcham, R. A., Nasdala, L., and Giester, G. (2013). Helium diffusion in natural zircon: radiation damage, anisotropy, and the interpretation of zircon (U-Th)/He thermochronology. Am. J. Sci. 313, 145–198. doi: 10.2475/03.2013.01
Huber, C., Bachmann, O., and Manga, M. (2009). Homogenization processes in silicic magma chambers by stirring and mushification (latent heat buffering). Earth Planet. Sci. Lett. 283, 38–43. doi: 10.1016/j.epsl.2009.03.029
Jaupart, C., and Provost, A. (1985). Heat focusing, granite genesis and inverted metamorphic gradients in continental collision zones. Earth Planet. Sci. Lett. 73, 385–397.
Johnson, K., Barnes, C. G., and Miller, C. A. (1997). Petrology, geochemistrym and genesis of high-Al tonalite and trondhjemites of the Cornucopia stock, Blue Mountains, northeastern Oregon. J. Petrol. 38, 1585–1611.
Karlstrom, L., Dufek, J., and Manga, M. (2010). Magma chamber stability in arc and continental crust. J. Volcanol. Geotherm. Res. 190, 249–270. doi: 10.1016/j.jvolgeores.2009.10.003
Karlstrom, L., Paterson, S. R., and Jellinek, A. M. (2017). A reverse energy cascade for crustal magma transport. Nat. Geosci. 20, 604–608. doi: 10.1038/ngeo2982
Kasbohm, J., and Schoene, B. (2018). Rapid eruption of the Columbia River flood basalt and correlation with the mid-Miocene climate optimum. Sci. Adv. 4:eaat8223. doi: 10.1126/sciadv.aat8223
Kass, R. E., Carlin, B. P., Gelman, A., and Neal, R. M. (1998). Markov Chain Monte Carlo in practice: a roundtable discussion. Am. Stat. 52, 93–100.
Keszthelyi, L., Self, S., and Thordarson, T. (2006). Flood lavas on Earth, Io and Mars. J. Geol. Soc. Lond. 163, 253–264. doi: 10.1144/0016-764904-503
Ladderud, J. A., Wolff, J. A., Rember, W. C., and Brueseke, M. E. (2015). Volcanic ash layers in the Miocene lake Clarkia beds: Geochemistry, regional correlation, and age of the Clarkia flora. Northw. Sci. 89, 309–323. doi: 10.3955/046.089.0402
Link, W. A., and Eaton, M. J. (2012). On thinning of chains in MCMC. Methods Ecol. Evol. 3, 112–115. doi: 10.1111/j.2041-210X.2011.00131.x
McDougall, I., and Harrison, T. M. (1999). Geochronology and Thermochronology by the 40Ar/39 Ar Method. New York, NY: Oxford University Press.
Metropolis, N., Rosenbluth, W., Rosenbluth, M. N., Teller, A. H., and Teller, E. (1953). Equation of state calculations by fast computing machines. J. Chem. Phys. 21, 1087–1092.
Morriss, M. C., and Karlstrom, L. (2018). “The Chief Joseph Dike Swarm of the Columbia River Basalts, and the legacy dataset of William H. Taubeneck,” in American Geophysical Union Fall Meeting Abstracts (V31H-0216)(Washington, DC).
Mosegaard, K., and Tarantola, A. (2002). “Probabilistic approach to inverse problems,” in International Handbook of Earthquake and Engineering Seismology, eds P. C. J. William H. K. Lee H. Kanamori and C. Kisslinger (Amsterdam: Academic Press), 237–265.
Murray, K. E., Braun, J., and Reiners, P. W. (2018). Toward robust interpretation of low-temperature thermochronometers in magmatic terranes. Geochem. Geophys. Geosyst. 19, 3739–3763. doi: 10.1029/2018GC007595
Perry-Houts, J., and Karlstrom, L. (2018). Anisotropic viscosity and time-evolving lithospheric instabilities due to aligned igneous intrusions. Geophys. J. Int. 216, 794–802. doi: 10.1093/gji/ggy466
Petcovic, H. L. (2004). Feeder Dikes to the Columbia River Flood Basalts: Underpinnings of a Large Igneous Province. PhD thesis, Oregon State University.
Petcovic, H. L., and Dufek, J. (2005). Modeling magma flow and cooling in dikes: implications for emplacement of Columbia River flood basalts. J. Geophys. Res. 110:B10201. doi: 10.1029/2004JB003432
Petcovic, H. L., and Grunder, A. L. (2003). Textural and thermal history of partial melting in tonalitic wallrock at the margin of a basaltic dike, Wallowa Mountains, Oregon. J. Petrol. 44, 2287–2312. doi: 10.1093/petrology/egg078
Petford, N., and Gallagher, K. (2001). Partial melting of mafic (amphibolitic) lower crust by periodic influx of basaltic magma. Earth Planet. Sci. Lett. 193, 483–499. doi: 10.1016/S0012-821X(01)00481-2
Reidel, S. P., Camp, V. E., Tolan, T. L., and Martin, B. S. (2013). The Columbia River flood basalt province: stratigraphy, areal extent, volume, and physical volcanology. Geol. Soc. Am. Spec. Pap. 497, 1–43. doi: 10.1130/2013.2497(1)
Reiners, P. W. (2005). Zircon (u−th)/he thermochronometry. Rev. Mineral. Geochem. 58, 151–179. doi: 10.2138/rmg.2005.58.6
Reiners, P. W. (2009). Nonmonotonic thermal histories and contrasting kinetics of multiple thermochronometers. Geochim. Cosmochim. Acta 73, 3612–3629. doi: 10.1016/j.gca.2009.03.038
Reiners, P. W., and Brandon, M. T. (2006). Using thermochronology to understand orogenic erosion. Annu. Rev. Earth Planet. Sci. 34, 419–466. doi: 10.1146/annurev.earth.34.031405.125202
Reiners, P. W., Spell, T., Nicolescu, S., and Zanetti, K. (2004). Zircon (U-Th)/He thermochronometry: He diffusion and comparisons with 40Ar/39Ar dating. Geochim. Cosmochim. Acta 68, 1857–1887. doi: 10.1016/j.gca.2003.10.021
Shuster, D. L., Flowers, R. M., and Farley, K. A. (2006). The influence of natural radiation damage on helium diffusion kinetics in apatite. Earth Planet. Sci. Lett. 249, 148–161. doi: 10.1016/j.epsl.2006.07.028
Taubeneck, W. H. (1964). Cornucopia stock, Wallowa Mountains, northeastern Oregon: field relationships. Geol. Soc. Am. Bull. 75, 1093–1116.
Taubeneck, W. H. (1970). “Dikes of Columbia River Basalt in northeastern Oregon, western Idaho, and southeastern Washington,” in Proceedings of the second Columbia River Basalt Symposium, eds E. H. Gilmor and D. Stradling (Cheney, WA: Eastern Washington State College), 73–96.
Thordarson, T., and Self, S. (1998). The Roza Member, Columbia River Basalt Group: a gigantic pahoehoe lava flow field formed by endogeneous processes? J. Geophys. Res. 103, 27411–27445.
Watson, E. B., and Cherniak, D. J. (2013). Simple equations for diffusion in response to heating. Chem. Geol. 335, 93–104. doi: 10.1016/j.chemgeo.2012.10.054
White, S. M., Crisp, J. A., and Spera, F. J. (2006). Long-term volumetric eruption rates and magma budgets. Geochem. Geophys. Geosyst. 7. doi: 10.1029/2005GC001002
Whittington, A. G., Homeister, A. M., and Nabelek, P. I. (2009). Temperature-dependent thermal diffusivity of the Earth's crust and implications for magmatism. Nature 458, 319–321. doi: 10.1038/nature07818
Wolf, R. A., Farley, K. A., and Kass, D. M. (1998). Modeling of the temperature sensitivity of the apatite (U-Th)/He thermochronometer. Chem. Geol. 148, 105–114.
Wylie, J. J., Helfrich, K. R., Daude, B., Lister, J. R., and Salzig, J. F. (1999). Flow localization in fissure eruptions. Bull. Volcanol. 60, 432–440.
Zak, J., Verner, K., Tomek, F., Holub, F. V., Johnson, K., and Schwartz, J. J. (2015). Simultaneous batholith emplacement, terrane/continent collision, and oroclinal bending in the Blue Mountains Province, North American Cordillera. Tectonics 34, 1107–1128. doi: 10.1002/2015TC003859
Appendix A
A.1. Assessment of MCMC Convergence and Parameter Values
Markov Chain Monte Carlo involves the production of a dependent sequence or chain of values which, if run for long enough time, will converge to the underlying posterior distribution (Mosegaard and Tarantola, 2002). Convergence of MCMC chains is impossible to guarantee in practice but several standard tools exist to assess convergence, the degree to which sampling has integrated over the joint posterior PDF (i.e., good parameter “mixing”), and whether the chain involves enough samples to adequetely cover the posterior (Kass et al., 1998).
We perform three tests to assess convergence of our MCMC inversions. As a first test, we computed the posterior distribution with different kept sample populations, experimenting with the number of ‘burn in' samples discarded and whether or not to “thin” the distribution (i.e., discard every kth sample, although this is likely unnecessary for sufficiently long chains, Link and Eaton, 2012). We have also experimented with different sampling step sizes (between 80 and 120 steps within uniform priors for each parameter), and logarithmically as well as linearly spaced steps. We run many MCMC chains, and the starting points for each chain are randomized. When the number of samples per chain is larger than ~ 104, for the tested range of thinning and step size, shapes of the posterior PDFs do not change much. This qualitative test provides some confidence that we are adequately sampling the true posterior.
A second, more quantitative test involves the autocorrelation for each parameter in each chain. Figure A1 shows the mean autocorrelation for each parameter over 70–75 independent chains, as a function of sample lag. Above lags of ~7 × 103, the mean autocorrelation for every parameter and both dikes has dropped to near zero and fluctuates about zero as lag increases further. This suggests randomized sampling and is in agreement with the qualitative threshold found in the first test.
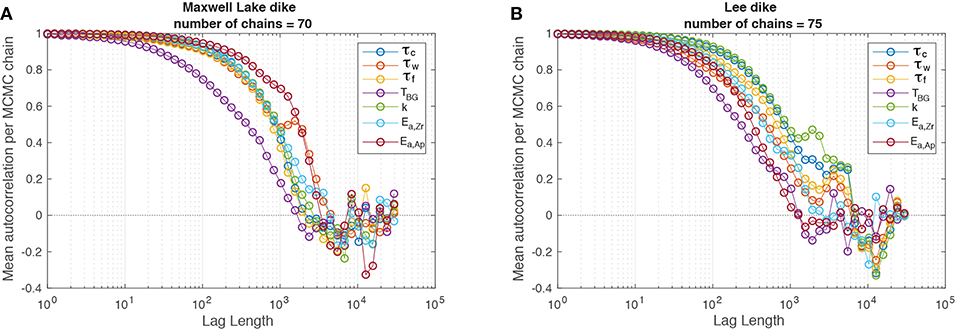
Figure A1. (A) Average autocorrelation of MCMC chains as a function of lag for the Maxwell Lake dike, for each parameter. Autocorrelation is calculated for each of 70 chains with randomized starting points, then averaged at each lag value to produce these curves. (B) Same as (A) for the Lee dike MCMC simulations, with 75 independent chains considered.
As a third test, we compute the Gelman and Rubin (1992) ‘Potential Scale Reduction Factor' for each parameter (Table 1). The Gelman-Rubin diagnostic is a weighted average of the within-chain variance and between-chain variances. Values below are often used as a criteria for convergence. As Table 1 shows, while most of the parameters do fall within this convergence criterion, there are notable exceptions. Most significantly, the activation energys Ea,Zr and Ea,Ap are far in excess of 1.2 and the background temperature TBG is close to but not under 1.2 for both dikes.
This could indicate that the MCMC has not converged for these parameters and longer chains are required. However, there are also some reasons to be wary of as a metric for convergence (Kass et al., 1998). The Gelman-Rubin diagnostic assumes the underlying PDF to be normally distributed and over-dispersed starting guesses for chains, which are not possible for all of our parameters on physical grounds: for example, we cannot take background temperatures TBG below 25 C, and above 100 C is implausible in the upper few km of crust. That the predicted posterior PDF for TBG is skewed toward the prior lower limit for the Lee dike, or that the flow unsteadiness parameter τw is screwed toward its lower limit for the Maxwell Lake dike, is likely a physical result. We thus have reason to suspect that may not be an accurate metric of convergence for all of our parameters, although do take the large values found for activation energies as another sign that these parameters are not well constrained by our inversions.
Keywords: Columbia River Flood Basalts, dike mechanics, Bayesian inversion, low temperature thermochronology, large igneous provinces, thermal modeling
Citation: Karlstrom L, Murray KE and Reiners PW (2019) Bayesian Markov-Chain Monte Carlo Inversion of Low-Temperature Thermochronology Around Two 8 – 10 m Wide Columbia River Flood Basalt Dikes. Front. Earth Sci. 7:90. doi: 10.3389/feart.2019.00090
Received: 30 November 2018; Accepted: 11 April 2019;
Published: 30 April 2019.
Edited by:
Mattia Pistone, Université de Lausanne, SwitzerlandReviewed by:
Tom Sheldrake, Université de Genéve, SwitzerlandCatherine Annen, Université Savoie Mont Blanc, France
Copyright © 2019 Karlstrom, Murray and Reiners. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Leif Karlstrom, bGVpZkB1b3JlZ29uLmVkdQ==
†Present Address: Kendra E. Murray, Department of Geosciences, Idaho State University, Pocatello, ID, United States
 Leif Karlstrom
Leif Karlstrom Kendra E. Murray
Kendra E. Murray Peter W. Reiners3
Peter W. Reiners3