- Jackson School of Geosciences, The University of Texas at Austin, Austin, TX, United States
In this study, we utilize high-resolution X-ray computed tomography (XCT) to track the progress of a leaching process within a pore network. Dissolution and leaching are difficult processes to observe with combined temporal and spatial context, particularly when dissolving material within a non-reactive pore network, and XCT is a uniquely suited technique for observing dissolution in situ, and extracting quantitative data on pore networks and the material in them in 3D. We XCT image two samples of porous diamond (carbonado) during a sequential acid leaching procedure designed to remove a diverse assemblage of pore-filling minerals. This experiment provides a unique perspective for observing mineral dissolution in 4D, allowing us to identify differences in mineral inclusions and pore network topology between carbonado samples based on dissimilar dissolution styles and rates. We are also able to observe the formation of fluorides during acid digestion, which can persist throughout acid leaching procedures and drastically affect yields for geochemical measurements of certain elements, most importantly REEs, U, Th, and Pb. We test various approaches to measuring porosity, finding that methods based on quantitative interpretation of CT numbers as partial porosity give more accurate results than purely binary segmentation, and that attempts to segment the pore network using visual criteria are scattered and unreliable. We document how image quality can be locally affected by material properties, with filled pores measurably blurrier than empty ones. Such local variation in point-spread function is important when segmenting XCT data for the purposes of quantification. Finally, we demonstrate that by comparing mass and X-ray attenuation loss it is possible to estimate the relative heavy-metal content of the leached material.
Introduction
Rock preparation methods for determining bulk elemental abundances and isotopic compositions involve either fusion or digestion and result in the complete destruction of the sample. Several acid digestion procedures exist (Potts and Cresser, 1987) and are optimized for dissolving a specific mineralogy (Pinto et al., 2012). Most involve sequential dissolution steps in various acids at high temperatures and usually use a hydrofluoric (HF) acid step to break down more refractory mineral phases (e.g., garnet, spinel, zircon, rutile, etc.). However, it has long been recognized that insoluble Ca, Mg, and Al fluoride complexes precipitate during this step and can incorporate significant amounts of rare earth elements (REEs), Rb, Sr, Y, Cs, Ba, Pb, Th, and U (Yokoyama et al., 1999; Krachler et al., 2002; Makishima and Nakamura, 2006). Precipitation of these insoluble fluorides can result in reduced yields of these elements, which can affect interpretation of rock petrogenesis and/or age (Boer et al., 1993). Several studies have quantified the composition of these precipitates using X-ray diffraction (XRD) and have developed digestion methods to avoid their formation or at least effectively dissolve them in a subsequent leaching step (Yokoyama et al., 1999; Krachler et al., 2002).
Because of the destructive nature of acid digestion, it is difficult to observe the dissolution process directly. Although most procedures are conducted on powders and complete dissolution is desired, intermediate phases like the aforementioned fluorides can precipitate during digestion, or some phases can persist through the entire process. In cases where the target for dissolution is mixed or embedded within a non-reactive matrix, spatial context can be important, as it provides the ability to study internal variation in acid digestion due to mineralogy or pore network topology. For instance, it is possible for refractory minerals to withstand a complete acid digestion procedure and result in incomplete yields of high field-strength elements (HFSEs) and REEs (Pinto et al., 2012). Similarly, the connectivity and permeability of a pore network can vary locally, leading to variation in reaction front penetration. Currently, there is no method for in situ determination of the effectiveness of acid digestion methods.
In this study, we provide the first time-integrated 3D imaging (i.e., 4D) of acid digestion in a porous medium using high-resolution X-ray computed tomography (XCT). XCT is a uniquely effective tool for imaging acid digestion, as other imaging techniques are destructive and/or simply not feasible given the nature of the material and process being imaged.
The medium we are studying is carbonado, a porous, polycrystalline diamond with an exceptionally diverse mineral assemblage filling and lining its pores. Using XCT, we are able to image the effects of reactive transport of various acids through a porous medium without altering the matrix, as diamond is inert to the acids used.
This experiment also presents a unique opportunity to examine how to best quantify the pore network and the materials within it using XCT data. We evaluate various strategies for measuring the filled and unfilled pores, and the effect of pore fillings on image sharpness. We also evaluate the ability of CT to discern information about the composition of leached material based on internal changes in X-ray attenuation. The results from this study not only contribute to a better understanding of acid digestion methods, but also shed light on properties of XCT data that affect quantitative interpretations.
Materials and Ct Data
Samples
Carbonado is an enigmatic variety of polycrystalline diamond found only in placer deposits and Mesoproterozoic metaconglomerates in Bahia, Brazil and the Central African Republic, with unknown primary origin (Trueb and Butterman, 1969; Trueb and De Wys, 1969, 1971). These highly porous dark nodules possess a narrow range of isotopically light carbon (δ13C −31 to −24 ‰), an inclusion suite reflecting crustal pressure-temperature conditions (e.g., kaolinite and florencite – a REE-rich aluminophosphate commonly formed from the hydrothermal breakdown of monazite) and unusually enriched in REEs and actinides filling the pore spaces, a loosely constrained crystallization age between 2.6 and 3.8 Ga (Ozima and Tatsumoto, 1997; Sano et al., 2002), and other atypical features. This unusual assortment of properties has led to a variety of formation theories, from extra-solar to deep mantle (Haggerty, 2014). The pore network in some carbonado specimens has been shown to be interconnected based on the successful removal of all inclusion-hosted magnetism after intense acid leaching (Dismukes et al., 1988). However, the origin of the inclusion material, whether as a product of the in situ breakdown of primary phases or as precipitates from infiltrating crustal fluids, remains unknown.
We have collected new 3D textural, geochemical, and isotopic data to investigate the age and origin of several carbonado specimens (Eckley, 2018). To acquire bulk geochemical and isotopic data on the pore-filling material, we subjected one African (C-16-C; 0.715 g) and one Brazilian sample (1–3; 1.001 g), both shown in Figure 1, to a multi-stage acid digestion procedure. We will refer to sample C-16-C and 1–3 as “sample A” and “sample B”, respectively, for the remainder of this paper. The samples were XCT imaged prior to leaching and after each acid leaching step to document the effects of the various acids on the mineral inclusion suite hosted within the pore network, and trace the progress of the reaction.

Figure 1. Stereomicroscope images of carbonado nodules used in this study (sample A, left; and sample B, right).
XCT Scanning
All scans were acquired at the University of Texas High-Resolution X-ray CT Facility using a Zeiss Xradia microXCT 400. X-rays were set at 80 kV and 10 W with 4 s (sample A; C-16-C in Eckley, 2018) and 2.5 s (sample B; 1–3 in Eckley, 2018) acquisition times per view (1261 views) using the LFOV objective; scan times were 1.8 and 1.1 h, respectively. X-rays were pre-filtered with a 0.35 mm SiO2 filter for sample A and unfiltered for sample B. The reconstructed data have a voxel size of 14.36 and 14.35 μm, respectively. Software corrections were applied to compensate for ring and beam hardening artifacts. The same reconstruction parameters were used for each scan.
X-ray computed tomography produces a continuous sequence of two-dimensional (2D) 16-bit images (slices), which when stacked together create a three-dimensional (3D) volume reflecting X-ray attenuation within the sample. X-ray attenuation is a function of a material’s atomic number and density, as well as the X-ray energy; denser, more attenuating material is assigned a higher CT number, which is usually visualized with brighter grayscales (Ketcham and Carlson, 2001). Ideally, each data voxel (pixel with volume) has a value proportional to the average X-ray linear attenuation coefficient of the material comprising that voxel. In reality, because of the finite resolution of XCT, the attenuation signal is blurred somewhat, and thus the signal within a voxel is also influenced by material in surrounding voxels (i.e., its neighborhood). The size of the neighborhood can be described by a point-spread function (PSF), the extent of which is affected by several inherent properties of XCT imaging (ASTM, 2011). This phenomenon is most important when features of interest are small with respect to the PSF, as the blurring will affect their detectability and appearance, and the appropriate strategy for measuring them (Ketcham and Mote, 2019).
Acid Digestion Procedures
After initial XCT imaging, samples were subjected to the following acid digestion procedure:
(Step 1) Cleaning: (6 N HCl for 2 h, 4:1 HF:HNO3 for 72 h; and aqua regia for 72 h at 110°C)
(Step 2) 7 days of 6 N HCl at 110°C
(Step 3) 7 days of 4:1 HF:HNO3 at 110°C
(Step 4) 7 days of aqua regia at 110°C
All steps were performed in sealed 15 mL SavillexTM beakers with screw tops in a ventilated oven using optima-grade 12 M HCl, optima-grade concentrated HF, and doubly-distilled 15.6 M HNO3. Before each step, sample masses were measured using a microbalance with 1 μg precision. Leachates were saved and the samples were ultrasonically rinsed in ultrapure water for 30 min. The water was combined with the leachate and saved for analysis. All leachates were evaporated to dryness on a hot plate at 110°C, re-dissolved in 1 mL of 1 N HNO3, and transferred in acid-cleaned 1.5 mL microcentrifuge tubes for subsequent dilution and geochemical analysis. All sample preparation was performed in the Radiogenic Isotope Clean Lab at the University of Texas at Austin. After each step, the samples were dried for at least 72 h on a hot plate at 140°C and reweighed. Next, to observe the effectiveness of each leaching step, both samples were rescanned using the same XCT parameters.
XCT Data Processing
The samples were scanned at random orientations at each stage, which required the TIFF slices for each scan to be reoriented, registered, and resampled to align with the initial XCT data sets. This task was performed in AvizoTM using the Register Images and Resample Transformed Image modules. The former is an automated registration function that computes an affine transformation to match a transformed image to a reference image using an iterative optimization algorithm that employs a hierarchical approach proceeding from coarse to fine quality. For computational efficiency, the two 3D volumes were manually pre-aligned as closely as possible using isosurfaces prior to using the alignment function. The newly registered dataset was then resampled to the original one so that they share the same coordinate system.
To exclude air-filled voxels exterior to the sample from the analysis, a mask encompassing the exterior was created in AvizoTM and expanded into the sample by two voxels. This was performed on the initial scans of both samples, and the respective masks were applied to all data volumes collected after the acid leaching steps. The results of image registration and masking are illustrated in Figure 2. Next, image subtraction calculations were performed in ImageJ to examine what material was removed during each acid leaching step.

Figure 2. Example XCT slices from sequential acid leaching steps of samples A (top) and B (bottom) after volume registration, resampling, and masking.
Results
Dissolution
Progressive XCT imaging the effects of acid digestion provides a 4D perspective of reactant infiltration and diffusion and dissolution styles. Figure 2 illustrates the effects of each step. The cleaning procedure (Step 1) removed pore-filling material from a relatively uniform ∼1 mm annulus in sample A; in sample B the annulus is somewhat more uneven, with shallower penetration in some regions such as the top, while on the left several bright inclusions remain after removal of the surrounding material. Nevertheless, in both scans there is a distinct boundary delineating the dissolution front and most affected pores are completely empty. For sample A, the extended HCl step (Step 2) penetrated deeper, but was not as effective as the cleaning step in completely removing all pore-filling material from the affected volume. There is a broad, 6-mm-diameter central region where inclusions remain but show much lower X-ray attenuation than evident in the same region in step 1. A smaller ∼2-mm-diameter core appears unaffected. In the intermediate region, the smaller pores appeared less distinct and the walls of the larger pores are lined with material. For sample B, the HCl step penetrated relatively uniformly by an additional ∼0.5 mm, and even removed some of the previously stranded inclusions. The dissolution front is well defined and, in contrast to sample A, there is no obvious region of partially demineralized pores. The HF:HNO3 step (Step 3) penetrated only slightly more deeply in sample A, and left most of the ∼2 mm core unaffected. Similar to Step 2, smaller pores are cloudy and some of the pore-lining material in larger pores was removed. Interestingly, randomly distributed, highly attenuating phases formed during this step, indicating dissolution, transfer, and re-precipitation of some high-Z material. Figure 3 highlights some of the largest instances of these new phases, as well as smaller ones that are more representative of the others in the remainder of the volume. For sample B, the HF:HNO3 step was similarly ineffective in removing material. Finally, the aqua regia step (Step 4) fully penetrated sample A and removed all remaining pore-filling material. For sample B, the aqua regia step penetrated slightly deeper and left an ∼0.5 mm annulus with cloudy smaller pores. The combined acid digestion procedure penetrated relatively uniformly, but left a large volume unaffected. Furthermore, in the affected rind, small, isolated, highly attenuating material remains in areas otherwise cleared in steps 2–4, similar to the remnants observed after the cleaning step (Step 1).
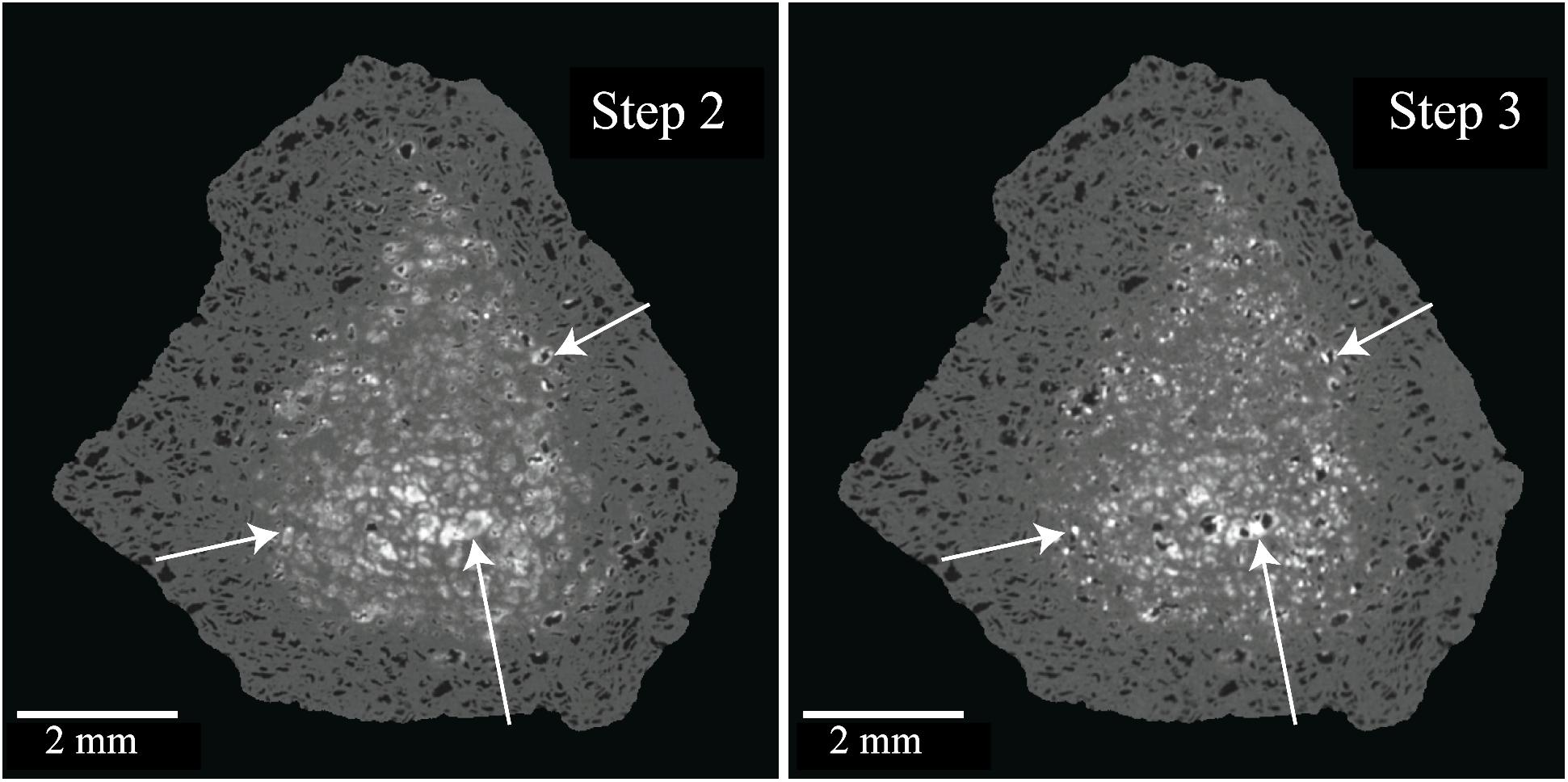
Figure 3. XCT slices through same location in samples A before (left) and B after (right) HF digestion step highlighting the formation of highly attenuating phases.
Figure 4 shows a close-up of the same region in sample A before and after leaching. The variation of CT numbers in the pores of the unleached sample reflect mixtures of various minerals of various compositions. Some pore fillings (for example, just above and to the left of the scale bar) have central regions with CT numbers close to the value for diamond; these are likely to be kaolinite (Ketcham and Koeberl, 2013). In the leached image the pores are fully empty; small pores appear less distinct from the diamond matrix than larger ones, but this is almost certainly due to blurring, not residual material. Interestingly, the pore-matrix boundaries for the empty pores in the leached sample appear sharper and more distinct than in the unleached specimen, even for those filled pores that have no obvious evidence of being multi-mineralic. The cause of this apparent increased blurring in the unleached sample may be due to local variation in the PSF (discussed later) and/or a heterogeneous distribution of mineral inclusions in the micro-porosity of the diamond matrix.

Figure 4. (A) XCT slice of sample A before acid leaching with (B) zoomed in area and (C,D) segmentation attempts (outlined in semi-transparent pink). (E) Same zoomed in area after acid leaching procedure with (F–H) segmentation attempts (filled in semi-transparent red).
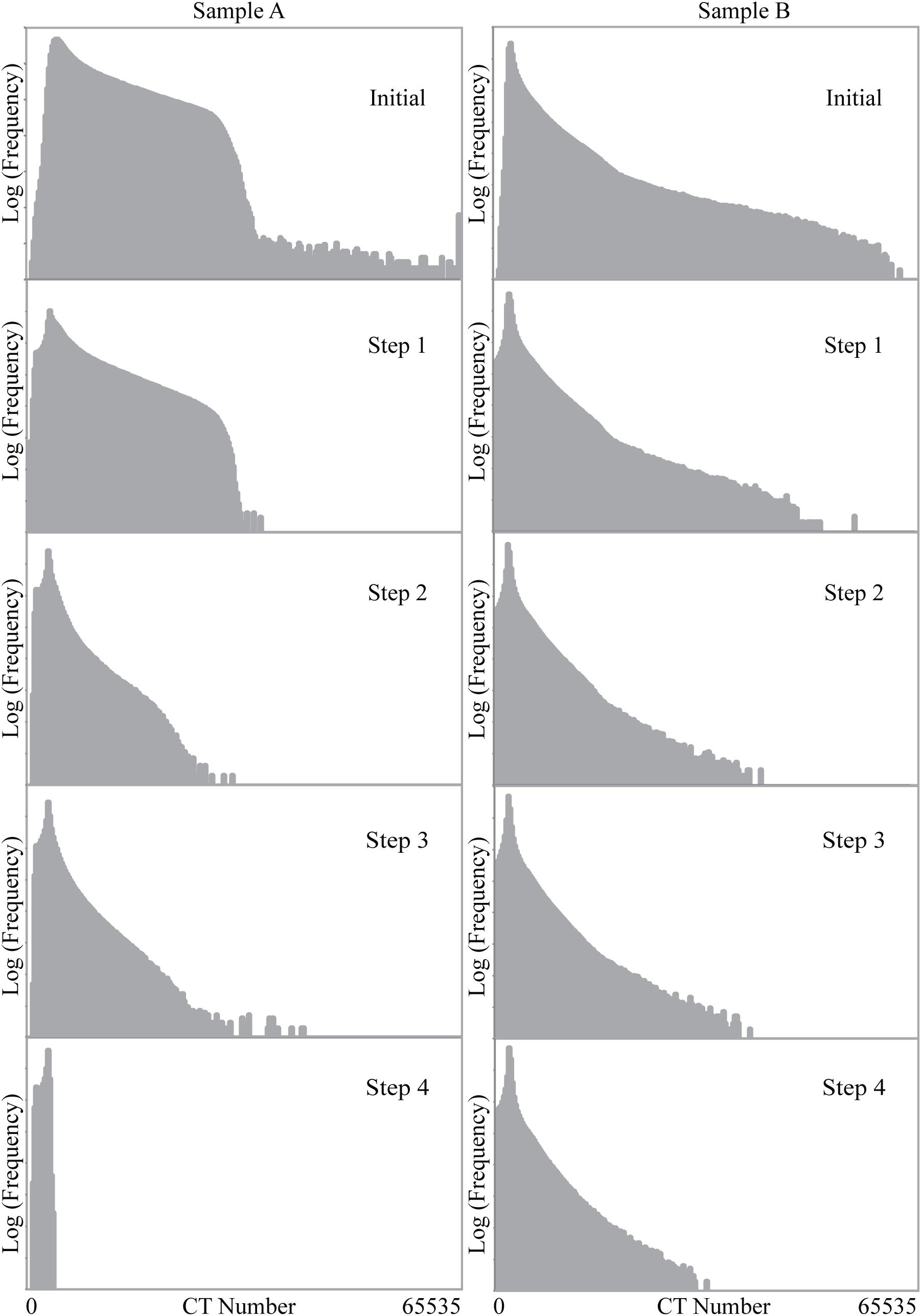
Figure 5 shows the histograms for each data set at each stage of the experiment, calculated using a 3D mask that captured only the diamond and omitted the outside air and container. The diamond peak is evident as the mode on the left side of each histogram, and the values to the right reflect the pore-filling material. The different shapes of these regions between sample B and A reflect the different amounts of low-Z and high-Z elements and minerals, and the extent to which they are intermixed in the pores. As the reaction progresses, the brighter values are progressively lost, with larger pores moving to the left side of the diamond mode. The precipitation of high-Z-concentrating fluorides resulted in rearranging the histogram values somewhat between sample A steps 2 and 3.
Quantitative Analysis
Quantifying Blurring in CT Data
Background
Blurring in XCT data is caused by the finite resolution of the technique stemming from various factors, including X-ray focal spot size, shape, and stability; detector size, crosstalk, and latency; gantry alignment and precision; image noise; and reconstruction algorithm and filter (Ketcham et al., 2010, ASTM, 2011; Ketcham and Mote, 2019). It can be usefully quantified as a blurring kernel. Various parameterizations are possible, but we keep to the convention introduced by Ketcham et al. (2010) of defining the PSF radius (rPSF) as 4σ for a standard Gaussian kernel, which corresponds visually to the approximate number of voxels required to pass fully from one material to another, or the number of voxels across which a flat interface will be blurred. Ketcham and Hildebrandt (2014) present a method for measuring rPSF using flat interfaces within a CT data set, and document minor but systematic variation within scans based on position, with areas closer to the center of rotation being slightly less blurry than edge regions due to greater data density. However, although the cited factors underlying rPSF are geometric in nature with no obvious relation to sample material, whether there is a link between rPSF and material properties has not been tested.
Knowledge of rPSF is not directly required for other calculations described below, but it does inform choices in data segmentation and interpretation. First, and most simply, it provides a simple and quantitative means of evaluating and comparing data quality and resolution. Second, it describes the extent of the region over which the signal from a given object is distributed, aiding the segmentation method described in the next section. Third, it helps determine when shape metrics may be impacted by blurring (Ketcham and Mote, 2019).
Measuring the Point-Spread Function
We measured the pore-diamond rPSF of mineral-filled and empty pores within a single XCT scan. After XCT imaging the cleaning step (Step 1), there was a ∼1 mm rind of completely empty pores in each sample, while interior pores seemed visually unaffected. We used the Line Traverse tool in Blob3D (Ketcham, 2005; Ketcham and Hildebrandt, 2014), which measures the PSF from the edge response function across a flat interface separating two materials, to measure the rPSF of empty and filled pores within these scans. We only measured the most visually homogeneous mineral-filled pores, as material heterogeneity can lead to excess apparent blurring. At least 10 traverses for both filled and empty pores were accumulated and only measurements with uncertainties around 1.0 voxel and angle between the traverse and interface normal less than 36° were accepted.
Point-Spread Function Results
The appearance of greater sharpness in the images of leached regions (Figure 4) is borne out in our PSF analysis (Figure 6). The rPSF values measured in the Step 1 scans for both samples were smaller for empty pores than for filled pores. The average rPSF for the empty pores is 2.61 and 2.11 voxels for samples A and B, respectively, whereas averages for the filled pores are almost double at 4.80 and 4.03 voxels, respectively. Figure 6 shows rPSF plotted against the absolute value of the percent difference between the normalized CT numbers (|ΔCTnorm|%) for adjacent phases in each traverse. While the data for sample A suggest a continuously rising rPSF with respect to |ΔCTnorm|, the sample B analyses, which extend to much higher |ΔCTnorm| values reflecting more attenuating inclusions, suggest a plateau.
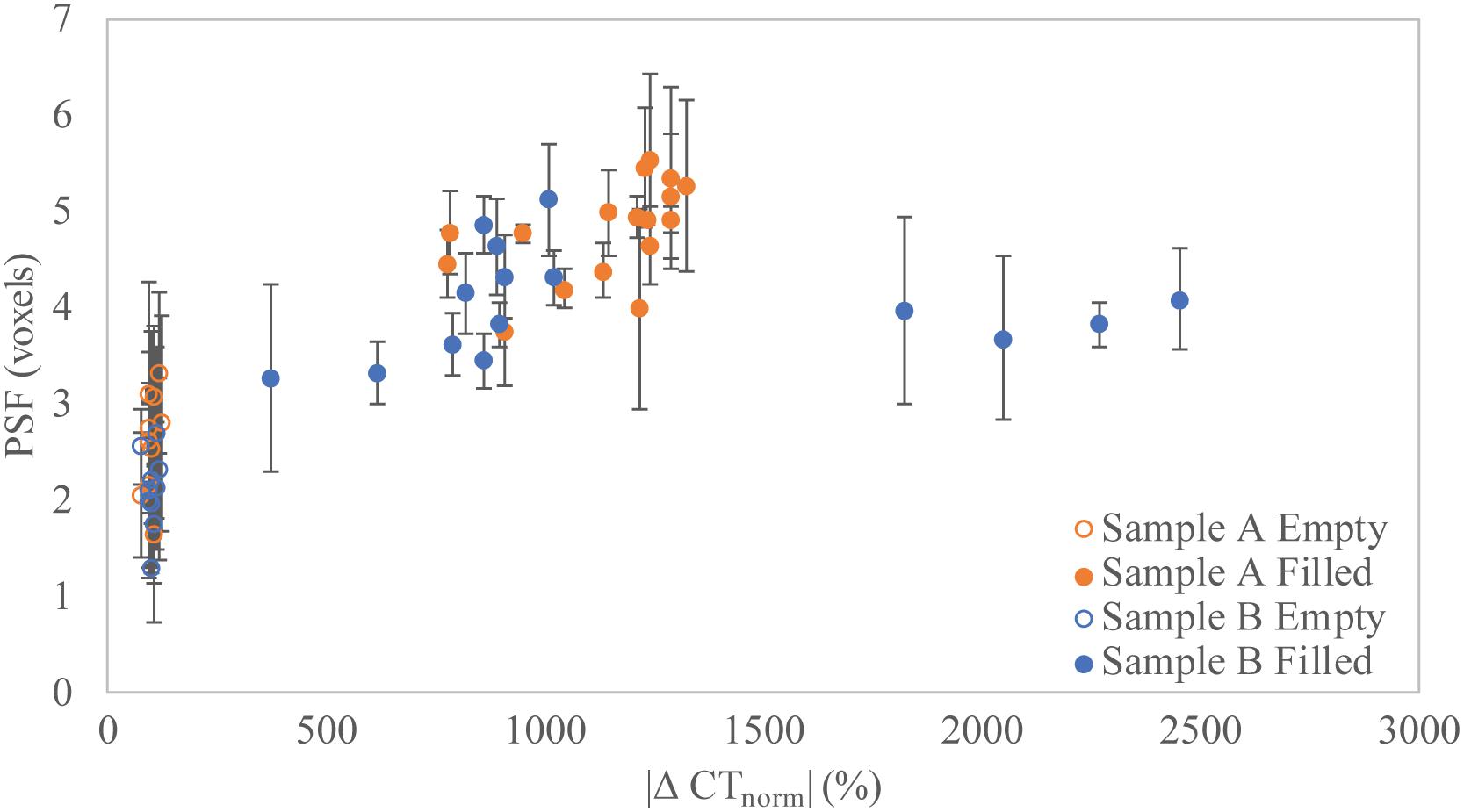
Figure 6. Relationship between PSF size (rPSF, voxels) versus attenuation difference (|ΔCTnorm|%) for individual traverses of empty and filled pores in both samples.
Measuring Porosity
Background
Porosity is not a straightforward quantity to measure in XCT data. In porous media, pore and throat sizes can vary over orders of magnitude, and almost always range down to near and below the XCT resolution limit. Several reviews discuss the challenges of quantifying XCT-imaged porosity, and illustrate the importance of careful analysis (Ashbridge et al., 2003; Taud et al., 2005; Iassonov et al., 2009; Brun et al., 2010; Wildenschild and Sheppard, 2013). Despite these limitations, multiple studies document the unique capabilities of XCT for visualizing and quantifying porosity in 3D (Wellington and Vinegar, 1987; Mooney, 2002; Taud et al., 2005; Wildenschild and Sheppard, 2013).
There are two general approaches to quantifying porosity using XCT: direct or binary segmentation, which delineates which voxels are porosity and which are not (Iassonov et al., 2009); and utilization of CT number information to discern partial porosity below the resolution limit (Wellington and Vinegar, 1987; Withjack, 1988). Binary segmentation is more conducive to pore network visualization and modeling, and when individual pores are visually evident in the data, it is usually the approach chosen, implicitly assuming that the below-resolution component of porosity can be neglected. Typically in such cases the segmentation is done using a global threshold CT number, with voxels below the threshold classified as porosity; ideally this threshold should be at the midpoint between the end-member CT numbers for pores and the solid matrix (ASTM, 2011), under the assumption that net attenuation is conserved. However, a strict midpoint will usually underestimate porosity, due to resolution effects. As pores approach the resolution limit, they begin to blur, appearing to grow fainter in the XCT data; this effect can be characterized as a convolution of the true specimen structure with the PSF (Ketcham and Mote, 2019). A segmentation that omits these small and dim but still visually evident pores is unsatisfying, and an analyst may be tempted to adjust the threshold to capture them. Some more sophisticated segmentation methods attempt to do a more careful job of distinguishing borderline voxels based on neighborhood criteria (Oh and Lindquist, 1999) or other local properties such as gradient, correlation, or entropy, but these are based on general statistical or mathematical models that do not necessarily reflect the actual physical situation. Iassonov et al. (2009) review and compare a range of these segmentation methods, and find that significant supervision and adaptation by a skilled operator is necessary to achieve good results.
The alternative quantification approach typically consists of calculating partial porosity on a voxel-by-voxel basis by assuming CT numbers are a linear mixture between solid and void, or whatever the pore-filling phase is (e.g., Withjack, 1988; Ketcham and Iturrino, 2005). This linear average method captures sub-voxel porosity more completely, but is degraded by image noise or by having multiple solid phases. It also does not provide a straightforward starting point to determine a pore-size distribution or conduct pore-network modeling.
An intermediate possibility is to combine segmentation with utilization of local CT number information. In the PVB (Partial Volume and Blurring) method (Ketcham and Mote, 2019), a broad segmentation is used to capture the entire CT number anomaly associated with a feature, including any attenuation dispersed among adjacent voxels by partial volume and blurring effects. The volume and shape of the feature are then determined based on a linear interpretation of the CT numbers within each segmented region. This approach has been successfully used to measure fracture apertures at sub-voxel resolution (Johns et al., 1993), and has more recently been adapted to measuring discrete small features such as gold particles (Ketcham and Mote, 2019). As the porosity in carbonado consists of virtually isolated pores connected only by very narrow sinuous passages along grain boundaries in the polycrystalline diamond matrix, we attempted to apply the PVB method for the first time to quantify porosity.
Application to Carbonado
We demonstrate the above methods and their outcomes on the scans for sample A, with both filled and empty (leached) porosity. Generally, porosity is measured on air- or fluid-filled voids, but occasionally samples may have partially or completely filled or mineralized pore space. By imaging a porous diamond before and after removal of pore-filling material with no matrix deformation, we are able to quantify how estimates vary depending on the nature of the pore-filling material (i.e., mineral inclusions or air). While measuring a mineral-filled pore seems counterintuitive for estimating porosity, the situation is analogous to studies that infiltrate a sample with a highly attenuating fluid (e.g., KI, NaI, Wood’s metal) to characterize porosity (Wellington and Vinegar, 1987; Withjack, 1988; Ramandi et al., 2016), or a case where an analyst needs to estimate pre-mineralization pore structure.
Carbonado porosity is highly variable as illustrated in Figure 3; pore sizes range from hundreds of μm to well below the XCT resolution limit, and the pore-filling material is a polymineralic assemblage that varies between and within individual pores (Ketcham and Koeberl, 2013). One of the dominant minerals, florencite, can contain several weight percent of rare earth and other elements with high atomic numbers (Z). Such high-Z phases are far more attenuating than other common pore-filling minerals such as kaolinite. Because of the diversity of pore-filling phases, no single CT number value can accurately represent the mineral-filled pore space for the initial scan. Nevertheless, we attempted to measure the effective porosity in the non-leached scan (Figure 3B) using a threshold (5916) that segmented the majority of XCT-resolvable filled pores. This threshold (Figure 3C) was arbitrarily determined using visual and geological criteria, recognizing that some pore-filling phases are only slightly more attenuating than diamond. This threshold omitted some locally bright regions representing diamond matrix with a relatively higher concentration of below-resolution filled pores, while also apparently over-segmenting larger pores filled with more attenuating material. In an attempt to compensate for the latter effect, we adjusted the initial segmentation by eroding it by one voxel in 3D (Figure 3D).
Segmenting pore space in the final scan was more straightforward, as there are only two phases, diamond and air (Figure 3E). Endmember CT number values for diamond (3479 ± 20) and air (1670 ± 35) were determined by measuring the average CT number value of several regions across multiple slices. For air, regions within larger, interior pores were used. For diamond, visually “flat” regions with no identifiable pores were used, although it is likely that even these regions had a small component of micro-porosity.
We experimented with segmenting the pore space in the final scan using various global thresholds determined both visually and mathematically. Our first attempt (Figure 3F) used the recommended midpoint CT number value (2575) between the two calculated end-member components. As expected, this value visually failed to include smaller pores, and so we simulated a typical user response by increasing threshold to 3000 (Figure 3G). This, however, led to over-segmented large pores, so a third attempt sought to compensate by eroding the selection by one voxel (Figure 3H). While the erosion step eliminated some very small pores, these were assumed to be volumetrically insignificant.
We also used the PVB method as implemented in Blob3D analysis software (Ketcham, 2005; Ketcham and Mote, 2019). In this workflow, pore space is slightly over-segmented (in this case, threshold at 3000 (Figure 4G), and expanding by one more voxel during the final data extraction step) to encompass the entire attenuation anomaly of every individual pore; i.e., out to an annular ring approximately rPSF beyond the central, unblurred region of the pore. Rather than simply counting all voxels selected as pore space, a partial porosity is calculated for each selected voxel using a linear interpolation between the endmember CT values for diamond and air. Volumes of individual pores are then determined as the sum of partial porosities within 3D-connected sets of voxels (blobs).
Finally, instead of directly segmenting XCT-resolvable pores, we used the linear average approach with endmember air and diamond values to calculate porosity globally. This calculation can be performed efficiently by simply using the sample-wide average CT number, excluding the exterior masked region. Intuitively, this method is most useful when quantifying the volume percentage of a phase of interest in a binary system (i.e., air and matrix).
We benchmarked these estimates using a simple bulk density method. As the fully leached diamond is a nearly pure mixture of diamond and air, we can determine porosity accurately based on its density deficit relative to solid diamond (3.51 g/cm3). To calculate the density of sample A after the complete digestion procedure, we measured its volume using AvizoTM and its mass using a microbalance with 10 μg precision. The diamond frame volume was segmented by using a midpoint CT number threshold between proximal exterior air and diamond near the sample boundary. To measure the entire sample’s envelope volume (diamond frame + pore space), we used the “fill volume” function in AvizoTM. Pores 3D-connected to the exterior had to be manually segmented and added to the sample volume; this increased the envelope volume by <0.1%.
Porosity Results
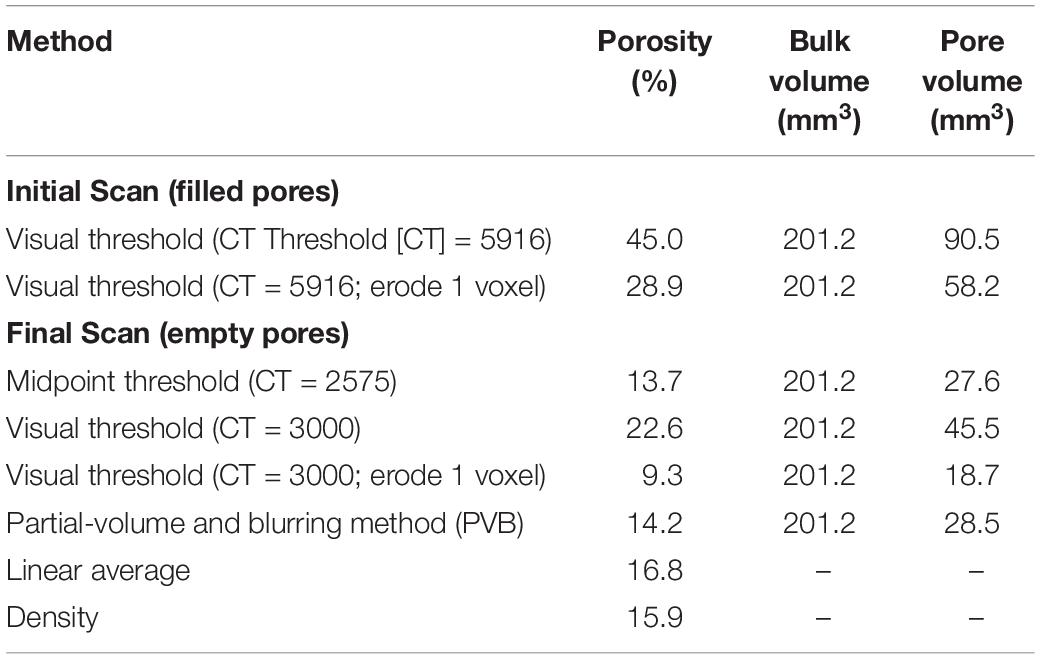
Estimates for porosity between and within the initial and final XCT scans for sample A varied greatly (Table 1). Based on mass and volume measurements, the density of the leached specimen was 2.98 g/cm3; assuming a diamond density of 3.51 g/cm3, this results in a porosity of 15.9%, which we take as the benchmark against which the other methods are evaluated (Table 1, bottom row).
Our “visually reasonable” threshold value for the initial scan with filled pores yielded a porosity of 45%; eroding that same threshold by one voxel reduced it to 29%. Because of the wide range of CT number values that comprise the pore-filling material, there is no appropriate global threshold for segmenting all of the XCT-resolvable pore space in the initial scan. Moreover, very small pores near rPSF are more affected by blurring, and some diamond regions may be made slightly brighter due to dispersed filled microporosity. Thus, as illustrated in Figure 3, in the attempt to capture small pores and low-Z pore fillings, the larger pores were grossly over-segmented, and even the attempt to scale back the overselection by erosion did not prevent a substantial overestimate of porosity.
The final scan for sample A is essentially pure air and diamond, allowing for more accurate quantification. The standard thresholding using the midpoint CT number between the two endmembers yielded a porosity of 13.7%, a slight underestimate of the benchmark value reflecting missed small pores. Thresholding based on a visually “reasonable” adjustment to capture these yielded an over-estimate of 22.6%, and the subsequent 1-voxel erosion step overcompensated, reducing the value to 9.3%. Finally, the PVB method improved on the standard segmentation value somewhat, probably due to capturing some of the smaller pores in an appropriate way, yielding a value of 14.2%. The linear average method using only mean CT numbers yielded a value of 16.8%, slightly above the density-derived benchmark.
Linking CT and Geochemical Data
Mass and Attenuation Loss
Mass loss was tracked by weighing the specimen after each leaching and drying step. We also performed geochemistry on the leaching acids (Eckley, 2018), to track the composition of lost material. Leachates were analyzed for a broad suite of elements, including all REE’s, Rb, Sr, Y, Zr, Nb, Cs, Ba, Hf, Ta, Pb, Th, U. We refer this suite of elements as “high-Z”, to distinguish them from other less dense, lower-attenuation elements extracted during leaching. During the cleaning step some insoluble residues formed in the dried HF acid, preventing a full accounting of the extracted high-Z elements in that step, but based on analysis of other another leached carbonado we estimate the missing material as roughly 23% of the amount measured in the other acids.
Attenuation loss was calculated by simply measuring the net drop in mean CT number in the masked regions of each scan. Because the two specimens were scanned with slightly different reconstruction parameters, we normalized the two measurement series by their respective differences between end-member diamond and air CT numbers.
Mass Versus Attenuation Loss Results
Figure 7 shows mean attenuation loss, normalized for the mean CT number difference between diamond and air for each sample, plotted versus total mass loss and lost mass of high-Z elements for each sample. As expected, higher amounts of removed mass are generally reflected in higher net loss of attenuation, demonstrating that CT can directly quantify material loss. However, the correlation is poorer with total loss than with the loss of high-Z elements. For sample A, the two lowest-attenuation-loss points (corresponding to leaching steps 4 and 3) are inverted with respect to total mass loss, but positively correlated as expected with respect to high-Z mass loss. The overall trends for both samples are also much more similar when only high-Z elements are considered. Note that the open high-Z-loss points in Figure 7A reflect that fact that some leached material remains unanalyzed, and thus these points under-report the true mass removal; moving them both slightly upward to account for the missing material would increase consistency within sample A and between samples. In sum, these features indicate that the high-Z component dominates the attenuation removal signal.
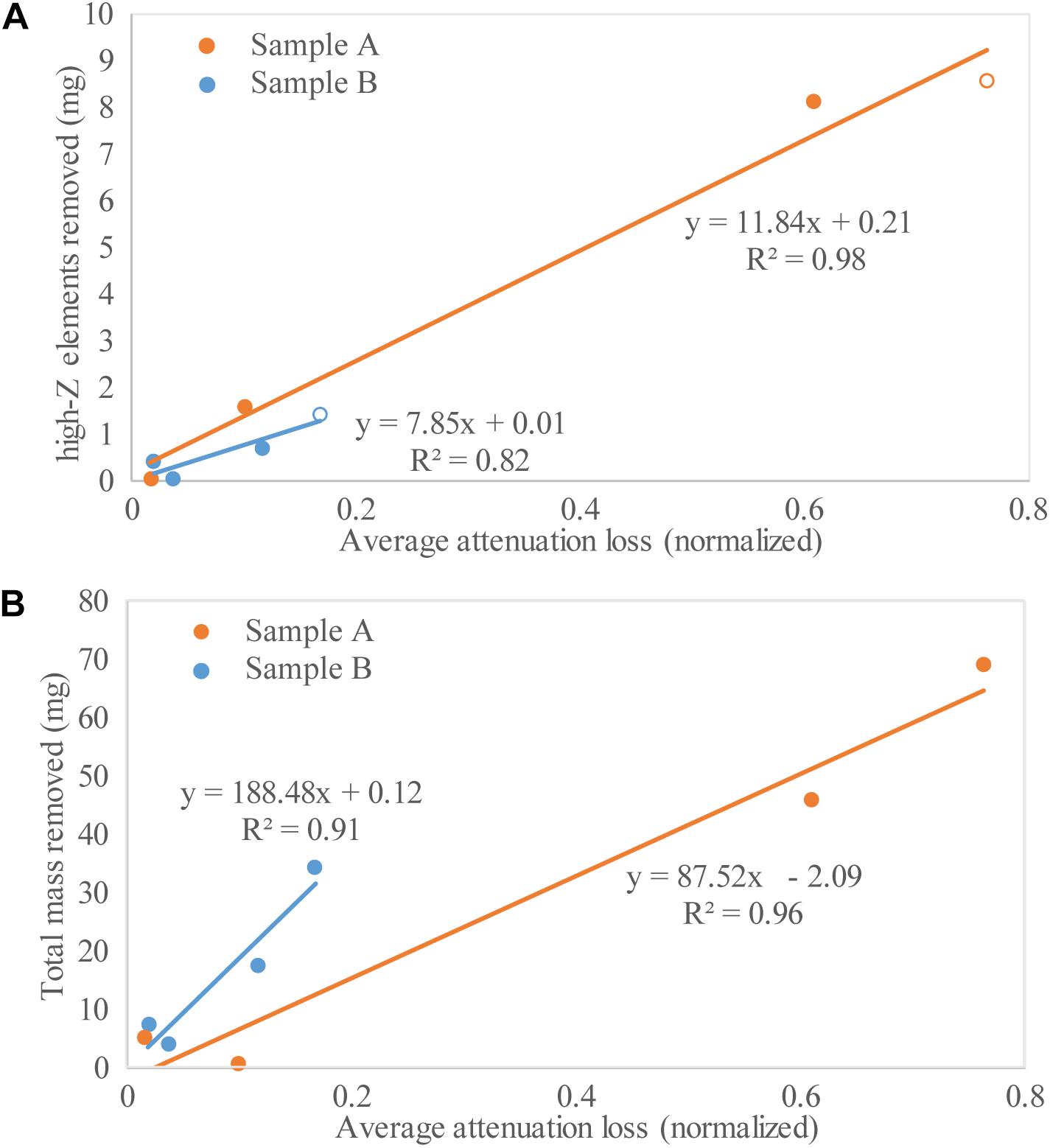
Figure 7. High-Z elements removed (A) and total mass removed (B) during acid leaching steps vs. average normalized attenuation loss for both samples.
Discussion
Dissolution Styles
Time-resolved XCT imaging provides a unique perspective for imaging acid digestion in carbonado in 4D. In sample A, there are no preferential fluid pathways that facilitated enhanced mineral dissolution, and acid transport is dominated by bulk volume diffusion through the pore network and along grain boundaries. The extended HCl and HF:HNO3 steps (Steps 2 and 3) resulted in a pair of reaction fronts, an outer one for total dissolution, and an inner one for partial removal of predominantly high-Z material. High-Z phases were preferentially leached and removed during Step 2 compared to Step 3, in which they were mostly just redistributed. This variation in behavior is likely due to a polymineralic assemblage dominated by disseminated silicate, phosphate, and oxide minerals (Ketcham and Koeberl, 2013). The partially cleared pores after Steps 2 and 3 were caused by different solubilities and reactivities of the diverse inclusion materials in the respective acids. Finally, the complete evacuation of the pores indicates that the entire sample A pore network is interconnected.
In sample B the dissolution front is less even, and some near-boundary inclusions were unaffected, likely reflecting a different pore structure, with tighter pathways to some portions of the sample and lower overall permeability, leading to locally and globally lower dissolution rates. Preferential dissolution of high-Z phases and partially cleared pores in Steps 2 and 3 as observed in sample A are not present, likely reflecting differences in both internal mineralogy and pore network topology. Although sample B did not fully leach, the steady progress of the reaction front indicates that the great majority of its pore network is probably also connected. Isolated inclusions bypassed by the reaction front across multiple leaches, however, may indicate one or more insoluble phases, or possibly small cavities not connected to the pore network and thus potentially containing primary material formed with the diamond.
Fluoride Precipitation
We observed the formation of highly attenuating phases after the HF:HNO3 digestion in sample A (Figure 3). Our 4D technique allowed us to observe how acids migrate and interact with the pore-filling material differently. There are three main processes during acid digestion: (1) infiltration of acid throughout the sample, (2) dissolution of material, and (3) diffusion of dissolved material throughout the solvent. However, during digestion where excess HF is present, it is known that Ca, Mg, and Al fluoride complexes precipitate out of solution and can remain insoluble in the HF-bearing solution. These newly formed compounds can incorporate significant amounts of high-Z elements (REEs, U, Th, and Pb), which we know comprise several wt.% of the bulk inclusion material. Thus, it is likely that these newly formed highly attenuating phases are fluorides with significant concentrations of high-Z elements. We are aware of no prior study where the formation of these compounds has been imaged in situ. Fortunately for our subsequent geochemical analyses, we were also able to observe that following HF digestion with an aqua regia digestion was effective at removing these materials, as insoluble fluorides can often persist throughout an entire acid digestion procedure.
Variation of Porosity Calculations
The nature of pore-filling material has a strong control on the quality of segmentation for calculating porosity using XCT. Significantly different values (up to 36%) were calculated between the initial and final scans. The high values for the initial scan were a result of several issues: a heterogeneous pore-filling material, a large range of pore sizes, and greater blurring of pore boundaries. Notably, both of our arbitrary but “reasonable” porosity estimates for the filled scan were highly inaccurate by a factor of 2–3×.
The binary nature (diamond and air) of the final scan allowed for more accurate segmentation and estimates for porosity closer to the density-derived benchmark value. The standard technique to threshold at the midpoint value yielded results comparable to the benchmark, and the estimate was further improved by the PVB method, which enabled appropriate quantification of some of the smaller pores. On the other hand, the visually assessed threshold resulted in a value ∼40% too high, and trying to compensate by eroding the result by one voxel overcorrected to a value ∼40% too low. Again, the “visual assessment” approach resulted in largely arbitrary values poorly linked to the actual porosity, demonstrating that porosity estimation is much sounder when based on physical principles than even informed guesswork.
Although demonstrated here on a simple two-phase system, the PVB method can be applied to more complex systems with little difficulty due to the simplicity of its underlying model. The input parameter it absolutely requires is an endmember CT number for the phase of interest, in this case air. It also requires the CT number of the surrounding material, which can also be entered by the user, or for complex materials it can be estimated adequately by averaging the CT numbers in the region immediately surrounding each segmented blob.
PSF Variation
Contrary to the assumption that the PSF can be considered generally uniform across a scan volume, we found it to be higher for filled versus unfilled pores (Figures 4B vs. 4E, 6). This is an interesting and unexpected observation and suggests that the PSF may be more complicated than previously thought, and affected by factors (discussed below) beyond scanning and reconstruction parameters.
Some component of excess blurring may be due to the pore fillings being inhomogeneous, but we were careful to only choose measurement locations where there was no obvious evidence of inhomogeneity, which would be apparent as an irregular transition. The most likely explanation lies in the unusually high amount of high-Z material in the pore fillings. One possibility is that the excess blurring is similar in origin to “metal artifacts” caused by photon starvation and edge gradient effects, although such artifacts usually appear directionally variable, which we do not observe here. Another, perhaps related, is that there may be additional blurring caused by coherent, or elastic scattering, in which the photon changes direction without losing energy. Coherent scattering is a second-order attenuation process compared to Compton scattering and the photoelectric effect, but it dominates over Compton scattering at low X-ray energies (∼30–100 keV) in high-Z materials, and can constitute several percent of total attenuation. Coherent scattering is more likely to occur at low angles, meaning that some photons with undiminished energy and only slight displacement are likely to reach the detector, the expected result of which would be blurring around high-scattering features.
Locally or contextually variable rPSF within a single scan can affect segmentation and quantitative measurements derived from XCT, including volume, surface area, and axis lengths. This concern is not only applicable to porous media, but to any XCT-based measurement.
Tracking Attenuation Loss
Although it is generally not practical to extract detailed compositional information from polychromatic XCT data, our experiments demonstrate some interesting new possibilities. In particular, we can distinguish that the high-Z component constitutes a major proportion of our leached attenuation signal, and by comparing attenuation with mass loss we may be able to derive quantitative information. In Figure 7, the fitted lines for sample B have a ∼3.3× greater change in slope from the total mass loss to the high-Z loss case compared to the change for sample A, implying that sample B has a lower high-Z content (a zero high-Z content would show the maximum change). This relation is corroborated in our geochemical data, which shows sample A to have a ∼8× greater high-Z content than sample B. Of course, this relation is only approximate, and a more rigorous calculation would require accounting for the different attenuation coefficients of each species as they vary over the X-ray spectrum used for scanning. However, it is clear that the general approach of comparing mass change to attenuation change in this manner has excellent potential for quick and spatially sensitive evaluation of leached heavy-metal content.
Conclusion
We present the first 4D imaging of acid digestion of pore-filling minerals in an inert porous medium. This technique not only allows us to further understand the physical nature of acid digestion, but also sheds light on inherent properties of XCT scanning. We find that, at least in carbonado, reactant infiltration is dominated by bulk volume diffusion through the pore network and along grain boundaries and is not focused along preferential reaction pathways, though it can be impeded by locally low permeability. For the first time, we image fluoride formation and subsequent destruction in situ. We demonstrate an approach for using CT to infer when and where preferential heavy metal leaching occurs. Finally, while the observations on dissolution style and pore network topology relate to carbonado, our experiments also provide general insights into the basics of XCT and the processing and interpretation of XCT data. We show that estimating porosity with XCT using seemingly reasonable but arbitrary criteria can be problematic, and that more reliable results are obtained by adhering to a more structured approach accounting for material end-members and blurring. We also document that the local degree of blurring within a scan can vary as a function of the material properties. This is important to consider not only when measuring porosity, but in any study where 3D quantitative data are extracted from discrete phases that have been segmented using general thresholding techniques.
Data Availability Statement
The datasets generated for this study can be found in the Digital Rocks Portal repository http://www.digitalrocksportal.org/projects/219, http://doi.org/10.17612/MPGF-FC78.
Author Contributions
SE planned and conducted the dissolutions and chemical analyses, conducted the image processing and analysis, and participated in data interpretation and writing. RK conceived of the experiment, provided the samples and funding, advised on image processing and analysis, and participated in data interpretation and writing.
Funding
This research was supported by the Geology Foundation of the Jackson School of Geosciences and UTCT facility was provided by the National Science Foundation grant EAR-1762458 to RK.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank J. Maisano for conducting the CT scans, and S. Loewy and N. Miller for overseeing the acid digestion and geochemical work.
References
Ashbridge, D. A., Thorne, M. S., Rivers, M. L., Muccino, J. C., and O’day, P. A. (2003). Image optimization and analysis of synchrotron X-ray computed microtomography (CμT) data. Comput. Geosci. 29, 823–836. doi: 10.1016/s0098-3004(03)00081-5
ASTM, (2011). Standard Gudie for Computed Tomography (CT) Imaging. ASTM Designation E 1441–1411. West Conshohocken, PA.: ASTM International.
Boer, R., Beukes, G., Meyer, F., and Smith, C. (1993). Fluoride precipitates in silicate wet-chemistry: implications on REE fractionation. Chem. Geol. 104, 93–98. doi: 10.1016/0009-2541(93)90144-8
Brun, F., Mancini, L., Kasae, P., Favretto, S., Dreossi, D., and Tromba, G. (2010). Pore3D: a software library for quantitative analysis of porous media. Nucl. Instrum. Methods Phys. Res. Sec. A 615, 326–332. doi: 10.1016/j.nima.2010.02.063
Dismukes, J., Gaines, P., Witzk, H., Leta, D., Kear, B., Behal, S., et al. (1988). Demineralization and microstructure of carbonado. Mater. Sci. Eng. A 105, 555–563. doi: 10.1016/0025-5416(88)90743-4
Eckley, S. A. (2018). 3D Textural and Geochemical Analyses on Carbonado Diamond: Insights from Pores and the Minerals within Them, Master’s Thesis, The University of Texas, Austin.
Haggerty, S. E. (2014). Carbonado: physical and chemical properties, a critical evaluation of proposed origins, and a revised genetic model. Earth Sci. Rev. 130, 49–72. doi: 10.1016/j.earscirev.2013.12.008
Iassonov, P., Gebrenegus, T., and Tuller, M. (2009). Segmentation of X-ray computed tomography images of porous materials: a crucial step for characterization and quantitative analysis of pore structures. Water Resour. Res. 45:W09415.
Johns, R. A., Steude, J. S., Castanier, L. M., and Roberts, P. V. (1993). Nondestructive measurements of fracture aperture in crystalline rock cores using X ray computed tomography. J. Geophys. Res. 98, 1889–1900. doi: 10.1029/92jb02298
Ketcham, R., and Mote, A. (2019). Accurate measurement of small features in X-ray Ct data volumes, demonstrated using gold grains. J. Geophys. Res. 124, 3508–3529.
Ketcham, R. A. (2005). Computational methods for quantitative analysis of three-dimensional features in geological specimens. Geosphere 1, 32–41.
Ketcham, R. A., and Carlson, W. D. (2001). Acquisition, optimization and interpretation of X-ray computed tomographic imagery: applications to the geosciences. Comput. Geosci. 27, 381–400. doi: 10.1016/s0098-3004(00)00116-3
Ketcham, R. A., and Hildebrandt, J. (2014). Characterizing, measuring, and utilizing the resolution of CT imagery for improved quantification of fine-scale features. Nucl. Instrum. Methods Phys. Res. Sec. B 324, 80–87. doi: 10.1016/j.nimb.2013.08.064
Ketcham, R. A., and Iturrino, G. J. (2005). Nondestructive high-resolution visualization and measurement of anisotropic effective porosity in complex lithologies using high-resolution X-ray computed tomography. J. Hydrol. 302, 92–106. doi: 10.1016/j.jhydrol.2004.06.037
Ketcham, R. A., and Koeberl, C. (2013). New textural evidence on the origin of carbonado diamond: an example of 3-D petrography using X-ray computed tomography. Geosphere 9, 1336–1347. doi: 10.1130/ges00908.1
Ketcham, R. A., Slottke, D. T., and Sharp, J. M. Jr. (2010). Three-dimensional measurement of fractures in heterogeneous materials using high-resolution X-ray computed tomography. Geosphere 6, 499–514. doi: 10.1130/ges00552.1
Krachler, M., Mohl, C., Emons, H., and Shotyk, W. (2002). Influence of digestion procedures on the determination of rare earth elements in peat and plant samples by USN-ICP-MS. J. Anal. At. Spectrom. 17, 844–851. doi: 10.1039/b200780k
Makishima, A., and Nakamura, E. (2006). Determination of major/minor and trace elements in silicate samples by ICP-QMS and ICP-SFMS applying isotope dilution-internal standardisation (ID-IS) and multi-stage internal standardisation. Geostand. Geoanal. Res. 30, 245–271. doi: 10.1111/j.1751-908x.2006.tb01066.x
Mooney, S. J. (2002). Three-dimensional visualization and quantification of soil macroporosity and water flow patterns using computed tomography. Soil Use Manag. 18, 142–151. doi: 10.1111/j.1475-2743.2002.tb00232.x
Oh, W., and Lindquist, B. (1999). Image thresholding by indicator kriging. IEEE Trans. Pattern Anal. Mach. Intell. 21, 590–602. doi: 10.1109/34.777370
Ozima, M., and Tatsumoto, M. (1997). Radiation-induced diamond crystallization: origin of carbonados and its implications on meteorite nano-diamonds. Geochim. Cosmochim. Acta 61, 369–376. doi: 10.1016/s0016-7037(96)00346-8
Pinto, F. G., Junior, R. E., and Saintpierre, T. D. (2012). Sample preparation for determination of rare earth elements in geological samples by ICP-MS: a critical review. Anal. Lett. 45, 1537–1556. doi: 10.1080/00032719.2012.677778
Potts, P., and Cresser, M. (1987). A handbook of silicate rock analysis. Anal. Chim. Acta 201, 363–363.
Ramandi, H. L., Mostaghimi, P., Armstrong, R. T., Saadatfar, M., and Pinczewski, W. V. (2016). Porosity and permeability characterization of coal: a micro-computed tomography study. Int. J. Coal Geol. 154, 57–68. doi: 10.1016/j.coal.2015.10.001
Sano, Y., Yokochi, R., Terada, K., Chaves, M. L., and Ozima, M. (2002). Ion microprobe Pb–Pb dating of carbonado, polycrystalline diamond. Precambrian Res. 113, 155–168. doi: 10.1016/s0301-9268(01)00208-x
Taud, H., Martinez-Angeles, R., Parrot, J., and Hernandez-Escobedo, L. (2005). Porosity estimation method by X-ray computed tomography. J. Petrol. Sci. Eng. 47, 209–217. doi: 10.1016/j.petrol.2005.03.009
Trueb, L., and De Wys, E. (1969). Carbonado: natural polycrystalline diamond. Science 165, 799–802. doi: 10.1126/science.165.3895.799
Trueb, L., and De Wys, E. (1971). Carbon from Ubangi-A microstructural study. Am. Mineral. 56, 1252–1256.
Wellington, S. L., and Vinegar, H. J. (1987). X-ray computerized tomography. J. Pet. Technol. 39, 885–898.
Wildenschild, D., and Sheppard, A. P. (2013). X-ray imaging and analysis techniques for quantifying pore-scale structure and processes in subsurface porous medium systems. Adv. Water Resour. 51, 217–246. doi: 10.1016/j.advwatres.2012.07.018
Withjack, E. (1988). Computed tomography for rock-property determination and fluid-flow visualization. SPE Format. Eval. 3, 696–704. doi: 10.2118/16951-pa
Keywords: X-ray CT, 4D imaging, pore networks, carbonado diamond, acid digestion, porosity segmentation
Citation: Eckley SA and Ketcham RA (2019) 4D Imaging of Mineral Dissolution in Porous Carbonado Diamond: Implications for Acid Digestion and XCT Measurement of Porosity and Material Properties. Front. Earth Sci. 7:288. doi: 10.3389/feart.2019.00288
Received: 21 June 2019; Accepted: 21 October 2019;
Published: 01 November 2019.
Edited by:
Lucia Mancini, Elettra Sincrotrone Trieste, ItalyReviewed by:
Katherine Dobson, Durham University, United KingdomBenoit Cordonnier, Nationaal Archief of the Netherlands, Netherlands
Copyright © 2019 Eckley and Ketcham. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Scott A. Eckley, c2Vja2xleUB1dGV4YXMuZWR1
 Scott A. Eckley
Scott A. Eckley Richard A. Ketcham
Richard A. Ketcham