- 1Bayerisches Geoinstitut, Universität Bayreuth, Bayreuth, Germany
- 2Institut des Sciences de la Terre (ISTE), Université de Lausanne, Lausanne, Switzerland
We investigate the impact of three coupled weakening mechanisms on the viscous detachment of a stalled lithospheric slab: structural weakening due to necking, material weakening due to grain size reduction, using a two-phase grain damage model, and thermal weakening due to shear heating (thermal damage). We consider a combined flow law of dislocation and diffusion creep. To understand and quantify the coupling of these three nonlinear weakening processes, we derive a mathematical model, which consists of three coupled nonlinear ordinary differential equations describing the evolution of slab thickness, grain size, and temperature. With dimensional analysis, we determine the dimensionless parameters which control the relative importance of the three weakening processes and the two creep mechanisms. We derive several analytical solutions for end-member scenarios that predict the detachment time, that is the duration of slab detachment until slab thickness becomes zero. These analytical solutions are then tested against numerical solutions for intermediate cases. The analytical solutions are accurate for end-member scenarios where one of the weakening mechanisms and one of the creep mechanisms is dominant. Furthermore, we use numerical solutions of the system of equations to systematically explore the parameter space with a Monte Carlo approach. The numerical approach shows that the analytical solutions typically never deviate by more than 50% from the numerical ones, even for scenarios where all three weakening and both creep mechanisms are important. When both grain and thermal damage are important, the two damage processes generate a positive feedback loop resulting in the fastest detachment times. For Earth conditions, we find that the onset of slab detachment is controlled by grain damage and that during later stages of slab detachment thermal weakening becomes increasingly important and can become the dominating weakening process. We argue that both grain and thermal damage are important for slab detachment and that both damage processes could also be important for lithosphere necking during continental rifting leading to break-up and ocean formation.
1. Introduction
Since the establishment of plate tectonic theory and early seismicity observations at subduction systems (Isacks and Molnar, 1969), slab detachment, also often called slab break-off, is considered as a prominent process associated with subduction systems. During slab detachment, the lower part of a subducting lithospheric plate detaches from its upper portion and sinks into the mantle. There is overall agreement that buoyancy forces within subducting slabs induce extensional stresses which can result in slab detachment. This process has been suggested to cause seismicity patterns in subduction zones (Isacks and Molnar, 1969), magmatism during orogeny (Davies and von Blanckenburg, 1995), rapid surface uplift (e.g., Fox et al., 2015; Sternai et al., 2019), the transition from Flysch to Molasse sedimentation in the European Alps (Schlunegger and Kissling, 2015), and abrupt changes in plate motions (McKenzie, 1969; Bercovici et al., 2015). The abruptness of these events suggests that slab detachment has to occur in equally short timescales. The occurrence of slab detachment has been suggested for various regions, among them the Mediterranean (Wortel and Spakman, 2000), the Pamir-Hindu Kush region (Kufner et al., 2016), and the European Alps (Lippitsch et al., 2003). However, geodynamic interpretations that consider slab detachment as controlling process are frequently contentious (see Garzanti et al., 2018, for a review). Also, indirect observations of slab detachment based on seismic tomography are sometimes contradictory, such as in the Central and Western Alps (Kästle et al., 2020), where seismic tomography is interpreted as showing a detached slab (Lippitsch et al., 2003) but also a continuous slab (Zhao et al., 2016). Some of the controversies concerning slab detachment are also due to the fact that the thermo-mechanical process of slab detachment is still incompletely understood.
Using simplified models, Wong A Ton and Wortel (1997) found that the rheology of the subducting lithosphere is the most important parameter affecting slab detachment, while buoyancy and resistive forces are less significant. To investigate the impact of additional processes, such as brittle failure, mineral phase transitions, partial melting, grain size reduction, or shear heating, and to study the inherent three-dimensionality of slab detachment, complex numerical models have been conducted in both 2D (e.g., Gerya et al., 2004; Andrews and Billen, 2009; Duretz et al., 2011) and 3D (e.g., Burkett and Billen, 2010; van Hunen and Allen, 2011; Capitanio and Replumaz, 2013; Duretz et al., 2014; von Tscharner et al., 2014; Chen and Gerya, 2016; Magni et al., 2017; Pusok et al., 2018). In general, these models confirm the finding of Wong A Ton and Wortel (1997) that slab rheology is the most important parameter controlling slab detachment. However, when standard olivine rheologies are employed, slab detachment is usually slow and occurs on time scales of tens of millions of years, thus resulting in large detachment depths (e.g., Schott and Schmeling, 1998; van Hunen and Allen, 2011), contrary to what is suggested from tomographic images and seismicity patterns. However, additional mechanisms have been suggested to significantly accelerate slab detachment, such as weakening due to grain size reduction (Bercovici et al., 2015, 2019; Bellas et al., 2018), elaborated viscoelastoplastic rheology models (Duretz et al., 2011, 2012), preexisting weak zones (Burkett and Billen, 2010) or thermal weakening due to shear heating (Gerya et al., 2004; Duretz et al., 2012). Shear heating can efficiently localize deformation and form large-scale shear zones under lithospheric deformation conditions (Thielmann and Kaus, 2012; Duretz et al., 2015, 2019; Kiss et al., 2019). In particular, the combined action of shear heating and grain size reduction may result in significant weakening of the slab and associated strain localization (Thielmann et al., 2015; Foley, 2018), which may even trigger earthquakes in slab detachment settings (Thielmann, 2018). Therefore, it seems important to include different ductile weakening effects in models of slab detachment. Shear heating and grain size reduction have been shown to result in comparable weakening (Duretz et al., 2012; Bercovici et al., 2015), but it is not yet clear which of these mechanisms ultimately control slab detachment under what conditions and whether these processes are competitive or collaborative processes (Kameyama et al., 1997; Thielmann et al., 2015; Foley, 2018; Thielmann, 2018).
While 2D and 3D numerical models capture the complex geometrical interactions during slab detachment, their computational expense makes it difficult to systematically investigate the impact of different weakening mechanisms and their mutual feedbacks. Furthermore, due to the many equations and parameters involved, such 2D and 3D models are often little transparent. In contrast, simple 0D and 1D models are usually more transparent and have proven to provide fundamental physical insight into the slab detachment process and to efficiently test the impact of different model parameters (Schmalholz, 2011; Duretz et al., 2012; Bercovici et al., 2015, 2019; Ribe and Xu, 2020).
While slab detachment is likely dominated by viscous necking, it has also been invoked to explain deep seismicity in various regions on Earth, such as e.g., the Hindu-Kush (Kufner et al., 2017), the Vrancea region (Mitrofan et al., 2016), or the Alboran slab in the Mediterranean (Sun and Bezada, 2020). The mechanisms resulting in the observed seismicity are still contentious, as brittle failure at this depth seems to be unlikely due to the high pressures and temperatures. However, since rocks are intrinsically viscoelastic, a significant local increase of strain rates during slab detachment could shift the rock deformation mechanism from effectively viscous to effectively elastic, and hence potentially cause brittle failure. Currently, it is still unclear which mechanism(s) result in seismicity generation, but two mechanisms are frequently favored, namely dehydration embrittlement and thermal runaway (see Zhan, 2019, and citations therein). Some intermediate-depth earthquakes pose, despite their depth, a significant seismic hazard (Frohlich, 2006) and it is hence important to identify their rupture mechanisms and the conditions favoring their occurrence.
Here, we investigate viscous slab detachment for a combination of dislocation creep and diffusion creep flow laws. We quantify the coupling of three nonlinear weakening mechanisms during slab detachment: (1) structural weakening due to a necking instability (see Schmalholz and Mancktelow, 2016, and citations therein) causing localized thinning of the slab, (2) weakening due to grain size reduction and grain size sensitive diffusion creep, referred to here as grain damage, and (3) weakening due to shear heating and temperature sensitive effective rock viscosities, referred to here as thermal damage. We consider a simple slab detachment setting and use a simple 0D mathematical model that allows us to comprehensively examine the parameter space. We derive a system of three coupled nonlinear differential equations that describe the evolution of grain size, temperature and slab thickness. We apply dimensional analysis to determine the controlling non-dimensional parameters. We further derive several analytical solutions for the duration of slab detachment, that is when the slab thickness is zero, for end-member scenarios where one of the weakening mechanisms or one of the two flow laws is dominant. Using a Monte Carlo simulation with 2 × 105 simulations, we are able to determine the most important parameters controlling slab detachment. Based on the results from these simulations, we derive empirical relationships that can be used to predict detachment times for a given set of parameters. Finally, we determine which mechanism is most likely to govern slab detachment.
2. Methods
In this section, we introduce our detachment model (section 2.1), together with the equations governing the evolution of slab thickness. In sections 2.2–2.4, we introduce the governing equations for rheology, for the evolution of grain interface curvature (as a proxy of grain size) and for the temperature evolution. In section 2.5, we non-dimensionalize the governing equations to derive a set of non-dimensional equations and parameters that will be used to investigate the impact of different parameters on the detachment process. The meaning of the derived non-dimensional parameters is discussed in section 2.6.
2.1. Detachment Model
We consider a vertical slab with initially zero velocity attached to a rigid surface; a so-called stalled slab. The slab has a length H, width D0 and density ρ1, which is larger than the density ρ2 of the surrounding mantle (see also Figure 1). Due to this density difference Δρ = ρ1 − ρ2, a negative buoyancy force per unit length, FB = ΔρgD0H, is induced, which causes the slab to sink and to stretch. For this configuration, localized thinning and necking will develop in the upper region of the slab where the buoyancy-driven stresses are highest. The extensional strain rate is related to the temporal evolution of the slab thickness D at the necking region by equation (Schmalholz, 2011):
where t is time. As the buoyancy force remains constant and the slab is considered much stronger than the surrounding, the deviatoric stress in the necking region is half the total stress, FB/D, and is given by (Turcotte and Schubert, 2014)
The initial state of the system is thus given by the initial stress and the mean temperature T0 of the slab. We will link the above two equations by rheological flow laws, which are mathematical relations between and τ and are described in the next section.
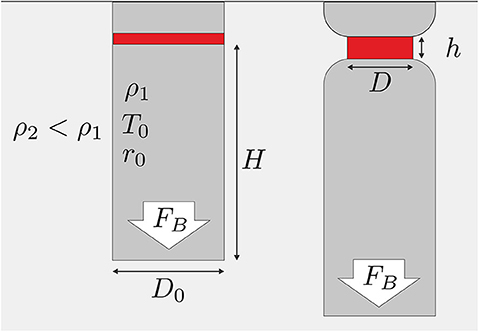
Figure 1. Model setup. (Left) Initial configuration of a slab with length H and thickness D0. The red region is the necking region with height h0 and thickness D0. (Right) Later stage, at which the thickness D of the necking region is significantly reduced and its height h increased.
2.2. Rheology
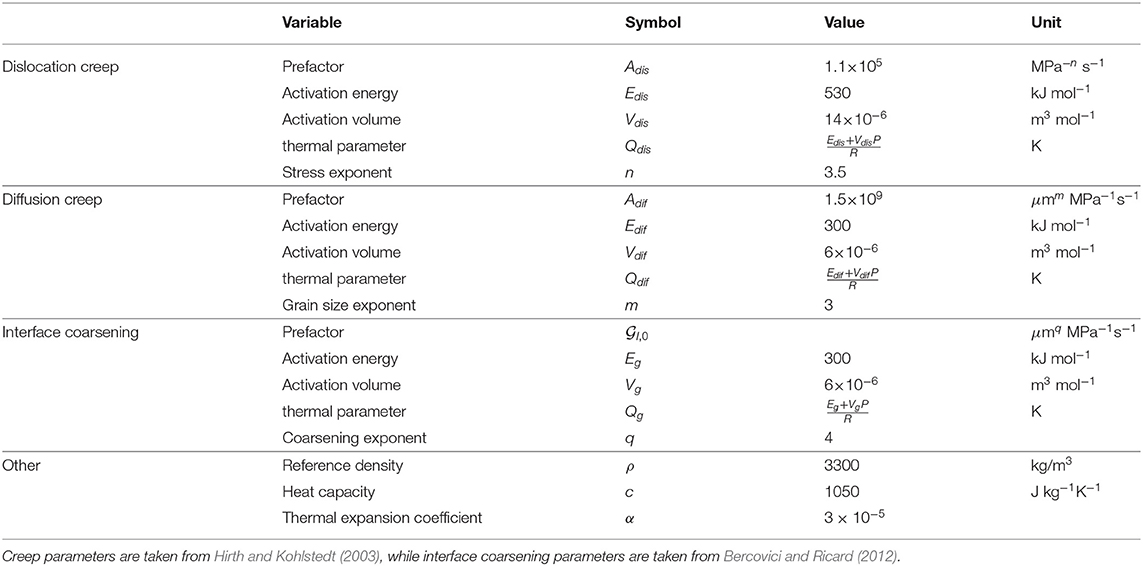
The buoyancy force FB induces deformation in the stalled slab. We assume that deformation is governed by a viscous composite rheology consisting of grain size insensitive dislocation and grain size sensitive diffusion creep (e.g., Hirth and Kohlstedt, 2003; Billen and Hirth, 2007; Kohlstedt and Hansen, 2015):
where the strain rate is a function of stress τ, temperature T, and grain size . Adis and Adif are rheological prefactors, n is the stress exponent of dislocation creep and m the grain size exponent (see also Table 1 for the definition of the different rheological parameters). Qdis and Qdif are the respective activation enthalpies divided by the gas constant R given by:
where P is pressure and Ei, Vi are activation energy and volume, respectively. The index i denotes either diffusion or dislocation creep. It is useful to define a transition grain size at which the contributions from dislocation and diffusion creep equally contribute to deformation:
Using this transition grain size, Equation (3) can be rewritten as:
where the ratio indicates whether dislocation creep () or diffusion creep () is the dominant deformation mechanism.
2.3. Grain Size Evolution
Grain size can significantly affect rock rheology if it is sufficiently small and if it changes with progressive deformation. The evolution of grain size is therefore crucial to determine the transient response of the rock to an applied stress. The reduction of the effective viscosity, quantifying viscous strength, due to a reduction in grain size is frequently termed grain damage. As mantle rocks are polymineralic, consisting of mostly olivine and pyroxene, we here treat grain size evolution using the two-phase grain size evolution law of Bercovici and Ricard (2012). This evolution law takes into account that a rock does not consist of a single mineral phase, but of at least two phases, which in the case of the mantle lithosphere corresponds to an olivine-pyroxene mixture. Due to the presence of pyroxene, the grain boundary mobility of olivine is strongly reduced due to Zener pinning. Due to this effect, the curvature of the grain boundaries is also significantly distorted, as illustrated in Figure 2. If we consider a single grain with radius , its interface curvature without the effect of secondary particles would equal . However, due to the presence of secondary particles with radius , this interface is significantly distorted and its mean interface curvature, or roughness, is quantified by r. In the “pinned state” limit, the system is assumed to be in a state where grain size evolution is controlled by the evolution of interface roughness r. Grain damage is therefore solely controlled by grain interface damage in the pinned state limit. Although we focus here on grain interface damage, we will use the more general term grain damage throughout the manuscript. If the secondary phase is dispersed (which we assume here), this effect results in interface roughness depending on the grain size of each phase as (see Bercovici and Ricard, 2012, Appendix G):
where is a factor which depends on the half width σ of the lognormal grain size distributions, which are assumed to have the same shape (see Bercovici and Ricard, 2012, Appendix F.4). Consequently, the grain sizes of both phases depend on r as (e.g., Bercovici and Ricard, 2012; Bercovici et al., 2015; Mulyukova and Bercovici, 2018):
where ϕi are the respective volume fractions of the two phases. With this definition, the mean grain size can be computed as:
Assuming a pyroxene content of 40 % and a half width of the lognormal grain size distributions of 0.8 (e.g., Bercovici and Ricard, 2013), the mean grain size is given by . Additionally assuming that both mineral phases have approximately the same rheological properties, we can—in analogy to the transition grain size (Equation 5)—define a transition interface roughness rt, which only differs by a constant prefactor from the transition grain size :
Therefore, the composite rheology can be re-written in the same manner as Equation (6), only replacing with :
In the “pinned state”, the grain size of either mineral phase is assumed to be solely determined by the interface curvature r. The interface curvature r evolves with time according to (Bercovici and Ricard, 2012):
where q is an effective grain growth exponent, γ the interfacial energy, η = 3ϕ1ϕ2 is a parameter that depends on the volume fraction ϕi of both phases, is the temperature-dependent interface coarsening rate given by (e.g., Mulyukova and Bercovici, 2017):
The deformational work rate Ψ, given by the product of and τ, is:
Both the work done in dislocation and diffusion creep contribute to grain damage and hence interface roughness. Last, the partitioning factor λI determines the relative amount of deformational work that is used for grain damage. This factor is relatively unconstrained and is most likely dependent on temperature (Rozel et al., 2011; Mulyukova and Bercovici, 2017), phase dispersion (Bercovici and Ricard, 2016; Bercovici and Skemer, 2017) as well as dislocation density (Chrysochoos and Belmahjoub, 1992; Holtzman et al., 2018). Given the missing constraints on most of these dependencies, we neglect these effects for simplicity.
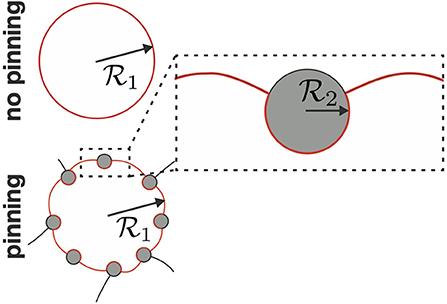
Figure 2. Sketch of the impact of Zener pinnning on grain interface roughness (after Bercovici and Ricard, 2012; Mulyukova and Bercovici, 2019). Shown is a sketch of a grain surrounded by secondary particles, with a zoom on the interface around one of the secondary particles.
In steady state, when grain damage and recovery balance each other such that dr/dt = 0, we can define a steady state roughness rs that has to fulfill the following equation:
This equation is not analytically solvable for rs for the general case. However, we can consider two particular cases, one where deformation is dominated by dislocation creep and another where diffusion creep is dominant. In the dislocation-dominated case (rs ≫ rt), the steady state interface roughness is given by:
whereas in the diffusion-dominated case (rs ≪ rt), it is:
Using Equations (16) and (17), we find that rs,dis and rs,dif are related by:
2.4. Thermal Evolution
Assuming adiabatic conditions, the temperature evolution in the necking region is given by:
Only the deformational work Ψ that is not used for grain damage results in heating, which is controlled by the coefficient 1 − λI (this coefficient is also frequently called the Taylor-Quinney coefficient). We neglect the surface energy that is released during interface coarsening as its contribution is likely negligible at typical interface roughnesses (Thielmann et al., 2015; Thielmann, 2018).
2.5. Reference State and Non-dimensionalization
The equations derived above contain a large number of material parameters. To identify potential trade-offs between different material parameters and to reduce their number it is useful to (i) define them in terms of a reference state and (ii) non-dimensionalize them using appropriate scales.
We use the initial state as the reference state with initial stress τ0, initial temperature T0 and initial grain interface transition roughness rt, 0. First, we express the temperature T as the sum of the initial temperature T0 and a temperature perturbation :
Using this, an Arrhenius term of the form can be rewritten as:
Second, with the above form of the Arrhenius term the flow law given in Equation (11) can be rewritten in terms of the reference state:
where we used Equation (10). Rewriting the rheology also allows to rewrite the grain size evolution Equation (12) in terms of the reference state:
where, using Equation (16), we can identify:
It is useful to define a normalized grain interface roughness and introduce , to obtain an equation for the evolution of the normalized interface roughness (which does not have any units):
Additionally, we can rewrite the relation between the steady state dislocation creep grain size and the steady state diffusion creep grain size given by Equation (18) in terms of normalized interface curvatures:
Using Equation (20) and the definition of the normalized grain interface roughness, the temperature Equation (19) can be written as:
Equating (1) and (22) yields:
This leaves us with three coupled ordinary differential equations for the three unknowns r, T, and D. While this notation may seem more complicated, it is significantly simplified when non-dimensionalizing Equations (26)–(29) with a set of characteristic scales for length, temperature, stress, and time, respectively, which are given by the initial slab thickness, initial slab temperature, initial slab stress, and the initial strain rate at the transition between diffusion and dislocation creep:
With the chosen characteristic temperature scale, the Arrhenius term can be rewritten as:
where . Replacing and non-dimensionalizing the respective quantities in Equations (24), (28), and (29) with the respective scales then yields
where we introduced for better readability. As is already a non-dimensional quantity, it does not have to be additionally non-dimensionalized. The superscript ′ indicates a non-dimensionalization with the characteristic scales in Equation (30), whereas ˆ indicates a normalization with the initial transition roughness rt, 0. We use two characteristic length scales because our model involves both the scale of the lithosphere thickness and the scale of a mineral grain, which can be more than ten orders of magnitude different. The two length scales are useful because they provide a more intuitive meaning of both the and D′. Additionally, the numerical treatment of this system of equations is made much easier, as values of and D′ do not attain extreme values prone to roundoff errors. The following non-dimensional numbers can be identified:
as well as the three non-dimensional exponents n, m, and q.
2.6. Nondimensional Parameters
It is worthwhile to discuss the meaning of the different non-dimensional parameters introduced in Equation (35) as well as the values they may take for Earth-like conditions. Due to their definition, the initial values for temperature and slab thickness are 0 and 1, respectively. The meaning of the non-dimensional initial temperature and interface curvature and are straightforward, with values of indicating that the initial deformation is mostly accommodated by dislocation creep and for mostly accommodated by diffusion creep. The values of δQg and δQdif indicate the respective temperature sensitivity of grain growth and diffusion creep with respect to dislocation creep. Values larger than 1 denote that dislocation creep is more sensitive to a temperature change than either grain growth or diffusion creep. This may, for example, be important during the necking process, as an increase in temperature due to shear heating may result in a switch from diffusion to dislocation creep.
The value for is the normalized steady state interface curvature in dislocation creep at the initial conditions, which is closely linked to the normalized steady state interface curvature in dislocation creep (see Equation 27). Depending on the initial grain size , the interface curvature will either increase () or decrease () to attain this steady state value. As for the initial interface curvature , values of indicate that the steady state interface curvature will favor dislocation creep. However, this is only true at the initial conditions. During the necking process, stress (being inversely proportional to the slab thickness D), temperature and interface curvature will change and thus also the transition curvature and steady state curvature. Whether deformation in these cases will be governed by dislocation or diffusion creep then depends on the values of n, m, and δQdif.
Finally, the damage numbers and determine the importance and speed of grain damage and temperature induced damage, respectively. Large values of the respective parameter denote fast and efficient weakening. Both the grain damage number and the thermal damage number can be considered as expressions of the available energies in the system. The grain damage number can be considered as the ratio between the specific deformation energy available for grain damage, given by the term λIτ0 and the energy stored in the grain interfaces, which is given by the term (Bercovici and Ricard, 2012). Hence, when the available specific deformation energy is also much larger than the energy stored in the interface (resulting in a large value of ), grain damage is more efficient. The same applies to the thermal damage number , which can be considered as the ratio between the specific deformation energy available for thermal damage, (1 − λI)τ0, and the specific thermal energy, ρcT0. Due to our choice of non-dimensionalization, this ratio is then additionally scaled by the factor Qdis/T0, also known as the Arrhenius number (e.g., Peters et al., 2016), which is in itself a measure of the ratio between activation energy and thermal energy. A large value of thus requires that (1) the system is highly temperature dependent (represented by large values of the Arrhenius number) and (2) the available deformation energy is much larger than the thermal energy.
To determine Earth-like ranges of , , , and , we assume slab lengths H of 100–500 km, mean slab temperatures T0 of 900–1,200 K and an interface partitioning factor λI within the range of 10−6 − 10−3 (e.g., Bercovici and Ricard, 2016; Mulyukova and Bercovici, 2017). There are at present no experimental constraints on the value of λI, thus its value is usually assumed based on indirect evidence. With the material parameters given in Table 1, we then compute the respective non-dimensional numbers for 105 random combinations of the input parameters to estimate their range. The resulting histograms for and , , and are shown in Figure 3. For the chosen parameters, ranges between 1 and 1,000, shows much less variation and varies between 1 and 10. and vary in the range of 10−3–10−2 and 50–70, respectively (see also Table 2).
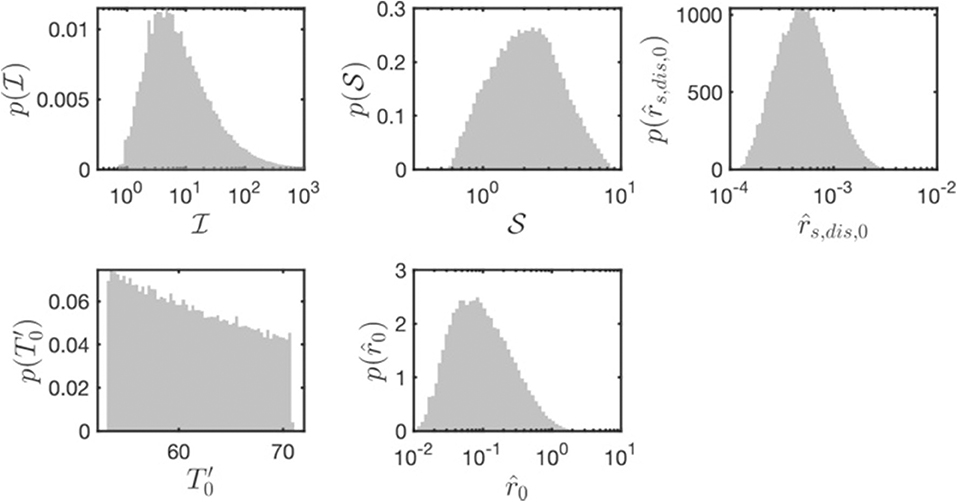
Figure 3. Probability density functions of the parameter ranges of the nondimensional numbers , , , and and for Earth-like parameters.

Table 2. Nondimensional model parameters and parameter ranges computed with the material parameters given in Table 1 and for slab lengths H of 100–500 km, average slab temperatures T of 900–1,200 K, pressures of 3–9 GPa, and partitioning factors λI ranging from 10−6 to 10−3.
2.7. Comparison to Previous Studies
Before applying these models to Earth, we will first have a general look at the system of equations given by (32)–(34). Unless otherwise noted specifically, the primes indicating non-dimensional values are dropped for the remainder of the paper for better readability. We can identify several particular cases that have been studied in the literature, the first being the analytical necking model by Schmalholz (2011). In this model, only dislocation (powerlaw) creep was considered, without taking into account either shear heating or grain size evolution. In this case, only (34) has to be considered, where the grain size dependent diffusion creep term is dropped. This is equivalent to setting and . As , the remaining Arrhenius term equals one (34), which results in:
The above equation corresponds to the equation derived in Schmalholz (2011). For n = 1, the detachment time td, that is the duration until the slab thickness becomes zero, is given by the characteristic time scale tc. For n > 1, the detachment time then depends on the powerlaw exponent as . Additionally considering shear heating (by setting ) then yields the following system of equations:
which corresponds to the system investigated by Duretz et al. (2012) (the thermal damage number is equal to A in their Equation 6). Finally, Bercovici et al. (2015) investigated the effect of grain damage and a composite dislocation/diffusion creep rheology on slab detachment, but not shear heating (, , ). In that case, (32)–(34) reduce to (due to the constant temperature, the respective Arrhenius terms equal 1):
This system of equations is equal to the one used in Bercovici et al. (2015), except that they additionally included the effect of the viscous resistance of the mantle to the sinking slab. The damage number used in their paper is equal to used here, whereas the used here equals their . Both the studies of Duretz et al. (2012) and Bercovici et al. (2015) concluded that the respective weakening mechanism resulted in a significant reduction of the detachment time.
3. Results
To determine the impact of different parameters on the necking process, we assessed their effect on the detachment time of the slab, td. We follow a two-fold approach which consists of (1) analytical considerations of several simplified cases and (2) a numerical Monte-Carlo approach to test the prediction potential of the analytical approximations. We solved the set of ordinary differential Equations (32)–(34) numerically using a stiff ordinary differential equation solver of the software Matlab. The numerical code can be found in the online repository on figshare (Thielmann and Schmalholz, 2020a).
3.1. Representative Slab Detachment Simulations
In Figure 4, we show a comparison of eight cases, where we chose different extreme parameters to illustrate their impact on the necking process. For all cases we assumed n = m = 3, q = 4, δQdis = δQg = 0.5 and an initial temperature T0 = 60. The different cases are: (1) a case without grain and thermal damage where deformation is dominated by dislocation creep (, , ), (2) a case without grain and thermal damage where deformation is dominated by diffusion creep (, , ), (3) a thermal damage case with dislocation creep governed deformation (, , , ), (4) a thermal damage case with diffusion creep governed deformation (, , , ), (5) an grain damage case initially in dislocation creep, but switching to diffusion creep (, , , ), (6) a case where weakening occurs via grain damage dominated by diffusion creep (, , , ), (7) a case where weakening equally occurs due to both damage mechanisms, with deformation starting initially in dislocation creep but likely to switch to diffusion creep due to a reduction in interface curvature (, , , ), and finally (8) a case where weakening equally occurs due to both damage mechanisms, with deformation starting initially in diffusion creep (, , , ).
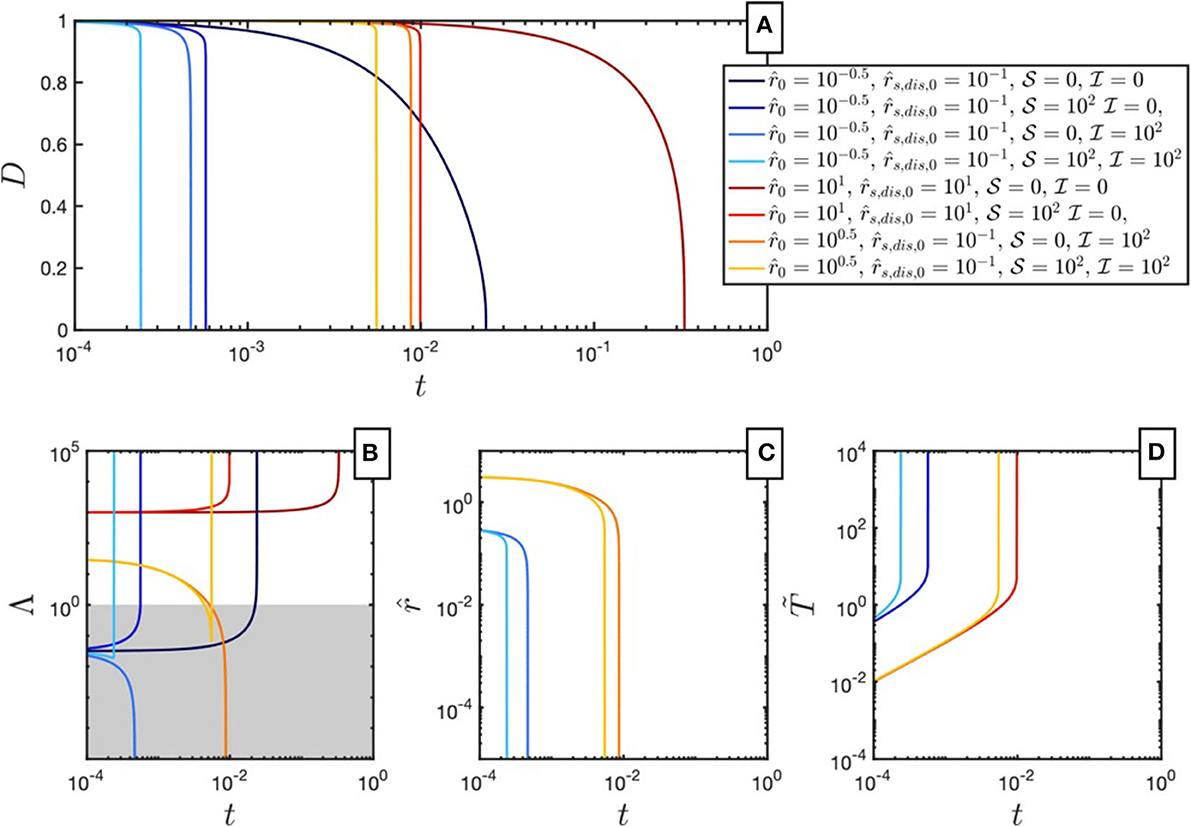
Figure 4. Comparison of eight simulations with different parameters for , , and . (A) Evolution of neck thickness D. (B) Evolution of , which denotes the importance of dislocation creep vs. diffusion creep during necking. (C) Evolution of interface curvature . (D) Evolution of the temperature perturbation . In (C,D), only the cases are shown where either interface roughness or temperature experience a change.
For the two non-damage cases, detachment times are longest. However, once a single or both damage mechanisms are activated, detachment times are significantly reduced. The reduction is largest when both interface and thermal damage are active. For all cases where damage is activated, we observe a very rapid, almost instantaneous detachment phase. As can be seen in Figure 4C, the interface curvature is significantly reduced if grain damage is active and rapidly approaches very small values. On the contrary, if thermal damage is active, temperatures significantly rise during the detachment phase (Figure 4D), which in some cases results in a switch from diffusion to dislocation creep at late detachment stages (Figure 4B).
While these examples qualitatively show the impact of both damage mechanisms on detachment times, we aim at quantifying these effects. We will first develop analytical approximations for td for several extreme cases before turning to numerical modeling. Even though Earth-like values for different nondimensional parameters are restricted (see Figure 3), we will also investigate regimes that go beyond these parameter ranges.
3.2. Analytical Considerations
3.2.1. Low Damage Numbers (, )
At low damage numbers, both Equations (32) and (33) can be neglected and the evolution of slab thickness is solely governed by Equation (34). Due to the low damage numbers, the interface curvature as well as the temperature perturbation remain at their initial values and 0. Depending on , deformation will either be dominated by diffusion or dislocation creep and the evolution of the slab thickness D is governed by:
which can be integrated to yield:
from which we can compute the detachment time td at which D = 0:
3.2.2. Shear Heating Dominated Weakening ()
In the case of shear heating dominated weakening, only Equation (32) can be neglected. The system of equations is then given by Equations (33) and (34). As in section 3.2.1, we will also distinguish between a diffusion and a dislocation dominated case. To understand the necking evolution in this case, we now examine it at the initial stages where temperature changes can be assumed to be small. The evolution of slab thickness in each case is then given by Equation (42). The evolution of temperature (Equation 33) reads as:
As we are only considering initial stages, we can additionally approximate the term e𝕋 using a Taylor series expansion around :
where we neglect higher order terms. Rewriting Equation (44) and inserting Equation (42) then results in:
which can be integrated using separation of variables to yield:
As can be seen in Figure 4, goes to infinity as D approaches zero when thermal damage is important. For the expressions of T(t) given above, the critical time tcrit at which T → ∞ is therefore an indicator of the detachment time td. This occurs when:
which yields the following expressions for tcrit:
For small values of , these expressions are equal to the low-damage case derived in section 3.2.1, thus reproducing the prediction of Schmalholz (2011) in the case of dislocation creep dominated deformation. For large values of , tcrit approaches values of , whereas in the case of dislocation creep dominated deformation, tcrit becomes independent of n and approaches values of .
3.2.3. Grain Damage Dominated Weakening
If grain damage dominates weakening during the detachment process, the necking process can be described by Equations (32) and (34). When deformation is governed by dislocation creep, grain damage does not affect the necking process. Necking within this regime can thus be described using Equation (42). In this case (and assuming that grain growth is negligible), grain size evolution is described by
which can be integrated to yield:
Using this equation, we can now determine the time tt at which the rheological transition between diffusion and dislocation creep is reached, which is the case when the dislocation and diffusion creep yield equal strain rates. If grain size evolution is sufficiently fast, this will be the case when . Inserting this value for in the above equation and solving for t results in:
Once this time is reached, the importance of diffusion creep will increase. To assess the necking behavior in this necking phase, we again consider its initial stage, where we assume that slab thickness D does not change significantly. In this case, only Equation (32) has to be considered. At , dislocation and diffusion creep yield the same strain rate so that Equation (32) can be rewritten as (additionally neglecting grain growth):
which, upon integration, results in the following expression for the evolution of :
For this equation, we can now define a critical time tcrit at which approaches zero:
The total detachment time for the case of grain damage dominated weakening with the initial deformation dominated by dislocation creep is therefore the sum of tt and tcrit:
If, on the other hand, the initial interface curvature , deformation at the initial stages will directly be governed by diffusion creep. In this case, Equation (32) can be written as (again neglecting grain growth):
which, can again be integrated and used to compute a critical time tt, which only slightly differs from the one derived above:
This critical time then represents the detachment time of the slab in the case of grain damage dominated weakening with the initial deformation dominated by diffusion creep.
In sections 3.2.1–3.2.3, we have derived a set of analytical predictions for the detachment time td for different deformation regimes using simple approximations. These predictions are summarized in Table 3.
3.3. Numerical Monte Carlo Study
As the analytical approximations derived above are based on several simplification, it is important to determine to which extent they are capable of predicting the detachment time td. To further quantify the impact of different material parameters on the detachment time td, we now turn to numerical modeling. Here we define td as the time it takes for the neck to reach a thickness of 1% of its original value. We determined the detachment time of 2 × 105 different simulations where we randomly varied , , and T0 within the ranges given in Table 2. Random numbers were drawn from uniform distributions using the Mersenne Twister pseudorandom number generator. As the number of non-dimensional parameters is still large, we used some simplifying assumptions: (1) Based on existing flow laws and two-phase growth laws for olivine (Hirth and Kohlstedt, 2003; Hiraga et al., 2010; Bercovici and Ricard, 2012), we assume fixed values for n, m, and q of 3.5, 3, and 4, respectively, (2) we assume that the activation energies for diffusion creep and interface coarsening are equal (δQdif = δQg = 0.566, e.g., Bercovici et al., 2019), and (3) at the initial conditions, grain size is large enough so that necking is dominated by dislocation creep ().
The results of this Monte Carlo simulation are shown in Figure 5, where we plot the detachment time of each simulation with respect to the grain and thermal damage numbers and as well as the initial dislocation dominated steady state interface roughness . Although the results are quite scattered, some potential underlying trends can be observed: (1) for small values of and , necking times seem to be insensitive to both values, (2) for values of and , necking times seem to primarily depend on (Figure 5A), (3) , and significantly reduce detachment times (Figure 5B), albeit not in all simulations and (4) if , necking times seem to be primarily affected by . To further explore these dependencies and to verify the previously derived analytical solutions, we will now consider three separate regimes: (1) a low grain damage regime, (2) a high grain damage, low thermal damage regime, and (3) a regime where both damage mechanisms play a role. As the initial grain size is fixed at a value of 2, thus favoring dislocation creep, our analysis will be concerned with the analytical solutions derived for cases where initial deformation is governed by dislocation creep.
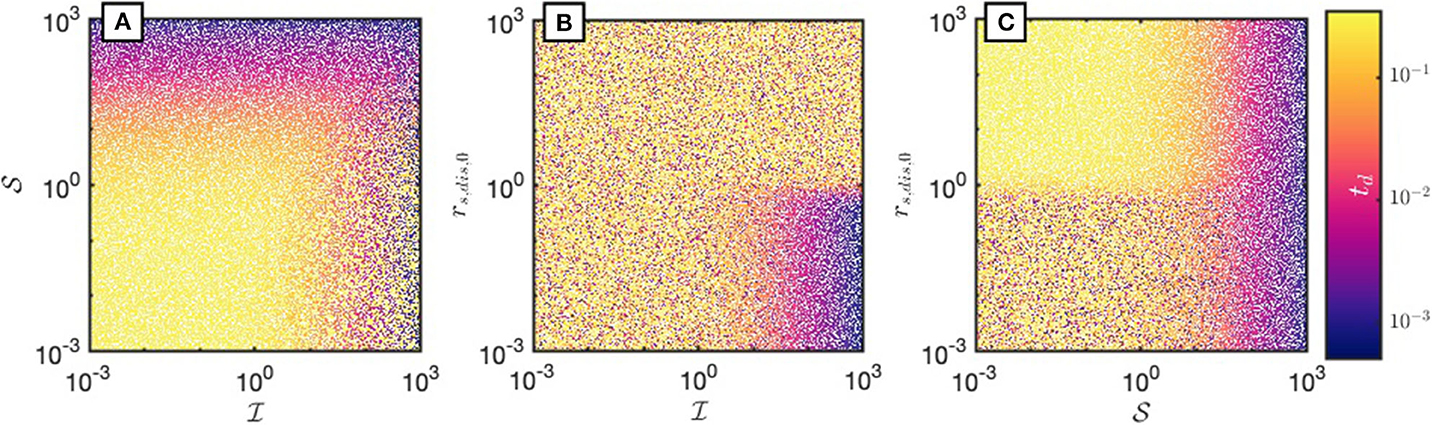
Figure 5. Detachment times td for a set of 2 × 105 simulations with different input parameters (see text for details). (A) td as a function of the grain damage parameter and thermal damage parameter . (B) td as a function of and . (C) td as a function of and .
3.3.1. Low Grain Damage ()
As derived in section 3.2.2, detachment times in this regime are independent of . In Figure 6A, we show the computed detachment times for all simulations with as a function of . In addition, the theoretical prediction of td using Equation (50) with is shown in gray. We see that, despite the simplifying assumptions made in deriving Equation (50), the analytical solution predicts the numerical result well and provides an accurate upper bound for td. Only at the transition from small to large values of , numerical results deviate from the analytical prediction by up to 35% (Figure 6B). Deviations are largest for simulations where a large value of is employed, indicating that in those cases grain damage already has an impact on the necking process. The larger deviations at values of around 1 reflect the approximation errors introduced while deriving the respective approximations. In general, at values of , detachment times are not influenced by thermal damage and thus are only dependent on the value of the stress exponent n, while at large values of , detachment times scale with .
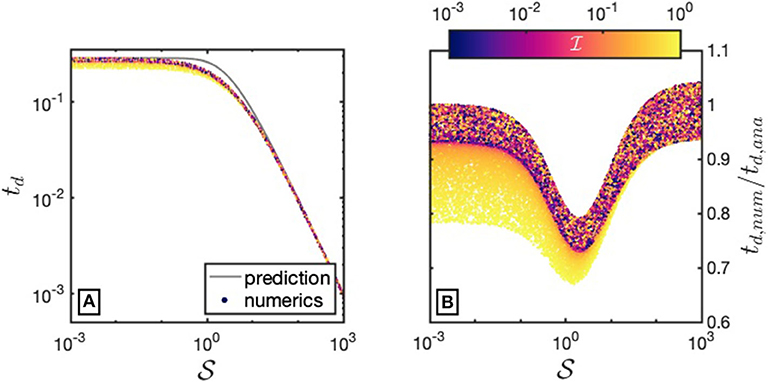
Figure 6. Detachment times td for a simulation subset with (low grain damage). (A) td as a function of the thermal damage parameter . Colors denote the value of for each simulation. The gray line denotes the analytical prediction for shear heating dominated weakening (Equation 50). (B) Ratio td,num/td,ana between the numerically computed detachment time and the analytically predicted one. As in (A), colors denote the value of for each simulation.
3.3.2. Large Grain Damage and Low Thermal Damage (, )
In this regime, detachment times should be largely independent of , but rather depend on . Due to the chosen value of , deformation in this regime is always dominated by dislocation creep at the initial stages, but may switch to diffusion creep depending on the value of . In Figure 7A, the detachment times for all simulations are shown, with their color denoting the employed value of . The two solid black lines show the predictions for td given by Equations (43) and (57). The first equation predicts the detachment time in the case of dislocation creep dominated deformation (which is grain size insensitive and thus independent of ), while the second equation predicts the detachment time in the case of deformation governed by dislocation creep at the initial stages, but switching to diffusion creep at later stages, thus essentially being governed by diffusion creep.
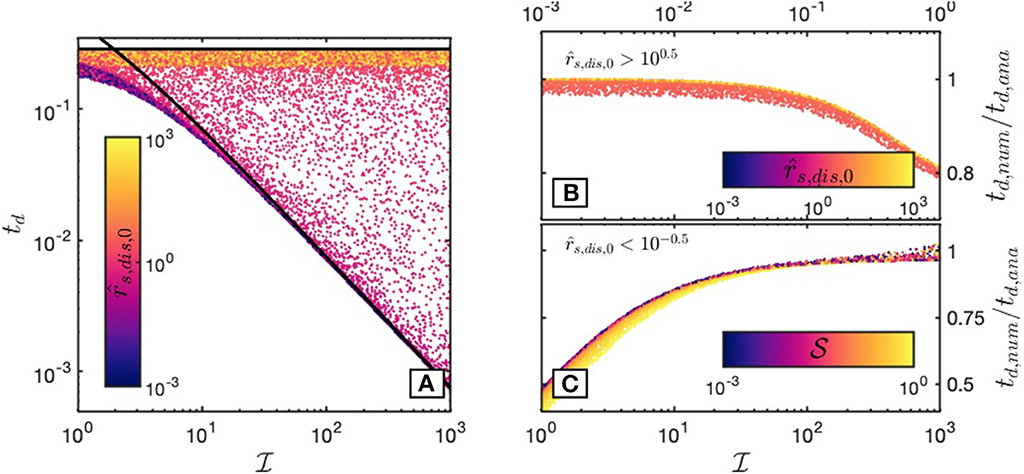
Figure 7. Detachment times td for a simulation subset with and (large grain damage, low thermal damage). (A) td as a function of the grain damage parameter . Colors denote the value of for each simulation (large values indicating that dislocation creep is more dominant during necking). The solid black lines denote the analytical predictions for grain damage dominated weakening (given by Equation 57) and damage insensitive necking (Equation 43). (B) Validity of the analytical detachment time prediction for a subset of the simulations shown in (A) with (dislocation creep controlled necking). Shown is the ratio td,num/td,ana between the respective numerically computed detachment time [given by Equation (50)] and the analytical prediction vs. the thermal damage parameter . Colors denote the value of the thermal damage parameter for each simulation. (C) Ratio td,num/td,ana but for a subset of the simulations shown in (A) with (diffusion creep controlled necking) vs. the grain damage parameter . Here, Equation (57) is appropriate to predict the detachment time.
The numerical results are quite scattered, but exhibit two main characteristics: at values of detachment times are independent of and are well predicted by Equation (50) for dislocation creep dominated deformation. This is illustrated in Figure 7B, where we plotted the ratio td,num/td,ana between the numerically computed and the predicted detachment time as a function of . Here, colors denote the value of for each simulation. As expected, the analytical prediction for td in this dislocation creep dominated regime fits best for small values of , while detachment times deviate from the prediction when approaches 1. For values of (diffusion dominated deformation), detachment times are well predicted by Equation (57) at values of and deviate from the analytical prediction as approaches 1 (Figure 7C). The analytical solutions thus predict detachment times well, except for the transition from grain damage dominated weakening to structural weakening (at ) or the transition between dislocation creep dominated deformation to diffusion creep dominated deformation (at rs, dis, 0 = 1).
3.3.3. Large Interface and Thermal Damage (, )
This regime is the most interesting one, as both interface and thermal damage will influence the necking process. Additionally, as Figure 3 indicates, detachment processes on Earth are most likely to lie within this regime. In Figure 8A, the detachment times of all simulations within this subset are shown, with colors denoting the value of . Although detachment times are very scattered, a clear pattern can be seen, with diffusion creep dominated simulations () representing a lower bound to detachment times. From this subset, we therefore extracted two additional subsets, one of which contained dislocation creep dominated simulations (), the other one containing diffusion creep dominated simulations (). In the case of dislocation creep dominated simulations, Equation (50) should predict the detachment time, since grain damage does not affect the rheology. In Figure 8B, the ratio td,num/td,ana between the numerically computed detachment times and the analytical prediction is plotted vs. thermal damage parameter . It can be seen that the analytical prediction predicts the detachment time very well, with deviations becoming larger as approaches 1. Similarly, for diffusion creep dominated simulations, Equation (57) provides a good prediction for td. The comparison between this prediction and the numerically computed results is shown in Figure 8C, where we plot the ratio td,num/td,ana between the numerically computed detachment times and the analytical prediction vs. the thermal damage parameter . Colors denote the ratio between the grain damage parameter and the thermal damage parameter . We can see that if is much larger than , detachment times are best predicted, with numerically computed detachment times becoming significantly decreased for (1) similar values of and and (2) for approaching 1. As could be already seen in Figure 4, this highlights the cumulative effect of grain and thermal damage.
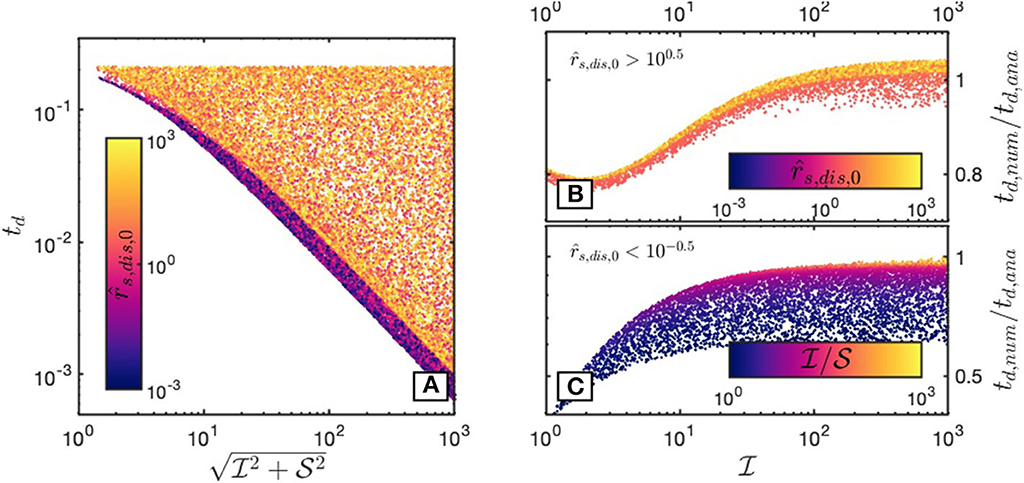
Figure 8. Detachment times td for a simulation subset with and (large interface and thermal damage). (A) td as a function of the combination of the grain damage parameter and the thermal damage parameter . Colors denote the value of for each simulation (large values indicating that dislocation creep is more dominant during necking). (B) Validity of the analytical detachment time prediction for a subset of the simulations shown in (A) with (dislocation creep controlled necking). Shown is the ratio td,num/td,ana between the respective numerically computed detachment time and the analytical prediction (given by Equation 50). (C) Same as (B), but for a subset of the simulations shown in (A) with (diffusion creep controlled necking). Here, Equation (57) is appropriate to predict the detachment time. Colors denote the ratio between the grain damage parameter and the thermal damage parameter.
In summary, the comparison between numerical model results and analytically derived detachment time predictions shows that the analytical predictions are capable to reasonably predict numerical model behavior for either dislocation creep dominated cases () or diffusion creep dominated cases (), when thermal and grain damage parameters attain extreme values. At the transition between dislocation creep and diffusion creep dominated regimes as well as when thermal and grain damage parameters take values around 1, numerically computed detachment times deviate strongest from the analytical predictions. However, these largest deviations typically never exceed 50%.
3.4. Impact of Thermal Diffusion
In the analysis presented above we have so far neglected thermal diffusion for simplicity, thus omitting the diffusion term in Equation (19) and its non-dimensional counterpart in Equation (34). During slab detachment, the cold slab will be heated due to thermal diffusion by the surrounding hotter mantle. This heating will weaken the slab and, hence, thermal diffusion may have a significant effect on the necking process (e.g., Gerya et al., 2004). However, thermal diffusion is only important, if the time scale of diffusive heating is not significantly longer than the time scale of slab detachment. To assess the time scale and importance of thermal diffusion during slab detachment and how it may affect detachment times, we here employ a simple analysis. First, we approximate the diffusion term using a simple finite difference approximation:
where Tm is the ambient mantle temperature and κ the thermal diffusivity. This term has units of K/s, which implies that it has to be multiplied with tc/Tc for non-dimensionalization. In non-dimensional form, this approximated diffusion term can be written as:
where is the diffusion time scale and tc is the characteristic time scale chosen for non-dimensionalization, here the dislocation creep strain rate at the initial conditions (see Equation 30). δTm = Tm/T0 is the ratio between the ambient mantle temperature and the slab temperature. Considering temperature diffusion thus introduces the two additional non-dimensional numbers tc/tdiff and δTm.
For Earth-like parameters, the range of δTm is relatively small and lies between ~ 1.3–1.8, while the range of tc/tdiff is significantly larger and may range between ~ 10−4and101. Values for tdiff are limited by the range of Earth-like values for thermal diffusivity and slab thickness. Both these properties cannot vary orders of magnitude, thus the variations in td are a result of variations in tc. This characteristic time scale is determined by the nonlinear rheology (see Equation 30) and yields large values for cold and short slabs and small values for long and warm slabs.
A large value of tc/tdiff implies that the slab may be significantly heated due to thermal diffusion. Due to this heating, the slab will be weakened and detachment times will be reduced. On Earth, thermal diffusion therefore may become important for cold and short slabs with long detachment times. This is also reflected in a value of 200 Ma for tdiff (assuming a slab with thickness 80 km and a thermal diffusivity of 10−6 m2s−1).
4. Discussion
4.1. Application to Earth
To determine the impact of grain size reduction and shear heating on slab detachment on Earth, we now compute detachment times for Earth-like parameter ranges. As shown in Figure 3, parameter ranges for and include values that span from ~ 10−1 to 102 and ~ 10−1 to 101, respectively, thus putting Earth-like detachment processes right within the transitional regime, where both grain and thermal damage are important. Employing the Earth-like parameters (Table 1) and assuming a range of slab lengths H and temperatures Tslab, we computed the resulting detachment times numerically for these transitional regimes. Additionally, as the value of the partitioning factor λI is highly unconstrained, we varied its value from 10−6 to 10−4. The results show that for the chosen parameters, the detachment times range between 10,000 and more than 10 billion years (Figures 9A–C), with the extremely long detachment times being a result of cold slab temperatures in short slabs. When thermal diffusion is considered, these extremely long detachment times are reduced to values less than ~100 million years for cold and short slabs (Figures 9A–C). As the value of λI is increased, detachment times decrease, but the effect is limited to very cold slab temperatures and short stalled slab lengths.
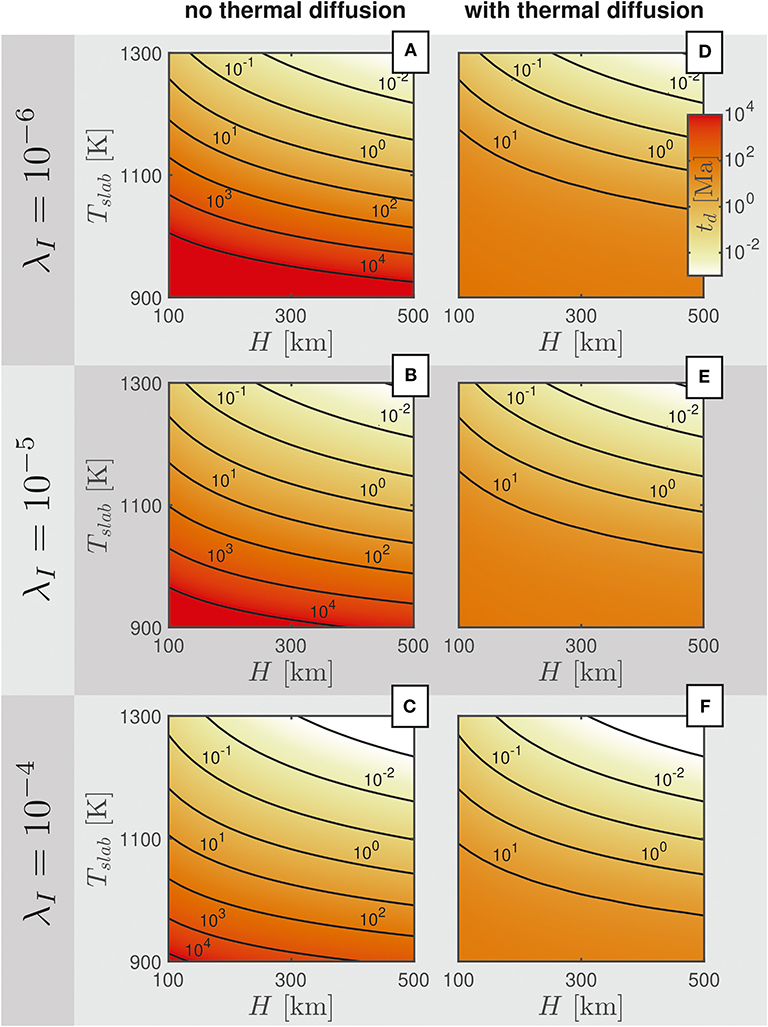
Figure 9. Application to Earth. Detachment times td for a range of slab lengths H and mean slab temperatures Tslab. Detachment times were computed using the parameters listed in Table 1. (A–C) Detachment times computed with three different values for λI, neglecting thermal diffusion. (D–F) Same as (A–C), but with thermal diffusion included.
To better illustrate the effect of thermal diffusion and variations in the partitioning factor λI, we show a comparison of six different cases in Figure 10, where we assumed a slab temperature of 1,100 K, a slab thickness of 80 km and an initial interface curvature of 1 cm. Increasing λI from 10−6 to 10−4 results in more than a 9-fold reduction of the detachment time (Figure 10A, thus highlighting the importance of this parameter. The effect of thermal diffusion can only be seen in simulations where λI is small and hence detachment times large. When looking at the evolution of the deformation mechanism ratio Λ (Figure 10B), which indicates dominant dislocation creep for Λ > 1, it becomes apparent that λI is crucial in determining the dominant deformation mechanism due to its strong impact on interface curvature (Figure 10C). The significant reduction in detachment time for the cases where indicates that the initial stages of slab detachment may be governed by grain damage. Indeed, interface curvature experiences a rapid decrease from 10−2 m to about 5·10−4 m at initial stages where slab thickness is reduced from 80 to 70 km (yellow line in Figure 10C). On the other hand, temperatures do not increase significantly at the initial necking stages. However, when a slab thickness of ~30 km is reached, temperatures start to increase significantly. This implies that while shear heating may not govern initial stages of slab detachment, it becomes important at later stages.
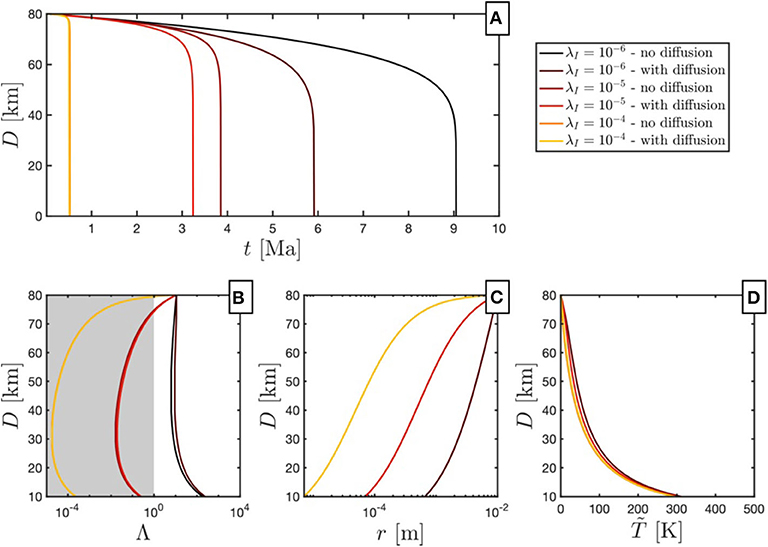
Figure 10. Examples of six simulations with a slab temperature of 1,100 K, a slab thickness of 80 km and an initial interface curvature of 1 cm are shown to illustrate the impact of thermal diffusion and the interface partitioning factor λI. (A) Evolution of neck thickness D vs. time. (B) Relationship between neck thickness D and deformation mechanism ratio Λ (with values smaller than 1 indicating diffusion creep dominated deformation. (C) Relationship between interface curvature r and D. (D) Relationship between temperature increase and neck thickness D. Non-visible lines in the respective plots lie on top of each other.
Seismic imaging has revealed several regions on Earth where high-velocity bodies have been identified in the upper mantle, among them the Northwestern US (Schmandt and Humphreys, 2011; Wang et al., 2013; Jiang et al., 2018), the Hindu-Kush (Lister et al., 2008; Kufner et al., 2017), the Mediterranean (Wortel and Spakman, 2000), the Carpathians (Sperner et al., 2001; Ismail-Zadeh et al., 2012), and the European Alps (Lippitsch et al., 2003; Kästle et al., 2020). These high velocity bodies are commonly interpreted as cold lithospheric material. However, their origin is often debated, as they could be interpreted as either subducted slabs or lithospheric drips (e.g., Sperner et al., 2001; Zandt et al., 2004; Lister et al., 2008; Lorinczi and Houseman, 2009; Kufner et al., 2017; Molnar and Bendick, 2019). Observations linked to slab detachment processes in these regions suggest slab detachment events occurring within a few million years after continental collision. Only in cases for which short slabs remain after a previous detachment event, longer “stalling times” in excess of tens of millions of years have been suggested (e.g., Jiang et al., 2018). This is in accordance with our results (see Figure 9), which also only predict detachment times in excess of 10 Ma for sufficiently short or cold slabs.
Despite the initial detachment process being mainly controlled by grain size, shear heating may have a strong impact on the “terminal stage of subduction” (Kufner et al., 2017), when elevated stresses result in increased viscous dissipation and thus heating. These elevated stresses together may not only trigger brittle failure and thus earthquakes, but may also trigger ductile instabilities at larger depths that have been proposed to be the cause for intermediate-depth earthquakes (Kelemen and Hirth, 2007; John et al., 2009; Deseta et al., 2014; Thielmann et al., 2015; Kufner et al., 2017; Ohuchi et al., 2017; Thielmann, 2018; Zhan, 2019). To further investigate this issue, it will be necessary to additionally take into account plastic failure, as the large stresses in the slab at final detachment stages may also result in brittle deformation.
4.2. Model Limitations
Owing to the simplicity of our model, computed detachment times should not be taken at face value, but rather as a first-order constraint. Due to the simplifying assumptions, our model most likely underestimates the time scales of the detachment process, as we do not account for additional forces such as (1) the viscous resistance of the mantle to the sinking slab (2) resistance of the asthenosphere to flow into the necking region of the slab and (3) the viscous resistance of the lower mantle when a slab tip reaches the bottom of the transition zone during detachment (e.g., Burkett and Gurnis, 2013). These effects could potentially slow down slab detachment (Bercovici et al., 2015). However, it is not clear to which extent these viscous forces would contribute to a delay in slab detachment. This is partly due to the nonlinear rheology of the mantle itself, which may be affected by dislocation creep and/or grain size reduction. In both cases, the viscosity of the mantle would be significantly reduced, thus reducing its resistance to the sinking slab (see also discussion in Bercovici et al., 2019).
The force balance assumed in our model may also be modified by other factors, such as the presence of positively buoyant crustal material at the top of the slab or negatively buoyant material due to the phase transition to eclogite at greater depths. Also, if the slab were not stalled, but rather subducting at a certain speed, the downward buoyancy force would be governed by their interplay with a number of other forces such as the viscous coupling of the plate at the surface to the asthenosphere and the coupling between subducting and overriding plate (e.g., Forsyth, 1975; Bercovici et al., 2019). Nevertheless, the fundamental interplay between the necking instability and the two damage processes will remain unchanged, whereas absolute time scales may change due to different stress levels in the slab. Combining the present model with the recent model by Ribe and Xu (2020) could potentially account for several of these effects.
One uncertainty for all mathematical models arises from the uncertainty of the different material parameters. Rheological parameters for dislocation and diffusion creep are to some extent constrained by laboratory experiments, but the extrapolation to tectonic time scales and the application to kilometer-scale heterogeneous rock units generates uncertainties. One of the largest parameter uncertainty of our model arises from the lack of constraints on the partitioning factor λI, which was assumed to be constant in this study. However, there is evidence that this factor depends on several other variables such as grain size, temperature, dislocation density, and phase mixing (see section 2.3). Some of these effects could potentially mitigate the effect of grain size reduction, as for example λI is thought to decrease at small grain sizes (Bercovici and Skemer, 2017) and larger temperatures (Mulyukova and Bercovici, 2018). Due to the strong effect of λI on model results, it is indispensable to obtain better constraints on this parameter, which could prove to be a challenge for experimental geoscientists. Additional constraints on the interplay between necking, grain damage and shear heating can also be obtained from structural geology (e.g., Linckens et al., 2015).
Despite the uncertainties of our model, it provides the means to analyze the fundamental physical relationship between necking, grain damage, and thermal weakening, all of which have a first-order impact on slab detachment. It also shows the importance of different material parameters (or combinations thereof), thus indicating which parameters are necessary to constrain accurately and which parameters are less important. This not only has implications for slab detachment, but also for other necking processes (e.g., Brune et al., 2016), where continental plate breakup, following lithosphere necking (e.g., Chenin et al., 2018), may be significantly accelerated due to the action of ductile weakening.
5. Conclusions
We have developed a fundamental mathematical model of slab detachment, considering structural weakening due to necking, thermal weakening due to shear heating (thermal damage) and microstructural weakening due to grain size reduction (grain damage; here represented by changes in interface curvature between two phases). Our model extends previously developed models (Schmalholz, 2011; Duretz et al., 2012; Bercovici et al., 2015) and is, to the best of our knowledge, the first model to link these three coupled weakening processes in a system of three nonlinear differential equations. The derived system of equations allows investigating the fundamental interplay of the three weakening mechanisms and to determine the conditions for which one, two or all three mechanisms are important. With dimensional analysis we determined the controlling dimensionless parameters of this system and we derived analytical solutions for the duration of slab detachment for several end-member regimes. We verified the controlling parameters and analytical solutions with a systematic numerical Monte-Carlo study. The analytical solutions for the detachment time are useful for understanding the fundamental control of the three weakening mechanisms and the involved parameters on slab detachment. Numerical solutions show that the analytical solutions are inaccurate for transitional regimes where more than one weakening mechanism is important. However, in these transitional regimes the analytical solutions typically do not deviate by more than 50% from the numerical solution, thus lying well within the range originating from uncertainties in the applied material parameters.
Both grain damage, due to grain size reduction, and thermal damage, due to shear heating, result in rapid detachment, showing that both damage mechanisms have a first order impact on the slab detachment process. Models where both damage mechanisms are equally active exhibit the shortest detachment times as a result of the positive feedback between necking, grain size reduction and shear heating. This positive feedback shows that both damage mechanisms should be considered in models of lithosphere necking.
For lithospheric-scale conditions on Earth, all three weakening mechanisms are presumably important during slab detachment. We find that for these conditions, grain damage and thermal weakening act in a collaborative manner, thus minimizing the detachment time. Grain damage is likely dominant during the initial stages of slab detachment, whereas thermal weakening becomes more important and presumably dominant during the later stages. Our results suggest that the typical duration of slab detachment is between 1 and 10 million years. Detachment times in excess of 10 Million years are only predicted for short (<≈200 km) and cold slabs, which is in broad agreement with results from other theoretical studies and indirect estimates based on geological and geophysical observations.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author. The code to create the datasets and figures used in this study are available on figshare (Thielmann and Schmalholz, 2020a,b).
Author Contributions
MT and SS designed the study, analyzed the data, and wrote the manuscript. MT derived the governing equations and performed simulations. All authors contributed to the article and approved the submitted version.
Funding
MT was funded by the Bayerisches Geoinstitut Visitor's program and SS by the University of Lausanne.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Colormaps were designed using the colorcet function (Kovesi, 2015).
References
Andrews, E., and Billen, M. I. (2009). Rheologic controls on the dynamics of slab detachment. Tectonophysics 464, 60–69. doi: 10.1016/j.tecto.2007.09.004
Bellas, A., Zhong, S., Bercovici, D., and Mulyukova, E. (2018). Dynamic weakening with grain-damage and implications for slab detachment. Phys. Earth Planet. Inter. 285, 76–90. doi: 10.1016/j.pepi.2018.09.001
Bercovici, D., Mulyukova, E., and Long, M. D. (2019). A simple toy model for coupled retreat and detachment of subducting slabs. J. Geodyn. 129, 275–289. doi: 10.1016/j.jog.2018.03.002
Bercovici, D., and Ricard, Y. (2012). Mechanisms for the generation of plate tectonics by two-phase grain-damage and pinning. Phys. Earth Planet. Inter. 202–203, 27–55. doi: 10.1016/j.pepi.2012.05.003
Bercovici, D., and Ricard, Y. (2013). Generation of plate tectonics with two-phase grain-damage and pinning: source–sink model and toroidal flow. Earth Planet. Sci. Lett. 365, 275–288. doi: 10.1016/j.epsl.2013.02.002
Bercovici, D., and Ricard, Y. (2016). Grain-damage hysteresis and plate tectonic states. Phys. Earth Planet. Inter. 253, 31–47. doi: 10.1016/j.pepi.2016.01.005
Bercovici, D., Schubert, G., and Ricard, Y. (2015). Abrupt tectonics and rapid slab detachment with grain damage. Proc. Natl. Acad. Sci. U.S.A. 112, 1287–1291. doi: 10.1073/pnas.1415473112
Bercovici, D., and Skemer, P. (2017). Grain damage, phase mixing and plate-boundary formation. J. Geodyn. 108, 40–55. doi: 10.1016/j.jog.2017.05.002
Billen, M. I., and Hirth, G. (2007). Rheologic controls on slab dynamics. Geochem. Geophys. Geosyst. 8:Q08012. doi: 10.1029/2007GC001597
Brune, S., Williams, S. E., Butterworth, N. P., and Müller, R. D. (2016). Abrupt plate accelerations shape rifted continental margins. Nature 536, 201–204. doi: 10.1038/nature18319
Burkett, E., and Gurnis, M. (2013). Stalled slab dynamics. Lithosphere 5, 92–97. doi: 10.1130/L249.1
Burkett, E. R., and Billen, M. I. (2010). Three-dimensionality of slab detachment due to ridge-trench collision: laterally simultaneous boudinage versus tear propagation. Geochem. Geophys. Geosyst. 11:Q11012. doi: 10.1029/2010GC003286
Capitanio, F. A., and Replumaz, A. (2013). Subduction and slab breakoff controls on Asian indentation tectonics and Himalayan western syntaxis formation. Geochem. Geophys. Geosyst. 14, 3515–3531. doi: 10.1002/ggge.20171
Chen, L., and Gerya, T. V. (2016). The role of lateral lithospheric strength heterogeneities in orogenic plateau growth: insights from 3-D thermo-mechanical modeling. J. Geophys. Res. 121, 3118–3138. doi: 10.1002/2016JB012872
Chenin, P., Schmalholz, S. M., Manatschal, G., and Karner, G. D. (2018). Necking of the lithosphere: a reappraisal of basic concepts with thermo-mechanical numerical modeling. J. Geophys. Res. 123, 5279–5299. doi: 10.1029/2017JB014155
Chrysochoos, A., and Belmahjoub, F. (1992). Thermographic analysis of thermomechanical couplings. Arch. Mech. 44, 55–68.
Davies, J. H., and von Blanckenburg, F. (1995). Slab breakoff: a model of lithosphere detachment and its test in the magmatism and deformation of collisional orogens. Earth Planet. Sci. Lett. 129, 85–102. doi: 10.1016/0012-821X(94)00237-S
Deseta, N., Andersen, T. B., and Ashwal, L. D. (2014). A weakening mechanism for intermediate-depth seismicity? Detailed petrographic and microtextural observations from blueschist facies pseudotachylytes, Cape Corse, Corsica. Tectonophysics 610, 138–149. doi: 10.1016/j.tecto.2013.11.007
Duretz, T., Gerya, T. V., and May, D. A. (2011). Numerical modelling of spontaneous slab breakoff and subsequent topographic response. Tectonophysics 502, 244–256. doi: 10.1016/j.tecto.2010.05.024
Duretz, T., Gerya, T. V., and Spakman, W. (2014). Slab detachment in laterally varying subduction zones: 3-D numerical modeling. Geophys. Res. Lett. 41, 1951–1956. doi: 10.1002/2014GL059472
Duretz, T., Räss, L., Podladchikov, Y. Y., and Schmalholz, S. M. (2019). Resolving thermomechanical coupling in two and three dimensions: spontaneous strain localization owing to shear heating. Geophys. J. Int. 216, 365–379. doi: 10.1093/gji/ggy434
Duretz, T., Schmalholz, S. M., and Gerya, T. V. (2012). Dynamics of slab detachment. Geochem. Geophys. Geosyst. 13:Q03020. doi: 10.1029/2011GC004024
Duretz, T., Schmalholz, S. M., and Podladchikov, Y. Y. (2015). Shear heating-induced strain localization across the scales. Philos. Mag. 1–16. doi: 10.1080/14786435.2015.1054327
Foley, B. J. (2018). On the dynamics of coupled grain size evolution and shear heating in lithospheric shear zones. Phys. Earth Planet. Inter. 283, 7–25. doi: 10.1016/j.pepi.2018.07.008
Forsyth, D., and Uyeda, S. (1975). On the relative importance of the driving forces of plate motion. Geophys. J. R. Astr. Soci. 43, 163–200. doi: 10.1111/j.1365-246X.1975.tb00631.x
Fox, M., Herman, F., Kissling, E., and Willett, S. D. (2015). Rapid exhumation in the Western Alps driven by slab detachment and glacial erosion. Geology 43, 379–382. doi: 10.1130/G36411.1
Frohlich, C. (2006). Deep Earthquakes. Cambridge: Cambridge University Press. doi: 10.1017/CBO9781107297562
Garzanti, E., Radeff, G., and Malusá, M. G. (2018). Slab breakoff: A critical appraisal of a geological theory as applied in space and time. Earth Sci. Rev. 177, 303–319. doi: 10.1016/j.earscirev.2017.11.012
Gerya, T. V., Yuen, D. A., and Maresch, W. V. (2004). Thermomechanical modelling of slab detachment. Earth Planet. Sci. Lett. 226, 101–116. doi: 10.1016/j.epsl.2004.07.022
Hiraga, T., Tachibana, C., Ohashi, N., and Sano, S. (2010). Grain growth systematics for forsterite-enstatite aggregates: effect of lithology on grain size in the upper mantle. Earth Planet. Sci. Lett. 291, 10–20. doi: 10.1016/j.epsl.2009.12.026
Hirth, G., and Kohlstedt, D. L. (2003). Rheology of the Upper Mantle and the Mantle Wedge: A View From the Experimentalists. Geophys. Monogr. Ser. Washington, DC: AGU. 83–105. doi: 10.1029/138GM06
Holtzman, B. K., Chrysochoos, A., and Daridon, L. (2018). A thermomechanical framework for analysis of microstructural evolution: application to olivine rocks at high temperature. J. Geophys. Res. 123, 8474–8507. doi: 10.1029/2018JB015613
Isacks, B., and Molnar, P. (1969). Mantle earthquake mechanisms and the sinking of the lithosphere. Nature. doi: 10.1038/2231121a0
Ismail-Zadeh, A., Matenco, L., Radulian, M., Cloetingh, S., and Panza, G. (2012). Geodynamics and intermediate-depth seismicity in Vrancea (the south-eastern Carpathians): current state-of-the art. Tectonophysics 530–531, 50–79. doi: 10.1016/j.tecto.2012.01.016
Jiang, C., Schmandt, B., Hansen, S. M., Dougherty, S. L., Clayton, R. W., Farrell, J., et al. (2018). Rayleigh and S wave tomography constraints on subduction termination and lithospheric foundering in central California. Earth Planet. Sci. Lett. 488, 14–26. doi: 10.1016/j.epsl.2018.02.009
John, T., Medvedev, S., Rüpke, L., and Andersen, T. B. (2009). Generation of intermediate-depth earthquakes by self-localizing thermal runaway. Nat. Geosci. 2, 137–140. doi: 10.1038/ngeo419
Kameyama, M., Yuen, D., and Fuijmoto, H. (1997). The interaction of viscous heating with grain-size dependent rheology in the formation of localized slip zones. Geophys. Res. Lett. 24, 2523–2526. doi: 10.1029/97GL02648
Kästle, E. D., Rosenberg, C., Boschi, L., Bellahsen, N., Meier, T., and El-Sharkawy, A. (2020). Slab break-offs in the Alpine subduction zone. Int. J. Earth Sci. 109, 587–603. doi: 10.1007/s00531-020-01821-z
Kelemen, P. B., and Hirth, G. (2007). A periodic shear-heating mechanism for intermediate-depth earthquakes in the mantle. Nature 446, 787–790. doi: 10.1038/nature05717
Kiss, D., Podladchikov, Y., Duretz, T., and Schmalholz, S. M. (2019). Spontaneous generation of ductile shear zones by thermal softening: Localization criterion, 1D to 3D modelling and application to the lithosphere. Earth Planet. Sci. Lett. 519, 284–296. doi: 10.1016/j.epsl.2019.05.026
Kohlstedt, D. L., and Hansen, L. N. (2015). “Constitutive equations, rheological behavior, and viscosity of rocks,” in Treatise on Geophysics, 2nd Edn, Vol. 2, ed G. Schubert (Oxford: Elsevier), 441–472.
Kufner, S.-K., Schurr, B., Haberland, C., Zhang, Y., Saul, J., Ischuk, A., et al. (2017). Zooming into the Hindu Kush slab break-off: A rare glimpse on the terminal stage of subduction. Earth Planet. Sci. Lett. 461, 127–140. doi: 10.1016/j.epsl.2016.12.043
Kufner, S.-K., Schurr, B., Sippl, C., Yuan, X., Ratschbacher, L., Akbar, A. M., et al. (2016). Deep India meets deep Asia: Lithospheric indentation, delamination and break-off under Pamir and Hindu Kush (Central Asia). Earth Planet. Sci. Lett. 435, 171–184. doi: 10.1016/j.epsl.2015.11.046
Linckens, J., Herwegh, M., and Müntener, O. (2015). Small quantity but large effect —How minor phases control strain localization in upper mantle shear zones. Tectonophysics 643, 26–43. doi: 10.1016/j.tecto.2014.12.008
Lippitsch, R., Kissling, E., and Ansorge, J. (2003). Upper mantle structure beneath the Alpine orogen from high-resolution teleseismic tomography. J. Geophys. Res. 108:277. doi: 10.1029/2002JB002016
Lister, G., Kennett, B., Richards, S., and Forster, M. (2008). Boudinage of a stretching slablet implicated in earthquakes beneath the Hindu Kush. Nat. Geosci. 1, 196–201. doi: 10.1038/ngeo132
Lorinczi, P., and Houseman, G. A. (2009). Lithospheric gravitational instability beneath the Southeast Carpathians. Tectonophysics 474, 322–336. doi: 10.1016/j.tecto.2008.05.024
Magni, V., Allen, M. B., van Hunen, J., and Bouilhol, P. (2017). Continental underplating after slab break-off. Earth Planet. Sci. Lett. 474, 59–67. doi: 10.1016/j.epsl.2017.06.017
McKenzie, D. P. (1969). Speculations on the consequences and causes of plate motions. Geophys. J. Int. 18, 1–32. doi: 10.1111/j.1365-246X.1969.tb00259.x
Mitrofan, H., Anghelache, M.-A., Chitea, F., Damian, A., Cadicheanu, N., and Visan, M. (2016). Lateral detachment in progress within the Vrancea slab (Romania): inferences from intermediate-depth seismicity patterns. Geophys. J. Int. 205, 864–875. doi: 10.1093/gji/ggv533
Molnar, P., and Bendick, R. (2019). Seismic moments of intermediate-depth earthquakes beneath the hindu kush: active stretching of a blob of sinking thickened mantle lithosphere? Tectonics 38, 1651–1665. doi: 10.1029/2018TC005336
Mulyukova, E., and Bercovici, D. (2017). Formation of lithospheric shear zones: Effect of temperature on two-phase grain damage. Phys. Earth Planet. Inter. 270, 195–212. doi: 10.1016/j.pepi.2017.07.011
Mulyukova, E., and Bercovici, D. (2018). Collapse of passive margins by lithospheric damage and plunging grain size. Earth Planet. Sci. Lett. 484, 341–352. doi: 10.1016/j.epsl.2017.12.022
Mulyukova, E., and Bercovici, D. (2019). The generation of plate tectonics from grains to global scales: a brief review. Tectonics 38, 4058–4076. doi: 10.1029/2018TC005447
Ohuchi, T., Lei, X., Ohfuji, H., Higo, Y., Tange, Y., Sakai, T., et al. (2017). Intermediate-depth earthquakes linked to localized heating in dunite and harzburgite. Nat. Geosci. 298:1407. doi: 10.1038/ngeo3011
Peters, M., Herwegh, M., Paesold, M. K., Poulet, T., Regenauer-Lieb, K., and Veveakis, M. (2016). Boudinage and folding as an energy instability in ductile deformation. J. Geophys. Res. 121, 3996–4013. doi: 10.1002/2016JB012801
Pusok, A. E., Kaus, B. J. P., and Popov, A. A. (2018). The effect of rheological approximations in 3-D numerical simulations of subduction and collision. Tectonophysics 746, 296–311. doi: 10.1016/j.tecto.2018.04.017
Ribe, N. M., and Xu, B. (2020). Subduction of non-Newtonian plates: thin-sheet dynamics of slab necking and break-off. Geophys. J. Int. 220, 910–927. doi: 10.1093/gji/ggz500
Rozel, A., Ricard, Y., and Bercovici, D. (2011). A thermodynamically self-consistent damage equation for grain size evolution during dynamic recrystallization. Geophys. J. Int. 184, 719–728. doi: 10.1111/j.1365-246X.2010.04875.x
Schlunegger, F., and Kissling, E. (2015). Slab rollback orogeny in the Alps and evolution of the Swiss Molasse basin. Nat. Commun. 6, 1–10. doi: 10.1038/ncomms9605
Schmalholz, S. M. (2011). A simple analytical solution for slab detachment. Earth Planet. Sci. Lett. 304, 45–54. doi: 10.1016/j.epsl.2011.01.011
Schmalholz, S. M., and Mancktelow, N. S. (2016). Folding and necking across the scales: a review of theoretical and experimental results and their applications. Solid Earth 7, 1417–1465. doi: 10.5194/se-7-1417-2016
Schmandt, B., and Humphreys, E. (2011). Seismically imaged relict slab from the 55 Ma Siletzia accretion to the northwest United States. Geology 39, 175–178. doi: 10.1130/G31558.1
Schott, B., and Schmeling, H. (1998). Delamination and detachment of a lithospheric root. Tectonophysics 296, 225–247. doi: 10.1016/S0040-1951(98)00154-1
Sperner, B., Lorenz, F., Bonjer, K., Hettel, S., Müller, B., and Wenzel, F. (2001). Slab break-off –abrupt cut or gradual detachment? New insights from the Vrancea Region (SE Carpathians, Romania). Terra Nova 13, 172–179. doi: 10.1046/j.1365-3121.2001.00335.x
Sternai, P., Sue, C., Husson, L., Serpelloni, E., Becker, T. W., Willett, S. D., et al. (2019). Present-day uplift of the European alps: evaluating mechanisms and models of their relative contributions. Earth Sci. Rev. 190, 589–604. doi: 10.1016/j.earscirev.2019.01.005
Sun, M., and Bezada, M. (2020). Seismogenic necking during slab detachment: evidence from relocation of intermediate-depth seismicity in the Alboran Slab. JGR 125:e2019JB017896. doi: 10.1029/2019JB01789
Thielmann, M. (2018). Grain size assisted thermal runaway as a nucleation mechanism for continental mantle earthquakes: impact of complex rheologies. Tectonophysics 746, 611–623. doi: 10.1016/j.tecto.2017.08.038
Thielmann, M., and Kaus, B. J. P. (2012). Shear heating induced lithospheric-scale localization: does it result in subduction? Earth Planet. Sci. Lett. 359–360, 1–13. doi: 10.1016/j.epsl.2012.10.002
Thielmann, M., Rozel, A., Kaus, B. J. P., and Ricard, Y. (2015). Intermediate-depth earthquake generation and shear zone formation caused by grain size reduction and shear heating. Geology 43, 791–794. doi: 10.1130/G36864.1
Thielmann, M., and Schmalholz, S. M. (2020a). Code for “Contributions of grain damage, thermal weakening and necking to slab detachment”. figshare.
Thielmann, M., and Schmalholz, S. M. (2020b). Figures for “Contributions of grain damage, thermal weakening and necking to slab detachment”. figshare.
Turcotte, D., and Schubert, G. (2014). “Stress and strain in solids,” in Geodynamics (Cambridge: Cambridge University Press), 92–129. doi: 10.1017/CBO9780511843877.003
van Hunen, J., and Allen, M. B. (2011). Continental collision and slab break-off: A comparison of 3-D numerical models with observations. Earth Planet. Sci. Lett. 302, 27–37. doi: 10.1016/j.epsl.2010.11.035
von Tscharner, M., Schmalholz, S. M., and Duretz, T. (2014). Three-dimensional necking during viscous slab detachment. Geophys. Res. Lett. 41, 4194–4200. doi: 10.1002/2014GL060075
Wang, Y., Forsyth, D. W., Rau, C. J., Carriero, N., Schmandt, B., Gaherty, J. B., et al. (2013). Fossil slabs attached to unsubducted fragments of the Farallon plate. Proc. Natl. Acad. Sci. U.S.A. 110, 5342–5346. doi: 10.1073/pnas.1214880110
Wong A Ton, S. Y. M., and Wortel, M. J. R. (1997). Slab detachment in continental collision zones: an analysis of controlling parameters. Geophys. Res. Lett. 24, 2095–2098. doi: 10.1029/97GL01939
Wortel, M., and Spakman, W. (2000). Subduction and slab detachment in the Mediterranean-Carpathian region. Science 290, 1910–1916. doi: 10.1126/science.290.5498.1910
Zandt, G., Gilbert, H., Owens, T. J., Ducea, M., Saleeby, J., and Jones, C. H. (2004). Active foundering of a continental arc root beneath the southern Sierra Nevada in California. Nature 431, 41–46. doi: 10.1038/nature02847
Zhan, Z. (2019). Mechanisms and implications of deep earthquakes. Annu. Rev. Earth Planet. Sci. 48:060314. doi: 10.1146/annurev-earth-053018-060314
Keywords: slab detachment, grain size evolution, shear heating, model, deep earthquakes
Citation: Thielmann M and Schmalholz SM (2020) Contributions of Grain Damage, Thermal Weakening, and Necking to Slab Detachment. Front. Earth Sci. 8:254. doi: 10.3389/feart.2020.00254
Received: 31 January 2020; Accepted: 09 June 2020;
Published: 16 July 2020.
Edited by:
Jeroen Van Hunen, Durham University, United KingdomReviewed by:
Sébastien Merkel, Lille University of Science and Technology, FranceMark Behn, Boston College, United States
Copyright © 2020 Thielmann and Schmalholz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Marcel Thielmann, bWFyY2VsLnRoaWVsbWFubkB1bmktYmF5cmV1dGguZGU=
 Marcel Thielmann
Marcel Thielmann Stefan M. Schmalholz
Stefan M. Schmalholz