Numerical Investigation on Fracture Mechanisms and Energy Evolution Characteristics of Columnar Jointed Basalts With Different Model Boundaries and Confining Pressures

To reveal the mechanical mechanisms and energy release characteristics underlying progressive failure of columnar jointed basalts (CJBs) with various model boundaries and confining pressures, by combining the meso-damage mechanics, statistical strength theory, and continuum mechanics, inhomogeneous CJB models with different dip angles to the column axis are constructed. In the cases of plane stress, plane strain, and between plane stress and plane strain, the gradual fracture processes of CJBs are simulated under different confining pressures and the acoustic emission (AE) rules are obtained. The results show that: 1) in the case of plane stress, the fracture process of CJBs along direction I orthogonal to the column axis: at the initial stage of loading, the vertical joints and the transverse joints in the CJB specimen are damaged. Then, more columns in the upper middle part are cracked; 2) in the case between plane stress and plane strain, the fracture process of CJBs along the direction parallel to the column axis: at the initial stage of loading, the columnar joints are damaged. Then, the area of the damaged and broken columns at the top of the specimen increases and the crushing degree intensifies; 3) for the case between plane stress and plane strain, the AE energy accumulation before the peak stress is higher than the plane strain state along the direction orthogonal to the column axis. Meanwhile, along the direction parallel to the column axis, this value becomes larger when changing from the state between plane stress and plane strain to the plane strain state. These achievements will certainly improve our understanding of the fracture mechanism and energy evolution of CJBs and provide valuable insights into the instability precursor of CJBs.

1 Introduction

A columnar jointed structure is a kind of tensile fracture-dominated structure with regular or irregular columns, which is common in volcanic lava. It is mostly found in basalt, and sometimes in intermediate acid lava, fused tuff, subvolcanic rock, and basic dike. Columnar jointed rock masses (CJRMs) usually present with the forms of quadrilateral prisms, pentagonal prisms, hexagonal prisms, etc. Actually, columnar joint structures are widely distributed in China, Australia, Israel, Brazil, the United States, Scotland, Northern Ireland, India, France, and Siberia, among other places (Huang et al., 2020). Figure 1 displays some representative field photographs of CJRMs (Gilman, 2009; Guy, 2010; Xu, 2010; Zavada et al., 2015; Weinberger and Burg, 2019). In Southwest China, many large-scale hydropower stations have been built in the areas filled with columnar jointed basalts (CJBs), such as the Baihetan Hydropower Station, Wudongde Hydropower Station, Jin’anqiao Hydropower Station in Lijiang, Yunnan, and the Xiluodu Hydropower Station in the canyon section of Jinsha River. With CJRMs being a special type of rock mass, their mechanical properties can be obtained from in situ tests, laboratory tests, numerical simulation, and some other methods (Min and Jing, 2003; Eshraghi and Zare, 2015; Liu and Shao, 2017; Yu et al., 2017; Yu et al., 2018).

FIGURE 1

FIGURE 1. Field photographs of the columnar jointed rock masses (CJRMs). (A) The CJRMs in Shandong, China (Xu 2010). (B) The CJRMs in Israel (Weinberger and Burg 2019). (C,D) The CJRMs of the Devils Tower in the United States (Zavada et al., 2015). (E) The CJRMs of the giant levee in Northern Ireland (Gilman 2009). (F) The CJRMs in France (Guy 2010).

For in situ tests, one of the most important purposes is to obtain the mechanical behaviors of CJBs (or CJRMs). However, it is difficult to prepare large-scale prototype specimens due to the disintegration of the rock mass under unloading relaxation conditions. In addition, the mechanical parameters obtained by in situ tests are generally discrete because of the spatial variability of the structures of CJRMs (Rajmeny et al., 2004). Xiao et al. (2017) monitored microseisms induced by the excavation of CJBs at an underground hydropower station. Hu et al. (2017) obtained rock cores through on-site dam foundation drilling, carried out uniaxial compression tests on basalt samples with primary hidden fractures, synchronously collected acoustic emission (AE) information during rock sample deformation and failure, and systematically analyzed the test results in combination with the structural characteristics of the samples. Xia et al. (2020a) studied the structural characteristics of CJBs in the drainage tunnel of the Baihetan Hydropower Station and their influence on longitudinal wave anisotropy. The valuable research data and results on the mechanical properties of CJRMs in practical engineering were obtained through the above field tests; however, the occurrence environment of engineering rock mass is always complex, and the sampling procedure might be affected by disturbance.

In laboratory tests, simplified small-scale structures have been adopted to represent regular or irregular columns. For example, Ji et al. (2017) used cement, fine sand, water, and a water reducer to make CJRM specimens, carried out uniaxial compression tests on them, and analyzed the strength changes and failure characteristics of specimens with different column dip angles. Ke et al. (2019) studied the effects of column dip angles and transverse joints on the anisotropic mechanical properties and failure mechanism of CJRM specimens through uniaxial compression tests. Xiao et al. (2014) and Xiao et al. (2015) obtained the deformation modulus and uniaxial compressive strength (CS) of CJRMs with different column dip angles through uniaxial and triaxial compression tests and analyzed the anisotropic characteristics of the deformation and strength of CJRMs. Huang et al. (2020), combined with Voronoi diagram random simulation and 3D printing technology to prepare irregular columnar joint network models, poured model and removed formwork and then used white latex and glue as the binder to bond the columns in order to obtain irregular CJRM specimens. Through uniaxial compression tests, the strength characteristics and failure modes of irregular CJRMs were studied. Xia et al. (2020b) proposed a suitable method to accurately reconstruct the structure of irregular CJRMs using three-dimensional printing (3DP) and similarity constant. Uniaxial compression tests were carried out on the reconstructed specimens, and the test results were compared with the field test results. Through the previous experimental tests, many useful research results were obtained for understanding the mechanical behaviors of CJRMs. However, the mechanical properties of rock matrix and joints in experimental tests are different from those of in situ rock mass. Meanwhile, issues of being time-consuming and diseconomy will be encountered.

For numerical tests, the selection of material parameters and constitutive relationships are important for the simulated results (Gong et al., 2018). Cui et al. (2016) used the joint network finite element as a tool to study the influence of various structural effect characterization parameters on the equivalent deformation modulus (EDM) of CJRMs. Zheng et al. (2010) established 3D discrete element numerical models of CJRMs. Through numerical simulations of bearing plate tests with different sizes, the effects of size and anisotropy on the test results were discussed. Ning et al. (2008) used the 3D distinct element code (3DEC) method to carry out numerical tests in order to study the random simulations of CJRMs and their characterization unit scale. Yan et al. (2012) established 3D discrete element models of CJRMs, carried out numerical simulations of triaxial compression tests, and studied the size effect of the macro equivalent elastic modulus of CJRMs. Through previous numerical simulations, some valuable achievements regarding the size effect, anisotropy, critical strength, etc., of CJRMs were obtained. However, revealing the fracture mechanisms and mechanical responses of CJBs suffering different model boundaries and confining pressures is still a challenging topic because of the complex structural characteristics. Meanwhile, energy release features provide a useful perspective to capture the precursory law of the fracture instability of CJBs.

Under different model boundaries and confining pressure conditions, the local deformation and peak strength of CJBs are different, and the fracture mechanisms and energy evolution rules are also different. In this study, based on the combination of meso-damage mechanics, statistical strength theory, and continuum mechanics, the images of CJBs with different dip angles along the directions orthogonal and parallel to the column axis are constructed and transformed into a series of numerical models. The heterogeneity of rock mass is taken into account by assigning the material mechanical parameters according to the specific statistical function. In the case of plane stress, the case between plane stress and plane strain, and the case of plane strain, the mechanical behaviors and AE released energy of CJBs in the directions orthogonal and parallel to the column axis are numerically simulated under confining pressure, and the progressive fracture process, failure mode, energy release rule, and instability precursor information are further analyzed.

2 Numerical Modeling

2.1 Rationale of the DIC-Improved RFPA

The advantages of the rock failure process analysis (RFPA) method lie in simulating the progressive failure process without assuming when and where the new cracks will generate and how they will propagate and connect with each other (Tang 1997; Tang and Kou, 1998; Tang et al., 2000; Li et al., 2011; Lang, 2018; Lang et al., 2019; Yu et al., 2015; Liang, 2005). In addition, the validity and reliability of the RFPA code have been assessed in a number of typical numerical tests (Tang and Kou, 1998; Tang et al., 2001; Xu et al., 2013). Also, RFPA has been widely applied in the stability analysis (Liu et al., 2017; Li et al., 2019), scale effect (Zhou et al., 2018), and anisotropy (Yang et al., 2015a; Yang et al., 2015b) of jointed rock masses.

Digital image correlation (DIC) was combined with the RFPA method to improve the model building capability. Clearly, the image import, gray threshold segmentation, and pixel processing were added into the RFPA method. In order to build a numerical model, it is necessary to transform the information of the image into the vectorized data for modeling. The digital image is composed of square pixels, as shown in Figure 2A. In the 3D space, if the image is considered to have a certain thickness t, each pixel can be regarded as a finite element mesh. The corner coordinates of each pixel were transformed into the physical positions of the corresponding element. According to the gray value of each pixel, it can be classified into rock or joint material and given corresponding material parameters. The transformed finite element meshes are presented in Figure 2B. The elastic moduli and strengths of the meso elements in the model were non-uniformly distributed. Namely, the parameters between adjacent elements were not necessarily equal. In this way, the heterogeneity of rock mass is simulated. The DIC-improved RFPA was based on the meso damage mechanics and the statistical strength theory. The maximum tensile stress criterion and the Mohr–Coulomb failure criterion were adopted as the failure criteria. When the minimum principal stress of a meso element exceeds its uniaxial tensile strength, the element will produce tensile damage, as shown in Figure 2C. If the stress state of the meso element satisfies the Mohr–Coulomb failure criterion, the meso element will produce shear damage, as shown in Figure 2D. Initially, the behavior of an element is linear elastic. After reaching the failure criteria, its bearing capacity remains a certain residual strength until completely damaged. As shown in Figures 2C,D, the residual strength coefficient can be 0–1, in theory. If it is 1, the stress–strain curve will show the ideal elastic–plastic characteristic.

FIGURE 2

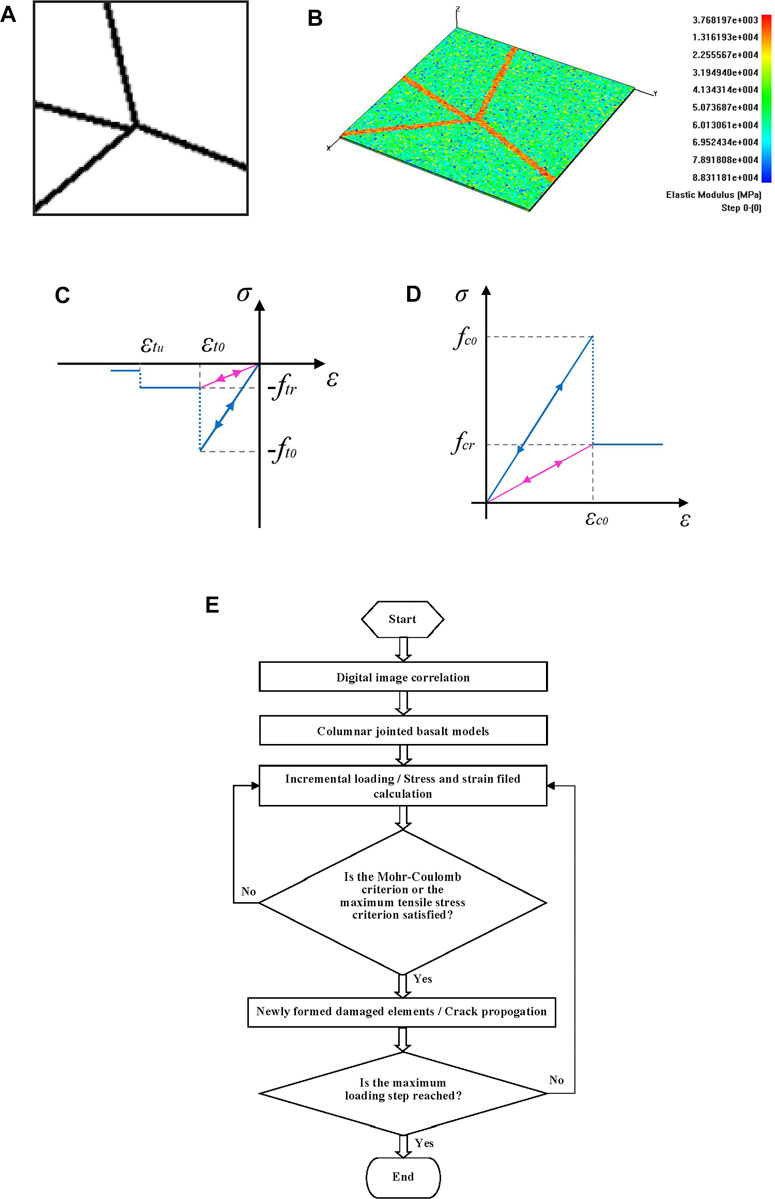
FIGURE 2. The digital image (A), the finite element model after digital image transformation (B), the tensile state of an element under uniaxial stress (C), the compressive state of an element under uniaxial stress (D), and the calculation flow diagram of the digital image correlation (DIC)-improved rock failure process analysis (RFPA) method (E).

2.2 Failure Criteria and Damage Behavior of the Meso Element

In the DIC-improved RFPA code, when an element is under uniaxial tension, the elastic–brittle damage constitutive relation will be adopted. The tensile damage function can be described using the following inequality:

${\sigma }_3\le f_t(1)$

where f_t is the uniaxial tensile strength. In this paper, the compressive stresses and strains are taken as positive.

Simultaneously, the Mohr–Coulomb criterion was applied to determine whether a meso element is damaged in the shear mode, and it can be expressed as follows:

${\sigma }_1-\frac{1+\sin \phi }{1-\sin \phi }{\sigma }_3-f_c\ge 0(2)$

where σ₁ and σ₃ are the major and minor principal stresses of the meso element, respectively, and φ and f_c are the internal friction angle and uniaxial CS, respectively.

In elastic damage mechanics, when the value of the stress increases to a specific value leading to the failure of the element, the elastic modulus of an element will degrade gradually as the damage evolves. The elastic modulus of the damaged material can be defined as follows:

$E=\left(1-D\right)E_0(3)$

where D represents the damage variable, E represents the elastic modulus of the damaged material element, and E₀ represents the elastic modulus of the undamaged material element.

Tensile damage will occur when the maximum tensile strain criterion is satisfied. According to the constitutive law, the damage variable D can be expressed as follows (Tang et al., 2015):

$\mathit{D}=\{\begin{array}{cc}0& \epsilon >{\epsilon }_{t0}\\ 1-\frac{\lambda {\epsilon }_{t0}}{\epsilon }& {\epsilon }_{tu}<\epsilon \le {\epsilon }_{t0}\\ 1& \epsilon \le {\epsilon }_{tu}\end{array}(4)$

where λ is the coefficient of residual strength given by λ = f_tr/f_t, f_t is the uniaxial tensile strength, f_tr is the residual tensile strength, ε_t0 is the elastic limit strain (or tensile threshold strain) given by ε_t0 = f_t/E₀, and ε_tu is the ultimate tensile strain describing the state when an element is fully damaged. The ultimate tensile strain can be defined as ε_tu = ηε_t0, where η is termed the ultimate strain coefficient.

Additionally, when a meso element is damaged in shear, the variable D can be calculated as follows (Tang et al., 2015):

$\mathit{D}=\{\begin{array}{cc}0& \epsilon <{\epsilon }_{c0}\\ 1-\frac{\lambda {\epsilon }_{c0}}{\epsilon }& \epsilon \ge {\epsilon }_{c0}\end{array}(5)$

where λ is also the coefficient of residual strength given by λ = f_cr/f_c, f_c is the uniaxial CS, f_cr is the residual CS, and ε_c0 is the compressive threshold strain given by ε_c0 = f_c/E₀.

The calculation flow diagram of the DIC-improved RFPA method is shown in Figure 2E. In the DIC-improved RFPA code, the AE count and AE energy are proportional to the number of damaged elements.

2.3 Validation of the Numerical Modeling

In the validation of the numerical simulation, the laboratory physical test of Ji et al. (2017) was used to verify the numerical test in this paper. The specimens used for the numerical validation in this paper included the directions orthogonal and parallel to the column axis. The case of plane strain was adopted. The width of the specimen was 50 mm, the height was 100 mm, and the diameter of the regular hexagonal column was 10 mm. Based on the DIC-improved RFPA method, the digital image was transformed into a finite element calculation model. The mechanical parameters of the finite element model were determined as follows by referring to relevant literatures (Zheng et al., 2010; Yan et al., 2012; Hu et al., 2017; Ji et al., 2017; Xiao et al., 2017; Ke et al., 2019; Xia et al., 2020a): for the material type of basalts, the values of the heterogeneity index, elastic modulus, Poisson’s ratio, uniaxial CS, the ratio of CS to tensile strength, and the friction angle were 5, 60 GPa, 120 MPa, 10, 0.2, and 56.15°, respectively; for the material type of joints, the values of the above parameters were 5, 15 GPa, 30 MPa, 10, 0.25, and 36°, respectively. The heterogeneity index was used to characterize the heterogeneity degree of the mechanical properties of rocks and joints. The smaller the heterogeneity index, the more inhomogeneous is the material.

The displacement-controlled loading was applied gradually in the numerical test until the occurrence of a macro specimen failure, and the ratio of the displacement loading amount in each step to the initial height of the specimen was 0.000017. A comparison of the obtained failure patterns by simulation and experiment is shown in Figure 3.

FIGURE 3

FIGURE 3. Comparison of the obtained failure patterns by simulation and experiment under uniaxial compression. (A) Physical test results of columnar jointed rock mass (CJRM) in the direction orthogonal to the column axis (Ji et al., 2017). (B) Damage diagram of the numerical test of CJRM (in this study). (C) Displacement diagram of the numerical test of CJRM (in this study). (D) Physical test results of CJRM with β = 15° in the direction parallel to the column axis (Ji et al., 2017). (E) Damage diagram of the numerical test of CJRM with β = 15° (in this study). (F) Displacement diagram of the numerical test of CJRM with β = 15° (in this study).

2.4 Numerical Configuration

In this study, the settings of numerical specimens are referred to the conditions of CJBs at the Baihetan Hydropower Station in China. The column length of the CJBs in Baihetan Hydropower Station is 0.5–3 m, and the column diameter is 13–25 cm. The calculation condition settings of CJBs with different model boundaries and confining pressures in numerical test are shown as follows. For the slice conditions of the model, three cases were considered: direction I, orthogonal to the column axis; direction II, orthogonal to the column axis; and the direction parallel to the column axis. For the boundary conditions of the model, three cases were considered: the case of plane stress, the case between plane stress and plane strain, and the case of plane strain. In the case between plane stress and plane strain, there were normal displacement constraints on one side of the model plane, which corresponds to the boundary of rock mass with a free surface, such as the underground cavern wall along the direction perpendicular to the axial direction of the cavern; in the case of plane strain, there were normal displacement constraints on both sides of the model plane, which correspond to the boundary of rock mass fixed along a direction, such as the surrounding rock along the axial direction of a cavern; in the case of plane stress, there are no displacement constraints along the normal direction of the model plane, which corresponds to the boundary of a thin rock slab.

The model size is 3 × 3 m, with confining pressures of 0, 4, and 8 MPa. The heterogeneity index of the column is 5 and the column dip angles are 0°, 15°, 30°, 45°, 60°, 75°, and 90°. The column is a regular hexagonal prism with a column diameter of 20 cm. The residual strength coefficients of the rocks and joints were set as 0.1 and 1, respectively. Specifically, the elastic–brittle–plastic constitutive relation is adopted for the rocks and the elastic–plastic constitutive relation adopted for joints.

In the numerical test, the element size of each model is the same. Taking a 3 × 3-m specimen as an example, the number of elements of the specimen is 608,400. Figure 4 shows the typical settings and boundary conditions of the numerical test of CJBs with different model boundaries and confining pressures. The regular hexagons in Figure 4C show the cross-sectional shape of the CJBs. In the numerical simulation, the local enlarged view in Figure 4C is similar to that in Figure 2B.

FIGURE 4

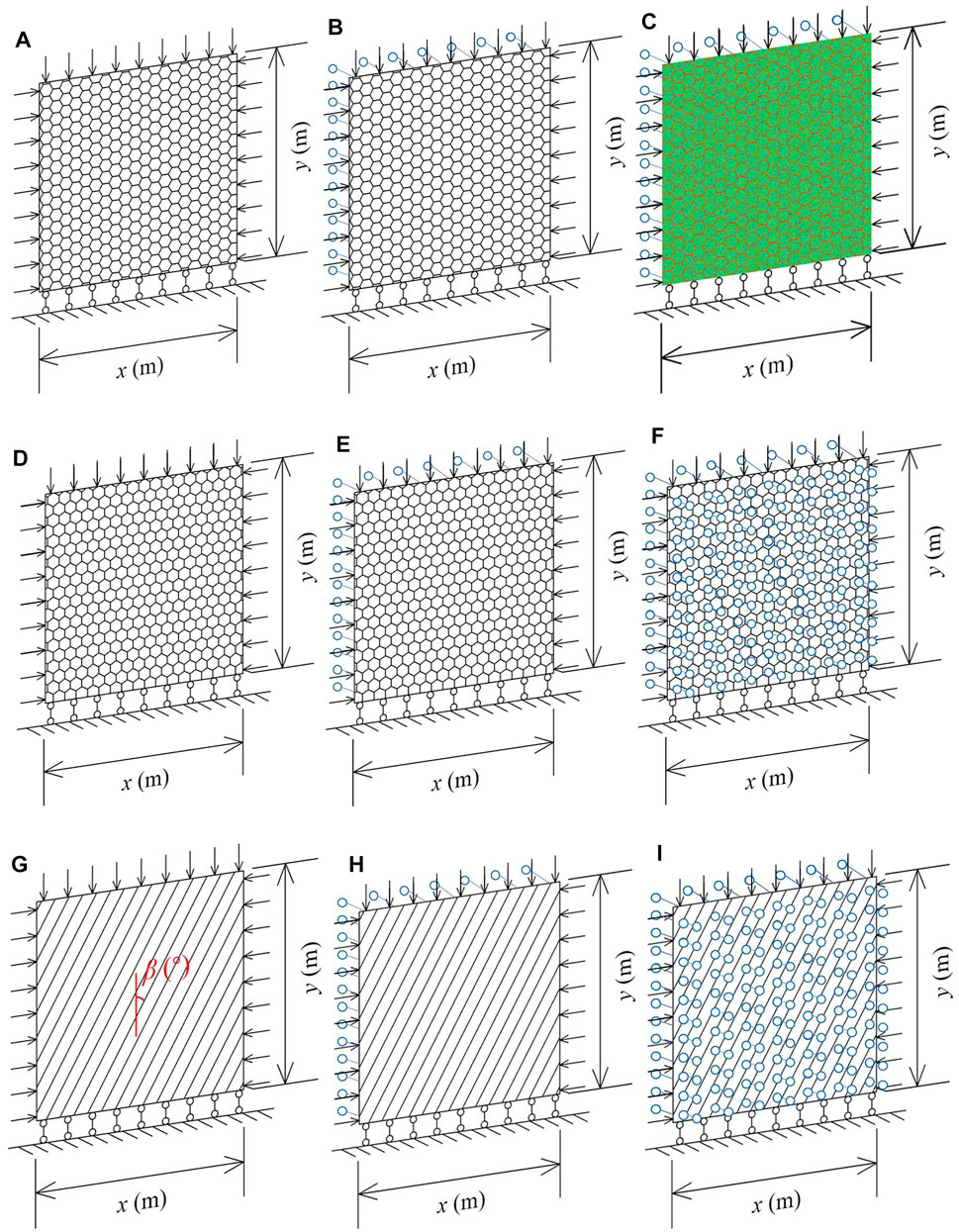
FIGURE 4. Typical settings and boundary conditions of the numerical test of columnar jointed basalts (CJBs) with different model boundaries and confining pressures. (A) The case of plane stress, direction I orthogonal to the column axis. (B) The case between plane stress and plane strain, direction I. (C) Schematic diagram of transforming the CJB images into the numerical model of CJBs. (D) The case of plane stress, direction II orthogonal to the column axis. (E) The case between plane stress and plane strain, direction II. (F) The case of plane strain, direction II. (G) The case of plane stress, the direction parallel to the column axis. (H) The case between plane stress and plane strain, the direction parallel to the column axis. (I) The case of plane strain, the direction parallel to the column axis.

The vertical displacement load was applied on the top of each model. The ratio of the displacement applied in each step to the initial lateral side length of the model is 0.000017, and the displacement load was applied gradually until the failure of specimen occurs. The criterion used to judge the failure of specimen is: if the specimen reaches the residual strength stage or the AE increases suddenly at a certain stage of loading, the overall instability failure of the specimen is considered to have occurred.

Generally, the mechanical parameters of the joint are lower than those of intact rock (Gui and Zhao, 2015). The joint parameters may influence the magnitude of the elastic modulus and compression strength of the jointed rock mass (Sun et al., 2012). However, the ratios of the mechanical properties between joint and intact rock have not been reported yet. Based on the above numerical verification and related literatures on CJBs, the mechanical parameters of rocks and joints are determined as described in Section 2.3.

3 Results and Analysis

3.1 Strength and Deformation Characteristics of CJBs With Different Model Boundaries and Confining Pressures

3.1.1 In the Direction Orthogonal to Column Axis: Strength and Deformation Characteristics of CJBs With Different Model Boundaries and Confining Pressures

In Figure 5, case I, case II, and case III correspond to the cases of plane stress, between plane stress and plane strain, and plane strain, respectively. As can be seen from Figure 5A, in the direction orthogonal to the column axis and with a confining pressure of 0 MPa, from the perspective of the different model boundaries, the CSs from small to large correspond to the case of plane stress, the case between plane stress and plane strain, and the case of plane strain, respectively. From the perspective of directions I and II orthogonal to the column axis, the CSs from small to large correspond to direction I and direction II, respectively.

FIGURE 5

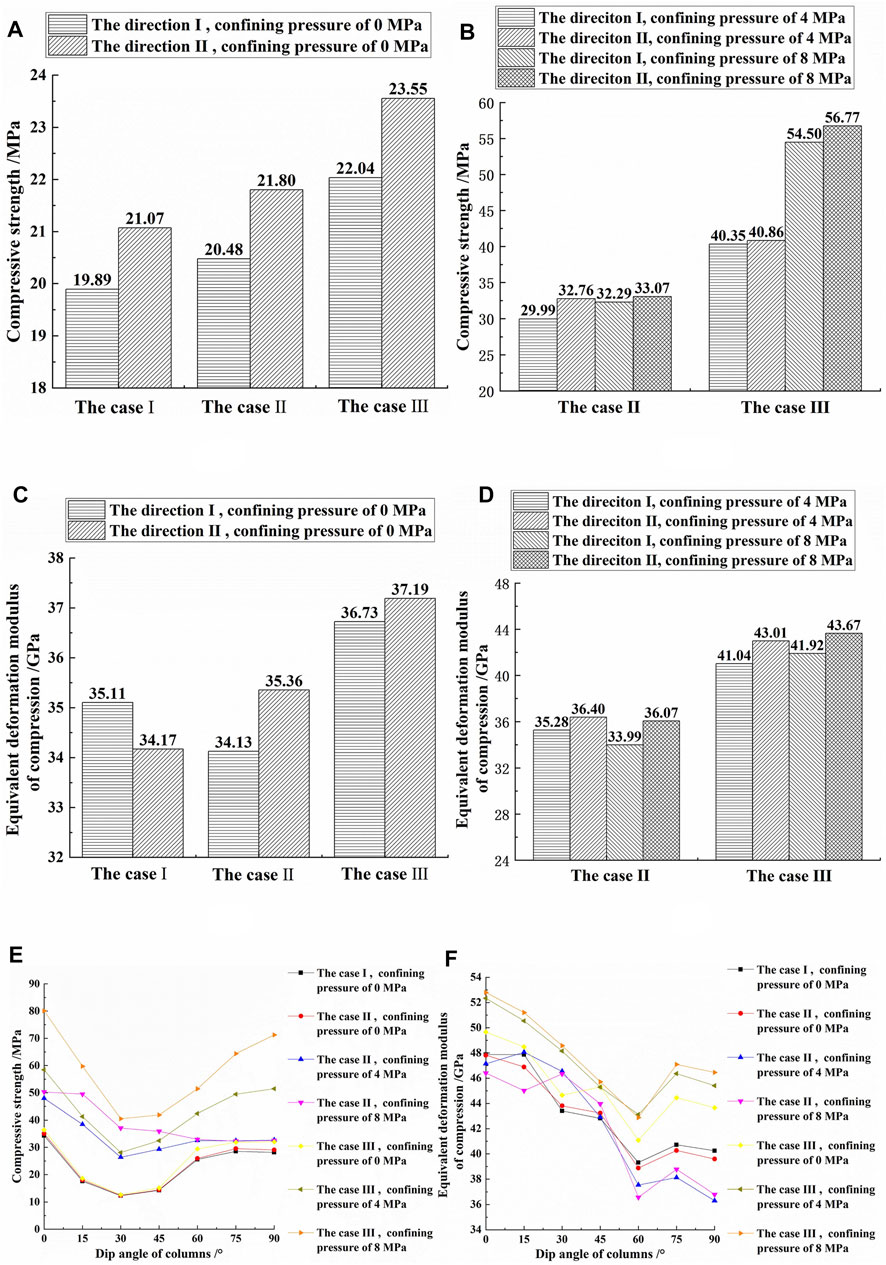
FIGURE 5. (A,B) Strengths of columnar jointed basalts (CJBs) with different model boundaries and confining pressures in the direction orthogonal to the column axis. (C,D) The equivalent deformation moduli of CJBs in the direction orthogonal to the column axis. (E,F) The strengths and equivalent deformation moduli of CJBs in the direction parallel to the column axis (case I, case II, and case III correspond to the case of plane stress, the case between plane stress and plane strain, and the case of plane strain, respectively).

Figure 5B presents the CSs, from the perspective of the different model boundaries, in the direction orthogonal to the column axis, with confining pressures of 4 and 8 MPa. The CSs from small to large correspond to the case between plane stress and plane strain and the case of plane strain, respectively. From the perspective of directions I and II orthogonal to the column axis, the CSs from small to large correspond to direction I and direction II, respectively. From the perspective of confining pressure, in the case between plane stress and plane strain, the increase of the CS was relatively small with the growth of confining pressure (the increase rates of CS were 7.67% and 0.95% in direction I and direction II, respectively); in the case of plane strain, the CS increased greatly with the growth of confining pressure (the increase rates of CS were 35.07% and 38.94% in direction I and direction II, respectively).

Figure 5C depicts the EDM, from the perspective of the different model boundaries, in the direction orthogonal to the column axis, with a confining pressure of 0 MPa. For direction I orthogonal to the column axis, the EDMs from small to large correspond to the case between plane stress and plane strain, the case of plane stress, and the case of plane strain, respectively; for direction II orthogonal to the column axis, the EDMs from small to large correspond to the case of plane stress, the case between plane stress and plane strain, and the case of plane strain, respectively. From the perspective of directions I and II, for the case of plane stress, the EDM in direction I was larger than that in direction II; for the case between plane stress and plane strain and the case of plane strain, the EDM in direction I was smaller than that in direction II. This phenomenon was mainly due to the case of plane stress, along the normal direction of the model plane, having free boundaries (without displacement constraints) on both sides of the model that are composed of heterogeneous elements. During the loading process, each element was deformed to any side of the model. Thus, the EDM in direction I is prone to be larger than that in direction II. Simultaneously, for the case between plane stress and plane strain and the case of plane strain, there was a normal displacement constraint on at least one side of the model plane. For direction II, oblique joints were damaged by shear and each stacked column suffered loading. Hence, the related EDM was larger.

Figure 5D shows the EDM, from the perspective of different model boundaries, in the direction orthogonal to the column axis, with confining pressures of 4 and 8 MPa. The EDMs from small to large correspond to the case between plane stress and plane strain and the case of plane strain, respectively. From the perspective of directions I and II, the EDMs from small to large correspond to direction I and direction II, respectively. From the perspective of confining pressure, in the case between plane stress and plane strain, the EDM decreased with the increase of confining pressure (in directions I and II, the reduction rates of EDM were −3.66% and −0.91%, respectively); in the case of plane strain, the EDM increased with the increase of confining pressure (in directions I and II, the increase rates of EDM were 2.14% and 1.53%, respectively).

In this study, the transverse anisotropy coefficient of compressive strength (TACCS) is defined as the CS in direction I divided by that in direction II. According to Figures 5A,B, when the confining pressure was 0 MPa, the TACCSs corresponding to the case of plane stress, the case between plane stress and plane strain, and the case of plane strain were 0.9440, 0.9394, and 0.9359, respectively; when the confining pressure was 4 MPa, the TACCSs corresponding to the case between plane stress and plane strain and the case of plane strain were 0.9154 and 0.9875, respectively; when the confining pressure was 8 MPa, the TACCSs corresponding to the case between plane stress and plane strain and the case of plane strain were 0.9764 and 0.9600, respectively. The above results show that the CS of CJBs roughly tended to be transversely isotropic with the increase of confining pressure.

The transverse anisotropy coefficient of equivalent deformation modulus (TACEDM) is defined as the EDM in direction I divided by that in direction II. Combined with Figures 5C,D, when the confining pressure was 0 MPa, the TACEDMs corresponding to the case of plane stress, the case between plane stress and plane strain, and the case of plane strain were 1.0275, 0.9652, and 0.9876, respectively; when the confining pressure was 4 MPa, the TACEDMs corresponding to the case between plane stress and plane strain and the case of plane strain were 0.9692 and 0.9542, respectively; when the confining pressure was 8 MPa, the TACEDMs corresponding to the case between plane stress and plane strain and the case of plane strain were 0.9423 and 0.9599, respectively. The above results show that the EDM of CJBs is basically transversely isotropic with the growth of confining pressure.

In Figure 6, case I, case II, and case III correspond to the case of plane stress, the case between plane stress and plane strain, and the case of plane strain, respectively. It can be seen from Figure 6A that, in the direction orthogonal to the column axis and with a confining pressure of 0 MPa, the stress–strain curves of the three model boundary conditions showed obvious brittle failure characteristics. As presented in Figure 6B, in the direction orthogonal to the column axis and with confining pressures of 4 and 8 MPa, the ductile failure characteristics of the stress–strain curves became more obvious with the increase of confining pressure for the case between plane stress and plane strain; for the case of plane strain, the brittle failure characteristics of the stress–strain curves were still obvious with the increase of confining pressure.

FIGURE 6

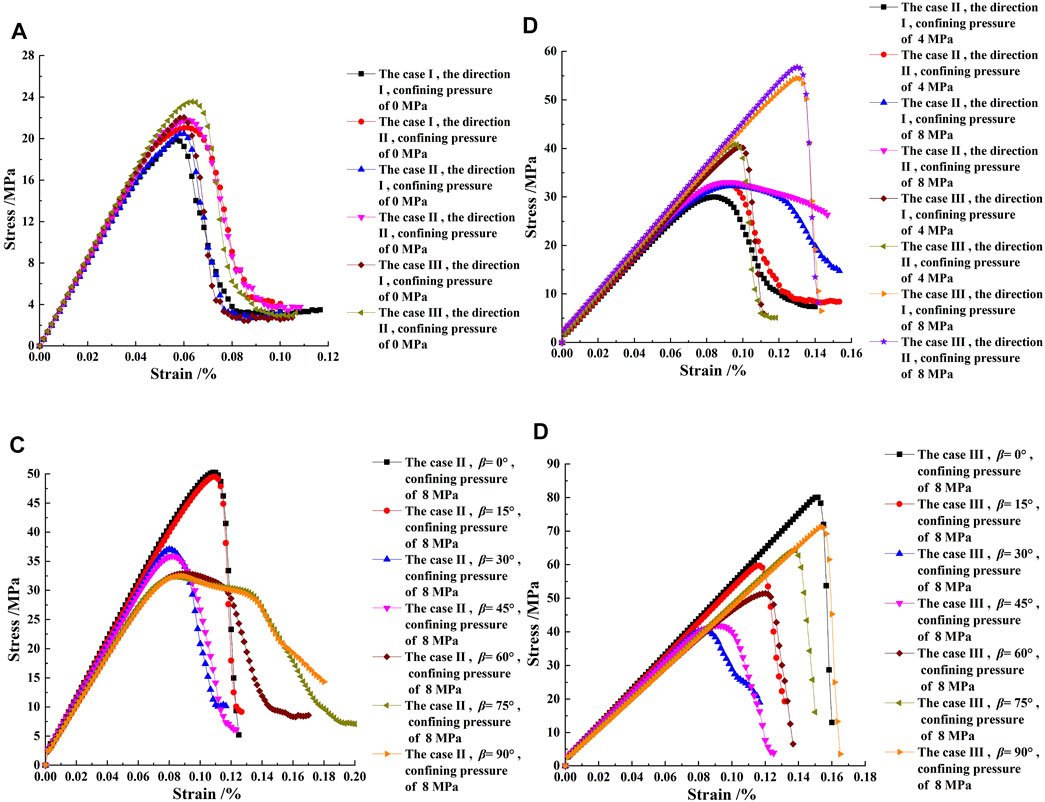
FIGURE 6. (A) The stress–strain curves of columnar jointed basalts (CJBs) with different model boundaries and a confining pressure of 0 MPa in the direction orthogonal to the column axis. (B) Confining pressures of 4 and 8 MPa. (C,D) The stress–strain curves of CJBs with different model boundaries and a confining pressure of 8 MPa in the direction parallel to the column axis (case I, case II, and case III correspond to the case of plane stress, the case between plane stress and plane strain, and the case of plane strain, respectively).

In direction I, when the confining pressures were 4 and 8 MPa, the stress curves showed the characteristics of ductile failure for the case between plane stress and plane strain, mainly because there was a displacement constraint on only one side along the normal direction of the model plane, and each element was allowed to deform to a certain extent outward the other side of the model during the failure process. For the case of plane strain, the stress curves showed the characteristics of brittle failure, mainly because there were displacement constraints on both sides along the normal direction of the model. Under loading, each element was extruded and deformed, resulting in the damage and fracture of the model. In practical engineering, such as the walls of an underground cavern, for the situation of large confining pressure and adverse geological structure, corresponding monitoring and reinforcement measures should be taken within a certain thickness range along the inner side of the walls of the underground cavern.

3.1.2 In the Direction Parallel to the Column Axis: Strength and Deformation Characteristics of CJBs With Different Model Boundaries and Confining Pressures

It can be seen from Figure 5E that, in the direction parallel to the column axis and with a confining pressure of 0 MPa, the CS of the three model boundary conditions changed in a U-shaped trend with the increase of the column dip angle, in which the CS reached the lowest value at β = 30° and changed slowly at the angle range β = 60°–90°. Furthermore, with confining pressures of 4 and 8 MPa, for the case between plane stress and plane strain, the CS decreased firstly and then changed slowly with the increase of the column dip angle, wherein it changed slowly at β ≥ 30°. With confining pressures of 4 and 8 MPa, for the case of plane strain, the CS showed a V-shaped change trend with the increase of the column dip angle, wherein it reached the lowest value at β = 30°.

As presented in Figure 5F, in the direction parallel to the column axis and with confining pressures of 0, 4, and 8 MPa, the EDM of three kinds of model boundaries roughly decreased firstly and then slightly increased (or changed) with the growth of the column dip angle, wherein it reached the lowest value at β = 60° (except for individual cases). From the perspective of the different model boundaries, the case of small EDM is the case between plane stress and plane strain, with confining pressures of 4 and 8 MPa; the case of large EDM is the case of plane strain, with confining pressures of 4 and 8 MPa.

According to Figures 6C,D, with a confining pressure of 8 MPa, the stress–strain curves of β = 75°–90° showed obvious ductile failure characteristics for the case between plane stress and plane strain, implying that, in these cases, the elements can be deformed to a certain extent outward the free side of the model boundary during the loading process. With a confining pressure of 8 MPa, the residual stages of the stress–strain curves did not exist for the case of plane strain, indicating severe instability failure, implying that, under the normal displacement constraints on both sides of the model, the elements will get severely damaged and fractured during the loading process. In practical projects, such as the walls of an underground cavern, for the case of large confining pressure and adverse geological structures, the damage and fracture of rock mass may occur within a certain thickness range along the inner side of the cavern wall, not just on the surface. Therefore, attention should be paid to the stress of rock mass within a certain thickness range along the inner side of the cavern wall, and the corresponding reinforcement measures should be taken when necessary.

3.2 In the direction orthogonal to the column axis: the fracture process and energy evolution of CJBs with different model boundaries and confining pressures

3.2.1 Direction I Orthogonal to the Column Axis: The Fracture Process and Energy Evolution of CJBs With Different Model Boundaries and a Confining Pressure of 0 MPa

Fracture Process and Energy Evolution of CJBs In Direction I Orthogonal to the Column Axis: The Case Between Plane Stress and Plane Strain, With a Confining Pressure of 0 MPa

Combined with Figures 7A,E–H, in direction I orthogonal to the column axis and with a confining pressure of 0 MPa, as the loading increases, when the stress reached point A of the stress–strain curve, the vertical joints in the specimen were damaged and cracked for the case between plane stress and plane strain. When the stress reached point B, the cracking of the vertical joints was further obvious. In addition, the transverse joints in the specimen were damaged, and damages also developed in the centers of several columns in the upper part of the specimen. When the stress reached the peak point C of the stress–strain curve, damage and fracture occurred in the centers of several columns in the upper part of the specimen. When the stress dropped to point D, the number of columns with damage and fracture increased in the upper part of the specimen. When the stress dropped to point E, the number of damaged and broken columns further increased in the upper part of the specimen, and these damaged and broken columns formed as strip areas. When the stress continued to drop to point F, in the upper part of the specimen, the fracture of the originally damaged and broken columns intensified, and other columns also developed from damage to fracture. It can be seen from Figure 7H that sedimentation mainly occurred between the top of the specimen and the fluctuating strip crushing area.

FIGURE 7

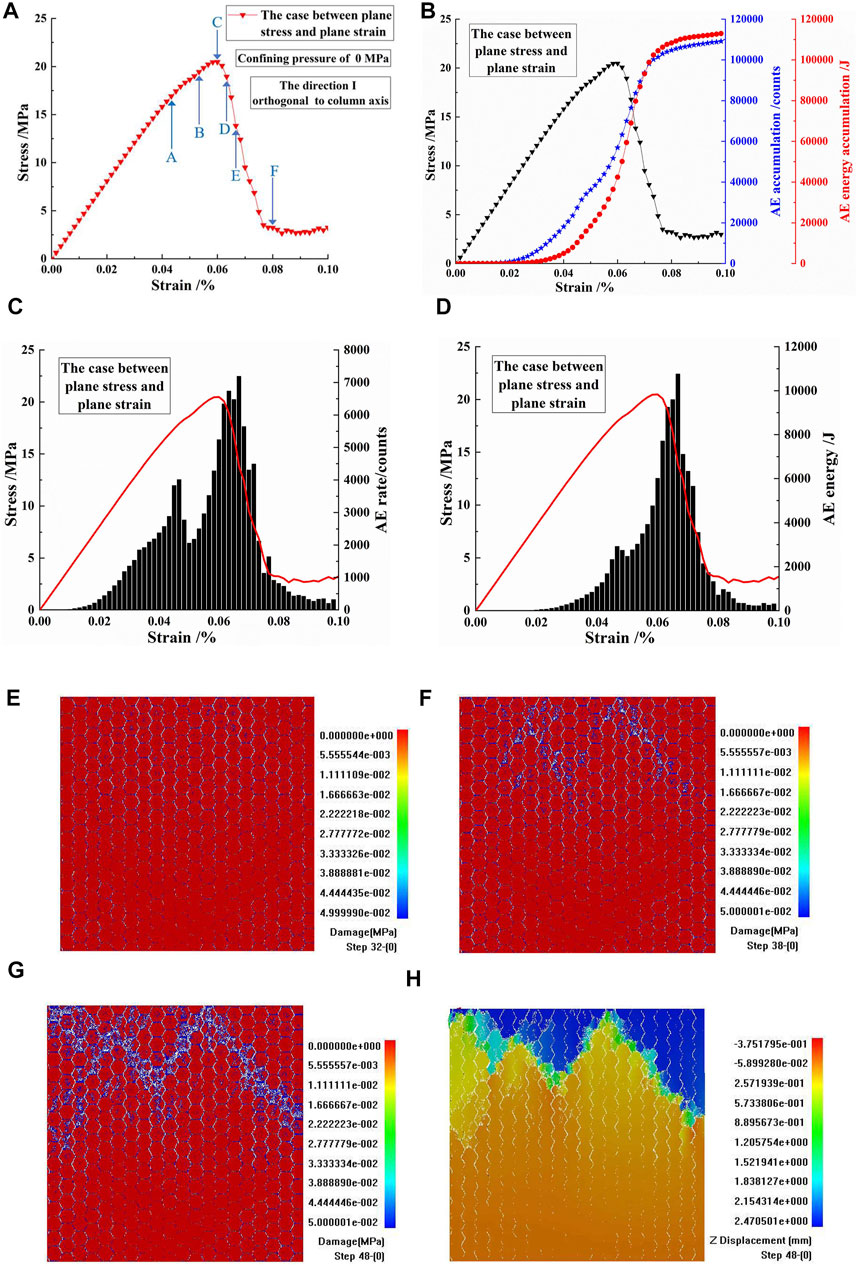
FIGURE 7. (A,B) The stress–strain curves, acoustic emission (AE) accumulations, and AE energy accumulations of columnar jointed basalts (CJBs) in direction I orthogonal to the column axis for the case between plane stress and plane strain, with a confining pressure of 0 MPa. (C, D) The stress–strain curve, AE rate, and AE energy of CJBs. (E–H) Damage and displacement diagrams corresponding to points B, D, and F of the stress–strain curve.

In this paper, firstly, the meso element strengths and elastic moduli are non-uniformly distributed according to the Weibull distribution function. Then, during the loading process, some elements will be damaged, resulting in many AE events. Hence, the AE number and energy can be obtained. As depicted in Figures 7B,C, the AE rates of the CJBs showed a distribution of double peaks in direction I for the case between plane stress and plane strain, with a confining pressure of 0 MPa. The first peak of the AE rate appeared before the peak stress of the stress–strain curve, and the second peak appeared in the drop stage after the peak stress of the stress–strain curve. The first peak of the AE rate was mainly controlled by the cracking of the vertical joints and the second peak mainly caused by the cracking of the columns in the upper part of the specimen.

Figure 7D shows that, in direction I and with a confining pressure of 0 MPa, for the case between plane stress and plane strain, the AE energies of the CJBs roughly showed a single peak distribution, in which the AE energy peak appeared in the drop stage after the peak stress of the stress–strain curve. The AE energy peak was mainly caused by the damage and fracture of the columns in the upper part of the specimen. In addition, combined with information on the AE rate and AE energy, it can be seen that, before the peak stress, the AE energy generated was relatively small because the cracking of vertical joints is mainly a tensile fracture, and there was no obvious peak of AE energy at this stage.

Fracture Process and Energy Evolution of CJBs In Direction I Orthogonal to the Column Axis: The Case of Plane Stress and the Case of Plane Strain, With a Confining Pressure of 0 MPa

Combined with Figures 8A,B, the stress–strain curves, the AE accumulations, and the AE energy accumulations of the CJBs were compared in direction I for the case of plane stress and the case of plane strain, with a confining pressure of 0 MPa. The stress–strain curves of the case of plane stress and that of the case of plane strain showed similar brittle failure characteristics. The AE accumulation of the case of plane stress was more than that of the case of plane strain. In terms of AE energy accumulation, that of the case of plane stress was also higher than that of the case of plane strain.

FIGURE 8

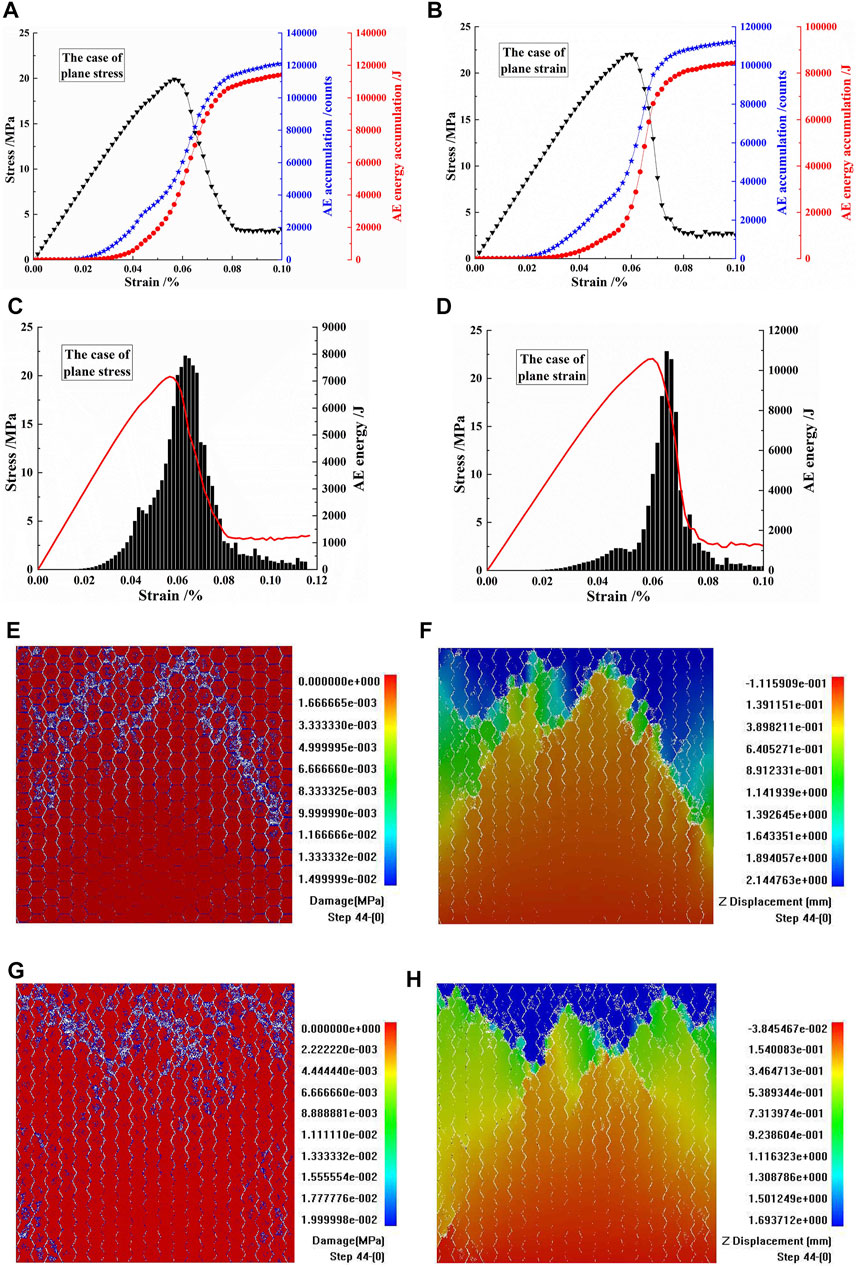
FIGURE 8. (A,B) The the stress–strain curves, acoustic emission (AE) accumulations, and AE energy accumulations of columnar jointed basalts (CJBs) in direction I orthogonal to the column axis for the case of plane stress and the case of plane strain, with a confining pressure of 0 MPa. (C,D) The stress–strain curves and AE energies of CJBs for the case of plane stress and the case of plane strain. (E,F) Damage and displacement diagrams for the case of plane stress. (G,H) Damage and displacement diagrams for the case of plane strain.

Figures 8C,D show the comparison of the AE energies of the CJBs in direction I for the case of plane stress and the case of plane strain, with a confining pressure of 0 MPa. In the case of plane stress, the peak value of AE energy was lower than that in the case of plane strain, but the peak shape of AE energy in the case of plane stress was wider, indicating that the time domain of high-energy release was longer. This is mainly because, in the case of plane stress, there were no displacement constraints on both sides along the normal direction of the model. During the process of vertical loading, the elements tend to tensile failure. On one hand, the AE energy caused by tensile failure was relatively small compared with compression-shear failure. On the other hand, the element damage occurred in many parts of the model.

Figures 8E,F present the analysis of the fracture process and displacement of the CJBs in direction I for the case of plane stress, with a confining pressure of 0 MPa. At the initial stage of loading, the vertical joints were damaged and cracked, and the transverse joints were damaged. At the middle stage of loading, several columns were damaged and cracked in the upper part of the specimen. At the late stage of loading, many columns in the middle and upper parts of the specimen were damaged and cracked. It can be seen from Figure 8F that the sedimentation mainly occurred between the specimen top and the fluctuating strip crushed area. Compared with that in the case between plane stress and plane strain, the sedimentation reached the lower part of the specimen in the case of plane stress.

Figures 8G,H depict the analysis of the fracture process and displacement of the CJBs in direction I for the case of plane strain, with a confining pressure of 0 MPa. At the initial stage of loading, the vertical joints were damaged and cracked, but the transverse joints were not damaged. At the middle stage of loading, several columns were damaged and cracked in the upper part of the specimen. At the late stage of loading, many columns in the upper part of the specimen were damaged and broken, and several columns were also damaged and broken on the left and right sides of the bottom of the specimen. It can be seen from Figure 8H that the sedimentation also mainly occurred between the specimen top and the fluctuating strip crushed area. Compared with that in the case between plane stress and plane strain, the sedimentation was located at a higher are of the specimen in the case of plane strain.

3.2.2 Direction I Orthogonal to the Column Axis: The Fracture Process and Energy Evolution of CJBs With Different Model Boundaries and a Confining Pressure of 8 MPa

Fracture Process and Energy Evolution of CJBs in Direction I Orthogonal to the Column Axis: The Case Between Plane Stress and Plane Strain and the Case of Plane Strain, With a Confining Pressure of 8 MPa

Combined with Figures 9A,B, the stress–strain curves, AE accumulations, and AE energy accumulations of the CJBs were compared in direction I for the case between plane stress and plane strain and the case of plane strain, with a confining pressure of 8 MPa. In the case between plane stress and plane strain, the ductile failure characteristic of the stress–strain curve was obvious; in the case of plane strain, the brittle failure characteristic of the stress–strain curve was clear. The AE accumulation in the case of plane strain was more than that in the case between plane stress and plane strain. The AE energy accumulation in the case of plane strain was higher than that in the case between plane stress and plane strain. From the perspective of the change trend of the AE energy accumulation, with the progress of loading, the AE energy accumulation in the case between plane stress and plane strain changed slowly at first and then grew; the AE energy accumulation in the case of plane strain changed slowly at first, then grew, and then increased sharply.

FIGURE 9

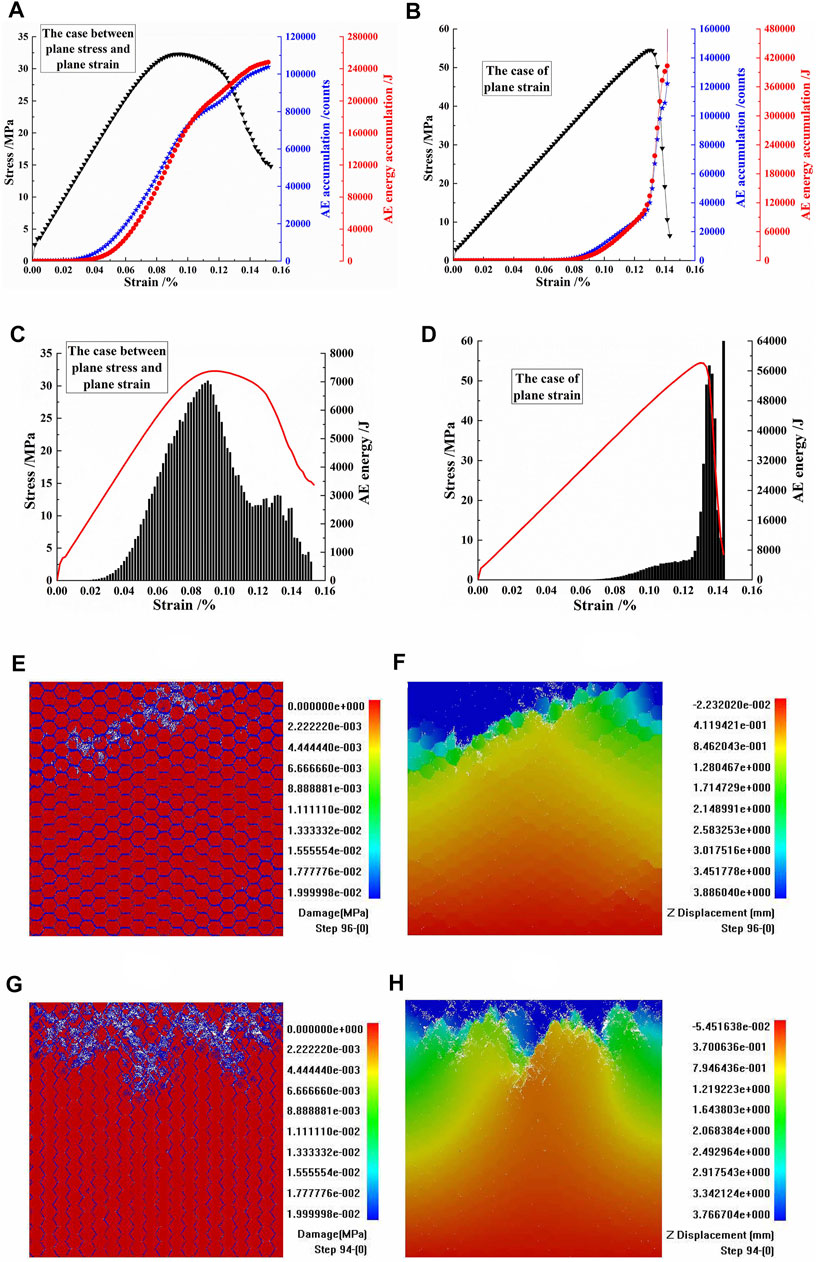
FIGURE 9. (A,B) The stress–strain curves, acoustic emission (AE) accumulations, and AE energy accumulations of columnar jointed basalts (CJBs) in direction I orthogonal to the column axis for the case between plane stress and plane strain and the case of plane strain, with a confining pressure of 8 MPa. (C,D) The stress–strain curves and AE energies of CJBs for the case between plane stress and plane strain and the case of plane strain. (E,F) Damage and displacement diagrams for the case between plane stress and plane strain. (G,H) Damage and displacement diagrams for the case of plane strain.

Figures 9C,D show the comparison of the the AE energies in direction I for the case between plane stress and plane strain and the case of plane strain, with a confining pressure of 8 MPa. The peak value of AE energy in the case between plane stress and plane strain was lower than that in the case of plane strain. In the case between plane stress and plane strain, the AE energy roughly showed a single peak distribution, and the AE energy peak tended to be before the peak stress of the stress–strain curve. In the case of plane strain, the AE energy also showed a single peak distribution, and the AE energy peak tended to be after the peak stress of the stress–strain curve.

According to Figures 9E, F, the fracture process and displacement of the CJBs were analyzed in direction I for the case between plane stress and plane strain, with a confining pressure of 8 MPa. At the initial stage of loading, damage of the transverse joints was obvious. At the middle stage of loading, the vertical joints were also damaged, and individual columns were damaged and broken in the upper part of the specimen. At the late stage of loading, the damaged and fractured columns increased in the upper part of the specimen. It can be seen from Figure 9F that the sedimentation mainly occurred between the specimen top and the strip crushed area.

Figures 9G,H present the analysis of the fracture process and displacement of the CJBs in direction I for the case of plane strain, with a confining pressure of 8 MPa. At the initial stage of loading, the vertical joints in the specimen were damaged. At the middle stage of loading, several columns in the upper part of the specimen were damaged and fractured. At the late stage of loading, the damaged and cracked columns increased in the upper part of the specimen. It can be seen from Figure 9H that the sedimentation mainly occurred between the top of the specimen and the fluctuating strip crushing area. Compared with that in the case between plane stress and plane strain, the sedimentation reached the lower part of the specimen in the case of plane strain.

3.2.3 Direction II Orthogonal to the Column Axis: The Fracture Process and Energy Evolution of CJBs With Different Model Boundaries and a Confining Pressure of 8 Mpa

Fracture Process and Energy Evolution of CJBs in Direction II Orthogonal to the Column Axis: The Case Between Plane Stress and Plane Strain and the Case of Plane Strain, With a Confining Pressure of 8 MPa

Combined with Figures 10A,B, the stress–strain curves, AE accumulations, and AE energy accumulations of the CJBs were compared in direction II orthogonal to the column axis for the case between plane stress and plane strain and the case of plane strain, with a confining pressure of 8 MPa. In the case between plane stress and plane strain, the ductile failure characteristic of the stress-strain curve was obvious; in the case of plane strain, the brittle failure characteristic of the stress–strain curve was clear. The AE accumulation in the case of plane strain was more than that in the case between plane stress and plane strain. The AE energy accumulation in the case of plane strain was higher than that in the case between plane stress and plane strain. From the perspective of the change trend of the AE energy accumulation, with the progress of loading, the AE energy accumulation in the case between plane stress and plane strain showed a trend of firstly slowly changing, then increasing, and then slowly growing; the AE energy accumulation in the case of plane strain changed slowly, then grew, and then increased sharply.

FIGURE 10

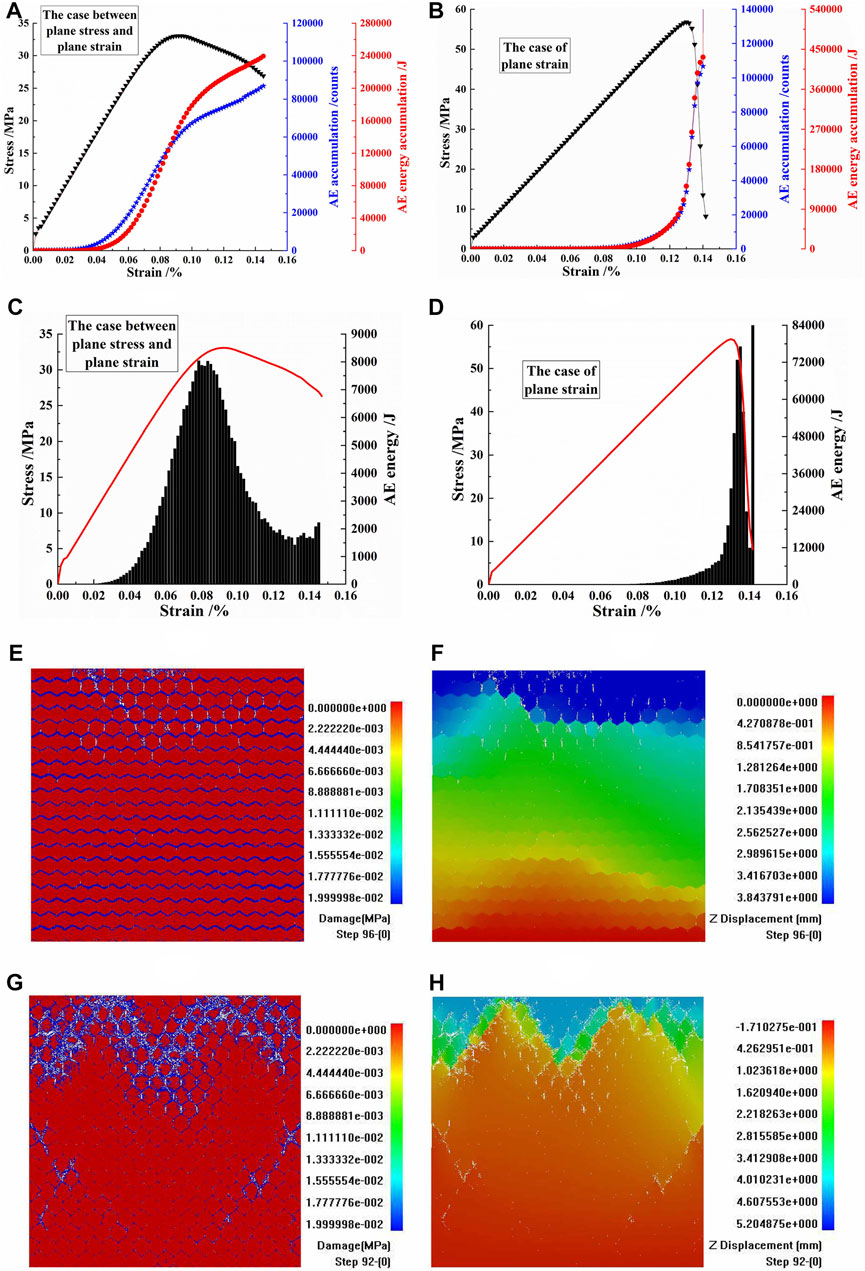
FIGURE 10. (A,B) The stress–strain curves, acoustic emission (AE) accumulations, and AE energy accumulations of columnar jointed basalts (CJBs) in direction II orthogonal to the column axis for the case between plane stress and plane strain and the case of plane strain, with a confining pressure of 8 MPa. (C,D) The stress–strain curves and AE energies of CJBs for the case between plane stress and plane strain and the case of plane strain. (E,F) Damage and displacement diagrams for the case between plane stress and plane strain. (G,H) Damage and displacement diagrams for the case of plane strain.

As depicted in Figures 10C,D, the AE energies of the CJBs were compared in direction II for the case between plane stress and plane strain and the case of plane strain, with a confining pressure of 8 MPa. The peak value of AE energy in the case between plane stress and plane strain was lower than that in the case of plane strain. In the case between plane stress and plane strain, the AE energy showed a single peak distribution, and the AE energy peak tended to be before the peak stress of the stress–strain curve. In the case of plane strain, the AE energy also showed a single peak distribution, and the AE energy peak tended to be after the peak stress of the stress–strain curve.

As shown in Figures 10E,F, the fracture process and displacement of the CJBs were analyzed in direction II for the case between plane stress and plane strain, with a confining pressure of 8 MPa. At the initial stage of loading, the damage of the transverse joints was obvious. At the middle stage of loading, some vertical joints were damaged and fractured in the upper part of the specimen. At the late stage of loading, several columns were damaged and fractured at the top and in the upper part of the specimen. It can be seen from Figure 10F that the sedimentation mainly occurred near the top and in the middle of the specimen.

According to Figures 10G,H, the fracture process and displacement of the CJBs were analyzed in direction II for the case of plane strain, with a confining pressure of 8 MPa. At the initial stage of loading, the damage of the joints was relatively weak. At the middle stage of loading, the damage and fracture of joints in the upper part of the specimen were obvious, and some vertical joints and their vicinity were damaged and fractured. At the late stage of loading, the other columns in the upper part of the specimen were also damaged and fractured, and the crushing was intensified. It can be seen from Figure 10H that the sedimentation mainly occurred between the specimen top and the fluctuating strip crushed area. Compared with that in the case between plane stress and plane strain, the range of sedimentation transmitted in the specimen was relatively limited in the case of plane strain.

3.3 In the Direction Parallel to the Column Axis: The Fracture Process and Energy Evolution of CJBs With Different Model Boundaries and Confining Pressures

3.3.1 Direction Parallel to the Column Axis: The Fracture Process and Energy Evolution of CJBs With Different Model Boundaries and a Confining Pressure of 0 MPa

Fracture Process and Energy Evolution of CJBs in the Direction Parallel to the Column Axis: The Case Between Plane Stress and Plane Strain, With a Confining Pressure of 0 MPa

Combined with Figures 11A,E–H, in the direction parallel to the column axis (β = 30°), for the case between plane stress and plane strain and with a confining pressure of 0 MPa, with the progress of loading, the columnar joints in the specimen were damaged when the stress reached point A of the stress–strain curve. When the stress reached point B near the peak point of the stress–strain curve, the columnar joints in the specimen showed a certain degree of damaged slip. When the stress dropped to point C, the damage, sliding, and cracking of the columnar joints were further obvious. When the stress continued to drop to point D, damages developed at the top of the specimen and at the edges of the columns near the middle of the specimen. When the stress dropped to point E, the originally damaged areas were fractured further. When the stress reached the point F, the originally fractured areas developed further. In addition, damage and fracture also developed in other areas of the specimen. It can be seen from Figure 11H that the sedimentation mainly occurred in the middle and upper parts of the specimen.

FIGURE 11

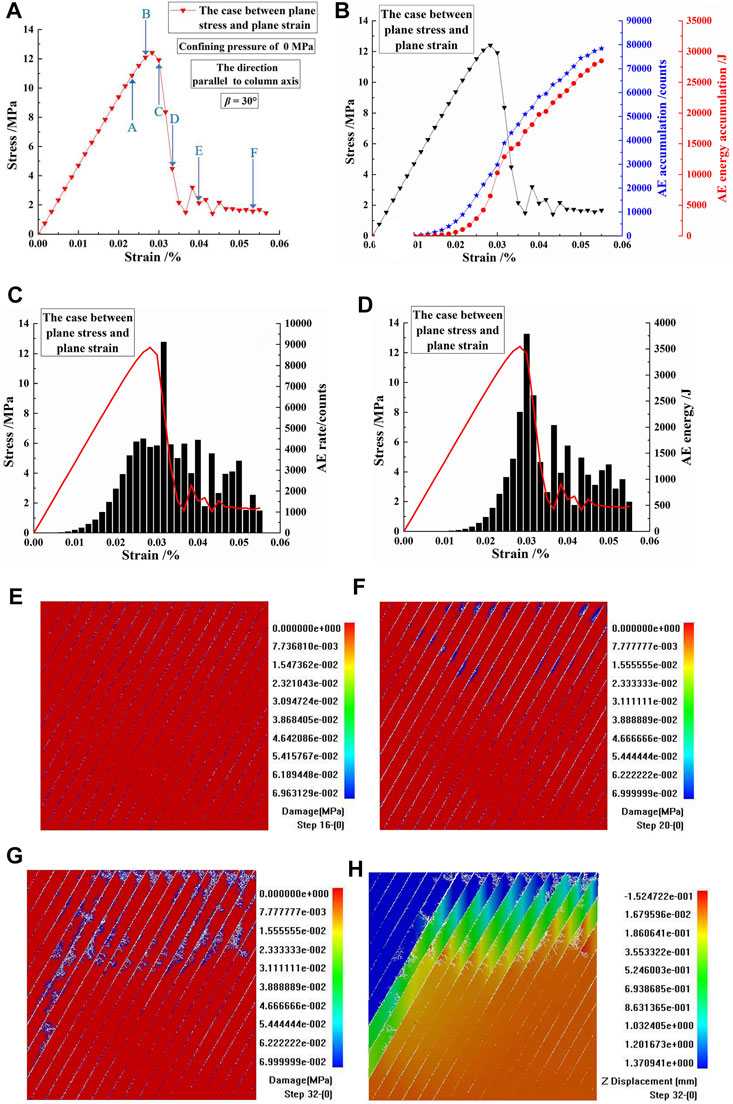
FIGURE 11. (A,B) The stress–strain curves, acoustic emission (AE) accumulations, and AE energy accumulations of columnar jointed basalts (CJBs) in the direction parallel to the column axis, β = 30°, for the case between plane stress and plane strain, with a confining pressure of 0 MPa. (C,D) The stress–strain curve, AE rate, and AE energy of CJBs, β = 30°, for the case between plane stress and plane strain. (E–H) Damage and displacement diagrams corresponding to points B, D, and F of the stress–strain curve, β = 30°, for the case between plane stress and plane strain.

As presented in Figures 11B,C, the AE rates of the CJBs showed a single peak distribution in the direction parallel to the column axis (β = 30°) for the case between plane stress and plane strain, with a confining pressure of 0 MPa. The peak value of the AE rate appeared in the drop stage after the peak stress of the stress–strain curve, and it was mainly caused by the damage and fracture of the column edges in the specimen.

It can be seen from Figure 11D that, in the direction parallel to the column axis (β = 30°), for the case between plane stress and plane strain and with a confining pressure of 0 MPa, the AE energies of the CJBs roughly showed a single peak distribution, in which the peak value of AE energy appeared in the drop stage after the peak stress of the stress–strain curve and was mainly caused by the damage, sliding, and cracking of the columnar joints in the specimen.

Fracture Process and Energy Evolution of CJBs in the Direction Parallel to the Column Axis: The Case of Plane Stress and the Case of Plane Strain, With a Confining Pressure of 0 MPa

As depicted in Figures 12A,B, in the direction parallel to the column axis (β = 30°), for the case of plane stress and the case of plane strain, with a confining pressure of 0 MPa, the stress–strain curves, the AE accumulations, and the AE energy accumulations of the CJBs were compared. In terms of the stress–strain curve, those in the case of plane stress and the case of plane strain showed similar brittle failure characteristics. The AE accumulation in the case of plane stress was more than that in the case of plane strain. The AE energy accumulation in the case of plane stress was also higher than that in the case of plane strain.

FIGURE 12

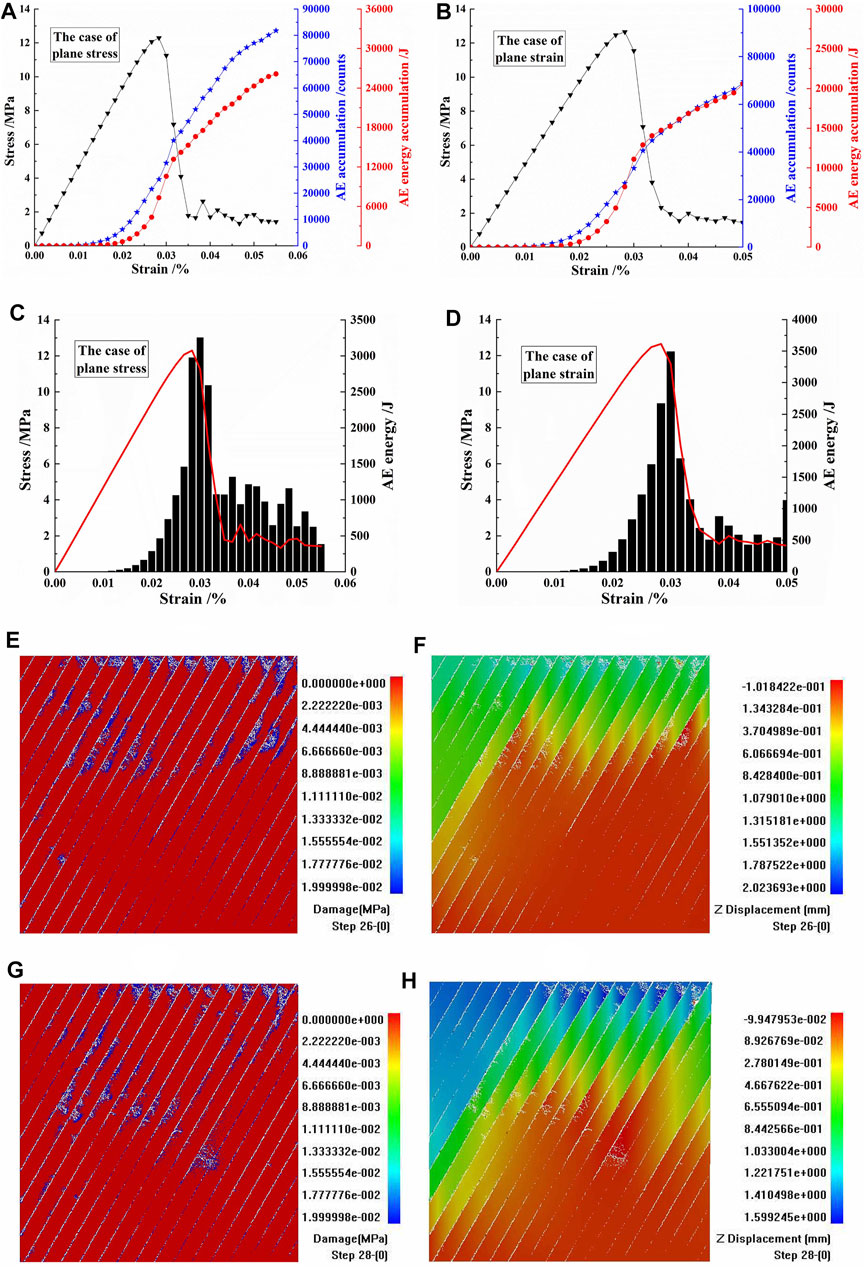
FIGURE 12. (A,B) The stress–strain curves, acoustic emission (AE) accumulations, and AE energy accumulations of columnar jointed basalts (CJBs) in the direction parallel to the column axis, β = 30°, for the case of plane stress and the case of plane strain, with a confining pressure of 0 MPa. (C,D) The stress–strain curves and AE energies of CJBs, β = 30°, for the case of plane stress and the case of plane strain. (E,F) Damage and displacement diagrams, β = 30°, for the case of plane stress. (G,H) Damage and displacement diagrams, β = 30°, for the case of plane strain.

Figures 12C,D show the comparison of the AE energies of the CJBs in the direction parallel to the column axis (β = 30°) for the case of plane stress and the case of plane strain, with a confining pressure of 0 MPa. In the case of plane stress, although the peak value of AE energy was lower than that in the case of plane strain, the AE energy was still high near the peak value in the case of plane stress, indicating that more energy was released in this stage.

Combined with Figures 12E,F, the fracture process and displacement of the CJBs were analyzed in the direction parallel to the column axis (β = 30°) for the case of plane stress, with a confining pressure of 0 MPa. At the initial stage of loading, the columnar joints were damaged and slipped. At the middle stage of loading, damage developed at the specimen top and at the edges of several columns in the middle and upper parts of the specimen. At the late stage of loading, fractures developed in the originally damaged areas. It can be seen from Figure 12F that the sedimentation mainly occurred in the upper part of the specimen.

According to Figures 12G,H, the fracture process and displacement of the CJBs were analyzed in the direction parallel to the column axis (β = 30°) for the case of plane strain, with a confining pressure of 0 MPa. At the initial stage of loading, the columnar joints were damaged and slipped. At the middle stage of loading, the slipped cracking of the columnar joints was further obvious, and damages developed at the specimen top and at the edges of several columns in the middle of the specimen. At the late stage of loading, fractures developed in the areas where the damages developed. It can be seen from Figure 12H that the sedimentation mainly occurred in the middle and upper parts of the specimen. Compared with that in the case of plane stress, the sedimentation reached the lower part of the specimen in the case of plane strain.

3.3.2 Direction Parallel to the Column Axis: The Fracture Process and Energy Evolution of CJBs With Different Model Boundaries and a Confining Pressure of 8 MPa

Fracture Process and Energy Evolution of CJBs in the Direction Parallel to the Column Axis: The Case Between Plane Stress and Plane Strain and the Case of Plane Strain, With a Confining Pressure Of 8 MPa

As presented in Figures 13A,B, the stress–strain curves, AE accumulations, and AE energy accumulations of the CJBs were compared in the direction parallel to the column axis (β = 30°) for the case between plane stress and plane strain and the case of plane strain, with a confining pressure of 8 MPa. For the case between plane stress and plane strain and the case of plane strain, the stress–strain curves showed certain ductile failure characteristics. In terms of AE accumulation, that in the case between plane stress and plane strain was slightly lower than that in the case of plane strain. For AE energy accumulation, the difference in the AE energy accumulations between the two kinds of model boundaries was relatively small. In terms of the change trend of the AE energy accumulation, with the progress of loading, the AE energy accumulation firstly changed slowly, then increased, and then again changed slowly in the case between plane stress and plane strain; in the case of plane strain, the AE energy accumulation changed slowly at first, then grew, and then increased sharply.

FIGURE 13

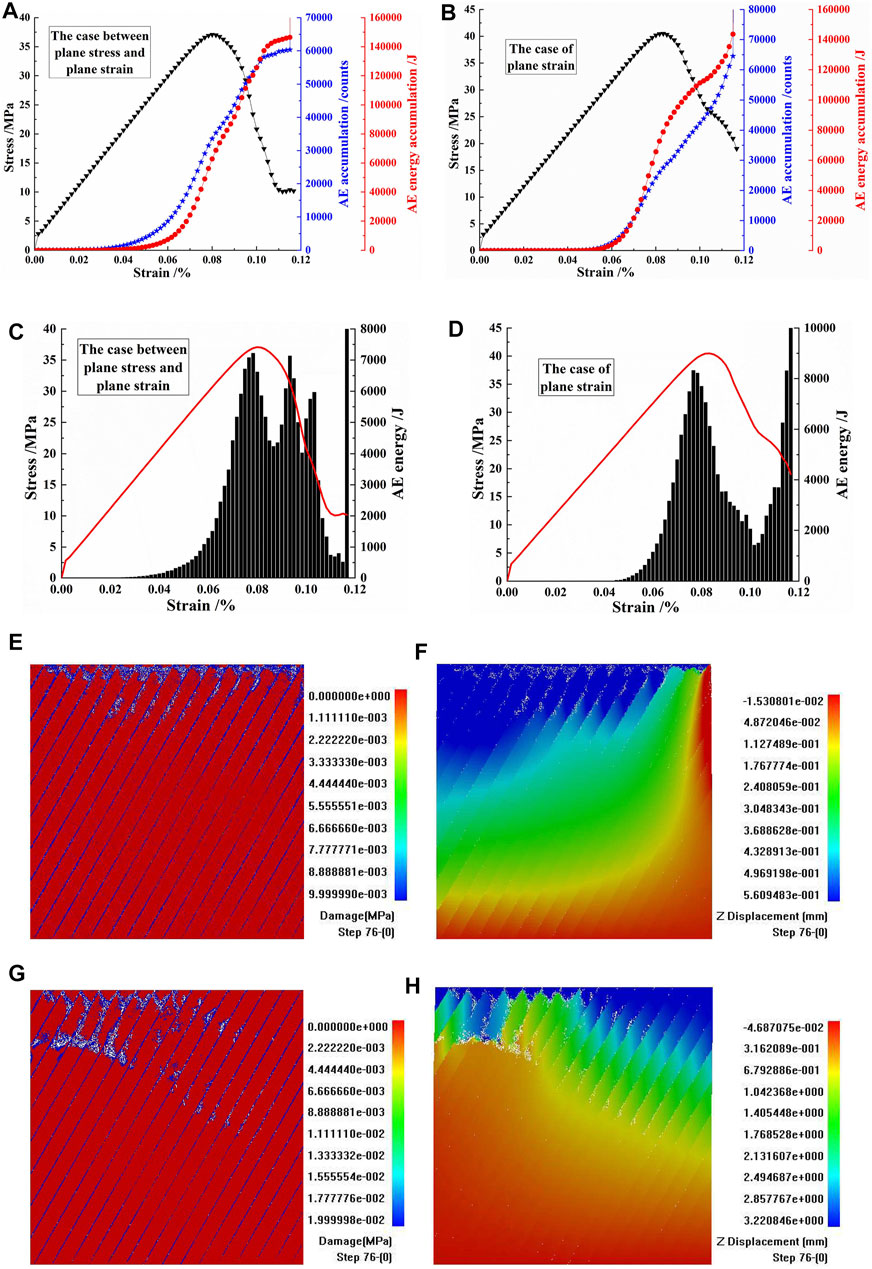
FIGURE 13. (A,B) The stress–strain curves, acoustic emission (AE) accumulations, and AE energy accumulations of columnar jointed basalts (CJBs) in the direction parallel to the column axis, β = 30°, for the case between plane stress and plane strain and the case of plane strain, with a confining pressure of 8 MPa. (C,D) The stress–strain curves and AE energies of CJBs, β = 30°, for the case between plane stress and plane strain and the case of plane strain. (E,F) Damage and displacement diagrams, β = 30°, for the case between plane stress and plane strain. (G,H) Damage and displacement diagrams, β = 30°, for the case of plane strain.

Figures 13C,D show the comparison of the AE energies of the CJBs in the direction parallel to the column axis (β = 30°) for the case between plane stress and plane strain and the case of plane strain, with a confining pressure of 8 MPa. In the case between plane stress and plane strain, the peak value of AE energy was lower than that in the case of plane strain. In the case between plane stress and plane strain, the AE energy showed a multi-peak distribution, in which the first peak value of AE energy tended to be before the peak stress of the stress–strain curve and the second and third peak values were in the drop stage after the peak stress of the stress–strain curve. In the case of plane strain, the AE energy showed a single peak distribution, and the peak value of AE energy tended to be before the peak stress of the stress–strain curve.

Combined with Figures 13E,F, the fracture process and displacement of the CJBs were analyzed in the direction parallel to the column axis (β = 30°) for the case between plane stress and plane strain, with a confining pressure of 8 MPa. At the initial stage of loading, the columnar joints were damaged. At the middle stage of loading, the columns at the specimen top were damaged and broken. At the late stage of loading, the damaged and broken columns at the top of the specimen increased and the crushing intensified, and in the upper part of the specimen, several column edges were damaged and broken. It can be seen from Figure 13F that the sedimentation mainly occurred in the middle and left of the upper part of the specimen.

Figures 13G,H show the analysis of the fracture process and displacement of the CJBs in the direction parallel to the column axis (β = 30°) for the case of plane strain, with a confining pressure of 8 MPa. At the initial stage of loading, the columnar joints were damaged. At the middle stage of loading, there were fractures in the columns on the left side of the specimen top and damage and fractures of several column edges on the left side of the upper part of the specimen. At the late stage of loading, near the top and the upper part of the specimen, two strip fractured zones were formed, and the fracturing intensified. It can be seen from Figure 13H that the sedimentation mainly occurred at the top and the right side of the middle and upper parts of the specimen.

3.4 The AE Accumulation and AE Energy Accumulation Before the Peak Stress of CJBs With Different Model Boundaries and Confining Pressures

3.4.1 In the Direction Orthogonal to the Column Axis: The AE Accumulations and AE Energy Accumulations Before the Peak Stress of CJBs With Different Model Boundaries and Confining Pressures

In Figure 14, case I, case II, and case III correspond to the case of plane stress, the case between plane stress and plane strain, and the case of plane strain, respectively. Figure 14A shows the AE accumulations before the peak stress in the direction orthogonal to the column axis and with a confining pressure of 0 MPa. For direction I, the AE accumulations before the peak stress from small to large correspond to the case of plane stress, the case of plane strain, and the case of between plane stress and plane strain, respectively; for direction II, the AE accumulations before the peak stress from small to large correspond to the case of plane stress, the case of between plane stress and plane strain, and the case of plane strain, respectively.

FIGURE 14

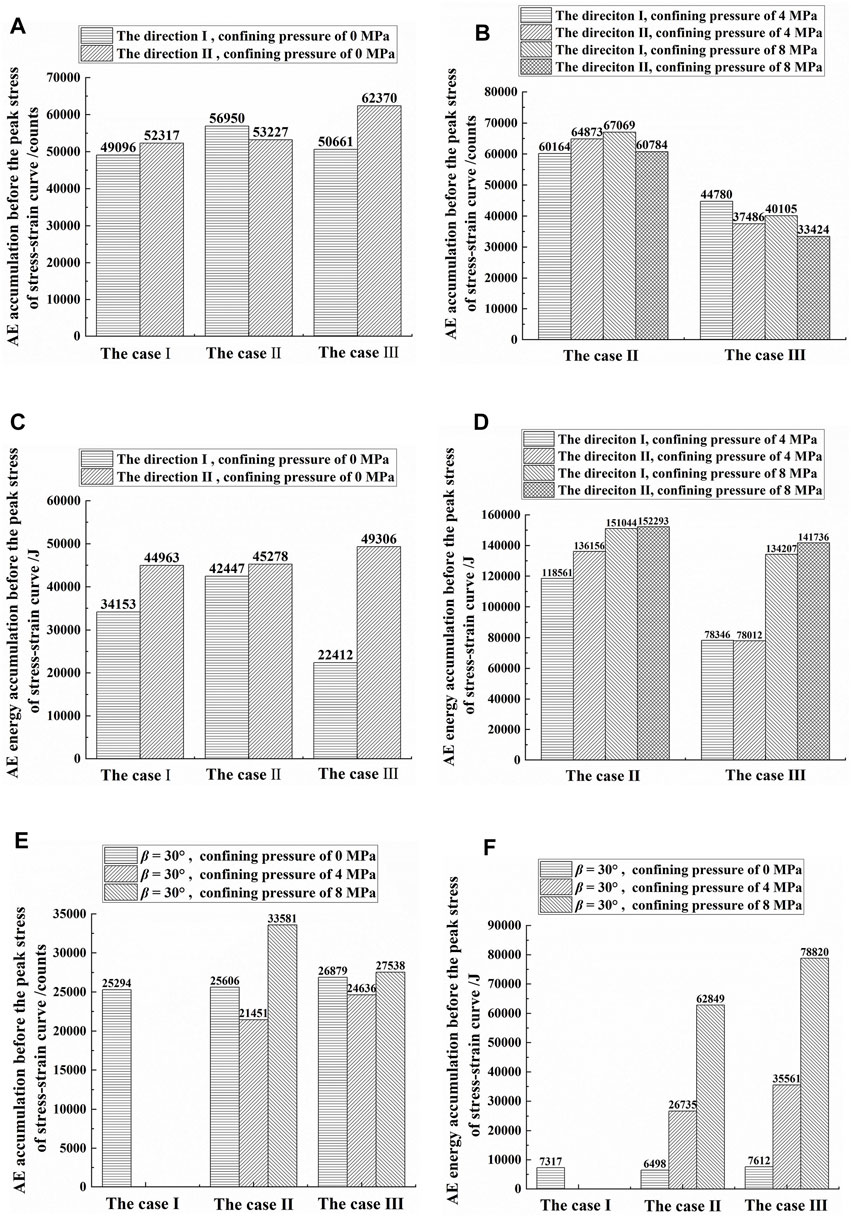
FIGURE 14. (A, B) Acoustic emission (AE) accumulations before the peak stress of columnar jointed basalts (CJBs) with different model boundaries and confining pressures in the direction orthogonal to the column axis. (C,D) The AE energy accumulations before the peak stress of CJBs. (E,F) The AE accumulations and AE energy accumulations before the peak stress of CJBs in the direction parallel to the column axis (case I, case II, and case III correspond to the case of plane stress, the case between plane stress and plane strain, and the case of plane strain, respectively).

Figure 14B displays the AE accumulations before the peak stress from the perspective of different model boundaries in the direction orthogonal to the column axis, with confining pressures of 4 and 8 MPa: in the case between plane stress and plane strain, the AE accumulation before the peak stress was more than that in the case of plane strain. The above result shows that, for the direction orthogonal to the column axis, in the monitoring of practical projects (such as underground caverns), the AE number near the wall may be higher than that in the surrounding rock inside the wall.

From the perspective of directions I and II for the case between plane stress and plane strain, with a confining pressure of 4 MPa, the AE accumulation before the peak stress in direction I was less than that in direction II, and with a confining pressure of 8 MPa, the AE accumulation before the peak stress in direction I was more than that in direction II. For the case of plane strain, with confining pressures of 4 and 8 MPa, the AE accumulation before the peak stress in direction I was more than that in direction II. From the perspective of confining pressure, except for individual cases, the AE accumulation before peak stress decreased with the increase of the confining pressure.

Figure 14C presents the AE energy accumulation before the peak stress in the direction orthogonal to the column axis and with a confining pressure of 0 MPa. For direction I, the AE energy accumulations before the peak stress from small to large correspond to the case of plane strain, the case of plane stress, and the case between plane stress and plane strain, respectively; for direction II, the AE energy accumulations before the peak stress from small to large correspond to the case of plane stress, the case between plane stress and plane strain, and the case of plane strain, respectively.

Figure 14D shows the AE energy accumulations before the peak stress from the perspective of the different model boundaries in the direction orthogonal to the column axis and with confining pressures of 4 and 8 MPa. In the case between plane stress and plane strain, the AE energy accumulation before the peak stress was higher than that in the case of plane strain. The above result shows that, for the direction orthogonal to the column axis, in the monitoring of practical projects (such as underground caverns), the AE energy near the wall may be higher than that in the surrounding rock inside the wall.

From the perspective of directions I and II, with confining pressures of 4 and 8 MPa, except for individual cases, the AE energy accumulation before the peak stress in direction I was lower than that in direction II. From the perspective of confining pressure, the AE energy accumulation before the peak stress increased with the growth of confining pressure.

3.4.2 In the Direction Parallel to the Column Axis: The AE Accumulations and AE Energy Accumulations Before the Peak Stress of CJBs With Different Model Boundaries and Confining Pressures

It can be seen from Figure 14E the AE accumulations before peak stress in the direction parallel to the column axis (β = 30°). With a confining pressure of 0 MPa, the AE accumulations before peak stress from small to large correspond to the case of plane stress, the case between plane stress and plane strain, and the case of plane strain, respectively; with a confining pressure of 4 MPa, the AE accumulations before peak stress from small to large correspond to the case between plane stress and plane strain and the case of plane strain, respectively; with a confining pressure of 8 MPa, the AE accumulations before peak stress from small to large correspond to the case of plane strain and the case between plane stress and plane strain, respectively.

Figure 14F depicts the AE energy accumulations before peak stress in the direction parallel to the column axis (β = 30°). With a confining pressure of 0 MPa, the AE energy accumulations before peak stress from small to large correspond to the case between plane stress and plane strain, the case of plane stress, and the case of plane strain, respectively. In the case of plane strain, the normal displacement constraints were set on both sides of the model plane, which will contribute to energy accumulation. Meanwhile, although there was normal displacement constraint on one side of the model plane for the case between plane stress and plane strain, the energy accumulation was also influenced by the rock heterogeneity, brittleness, etc., compared with the case of plane stress. Under the applied material properties and boundary conditions, the AE energy accumulations before peak stress of the case between plane stress and plane strain were the smallest. With confining pressures of 4 and 8 MPa, the AE energy accumulations before peak stress from small to large correspond to the case between plane stress and plane strain and the case of plane strain, respectively. The above results show that, for the direction parallel to the column axis, in the monitoring of practical projects (such as underground caverns), the AE number near the wall may be lower or higher than that in the surrounding rock inside the wall; however, the AE energy near the wall may be lower than that in the surrounding rock inside the wall.

4 Discussion

4.1 Effects of Different Model Boundaries and Confining Pressures on the Strength and Deformation of Jointed Rock Mass

In terms of CS, in the direction orthogonal to the column axis, with a confining pressure of 0 MPa and from the perspective of different model boundaries, the CSs from small to large correspond to the case of plane stress, the case between plane stress and plane strain, and the case of plane strain, respectively. When the confining pressures were 4 and 8 MPa, the CSs from small to large correspond to the case between plane stress and plane strain and the case of plane strain, respectively.

In terms of EDM, in the direction orthogonal to the column axis, with a confining pressure of 0 MPa and from the perspective of different model boundaries, for direction I, the EDMs from small to large correspond to the case between plane stress and plane strain, the case of plane stress, and the case of plane strain, respectively; for direction II, the EDMs from small to large correspond to the case of plane stress, the case between plane stress and plane strain, and the case of plane strain, respectively. When the confining pressures were 4 and 8 MPa, the EDMs from small to large correspond to the case between plane stress and plane strain and the case of plane strain, respectively.

In the direction parallel to the column axis, with a confining pressure of 0 MPa, the CS of the three model boundary conditions changed in a U-shaped trend with the increase of the column dip angle. Furthermore, with confining pressures of 4 and 8 MPa, the CS decreased firstly and then changed slowly with the increase of the column dip angle in the case between plane stress and plane strain. In the case of plane strain, the CS showed a V-shaped change trend with the increase of the column dip angle.

In the direction parallel to the column axis, with confining pressures of 0, 4, and 8 MPa, the EDM of three kinds of model boundaries roughly decreased firstly and then slightly increased (or changed) with the increase of the column dip angle. From the perspective of the different model boundaries, the case of small EDM is the case between plane stress and plane strain with confining pressures of 4 and 8 MPa, and the case of large EDM is the case of plane strain with confining pressures of 4 and 8 MPa.

In Figure 15, cases II and III correspond to the case between plane stress and plane strain and the case of plane strain, respectively. In the case between plane stress and plane strain, only one side along the thickness direction of the model was subject to normal displacement constraints, while the other side was free. In the case of plane strain, normal displacement constraints were applied on both sides along the thickness direction of the model. As shown in Figure 15, in the case between plane strain and plane stress and the case of plane strain, with a confining pressure of 4 MPa, the numerical test results in this paper were compared with the laboratory physical test results of Xiao et al. (2014) and Zhu et al. (2021). Xiao et al. (2014) used a mixture of gypsum, cement, and water to make columns according to a mass ratio of 3:1:3.2, then bonded them with cement slurry, cut and polished to obtain cylindrical specimens with a diameter of 50 mm and a height of 100 mm, and carried out a uniaxial compression test. However, in their research, the cement slurry was used to simulate joints. Cement slurry may have a great constraint on the deformation of jointed rock mass specimens, which may be quite different from the actual mechanical properties of the joints. Zhu et al. (2021) studied the mechanical properties and failure characteristics of CJRM specimens under 3D stress through a physical model test. The results showed that, under confining pressure, with the increase of column dip angle, the CSs of the specimens roughly decreased firstly and then changed slowly. However, in their research, the column material was made of gypsum, sand, and water in a certain proportion, and its mechanical properties under confining pressure may be different from that of the actual CJB material. Zhou et al. (2017) used an improved equivalent continuum model method to carry out triaxial compression numerical tests on cylindrical specimens of intact layered rock mass and layered rock mass with a weak surface. The results showed that the CSs of the two kinds of specimens changed in different degrees of U-shaped trend with the increase of the bedding dip angle. Hu et al. (2020) used the FLAC3D (fast Lagrangian analysis of continua in three dimensions) program to carry out triaxial compression numerical tests on cylindrical specimens of layered rock mass. The results showed that with the increase of confining pressure, the CS of the specimens increased significantly, but the change of EDM was small. However, the case between plane stress and plane strain has not been considered in their research. Feng et al. (2020) comprehensively evaluated the effects of the intermediate principal stress and the minimum principal stress on the failure strength of granite, marble, and sandstone under true triaxial conditions. The results showed that, when the intermediate principal stress remained unchanged and the minimum principal stress increased, the failure strength of the specimens roughly increased; when the minimum principal stress remained unchanged and the intermediate principal stress increased, the failure strength of the specimens increased firstly and then decreased. These results provide the references for the numerical result analysis of the CJBs with different model boundaries and confining pressures in this paper. Compared with the case of plane stress, the CJBs in the case between plane stress and plane strain were equivalent to the increase of the intermediate principal stress; compared with the case between plane stress and plane strain, the CJBs with confining pressure in the case of plane strain were equivalent to the increase of the minimum principal stress or the intermediate principal stress. Makhnenko and Labuz (2014) analyzed the change of the mechanical properties of limestone under plane strain compression and triaxial compression. The results showed that, with the increase of the minimum principal stress or the intermediate principal stress, the strength of the specimen roughly increased, which also provide the references for the numerical result analysis of the CJBs with different model boundaries and confining pressures in this paper. Tonon (2004) analyzed the influence of anisotropic rock mass on the tunnel in the case of plane strain, but in his research, the heterogeneity of rock mass was not considered and the meso damage was not further combined in the analysis.

FIGURE 15

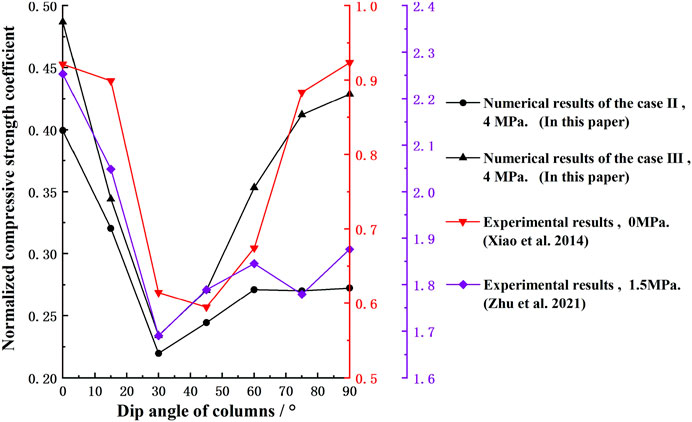
FIGURE 15. Comparison between the numerical test results and laboratory physical test results of columnar jointed basalts (CJBs) (cases II and III correspond to the case between plane stress and plane strain and the case of plane strain, respectively).

The deformation and failure of CJBs are not only related to the model boundaries and confining pressures but also influenced by the model size, the change of rock and joint mechanical properties, rock meso constitutive law, column diameter, column irregularity, etc. Because of the topic limitation, the relevant research has not been carried out in this work, but needs to be conducted in the future.

4.2 Effects of Different Model Boundaries and Confining Pressures on the Fracture Mechanism of Jointed Rock Mass

For the fracture process of CJBs along the direction orthogonal to the column axis with different model boundaries and confining pressures: 1) when the confining pressure was 0 MPa under the plane stress state, at the initial stage of loading, the vertical joints and transverse joints were damaged and cracked for the CJBs along direction I. At the middle stage of loading, several columns in the upper part of the specimen were also obviously damaged. At the late stage of loading, many columns in the middle and upper parts of the specimen failed and a final failure pattern occurred; 2) when the confining pressure was 8 MPa under the boundaries between plane stress and plane strain, the damage of the transverse joints was obvious for the CJBs along direction I. With the loading increasing, the vertical joints were also damaged, and the damaged and fractured columns continued to increase in the upper part of the specimen; 3) when the confining pressure was 8 MPa, for the CJBs along direction II, the damage and fracture of the joints in the upper part of the specimen became obvious with the loading increasing, and the other columns in the upper part of the specimen were also damaged and the crushing was intensified.

For the fracture process of the CJBs along the direction parallel to the column axis with different model boundaries and confining pressures: 1) when the confining pressure was 0 MPa, for the CJBs with β = 30° under the plane stress state, at the initial stage of loading, the columnar joints in the specimen were damaged and slipped. In the middle stage of loading, damage developed at the top of the specimen and at the edges of several columns in the middle and upper parts of the specimen. At the late stage of loading, new cracks appeared in the areas where the damage developed; 2) when the confining pressure was 8 MPa, for the CJBs with β = 30° under the state between plane stress and plane strain, at the initial stage of loading, the columnar joints were damaged, and then the damage of the columns at the top of the specimen developed and the crushing intensified; 3) when the confining pressure was 8 MPa, for the CJBs with β = 30° under the plane strain state, there were fractured columns occurring on the left side of the specimen top, and damage and fracture of several column edges happened on the left side of the upper part of the specimen, and then near the top and in the upper part of the specimen, two strip fractured zones were formed and the fracturing intensified.

Xiao et al. (2014) and Xiao et al. (2015) studied the deformation and strength anisotropy of CJRMs under uniaxial compression and conventional triaxial compression and analyzed their failure patterns. However, in their research, cement slurry was used to simulate joints, which may be quite different from the mechanical properties of actual joints and affect the fracture mechanism of CJRMs. Huang et al. (2020) used 3DP technology to prepare the molds. They poured white cement slurry, removed the molds, and then bonded the columns with white latex and glue, then carried out the tests of mechanical properties of irregular CJRMs. However, in their research, the bonding effect of white latex or glue may also be quite different from the mechanical properties of actual joints and affect the fracture mechanism of CJRMs. Ji et al. (2017) used cement, fine sand, water, and a water reducer to make regular hexagonal prisms and then bonded the columns with white cement slurry to form CJRM specimens. Uniaxial compression tests were carried out and the failure patterns of CJRMs were analyzed. Zhu et al. (2021) studied the mechanical properties and failure characteristics of CJRM specimens under 3D stress through physical model tests. Xia et al. (2020b) reconstructed irregular CJRMs using 3DP technology and then carried out uniaxial compression tests to analyze the fracture characteristics of irregular CJRMs. However, the above physical tests cannot reflect the progressive fracture process of the specimens. Hu et al. (2020) used the FLAC3D program to carry out triaxial compression numerical tests on cylindrical specimens of layered rock mass and analyzed the failure patterns of the specimens. However, the progressive fracture processes of the specimens were not presented in their study. Zhou et al. (2017) used an improved equivalent continuum model method to carry out uniaxial and triaxial compression numerical tests on cylindrical specimens of intact layered rock mass and layered rock mass with a weak surface and analyzed the evolution of the failure patterns. However, in their research, the factors such as rock heterogeneity and meso damage were not comprehensively considered.

4.3 Effects of Different Model Boundaries and Confining Pressures on the AE of Jointed Rock Mass

For the energy release of CJBs along the direction orthogonal to the column axis with different model boundaries and confining pressures: 1) when the confining pressure was 0 MPa, in the case of plane stress, the peak value of AE energy was lower than that in the case of plane strain, but the area under the AE energy curve was larger, indicating that more energy was released at this stage; 2) when the confining pressure was 8 MPa, the peak value of AE energy in the case between plane stress and plane strain was lower than that in the case of plane strain and showed a single peak distribution. Simultaneously, its AE energy peak tended to be before the peak stress of the stress–strain curve. In the case of plane strain, the AE energy distribution showed a single peak distribution as well, but the AE energy peak tended to be after the peak stress of the stress–strain curve.

For the energy evolution of the CJBs along the direction parallel to the column axis with different model boundaries and confining pressures: 1) when the confining pressure was 0 MPa, for the AE energies of CJBs with β = 30°, in the case of plane stress, although the peak value of AE energy was lower than that in plane strain, the accumulated AE energy was still high near the peak value, which indicates that more energy was released at this stage; 2) when the confining pressure was 8 MPa, for the AE energies of CJBs with β = 30°, when the boundaries are between plane stress and plane strain, the peak value of AE energy was lower than that in plane strain and the AE energy showed a multi-peak distribution. Furthermore, the AE energy showed a single peak distribution under the plane strain state, and the peak value of AE energy tended to be before the peak stress of the stress–strain curve.

Zhu et al. (2021) studied the mechanical properties and failure characteristics of CJRM specimens under 3D stress through physical model tests. However, the evolution of the AE energy in the progressive fractured process of CJRMs was not considered in their research. Duan et al. (2018) used the discrete element method to study the stress stability of boreholes in different directions in anisotropic rock mass and analyzed the stress–strain curves of specimens with different dip angles and the variation trend of the number of different types of microcracks during loading. The results showed that the number of microcracks increased slowly before the peak stress and increased sharply near the peak stress. To some extent, the change of the number of microcracks represents the evolution process of AE energy. Therefore, the research results showed certain similarity with the numerical test results in this paper. The laboratory physical test results of Feng et al. (2021), Song et al. (2020), Li S. et al. (2019), and Li D. et al. (2019) and the PFC2D (particle flow code in two dimensions) numerical test results of Wen et al. (2016) also showed that, under uniaxial compression, the AE peak of a single joint specimen with different joint dip angles roughly appeared near the peak stress of the stress–strain curve. However, when the joint dip angles were 30° and 45°, the AE results of the numerical tests of Wen et al. (2016) did not obviously show this characteristic, which may be related to the numerical test method used. The laboratory physical test results of Chen et al. (2020) showed that, under different confining pressures, the AE peak of pre-cut cracked granite specimens roughly appeared near the peak stress of the stress–strain curve, which had certain similarity with the numerical test results in this paper. The laboratory physical test results of Wang et al. (2019) showed that, when the confining pressure was small, the AE of the specimen showed a multi-peak distribution; with the increase of the confining pressure, the AE of the specimen concentrated in a certain section of the stress–strain curve. However, the factor of joint was not considered in their research, so there are certain differences with the results in this paper.

5 Conclusion

By combining the meso-damage mechanics, statistical strength theory, and continuum mechanics, a series of heterogeneous numerical models of CJBs with different column dip angles were established. In the cases of plane stress, plane strain and between plane stress, and plane strain, the fracture process and energy evolution of CJBs with joints orthogonal and parallel to the column axis were numerically simulated under confining pressure, and the AE events and energy accumulation before and after the peak stress of CJBs were obtained. The main conclusions can be summarized as follows:

For the fracture process of the CJBs along the direction orthogonal to the column axis with different model boundaries and confining pressures: 1) when the confining pressure was 0 MPa under the plane stress state, for the CJBs along direction I, the vertical joints and transverse joints were damaged and cracked at the initial stage of loading. At the middle stage of loading, several columns in the upper part of the specimen were also obviously damaged. At the late stage of loading, many columns in the middle and upper parts of the specimen failed and a final failure pattern occurred; 2) when the confining pressure was 8 MPa under the boundaries between plane stress and plane strain, for the CJBs along direction I, the damage of the transverse joints was obvious. With the loading increasing, the vertical joints were also damaged, and the damaged and fractured columns continued to increase in the upper part of the specimen; 3) when the confining pressure was 8 MPa, for the CJBs along direction II, with the loading increasing, the damage and fracture of the joints in the upper part of the specimen became obvious; the other columns in the upper part of the specimen were also damaged and the crushing was intensified.

For the fracture process of the CJBs along the direction parallel to the column axis with different model boundaries and confining pressures: 1) when the confining pressure was 0 MPa, for the CJBs with β = 30° under the plane stress state, the columnar joints in the specimen were damaged and slipped at the initial stage of loading. In the middle stage of loading, damage developed at the top of the specimen and at the edges of several columns in the middle and upper parts of the specimen. At the late stage of loading, new cracks appeared in the areas where damage developed; 2) when the confining pressure was 8 MPa, for the CJBs with β = 30° under the state between plane stress and plane strain, at the initial stage of loading, the columnar joints were damaged and then damage of the columns at the top of the specimen developed and the crushing intensified; 3) when the confining pressure was 8 MPa, for the CJBs with β = 30° under the plane strain state, there were fractured columns occurring on the left side of the specimen top. Damage and fracture of several column edges happened on the left side of the upper part of the specimen, and then near the top and in the upper part of the specimen, two strip fractured zones were formed and the fracturing intensified.

For the AE energy accumulation before the peak stress of the CJBs with different model boundaries and confining pressures: 1) when the confining pressures were 4 and 8 MPa, the AE energy accumulation of the CJBs along the direction orthogonal to the column axis in the case between plane stress and plane strain before the peak stress was higher than that in the plane strain state; 2) when the confining pressures were 4 and 8 MPa, the AE energy accumulation of the CJBs along the direction parallel to the column axis (β = 30°) under plane strain was higher than that in the case between plane stress and plane strain. Therefore, the released AE energy can provide valuable insights into the instability precursor of CJBs.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

YW conducted the numerical simulations and wrote the first draft. BG supervised the study and revised the draft. CT gave critical reviews to improve the study. All authors approved the submitted version.

Funding

This study was financially supported by the National Key Research and Development Program of China (Grant No. 2018YFC1505301), the National Natural Science Foundation of China (Grant Nos. 42050201 and 51627804) and the China Postdoctoral Science Foundation (Grant No. 2020M680950), for which the authors are very grateful.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

AE, acoustic emission; CJBs, columnar jointed basalts; CJRMs, columnar jointed rock masses; CS, compressive strength; EDM, equivalent deformation modulus; TACCS, transverse anisotropy coefficient of compressive strength; TACEDM, transverse anisotropy coefficient of equivalent deformation modulus; σ, stress (MPa); f_cr, residual compressive strength; f_tr, residual tensile strength; f_c0, uniaxial compressive strength; f_t0, uniaxial tensile strength; ε, strain; ε_c0, strain at f_c0; ε_t0, strain at f_t0; ε_tu, ultimate tensile strain.

References

Chen, G., Sun, X., Wang, J., Wang, D., and Zhu, Z. (2020). Detection of Cracking Behaviors in Granite with Open Precut Cracks by Acoustic Emission Frequency Spectrum Analysis. Arab. J. Geosci. 13, 258. doi:10.1007/s12517-020-5253-8

CrossRef Full Text | Google Scholar

Cui, Z., Wei, Q., Hou, J., Sheng, Q., and Li, L. Q. (2016). Structural Effect on Equivalent Modulus of Deformation of Columnar Jointed Rock Mass with Jointed Finite Element Method. Rock Soil Mech. 37 (10), 2921–2928+2936. doi:10.16285/j.rsm.2016.10.025

CrossRef Full Text | Google Scholar

Duan, K., Wu, W., and Kwok, C. Y. (2018). Discrete Element Modelling of Stress-Induced Instability of Directional Drilling Boreholes in Anisotropic Rock. Tunn. Undergr. Space Technol. 81, 55–67. doi:10.1016/j.tust.2018.07.001

CrossRef Full Text | Google Scholar

Eshraghi, A., and Zare, S. (2015). Face Stability Evaluation of a TBM-Driven Tunnel in Heterogeneous Soil Using a Probabilistic Approach. Int. J. Geomech. 15. doi:10.1061/(asce)gm.1943-5622.0000452

CrossRef Full Text | Google Scholar

Feng, F., Li, X. B., Du, K., Li, D. Y., Rostami, J., and Wang, S. F. (2020). Comprehensive Evaluation of Strength Criteria for Granite, Marble, and Sandstone Based on Polyaxial Experimental Tests. Int. J. Geomech. 20 (2), 04019155. doi:10.1061/(asce)gm.1943-5622.0001544

CrossRef Full Text | Google Scholar

Feng, Z., Chen, X., Fu, Y., Qing, S., and Xie, T. (2021). Acoustic Emission Characteristics and Joint Nonlinear Mechanical Response of Rock Masses under Uniaxial Compression. Energies 14, 200. doi:10.3390/en14010200

CrossRef Full Text | Google Scholar

Gilman, J. J. (2009). Basalt Columns: Large Scale Constitutional Supercooling? J. Volcanology Geothermal Res. 184, 347–350. doi:10.1016/j.jvolgeores.2009.04.017

CrossRef Full Text | Google Scholar

Gong, B., Wang, S., Sloan, S. W., Sheng, D., and Tang, C. a. (2018). Modelling Coastal Cliff Recession Based on the GIM-DDD Method. Rock Mech. Rock Eng. 51, 1077–1095. doi:10.1007/s00603-017-1382-0

CrossRef Full Text | Google Scholar

Gui, Y., and Zhao, G. F. (2015). Modelling of Laboratory Soil Desiccation Cracking using DLSM with a Two-Phase Bond Model. Comput. Geotech. 69, 578–587. doi:10.1016/j.compgeo.2015.07.001

CrossRef Full Text | Google Scholar

Guy, B. (2009). Comments on "Basalt Columns: Large Scale Constitutional Supercooling? by John Gilman (JVGR, 2009) and Presentation of Some New Data. J. Volcanol. Geotherm. Res. 184, 347–350. doi:10.1016/j.jvolgeores.2009.09.021

CrossRef Full Text | Google Scholar

Hu, S., Tan, Y., Zhou, H., Ru, W., Ning, J., Wang, J., et al. (2020). Anisotropic Modeling of Layered Rocks Incorporating Planes of Weakness and Volumetric Stress. Energy Sci Eng 8, 789–803. doi:10.1002/ese3.551

CrossRef Full Text | Google Scholar

Hu, W., Wu, A. Q., Chen, S. H., Huang, S. L., and Zhang, L. J. (2017). Mechanical Properties of Columnar Jointed basalt Rock with Hidden Fissures under Uniaxial Loading. Chin. J. Rock Mech. Eng. 36 (08), 1880–1888. doi:10.13722/j.cnki.jrme.2017.0149

CrossRef Full Text | Google Scholar

Huang, W., Xiao, W. M., Tian, M. T., and Zhang, L. H. (2020). Model Test Research on the Mechanical Properties of Irregular Columnar Jointed Rock Masses. Rock Soil Mech. 41 (07), 2349–2359. doi:10.16285/j.rsm.2019.1493

CrossRef Full Text | Google Scholar

Ji, H., Zhang, J. C., Xu, W. Y., Wang, R. B., Wang, H. L., Yan, L., et al. (2017). Experimental Investigation of the Anisotropic Mechanical Properties of a Columnar Jointed Rock Mass: Observations from Laboratory-Based Physical Modelling. Rock Mech. Rock Eng. 50, 1919–1931. doi:10.1007/s00603-017-1192-4

CrossRef Full Text | Google Scholar

Ke, Z. Q., Wang, H. L., Xu, W. Y., Lin, Z. N., and Ji, H. (2019). Experimental Study of Mechanical Behaviour of Artificial Columnar Jointed Rock Mass Containing Transverse Joints. Rock Soil Mech. 40 (02), 660–667. doi:10.16285/j.rsm.2017.1645

CrossRef Full Text | Google Scholar

Lang, Y. X., Liang, Z. Z., Duan, D., and Cao, Z. L. (2019). Three-dimensional Parallel Numerical Simulation of Porous Rocks Based on CT Technology and Digital Image Processing. Rock Soil Mech. 40 (03), 1204–1212. doi:10.16285/j.rsm.2017.1728

CrossRef Full Text | Google Scholar

Lang, Y. X. (2018). Numerical Tests of Three-Dimensional Microscopic Model of Porous Rock Based on CT Digital Image Processing. China: Dalian University of Technology.

Google Scholar

Li, D., Wang, E., Kong, X., Ali, M., and Wang, D. (2019b). Mechanical Behaviors and Acoustic Emission Fractal Characteristics of Coal Specimens with a Pre-existing Flaw of Various Inclinations under Uniaxial Compression. Int. J. Rock Mech. Mining Sci. 116, 38–51. doi:10.1016/j.ijrmms.2019.03.022

CrossRef Full Text | Google Scholar

Li, L. C., Yang, T. H., Liang, Z. Z., Zhu, W. C., and Tang, C. N. (2011). Numerical Investigation of Groundwater Outbursts Near Faults in Underground Coal Mines. Int. J. Coal Geol. 85 (3-4), 276–288. doi:10.1016/j.coal.2010.12.006

CrossRef Full Text | Google Scholar

Li, S., Zhang, D., Bai, X., Zhang, X., Chu, Y., and Guo, K. (2019a). Experimental Study on Mechanical Properties, Acoustic Emission Energies and Failure Modes of Pre-cracked Rock Materials under Uniaxial Compression. Pure Appl. Geophys. 176, 4519–4532. doi:10.1007/s00024-019-02201-8

CrossRef Full Text | Google Scholar

Liang, Z. Z. (2005). Three-dimensional Failure Process Analysis of Rock and Associated Numerical Tests. Shenyang, Liaoning, China: Northeastern University.

Google Scholar

Liu, X., Tang, C. a., Li, L., Lv, P., and Liu, H. (2017). Microseismic Monitoring and 3D Finite Element Analysis of the Right Bank Slope, Dagangshan Hydropower Station, during Reservoir Impounding. Rock Mech. Rock Eng. 50, 1901–1917. doi:10.1007/s00603-017-1191-5

CrossRef Full Text | Google Scholar

Liu, Z., and Shao, J. (2017). Strength Behavior, Creep Failure and Permeability Change of a Tight Marble under Triaxial Compression. Rock Mech. Rock Eng. 50, 529–541. doi:10.1007/s00603-016-1134-6

CrossRef Full Text | Google Scholar

Makhnenko, R., and Labuz, J. (2014). Plane Strain Testing with Passive Restraint. Rock Mech. Rock Eng. 47, 2021–2029. doi:10.1007/s00603-013-0508-2

CrossRef Full Text | Google Scholar

Min, K.-B., and Jing, L. (2003). Numerical Determination of the Equivalent Elastic Compliance Tensor for Fractured Rock Masses Using the Distinct Element Method. Int. J. Rock Mech. Mining Sci. 40, 795–816. doi:10.1016/s1365-1609(03)00038-8

CrossRef Full Text | Google Scholar

Ning, Y., Xu, W. Y., Zheng, W. T., Meng, G. T., Shi, A. C., and Wu, G. Y. (2008). Study of Random Simulation of Columnar Jointed Rock Mass and its Representative Elementary Volume Scale. Chin. J. Rock Mech. Eng. 26 (06), 1202–1208. doi:10.13722/j.cnki.jrme.2007.0302

CrossRef Full Text | Google Scholar

Rajmeny, P. K., Singh, U. K., and Rathore, S. S. (2004). A New Model to Estimate Rock Mass Strength Accounting for the Scale Effect. Int. J. Rock Mech. Mining Sci. 41, 1013–1021. doi:10.1016/j.ijrmms.2004.03.008

CrossRef Full Text | Google Scholar

Song, H., Zhao, Y., Elsworth, D., Jiang, Y., and Wang, J. (2020). Anisotropy of Acoustic Emission in Coal under the Uniaxial Loading Condition. Chaos, Solitons & Fractals 130, 109465. doi:10.1016/j.chaos.2019.109465

CrossRef Full Text | Google Scholar

Sun, P. F., Yang, T. H., Yu, Q. L., and Shen, W. (2012). Numerical Research on Anisotropy Mechanical Parameters of Fractured Rock Mass. Adv. Mater. Res. 524–527, 310–316. doi:10.4028/www.scientific.net/AMR.524-527.310

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, C. A., and Kou, S. Q. (1998). Crack Propagation and Coalescence in Brittle Materials under Compression. Eng. Fract. Mech. 61 (3-4), 311–324. doi:10.1016/s0013-7944(98)00067-8

CrossRef Full Text | Google Scholar

Tang, C. A., Lin, P., Wong, R. H. C., and Chau, K. T. (2001). Analysis of Crack Coalescence in Rock-like Materials Containing Three Flaws-Part II: Numerical Approach. Int. J. Rock Mech. Mining Sci. 38 (7), 925–939. doi:10.1016/s1365-1609(01)00065-x

CrossRef Full Text | Google Scholar

Tang, C. A., Liu, H., Lee, P. K. K., Tsui, Y., and Tham, L. G. (2000). Numerical Studies of the Influence of Microstructure on Rock Failure in Uniaxial Compression - Part I: Effect of Heterogeneity. Int. J. Rock Mech. Mining Sci. 37 (4), 555–569. doi:10.1016/s1365-1609(99)00121-5

CrossRef Full Text | Google Scholar

Tang, C. (1997). Numerical Simulation of Progressive Rock Failure and Associated Seismicity. Int. J. Rock Mech. Mining Sci. 34 (2), 249–261. doi:10.1016/s0148-9062(96)00039-3

CrossRef Full Text | Google Scholar

Tang, C., Tang, S., Gong, B., and Bai, H. (2015). Discontinuous Deformation and Displacement Analysis: From Continuous to Discontinuous. Sci. China Technol. Sci. 58, 1567–1574. doi:10.1007/s11431-015-5899-8

CrossRef Full Text | Google Scholar

Tonon, F. (2004). Does Elastic Anisotropy Significantly Affect a Tunnel's Plane Strain Behavior? Transportation Res. Rec. 1868, 156–168. doi:10.3141/1868-17

CrossRef Full Text | Google Scholar

Wang, Q., Chen, J., Guo, J., Luo, Y., Wang, H., and Liu, Q. (2019). Acoustic Emission Characteristics and Energy Mechanism in Karst limestone Failure under Uniaxial and Triaxial Compression. Bull. Eng. Geol. Environ. 78, 1427–1442. doi:10.1007/s10064-017-1189-y

CrossRef Full Text | Google Scholar

Weinberger, R., and Burg, A. (2019). Reappraising Columnar Joints in Different Rock Types and Settings. J. Struct. Geology. 125, 185–194. doi:10.1016/j.jsg.2018.04.015

CrossRef Full Text | Google Scholar

Wen, Z. J., Wang, X., Li, Q. H., Lin, G., Chen, S. J., and Jiang, Y. J. (2016). Simulation Analysis On The Strength And Acoustic Emission Characteristics Of Jointed Rock Mass. Teh. Vjesn. 23, 1277–1284. doi:10.17559/tv-20160826112410

CrossRef Full Text | Google Scholar

Xia, Y., Zhang, C., Zhou, H., Chen, J., Gao, Y., Liu, N., et al. (2020a). Structural Characteristics of Columnar Jointed basalt in Drainage Tunnel of Baihetan Hydropower Station and its Influence on the Behavior of P-Wave Anisotropy. Eng. Geology. 264, 105304. doi:10.1016/j.enggeo.2019.105304

CrossRef Full Text | Google Scholar

Xia, Y., Zhang, C., Zhou, H., Hou, J., Su, G., Gao, Y., et al. (2020b). Mechanical Behavior of Structurally Reconstructed Irregular Columnar Jointed Rock Mass Using 3D Printing. Eng. Geology. 268, 105509. doi:10.1016/j.enggeo.2020.105509

CrossRef Full Text | Google Scholar

Xiao, W. M., Deng, R. G., Fu, X. M., and Wang, C. Y. (2015). Experimental Study of Deformation and Strength Properties of Simulated Columnar Jointed Rock Masses under Conventional Triaxial Compression. Chin. J. Rock Mech. Eng. 34 (S1), 2817–2826. doi:10.13722/j.cnki.jrme.2014.0316

CrossRef Full Text | Google Scholar

Xiao, W. M., Deng, R. G., Fu, X. M., and Wang, C. Y. (2014). Model Experiments on Deformation and Strength Anisotropy of Columnar Jointed Rock Masses under Uniaxial Compression. Chin. J. Rock Mech. Eng. 33 (05), 957–963. doi:10.13722/j.cnki.jrme.2014.05.011

CrossRef Full Text | Google Scholar

Xiao, Y.-X., Feng, X.-T., Chen, B.-R., Feng, G.-L., Yao, Z.-B., and Hu, L.-X. (2017). Excavation-induced Microseismicity in the Columnar Jointed basalt of an Underground Hydropower Station. Int. J. Rock Mech. Mining Sci. 97, 99–109. doi:10.1016/j.ijrmms.2017.04.012

CrossRef Full Text | Google Scholar

Xu, T., Ranjith, P. G., Wasantha, P. L. P., Zhao, J., Tang, C. A., and Zhu, W. C. (2013). Influence of the Geometry of Partially-Spanning Joints on Mechanical Properties of Rock in Uniaxial Compression. Eng. Geology. 167, 134–147. doi:10.1016/j.enggeo.2013.10.011

CrossRef Full Text | Google Scholar

Xu, X.-W. (2010). Columnar Jointing in basalt, Shandong Province, China. J. Struct. Geology. 32, 1403. doi:10.1016/j.jsg.2007.05.010

CrossRef Full Text | Google Scholar

Yan, D. X., Xu, W. Y., Wang, W., Shi, C., Shi, A. C., and Wu, G. Y. (2012). Research of Size Effect on Equivalent Elastic Modulus of Columnar Jointed Rock Mass. Chin. J. Geotechnical Eng. 34 (2), 243–250. doi:10.11779/CJGE201102016

CrossRef Full Text | Google Scholar

Yang, J. P., Chen, W. Z., Yang, D. S., and Yuan, J. Q. (2015a). Numerical Determination of Strength and Deformability of Fractured Rock Mass by FEM Modeling. Comput. Geotech. 64, 20–31. doi:10.1016/j.compgeo.2014.10.011

CrossRef Full Text | Google Scholar

Yang, T., Wang, P., Xu, T., Yu, Q., Zhang, P., Shi, W., et al. (2015b). Anisotropic Characteristics of Jointed Rock Mass: A Case Study at Shirengou Iron Ore Mine in China. Tunnelling Underground Space Technology 48, 129–139. doi:10.1016/j.tust.2015.03.005

CrossRef Full Text | Google Scholar

Yu, Q. L., Yang, T. H., Tang, S. B., Liu, H. L., Liang, Z. Z., Zheng, X., et al. (2015). The 3D Reconstruction Method for Quasi-Brittle Material Structure and Application. Eng. Mech. 32 (11), 51–62+114. doi:10.6052/j.issn.1000-4750.2014.06.0474

CrossRef Full Text | Google Scholar

Yu, Y., Chen, B. R., Xu, C. J., Diao, X. H., Tong, L. H., and Shi, Y. F. (2017). Analysis for Microseismic Energy of Immediate Rockbursts in Deep Tunnels with Different Excavation Methods. Int. J. Geomech. 17. doi:10.1061/(asce)gm.1943-5622.0000805

CrossRef Full Text | Google Scholar

Yu, Y., Geng, D. X., Tong, L. H., Zhao, X. S., Diao, X. H., and Huang, L. H. (2018). Time Fractal Behavior of Microseismic Events for Different Intensities of Immediate Rock Bursts. Int. J. Geomech. 18. doi:10.1061/(asce)gm.1943-5622.0001221

CrossRef Full Text | Google Scholar

Závada, P., Dědeček, P., Lexa, J., and Keller, G. R. (2015). Devils Tower (Wyoming, USA): A Lava Coulée Emplaced into a Maar-Diatreme Volcano? Geosphere 11, 354–375. doi:10.1130/ges01166.1

CrossRef Full Text | Google Scholar

Zheng, W. T., Xu, W. Y., Ning, Y., and Meng, G. T. (2010). Scale Effect and Anisotropy of Deformation Modulus of Closely Jointed Basaltic Mass. J. Eng. Geology. 18 (04), 559–565. doi:10.13544/j.cnki.jeg.2009-127

CrossRef Full Text | Google Scholar

Zhou, J., Wei, J., Yang, T., Zhu, W., Li, L., and Zhang, P. (2018). Damage Analysis of Rock Mass Coupling Joints, Water and Microseismicity. Tunnelling Underground Space Technology 71, 366–381. doi:10.1016/j.tust.2017.09.006

CrossRef Full Text | Google Scholar

Zhou, Y.-Y., Feng, X.-T., Xu, D.-P., and Fan, Q.-X. (2017). An Enhanced Equivalent Continuum Model for Layered Rock Mass Incorporating Bedding Structure and Stress Dependence. Int. J. Rock Mech. Mining Sci. 97, 75–98. doi:10.1016/j.ijrmms.2017.06.006

CrossRef Full Text | Google Scholar

Zhu, Z., Lu, W., He, Y., and Que, X. (2021). Experimental Study on the Strength Failure Characteristics of Columnar Jointed Rock Masses under Three-Dimensional Stress. KSCE J. Civ. Eng. 25, 2411–2425. doi:10.1007/s12205-021-0821-3

CrossRef Full Text | Google Scholar