- 1Sinosteel Maanshan General Institute of Mining Research Co., LTD, Maanshan, China
- 2State Key Laboratory of Safety and Health for Metal Mines, Maanshan, China
- 3322 Geological Team of Anhui Provincial Bureau of Geology and Mineral Exploration, Maanshan, China
- 4School of Mining Engineering, Anhui University of Science and Technology, Huainan, China
- 5School of Resources and Environmental Engineering, Jiangxi University of Science and Technology, Ganzhou, China
The application of tailings-geotextile composites can effectively reduce tailings dam safety accidents. In this paper, the tailings dam of the Gushan Iron Mine is the research background. The construction of tailings-geotextile composites was briefly studied. Based on the existing experimental data, the permeability and physical properties of the composite material were analyzed, and the model of the composite material was generalized. The seepage characteristics of the composite were analyzed by using the numerical simulation method of the seepage field. Finally, the overall stability of the composite during the construction and storage phases was investigated. The conclusions are as follows: 1) In the early stage of stacking, the permeability coefficient of the composite body increases with the increase in filling tension; in the later stage, under the action of excess pore pressure, the composite body still exhibits strong permeability; 2) In the early stage of stacking, the height of the composite body is low, and the relative position of the saturated zone is relatively high; as the composite continues to rise or the stacking time increases, the lower part of the composite is gradually consolidated, and the position of the saturated zone is gradually raised; when the stacking is stopped, the saturated zone gradually decreases until it is close to the original position; 3) With the increase in the stacking height of the composite, the safety factor decreases rapidly; when the stacking height is 22.0 m, it decreases to the minimum; with time, the stability of the composite will gradually increase. This study helps people understand tailings-geotextile composites, and it has significant reference value for practical engineering.
1 Introduction
A tailings dam, like a dam structure used for pile mine wastes in the case of dam failure, will bring immeasurable loss (Rahardjo et al., 2005; Cao et al., 2019; Yang et al., 2021). At present, tailings disposal technologies mainly include open-pit tailings discharge, wet discharge of tailings ponds, and dry stacking of tailings (Duan et al., 2013). Among them, tailings-geotextile composite heap dry backfilling materials technology can enhance the penetration of consolidation characteristics, and chambers rapidly drain the water body, effectively improve the safety and stability of tailings dam. In recent years, due to the demand for practical engineering, research on tailings-geotextile composites and their properties has developed rapidly (Wang et al., 2022; Wu et al., 2022).
Researchers mainly study the properties of the composite through direct shear and pull-out tests, but triaxial compression tests are also an effective means to study the properties of the composite. For example, Koerner (2000) performed a triaxial test and analyzed the influence of confining pressure, the influence law of the soil, and the complex shear strength index; Khedkar and Mandal (2009) compared the three kinds of pure sand under confining pressure and single complex and double complex stress-strain curves; Khaniki and Daliri (2013) analyzed the influence of confining pressure on the shear strength index of plain soil and composite through the triaxial test of composite; Chen et al. (2014) conducted consolidation drainage and consolidation undrained tests, respectively, and analyzed the shear complex microstructure in the process of change; and Nouri et al. (2016) studied the triaxial monotonous mechanical properties of the composite drainage conditions.
In terms of model testing, scholars have also conducted much work, and useful conclusions have been drawn. Pincus et al. (1993) studied a large chamber to enhance the soil confining effect for large chamber reinforced silica sand and limestone; Liu et al. (2014), Chen et al. (2015), Zhao et al. (2016), and Li et al. (2022) carried out model tests of the overtopping failure of the tailings dam. Zhao et al. revealed that the composite can effectively reduce the flood overtopping damage of the tailings dam.
Due to the complex interaction mechanism between the tailings-geotextile composite and the surrounding tailings, researchers still have an insufficient understanding of its physical structure stability. This paper takes the Gushan Iron Mine tailings dam as the research background. According to the existing test data, the permeability and physical and mechanical properties of the composite are analyzed, and the model of the composite is generalized. Second, the seepage characteristics of the composite were analyzed by a numerical simulation method. Finally, the overall stability of the composite during the construction and storage phases is investigated.
2 Construction of tailings-geotextile composites
2.1 Selection of geosynthetics
Geosynthetics are various types of geotechnical products made of synthetic polymers (such as plastics, chemical fibers, synthetic rubber, etc.) as raw materials. Because the geotechnical materials in the tailings-geotextile composite dry stack need to meet the requirements of high strength and good anti-aging properties, the geotechnical materials need to be made of polyester chemical materials. Due to the same porosity, the penetration rate of woven polyester geotextile is higher than that of nonwoven type, so in the composite dry pile of tailings-geotextile, we choose woven polyester geotextile to make geosynthetic material (Liu et al., 2002).
To increase the strength of the composite and the frictional resistance between layers, we added reinforcement materials, such as geobelt or geogrids, between the monomers. To increase the permeability of the complex, we need to add drainage strips, drain pipes, or plastic blind trenches to the complex.
2.2 Research on the stacking technology of complexes
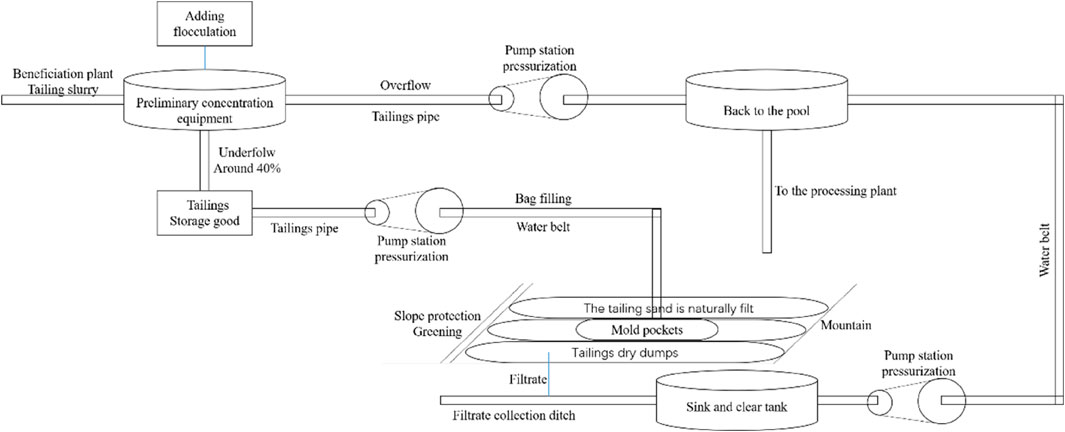
The tailings-geotextile composite dry stacking is a process of converting tailings from suspended liquid to a solid state. The technological process is to first concentrate the tailings produced by the dressing plant into 20%–40% slurry, and then the slurry is pressed into the geoform bag by the slurry pump. Under the action of slurry pressure, self-gravity, and external force, the water in the slurry is discharged through the geotechnical bag. As the water content of the slurry gradually decreases and the slurry concentration increases, the tailings gradually consolidate, and the tailings and geotextile gradually become reinforced soil, forming a tailings-geotextile composite with higher strength (Figure 1).
From the dry stacking process of the tailings-geotextile composite, it can be seen that the whole process can be divided into the initial concentration stage of tailings slurry, the stage of tailings slurry transportation, the stage of tailings slurry filling and sedimentation dehydration and compaction consolidation and the final greening and reclamation stage. From the system point of view, it can be divided into a dense system, conveying system, natural filter press system, and auxiliary system (including greening, wastewater recovery, monitoring, and other subsystems).
2.2.1 Initial concentration process of tailings slurry
The concentration of tailings pulp produced by the dressing plant is generally low, and the original pulp needs to be concentrated to a concentration of 20%–40% by thickening equipment.
2.2.2 Tailings slurry transportation process
The tailings conveying process mainly includes conveying equipment, conveying concentration, and conveying pressure. Among them, the slurry transport concentration is an important index affecting the dry pile of tailings geotextiles. Through the experimental test, this study chose a pulp conveying concentration of 25%∼35%.
2.2.3 Tailings slurry filling and sedimentation dehydration and compaction consolidation process
In this study, the following points should be noted. The size of the geotechnical bag is generally 60∼600 m3; when the slurry concentration is 30%, the flow rate of the slurry is approximately 2 m/s; the better the permeability and consolidation of the tailings are, the larger the layer thickness of the composite should be.
3 Characteristics of composite and analysis of models
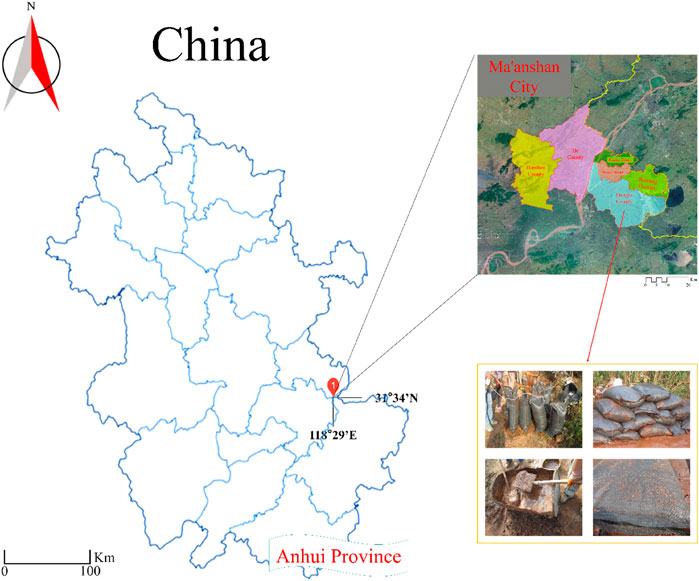
This study was carried out at the tailings dam of the Gushan Iron Mine in Anhui Province (Figure 2).
3.1 Research on the permeability characteristics of the composite
When conducting the composite permeability test on-site, we used slurry (taking tailings slag as raw material) pumps to fill 20 m × 4 m mold bags, and the seepage water was measured by a water meter. The specific test plan is as follows (Figure 3):
3.1.1 Experimental preparation
(1) Before sampling, use the sample bucket to sample 40 samples in situ;
(2) Sew the geotextile into a bucket bag with a bag length of 1,000 mm and a width of 800 mm.
3.1.2 Experimental body stacking
(1) Level the test site, and then lay geomembrane to collect seepage water;
(2) Divide the tailings sample into several equal parts with a bench scale, each 52.45 kg of tailings;
(3) Pour the tailings into the mixing tank, add 11.65 kg of water to the tailings;
(4) Pour the prepared tailings slurry into the geotextile bag; start the timer at the same time.
(5) Seal the geotextile bag and place it horizontally;
(6) In the process of horizontal placement, the water seepage amount of the complex per unit time is collected through the geomembrane;
(7) Repeat steps 3–5 to bag the slurry, spread it out, and stack it in layers. There are 4 layers in total in this experiment.
(8) After the complex is built up, it is left to stand for dehydration, and the test is carried out.
Figure 4A shows the variation in porosity with time for composites of different heights (taking the average value of multiple measurements). The rate of decrease in the void ratio of composites with different heights is not the same. Under the action of self-gravity, the void ratio of the upper part of the composite is slightly higher than that of the lower part of the composite.
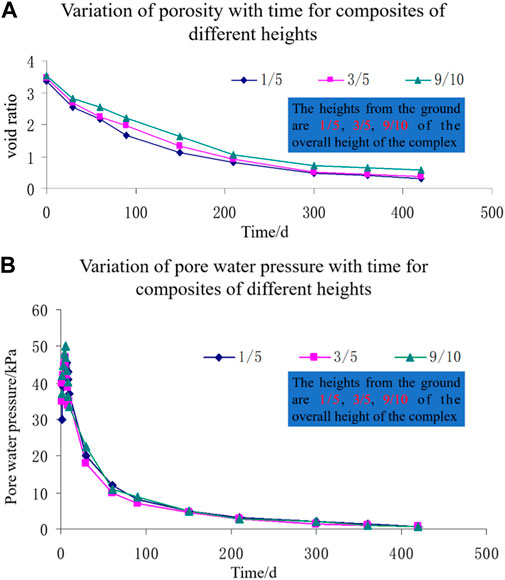
FIGURE 4. Variation curve of porosity and pore water pressure; (A) Variation of porosity with time for composites of different heights; (B) Variation of pore water pressure with time for composites of different heights.
Figure 4B shows the variation in pore water pressure with time for composites of different heights (taking the average value of multiple measurements). The pore water pressure at the bottom of the complex is higher than that at the top. This shows that the greater the external force applied to the complex, the faster the complex is excreted. External pressure aids in the drainage of the complex.
Based on the above analysis and experimental phenomena, we can conclude the following:
(1) In the absence of packing pressure, the flow regime of water passing through the composite is very close to laminar flow. In the later stage, the water permeability of the composite decreases obviously with the increasing sand filling amount. However, the permeability of the composite will gradually increase under the action of filling pressure or external vibration force. When it increases to a certain value, the permeability of the composite gradually decreases and finally tends to be stable.
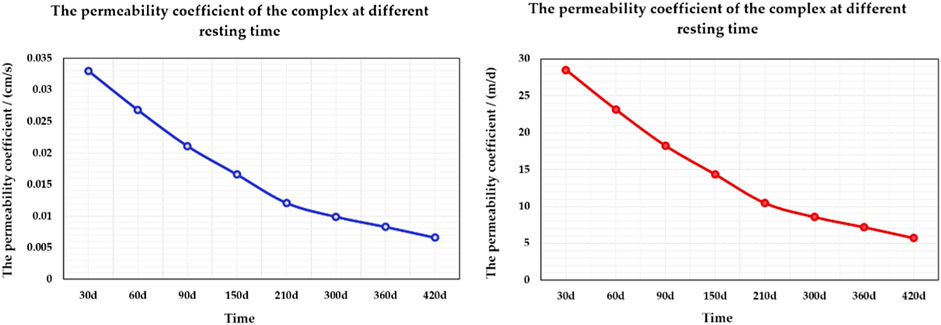
(2) In the early stage of filling, the permeability coefficient of the composite body is relatively large; as the tailings in the composite body are consolidated, the water content decreases, and the reverse filter layer is gradually formed near the geotextile. The permeability coefficient of the composite body gradually decreases (Figure 5). After the tailings are consolidated, the permeability of the composite is very weak and even becomes a relative water barrier.
3.2 Research on the physical and mechanical properties of the composite
In this study, the tailings-geotextile composite is a composite material composed of geotextile and tailings. Zhang et al. (2012) conducted a triaxial numerical simulation of the shear strength of the composite, Zhu et al. (2013) studied the interfacial friction strength characteristics of the composite woven bag, and Qin and Fu (2016) conducted a consolidation test of the composite (the above research is the source of some basic data of this paper). This leads to the following conclusions.
The physical and mechanical properties of the composite show the characteristics of the tailings-geotextile composite material. The deformation of the same composite decreases with the increasing strength of the geotextile. The strength of the composite increases gradually with increasing consolidation time. However, the geotextile has a limited effect on the increase in the internal friction angle of the composite, and it has a greater effect on the increase in cohesion. The effect of geotextiles on improving the shear strength of tailings sand is mainly reflected in increasing the “cohesion” of tailings, while the friction angle remains unchanged.
3.3 Model research
From the engineering characteristics of the tailings geotextile composite dry heap, the composite can be generalized into the following three models during stability analysis (Zhang, 2019):
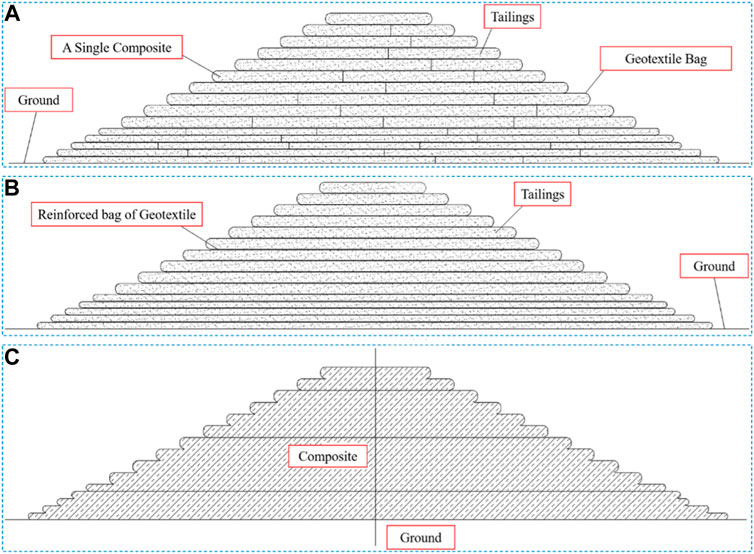
3.3.1 Masonry model
The composite is layered and superimposed by tailings and geotextiles at different times. The composite has the characteristics of layering. The entire composite can be regarded as a single filling body. (Figure 6A). The model needs to know the physical and mechanical parameters, infiltration parameters, friction parameters between monomers, foundation parameters, and environmental parameters of a single dry stack during composite analysis.
3.3.2 Reinforcing model
The reinforcement model is to generalize the tailings in the composite into a whole (if there are areas with different physical and mechanical properties, the composite can be divided according to the properties), and the geotextile in the composite is generalized into the reinforcement of the tailings, that is, reinforcement (Figure 6B). The model needs to know the physical and mechanical parameters of tailings and geotextiles, infiltration parameters, grip performance parameters, foundation parameters, and environmental parameters between tailings and geotextiles during composite analysis.
3.3.3 Overall model
The overall model is to generalize the composite into an enhanced “tailings body”. If the complex is homogeneous, it can be generalized as a whole; if there are regions with different physical and mechanical properties, the complexes with the same properties can be divided into a region and then combined into a whole (Figure 6C). When analyzing the model, it is necessary to know the physical and mechanical parameters, infiltration parameters, foundation parameters, and environmental parameters of the complex.
It is theoretically feasibleanalyzelyse and compare the above three models and can be selected according to the known conditions in the specific analysis. Using the first and third models, a large number of medium-sized composite material tests need to be done before the analysis and calculation. For example, considering the time strength, the test volume is larger and more complicated. Generally, it is difficult to have the required model before design. Parameters can only be designed based on empirical data. When using the second model, only some small experiments are needed, and the analytical parameters are easier to obtain.
4 Numerical simulation analysis of composite seepage
4.1 Overview
The seepage of the tailings-geotextile composite dry heap is mainly divided into two stages: the construction stage and the storage stage. In these two phases, in addition to the same boundary conditions of groundwater source recharge and rainwater recharge, they are also recharged by the construction water source on the upper part of the complex during the construction phase.
Both rainfall and construction water supply are intermittently supplied, and a large number of experimental studies show that intermittent water supply makes the medium in a saturated-unsaturated state. Studies have shown that the stability of the slope is greatly influenced by the internal groundwater (infiltration line or saturation zone). Therefore, it is necessary analyze lyse and studies the changes in water in the composite.
Due to the nonlinearity of the governing equations of saturated-unsaturated seepage, the complexity of the solution domain boundary, and the wide application of electronic computers, numerical methods have become the dominant method for solving saturated-unsaturated seepage fields. To ensure the solution accuracy of the numerical method, it is necessary to establish a suitable saturated-unsaturated mathematical and physical model according to the actual situation.
In porous media, the motion law of saturated water generally conforms to Darcy’s law (Gray and O’Neill, 1976; Whitaker, 1986). According to Darcy’s law, the basic equation of unsaturated seepage in a continuum can be extended to Eq. 1.
θ—the volumetric moisture contentt—timeH—the total head, H = h + zz—the position headh—pressure headK—the permeability coefficientx, y, z—the coordinates
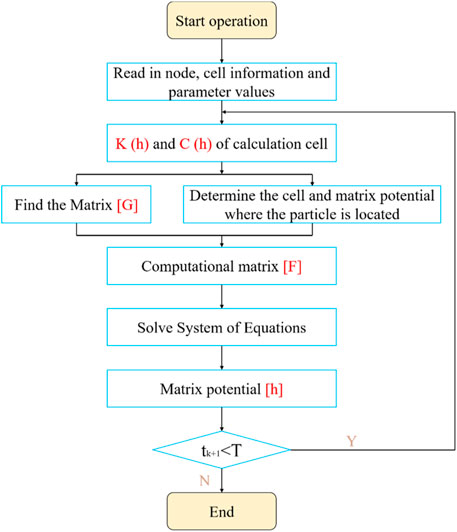
This equation is a basic equation with matrix potential having the dependent variable. In the specific operation, it is solved according to the characteristic finite element principle. The block diagram of the finite element program is shown in Figure 7.
4.2 Basic parameters for the numerical simulation of composite seepage
4.2.1 Model size
The composite size is shown in Figure 8A. The height of the pile is 40 m, the slope ratio is 1:2, and the height of a single bag of the complex is 1.0 m. It takes 30 days to pile up 0∼4.0, 4.0∼8.0, 8.0∼12.0 m, and 12∼16.0 and 16.0 m, respectively. It takes 60 days for each of ∼22.0 m, 90 days for 22.0∼28.0 m, and 60 days for 28.0∼34.0 and 34.0∼40.0 m.
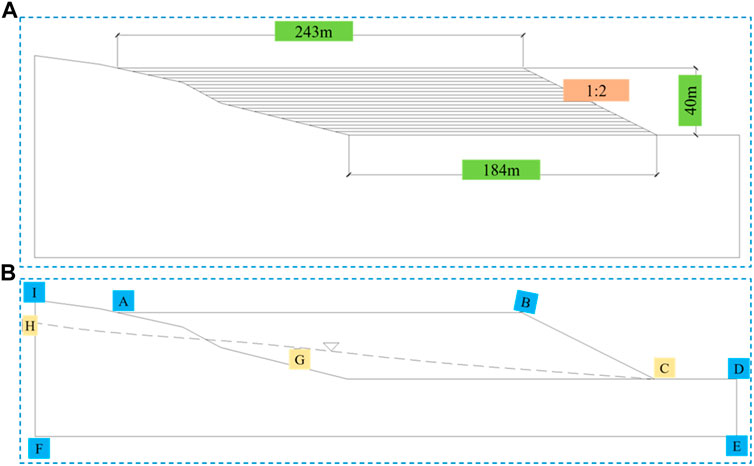
FIGURE 8. Basic parameters for numerical simulation of composite seepage; (A) Schematic diagram of the assumed composite geometry; (B) Schematic diagram of hypothetical complex hydrogeological boundary conditions.
4.2.2 Boundary conditions
The hydrogeological conditions of the complex are shown in Figure 8B. D-E-F-H-I is the flow boundary, I-A-B-C-D is the rainfall infiltration boundary, where B-C-D is the boundary of the saturated escape surface, and the dotted line H-G-C is the saturated infiltration water surface formed by groundwater, the upper part is the unsaturated area, and the lower part is the saturated area.
4.2.3 Calculation parameters
The permeability coefficients of the composite at different times are shown in Figure 5. In the analysis, the foundation permeability coefficient is assumed to be 5e-7 cm/s, that is, it is assumed to be a relative water barrier. The permeability coefficient of the geotextile is taken as the permeability coefficient of sample A: 1.02e-2 cm/s. In this analysis, the rain intensity is 0.22 mm/min, and the water replenishment intensity of the upper construction is 38.6 m3/d/m, that is, the water replenishment intensity is 26.79 mm/min. The impact of groundwater was not considered in the study.
4.3 Numerical simulation results and analysis
The study simulated the changes in the saturation zone of the hypothetical complex at 30, 60, 90, 150, 210, 300, 360, and 420 days. The simulation results are shown in Figure 9.
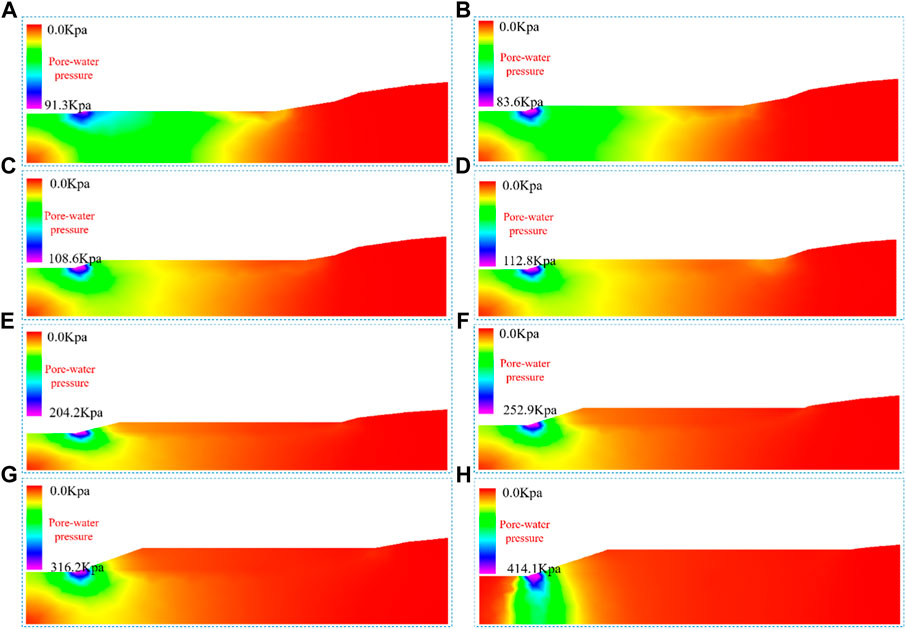
FIGURE 9. Simulation results of infiltration lines of composites at different times and heights; (A) 30 days of stacking (stacking height 4 m); (B) 60-days stacking (stacking height 8 m); (C) 90-days stacking (stacking height) 12 m high); (D) 150 days (height 16 m); (E) 210 days (height 22 m); (F) 300 days (height 28 m); (G) 360 days (height 34 m); (H) 420 days of stacking (height 40 m).
According to the process of composite dry stacking, the composite is mainly supplied by slurry water and rainwater during the construction and storage stages. When there is no direct water supply around the composite, the saturated-unsaturated theory can be used to simulate and analyze the water movement in the composite (Srivastava and Yey, 1991; Diersch and Perrochet, 1999; He et al., 2015).
From Figures 9A–H, it can be seen that under the action of only rainwater and slurry water, the following rules exist:
(1) In the initial stage of stacking, due to the large permeability coefficient of tailings and the small height of the complex, the relative position of the saturated zone is relatively high;
(2) With time, the composite body increases continuously, the lower composite body gradually consolidates, its permeability coefficient gradually decreases, almost becomes an impermeable layer, and the saturated zone gradually rises; when the stacking is stopped, due to the lack of a water source in the upper part Replenishment, the saturation zone gradually declines until it is close to the original position.
(3) When rainwater or slurry water is continuously replenished, seepage water or rainwater gathers from the surface of the lower complex to the bottom of the slope. If there is no drainage channel at the bottom of the slope, it accumulates at the bottom of the slope, and the water flow at the bottom of the slope infiltrates in a near-vertical direction.
In other words, when the permeability coefficient of tailings in the complex is large, the relative position of the infiltration line is high (Kansoh et al., 2020); as the dam body continues to rise, the lower complex is gradually consolidated, and its permeability coefficient gradually decreases, and the lower part is almost impermeable, the infiltration line is gradually raised; when the stacking is stopped, due to the lack of water supply in the upper part, the infiltration line gradually decreases until it is close to the original infiltration line (Shakesby and Whitlow, 1991; Chen et al., 2011). When rainwater or slurry water is continuously replenished, seepage water or rainwater gathers from the surface of the lower complex to the bottom of the slope. In the absence of a drainage channel at the bottom of the slope, it accumulates at the bottom of the slope, and the water flow at the bottom of the slope infiltrates in a near-vertical direction. According to the above research results, the influence of groundwater may not be considered in the overall stability analysis of the composite (Čarman et al., 2014).
5 Stability studies
5.1 Basic assumptions and methods of analysis
5.1.1 Basic assumption
In Section 2, composites are generalized into masonry, comprehensive and reinforced models according to their properties. Since the complex is filled with tailings and nonrigid bodies, it is difficult to model mathematically when generalized as a masonry model. Therefore, the composite is generalized into a reinforced model and an overall model for stability analysis in this study.
For the above model, the following assumptions were made in the analysis:
(1) The single composite is very long, and the layered height is not large, less than 3 m, which simplifies the stability as a two-dimensional plane problem;
(2) Generalize the complex of each stage (including the final stage) into a tailings heap;
(3) The geotextiles are generalized as reinforcement, and the tensile strength of the reinforcement is twice the tensile strength of the single-layer; the vertical spacing of the reinforcement is the layer height, and the horizontal spacing is zero;
(4) The geotextile wraps the layered tailings. We assume that the anchoring force of the tendon is greater than the gripping force between the tailings and the geotextile and consider a single composite as a whole;
(5) The strengthening effect of the geotextile at the end of the composite body on the tailings is used as a safety reserve, and its influence is not considered in the stability calculation;
(6) The influence of the foundation on the composite is not considered, that is, the foundation is considered to be free from deformation and damage;
(7) Does not consider the effect of groundwater on the stability of the complex;
(8) The effect of horizontal thrust on the complex is not considered;
(9) In practical engineering, the effects of (6) and (7) should be considered. When the dry pile is used as a dam body or retaining wall, the influence of (8) should be considered, and the problem of foundation settlement should also be considered;
(10) In this study, in addition to the above assumptions, the assumptions and applicable conditions of specific calculation methods are also met.
5.1.2 Methods of analysis
There are many methods for slope stability analysis, such as the limit equilibrium method, numerical analysis method, stochastic analysis method, and fuzzy analysis method (Hu et al., 2021; Zhang et al., 2022). However, the specification adopts the most widely used limit equilibrium method, so this study adopts the Swedish slice method with similar assumptions to analyze the stability of the complex.
5.2 Basic parameters
5.2.1 Geometric model and parameters
The geometric model, process, and parameters are shown in Section 4.2 and Figure 8A.
5.2.2 Constraints
Constraints see basic assumptions.
5.2.2 Physical and mechanical parameters
The tailings-geotextile composite is shown in Table 1, and the tensile strength of the geotextile is 19 kN/m. The shear strength comparison of pure tailings and tailings geotextile composites is shown in Figure 10.
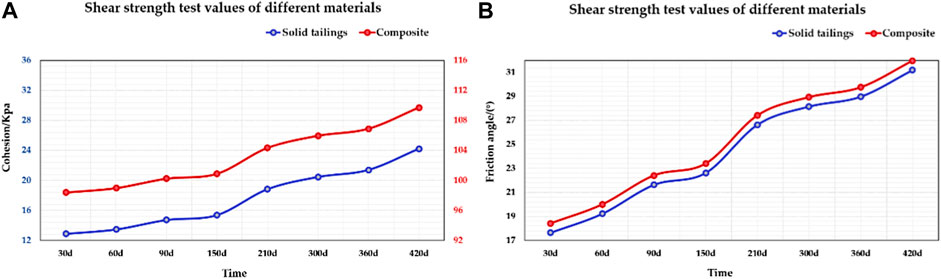
FIGURE 10. The shear strength comparison of pure tailings and tailings geotextile composites; (A) cohesion test values of different materials; (B) friction angle test value of different materials.
When calculating and analyzing, there are two ways to set the physical and mechanical parameters of the composite dry stack:
(1) The parameters of the tailings and the geotextile are set separately; that is, the geotextile is generalized into the reinforcement in the tailings body and then substituted into the respective physical and mechanical parameters.
(2) Mixing settings according to the composite parameters, that is, substituting the comprehensive physical and mechanical parameters of the mixture.
5.3 Stability calculation results and analysis
According to the previous assumptions, we study and analyze the stability of the composite model at different times and heights (the overall algorithm and the reinforcement algorithm). The law of composite height and safety factor with consolidation time is shown in Figure 11.
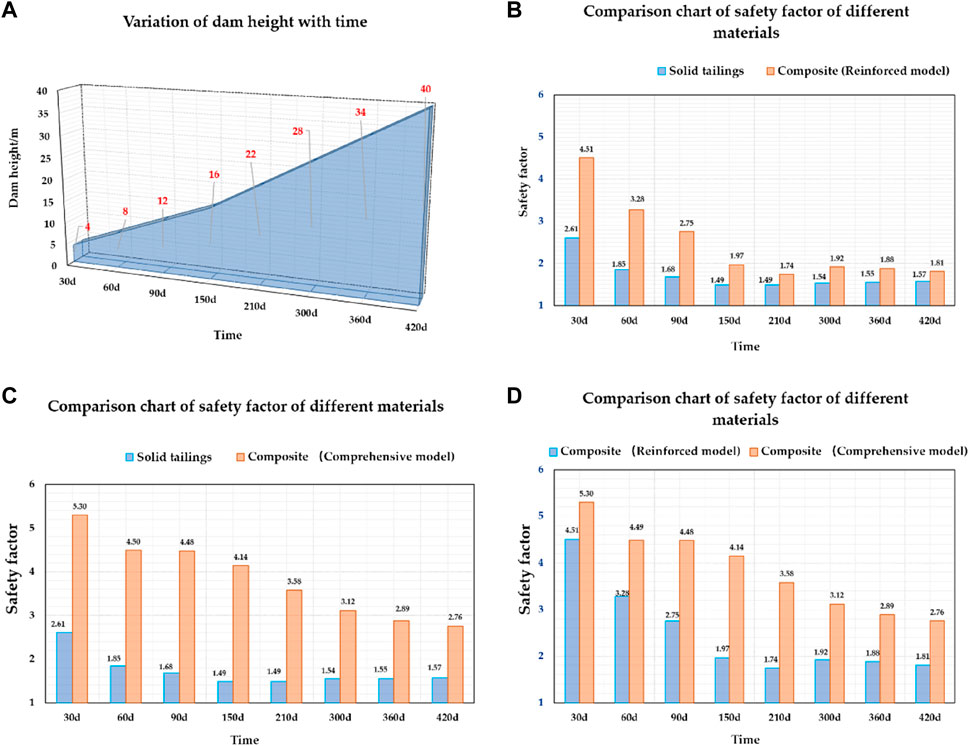
FIGURE 11. Variation in the safety factor with time and dam height; (A) Variation of dam height with time; (B) Comparison chart of safety factor for solid tailings and composite-reinforced model; (C) Comparison chart of safety factor for solid tailings and composite-comprehensive model; (D) Comparison chart of safety factor for composite-reinforced model and composite-comprehensive model.
Figure 11 shows the following:
(1) During the stacking process of the complex, its safety and stability change with time and height; in the initial stage of stacking, with the increase in stacking height, the safety factor of the composite decreases rapidly, and the decreasing speed decreases at approximately 180 days. After 210 days (the stacking height is 22.0 m), the left and right sides are reduced to their minimum values. If the stacking is stopped at this time, the stability of the composite will gradually increase until it is stable. Therefore, the use of spaced stacking helps to enhance the stability of the composite.
(2) Under the condition of equal consolidation, the composite body has better stability than the pure tailings dry heap.
(3) Due to the limitation of assumptions, experimental data, and environmental conditions, the safety factor of the composite calculated by the reinforcement model is more conservative than the calculation result of the overall model. Experimental study of physical and mechanical properties.
6 Conclusion
This paper studies the overall stability of a tailings composite dry stack. It can be concluded that:
(1) The materials (tailings, geotextiles) that make up the composite and its stacking process have a great influence on the permeability of the composite. The general rule is that in the early stage of composite stacking, the permeability coefficient of the composite body increases with increasing filling tension; in the later stage, it gradually decreases until it is stable.
(2) The numerical simulation analysis of the seepage field of the complex shows that in the early stage of complex stacking, although the tailings permeability coefficient in the complex is large, the relative position of the saturated zone is relatively high due to the low height of the complex; with the continuous rise of the composite or the increase of the stacking time, the lower part almost becomes an impermeable layer, and the position of the saturated zone gradually increases; when the stacking is stopped, due to the lack of water supply in the upper part, the saturation zone gradually decreases until it is close to the original position.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
Drafting of manuscript: YZ and CY; planning and supervision of the research: JJ and SH; analysis and interpretation of data: XH; acquisition of data: XW; Model construction: TZ.
Funding
The work was supported by the Major science and technology projects of Anhui Province (No.201903a07020008) and the Transportation Science and Technology Project Foundation of Fujian Provincial (No.201911).
Conflict of interest
Author YZ, XW, and CY were employed by Sinosteel Maanshan General Institute of Mining Research Co., LTD, China.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We also thank Xiao Gu for their assistance in the test. Finally, we would like to thank the handling editor and reviewers whose valuable and constructive comments greatly improved this article.
References
Cao, G., Wang, W., Yin, G., and Wei, Z. (2019). Experimental study of shear wave velocity in unsaturated tailings soil with variant grain size distribution. Constr. Build. Mater. 228, 116744. doi:10.1016/j.conbuildmat.2019.116744
Čarman, M., Jemec Auflič, M., and Komac, M. (2014). Landslides at a uranium mill tailing deposit site Boršt (Slovenia) detected by radar interferometry. Landslides 11, 527–536. doi:10.1007/s10346-013-0454-9
Chen, R., Zhang, B. Z., Lei, W. D., and Luo, W. B. (2011). Response of soil suction to heavy rainfalls in a tailings dam. Adv. Mat. Res. 250–253, 1681–1685. doi:10.4028/www.scientific.net/amr.250-253.1681
Chen, X., Zhang, J., and Li, Z. (2014). Shear behaviour of a geogrid-reinforced coarse-grained soil based on large-scale triaxial tests. Geotext. Geomembranes 42, 312–328. doi:10.1016/j.geotexmem.2014.05.004
Chen, S., Zheng, Y., Wang, C., and Hsu, T. Y. (2015). A large-scaletest on overtopping failure of two artificialdams in Taiwan. Eng. Geol. Soc. Territ. 2, 1177–1181. doi:10.1007/978-3-319-09057-3_206
Diersch, H.-J. G., and Perrochet, P. (1999). On the primary variable switching technique for simulating unsaturated-saturated flows. Adv. Water Resour. 23, 271–301. doi:10.1016/S0309-1708(98)00057-8
Duan, W., Guo, J., and Wang, B. (2013). Stacking process of metal mine tailings in China and its development trend. Metal. Mine 12, 118–122.
Gray, W. G., and O’Neill, K. (1976). On the general equations for flow in porous media and their reduction to Darcy’s Law. Water Resour. Res. 12, 148–154. doi:10.1029/WR012i002p00148
He, W., Shao, H., Kolditz, O., Wang, W., and Kalbacher, T. (2015). Comments on “A mass-conservative switching algorithm for modeling fluid flow in variably saturated porous media, K. Sadegh Zadeh, Journal of Computational Physics, 230 (2011)”. J. Comput. Phys. 295, 815–820. doi:10.1016/j.jcp.2015.04.019
Hu, Q., Wu, Y., Miao, F., Zhang, L., and Li, L. (2021). Stability analysis of concave slope based on Mein-Larson infiltration model. Chin. J. Geol. hazard control 32, 26–35. doi:10.16031/j.cnki.issn.1003-8035.2021.06-04
Kansoh, R. M., Elkholy, M., and Abo-Zaid, G. (2020). Effect of shape parameters on failure of earthen embankment due to overtopping. KSCE J. Civ. Eng. 24, 1476–1485. doi:10.1007/s12205-020-1107-x
Khaniki, A. K., and Daliri, F. (2013). Analytical and experimental approaches to obtain the ultimate strength of reinforced Earth elements. KSCE J. Civ. Eng. 17, 1001–1007. doi:10.1007/s12205-013-0181-8
Khedkar, M. S., and Mandal, J. N. (2009). Behaviour of cellular reinforced sand under triaxial loading conditions. Geotech. Geol. Eng. (Dordr). 27, 645–658. doi:10.1007/s10706-009-9264-1
Koerner, R. M. (2000). Emerging and future developments of selected geosynthetic applications. J. Geotech. Geoenviron. Eng. 126, 293–306. doi:10.1061/(asce)1090-0241(2000)126:4(293)
Li, Q., Geng, J., Song, D., Nie, W., Saffari, P., and Liu, J. (2022). Automatic recognition of erosion area on the slope of tailings dam using region growing segmentation algorithm. Arab. J. Geosci. 15, 438. doi:10.1007/s12517-022-09746-4
Liu, L., Wang, W., Chu, C., and Chi, J. (2002). Study on relation between pore size distribution and permeability of nonwoven geotextile. J. Qingdao Univ., 48–52. doi:10.13306/j.1006-9798.2002.01.014
Liu, L., Zhang, H., Zhong, D., and Miao, R. (2014). Research on tailings dam break due to overtopping. J. Hydraulic Eng. 45, 675–681. doi:10.13243/j.cnki.slxb.2014.06.006
Nouri, S., Nechnech, A., Lamri, B., and Lopes, M. L. (2016). Triaxial test of drained sand reinforced with plastic layers. Arab. J. Geosci. 9, 53. doi:10.1007/s12517-015-2017-y
Pincus, H., Bathurst, R., and Karpurapu, R. (1993). Large-scale triaxial compression testing of geocell-reinforced granular soils. Geotech. Test. J. 16, 296. doi:10.1520/GTJ10050J
Qin, K., and Fu, K. (2016). Application of tailings geotextile composite in the treatment of a tailings pond. Mod. Min. 32, 214–215.
Rahardjo, H., Lee, T. T., Leong, E. C., and Rezaur, R. B. (2005). Response of a residual soil slope to rainfall. Can. Geotech. J. 42, 340–351. doi:10.1139/t04-101
Shakesby, R. A., and Whitlow, J. R. (1991). Failure of a mine waste dump in Zimbabwe: causes and consequences. Environ. Geol. Water Sci. 18, 143–153. doi:10.1007/BF01704668
Srivastava, R., and Yey, T. C. J. (1991). Analytical solutions for one-dimensional, transient infiltration towards the water table in homogeneous and layered soils. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 28, A350. doi:10.1016/0148-9062(91)91285-Y
Wang, W., Cao, G., Li, Y., Zhou, Y., Lu, T., Wang, Y., et al. (2022). Experimental study of dynamic characteristics of tailings with different reconsolidation degrees after liquefaction. Front. Earth Sci. (Lausanne). 10. doi:10.3389/feart.2022.876401
Whitaker, S. (1986). Flow in porous media I: a theoretical derivation of Darcy’s law. Transp. Porous Media 1, 3–25. doi:10.1007/BF01036523
Wu, J., Li, L., and Wang, J. (2022). Dynamic shear characteristics of interface between different geosynthetics and recycled concrete aggregate. J. Vib. Shock 41, 279–287. doi:10.13465/j.cnki.jvs.2022.01.035
Yang, C., Zhang, C., Li, Q., Yu, Y., Ma, C., and Duan, Z. (2021). Disaster mechanism and prevention methods of large-scale high tailings dam tailings geotextiles woven bags. Rock Soil Mech. 42, 1–17. doi:10.16285/j.rsm.2020.1653
Zhang, M., Zhou, Y., Xu, C., and Cao, Z. (2012). True triaxial numerical experiment of tailing geotextile compound in an lron mine. Metal. Mine 11, 132–134.
Zhang, Z., Lin, Y., He, H., Zhang, H., and Yang, G. (2022). Instability characteristics and stability analysis of expansive soil slope. J. Central South Univ. Sci. 53, 104–113. doi:10.11817/j.issn.1672-7207.2022.01.006
Zhang, L. (2019). Multi-scale Analysis of mechanical properties of textile geotextiles reinforced tailing sand. Liaoning Technical University, MA thesis. doi:10.27210/d.cnki.glnju.2019.000040
Zhao, Y., Jing, X., Zhou, X., Cai, Z., and Liu, K. (2016). Experimental study on blocking action of bar strip on tailings dam overtopping. China Saf. Sci. J. 26, 94–99. doi:10.16265/j.cnki.issn1003-3033.2016.01.016
Keywords: tailings-geotextile composites, tailings dam, seepage characteristics, numerical simulation, stability
Citation: Zhou Y, Ji J, Hu X, Hu S, Wu X, Yuan C and Zhu T (2022) Comprehensive analysis of the stability of tailings-geotextile composite—Iron Mine Tailings Dam in Gushan, Anhui, China. Front. Earth Sci. 10:931714. doi: 10.3389/feart.2022.931714
Received: 29 April 2022; Accepted: 08 July 2022;
Published: 26 August 2022.
Edited by:
Haijun Qiu, Northwest University, ChinaReviewed by:
Wensong Wang, Chengdu University of Technology, ChinaLei Wang, Ludong University, China
Wei Lu, Shandong University, China
Copyright © 2022 Zhou, Ji, Hu, Hu, Wu, Yuan and Zhu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Canming Yuan, MzE4NzgwNTk5MUBxcS5jb20=
 Yuxin Zhou1,2
Yuxin Zhou1,2 Xuelong Hu
Xuelong Hu Canming Yuan
Canming Yuan