Raindrop size distribution characteristics in summer of a nival glacial zone in eastern Tianshan, Central Asia

Precipitation is a key component of the hydrological cycle, which is critical to understanding its formation and evolution. In this study, based on the observation data of the PWS100 located at the meteorological observation site at the terminal of Urumqi Glacier No. 1, eastern Tianshan Mountains, the statistical characteristics of the summer raindrop size distribution (DSD) were analyzed, and the DSD characteristics of five different rainfall rates(R) and two rainfall types (convective and stratiform) were investigated for the daytime and nighttime. The average raindrop spectral width was the largest in class III (1 < R < 5 mm h⁻¹). The result showed that the raindrop concentration increased with the rainfall rate. The maximum raindrop concentration was at class IV (5 < R < 10 mm h⁻¹), when the raindrop diameter was higher than 1.74 mm. The small and medium size raindrops played a dominant role in precipitation composition in the head watershed of the Urumqi River, contributing 98% of the total raindrop. The convective precipitation at the headwaters was divided into continental clusters. The stratiform/convective D_m-log₁₀N_w was characterized by a large mass-weighted mean diameter D_m = 1.523/2.608, and a generalized intercept log₁₀N_w = 2.841/3.469. N(D) of convective precipitation was significantly different between the daytime and nighttime, while that of stratiform precipitation was almost the same. The constraint relationship between R-D_m and R-log₁₀N_w of these two precipitation types was deduced, the exponent of the R-log₁₀N_w relationship of the two precipitation types was negative, and the D_m value of stratiform precipitation tended to be stable at a higher rainfall rate (1–2 mm). Finally, we deduced the power-law relationship between radar reflectivity (Z) and rain rate (R) [Z = A*R^b] for stratiform and convective precipitation at the headwaters. Z = 698.8R^2.0 was for stratiform, and Z = 47.1R^2.0 was for convective. These results, for the first time, offer insights into the microphysical nature of precipitation in the head watershed of the Urumqi River during the summer and provide essential information that could be useful for precipitation retrievals based on weather radar observations.

Introduction

Precipitation is one of the most active elements in the atmosphere and plays an important role in various atmospheric processes (Liu and Fu., 2007). Moreover, it is crucial in hydrothermal conditions on a basin scale. In addition, it is an indispensable input parameter in research such as climate analysis, water resource evaluation, water cycle, water balance, and hydrological model (Yang et al., 1992; Liu et al., 2011). Over the past few years, the spatial and temporal distribution of precipitation in large-scale climate models made huge improvements (Liepert and Previdi., 2012; Climate change, 2013). Since the properties of precipitation vary on a small scale usually smaller than the model’s resolution, there was still a lack of confidence in the representation of the precipitation and related microphysical processes in these climate models (Stocker et al., 2013). The instruments such as radar and disdrometers can provide a great opportunity to address this problem by characterizing the spatiotemporal variability of precipitation with the high resolution (Penide et al., 2013a; Giangrande et al., 2014). The microscale structure of precipitation can be characterized by the raindrop size distribution (DSD), which is a fundamental characterization of precipitation microphysics and an important aspect of precipitation research. The DSD is highly correlated with the bulk microphysical properties of precipitation (liquid water content W, rainfall rate R, radar reflectivity Z, and total number concentration N_t). On the other hand, DSD specifies the expected number of raindrops per unit of size (diameter) interval and per unit volume of air, which attributes to the comprehension of the mechanisms at upper levels (Caracciolo et al., 2006; Uijlenhoet and Torres., 2006; Adirosi et al., 2015). The DSD study established quantitative precipitation estimation (QPE) algorithms for radar measurements through radar reflectivity (Z), rain rate (R) relations [Z = A*R^b] and played a significant role in improving microphysical parameterization in modeling studies (Ryzhkov and Zrnić., 1995; Fadnavis et al., 2014; Tapiador et al., 2014; Wainwright et al., 2014; Boodoo et al., 2015; McFarquhar et al., 2015; Ji et al., 2019). In addition, three-parameter gamma distribution has been used in the rainfall estimation algorithms of the Tropical Rainfall Measuring Mission (TRMM) precipitation radar (Iguchi et al., 2000; Kozu et al., 2009) and in the Global Precipitation Measurement (GPM) Dual-frequency Precipitation Radar (DPR) (Nakamura and Iguchi., 2007; Hou et al., 2008; Liao et al., 2014; Dolan et al., 2018; Petersen et al., 2018; Yamaji et al., 2018).

Over the last several decades, many studies have been carried out on the characteristics of DSD distribution. Characteristics of the DSD distribution were found to vary with climate types, topographic conditions, geographical location (ocean vs. land) and precipitation types (Tokay and Short., 1996; Bringi et al., 2003; Penide et al., 2013b; Kumar and Reddy., 2013; Porcù et al., 2014; Jameson et al., 2015; Janapati et al., 2017; Seela et al., 2017). Tokay and Short (1996) analyzed the overall rainfall parameters of tropical rainfall by using the gamma distribution fitting experiment DSD and put forward the judgment basis for distinguishing the convective and the stratiform type. Caracciolo et al. (2006) improved this method by applying higher-order DSD moments to mid-latitude regions. Kim et al. (2022) analyzed the difference in the microphysical development characteristics of orographic rainfall between the windward and leeward slope of a mountain, and found that the number concentration of raindrops smaller than 1 mm was relatively lower in mountainous areas, compared to low-altitude coastal areas and adjacent areas. DSD variations in easterly and westerly monsoon wind regimes of an oceanic station at Palau islands were inspected by Krishna et al. (2016), and they revealed profound differences in microphysical characteristics between these two seasons. The characteristics of the DSD on the Tibetan Plateau using the raindrop spectrum data collected in Lhasa (3,600 m a.s.l) and Nyingchi (3,300 m a.s.l) during the rainy season in 2010 was studied by Porcù et al. (2014), and found that the collision rupture of precipitation occurred at relatively low rainfall rates. Moreover, the DSD characteristics of Naqu (4,500 m a.s.l) and Motuo (1,275 m a.s.l) in the hinterland of the Tibetan Plateau had shown that the shape of the average DSD under different rainfall rates was similar and the concentration of large raindrop number increased with the increase of rainfall intensity (Chen et al., 2017; Wang et al., 2021), and the DSD exhibit little variance during the daytime and nighttime for stratiform precipitation, with large variance for convective precipitation (Chen et al., 2017). Mao et al. (2022) studied the DSD characteristics of Qilian mountains on the southern slopes, northern slopes and inside, and found that the number concentration of small and large raindrops on the inside and south slope were greater than on the north slope, but midsize raindrops were fewer. The DSD spectrum of inside mountains was more variable and significantly differ from the north slopes. Tang et al. (2014) compared the DSD characteristics of stratiform and convective precipitation in different climate regions (including North China, South China, the Loess Plateau, and Mongolian Plateau transition zone), and the results further confirmed the existence of DSD had significant differences in different climate regions with different precipitation types. Wen et al. (2017) studied the DSD characteristics of summer and winter precipitation in the North China Plain, and pointed out that with the decrease of height, the radar reflectivity of stratiform rainfall increased while liquid water content and rainfall rate decreased, the reason was that the actual drop fall velocity was relative to the ambient air flows in real atmosphere, updrafts could decrease the fall velocity of raindrops, resulting in an underestimation of the drop size. The DSD characteristics of Zhuhai in the southern China studied by Zhang et al. (2019) found that, compared with eastern and northern China, the DSD characteristics of Southern China were relatively small and high concentration of raindrops, and the convective rain in the monsoon season could be identified as a maritime convective cluster.

Although there have been many studies such as those mentioned above, as far as China is concerned, the previous studies on the distribution characteristics of DSD mainly focus on the temperate and subtropical coastal areas of northern, southern, and eastern China and parts of the Qinghai-Tibet Plateau. While in the cold alpine regions, the characteristics of DSD in typical continental glacial regions were poorly studied. The head watershed of the Urumqi River has a complex topography and a cold climate, and snowfall accounts for about 43% of the total summer rainfall. The research in recent years was mainly focused on glacier variation (e.g., mass balance, ice temperature, albedo, etc.) and hydrological processes (Wang et al., 2018; Xu et al., 2018; Xu et al., 2019; Jia et al., 2020a; Wang et al., 2020; Yang et al., 2021; Li et al., 2022). The research on precipitation mainly focused on precipitation calibration (Yang et al., 1988; Yang et al., 1991; Goodison and Metcalfe, 1992; Yang et al., 1998; Ye et al., 2004) and its characteristics (Yang et al., 1992; Li et al., 2007; Li et al., 2011; Liu et al., 2011; Feng et al., 2013; Zhang et al., 2014; Jia et al., 2020b). We have not found any research on the microphysical processes of precipitation. In 2017, we set up the PWS100 present weather Sensor (Agnew and Space, 2013; Johannsen et al., 2020; Zhao et al., 2021) (produced by Campbell Scientific in the meteorological observation field) on the flat moraine ridge at the terminal of Urumqi Glacier No. 1 and collected DSD data for 3 years (2017–2019). This helped us to carry out the present study with principal objectives: 1) analyze the distribution characteristics of DSD and integral rainfall parameters of summer precipitation in the source region of the Urumqi River. 2) Establish a range of D_m and log₁₀N_w values for the maritime and continental cluster by measuring large-scale DSD characteristics, 3) classify summer precipitation into stratiform and convective types, and 4) derive power-law relationships for radar reflectivity (Z) and rainfall rate (R), compare with Z-R in other regions and analyze the differences.

Instruments and methods

Observation site

The observation site (43.12°N, 86.82°E, 3 835 m a.s.l) is located in the source area of the Urumqi River in the southeastern part of the Tianshan Mountains in the central region of Asia. There are seven glaciers in the head watershed region, among which the Urumqi Glacier No. 1 (43°06′N, 86°49′E) is the largest, and it is the “reference glacier” of the World Glacier Monitoring Service (WGMS) in the arid regions of Central Asia and one of the ten major modern glaciers monitored globally (Li et al., 2010). Annual precipitation is about 468 mm on average, the summer season contributed approximately about 77% (Li et al., 2007) (Figure 1).

FIGURE 1

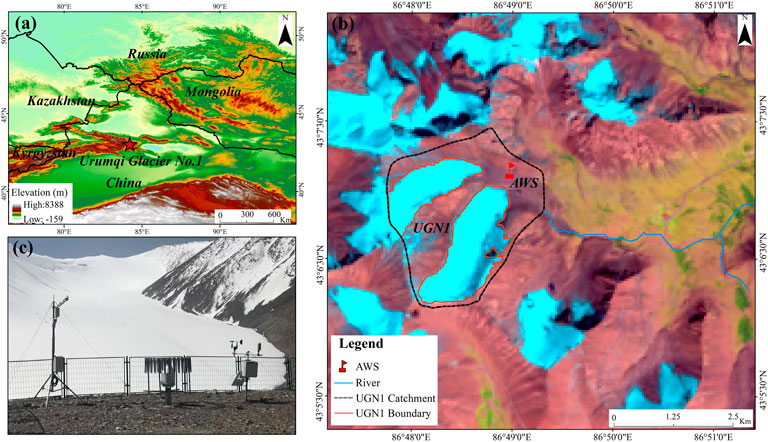
FIGURE 1. In (A) location of the observation site; in (B) AWS means Automatic Weather Station and UGN1 means Urumqi glacier NO.1; and in (C) the instruments in the automatic weather station [AWS in (B)], from left to right are PWS100, T-200b, and Wind monitor.

PWS100 disdrometer and dataset

The DSD data used in this paper were obtained from PWS100 produced by Campbell Scientific (particle diameter, falling velocity and drops count of raindrops). The instrument was installed in the meteorological observation field on the moraine ridge at the terminal of the Urumqi Glacier No. 1, and equipped with Geonor T-200B series precipitation gauges, Young 05103 wind monitor, HC2-S3 temperature and humidity sensor, and other instruments (Figure 1B). Table 1 were meteorological parameters, comparison of precipitation and precipitation days between T-200B and PWS100, the correlation between the two instruments was 0.8. The PWS100 disdrometer observation is based on the laser Doppler measurement principle, which can automatically measure the amount of precipitation and visible meteorological factors. The instrument configuration defines an area of 40 cm² by overlap measurement regions of two detectors. Thus, the PWS100 is capable of classifying precipitation as rain, snow, hail, etc., and it delivers output messages about the type of particles detected. Using advanced detection technology and a fuzzy logic, the PWS100 disdrometer can measure the size and speed of raindrops with an accuracy of 5% (Ellis et al., 2006). The rainfall total resolution was 0.0001 mm, and the accuracy was better than 10% (Campbell Scientific, Inc., 2015). When connected to the air temperature and humidity sensor, making the measurement is more accurate (Ellis et al., 2006). The nominal detection size and velocity of individual particles range from 0.1 to 30 mm and 0.1–30 m s⁻¹, respectively. The outputs are arranged in 34 by 34 size and velocity bins.

TABLE 1

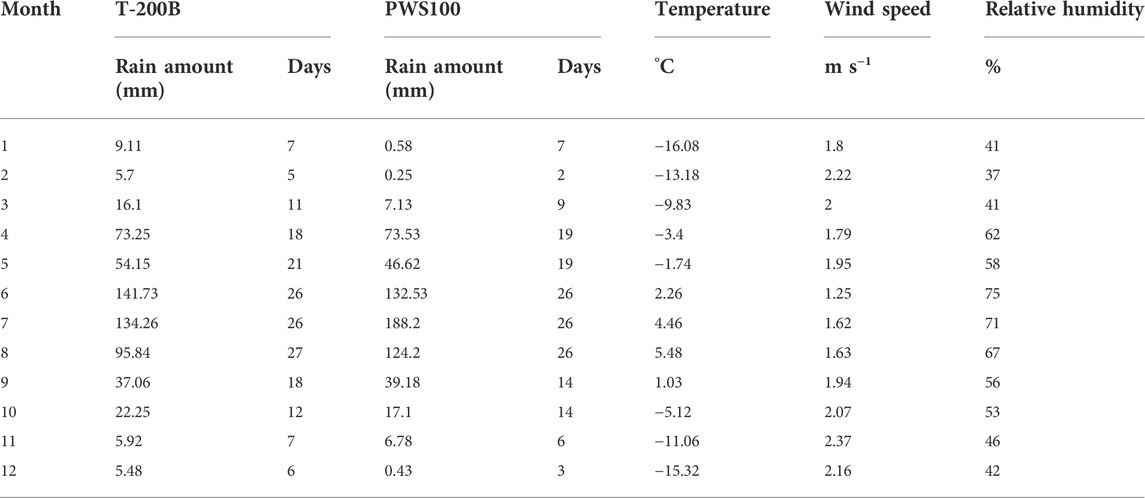
TABLE 1. Meteorological parameters, comparison of rain amount and precipitation days between T-200B and PWS100.

The data selected in this paper were the observation results of the disdrometer in the summer of 2017–2019, with a time resolution of 1 min. When a particle is partially within the beam, it can be misclassified as a small particle that falls faster than other particles observed at that size (Yuter et al., 2006). Moreover, during heavy rains, strong winds and splashes on the surface of the instrument may produce unrealistically slow falling large particles (Friedrich et al., 2013). Therefore, in its built-in algorithm, PWS100 assumes that similar distortions will occur when raindrops fall, and its internal algorithm excludes precipitation particles with abnormal velocity and simultaneously outputs incorrect particle numbers and unknown particle numbers (Campbell Scientific, Inc., 2015). This may result in a low number of raindrops less than 0.4 mm (Montero-Martinez et al., 2009; Montero-Martinez and Eduardo, 2016). To minimize the effects of edge fall, wind, and splash, first, we removed data with minute raindrop counts below 10 and rainfall rates less than 0.1 mm h⁻¹. Secondly, precipitation particles with diameters below 0.45 mm and above 6 mm were excluded. Finally, the disdrometer data with precipitation duration of less than thirty minutes were excluded. After these steps, there must be no precipitation period of at least one hour between each rainfall event to reduce statistical error according to the previous studies (Atlas et al., 1973; Chen et al., 2013; Chen et al., 2016; Tang et al., 2014). The total number of samples available for this study was 40,214.

Methods

The number concentration of raindrops can be obtained by the following equation:

$N\left(D_i\right)={\displaystyle \sum _{j=1}^{34}\frac{n_{ij}}{{\upsilon }_j\cdot S\cdot t\cdot \mathit{\Delta }{\mathit{D}}_{\mathit{i}}}}(1)$

where N(D_i) (mm⁻¹m⁻³) is the number concentration of raindrops per unit volume per unit size interval for raindrop diameter D_i (mm); n_ij is the number of raindrops within the size bin i and velocity bin j; S(m²) and t(s) are the sampling area (set to 40 cm² in this study) and sampling time (set to 60 s in this study), respectively; and v_j (m s⁻¹) is the falling speed for velocity bin j. and ∆D_i (mm) is the interval between the diameter classes. In this study, the falling speed measurements from the PWS100 disdrometer are not used because of measurement error. Instead, the model-based velocity relation proposed by Atlas et al. (1973) as shown in below.

$\upsilon \left(D_i\right)=9.65-10.3\exp \left(-0.6D_i\right)(2)$

The integral rainfall parameters including the liquid water content W (g m⁻³), rain rate R (mm h⁻¹), radar reflectivity factor Z (mm⁶ m⁻³) and total concentration of raindrops N_t (m⁻³) can be derived from N(D_i) as follows.

$W=\frac{\pi }{6}\times {10}^{-3}{\displaystyle \sum _{i=1}^{34}{D}_i^{3}N\left(D_i\right)\mathit{\Delta }{D}_i}(3)$

$\mathit{R=6}\pi \times \mathrm{1}{\mathrm{0}}^{\mathrm{-4}}{\displaystyle \sum _{i=1}^{34}{D}_i^3{V}_{i}N\left(D_i\right)\mathit{\Delta }{D}_i}(4)$

$Z={\displaystyle \sum _{i=1}^{34}{D}_i^{6}N\left(D_i\right)\mathit{\Delta }{D}_i}(5)$

$N_t{\displaystyle \sum _{i=1}^{34}N\left(D_i\right)\mathit{\Delta }{D}_i}(6)$

The three-parameter gamma distribution is the most commonly accepted model for describing the measured raindrop spectra, and it is generally enough to describe the DSD fluctuations observed on small scale and has the capability of describing a broader variation in DSD (Ulbrich and Atlas., 1998), which is expressed as

$N\left(D\right)=N_0{D}^{\mathrm{\mu }}\exp \left(-\Lambda D\right)(7)$

where N₀ is the intercept parameter in a unit of m⁻³ mm^−(1+µ), its related to the total number of rainfall particles; μ is the shape parameter (dimensionless), when μ is above zero, the curve is curved upward, and it is the opposite when the value of μ is below 0; Λ is the slope parameter in a unit of mm⁻¹, which represents the distribution characteristics of particles, and Λ decreases with the increase of rainfall rate, indicating that the number of large raindrops increases with the increase of rainfall rate; D (mm) is the diameter of the raindrop. Due to its ability to proportionally fit the moment of the above integral rainfall parameters, the method of moments (MoM) is considered in this study. In general, the nth moment of the DSD, M_n, is defined as:

$M_n={\displaystyle {\int }_0^{\infty }{D}^{n}N\left(D\right)dD={\displaystyle \sum _{i=1}^{34}N\left(D_i\right){\mathit{D}}_{\mathit{i}}^{\mathit{n}}\mathit{\Delta }{D}_i}}(8)$

Three moments are required to compute the Gamma distribution parameters. In this paper, the third, fourth, and sixth moments are used to calculate the Gamma parameter (Seela et al., 2018; Montero-Martinez et al., 2021; Wang et al., 2021). The 2/4/6 moment is also used to fit Gamma parameters in many studies (Chen et al., 2017; Wen et al., 2017; Zhang et al., 2019). However, Cao and Zhang (2009) showed that there was no significant difference between the 2/4/6 moment estimator and the 3/4/6 moment estimator. The formulas for the three parameters of the Gamma distribution are as follows (Kozu and Nakamura., 1991):

$\mu =\frac{11G-8+\sqrt{G\left(G+8\right)}}{2\left(1-G\right)}(9)$

where,

$G=\frac{M_4^3}{M_3^2{M}_6}(10)$

$\Lambda =\left(\mu +4\right)\frac{M_3}{M_4}(11)$

$N_0=\frac{{\Lambda }^{\mu +4}{M}_3}{\Gamma \left(\mu +4\right)}(12)$

where, Г(x) is expressed as:

$\Gamma \left(x\right)=\sqrt{2\pi }{e}^{-x}{x}^{x-\frac{1}{2}}(13)$

The normalized intercept parameter N_w in the unit of mm⁻¹ m⁻³ and the mass-weighted mean diameter D_m (mm) were defined by Bringi et al. (2003) as:

$N_w=\frac{4^4}{\pi {\rho }_w}\left(\frac{{10}^{3}W}{D_m^4}\right)(14)$

where, ρ_ω (1.0 g cm⁻¹) is the density of the water.

$D_m=\frac{M_4}{M_3}(15)$

Results

Raindrop size distribution properties for the different rainfall rates

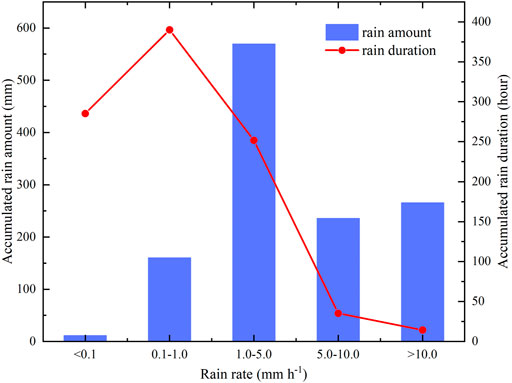
Previous studies showed that the properties of DSD depend on rainfall rates and manifest as temporal and spatial variability (Tokay and Short., 1996; Bringi et al., 2003; Nzeukou et al., 2004). To examine the characteristics of the DSD for different rainfall regimes over the head watershed of the Urumqi River, the rain-rate was divided into five classes: class I (R < 0.1 mm h⁻¹), class II (0.1 < R < 1 mm h⁻¹), class III (1 < R < 5 mm h⁻¹), class Ⅳ (5 < R < 10 mm h⁻¹) and class V (R > 10 mm h⁻¹). The accumulated rainfall duration (977 h) and rain amount (1242 mm) for the five rainfall rate classes are shown in Figure 2. The longest precipitation duration is class II (0.1 < R < 1 mm h⁻¹) and class I (<0.1 mm h⁻¹) of precipitation, accounting for 69.1% of the total rain amount duration in the study period, but the rain amount only accounts for 13.8% of the overall. Class III (1 < R < 5 mm h⁻¹) had the largest accumulated rainfall amount, accounting for more than 45.8% of the total rainfall, but the precipitation duration only accounts for 25.1% of the total. In addition, although class V (R > 10 mm h⁻¹) had the shortest precipitation duration (14 h), the precipitation accounts for 21.4% of the total precipitation. The average rainfall rates of the five classes were 0.04, 0.41, 2.26, 6.67, and 18.50 mm h⁻¹, respectively.

FIGURE 2

FIGURE 2. Accumulated duration (red) and rain amount (blue) for five rain-rate regimes.

To discern the characteristics of DSD among different rainfall rates, we calculated the averaged size spectra of each rain-rate class and put them on the same figure (Figure 3). The corresponding integral rainfall parameters computed from the average spectra are shown in Table 2. We can know that the spectral widths of the five rainfall rates don’t widen with the increase of rainfall rates compared to Motuo and Naqu (Chen et al., 2017; Wang et al., 2021), but first, widen and then narrow, and at class III reaches the maximum value. With the increase in rainfall rates, the concentration of raindrops showed an increasing-decreasing-increasing distribution shape when the particle diameter is below 1.22 mm. However, the raindrop concentration is different from the trend proposed by Wang et al. (2021) and Chen et al. (2017). The raindrop concentration increased with the rainfall rate and the largest was at class V, of which the mass-weighted mean diameter is above 1.74 mm. In this paper, with the enhancement of rainfall rate, although the raindrop concentration also showed an increasing trend, the maximum raindrop concentration was at class Ⅳ. The liquid water content W, radar reflectivity factor Z, and the mass-weighted mean diameter D_m reach the maximum value at class Ⅳ, while the total concentration of raindrops N_t and the normalized intercept parameter N_w increased with the increase in rainfall rate.

FIGURE 3

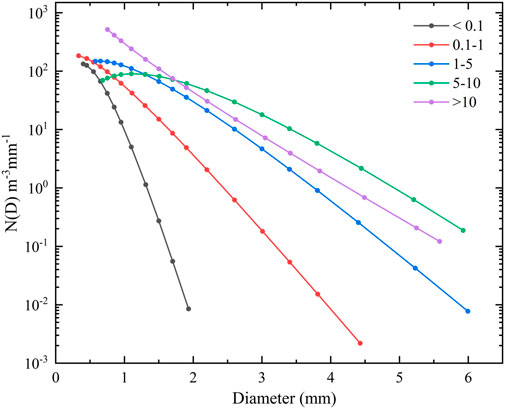
FIGURE 3. The average raindrop size distribution for the five rainfall rate classes in the head watershed of the Urumqi River basin.

TABLE 2

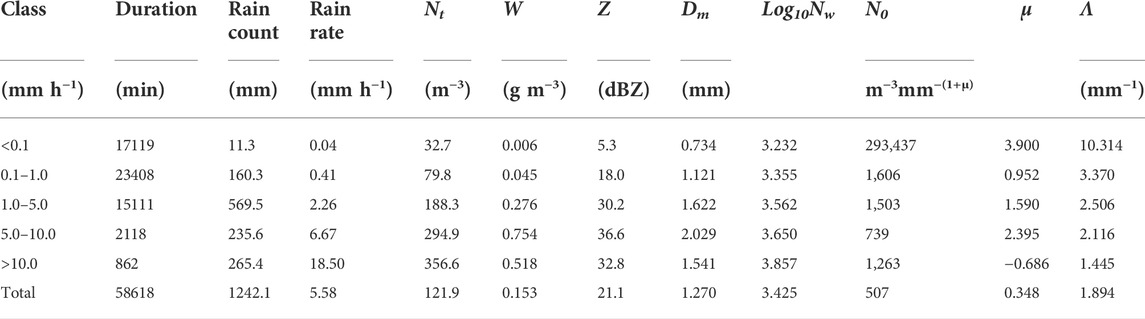
TABLE 2. Integral rain parameters obtained from the average raindrop size distribution for the five precipitation rate classes and the total data.

The relation between terminal fall velocity and drop size as that in Atlas et al. (1973) was used in our research, whereas the actual drop fall velocity was relative to the ambient air flows in real atmosphere. Updrafts could decrease the fall velocity of raindrops, resulting in an underestimation of the drop size. Furthermore, the liquid water content and rainfall rate were proportional to the third DSD moments in Eq. 3 and the third velocity-weighted DSD moments in Eq. 4, respectively. Therefore, these two bulk properties were also underestimated in case of updrafts. This effect would also be due to enhanced collision process aloft or strong attenuation along the path in the convective rainfall.

To further understand the distribution of DSD and its relative contribution to the total rainfall, we divided the droplet diameter of the observed samples at the headwaters of the Urumqi River into six classes, and the corresponding diameter values were shown in Figure 4. The raindrop diameter < 1 mm contributes the most to the precipitation, accounting for 83% of the total concentration of raindrops and 20% of the rainfall rate. In addition, particles with a diameter class of 1–2 mm contributed 15% to the total raindrop concentration but contributed 39% to the rainfall rate.

FIGURE 4

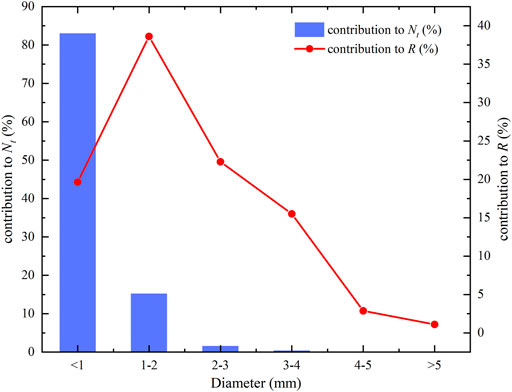
FIGURE 4. Relative contribution of each size class to the rain rate R (solid red line) and total drop contribution N_t (blue histogram) in the head watershed at the Urumqi River basin.

Raindrop size distribution variation in stratiform and convective precipitation

Previous studies showed a clear distinction between convective and stratiform precipitation (Tokay and Short, 1996; Maki et al., 2001; Ulbrich and Atlas, 2007). DSD characteristics of different rain types over a wide range of climatic regimes were studied by Bringi et al. (2003), and they found distinct variations between stratiform and convective regimes of the maritime and continental clusters. As the microphysical characteristics of raindrop spectra vary from stratiform to convective precipitation, the total dataset was further divided into convective rain type and stratiform rain type to analyze DSD characteristics according to the time series of rainfall rates. Many precipitation classification schemes have been proposed by previous researchers through different types of instruments (e.g., Disdrometer, profiler, and radar) (Tokay and Short, 1996; Bringi et al., 2003; Campos et al., 2006; Das et al., 2017). In this study, the classification method of Bringi et al. (2003) was used to classify precipitation into convective and stratiform. Specifically, the precipitation was classified as stratiform if the R values are between 0.5 and 5 mm h⁻¹ and the standard deviation (σR) is < 1.5 mm h⁻¹ over at least ten consecutive 1 min DSD samples. It was classified as convective rain when the R values were higher than 5 mm h⁻¹ and the standard deviation (σR) was more than 1.5 mm h⁻¹ over the same period. The results displayed after classification that the stratiform precipitation lasted 19228 min, accounting for 47% of the total amount of stratiform precipitation duration. The precipitation amount was 506 mm (40%), and the average rainfall rate was 1.57 mm h⁻¹. The duration of convective precipitation was 390 min, the cumulative precipitation was 38 mm (accounting for 3%), and the average rainfall rate was 5.87 mm h⁻¹.

The average raindrop spectra for the stratiform and convective precipitation types in the head watershed of the Urumqi River were shown in Figure 5. Stratiform precipitation exhibits broader spectra than Convective precipitation. The concentration of convective precipitation drops decreased with the increase of median diameter, while the concentration of stratiform precipitation drops increased first (the largest diameter was 1.6 mm) and then decreased. Moreover, when the diameter was smaller than 1.5 mm, the raindrop concentration of stratiform precipitation was greater than that of convective precipitation. However, when the diameter was above 1.5 mm, the raindrop concentration of convective precipitation was always higher than that of stratiform precipitation with the increase in diameter. The integral rain parameters obtained from the average spectra were listed in Table 3. The total concentration of raindrops N_t (m⁻³), liquid water content W (g m⁻³), and radar reflectivity factor Z (dBZ) for stratiform precipitation were 150.0, 0.216, and 27.5, respectively; and for convective precipitation were 309.7, 1.124, and 42.4, respectively.

FIGURE 5

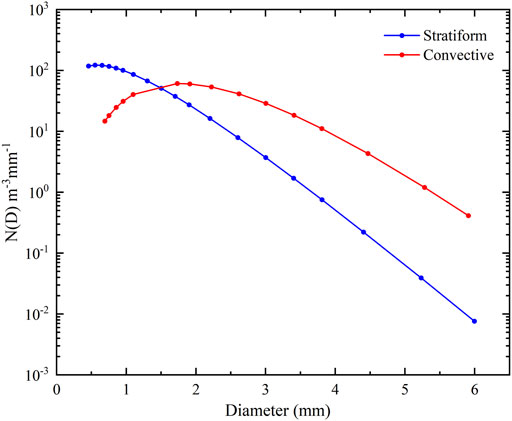
FIGURE 5. Average raindrop size spectra for the stratiform (blue line) and convective (red line) precipitation types in the head watershed of the Urumqi River basin.

TABLE 3

TABLE 3. Integral rain parameters obtained from the average raindrop size distribution for the stratiform and convective precipitation types.

The mean values of log₁₀N_w and D_m for the convective and stratiform precipitation types in the head watershed of the Urumqi River were compared (Figure 6). The red and blue symbols denote the results from the stratiform and convective precipitation data, respectively. Two outlined dark grey rectangles, corresponding to the maritime-like (D_m:1.5–1.75 mm; log₁₀N_w:4–4.5 m⁻³mm⁻¹) and continental-like (D_m: 2–2.75 mm; log₁₀N_w: 3–3.5 m⁻³mm⁻¹) convective clusters defined by Bringi et al. (2003), were superimposed upon the scatterplot. The D_m value of convective precipitation in the headwaters was larger than that of stratiform precipitation. In terms of stratiform precipitation, D_m and N_w in the headwaters are different from those in other parts of China. The stratiform precipitation in headwaters had a large D_m and a small N_w value, indicating that the precipitation was formed by the melting of large and dry snowflakes. The larger liquid water content causes the raindrops to collide and coalesce during the falling process, which increases the mass-weighted mean diameter of raindrops and reduced the raindrops’ concentration to a certain extent, leading to the smaller N_w. Based on the present observations and comparison to the study of Bringi et al. (2003), the convective precipitation in the head watershed of the Urumqi River could be identified as continental-like precipitation.

FIGURE 6

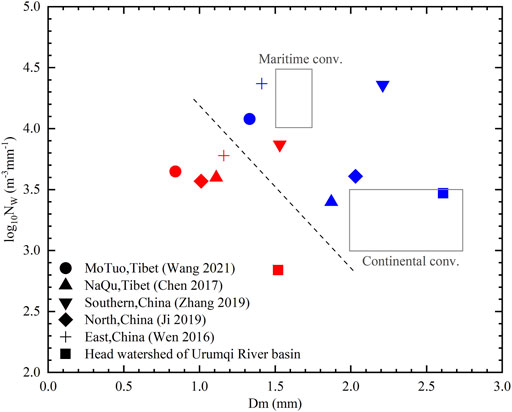
FIGURE 6. The average values of log₁₀N_w and D_m from the present study and previous literature are distinguished by the different symbols, as explained in the legend. The blue/red symbols represent convective/stratiform precipitation. The outlined dark grey rectangles correspond to the maritime and continental convective clusters.

Figure 7 showed the relative frequency histogram of D_m and log₁₀N_w for the whole data set and convective and stratiform subsets calculated from the disdrometer. In addition, three key parameters, such as mean, standard deviation, and skewness were used. As shown in Figures 7A,B, for the whole dataset, the mean value of D_m and N_w is 1.54 mm and 2.85, respectively. The D_m was larger and the log₁₀N_w was smaller than the value proposed by Zhang et al. (2019) in South China (1.46 and 3.86). The histogram of D_m had a highly positive skewness, and on the contrary, the log₁₀N_w was slightly negative skewness. The standard deviation of D_m and log₁₀N_w were large (0.83 mm and 0.44, respectively), indicating high variability in D_m and log₁₀N_w. The convective histogram and stratiform histogram of D_m were both positively skewed (0.19 and 1.24); however, the log₁₀N_w skewness of convective and stratiform precipitation was different, with convective precipitation being positively skewed (0.51) and stratiform precipitation being negatively skewed (−0.11). Meanwhile, the D_m value of the three datasets are all bimodal.

FIGURE 7

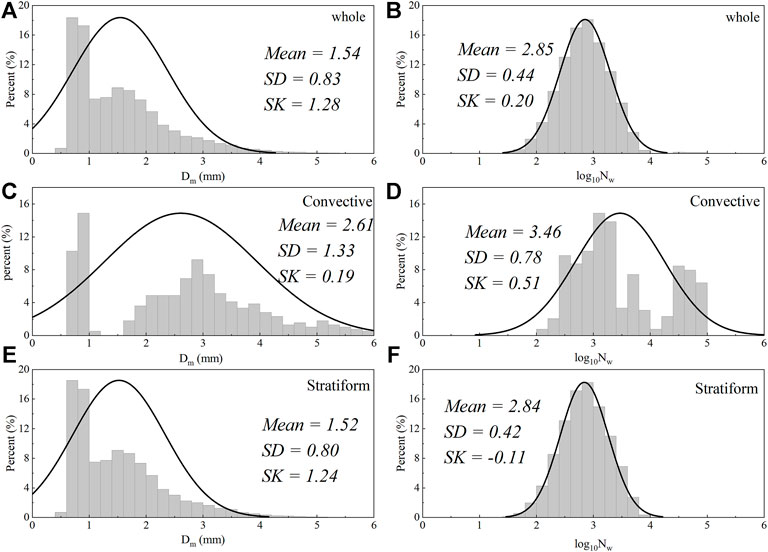
FIGURE 7. Histogram of D_m and log₁₀N_w for the (A,B) whole data set and (C,D) convective and (E,F) stratiform subsets calculated from the PWS100 disdrometer datasets.

Figure 8 is a scatter plot of the D_m -R and log₁₀N_w-R relationships of convective and stratiform precipitation obtained by the PWS100 disdrometer. The red solid line was the corresponding power-law relationship fitted by the least-squares method. In terms of the log₁₀N_w-R relationship, which are more scattered, especially for convective precipitation. The coefficient of convective precipitation was larger than that of stratiform precipitation but the index was smaller. Notably, the exponent of the log₁₀N_w-R relationship was negative, indicating that log₁₀N_w-R was lower at higher rainfall rates, which were related to collision and coalescence mechanisms during precipitation. As far as the D_m-R relationship was concerned, the scatter was not as spread out as the log₁₀N_w-R relationship. The index of the power-law relationship was positive, indicating that large particles contribute the most to the rainfall rate. The D_m value of convective precipitation increased with the increase in rainfall rates, while the D_m value of stratiform precipitation tended to be stable (1–2 mm) at higher rainfall rates. This indicated that the DSD tended to be in an equilibrium state.

FIGURE 8

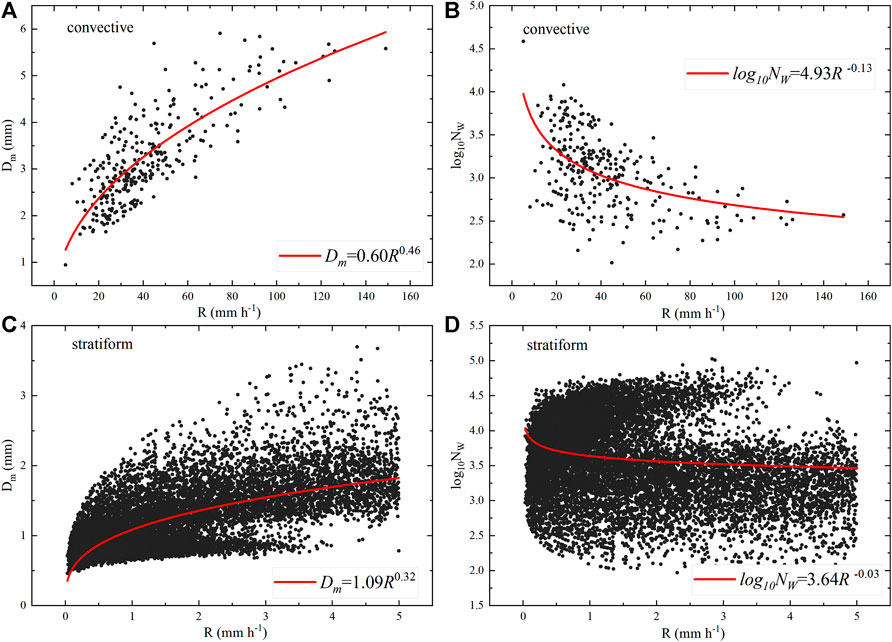
FIGURE 8. Scatter plots of D_m vs. R and log₁₀N_w vs. R for convective (A,B) and stratiform (C,D) rain types. The solid red lines indicate the fitting power-law relationships in the head watershed of Urumqi River using the least-squares method are also provided in each panel.

Diurnal variation of raindrop size distribution

To study the DSD difference between daytime and nighttime rainfall in the source area of the Urumqi River, the convective precipitation and stratiform precipitation were further divided into two types: daytime and nighttime. The separation of day and night was based on the local mean sunrise and sunset time in summer, with the beginning times at approximately 0700 and 2100 BST (UTC + 8), respectively. A rain event was considered a daytime event (nighttime event) if all the spectra were from daytime hours (nighttime hours). The classification results were shown in Table 4. The duration of daytime precipitation is 25,400 min, the cumulative precipitation is 825.1 mm, and the average rainfall rate is 1.95 mm h⁻¹, accounting for 62% and 65% of the precipitation in headwater, respectively. The night precipitation lasted 15,260 min, the accumulated precipitation is 439.1 mm, and the average rainfall rate is 1.72 mm h⁻¹, accounting for 38% and 35% of the precipitation in headwater, respectively.

TABLE 4

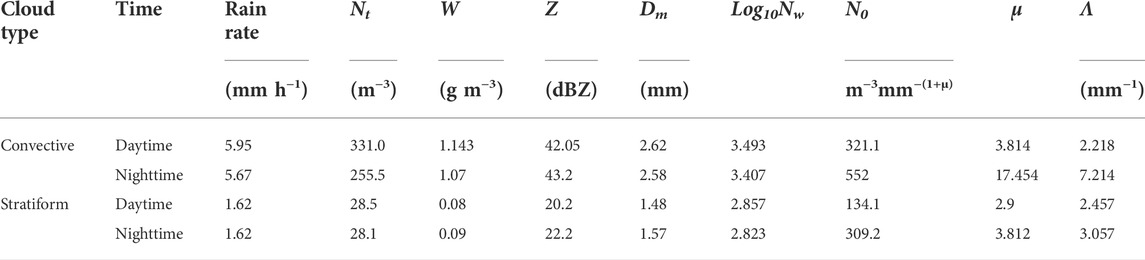
TABLE 4. Integral rain parameters obtained from the average raindrop size distribution for the daytime and nighttime precipitation types.

The average raindrop spectra for daytime and nighttime precipitation types in the head watershed of the Urumqi River are shown in Figure 9. The integral rain parameters obtained from the average spectra are listed in Table 4. For stratiform precipitation, daytime and nighttime precipitation had the same spectral width and curve trend, and the raindrop concentration decreases with the increase of particle diameter. For convective precipitation, the shape of the spectral curve was very different during daytime than at nighttime. When the diameter of raindrops is less than 1.5 mm, the concentration of raindrops in the daytime is much higher than that in the nighttime, and when the diameter of raindrops is about 2 mm, the concentration of raindrops in nighttime is higher than that in the daytime. Second, there are higher N_t and W and smaller Z values during the daytime than at night. The daytime/nighttime D_m-log₁₀N_w relationship of stratiform precipitation is 1.48–2.857/1.57–2.823, and the day/night D_m-log₁₀N_w relationship of convective precipitation is 2.62–3.493/2.58–3.407. In addition, regardless of daytime or nighttime precipitation, convective precipitation has larger N_t, W, Z, and D_m-log₁₀N_w values than stratiform precipitation.

FIGURE 9

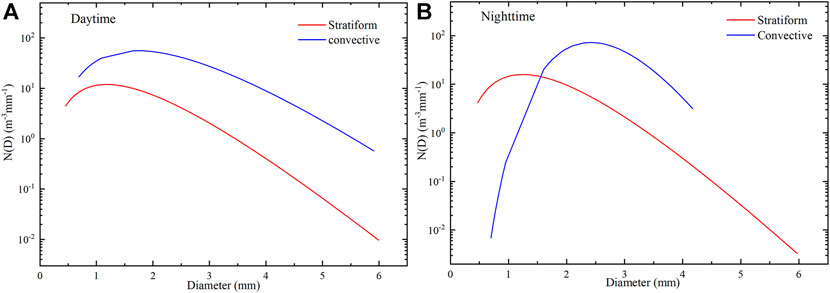
FIGURE 9. Average raindrop size spectra for the daytime (A) and nighttime (B) precipitation types in the head watershed at the head watershed of the Urumqi River. The solid red line and solid blue line represent stratiform and convective precipitation, respectively.

Radar reflectivity and rain rate relations

The coefficients (A) and indices (b) of the radar reflectivity-rain rate (Z = A*R^b) power-law relation are strongly affected by many factors, such as geographic location, atmospheric conditions, and raindrop spectrometer type (Uijlenho, 2001; Chandrasekar et al., 2003; Rosenfeld and Ulbrich 2003; Tokay et al., 2008), which is also strongly dependent on the variability of DSD (Steiner et al., 2004; Lee and Zawadzki., 2005). The power-law relationship between Z-R has been widely applied in radar QPE algorithms. For example, the relationship of Z = 300R^1.4 proposed by Fulton et al. (1998) was utilized by the Next Generation Weather Radar (NEXRAD) in midlatitudes for convective rain, and the relationship of Z = 200R^1.6 was recommended in midlatitude areas for stratiform rain (Marshall and Palmer., 1948). Wu and Liu (2017) proposed that the Z-R relationship of stratiform and convective precipitation were Z = 170R^1.3 and Z = 70R^1.8, respectively, through the study of raindrop spectrum data in Naqu, Qinghai-Tibet Plateau; while Wang et al. (2021) reported the Z-R relationships of stratiform and convective precipitation in Motuo over the TP are Z = 114R^1.8and Z = 53.7R^1.7, respectively. Therefore, the uncertainty of rainfall rate estimated by radar can be minimized by establishing the optimal reflectivity factor-rainfall rate (Z-R) relationship in specific locations, seasons, and precipitation types. Due to the complex topography of the alpine mountains and relatively limited observations, it is of great significance to research the Z-R relationship of precipitation in the head watershed of the Urumqi River basin based on the DSD observation data.

Scatterplots of the rain rate R and radar reflectivity factor Z, as well as the fitted power-law relationships using the least-squares method for the stratiform and convective rain types in the head watershed of the Urumqi River, are shown in Figure 10. The Z-R relationships of Naqu reported by Wu and Liu (2017) and the Z-R relationships of Motuo reported by Wang et al. (2021) are also imposed upon Figure 9 as a solid blue line and solid purple line. Compared with other study areas, the stratiform precipitation in the source area of the Urumqi River has a larger coefficient and index (A: 698.8, b: 2.0), while the convective precipitation has a smaller coefficient and a larger index (A: 47.1, b: 2.0). Compared with other regions, the D_m-N_w value in the source region of the Urumqi River is larger and the N_w value is smaller, which corresponds to the D_m-N_w relationship in Figure 5, which further indicates that the diversity of the Z-R relationship is mainly caused by the variability of DSD. For stratiform precipitation, the empirical relationship Z = 200R^1.6 underestimates precipitation at a rainfall rate below 0.1 mm h⁻¹, while it overestimates precipitation at a rainfall rate above 0.1 mm h⁻¹, it is contrary to Wang et al. (2021). In terms of convective precipitation, compared with Naqu and Motuo, the Heyuan region has a smaller coefficient and a larger exponent, which may be related to the abundance of large raindrops in the Heyuan region. This indicates that under the same rainfall rates, the Heyuan area has higher radar reflectivity than the above two areas. The empirical relationship Z = 300R^1.4 underestimates the convective precipitation in the head watershed of the Urumqi River.

FIGURE 10

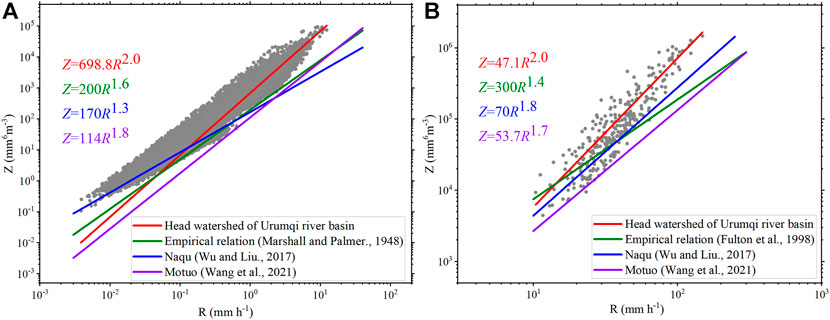
FIGURE 10. Z-R relation scatterplots for (A) stratiform and (B) convective precipitation. The solid red lines indicate the fitting power-law relationships in the head watershed of the Urumqi River using the least-squares method. The solid green lines indicate the empirical relations (Z = 200R^1.60 for stratiform precipitation and Z = 300R^1.40 for convective precipitation). The solid blue lines indicate the fitting power-law relationships in Naqu, as reported by Wu and Liu (2017). The solid purple lines indicate the fitting power-law relationships in Motuo, as reported by Wang et al. (2021).

Discussion

The statistical characteristics of DSD observed in summer in the head watershed of Urumqi River Basin were documented using observations from the PWS100. The DSD measured by PWS100 indicated that it consists of a lower number concentration (especially around 1 mm in diameter) compared to the rest of China. This may be related to the fact that snowflakes, hail, and other large-diameter particles account for 43% of the total particles in the summer precipitation in the source area of the Urumqi River Basin. The DSD of convective precipitation in the headwaters of the Urumqi River was more like a continental-like cluster (derived from the D_m-log₁₀N_w relationship), which further illustrated the close relationship between DSD and geographic location. On the other hand, the Z-R power-law relationship, which was derived from the disdrometer, was also different from other regions, with larger coefficients and exponents for stratiform precipitation, and smaller coefficients and larger exponents for convective precipitation. Previous study has shown that coefficients may vary with weather conditions, geographic location, and other possible reasons, such as quality control and physical properties of the raindrop.

As aforementioned, we excluded data with diameters below 0.45 mm and above 6 mm for quality control, partly, because the PWS100 excluded precipitation particles with abnormal velocities and sizes in its built-in algorithm (Campbell Scientific Inc., 2015), which may result in lower numbers of raindrops smaller than 0.4 mm (Montero-Martínez et al., 2009; Montero-Martinez and Eduardo, 2016). On the other hand, there were few precipitation particles with a diameter above 6 mm observed by PWS100. Therefore, it should be noted that the DSD measured by PWS100 in this study is not complete. Moreover, Schönhuber et al. (2007) found similar results when analyzing DSD features by 2DVD (2D-video-distrometer), which underestimated droplets with diameters less than 0.3 mm and thus the concentration of small droplets.

The decrease of air pressure and density over the head watershed of the Urumqi River impacts on the microphysical processes responsible for the precipitation formation, coalescence, and fall velocity of drops. An empirical relationship between raindrop diameter and terminal velocity at different pressure levels derived by Beard, (1977) shows that, for large size raindrops, the 600 hPa raindrop velocity was expected to increase by 30% compared to the 1000 hPa raindrop velocity. This may affect the collision fragmentation mechanism and particle size of raindrops (Porcù et al., 2013), and some features can also be found in Figure 7. Compared with other research areas, the DSD characteristics of the head watershed of the Urumqi River showed a lower concentration of raindrops. Besides height difference, the topographic effect in the headwaters also played an important role in the variability of DSD characteristics.

Conclusion

The statistical characteristics of DSD were analyzed by using the observation data of the PWS100 Present Weather Sensor, which located at the meteorological observation site at the terminal of the Urumqi Glacier No. 1. The data selected for study were the observation results of the disdrometer measurements in the summer of 2017–2019, with a time resolution of 1 min. The DSD characteristics of the continental glacial belt in the eastern Tianshan Mountains were analyzed. The total number of samples available after quality control was 40214 min, corresponding to a total rainfall of 1242 mm. The main conclusions were as follows:

(1) The rainfall rate was divided into five classes. The spectral width of the five rainfall rates did not increase with the increase of the rainfall rate, but increased first and then decreased and reached its maximum at class IV. The first two categories accounted for 69.1% of the total precipitation duration, and the rainfall rate was less than 1 mm h⁻¹, while class III contributed the most to the rainfall, accounting for 45.8% of the total precipitation. The precipitation in the headwaters (3 835 m a.s.l) was dominated by small raindrops (under 2 mm), which contributed 98% to the concentration of raindrops.

(2) The precipitation data in the headwaters were further divided into two types: stratiform and convective. In terms of the D_m-log₁₀N_w relationship between stratiform and convective, compared with other study areas, the D_m-log₁₀N_w value of the headwaters showed a smaller log₁₀N_w and a larger D_m. The convective precipitation in the head watershed of the Urumqi River could be identified as continental-like precipitation. In addition, the slope of the log₁₀N_w-R relationship for these two precipitation types was negative. The D_m value of stratiform precipitation tended to be stable at higher rainfall rates (1–2 mm). And the particle diameter of raindrops, at low rainfall rates, in stratiform precipitation may be larger due to the higher raindrop concentration.

(3) Both of the convective and stratiform spectra were further subdivided into daytime and nighttime types to investigate the differences in DSDs between daytime and nighttime rains over the head watershed of the Urumqi River. For stratiform precipitation, the spectral widths of daytime and nighttime precipitation were the same, while convective precipitation showed a large difference between daytime and nighttime. When the diameter of raindrops was below 1.5 mm, the concentration of raindrops in the daytime was much higher than that in the nighttime, and the spectral width in the daytime was larger than that in the nighttime. The daytime/nighttime D_m-log₁₀N_w for stratiform precipitation were 1.48–2.857 and 1.57–2.823, respectively; and for convective precipitation were 2.62–3.493 and 2.58–3.407, respectively.

(4) The coefficient A and index b in the Z-R relationship for stratiform precipitation (Z = 698.8R^2.0) were larger than those in the empirical relationship (Marshall and Palmer., 1948) for Z = 200R^1.6, which underestimated the rainfall rate below 0.1 mm h⁻¹ and overestimated precipitation above 0.1 mm h⁻¹. The empirical relationship Z = 300R^1.4 underestimated the convective precipitation in the source region (Z = 47.1R^2.0). When the type of precipitation changed from stratiform to convective, coefficient A decreased and the exponent b remain unchanged.

Notably, there are certain limitations in this study that should be mentioned. For instance, the PWS100 disdrometer underestimates the number of small drops (below 0.4 mm), which likely affects the spectral shape of the DSD and resulting microphysical parameters. Therefore, different instruments (i.e., 2DVD, Thies and MRR, etc.) should be considered and the DPR observations should be verified in future work. Lastly, the DSD characteristics during the different seasons in the head watershed of the Urumqi River should be determined in future research.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

Conceptualization: PC and ZL; Data curation: PC; Formal analysis: PC, Methodology: PC, Resources: PW, JP, and YJ Software: PC and YJ; Visualization: PC; Writing original draft: PC and MY; Writing review and editor: PC and PW.

Funding

This work was supported by the Innovative Research Groups of the National Natural Science Foundation (41721091), the National Natural Science Foundation of China (Grant Nos 41761134093 and 41471058), the Second Tibetan Plateau Scientific Expedition and Research (Grant No. 2019QZKK0201), the State Key Laboratory of Cryospheric Science funding (SKLCS-ZZ-2020), the Strategic Priority Research Program of Chinese Academy of Sciences (Class A, Grant Nos XDA20060201 and XDA20020102), Natural Science Foundation of Gansu Province (21JR7RA059), National Science and Technology Basic Resources Survey Program of China (2019FY100202), the Third Comprehensive Scientific Investigation Project of Xinjiang (2021XJKK0801).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adirosi, E., Baldini, L., Lombardo, F., Russo, F., Napolitano, F., Volpi, E., et al. (2015). Comparison of different fittings of drop spectra for rainfall retrievals. Adv. water Resour. 83, 55–67. doi:10.1016/j.advwatres.2015.05.009

CrossRef Full Text | Google Scholar

Agnew, J., and Space, R. A. L. (2013). Final report on the operation of a Campbell Scientific PWS100 present weather sensor at Chilbolton Observatory[J]. Swindon, UK: Science & Technology Facilities Council.

Google Scholar

Atlas, D., Srivastava, R. C., and Sekhon, R. S. (1973). Doppler radar characteristics of precipitation at vertical incidence. Rev. Geophys. 11 (1), 1–35. doi:10.1029/rg011i001p00001

CrossRef Full Text | Google Scholar

Beard, K. V. (1977). Terminal velocity adjustment for cloud and precipitation drops aloft. J. Atmos. Sci. 34 (8), 1293–1298. doi:10.1175/1520-0469(1977)034<1293:tvafca>2.0.co;2

CrossRef Full Text | Google Scholar

Boodoo, S., Hudak, D., Ryzhkov, A., Zhang, P., Donaldson, N., Sills, D., et al. (2015). Quantitative precipitation estimation from a C-band dual-polarized radar for the 8 july 2013 flood in toronto, Canada. J. Hydrometeorol. 16 (5), 2027–2044. doi:10.1175/jhm-d-15-0003.1

CrossRef Full Text | Google Scholar

Bringi, V. N., Chandrasekar, V., Hubbert, J., Gorgucci, E., Randeu, W. L., and Schoenhuber, M. (2003). Raindrop size distribution in different climatic regimes from disdrometer and dual-polarized radar analysis. J. Atmos. Sci. 60 (2), 354–365. doi:10.1175/1520-0469(2003)060<0354:rsdidc>2.0.co;2

CrossRef Full Text | Google Scholar

Campbell Scientific, Inc (2015). PWS100 present weather sensor; instruction manual[M]. Revision 9/15. Logan, UT, USA: Campbell Scientific, Inc.

Google Scholar

Campos, E. F., Zawadzki, I., Petitdidier, M., and Fernandez, W. (2006). Measurement of raindrop size distributions in tropical rain at Costa Rica. J. Hydrology 328 (1-2), 98–109. doi:10.1016/j.jhydrol.2005.11.047

CrossRef Full Text | Google Scholar

Cao, Q., and Zhang, G. (2009). Errors in estimating raindrop size distribution parameters employing disdrometer and simulated raindrop spectra. J. Appl. Meteorology Climatol. 48 (2), 406–425. doi:10.1175/2008jamc2026.1

CrossRef Full Text | Google Scholar

Caracciolo, C., Prodi, F., Battaglia, A., and Porcu', F. (2006). Analysis of the moments and parameters of a gamma DSD to infer precipitation properties: A convective stratiform discrimination algorithm. Atmos. Res. 80 (2-3), 165–186. doi:10.1016/j.atmosres.2005.07.003

CrossRef Full Text | Google Scholar

Chandrasekar, V., Meneghini, R., and Zawadzki, I. (2003). Global and local precipitation measurements by radar[m]//radar and atmospheric science: A collection of essays in honor of david Atlas. Boston, MA: American Meteorological Society, 215–236.

CrossRef Full Text | Google Scholar

Chen, B., Hu, Z., Liu, L., and Zhang, G. (2017). Raindrop size distribution measurements at 4, 500 m on the Tibetan Plateau during TIPEX‐III[J]. J. Geophys. Res. Atmos. 122 (20), 11092–11106.

CrossRef Full Text | Google Scholar

Chen, B., Wang, J., and Gong, D. (2016). Raindrop size distribution in a midlatitude continental squall line measured by Thies optical disdrometers over east China. J. Appl. Meteorology Climatol. 55 (3), 621–634. doi:10.1175/jamc-d-15-0127.1

CrossRef Full Text | Google Scholar

Chen, B., Yang, J., and Pu, J. (2013). Statistical characteristics of raindrop size distribution in the meiyu season observed in eastern China. J. Meteorological Soc. Jpn. 91 (2), 215–227. doi:10.2151/jmsj.2013-208

CrossRef Full Text | Google Scholar

Climate change (2013). “The physical science basis,” in Working Group I contribution to the fifth assessment report of the intergovernmental panel on climate change[M] (Cambridge University Press). 2014.

Google Scholar

Das, S. K., Konwar, M., Chakravarty, K., and Deshpande, S. M. (2017). Raindrop size distribution of different cloud types over the Western Ghats using simultaneous measurements from Micro-Rain Radar and disdrometer. Atmos. Res. 186, 72–82. doi:10.1016/j.atmosres.2016.11.003

CrossRef Full Text | Google Scholar

Dolan, B., Fuchs, B., Rutledge, S. A., Barnes, E. A., and Thompson, E. J. (2018). Primary modes of global drop size distributions. J. Atmos. Sci. 75 (5), 1453–1476. doi:10.1175/jas-d-17-0242.1

CrossRef Full Text | Google Scholar

Ellis, R. A., Sandford, A. P., Jones, G. E., Richards, J., Petzing, J., and Coupland, J. M. (2006). New laser technology to determine present weather parameters. Meas. Sci. Technol. 17 (7), 1715–1722. doi:10.1088/0957-0233/17/7/009

CrossRef Full Text | Google Scholar

Fadnavis, S., Deshpande, M., Ghude, S. D., and Ernest Raj, P. (2014). Simulation of severe thunder storm event: A case study over pune, India. Nat. Hazards (Dordr). 72 (2), 927–943. doi:10.1007/s11069-014-1047-1

CrossRef Full Text | Google Scholar

Feng, F., Li, Z. Q., Jin, S., Feng, Q., and Liu, W. (2013). Characteristics of δ18O and δD in precipitation and its water vapor sources in the upper Urumqi River basin, Eastern Tianshan[J]. Adv. water Sci. 24 (5), 634–641.

Google Scholar

Friedrich, K., Kalina, E. A., Masters, F. J., and Lopez, C. R. (2013). Drop-size distributions in thunderstorms measured by optical disdrometers during VORTEX2. Mon. weather Rev. 141 (4), 1182–1203. doi:10.1175/mwr-d-12-00116.1

CrossRef Full Text | Google Scholar

Fulton, R. A., Breidenbach, J. P., Seo, D. J., Miller, D. A., and O’Bannon, T. (1998). The WSR-88d rainfall algorithm. Weather Forecast. 13 (2), 377–395. doi:10.1175/1520-0434(1998)013<0377:twra>2.0.co;2

CrossRef Full Text | Google Scholar

Giangrande, S. E., Bartholomew, M. J., Pope, M., Collis, S., and Jensen, M. P. (2014). A summary of precipitation characteristics from the 2006–11 northern Australian wet seasons as revealed by ARM disdrometer research facilities (Darwin, Australia). J. Appl. Meteorology Climatol. 53 (5), 1213–1231. doi:10.1175/jamc-d-13-0222.1

CrossRef Full Text | Google Scholar

Goodison, B. E., and Metcalfe, J. R. (1992). The WMO solid precipitation inter-comparison: Canadian assessment[R]. Geneva: WMO, 221–225. WMO/TD No.462.

Google Scholar

Hou, A. Y., Skofronick-Jackson, G., and Kummerow, C. D. (2008). “Global precipitation measurement[M]//Precipitation,” in Advances in measurement, estimation and prediction (Berlin, Heidelberg: Springer), 131–169.

Google Scholar

Iguchi, T., Kozu, T., Meneghini, R., Awaka, J., and Okamoto, K. (2000). Rain-profiling algorithm for the TRMM precipitation radar. J. Appl. Meteor. 39 (12), 2038–2052. doi:10.1175/1520-0450(2001)040<2038:rpaftt>2.0.co;2

CrossRef Full Text | Google Scholar

Jameson, A. R., Larsen, M. L., and Kostinski, A. B. (2015). Disdrometer network observations of finescale spatial–temporal clustering in rain. J. Atmos. Sci. 72 (4), 1648–1666. doi:10.1175/jas-d-14-0136.1

CrossRef Full Text | Google Scholar

Janapati, J., Reddy, V., Reddy, K., Reddy K., K., Lin, P. L., Rao T., N., et al. (2017). A study on raindrop size distribution variability in before and after landfall precipitations of tropical cyclones observed over southern India. J. Atmos. Solar-Terrestrial Phys. 159, 23–40. doi:10.1016/j.jastp.2017.04.011

CrossRef Full Text | Google Scholar

Ji, L., Chen, H., Li, L., Chen, B., Xiao, X., Chen, M., et al. (2019). Raindrop size distributions and rain characteristics observed by a PARSIVEL disdrometer in beijing, northern China. Remote Sens. 11 (12), 1479. doi:10.3390/rs11121479

CrossRef Full Text | Google Scholar

Jia, Y. F., Li, Z. Q., Jin, S., Xu, C., Deng, H., and Zhang, M. (2020a). Runoff changes from Urumqi glacier no. 1 over the past 60 years, eastern tianshan, central Asia. Water 12 (5), 1286. doi:10.3390/w12051286

CrossRef Full Text | Google Scholar

Jia, Y. F., Li, Z. Q., Xu, C. H., Jin, S., and Deng, H. (2020b). A comparison of precipitation measurements with a PWS100 laser sensor and a geonor T-200B precipitation gauge at a nival glacial zone in eastern tianshan, central Asia. Atmosphere 11 (10), 1079. doi:10.3390/atmos11101079

CrossRef Full Text | Google Scholar

Johannsen, L. L., Zambon, N., Strauss, P., Dostal, T., Neumann, M., Zumr, D., et al. (2020). Comparison of three types of laser optical disdrometers under natural rainfall conditions. Hydrological Sci. J. 65 (4), 524–535. doi:10.1080/02626667.2019.1709641

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, H. J., Jung, W., Suh, S. H., Lee, D. I., and You, C. H. (2022). The characteristics of raindrop size distribution at windward and leeward side over mountain area. Remote Sens. 14 (10), 2419. doi:10.3390/rs14102419

CrossRef Full Text | Google Scholar

Kozu, T., Iguchi, T., Shimomai, T., and Kashiwagi, N. (2009). Raindrop size distribution modeling from a statistical rain parameter relation and its application to the TRMM precipitation radar rain retrieval algorithm. J. Appl. Meteorology Climatol. 48 (4), 716–724. doi:10.1175/2008jamc1998.1

CrossRef Full Text | Google Scholar

Kozu, T., and Nakamura, K. (1991). Rainfall parameter estimation from dual-radar measurements combining reflectivity profile and path-integrated attenuation. J. Atmos. Ocean. Technol. 8 (2), 259–270. doi:10.1175/1520-0426(1991)008<0259:rpefdr>2.0.co;2

CrossRef Full Text | Google Scholar

Krishna, U. V. M., Reddy, K. K., Seela, B. K., Shirooka, R., Lin, P. L., and Pan, C. J. (2016). Raindrop size distribution of easterly and westerly monsoon precipitation observed over Palau islands in the Western Pacific Ocean. Atmos. Res. 174, 41–51. doi:10.1016/j.atmosres.2016.01.013

CrossRef Full Text | Google Scholar

Kumar, S. B., and Reddy, K. K. (2013). Rain drop size distribution characteristics of cyclonic and north east monsoon thunderstorm precipitating clouds observed over Kadapa (14.47°N, 78.82°E), Tropical semi-arid region of India. Mausam 64 (1), 35–48. doi:10.54302/mausam.v64i1.653

CrossRef Full Text | Google Scholar

Lee, G. W., and Zawadzki, I. (2005). Variability of drop size distributions: Time-scale dependence of the variability and its effects on rain estimation. J. Appl. Meteorol. Climatol. 44 (2), 241–255. doi:10.1175/jam2183.1

CrossRef Full Text | Google Scholar

Li, H. L., Wang, P. Y., Li, Z. Q., Jin, S., Xu, C., Liu, S., et al. (2022). An application of three different field methods to monitor changes in Urumqi Glacier No. 1, Chinese Tien Shan, during 2012–18. J. Glaciol. 68 (267), 41–53. doi:10.1017/jog.2021.71

CrossRef Full Text | Google Scholar

Li, X. Y., Ding, Y. J., Ye, B. S., and Han, T. (2011). Changes in physical features of Glacier No. 1 of the Tianshan Mountains in response to climate change. Chin. Sci. Bull. 56 (26), 2820–2827. doi:10.1007/s11434-011-4621-x

CrossRef Full Text | Google Scholar

Li, Z. Q., Li, C. J., Li, Y. F., Wang, F., and Huilin, L. (2007). Preliminary results from measurements of selected trace metals in the snow–firn pack on Urumqi glacier No.1, eastern Tien Shan, China[J]. J. Glaciol. 53, 368–373.

Google Scholar

Li, Z. Q., Wang, W. B., Zhang, M. J., Wang, F., and Li, H. (2010). Observed changes in streamflow at the headwaters of the Urumqi River, eastern Tianshan, central Asia[J]. Hydrological Process. Int. J. 24 (2), 217–224.

Google Scholar

Liao, L., Meneghini, R., and Tokay, A. (2014). Uncertainties of GPM DPR rain estimates caused by DSD parameterizations. J. Appl. Meteorology Climatol. 53 (11), 2524–2537. doi:10.1175/jamc-d-14-0003.1

CrossRef Full Text | Google Scholar

Liepert, B. G., and Previdi, M. (2012). Inter-model variability and biases of the global water cycle in CMIP3 coupled climate models. Environ. Res. Lett. 7 (1), 014006. doi:10.1088/1748-9326/7/1/014006

CrossRef Full Text | Google Scholar

Liu, J. F., Chen, R. S., and Qin, W. W. (2011). Study on the vertical distribution of precipitation in mountainous regions using TRMM data[J]. Adv. water Sci. 22 (4), 447–454.

Google Scholar

Liu, Q., and Fu, Y. F. (2007). Study on Asian summer precipitation based on TRMM/TMI[J]. Sci. China press 37 (1), 111–122.

Google Scholar

Maki, M., Keenan, T. D., Sasaki, Y., and Nakamura, K. (2001). Characteristics of the raindrop size distribution in tropical continental squall lines observed in Darwin, Australia. J. Appl. Meteor. 40 (8), 1393–1412. doi:10.1175/1520-0450(2001)040<1393:cotrsd>2.0.co;2

CrossRef Full Text | Google Scholar

Mao, W., Zhang, W., and Kou, M. (2022). Statistical characteristics of raindrop size distribution during rainy seasons in Complicated Mountain Terrain[J]. Hydrology Earth Syst. Sci. Discuss., 1–24.

Google Scholar

Marshall, J. S., and Palmer, W. M. K. (1948). The distribution of raindrops with size[J]. J. Meteor. 5, 165–166. doi:10.1175/1520-0469(1948)005<0165:tdorws>2.0.co;2

CrossRef Full Text | Google Scholar

McFarquhar, G. M., Hsieh, T. L., Freer, M., Mascio, J., and Jewett, B. F. (2015). The characterization of ice hydrometeor gamma size distributions as volumes in N0–λ–μ phase Space: Implications for microphysical process modeling. J. Atmos. Sci. 72 (2), 892–909. doi:10.1175/jas-d-14-0011.1

CrossRef Full Text | Google Scholar

Montero-Martínez, G., Gómez-Balvás, S. S., and García-García, F. (2021). Study of rain classification and the tendency of gamma DSD parameterizations in Mexico. Atmos. Res. 252, 105431. doi:10.1016/j.atmosres.2020.105431

CrossRef Full Text | Google Scholar

Montero-Martínez, Guillermo, Eduardo, F. T., and Garcia-Garcia, F. (2016). A comparison of two optical precipitation sensors with different operating principles: The PWS100 and the OAP-2DP. Atmos. Res. 178, 550–558. doi:10.1016/j.atmosres.2016.05.007

CrossRef Full Text | Google Scholar

Montero-Martínez, Guillermo, Kostinski, A. B., Shaw, R. A., and Garcia-Garcia, F. (2009). Do all raindrops fall at terminal speed?[J]. Geophys. Res. Lett. 36 (11), L11818. doi:10.1029/2008gl037111

CrossRef Full Text | Google Scholar

Nakamura, K., and Iguchi, T. (2007). Dual-wavelength radar algorithm[M]//Measuring precipitation from space. Dordrecht: Springer, 225–234.

CrossRef Full Text | Google Scholar

Nzeukou, A., Sauvageot, H., Ochou, A. D., and Kebe, C. M. F. (2004). Raindrop size distribution and radar parameters at Cape Verde. J. Appl. Meteor. 43 (1), 90–105. doi:10.1175/1520-0450(2004)043<0090:rsdarp>2.0.co;2

CrossRef Full Text | Google Scholar

Penide, G., Kumar, V. V., Protat, A., and May, P. T. (2013b). Statistics of drop size distribution parameters and rain rates for stratiform and convective precipitation during the north Australian wet season. Mon. weather Rev. 141 (9), 3222–3237. doi:10.1175/mwr-d-12-00262.1

CrossRef Full Text | Google Scholar

Penide, G., Protat, A., Kumar, V. V., and May, P. T. (2013a). Comparison of two convective/stratiform precipitation classification techniques: Radar reflectivity texture versus drop size distribution–based approach. J. Atmos. Ocean. Technol. 30 (12), 2788–2797. doi:10.1175/jtech-d-13-00019.1

CrossRef Full Text | Google Scholar

Petersen, W. A., Gatlin, P. N., Wolff, D. B., Tokay, A., and Grecu, M., A radar-based evaluation of GPM retrievals of the rain drop size distribution[C]//European Conference on Radar in Meteorology and Hydrology. 2018 (MSFC-E-DAA-TN56720).

Google Scholar

Porcù, F., D'Adderio, L. P., Prodi, F., and Caracciolo, C. (2014). Rain drop size distribution over the Tibetan Plateau. Atmos. Res. 150, 21–30. doi:10.1016/j.atmosres.2014.07.005

CrossRef Full Text | Google Scholar

Porcù, F., D’adderio, L. P., Prodi, F., and Caracciolo, C. (2013). Effects of altitude on maximum raindrop size and fall velocity as limited by collisional breakup. J. Atmos. Sci. 70 (4), 1129–1134. doi:10.1175/jas-d-12-0100.1

CrossRef Full Text | Google Scholar

Rosenfeld, D., and Ulbrich, C. W. (2003). And rainfall estimation opportunities[m]//radar and atmospheric science: A collection of essays in honor of david Atlas. Boston, MA: American Meteorological Society, 237–258.Cloud microphysical properties, processes,

CrossRef Full Text | Google Scholar

Ryzhkov, A. V., and Zrnić, D. S. (1995). Comparison of dual-polarization radar estimators of rain. J. Atmos. Ocean. Technol. 12 (2), 249–256. doi:10.1175/1520-0426(1995)012<0249:codpre>2.0.co;2

CrossRef Full Text | Google Scholar

Schönhuber, M., Lammer, G., and Randeu, W. L. (2007). One decade of imaging precipitation measurement by 2D-video-distrometer. Adv. Geosci. 10, 85–90. doi:10.5194/adgeo-10-85-2007

CrossRef Full Text | Google Scholar

Seela, B. K., Janapati, J., Lin, P. L., Reddy, K., Shirooka, R., and Wang, P. K. (2017). A comparison study of summer season raindrop size distribution between Palau and Taiwan, two islands in western Pacific[J]. J. Geophys. Res. Atmos. 122 (21), 11787–11805.

CrossRef Full Text | Google Scholar

Seela, B. K., Janapati, J., Lin, P. L., Wang, P. K., and Lee, M-T. (2018). Raindrop size distribution characteristics of summer and winter season rainfall over north Taiwan[J]. J. Geophys. Res. Atmos. 123 (20), 11602–11624. doi:10.1029/2018jd028307

CrossRef Full Text | Google Scholar

Steiner, M., Smith, J. A., and Uijlenhoet, R. (2004). A microphysical interpretation of radar reflectivity–rain rate relationships. J. Atmos. Sci. 61 (10), 1114–1131. doi:10.1175/1520-0469(2004)061<1114:amiorr>2.0.co;2

CrossRef Full Text | Google Scholar

Stocker, T. F., Qin, D., and Plattner, G. K. (2013). Technical summary[M]//Climate change 2013: The physical science basis. Contribution of working Group I to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, 33–115.

Google Scholar

Tang, Q., Xiao, H., Guo, C., and Feng, L. (2014). Characteristics of the raindrop size distributions and their retrieved polarimetric radar parameters in northern and southern China. Atmos. Res. 135, 59–75. doi:10.1016/j.atmosres.2013.08.003

CrossRef Full Text | Google Scholar

Tapiador, F. J., Haddad, Z. S., and Turk, J. (2014). A probabilistic view on raindrop size distribution modeling: A physical interpretation of rain microphysics. J. Hydrometeorol. 15 (1), 427–443. doi:10.1175/jhm-d-13-033.1

CrossRef Full Text | Google Scholar

Tokay, A., Bashor, P. G., Habib, E., and Kasparis, T. (2008). Raindrop size distribution measurements in tropical cyclones. Mon. Weather Rev. 136 (5), 1669–1685. doi:10.1175/2007mwr2122.1

CrossRef Full Text | Google Scholar

Tokay, A., and Short, D. A. (1996). Evidence from tropical raindrop spectra of the origin of rain from stratiform versus convective clouds. J. Appl. Meteor. 35 (3), 355–371. doi:10.1175/1520-0450(1996)035<0355:eftrso>2.0.co;2

CrossRef Full Text | Google Scholar

Uijlenhoet, R. (2001). Raindrop size distributions and radar reflectivity–rain rate relationships for radar hydrology. Hydrol. Earth Syst. Sci. 5 (4), 615–628. doi:10.5194/hess-5-615-2001

CrossRef Full Text | Google Scholar

Uijlenhoet, R., and Torres, D. S. (2006). Measurement and parameterization of rainfall microstructure. J. hydrology 328 (1-2), 1–7. doi:10.1016/j.jhydrol.2005.11.038

CrossRef Full Text | Google Scholar

Ulbrich, C. W., and Atlas, D. (2007). Microphysics of raindrop size spectra: Tropical continental and maritime storms. J. Appl. Meteorology Climatol. 46 (11), 1777–1791. doi:10.1175/2007jamc1649.1

CrossRef Full Text | Google Scholar

Ulbrich, C. W., and Atlas, D. (1998). Rainfall microphysics and radar properties: Analysis methods for drop size spectra. J. Appl. Meteor. 37 (9), 912–923. doi:10.1175/1520-0450(1998)037<0912:rmarpa>2.0.co;2

CrossRef Full Text | Google Scholar

Wainwright, C. E., Dawson, D. T., Xue, M., and Zhang, G. (2014). Diagnosing the intercept parameters of the exponential drop size distributions in a single-moment microphysics scheme and impact on supercell storm simulations. J. Appl. Meteorology Climatol. 53 (8), 2072–2090. doi:10.1175/jamc-d-13-0251.1

CrossRef Full Text | Google Scholar

Wang, G., Zhou, R., Zhaxi, S., and Liu, S. (2021). Raindrop size distribution measurements on the Southeast Tibetan Plateau during the STEP project. Atmos. Res. 249, 105311. doi:10.1016/j.atmosres.2020.105311

CrossRef Full Text | Google Scholar

Wang, P. Y., Li, Z. Q., Schneider, C., Li, H., Hamm, A., Jin, S., et al. (2020). A test study of an energy and mass balance model application to a site on Urumqi Glacier No. 1, Chinese Tian Shan. Water 12 (10), 2865. doi:10.3390/w12102865

CrossRef Full Text | Google Scholar

Wang, P. Y., Li, Z. Q., Zhou, P., Li, H., Yu, G., Xu, C., et al. (2018). Long-term change in ice velocity of Urumqi glacier No. 1, tian Shan, China. Cold Regions Sci. Technol. 145, 177–184. doi:10.1016/j.coldregions.2017.10.008

CrossRef Full Text | Google Scholar

Wen, G., Xiao, H., Yang, H., Bi, Y., and Xu, W. (2017). Characteristics of summer and winter precipitation over northern China. Atmos. Res. 197, 390–406. doi:10.1016/j.atmosres.2017.07.023

CrossRef Full Text | Google Scholar

Wu, Y., and Liu, L. (2017). Statistical characteristics of raindrop size distribution in the Tibetan Plateau and southern China. Adv. Atmos. Sci. 34 (6), 727–736. doi:10.1007/s00376-016-5235-7

CrossRef Full Text | Google Scholar

Xu, C. H., Li, Z. Q., Li, H. L., Wang, F., and Zhou, P. (2019). Long-range terrestrial laser scanning measurements of annual and intra-annual mass balances for Urumqi Glacier No. 1, eastern Tien Shan, China. Cryosphere 13 (9), 2361–2383. doi:10.5194/tc-13-2361-2019

CrossRef Full Text | Google Scholar

Xu, C. H., Li, Z. Q., Wang, P. Y., Anjum, M. N., and Wang, F. (2018). Detailed comparison of glaciological and geodetic mass balances for Urumqi Glacier No.1, eastern Tien Shan, China, from 1981 to 2015. Cold Regions Sci. Technol. 155, 137–148. doi:10.1016/j.coldregions.2018.08.006

CrossRef Full Text | Google Scholar

Yamaji, M., Kubota, T., Takahashi, H. G., Hamada, A., and Takayabu, Y. N. (2018). Drop size distribution observed by dual-frequency precipitation radar onboard global precipitation measurement core satellite[C]//Remote Sensing and Modeling of the Atmosphere, Oceans, and Interactions VII. Int. Soc. Opt. Photonics 10782, 107820H.

Google Scholar

Yang, D. Q., Goodison, B. E., and Benson, C. (1998). Adjustment of daily precipitation data at 10 climate stations in Alaska: Application of World Meteorological Organization intercomparison results. Water Resour. Res. 34 (2), 241–256. doi:10.1029/97wr02681

CrossRef Full Text | Google Scholar

Yang, D. Q., Kang, E. S., and Felix, B. (1992). Characteristics of precipitation in the source area of Urumqi river basin[J]. J. Glaciol. Geocryol. (03), 258–266.

Google Scholar

Yang, D. Q., Shi, Y. F., and Kang, E. S. (1991). Results of solid precipitation measurement intercomparison in the alpine area of Urumqi River Basin[J]. Chin. Sci. Bull. 36 (13), 1105–1109.

Google Scholar

Yang, D. Q. (1988). Research on analysis and correction of systematic errors in precipitation measurement in Urumqi River basin, tianshan[D]. Thesis (Lanzhou, China: Lanzhou Institute of Glaciology and Geocryology, Chinese Academy of Sciences), 169.

Yang, M., Li, Z. Q., Anjum, M. N., Zhang, X., Gao, Y., and Xu, C. (2021). On the importance of subsurface heat flux for estimating the mass balance of alpine glaciers. Glob. Planet. Change 207, 103651. doi:10.1016/j.gloplacha.2021.103651

CrossRef Full Text | Google Scholar

Ye, B. S., Yang, D. Q., Ding, Y. Z., Han, T., and Koike, T. (2004). A bias-corrected precipitation climatology for China. J. Hydrometeorol. 5, 1147–1160. doi:10.1175/jhm-366.1

CrossRef Full Text | Google Scholar

Yuter, S. E., Kingsmill, D. E., Nance, L. B., and Loffler-Mang, M. (2006). Observations of precipitation size and fall speed characteristics within coexisting rain and wet snow. J. Appl. Meteorology Climatol. 45 (10), 1450–1464. doi:10.1175/jam2406.1

CrossRef Full Text | Google Scholar

Zhang, A., Hu, J., Chen, S., Hu, D., Liang, Z., Huang, C., et al. (2019). Statistical characteristics of raindrop size distribution in the monsoon season observed in southern China. Remote Sens. 11 (4), 432. doi:10.3390/rs11040432

CrossRef Full Text | Google Scholar

Zhang, G. F., Li, Z. Q., and Wang, W. B. (2014). Rapid decrease of observed mass balance in the Urumqi glacier No. 1, tianshan mountains, central Asia. Quat. Int. 349, 135–141. doi:10.1016/j.quaint.2013.08.035

CrossRef Full Text | Google Scholar

Zhao, Y., Chen, R., Han, C., Wang, L., Guo, S., and Liu, J. (2021). Correcting precipitation measurements made with Geonor T-200B weighing gauges near the August-one ice cap in the Qilian Mountains, Northwest China[J]. J. Hydrometeorol. 22 (8), 1973–1985. doi:10.1175/jhm-d-20-0271.1

CrossRef Full Text | Google Scholar