Dynamic resilient modulus of subgrade silty clay for heavy-haul railway: an experimental investigation and the predicted method

A large-scale series of cyclic triaxial tests were conducted to explore the evolution of the dynamic resilient modulus of silty clay for the heavy-haul railway subgrade. A novel loading sequence for measuring the dynamic resilient modulus was established, which characterized the dynamic stress state of the subgrade induced by the heavy-haul train load. In the experimental investigation, the deviatoric stresses, confining stress, initial moisture content, and compaction degree were considered as variables, and the effects of the aforementioned variables were evaluated quantitatively. The experimental results showed that the dynamic resilient modulus was negatively related to deviatoric stresses and initial moisture content, where the average decreased rates were 14.65% and 27.79% with the increase in deviatoric stresses from 60 kPa to 150 kPa and increase in the initial moisture content from 9.8% to 15.8%, respectively. Furthermore, the dynamic resilient modulus was positively related to confining stress and compaction degree, where the average increased rates were 23.25% and 27.48% with the increase in confining stress from 20 kPa to 60 kPa and increase in compaction degree from 0.91 to 0.95. To provide a better application, the two high-accuracy predicted methods were established through the empirical model and artificial neural network approach including the aforementioned variables. This study can provide useful guidelines for the effective and safe design of the heavy-haul railway subgrade filled with silty clay.

1 Introduction

The heavy-haul train is a meaningful approach to improving the capacity and efficiency of railway transportation (Krechowiecki-Shaw et al., 2016). The subgrade is usually considered as the important support to undertake the cyclic load transmitted from the superstructure such as track and ballast, and its stability is critical for the safe operation of heavy-haul railways (Leng et al., 2017; Bian et al., 2018; Thevakumar et al., 2021; Li et al., 2022). Compared with the common railway, the cyclic stress is higher and the action depth is bigger in the subgrade induced by a heavy-haul train load (Zhao et al., 2021; Cui et al., 2022; Cui et al., 2023). The dynamic resilient modulus is a key parameter for evaluating the mechanical performance and service life of the subgrade for railways and pavement structures (Han and Vanapalli, 2016; Nie et al., 2021; Wang et al., 2022; Indraratna et al., 2023a). Therefore, it is necessary to reveal the evolution of the dynamic resilient modulus of the heavy-haul railway subgrade and establish the predicted method on the dynamic resilient modulus.

The concept of dynamic resilient modulus was proposed by Seed and applied for evaluating the dynamic performance of the subgrade, which was defined as the ratio of the amplitude of deviatoric stresses to resilient strain (Seed et al., 1962). Subsequently, numerous scholars studied the evolution and estimation of the dynamic resilient modulus of subgrade soils and structures subjected to the traffic load. According to the previous research, several effects on the dynamic resilient modulus were mainly divided into the types of subgrade soils, stress levels exposed to soil specimens, and physical conditions of soils such as initial moisture content and compaction degree (Li and Selig, 1994; Kim and Kim, 2007; Ng et al., 2013; Zhang et al., 2018; Zhang et al., 2019a; Zhang et al., 2019b; Liu et al., 2019; Chen et al., 2020). Furthermore, numerous prediction models on the dynamic resilient modulus were established and validated, where these models were divided into three categories, such as models based only on the statistical relationship between the dynamic resilient modulus and physical properties (CBR, etc.), models considering the applied stress state (deviatoric stresses, confining stress, suction stress, etc.), and models extending the independent stress state variable approach. Recently, with the development of the experimental data scale and artificial neural network (ANN) method, many data-driven models have been successfully used for predicting the dynamic resilient modulus of subgrade soils, where the ANN model can capture the complex non-linear relationships of high-dimensional data to promote prediction accuracy (Khasawneh and Al-jamal, 2019; Ren et al., 2019; Zhang J.-h. et al., 2021; Zhang Q. et al., 2021; Heidarabadizadeh et al., 2021; Zou et al., 2021; Khan et al., 2022; Indraratna et al., 2023b).

However, the research results mentioned previously were obtained and analyzed based on the conventional cyclic stress levels induced by normal traffic load, where the high cyclic stress levels induced by the heavy-haul train load were little considered, especially for subgrade silty clay. Therefore, the objective of this paper is to reveal the evolution of the dynamic resilient modulus including the effect variables of deviatoric stresses, confining stress, moisture content, and compaction degree by using a series of cyclic triaxial tests conducted on subgrade silty clay. In addition, based on the experimental results, the predicted methods for predicting the dynamic resilient modulus were proposed through the empirical model and ANN approach, which can supply the fundamental reference for the subgrade design of the heavy-haul railway.

2 Experimental investigation

2.1 Preparation of the specimen

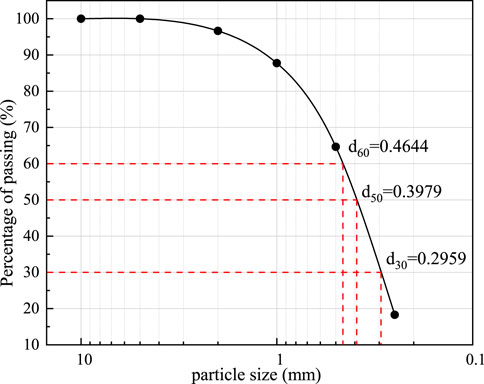
The soil tested in this paper was taken from the subgrade site of the Datong–Qinhuangdao heavy-haul railway, as shown in Figure 1, and the field tests of the dynamic response of the heavy-haul subgrade were conducted by our team here (Cui et al., 2023). According to the Chinese Standard TB 10102–2010 (Code for Soil Test of Railway Engineering), the basic physical properties of the tested soil were obtained and listed in Figure 2 and Table 1.

FIGURE 1

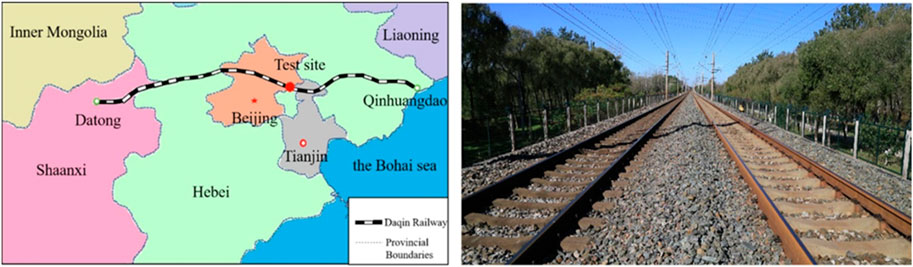
FIGURE 1. Location of subgrade silty clay sampling (Cui et al., 2023).

FIGURE 2

FIGURE 2. Gradation curve of soil samples.

TABLE 1

TABLE 1. Basic physical properties of the tested soil.

Considering the variations in the compaction degree and moisture content of subgrade soil during the service period, the compaction degrees are set as 0.91, 0.93, and 0.95, and the initial moisture contents are set as 10%, 13% (optimal moisture content), and 16%, respectively.

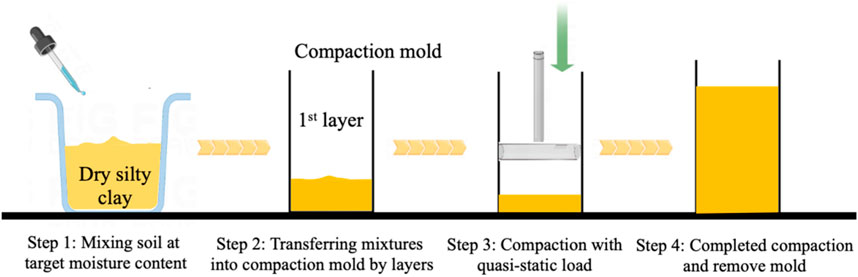
The specimens were unsaturated cylinders with 39.1 mm diameter and 80 mm height under the target compaction degree and initial moisture content. Meanwhile, the predetermined silty clays were compacted into five layers with equal thickness and quality of any layer to ensure the uniform distribution of soil particles and water, as shown in Figure 3.

FIGURE 3

FIGURE 3. Schematic illustration of specimen compaction.

2.2 Cyclic triaxial test

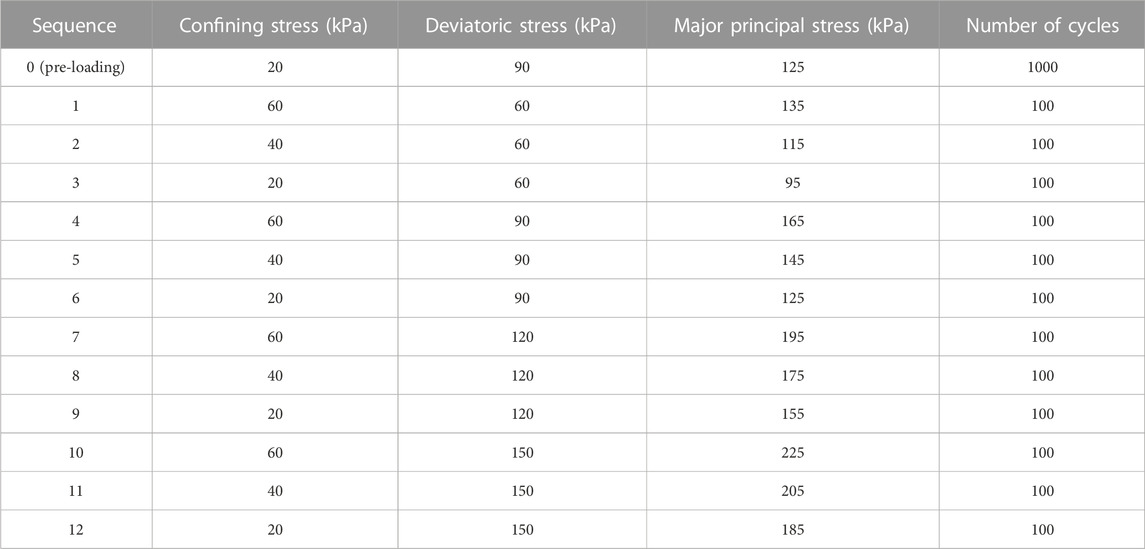
Due to the stress dependence of the dynamic resilient modulus, the loading condition is crucial to measure and determine the dynamic resilient modulus reasonably by using the cyclic triaxial test. According to the stress state obtained from the field test and numerical simulation, and considering the expansion of railway capacity such as the 400 kN axle load train in Australia, the deviatoric stresses are set as 60 kPa, 90 kPa, 120 kPa, and 150 kPa, and the confining stresses are set as 20 kPa, 40 kPa, and 60 kPa (Indraratna et al., 2021; Zhao et al., 2021; Cui et al., 2023). Meanwhile, the additional 15 kPa static deviatoric stresses are added to simulate the superstructure. The loading frequency is set as 1 Hz, which can be usually calculated by the passing speed of the heavy-haul train. Before the formal loading, a pre-loading phase of 1000 cycles is adopted to eliminate the initial plastic strain and reduce the variability of specimens. In general, the loading sequence is listed in Table 2. It is shown that the dynamic resilient modulus is defined and calculated as follows:

$M_R=\frac{{\sigma }_d}{{\epsilon }_d},(1)$

where M_R is the dynamic resilient modulus (MPa), σ_d is the deviatoric stress (kPa), σ_d = σ₁˗σ₃, where σ₁ and σ₃ are the major principal stress and confining stress (kPa), respectively, and εd is the average resilient deformation recorded in the last five cyclic loadings.

TABLE 2

TABLE 2. Loading sequence for heavy-haul railway subgrade soils.

3 Results and analysis

3.1 Effect of deviatoric stresses

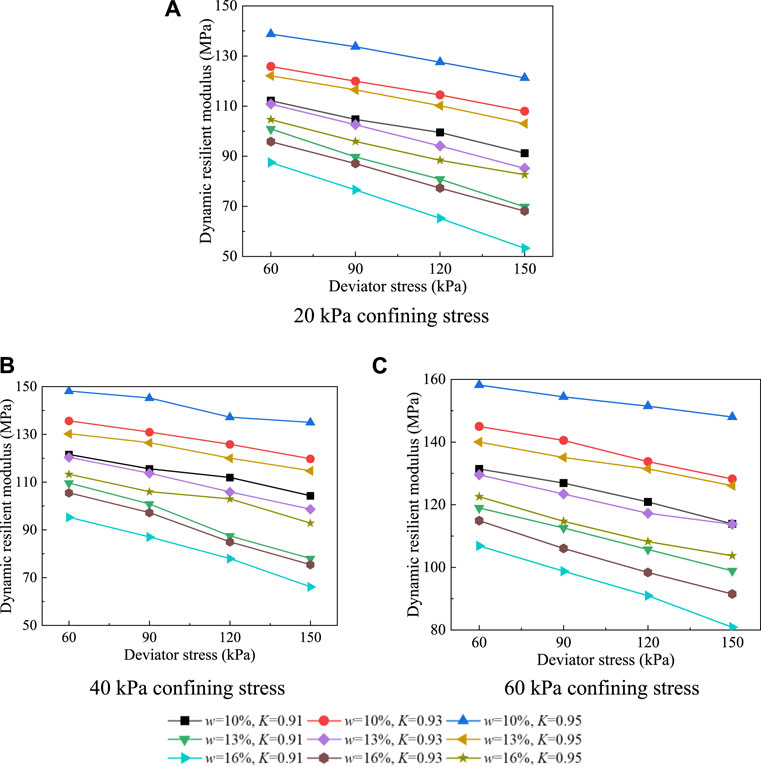
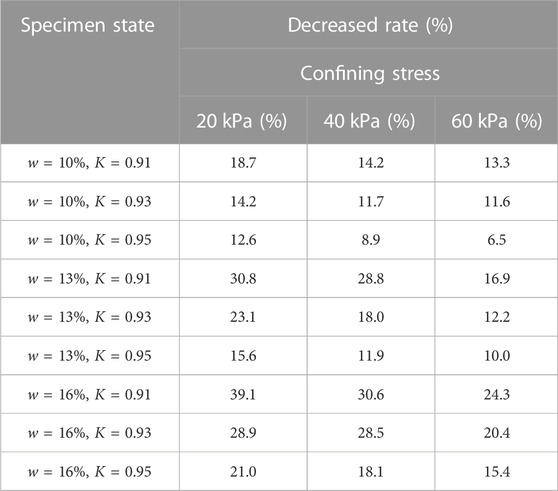
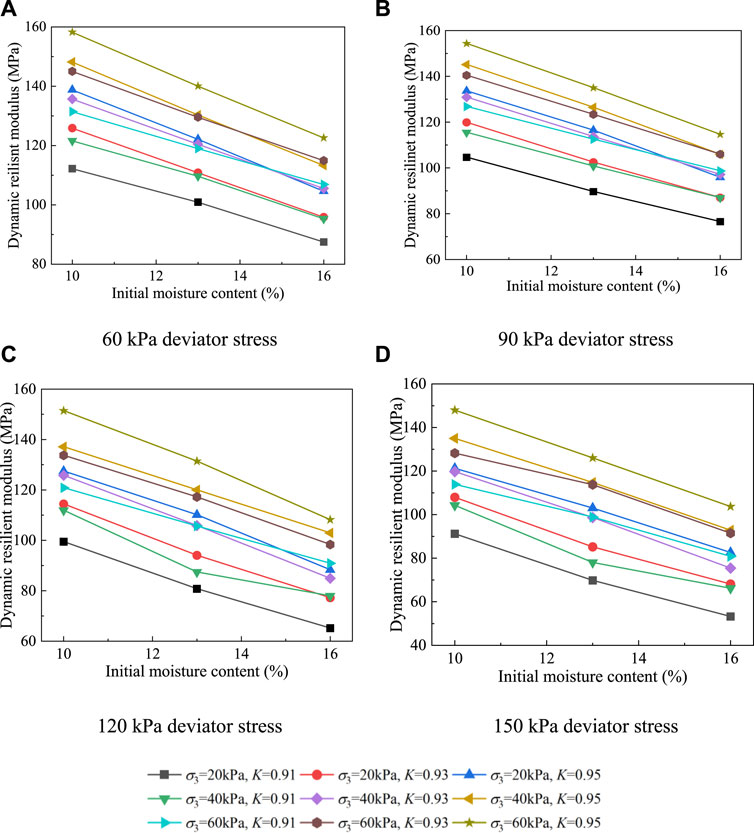
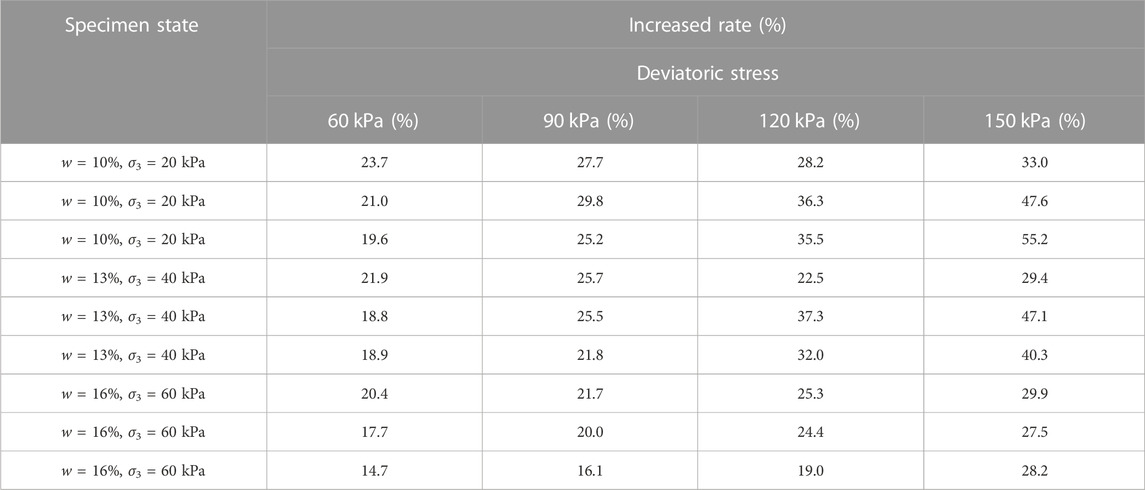
Figure 4 shows the effect of deviatoric stresses on the dynamic resilient modulus of subgrade silty clay at different confining stresses and physical states (initial moisture content w and compaction degree K). It can be seen that with the increase in deviatoric stresses, the dynamic resilient modulus decreases under any stress and physical states. Because the increase in deviatoric stresses makes the resilient strain increase during every cycle of loading, there is a decrease in the dynamic resilient modulus according to the calculation by Eq. 1. Then, the decreased rate is introduced and defined as the ratio of variation in the dynamic resilient modulus with an increase in maximum deviatoric stresses to the values of dynamic resilient modulus with minimum deviatoric stresses. Through the calculation, the results of the decreased rate due to the deviatoric stresses are tabulated in Table 3. It can be concluded that the average decreased rate is 14.65% when the deviatoric stresses increase from 60 kPa to 150 kPa. In addition, the maximum value of the decreased rate is up to 39.1% when confining stress, moisture content, and compaction degree are 20 kPa, 15.8%, and 0.91, respectively, which means that the deviatoric stress level must be considered in the subgrade design and be controlled and limited in a safe range, such as promoting the stiffness of track or ballast.

FIGURE 4

FIGURE 4. Effect of deviatoric stresses on the dynamic resilient modulus.

TABLE 3

TABLE 3. Effect of deviatoric stresses on the decreased rate.

3.2 Effect of confining stress

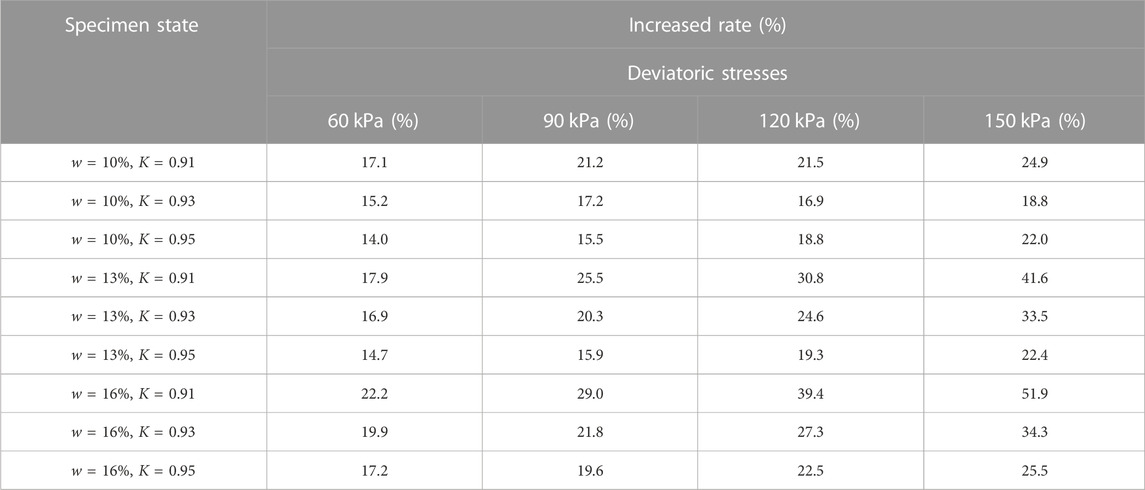
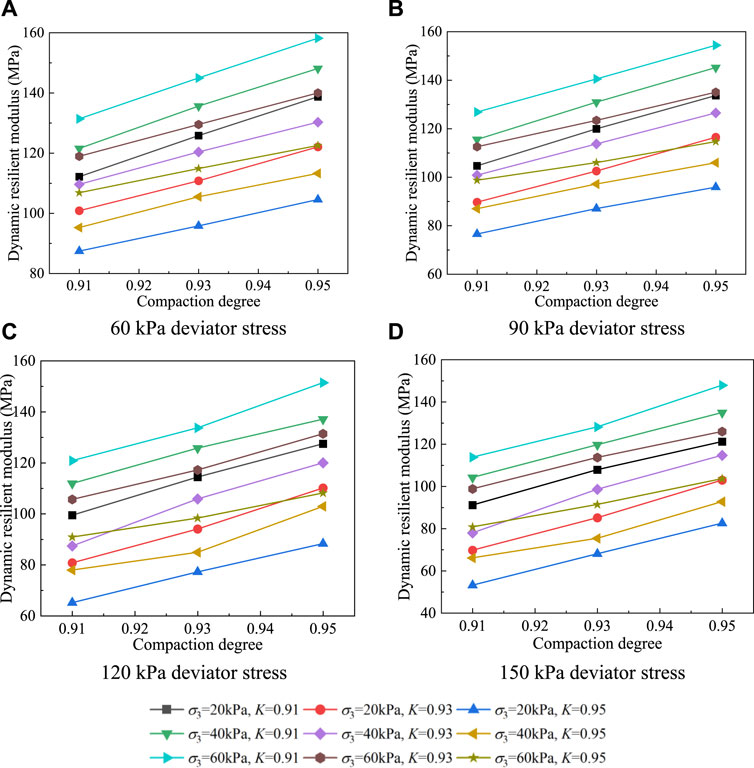
Figure 5 shows the effect of confining stress on the dynamic resilient modulus when the other states of the specimen are the same. It can be seen that the dynamic resilient modulus increases with the increase in confining stress, which is because the confining stress can restrict the deformation of the specimen subjected to the cyclic loading, leading to a decrease in the value of resilient strain with every cycle loading. Similar to the quantitative analysis mentioned previously, the increased rate is defined as the ratio of the variation in the dynamic resilient modulus with an increase in the maximum confining stress to the values of the dynamic resilient modulus with minimum confining stress. Table 4 shows the calculated results of increased rates of every test condition. It can be known that the average increased rate is 23.25% when the confining stress increases from 20 kPa to 60 kPa. In addition, the maximum value of increased rate due to the confining stress is up to 51.9% at the state of 150 kPa deviatoric stresses, 15.8% initial moisture content, and 0.91 compaction degree, where this state of the tested specimen can be regarded as the most unfavorable condition among the designed test conditions. Therefore, increasing the confining stress level can be taken as an effective measurement to guarantee subgrade stability, such as the subgrade structures with prestress (Dong et al., 2023) (as shown in Figure 6).

FIGURE 5

FIGURE 5. Effect of confining stress on the dynamic resilient modulus.

TABLE 4

TABLE 4. Effect of confining stress on the increased rate.

FIGURE 6

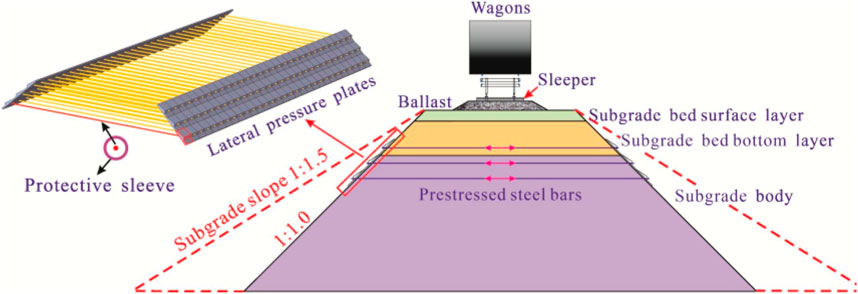
FIGURE 6. Schematic drawing of the prestressed subgrade structure (Dong et al., 2023).

3.3 Effect of initial moisture content

Figure 7 shows the relationships between the dynamic resilient modulus and different moisture content. It can be proven that the dynamic resilient modulus decreases with the increase in the initial moisture content obviously. The reason for this phenomenon is that when the initial moisture content increases, the water film on the soil particle surface thickens and friction between the soil particles decreases. Then, the soil particles move easily, and deformation increases under the cyclic loading, resulting in the decrease in the dynamic resilient modulus and degrade in performance. Similarly, the decreased rate is also used, where the calculation is the same as that mentioned previously as the ratio of variation in dynamic resilient modulus with an increase in the maximum initial moisture content to the values of dynamic resilient modulus with the minimum initial moisture content. As tabulated in Table 5, it can be concluded that the average decreased rate is 27.79% when the initial moisture content increases from 10% to 16%. In addition, the maximum decreased rate is up to 41.6% due to the increase in the initial moisture content. Furthermore, it is well known that if the initial moisture content is higher, the sensitivity of freeze–thaw or drying–wetting cycles of subgrade soil is more obvious to soften the mechanical performance of the subgrade under the coupled effect of the heavy-haul train load and environmental load (Ding et al., 2020; Hao et al., 2022; Abbey et al., 2023; Ha et al., 2023). Thus, it is suggested that the subgrade silty clay should be treated by additional mixtures or the drainage materials should be used in the subgrade structure to control the moisture content level during the service period of the heavy-haul railway (Changizi et al., 2021; Wu et al., 2021; Zhang et al., 2023).

FIGURE 7

FIGURE 7. Effect of the initial moisture content on the dynamic resilient modulus.

TABLE 5

TABLE 5. Effect of the initial moisture content on the decreased rate.

3.4 Effect of compaction degree

Figure 8 shows the effect of confining stress on the dynamic resilient modulus when the other tested conditions are the same. Obviously, it can be known that the dynamic resilient modulus is positively related to the compaction degree. The mechanism is that when the compaction degree of the soil specimen is larger, the pores and contact force between the soil particles are smaller and stronger, respectively, which promote the resistance on deformation of the specimen under cyclic loading. Table 6 presents the increased rates due to the increase in the compaction degree, where this increased rate is decided as the ratio of variation in the dynamic resilient modulus with an increase in the maximum compaction degree to the values of dynamic resilient modulus with the minimum compaction degree. The average increased rate is 27.48%, and the maximum value is up to 47.6%. Hence, the construction of the heavy-haul railway subgrade must improve the compaction quality to reach the designed compaction degree, such as the development of intelligent compaction technology.

FIGURE 8

FIGURE 8. Effect of compaction degree on the dynamic resilient modulus.

TABLE 6

TABLE 6. Effect of compaction degree on the increased rate.

4 Predicted method

4.1 Empirical model

In the existing empirical model for predicting the dynamic resilient modulus of subgrade soils, the most widely used model is the three-parameter universal model proposed by NCHRP 1–28A, as shown in the following equation:

$M_R=k_1{P}_a{\left(\frac{\theta }{P_a}\right)}^{k_2}{\left(\frac{{\tau }_{oct}}{P_a}+1\right)}^{k_3},(2)$

where $P_a=101.3$ kPa is the atmospheric pressure; $\theta$ is the bulk stress, $\theta ={\sigma }_1+{\sigma }_2+{\sigma }_3$ (${\sigma }_1$ is the major principal stress, ${\sigma }_2$ is the intermediate principal stress, and ${\sigma }_3$ is the confining stress); ${\tau }_{oct}$ is the octahedral shear stress, ${\tau }_{oct}=\sqrt{2}/3\left({\sigma }_1-{\sigma }_3\right)=\sqrt{2}/3{\sigma }_d$; and $k_1$, $k_2$, and $k_3$ are the regression coefficients.

According to the aforementioned analysis, the effects of the compaction degree and initial moisture content are important in relation to the dynamic resilient modulus and should be introduced into the prediction model. Thus, the novel empirical model is proposed by modifying the three-parameter model as follows:

$M_r=k_1{P}_a{K}^{k_2}{\left(\frac{w}{w_{opt}}\right)}^{k_3}{\left(\frac{\theta }{P_a}\right)}^{k_4}{\left(\frac{{\tau }_{oct}}{P_a}+1\right)}^{k_5},(3)$

where K is the compaction degree, w is the initial moisture content, w_opt is the optimal moisture content, and parameters k₁–k₅ are the regression coefficients.

In the proposed model, the coefficient k₁ is a positive value to adjust the fitting results. Then, it has been concluded that the dynamic resilient modulus is positively related to the compaction degree and confining stress, where the coefficients k₂ and k₄ are the positive values. Furthermore, the coefficients k₃ and k₅ are negative values due to the softening effect on the dynamic resilient performance of subgrade soils caused by the increase in the initial moisture content and deviatoric stresses.

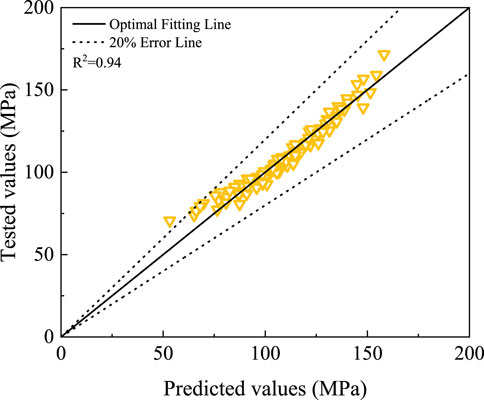
Through non-linear regression fitting, the regression coefficients are obtained based on the experimental data, and fitted results are shown in Table 7 and Figure 9. According to the comparison between the tested values and predicted values, the proposed empirical model is acceptable and accurate to be applied for predicting the dynamic resilient modulus of subgrade silty clay.

TABLE 7

TABLE 7. Regression coefficients of the proposed empirical model.

FIGURE 9

FIGURE 9. Comparison between the tested values and predicted values.

4.2 ANN model

4.2.1 Basic principle

The error backpropagation network is the most well-known feedforward network, which was proposed by Rumelhart et al. (1986), and it has good multi-dimensional function mapping capabilities. This network uses the square of the error as the objective function, employs the gradient descent method to find the minimum value of the objective function, and continuously modifies the connection weight to reduce the difference between the network output and objective output. However, the convergence speed of the BP network is slow, and it is easy to fall into the local optimum. Ding et al. (2011) optimized the BP network by using the genetic algorithm (GA), and the results showed that this method was less likely to fall into a local optimum and it had superior generalization capability.

This paper uses the genetic algorithm to optimize the input initial weights and thresholds of the BP network. The algorithm flowchart is shown in Figure 10: the network is initialized first, and then, the initial weights and thresholds are generated; the second process is the GP process, the numerical values are encoded, the initial population is created, the fitness function is established, and finally, the individuals with high fitness for replication are selected, intersected, and mutated to update the new populations in this process; and finally, the optimal weight and threshold for the BP algorithm are output if the termination condition is met; otherwise, the aforementioned operation is repeated.

FIGURE 10

FIGURE 10. GA–BP algorithm flowchart.

The input value is normalized and transmitted forward to the hidden layer, and this input value is then non-linearly transformed to output by the activation function, and the relationship between the input and output is shown as follows:

$y_j=f\left({\displaystyle \sum _{i=1}^n}{w}_{ji}{x}_i\right)+b_j,(4)$

where y_i is the actual output variable of neurons; f is the activation function, and the sigmoid function is used as the activation function; w_ji is the network weight; x_j is the input variable of the neuron; and b_j is the network threshold.

The loss function is used to calculate the network error, as given in the following equation:

$E_{total}=\frac{1}{2}{\displaystyle \sum _{k=1}^m}\left(T_k-O_k\right),(5)$

where E_total is the sum of squares of network errors and m is the number of output nodes; T_k is the target output; and O_k is the output of the k output layer.

The training completes if the termination condition is met; otherwise, the network weights and thresholds are backpropagated to the input layer to update the network and repeat it to meet the objective value by using the gradient descent method shown as follows:

$w_{ij}\left(l+1\right)=w_{ij}\left(l\right)-\eta \frac{\partial E_{total}}{\partial w_{ij}\left(l\right)},(6)$

$w_{jk}\left(l+1\right)=w_{jk}\left(l\right)-\eta \frac{\partial E_{total}}{\partial w_{jk}\left(l\right)},(7)$

$b_q\left(l+1\right)=b_q\left(l\right)-\eta \frac{\partial E_{total}}{\partial b_q\left(l\right)},(8)$

where w_ij(l), w_ij(l+1), w_jk(l), w_jk(l+1), b_q(l), and b_q(l+1) are the connection weights of input layer neuron i and hidden layer neuron j, the connection weights between the hidden layer neuron j and the output layer neuron k in the lth and l+1st iteration, and the qth offset in the lth and l+1st iteration, respectively; η is the learning rate, usually equal to 0.1.

4.2.2 Construction of the ANN

The GA–BP model in this paper contains three network layers, including an input layer, a hidden layer, and an output layer, as shown in Figure 11. It can be seen previously that the important factors affecting the dynamic resilient modulus are the compaction degree K, initial moisture content w, bulk stress θ, and octahedral shear stress τ_oct. Therefore, these four parameters are the input of the neural network. The number of nodes in the hidden layer n₂ is twice the number of nodes in the input layer and plus 1 so that n₂=9, and the output layer value is the dynamic resilient modulus (Zhang J.-h. et al., 2021).

FIGURE 11

FIGURE 11. Structure diagram of the ANN.

The mapping relationship between the input layer and the output layer is shown in the following equations:

$f\left(z\right)=\frac{1}{1+e^{-z}},(9)$

$y=f_{HO}\left(b_k+{\displaystyle \sum _{j=1}^9}{w}_{j1}{f}_{IH}\left(b_j+{\displaystyle \sum _{i=1}^4}{w}_{ij}{x}_i\right)\right).(10)$

Among them, f_IH and f_HO are the sigmoid functions between the input layer and the hidden layer, as well as between the hidden layer and the output layer, respectively; w_ij and w_j1 are the connection weights between the input layer and the hidden layer, as well as between the hidden layer and the output layer, respectively; b_j and b_k are the offset of the hidden layer and the output layer, respectively; and x_i is the input variable.

4.2.3 Training results and validation

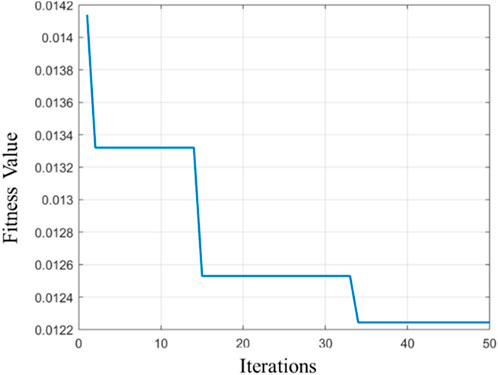
As shown in Figure 12, the population fitness decreases at the 1st, 14th, and 33rd generations, with fitness values declining by 5.8%, 4.5%, and 2.3%, respectively. It can be seen that the genetic algorithm has a certain optimization effect on the initial weights and thresholds of the input BP neural network.

FIGURE 12

FIGURE 12. Fitness curve of the established GA–BP model.

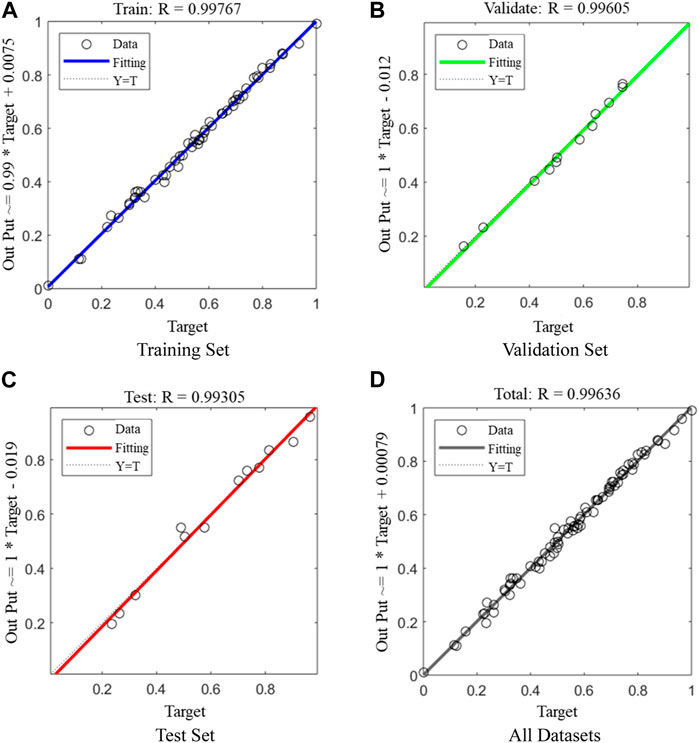
Figure 13 shows the target value and output values of the training set, validation set, testing set, and all datasets, where the values of R² are all above 0.99. Compared with R² = 0.94 in the empirical model proposed previously, the accuracy of dynamic resilient modulus given by the GA–BP model is better. The prediction method based on ANNs has higher accuracy compared to traditional methods, and more importantly, its scalability is great. In subsequent research, if other physical or environmental factors, such as freeze–thaw cycles, are considered, it can still have high accuracy with sufficient training datasets. However, traditional prediction methods need to re-establish prediction formulas. Therefore, the prediction model based on ANNs has greater potential in future research, and we will also conduct further research on this method in the future.

FIGURE 13

FIGURE 13. Comparison between target values and output values.

In order to improve the practicality and usability of the GA–BP model, the graphical user interface (GUI) is designed and developed, as shown in Figure 14, which provides the application and tool to obtain the value of dynamic resilient modulus easily for practicing engineers.

FIGURE 14

FIGURE 14. GUI for predicting the dynamic resilient modulus by the GA–BP model.

5 Conclusion

In order to explore the evolution of the dynamic resilient modulus of subgrade silty clay subjected to a heavy-haul train load, a series of cyclic triaxial tests were conducted considering the deviatoric stresses, confining stress, initial moisture content, and compaction degree as experimental variables. The main conclusions are as follows:

1) The dynamic resilient modulus is positively related to the confining stress and compaction degree, where the average increased values of each other are 23.25% and 27.48%, respectively.

2) The dynamic resilient modulus decreases with the increase in deviatoric stresses and initial moisture content, where the average decreased values of each other are 14.65% and 27.79%, respectively.

3) Based on the experimental results, the predicted methods are established and validated by the empirical model and GA–BP model. The two prediction models have high accuracy for predicting the dynamic resilient modulus, where the GA–BP model is better (R²=0.99) than the empirical model (R²=0.94).

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

JH: conceptualization, writing–original draft, and writing–review and editing. HW: data curation and writing–review and editing. XZ: methodology, supervision, and writing–original draft. TY: writing–original draft. XJ: software and writing–review and editing. CL: writing–original draft. XL: formal analysis, methodology, and writing–review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (Nos. 52178429, U22A20235, and 52027813) and the Natural Science Foundations of Shandong Province, China (No. ZR2020ME242).

Conflict of interest

Authors JH, HW, TL, XJ, and CL were employed by Shandong High-speed Construction Management Group Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbey, S. J., Amakye, S. Y. O., Eyo, E. U., Booth, C. A., and Jeremiah, J. J. (2023). Wet–dry cycles and microstructural characteristics of expansive subgrade treated with sustainable cementitious waste materials. Materials 16 (8), 3124. doi:10.3390/ma16083124

PubMed Abstract | CrossRef Full Text | Google Scholar

Bian, X., Li, W., Hu, J., Liu, H., Duan, X., and Chen, Y. (2018). Geodynamics of high-speed railway. Transp. Geotech. 17, 69–76. doi:10.1016/j.trgeo.2018.09.007

CrossRef Full Text | Google Scholar

Changizi, F., Ghasemzadeh, H., and Ahmadi, S. (2021). Evaluation of strength properties of clay treated by nano-SiO2 subjected to freeze–thaw cycles. Road Mater. Pavement Des. 23, 1221–1238. doi:10.1080/14680629.2021.1883466

CrossRef Full Text | Google Scholar

Chen, W.-B., Feng, W.-Q., and Yin, J.-H. (2020). Effects of water content on resilient modulus of a granular material with high fines content. Constr. Build. Mater., 236. doi:10.1016/j.conbuildmat.2019.117542

CrossRef Full Text | Google Scholar

Cui, X., Du, Y., Bao, Z., Xiao, Y., Hao, J., Li, X., et al. (2023). Field evaluation of the three-dimensional dynamic stress state of the subgrade induced by the heavy-haul train load. Transp. Geotech. 38, 100903. doi:10.1016/j.trgeo.2022.100903

CrossRef Full Text | Google Scholar

Cui, X., Li, X., Hao, J., Wang, Y., Bao, Z., Du, Y., et al. (2022). Dynamic response of unsaturated poroelastic ground underlying uneven pavement subjected to vehicle load. Soil Dyn. Earthq. Eng. 156, 107164. doi:10.1016/j.soildyn.2022.107164

CrossRef Full Text | Google Scholar

Ding, L.-q., Han, Z., Zou, W.-l., and Wang, X.-q. (2020). Characterizing hydro-mechanical behaviours of compacted subgrade soils considering effects of freeze-thaw cycles. Transp. Geotech. 24, 100392. doi:10.1016/j.trgeo.2020.100392

CrossRef Full Text | Google Scholar

Ding, S., Su, C., and Yu, J. (2011). An optimizing BP neural network algorithm based on genetic algorithm. Artif. Intell. Rev. 36 (2), 153–162. doi:10.1007/s10462-011-9208-z

CrossRef Full Text | Google Scholar

Dong, J., Xu, F., Zhang, Q., Leng, W., Li, Y., Wu, S., et al. (2023). Study on vibration characteristics of fine breccia soil subgrade reinforced with a new prestressed structure under train cyclic loading. Constr. Build. Mater. 2023, 397. doi:10.1016/j.conbuildmat.2023.132364

CrossRef Full Text | Google Scholar

Han, Z., and Vanapalli, S. K. (2016). State-of-the-art: prediction of resilient modulus of unsaturated subgrade soils. Int. J. Geomechanics 16 (4). doi:10.1061/(asce)gm.1943-5622.0000631

CrossRef Full Text | Google Scholar

Hao, J., Cui, X., Bao, Z., Jin, Q., Li, X., Du, Y., et al. (2023). Dynamic resilient modulus of heavy-haul subgrade silt subjected to freeze-thaw cycles: experimental investigation and evolution analysis. Soil Dyn. Earthq. Eng. 2023, 173. doi:10.1016/j.soildyn.2023.108092

CrossRef Full Text | Google Scholar

Hao, J., Cui, X., Qi, H., Zheng, Y., and Bao, Z. (2022). Dynamic behavior of thawed saturated saline silt subjected to freeze-thaw cycles. Cold Regions Sci. Technol., 194. doi:10.1016/j.coldregions.2021.103464

CrossRef Full Text | Google Scholar

Heidarabadizadeh, N., Ghanizadeh, A. R., and Behnood, A. (2021). Prediction of the resilient modulus of non-cohesive subgrade soils and unbound subbase materials using a hybrid support vector machine method and colliding bodies optimization algorithm. Constr. Build. Mater., 275. doi:10.1016/j.conbuildmat.2020.122140

CrossRef Full Text | Google Scholar

Indraratna, B., Armaghani, D. J., Gomes Correia, A., Hunt, H., and Ngo, T. (2023a). Prediction of resilient modulus of ballast under cyclic loading using machine learning techniques. Transp. Geotech., 38. doi:10.1016/j.trgeo.2022.100895

CrossRef Full Text | Google Scholar

Indraratna, B., Armaghani, D. J., Gomes Correia, A., Hunt, H., and Ngo, T. (2023b). Prediction of resilient modulus of ballast under cyclic loading using machine learning techniques. Transp. Geotech. 38, 100895. doi:10.1016/j.trgeo.2022.100895

CrossRef Full Text | Google Scholar

Indraratna, B., Ngo, T., Ferreira, F. B., Rujikiatkamjorn, C., and Tucho, A. (2021). Large-scale testing facility for heavy haul track. Transp. Geotech., 28. doi:10.1016/j.trgeo.2021.100517

CrossRef Full Text | Google Scholar

Khan, K., Jalal, F. E., Khan, M. A., Salami, B. A., Amin, M. N., Alabdullah, A. A., et al. (2022). Prediction models for evaluating resilient modulus of stabilized aggregate bases in wet and dry alternating environments: ANN and GEP approaches. Materials 15 (13), 4386. doi:10.3390/ma15134386

PubMed Abstract | CrossRef Full Text | Google Scholar

Khasawneh, M. A., and Al-jamal, N. F. (2019). Modeling resilient modulus of fine-grained materials using different statistical techniques. Transp. Geotech. 21, 100263. doi:10.1016/j.trgeo.2019.100263

CrossRef Full Text | Google Scholar

Kim, D., and Kim, J. R. (2007). Resilient behavior of compacted subgrade soils under the repeated triaxial test. Constr. Build. Mater. 21 (7), 1470–1479. doi:10.1016/j.conbuildmat.2006.07.006

CrossRef Full Text | Google Scholar

Krechowiecki-Shaw, C. J., Jefferson, I., Royal, A., Ghataora, G. S., and Alobaidi, I. M. (2016). Degradation of soft subgrade soil from slow, large, cyclic heavy-haul road loads: a review. Can. Geotechnical J. 53 (9), 1435–1449. doi:10.1139/cgj-2015-0234

CrossRef Full Text | Google Scholar

Leng, W., Xiao, Y., Nie, R., Zhou, W., and Liu, W. (2017). Investigating strength and deformation characteristics of heavy-haul railway embankment materials using large-scale undrained cyclic triaxial tests. Int. J. Geomechanics 17 (9). doi:10.1061/(asce)gm.1943-5622.0000956

CrossRef Full Text | Google Scholar

Li, D., and Selig, E. T. (1994). Resilient modulus for fine-grained subgrade soils. J. Geotechnical Eng. 120 (6), 939–957. doi:10.1061/(asce)0733-9410(1994)120:6(939)

CrossRef Full Text | Google Scholar

Li, J., Zhang, J., Zhang, A., and Peng, J. (2022). Evaluation on deformation behavior of granular base material during repeated load triaxial testing by discrete-element method. Int. J. Geomechanics 22 (11). doi:10.1061/(asce)gm.1943-5622.0002539

CrossRef Full Text | Google Scholar

Liu, X., Zhang, X., Wang, H., and Jiang, B. (2019). Laboratory testing and analysis of dynamic and static resilient modulus of subgrade soil under various influencing factors. Constr. Build. Mater. 195, 178–186. doi:10.1016/j.conbuildmat.2018.11.061

CrossRef Full Text | Google Scholar

Ng, C. W. W., Zhou, C., Yuan, Q., and Xu, J. (2013). Resilient modulus of unsaturated subgrade soil: experimental and theoretical investigations. Can. Geotechnical J. 50 (2), 223–232. doi:10.1139/cgj-2012-0052

CrossRef Full Text | Google Scholar

Nie, R., Sun, B., Leng, W., Li, Y., and Ruan, B. (2021). Resilient modulus of coarse-grained subgrade soil for heavy-haul railway: an experimental study. Soil Dyn. Earthq. Eng., 150. doi:10.1016/j.soildyn.2021.106959

CrossRef Full Text | Google Scholar

Ren, J., Vanapalli, S. K., Han, Z., Omenogor, K. O., and Bai, Y. (2019). The resilient moduli of five Canadian soils under wetting and freeze-thaw conditions and their estimation by using an artificial neural network model. Cold Regions Sci. Technol., 168. doi:10.1016/j.coldregions.2019.102894

CrossRef Full Text | Google Scholar

Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986). Learning representations by back-propagating errors. Nature 323 (6088), 533–536. doi:10.1038/323533a0

CrossRef Full Text | Google Scholar

Seed, H. B., Chan, C. K., and Lee, C. E. (1962). “Resilience characteristics of subgrade soils and their relation to fatigue failures in asphalt pavements,” in Proceedings international conference on structural design of asphalt pavement, University of Michigan.

Google Scholar

Thevakumar, K., Indraratna, B., Ferreira, F. B., Carter, J., and Rujikiatkamjorn, C. (2021). The influence of cyclic loading on the response of soft subgrade soil in relation to heavy haul railways. Transp. Geotech. 29, 100571. doi:10.1016/j.trgeo.2021.100571

CrossRef Full Text | Google Scholar

Wang, M., Yu, Q., Xiao, Y., and Li, W. (2022). Resilient modulus behavior and prediction models of unbound permeable aggregate base materials derived from tunneling rock wastes. Materials 15 (17), 6005. doi:10.3390/ma15176005

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, H., Li, Z., Song, W., and Bai, S. (2021). Effects of superabsorbent polymers on moisture migration and accumulation behaviors in soil. J. Clean. Prod., 279. doi:10.1016/j.jclepro.2020.123841

CrossRef Full Text | Google Scholar

Zhang, J., Peng, J., Liu, W., and Lu, W. (2019a). Predicting resilient modulus of fine-grained subgrade soils considering relative compaction and matric suction. Road Mater. Pavement Des. 22 (3), 703–715. doi:10.1080/14680629.2019.1651756

CrossRef Full Text | Google Scholar

Zhang, J., Peng, J., Zeng, L., Li, J., and Li, F. (2019b). Rapid estimation of resilient modulus of subgrade soils using performance-related soil properties. Int. J. Pavement Eng. 22 (6), 732–739. doi:10.1080/10298436.2019.1643022

CrossRef Full Text | Google Scholar

Zhang, J., Peng, J., Zheng, J., and Yao, Y. (2018). Characterisation of stress and moisture-dependent resilient behaviour for compacted clays in South China. Road Mater. Pavement Des. 21 (1), 262–275. doi:10.1080/14680629.2018.1481138

CrossRef Full Text | Google Scholar

Zhang, J.-h., Hu, J.-k., Peng, J.-h., Fan, H.-s., and Zhou, C. (2021a). Prediction of resilient modulus for subgrade soils based on ANN approach. J. Central South Univ. 28 (3), 898–910. doi:10.1007/s11771-021-4652-7

CrossRef Full Text | Google Scholar

Zhang, Q., Leng, W., Zhai, B., Xu, F., Dong, J., and Yang, Q. (2021b). Evaluation of critical dynamic stress and accumulative plastic strain of an unbound granular material based on cyclic triaxial tests. Mater. (Basel) 14 (19), 5722. doi:10.3390/ma14195722

CrossRef Full Text | Google Scholar

Zhang, X.-n., Cui, X.-z., Ding, L.-q., Luan, J.-y., Wang, Y.-l., Jiang, P., et al. (2023). Effects of a novel hybrid polymer material on the hydro-mechanical behavior of subgrade silts considering freeze-thaw cycles. Cold Regions Sci. Technol. 205, 103698. doi:10.1016/j.coldregions.2022.103698

CrossRef Full Text | Google Scholar

Zhao, H. Y., Indraratna, B., and Ngo, T. (2021). Numerical simulation of the effect of moving loads on saturated subgrade soil. Comput. Geotechnics 131, 103930. doi:10.1016/j.compgeo.2020.103930

CrossRef Full Text | Google Scholar

Zou, W.-l., Han, Z., Ding, L.-q., and Wang, X.-q. (2021). Predicting resilient modulus of compacted subgrade soils under influences of freeze–thaw cycles and moisture using gene expression programming and artificial neural network approaches. Transp. Geotech., 28. doi:10.1016/j.trgeo.2021.100520

CrossRef Full Text | Google Scholar