Experimental study of dynamic shear stiffness decay characteristics of interbedded soil: a case study in Yangtze River floodplain

To explore the characteristics of the dynamic shear modulus of river-phase (as opposed to estuarine) floodplain interbedded soil, undisturbed interbedded soil from the floodplain of the Yangtze River in Nanjing was subjected to strain-controlled cyclic triaxial tests to investigate how the initial effective confining pressure (σʹ_m), consolidation ratio (k_c), and degree of consolidation (U) influence the maximum dynamic shear modulus G_max and the dynamic shear modulus ratio G/G_max. The results show that for this soil, G decreases with increasing strain amplitude, and for a given strain amplitude, G increases with increasing σʹ_m, k_c, and U. Compared with soil from the Yangtze estuary, k_c has a greater effect on G_max of the floodplain interbedded soil. Finally, a modified Martin-Davidenkov model is proposed for predicting G/G_max of river-phase floodplain interbedded soil under different σʹ_m, k_c, and U.

Introduction

River-phase (as opposed to estuarine) floodplain soil is a typical example of the interbedded soil that is found in deltas, coastal regions, river floodplains, and lakes. In the floodplain of a river (Li et al., 2014; Tankiewicz, 2016; Boulanger and DeJong, 2018; Bucci, Villamor, and Almond, 2018; Beyzaei et al., 2020) the annual alternation between dry periods and ones when water is abundant causes the sediment and organic matter content of the water to change periodically, which also leads to similar cyclic variations in the hydrodynamic conditions. Consequently, the sediment exhibits differences in composition, thickness, particle size, and color, creating a unique and intuitive stratified structure. This process repeats numerously over time, leading to alternating, regular, and repetitive deposits of sandy soil and clayey soil.

Many underground structures near rivers and in coastal cities are in interbedded soil. Also, the foundations of coastal harbors and bridges often penetrate interbedded soil, and numerous marine engineering activities involve such soil. Studies have shown that stratified sites have obvious special characteristics in terms of the deformation of foundation supporting structures (Wan et al., 2022a), the stability of tunnel excavation and slopes, and the site liquefaction resistance (Beyzaei et al., 2018; Boulanger et al., 2019; Tasiopoulou et al., 2019; Beyzaei et al., 2020; Ecemis, 2021; Zhou et al., 2021).

Various scholars have conducted tests to determine the static and dynamic characteristics of interlayered soil. Tankiewicz (2015) conducted static triaxial tests on interbedded soil, with the observed failure modes revealing pronounced strength anisotropy and with considerable variability noted in the sample failure modes and shear strength values; also, the permeability and shear strength anisotropy of the interbedded soil surpassed those of many other soil types. Ma et al. (2019) conducted a series of ring shear tests on remolded overconsolidated soft interlayers, investigating the influence of remolded water content and consolidation stress on shear behavior under drained conditions. They found that water content can weaken the shear strength of soft interlayers, with cohesion being more sensitive to changes in water content compared to the friction angle; also, consolidation stress is an important factor influencing the strain-softening and strain-hardening behaviors of soft interlayers. Via extensive cyclic triaxial testing, Duong et al. (2016) explored how water content and fines content affected the resilient modulus of interlayer soil sampled from a railway substructure in France. The conclusions indicate that under unsaturated conditions, soil with high fines content exhibits a higher resilient modulus because of the influence of capillary suction. However, as the soil approaches saturation, fine particles negatively affect the resilient modulus. This suggests that protective drainage measures must be implemented for interlayer soil when its mechanical performance is satisfactory under unsaturated conditions but unsatisfactory under saturated conditions. Studying the mechanical properties of soil via techniques such as X-ray diffraction (XRD), energy-dispersive X-ray analysis (EDXA), and scanning electron microscopy (SEM) offers a multifaceted advantage. These methods provide precise information on mineral composition, elemental distribution, and microstructure, offering crucial support for a comprehensive understanding of the chemical and mechanical properties of soil. Sun et al. (2022) used XRD, EDXA, concentration monitoring, triaxial compression tests, unconfined compressive tests, and SEM to investigate the mineral composition, mechanical properties, and microstructure of weak interlayers in various acidic environments. The results showed that the pH value of the solution and the immersion time were significant factors influencing the undrained strength of the samples. Moreover, as the immersion time increased, microscopic structural parameters showed a decrease in the area of mineral particles and a simultaneous rise in the pore ratio. These microstructural changes observed in images and parameters were consistent with the macroscopic physical and mechanical properties of the samples. The interlayers can be as thin as few millimeters, and conventional in situ investigation techniques such as CPT and sonic borings fail to characterize the laminar structure (Beyzaei et al., 2020). To address this challenge, Tankiewicz (2016) conducted a thorough investigation using high-quality samples. Through the application of SEM and computed microtomography, intricate 3D models were reconstructed, unveiling the detailed nature of the varved clay structure. Furthermore, the mechanical properties of individual layers were scrutinized at the layer-thickness scale using nanoindentation (Tankiewicz, 2018).

The dynamic shear modulus (DSM) is important for evaluating the response behavior of soil under dynamic loads. In-depth research on the DSM helps to accurately predict the behavior of soil under different dynamic conditions, providing effective guidance and an evaluation basis for earthquake engineering, infrastructure construction, and soil–structure interaction. Geotechnical assessments based on established knowledge of non-interbedded soil can lead to confusion in practice. For instance, conventional liquefaction assessment procedures predicted site liquefaction that did not occur during earthquake events (Beyzaei et al., 2020; Ecemis, 2021). Challenges have also emerged in predicting the stability and consolidation behavior of embankments (Ladd and Foott, 1977) and estimating the side resistance of drilled shafts (Mackiewicz and Lehman-Svoboda, 2012). Consequently, establishing a distinct dynamic evaluation procedure for interbedded soil becomes imperative, especially for that in the floodplain of the Yangtze River, whose dynamic properties remain poorly understood.

Based on the aforementioned studies, this paper investigates the characteristics of the DSM (G) of interbedded soil in the floodplain of the Yangtze River under different values of the initial effective confining pressure (σʹ_m), consolidation ratio (k_c), and degree of consolidation (U). The degree of consolidation U is an important parameter for evaluating the soil consolidation level, which directly affects the bearing capacity and deformation characteristics of the soil body. For example, in bridge construction, the degree of consolidation U of the riverbed soil needs to be evaluated first to ensure that the soil body has sufficient support to carry the weight of the bridge. Similarly, in high fill projects, by adjusting the degree of consolidation of the fill, settlement can be effectively controlled to ensure a smooth road. The use of U as an influencing factor reflects the effect of stress history on the dynamic properties of the soil in this interlayer, and also effectively reduces the consolidation time and improves the testing efficiency, which is very important in the context of the increasing demand for testing of geodynamic parameters.Considering U as an influencing factor reflects the influence of stress history on the dynamic properties of this interbedded soil while also effectively shortening the time used for consolidation; this improves the testing efficiency, which is very important given the increasing demand for testing the dynamic parameters of soil.

Test program and procedures

Test material

Undisturbed river-phase floodplain interbedded soil (FIS) is the main stratum for urban subsurface space development (Wan et al., 2022b). The soil samples tested in the study reported herein were obtained from the Central Business District of Jiangbei New District in Nanjing, China, as shown in Figure 1. The original river-phase FIS is gray-brown in appearance, with obvious horizontal stratification and sand sandwich structure, which is typical of river-phase FIS. The specific gravity (G_s), natural water content (w₀), and natural wet density (ρ₀) were determined according to D2216 (ASTM, 2019), D854 (ASTM, 2014), and D1556/D1556M (ASTM, 2015), respectively, and the natural density of the samples was 1.76 g/cm⁻³, the water content was 42.06%, the specific gravity was 2.71, the initial void ratio was 1.19, and the plasticity index was 17.18.

Figure 1

Figure 1. Geographical sampling locations.

Test apparatus

In this study, multi-stage strain-controlled cyclic triaxial tests were conducted using the HCA-300 multifunctional cyclic triaxial instrument developed by GCTS, which can perform conventional static/cyclic triaxial tests and synchronous coupled bidirectional vibration loading torsion shear tests. The HCA-300 cyclic triaxial instrument and its main technical indicators are shown in Figure 2. The system hardware comprises a test platform, a pressure control cabinet, a computer, an acquisition system, a hydraulic source, and a vacuum pump; the system software comprises a digital servo controller and the GCTS CATS software. The HCA-300 cyclic triaxial instrument uses electro-hydraulic servo closed-loop control, which allows direct testing of the axial stress σ_d and axial strain ε of specimens. During cyclic loading, the σ_d values of a specimen are picked up by the built-in small-range axial force transducer, and the ε values are picked up by the small-range LVDT displacement transducer. See (Chen et al., 2019) for more details about the HCA-300 system.

Figure 2

Figure 2. Test apparatus and main technical indicators.

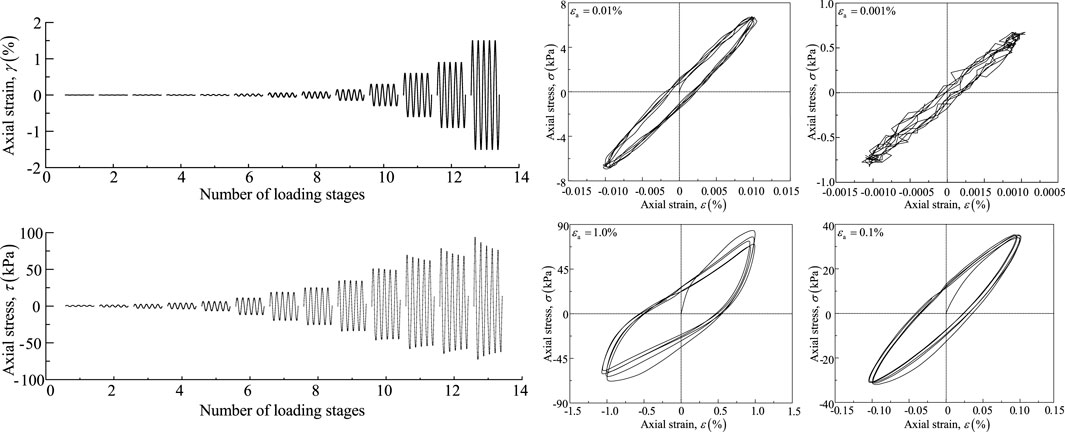
For a cylindrical specimen, the shear stress τ and shear strain γ in the 45° plane of the specimen during loading are calculated as Equation 1:

$\left\{\begin{array}{l}\tau ={\sigma }_{\mathrm{d}}/2\\ \gamma =\left(1+\nu \right)\epsilon \end{array}\right.,(1)$

where ν is Poisson’s ratio; for the in situ interbedded soil of the Yangtze River floodplain, we take ν = 0.42 (Zhuang et al., 2020). In the equivalent linear dynamic viscoelastic ontological model, the shear modulus is calculated as Equation 2 (D3999/D3999M-11 ASTM, 2013)

$G=\frac{\tau }{\gamma },(2)$

and the typical strain, stress, and strain–stress time-dependent curves are shown in Figure 3.

Figure 3

Figure 3. Measured time histories of test results for a typical specimen.

Test program and method

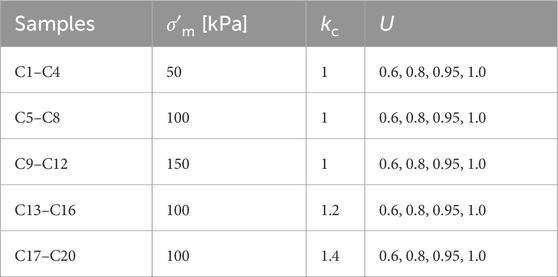
To investigate how G of FIS vary with consolidation degree U, five sets of tests with different U were performed according to the test program given in Table 1. The test steps were as follows. 1) Make the in situ FIS sample into a solid cylindrical specimen that has a standard size of 50 mm × 100 mm and is saturated. 2) Install the specimen into the base of the instrument, connect the top with the displacement transducer and the driving device, and close the pressure chamber. 2) After installation and according to the test conditions of the specimen, apply confining pressure to achieve different degrees of consolidation, with consolidation being completed after reaching the pre-set U. 4) The specimen is subjected to strain-controlled cyclic loading, with the amplitude of axial strain increasing in steps from 1 × 10⁻⁵ to 1 × 10⁻². Each level of cyclic loading was five cycles with a frequency of 0.5 Hz.

Table 1

Table 1. Dynamic triaxial test scheme for controlling degree of consolidation.

Control methods for consolidation degree

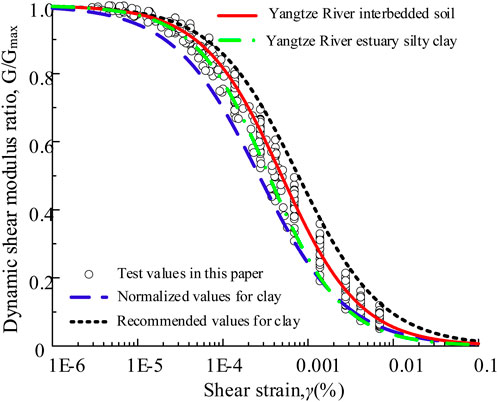
Figure 4 shows the time histories of the axial displacement of completely consolidated FIS under different consolidation conditions. These axial displacement curves are then normalized to obtain the consolidation degree as a function of time (t), as shown in Figure 5. As can be seen, the U development trend is insensitive to the initial stress conditions, and U can be transformed into a function of the consolidation time t. Referring to the universal expression for the average consolidation degree of a soft clay foundation (Martin and Seed, 1983), the relationship between consolidation degree and time is fitted to obtain an exponential function of the form as Equation 3

$U=1-k{\mathrm{e}}^{-bt},(3)$

where k and b are the shape coefficients of the curves. This is how U was controlled in the present study. The reference intervals for the consolidation time for different values of U are given in Figure 5, and as can be seen, the consolidation time used for the specimens is greatly reduced as U decreases.

Figure 4

Figure 4. Consolidation displacement curves of Yangtze River floodplain interbedded soil (FIS) under different consolidation conditions.

Figure 5

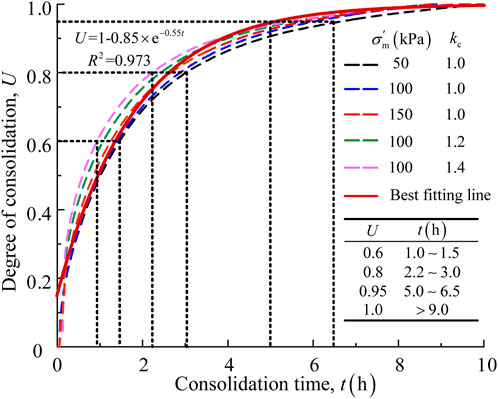
Figure 5. Consolidation curves and fitting for Yangtze River FIS under different initial stress conditions.

Test results and analysis

Effect of initial consolidation conditions on dynamic shear modulus

Figure 6 shows the distribution of the DSM G of the undisturbed FIS over a wide range of shear strain γ under different values of U. As can be seen, γ plays an important role in the development of G: for given U, each specimen exhibits decaying G with increasing γ. Also, for given γ, G increases with increasing U, which indicates that the larger the value of U, the greater the cementation degree between soil particles and the more stable the particle fabric, which contribute to greater stiffness for resisting shear deformation. In addition, comparing among the subplots in Figure 6 reveals the interesting phenomenon that increasing σʹ_m or k_c results in G increasing more for a given increase in U.

Figure 6

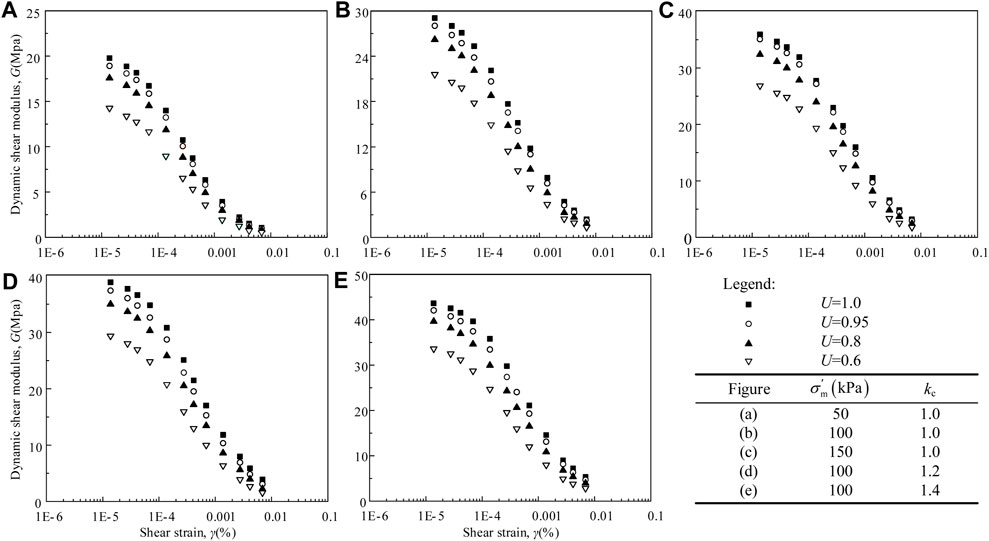
Figure 6. Test results for Yangtze River FIS with different degrees of consolidation. (A) σʹ_m = 50 kPa and k_c = 1.0; (B) σʹ_m = 100 kPa and k_c = 1.0; (C) σʹ_m = 150 kPa and k_c = 1.0; (D) σʹ_m = 100 kPa and k_c = 1.2; (E) σʹ_m = 150 kPa and k_c = 1.4.

Effect of initial consolidation conditions on maximum dynamic shear modulus

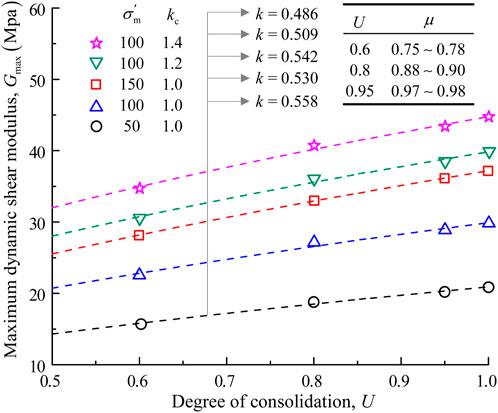
The maximum DSM G_max is the DSM when the strain percentage is less than 10⁻⁵, in which case the soil is considered to be in a purely elastic state. and so in this study G_max was obtained using the extrapolation method at 0.0001% strain (Hardin and Drnevich, 1972). Figure 7 shows the variation of G_max with U in the FIS with different values of σʹ_m and k_c. It is obvious that G_max is closely related to U: it increases with increasing U, and the data suggest an exponential correlation between G_max and U. Also, the growth rate of G_max with increasing U is insensitive to σʹ_m or k_c. The proposed relationship between U and G_max for FIS under different initial stress conditions is described as Equation 4

$G_{\max }=A_1\cdot U^k,(4)$

where A₁ and k are fitting parameters. The coefficient A₁ equals G_max when U = 1, and the stress exponent k describes how U affects the growth rate of G_max. Regression analysis suggests fixing k at 0.5 for different σʹ_m or k_c. To estimate G_max empirically under different U, those values are denoted as G_max,U, and G_max for U = 1 (100%) is denoted as G_max,100%. Then G_max,U is determined as Equation 5

$G_{\max ,\mathrm{U}}=\mu \cdot G_{\max ,100\%},(5)$

where μ is the G_max reduction coefficient. Figure 7 gives the recommended values of μ for FIS with different values of U for engineering applications.

Figure 7

Figure 7. Relationship between G_max and degree of consolidation U of Yangtze River FIS.

Expression for and parameters of dynamic shear modulus ratio

To characterize quantitatively the variation of the nonlinear and hysteretic characteristics of river-phase floodplain soil at different U, the three-parameter Martin–Davidenkov model (Hardin and Drnevich, 1972) is selected to fit the relationship between G/G_max and γ as shown in Equation 6

$\frac{G}{G_{\max }}=1-{\left[\frac{{\left(\gamma /{\gamma }_0\right)}^{2\beta }}{1+{\left(\gamma /{\gamma }_0\right)}^{2\beta }}\right]}^{\alpha },(6)$

where α, β, and γ₀ are best-fit parameters that control the shape of the G/G_max–γ curve concerning the soil properties; γ₀ is commonly known as the reference shear strain and is generally taken to be the value of γ₀ at G/G_max = 0.5.

As shown in Figure 8, U has a significant effect on G/G_max. For a given strain amplitude, G/G_max of the FIS increases with increasing U; i.e., the Yangtze River FIS presents stronger nonlinear characteristics as U increases. Also, for given U, the G/G_max–γ curve rises with increasing σʹ_m or k_c.

Figure 8

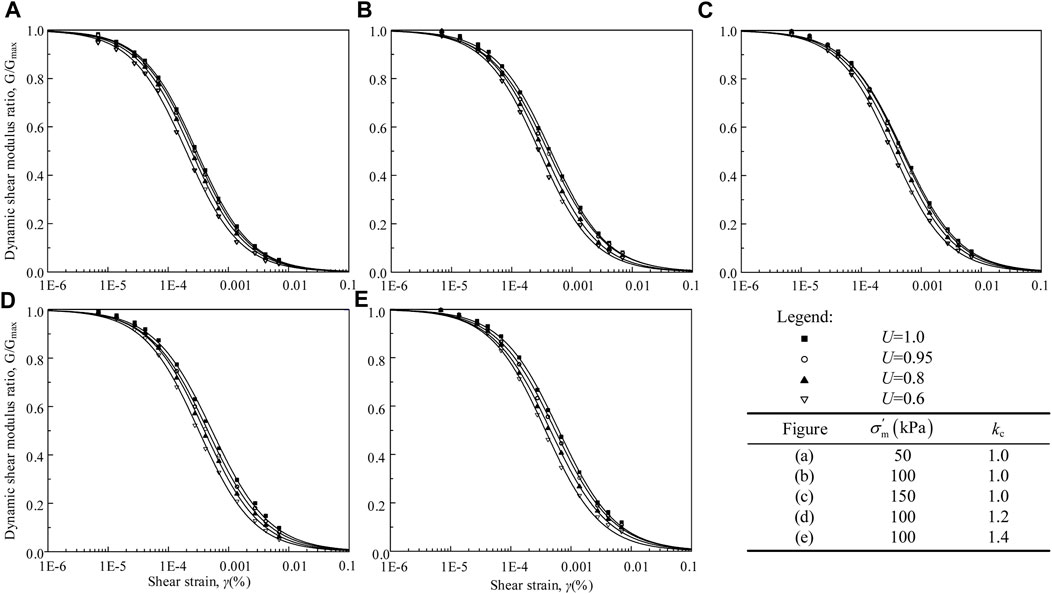
Figure 8. Relationship between G/G_max and γ for Yangtze River FIS with different degrees of consolidation. (A) σʹ_m = 50 kPa and k_c = 1.0; (B) σʹ_m = 100 kPa and k_c = 1.0; (C) σʹ_m = 150 kPa and k_c = 1.0; (D) σʹ_m = 100 kPa and k_c = 1.2; (E) σʹ_m = 150 kPa and k_c = 1.4.

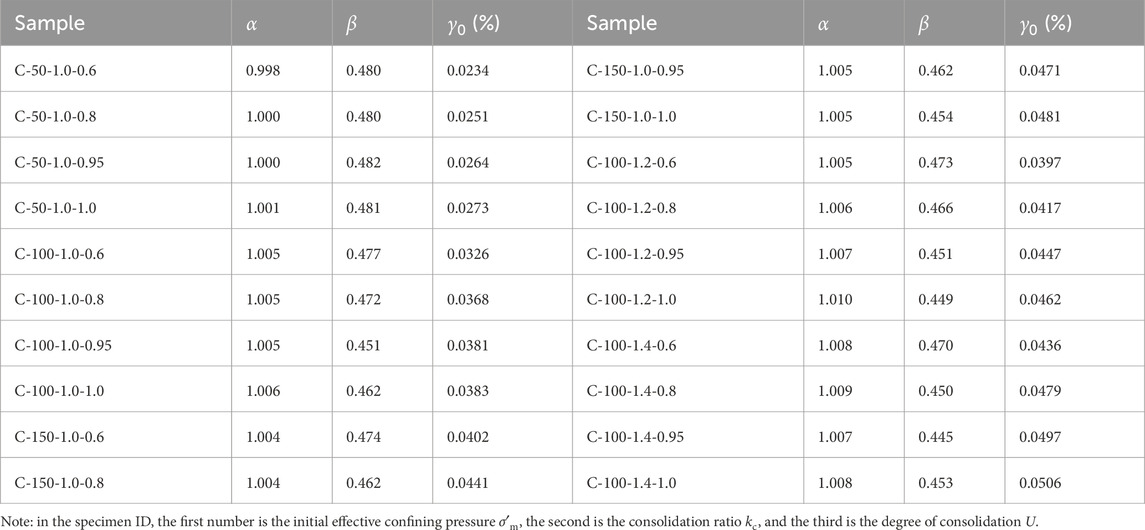
Table 2 lists the values of the fitting parameters α and β for all the tested soil samples. The values of α range from 0.998 to 1.010 and those of β range from 0.445 to 0.482, which indicates that U has little effect on α and β. Therefore, for the Yangtze River FIS, α and β can be regarded as 1.0 and 0.47, respectively. Figure 9 shows the variation of γ₀ with U under different σʹ_m and k_c. As can be seen, for given σʹ_m and k_c, γ₀ increases with increasing U, and for given U, γ₀ increases with increasing σʹ_m and k_c. To quantify the relationship between U and γ₀, the latter is normalized by considering the effects of σʹ_m and k_c and is expressed as Equation 7

${\gamma }_0^{\prime }=\frac{{\gamma }_0}{{\left(\frac{{{\sigma }^{\prime }}_m}{P_a}\right)}^n{\left(k_{\mathrm{c}}\right)}^m},(7)$

where n and m are related to the soil properties and are taken herein as n = 0.5 and m = 0.84, and P_a = 100 kPa as the value of standard atmospheric pressure. Figure 10 shows the relationship between γʹ₀ and U, which as can be seen is a power law of the form as shown in Equation 8

${\gamma }_0^{\prime }=p\cdot U^q,(8)$

where p and q are the fitting parameters, with p = 0.0436 and q = 0.7468.

Table 2

Table 2. Parameters of Davidenkov model for predicting G/G_max–γ curve.

Figure 9

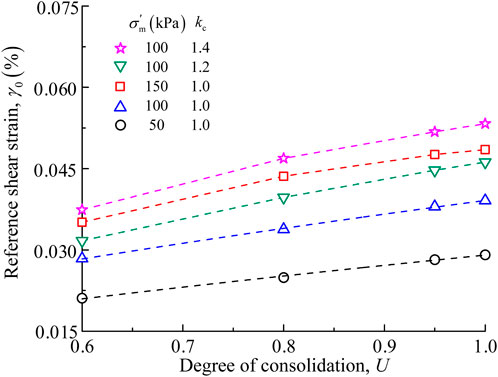
Figure 9. Relationships between consolidation degree U and reference shear strain γ₀ under different values of σʹ_m and k_c.

Figure 10

Figure 10. Relationship between U and normalized reference shear strain γʹ₀.

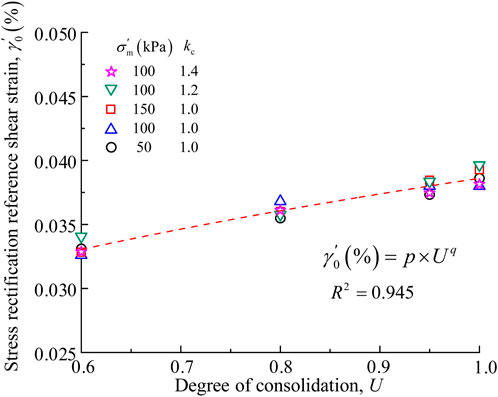
Figure 11 compares G/G_max of the present FIS with that of silt clay from the Yangtze estuary (σʹ_m = 50∼200 kPa), as well as recommended values given by Yuan et al. (Shun et al., 2004) and normalized values given by the China Earthquake Administration (GB, 1999). As can be seen, the distribution range of the G/G_max–γ curves for the FIS is within the statistical range of the recommended and standardized values for clayey soil. Compared with the Yangtze estuary silty clay, the FIS decays less rapidly and has larger G/G_max at large strain, which indicates that the nonlinear properties of the FIS in the Yangtze River are weaker than those of the silty clay at the Yangtze estuary. Overall, the empirical equations given herein can be used for predictions regarding the FIS in the Yangtze River.

Figure 11

Figure 11. G/G_max–γ curves for different clay soils.

Conclusion

In this study, the characteristics of the DSM G of river-phase FIS with differing consolidation degree U were investigated, and the variations of the maximum DSM G_max and the normalized DSM ratio G/G_max with different U were analyzed. The main conclusions are as follows.

Under different values of the consolidation ratio, the development of U of Yangtze River FIS with consolidation time is almost the same. A quantitative method for relating U and the consolidation time was established and gives the corresponding reference time.

The Yangtze River FIS with different U shows nonlinear characteristics of “low shear modulus” in the strain range of 10⁻⁵ to 10⁻⁴. As the shear strain γ increases, the DSM G decreases, and at different strain levels, G increases with increasing U.

For Yangtze River FIS, G_max is affected by U and increases gradually with increasing U. Taking the G_max value at a consolidation degree of 100% as a reference, the reference range for the reduction coefficient μ of G_max of soft soil in the Yangtze River floodplain corresponding to different consolidation degrees is provided.

Finally, the G/G_max–γ curves of Yangtze River FIS show a “low to high” change with increasing U, and the nonlinear characteristics of the soil weaken gradually. Compared with conventional clayey soils, the FIS has more-obvious nonlinear characteristics.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

HL: Resources, Visualization, Writing–original draft. ZH: Writing–review and editing. DC: Investigation, Resources, Validation, Visualization, Writing–review and editing. RZ: Data curation, Investigation, Writing–review and editing. QW: Project administration, Supervision, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (52008206).

Conflict of interest

Authors LH and CD were employed by Zhejiang Institute of Communications Co., Ltd. Author HZ was employed by China Nuclear Power Engineering Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

ASTM (2013). Standard test methods for the determination of the modulus and damping properties of soils using the cyclic triaxial apparatus. West Conshohocken, PA: ASTM. ASTM D3999/D3999M-11.

Google Scholar

ASTM (2014). Standard test methods for specific gravity of soil solids by water pycnometer. West Conshohocken, PA: ASTM. ASTM D854-14.

Google Scholar

ASTM (2015). “Standard test method for density and unit weight of soil in place by sand-cone method,” in Astm D1556/D1556M-15E0 (West Conshohocken, PA: ASTM).

Google Scholar

ASTM (2019). Standard test Method for laboratory Determination of water (moisture) Content of Soil and Rock by mass. ASTM d2216-19. West Conshohocken, PA: ASTM.

Google Scholar

Beyzaei, C. Z., Bray, J. D., Ballegooy, S. V., Misko, C., and Sarah, B. (2018). Depositional environment effects on observed liquefaction performance in silt swamps during the canterbury earthquake sequence. Soil Dyn. Earthq. Eng. 107, 303–321. doi:10.1016/j.soildyn.2018.01.035

CrossRef Full Text | Google Scholar

Beyzaei, C. Z., Bray, J. D., Cubrinovski, M., Sarah, B., Mark, S., Mike, J., et al. (2020). Characterization of silty soil thin layering and groundwater conditions for liquefaction assessment. Can. Geotechnical J. 57 (2), 263–276. doi:10.1139/cgj-2018-0287

CrossRef Full Text | Google Scholar

Boulanger, R. W., and DeJong, J. T. (2018). Inverse filtering procedure to correct cone penetration data for thin-layer and transition effects. Cone penetration testing. Boca Raton, FL: CRC Press.

Google Scholar

Boulanger, R. W., Munter, S. K., Krage, C. P., and DeJong, J. T. (2019). Liquefaction evaluation of interbedded soil deposit: cark canal in 1999 M7.5 kocaeli earthquake. J. Geotechnical Geoenvironmental Eng. 145 (9), 5019007. doi:10.1061/(ASCE)GT.1943-5606.0002089

CrossRef Full Text | Google Scholar

Bucci, M. G., Villamor, P., Almond, P., Tuttle, M., Stringer, M., Ries, W., et al. (2018). Associations between sediment architecture and liquefaction susceptibility in fluvial settings: the 2010-2011 canterbury earthquake sequence, New Zealand. Eng. Geol. 237, 181–197. doi:10.1016/j.enggeo.2018.01.013

CrossRef Full Text | Google Scholar

Chen, G. X., Zhao, D. F., Chen, W. Y., and Juang, C. H. (2019). Excess pore-water pressure generation in cyclic undrained testing. J. Geotechnical Geoenvironmental Eng. 145 (7), 04019022. doi:10.1061/(ASCE)GT.1943-5606.0002057

CrossRef Full Text | Google Scholar

Duong, T. V., Cui, Y. J., Tang, A. M., Dupla, J. C., Jean, C., Nicolas, C., et al. (2016). Effects of water and fines contents on the resilient modulus of the interlayer soil of railway substructure. Acta Geotech. 11, 51–59. doi:10.1007/s11440-014-0341-0

CrossRef Full Text | Google Scholar

Ecemis, N. (2021). Experimental and numerical modeling on the liquefaction potential and ground settlement of silt-interlayered stratified sands. Soil Dyn. Earthq. Eng. 144 (10), 106691. doi:10.1016/j.soildyn.2021.106691

CrossRef Full Text | Google Scholar

GB (1999). Technical specification for seismic safety evaluation of engineering sites. GB 17741. (in Chinese).

Google Scholar

Hardin, B. O., and Drnevich, V. P. (1972). Shear modulus and damping in soils: design equations and curves. Geotech. Spec. Publ. 98 (118), 667–692. doi:10.1061/JSFEAQ.0001760

CrossRef Full Text | Google Scholar

Ladd, C. C., and Foott, R. (1977). Foundation design of embankments constructed on varved clays. Washington, DC: Federal Highway Administration.

Google Scholar

Li, S., Xu, B. Z., Liu, J. T., and Zhou, Y. R. (2014). Study of characteristics of laminated soil in south China sea. Rock Soil Mech. 35 (S1), 203–208. (in Chinese). doi:10.16285/j.rsm.2014.s1.014

CrossRef Full Text | Google Scholar

Ma, C., Zhan, H. B., Zhang, T., and Yao, W. M. (2019). Investigation on shear behavior of soft interlayers by ring shear tests. Eng. Geol. 254, 34–42. doi:10.1016/j.enggeo.2019.04.002

CrossRef Full Text | Google Scholar

Mackiewicz, S. M., and Lehman-Svoboda, J. (2012). Measured versus predicted side resistance of drilled shafts in a heterogeneous soil profile. Geocongress, 2412–2421. doi:10.1061/9780784412121.247

CrossRef Full Text | Google Scholar

Martin, P. P., and Seed, H. B. (1983). One-dimensional dynamic ground response analyses. J. Geotechnical Eng. Div. 108 (7), 935–952. doi:10.1061/AJGEB6.0001316

CrossRef Full Text | Google Scholar

Shun, J., Yuan, X. M., and Shun, Y. (2004). Comparison of the rationality between recommended and standard values for soil dynamic shear modulus and damping ratio. Earthq. Eng. Eng. Vib. 24 (2), 9. (in Chinese). doi:10.13197/j.eeev.2004.02.022

CrossRef Full Text | Google Scholar

Sun, S. R., Wang, W. C., Wei, J. H., Song, J. L., Yu, Y. X., H, W., et al. (2022). Experimental study on microstructure response and mechanical properties of weak interlayer in acidic environment. Nat. Hazards 112 (1), 327–348. doi:10.1007/s11069-021-05183-w

CrossRef Full Text | Google Scholar

Tankiewicz, M. (2015). Experimental investigation of strength anisotropy of varved clay. Procedia Earth Planet. Sci. 15, 732–737. doi:10.1016/j.proeps.2015.08.116

CrossRef Full Text | Google Scholar

Tankiewicz, M. (2016). Structure investigations of layered soil-varved clay. Ann. Warsaw Univ. Life Sci. - SGGW. Land Reclam. 48 (4), 365–375. doi:10.1515/sggw-2016-0028

CrossRef Full Text | Google Scholar

Tankiewicz, M. (2018). Application of the nanoindentation technique for the characterization of varved clay. Open Geosci. 10, 902–910. doi:10.1515/geo-2018-0071

CrossRef Full Text | Google Scholar

Tasiopoulou, P., Giannakou, A., Chacko, J., and Sjoerd, D. W. (2019). Liquefaction triggering and post-liquefaction deformation of laminated deposits. Soil Dyn. Earthq. Eng. 124, 330–344. doi:10.1016/j.soildyn.2018.04.044

CrossRef Full Text | Google Scholar

Wan, X., Ding, J. W., Hong, Z. S., Huang, C., Shang, S. L., and Ding, C. (2022a). Dynamic response of a low embankment subjected to traffic loads on the Yangtze River floodplain, China. Int. J. Geomechanics 22 (6), 04022065. doi:10.1061/(ASCE)GM.1943-5622.0002357

CrossRef Full Text | Google Scholar

Wan, X., Ding, J. W., Jiao, N., Sun, S., Liu, J. Y., and Guo, Q. Y. (2022b). Observed performance of long-zoned excavation with suspended waterproof curtain in Yangtze River floodplain. J. Perform. Constr. Facil. 36 (3), 04022018. doi:10.1061/(ASCE)CF.1943-5509.0001725

CrossRef Full Text | Google Scholar

Zhou, H., Wotherspoon, L. M., Hayden, C. P., McGann, C. R., Stolte, A., and Haycock, L. (2021). Assessment of existing SPT-CPT correlations using a New Zealand database. J. Geotechnical Geoenvironmental Eng. 147 (11), 4021131. doi:10.1061/(ASCE)GT.1943-5606.0002650

CrossRef Full Text | Google Scholar

Zhuang, H. Y., Yang, J., Chen, S., Li, H. X., Zhao, K., and Chen, G. X. (2020). Liquefaction performance and deformation of slightly sloping site in floodplains of the lower reaches of Yangtze River. Ocean. Eng. 217, 107869. doi:10.1016/j.oceaneng.2020.107869

CrossRef Full Text | Google Scholar