Investigation on the AE characteristics and progressive failure behaviors of tunnels by strength reduction method

The fracture features and failure mechanisms of tunnels excavated in shallow and deep rock masses are investigated using a series of three-dimensional heterogeneous models that incorporate cross section, tunnel alignment, faults and tunnel support system. The strength reduction method is embedded in the rock failure process analysis method to achieve the gradual fracture process, macro failure mode and safety factor, and to reproduce the characteristic fracture phenomenon of surrounding rock masses. The mechanical mechanisms and acoustic emission energy of deep rocks at the different stages of the whole formation process of zonal disintegration are further discussed. The results indicate that the zonal disintegration process is triggered by the stress redistribution; cross section influences the stress buildup, stress shadow and stress transfer as well as the failure mode of surrounding rock mass; the dip of faults and tunnel support system can affect zonal disintegration pattern near the tunnel surface along their strikes; the twin-tunnel layout makes zonal disintegration pattern more intricate. These insights advance our understanding of the zonal disintegration in deep engineering.

1 Introduction

As transportation networks expand into hilly and mountainous regions, the development of tunnels is experiencing rapid growth. However, the construction of mountain tunnels often encounters complex geological challenges, including high ground stress, weak and fragmented surrounding rock, and well-developed geological structures. These conditions significantly increase the difficulty and risk of tunnel construction, requiring advanced engineering techniques and careful planning to ensure safety and stability (Karahan and Gokceoglu, 2025; Basirat, 2025; Feng et al., 2025a; Liu et al., 2023). The deformation of surrounding rock is substantial and persistent after tunnel excavation in high ground stress and weak shattered surrounding rock, resulting in a constant rise in stress on the supporting structures. Initial support could shatter, surrounding rock could intrude into the tunnel clearance, and even severe engineering disasters could happen if the stress surpasses the bearing capacity of surrounding rock and lining, posing huge threats to the safety of tunnel structures and constructors (Xue et al., 2024; Ko and Jeong, 2017). Hence, more attention should be given to the failure mechanism in a detailed geotechnical engineering analysis. Subsurface construction is technically possible and has fewer problems with land expropriation and environmental effects, which are key issues in today’s development projects (Kovari, 1994). Tunnel engineering parameters such as displacement stress distribution, properties of adjacent rock masses, faults, tunnel cross section, and others should be taken into account in tunnel design (Deng et al., 2021; Hu et al., 2021). Squeezing situations and excessive loads around the excavation may impair the integrity of deep tunnels with large overburden and poor rock mass characteristics, causing extensive collapse (Chen et al., 2013; He et al., 2021). The primary challenge in deep excavation lies in accurately understanding and simulating the rock failure process. This is essential for designing an effective rock support system that ensures both the stability of the construction and cost-efficiency. By comprehensively analyzing the mechanisms of rock failure, engineers can develop tailored support solutions that mitigate risks and optimize the construction process, ultimately achieving a balance between safety and economic viability (Armand et al., 2014; Fujiyama and Kaku, 2023; Liu et al., 2024a). From literature, it can be found that numerous research and laboratory tests were conducted on different design parameters of tunnel design (Lin et al., 2015; Qian and Zhou, 2018; Feng et al., 2025b; Liu et al., 2024).

The process of tunnel stability and crack propagation of an underground tunnel has been investigated by many researchers from the perspective of the cross-sectional shape of the tunnel. Wang et al. (2018) performed a field test on 50 sections of a tunnel built using clay layers with high plasticity. They analyzed the deformation features of adjacent rocks and the influencing laws induced by burial depth, soft clay invasion thickness, and atmospheric precipitation. Ova (2004) discussed the influence of various cross-sectional shapes of the tunnel (including circles and horseshoes) on the tunnel of the Hanoi metro system and stated that circular tunnels are more appropriate when earthquake happened. Mobaraki and Vaghefi (2015) examined and compared semi-ellipse, circular, and horseshoe shape tunnels and discovered that the circular and horseshoe tunnels are less resistant to demolition than the box shape tunnel. Yang et al. (2019) investigated dynamic behavior on tunnel models with three distinct cross-sectional shapes (circle, rectangle, and horseshoe) and stated that cross-sectional shape effects on tunnel response are primarily in the nearfield, and that the influence reduces as the distance from the excitation source increases. Chen et al. (2022) revealed the fracture features and mechanisms of circle tunnels excavated in deep jointed rock masses by employing a series of three-dimensional heterogeneous models considering different joint dip angles. Lu et al. (2014) analyzed the optimal shape of a tunnel that meets the optimization criterion by using the conformal mapping method for a plane elasticity complex function.

However, there is still a gap in research on the influence of section shape on deep and shallow tunnel stability. Clearly, while individual studies have examined specific tunnel shapes, there is a lack of comprehensive comparative studies that systematically evaluate the performance of different shapes under identical conditions, and there is limited research on how the optimal shape changes with depth. Meanwhile, most studies assume homogeneous ground conditions, but real-world geological settings are often heterogeneous, with varying rock properties. As mining depth and stress environment increase in complexity, the effect of stress magnitude and loading rate on the stability of tunnels with different cross-sectional shapes needs a comparative study (Bobet, 2011; Kim et al., 2020). Thus, this research aims to quantify the effects of section shape on the process of crack propagation and tunnel failure, by examining stress redistribution, displacement, geometric characteristics and their effects on the crack propagation, and development of damage (Lin et al., 1984; Tang, 1997; Jia and Zhu, 2015).

Structural planes are a critical geological risk factor that can influence the stability of tunnel, slope, dam construction, etc., and substantially lower the strength of rock masses (Wang et al., 2023a; Feng et al., 2024; Yu et al., 2024). In tunnels, faults can enlarge stress relaxation zones during excavation and create instabilities in ground stress that may lead to collapse. Due to their low shear and tensile strength, as well as the loosening of the rock mass caused by excavation-induced unloading, rock masses are prone to sliding along structural planes or experiencing detachment, flexing, and fracturing. These behaviors are particularly concerning in deep excavations, where the redistribution of stress can destabilize the surrounding rock, leading to potential failures. Understanding these mechanisms is critical for implementing effective stabilization measures to prevent structural collapse and ensure the safety and integrity of the excavation site (Wu et al., 2019; Li et al., 2024; Zhang et al., 2024; Zhong et al., 2025). Under some conditions, the faults may cause big disasters for tunnel construction. Zhang et al. (2020) performed scaled model tests to investigate the effect of a fault and grouting on the stability of a tunnel. Seo et al. (2016) conducted a parametric study using two-dimensional discontinuous deformation analysis to study the effects of the attribute of joints in a rock mass on the stability of a tunnel excavated in the rock mass. Manouchehrian and Ming (2018) investigated the influence of some parameters of a fault on tunnel stability.

Complex geological conditions have been encountered in the development of underground space in recent years, especially in squeezing ground areas, resulting in many tunnel construction problems such as excessive deformation, support structure failure, and even collapse (Mahabadi et al., 2012; Luo et al., 2020). The type of support, the excavation method, and the nature of the ground are all interdependent. However, some types of lining are better than others depending on the tunnel layout and construction method (Barton et al., 1995; Wu and Shao, 2019; Zhang and Zhao, 2015; Ghorasaini and Singh, 2019). A thorough understanding of the primary influencing factors and mechanisms of structural deterioration in such challenging geological conditions is essential to minimize problems during tunnel excavation (Shaalan et al., 2019; Chakeri et al., 2011; Simser, 2019). Tunneling or constructing underground structures in tight ground often presents significant technical challenges due to the complex and unpredictable nature of the geology, which can lead to numerous tunneling difficulties. Rational design in these scenarios requires a comprehensive knowledge of support system requirements, criteria for effective performance, familiarity with the capabilities of available systems, and analysis methods validated by practical experience. Future advancements in tunneling practices are expected to stem from a clear understanding of the limitations and requirements of current methodologies.

In this study, the extensive investigation into the fracture characteristics and failure mechanisms of tunnels excavated within deep rock formations are conducted. A comprehensive series of three-dimensional heterogeneous models that incorporate various parameters such as cross-section profiles, tunnel alignments, fault structures, and tunnel support systems are utilized. To simulate the gradual fracture process, macro failure modes, and safety factors, the strength reduction method is integrated into the rock failure process analysis (RFPA) method. This approach allows to accurately replicate the distinct fracture phenomena commonly observed in deep rock masses. Furthermore, our research delves into the mechanical mechanisms at play and the acoustic emission (AE) energy patterns exhibited by the surrounding rock formations throughout the various stages of zonal disintegration. This analysis sheds light on the intricate processes affecting the stability of deep rock tunnels.

2 Methodology

The tectonic denudation hilly area between the two major water systems of the Yangtze River and Jialing River is where the planned Hongyancun tunnel and Xietaizi connection ramp project pass through. The landform of the project site is a structural denudation shallow hill landform, with no adverse geological events such as landslides or faults, and with typical layer succession. The site rock and soil mass are stable overall. The site features an undulating original terrain with elevations ranging from 260 m to 360 m, resulting in a relative height difference of approximately 100 m. The area has undergone significant infrastructure engineering activities and transformations. Two primary gullies are present in the original terrain: one is located within the current site, specifically in the residential area of Xiexin Yunqigu, where the gully has been backfilled. The other gully is situated in the northeast part of the laboratory of the China Post Engineering College and has been repurposed as a training ground for an aircraft school following backfilling. This gully’s centerline runs diagonally, intersecting the X-B ramp at K0 + 250, then the X-A ramp at K1 + 650 to the southeast, and finally extending further to intersect the X-C ramp at K2 + 050. The gully is characterized by a wide and gentle topography, with its centerline elevation originally around 290 m. Currently, the gully has been backfilled to an elevation of 305 m–315 m. The surrounding rock of the tunnel is mainly sandy mudstone with relatively complete block mosaic structure. The classification of surrounding rock is grade IV. The moderately weathered sandy mudstone at the top of the tunnel is 12 m∼17 m thick. The possible problems of site and foundation stability caused by engineering construction are mainly the stability of the underground tunnel and subgrade slope, which should be considered in a reasonable design. The construction site of the Hongyancun tunnel is shown in Figure 1.

Figure 1

Figure 1. The underground tunnel excavation.

In order to solve the stability problem related to rock engineering structures, we combined the fundamental principles of strength reduction method into the RFPA method (Tang et al., 2020; Feng et al., 2022). RFPA has been applied in simulating rock failure by many researchers (Wang et al., 2023b; Liu et al., 2024b; Gong et al., 2025a; Gong et al., 2025b). We also employed the AE event rate as the criterion for rock engineering failure. The main feature of the RFPA improved by strength reduction method for stability analysis of rock engineering is that they can obtain the factor of safety without any assumption for the shape and location of the failure surface. We initially considered that all FEM elements were elastic, with their elastic properties defined by Young’s modulus and Poisson’s ratio. We used the maximum tensile strain (or stress) criterion and the Mohr-Coulomb criterion to set the damage criteria. In the tensile failure mode, element damage was evaluated based on the maximum tensile strain criterion. For elements remaining intact under tensile conditions, shear-induced failure was subsequently assessed using the Mohr-Coulomb strength criterion.

The essential notion of strength reduction is introduced into the constitutive model of the element as an alternate solution to the failure analysis problem connected to geological or rock engineering. Each element is subjected to the shear strength reduction technique, and the constitutive model’s strength f₀ is determined linearly using Equation 1:

$f_0^{trial}=\frac{f_0}{f_s^{trial}}(1)$

In the formula, f_s^trial is the trial safety factor and f₀^trial is the trial strength of the element. The trial strength f₀^trial will be used in RFPA to investigate the strength of the rock masses.

Two kinds of cavities with different section shapes are selected, i.e., circular cavity and horseshoe cavity. The section size and boundary condition of the cavity are shown in Figure 2. We established numerical models with the size of 15 m × 15 m × 15 m in the X, Y and Z directions, respectively, and divided them into 100 × 100 × 100 = 100,000 units. In RFPA, the rock is assumed to be composed of many mesoscopic elements of the same size, and the mechanical properties of these elements are assumed to follow a given Weibull distribution (Gong et al., 2024; Gong et al., 2025c).

Figure 2

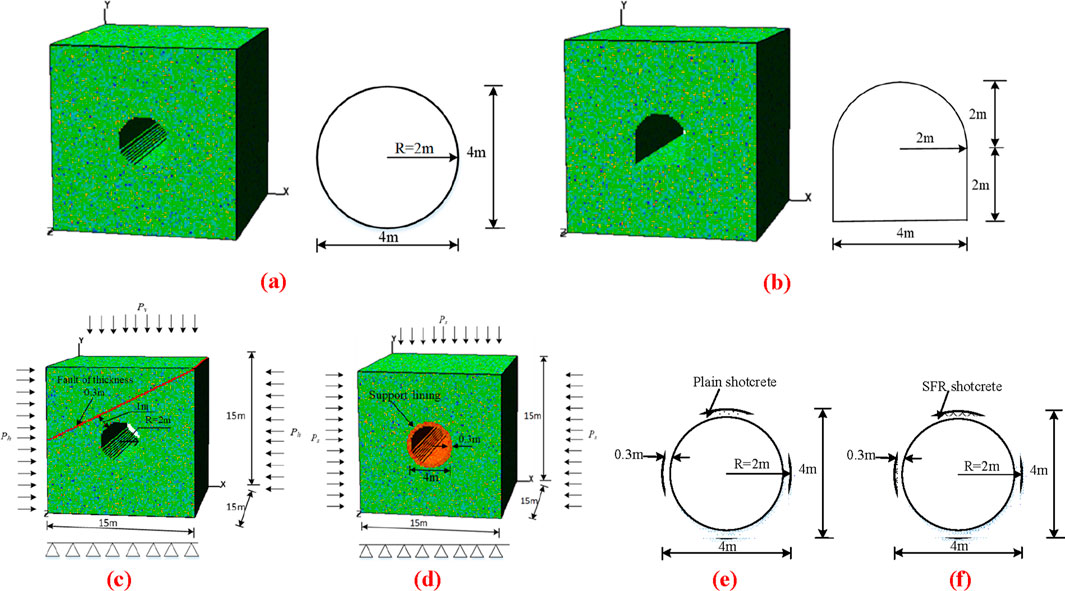
Figure 2. Configuration of cross sections and numerical models. (A) Model (M_C). (B) Model (M_H). (C) Model (M_F). (D) Model (M_P and M_S). (E) Plain concrete. (F) SFR concrete.

For shallow tunnel, we applied vertical stress of 2.75 MPa on the upper part of the model, horizontal stress of 4 MPa on both sides, and fixed the bottom, respectively, i.e., models M_C0 and M_H0. For deep tunnel, the vertical stress is kept unchanged and the horizontal stress of 8 MPa is applied, i.e., models M_C1 and M_H1. The rock mass yield criterion is based on the Mohr-Coulomb criterion. The parameters of rock mass are determined according to the field test and relevant literature (Liang, 2005), as shown in Table 1.

Table 1

Table 1. Physical and mechanical parameters of numerical simulation.

Numerical simulations employed the strength reduction method with a constant boundary stress condition. Both the rock mass strength and joint strength were progressively reduced at an increment of 0.01 until instability occurred, which was determined based on the critical number of failed elements. The corresponding safety factor was then calculated. A comprehensive parametric study was conducted to investigate: (1) the stability influence of faults (M_F) positioned 1 m above the tunnel with varying dip angles (α = 0°, 30°, 60°, 90°) and (2) the effect of lateral pressure coefficients (k = 0.8, 1.0, 1.2, 1.4). The model geometry and boundary conditions are illustrated in Figures 2A, B and 2D. Material parameters for both rock mass and joints were determined through field tests and validated against existing literature (Liang, 2005), with detailed mechanical properties provided in Table 2.

Table 2

Table 2. Physical and mechanical parameters of fault.

The failure mechanisms of both rigid and flexible tunnel support systems were numerically analyzed, respectively, i.e., Models M_P and M_S. As illustrated in Figures 2E,F, the circular tunnel support system was evaluated under plane strain conditions. Two distinct support configurations were modeled: (1) rigid support: conventional plain concrete lining and (2) flexible support: steel fiber-reinforced (SFR) concrete lining. The SFR concrete demonstrates post-cracking tensile strength. The fibers within it function as micro-reinforcements, effectively distributing stresses in a more uniform manner and regulating crack propagation. Concurrently, SFR concrete can be regarded as a single composite material featuring homogenized properties. This approach significantly reduces computational complexity when contrasted with modeling discrete rebars and their complex interactions with concrete.

In this simulation, the thickness of the support lining under consideration is set at 0.3 m. The calculation domain is discretized into 100 × 100 × 100 quadrilateral isoparametric elements. A static loading scheme is implemented in the numerical model to mimic the deep - seated ground stress environment of the rock mass surrounding the laneway. The bottom of the model is fully fixed. A uniform static load of 8 MPa is applied on both lateral sides of the model, while a vertical load of 2.75 MPa is imposed on the model’s top surface. The average self-weight of the overburden strata in the model is assumed to be 25 kN/m³. The mechanical parameters of the elements are assigned following a Weibull distribution, and the values of the physical and mechanical parameters are determined based on in-situ tests and relevant literature (Liang, 2005), as presented in Table 3. Three distinct models with horizontal, inclined, and vertical alignments are designed. In each model, a circular tunnel with a radius of 2.00 m is excavated along the respective alignment. As depicted in Figure 3, the distances L between the centers of two adjacent tunnels are 2.00 m for the horizontal alignment, 2.83 m for the inclined alignment, and 2.00 m for the vertical alignment.

Table 3

Table 3. Physical and mechanical parameters of model material.

Figure 3

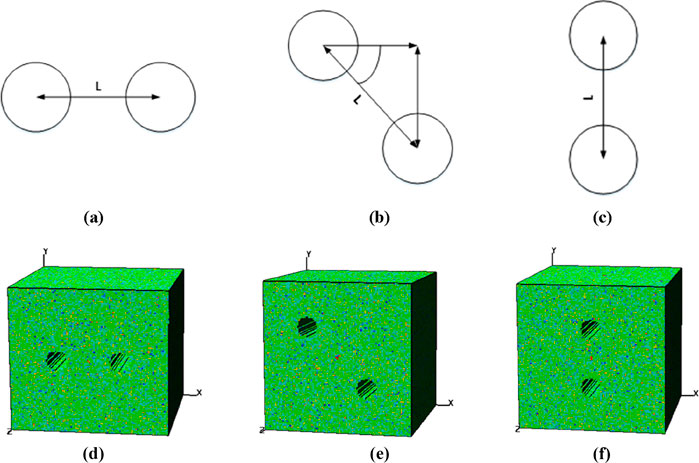
Figure 3. Configuration and numerical model of twin tunnels. (a) Horizontal alignment. (b) Inclined alignment. (c) Vertical alignment. (d) Model of horizontal alignment. (e) Model of inclined alignment. (f) Model of vertical alignment.

3 Results and discussion

3.1 Section optimization effect

3.1.1 Failure process of tunnels with circular cavity

The maximum principal stress diagram and its corresponding AE diagram of tunnels with circular cavity are shown in Figure 4. In the AE diagrams, the red and blue dots represent the locations of AE events. The red color means that the AE event is generated because the tensile failure happens, while the blue color indicates that the AE event occurs because the compression-shear failure is triggered. The failure process of circular cavity in shallow tunnel are similar to the top of horseshoe where roof damage precedes the floor damage and is more severe than the latter. Discontinuous spalling occurred at the mid height of the side wall of the circular tunnel after excavation, and micro cracks in the surrounding rock were initially generated from the mid height of the side wall at the 66th reduction step. Under the increasing external load, the cracks then extended concentrically to greater depth in the rock mass surrounding the tunnel. At 74th step, the zonal disintegration becomes obviously and continuously, the cracks penetrated on the deep masses of surrounding rock. The cracks of the sidewall, bottom and roof are completely detached from the surrounding rock resulting in the tunnel losing its stability.

Figure 4

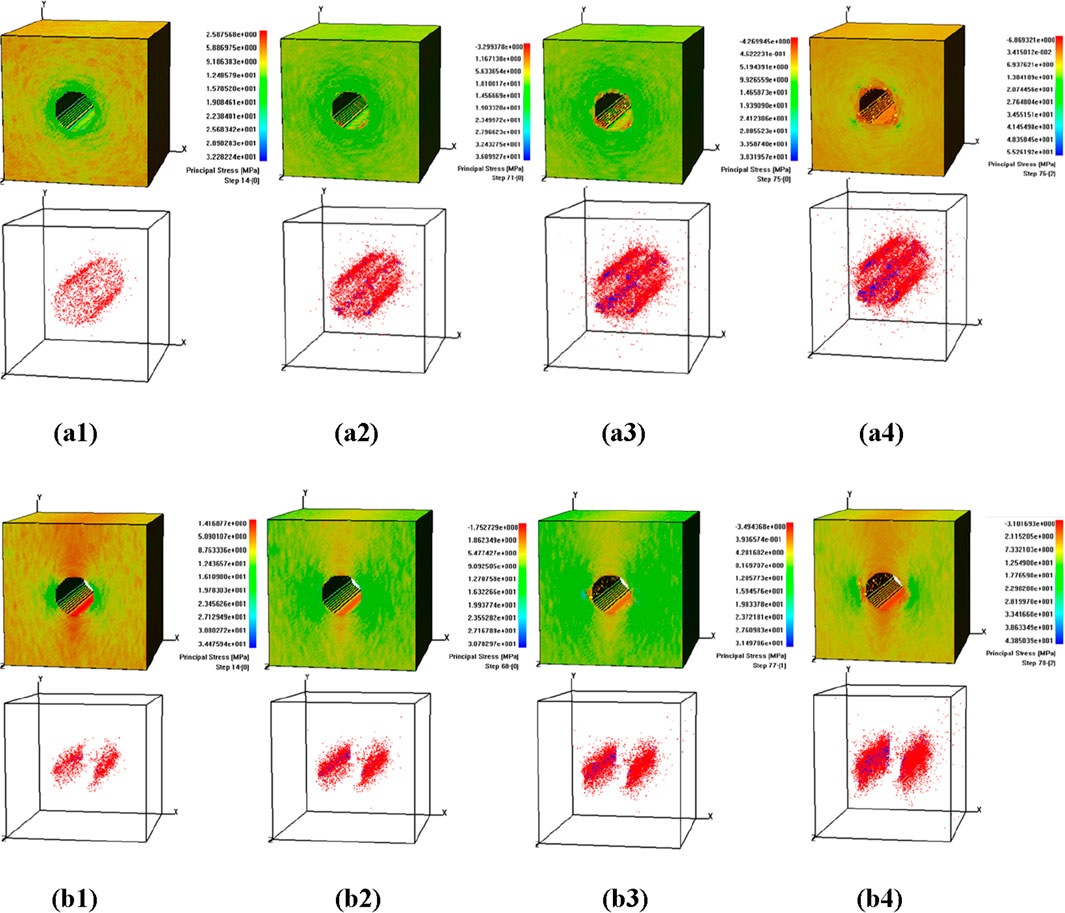
Figure 4. Shear stress and AE diagram of shallow (series (a)) and deep (series (b)) circular tunnels. (a1) Step 14. (a2) Step 71. (a3) Step75. (a4) Step 76-2. (b1) Step 14. (b2) Step 68. (b3) Step77. (b4) Step 78.

The maximum principal stress diagram and its corresponding acoustic emission diagram in the failure process of circular cavity in deep tunnel are shown in Figure 4. Due to the excavation under high overburden stresses in deep tunneling, the distribution of the zonal disintegration tends to appear on all the periphery of model due to the rock overstressing. The failure process is somehow similar to the shallow tunnel, it also shows the continuous damage evolution under the loading state. At the 73rd step, the concentration of the stress tends to appear at both the sidewall, the zonal disintegration in the left and right sidewall of tunnel seems to begin simultaneously. When the strength of the rock mass continues weakening and at the 77-1st step, the cracks in the left sidewall develop into deeper surrounding rock, the disintegration on the roof and bottom is not prominent. Finally, at the 78-2nd step, the side wall, the vault and invert of the tunnel completely lose their stability.

3.1.2 Failure process of tunnels with horseshoe cavity

For the shallow tunnel with horseshoe cavity in Figure 5, continuous spalling is found to occur at the foot of the tunnel and micro cracks in the surrounding rock are initially generated from the foot of the side wall at the 42nd step. Under the increasing external load, the cracks develop upwards to form a conjugate sliding shape at the foot of the arch roof, where the cracks finally coalesce. At the 59th reduction step, cracks are initially generated at the two right sides of the tunnel base, the vault is next damaged. However, the cracks at the top of horseshoe shaped tunnels generate and propagate to form smaller triangular zonal disintegration. Similarly, with the further reduction of the surrounding rock strength, the stress transfers to the deeper part of the further reduction of the surrounding rock again. When the strength of the rock mass continues weakening and at the 75-7th step, the roof and floor of the tunnel are obviously damaged, the right bottom corner displays the detachment. The tunnel detaches from the surrounding rock and completely loses its stability.

Figure 5

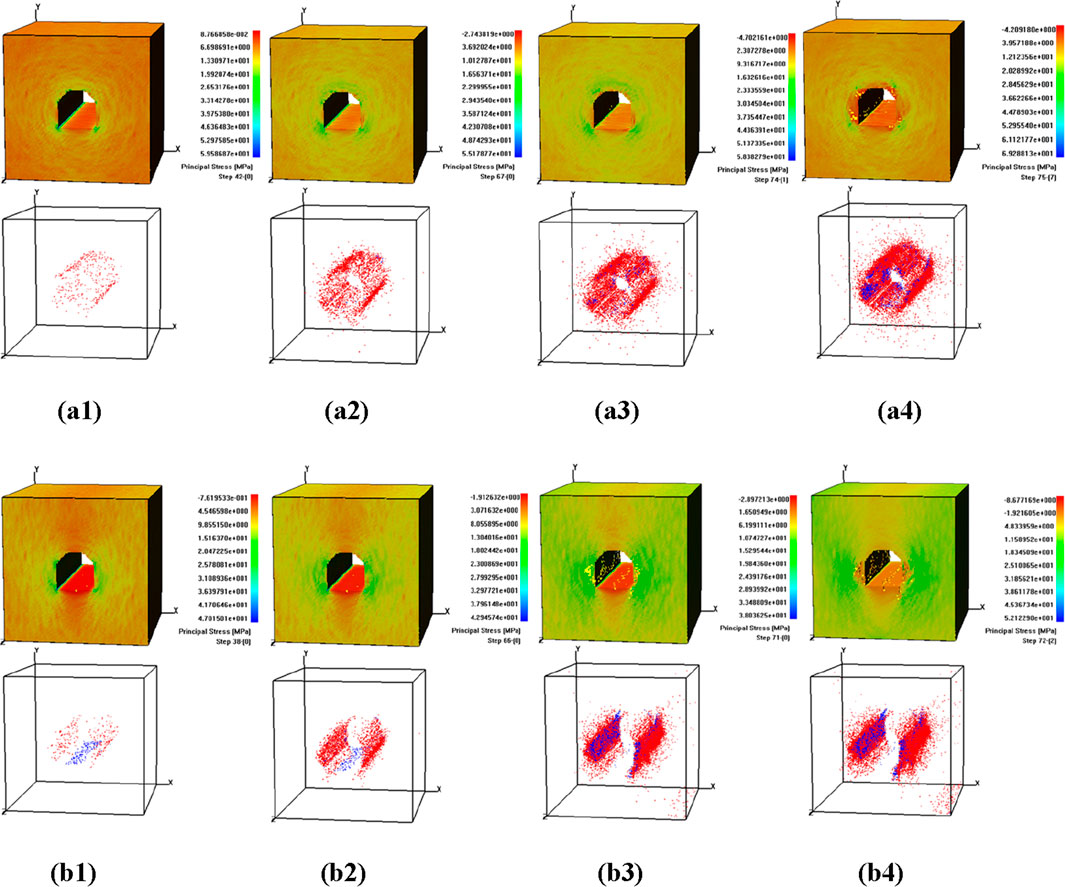
Figure 5. Shear stress and AE diagram of shallow (series (a)) and deep (series (b)) horseshoe cavity. (a1) Step 42. (a2) Step 67. (a3) Step74. (a4) Step 75. (b1) Step 38. (b2) Step 66. (b3) Step71. (b4) Step 72.

For deep tunnel, the zonal disintegration with horseshoe cavity in Figure 5 seems to appear early than the shallow tunnel. Unlike the shallow tunnel, the concentration of stress tends to appear at floor and the bottom of the tunnel. Then, the cracks extend to the center of the roof and floor of the tunnel. Then, zonal disintegrations starting from the cavity wall are mainly on the left sides along the joint extension. Under the increasing external load, the cracks also develop on the left side wall of the tunnel to some extent. The zonal disintegration on the left and right sidewall shows the huge damages, which is highly consistent with the classical rib spalling during tunnel excavation in Figure 6. The middle part of the floor also shows the ridgeline damages but unlike the shallow tunnel, the roof of the tunnel does not generate damages. Finally, considering that the zonal fractures of surrounding rocks generally happen in high-stress environments in deep engineering, which may result in unimaginable accidents, it is necessary to further study more effective support methods.

Figure 6

Figure 6. The classical rib spalling during tunnel excavation.

3.1.3 AE distribution and safety factor

Figure 7 presents the AE counts and accumulated energy from excavation to instability in shallow and deep tunnels with different cross-sections. The safety factors are: 4.00 (M_C0), 2.38 (M_H0), 1.44 (M_C1), and 3.00 (M_H1). Before macro-instability, over 2,000 AE events occur, with a sharp upward trend preceding failure, indicating clear precursory characteristics in heterogeneous rock. AE energy is released from damaged elements, but the quantity, distribution continuity, and accumulated energy frequency vary significantly. Circular tunnels exhibit better AE distribution continuity than horseshoe-shaped ones, suggesting lower stability in the latter. Circular tunnels also fail later, confirming their superior stability. Figure 7 shows a rapid increase in AE counts and energy ratios before macroscopic failure. This occurs because stress redistribution under load creates localized concentrations, triggering microcracking. As microcracks coalesce into larger fractures, AE activity intensifies, accelerating as failure approaches. This process leads to a sharp rise in AE signals just before collapse.

Figure 7

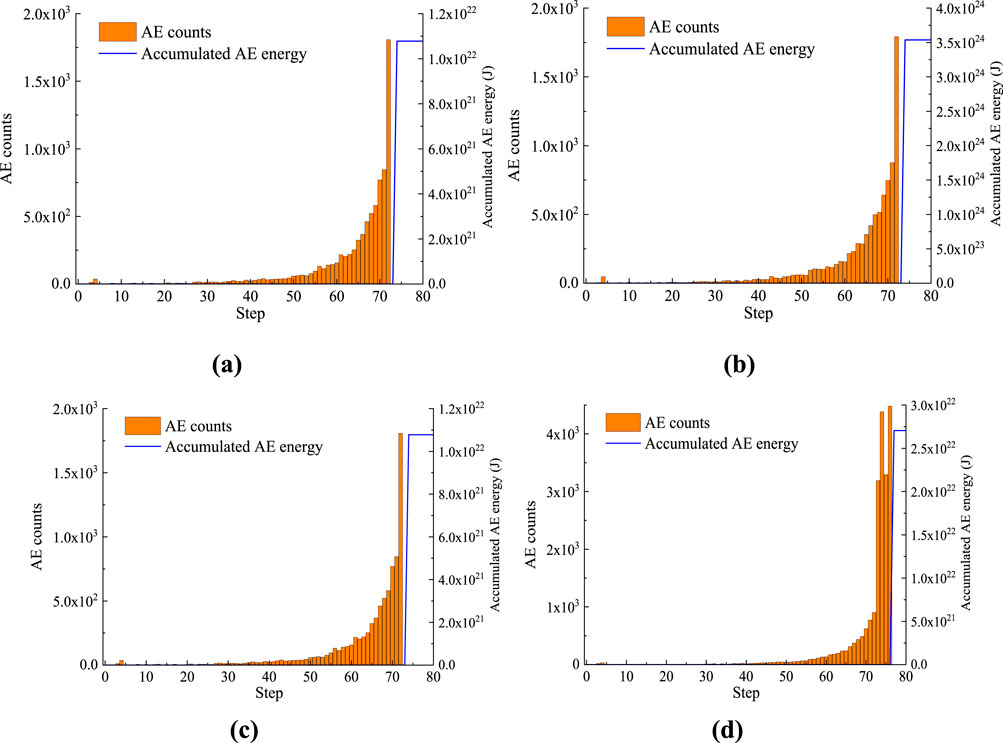
Figure 7. AE results of circular and horseshoe cavities. (a) Shallow circular tunnel. (b) Deep circular tunnel. (c) Shallow horseshoe tunnel. (d) Deep horseshoe tunnel.

3.2 Influence of existing fault

3.2.1 Effect of dip angles on the stability of tunnel

Fault located at different locations can lead to different influences on the deformation, stress and zonal disintegration of surrounding rock mass. Figure 8 shows the stress distribution of surrounding rock under different fault dip angles and their corresponding acoustic emissions at failure state. It can be seen that during the initial excavation, the surrounding rock stress is concentrated at the arch waist, and the stress shows symmetry. Under the increasing external load, the surrounding rock is damaged at the arch waist, and the stress concentration area also moves to the tip of the propagation crack. At the same time, there is also a high stress area at the fault, and finally a through crack appears between the tunnel and the fault. It can also be seen from the figure that the stress concentration degree of surrounding rock near the fault side is significantly higher than that on the without fault side.

Figure 8

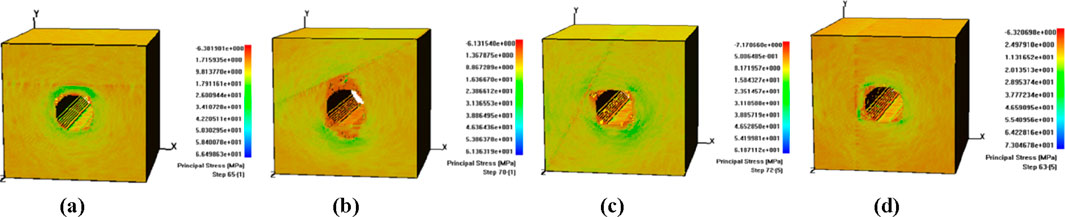
Figure 8. Shear stress diagrams with different dip angles of fault. (a) α = 0°. (b) α = 30°. (c) α = 60°. (d) α = 90°.

When α = 0°, the stress first appears in the arch waist and shows symmetry, which leads to damage and then extends to both sides; with the increase of fault dip angle, the stress distribution changes from the symmetrical distribution of intact rock mass and close to the fault stress migration. From the acoustic emission distribution in Figure 9, we can understand that the fault has great influence on the transmission of stress, strain and strain energy. When the tunnel is excavated, the rock mass between the fault and the tunnel will bear greater stress and store more energy, resulting in large deformation of the rock mass in this area, collapse or even rock burst at the tunnel boundary can occur, and the crack extends to the depth, which may eventually cause the relative sliding of the upper and lower walls of the fault.

Figure 9

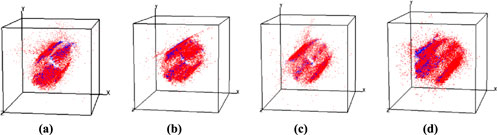
Figure 9. Acoustic emission distribution with different dip angles of fault. (a) α = 0°. (b) α = 30°. (c) α = 60°. (d) α = 90°.

3.2.2 Effect of lateral pressure coefficient on the stability of tunnel

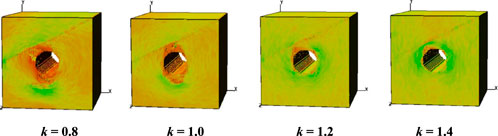
A series of lateral pressure coefficient of 0.8, 1.0, 1.2 and 1.4 are applied on models with dip angle of 30°, respectively, and the failure patterns at four typical reduction steps are shown in Figure 10. When k = 0.8 and k = 1.0, the detachment of joints is confined in the regions near the left shoulder of tunnel. At k = 1.2, cracks initiate at the bottom of left sidewall and the jointed place of right sidewall. For k = 1.4, fractures only occur at roof of tunnels, and there are no fracture zones at both sidewalls. The failure pattern of tunnel is spalling, flexing and breaking of tunnel rock mass, for which the shape of fractured zones on the roof is triangle. The faults have obvious effect on the failure mode of tunnel, and the high tectonic stress will have dominate effect on the failure of tunnel.

Figure 10

Figure 10. Effect of lateral pressure coefficient on the stability of tunnel.

3.3 Tunnel support system

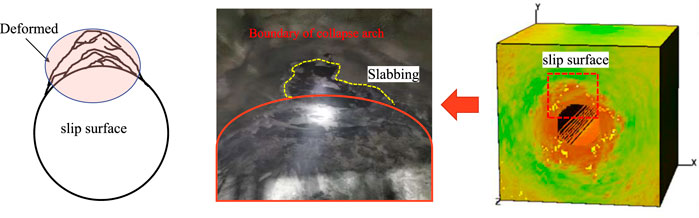
The numerical results that portray the failure process of the surrounding rock of the laneway are presented in Figure 11. In this simulation, plain shotcrete serves as the rigid support under static loading conditions. As the external load gradually increases, due to the inherent heterogeneity of the model, the relatively weaker units within the rigid support start to sustain minor damage. By the 86-7th loading step, a large number of units in the rigid roof suddenly fail. The damage is especially conspicuous at all four corners of the vault. As the damage continues to develop and reaches the 86-23rd reduction step, the laneway roof undergoes substantial deformations and widespread failure. Meanwhile, both sides of the laneway also suffer significant destruction. At this point, the rigid support is forced outward and loses its ability to bear loads. An instance of slabbing during the excavation of a circular tunnel is shown in Figure 12, which further clarifies the failure mechanism.

Figure 11

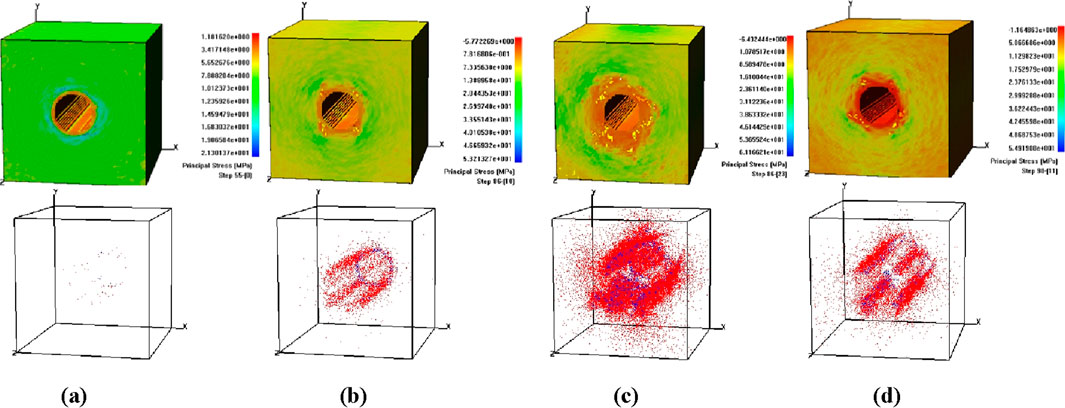
Figure 11. Shear stress diagram and acoustic emission distribution of rigid tunnel support. (a) Step 55. (b) Step 86-7. (c) 86-23. (d) Step 98-11.

Figure 12

Figure 12. An example of slabbing during circle tunnel excavation.

As external load increases, laneway undergoes shear failure. However, the flexible support shows far less element damage. Under static loading, only a few roof units of the flexible support are damaged. By the 98-11th reduction step, damage emerges at the tunnel’s bottom and top left corner, yet sidewalls and roof remain largely intact, with no collapse or spalling. The steel fiber-reinforced flexible support stays undamaged, enhancing rock load - bearing. Tensile stress dominates its failure area. As load rises, it uses tensile properties to absorb deformation energy, preventing fractures. For varying excavation conditions, grouted rock bolts and lattice girders can be used for support.

3.4 Influence of tunnel alignment

3.4.1 Tunnels with horizontal alignment

The maximum principal stress diagram and corresponding acoustic emission diagram in the failure process with horizontal alignment tunnel are shown in Figure 13. With the rock mass strength weakening under the triaxial stress state, from which can be observed that the first fractured zone adjacent to the tunnel wall appear at the 39th reduction step. Then, the stress and damage from the cavity wall on both sides along the joint extension, left and right sides of the expansion rate are similar. When the damages continue and reach the 81st reduction step, the damage in both side of tunnel begins to appear. When the compressive/tensile strength continues reducing to the 87th step, the rock mass at a certain distance away from the first fracture starts to show the obvious damages. When it reaches to the 87-19 reduction step, the tunnel loses stability from the bottom and along the horizontal line of the two tunnels.

Figure 13

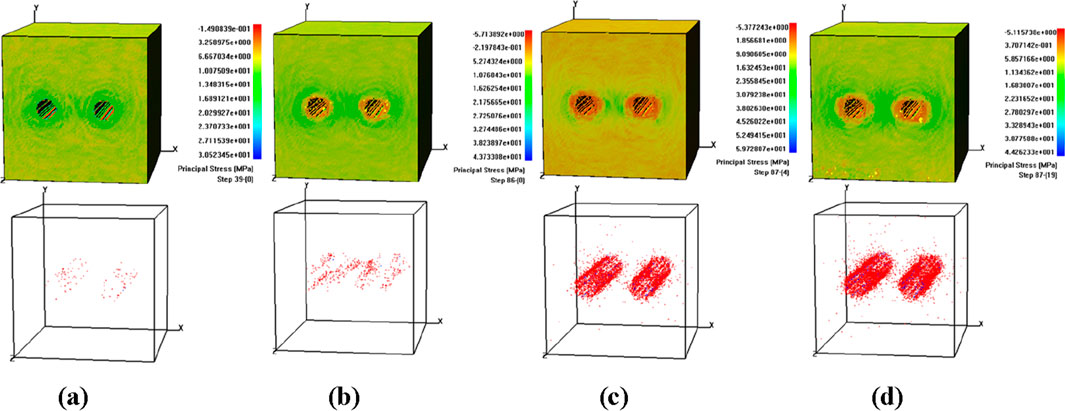
Figure 13. Shear stress and AE diagram of horizontally aligned tunnel. (a) Step 39. (b) Step 86. (c) Step87-4. (d) Step 87-19.

3.4.2 Tunnels with inclined alignment

The shear stress and AE diagram of inclined aligned tunnel are shown in Figure 14. The strength of the rock mass contuses weakening and when reaches the 85 reduction step, the damage in both the tunnel becomes obvious. However, the upper left tunnel shows the damage mainly on the right wall and the lower right tunnel shows the damage on the and left wall. When it reaches the 85th reduction step, the bottom of both the tunnel shows the obvious damage, the damage on the lower tunnel is more prominent, the roof wall starts to detach from the surrounding rock. At the reduction step 87-6, the tunnel completely loses its stability and along with the radial damages around cavity, the damage seems to be more concentrated diagonally and around the cavity.

Figure 14

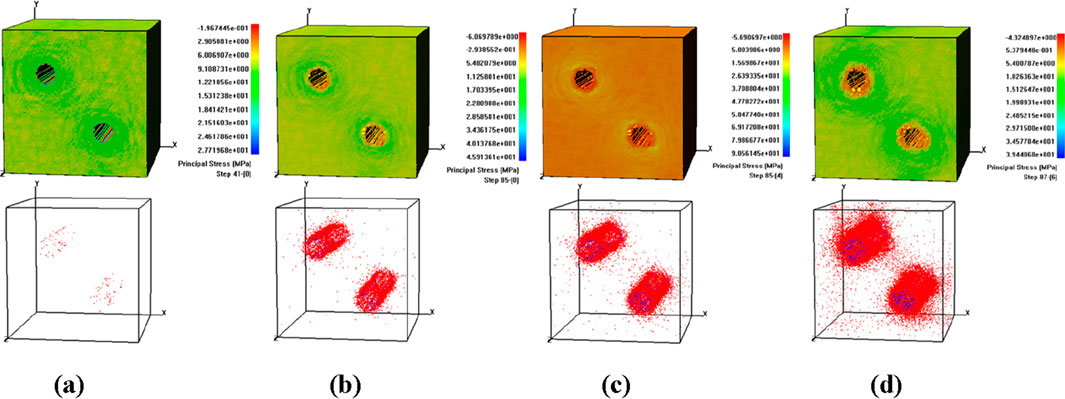
Figure 14. Shear stress and AE diagram of vertically inclined tunnel. (a) Step 41. (b) Step 85-1. (c) Step 85-4. (d) Step 87-6.

3.4.3 Tunnels with vertical alignment

The shear stress and AE diagram of vertically aligned tunnel are shown in Figure 15. When it reaches the 85-4 reduction step, the damage on the lower tunnel is more severe than the upper tunnel, the floor of the tunnel completely detaches, and the vault collapses. Compared with the horizontal tunnel, the zonal fracture modes of vertical aligned tunnel show similarities to a certain extent. Consequently, the rapture area of the fracture ring located above the tunnel develops along the vertical line of the tunnel.

Figure 15

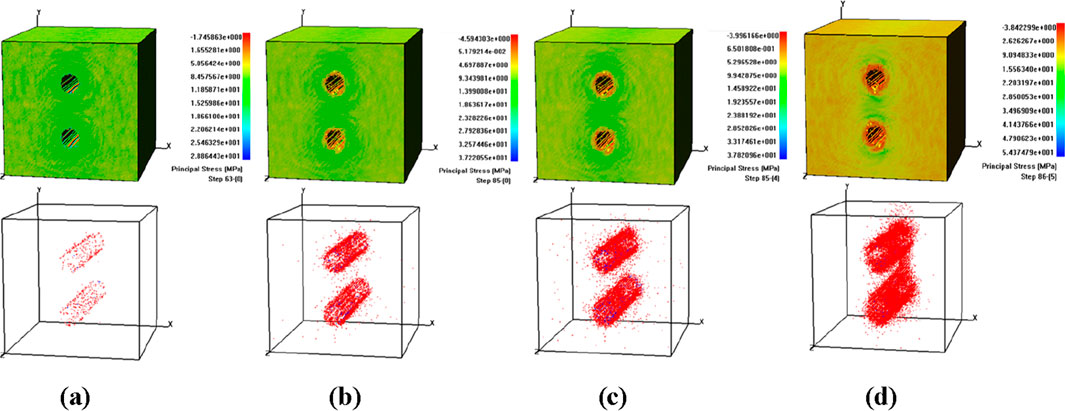
Figure 15. Shear stress and AE diagram of vertically aligned tunnel. (a) Step 63. (b) Step 85. (c) Step 85-4. (d) Step 86-5.

4 Conclusion

To understand the fracture features and reveal the failure mechanisms of circle tunnels excavated in deep rock masses, a series of three-dimensional heterogeneous models considering the effects of the tunnel cross section, tunnel spacing, tunnel alignment, support system, dip angle of faults and the lateral pressure coefficient of faulted rock mass on the stability of the tunnel are established. The strength reduction method is embedded to achieve the gradual fracture process, final failure mode and safety factor and to reproduce the characteristic fracture phenomenon of tunnels under high geo-stress level, i.e., zonal disintegration. The following conclusions could be drawn:

(1) The circle cross-section is considered to be the optimal cross-section because the force around the vault and the arch bottom is symmetrical. The horseshoe cross-section should be avoided in the tunnel design. Meanwhile, because of obvious obstruction, the rock mass between the fault and the tunnel bears high stress, and the tunnel cavity is easy to be damaged near the fault, and the degree of damage is severe. When k = 0.8 and 1.0, the detachment of joints is confined in the regions near the left shoulder of tunnel. At k = 1.2, cracks initiate at the bottom of left sidewall and the jointed place of right sidewall. For k = 1.4, fractures only occur at roof of tunnels, and there are no fracture zones at both sidewalls.

(2) The alignment of a tunnel significantly influences its stability, with zonal fracture modes along the tunnel alignment exhibiting certain similarities. Overall, the rupture area of the fracture ring above the tunnel tends to develop in alignment with the tunnel’s longitudinal axis. Additionally, an analysis of stress distribution, fracture progression, and cumulative acoustic emissions highlights distinct behavioral patterns in the tunnel support systems. These patterns provide critical insights into the interaction between the tunnel structure and the surrounding rock mass, aiding in the design of more effective support strategies.

(3) In terms of the rigid support, significant deformation and eventual collapse of the roof are observed, alongside noticeable damage to the two tunnel sidewalls. In contrast, the flexible support structure demonstrates minimal and controllable deformation, resulting in an overall stable condition of the laneway. To address the varying ground conditions and stress regimes encountered during excavation, the grouted rock bolts can be used to rigidly anchor the rock mass and transfer loads to deep stable zones, and lattice girders can be installed as rigid structural elements to support the tunnel roof and walls.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

XF: Data curation, Formal Analysis, Funding acquisition, Investigation, Writing – original draft. YP: Investigation, Writing – original draft. BG: Conceptualization, Methodology, Supervision, Writing – review and editing. XC: Software, Validation, Writing – review and editing. WD: Project administration, Resources, Writing – review and editing. HL: Formal Analysis, Visualization, Writing – review and editing. FR: Formal Analysis, Validation, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The present work was financially supported by the Beijing Natural Science Foundation, China (Grant No. 2244099), the China Postdoctoral Science Foundation, China (Grant No. 2023TQ0025) and the Major National Science and Technology Project for Deep Earth: Mobile tailings-waste homogeneous filling and rock pressure coordination control technology, China (Grant No. 2024ZD1003805).

Conflict of interest

Author YP was employed by China Communication Construction 4th Harbour Engineering Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Armand, G., Leveau, F., Nussbaum, C., de La Vaissiere, R., Noiret, A., Jaeggi, D., et al. (2014). Geometry and properties of the excavation-induced fractures at the Meuse/Haute-Marne URL Drifts. Rock Mech. Rock Eng. 47 (1), 21–41. doi:10.1007/s00603-012-0339-6

CrossRef Full Text | Google Scholar

Barton, N., Grimstad, E., and Palmstrom, A. (1995). “Design of tunnel support,” in Chapter of sprayed concrete: properties, design and application. Editors S. A. Austin, and P. J. Robins (Dunbeath, UK: Whittles Publishing).

Google Scholar

Basirat, R. (2025). Analysis of tunnel lining internal forces under the influence of S and P-waves: an analytical solution and quasi-static numerical method. Rock Mech. Bull. 4 (1), 100168. doi:10.1016/j.rockmb.2024.100168

CrossRef Full Text | Google Scholar

Bobet, A. (2011). Lined circular tunnels in elastic transversely anisotropic rock at depth. Rock Mech. Rock Eng. 44 (2), 149–167. doi:10.1007/s00603-010-0118-1

CrossRef Full Text | Google Scholar

Chakeri, H., Hasanpour, R., Hindistan, M. A., and Ünver, B. (2011). Analysis of interaction between tunnels in soft ground by 3D numerical modeling. Bull. Eng. Geol. Environ. 70 (3), 439–448. doi:10.1007/s10064-010-0333-8

CrossRef Full Text | Google Scholar

Chen, B., Gong, B., Wang, S., and Tang, C. (2022). Research on zonal disintegration characteristics and failure mechanisms of deep tunnel in jointed rock mass with strength reduction method. Mathematics 10, 922. doi:10.3390/math10060922

CrossRef Full Text | Google Scholar

Chen, X., Wang, Y., Zhang, Q., Li, S., and Nordlund, E. (2013). Analogical model test and theoretical analysis on zonal disintegration based on filed monitoring in deep tunnel. Eur. J. Environ. Civ. Eng. 17, s33–s52. doi:10.1080/19648189.2013.834584

CrossRef Full Text | Google Scholar

Deng, P., Liu, Q., Huang, X., Liu, Q., Ma, H., and Li, W. (2021). Acquisition of normal contact stiffness and its influence on rock crack propagation for the combined finite-discrete element method (FDEM). Eng. Fract. Mech. 242, 107459. doi:10.1016/j.engfracmech.2020.107459

CrossRef Full Text | Google Scholar

Feng, X., Gong, B., Cheng, X., Zhang, H., and Tang, C. (2022). Anisotropy and microcrack-induced failure precursor of shales under dynamic splitting. Geomatics, Nat. Hazards Risk 13 (1), 2864–2889. doi:10.1080/19475705.2022.2137440

CrossRef Full Text | Google Scholar

Feng, X., Gong, B., Liang, Z., Wang, S., Tang, C., Li, H., et al. (2024). Study of the dynamic failure characteristics of anisotropic shales under impact Brazilian splitting. Rock Mech. Rock Eng. 57, 2213–2230. doi:10.1007/s00603-023-03673-w

CrossRef Full Text | Google Scholar

Feng, X., Liu, H., Chen, X., Che, C., Xia, K., Guo, Q., et al. (2025b). Acoustic emission characteristics and cracking mechanism analysis of anisotropic shale containing a circular hole under uniaxial compression. Theor. Appl. Fract. Mech. 135, 104771. doi:10.1016/j.tafmec.2024.104771

CrossRef Full Text | Google Scholar

Feng, X., Liu, H., Wang, P., Zhang, S., Zhu, Q., Tang, C., et al. (2025a). Failure behaviors of anisotropic shale with a circular cavity subjected to uniaxial compression. J. Rock Mech. Geotechnical Eng. 17 (1), 357–369. doi:10.1016/j.jrmge.2024.03.042

CrossRef Full Text | Google Scholar

Fujiyama, T., and Kaku, K. (2023). Current status of the geological disposal programme and an overview of the safety case at the pre-siting stage in Japan. Rock Mech. Bull. 2 (3), 100062. doi:10.1016/j.rockmb.2023.100062

CrossRef Full Text | Google Scholar

Ghorasaini, D., and Singh, A. B. (2019). Geotechnical engineering design of a tunnel support system - a case study of Bheri Babai Headrace Tunnel. Int. J. Eng. Trends Technol. 67 (4), 33–37. doi:10.14445/22315381/ijett-v67i4p208

CrossRef Full Text | Google Scholar

Gong, B., Wang, Y., Chen, X., Song, W., Wang, K., and Yu, J. (2025b). Analysis of sensitivity factors on CJB mechanical behavior from specimen scale to engineering scale. Eng. Fract. Mech. 314, 110673. doi:10.1016/j.engfracmech.2024.110673

CrossRef Full Text | Google Scholar

Gong, B., Zhao, T., Thusyanthan, I., and Tang, C. (2024). Modelling rock fracturing by a novel implicit continuous to discontinuous method. Comput. Geotechnics 166, 106035. doi:10.1016/j.compgeo.2023.106035

CrossRef Full Text | Google Scholar

Gong, B., Zhao, T., Thusyanthan, I., Tang, C., and Zhou, G. G. D. (2025a). The random RFPA method for modelling rock failure. Rock Mech. Rock Eng. doi:10.1007/s00603-025-04400-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Gong, B., Zhao, T., Thusyanthan, I., Tang, C., and Zhou, G. G. D. (2025c). Integrating RFPA and DEM in adaptive RDFA modeling of rock fracturing process. Rock Mech. Rock Eng. 58, 2569–2587. doi:10.1007/s00603-024-04239-0

CrossRef Full Text | Google Scholar

He, S., Lai, J., Zhang, Y., Wang, K., Xu, W., Wang, L., et al. (2021). Damage behaviors, prediction methods and prevention methods of rockburst in 13 deep traffic tunnels in China. Eng. Fail. Anal. 121, 105178. doi:10.1016/j.engfailanal.2020.105178

CrossRef Full Text | Google Scholar

Hu, Y., Wang, Q., Wang, M., and Liu, D. (2021). A study on the thermo-mechanical properties of shotcrete structure in a tunnel, excavated in granite at nearly 90 °C temperature. Tunn. Undergr. Space Technol. 110, 103830. doi:10.1016/j.tust.2021.103830

CrossRef Full Text | Google Scholar

Jia, P., and Zhu, W. C. (2015). Mechanism of zonal disintegration around deep underground excavations under triaxial stress – insight from numerical test. Tunn. Undergr. Space Technol. 48, 1–10. doi:10.1016/j.tust.2015.01.005

CrossRef Full Text | Google Scholar

Karahan, S., and Gokceoglu, C. (2025). Assessment for shallow and large tunnel construction in weak ground conditions: application of tunnel boring machines. Deep Undergr. Sci. Eng. 4 (1), 132–148. doi:10.1002/dug2.12083

CrossRef Full Text | Google Scholar

Kim, K., Rutqvist, J., and Birkholzer, J. (2020). Lattice modeling of excavation damage in argillaceous clay formations: influence of deformation and strength anisotropy. Tunn. Undergr. Space Technol. 98, 103196. doi:10.1016/j.tust.2019.103196

CrossRef Full Text | Google Scholar

Ko, J., and Jeong, S. (2017). A study on rock mass classifications and tunnel support systems in unconsolidated sedimentary Rock. Sustainability 9, 573. doi:10.3390/su9040573

CrossRef Full Text | Google Scholar

Kovari, K. (1994). Erroneous concepts behind the new Austrian tunnelling method. Tunnels &Tunnelling 26 (11), 38–42.

Google Scholar

Li, Y., Zhu, H., Zhang, S., Chen, B., and Buchu Zhang, B. (2024). Shear mechanical behavior and fracturing path of red sandstone treated by joninted effect of water-fractures. Int. J. Coal Sci. and Technol. 11, 77. doi:10.1007/s40789-024-00726-5

CrossRef Full Text | Google Scholar

Liang, Z. Z. (2005). “Three-dimensional failure process analysis of rock and associated numerical tests,”. Ph.D. Thesis (Shenyang, China: Northeastern University).

Google Scholar

Lin, P., Liu, H., and Zhou, W. (2015). Experimental study on failure behaviour of deep tunnels under high in-situ stresses. Tunn. Undergr. Space Technol. 46, 28–45. doi:10.1016/j.tust.2014.10.009

CrossRef Full Text | Google Scholar

Lin, Y. J., Paddock, E. F., and King, E. L. (1984). Meiotic chromosome configurations in a triploid Rhoeo. Genetica 63 (2), 113–119. doi:10.1007/bf00605895

CrossRef Full Text | Google Scholar

Liu, H., Feng, X., Liu, L., Li, T., and Tang, C. (2023). Mechanical properties and failure characteristics of anisotropic shale with circular hole under combined dynamic and static loading. Int. J. Rock Mech. Min. Sci. 170, 105524. doi:10.1016/j.ijrmms.2023.105524

CrossRef Full Text | Google Scholar

Liu, H., Feng, X., Miao, S., Hu, J., Zhao, J., Zhang, Y., et al. (2024). Study on the dynamic fracture behavior of anisotropic CCNBD shale specimens under different impact angles. Theor. Appl. Fract. Mech. 133, 104616. doi:10.1016/j.tafmec.2024.104616

CrossRef Full Text | Google Scholar

Liu, X., Gong, B., Song, K., and Liu, H. (2024b). Indirect tensile strength test on heterogeneous rock using square plate sample with a circular hole. Lithosphere 2024 (3). doi:10.2113/2024/lithosphere_2023_322

CrossRef Full Text | Google Scholar

Liu, X., Zhang, X., Wang, L., Qu, F., Shao, A., Zhao, L., et al. (2024a). Research progress and prospects of intelligent technology in underground mining of hard rock mines. Green Smart Min. Eng. 1 (1), 12–26. doi:10.1016/j.gsme.2024.03.007

CrossRef Full Text | Google Scholar

Lu, A. Z., Chen, H. Y., Qin, Y., and Zhang, N. (2014). Shape optimisation of the support section of a tunnel at great depths. Comput. Geotechnics 61 (1), 190–197. doi:10.1016/j.compgeo.2014.05.011

CrossRef Full Text | Google Scholar

Luo, Y., Chen, J., Shi, Z., Li, J., and Liu, W. (2020). Mechanical characteristics of primary support of large span loess highway tunnel: a case study in Shaanxi Province, Loess Plateau, NW China primary. Tunn. Undergr. Space Technol. 104 (1), 103532. doi:10.1016/j.tust.2020.103532

CrossRef Full Text | Google Scholar

Mahabadi, O. K., Lisjak, A., Munjiza, A., and Grasselli, G. (2012). Y-Geo: new combined finite-discrete element numerical code for geomechanical applications. Int. J. Geomechanics 12 (6), 676–688. doi:10.1061/(asce)gm.1943-5622.0000216

CrossRef Full Text | Google Scholar

Manouchehrian, A., and Ming, C. (2018). Numerical modeling of rockburst near fault zones in deep tunnels. Tunn. Undergr. Space Technol. 80, 164–180. doi:10.1016/j.tust.2018.06.015

CrossRef Full Text | Google Scholar

Mobaraki, B., and Vaghefi, M. (2015). Numerical study of the depth and cross-sectional shape of tunnel under surface explosion. Tunn. Undergr. Space Technol. incorporating Trenchless Technol. Res. 47, 114–122. doi:10.1016/j.tust.2015.01.003

CrossRef Full Text | Google Scholar

Ova, O. G., and Ova, G. (2004). Quality in tunnelling: ITA-AITES working group 16 final report. Tunn. Undergr. Space Technol. 19 (3), 239–272. doi:10.1016/j.tust.2004.01.002

CrossRef Full Text | Google Scholar

Qian, Q., and Zhou, X. (2018). Failure behaviors and rock deformation during excavation of underground cavern group for Jinping I Hydropower Station. Rock Mech. Rock Eng. 51 (8), 2639–2651. doi:10.1007/s00603-018-1518-x

CrossRef Full Text | Google Scholar

Seo, Y. S., Yun, H. S., Ban, J. D., and Lee, C. K. (2016). Mechanical properties of fault rocks in Korea. J. Eng. Geol. 26 (4), 571–581. doi:10.9720/kseg.2016.4.571

CrossRef Full Text | Google Scholar

Shaalan, H. H., Ismail, M. A. M., and Azit, R. (2019). Effect of tunnel overburden stress on the rock brittle failure depth. Arabian J. Geosciences 12 (4), 108. doi:10.1007/s12517-019-4246-y

CrossRef Full Text | Google Scholar

Simser, B. P. (2019). Rockburst management in Canadian hard rock mines. J. Rock Mech. Geotechnical Eng. 11 (5), 1036–1043. doi:10.1016/j.jrmge.2019.07.005

CrossRef Full Text | Google Scholar

Tang, C. (1997). Numerical simulation of progressive rock failure and associated seismicity. Int. J. Rock Mech. Min. Sci. 34 (2), 249–261. doi:10.1016/s0148-9062(96)00039-3

CrossRef Full Text | Google Scholar

Tang, C. A., Webb, A. A. G., Moore, W. B., Wang, Y. Y., Ma, T. H., and Chen, T. T. (2020). Breaking Earth’s shell into a global plate network. Nat. Commun. 11 (1), 3621. doi:10.1038/s41467-020-17480-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, G., Yuan, M., Miao, Y., Wu, J., and Wang, Y. (2018). Experimental study on seismic response of underground tunnel-soil-surface structure interaction system. Tunn. Undergr. Space Technol. 76, 145–159. doi:10.1016/j.tust.2018.03.015

CrossRef Full Text | Google Scholar

Wang, Y. Y., Gong, B., Tang, C. A., and Yang, X. Y. (2023b). Size effect and lateral pressure effect on the mechanical resistance of columnar jointed basalt. Int. J. Rock Mech. Min. Sci. 171, 105571. doi:10.1016/j.ijrmms.2023.105571

CrossRef Full Text | Google Scholar

Wang, Y. Y., Gong, B., Yang, X., and Tang, C. (2023a). Investigation into the multistage mechanical damage behavior of columnar jointed basalts with different meso-constitutive relations and model sizes. Lithosphere 2023 (1), 8711959. doi:10.2113/2023/8711959

CrossRef Full Text | Google Scholar

Wu, K., and Shao, Z. (2019). Study on the effect of flexible layer on support structures of tunnel excavated in viscoelastic rocks. J. Eng. Mech. 145 (10), 04019077. doi:10.1061/(asce)em.1943-7889.0001657

CrossRef Full Text | Google Scholar

Wu, N., Liang, Z., Li, Y., Qian, X., and Gong, B. (2019). Effect of confining stress on representative elementary volume of jointed rock masses. Geomechanics Eng. 18 (6), 627–638. doi:10.12989/gae.2019.18.6.627

CrossRef Full Text | Google Scholar

Xue, Y., Yan, F., Qi, C., Zhang, H., Zhao, X., and Chen, J. (2024). Research on the bearing capacity characteristics of initial support for horseshoe-shaped tunnel prefabrication. Deep Undergr. Sci. Eng. 3 (4), 426–438. doi:10.1002/dug2.12110

CrossRef Full Text | Google Scholar

Yang, W., Zhang, C., Liu, D., Tu, J., Yan, Q., Fang, Y., et al. (2019). The effect of cross-sectional shape on the dynamic response of tunnels under train induced vibration loads. Tunn. Undergr. space Technol. 90, 231–238. doi:10.1016/j.tust.2019.05.006

CrossRef Full Text | Google Scholar

Yu, J., Gong, B., Cao, C., and Tang, C. (2024). A novel cohesive interlayer model considering friction. Int. J. Solids Struct. 305, 113049. doi:10.1016/j.ijsolstr.2024.113049

CrossRef Full Text | Google Scholar

Zhang, C., Chen, Y., Wang, Y., and Bai, Q. (2024). Discrete element method simulation of granular materials considering particle breakage in geotechnical and mining engineering: a short review. Green Smart Min. Eng. 1 (2), 190–207. doi:10.1016/j.gsme.2024.06.003

CrossRef Full Text | Google Scholar

Zhang, Q. B., and Zhao, J. (2015). A review of dynamic experimental techniques and mechanical behaviour of rock materials. Rock Mech. Rock Eng. 47, 1411–1478. doi:10.1007/s00603-013-0463-y

CrossRef Full Text | Google Scholar

Zhang, Y., Zhao, C., Jiang, M., Zhang, J., Chen, C., Zheng, X., et al. (2020). Constant-resistance, rigid, and flexible coupling support technology for soft rock entrances in deep coal mines: a case study in China. Adv. Mater. Sci. Eng. 2020, 6212456. doi:10.1155/2020/6212456

CrossRef Full Text | Google Scholar

Zhong, T., Li, Z., Song, D., Khan, M., He, X., Chen, Z., et al. (2025). Mechanism of rock burst vertical damage induced by layered crack structures of the steeply inclined extremely thick coal seams. Int. J. Coal Sci. and Technol. 12, 24. doi:10.1007/s40789-025-00760-x

CrossRef Full Text | Google Scholar