A comprehensive study on the largest amplitude traceable short gravimetric calibration line in China

Relative gravimeter must be calibrated periodically on a gravimetric calibration line with a tiny uncertainty. We created a new gravimetric calibration baseline with a 326 milligal gravity difference in Jiugong Mountain, central China. The baseline consisted of four absolute gravimetry stations and eight basic relative gravimetry stations. Firstly, we carried out metrological parameters calibration (laser length and atomic clock) for FG5X(#265) and A10(#057) gravimeter with beat frequency experiment and atomic clock comparison respectively. Then we compared absolute gravity measurement from A10#057 and FG5X#265. We obtained a normalized error (i.e., the ratio of the gravity difference over the expended uncertainty of the difference) of 0.58, indicating that the discrepancy between both measurements lies within the measurement uncertainties. In order to precisely characterize the 4 absolute gravity stations, we conducted i) vertical and horizontal gravity gradients, and ii) we estimated the seismic background noise level. Finally, we have conducted relative gravimetric survey using Scincrex CG6(#236 and #238) constrained by FG5X and A10 absolute gravimeter to fulfill metrological traceability of the calibration line. The findings show that the basic relative station’s and absolute stations’ respective errors on the gravitational acceleration are 3 μGal and 5 μGal. For each gravity difference, the average biases between the FG5X-265 and CG-6 gravimeter are included in the uncertainty of the absolute observations.

1 Introduction

High-precision gravity survey plays an irreplaceable role in national basic surveying and mapping, geodynamics research, analysis of the Earth’s internal structure, resource exploration, aerospace science, etc., (Crossley et al., 2013). However, it is important to calibrate scale factor of relative gravimeter to achieve high precision gravity survey where the scale factor can translate original gravity reading (spring lengths, counter units, electrical units) into acceleration units (Terada et al., 2015). Therefore, the construction of gravity baseline is indispensable. When building the gravity baseline, two primary factors need to be taken into account. Firstly, the difference between the gravity segments of the two absolute points should be as great as possible; secondly, the travel time between the first and last absolute points should be as short as possible in order to minimize the impact of long-term instrument drift. Through the difference in gravity segment of the north-south long baseline field with a large latitude difference is larger, its practicability is not high due to it covers several thousand kilometers (Cheraghi et al., 2020). Thus, the short baseline field established by relying on the elevation difference becomes an popular way for calibration the relative gravimeter.

Many countries or regions have established their own gravity short baseline fields, such as Germany (Timmen et al., 2006), Switzerland (Marti et al., 2016), Poland (Sas et al., 2009), Japan (Net, 2018), Turkey (Dogan et al., 2013) and so on. At the same time, China has also established six gravity short baseline fields. Among them, the Lushan gravity baseline established in 1985 is the most widely used, with a maximum gravity difference of 229mGal (Wang et al., 2014). The gravity baseline needs to be built in a place with stable geological structure. However, the Lushan gravity baseline is located in a famous natural scenic spot in China, the expansion of the scenic spot has caused large changes in the gravity value. Therefore, it is necessary to build a new gravity baseline with a larger gravity difference. We conducted detailed geological surveys in the Jiugong Mountain area in the early stage. The results show that the Jiugongshan gravity baseline is located on a stable block inside the Mufu uplift. The northeast-trending Yanglin fault and Hengshi fault spread in the site area are Pre-Quaternary structures, which are defined as non-seismic structures and will not affect Gravity baseline stability. In 2022, we designed and built a gravity baseline with 4 absolute gravity points, eight relative gravity points, and a maximum gravity difference of more than 326 mGal in Jiugong Mountain, China (as shown in Figure 1). From the bottom to the top of the mountain, a single round trip only takes two and a half hours. It is very suitable for dynamic testing or calibration of various relative gravimeters. In this study, we will introduce in detail the entire process of the gravity acceleration value measurement of the Jiugongshan gravity baseline, which also includes the measurement of vertical and horizontal gravity gradients, geodetic coordinates and background noise levels.

Figure 1

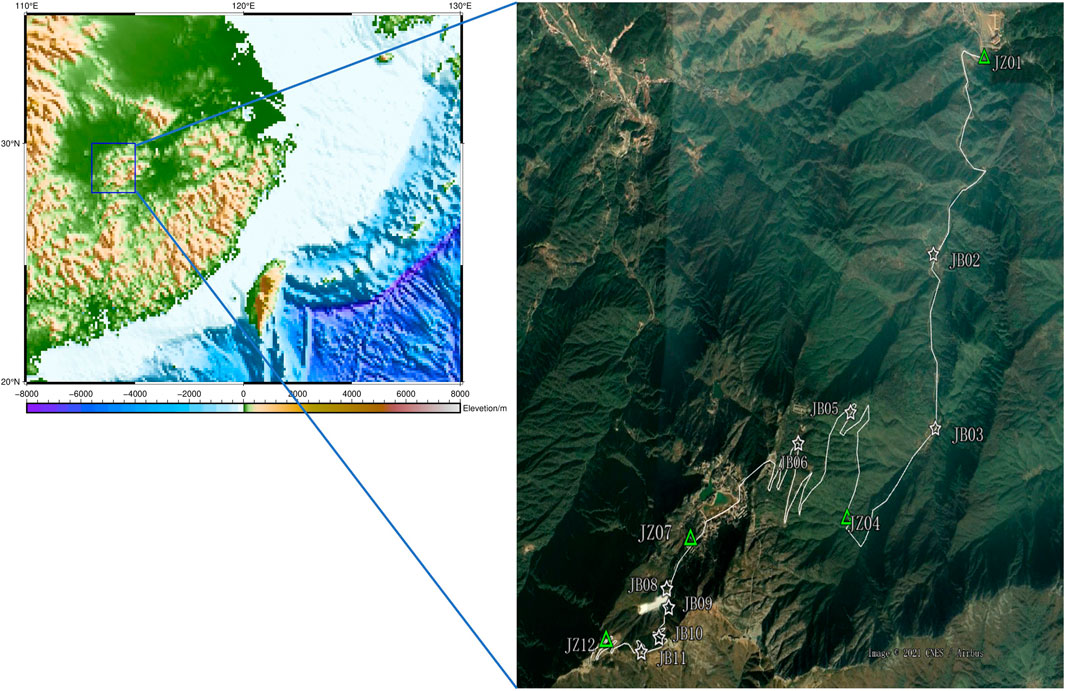
Figure 1. Location of the Jiugongshan gravity baseline stations. The green triangle represents the absolute gravity points and the white represents the relative gravity points.

2 Calibration of measurement parameters of absolute gravimeter

In order to ensure i) the best accuracy, ii) the smallest uncertainty and iii) the traceability of the gravity acceleration measurement value, the absolute gravimeter neds to be calibrated. Special attention must be paid to the length and the time reference. The reference true value is obtained by weighting the multiple measurement results of FG5X-232 and the FG5X-232 has participated in many international absolute gravity comparisons, including the third European absolute gravity comparison in Walfdange, Luxembourg, the 2017 CIPM(International Bureau of Weights and Measures) Key Comparison of Absolute Gravimeters. Meanwhile, it has participated in many absolute gravity comparisons in the Asia-Pacific region, and its measurement values can be traced to the BIPM KCRVs.

FG5X (#265) and A10 (#057) were both purchased from micro-g company in the spring of 2022. Their relevant parameters (laser wavelength and rubidium clock frequency) have been calibrated by the manufacturer and were tested between April 18 and 22, 2022. Relevant acceptance testing work was carried out at the Wuhan Seismological Observatory on the same day. The test results (Zhang et al., 2023) show that the set scatter of A10 (#057) is 1.90 μGal, and the measurement accuracy is −4.03 μGal with the calibration of the Laser frequency shift (compared with the reference true value). The set scatter of FG5X is 0.84 μGal, and the measurement accuracy is 2.01 μGal, which meets the nominal accuracy of the instrument.

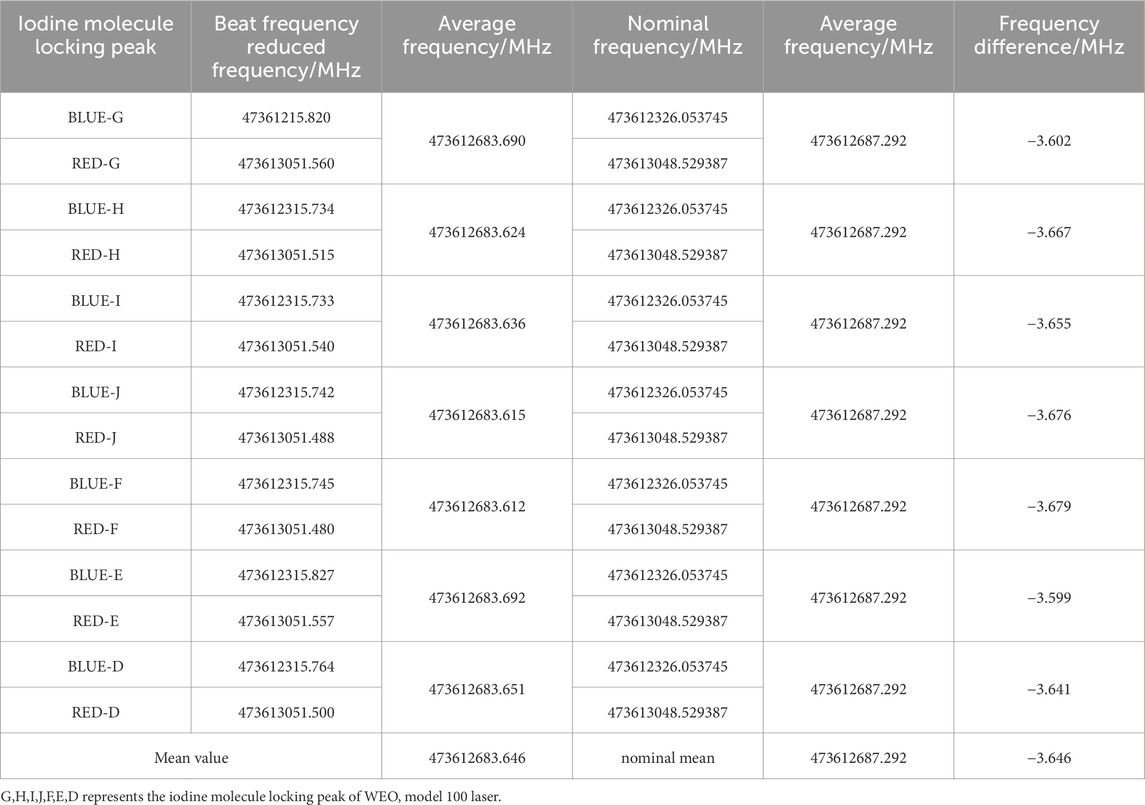
In March 2023, we conducted the gravity acceleration value measurement of the Jiugongshan gravity baseline, considering that the laser wavelength and rubidium clock frequency may drift over time. We conducted an experiment on beat frequency between WEO model 100 laser for FG5X gravimeter and ML-1 polarization stabilized laser for A10 gravimeter. The Model 100 Iodine-Stabilized He-Ne laser of the FG5X absolute gravimeter does not require calibration. Its frequency stability reaches 2.5 parts in 10¹¹, making its gravity measurement accuracy reach 0.2 μGal. It is currently the length reference standard of the BIPM (Niebauer et al., 1995). Historical research (Niebauer et al., 1995) shows that the ML-1 laser will produce a frequency drift of about 5 MHz/year, which will produce a gravity measurement deviation of about 2.07 μGal/MHz. Therefore, the laser wavelength of the A10 absolute gravimeter must be calibrated (Falk et al., 2009; Sekowski et al., 2012).

According to the optical path shown in Figure 2, the beat frequency measurement system was constructed. The laser generated by the WEO-100 iodine molecular laser of FG5X-265 and the laser generated by the ML-1 laser of A10-057 are converged to the photoelectric conversion module. Then an oscilloscope and frequency counter were used to measure the frequency difference signal generated by the beat frequency. The results of the beat frequency measurement are shown in Table 1. The frequency difference measured by the beat frequency of the ML-1 laser of the A10-057 absolute gravimeter and the WEO-100 laser is 473612683.646 MHz. The frequency calibrated by the micro-g company in 2022 is 473612687.300 MHz. The frequency difference between the two calibration results is −3.646 MHz, which will produce a deviation of about 7.5 μGal in the absolute gravity measurement value. The Model 100 achieves an absolute frequency accuracy of 2.5 parts in 10¹¹, corresponding to approximately 12 kHz. This precision aligns with the frequencies established by the 1997 Comité International des Poids et Mesures (CIPM) Mise en Pratique (http://www.winterseo.com/m100.html). Thus, ignoring the wavelength stability of WEO-100, the uncertainty of this calibration result mainly comes from the repeatability of the experimental results. The standard deviation of the beat frequency result is 0.033 Mhz, which brings the uncertainty of the gravity measurement to no more than 0.1 μGal.

Figure 2

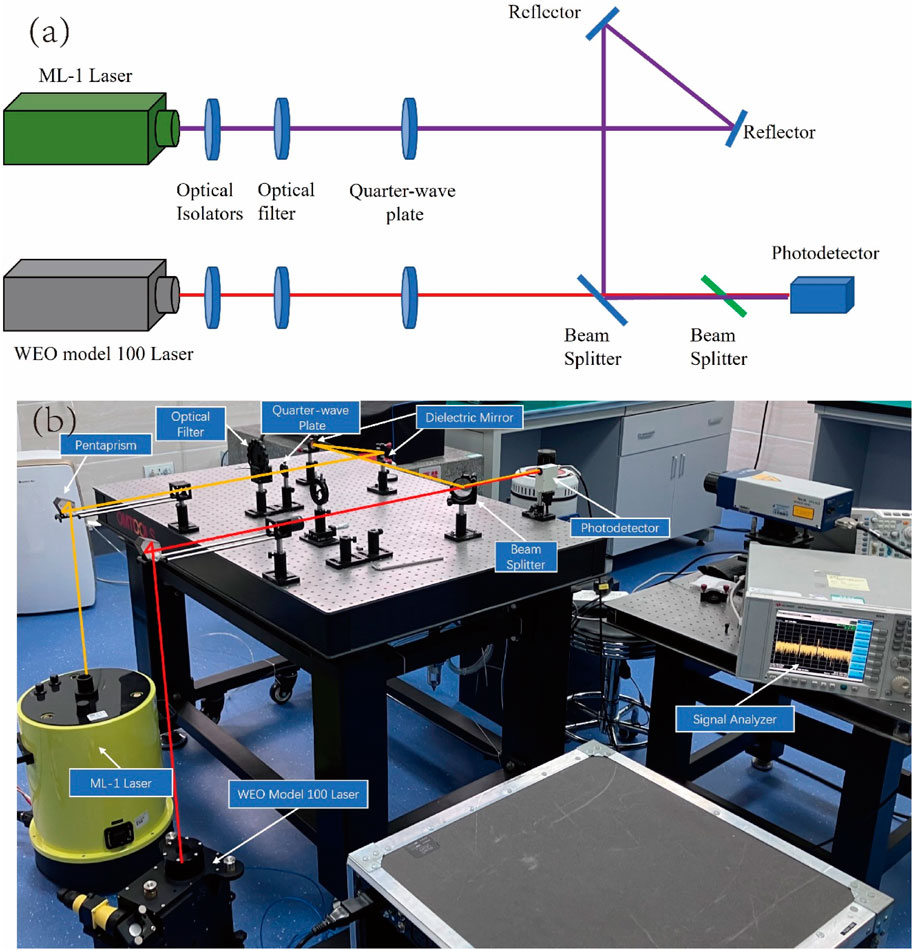
Figure 2. Beat frequency experimental optical path design diagram (a) and experimental site diagram (b).

Table 1

Table 1. A10-057 LASER beat frequency measurement results.

FG5X-265 and A10-057 absolute gravimeters use the same FRK-L rubidium atomic clock, whose frequency stability is 3 × 10⁻¹⁰ (Niebauer et al., 1995). We use the Meridian II Precision TimeBase (with Frequency accuracy less than 6 × 10⁻¹⁴) to calibrated and test the frequency stability of the rubidium atomic clock. After calibration, the rubidium clock frequency of A10-057 is 10000000.00047 Hz, and the rubidium clock frequency of FG5X-265 is 10000000.00170 Hz. The frequency stability of both is better than 1.7 × 10⁻¹⁰, and the impact on the gravity measurement results is less than 0.3 μGal.

3 Gravity datum measurement

We used FG5X-265 and A10-057 absolute gravimeters to simultaneously measure absolute gravity values at the center point and southwest point of each absolute gravity station of the calibration line. (See Figure 3). where the FG5X#265 measuring on the “center point” with the A10#057 measuring on the “south west point”, 80 cm away from FG5X, 20 cm for other site. In order to accurately correct the influence of environmental factors such as solid tides, we conducted high-precision coordinate measurements (for Solid tide, sea tide correction, normal pressure calculation).

Figure 3

Figure 3. Absolute gravity measurement at JZ07 station (A) where the FG5X#265 measuring on the “center point” with the A10#057 measuring o, the “south west point”, 80 cm away from FG5X, 20 cm for other site, vertical (B) and horizontal (C) gradient measurement at JZ01 station.

In order to perform height difference correction, or horizontal correction required for transferring measured absolute gravity values between the A10-057 and the FG5X-265 measurement point, we also conducted vertical and horizontal gravity gradient measurement.

3.1 Vertical and horizontal gradient measurements

Vertical gradient is a basic parameter in the absolute gravimeter measurement model based on free-falling interferometry, and its accurate measurement plays an important role in improving the accuracy of absolute gravity measurement (Vitushkin, 2014). The global average value of the vertical gravity gradient is close to 3.09 μGal/cm. However, absolute gravity measurements are conducted in a mountainous area with uneven mass distribution, which makes the actual gravity vertical gradient value deviate greatly from the theoretical value (Torge et al., 2023). As shown in Figure 3B, two Burris relative gravimeters (#514 and #758) calibrated by the factory were used to conduct vertical gradient measurements (120 cm and 72 cm) and horizontal gradient measurements (20 cm and 80 cm) between the FG5 measurement point and A10 measurement point respectively.

The measurement method refers to the traditional high-low-high or low-high-low mode (Dogan et al., 2013). In order to accurately control the height difference, we use a level control point outside the surface of gravimeter. We use an optical level (with a micrometer, the resolution is 0.01 mm) to accurately control the height difference between gravity measurements points. The height difference uncertainty is 0.01 cm, eliminating the mutual coupling of horizontal gradient and vertical gradient caused by the uneven observation surface. Each instrument measures eight measurement rounds with a total of 4 effective gravity campaign. Each measurement round is treated as an independent measurement section for adjustment calculation and linear drift correction.

The vertical gradient and horizontal gradient measurement results of each measurement point are shown in Table 2. We found that the largest uncertainty affecting vertical gradient measurement comes from the repeatability of the measuring instrument, which corresponds to the standard deviation of repeated gravity measurement. For the Burris relative gravimeter, the worst repeatability is 3 μGal. For a single instrument, the relative uncertainty of the gravity vertical gradient obtained from one measurement round about 0.7%, equivalent to 0.03 μGal/cm. With a level, the height difference error can be limited to 0.01 cm, and its effect on the vertical gradient is insignificant, impacting the vertical gradient of gravity by less than 0.01%. When using a general steel tape, the height difference error is within 0.2 cm, but the impact on the vertical gravity gradient is less than 0.2%, and the uncertainty contributed by it is approximately equal to 1/3 of the uncertainty component introduced by repeatability. Thus, it is reasonable whether using a level or steel tape in this case because the uncertainty introduced by the height difference error on the gravity vertical gradient cannot be ignored. However, the gravity horizontal gradient variation is less than 5 μGal for a relative gravity point, and the uncertainty introduced by the repeatability of the 3 μGal gravimeter accounts for more than 50%. Therefore, the uncertainty of the results given by the gravity horizontal gradient measurement only takes into account the error come from gravimeter.

Table 2

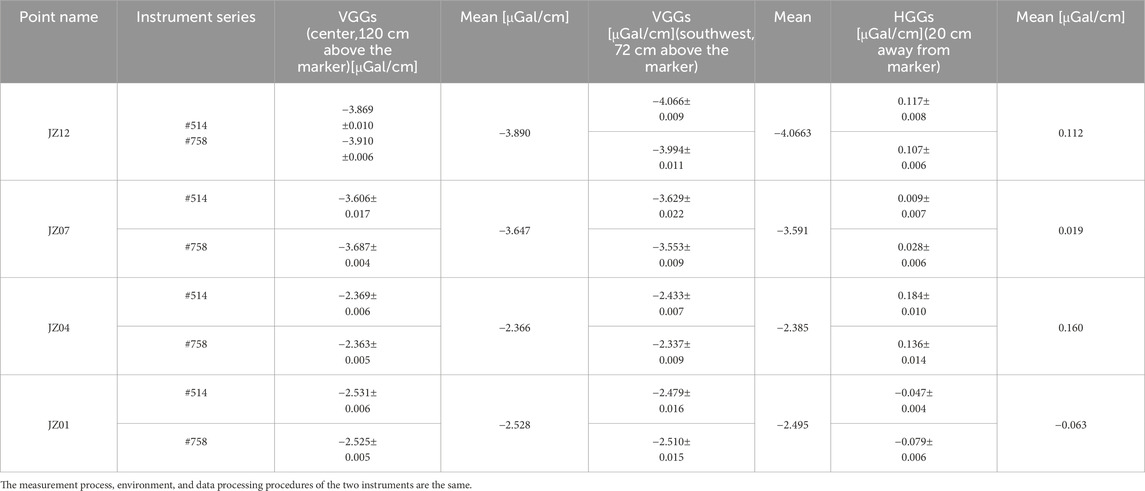
Table 2. Vertical and horizontal gravity gradients of Jiugong mountain calibreation baseline absolute gravity stations.

3.2 Absolute gravity measurement

From March 7 to 11, 2023, we used FG5X-265 and A10-057 absolute gravimeters to measure four absolute gravity measurement points at the Jiugongshan gravity baseline. Both the FG5-265 and A10-057 absolute gravimeters have undergone acceptance testing and metrological calibration before measurement, and there is no obvious systematic error. We place the FG5X-265 absolute gravimeter at the center of the gravity station, and the A10-057 absolute gravimeter at the southwest point about 20 cm away. The two instruments start measuring at the same time for 25 h with 100 drops each hour, and the effective number of drops for each instrument is not less than 2400 times (2.5σ reject). Subsequently, the absolute gravity data was processed using “g” version 9.0 from Micro-g Solutions Inc., and the environmental impact was processed through the built-in model of the “g” software; the ETGTAB method was used for solid tide correction and the precise coordinate values measured following the procedure described in Section 3.1. (Terada et al., 2015). The ocean tide model is processed using the FES2004 model (Terada et al., 2015), and the atmospheric gravity effect is calculated by the empirical atmospheric admittance value (−0.3 μGal/hPa) (Boy et al., 2002); the earth’s polar motion is corrected using the polar motion coordinates published by IERS (http://www.iers.org), the amplitude factor is 1.16 (Wahr, 1985). Finally, the gravity value is calculated to the center of the gravity station through the vertical gradient and horizontal gradient correction (Table 2). The measurement results are shown in Table 3. The uncertainty of the FG5 measurement results is 5 μGal, and the uncertainty of the A10 measurement results is better than 11 μGal (including the uncertainty of gravity gradient). Taking the value measured by FG5-265 as the reference value, the maximum difference between the two gravimeters is 7.05 μGal (point JZ12). The normalized error (i.e., the ratio of the gravity difference over the extended uncertainty of the gravity difference, Wu et al., 2020) is 0.58, which is less than 1, so that the absolute gravity measurement results are reliable.

Table 3

Table 3. Gravity values transferred at the central point of absolute gravity stations of the Jiugong calibration line.

4 Relative gravity joint measurement under absolute gravity constraints

The relative gravimeter is a lightweight instrument used to measure the relative changes, which requires regular calibration of the instrument constants. We followed the A-B-C. C-B-A observation routine with 4 gravity campaign. As Figure 4 shows, the distance between the two CG6 gravimeters was 40cm, and effective measurement height of CG6 and Sino-G5 gravimeter was 30.6cm and 42.3 cm respectively. The observation equation of the gravity measurement network is shown in Equation 1, where t is the time of measurement; i the serial number of gravimeter, j the location of the gravity station, k the code of gravity point, $\delta$ the scale factor, $D$ linear drift rate, $g_{\mathrm{t}}$ 、 $g_{\mathrm{a}}$ 、 $g_{\text{hg}}$ 、 $g_{\text{vg}}$ the theoretical solid tide, air pressure, vertical gradient, and horizontal gradient correction respectively. And the g_R(i,j) refers to the gravity difference measured by the relative gravimeter #i at location #j.

$\delta {g_R}_{\left(i,j\right)}^k+D_{\left(i,j\right)}*dt+g_{0\left(i,j\right)}+{g_{\mathrm{t}}}_{\left(i,j\right)}^k+{g_{\mathrm{a}}}_{\left(i,j\right)}^k+{g_{\text{hg}}}_{\left(i,j\right)}^k+{g_{\text{vg}}}_{\left(i,j\right)}^k=g^k(1)$

Figure 4

Figure 4. Relative gravity measurements (left, relative gravity point in the field; right, absolute benchmark point).

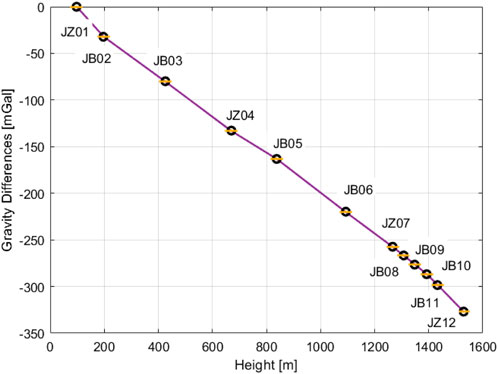
We use least squares indirect adjustment algorithm to process the relative gravity data constrained by the absolute values (JZ01∼JZ12) measured by FG5X-265 (Terada et al., 2015). Scale factor, gravity differences and the corresponding medium error are obtained through least square fitting in which the zero-drift coefficient is independently calculated through each campaign. Specifically, the weight of the absolute point observation results is weighted with 2 μGal, and 5 μGal for the relative gravity measurement point. The weight is reweighted based on the posterior error results after the initialization until the change in gravity point value after adjustment does not exceed 1 × 10^-5 μGal. The results are presented in Figure 5. The gravity difference of the 12 measurements of the Jiugongshan gravity baseline is 326.934 mGal, and the uncertainty is better than 3 μGal, where he uncertainty comes from the standard deviation of the combined least square adjustment result and the repeatability of the relative gravimeter.

Figure 5

Figure 5. The gravity differences at adjacent stations of Jiugong gravity calibration baseline.

5 Background noise measurement

From 7 March 2023 to 13 March 2023, the Güralp-40TDE (#4216) seismometer was applied to conduct background vibration and noise measurement on the 4 absolute gravity stations. The seismometer’s measurement period encompasses the entire absolute gravity measurement period. On the one hand, it is used to detect abnormal vibration signals during the absolute gravity measurement process. On the other hand, it can evaluate the acceleration noise level of the gravity baseline of Jiugong Mountain. The Güralp-40TDE seismometer has undergone instrument frequency response calibration by Güralp Inc.(calibration certificate number: F044055) before measurement, and its sensitivity amplitude and zero and pole points have been precisely calibrated where the sensitivity amplitude is 2 × 1606 V/m/s, and the frequency band is (1–100) Hz. Previous researchers usually used the power spectral density (PSD) of the seismometer’s quiet period observation data to evaluate the noise level of the observation point (Peterson, 1993; Vassallo et al., 2012) which reflects the noise level of the entire observation period. Presently, the probability density function method of noise power spectrum (PSD-PDF) is widely used to evaluate the noise level of seismic stations (McNamara and Buland, 2004). The background noise measurement results are shown in Figure 6. The high-frequency noise above 10 Hz is mainly related to signals such as human activities. Vibration observation results show that, in addition to high-frequency noise above 1 Hz approaching the global new high-noise model, the noise in the low-frequency band of 0.01–1 Hz is smaller and has less impact on the gravity observation frequency band. The noise levels of (1–10) Hz are all lower than 120 dB, that is, (1 × 10⁻⁶ m/s²),so the vibration isolation foundation of the absolute gravity observation site provides a very quiet absolute gravity observation environment, which is equivalent to the vibration noise level of the gravity measurement base of the Chinese Academy of Metrology (Wu et al., 2020).

Figure 6

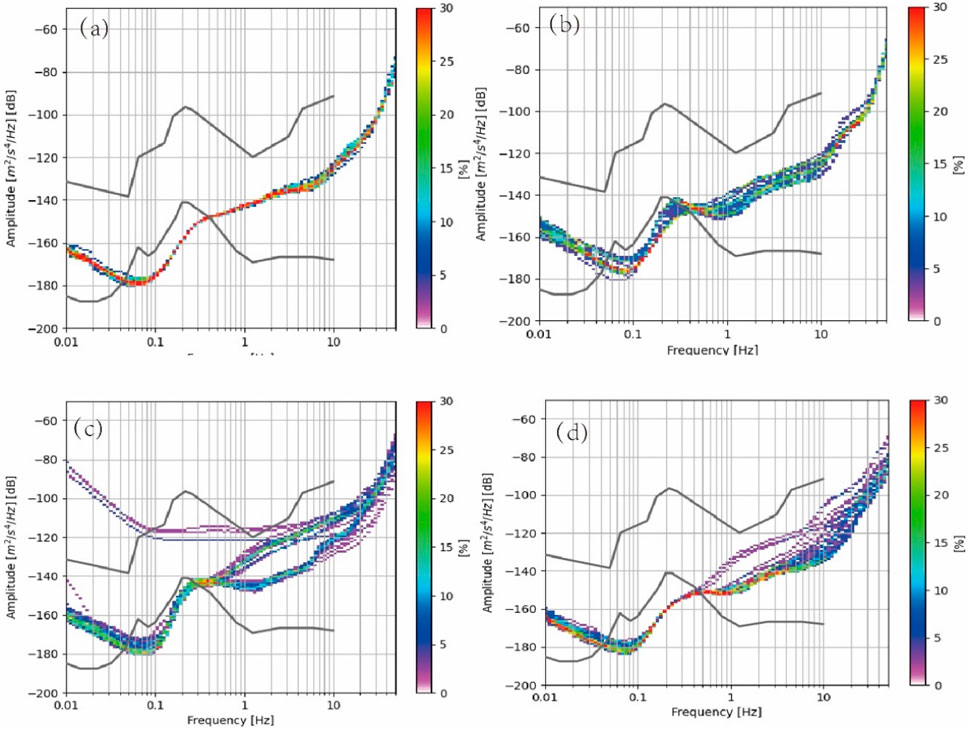
Figure 6. Results of absolute gravity point noise level estimation. (A) JZ01; (B) JZ04; (C) JZ07; (D) JZ12. The upper and lower black curves represent the NHNM model and the NLNM model respectively (Peterson, 1993).

6 Discussion and conclusion

This article introduces in detail the construction of the Jiugongshan gravity short baseline field with the largest gravity difference in China. It includes the measurement of gravity acceleration measurement values, high-precision coordinate measurement based on GNSS measurements, relative gravity joint measurement and horizontal and vertical gradient based on CG-6 and Burris. The measurement results show that 1) The indirect adjustment results of the GNSS measurement network show that the uncertainty of the gravity point coordinate measurement results of the gravity baseline grid is better than 0.05″; 2) The gravity vertical gradient measurement shows that the repeatability of the gravimeter is the main source of measurement uncertainty accounting for about 0.7%. When the height difference is controlled below 0.1 cm, the relative uncertainty component introduced by the height difference measurement error is about 0.1%, and its impact on the gravity vertical gradient measurement results can be neglected. 3) The relative gravity joint measurement results under the absolute gravity constraint show that the uncertainty of the difference in the gravity section of the Jiugongshan gravity baseline is better than 3 μGal, and the average uncertainty is 2 μGal; 4) The background noise level measured by the Güralp 40TDE seismometer shows that the noise level of the Jiugongshan gravity baseline at (1–10) Hz is lower than 120 dB (1 × 10⁻⁶ m/s²), which is consistent with the Changping Park of the China Institute of Metrology.

The establishment of a high-precision gravity baseline can be used for calibrating scale factor, dynamic drift rate and dynamic observation accuracy of various gravimeters or accelerometers. Since the maximum gravity difference is 326.9338 mGal with 0.0064 mGal uncertainty, the uncertainty of the factor calibration result is theoretically better than 2.0 × 10⁻⁵, which can satisfy most relative gravimeters currently on the market. However, the hydrological cycle has certainty an effect on the gravity and the gradient measurement (Reich et al., 2019). It is necessary to focus on the stability of our calibration line over time, especially in dry and wet season.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

ZL: Conceptualization, Data curation, Investigation, Methodology, Writing–original draft, Writing–review and editing. JG: Formal Analysis, Validation, Writing–original draft, Writing–review and editing. JL: Project administration, Supervision, Conceptualization, Investigation, Writing–original draft. JH: Investigation, Conceptualization, Writing–review and editing. XZ: Conceptualization, Resources, Visualization, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was Supported by Open Fund of Wuhan, Gravitation and Solid Earth Tides, National Observation and Research Station (WHYWZ202212).

Conflict of interest

Authors ZL, JG, JL, JH, and XZ were employed by Wuhan Institute of Seismic Metrology and Measurement Engineering Co., Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Boy, J. P., Gegout, P., and Hinderer, J. (2002). Reduction of surface gravity data from global atmospheric pressure loading. Geophys. J. Int. 149, 534–545. doi:10.1046/j.1365-246X.2002.01667.x

CrossRef Full Text | Google Scholar

Cheraghi, H., Hinderer, J., Saadat, S. A., Bernard, J. D., Djamour, Y., Tavakoli, F., et al. (2020). Stability of the calibration of scintrex relative gravimeters as inferred from 12 Years of measurements on a large amplitude calibration line in Iran. Pure Appl. Geophys. 177, 991–1004. doi:10.1007/s00024-019-02300-6

CrossRef Full Text | Google Scholar

Crossley, D., Hinderer, J., and Riccardi, U. (2013). The measurement of surface gravity. Rep. Prog. Phys. 76, 046101. doi:10.1088/0034-4885/76/4/046101

PubMed Abstract | CrossRef Full Text | Google Scholar

Dogan, U., Ergintav, S., Arslan, G., Demir, D. O., Karaboce, B., Bilgic, E., et al. (2013). Establishment of a gravity calibration baseline with the constrain of absolute gravity measurements after 17 August 1999 Izmit earthquake in Marmara region, Turkey. Acta Geod. geophys. 48, 377–388. doi:10.1007/s40328-013-0033-5

CrossRef Full Text | Google Scholar

Falk, R., uller, J. M. ¨, Lux, N., Wilmes, H., and Wzionek, H. (2009). “Precise gravimetric surveys with the field absolute gravimeter A-10,” in IAG scientific assembly symposium 2009 “geodesy for planet earth (Buenos Aires, Argentina: Springer). 31 August – 4 September 2009.

Google Scholar

Marti, U., Baumann, H., Bürki, B., and Gerlach, C. (2016). “A first traceable gravimetric calibration line in the Swiss alps,” in Igfs 2014: proceedings of the 3rd international gravity field service (IGFS) (Shanghai, China: Springer), 17–25. June 30-July 6, 2014.

Google Scholar

McNamara, D. E., and Buland, R. P. (2004). Ambiente noise levels in the continental United States. Bull. Seismol. Soc. Am. 94, 1517–1527. doi:10.1785/012003001

CrossRef Full Text | Google Scholar

Net, S. (2018). Construction of the Japan gravity standardization net 2016 toshihiro YAHAGI, kenji YOSHIDA, takayuki MIYAZAKI, yoshifumi HIRAOKA and, 49–58.

Google Scholar

Niebauer, T. M., Sasagawa, G. S., Faller, J. E., Hilt, R., and Klopping, F. (1995). A new generation of absolute gravimeters. Metrologia 32, 159–180. doi:10.1088/0026-1394/32/3/004

CrossRef Full Text | Google Scholar

Peterson, J. R. (1993). Observations and modeling of seismic background noise. doi:10.3133/ofr93322

CrossRef Full Text | Google Scholar

Reich, M., Mikolaj, M., Blume, T., and Güntner, A. (2019). Reducing gravity data for the influence of water storage variations beneath observatory buildings. Geophysics 84 (1), EN15–EN31. doi:10.1190/geo2018-0301.1

CrossRef Full Text | Google Scholar

Sas, A., Sas-Uhrynowski, A., Cisak, M., and Siporski, L. (2009). Vertical gravimetric calibration baseline in the Tatra Mountains of Poland. Geoinf. Issues 1, 19–32. doi:10.34867/gi.2009.2

CrossRef Full Text | Google Scholar

Sekowski, M., Krynski, J., Dykowski, P., and Makinen, J. (2012). Effect of laser and clock stability and meteorological conditions on gravity surveyed with the A10 free-fall gravimeter – first results. Rep. Geodesy 92 (1).

Google Scholar

Terada, Y., Kato, T., Nagai, T., Koshimura, S., Imada, N., Hiromu, S., et al. (2015). First SixMonths of superconducting gravimetry in Argentina. Int. Assoc. Geod. Symp., 145–153. doi:10.1007/1345

CrossRef Full Text | Google Scholar

Timmen, L., Flury, J., Peters, T., and Gitlein, O. (2006). A new absolute gravity base in the German Alps. Contrib. Geophys. Geod. 36, 7–20.

Google Scholar

Torge, W., Müller, J., and Pail, R. (2023). Geodesy, Berlin, Boston: De Gruyter Oldenbourg. doi:10.1515/9783110723304

CrossRef Full Text | Google Scholar

Vassallo, M., Festa, G., and Bobbio, A. (2012). Seismic ambient noise analysis in southern Italy. Bull. Seismol. Soc. Am. 102, 574–586. doi:10.1785/0120110018

CrossRef Full Text | Google Scholar

Vitushkin, L. F. (2014). Absolute gravity measurements. Encycl. Geod. 117, 1–8. doi:10.1007/978-3-319-02370-0_25-1

CrossRef Full Text | Google Scholar

Wahr, J. M. (1985). Deformation induced by polar motion. J. Geophys. Res. Solid Earth 90, 9363–9368. doi:10.1029/jb090ib11p09363

CrossRef Full Text | Google Scholar

Wang, L. S., Chen, C., Kaban, M. K., Du, J. S., Liang, Q., and Thomas, M. (2014). The use of the A10-022 absolute gravimeter to construct the relative gravimeter calibration baselines in China. Metrologia 51, 203–211. doi:10.1088/0026-1394/51/3/203

CrossRef Full Text | Google Scholar

Wu, S., Feng, J., Li, C., Su, D., Wang, Q., Hu, R., et al. (2020). The results of CCM.G-K2.2017 key comparison. Metrologia 57, 07002. doi:10.1088/0026-1394/57/1A/07002

CrossRef Full Text | Google Scholar

Zhang, X., Zhou, H., Jiang, Y., Zhai, D., Wei, G., Li, H., et al. (2023). First acceptance testing of multiple A10 absolute gravimeters in China and analysis of the comparison results. Geod. Geodyn. 14, 401–410. doi:10.1016/j.geog.2023.02.001

CrossRef Full Text | Google Scholar