Influence of borehole trajectory and pressure on the characteristics of drilling induced fractures

Research on the identification and classification of drilling-induced fractures plays a critical role in clarifying the mechanisms of wellbore instability and drilling fluid loss, while also supporting the analysis of imaging logging data and reservoir evaluation. In this study, a prediction model for the occurrence of drilling induced fractures is established by using linear elastic wellbore stress model combined with the tensile failure criterion of wellbore surrounding rock. The influences of engineering parameters, specifically borehole trajectory and bottom-hole pressure, on the distribution of principal stresses around the wellbore, as well as the angle between drilling-induced fractures and the borehole axis are investigated. The findings reveal that the induced fractures exhibit a highly organized pattern, typically forming at 180° intervals with a nearly symmetrical, downward-diffusing arrangement. This pattern provides a solid theoretical basis for the identification and classification of these fractures. In addition, under low bottom-hole pressure, the well tends to form feather-shaped induced fractures. As the pressure of the liquid column increases, the angle between these fractures and the borehole axis decreases while their length expands, eventually evolving into a “J”-shaped fracture. Accurate detection and identification of such induced fractures are crucial for reliably interpreting fracture networks and evaluating reservoirs in unconventional oil and gas fields.

1 Introduction

Natural fractures in the formation significantly contribute to borehole instability and drilling fluid losses. Triaxial mechanical tests on fractured rocks indicate that the stress required to reinitiate failure along these pre-existing fracture surfaces is 43%–55% lower than that for intact core samples (Bai, 2020; Dong et al., 2025; Fengjiao et al., 2023; Fontoura et al., 2002; Guan and Sheng, 2017; Huang et al., 2019; Li, 2020). Due to the lower tensile strength of natural fractures compared to the rock’s tensile strength, natural fractures tend to open preferentially under certain conditions, thereby controlling the spatial characteristics of fracture propagation (Qin, 2006; Al-Ajmi and Zimmerman, 2006; Ewy, 1999; Lee et al., 2012; He et al., 2015; Setiawan and Zimmerman, 2018). Improving the understanding of fractures is beneficial for further research on reservoir evaluation, geological understanding, and reservoir knowledge across various geological historical periods (Liu et al., 2016; Liu et al., 2018; Lu et al., 2020; Moos et al., 2003; Noohnejad et al., 2021; Qiu et al., 2011; Sheng et al., 2006). Current methods for analyzing natural fractures in formations often lack precision (Sheng et al., 2017; Sheng et al., 2018; Tabatabaee et al., 2018; Wei et al., 2013; Wen, 2012; Wu et al., 2024; Wen, 2012). In contrast, imaging logging offers an intuitive two-dimensional visualization of the borehole wall, providing a reliable foundation for accurately identifying and extracting geological features—such as rock structure, stratification, pore networks, and fractures—which in turn leads to superior geological interpretations (Singh et al., 2019; Chen et al., 2015; Liu et al., 2016; Zhou et al., 2018; Lu et al., 2013; Økland and Cook, 1998; Zhang, 2013; Amadei, 2012). In reservoir evaluation, it is crucial to more accurately and effectively identify effective fractures and discern and eliminate the influence of drilling-induced fractures (Zhang et al., 2021b; Zhang et al., 2023; Zhao et al., 2020Ai, 2015Al-Ajmi and Al-Harthy, 2010). Due to the strong heterogeneity of the Ordovician carbonate rocks in the Shunbei oil and gas field, the diversity of reservoir space types, and the varying shapes of fractures, detecting and identifying fractures are particularly challenging (Wu et al., 2024; Xia, 2018; Zhang et al., 2017; Zhang et al., 2021a). Therefore, the correct identification of induced fractures is essential (Huang et al., 2012; Liu et al., 2016; Ebrahimi et al., 2020; Denney, 2005; Udegbunam et al., 2013; Ma et al., 2021; Chen et al., 2019).

In the realm of borehole stability, Lee et al. (2012) proposed a wellbore stability model for formations with anisotropic strength and predicted collapse positions in different drilling directions. He et al. (2015) explored the impact of water content on weak planes and wellbore stability by developing a model that accounts for these planes. Their comparison of slip failure along weak planes versus shear failure in intact rock revealed that cross-dip wells are less stable than up-dip or down-dip wells in a strike-slip stress regime, and that higher water content leads to increased collapse pressure. Setiawan and Zimmerman (2018) introduced a transversely isotropic well stress model for shale reservoirs, employing a three-dimensional Mogi-Coulomb criterion to assess borehole collapse pressure while considering the effects of weak surface structures on rock strength. Singh et al. (2019) presented an analytical solution for wellbore stability in rock masses exhibiting elastic-perfectly plastic and elastic-brittle behavior using a 3D failure criterion. Their findings indicate that the plastic zone predicted by the Mogi-Coulomb criterion is about 13%–20% smaller than that estimated by the Mohr-Coulomb criterion, with intermediate principal stress contributing to improved wellbore stability and wellbore column pressure significantly affecting the plastic zone radius. Additionally, Chen et al. (2015) together with Ding et al. (2018) developed a model for wellbore stability that incorporates multiple weak planes, demonstrating that when more than four such planes are present, the collapse pressure is predominantly controlled by these features and increases gradually. Liu et al. (2016) developed a wellbore stress distribution model in a transversely isotropic formation drilled at an arbitrary angle to the weak planes. They studied both controllable factors (internal pressure, dipping angle, and dipping direction) and uncontrollable factors (weak planes occurrence and in situ stress), concluding that a proper lower critical mud weight is essential for ensuring wellbore stability. Zhou et al. (2018) investigated how rock elastic transverse isotropy influences pore pressure distribution and seepage stresses, emphasizing that anisotropic seepage in shales with bedding and fractures requires a lower internal critical mud weight than that applied at the borehole wall. Similarly, Lu et al. (2013) found that porous flow in shale formations exacerbates wellbore instability, with the critical mud weight highly sensitive to the presence of weak planes. Økland and Cook (1998) showed through thick-walled cylinder tests that wells drilled within 15° of the bedding-parallel direction are particularly unstable, necessitating a higher mud density to prevent losses. Borehole stability analysis typically begins by calculating the stress tensor on the wellbore wall after drilling, followed by applying a strength criterion to compare principal stresses with rock strength. Zhang (2013) noted that when weak bedding planes are present, the maximum slip failure direction deviates from the minimum stress direction, and the overlap of shear failure in intact rock with sliding failure along weak planes enlarges unstable areas. Although Lu et al. (2013) also observed that porous flow in fractured formations further undermines stability, their study did not consider elastic anisotropy and natural fractures in bedding. Static stability models often overlook the hydraulic effects of drilling fluids on pore pressure and rock failure. To address this, Kanfar et al. (2015) developed a time-dependent numerical model that incorporates the transverse isotropy of shales, revealing significant differences in pore pressure compared to isotropic models and leading to different critical mud pressure recommendations, despite not accounting for thermal and chemical gradients. Higgins et al. (2008) further demonstrated that models including anisotropy capture subtle stress variations more accurately, which is crucial for well completion decisions. Additionally, Dokhani et al. (2016) incorporated the interaction between aqueous fluids and clay minerals into their model, treating shale as an isotropic medium with strength anisotropy defined by an extended Jaeger’s criterion and a bedding plane angle (β) relative to the maximum principal stress. Given the finely laminated structure, natural fractures, low permeability, and cation exchange capacity of shales, it is essential to account for the combined effects of natural fractures and bedding planes on near-wellbore stresses. Finally, Huang et al. (2012) analyzed stress distributions around boreholes in layered rocks with water-based drilling fluids, highlighting the critical roles of borehole inclination, hydraulic conductivity, and water activity in determining a safe mud pressure window.

Both domestic and international scholars have extensively studied fracture identification, highlighting that each fracture type possesses unique features that significantly affect oil and gas exploration and production. During drilling, fractures are typically classified as natural or induced based on their origin (Gao et al., 2021; Gao et al., 2024). Currently, imaging logging is the most precise method for detecting fractures, providing images that reveal a broad spectrum of geological events as well as drilling-induced disturbances on the wellbore. Drilling-induced tensile fractures are formed under the influence of ground stress during the drilling process and occur simultaneously with the drilling operation. These fractures typically develop parallel to the wellbore, appearing symmetrically at 180° intervals. Drilling-induced tensile fractures occur only when there is a significant disparity in horizontal stresses, and they usually extend less than 1 cm into the surrounding formation. If the bottom-hole pressure is maintained below the minimum principal stress, these fractures will not propagate further, thereby preventing drilling fluid loss. Unlike natural fractures, induced fractures form as a result of stress changes during drilling, following predictable patterns that can be modeled under different operating conditions.

Research on predicting the initiation locations and morphologies of drilling-induced fractures around wellbores remains limited. A thorough understanding of the mechanisms behind fracture formation and propagation is essential for ground stress inversion, determining optimal drilling fluid density windows, and optimizing the particle size distribution of sealing materials. This knowledge also aids in classifying fracture types and precisely determining their orientations from imaging logging data, which is critical for reliable reservoir evaluation. Consequently, this study develops a prediction model for drilling-induced fractures, investigating the impact of engineering parameters such as wellbore trajectory and borehole pressure on fracture characteristics. It further provides quantitative criteria to assess the effectiveness of drilling fluid leak prevention and plugging strategies based on these fracture features.

2 Drilling-induced fractures prediction model

2.1 Coordinate transformation

To determine the stress distribution characteristics around the wellbore, it is first necessary to transform the in situ stresses into the global coordinate system. As illustrated in Figure 1, X_G-Y_G-Z_G represents the global coordinate system, where X_G points north, Y_G points east, and Z_G is vertical. X_S-Y_S-Z_S represents the in situ stress coordinate system, corresponding to the maximum horizontal stress, minimum horizontal stress, and vertical stress, respectively. To transform the in situ stresses into the global coordinate system, three coordinate transformations are required. First Step, rotate the global coordinate system around the Z_G axis by an angle α₁, resulting in the X′-Y′-Z′ coordinate system. Second Step, rotate the X′-Y′-Z′ coordinate system around the Y′ axis by an angle β₁, yielding the X″-Y″-Z″ coordinate system. Third Step, rotate the X″-Y″-Z″ coordinate system around the X″ axis by an angle β₁. This series of transformations converts the X_G-Y_G-Z_G coordinate system into the X_s-Y_s-Z_s coordinate system. This transformation process enables the accurate determination of the stress distribution around the wellbore in relation to the global geographic orientation.

Figure 1

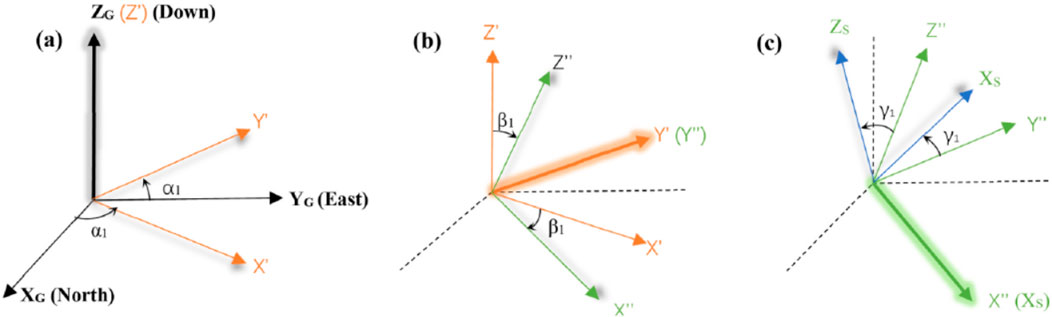
Figure 1. Three steps of the transformation between the global coordinate system (GCS) and the in situ stress coordinate system (ICS) (a) rotation about the Z_G axis (b) rotation about the Y′ axis (c) rotation about the X″ axis.

Based on geometric knowledge, a transformation matrix R₁ is established, as shown in Equation 1,

$R_1=\left[\begin{array}{ccc}\cos {\alpha }_1\cos {\beta }_1& \sin {\alpha }_1\cos {\beta }_1& -\sin {\beta }_1\\ \cos {\alpha }_1\sin {\beta }_1\sin {\gamma }_1-\sin {\alpha }_1\cos {\gamma }_1& \sin {\alpha }_1\sin {\beta }_1\sin {\gamma }_1+\cos {\alpha }_1\cos {\gamma }_1& \cos {\beta }_1\sin {\gamma }_1\\ \cos {\alpha }_1\sin {\beta }_1\cos {\gamma }_1-\sin {\alpha }_1\sin {\gamma }_1& \sin {\alpha }_1\sin {\beta }_1\cos {\gamma }_1+\cos {\alpha }_1\sin {\gamma }_1& \cos {\beta }_1\cos {\gamma }_1\end{array}\right](1)$

Using the stress tensor σ_G to represent the components of stress in the global coordinate system and σ_S to represent the components of stress in the stress coordinate system, the transformation relationship between them can be expressed as shown in Equation 2,

${\sigma }_{\mathrm{G}}=R_1^T{\sigma }_S{R}_1(2)$

Where ${\sigma }_S=\left[{\sigma }_{\mathrm{H}},0,0;0,{\sigma }_h,0;0,0,{\sigma }_v\right]$, σ_H represents the maximum horizontal stress, measured in MPa; σ_h represents the minimum horizontal stress, measured in MPa; and σ_v represents the vertical stress, measured in MPa.

After transforming the stress into the global coordinate system, it should be further transformed into the wellbore coordinate system for analysis. The transformation relationship between the global coordinate system (GCS) and the wellbore coordinate system (BCS) is shown in Figure 2, where X_B-Y_B-Z_B represents the wellbore coordinate system, α₂ represents the angle between the wellbore inclination and the true north direction, usually referred to as the wellbore azimuth angle; β₂ represents the angle between the wellbore axis and the vertical direction, typically referred to as the well deviation angle. Using σ_B to represent the stress tensor in the wellbore coordinate system, according to the study by Lee et al. (2012), the transformation relationship between σ_B and σ_G is expressed as shown in Equation 3,

${\sigma }_B=R_2{\sigma }_{\mathrm{G}}{R}_2^T(3)$

Figure 2

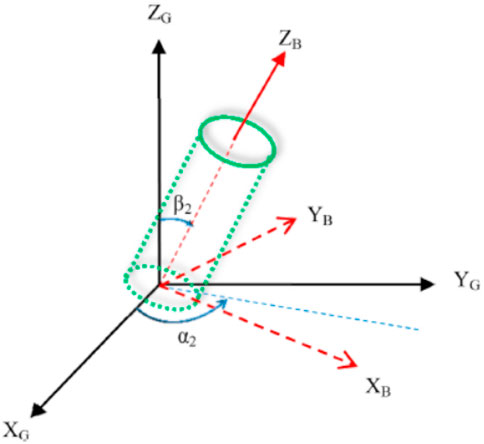
Figure 2. Transformation between global coordinate system (GCS) and borehole coordinate system (BCS).

The transformation matrix R₂ is represented as shown in Equation 4.

$R_2=\left[\begin{array}{ccc}\cos {\alpha }_2\cos {\beta }_2& \sin {\alpha }_2\cos {\beta }_2& \sin {\beta }_2\\ \sin {\alpha }_2& \cos {\alpha }_2& 0\\ \cos {\alpha }_2\sin {\beta }_2& \sin {\alpha }_2\sin {\beta }_2& \cos {\beta }_2\end{array}\right](4)$

2.2 Wellbore stress distribution

The representation of stress tensors around the wellbore in polar coordinates is more convenient. Therefore, after transforming the stress from the global coordinate system to the wellbore coordinate system, the stress tensor σ_B, i.e., [σ_x, σ_y, σ_z, τ_xy, τ_xz, τ_yz], needs to be further transformed into polar coordinates. Due to the disturbance of the original stress state by drilling through the formation, the stress redistributes around the wellbore and creates stress concentration effects. According to Biot’s effective stress theory, the equation for the effective stress around the wellbore at any inclination angle is expressed as shown in Equation 5,

$\left\{\begin{array}{l}{\sigma }_r=\frac{\left({\sigma }_x+{\sigma }_y\right)}{2}\left(1-\frac{r_w^2}{r^2}\right)+\frac{\left({\sigma }_x-{\sigma }_y\right)}{2}\left(1-4\frac{r_w^2}{r^2}+3\frac{r_w^4}{r^4}\right)\cos 2\theta \\ +{\tau }_{xy}\left(1-4\frac{r_w^2}{r^2}+3\frac{r_w^4}{r^4}\right)\sin 2\theta +P_w\frac{r_w^2}{r^2}-\alpha P_p\\ {\sigma }_{\theta }=\frac{\left({\sigma }_x+{\sigma }_y\right)}{2}\left(1+\frac{r_w^2}{r^2}\right)-\frac{\left({\sigma }_x-{\sigma }_y\right)}{2}\left(1+3\frac{r_w^4}{r^4}\right)\cos 2\theta \\ +{\tau }_{xy}\left(1+3\frac{r_w^4}{r^4}\right)\sin 2\theta -P_w\frac{r_w^2}{r^2}-\alpha P_p\\ {\sigma }_z={\sigma }_{zz}-2\nu \left({\sigma }_x-{\sigma }_y\right)\frac{r_w^2}{r^2}\cos 2\theta -4\nu {\tau }_{xy}\frac{r_w^2}{r^2}\sin 2\theta -\alpha P_p\\ {\tau }_{r\theta }=\left[\frac{\left({\sigma }_x+{\sigma }_y\right)}{2}\sin 2\theta +{\tau }_{xy}\cos 2\theta \right]\left(1+2\frac{r_w^2}{r^2}-3\frac{r_w^4}{r^4}\right)\\ {\tau }_{rz}=\left[{\tau }_{yz}\sin \theta +{\tau }_{xz}\cos \theta \right]\left(1-\frac{r_w^2}{r^2}\right)\\ {\tau }_{\theta z}=\left[-{\tau }_{xz}\sin \theta +{\tau }_{yz}\cos \theta \right]\left(1+\frac{r_w^2}{r^2}\right)\end{array}\right.(5)$

In the equation, r_w represents the wellbore radius, measured in meters; r represents the distance from any point around the wellbore to the wellbore axis, measured in meters; P_w represents the bottomhole fluid column pressure, measured in MPa; Pp represents the pore pressure of the formation, measured in MPa; θ represents the azimuth angle around the wellbore, i.e., the angle, measured in degrees, from a point around the wellbore rotating clockwise to the X_b coordinate axis; α represents the Biot’s effective stress coefficient, which ranges from 0 to 1 and is dimensionless.

Once the stress distribution around the wellbore is determined, these values must be incorporated into rock strength criteria to evaluate the formation’s stability. Because these criteria are typically expressed in terms of principal stresses, the wellbore stresses need to be transformed accordingly. Equation 6 shows how to convert stresses from polar coordinates into principal stresses,

$\left\{\begin{array}{l}{\sigma }_i={\sigma }_r\\ {\sigma }_j=\left({\sigma }_{\theta }+{\sigma }_z\right)/2+\sqrt{{\left({\sigma }_{\theta }+{\sigma }_z\right)}^2+4{\tau }_{\theta z}^2}/2\\ {\sigma }_k=\left({\sigma }_{\theta }+{\sigma }_z\right)/2-\sqrt{{\left({\sigma }_{\theta }+{\sigma }_z\right)}^2+4{\tau }_{\theta z}^2}/2\end{array}\right.(6)$

The relative magnitudes of the three principal stresses at any point around the wellbore vary with changes in the bottomhole fluid column pressure. To accurately distinguish between the three principal stresses around the wellbore, substitute the expression ${\sigma }_i,{\sigma }_j,{\sigma }_k$ obtained from Equation 6 into Equation 7,

$\left\{\begin{array}{l}{\sigma }_1=\max \left({\sigma }_i,{\sigma }_j,{\sigma }_k\right)\\ {\sigma }_3=\min \left({\sigma }_i,{\sigma }_j,{\sigma }_k\right)\\ {\sigma }_2={\sigma }_i+{\sigma }_j+{\sigma }_k-{\sigma }_1-{\sigma }_3\end{array}\right.(7)$

2.3 Induced fracture orientation determination

To differentiate between types of tensile failure in the wellbore wall, it is necessary to quantitatively analyze the relationship between the three principal stresses around the wellbore. Additionally, it is important to compare the minimum principal stress around the wellbore with the tensile strength of the rock, as shown in Equation 8,

${\sigma }_3\le -{\sigma }_t(8)$

When σ_r equals σ₃ and Equation 8 holds true, drilling-induced fractures occur around the wellbore. If the hydrostatic pressure exceeds the formation pressure, it may lead to drilling fluid loss. The relationship between the angle of induced fractures and the well axis stress is expressed as shown in Equation 9,

$\tan 2\omega =\frac{2{\tau }_{\theta z}}{{\sigma }_z-{\sigma }_{\theta }}(9)$

In which, $\omega$ represents the angle between the drilling-induced fractures and the wellbore axis, measured in degrees, as shown in Figure 3. This angle represents the orientation between the maximum principal stress around the wellbore and the wellbore axis. By incorporating in situ stress, wellbore trajectory, and fluid column pressure, the principal stresses at different points around the wellbore can be determined. This enables the identification of tensile failure types and the calculation of the angle at each point relative to the wellbore axis, ultimately predicting the morphology of drilling-induced fractures under these conditions.

Figure 3

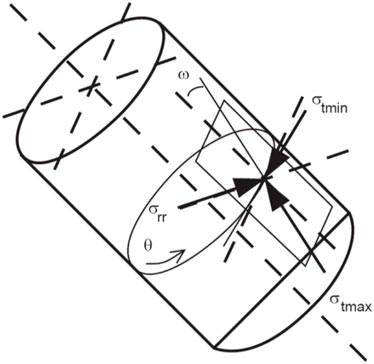
Figure 3. The angle between the minimum principal stress acting on the borehole wall and the borehole axis in any trajectory (Zoback, 2007).

It is worth noting that this study assumes the formation rock to be a linear elastic medium and does not consider the effects of temperature, fluid interactions, chemical influences, or formation exposure time on the stress distribution around the wellbore. Additionally, given the characteristics of rock being strong in compression but weak in tension, as well as the natural development of fractures, it is generally assumed that cracks will form when the rock experiences tensile stress.

2.4 Model verification

Based on the MATLAB 2022a platform, a wellbore-induced fracture prediction model was developed and implemented. To verify the accuracy of the program, the data from Table 1 was used as input for the model. The program was then employed to calculate the circumferential, radial, and vertical stresses around a vertical wellbore. The results were compared with those obtained using Equation 5 to ensure the correctness of the developed program.

Table 1

Table 1. Inputting parameters.

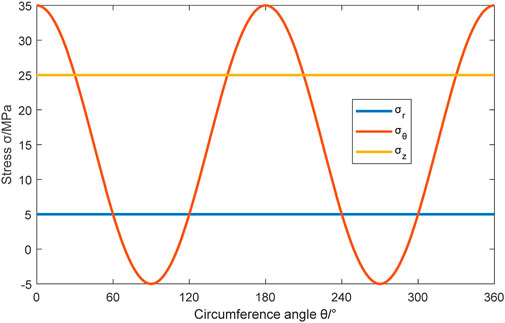
The circumferential, radial, and vertical stresses on the wellbore wall of a vertical well, as calculated using the program developed in this study, are shown in Figure 4. Similarly, for a vertical well in the direction of the minimum horizontal in situ stress, the calculation process and results for wellbore circumferential stress, based on Equation 5, are presented in Equation 10,

$\left\{\begin{array}{l}{\sigma }_r=\frac{{\sigma }_{\mathrm{H}}+{\sigma }_{\mathrm{h}}}{2}\times 0+\frac{{\sigma }_{\mathrm{H}}-{\sigma }_{\mathrm{h}}}{2}\times 0\times \cos 2\theta +0\times 0\times \sin 2\theta +P_w\\ \times 1-P_p=5\text{MPa}\\ {\sigma }_{\theta }=\frac{\left({\sigma }_{\mathrm{H}}+{\sigma }_{\mathrm{h}}\right)}{2}\times 2-\frac{\left({\sigma }_{\mathrm{H}}-{\sigma }_{\mathrm{h}}\right)}{2}\times 4\cos 2\theta +0\times 4\sin 2\theta -P_w\\ \times 1-P_p=35\text{MPa}\\ {\sigma }_z={\sigma }_{\mathrm{v}}-2\nu \left({\sigma }_{\mathrm{H}}-{\sigma }_{\mathrm{h}}\right)\times 1\times \cos 2\theta -4\nu \times 0\times 1\\ \times \sin 2\theta -\alpha P_p=25\text{MPa}\end{array}\right.(10)$

Figure 4

Figure 4. Stresses around wellbore wall for vertical well.

Comparing the results obtained from Equation 5 with those shown in Figure 4 reveals a perfect match, confirming the accuracy of the developed model and calculation program, including the coordinate transformation equations and principal stress calculations.

3 Results and analysis

Based on this model, the study further explores the effects of different wellbore trajectories and fluid column pressures on the principal stresses around the wellbore, the initiation angle of induced fractures, and their occurrence. The variation patterns of wellbore principal stresses and induced fracture orientations with changes in wellbore trajectory and fluid column pressure are discussed in the following sections.

3.1 The impact of wellbore trajectory

This study investigates the locations and morphologies of drilling-induced fractures in a normal fault environment. Assuming a fluid column pressure of 50 MPa in the wellbore, the remaining parameters from Table 1 are used to analyze the effects of borehole trajectory and pressure on the characteristics of drilling-induced fractures. Utilizing the drilling-induced fracture prediction model established in this study and inputting the parameters from Table 1, the variation trends of the principal stresses on the wellbore wall and the angles between induced fractures and the wellbore axis along the circumferential angle of the wellbore are depicted in Figure 5–20. The dual vertical axes in the diagrams respectively quantify two critical parameters: the left axis measures principal stress magnitudes, while the right axis (purple crosses) tracks angular deviation between drilling-induced fractures and the wellbore axis. Rock mechanics analysis reveals these fractures initiate when tangential stress at the borehole wall exceeds the tensile strength threshold. Specifically, fracture propagation commences as the minimum principal stress transitions from compressive to tensile domain, a fundamental principle derived from tensile failure criteria in wellbore stability studies.

Figure 5

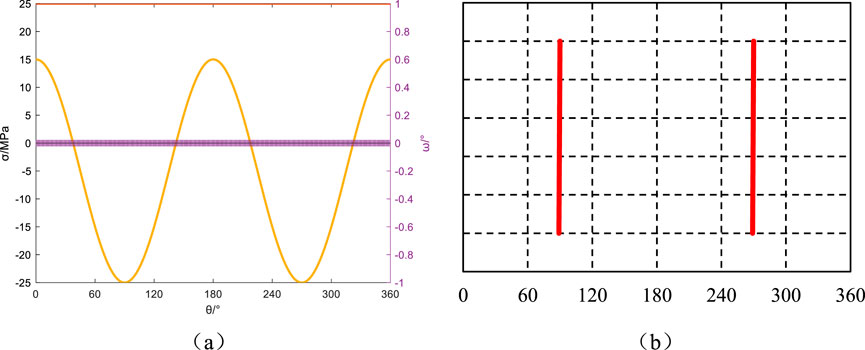
Figure 5. Azimuth angle αb = 0°, Well inclination angle βb = 0°: Principal stresses around the wellbore, induced fractures, and their angles relative to the wellbore axis. (a) Principal stress and induced fracture angle, (b) Induced fracture.

Figure 6

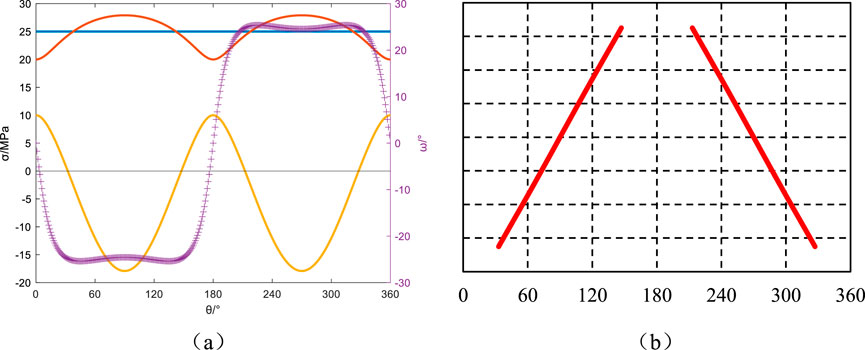
Figure 6. Azimuth angle αb = 0°, Well inclination angle βb = 30°: Principal stresses around the wellbore, induced fractures, and their angles relative to the wellbore axis. (a) Principal stress and induced fracture angle, (b) Induced fracture.

Figure 7

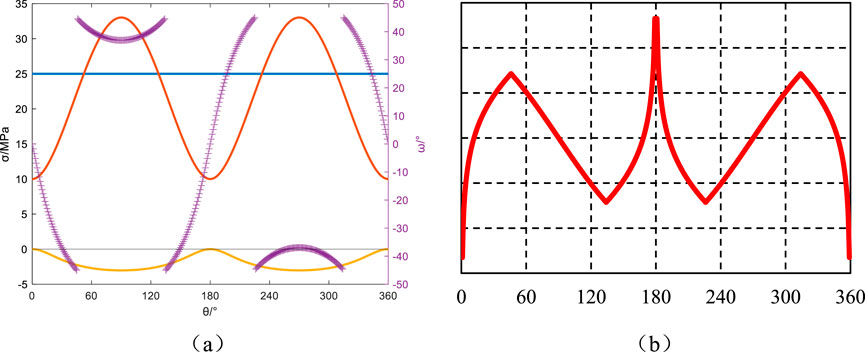
Figure 7. Azimuth angle αb = 0°, Well inclination angle βb = 60°: Principal stresses around the wellbore, induced fractures, and their angles relative to the wellbore axis. (a) Principal stress and induced fracture angle, (b) Induced fracture.

Figure 8

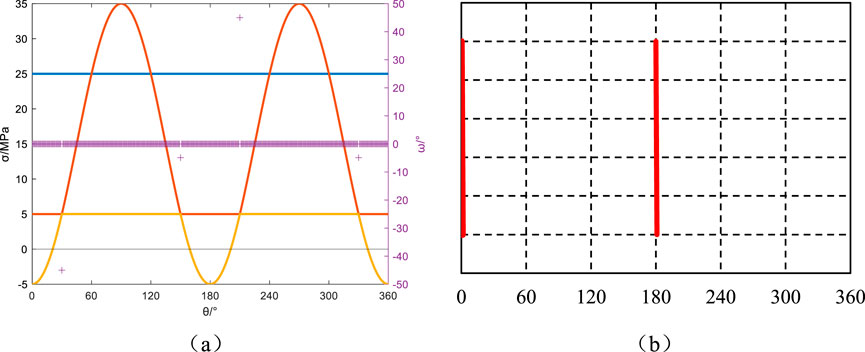
Figure 8. Azimuth angle αb = 0°, Well inclination angle βb = 90°: Principal stresses around the wellbore, induced fractures, and their angles relative to the wellbore axis. (a) Principal stress and induced fracture angle, (b) Induced fracture.

Figure 9

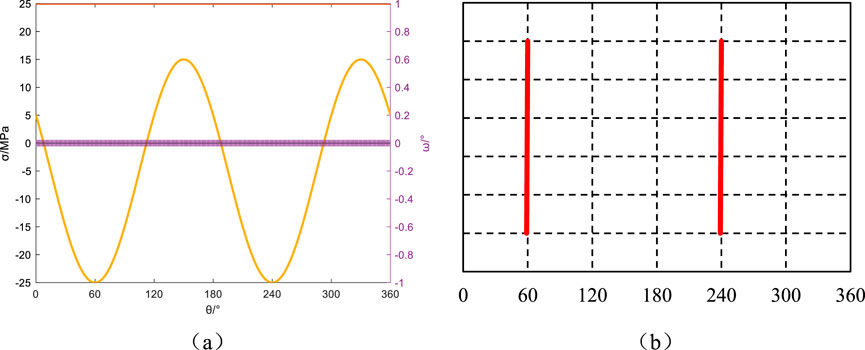
Figure 9. Azimuth angle αb = 30°, Well inclination angle βb = 0°: Principal stresses around the wellbore, induced fractures, and their angles relative to the wellbore axis. (a) Principal stress and induced fracture angle, (b) Induced fracture.

Figure 10

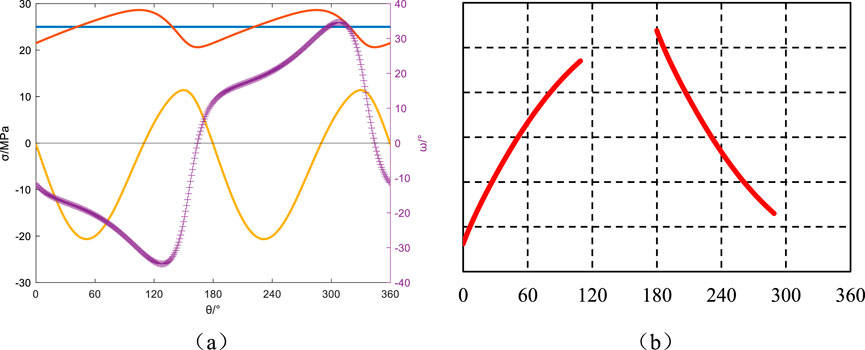
Figure 10. Azimuth angle αb = 30°, Well inclination angle βb = 30°: Principal stresses around the wellbore, induced fractures, and their angles relative to the wellbore axis. (a) Principal stress and induced fracture angle, (b) Induced fracture.

Figure 11

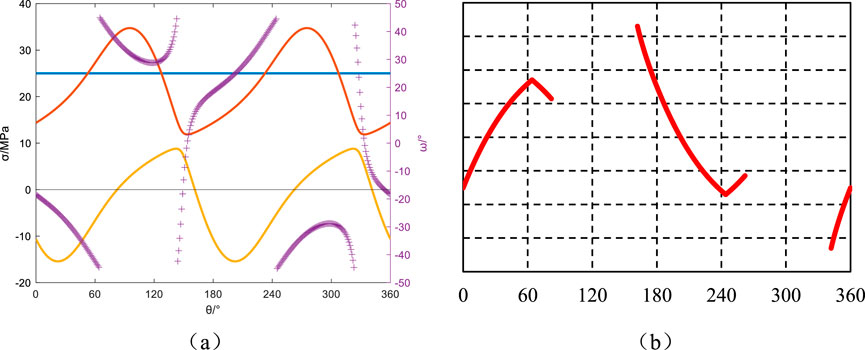
Figure 11. Azimuth angle αb = 30°, Well inclination angle βb = 60°: Principal stresses around the wellbore, induced fractures, and their angles relative to the wellbore axis. (a) Principal stress and induced fracture angle, (b) Induced fracture.

Figure 12

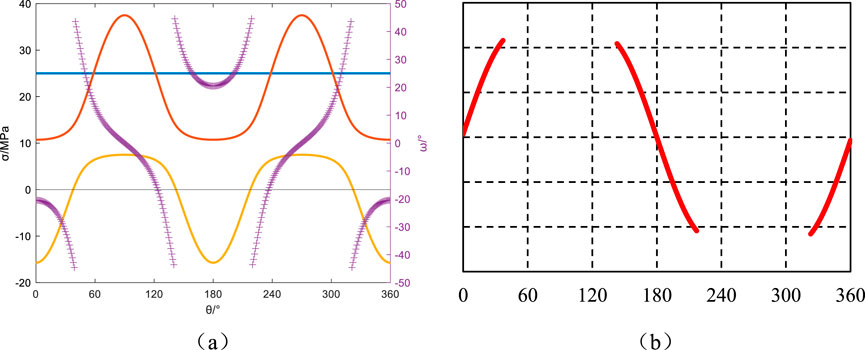
Figure 12. Azimuth angle αb = 30°, Well inclination angle βb = 90°: Principal stresses around the wellbore, induced fractures, and their angles relative to the wellbore axis. (a) Principal stress and induced fracture angle, (b) Induced fracture.

Figure 13

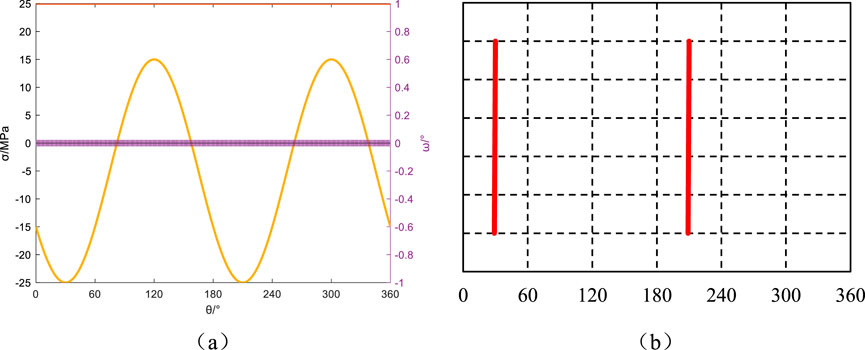
Figure 13. Azimuth angle αb = 60°, Well inclination angle βb = 0°: Principal stresses around the wellbore, induced fractures, and their angles relative to the wellbore axis. (a) Principal stress and induced fracture angle, (b) Induced fracture.

Figure 14

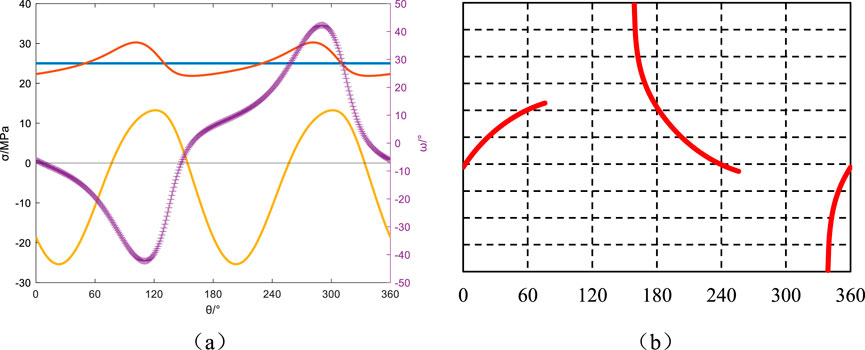
Figure 14. Azimuth angle αb = 60°, Well inclination angle βb = 30°: Principal stresses around the wellbore, induced fractures, and their angles relative to the wellbore axis. (a) Principal stress and induced fracture angle, (b) Induced fracture.

Figure 15

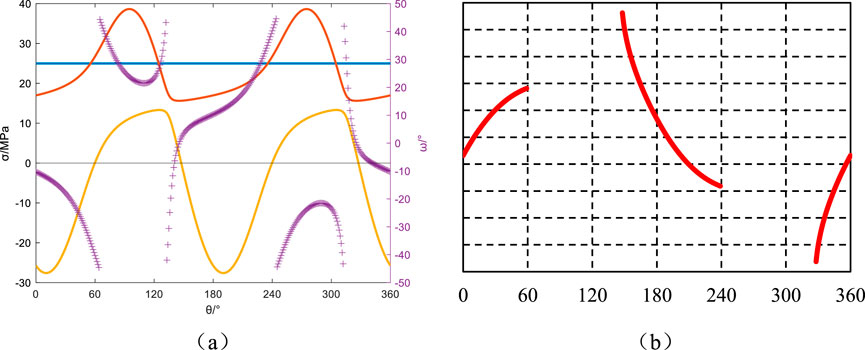
Figure 15. Azimuth angle αb = 60°, Well inclination angle βb = 60°: Principal stresses around the wellbore, induced fractures, and their angles relative to the wellbore axis. (a) Principal stress and induced fracture angle, (b) Induced fracture.

Figure 16

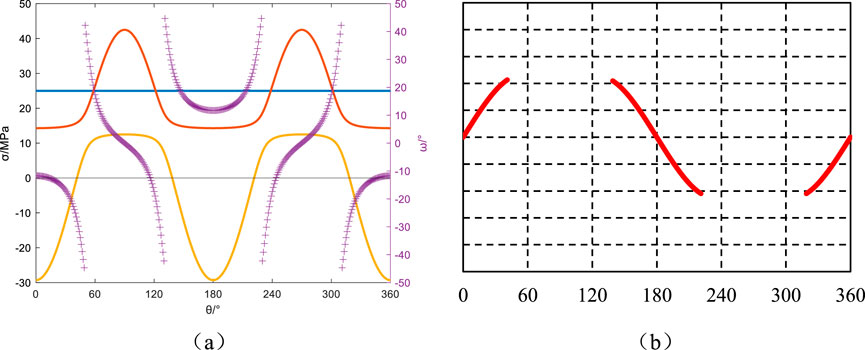
Figure 16. Azimuth angle αb = 60°, Well inclination angle βb = 90°: Principal stresses around the wellbore, induced fractures, and their angles relative to the wellbore axis. (a) Principal stress and induced fracture angle, (b) Induced fracture.

Figure 17

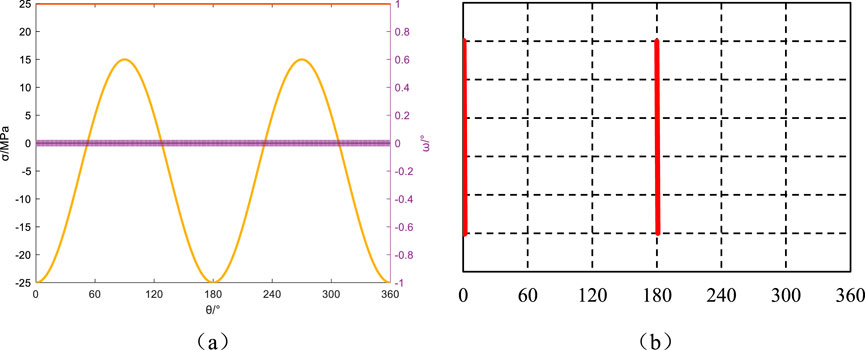
Figure 17. Azimuth angle αb = 90°, Well inclination angle βb = 0°: Principal stresses around the wellbore, induced fractures, and their angles relative to the wellbore axis. (a) Principal stress and induced fracture angle, (b) Induced fracture.

Figure 18

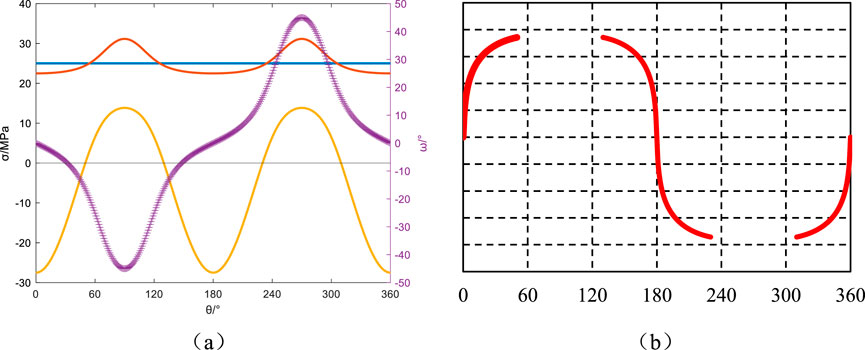
Figure 18. Azimuth angle αb = 90°, Well inclination angle βb = 30°: Principal stresses around the wellbore, induced fractures, and their angles relative to the wellbore axis. (a) Principal stress and induced fracture angle, (b) Induced fracture.

Figure 19

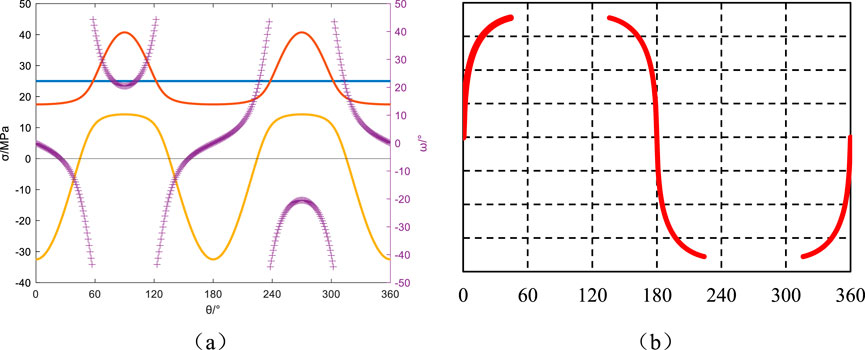
Figure 19. Azimuth angle αb = 90°, Well inclination angle βb = 60°: Principal stresses around the wellbore, induced fractures, and their angles relative to the wellbore axis. (a) Principal stress and induced fracture angle, (b) Induced fracture.

Figure 20

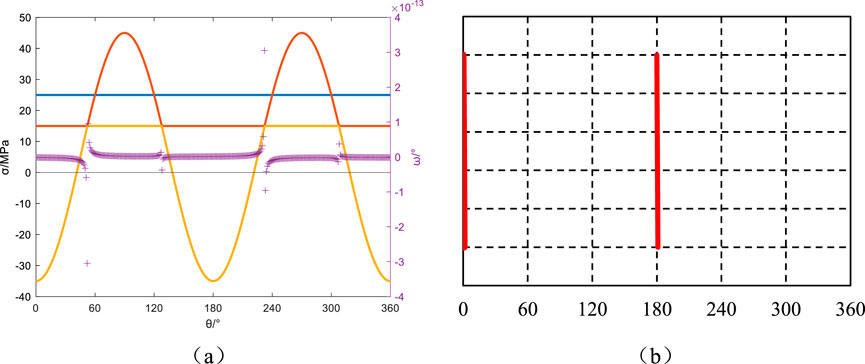
Figure 20. Azimuth angle αb = 90°, Well inclination angle βb = 90°: Principal stresses around the wellbore, induced fractures, and their angles relative to the wellbore axis. (a) Principal stress and induced fracture angle, (b) Induced fracture.

From Figure 5a, it can be observed that the first and second principal stresses around the wellbore do not vary with the circumferential angle. The third principal stress reaches its maximum value in the direction of minimum horizontal in situ and its minimum value in the direction of maximum horizontal in situ. The angle ω between induced fractures and the wellbore axis remains 0 throughout. This indicates that a vertical fracture is generated in the direction of maximum horizontal in situ, as depicted in Figure 5b.

Maintaining the drilling direction constant, but varying the well deviation angle, the wellbore’s principal stresses, the angle between induced fractures and the wellbore axis, and the induced fracture orientations for well deviation angles of 30°, 60°, and 90° are illustrated in Figures 6–8, respectively. The mechanical response exhibits distinct patterns across different well orientations. At βb = 30° deviation, circumferential stress analysis shows dual stress minima at 90°/270° azimuths. Stress state transition initiates fracture development with maintained near-orthogonal fracture-wellbore alignment (θ ≈ 90°), producing characteristic feather-textured fracture patterns as documented in Figures 6a,b. Notably, increasing deviation to β_b = 60° induces comprehensive tensile transformation (σ_min<0 throughout azimuths), driving θ fluctuations exceeding 60°. This mechanically governed instability generates multi-axial fracture intersections shown in Figures 7a,b, demonstrating progressive complexity with inclination angle. The horizontal well configuration (β_b = 90°) presents polar stress minima at 0°/180° positions. Theta maintains perfect coaxial alignment (θ≡0°) during wellbore rotation, forming vertically oriented fracture planes that bisect the borehole circumference (Figures 8a,b). This orientation-dependent fracture geometry evolution follows fundamental principles of anisotropic stress redistribution in inclined boreholes.

Keeping the wellbore azimuth angle at 30° and varying the well deviation angle to 0°, 30°, 60°, and 90°, the principal stresses around the wellbore, induced fractures, and their angles with the wellbore axis are depicted in Figures 9–12. When the well deviation angle β_b = 0°, the minimum principal stress around the wellbore reaches its minimum values at 60° and 240° around the wellbore. The angle between induced fractures and the wellbore axis remains 0°, resulting in two vertical fractures at positions 60° and 240° around the wellbore. For a well deviation angle of β_b = 30°, the minimum principal stress around the wellbore transitions to tensile stress in the range of 0°–108° and 181°–289° around the wellbore. Mechanical analysis reveals pronounced angular instability in fracture trajectory deviation (Δθ>45°), yielding distinctive hooked fracture geometries. This bifurcation pattern, encompassing both J-type curvature and mechanical fishhook configurations, arises from critical stress anisotropy conditions documented in Figures 10a,b. The observed morphological bifurcation demonstrates fundamental fracture path selection mechanisms governed by near-wellbore stress tensor reconfiguration. With a well deviation angle of β_b = 60°, the minimum principal stress around the wellbore transitions to tensile stress in the ranges of 0°–82°, 163°–262°, and 323°–360° around the wellbore. Similar to the previous case, the angle between induced fractures and the wellbore axis undergoes significant variations, resulting in induced fracture orientations resembling “J-shaped” fractures. The induced fractures exhibit inflection points at 60° and 240°, forming more pronounced “J-shaped” fractures, as depicted in Figures 11a,b. In horizontal well configurations (β_b = 90°), fracture trajectory angularity demonstrates constrained variability (Δθ<10°), manifesting hybrid fracture morphologies that bridge classical feather-textured patterns and mechanical “fishhook” configurations. This transitional morphology emerges from the unique stress coupling effects inherent to horizontal borehole geometries.

Maintaining the wellbore azimuth angle at 60°, the variations in principal stresses around the wellbore and induced fracture orientations with respect to the circumferential angle for well deviation angles of 0°, 30°, 60°, and 90° are illustrated in Figures 13–16. The mechanical response exhibits systematic dependence on wellbore orientation relative to in situ stress fields. In vertical wells (β_b = 0°), coaxial alignment with the principal in situ stress orientation induces fracture propagation vectors parallel to the borehole axis through geomechanical coupling. At intermediate inclinations (β_b = 30°,60°), stress anisotropy intensification during tensile state transition triggers angular instability (Δθ>30°), forming characteristic J-curvature fractures through stress-dependent path selection mechanisms, as quantitatively verified in Figure 10b. Conversely, horizontal wells (β_b = 90°) demonstrate constrained trajectory deviation (Δθ<10°) under compressive-tensile stress tensor reconfiguration. This transitional regime produces hybrid fracture architectures blending feather-textured discontinuities with incipient hook-shaped geometries, reflecting progressive stress decoupling in high-angle completions.

The wellbore azimuth angle is 90°, and the well deviation angles are 0°, 30°, 60°, and 90°. The principal stresses around the wellbore and the induced fracture orientations for these angles are depicted in Figures 17–20. In stress-aligned well configurations, the borehole axis maintains strict parallelism with principal in situ stress orientations: vertical stress correspondence at βb = 0° (Figures 17a,b) and maximum horizontal stress alignment at β_b = 90° (Figures 20a,b). This geometric optimization induces dual fracture initiation with perfect coaxial propagation through stress-controlled failure mechanisms. The resultant fracture planes exhibit diametric symmetry with exact 180° phasing, forming textbook hydraulic fracture patterns through geomechanical resonance. When the well deviation angles are 30° (Figures 18a,b) and 60° (Figures 19a,b) , the minimum principal stress around the wellbore reaches its minimum value at the circumferential angles of 0° and 180°. When the minimum principal stress transitions to tensile stress, the angle between induced fractures and the wellbore axis is close to 0° at the 0° (Figures 17a,b) and 180° (Figures 20a,b) positions, exhibiting minimal variation. As the circumferential angle increases, the variation becomes more significant, resulting in induced fracture orientations resembling sine curves, as predicted in Figures 18b, 19b. This makes them easily mistaken for natural fractures.

When analyzing the induced fractures around the wellbore formed by different trajectories, it is evident that if the wellbore axis is parallel to any principal in situ stress direction, such that no shear stress is induced around the wellbore, the angle between the induced fractures and the wellbore axis will remain at 0°. As a result, two symmetrically distributed fractures parallel to the wellbore axis are typically produced. When the variation in the angle between the induced fractures and the wellbore axis is within 10°, feather-like fractures appear. Once this angular variation exceeds 10°, “J-shaped” fractures are formed. Furthermore, when the angle between the induced fractures and the wellbore axis approaches 0° at the minimum principal stress extremum around the wellbore and then changes sharply either increasing or decreasing, the fractures tend to follow an approximately sine-curve pattern. Moreover, the induced fractures usually occur in pairs symmetrically arranged at 180° intervals.

3.2 The impact of bottomhole fluid column pressure

Bottomhole fluid column pressure is one of the most direct, effective, and controllable measures to maintain wellbore stability. It directly determines complex scenarios such as erosion or shear collapse of the wellbore wall and loss of drilling fluid. The authors studied the influence of bottomhole fluid column pressure on the development of drilling-induced fractures. The induced fracture orientations of a wellbore with azimuth angle α_b = 0° and well deviation angle β_b = 30° under different bottomhole pressures are illustrated in Figure 21. Analysis indicates that feather-like fractures are consistently formed under various bottomhole pressures. As the bottomhole fluid column pressure rises, the angle between the drilling-induced fractures and the wellbore axis progressively diminishes, while the length of these induced fractures gradually increases. The induced fractures are symmetrically distributed within the wellbore, with a spacing of 180° between them.

Figure 21

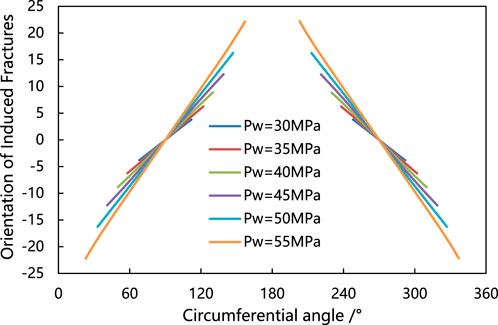
Figure 21. The orientation angle α_b = 0°, inclination angle β_b = 30°, and the orientation of induced fractures during directional drilling changes with the variation of bottom hole pressure.

The variations in drilling-induced fracture orientations of a wellbore with azimuth angle α_b = 30° and well deviation angle β_b = 30° under different bottomhole pressures are depicted in Figure 22. Analysis indicates that feather-like fractures are consistently formed under various bottomhole pressures. As the bottomhole fluid column pressure rises, the angle between the drilling-induced fractures and the wellbore axis progressively diminishes, while the length of these induced fractures gradually increases. The induced fractures are symmetrically distributed within the wellbore, with a spacing of 180° between them.

Figure 22

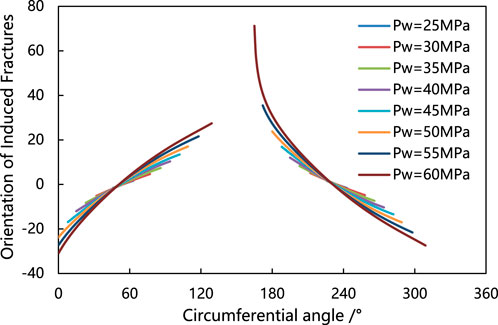
Figure 22. The azimuth angle α_b = 30°, inclination angle β_b = 30°, and the orientation of induced fractures in the wellbore change with variations in bottom hole pressure.

4 Conclusion

The identification and classification research of drilling-induced fractures is of great significance for clarifying the mechanisms of wellbore instability and drilling fluid loss, analyzing imaging logging data, and reservoir evaluation. This study adopts a linear elastic per-wellbore stress model and combines it with the tensile failure criterion of the wellbore surrounding rock to establish a predictive model for the occurrence of drilling-induced fractures around the wellbore. The influence of different engineering parameters such as wellbore trajectories and bottomhole pressures on the distribution of principal stresses around the wellbore, the angle and occurrence of drilling-induced fractures relative to the wellbore axis has been investigated. The main conclusions of this study are as follows, Drilling-induced fractures result from the combined effects of in situ stresses and engineering disturbances. They have a close relationship with in situ stresses and typically occur in pairs symmetrically arranged at 180° intervals. This organized arrangement provides a solid basis for identifying and classifying drilling-induced fractures, distinguishing them from natural fractures. When the wellbore axis is parallel to any principal in situ stress direction, with no shear stress induced around the wellbore, the angle between the drilling-induced fractures and the wellbore axis remains 0°. Consequently, two symmetrically distributed fractures parallel to the wellbore axis are usually formed. Feather-like fractures occur when the variation in the angle between the drilling-induced fractures and the wellbore axis is within 10°. When this variation exceeds 10°, “J-shaped” fractures are formed. Fractures approximately follow a sine curve when the angle between the drilling-induced fractures and the wellbore axis approaches 0° at the minimum principal stress extremum around the wellbore and then changes sharply either increasing or decreasing. With relatively low bottomhole pressure, feather-like drilling-induced fractures occur in the wellbore. As the pressure of the fluid column inside the well increases, the angle between the drilling-induced fractures and the wellbore axis gradually decreases, resulting in an increase in fracture length. Eventually, they transform into “J-shaped” fractures.

In reservoir evaluation, it is very important to more accurately and effectively identify effective fractures and distinguish and exclude the influence of drilling-induced fractures. Especially for unconventional reservoirs with strong heterogeneity, diverse types of storage spaces, and various fracture morphologies, the detection and identification of fractures are particularly difficult. Therefore, the correct identification of induced fractures is particularly important. The predictive model for the occurrence of drilling-induced fractures established in this paper can help reasonably and correctly interpret effective fractures in unconventional reservoirs and reservoir evaluation.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YL: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing. JW: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing. ZZ: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing. ML: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing. XZ: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing. XG: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing. MZ: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This paper is supported by the team construction project of the young innovative talents inducing and cultivating program of Shandong Province “Research and Innovation Team of Complex Oil and Gas Well Drilling Engineering” (Grant No. 2019035).

Conflict of interest

Author MZ was employed by Sinopec Research Institute of Petroleum Engineering Co., Ltd., China Petroleum and Chemical Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ai, E. (2015). Research on early warning theory and method of wellbore instability in shale. Xian, Shanxi: Xi'an Shiyou University Master's thesis.

Google Scholar

Al-Ajmi, A., and Zimmerman, R. (2006). A new 3D stability model for the design of non-vertical wellbores. Eng. and Technol. Environ. Eng.

Google Scholar

Al-Ajmi, A. M., and Al-Harthy, M. H. (2010). Probabilistic wellbore collapse analysis. J. Petroleum Sci. Eng. 74 (3-4), 171–177. doi:10.1016/j.petrol.2010.09.006

CrossRef Full Text | Google Scholar

Amadei, B. (2012). “Rock anisotropy and the theory of stress measurements,”, 2. Springer Science and Business Media. doi:10.1007/978-1-4615-1633-4

CrossRef Full Text | Google Scholar

Bai, G. (2020). Optimization method for drilling fluid density design in Wei 202,204 shale gas well area. Drill. Fluid and Complet. Fluid 37 (2), 196–201.

Google Scholar

Chen, P., Ma, T., and Xia, H. (2015). A collapse pressure prediction model for horizontal shale gas wells with multiple weak planes. Nat. Gas. Ind. B 2 (1), 101–107. doi:10.1016/j.ngib.2014.12.003

CrossRef Full Text | Google Scholar

Chen, Y., Deng, C., and Ma, T. (2019). Reliability theory-based evaluation method for wellbore instability risk. Nat. Gas. Ind. 39 (11), 97–104.

Google Scholar

Denney, D. (2005). Safe operating window: wellbore stability is more than just fluid density. J. petroleum Technol. 57 (09), 69–71. doi:10.2118/0905-0069-jpt

CrossRef Full Text | Google Scholar

Ding, Y., Luo, P., Liu, X., and Liang, L. (2018). Wellbore stability model for horizontal wells in shale formations with multiple planes of weakness. J. Nat. Gas Sci. Eng., S187551001830043X. doi:10.1016/j.jngse.2018.01.029

CrossRef Full Text | Google Scholar

Dokhani, V., Yu, M., and Bloys, B. (2016). A wellbore stability model for shale formations: accounting for strength anisotropy and fluid induced instability. J. Nat. Gas Sci. Eng. 32, 174–184. doi:10.1016/j.jngse.2016.04.014

CrossRef Full Text | Google Scholar

Dong, Z., Tian, S., Xue, H., Lu, S., Liu, B., Erastova, V., et al. (2025). A novel method for automatic quantification of different pore types in shale based on SEM-EDS calibration. Mar. Petroleum Geol. 173, 107278. doi:10.1016/j.marpetgeo.2024.107278

CrossRef Full Text | Google Scholar

Ebrahimi, M. A., Ahmadi, M., and Ameri, M. J. (2020). Application of unconditional simulation methods for quantifying the uncertainties in mud window design of gas reservoirs based on 3-dimensional mechanical earth modeling. J. Nat. Gas Sci. Eng. 76, 103186. doi:10.1016/j.jngse.2020.103186

CrossRef Full Text | Google Scholar

Ewy, R. T. Wellbore-stability predictions by use of a modified lade criterion (1999). Spe Drill. and Complet., 14(2):85–91. doi:10.2118/50671-PA

CrossRef Full Text | Google Scholar

Fengjiao, W., He, X., Liu, Y., Meng, X., and Liu, L. (2023). Mechanism of low chemical agent adsorption by high pressure for hydraulic fracturing-assisted oil displacement technology: a study of molecular dynamics combined with laboratory experiments. Langmuir 39 (46), 16628–16636. doi:10.1021/acs.langmuir.3c02634

CrossRef Full Text | Google Scholar

Fontoura, S. A. B., Holzberg, B. B., Teixeira, É. C., and Frydman, M. (2002). “Probabilistic analysis of wellbore stability during drilling,” in SPE/ISRM rock mechanics conference (OnePetro).

Google Scholar

Gao, R., Bai, D., Yu, B., Tai, Y., Meng, X., and Zhang, W. (2024). Ground fracturing of multi-strata for strong ground pressure control in extra-thick coal seams with hard roofs: numerical simulation and case study. Eng. Fract. Mech. 303, 110129. doi:10.1016/j.engfracmech.2024.110129

CrossRef Full Text | Google Scholar

Gao, R., Kuang, T., Meng, X., and Huo, B. (2021). Effects of ground fracturing with horizontal fracture plane on rock breakage characteristics and mine pressure control. Rock Mech. Rock Eng. 54 (6), 3229–3243. doi:10.1007/s00603-020-02294-x

CrossRef Full Text | Google Scholar

Guan, Z. C., and Sheng, Y. N. (2017). Study on evaluation method for wellbore stability based on uncertainty analysis. J. Appl. Sci. Eng. 20 (4), 453–457. doi:10.1080/13321349.2017.1373419

CrossRef Full Text | Google Scholar

He, S., Wei, W., Zhou, J., Zhen, H., and Ming, T. (2015). A model for analysis of wellbore stability considering the effects of weak bedding planes. J. Nat. Gas Sci. and Eng. 27 (part_P2), 1050–1062. doi:10.1016/j.jngse.2015.09.053

CrossRef Full Text | Google Scholar

Higgins, S. M., Goodwin, S. A., Bratton, T. R., and Tracy, G. W. (2008). “Anisotropic stress models improve completion design in the Baxter Shale,” in SPE annual technical conference and exhibition (Richardson, TX, United States: Society of Petroleum Engineers (SPE)).

Google Scholar

Huang, L., Yu, M., Miska, S. Z., Takach, N. E., and Bloys, J. B. (2012). “Parametric sensitivity study of chemo-poro-elastic wellbore stability considering transversely isotropic effects in shale formations,” in SPE Canadian unconventional Resources conference (Richardson, TX, United States: Society of Petroleum Engineers).

Google Scholar

Huang, Y., Sheng, Y., Guan, Z., Luo, M., Li, W., and Deng, W. (2019). Quantitative risk evaluation of wellbore stability in Yingqiong Basin. Fault-Block Oil and Gas Field 26 (3), 380–384.

Google Scholar

Lee, H., Ong, S. H., Azeemuddin, M., and Goodman, H. (2012). A wellbore stability model for formations with anisotropic rock strengths. J. Petroleum Sci. Eng. 96, 109–119. doi:10.1016/j.petrol.2012.10.011

CrossRef Full Text | Google Scholar

Li, W. (2020). Analysis and risk assessment of wellbore stability based on uncertainty of lithology parameters. East China: China University of Petroleum.

Google Scholar

Liu, M., Jin, Y., Lu, Y., Chen, M., Hou, B., Chen, W., et al. (2016). A wellbore stability model for a deviated well in a transversely isotropic formation considering poroelastic effects. Rock Mech. Rock Eng. 49 (9), 3671–3686. doi:10.1007/s00603-016-1019-8

CrossRef Full Text | Google Scholar

Liu, X., Yi, R., Zhou, X., and Wang, R. (2018). “Application of Bayesian network method in optimal completion of gas wells,” in Proceedings of the 2018 national natural gas academic annual conference (04 engineering Technology).

Google Scholar

Lu, Y., Xiao, X., Zhao, L., Jin, Y., and Chen, M. (2020). Influence of temperature on the stability of wellbore in ultra-deep fractured formations. Drill. Fluid and Complet. Fluid 37 (2), 160–167.

Google Scholar

Lu, Y. H., Chen, M., Jin, Y., Ge, W. F., An, S., and Zhou, Z. (2013). Influence of porous flow on wellbore stability for an inclined well with weak plane formation. Petroleum Sci. Technol. 31 (6), 616–624. doi:10.1080/10916466.2010.520912

CrossRef Full Text | Google Scholar

Ma, T., Zhang, Y., Qiu, Y., Liu, Y., and Chen, P. (2021). Risk assessment method for inclined wellbore instability based on reliability theory. Acta Pet. Sin. 42 (11), 1486–1498.

Google Scholar

Moos, D., Peska, P., Finkbeiner, T., and Zoback, M. (2003). Comprehensive wellbore stability analysis utilizing quantitative risk assessment. J. Petroleum Sci. Eng. 38(3-4): 97–109. doi:10.1016/s0920-4105(03)00024-x

CrossRef Full Text | Google Scholar

Noohnejad, A., Ahangari, K., and Gosht asbi, K. (2021). Integrated mechanical earth model and quantitative risk assessment to successful drilling. J. Petroleum Explor. Prod. 11 (1), 219–231. doi:10.1007/s13202-020-01043-7

CrossRef Full Text | Google Scholar

Økland, D., and Cook, J. M. (1998). “Bedding-related borehole instability in high-angle wells,” in SPE/ISRM rock mechanics in petroleum engineering (Richardson, TX, United States: Society of Petroleum Engineers).

Google Scholar

Qin, J. (2006). Identification of drilling induced fractures using imaging logging technology. Inn. Mong. Petrochem. Ind. 32 (10), 116–117.

Google Scholar

Qiu, K., Chen, M., and Jin, Y. (2011). Collapse pressure model of wellbore based on statistical damage. Rock Soil Mech. 32 (7), 2029–2033.

Google Scholar

Setiawan, N. B., and Zimmerman, R. W. (2018). Wellbore breakout prediction in transversely isotropic rocks using true-triaxial failure criteria. Int. J. Rock Mech. Min. Sci. 112, 313–322. doi:10.1016/j.ijrmms.2018.09.022

CrossRef Full Text | Google Scholar

Sheng, Y., Guan, Z., Luo, M., Li, W., and Ju, R. (2018). Sensitivity analysis of wellbore stability reliability random variables based on Monte Carlo method. Drill. and Prod. Technol. 40 (1), 14–19.

Google Scholar

Sheng, Y., Guan, Z., Xu, Y., Wang, Q., and Zhang, B. (2017). Discussion on uncertainty analysis method of wellbore stability problems. Fault-Block Oil and Gas Field 24 (6), 847–850.

Google Scholar

Sheng, Y., Reddish, D., and Lu, Z. (2006). Assessment of uncertainties in wellbore stability analysis[M]//Modern trends in geomechanics. Berlin, Heidelberg: Springer, 541–557.

CrossRef Full Text | Google Scholar

Singh, A., Rao, K. S., and Ayothiraman, R. (2019). An analytical solution to wellbore stability using Mogi-Coulomb failure criterion. J. Rock Mech. Geotechnical Eng. 11, 1211–1230. doi:10.1016/j.jrmge.2019.03.004

CrossRef Full Text | Google Scholar

Tabatabaee, M. S. S., Nikolaev, N., and Khormali, A. (2018). “A comprehensive uncertainty assessment of wellbore stability models,” in Saint petersburg 2018: innovations in geosciences and time for breakthrough, 44298.

Google Scholar

Udegbunam, J. E., Fjelde, K. K., Arild, Ø., Ford, E., and Lohne, H. P. (2013). Uncertainty-based approach for predicting the operating window in UBO well design. SPE Drill. and Complet. 28 (04), 326–337. doi:10.2118/161997-PA

CrossRef Full Text | Google Scholar

Wei, K., Guan, Z., Liao, H., Shi, Y., and Liu, Y. (2013). Evaluation method of wellbore instability risk. J. China Univ. Petroleum Ed. Nat. Sci. 37 (2), 62–66.

Google Scholar

Wen, Q. (2012). Research on risk assessment of complex geological drilling systems in deep wells based on soft computing theory Doctoral dissertation. East China: Qingdao: China University of Petroleum.

Google Scholar

Wu, W., Wang, T., Bai, J., Liu, J., Wang, X., Xu, H., et al. (2024). Failure characteristics and cooperative control strategies for gob-side entry driving near an advancing working face: a case study. Processes 12, 1398. doi:10.3390/pr12071398

CrossRef Full Text | Google Scholar

Xia, P. (2018). Impact fracture law and safety analysis of bare-eye wellbore in shale gas well Master's thesis. East China: China University of Petroleum.

Google Scholar

Zhang, J. (2013). Borehole stability analysis accounting for anisotropies in drilling to weak bedding planes. Int. J. Rock Mech. and Min. Sci. 60 (2), 160–170. doi:10.1016/j.ijrmms.2013.01.012

CrossRef Full Text | Google Scholar

Zhang, M., Fan, X., Zhang, Q., Yang, B., Zhao, P., Yao, B., et al. (2021a). Influence of multi-planes of weakness on unstable zones near wellbore wall in a fractured formation. J. Nat. Gas Sci. Eng. 93, 104026. doi:10.1016/j.jngse.2021.104026

CrossRef Full Text | Google Scholar

Zhang, M., Fan, X., Zhang, Q., Yang, B., Zhao, P., Yao, B., et al. (2021b). Parametric sensitivity study of wellbore stability in transversely isotropic medium based on poly-axial strength criteria. J. Petroleum Sci. Eng. 197, 108078. doi:10.1016/j.petrol.2020.108078

CrossRef Full Text | Google Scholar

Zhang, M., Li, D., Liu, J., Zhang, D., Zhang, Y., and Cui, K. (2023). The modification of Mohr-Coulomb criteria based on shape function and determination method of undetermined parameters. Mech. Mater. 185, 104772. doi:10.1016/j.mechmat.2023.104772

CrossRef Full Text | Google Scholar

Zhang, M. M., Liang, L. X., and Liu, X. J. (2017). Analysis of the influence of different rock shear failure criteria on wellbore collapse pressure. Chin. J. Rock Mech. Eng. 36 (S1), 3485–3491.

Google Scholar

Zhao, L., Wang, Q., Guo, Z., Fang, C., and Cao, H. (2020). Evaluation of wellbore stability in laminated shale formations based on finite collapse width. Sci. Technol. Rev. 38 (11), 122–130. doi:10.16651/j.cnki.issn0253-2778.2020.11.027

CrossRef Full Text | Google Scholar

Zhou, J., He, S., Tang, M., Huang, Z., Chen, Y., Chi, J., et al. (2018). Analysis of wellbore stability considering the effects of bedding planes and anisotropic seepage during drilling horizontal wells in the laminated formation. J. Petroleum Sci. Eng. 170, 507–524. doi:10.1016/j.petrol.2018.06.034

CrossRef Full Text | Google Scholar

Zoback, M. D. (2007). Reservoir geomechanics. Cambridge University Press. doi:10.1017/CBO9780511535596

CrossRef Full Text | Google Scholar