Identification and parameter estimation for electrical anisotropy in two-dimensional magnetotelluric models

When the subsurface media contain electrical anisotropic structure, magnetotelluric isotropic inversion fails to recover the electrical anisotropic structure and may distort the image of isotropic structures. Besides, due to the diversity and uncertainty in inversion caused by multi-parameterization, mature and practical anisotropic inversion procedure is lacking at the case with anisotropic angle. Here, four two-dimensional models were constructed with mixed electrical anisotropic/isotropic structures including azimuthal anisotropy case. Phase tensor and real induction vector analyses, as well as two-dimensional isotropic and one-dimensional anisotropic inversions, were performed to identify and estimate the electrical anisotropic parameters. Based on the equivalence concept of electrical anisotropy, the extracted anisotropic structure was equivalent to isotropic structure with alternating high- and low-resistivity anomalies. These equivalent anomalies were then added into two-dimensional isotropic inversion as a priori information. Consequently, the isotropic structure of the true model is well recovered. The proposed method can identify and estimate the electrical anisotropy structure as well as the isotropic structure to a certain extent in two-dimensional magnetotelluric models. This study provides a novel approach for analyzing electrical anisotropy in magnetotelluric data.

1 Introduction

An increasing number of studies have presented the multi-scale electrical anisotropy characteristics of lithospheric composition and structure (Jones, 2012; Martí, 2014), such as the directional arrangement of specific mineral rocks or geological structures, and the spatial dominance distribution of geological fluids or volatile components (Nover, 2005; Wannamaker, 2005; Martí, 2014; Pommier, 2014). The magnetotelluric method is a passive exploration technique that utilizes a broad spectrum of naturally occurring geomagnetic variations as a power source for electromagnetic induction in the Earth. It measures natural electric and magnetic fields in orthogonal directions at the Earth’s surface. Based on the theory of skin depth (i.e., the penetration depth of electromagnetic fields into the Earth approximately expressed as $503\sqrt{\rho T}$, where $\rho$ is the average resistivity of medium and $T$ the period), it can determine subsurface electrical resistivities at depths ranging from a few tens of meters to several hundreds of kilometers. Lots of studies have presented the existence of electrical anisotropy within real magnetelluric data (e.g., Bhattacharya, 2005; Heinsong and White, 2005; Frederiksen et al., 2006; Padilha et al., 2006; Wannamaker et al., 2008; Brasse et al., 2009; Häuserer and Junge, 2011; Le Pape et al., 2012; Naif et al., 2013; Liu, 2016; Chave and Jones, 2018; Liu et al., 2019). Undoubtedly, studying the electrical anisotropy in the Earth’s interior can provide crucial clues to reveal the lithospheric deformation history and evolution process (e.g., Tommasi et al., 1999; Hamilton et al., 2006; Jones, 2006; Jones, 2012), as well as provide fundamental information and key constraints for lithospheric composition and structure and geodynamic models (e.g., Mareschal et al., 1995; Becker et al., 2006; Heise and Ellis, 2016).

Identifying electrical anisotropy in magnetotelluric data has been a global research focus (e.g., Bahr and Duba, 2000; Bahr and Simpson, 2002; Liu et al., 2019). The over-quadrant phenomenon of impedance phase (i.e., the phase variations of Zxy or Zyx components exceeding 90°) was first observed in specific two-dimensional or three-dimensional anisotropic models with upper and lower structural relationships (Pek and Verner, 1997; Heise and Pous, 2003; Kumar and Manglik, 2012). Additionally, the real induction vectors and phase tensors can be used to indicate the presence of electrical anisotropy. Pek (2009) found that, in a two-dimensional anisotropic medium, the real induction vector deviated from the principal axes of both the regional impedance tensor and the anisotropy body, with the degree of deviation depending on the depth and horizontal extent of the anisotropic body. Based on the consistent phase differences and induction vectors, Yin et al. (2014) determined the electrical anisotropy within real magnetotelluric data. Liu et al. (2019) discriminated the electrical anisotropy from the spatially continuous directions of phase tensors and real induction vectors. Furthermore, numerous theoretical modeling studies have shown that isotropic inversion of magnetotelluric responses from a resistivity model with anisotropy will produce equivalent isotropic anomalies, i.e., alternating high- and low-resistivity anomalies (Eisel and Haak, 1999; Heise and Pous, 2003; Martí, 2014). This phenomenon facilitates the identification and parameter estimation of electrical anisotropy (Heise and Pous, 2003; Heise et al., 2006). Conversely, the occurrence of such alternating resistivity structures does not necessarily indicate the presence of electrical anisotropy. Comeau and Becken (2020) conducted two-dimensional magnetotelluric imaging in the Bulnay region of Mongolia and identified distinct low-resistivity bands in the lower crust. These features persisted even when anisotropy was incorporated into the modeling. They suggested that regional lower crustal fluid flow is primarily governed by tectonic deformation and compaction processes, rather than lithological-structural heterogeneity.

For quantitative interpretation, the three-dimensional modeling has gradually matured (e.g., Löwer and Junge, 2017; Cao et al., 2017; Cao et al., 2018; Xiao et al., 2018; Han et al., 2018; Xiao et al., 2019a; Xiao et al., 2019b; Yu, 2021; Zhou, 2022; Zhu et al., 2023). However, progress in anisotropic inversions remains slow. The main challenge is recovering the true electrical anisotropic structure without introducing artificial anomalies (Yin, 2003; Pek et al., 2011; Chen and Weckmann, 2012; Xie et al., 2022). One-dimensional anisotropic inversion accounting for azimuthal anisotropy case has become relatively mature, where the most representative and widely adopted method is the improved Occam inversion method developed by Pek and Santos (2006). Mature two-dimensional anisotropic inversion has been applied in some practical applications, but only in the case where the resistivity anisotropy direction is either parallel or perpendicular to the regional electrical principal axis (e.g., Baba et al., 2006; Key et al., 2013; Naif et al., 2013; Key, 2016; Johansen et al., 2019). Besides, for two-dimensional electrical anisotropic media, two-dimensional isotropic inversion will not only fail to recover the electrical anisotropic structure but also possibly distort the imaging of the electrical isotropic structure (Heise and Pous, 2003; Löwer and Junge, 2017; Miensopust and Jones, 2011). Therefore, considering the multiplicity and instability of inversions, it is crucial to find a way to identify and estimate anisotropic parameters, and simultaneously recover electrical anisotropic/isotropic structures.

Based on four two-dimensional theoretical models with mixed electric anisotropic/isotropic structures including azimuthal anisotropy case, we aim to identify and estimate electrical anisotropy through phase tensor and induction vector analyses, as well as two-dimensional isotropic and one-dimensional anisotropic inversions. Ultimately, the extracted electrical anisotropic parameters were equivalent to isotropic structures with alternating high- and low-resistivity anomalies, which were used as prior information for the isotropic inversion to recover the electrical isotropic structure.

2 Theoretical electrical anisotropy model

In orogenic belts and subduction zones, the crust and upper mantle are influenced by various geological processes, such as stress motion, magma intrusion, and migration of mantle fluids. These processes may include the transports of liquid-melt, graphite, and metallic sulfides, as well as the directional alignments of specific geological structures, which can result in observable electrical anisotropy (e.g., Wannamaker, 2005; Yin et al., 2014; Liu et al., 2021). For example, in Tibetan Plateau of SW China, the flow of soft materials (either molten or partially molten) under shear stress in the lower crust can lead to resistivity variations in different directions (Meyer et al., 1998; Yin et al., 2008a; Yin et al., 2008b; Zhao et al., 2011). Additionally, in Western Junggar of NW China, ancient subducted slabs modified by magmatic activity, can produce electrical anisotropy in the upper crust (Liu, 2016; Liu et al., 2019). Based on the typical characteristics of electrical anisotropy observed in Tibetan Plateau and Western Junggar, this study constructed four two-dimensional theoretical models with mixed azimuthal electrical anisotropy structures and electrical isotropy structures, as illustrated in Figure 1. Model A, referred to the electrical anisotropy in Tibetan Plateau, includes a high-resistivity (300 $\left.\mathrm{\Omega }.\mathrm{m}\right)$ upper crust (0–20 km) embedded with an isotropic low-resistivity body of 10 $\mathrm{\Omega }.\mathrm{m}$, an azimuth anisotropic mid-lower crust (20–40 km) with the principal axes resistivities of 10 $\mathrm{\Omega }.\mathrm{m}$, 300 $\mathrm{\Omega }.\mathrm{m}$, and 10 $\mathrm{\Omega }.\mathrm{m}$, respectively, and a 10 $\mathrm{\Omega }.\mathrm{m}$ half-space below 40 km. When the azimuth angle ${\alpha }_s$ of anisotropic layer is 0° and 30°, the models are referred to Model A1 and Model A2, respectively. Model B, referred to the electric anisotropy in Western Junggar, has the consistent structure scales bodies with Model A. The differences are that the isotropic body and the anisotropic layer in Model A are changed to the anisotropic body and the isotropic layer. Similarly, the anisotropic bodies with ${\alpha }_s$ = 0° and ${\alpha }_s$ = 30° are designated as Models B1 and B2, respectively.

Figure 1

Figure 1. Schematic representation of two-dimensional electrical anisotropic models used in this study. (a) Model A represents an anisotropic layer within an isotropic structure, while (b) Model B features an anisotropic body within an isotropic layer. The black inverted triangles indicate the locations of magnetotelluric sites.

For the four typical models, the two-dimensional finite difference method (Pek and Verner, 1997) was utilized to calculate the response functions at 51 stations with a space of 2 km. The response periods ranged from 0.015 s to 2000 s logarithmically divided into 30 spaced periods.

3 Identification and parameter estimation for electrical anisotropy

3.1 Forward response analysis

The magnetotelluric forward responses for the four models were analyzed using phase tensor ellipses (Caldwell et al., 2004; Booker, 2014) and real induction vectors (Wiese, 1962) as illustrated in Figure 2. Phase tensor ellipses are plotted for the magnetotelluric stations with long axes (maximum phase ${\mathrm{\varphi }}_{\mathit{max}}$) normalized and filled by colors representing the values of the skew angle $\mathrm{\psi }$ (left slide) and the minimum phase ${\mathrm{\varphi }}_{\mathit{min}}$ (right slide). In a two-dimensional case, ${\mathrm{\varphi }}_{\mathit{max}}$ and ${\mathrm{\varphi }}_{\mathit{min}}$ refer to the magnetotelluric phases of transverse electric (TE) and transverse magnetic (TM) modes and the skew angle $\mathrm{\psi }$ is 0° (Caldwell et al., 2004). The real induction vectors follow Wiese convention (Wiese, 1962), where the vectors point away from low-resistivity structures.

Figure 2

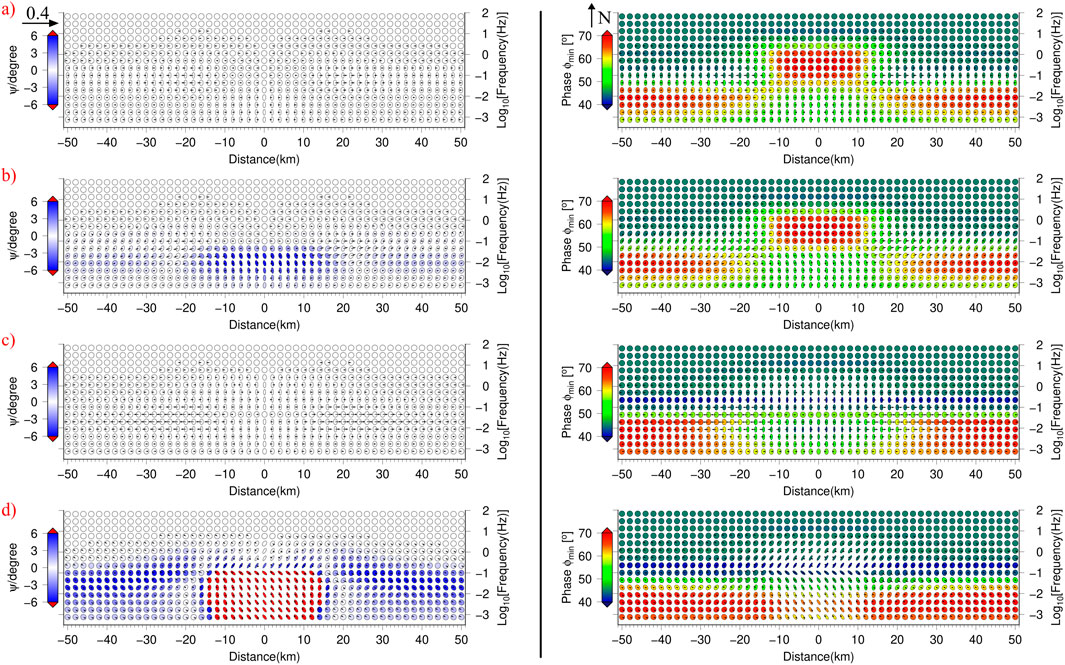
Figure 2. The phase tensor ellipses and real induction vectors from the anisotropic models A1 (a), A2 (b), B1 (c) and B2 (d). The long axes of ellipses are normalized and the fill colors represent the skew angle $\mathrm{\psi }$ (left) and the minimum phase ${\mathrm{\varphi }}_{\mathit{min}}$ (right), respectively. The black arrow represents the Wiese real induction vector.

For the axial anisotropy Models A1 and B1 (Figures 2a,c), the phase tensor ellipses within the anisotropic regions present consistent long-axis orientation directing towards true north, with skew angle value of zero. In contrast, the one-dimensional electrical isotropic regions beneath the anisotropic body or layer exhibit distorting features with consistent long-axis orientation in certain areas. For the Model A1, the minimum phase indicates the presence of a relatively low-resistivity body within the vertical range of 5–20 km (as calculated using the skin depth formula) and the horizontal range of −15 to 15 km. In comparison, the high-resistivity layer situated beneath the anisotropic body in the Model B1 cannot be distinguished from minimum phase.

In the context of azimuthal anisotropy Models A2 and B2 (Figures 2b,d), the phase tensor ellipses within the anisotropic regions present consistent long-axis orientation directing towards 30° east of north. However, beneath these regions, the orientation of the phase tensor ellipses shifts to 30° west of north. Notably, the skew angle is no longer zero beneath the anisotropic body or layer. Especially, for the Model B2, the absolute value of skew angle exceeds 6°. Without considering anisotropy, this may mislead that three-dimensional interpretation is necessary. This suggests that azimuthal anisotropy can induce substantial changes in dimensionality analysis within the anisotropic region and its surrounding. Moreover, the minimum phase can indicate the presence of a low-resistivity body located above the azimuthal anisotropic layer in Model A2. In contrast, the high-resistivity layer beneath the anisotropic body in the Model B2 remains unclear from the minimum phase.

Furthermore, for all four models, the real induction vectors (Figure 2) are primarily oriented perpendicular to the structural strike or the direction of minimum resistivity anisotropy, indicating strong response to anomaly body. The values of the real induction vectors reach their maximum at the boundaries of these bodies.

3.2 Two-dimensional isotropic inversion

To explore the distortion patterns when inverting the responses of an anisotropic model using isotropic inversion, we performed two-dimensional isotropic Occam inversion (DeGroot-Hedlin & Constable, 1990). The impedance data from Models A2 and B2 were rotated by 30° to align with the anisotropic direction. Both apparent resistivity and phase were assigned to 5% error floor. The inversion results are presented in Figure 3.

Figure 3

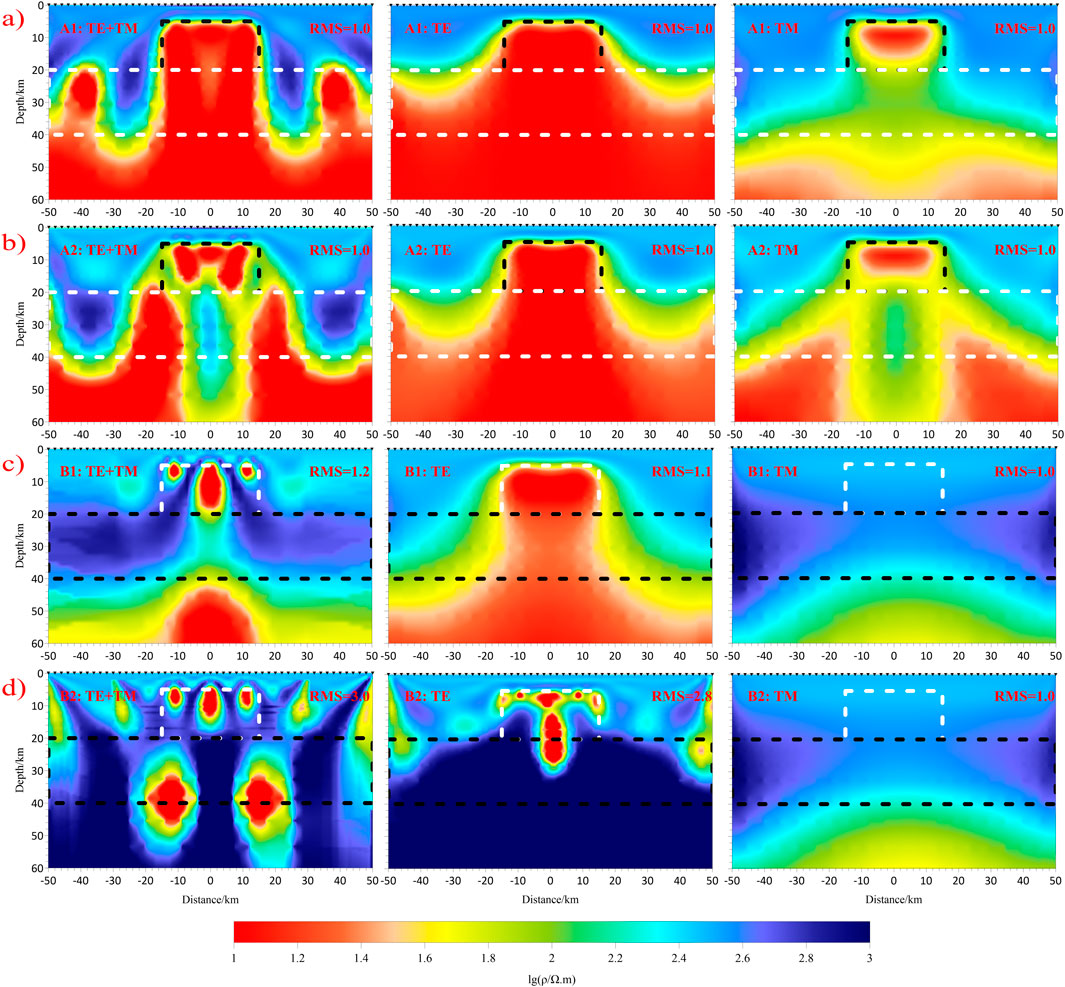
Figure 3. Two-dimensional isotropic inversion results of different polarization modes for Models A1 (a), A2 (b), B1 (c), and B2 (d). Black inverted triangles indicate magnetotelluric sites, white rectangles represent the true anisotropic areas, and black rectangles denote the true isotropic areas.

Within the electrically anisotropic body (Model B) and the layer (Model A), the inversion results of joint TE+TM modes manifest as vertical dyke isotropic structures characterized by alternating high- and low-resistivity anomalies. The inverted high- and low-resistivity dykes have resistivities of ∼635 $\mathrm{\Omega }.\mathrm{m}$ and ∼5 $\mathrm{\Omega }.\mathrm{m}$, respectively. The average widths of the dykes are ∼20 km for Model A and ∼6 km for Model B. Moreover, consistent with the forward response analysis, the isotropic inversion results suggest that electrical anisotropy does not significantly affect the imaging of the overlying isotropic structure. The isotropic inversions of different polarization modes for Models A1 (Figure 3a) and A2 (Figure 3b) can effectively recover the overlying isotropic low-resistivity body. However, electrical anisotropy would distort the imaging of underlying isotropic regions. The inversion results of different polarization modes for Model B1 (Figure 3c) show that the high-resistivity layer beneath the electrical anisotropic body is disrupted and the deep isotropic half-space cannot be well recovered. Besides, in contrast to axial anisotropy (Model B1), azimuthal anisotropy can produce a more pronounced distortion in the imaging of underlying isotropic structure (Figure 3d). The inversion results of TE+TM modes reveal two low-resistivity false anomalies within the high-resistivity layer, while the inversion results of TE mode present a “T-shaped” low-resistivity anomaly within the region of the anisotropic body region.

3.3 One-dimensional anisotropic inversion

Currently, mature and practical two-dimensional anisotropic inversion is limited to cases with axial anisotropy. One-dimensional anisotropic inversion is relatively well-developed and can account for azimuthal anisotropy case. The spatial consistency of the inversion results plays a crucial role in identifying electrical anisotropy and estimating anisotropic parameters. To estimate the electrical anisotropic parameters, one-dimensional anisotropic inversion (Pek and Santos, 2006) was conducted for all stations from the four models. The pseudo two-dimensional images are shown in Figure 4, where the inversion results for the rightmost and central stations of each model are also presented. The background color represents the logarithmic difference between the maximum and minimum resistivities. The more intense red hue indicates a higher degree of anisotropy. The filling color of small square above the background represents the azimuthal angle of the minimum resistivity at various depths. The north is defined as 0° and the clockwise direction is positive.

Figure 4

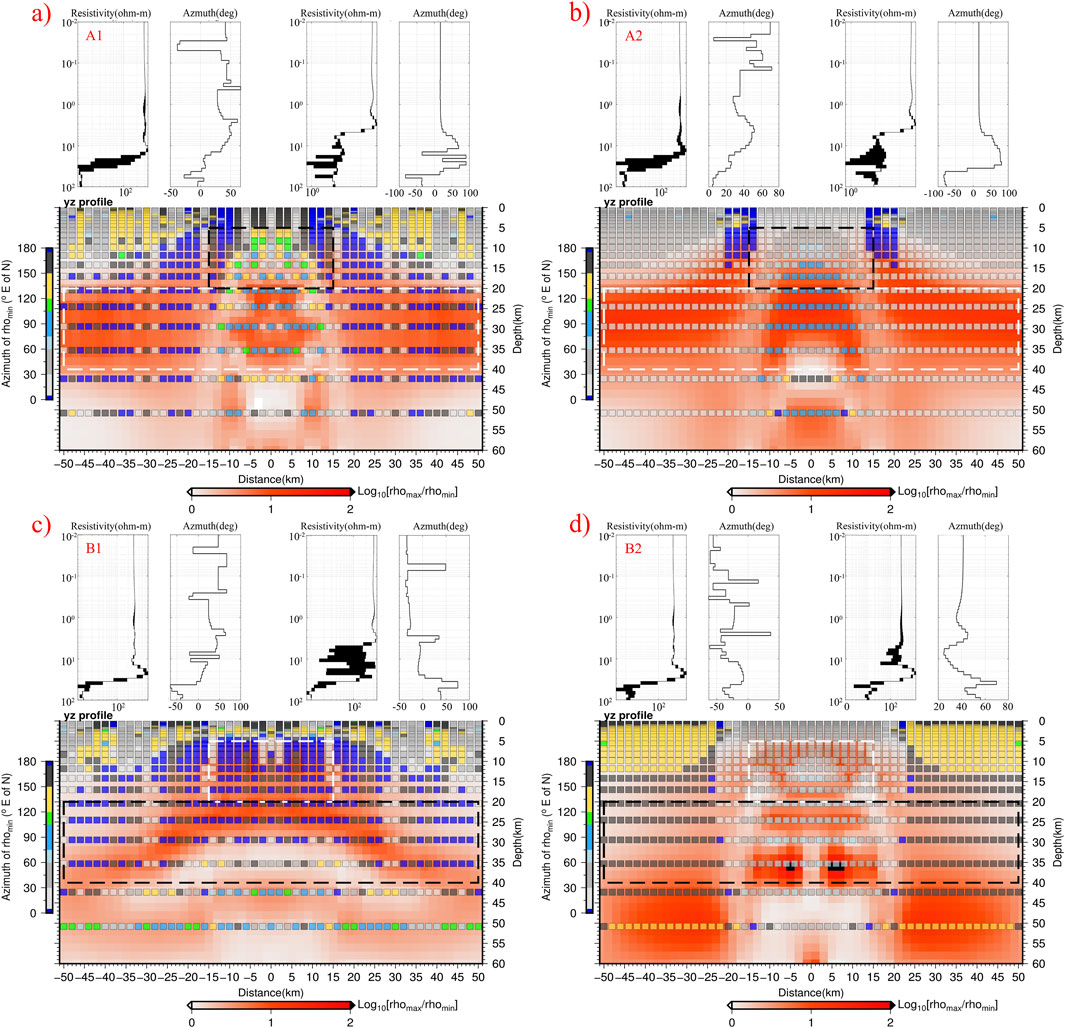
Figure 4. One-dimensional anisotropy inversion results for Models A1 (a), A2 (b), B1 (c) and B2 (d). Profile represents the pseudo two-dimensional imaging of one-dimensional inversion results. Background color of profile shows the difference between maximum and minimum resistivities in logarithmic domain. The darker red indicates stronger electrical anisotropy. The overlaid small squares with colors indicate the azimuthal angles of minimum resistivities. The white and black dotted lines represent the locations of anisotropic and isotropic anomalies, respectively. The two plots above each profile show the one-dimensional inversion results at the y = 50 km and y = 0 km stations.

For the Model A1 (Figure 4a), an electrical anisotropy layer can be observed at depths ranging from 20 to 40 km. The azimuth of minimum resistivity is primarily oriented at 0° or 180°, which is consistent with that of true electrical anisotropy. Moreover, the inversion results of the two typical stations (y = 50 km and y = 0 km) show that the background resistivity at depths of 0–20 km is about 300 $\mathrm{\Omega }.\mathrm{m}$, and a low-resistivity body of about 10 $\mathrm{\Omega }.\mathrm{m}$ is embedded at depths of 5–20 km in the middle area. The minimum and maximum resistivities at depths of 20–40 km are around 5 $\mathrm{\Omega }.\mathrm{m}$ and 280 $\mathrm{\Omega }.\mathrm{m}$, respectively. For the Model A2 (Figure 4b), the inversion results are similar to those from Model A1. A layer with relatively high electrical anisotropy at depths of 20–40 km can also be identified with an azimuth angle of ∼30°. However, large-scale false anisotropic anomalies also appear in the underlying region. The bottom boundary of the anisotropic layer can be determined through a combination of forward response analysis and two-dimensional isotropic inversion.

For the Model B1 (Figure 4c), electrical anisotropy is evident at depths greater than 5 km, with the minimum resistivity azimuth predominantly oriented at 0° or 180°. Combined with the results from both the forward response analysis and two-dimensional isotropic inversion, it can be inferred that there is an axial anisotropic body, extending horizontally from −15 km to 15 km and vertically from 5 km to 20 km. From the inversion results of the two typical stations (y = 50 km and y = 0 km), the minimum and maximum resistivities of this anisotropic body can be obtained with values of ∼15 $\mathrm{\Omega }.\mathrm{m}$ and ∼290 $\mathrm{\Omega }.\mathrm{m}$, respectively. Besides, the inversion results for Model B2 are similar to those for Model B1, except that the minimum resistivity azimuth within the anisotropic region is primarily oriented at 30°.

4 Isotropic constraint inversion under equivalent concept

4.1 Isotropic equivalence of electrical anisotropy

Theoretical model studies have shown that any microscopic anisotropic model can be effectively simulated using complex isotropic structures (Eisel and Haak, 1999; Weidelt, 1999; Heise and Pous, 2003; Martí, 2014). This equivalence between microscopic anisotropy and isotropy arises primarily from the limited resolution of the magnetotelluric method at the relevant detection depths (Weidelt, 1999). Eisel and Haak (1999) noted that once a macroscopic anisotropic structure, such as dyke structures with alternating high- and low-resistivities, is recovered through two-dimensional isotropic inversion, the approximate values of the microscopic anisotropic resistivities can be derived using the resistivities and average dyke widths from the inversion. The fundamental formula for estimating axial resistivities is as follows:

${\rho }_{\max }=\frac{{\rho }_1{d}_1+{\rho }_2{d}_2}{d_1+d_2},{\rho }_{\min }=\frac{{\rho }_1{\rho }_2\left(d_1+d_2\right)}{{\rho }_1{d}_1+{\rho }_2{d}_2}(1)$

In the above, ${\rho }_1$ and $d_1$ represent the resistivity and width of high-resistivity dykes from the inversion, while ${\rho }_2$ and $d_2$ are the resistivity and width of the low-resistivity dykes.

The two-dimensional inversions of TE+TM modes for the four models effectively fit the anisotropic response data by employing a vertical dyke structure with alternating high- and low-resistivities (Figure 3), where ${\rho }_1\approx 635\mathrm{\Omega }.\mathrm{m}$, ${\rho }_2\approx 5\mathrm{\Omega }.\mathrm{m}$, and $d_1\approx d_2$. The average dyke widths are 20 km and 6 km for Model A and Model B. Utilizing Equation 1, we can obtain ${\rho }_{\mathit{max}}\approx 320\mathrm{\Omega }.\mathrm{m}$ and ${\rho }_{\mathit{min}}\approx 10\mathrm{\Omega }.\mathrm{m}$. From the one-dimensional anisotropic inversions, the anisotropic layer in Model A presents ${\rho }_{\mathit{max}}\approx 280\mathrm{\Omega }.\mathrm{m}$ and ${\rho }_{\mathit{min}}\approx 5\mathrm{\Omega }.\mathrm{m}$, while the anisotropic body in Model B shows ${\rho }_{\mathit{max}}\approx 290\mathrm{\Omega }.\mathrm{m}$ and ${\rho }_{\mathit{min}}\approx 15\mathrm{\Omega }.\mathrm{m}$. By taking the arithmetic mean of the anisotropic resistivities obtained from two-dimensional isotropic and one-dimensional anisotropic inversions, the final optimized anisotropic resistivities for Model A and Model B are ${\rho }_{\mathit{max}}\approx 300\mathrm{\Omega }.\mathrm{m}$ and ${\rho }_{\mathit{min}}\approx 7.5\mathrm{\Omega }.\mathrm{m}$, and ${\rho }_{\mathit{max}}\approx 305\mathrm{\Omega }.\mathrm{m}$ and ${\rho }_{\mathit{min}}\approx 7.5\mathrm{\Omega }.\mathrm{m}$, respectively. These values are close to the true anisotropic resistivities.

4.2 Constraint inversion

From the results of two-dimensional isotropic inversion (Figure 3), it is obvious that the anisotropic layer in Model A does not influence the image of overlying isotropic structure. However, the anisotropic body in Model B distorts the imaging of the underlying isotropic medium. Therefore, this study focuses on the recovery of isotropic structures in Models B1 and B2. The basic idea is that the equivalent isotropic results of electrical anisotropy are first added into two-dimensional isotropic inversion as a priori information, as shown in the top two panels of Figure 5. Then, constraint isotropic inversion is conducted to suppress the influence of anisotropy and recover the isotropic structure distorted by anisotropy.

Figure 5

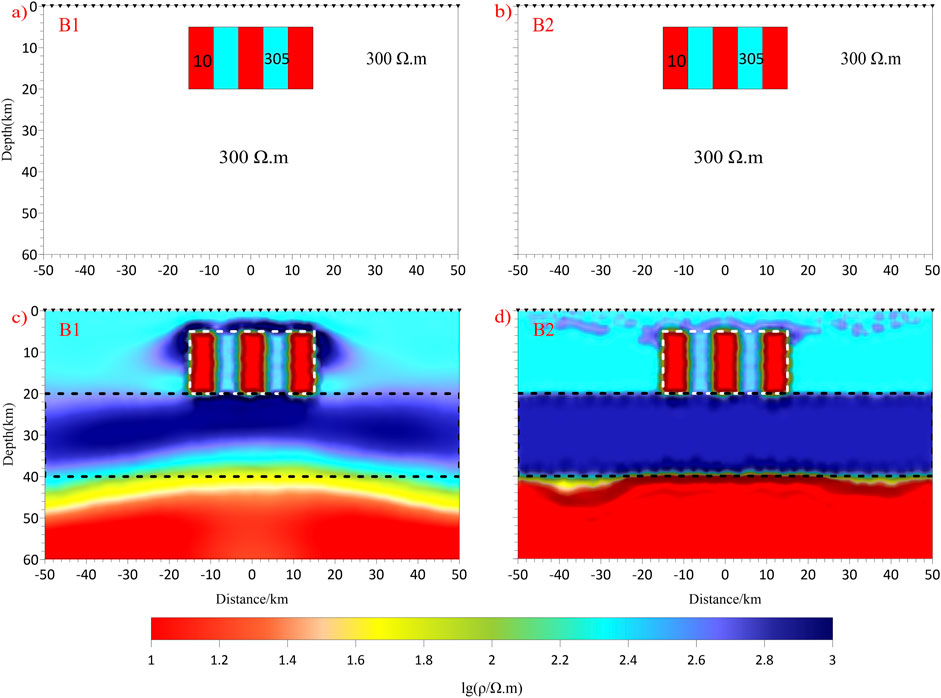
Figure 5. Two-dimensional isotropic constraint inversion results for Models B1 and B2. (a, b) show the prior models for Model B1 and Model B2, respectively, incorporating the equivalent structures proposed in this study, where the resistivity of the low-resistivity dykes is 10 $\mathrm{\Omega }.\mathrm{m}$ and the high-resistivity dykes is 300 $\mathrm{\Omega }.\mathrm{m}$. (c) Constraint inversion results for Model B1; (d) Constrained inversion results for Model B2.

When the anisotropic body in Model B was equivalent to isotropic structures with alternating high- and low-resistivity bands of 635 $\mathrm{\Omega }.\mathrm{m}$ and 5 $\mathrm{\Omega }.\mathrm{m}$, respectively, the constraint inversion cannot recover the underlying structure. After numbers of simulations, we found that replacing the equivalent high- and low-resistivities as approximate ${\rho }_{\mathit{max}}$ and ${\rho }_{\mathit{min}}$ in the constraint inversion can effectively recover the underlying isotropic structure. In this case, the prior model can produce relatively small initial misfit. Here, we adopted 305 $\mathrm{\Omega }.\mathrm{m}$ and 10 $\mathrm{\Omega }.\mathrm{m}$ as the final equivalent high- and low-resistivities for prior model (Figures 5a,b).

The constraint inversion results are shown in Figure 5. Compared with the unconstrained inversion results (Figure 3), it can be seen that the constraint inversions can well recover the resistivity values and geometrical features of the isotropic high-resistivity layer and low-resistivity half-space beneath the anisotropic body. Therefore, combined with the results of identification and parameter estimation for electrical anisotropy as previously mentioned, both electrical anisotropy and isotropic electrical structures in the models B1 and B2 have been successfully recovered to a certain content.

5 Discussion

The phase tensor analysis shows that the major axes of ellipses maintain consistent orientations within anisotropic regions. For axial anisotropy, the major axes of the ellipses align with the strike direction, while the skew angles have an absolute value of 0°. In contrast, for azimuthal anisotropy, the major axes are perpendicular to the anisotropic direction (the direction of lowest resistivity). Meanwhile, the skew angles have absolute values greater than 0° (even exceeding 6°). Without considering anisotropy, this may mislead that three-dimensional interpretation is necessary. Moreover, the real induction vectors reach maximum amplitudes at the boundaries of anomalous bodies (including anisotropic bodies), with directions always perpendicular to anisotropic direction. Significantly, the modeling reveals a new finding that electrical anisotropy anomaly can severely distort the phase tensors and real induction vectors of its underlying region but not above it.

When isotropic inversion is applied to magnetotelluric responses from an electrical anisotropy model, it fails to recover the anisotropic structure and distorts the imaging of isotropic structure below anisotropic body. However, two-dimensional isotropic inversion of TE+TM modes generally produces vertically alternating high- and low-resistivity anomalies within anisotropic region. By combining the spatial variation patterns of phase tensors and real induction vectors (particularly the spatial consistency or continuity of responses across different sites and periods) with the two-dimensional isotropic inversions, the type and boundary of electrical anisotropy can be roughly identified. Moreover, one-dimensional anisotropic inversion can reveal electrical anisotropy structure to a certain extent. The minimum and maximum resistivities and the orientation of the anisotropy anomaly can be approximately obtained from the spatial variations of one-dimensional anisotropic inversion results. However, due to fake anomalies below the anisotropic structure in the one-dimensional anisotropic inversion results, the lower boundary cannot be obtained, which can be detected from response analyses or two-dimensional isotropic inversion results. Therefore, based on the above processes, the anisotropic body and its parameters can be identified and estimated.

On the other hand, based on phase tensor and real induction vector analyses, as well as the results of two-dimensional isotropic and one-dimensional anisotropic inversions, it is obvious that the anisotropic structure can affect the isotropic structure below it. Following the principle of anisotropic equivalence (Eisel and Haak, 1999; Heise and Pous, 2003; Martí, 2014), the anisotropic structure can be equivalent to isotropic alternating high- and low-resistivity anomalies. By isotropic constraint inversion, the isotropic structure can be obtained. Thus, combined with the identification and parameter estimation for electrical anisotropy, the anisotropic and isotropic structures in the true models can be well recovered to a certain content.

This study involves multiple inversion steps, including one-dimensional anisotropic inversion and two-dimensional unconstrained and constrained isotropic inversions. The selected inversion codes are mature and widely applied with less computational costs (about 2 h for all steps on a normal desktop computer in this study). Moreover, the proposed approach is based on the assumption that electrical anisotropy can be equivalently represented by isotropic resistivity structures (Eisel and Haak, 1999; Weidelt, 1999; Heise and Pous, 2003). The theoretical modeling tests in this study indicate the validation of the assumption. Nevertheless, considering the complexity of real geological settings, the applicability of the assumption requires further studies. Furthermore, the proposed method in this study lacks the validation in real magnetotelluric data, which will be a focus in future research. Anyway, when the proposed method is used in real data, the existence of electrical anisotropy should be firstly identified and then the validation of quantitative interpretation can be studied.

6 Conclusion

It is worth noting that this study only considers the azimuthal anisotropy, which is the most common and significant case for magnetotelluric method based on plane wave theory. Following the line of evidence discussed above, several conclusions are obtained:

1. Electrical anisotropic bodies can distort the magnetotelluric responses of the underlying isotropic structure, misleadingly indicating that three-dimensional interpretation is necessary. Two-dimensional isotropic inversion of TE+TM modes can fit the anisotropic responses by introducing vertically isotropic structure with alternating high- and low-resistivity anomalies but produce fake anomalies in the underlying isotropic part.

2. Combined phase tensor and real induction vector analyses with two-dimensional isotropic and one-dimensional anisotropic inversions, the anisotropic structure and its parameters can be well identified and estimated.

3. Compared with the unconstrained isotropic inversion results, the resistivity values and geometrical features of isotropic parts beneath the anisotropic body can be reasonably recovered by constrained isotropic inversions based on the assumption that anisotropic structures can be treated as equivalent isotropic structures.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

XJ: Conceptualization, Formal Analysis, Investigation, Methodology, Validation, Visualization, Writing – original draft, Writing – review and editing. ZX: Formal Analysis, Supervision, Writing – review and editing. ZH: Formal Analysis, Supervision, Writing – review and editing. WZ: Investigation, Validation, Writing – review and editing. YL: Conceptualization, Funding acquisition, Investigation, Project administration, Supervision, Validation, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This study was supported by the National Key Research and Development Program of China (No. 2024YFF0807300) and the National Natural Science Foundation of China with grants 42430307 and 41904079.

Acknowledgments

We are grateful for the constructive comments and insightful suggestions provided by the reviewers, which significantly enhanced the quality of this paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Baba, K., Chave, A. D., Evans, R. L., Hirth, G., and Mackie, R. L. (2006). Mantle dynamics beneath the east pacific rise at 17°S: insights from the mantle electromagnetic and tomography (MELT) experiment. J. Geophys. Res. Solid Earth 111 (B2), B02101. doi:10.1029/2004jb003598

CrossRef Full Text | Google Scholar

Bahr, K., and Duba, A. (2000). Is the asthenosphere electrically anisotropic? Earth Planet. Sci. Lett. 178, 87–95. doi:10.1016/s0012-821x(00)00070-4

CrossRef Full Text | Google Scholar

Bahr, K., and Simpson, F. (2002). Electrical anisotropy below slow and fast moving plates: paleo flow in the upper mantle. Science 295, 1270–1272. doi:10.1126/science.1066161

PubMed Abstract | CrossRef Full Text | Google Scholar

Becker, T. W., Chevrot, S., Schulte-Pelkum, V., and Blackman, D. K. (2006). Statistical properties of seismic anisotropy predicted by upper mantle geodynamic models. J. Geophys. Res. Solid Earth 111, B08309. doi:10.1029/2005jb004095

CrossRef Full Text | Google Scholar

Bhattacharya, B. B. (2005). Electrical anisotropy of asthenosphere in a region of window to mantle underneath Eastern Indian Craton. Phys. Earth Planet. Interiors 152 (1), 43–61. doi:10.1016/j.pepi.2005.06.001

CrossRef Full Text | Google Scholar

Booker, J. R. (2014). The magnetotelluric phase tensor: a critical review. Surv. Geophys. 35 (1), 7–40. doi:10.1007/s10712-013-9234-2

CrossRef Full Text | Google Scholar

Brasse, H., Kapinos, G., Li, Y., Mütschard, L., Soyer, W., and Eydam, D. (2009). Structural electrical anisotropy in the crust at the South-Central Chilean continental margin as inferred from geomagnetic transfer functions. Phys. Earth Planet. Interiors 173 (1), 7–16. doi:10.1016/j.pepi.2008.10.017

CrossRef Full Text | Google Scholar

Caldwell, T. G., Bibby, H. M., and Brown, C. (2004). The magnetotelluric phase tensor. Geophys. J. Int. 158 (2), 457–469. doi:10.1111/j.1365-246x.2004.02281.x

CrossRef Full Text | Google Scholar

Cao, H., Wang, K., Wang, T., and Hua, B. (2018). Three-dimensional magnetotelluric axial anisotropic forward modeling and inversion. J. Appl. Geophys. 153 (1), 75–89. doi:10.1016/j.jappgeo.2018.04.015

CrossRef Full Text | Google Scholar

Cao, X., Yin, C., Zhang, B., Huang, X., Ren, X., Qiu, C., et al. (2017). “A goal-oriented adaptive finite-element algorithm for 3D anisotropic MT modelling,” in 79th EAGE Conference and Exhibition, France.

Google Scholar

Chave, A. D., and Jones, A. (2018). The magnetotelluric method: theory and practice. Cambridge, United Kingdom: Cambridge Univ. Press, 604.

Google Scholar

Chen, X., and Weckmann, U. (2012). Constriant inversion of 2D magnetotelluric data with anisotropic conductivities. Darwin, Australia: American Geophysical Union. Extended Abstract 21 st Workshop.

Google Scholar

Comeau, M. J., Becken, M., Connolly, J. A. D., Grayver, A. V., and Kuvshinov, A. V. (2020). Compaction-driven fluid localization as an explanation for lower crustal electrical conductors in an intracontinental setting. Geophys. Res. Lett. 47. doi:10.1029/2020gl088455

CrossRef Full Text | Google Scholar

DeGroot-Hedlin, C., and Constable, S. (1990). Occam's inversion to generate smooth, two-dimensional models from magnetotelluric data. Geophysics 55 (12), 1613–1624. doi:10.1190/1.1442813

CrossRef Full Text | Google Scholar

Eisel, M., and Haak, V. (1999). Macro-anisotropy of the electrical conductivity of the crust: a magnetotelluric study of the German Continental Deep Drilling site (KTB). Geophys. J. R. Astronomical Soc. 136 (1), 109–122. doi:10.1046/j.1365-246x.1999.00707.x

CrossRef Full Text | Google Scholar

Frederiksen, A. W., Ferguson, I. J., Eaton, D., Miong, S. K., and Gowan, E. (2006). Mantle fabric at multiple scales across an archean–proterozoic boundary, grenville front, Canada. Phys. Earth Planet. Interiors 158 (2), 240–263. doi:10.1016/j.pepi.2006.03.025

CrossRef Full Text | Google Scholar

Hamilton, M. P., Jones, A. G., Evans, R. L., Fourie, C., Garcia, X., Mountford, A., et al. (2006). Electrical anisotropy of South African lithosphere compared with seismic anisotropy from shear-wave splitting analyses. Phys. Earth Planet. Interiors 158 (2), 226–239. doi:10.1016/j.pepi.2006.03.027

CrossRef Full Text | Google Scholar

Han, B., Li, Y., and Li, G. (2018). 3D forward modeling of magnetotelluric fields in general anisotropic media and its numerical implementation in Julia. Geophysics 83 (4), F29–F40. doi:10.1190/geo2017-0515.1

CrossRef Full Text | Google Scholar

Häuserer, M., and Junge, A. (2011). Electrical mantle anisotropy and crustal conductor: a 3-D conductivity model of the Rwenzori Region in western Uganda. Geophys. J. Int. 185 (3), 1235–1242. doi:10.1111/j.1365-246x.2011.05006.x

CrossRef Full Text | Google Scholar

Heinsonq, , and White, A. (2005). Electrical resistivity of the Northern Australian lithosphere: crustal or mantle heterogeneity? Earth Planet. Sci. Lett. 232 (1), 157–170. doi:10.1016/j.epsl.2004.12.029

CrossRef Full Text | Google Scholar

Heise, W., Caldwell, T. G., Bibby, H. M., and Brown, C. (2006). Anisotropy and phase splits in magnetotellurics. Phys. Earth Planet. Interiors 158 (2), 107–121. doi:10.1016/j.pepi.2006.03.021

CrossRef Full Text | Google Scholar

Heise, W., and Ellis, S. (2016). On the coupling of geodynamic and resistivity models: a progress report and the way forward. Surv. Geophys. 37 (1), 81–107. doi:10.1007/s10712-015-9334-2

CrossRef Full Text | Google Scholar

Heise, W., and Pous, J. (2003). Anomalous phases exceeding 90° in magnetotellurics: anisotropic model studies and a field example in magnetotellurics: anisotropic model studies and a field example. Geophys. J. Int. 155 (1), 308–318. doi:10.1046/j.1365-246x.2003.02050.x

CrossRef Full Text | Google Scholar

Johansen, S. E., Panzner, M., Mittet, R., Amundsen, H. E. F., Lim, A., Vik, E., et al. (2019). Deep electrical imaging of the ultraslow-spreading Mohns Ridge. Nature 567 (7748), 379–383. doi:10.1038/s41586-019-1010-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Jones, A. G. (2006). Electromagnetic interrogation of the anisotropic Earth: looking into the Earth with polarized spectacles. Phys. Earth Planet. Interiors 158 (s2–4), 281–291. doi:10.1016/j.pepi.2006.03.026

CrossRef Full Text | Google Scholar

Jones, A. G. (2012). Distortion decomposition of the magnetotelluric impedance tensors from a one-dimensional anisotropic Earth. Geophys. J. Int. 189, 268–284. doi:10.1111/j.1365-246x.2012.05362.x

CrossRef Full Text | Google Scholar

Key, K. (2016). MARE2DEM: a 2-D inversion code for controlled-source electromagnetic and magnetotelluric data. Geophys. J. Int. 207 (1), 571–588. doi:10.1093/gji/ggw290

CrossRef Full Text | Google Scholar

Key, K., Constable, S., Liu, L., and Pommier, A. (2013). Electrical image of passive mantle upwelling beneath the northern East Pacific Rise. Nature 495 (7442), 499–502. doi:10.1038/nature11932

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, G. P., and Manglik, A. (2012). Electrical anisotropy in the main central thrust zone of the Sikkim himalaya: inference from anomalous MT phase. J. Asian Earth Sci. 57 (57), 120–127. doi:10.1016/j.jseaes.2012.06.017

CrossRef Full Text | Google Scholar

Le Pape, F., Jones, A. G., Vozar, J., and Wenbo, W. (2012). Penetration of crustal melt beyond the kunlun fault into northern tibet. Nat. Geosci. 5 (5), 330–335. doi:10.1038/ngeo1449

CrossRef Full Text | Google Scholar

Liu, S. Y., Xu, Y., Yang, B., Guo, Z., Shi, Y., and Liu, Y. (2021). Deciphering fine electrical conductivity structuresin the crust from MT data using the equivalent conductivity formula. J. Geophys. Res. Solid Earth 126 (10). doi:10.1029/2021jb022519

CrossRef Full Text | Google Scholar

Liu, Y. (2016). Investigation of lithospheric electrical anisotropy in Western Junggar. Ph.D. thesis (Wuhan: China University of Geosciences). (in Chinese with English abstract).

Google Scholar

Liu, Y., Liu, J. P., Chen, C., Wang, G., Liao, Q., and Zhang, X. (2019). The application of audio magnetotelluric for 3D geological mapping in the Gobi Desert area. Geol. J. 55, 7335–7345. doi:10.1002/gj.3627

CrossRef Full Text | Google Scholar

Löwer, A., and Junge, A. (2017). Magnetotelluric transfer functions: phase tensor and tipper vector above a simple anisotropic three-dimensional conductivity anomaly and implications for 3D isotropic inversion. Pure Appl. Geophys. 174 (5), 2089–2101. doi:10.1007/s00024-016-1444-3

CrossRef Full Text | Google Scholar

Mareschal, M., Kellrttt, R., Kurtz, R. D., Ludden, J. N., Ji, S., and Bailey, R. C. (1995). Archaean cratonic roots, mantle shear zones and deep electrical anisotropy. Nature 375 (6527), 134–147. doi:10.1038/375134a0

CrossRef Full Text | Google Scholar

Martí, A. (2014). The role of electrical anisotropy in magnetotelluric responses: from modelling and dimensionality analysis to inversion and interpretation. Surv. Geophys. 35 (1), 179–218.

CrossRef Full Text | Google Scholar

Meyer, B., Tapponnier, P., Bourjot, L., Métivier, F., Gaudemer, Y., Peltzer, G., et al. (1998). Crustal thickening in Gansu-Qinghai, lithosphericmantle subduction, and oblique, strike-slip controlled growth of the Tibet plateau. Geophys. J. Int. 135 (1), 1–47. doi:10.1046/j.1365-246x.1998.00567.x

CrossRef Full Text | Google Scholar

Miensopusτ, M. P., and Jones, A. G. (2011). Artefacts of isotropic inversion applied to magnetotelluric data from an anisotropic Earth. Geophys. J. Int. 187 (2), 677–689. doi:10.1111/j.1365-246x.2011.05157.x

CrossRef Full Text | Google Scholar

Naif, S., Key, K., Constable, S., and Evans, R. L. (2013). Melt-rich channel observed at the lithosphere-asthenosphere boundary. Nature 495 (7441), 356–359. doi:10.1038/nature11939

PubMed Abstract | CrossRef Full Text | Google Scholar

Nover, G. (2005). Electrical properties of crustal and mantle rocks—a review of laboratory measurements and their explanation. Surv. Geophys. 26 (5), 593–651. doi:10.1007/s10712-005-1759-6

CrossRef Full Text | Google Scholar

Padilha, A. L., Vitorello, Í., Pádua, M. B., and Bologna, M. S. (2006). Lithospheric and sublithospheric anisotropy beneath central-southeastern Brazil constrained by long period magnetotelluric data. Phys. Earth Planet. Interiors 158 (2), 190–209. doi:10.1016/j.pepi.2006.05.006

CrossRef Full Text | Google Scholar

Pek, J. (2009). “Effects of electrical anisotropy upon magnetotelluric data: modelling and experiments,” in Modern methods of electromagnetic data measurement, processing and interpretation. Editor V. V. Spichak (Moscow: Librokom Publ), 110–135. (in Russian).

Google Scholar

Pek, J., and Santos, F. A. M. (2006). Magnetotelluric inversion for anisotropic conductivities in layered media. Phys. Earth Planet. Interiors 158 (2), 139–158. doi:10.1016/j.pepi.2006.03.023

CrossRef Full Text | Google Scholar

Pek, J., Santos, F. A. M., and Li, Y. G. (2011). “Non-linear conjugate gradient magnetotelluric inversion for 2-D anisotropic conductivities,” in Schmicker-Weidelt-Kolloquium, Nustadt and der Weinstral (GFZ), NY, United States, 187–206.

Google Scholar

Pek, J., and Verner, T. (1997). Finite-difference modelling of magnetotelluric fields in two-dimensional anisotropic media. Geophys. J. Int. 128 (3), 505–521. doi:10.1111/j.1365-246x.1997.tb05314.x

CrossRef Full Text | Google Scholar

Pommier, A. (2014). Interpretation of magnetotelluric results using laboratory measurements. Surv. Geophys. 35 (1), 41–84. doi:10.1007/s10712-013-9226-2

CrossRef Full Text | Google Scholar

Tommasi, A., Tikoff, B., and Vauchez, A. (1999). Upper mantle tectonics: three-dimensional deformation, olivine crystallographic fabrics and seismic properties. Earth Planet. Sci. Lett. 168, 173–186. doi:10.1016/s0012-821x(99)00046-1

CrossRef Full Text | Google Scholar

Wannamaker, P. E. (2005). Anisotropy versus heterogeneity in continental solid Earth electromagnetic studies: fundamental response characteristics and implications for physicochemical state. Surv. Geophys. 26 (6), 733–765. doi:10.1007/s10712-005-1832-1

CrossRef Full Text | Google Scholar

Wannamaker, P. E., Hasterok, D. P., Johnston, J. M., Stodt, J. A., Hall, D. B., Sodergren, T. L., et al. (2008). Lithospheric dismemberment and magmatic processes of the Great Basin-Colorado Plateau transition, Utah, implied from magnetotellurics. Geochem. Geophys. Geosystems 9 (5), 620–628. doi:10.1029/2007gc001886

CrossRef Full Text | Google Scholar

Weidelt, P. (1999). “3D conductivity models: implications of electrical anisotropy,” in Three-dimensional electromagnetics. Editors M. Oristaglio, and B. Spies (Tulsa, OK, United States: SEG), 119–137.

Google Scholar

Wiese, H. (1962). Geomagnetiseche Tiefentellurik Teil II: Die Streichrichtung der untergrundstrukturen des elektrischen Widerstandes, erschlossen aus geomagnetischen Variationen. Geofis. Pura E Appl. 52 (1), 83–103. doi:10.1007/bf01996002

CrossRef Full Text | Google Scholar

Xiao, T. J., Hiu, Y., Wang, Y., and Fu, L. Y. (2018). Three-dimensional magnetotelluric modeling in anisotropic media using edge-based finite element method. J. Appl. Geophys. 149, 1–9. doi:10.1016/j.jappgeo.2017.12.009

CrossRef Full Text | Google Scholar

Xiao, T. J., Huang, X. Y., and Wang, Y. (2019a). 3D MT modeling using the T–Ω method in general anisotropic media. J. Appl. Geophys. 160, 171–182. doi:10.1016/j.jappgeo.2018.11.012

CrossRef Full Text | Google Scholar

Xiao, T. J., Huang, X. Y., and Wang, Y. (2019b). Three-dimensional magnetotelluric modelling in anisotropic media using the A-phi method. Explor. Geophys. 50 (1), 31–41. doi:10.1080/08123985.2018.1564274

CrossRef Full Text | Google Scholar

Xie, J., Cai, H., Hu, X., Han, S., and Liu, M. (2022). Three-dimensional magnetotelluric inversion for triaxial anisotropic medium in data space. Minerals 12, 734. doi:10.3390/min12060734

CrossRef Full Text | Google Scholar

Yin, A., Dang, Y., Wang, L., Jiang, W. M., Zhou, S. P., Chen, X. H., et al. (2008a). Cenozoic tectonic evolution of Qaidam basin and its surrounding regions (Part 1): the southern Qilian Shan-Nan Shan thrust belt and northern Qaidam basin. Geol. Soc. Am. Bull. 120, 813–846. doi:10.1130/b26180.1

CrossRef Full Text | Google Scholar

Yin, A., Dang, Y., Zhang, M., Chen, X. H., and McRivette, M. W. (2008b). Cenozoic tectonic evolution of the Qaidam basin and its surrounding regions (Part 3): structural geology, sedimentation, and regional tectonic reconstruction. Geol. Soc. Am. Bull. 120 (7−8), 847–876. doi:10.1130/b26232.1

CrossRef Full Text | Google Scholar

Yin, C. C. (2003). Inherent nonuniqueness in magnetotelluric inversion for 1D anisotropic models. Geophysics 68 (1), 138–146. doi:10.1190/1.1543201

CrossRef Full Text | Google Scholar

Yin, Y., Unsworth, M., Liddell, M., Pana, D., and Craven, J. A. (2014). Electrical resistivity structure of the Great Slave Lake shear zone, northwest Canada: implications for tectonic history. Geophys. J. Int. 199 (1), 178–199. doi:10.1093/gji/ggu251

CrossRef Full Text | Google Scholar

Yu, G. (2021). Two-dimensional anisotropic magnetolluric inversion and applications in northern tibet. Ph.D. thesis (Beijing, China: Institute of Geology, China Earthquake Administration). (in Chinese with English Abstract).

Google Scholar

Zhao, W., Kumar, P., Mechie, J., Kind, R., Meissner, R., Wu, Z., et al. (2011). Tibetan plate overriding the Asian plate in central and northern Tibet. Nat. Gioscience 4, 870–873. doi:10.1038/ngeo1309

CrossRef Full Text | Google Scholar

Zhou, J. (2022). Three-dimensional anisotropic finitie element modeling and inversion of magnetotelluric data. Ph.D. thesis (Wuhan, China: China University of Geosciences). (in Chinese with English Abstract).

Google Scholar

Zhu, Y., Shao, G., Wang, X., and Zhang, W. (2023). A rapid 3D magnetotelluric forward approach for arbitrary anisotropic conductivities in the Fourier domain. Front. Earth Sci. 11. doi:10.3389/feart.2023.1183191

CrossRef Full Text | Google Scholar