- National Institute of Natural Hazards, Ministry of Emergency Management of China, Beijing, China
The 2021 Maduo earthquake (Mw = 7.4) is the first sudden and abrupt supershear rupture ever documented in the history of seismology, in which subshear rupture changed to supershear within a short time and short distance. However, the mechanism for this special phenomenon remains unclear although previous workers have done much work on it. For this reason, we use the finite element method to study the effects of fault geometry near the epicenter of the earthquake on the generation of rupture scenarios and use the grid-search approach to find the optimal model. Our simulation results show that the special fault geometry with a curved bend near the epicenter in the eastern segment of the fault induced supershear rupture transition at ∼3–5 s after the rupture nucleation, leading to the abrupt and sudden occurrence of the supershear rupture in the earthquake, whereas the westward-going rupture behaved as subshear in general. Additionally, the modeling results suggest that the co-seismic slips along the fault are mainly controlled by unevenly distributed dynamic friction coefficients. The modeling results also suggest that the other complex geometry of the fault, such as stepovers, cannot encourage the abrupt supershear rupture in the Maduo earthquake. Therefore, in this work, we may provide a new perspective for the study of the dynamic mechanism of supershear rupture.
1 Introduction
The Maduo earthquake (also called Madoi earthquake) (Mw = 7.4) was the largest earthquake to strike China since the 2008 Wenchuan event, and it occurred on 22 May 2021. The epicenter is located at 34.6ºE, 98.2ºN with a focal depth of 10 km in the inner region of the Bayan Har Block (BHB), northern Tibetan Plateau, according to the U.S. Geological Survey (USGS) (https://earthquake.usgs.gov/earthquakes/search/). Based on the post-seismic geological investigations (Li et al., 2021) and aftershock relocation (Wang et al., 2021) the seismogenic fault is assumed as the Kunlun Mountain Pass-Jiangcuo Fault (KMPJF) (Zhao et al., 2021) extending west–east for ∼160 km, approximately 70 km south of the East Kunlun Fault on the northern boundary of the BHB within the Tibetan Plateau (Pan et al., 2021; Yuan et al., 2022), as shown in Figure 1A. Thanks to the earthquake being located in the remote, high-altitude, sparsely populated, sterile, and windy region, this strong event caused no fatalities although some local buildings and roads were severely damaged (Pan et al., 2022).
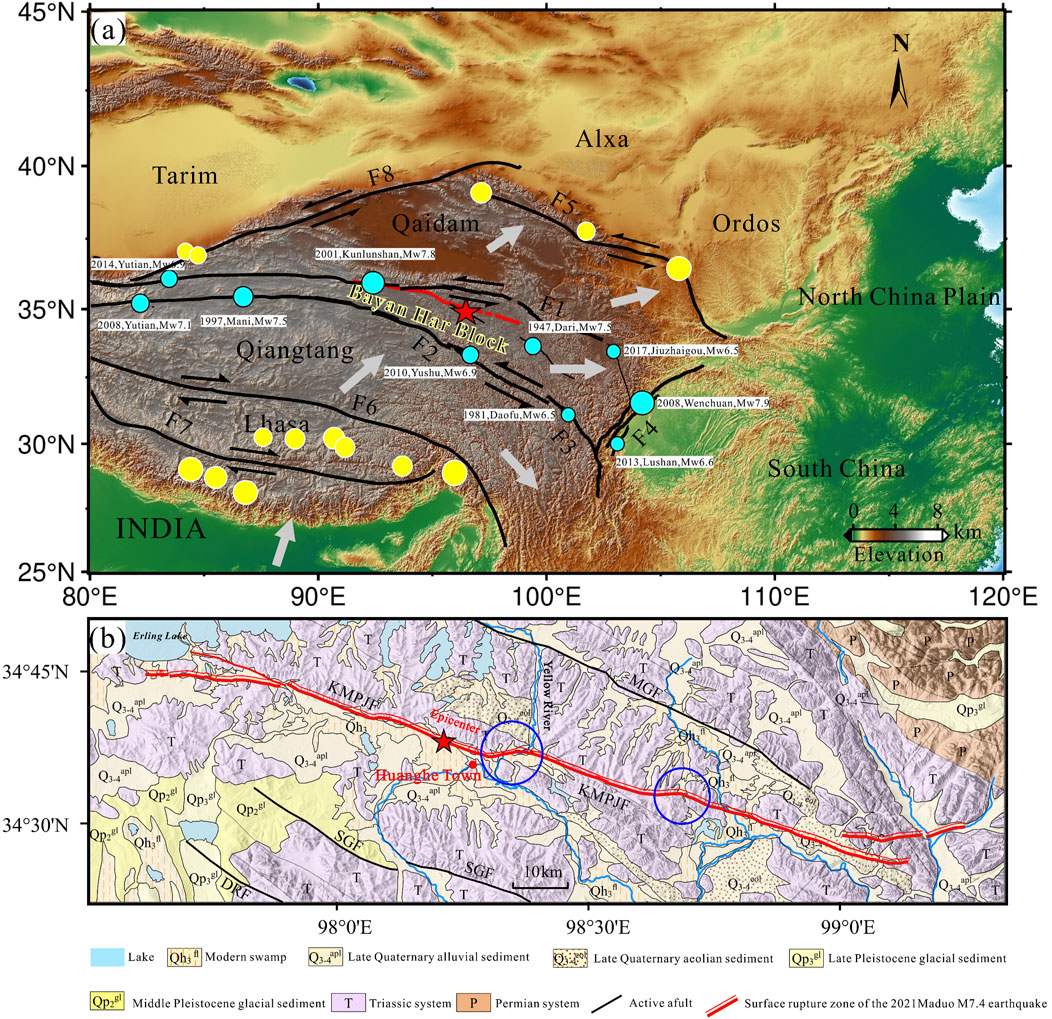
Figure 1. (a) Main blocks of the Tibetan Plateau and the surrounding terrain. Blue circles mark major earthquakes that have occurred on the boundary faults of the Bayan Har Block since 1980. Yellow circles stand for earthquakes (M ≥ 7.0) in the Tibetan Plateau since 1900, excluding the Bayan Har Block. The gray arrows denote the direction of block movement. The red line represents the seismogenic fault of the 2021 Maduo earthquake, and the red star marks the epicenter. F1: East Kunlun fault, F2: Ganzi-Yushu fault, F3: Xianshuihe fault, F4: Longmenshan fault, F5: Haiyuan fault, F6: Jiali fault, F7: Karakorum fault, and F8: Altyn Tagh fault. (b) Surface rupture and geological landscape of the 2021 Maduo earthquake (modified from G. Chen et al., 2022b). MGF: Maduo Fault, KMPJF: Kunlun Mountain Pass-Jiangcuo Fault, SGF: South Gander Fault, DRF: Dari Fault.
As we know, the BHB is bordered by the East Kunlun Fault, the Ganzi-Yushu Fault, the Xianshuihe Fault, and the Longmenshan Fault to the north, the south, and the east, respectively, where strong earthquakes frequently occur. Historically, many strong earthquakes with magnitudes (M ≥ 7.0) have occurred along the boundaries of the block. Particularly, in recent years, some large events stroked the boundary of the BHB, such as the 1997 Mani earthquake (Mw = 7.5), the 2001 Kunlunshan earthquake (Mw = 7.8), the 2008 Wenchuan earthquake (Mw = 7.9), and the 2008 Yutian earthquake (Mw = 7.1). In contrast, earthquakes are rare in the inner part of the block, which is mainly due to the relative rigid deformation in the intra-block (Xu et al., 2008). Until the 2021 Maduo Mw 7.4 earthquake, there had been no earthquakes (M ≥ 7.0) in the inner region of the BHB since the 1947 Dari earthquake (Mw = 7.5) (Liang et al., 2020).
After the earthquake, research workers have studied the propagation velocity of the rupture by using many inversion methods. For example, using a multi-array back projection inversion method, Zhang et al. (2022) found that the Maduo earthquake had characteristics of supershear rupture (4.0 km/s) along the southeast segment and subshear rupture (2.4 km/s) in the northwest segment. Yue et al. (2022) employed a joint inversion technique and concluded that the Maduo earthquake displayed characteristics of unilateral supershear rupture, with the southeast segment exhibiting supershear behavior (4.6 km/s) and the northwest segment showing subshear behavior (2.0 km/s). Lyu et al. (2022) utilized high-frequency GNSS data and 3D InSAR deformation analysis, and indicated that the Maduo earthquake exhibited overall subshear characteristics (2.8 km/s), with the northwest segment showing subshear rupture (2.2 km/s) and the southeast segment showing supershear rupture (3.8 km/s).
Nevertheless, research workers have reached the general consensus that the 2021 Maduo earthquake has characteristics of bilateral rupture with supershear speed in the southeast segment of the fault; however, some research workers (e.g., Chen et al., 2022a) did not think so. Furthermore, according to the latest research on rupture propagation speed (Cheng et al., 2023; Zhang et al., 2022), the fast supershear rupture of the Maduo quake occurred suddenly and immediately after the slow rupture initiation (approximately 3–4 s) (Cheng et al., 2023), without a long transitional length in which subshear rupture transforms into supershear rupture (e.g., Andrews, 1976; Burridge, 1973; Dunham, 2007; Rosakis et al., 2023). This supershear rupture occurred suddenly, sharing a similar rupture transition with the first mainshock of the 2023 Turkey double earthquake event, where the rupture transitioned abruptly from subshear to supershear after a very short transition distance in the early stages of the earthquake (Rosakis et al., 2023). This is markedly different from the rupture jumps exhibited by the second mainshock of the 2023 Turkey double earthquake event (Toker et al., 2023). Cheng et al. (2023) declared that “the Maduo event is the first case of abrupt supershear rupture” in seismic documents. Traditionally, rupture speed exceeds the shear wave velocity after traveling a long distance and then transforms into supershear. This typically occurs in long straight and simple fault segments (Bouchon et al., 2001; Bouchon et al., 2010; Das, 2015; Robinson et al., 2010).
What makes the Maduo earthquake so particular from other previous supershear rupture earthquakes such as the 1999 Izmit earthquake (Mw = 7.6) and the 2001 Kunlun event (Mw = 7.8) (Bouchon and Vallée, 2003; Bouchon et al., 2000)? What causes the rupture velocity to suddenly exceed the S-wave velocity into a supershear rupture? These questions have not been satisfactorily answered so far. For this goal, in this work, we first investigate the causative faults for the Maduo earthquake and then establish numerical models to simulate spontaneous rupture along the fault. Finally, we investigate the simulated rupture propagation scenarios and explore the critical factors that influence abrupt supershear rupture. Undoubtedly, in this study, we provide new insights into the dynamics of earthquakes, which is of great significance for further research and alleviation of seismic hazards.
2 Geodynamic background
The continuous collision between India and Eurasia has uplifted the Tibetan Plateau and formed the subsequent eastward extrusion. Meanwhile, with the activation of several faults, the northern part of the Karakorum-Jiali fault zone (KJFZ) was divided into three main blocks, including the BHB (Replumaz and Tapponnier, 2003). In northern Tibet, the East Kunlun Fault (EKF), Ganzi-Yushu-Xianshuihe fault (GYXF), the Altyn Tagh fault (ATF), and the Longmenshan thrust fault (LMF) are the boundary faults of the BHB (Figure 1A). GPS observational results (Wang and Shen, 2020) showed that the eastward motion of the BHB is one of the fastest moving blocks within the Tibetan Plateau (Deng et al., 2010), inducing the highest and strongest seismicity along the boundary of the BHB. In the recent 25 years, eight strong earthquakes (Mw ≥ 6.5) occurred along the boundary of the BHB, as shown in Figure 1A. However, the Maduo earthquake (Mw = 7.4) occurred in the inner part of the BHB rather than along its boundary. The main dynamic mechanism is as follows.
Figure 1B shows that the causative fault of the Maduo event, KMPJF, is a left-lateral strike-slip fault with a low slip rate of less than ∼1 mm/yr in the interseismic period (e.g., Li et al., 2023; Ren et al., 2022). Meanwhile, to the north of KMPJF lies a high active EKF with the slip rate as high as ∼10–12 mm/yr (Der Woerd et al., 2002; Wang and Shen, 2020), and to the south of KMPJF, the GYXF is located, with the slip rate of 9.7–12.7 mm/yr (Wang et al., 2009; Wen et al., 2003). Accordingly, KMPJF is tectonically loaded and sheared by the two fast-moving sinistral strike-slip faults (EKF and GYXF), accumulating a large amount of elastic energy. Once the shear stress on the surface of KMPJF exceeds the frictional strength, the fault will produce a spontaneous rupture, releasing elastic energy, and a strong earthquake such as the 2021 Maduo event will occur.
In this study, we will simulate the rupture scenarios based on the previous observational results and present the main factor which influences the first-order feature of rupture behavior.
3 Model setup and calculation method
The finite element method (FEM) is widely used in simulating the spontaneous rupture process of faults as it can handle dynamic rupture mechanics problems related to geometric and material nonlinearities, as well as frictional contact. The geometric nonlinearity of faults is a significant factor influencing rupture propagation. Numerical simulations using the FEM have shown that fault bends promote supershear rupture (Zhu and Yuan, 2020). Similarly, the FEM has been applied to investigate the effects of material heterogeneity on both sides of the fault on the rupture process (Zhang and Zhu, 2019). The FEM not only excels in dealing with nonlinear problems but also performs well in addressing fluid–solid coupling issues. For instance, Pampillón et al. (2018) used the FEM to simulate the spontaneous rupture process of faults induced by water injection in poro-elastic media. Despite its significant advantages in simulating spontaneous fault ruptures, the FEM has certain limitations. First, the accuracy and results of the FEM highly depend on the quality of mesh generation. Inappropriate mesh arrangement can introduce numerical errors or even cause instability, especially in areas with high stress gradients during fault rupture. Second, dynamic fault rupture simulations often require very fine meshes and small time step, leading to high computational costs and resource consumption, which limits the practical simulation of large-scale or long-duration processes. Fortunately, with the development of the high-performance parallel computing technology and adaptive mesh refinement techniques, the computational efficiency and accuracy of the FEM can be significantly improved. In order to investigate why supershear rupture occurred just after the rupture initiation without long transitional distance in the 2021 Maduo earthquake, we simplify the actual complex seismogenic fault and then establish the finite element model.
The predominant fault motion in the Maduo event is a sense of strike-slip (Li et al., 2021). The basic rupture trace has a characteristic of two distinct bends (e.g., Chen et al., 2022a), as depicted in Figure 1B. Based on the significant fault bend structures of the causative fault of the 2021 Maduo quake from previous results (Chen et al., 2022b; Liu et al., 2022), we established a fault bend model (named Model 1 for convenience) to investigate the influence of the fault structure on the rupture scenarios of the earthquake. As our research focuses mainly on the mechanism of sudden supershear transition on the eastern section of the fault, we only consider the key portions of the seismogenic fault, ignoring the detailed branching segments. The fault bend near the nucleation zone on the eastern fault is taken into account, but the fault is presumed as a straight line onto the west of the nucleation zone. The specific fault geometry is chosen as illustrated in Figure 2.
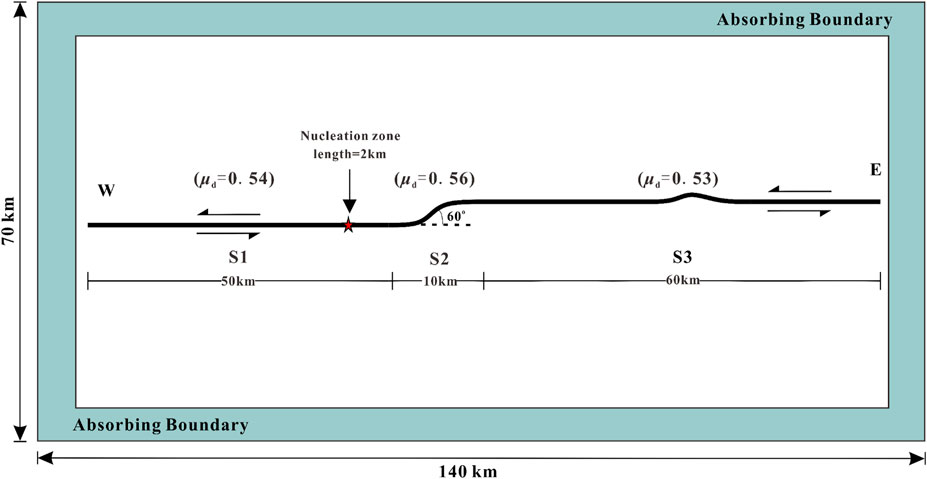
Figure 2. Model setup and boundary conditions. The model has a rectangular shape measuring 140 km × 70 km. Bold black curves in the figure represent seismogenic fault segments.
As the causative fault is almost vertical strike-slip, we abstract the actual three-dimensional problem into a two-dimensional plane strain model and use smooth curves replacing the multi-segment surface of the fault in order to speed up the calculation. Based on the fault traces obtained from geodetic measurements (Figure 1B), we simplified the fault into a curved segment. We retained the prominent fault bend in the central part of the fault and the curvature in the eastern segment of the fault. In modeling, we choose the surface where the source is located as the model plane (Figure 2). The whole rupture length is assigned to be 120 km, consisting of a straight segment to the west of the epicenter and a curved segment to the east of the epicenter. The seismogenic fault in the model is subdivided into fault segments of S1–S3, as illustrated in Figure 2. As can be observed from the figure, the geometry of the FEM model is 140 km × 70 km, including the causative fault of the 2021 Maduo quake. The model employs a triangulated mesh to eliminate the hourglass mode, as indicated by previous studies (Zhu, 2018; Zhu and Yuan, 2020). To distinguish the cohesive zone and enhance the computational efficiency, a densely meshed region is established around the fault zone, gradually transitioning to a sparser mesh outward. The element length is set to be 60 m along the seismogenic fault and 300 m in the peripheral areas. Notably, all meshes around the model are equipped with absorbing boundaries (Zhu, 2018; Zhu and Yuan, 2020).
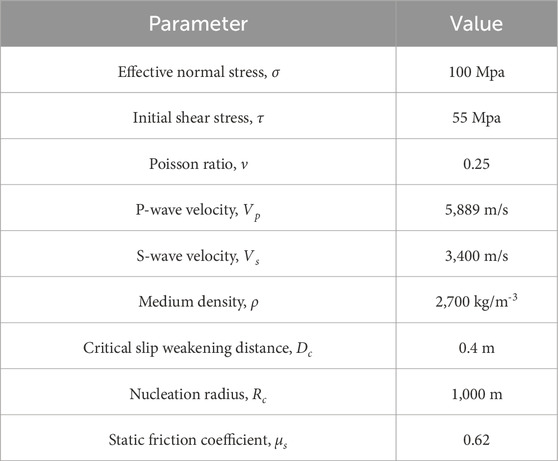
Initial stresses are crucial factors in simulations of dynamic rupture propagation (Duan, 2010; Yamashita, 1976; Zhu, 2018; Zhu and Yuan, 2020). However, direct measurement of the absolute initial stress is challenging, despite the availability of some shallow in situ stress data from borehole surveying (Heidbach et al., 2016). Considering the relatively small domain of the study region and minimal variations in principal strain rates (Zhu and Shi, 2011), we suppose that the variation of the initial stresses in the study area is not significant, which means that it can be neglected. Consequently, we consider that the initial stresses in the study area are uniformly distributed during modeling. The values of these initial stresses can be determined from former numerical simulations (Finzi and Langer, 2012; Yuan and Zhu, 2017). Based on the velocity structure of seismic waves in and around the KMPJF, the S-wave velocity in the area is determined to be 3.4 km/s. It should be noted that we suppose the entire model medium to be linear homogeneous elastic. Also, all model parameters are listed in Table 1. In addition, we selected the widely used linear slip-weakening friction law in dynamic simulations (e.g., Harris and Day, 1993; Zhu, 2018). In this study, simulations are conducted with the finite element software ABAQUS/Explicit (Yuan and Zhu, 2017; Zhu, 2018).
Based on the work by K. Chen et al. (2022), the residual shear strength of the fault (the strength transitioning from static to dynamic friction) is equivalent to the initial shear stress. With current detection techniques, the friction coefficient along the fault during the actual fault rupture process cannot be determined. Therefore, we vary the dynamic frictional coefficient from 0.40 to 0.60 with step of 0.01 along different segments (from S1 to S3) of the fault, with the static friction coefficient set at 0.62. Therefore, this grid-search approach will produce several models for simulations; among them , the one whose simulated fault slips fit the observed data best is regarded as the optimal model.
4 Simulation results
Through a mass of FEM calculations, we finally found the optimal model in which the simulated slips along the fault fitted the observed data from the study by Jin and Fialko (2021) best with the root-mean-square-error of 0.63 m. In addition, the optimal model presented that the dynamic frictional coefficients along fault segments S1, S2, and S3 are 0.54, 0.56, and 0.53, respectively. In the following, based on the optimal model, we will analyze the rupture behaviors in detail and uncover what factor led to the abrupt supershear rupture transition within a short distance in the 2021 Maduo earthquake.
4.1 Rupture processes across the fault bend
Figure 3 shows a series of snapshots of the contour map of particle motions in the optimal model at different times. From the figure, it can be observed that the ruptures, expanding in both the east and west directions along the fault before reaching the fault bend, are subshear, with the propagation speed of 2.6 km/s. At the time of ∼3 s, the eastward-going rupture reached the first fault bend, and there is a significant change in the rupture behavior compared with the corresponding westward-going rupture, as shown in Figure 3B. Within the time of 4–6 s, a clear Mach wave can be observed (Figures 3C, D), signifying the appearance of supershear rupture. The rupture propagation velocity along the eastern section of the fault is derived as 5.26 km/s, which is greater than the shear wave velocity of the local medium with the value of 3.4 km/s. However, along the entire western segment of the fault rupture propagation, no Mach waves can be observed, indicating subshear rupture behavior with the propagation velocity of 3.0 km/s, which is less than the shear wave speed. As time progresses, rupture continued to propagate in both directions. When the time approached 9 s, the eastward-going rupture reached the second fault bend, which did not block rupture expansion, and continued to propagate eastward at a supershear speed with evident Mach waves, as shown in Figures 3E–H. By the time of ∼16 s, ruptures on both sides reached the ends of the fault and were finally arrested. Throughout the entire rupture process, subshear rupture occurs on the western side of the nucleation zone, with a calculated average rupture speed of 3.1 km/s. In contrast, on the eastern side, supershear rupture occurs with a rupture velocity of 5.3 km/s, and it occurred ∼3 s after nucleation, which is in good agreement with the observational ones (Cheng et al., 2023).
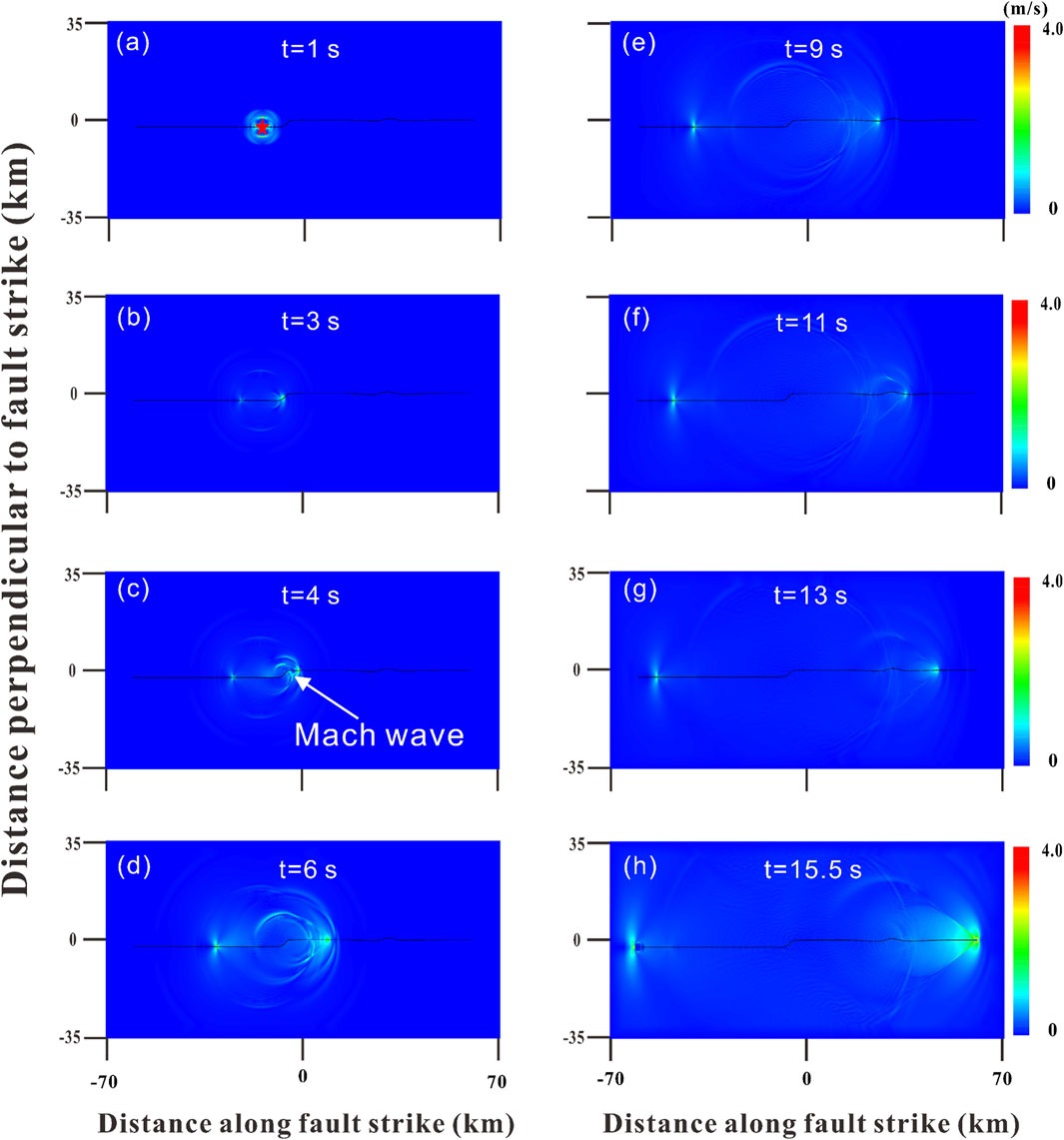
Figure 3. Snapshots of contour map of particle velocities at different moments during the fault rupture process in the optimum model. (a,b) subshear rupture process .(c–h) supershear rupture process. The black lines in the figure stand for fault, and the red star marks nucleation position.
Both observational results and our numerical simulations indicate that the 2021 Maduo earthquake involved supershear rupture. Interestingly, the transition process of this supershear rupture shares similarities with the first mainshock of the highly notable 2023 Turkey doublet earthquake. In both mainshocks of the 2023 Turkey doublet earthquake, supershear rupture occurred, but the characteristics of the supershear rupture differed between the two events. The first mainshock occurred on a branch fault, and the rupture transitioned from subshear to supershear after propagating a very short distance (Rosakis et al., 2023), which is consistent with our simulation results of the supershear transition process in the 2021 Maduo earthquake. Subsequently, the rupture propagated from the branch fault to the main fault, spreading bilaterally along the main fault. The rupture on the main fault exhibited intermittent supershear behavior, with alternating subshear and supershear phases (Wang et al., 2023; Delouis et al., 2023). The second mainshock also involved supershear rupture. Toker et al. (2023) indicated that the rupture velocity of the second mainshock suddenly transitioned from supershear to subshear during propagation, exhibiting a rupture jump phenomenon. A significant difference in the geometric configuration of the seismogenic faults between the 2021 Maduo earthquake and the first mainshock of the 2023 Turkey double earthquakes is that the former exhibits a distinct fault bend structure near the epicenter. Our simulation results demonstrate that the rupture transitioned from subshear to supershear as it propagated through the fault bend.
Furthermore, we displayed the calculated slips along the fault with the corresponding observed results from InSAR data from studies of Chen et al. (2021) and Jin and Fialko (2021), as shown in Figures 4A, B. It is observed that the simulated slips generally match the measurement data well, confirming that the simulated results represent the first-order rupture propagation feature in the Maduo earthquake.
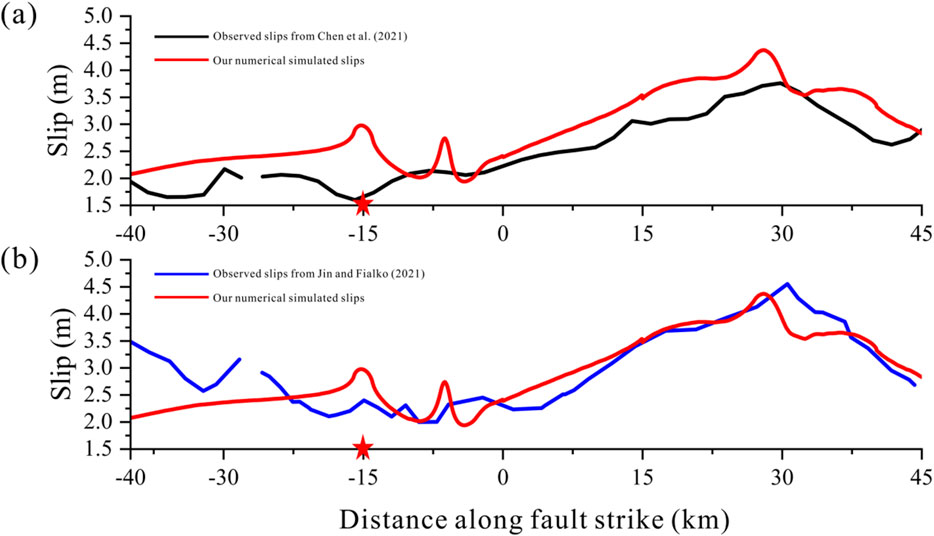
Figure 4. (a, b)Comparison of numerical simulated slips with the observed InSAR data. The red stars stand for the epicenter location, the red lines represent the simulated slips, and the black and blue curves denote the observed data. (a)InSAR data from the study by Chen et al., 2021; (b)InSAR data from the study by Jin and Fialko, 2021.
In sum, the optimal model was found by means of the grid-search approach. It provided the basic characteristics of the rupture scenario of the Maduo event and best matched the abrupt occurrence of supershear rupture with the observed results.
4.2 The influence of fault stepover
Fault stepovers have a significant influence on supershear rupture transition (Harris and Day, 1993; Knuepfer, 1989; Segall and Pollard, 1980; Yuan and Zhu, 2017). According to geological field surveys, it is found that there is a 2–3 km fault stepover between the faults on either side of the epicenter in the Maduo quake (Li et al., 2021; Yuan et al., 2022). Therefore, there is a possibility that the generation of supershear rupture is associated with the fault stepovers along the fault. To investigate this case, we established model 2, in which fault stepover is included, as shown in Figure 5. The model parameters and initial conditions remained the same as those in model 1.
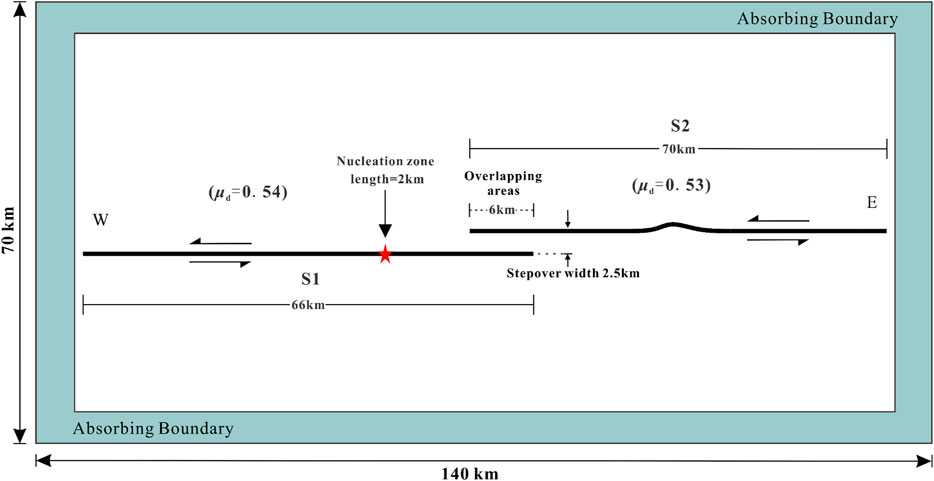
Figure 5. Model geometry and boundary conditions in model 2, in which fault stepover is included. Bold black curves in the figure represent seismogenic fault segments. Red star marks nucleation position.
By means of FEM simulations, we obtained the rupture propagation scenario in model 2. The snapshots of the contour map of particle velocities at different moments are displayed in Figure 6. We observed that propagation of rupture along the entire fault can be subdivided into two stages. Within the time period of ∼16 s after nucleation, it is seen that the rupture propagated only along the fault S1, in which the fault stepover prevented the rupture continuous propagation along S2, as shown in Figures 6A–6. However, at the time of 19 s, a new rupture was nucleated again and clearly seen along the fault S2, as shown in Figure 6E. Then, the rupture goes eastward with time, and clear Mach waves were observed at the moments of ∼22 s and afterward, as shown in Figures 6G–I, suggesting the appearance of supershear rupture. The rupture propagation speed is calculated to be 5.5 km/s, which is much greater than the shear wave velocity (3.4 km/s). In contrast, no Mach waves were seen along the fault S1 with the propagation speed of 2.9 km/s. This simulated result is consistent with that of previous studies (e.g., Harris and Day, 1993; Knuepfer, 1989; Segall and Pollard, 1980; Yuan and Zhu, 2017).
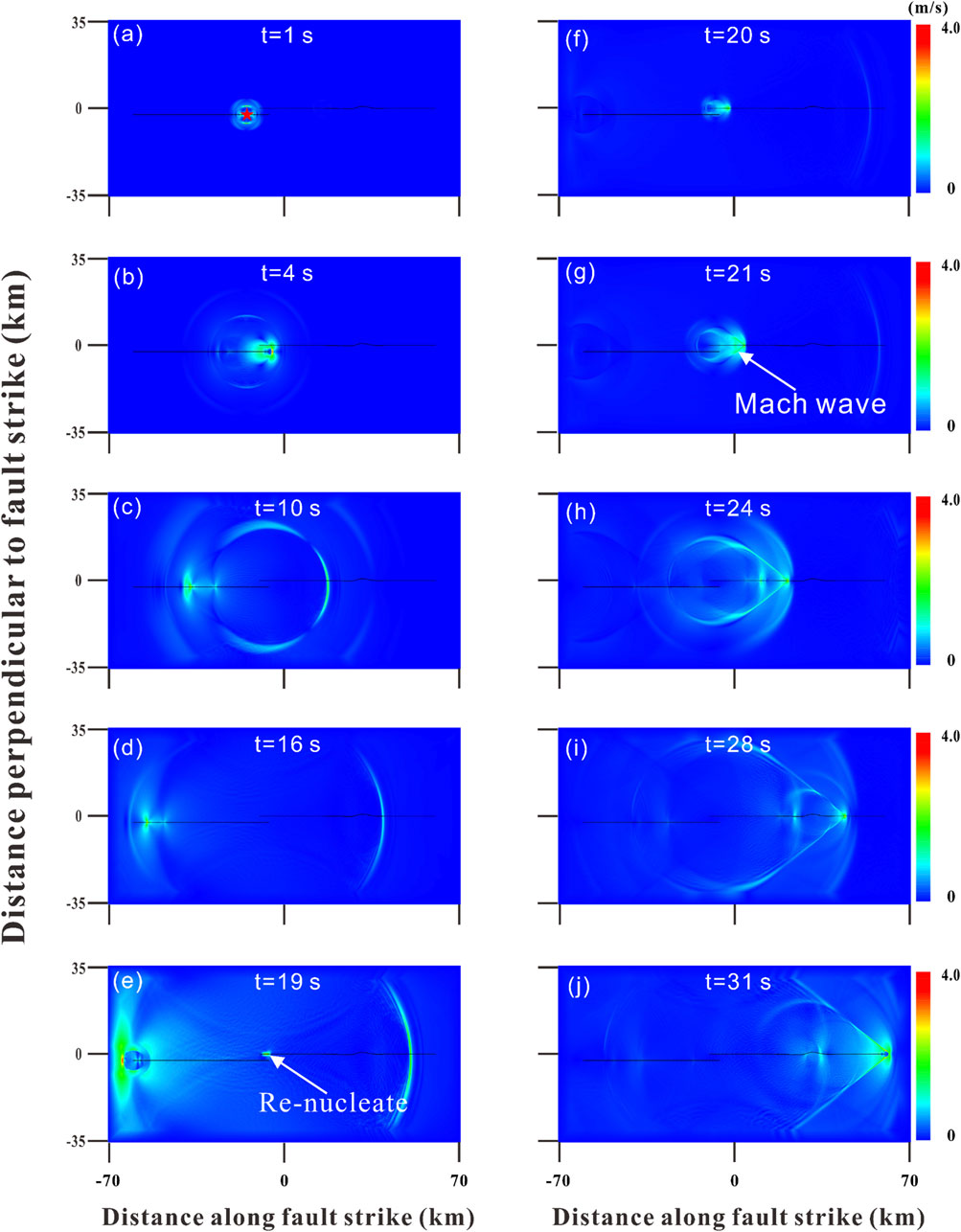
Figure 6. Snapshots of contour map of particle velocities at different moments during the fault rupture process in the model 2. (a–f)subshear rupture process. (g–j)supershear rupture process. The black lines in the figure stand for fault, and the red star marks nucleation position.
From the above rupture scenario, we can see that the supershear rupture occurred at the time of 22 s after the earthquake nucleation, which does not match the seismic inversion results in which the supershear rupture took place within 3–4 s after the nucleation (Cheng et al., 2023).
In brief, from the above simulated results of models 1 and 2, we presume that the fault bend near the epicenter may be responsible for the generation of the abrupt and sudden supershear rupture in the 2021 Maduo earthquake.
4.3 Mechanism for abrupt supershear rupture
From the above numerical simulated results, it is evident that both fault structures in model 1 and model 2 can generate supershear rupture on the eastern segment of the fault. However, the key difference between them lies in the moment of supershear rupture occurrence. In model 2, there exists a time delay of ∼15 s when the rupture travels across the fault stepover, and the supershear rupture occurs at 20 s after the nucleation. However, in model 1, the occurrence of the supershear rupture is at 3.5 s after nucleation, which matches well with the seismic inversion results (Cheng et al., 2023; Zhang et al., 2022). Furthermore, the modeled fault slips of model 1 are in good agreement with the inversion results. Therefore, we conclude that the fault bend structure may be responsible for the generation of abrupt supershear rupture in the earthquake.
To know why the fault bend near the epicenter in model 1 can encourage supershear transition from subshear to supershear rupture, the nondimensional seismic S ratio is calculated along the fault, which is an important indicator for determining whether a rupture along a fault can transition into a supershear one. S = (τy-τ0)/(τ0-τd), where τy and τ0 represents the peak strength and initial loading stress, respectively, τy = μsσ, τ0 = τ; τd represents the residual strength, and τd = μdσ. In a uniformly isotropic fault, supershear rupture occurs when the S value is below a threshold of 1.77 in 2D (Andrews, 1985; Zhu, 2018) when the fault width is large enough (Xu et al., 2015; Zhu, 2018). The stress changes on the fault surface have a significant impact on the rupture propagation process. Figure 7A illustrates the stress variations on the fault surface during the rupture propagation. From the figure, it can be concluded that as the rupture passes through the fault bend (−10 km to 0), the stress state on the fault surface undergoes noticeable changes. Both the normal stress and shear stress exhibit an initial increase followed by a decrease. Such changes are bound to cause variations in the seismic S ratio. Figure 7B shows the seismic S ratio along fault strike. It is obvious that the seismic S ratio has a significant decrease along the fault bend on the eastern side of the nucleation zone with values from ∼7.5 to ∼1.0, which falls below the threshold (1.77) required for supershear rupture to occur, leading to a sudden supershear rupture during the Maduo event.
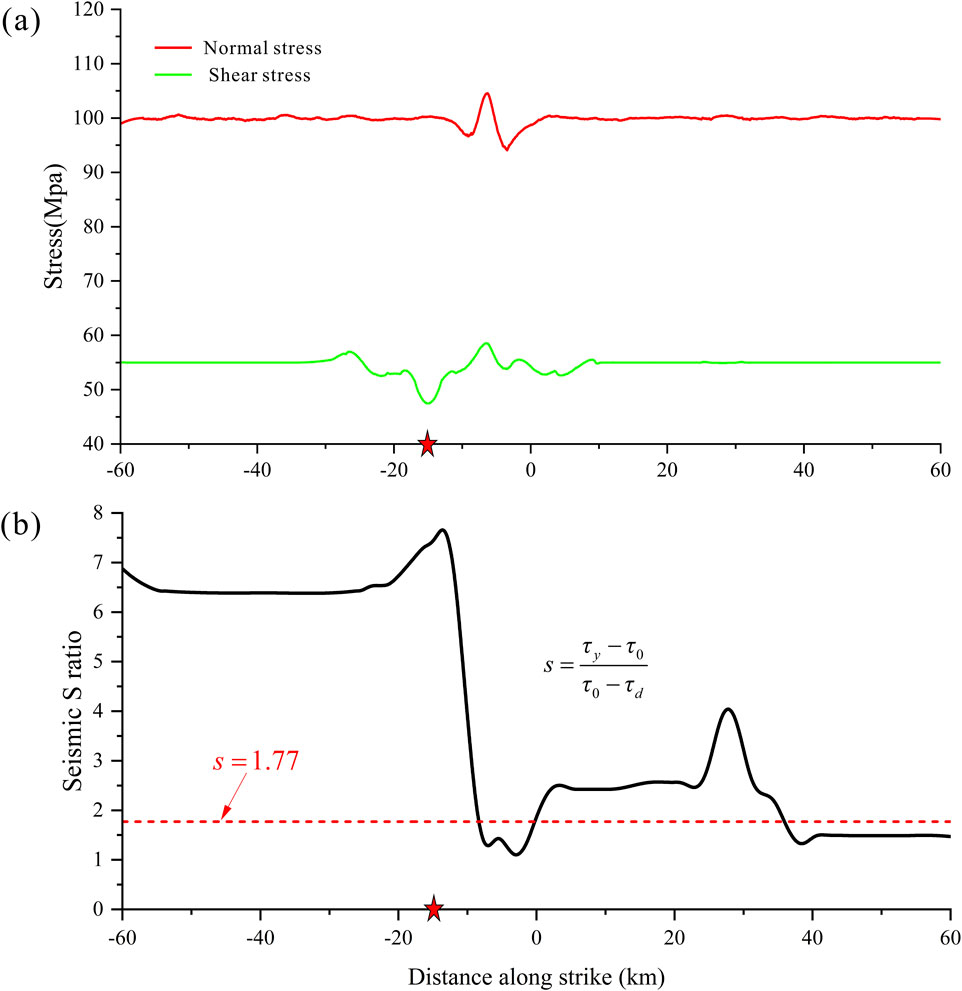
Figure 7. (a) Stress changes in the fault during the rupture process in model 1. (b) Seismic S ratio scattered along the fault strike. The red line stands for the threshold value of 1.77. The red star indicates the location of the epicenter.
In short, we presume that a fault bend along the seismogenic fault of the Maduo earthquake is responsible for the abrupt supershear rupture transition.
5 Discussions and conclusions
In order to furtherly confirm the supershear rupture caused by the fault bend in the Maduo earthquake, we will compare and analyze the different rupture scenarios under the following two cases.
At first, we ignored the complex bend structures in the middle of the fault and assumed that the entire fault is a straight line. Therefore, we established a new model named model 3, in which all other model parameters are the same as those for model 1, except for the fault geometry. Based on FEM computations, the average rupture velocity along the fault on the western segment of the nucleation zone is 3.0 km/s and that on the east side is 3.1 km/s, both of which are lower than the S-wave speed, indicating a subshear rupture along the entire fault. Figure 8 shows snapshots of the contour map of particle velocities at different moments during the fault rupture propagation in model 3, where no Mach waves can be seen, corresponding to the subshear rupture expansion in model 3. Hence, a simple geometry of fault structure with a straight line is excluded in producing supershear rupture in the Maduo event.
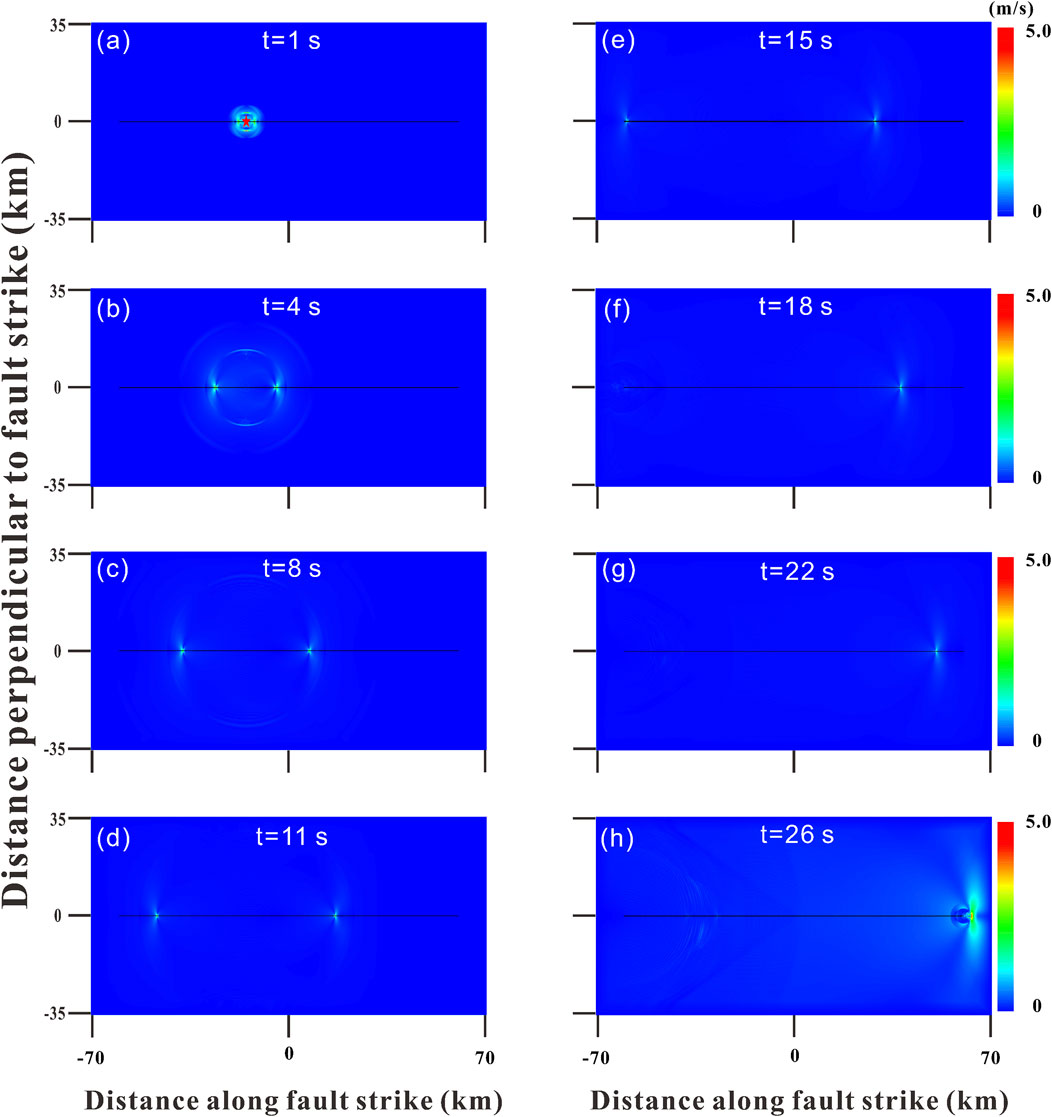
Figure 8. (a–h) Snapshots of contour maps of particle velocities at different moments during the fault rupture process in model 3. The black line in the figure stands for fault, and the red star marks nucleation position.
Next, based on model 1, we constructed model 4, in which we changed the static friction coefficient of the fault in model 1 from 0.62 to 0.60 while keeping all the other model parameters unchanged. Using the new model, we recalculated the spontaneous fault rupture propagation scenario since the nucleation of the rupture. Figure 9 displays the snapshots of contour images of particle vibration velocities at different moments in model 4. It can be seen that the fault rupture process did not vary significantly under the case of the reduction of static friction coefficient, and the supershear rupture still occurred when rupture traveled through the fault bend near the epicenter. It is noted that the supershear rupture occurred ∼2 s after the nucleation, and this supershear rupture transition is even earlier than that in model 1. It is evident that the variation in the static friction coefficients along the fault did not change the supershear rupture style but only changed the occurrence time of subshear rupture.
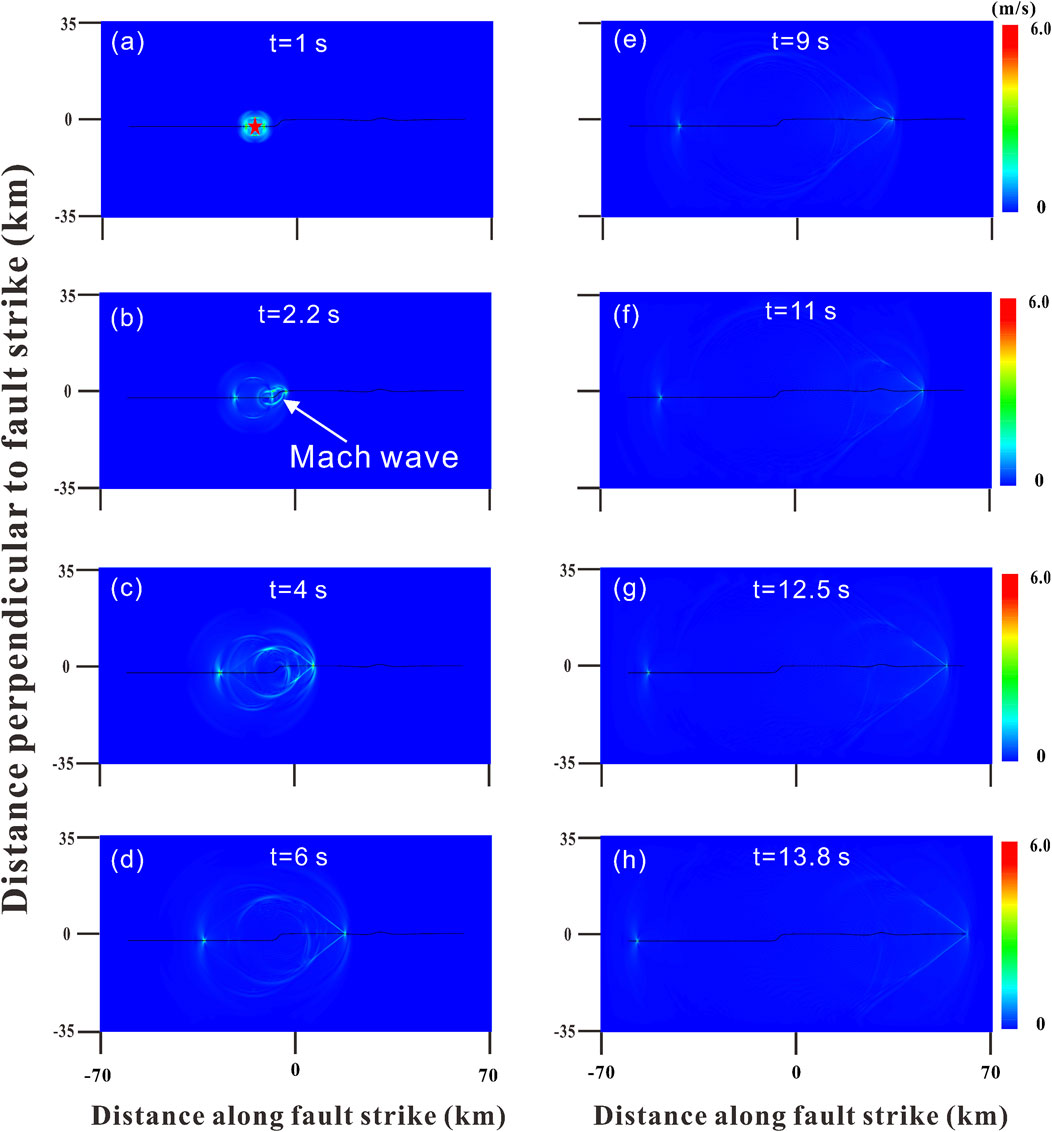
Figure 9. Snapshots of contour map of particle velocities at different moments during the fault rupture process in the model 4. (a,b) subshear rupture process. (c–h) supershear rupture process. The black lines in the figure stand for fault, and the red star marks nucleation position.
In addition, the Earth’s free surface often induces supershear rupture transition (Cui and Zhu, 2022; Kaneko and Lapusta, 2010; Olsen et al., 1997). In general, it needs a long enough distance along fault strike for a subshear rupture to change into a supershear one (Xu et al., 2015). However, the transition distance for supershear rupture is very short in the 2021 Maduo earthquake (Cheng et al., 2023). Then, it is unlikely that the Earth’s free surface encouraged the occurrence of supershear rupture in the Maduo event.
Therefore, it can be concluded that the optimal model, fitting the observed fault slips best, matches the time and position of the occurrence of supershear rupture well with the results observed in this work. Consequently, it is presumed that the fault bend near the epicenter is responsible for the occurrence of the sudden and abrupt supershear rupture in the 2021 Maduo earthquake.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
Author contributions
KW: Conceptualization, Investigation, Methodology, Validation, and Writing – original draft. SZ: Funding acquisition, Investigation, Methodology, Visualization, and Writing – original draft. JH: Funding acquisition, Investigation, Methodology, Validation, Writing - review and editing
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This research was supported by the National Natural Science Foundation of China (42374074 and 41874060), the Centralized management project from the Ministry of Finance of P.R.C, and the Construction projects for spatial information platform.
Acknowledgments
The authors thank H. Chen and Z. Jin for sharing their InSAR results.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Andrews, D. (1976). Rupture velocity of plane strain shear cracks. J. Geophys. Res. 81 (32), 5679–5687. doi:10.1029/jb081i032p05679
Andrews, D. (1985). Dynamic plane-strain shear rupture with a slip-weakening friction law calculated by a boundary integral method. Bull. Seismol. Soc. Am. 75 (1), 1–21. doi:10.1785/bssa0750010001
Bouchon, M., Bouin, M. P., Karabulut, H., Toksöz, M. N., Dietrich, M., and Rosakis, A. J. (2001). How fast is rupture during an earthquake? New insights from the 1999 Turkey earthquakes. Geophys. Res. Lett. 28 (14), 2723–2726. doi:10.1029/2001gl013112
Bouchon, M., Karabulut, H., Bouin, M. P., Schmittbuhl, J., Vallée, M., Archuleta, R., et al. (2010). Faulting characteristics of supershear earthquakes. Tectonophysics 493 (3-4), 244–253. doi:10.1016/j.tecto.2010.06.011
Bouchon, M., Toksöz, N., Karabulut, H., Bouin, M. P., Dietrich, M., Aktar, M., et al. (2000). Seismic imaging of the 1999 Izmit (Turkey) rupture inferred from the near-fault recordings. Geophys. Res. Lett. 27 (18), 3013–3016. doi:10.1029/2000gl011761
Bouchon, M., and Vallée, M. (2003). Observation of long supershear rupture during the magnitude 8.1 Kunlunshan earthquake. Science 301 (5634), 824–826. doi:10.1126/science.1086832
Burridge, R. (1973). Admissible speeds for plane-strain self-similar shear cracks with friction but lacking cohesion. Geophys. J. Int. 35 (4), 439–455. doi:10.1111/j.1365-246x.1973.tb00608.x
Chen, G., Li, Z., Xu, X., Sun, H., Ha, G., Guo, P., et al. (2022a). Co-seismic surface deformation and late Quaternary accumulated displacement along the seismogenic fault of the 2021 Madoi M7. 4 earthquake and their implications for regional tectonics. Chin. J. Geophys. 65 (8), 2984–3005. doi:10.6038/cjg2022P0873
Chen, H., Qu, C., Zhao, D., Ma, C., and Shan, X. (2021). Rupture kinematics and coseismic slip model of the 2021 Mw 7.3 Maduo (China) earthquake: implications for the seismic hazard of the Kunlun fault. Remote Sens. 13 (16), 3327. doi:10.3390/rs13163327
Chen, K., Avouac, J. P., Geng, J., Liang, C., Zhang, Z., Li, Z., et al. (2022b). The 2021 Mw 7.4 madoi earthquake: an archetype bilateral slip-pulse rupture arrested at a splay fault. Geophys. Res. Lett. 49 (2), e2021GL095243. doi:10.1029/2021gl095243
Cheng, C., Wang, D., Yao, Q., Fang, L., Xu, S., Huang, Z., et al. (2023). The 2021 Mw 7.3 madoi, China earthquake: transient supershear ruptures on a presumed immature strike-slip fault. J. Geophys. Res. Solid Earth 128 (2), e2022JB024641. doi:10.1029/2022jb024641
Cui, Z., and Zhu, S. (2022). Effect of real-world frictional strengthening layer near the Earth's free surface on rupture characteristics with different friction laws: implication for scarcity of supershear earthquakes. Tectonophysics 837, 229447. doi:10.1016/j.tecto.2022.229447
Das, S. (2015). Supershear earthquake ruptures–Theory, methods, laboratory experiments and fault superhighways: an update. Perspect. Eur. Earthq. Eng. Seismol. 2, 1–20. doi:10.1007/978-3-319-16964-4_1
Deng, Q., Xiang, G., Gui-Hua, C., and Hu, Y. (2010). Recent tectonic activity of Bayankala fault block and the Kunlun Wenchuan earthquake series of the Tibetan Plateau. Earth Sci. Front. 17 (5), 163. doi:10.1017/S0004972710001772
Der Woerd, J. V., Tapponnier, P. J., Ryerson, F., Meriaux, A.-S., Meyer, B., Gaudemer, Y., et al. (2002). Uniform postglacial slip-rate along the central 600 km of the Kunlun Fault (Tibet), from 26Al, 10Be, and 14C dating of riser offsets, and climatic origin of the regional morphology. Geophys. J. Int. 148 (3), 356–388. doi:10.1046/j.1365-246x.2002.01556.x
Duan, B. (2010). Role of initial stress rotations in rupture dynamics and ground motion: a case study with implications for the Wenchuan earthquake. J. Geophys. Res. Solid Earth 115 (B5). doi:10.1029/2009jb006750
Dunham, E. M. (2007). Conditions governing the occurrence of supershear ruptures under slip-weakening friction. J. Geophys. Res. Solid Earth 112 (B7). doi:10.1029/2006jb004717
Finzi, Y., and Langer, S. (2012). Damage in step-overs may enable large cascading earthquakes. Geophys. Res. Lett. 39 (16). doi:10.1029/2012gl052436
Harris, R. A., and Day, S. M. (1993). Dynamics of fault interaction: parallel strike-slip faults. J. Geophys. Res. Solid Earth 98 (B3), 4461–4472. doi:10.1029/92jb02272
Heidbach, O., Rajabi, M., Reiter, K., Ziegler, M., and Team, W. (2016). World stress map database release 2016. GFZ Data Serv. 10, 1. doi:10.5880/WSM.2016.001
Jin, Z., and Fialko, Y. (2021). Coseismic and early postseismic deformation due to the 2021 M7. 4 Maduo (China) earthquake. Geophys. Res. Lett. 48 (21), e2021GL095213. doi:10.1029/2021gl095213
Kaneko, Y., and Lapusta, N. (2010). Supershear transition due to a free surface in 3-D simulations of spontaneous dynamic rupture on vertical strike-slip faults. Tectonophysics 493 (3-4), 272–284. doi:10.1016/j.tecto.2010.06.015
Knuepfer, P. L. (1989). Implications of the characteristics of end-points of historical surface fault ruptures for the nature of fault segmentation. Fault Segmentation Controls Rupture Initiation Termin. U.S. Geological Survey Open File Report 89, 193–228.
Li, C., Li, T., Shan, X., and Zhang, G. (2023). Extremely large off-fault deformation during the 2021 M w 7.4 maduo, Tibetan plateau, earthquake. Seismol. Soc. Am. 94 (1), 39–51. doi:10.1785/0220220139
Li, Z., Ding, K., Zhang, P., Wen, Y., Zhao, L., and Chen, J. (2021). Coseismic deformation and slip distribution of 2021 Mw 7.4 Madoi earthquake from GNSS observation. Geomatics Inf. Sci. Wuhan Univ. 46 (10), 1489–1497. doi:10.13203/j.whugis20210301
Liang, M. J., Yang, Y., Du, F., Gong, Y., Sun, W., Zhao, M., et al. (2020). Late quaternary activity of the central segment of the Dari fault and restudy of the surface rupture zone of the 1947 M7 3/4 Dari earthquake, Qinghai province. Seismol. Geol. 42 (3), 703–714. doi:10.3969/j.issn.0253-4967.2020.03.011
Liu, J., Hu, J., Li, Z., Ma, Z., Wu, L., Jiang, W., et al. (2022). Complete three-dimensional coseismic displacements due to the 2021 Maduo earthquake in Qinghai Province, China from Sentinel-1 and ALOS-2 SAR images. Sci. China Earth Sci. 65 (4), 687–697. doi:10.1007/s11430-021-9868-9
Lyu, M., Chen, K., Xue, C., Zang, N., Zhang, W., and Wei, G. (2022). Overall subshear but locally supershear rupture of the 2021 Mw 7.4 Maduo earthquake from high-rate GNSS waveforms and three-dimensional InSAR deformation. Tectonophysics 839, 229542. doi:10.1016/j.tecto.2022.229542
Olsen, K., Madariaga, R., and Archuleta, R. J. (1997). Three-dimensional dynamic simulation of the 1992 Landers earthquake. Science 278 (5339), 834–838. doi:10.1126/science.278.5339.834
Pampillón, P., Santillán, D., Mosquera, J. C., and Cueto-Felgueroso, L. (2018). Dynamic and quasi-dynamic modeling of injection-induced earthquakes in poroelastic Media. J. Geophys. Res. Solid Earth 123, 5730–5759. doi:10.1029/2018jb015533
Pan, J., Bai, M., Li, C., Liu, F., Li, H., Liu, D., et al. (2021). Coseismic surface rupture and seismogenic structure of the 2021-05-22 Maduo (Qinghai) Ms 7.4 earthquake. Acta Geol. Sin. 95 (6), 1655–1670. doi:10.19762/j.cnki.dizhixuebao.2021166
Pan, J., Li, H., Chevalier, M.-L., Tapponnier, P., Bai, M., Li, C., et al. (2022). Co-seismic rupture of the 2021, M 7.4 Maduo earthquake (northern Tibet): short-cutting of the Kunlun fault big bend. Earth Planet. Sci. Lett. 594, 117703. doi:10.1016/j.epsl.2022.117703
Ren, J., Xu, X., Zhang, G., Wang, Q., Zhang, Z., Gai, H., et al. (2022). Coseismic surface ruptures, slip distribution, and 3D seismogenic fault for the 2021 Mw 7.3 Maduo earthquake, central Tibetan Plateau, and its tectonic implications. Tectonophysics 827, 229275. doi:10.1016/j.tecto.2022.229275
Replumaz, A., and Tapponnier, P. (2003). Reconstruction of the deformed collision zone between India and Asia by backward motion of lithospheric blocks. J. Geophys. Res. Solid Earth 108 (B6). doi:10.1029/2001jb000661
Robinson, D., Das, S., and Searle, M. (2010). Earthquake fault superhighways. Tectonophysics 493 (3-4), 236–243. doi:10.1016/j.tecto.2010.01.010
Rosakis, A. J., Abdelmeguid, M., and Elbanna, A. (2023). Evidence of early supershear transition in the Feb 6th 2023 Mw 7.8 Kahramanmaraş Turkey earthquake from near-field records. doi:10.31223/X5W95G
Segall, P., and Pollard, D. (1980). Mechanics of discontinuous faults. J. Geophys. Res. Solid Earth 85 (B8), 4337–4350. doi:10.1029/jb085ib08p04337
Wang, H., Wright, T., and Biggs, J. (2009). Interseismic slip rate of the northwestern Xianshuihe fault from InSAR data. Geophys. Res. Lett. 36 (3). doi:10.1029/2008gl036560
Wang, M., and Shen, Z. K. (2020). Present-day crustal deformation of continental China derived from GPS and its tectonic implications. J. Geophys. Res. Solid Earth 125 (2), e2019JB018774. doi:10.1029/2019jb018774
Wang, W., Fang, L., Wu, J., Tu, H., Chen, L., Lai, G., et al. (2021). Aftershock sequence relocation of the 2021 Ms 7.4 Maduo earthquake, Qinghai, China. Sci. China Earth Sci. 64, 1371–1380. doi:10.1007/s11430-021-9803-3
Wen, X., Xu, X., Zheng, R., Xie, Y., and Wan, C. (2003). Average slip-rate and recent large earthquake ruptures along the Garzê-Yushu fault. Sci. China Ser. D Earth Sci. 46, 276–288. doi:10.1360/03dz0022
Xu, J., Zhang, H., and Chen, X. (2015). Rupture phase diagrams for a planar fault in 3-D full-space and half-space. Geophys. J. Int. 202 (3), 2194–2206. doi:10.1093/gji/ggv284
Xu, X., Wen, X., Chen, G., and Yu, G. (2008). Discovery of the Longriba fault zone in eastern Bayan Har block, China and its tectonic implication. Sci. China Ser. D Earth Sci. 51 (9), 1209–1223. doi:10.1007/s11430-008-0097-1
Yamashita, T. (1976). On the dynamical process of fault motion in the presence of friction and inhomogeneous initial stress. I. Rupture propagation. J. Phys. Earth 24 (4), 417–444. doi:10.4294/jpe1952.24.417
Yuan, J., and Zhu, S. (2017). Numerical simulation of seismic supershear rupture process facilitated by a fault stepover. Chin. J. Geophys. 60 (1), 212–224. doi:10.6038/cjg20170118
Yuan, Z., Li, T., Su, P., Sun, H., Ha, G., Guo, P., et al. (2022). Large surface-rupture gaps and low surface fault slip of the 2021 Mw 7.4 Maduo earthquake along a low-activity strike-slip fault, Tibetan Plateau. Geophys. Res. Lett. 49 (6), e2021GL096874. doi:10.1029/2021gl096874
Yue, H., Shen, Z. K., Zhao, Z., Wang, T., Cao, B., Li, Z., et al. (2022). Rupture process of the 2021 M7. 4 Maduo earthquake and implication for deformation mode of the Songpan-Ganzi terrane in Tibetan Plateau. Proc. Natl. Acad. Sci. 119 (23), e2116445119. doi:10.1073/pnas.2116445119
Zhang, Q., and Zhu, S. (2019). FEM simulations of spontaneous rupture propagations along the fault with dissimilar anisotropic materials[J]. Chin. J. Geophys., 62(12): 4706–4717. doi:10.6038/cjg2019N0020
Zhang, X., Feng, W., Du, H., Samsonov, S., and Yi, L. (2022). Supershear rupture during the 2021 MW 7.4 Maduo, China, earthquake. Geophys. Res. Lett. 49 (6), e2022GL097984. doi:10.1029/2022gl097984
Zhao, D., Qu, C., Chen, H., Shan, X., Song, X., and Gong, W. (2021). Tectonic and geometric control on fault kinematics of the 2021 Mw7. 3 Maduo (China) earthquake inferred from interseismic, coseismic, and postseismic InSAR observations. Geophys. Res. Lett. 48 (18), e2021GL095417. doi:10.1029/2021gl095417
Zhu, S. (2018). Why did the most severe seismic hazard occur in the Beichuan area in the 2008 Wenchuan earthquake, China? Insight from finite element modelling. Phys. Earth Planet. Interiors 281, 79–91. doi:10.1016/j.pepi.2018.05.005
Zhu, S., and Shi, Y. (2011). Estimation of GPS strain rate and its error analysis in the Chinese continent. J. Asian Earth Sci. 40 (1), 351–362. doi:10.1016/j.jseaes.2010.06.007
Keywords: fault bend, abrupt and sudden supershear rupture, finite element method, 2021 Maduo earthquake, grid-search approach
Citation: Wu K, Zhu S and Huang J (2025) Mechanism of abrupt supershear rupture for the 2021 Maduo earthquake (Mw=7.4) in the northern Tibetan Plateau. Front. Earth Sci. 13:1533639. doi: 10.3389/feart.2025.1533639
Received: 24 November 2024; Accepted: 28 March 2025;
Published: 29 April 2025.
Edited by:
Aydın Büyüksaraç, Çanakkale Onsekiz Mart University, TürkiyeReviewed by:
Stephane Dominguez, UMR5243 Géosciences Montpellier, FranceMustafa Toker, Yüzüncü Yıl University, Türkiye
Copyright © 2025 Wu, Zhu and Huang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jianping Huang, amlhbnBpbmdodWFuZ0BuaW5obS5hYy5jbg==
 Kai Wu
Kai Wu Shoubiao Zhu
Shoubiao Zhu Jianping Huang
Jianping Huang