Triaxial compression test of shear strength parameters of rock-fill materials considering scale effect

Soil mass stability refers to the ability of soil to resist deformation and failure under external loads, and it is a fundamental consideration in geotechnical engineering, particularly for large-scale infrastructure such as earth-rock dams and slopes. This stability is primarily determined by the soil’s shear strength, which defines the internal resistance of the soil to sliding along potential failure planes. A major challenge in accurately predicting the shear strength of coarse-grained soils is the scale effect, where laboratory test results on small-scale specimens may not fully represent the behavior of large-scale soil masses encountered in real-world applications. To address this issue, this study investigates the influence of two key factors—the maximum particle diameter (d_max) and the gradation structure, quantified by the gradation area (S)—on the shear strength of coarse-grained soils. We designed 21 distinct soil specimens with varying d_max and S values to simulate natural soil gradations, and conducted large-scale triaxial compression tests to explore the relationship between these parameters and shear strength indicators, namely, cohesion (c) and internal friction angle (φ). The results show that increasing d_max enhances both cohesion and internal friction due to stronger interlocking between particles, while a higher gradation area (S), reflecting a broader particle size distribution, reduces these parameters as uneven stress distribution weakens the soil structure. Based on these observations, we propose a shear strength prediction model that incorporates the scale effect, which has been validated using independent datasets from a range of coarse-grained soils.

1 Introduction

In large-scale engineering projects, such as high earth-rock dams, measuring the shear strength of coarse-grained soils poses significant challenges due to limitations in existing test instruments, which cannot replicate the real-life gradation of soil particles. Scaling down the gradation for laboratory tests results in discrepancies that hinder the accurate determination of shear strength parameters, which are crucial for designing safe and reliable geotechnical structures.

Contemporary progress in soil mechanics and geotechnical engineering has significantly enhanced our knowledge of coarse-grained soil’s properties and behaviors. The wide application of coarse-grained soil in engineering, especially in high earth-rock dams, has made its shear strength a key research focus. In practical applications, particularly in high earth-rock dams, the maximum particle diameter of coarse-grained soil can range from 800 to 1,000 mm (Guo, 2003). However, the size limitations of existing test instruments render it impossible to directly measure the shear strength parameters of coarse-grained soil through tests, and the original gradation must be scaled down (Ministry of Housing and Urban-Rural Development of the People’s Republic of China, State Administration for Market Regulation, 2019). According to the existing research, however, the test results after scaling cannot accurately reflect the strength with the original gradation regardless of the scaling method, i.e., the scale effect. Consequently, investigating the impact of the scale effect on the shear strength of coarse-grained soil is essential.

International scholars have been rigorously investigating the implications of the scale effect on the strength of coarse-grained materials. In experiments using specimens with consistent dry density, a trend emerges showing a decline in shear strength as the maximum particle diameter increases. For example, Marsal (1967), Marschi et al. (1972), Varadarajan et al. (2003), Kong et al. (2019), and Meng and Shi (1983) proved through experiments that the shear strength decreased with the increase of the particle d_max.

Despite using specimens with equivalent relative density, there remains a lack of agreement on how the scale effect impacts shear strength (Weng et al., 2009). Opinions among researchers vary; Li et al. (2001) and Li et al. (2008), for instance, argue that the internal friction angle φ rises as the maximum particle diameter d_max increases. On the other hand, Lee (1992) and Hu et al. (2011) argue that the maximum particle diameter d_max has negligible impact on the peak internal friction angle φ. Meanwhile, Wei et al. (2008) discovered that φ increases with reduced fine particle content, and Li and Xing (2006) found that φ remains stable at low levels of fine particle content but decreases rapidly with an increase in this content.

In summary, to summarize, the complexities involved in scaling methods, gradation properties, and specimen preparation density make it challenging to quantitatively define the relationship between the mechanical properties of scaled specimens and their original gradation counterparts. This results in a gap in the quantitative understanding of shear strength variation in coarse-grained soil post-scaling (Marsal, 1967; Marschi et al., 1972; Li et al., 2008). Consequently, there is a significant need for quantitative experimental research to investigate the scale effect’s impact on the shear strength of coarse-grained soil.

Zhu et al. (2018) collated the common soil gradation curve patterns observed in global engineering endeavors and introduced an equation to precisely characterize coarse-grained soil gradation, as shown in Equation 1.

$P=\frac{1}{\left(1-b\right){\left(d_{\max }/d\right)}^m+b}\times 100\%(1)$

In this context, P represents the proportion of soil particles smaller than a given diameter d (%), d signifies the diameter of the soil particles (mm), d_max is the maximum diameter within the soil mass (mm), while b and m are parameters in the gradation equation, influencing the gradation curve’s shape and slope.

As noted by Wu et al. (Wu et al., 2019; Shi et al., 2024; Shi et al., 2023; Wu et al., 2020a; Wu et al., 2020b), the key variances between scaled specimens and their original-gradation counterparts are evident in aspects such as maximum particle diameter and particle gradation structure, independent of the specified scaling methods (China Planning Press). Consequently, the scale effect is seen as a consequence of the interplay between changes in the specimen’s maximum particle diameter and its gradation structure.

This study undertook a detailed exploration of the scale effect on coarse-grained soil’s shear strength by designing 21 different groups of specimens, each varying in maximum particle diameter or gradation structure, yet maintaining consistent initial relative compaction. Triaxial shear tests were then executed on these specimens. The study applied a single-variable method to specifically assess the impacts of maximum particle diameter and gradation structure on the coarse-grained soil’s shear strength, aiming to quantitatively determine the laws influencing the scale effect on this property. Additionally, the study extrapolated the shear strength of the original-gradation coarse-grained soil in actual field conditions from the results of these indoor tests. It is anticipated that the outcomes of this research will significantly reduce the scale effect on coarse-grained soil’s shear strength, leading to improvements in the safety and reliability of geotechnical engineering designs.

The outcomes of this research are expected to offer valuable insights into reducing the scale effect on the shear strength of coarse-grained soil, which in turn could enhance the safety and reliability of geotechnical engineering designs, particularly in large-scale projects such as tunnels, embankments, and dams.

2 Coarse-grained soil triaxial test

2.1 Test equipment

The experimental trials were carried out on a DJSZ-150 large-scale triaxial testing machine, suitable for both dynamic and static analyses of coarse-grained soil, showcased in Figure 1, located at the Kunming Institute’s Geotechnical Engineering Experiment Center.The testing machine can facilitate dynamic and static loading on soil specimens with a size of Ф300 mm × 600 mm and can achieve different stress path conditions. It includes axial loading systems, a confining pressure loading system, and a loading servo control system. The testing machine can provide a maximum confining pressure of 3.0 MPa and static loads of 0–1,500 kN, and the test data are automatically acquired by computer. According to the Standard for Geotechnical Testing Method (GB/T50123-2019) (China Planning Press), the particle size of the tested soil material should be less than 1/5 to 1/6 of the instrument size, that is, the testing machine can facilitate triaxial consolidation drained shear tests on specimens with a maximum particle diameter of 60 mm. Through preliminary tests, the confining pressure of this test was determined as 400, 800, and 1,200 kPa, and the loading rate was set to 1 mm/min.

Figure 1

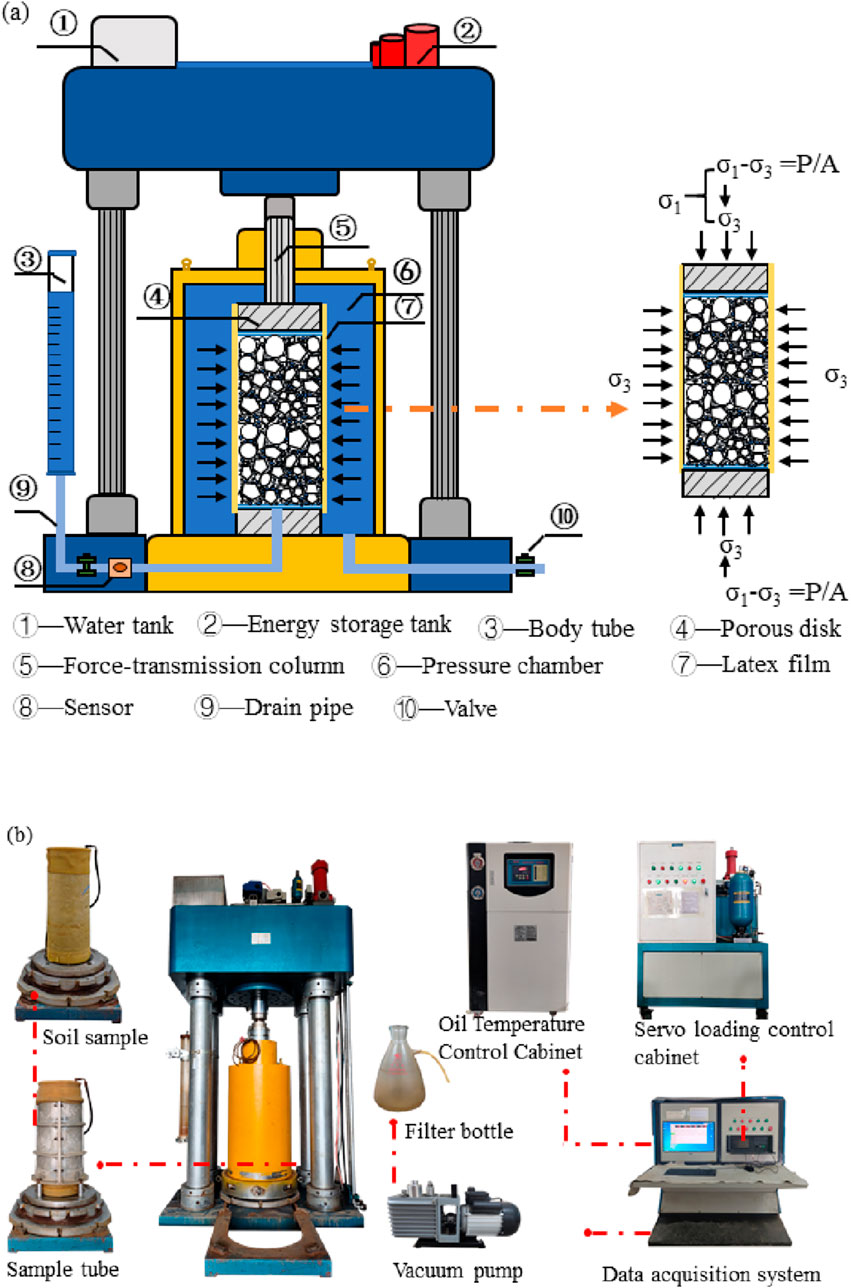
Figure 1. DJSZ-150 large coarse grained soil dynamic and static triaxial testing machine structure principle diagram (A) and physical diagram (B).

2.2 Test materials

The test material was selected from the rockfill material for the dam of the Lincang Daqiaopo Reservoir in Yunnan Province, granular gravel obtained after blasting and processing. This sample originates from slightly weathered granite, exhibiting an average saturated uniaxial compressive strength of 50 MPa, along with a softening coefficient of 0.79, and a specific gravity of 2.70. Particle screening tests were conducted on the obtained original-gradation specimens using a sieve shaker, and the particle fractions with particle diameters of 60∼40 mm, 40∼30 mm, 30∼20 mm, 20∼10 mm, 10∼ 5 mm, 5∼2 mm, and <2 mm were retained as soil material for specimen preparation (Figure 2).

Figure 2

Figure 2. Different particle group test soil material.

2.3 Test protocol

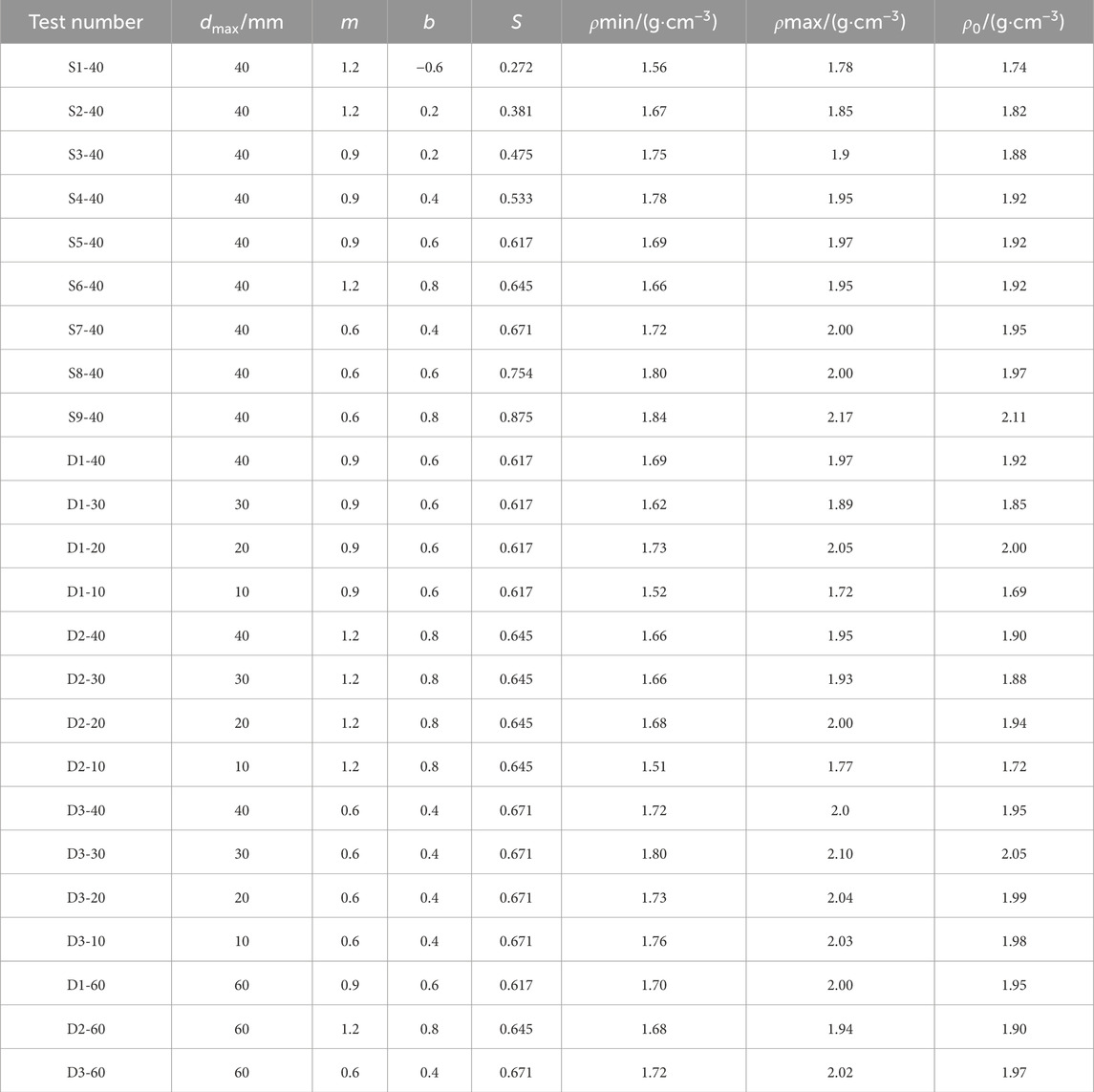
Previous studies indicates that both the maximum particle diameter and gradation area significantly influence the strength of coarse-grained soil. In the earth-rock dam project, the commonly used value intervals of the grading parameters m and b of coarse-grained soil are: 0 < m < 2 and −2 < b < 1. Therefore, this paper designs a total of 21 groups of grading samples by setting a series of parameters m and b. The maximum and minimum dry densities of these soil specimens were established through compaction testing. A relative compaction rate of 0.85 was maintained throughout the preparation of specimens for the triaxial compression tests. Gradation parameters and densities used in preparing the 21 groups of specimens are systematically listed in Table 1. Groups S1-40 through S9-40, encompassing nine specimen sets, share the same maximum particle diameter but differ in gradation areas. Their gradation curves are illustrated in Figure 3A. The specimen groups D1-40 to D1-10, D2-40 to D2-10, and D3-40 to D3-10, each comprising four specimens, are categorized by consistent gradation areas but varying maximum particle diameters, adding up to 12 specimens in these three groups. Their gradation curves can be viewed in Figure 3B. D1-60, D2-60, and D3-60 are three groups of specimens for validation experiments, and their corresponding gradation curves are shown in Figure 3C.

Table 1

Table 1. Summary of test soil sample gradation parameters and sample preparation density.

Figure 3

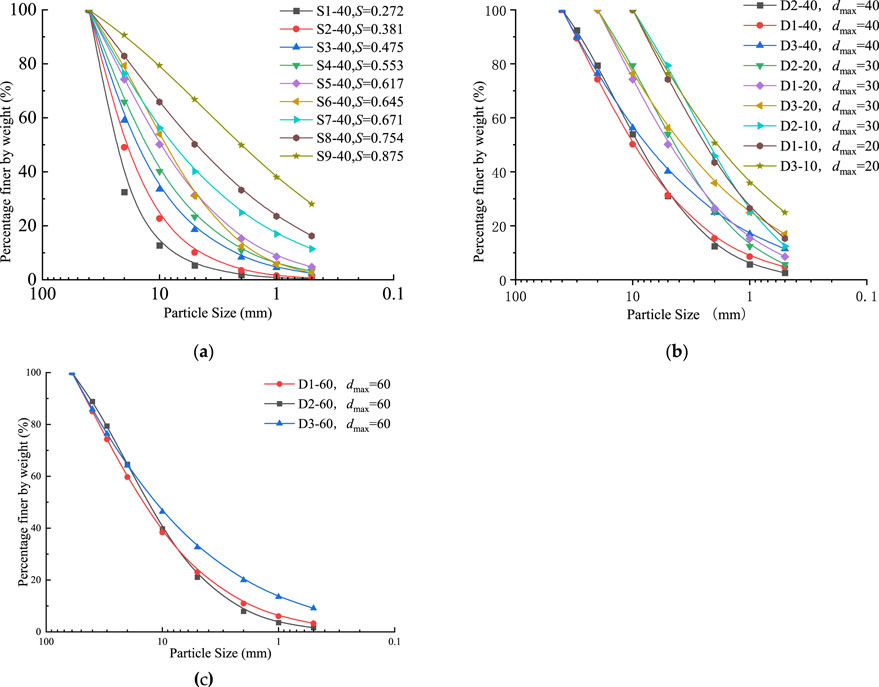
Figure 3. Particle gradation cumulative curve of rockfill material. (A), (B), and (C) correspond to S1-40∼S9-40, D1-40∼D1-10, D2-40∼D2-10, D3-40∼D3-10 and D1-60∼D3-60, respectively.

3 Scale effect research methods

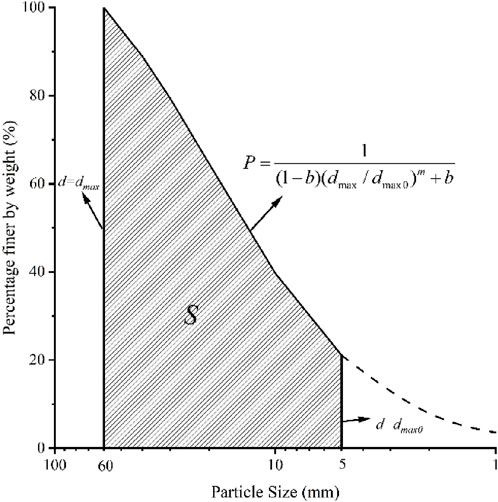
The gradation area S is enclosed by the gradation equation curve, the horizontal axis of the coordinates, the maximum particle diameter line d = d_max, and the d = d_max0 line (Wu et al., 2019; Wu et al., 2020a), as shown in Figure 4. It can be calculated as follows:

$S=\frac{\ln \left(1-kb\right)-\ln \left(1-b\right)}{mb\ln 10}(2)$

where

$k=\frac{1}{\left(1-b\right){\left(d_{\max }/d_{\max 0}\right)}^m+b}(3)$

Figure 4

Figure 4. Schematic diagram of gradation curve area.

As per Equations 2, 3, the gradation area S is defined by the variables d_max, m, and b. When d/d_max0 is set as a fixed value, S becomes exclusively dependent on the gradation parameters b and m. The gradation area S, being indicative of changes in gradation structure, which is governed by parameters b and m, acts as a key characteristic parameter in this context.

Parameters d_max and S, as outlined in Equations 2, 3, serve to quantitatively assess the impacts of maximum particle diameter d_max and gradation structure on the strength attributes of coarse-grained soil. Through correlating d_max and S with shear strength parameters like cohesion (c) and internal friction angle (φ), one can elucidate the governing principles of gradation structure on the strength of coarse-grained soil.

Guo (2003) proposed a boundary particle diameter of 5 mm to distinguish between sand and gravel. Based on this definition, this study established a maximum particle diameter d_max of 40 mm and a reference diameter d_max0 of 5 mm. This configuration enables the use of the single-variable method to investigate the effects of maximum particle diameter on the shear strength parameters of coarse-grained soil. The method requires that the gradation area S remains constant before and after scaling to ensure accurate comparisons.

To conclude, the application of the single-variable method, coupled with testing a range of specimens either having identical maximum particle diameters but varying gradation areas, or uniform gradation areas with differing maximum particle diameters, offers a viable approach to investigate how maximum particle diameter and gradation structure correlate with shear strength parameters.

4 Analysis of test results

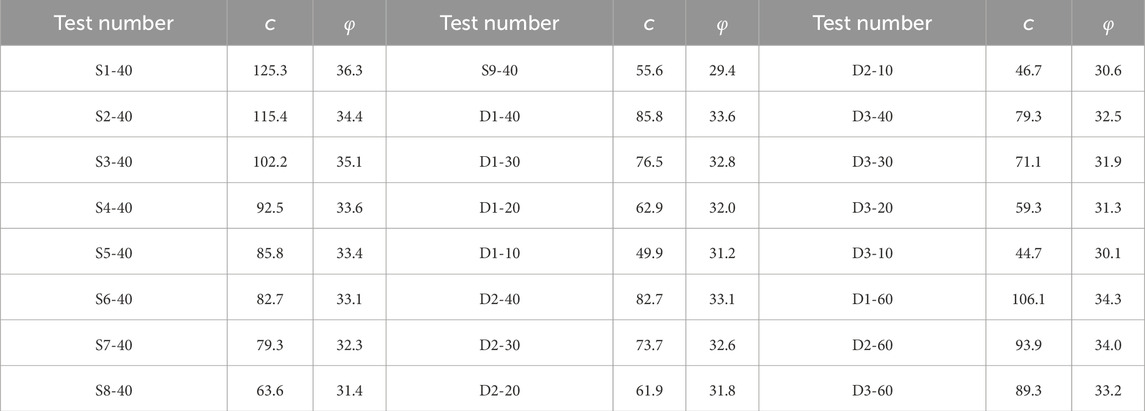
Table 2 presents the values of soil C and fai obtained from 21 sets of large-scale triaxial tests.

Table 2

Table 2. Detailed values of shear strength indicators for each group of styles.

4.1 The association between shear strength parameters and maximum particle diameter

The triaxial compression test results for specimens D1-40 to D3-10 allow for summarizing the relationship between the maximum particle diameter d_max and the shear strength parameters c and φ, which are presented as discrete data points in Figures 5A,B. As evidenced by Figure 5, there is a notable influence of maximum particle diameter on the shear strength attributes of coarse-grained soil, with a discernible increase in cohesion c and internal friction angle φ accompanying the rise in maximum particle diameter, independent of changes in gradation structure. Jiang et al. (Wu et al., 2020b) conducted large-scale direct shear tests on rockfill materials, and their results mirrored the trends in c and φ changes in relation to d_max variations, corroborating the experimental findings of this study. In addition, through the use of DEM numerical simulations, Wang et al. (Jiang et al., 2023) investigated the scale effect on coarse-grained materials and concluded that increases in d_max correspond with rises in both c and φ.

Figure 5

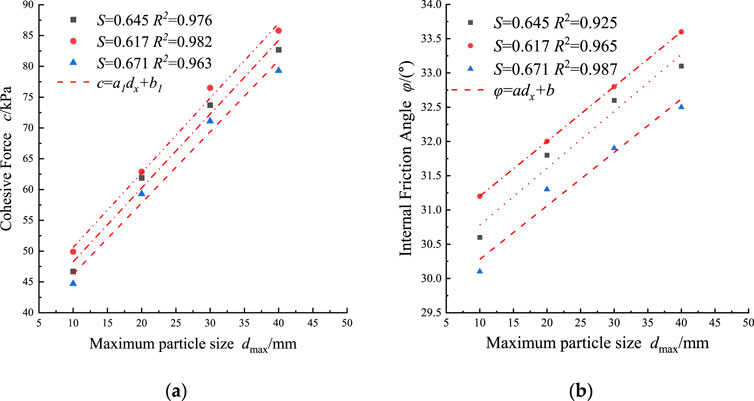
Figure 5. The relationship between the maximum particle size d_max and shear strength parameters c (A) and φ (B).

Further analysis of the influence law of d_max on c and φ suggested that the relationships of d_max with c and φ were linear. Thus, the relationships of coarse-grained soil d_max with c and φ can be expressed as:

$\left.\begin{array}{l}c=a_1\left(d_{\max }-d_{\max 0}\right)+c_0\\ \phi =a_2\left(d_{\max }-d_{\max 0}\right)+{\phi }_0\end{array}\right\}(4)$

In this equation, d_max0 = 5 mm serves as the boundary diameter distinguishing sand from gravel. The parameters a₁, a₂, c₀, and φ₀ are defined where c₀ (kPa) and φ₀ (°) signify the cohesion c and internal friction angle φ for a specimen with maximum particle diameter d_max = 5 mm. Additionally, a₁ (kPa) and a₂ (°) indicate the rate of change in cohesion c and internal friction angle φ for specimens where d_max is 5 mm.

Equation 4 was employed to fit the test data from specimens D1-40 to D3-10. This fitting is visually represented in Figure 5, while the statistical outcomes of the fitting are detailed in Table 3. Examination of Figure 5 reveals that the fitting curves closely match the data points. The errors between the fitted values of c₀ and φ₀ and their respective test data points are below 4% and 2%, achieving determination coefficients greater than 0.963.Therefore, Equation 4 effectively quantifies the impact of d_max on the parameters c₀ and φ₀, in relation to the scale effect.

Table 3

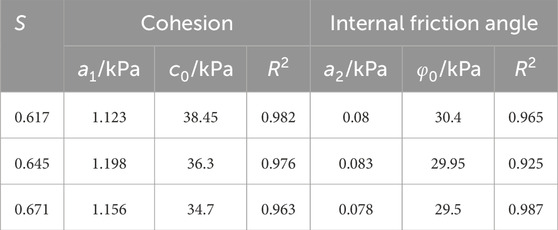
Table 3. Fitting results of Equation 4 for gravel soils.

4.2 The association between shear strength parameters and the gradation area

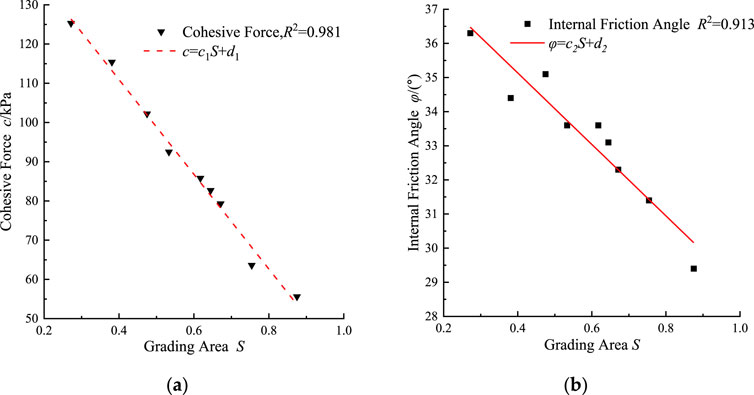
From the triaxial compression tests conducted on soil specimens S1-40 to S9-40, which possess an identical d_max, the trends showing how the cohesion c and internal friction angle φ of coarse-grained soil vary with the gradation area S are captured and illustrated as distinct points in Figures 6A,B. It can be observed from Figure 6 that c and φ decrease with the increase of the gradation area S, exhibiting linear relationships. Apparently, the gradation area S has significant effects on the coarse-grained soil shear strength parameters (cohesion c and internal friction angle φ).

Figure 6

Figure 6. The relationship between gradation area S and shear strength parameters c (A) and φ (B).

By fitting the test data, the relationships of coarse-grained soil c and φ with soil gradation area S can be expressed as:

$\left.\begin{array}{l}c=b_{1}S+d_1\\ \phi =b_{2}S+d_2\end{array}\right\}(5)$

where b₁, b₂, d₂, and d₂ are all parameters of the equation.

The test data from soil specimens S1-40 through S9-40 were analyzed using Equation 5. The fitting curves derived from this analysis are depicted in Figure 6, with detailed statistical outcomes presented in Table 4. As evidenced in Figure 6, there is a pronounced congruence between the fitting curves and the experimental data points. The deviations between the fitted and observed values for cohesion c and internal friction angle φ are less than 2% and 9%, respectively. Additionally, the coefficients of determination associated with these fits exceed 0.913. Consequently, the influence of gradation structure on the parameters of cohesion c and internal friction angle φ, particularly in relation to scale effects, can be quantitatively described using Equation 5.

Table 4

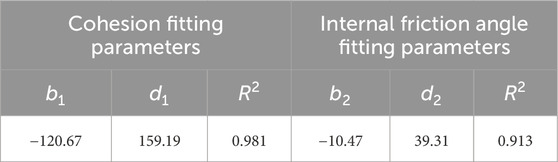
Table 4. Fitting results of Equation 5 for gravel soils.

4.3 Establishment of empirical formula for shear strength

To summarize, the relationships between the cohesion c and internal friction angle φ of coarse-grained soil, and the gradation area S, are consistent with Equation 5, provided the maximum particle diameter remains constant. In Equation 4, c₀ and φ₀ represent the baseline values of cohesion c and internal friction angle φ when the maximum particle diameter d_max is 5 mm. The dependency of these parameters on the gradation area S is thus effectively captured by Equation 5. Consequently, the combined effects of maximum particle diameter and gradation structure on the shear strength of coarse-grained soil can be quantitatively assessed using the following equation:

$\left.\begin{array}{l}c=a_1\left(d_{\max }-d_{\max 0}\right)+b_{1}S+d_1\\ \phi =a_2\left(d_{\max }-d_{\max 0}\right)+b_{2}S+d_2\end{array}\right\}(6)$

Strength parameters for the 21 sets of coarse-grained soil specimens were analyzed and fitted using Equation 6, with the findings detailed in Table 5.

Table 5

Table 5. Fitting results of Equation 6 for gravel soils.

In Figure 7, there is a juxtaposition of the measured shear strength parameters from diverse gradations of coarse-grained soil and the soil specimens D1-60 to D3-60, against the outcomes calculated using the formula. It can be observed from Figure 7 that the fitted values of cohesion c and internal friction angle φ derived from Equation 6 have errors with the corresponding test points below 3% and 8%, reaching determination coefficients above 0.924, which is in an acceptable range. Consequently, Equation 6 effectively quantifies the scale effect’s impact on the shear strength of coarse-grained soil.

Figure 7

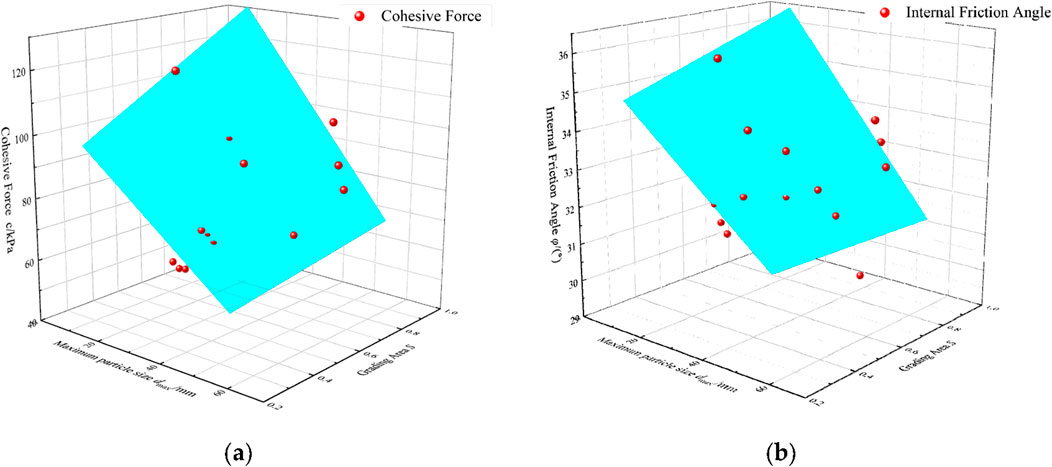
Figure 7. The comparison between the measured values of shear strength parameters c (A) and φ (B) and the formula calculation results.

The utilization of Equation 6 to characterize the cumulative influence of the maximum particle diameter and gradation structure on the shear strength of soil masses is of substantial practical significance. By performing shear strength tests on scaled soil materials to ascertain their material parameters, it is feasible to infer the shear strength parameters of coarse-grained soil with original gradation in situ using Equation 6. This methodology effectively reduces the scale effect on the shear strength of soil masses, thereby augmenting the safety and reliability of geotechnical engineering endeavors.

5 Shear strength empirical formula verification

While this research focused solely on gravel material for shear strength testing, additional test data from various types of coarse-grained soil are needed to confirm the applicability of the proposed shear strength prediction formula. Jiang et al. (Shi et al., 2023) performed large-scale direct shear tests on sandy pebble materials, varying in maximum particle diameters and gradation structures. Shear strength tests of sandy pebble materials with d_max values of 40, 20, and 10 mm from Jiang et al. (Shi et al., 2023) were analyzed using Equation 6. The parameters derived from this fitting are listed in Table 6, and the corresponding fitting curves are illustrated in Figure 8.

Table 6

Table 6. Fitting results of Equation 6 for sand pebble soils.

Figure 8

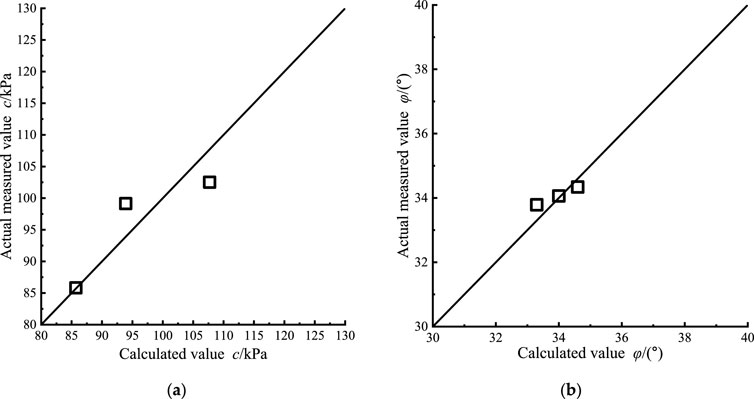
Figure 8. The measured and calculated values of shear strength parameters c (A) and φ (B) of sandy pebble soil.

To assess the validity and simplicity of our proposed formula, we compared it with the model presented by Jiang et al. (Shi et al., 2023). While Jiang’s model provides a comprehensive approach, the formula proposed in this study offers a more straightforward and less complex method for predicting shear strength, without compromising accuracy. This makes our approach particularly advantageous for practical applications where computational efficiency is critical.

It can be observed from Figure 8 that the errors between the fitted c and φ values derived from Equation 6 and the corresponding test values are basically below 14% and 24%, reaching determination coefficients above 0.763, with relatively good fitting effects. Apparently, Equation 6 can accurately describe the relationship between the shear strength and gradation of any type of coarse-grained soil.

An analysis of Figure 9 reveals a close alignment between the predicted and actual measured values, with the error margins for cohesion c and internal friction angle φ being 3.15% and 1.81%, respectively. The above comparative analysis demonstrated the high reliability of the established coarse-grained soil shear strength prediction model considering the scale effect and its applicability to different types of soil (Zheng et al., 2024a; Zheng et al., 2024b; Wu et al., 2024; Wu et al., 2022; Wu et al., 2020c). Therefore, the shear strength parameters of coarse-grained soil with any gradation can be well predicted by Equation (6) after conducting shear strength tests on a series of scaled specimens of the same coarse-grained soil material to determine the various parameters of Equation 6.

Figure 9

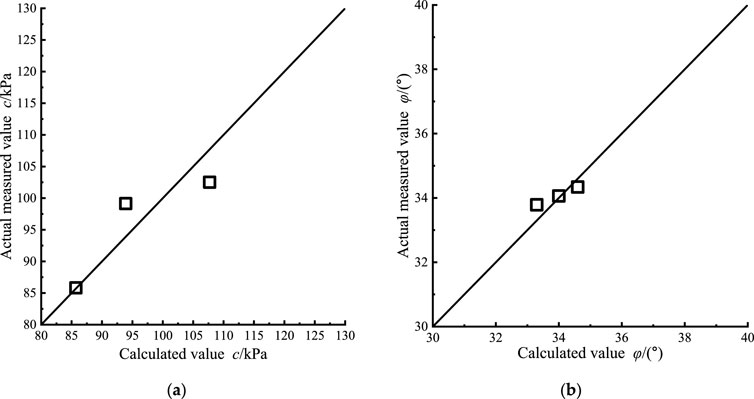
Figure 9. The predicted values of shear strength parameters c (A) and φ (B) are compared with the measured values when the test soil d_max = 60 mm.

6 Discussion

This study investigates the shear strength characteristics of coarse-grained soils and compares the findings with existing research. The results show that the shear strength of coarse-grained soils is influenced by various factors, including soil type, dry density, particle gradation, shear rate, coarse particle content, and moisture content. Consistent with the findings of Wang and Zhuang (2021), this study shows that sand and gravel soils exhibit significant differences in shear strength, with sand having a higher internal friction angle, while gravel soils demonstrate higher shear strength due to particle interlocking. Additionally, this study confirms that increased dry density significantly enhances both the internal friction angle and cohesion, which aligns with the conclusions of Gu et al. (2017) and Li and Selig (1996), highlighting the important role of dry density in shear strength. The study also verifies the scale effect, where larger sample sizes result in lower shear strength, which is consistent with the findings in Wang and Zhang (2020). Overall, the influence of particle gradation and compaction on shear strength is particularly significant in slope stability analysis, supporting the conclusions of Marsal (1967), Marschi et al. (1972), and Indraratna et al. (1998), which emphasize the importance of these factors in engineering applications.

However, there are some limitations in this study. First, the selection and scale of the experimental samples may affect the generalizability of the results, especially given the lack of consideration for larger-scale samples, which may impact the representativeness of the data. Second, while this study focused on the impact of dry density and particle gradation, other geotechnical factors, such as pore water pressure and stress history, were not thoroughly considered. These factors could significantly influence shear strength under different environmental conditions. Finally, although the study provides laboratory data, it lacks field validation, which could introduce discrepancies between laboratory results and actual engineering conditions. Future research should incorporate field data or case studies to further validate the conclusions of this study.

7 Conclusion

Employing the continuous gradation formula for coarse-grained soil, the research crafted 21 distinct groups of specimens, characterized by maximum particle diameters d_max of 40, 30, 20, and 10 mm. The shear strength of these coarse-grained soil specimens, varying in gradation structure and maximum particle diameter but unified in relative density, was quantitatively assessed using a large-scale triaxial testing machine for coarse-grained soil. The following four conclusions were reached:

(1) Variations in the maximum particle diameter and the gradation structure substantially contribute to the scale effect observed in coarse-grained soil. Therefore, applying the single-variable approach to investigate the impacts of maximum particle diameter and gradation structure on coarse-grained soil’s shear strength offers a quantitative insight into the scale effect’s influence on this attribute.

(2) With constant gradation areas S, implying no changes in gradation structure, there is a gradual increase in both cohesion c and internal friction angle φ with the rising maximum particle diameter d_max, exhibiting a linear correlation with d_max with an error of less than 8%.

(3) With fixed maximum particle diameters d_max, an escalation in the gradation area S leads to a reduction in both cohesion c and internal friction angle φ, each maintaining a linear association with d_max. with an error of less than 9%.

(4) This research develops a model for predicting the shear strength of coarse-grained soil, incorporating the effects of maximum particle diameter and gradation structure. The model’s effectiveness in predicting the shear strength of coarse-grained soil across all gradations was confirmed with related test data from existing literature, and its adaptability to diverse coarse-grained soil types was examined. Relative to prior research findings, this model offers more straightforward calculations and enhanced applicability in practical engineering scenarios.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

XL: Data curation, Formal Analysis, Funding acquisition, Validation, Writing–review and editing. XS: Data curation, Funding acquisition, Validation, Writing–review and editing. JD: Funding acquisition, Methodology, Writing–review and editing. YS: Project administration, Supervision, Writing–original draft. HJ: Investigation, Project administration, Writing–review and editing. JG: Data curation, Writing–review and editing. MJ: Data curation, Methodology, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work is supported by the Guangxi Science and Technology Base and Talent Project (No. 2021AC19244) and Special Basic Cooperative Research Programs of Yunnan Provincial Undergraduate Universities’ Association (No. 202301BA070001-012, No. 202101BA070001-137).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Gu, F., Zhang, Y., Luo, X., Sahin, H., and Lytton, R. L. (2017). Characterization and prediction of permanent deformation properties of unbound granular materials for pavement ME design. Constr. Build. Mater. 155, 584–592. doi:10.1016/j.conbuildmat.2017.08.116

CrossRef Full Text | Google Scholar

Guo, Q. G. (2003). Engineering properties and application of coarse-grained soil. Beijing, China: China Water Power Press.

Google Scholar

Hu, W., Dano, C., Hicher, P.-Y., Le, J.-Y., François, D., and Merliot, E. (2011). Effect of sample size on the behavior of granular materials. Geotech. Test. J. 34 (3), 186–197. doi:10.1520/GTJ103095

CrossRef Full Text | Google Scholar

Indraratna, B., Ionescu, D., and Christie, H. D. (1998). Shear behavior of railway ballast based on large-scale triaxial tests. J. Geotech. Geoenviron. Eng. 124 (5), 439–449. doi:10.1061/(asce)1090-0241(1998)124:5(439)

CrossRef Full Text | Google Scholar

Jiang, M. J., Ji, E. Y., Wang, T. C., Li, S. Y., Zhu, J. G., and Mei, G. X. (2023). Experimental study on laws of scale effects of shear strength of coarse-grained soils. Chin. J. Geotech. Eng. 45 (4), 855–861. doi:10.11779/CJGE20220102

CrossRef Full Text | Google Scholar

Kong, X. J., Ning, F. W., Liu, J. M., Zou, D. G., and Zhou, C. G. (2019). Scale effect of rockfill materials using super-large triaxial tests. Chin. J. Geotech. Eng. 41 (2), 255–261. doi:10.11779/CJGE201902002

CrossRef Full Text | Google Scholar

Lee, D. M. (1992). The angles of friction of granular fills. Cambridge, MA: University of Cambridge.

Google Scholar

Li, C., He, C. R., Wang, C., and Zhao, H. F. (2008). Study of scale effect of large-scale triaxial test of coarse-grained materials. Rock Soil Mech. 29 (S1), 563–566. doi:10.16285/j.rsm.2008.s1.103

CrossRef Full Text | Google Scholar

Li, D., and Selig, E. T. (1996). Cumulative plastic deformation for fine-grained subgrade soils. J. Geotech. Eng. 122 (12), 1006–1013. doi:10.1061/(asce)0733-9410(1996)122:12(1006)

CrossRef Full Text | Google Scholar

Li, N. H., Zhu, T., and Mi, Z. K. (2001). Strength and deformation properties of transition zone material of Xiaolangdi Dam and scale effect. Hydroelectr. Energy 19 (2), 39–42. doi:10.20040/j.cnki.1000-7709.2001.02.012

CrossRef Full Text | Google Scholar

Li, Z., and Xing, Y. C. (2006). Effects of dry density and percent fines on shearing strength of sandy cobble and broken stone. Rock Soil Mech. 27 (12), 2255–2260. doi:10.16285/j.rsm.2006.12.032

CrossRef Full Text | Google Scholar

Marsal, R. J. (1967). Large scale testing of rockfill materials. J. Soil Mech. Found. Div. 93 (2), 27–43. doi:10.1061/JSFEAQ.0000958

CrossRef Full Text | Google Scholar

Marschi, N. D., Chan, C. K., and Seed, H. B. (1972). Evaluation of properties of rockfill materials. J. Soil Mech. Found. Div. 98 (1), 95–114. doi:10.1061/JSFEAQ.0001735

CrossRef Full Text | Google Scholar

Meng, X. Q., and Shi, Y. W. (1983). Shear strength of sandy-gravels in Shitouhe River dam. Chin. J. Geotech. Eng. 5 (1), 90–101.

Google Scholar

Ministry of Housing and Urban-Rural Development of the People’s Republic of China, State Administration for Market Regulation (2019). Standard for geotechnical testing method (GB/T 50123–2019). Beijing, China: China Planning Press.

Google Scholar

Shi, J. W., Wang, J. P., Chen, Y. H., Shi, C., Lu, H., Ma, S. K., et al. (2023). Physical modeling of the influence of tunnel active face instability on existing pipelines. Tunn. Undergr. Space Technol. 140, 105281. doi:10.1016/j.tust.2023.105281

CrossRef Full Text | Google Scholar

Shi, J. W., Zhong, X. C., Lu, H., Ni, X. D., and Shi, C. (2024). Influence of joint stiffness on three-dimensional deformation mechanisms of pipelines under tunnel active face instability. Can. Geotech. J. 62, 1–18. doi:10.1139/cgj-2024-0092

CrossRef Full Text | Google Scholar

Varadarajan, A., Sharma, K. G., Venkatachalam, K., and Gupta, A. K. (2003). Testing and modeling two rockfill materials. J. Geotech. Geoenviron. Eng. 129 (3), 206–218. doi:10.1061/(ASCE)1090-0241(2003)129:3(206)

CrossRef Full Text | Google Scholar

Wang, F., and Zhang, J.-q. (2020). Study on breakage behaviour of original rockfill materials considering size effect on particle strength. Rock Soil Mech. 41 (1), 87–94. doi:10.16285/j.rsm.2018.7240

CrossRef Full Text | Google Scholar

Wang, K., and Zhuang, Y. (2021). Characterizing the permanent deformation response-behavior of subgrade material under cyclic loading based on the shakedown theory. Constr. Build. Mater. 311, 125325. doi:10.1016/j.conbuildmat.2021.125325

CrossRef Full Text | Google Scholar

Wei, H. Z., Wang, R., Hu, M. J., Zhao, H. Y., and Xu, X. Y. (2008). Strength behaviour of gravelly soil with different coarse-grained contents in Jiangjiagou Ravine. Rock Soil Mech. 29 (1), 48–51+57. doi:10.16285/j.rsm.2008.01.030

CrossRef Full Text | Google Scholar

Weng, H. Y., Zhu, J. G., Yu, T., and Wang, G. Q. (2009). Status quo and tendency of studies on scale effects of coarse-grained materials. J. Hohai Univ. Nat. Sci. 37 (4), 425–429. doi:10.3876/j.issn.1000-1980.2009.04.013

CrossRef Full Text | Google Scholar

Wu, E. L., Zhu, J. G., Guo, W. L., and Chen, G. (2019). Experimental study on effect of scaling on compact density of coarse-grained soils. Chin. J. Geotech. Eng. 41 (9), 1767–1772. doi:10.11779/CJGE201909023

CrossRef Full Text | Google Scholar

Wu, L. Q., Ye, F., and Lin, W. Q. (2020a). Experimental study on scale effect of mechanical properties of rockfill materials. Chin. J. Geotech. Eng. 42 (S2), 141–145. doi:10.11779/CJGE2020S2025

CrossRef Full Text | Google Scholar

Wu, E. L., Zhu, J. G., Guo, W. L., and Lu, Y. Y. (2020b). Experimental study of compaction characteristics of coarse-grained soil based on gradation equation. Rock Soil Mech., 41 (1), 214–220. doi:10.16285/j.rsm.2018.2358

CrossRef Full Text | Google Scholar

Wu, J. Y., Jing, H. W., Yin, Q., Yu, L. Y., Meng, B., and Li, S. C. (2020c). Strength prediction model considering material, ultrasonic and stress of cemented waste rock backfill for recycling gangue. J. Clean. Prod. 276, 123189. doi:10.1016/j.jclepro.2020.123189

CrossRef Full Text | Google Scholar

Wu, J. Y., Jing, H. W., Gao, Y., Meng, Q. B., Yin, Q., and Du, Y. (2022). Effects of carbon nanotube dosage and aggregate size distribution on mechanical property and microstructure of cemented rockfill. Cem. Concr. Compos. 127, 104408. doi:10.1016/j.cemconcomp.2022.104408

CrossRef Full Text | Google Scholar

Wu, J. Y., Wong, H. S., Zhang, H., Yin, Q., Jing, H. W., and Ma, D. (2024). Improvement of cemented rockfill by premixing low-alkalinity activator and fly ash for recycling gangue and partially replacing cement. Cem. Concr. Compos. 145, 105345. doi:10.1016/j.cemconcomp.2023.105345

CrossRef Full Text | Google Scholar

Zheng, Z., Bin, D., Hong, L., Wang, W., Huang, S., and Shaojun, L. (2024a). Microdynamic mechanical properties and fracture evolution mechanism of monzogabbro with a true triaxial multilevel disturbance method. Int. J. Min. Sci. Technol. 34 (3), 385–411. doi:10.1016/j.ijmst.2024.01.001

CrossRef Full Text | Google Scholar

Zheng, Z., Li, R., Pan, P., Qi, J., Su, G., and Zheng, H. (2024b). Shear failure behaviors and degradation mechanical model of rockmass under true triaxial multi-level loading and unloading shear tests. Int. J. Min. Sci. Technol. 34 (10), 1385–1408. doi:10.1016/j.ijmst.2024.10.002

CrossRef Full Text | Google Scholar

Zhu, J. G., Guo, W. L., Wen, Y. F., Yin, J. H., and Zhou, C. (2018). New gradation equation and applicability for particle-size distributions of various soils. Int. J. Geomech. 18 (2), 04017155. doi:10.1061/(ASCE)GM.1943-5622.0001082

CrossRef Full Text | Google Scholar