Field testing and numerical modeling of vehicle-induced vibrations on an ancient seawall via an approach slab

The Yanguan Ancient Seawall at the Qiantang River estuary is a nationally protected cultural heritage and an in-service flood defense. Construction activities, such as vehicle crossings, pose risks of vibration-induced damage to this aging structure. In this study, a three-dimensional finite element model was developed to evaluate the vibrations caused by moving vehicles on the seawall. The model represents the seawall’s discrete-continuum structural characteristics by modeling rubble stone blocks with solid elements and bonding mortar with cohesive zone elements. Additionally, a custom Vehicle-Road Interaction element was introduced to simulate both vertical and tangential wheel–road contact forces for vehicles crossing the inclined approach slab. Field vibration measurements were used to validate the model, demonstrating that it can accurately reproduce the observed vibration response. The validated model was then applied to investigate the seawall’s vibration behavior under various approach slab inclination angles. The results provide a scientific basis for designing vibration mitigation measures and inform strategies to protect this cultural heritage structure.

1 Introduction

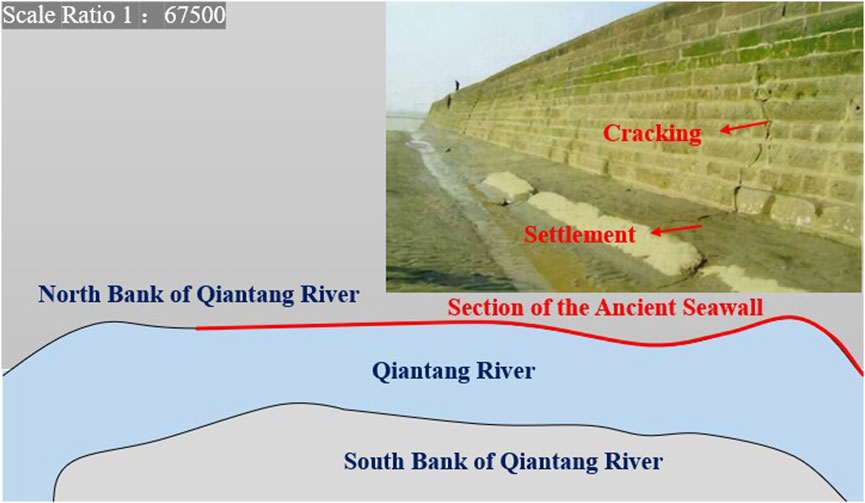
The seawalls along the Qiantang River serve as critical flood defense structures in the estuary region, protecting against tidal surges, typhoons, storm surges, and flooding events (Figure 1). Over time, these ancient seawalls have experienced significant structural degradation due to the combined effects of evolving natural conditions (Pan et al., 2013; Yu et al., 2010), intensive human activities (Zou and Shen, 2017; Zheng et al., 2014), and the high-energy tidal bores characteristic of the Qiantang River (Chen and Pan, 2008). Such factors have led to breaches in embankments and the destruction of protective aprons, thereby compromising the functional integrity of many seawall sections.

Figure 1

Figure 1. Structural issues in the Yanguan ancient seawall section along the Qiantang River.

Figure 2

Figure 2. Schematic diagram of the vibration monitoring setup during approach slab crossing.

To address these challenges, the Zhejiang Province government in China initiated the “Billion Seawalls Reinforcement Project,” prioritizing the Yanguan ancient seawall segment along the Qiantang River. This large-scale initiative aims to upgrade the Yanguan seawall’s flood defense standard from a 100-year to a 300-year return period. The reinforcement process involves several construction activities, including the installation of approach slabs spanning the seawall and vehicle crossings behind structure. However, dynamic loads generated by construction vehicles may induce excessive vibrations in the ancient seawall, posing risks of structural deterioration, such as cracking and severe damage to this nationally protected cultural relic.

Research on the vibration and deformation of historical structures has primarily focused on the effects of seismic and traffic loads on ancient buildings. For instance, Calik et al. (2020) and Bayraktar et al. (2018) evaluated the dynamic behavior of masonry heritage buildings under environmental and seismic vibrations, while Li et al. (2010) reported that subway-induced vibrations in ancient structures can be an order of magnitude greater than those from road traffic. Ali et al. (2013) identified structural improvements, such as vertical members and relatively thin horizontal bands, that enhance the seismic performance of rubble masonry houses through shaking table tests. Kowalska-Koczwara and Stypula (2016) measured vibrations of a historic church and proposed protective measures. Existing research predominantly employs numerical simulations (Zhao et al., 2013; Sadeghi and Esmaeili, 2017; Ma et al., 2018; Günaydin et al., 2022; Montabert et al., 2024) and on-site measurements (Hinzen, 2014; Krentowski et al., 2023) to analyze the vibrational impacts of subway trains on ancient city towers (Xin et al., 2019), bell towers (De Angelis et al., 2022), and other brick and stone cultural relic structures (Poovarodom et al., 2024). However, very limited research has been conducted on nationally protected relics like the Qiantang ancient seawall, which serves dual roles as a cultural monument and a flood defense structure.

The Qiantang ancient seawall is a masonry structure composed of rigid stone blocks bonded locally with sticky rice mortar, classifying it as a gravity retaining wall. While the stone blocks exhibit discrete characteristics, the overall wall structure demonstrates continuum behavior. This unique combination of discrete and continuous characteristics complicates the analysis of the seawall’s deformation and vibration. Conventional methods based solely on continuum or discrete media theories are insufficient for directly predicting its dynamic behavior. For masonry structures with such discrete-continuous characteristics, researchers often employ decoupled modeling approaches to develop finite element models. Page (1978) first propose a decoupled finite element model for clay brick masonry. Lotfi and Shing, 1994 (12) introduced the use of zero-thickness interface elements to simulate mortar joints. Building on Lotfit’s work, Lourenço and Rots, (1994) combined blocks with half the thickness of their mortar joints and represented them using continuum elements. Andreotti et al. (2018) adopted a decoupled modeling approach, using continuum elements for masonry walls and zero-thickness bonding interfaces for mortar, successfully simulating damage mechanisms and failure phenomena at mortar joints.

Despite these advancements, limited studies have investigated the impact of vehicle-induced vibrations on the structural integrity of ancient seawalls. There is currently no precedent for assessing the vibration effects caused by moving vehicles during the reinforcement and upgrade of such structures. Consequently, it is essential to develop an analysis method that incorporates the key characteristics of moving vehicle loads and the discrete-continuous nature of the ancient seawall structure.

In this study, solid elements and cohesive zone elements were employed to discretize the stone blocks and sticky rice mortar of the ancient seawall, respectively. A 3D finite element model reflecting the discrete-continuous structural characteristics of the seawall was developed using the general-purpose finite element software ABAQUS. Additionally, a vehicle-road coupled element capable of considering vertical and tangential wheel-road contact forces was implemented via the ABAQUS User Element (UEL) interface. This approach resulted in a 3D numerical analysis method capable of predicting the vibration effects of moving vehicles on the ancient seawall. The study also evaluated the vibration response levels of the seawall under different inclination angles of the approach slab spanning the seawall crest, providing scientific evidence for the vibration protection of cultural relics.

2 Measured vibrations of the ancient seawall induced by approach slab crossing

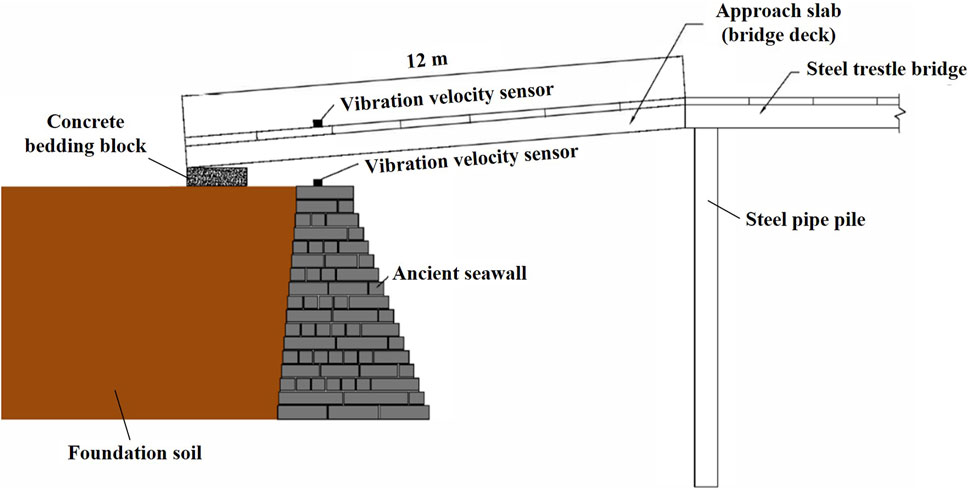
In the transverse direction of the ancient seawall, a steel trestle bridge extends into the river for soil excavation. To avoid direct vehicle loading on the ancient seawall crest, an approach slab is installed between the trestle bridge and the road behind the seawall. However, the vibrations induced by vehicles crossing the approach slab propagate to the ancient seawall, potentially compromising its structural stability. This section focuses on measuring the vibration levels of the ancient seawall structure caused by vehicles traversing the approach slab.

The vibration measurements used for model validation were obtained from our prior on-site experiment conducted on the Yanguan seawall (Figure 2). In this field test, a three-axle truck (total weight 25 t, ∼10 t per axle) was driven over a newly installed approach slab at a controlled speed of 5 km/h. The truck’s travel path aligned with the centerline of the approach slab. The speed of 5 km/h was selected to simulate typical slow-moving construction vehicles, which are common in reinforcement projects. A total of 6 vibration sensors (servo-velocity meters, model XYZ-123) were deployed: three on the approach slab and three on the seawall top, aligned with the vertical (Z), along-dike horizontal (X), and cross-dike horizontal (Y) directions. Each sensor was factory-calibrated and checked with a standard vibration calibrator (yielding a calibration error <2%) prior to installation. The data acquisition system recorded signals at 1,000 Hz, and care was taken to securely attach sensors to avoid any spurious readings. We estimate the measurement uncertainty in velocity to be within ±5% based on the sensor specifications and repeatability tests.

The time-history curves of the vertical vibration velocity (Z) and horizontal vibration velocities (X and Y) on the approach slab surface under the crossing condition are shown in Figure 3. The results indicate that the vibrations induced by the vehicle crossing are predominantly in the vertical direction, with the vertical vibration velocity significantly exceeding the horizontal components. Specifically, the peak vertical vibration velocity reaches 77.5770 mm/s, which is 17.25 times greater than the peak horizontal vibration velocity in the X direction (4.4985 mm/s) and 21.6 times greater than that in the Y direction (3.5910 mm/s). These ratios highlight the significant disparity between the vertical and horizontal vibration components, emphasizing the need to focus on mitigating vertical vibrations to protect the structural integrity of the seawall.

Figure 3

Figure 3. Time-history curves of approach slab surface vibration under the crossing condition.

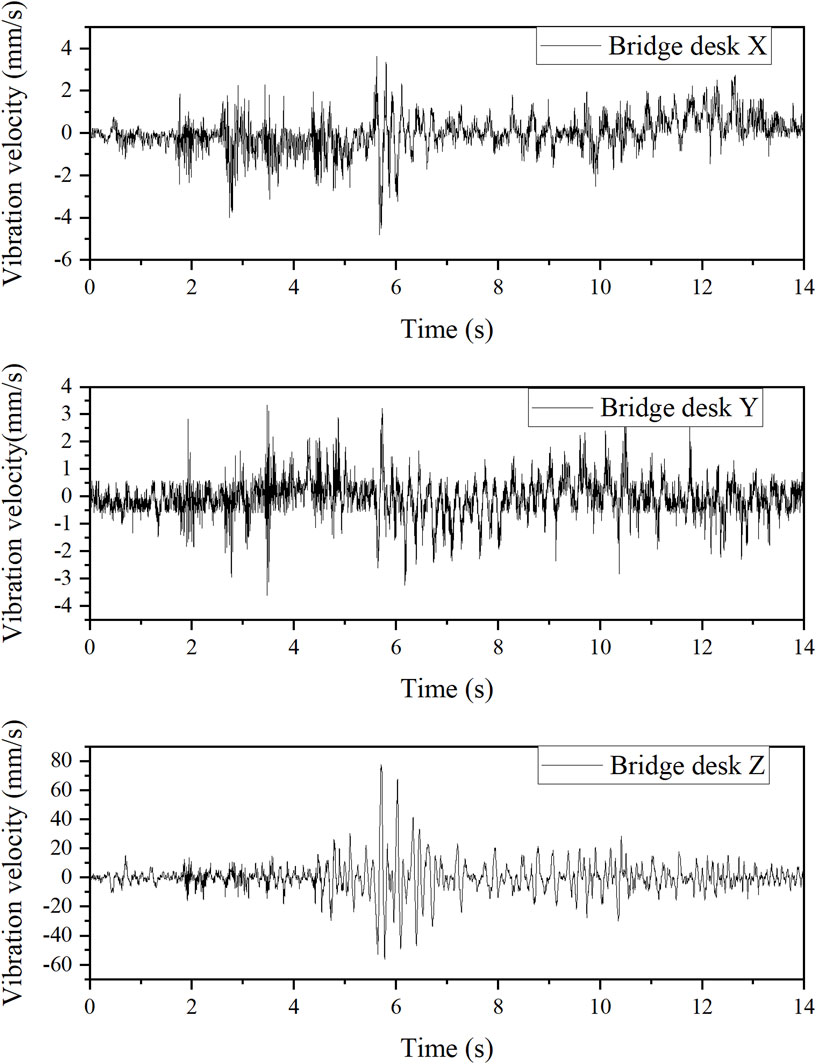
The time-history curves of the vertical vibration velocity (Z) and horizontal vibration velocities (X and Y) of the ancient seawall structure under the approach slab crossing condition are presented in Figure 4. The results reveal a significant increase in vibration velocities in all three directions, contradicting typical observations where vertical vibrations often dominate in similar scenarios. This anomaly suggests that specific structural or loading conditions may amplify horizontal vibrations. Notably, the peak vibration velocity in the horizontal X direction (1.4800 mm/s) is 30.52 times greater than that in the horizontal Y direction (0.0485 mm/s) and 4.45 times greater than that in the vertical Z direction (0.3324 mm/s). This finding highlights the vulnerability of the seawall to transverse vibrations, which could lead to structural degradation or failure over time if not mitigated.

Figure 4

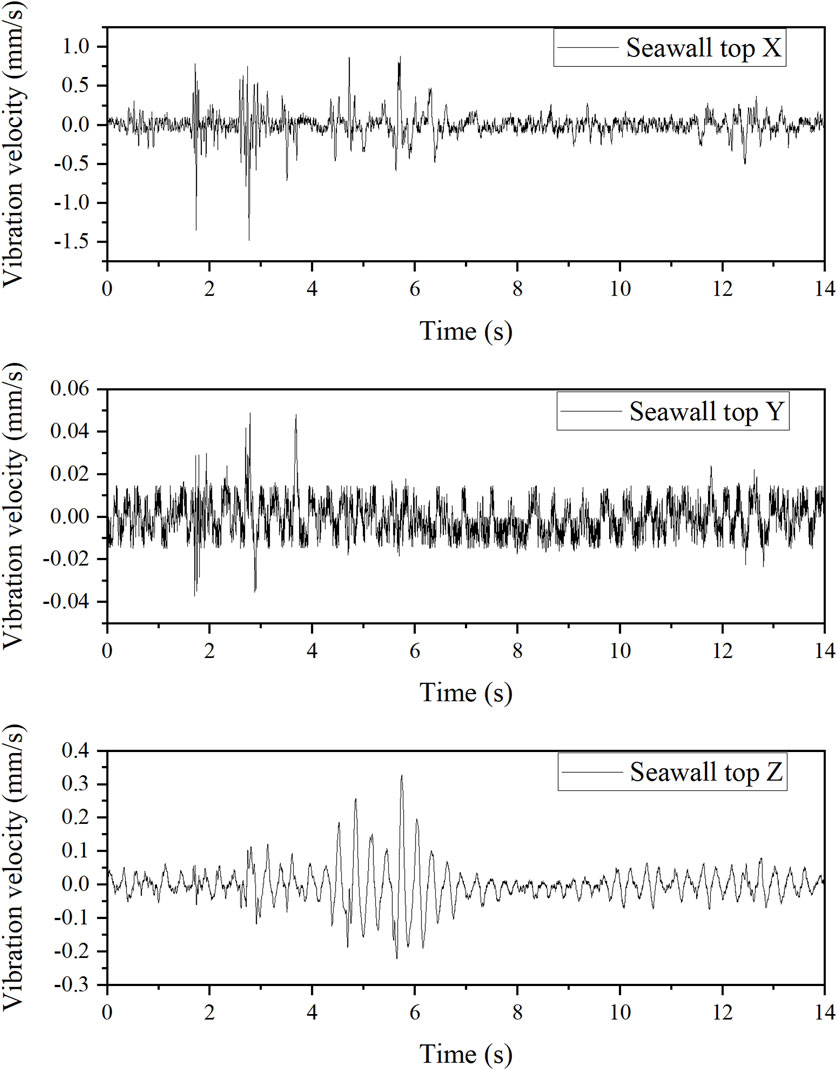
Figure 4. Time-history curves of forced vibration of the ancient seawall top under the approach slab crossing condition.

3 Vehicle-road coupling element considering vertical and tangential wheel-road contact forces

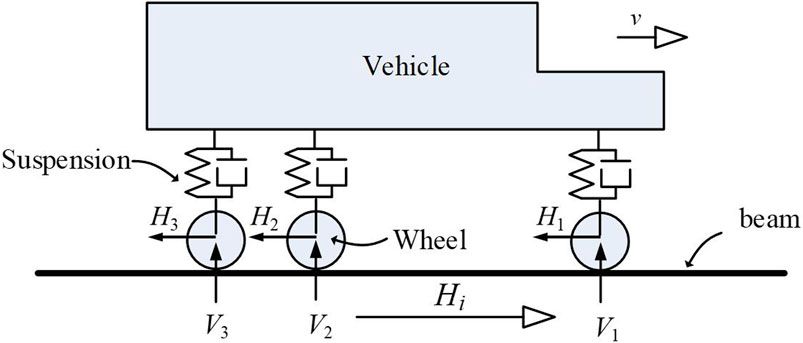
During construction, vehicles crossing the approach slab operate at an inclined angle relative to the ground, resulting in significant tangential forces between the wheels and the road. To accurately model these interactions, a Vehicle-Road Interaction (VRI) element is required, which can simultaneously account for both vertical and tangential wheel-road forces. The derivation of the VRI element’s governing equations follows the general approach of Yang and Wu (2001) for vehicle-bridge interaction, and we reference that work for standard derivation steps. Here we highlight the new elements introduced by our study, notably the numeical implementation of the VRI element in Abaqus via the user-defined element subroutine.

As shown in Figure 5, the vehicle moves at a constant velocity $v$ on a beam. The vehicle is modeled as a multi-rigid-body system, consisting of two rigid mass blocks representing the vehicle body and another rigid mass block for the wheels. These two components are connected by a suspension system, which is modeled using springs and dampers. The mass, stiffness, and damping matrices of the vehicle model are denoted as $m_v$, $k_v$, and $c_v$ respectively. The finite element dynamic control equation for the vehicle’s motion governed by Newton’s second law can be expressed as:

$\left[m_v\right]\left\{{\ddot{d}}_v\right\}+\left[c_v\right]\left\{{\dot{d}}_v\right\}+\left[k_v\right]\left\{d_v\right\}=\left\{f_v\right\}(1)$

where, $\left\{dv\right\}$ represents the displacement vector of the vehicle, which can be decomposed as $\left\{dv\right\}={〈〈d_u〉〈d_w〉〉}^T$, where subscripts $u$ and $w$ denote the displacements of the vehicle body and wheels, respectively. The load vector $\left\{fv\right\}$ can be further expressed as (Equation 2):

$\left\{f_v\right\}=\left\{f_e\right\}+\left[l\right]\left\{f_c\right\}(2)$

where $\left\{f_c\right\}=\left\{\begin{array}{cccc}{V}_1& V_2& \dots & V_{\mathrm{n}}\end{array}\right.{\}}^T$ is the contact force vector between the tires and the road surface, $\left[l\right]$ is the coordinate transformation matrix, and $\left\{f_e\right\}$ represents external loads other than the contact forces.

Figure 5

Figure 5. Schematic of the vehicle-road coupling unit.

3.1 Vehicle-road coupling element

Based on the degrees of freedom of the vehicle body and wheels, Equation 1 can be rewritten as:

$\begin{array}{ll}\hfill & \left[\begin{array}{cc}\left[m_{uu}\right]& \left[m_{uw}\right]\\ \left[m_{wu}\right]& \left[m_{ww}\right]\end{array}\right]{\left\{\begin{array}{c}\left\{{\ddot{d}}_u\right\}\\ \left\{{\ddot{d}}_w\right\}\end{array}\right\}}_{t+\Delta t}+\left[\begin{array}{cc}\left[c_{uu}\right]& \left[c_{uw}\right]\\ \left[c_{wu}\right]& \left[c_{ww}\right]\end{array}\right]{\left\{\begin{array}{c}\left\{{\dot{d}}_u\right\}\\ \left\{{\dot{d}}_w\right\}\end{array}\right\}}_{t+\Delta t}\hfill \\ \hfill & +\left[\begin{array}{cc}\left[k_{uu}\right]& \left[k_{uw}\right]\\ \left[k_{wu}\right]& \left[k_{ww}\right]\end{array}\right]{\left\{\begin{array}{c}\left\{d_u\right\}\\ \left\{d_w\right\}\end{array}\right\}}_{t+\Delta t}=\left\{\begin{array}{c}\left\{f_{ue}\right\}\\ \left\{f_{we}\right\}\end{array}\right\}+\left[\begin{array}{c}\left[l_u\right]\\ \left[l_w\right]\end{array}\right]{\left\{f_c\right\}}_{t+\Delta t}\hfill \end{array}(3)$

where, $\left\{f_{ue}\right\}$ and $\left\{f_{we}\right\}$ represent external loads acting on the vehicle body and wheels, respectively. The first row of Equation 3 corresponds to the vibration control equation for the vehicle body, while the second row corresponds to that for the wheels. Since contact forces only act on the wheels, $\left[l_u\right]=\left[0\right]$. Expanding the first row of Equation 3 yields:

${\left[m_{uu}\right]\left\{{\ddot{d}}_u\right\}}_{t+\Delta t}+{\left[c_{uu}\right]\left\{{\dot{d}}_u\right\}}_{t+\Delta t}+{\left[k_{uu}\right]\left\{d_u\right\}}_{t+\Delta t}={\left\{f_{ue}\right\}}_{t+\Delta t}-{\left\{q_{uc}\right\}}_{t+\Delta t}(4)$

where (Equation 5):

${\left\{q_{uc}\right\}}_{t+\Delta t}=\left[m_{uw}\right]{\left\{{\ddot{d}}_w\right\}}_{t+\Delta t}+{\left[c_{uw}\right]\left\{{\dot{d}}_w\right\}}_{t+\Delta t}+{\left[k_{uw}\right]\left\{d_w\right\}}_{t+\Delta t}(5)$

Let $\left\{\Delta d_u\right\}$ denote the displacement increment from time $t$ to $t+\Delta t$, where $\Delta t$ is the time step. Using the Newmark time-step integration method, the acceleration, velocity, and displacement of the vehicle body at $t+\Delta t$ can be expressed as:

${\left\{{\ddot{d}}_u\right\}}_{\mathrm{t}+∆\mathrm{t}}=a_0\left\{∆d_u\right\}-a_1{\left\{{\dot{d}}_u\right\}}_t-a_2{\left\{{\ddot{d}}_u\right\}}_t(6)$

${\left\{{\dot{d}}_u\right\}}_{t+\Delta t}={\left\{{\dot{d}}_u\right\}}_t+a_3{\left\{{\ddot{d}}_u\right\}}_t+a_4{\left\{{\ddot{d}}_u\right\}}_{t+\Delta t}(7)$

${\left\{d_u\right\}}_{t+\Delta t}={\left\{d_u\right\}}_t+\left\{∆d_u\right\}(8)$

where in the equations provided, the superscript $t$ denotes variables known at the current time step. The coefficients in the Newmark time-step integration method can be determined by the parameters $\beta$ and $\gamma$ ().

Substitute Equations 6–8 into Equation 4 yields Equations 10a, 10b:

$\left[{\mathrm{\Psi }}_{uu}\right]\left\{∆d_u\right\}={\left\{f_{ue}\right\}}_{t+\Delta t}-{\left\{q_{uc}\right\}}_{t+\Delta t}+{\left\{q_u\right\}}_t(9)$

where (Equation 10),

$\left[{\mathrm{\Psi }}_{uu}\right]=a_0\left[m_{uu}\right]+a_5\left[c_{uu}\right]+\left[k_{uu}\right](\mathrm{10a})$

${\left\{Q_u\right\}}_t=\left[m_{uu}\right]\left({a_1\left\{{\dot{d}}_u\right\}}_t+{a_2\left\{{\ddot{d}}_u\right\}}_t\right)+\left[c_{uu}\right]\left({a_6\left\{{\dot{d}}_u\right\}}_t+{a_7\left\{{\ddot{d}}_u\right\}}_t\right)-\left[k_{uu}\right]{\left\{d_u\right\}}_t(\mathrm{10b})$

By solving Equation 11, the displacement increments $t+\Delta t$ at $\left\{\Delta d_u\right\}$ can be obtained. Substituting this result back into Equations 6–8 provides the vehicle’s vibration response at.

$\left\{{∆d}_u\right\}={\left[{\mathrm{\Psi }}_{uu}\right]}^{-1}\left({\left\{f_{ue}\right\}}_{t+∆t}-{\left\{q_{uc}\right\}}_{t+∆t}+{\left\{q_u\right\}}_t\right)(11)$

Substituting Equation 11 into Equations 6–8 provides the vehicle’s vibration response at $t+\Delta t$:

${\left\{{\ddot{d}}_u\right\}}_{t+∆t}=a_0{\left[{\mathrm{\Psi }}_{uu}\right]}^{-1}\left({\left\{f_{ue}\right\}}_{t+∆t}-{\left\{q_{uc}\right\}}_{t+∆t}+{\left\{q_u\right\}}_t\right)-a_1{\left\{{\dot{d}}_u\right\}}_t-a_2{\left\{{\ddot{d}}_u\right\}}_t(\mathrm{12a})$

${\left\{{\dot{D}}_u\right\}}_{t+∆t}=a_5{\left[{\mathrm{\Psi }}_{uu}\right]}^{-1}\left({\left\{f_{ue}\right\}}_{t+∆t}-{\left\{q_{uc}\right\}}_{t+∆t}+{\left\{q_u\right\}}_t\right)-a_6{\left\{{\dot{d}}_u\right\}}_t-a_7{\left\{{\ddot{d}}_u\right\}}_t(\mathrm{12b})$

${\left\{D_u\right\}}_{t+∆t}={\left[{\mathrm{\Psi }}_{uu}\right]}^{-1}\left({\left\{f_{ue}\right\}}_{t+∆t}-{\left\{q_{uc}\right\}}_{t+∆t}+{\left\{q_u\right\}}_t\right)+{\left\{d_u\right\}}_t(\mathrm{12c})$

Substituting Equation 12a into the second row of Equation 3 (the wheel vibration control equation), the wheel-road contact force at $t+\Delta t$ can be expressed as:

${\left\{f_c\right\}}_{t+\Delta t}=\left[m_c\right]{\left\{{\ddot{d}}_w\right\}}_{t+\Delta t}+\left[c_c\right]{\left\{{\dot{d}}_w\right\}}_{t+\Delta t}+\left[k_c\right]{\left\{d_w\right\}}_{t+\Delta t}+{\left\{p_c\right\}}_{t+\Delta t}+{\left\{q_c\right\}}_t(13)$

where, the mass, damping, and stiffness matrices are defined in Equations 14a, 14b as:

$\left[m_c\right]={\left[l_w\right]}^{-1}\left(\left[m_{ww}\right]-\left[{\mathrm{\Psi }}_{wu}\right]{\left[{\mathrm{\Psi }}_{uu}\right]}^{-1}\left[m_{uw}\right]\right)(\mathrm{14a})$

$\left[C_c\right]={\left[l_w\right]}^{-1}\left(\left[c_{ww}\right]-\left[{\mathrm{\Psi }}_{wu}\right]{\left[{\mathrm{\Psi }}_{uu}\right]}^{-1}\left[c_{uw}\right]\right)(\mathrm{14b})$

$\left[K_c\right]={\left[l_w\right]}^{-1}\left(\left[k_{ww}\right]-\left[{\mathrm{\Psi }}_{wu}\right]{\left[{\mathrm{\Psi }}_{uu}\right]}^{-1}\left[k_{uw}\right]\right)(\mathrm{14c})$

The equivalent load vectors are expressed in Equation 15:

${\left\{p_c\right\}}_{t+∆t}={\left[l_w\right]}^{-1}\left(\left[{\mathrm{\Psi }}_{wu}\right]{\left[{\mathrm{\Psi }}_{uu}\right]}^{-1}{\left\{f_{ue}\right\}}_{t+∆t}-{\left\{f_{we}\right\}}_{t+∆t}\right)(\mathrm{15a})$

${\left\{Q_c\right\}}_t={\left[l_w\right]}^{-1}\left(\left[{\mathrm{\Psi }}_{wu}\right]{\left[{\mathrm{\Psi }}_{uu}\right]}^{-1}{\left\{q_u\right\}}_t-{\left\{q_w\right\}}_t\right)(\mathrm{15b})$

where (Equations 16a, 16b),

$\left[{\mathrm{\Psi }}_{wu}\right]=a_0\left[m_{wu}\right]+a_5\left[c_{wu}\right]+\left[k_{wu}\right](\mathrm{16a})$

${\left[Q_w\right]}_t=\left[m_{wu}\right]\left(a_1{\left\{{\dot{d}}_u\right\}}_t+a_2{\left\{{\ddot{d}}_u\right\}}_t\right)+\left[c_{wu}\right]\left(a_6{\left\{{\dot{d}}_u\right\}}_t+a_7{\left\{{\ddot{d}}_u\right\}}_t\right)-\left[k_{wu}\right]{\left\{d_u\right\}}_t(\mathrm{16b})$

From Equation 13, it is evident that the wheel-road contact force $t+\Delta t$ depends not only on the wheel vibration response at $\left\{f_c{\}}_{t+\Delta t}\right.$ ($\left\{{\ddot{d}}_w{\}}_{t+\Delta t}\right.$, $\left\{{\dot{d}}_w{\}}_{t+\Delta t}\right.$, and $\{d_w{\}}_{t+\Delta t}$) and the external load $\{p_c{\}}_{t+\Delta t}$, but also on the known quantities at time $t$. Assuming the wheel remains in contact with the road, the relationship between the wheel displacement $\left\{d_w\right\}$ and the road surface displacement at the contact point $\left\{d_c\right\}$ is expressed in Equation 17:

$\left\{d_w\right\}=\left[\mathrm{\Gamma }\right]\left\{d_c\right\}(17)$

where, $\left[\mathrm{\Gamma }\right]$ is a transformation matrix with elements of 1 or 0. Substituting this into Equation 13 establishes the relationship between the contact force and the contact displacement (Equation 18):

${\left\{f_c\right\}}_{t+∆t}=\left[m_c\right]{\left\{{\ddot{d}}_c\right\}}_{t+∆t}+\left[c_c\right]{\left\{{\dot{d}}_c\right\}}_{t+∆t}+\left[k_c\right]{\left\{d_c\right\}}_{t+∆t}+{\left\{p_c\right\}}_{t+∆t}+{\left\{q_c\right\}}_t(18)$

where the contact force for the i-th wheel/bridge deck at $V_{i,t+\Delta t}$ ($i=1,\dots ,\mathrm{n}$) can then be expressed as:

$V_{I,t+∆t}=p_{ci,t+∆t}+q_{ci,t}+{\displaystyle \sum _{j=1}^{\mathrm{n}}}\left(m_{cij}{\ddot{d}}_{cj,t+∆t}+c_{cij}{\dot{d}}_{cj,t+∆t}+k_{cij}{d}_{cj,t+∆t}\right)(19)$

In summary, the vehicle-road interaction model presented here effectively incorporates both vertical and tangential forces, providing a comprehensive framework for understanding the complex dynamics between the vehicle and the road surface.

3.2 Wheel-road contact force

The contact force expressed in Equation 19 directly acts on the road surface, which is discretized into Euler-Bernoulli (E-B) beam elements. Each i-th beam element is assumed to experience only the i-th contact force. The size of the beam elements must be adjusted so that each element interacts with at most one wheel. The vibration control equation for the i-th E-B beam element is expressed as:

$\left[M_{bi}\right]{\left\{{\ddot{d}}_{bi}\right\}}_{t+∆t}+\left[c_{bi}\right]{\left\{{\dot{d}}_{bi}\right\}}_{t+∆t}+\left[k_{bi}\right]{\left\{d_{bi}\right\}}_{t+∆t}={\left\{f_{bi}\right\}}_{t+∆t}-{\left\{f_{bci}\right\}}_{t+∆t}(20)$

where, $\left[m_{bi}\right]$, $\left[c_{bi}\right]$, $\left[k_{bi}\right]$ are the mass, damping, and stiffness matrices of the i-th E-B beam element; $\left\{d_{bi}\right\}$ is the nodal displacement vector of the beam element at time $t+\Delta t$; $\left\{f_{bi}\right\}$ is the equivalent nodal external load vector at time $t+\Delta t$; $\left\{f_{bci}\right\}$ is the equivalent nodal load vector contributed by the contact force $V_i$ at the current time step, defined as:

${\left\{F_{bci}\right\}}_{t+∆t}=\left\{N_{ci}^h\right\}{H}_{I,t+∆t}+\left\{N_{ci}^v\right\}{V}_{I,t+∆t}(21)$

where, $H_i={\mu }_i{V}_i$ represents the tangential wheel-road contact force, where ${\mu }_i$ is the coefficient of friction. $\left\{N_i^v\right\}$ is the Hermite interpolation function for the E-B beam element, which only has non-zero components for vertical degrees of freedom. All other translational and rotational degrees of freedom are set to zero. This assumes that the vertical contact force is distributed as vertical nodal loads without causing horizontal forces or bending moments at the nodes. Therefore, Equation 21 can be rewritten as:

${\left\{F_{bci}\right\}}_{t+∆t}=\left\{N_{ci}^h\right\}{\mu }_i{V}_{I,t+∆t}+\left\{N_{ci}^v\right\}{V}_{I,t+∆t}=\left({\mu }_i\left\{N_{ci}^h\right\}+\left\{N_{ci}^v\right\}\right)V_{I,t+∆t}(22)$

where, $\left\{N_{ci}^h\right\}=\left\{N^h\left({\xi }_i\right)\right\}$ represents the interpolation function. For E-B beam elements, the nodal degrees of freedom include horizontal displacement, vertical displacement, and rotation. The two interpolation functions related to horizontal displacement are $N_1^h\left(\xi \right)=1-\xi$ and $N_2^h\left(\xi \right)=\xi$, where $\xi =\frac{x-x_1}{l}$. Thus the interpolation function can be expressed in Equation 23:

$\left\{N_{ci}^h\right\}={\left\{1-\xi ,0,0;\xi ,0,0\right\}}^T(23)$

Based on Equation 22, the equivalent nodal load vector can be expressed in Equation 24 as:

$\begin{array}{ll}\hfill & {\left\{f_{bci}\right\}}_{t+\Delta t}=\left({\mu }_i\left\{N_{ci}^h\right\}+\left\{N_{ci}^v\right\}\right)\left[p_{ci,t+\Delta t}+q_{ci,t}+{\displaystyle \sum _{j=1}^{\mathrm{n}}}\left(\begin{array}{c}{m}_{cij}〈N_{cj}^v〉{\left\{{\ddot{d}}_{bj}\right\}}_{t+\Delta t}\\ +c_{cij}〈N_{cj}^v〉{\left\{{\dot{d}}_{bj}\right\}}_{t+\Delta t}\\ +k_{cij}〈N_{cj}^v〉{\left\{d_{bj}\right\}}_{t+\Delta t}\end{array}\right)\right]\hfill \\ \hfill & =\left({\mu }_i\left\{N_{ci}^h\right\}+\left\{N_{ci}^v\right\}\right)\left(p_{ci,t+\Delta t}+q_{ci,t}\right)\hfill \\ \hfill & +{\displaystyle \sum _{j=1}^{\mathrm{n}}}\left[\begin{array}{c}{\mu }_i\left\{N_{ci}^h\right\}{m}_{cij}〈N_{cj}^v〉{\left\{{\ddot{d}}_{bj}\right\}}_{t+\Delta t}+\left\{N_{ci}^v\right\}{m}_{cij}〈N_{cj}^v〉{\left\{{\ddot{d}}_{bj}\right\}}_{t+\Delta t}\\ +{\mu }_i\left\{N_{ci}^h\right\}{c}_{cij}〈N_{cj}^v〉{\left\{{\dot{d}}_{bj}\right\}}_{t+\Delta t}+\left\{N_{ci}^v\right\}{c}_{cij}〈N_{cj}^v〉{\left\{{\dot{d}}_{bj}\right\}}_{t+\Delta t}\\ +{\mu }_i\left\{N_{ci}^h\right\}{k}_{cij}〈N_{cj}^v〉{\left\{d_{bj}\right\}}_{t+\Delta t}+\left\{N_{ci}^v\right\}{k}_{cij}〈N_{cj}^v〉{\left\{d_{bj}\right\}}_{t+\Delta t}\end{array}\right]\hfill \end{array}(24)$

where the subscript $c$ denotes interpolation functions determined by the contact point coordinates. The vertical interpolation function $\left\{N_{ci}^v\right\}$ is defined in Equation 25 as:

$\left\{N_{ci}^v\right\}=\left\{N^v\left(\overline{x}\right)\right\}={〈1-3{\overline{x}}^2+2{\overline{x}}^3,0,0,3{\overline{x}}^2-2{\overline{x}}^3,0,0〉}^{\mathrm{T}}(25)$

where, $\overline{x}=\frac{x}{L}$ represents the local coordinate of the wheel-road contact point within the current E-B beam element, and $L$ is the element length. Substituting Equation 19 into Equations 20, 21 can be rewritten as:

$\begin{array}{ll}\hfill & \left[m_{bi}\right]{\left\{{\ddot{d}}_{bi}\right\}}_{t+∆t}+\left[c_{bi}\right]{\left\{{\dot{d}}_{bi}\right\}}_{t+∆t}+\left[k_{bi}\right]{\left\{d_{bi}\right\}}_{t+∆t}\hfill \\ \hfill & ={\left\{f_{bi}\right\}}_{t+∆t}-{\displaystyle \sum _{j=1}^{\mathrm{n}}}\left(\left[m_{cij}^{*}\right]\left\{{\ddot{d}}_{bj}\right\}+\left[c_{cij}^{*}\right]\left\{{\dot{d}}_{bj}\right\}+\left[k_{cij}^{*}\right]\left\{d_{bj}\right\}\right)-{\left\{p_{ci}^{*}\right\}}_{t+∆t}-{\left\{q_{ci}^{*}\right\}}_t\hfill \end{array}(26)$

where the superscript indicates structural matrices and load vectors influenced by the moving wheel. These are defined as:

$\left[m_{cij}^{*}\right]={\mu }_i\left\{N_{ci}^h\right\}{m}_{cij}〈N_{ci}^v〉+\left\{N_{ci}^v\right\}{m}_{cij}〈N_{cj}^v〉(\mathrm{27a})$

$\left[C_{cij}^{*}\right]={\mu }_i\left\{N_{ci}^h\right\}{c}_{cij}〈N_{ci}^v〉+\left\{N_{ci}^v\right\}{c}_{cij}〈N_{cj}^v〉(\mathrm{27b})$

$\left[K_{cij}^{*}\right]={\mu }_i\left\{N_{ci}^h\right\}{k}_{cij}〈N_{ci}^v〉+\left\{N_{ci}^v\right\}{k}_{cij}〈N_{cj}^v〉(\mathrm{27c})$

${\left\{P_{ci}^{*}\right\}}_{t+∆t}={{\mu }_i\left\{N_{ci}^h\right\}p}_{ci,t+∆t}+\left\{N_{ci}^v\right\}{p}_{ci,t+∆t}(\mathrm{27d})$

${\left\{Q_{ci}^{*}\right\}}_t={{\mu }_i\left\{N_{ci}^h\right\}q}_{ci,t}+\left\{N_{ci}^v\right\}{q}_{ci,t}(27e)$

Equation 26 represents the vibration control equation of the beam element incorporating the degrees of freedom of the vehicle (hereafter referred to as the VRI element). The contribution of the vehicle to the beam element is reflected in the structural matrices and equivalent load vectors on the right-hand side of Equation 26. As shown in Equation 27a, these terms depend on the real-time position x of the wheel. Therefore, the variables marked with * must be updated in real time according to the wheel’s position when forming the VRI element.

4 Numerical analysis model of the ancient seawall considering discrete-continuous characteristics

4.1 Contact elements and crack simulation

The ancient seawall is essentially a masonry structure composed of stone blocks. While the individual blocks exhibit discrete characteristics, the overall wall structure demonstrates continuum behavior. To account for these characteristics, a simplified decoupled modeling approach is adopted to establish the finite element analysis model of the ancient seawall. The masonry blocks are modeled individually, while the mortar layers are treated as contact elements acting between solid elements.

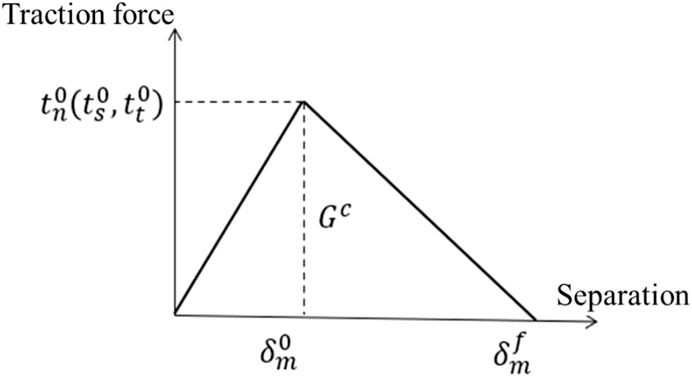
As shown in Figure 6, the “traction-separation model” in ABAQUS is used to describe the relationship between normal stress, shear stress, and relative displacement at the contact interface. The parameters of this model include ${\delta }_m^f$, which represents the nodal separation at complete interface failure; ${\delta }_m^0$, which denotes the nodal separation at the onset of interface damage; $t_n^0$, the tensile strength of the mortar; $t_s^0$ and $t_t^0$, the shear strengths of the mortar, and $G$, the shear modulus.

Figure 6

Figure 6. Linear damage evolution in the traction-separation model.

4.2 Finite element elements and constitutive models

The ancient seawall’s stone blocks and contact interfaces are discretized using C3D8R elements for the stone blocks and COH3D8 elements for the cohesive contact interfaces, respectively. The stone block elements employ the Drucker-Prager model, while the constitutive behavior of the interface elements follows the linear damage evolution shown in Figure 6. To simulate the degraded mechanical properties of the interface, initial damage and damage evolution laws are defined in the contact properties.

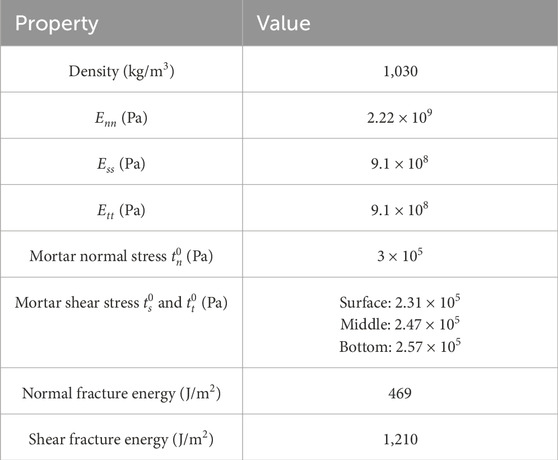
The parameters used in the model were drawn from a combination of literature values and site-specific data. For the seawall’s stone blocks, density and elastic properties follow typical values for granite masonry reported by Xie (2013), while strength parameters were calibrated against the compressive strength of the actual stones. The sticky-rice lime mortar interface parameters (Table 3) are based on experimental studies of historical mortars (Xie, 2013), ensuring realistic tensile and shear failure behavior.

The material properties of the stone blocks and cohesive contact models are detailed in Tables 1–3. This combination of constitutive models ensures that both the discrete behavior of the blocks and the continuum behavior of the mortar layers are accurately represented.

Table 1

Table 1. Material properties of the block layer in the ancient seawall structure.

Table 2

Table 2. Parameters of the plastic hardening material model for the stone blocks.

Table 3

Table 3. Material properties of the mortar layer for cohesive contact interfaces.

4.3 Model development and mesh generation

The schematic diagram of the ancient seawall model is shown in Figure 7. The model features a trapezoidal cross-section in the transverse direction, with bottom width of the model is 3.84 m, the top width is 1.44 m, and the height is 5.44 m. The model extends 5.7 m along the longitudinal direction of the seawall that encapsulates five masonry cycles of the prototype, which ensures that the model captures the representative structural behavior of the seawall.

Figure 7

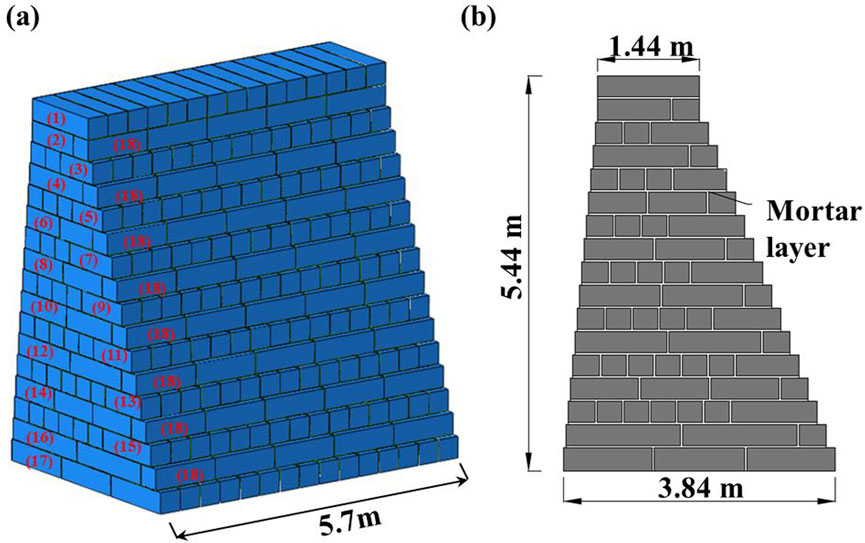
Figure 7. Schematic diagram of the model of the ancient seawall. (A) 3D illustration of the model dimensions, showing a longitudinal extension of 5.7 m. (B) Cross-sectional view of the model, showing a base width of 3.84 m, a top width of 1.44 m, and a height of 5.44 m.

The stone blocks in the model are simulated using stretcher and header bonding. Each block is rectangular with a cross-sectional size of 380 mm × 320 mm. However, the model includes 18 different block lengths, which are detailed in Table 4, to reflect the variability in block dimensions observed in the prototype. These dimensions were measured from the actual seawall (field survey data) – hence they reflect the real block size distribution. Figure 8 illustrates the structural mesh of the ancient seawall and the cohesive zone model, which provides a detailed representation of the contact behavior between the blocks and mortar layers.

Table 4

Table 4. Length specifications of boulders in the ancient seawall model.

Figure 8

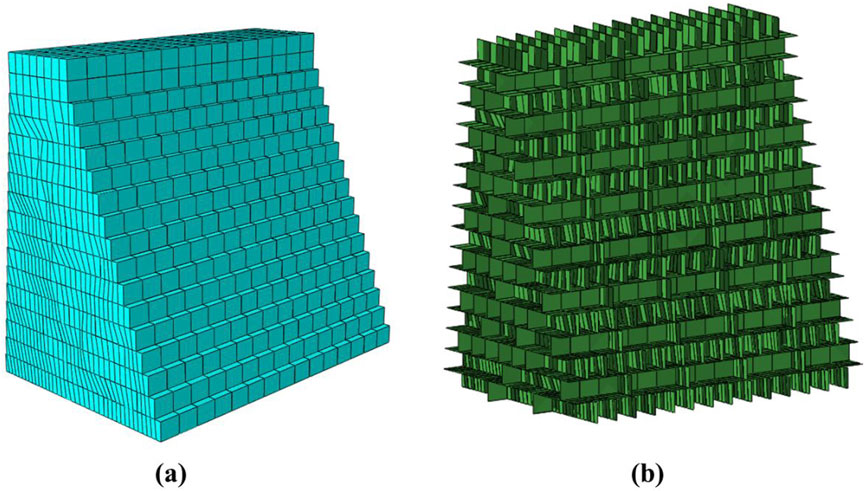
Figure 8. (A) Structural gridding of the ancient seawall; (B) Modelling of cohesive zones in the ancient seawall.

5 Simulation and validation of the approach slab crossing condition

5.1 Establishment of the approach slab crossing model

5.1.1 Soil model behind the ancient seawall

As illustrated in Figure 9, a soil model measuring 5.7 m in length, 12 m in width, and 5.44 m in height is constructed. This model primarily focuses on studying the impact of the approach slab crossing on the structure of the ancient seawall, excluding the effects of the road behind the embankment. Backfill soil properties (Tables 5–6) were obtained from in-situ geotechnical tests and are representative of the silty clay at the site. To simplify the analysis, only the properties of the fill soil are considered, as detailed in Table 5. The material property parameters for the soil model are presented in Table 6.

Figure 9

Figure 9. Soil modeling behind the embankment.

Table 5

Table 5. Physical and mechanical properties of the soil layer behind the embankment.

Table 6

Table 6. Material property parameters of the soil model behind the embankment.

5.1.2 Approach slab model

The approach slab consists of four components: longitudinal beams, crossbeams, the plate surface, and concrete bedding blocks. The modeling and meshing of each component are illustrated in Figures 10A–D. The longitudinal beams, crossbeams, and steel plate were modeled using a Young’s modulus of 206 GPa and a Poisson’s ratio of 0.3. The concrete bedding blocks were assigned a Young’s modulus of 20 GPa and a Poisson’s ratio of 0.2. A coefficient of friction of 0.2 was used to simulate the interaction between the wheels and the plate surface.

Figure 10

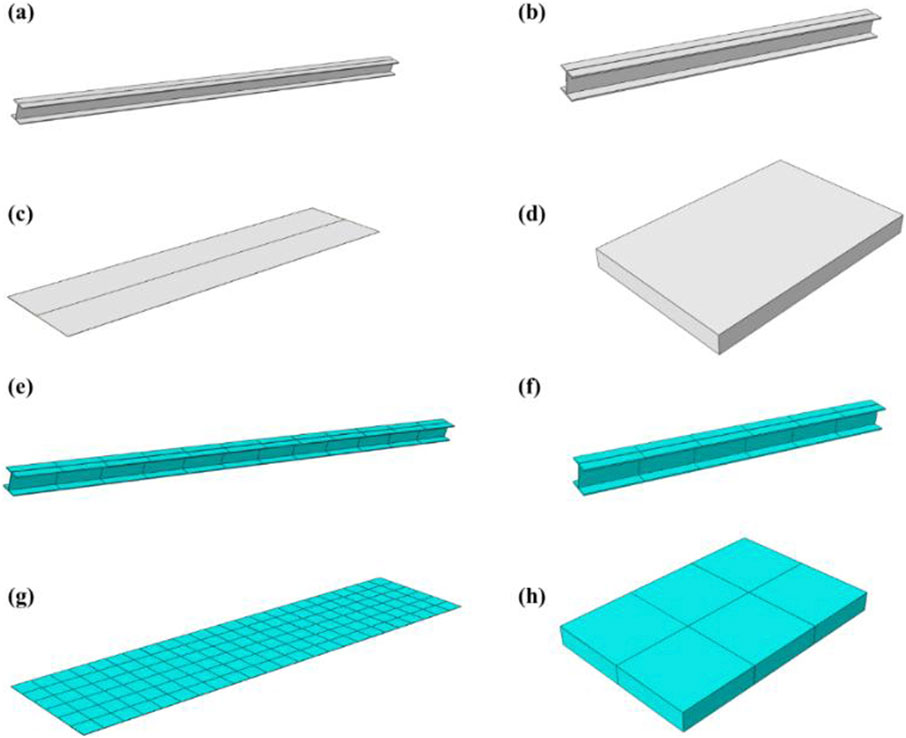
Figure 10. (A) Longitudinal beam model; (B) Crossbeam model; (C) Plate model; (D) Concrete bedding block model; (E) Longitudinal beam meshing; (F) Crossbeam meshing; (G) Plate meshing; (H) Concrete bedding block meshing.

5.1.3 Overall Model

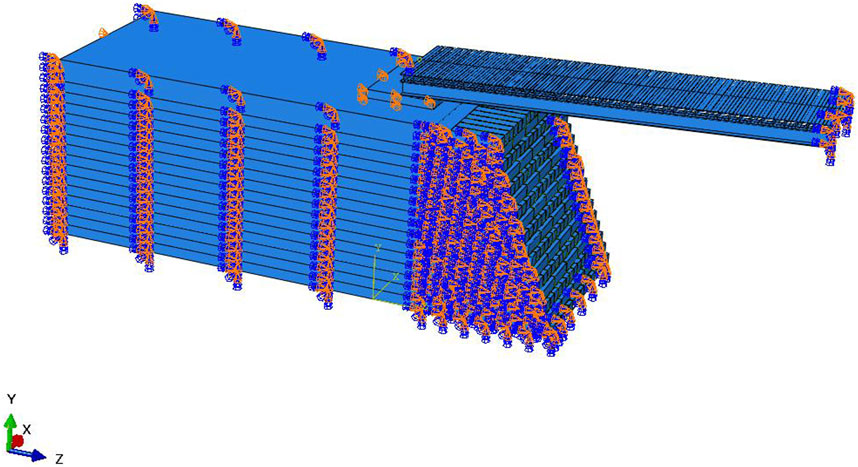
The individual components are assembled to form the complete approach slab structure, integrating with the subsurface soil and the ancient seawall, as shown in Figure 11. To accurately simulate the actual constraints between the seawall and the approach slab, the following boundary conditions are imposed: the bottom surfaces of the soil and ancient seawall are constrained in all six degrees of freedom; the lateral surfaces of both the soil and the seawall are constrained similarly; two degrees of freedom are constrained on the side surface of the concrete bedding block; one degree of freedom is constrained at the back surface of the soil; and all six degrees of freedom are constrained at the outer end of the approach slab.

Figure 11

Figure 11. Boundary condition settings for the approach slab crossing model.

5.2 Simulation of the approach slab crossing and comparison with measured results

By integrating the VRI elements into the approach slab crossing model, a simulation analysis is performed under a load condition of 10 t per axle and a vehicle speed of 5 km/h. Vibration velocities at the slab surface and the seawall top are extracted and compared with the on-site measured results. The vertical vibration velocity (Z) of the slab surface and the horizontal vibration velocity (X) at the seawall top are identified as the dominant directions of vibration. Figures 12, 13 show that the simulated and measured vibration time histories are in close agreement. Quantitatively, the simulation’s peak vertical velocity on the slab is 77.6 mm/s, which differs by only +0.5 mm/s (+0.6%) from the measured peak (78.1 mm/s). The peak horizontal velocity at the seawall top is 1.48 mm/s in the simulation versus 1.45 mm/s measured (a 2% difference). These quantitative metrics confirm that the model accurately reproduces both the amplitude and the temporal pattern of the vibrations observed in the field.

Figure 12

Figure 12. Comparison of slab surface vibration simulation results with measured results (vertical direction Z).

Figure 13

Figure 13. Comparison of simulation results and measured results of vibration on seawall top (horizontal direction X).

6 Analysis of vibration levels under different approach slab angles

To account for actual site conditions, the vehicle configuration is maintained with an axle load of 10 t and a speed of 5 km/h. The approach slab angle is varied across four scenarios (3°, 4°, 5°, and 6°) to analyze the vibration response of the ancient seawall structure at different angles. The peak vibration velocities on the slab surface and seawall top under each condition are summarized in Table 7. Interestingly, increasing the slab angle beyond 5° led to a decrease in the peak vibration (Table 7). This trend can be explained by the dynamics of the vehicle–slab interaction: at steeper angles, the vehicle’s suspension system and tire deformation play a greater role in absorbing the energy. Essentially, once the approach angle becomes large enough, a portion of the vehicle’s weight transfer is alleviated by the suspension compressing more significantly upon impact, resulting in slightly lower force transmitted to the seawall. Another contributing factor might be intermittent wheel contact at the steepest angle–the truck’s wheels could lose firm contact momentarily, reducing the effective impulse delivered to the structure. Vehicle-induced vibrations primarily cause vibrations in the slab surface along the horizontal X direction and vertical Z direction, with the vertical Z direction being the dominant vibration direction. The vibration peak velocity in the Z direction is significantly higher than that in the horizontal X and Y directions. On the seawall top, the horizontal X direction dominates the vibration response, with its peak vibration velocity exceeding those in the vertical Z and horizontal Y directions. This highlights the importance of horizontal vibrations in the dynamic behavior of the seawall.

Table 7

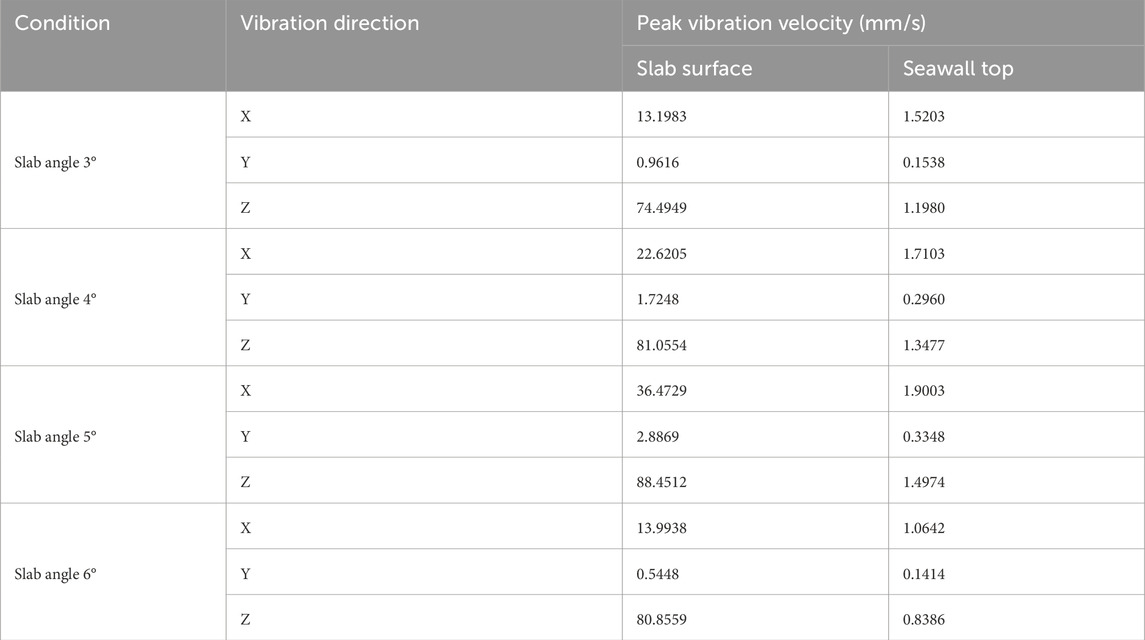
Table 7. Peak vibration velocities for an axle load of 10 t, vehicle speed of 5 km/h, and varying approach slab angles.

The simulation of a 3° slab angle, combined with a vehicle axle load of 10 t and a speed of 5 km/h, is simulated to analyze the vibration velocity trends, as depicted in Figure 14. The results reveal that the slab surface vibration velocity peaks at the center of the plate, while the vibration velocity on the seawall top attains its maximum at approximately 3 s after the vehicle begins crossing the slab. This peak is attributed to the second and third axles of the vehicle successively move onto the slab, based on the vehicle’s speed and axle spacing. Following these initial peaks, the subsequent vibration velocities diminish, indicating that the impact of the vehicle-induced vibrations decreases over time. Furthermore, the overall vibration pattern observed at the seawall top is consistent with the behavior recorded on the slab surface, highlighting a strong correlation between the two structural components in their dynamic responses.

Figure 14

Figure 14. Simulation results for a 10 t axle load, 5 km/h vehicle speed, and a 3° approach slab angle.

Our observation that vertical vibrations dominate on the approach slab is consistent with prior field measurements on this seawall and with traffic-induced vibration studies on similar structures (Zhu et al., 2023). In contrast, the seawall top experienced a significant horizontal vibration (along the wall’s length), a behavior not commonly seen in more monolithic structures like buildings (where vertical components usually prevail under vehicle loading, as noted by Li et al., 2010). This discrepancy may be attributed to the seawall’s discrete block construction and relatively flexible response in the transverse direction, which can amplify horizontal motions. By comparing our results with these studies, it is evident that the Yanguan seawall exhibits a unique dynamic response that bridges characteristics of both masonry buildings and geotechnical structures.

The insights from the above resulys offer valuable guidance for designing safer reinforcement strategies for heritage structures. Specifically, the results show that optimizing the approach slab angle (e.g., keeping it at or below 5°) can help minimize the vibration transmitted to the ancient seawall. Furthermore, the validated model provides a tool to evaluate other influencing parameters, such as axle loads and speed, in future planning. These findings can inform traffic control strategies and construction planning for projects near or on vulnerable cultural relics, thereby contributing to their long-term preservation.

7 Limitations and future work

This study has a few limitations that suggest avenues for further research. First, the numerical model was validated for a specific vehicle load (10 t per axle) and speed (5 km/h); the effects of heavier vehicles and higher speeds were not directly examined and should be investigated in future work to ensure the seawall’s safety under more extreme conditions. Second, some simplifying assumptions were made: for example, the foundation beyond the modeled soil domain was assumed fixed, and long-term material degradation was not considered. Future studies could incorporate varying boundary conditions–such as more extensive soil domains or the influence of adjacent seawall sections–to evaluate their impact on the vibration response. A systematic sensitivity analysis on model parameters (e.g., stone–mortar interface properties, damping ratios) is also recommended to assess the robustness of the conclusions. Moreover, while this work focused on characterizing the vibrations, it did not examine specific mitigation measures; hence, exploring vibration reduction techniques (like damping layers or speed restrictions) would be a valuable next step. Addressing these points in subsequent research will broaden the applicability of the proposed model and contribute to more effective protection strategies for this and other ancient seawall structures.

8 Conclusion

This study presents a three-dimensional numerical analysis method to assess the vibration effects induced by moving vehicles on the Yanguan ancient seawall during its upgrading and reconstruction as part of the Qiantang River seawall reinforcement project. The analysis specifically focuses on the approach slab crossing condition, a critical construction scenario. The methodology was validated against field-measured vibration data collected during the construction process. The primary conclusions of this study are as follows:

(1) A VRI element, capable of accounting for both vertical and tangential wheel-road contact forces, was successfully developed using the UEL interface in ABAQUS. This element was integrated into a three-dimensional finite element model of the ancient seawall. The model discretized rubble stones and sticky rice mortar using solid elements and cohesive zone elements, respectively, effectively capturing the discrete-continuum structural characteristics of the seawall’s composition.

(2) A three-dimensional finite element model of the approach slab crossing condition was constructed and validated through a comparison with field-measured vibration results. The numerical simulation results closely aligned with the measured data, successfully replicating the observed trends and peak vibration values. This validation demonstrates the model’s reliability in predicting the structural vibrations of the ancient seawall under construction-induced loads.

(3) The validated numerical model was used to simulate and predict the vibration responses of the ancient seawall under different approach slab angles. These simulations provided critical insights into vibration behavior and served as a basis for ensuring the structural safety of the seawall during construction. Furthermore, the findings also contribute valuable scientific evidence for heritage conservation, supporting the safe restoration and preservation of this historically significant structure.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

WL: Funding acquisition, Writing – original draft. QC: Methodology, Validation, Writing – original draft. MH: Data curation, Investigation, Writing – original draft. YX: Conceptualization, Software, Writing – original draft. BL: Data curation, Methodology, Writing – original draft. LS: Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

Authors QC, MH, YX, and BL were employed by PowerChina Huadong Engineering Corporation.

Authors QC, MH, YX, and BL were employed by Zhejiang Huadong Engineering Construction Management Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ali, Q., Khan, A. N., Ashraf, M., Ahmad, A., Alam, B., Ahmad, N., et al. (2013). Seismic performance of stone masonry buildings used in the Himalayan belt. Earthq. Spectra 29 (4), 1159–1181. doi:10.1193/091711eqs228m

CrossRef Full Text | Google Scholar

Andreotti, G., Graziotti, F., and Magenes, G. (2018). Detailed micro-modelling of the direct shear tests of brick masonry specimens: the role of dilatancy. Eng. Struct. 168, 929–949. doi:10.1016/j.engstruct.2018.05.019

CrossRef Full Text | Google Scholar

Bayraktar, A., Calik, I., Türker, T., and Yildirim, F. (2018). Restoration effects on experimental dynamic characteristics of masonry stone minarets. Mater. Struct. 51 (6), 141. doi:10.1617/s11527-018-1272-2

CrossRef Full Text | Google Scholar

Calik, I., Bayraktar, A., Türker, T., and Yildirim, F. (2020). Ambient vibration based-simplified frequency formulas for historical masonry stone mosques with timber truss roofs. J. Archit. Conservation 26 (3), 247–264. doi:10.1080/13556207.2020.1790145

CrossRef Full Text | Google Scholar

Chen, L., and Pan, C. (2008). Research on river bed regulation in strong tidal reaches of Qiantang River [In Chinese]. Ocean Eng. 111 (2), 96–101.

Google Scholar

De Angelis, A., Lourenço, P. B., Sica, S., and Pecce, M. R. (2022). Influence of the ground on the structural identification of a bell-tower by ambient vibration testing. Soil Dyn. Earthq. Eng. 155, 107102. doi:10.1016/j.soildyn.2021.107102

CrossRef Full Text | Google Scholar

Günaydin, M., Genç, A. F., Altunışık, A. C., Haciefendioğlu, K., Okur, F. Y., Okur, E., et al. (2022). Structural condition assessment of a historical masonry school building using experimental and numerical methods. J. Civ. Struct. Health Monit. 12 (5), 1083–1113. doi:10.1007/s13349-022-00597-x

CrossRef Full Text | Google Scholar

Hinzen, K.-G. (2014). Subway-induced vibrations in cologne cathedral. Seismol. Res. Lett. 85, 631–638. doi:10.1785/0220140003

CrossRef Full Text | Google Scholar

Kowalska-Koczwara, A., and Stypula, K. (2016). “Protection of historic buildings against environmental pollution of vibrations,” in 1st international conference on the sustainable energy and environment development (SEED 2016) (Les Ulis, France: EDP Sciences). doi:10.1051/e3sconf/2016100004300043

CrossRef Full Text | Google Scholar

Krentowski, J. R., Knyziak, P., Pawłowicz, J. A., and Gavardashvili, G. (2023). Historical masonry buildings’ condition assessment by non-destructive and destructive testing. Eng. Fail. Anal. 146, 107122. doi:10.1016/j.engfailanal.2023.107122

CrossRef Full Text | Google Scholar

Li, K., Liu, W., Liu, W., and Chen, Y. (2010). “Tests and analysis of metro-induced vibration effects on surrounding historic buildings,” in Key technologies of railway engineering – high speed railway, heavy haul railway and urban rail transit (Beijing, China: China Railway Publishing House), 921–926.

Google Scholar

Lotfi, H. R., and Shing, P. B. (1994). Interface model applied to fracture of masonry structures. J. Struct. Eng. 120 (1), 63–80. doi:10.1061/(asce)0733-9445(1994)120:1(63)

CrossRef Full Text | Google Scholar

Lourenço, P. B., and Rots, J. G. (1997). Multisurface interface model for analysis of masonry structures. J. Eng. Mech. 123 (7), 660–668. doi:10.1061/(asce)0733-9399(1997)123:7(660)

CrossRef Full Text | Google Scholar

Ma, M., Cao, Y., Sun, X., and Liu, W. (2018). “Prediction of metro train-induced vibrations on a historic building: the case of the Round City and Chengguang Hall in Beijing,” in Recent developments in railway track and transportation engineering, sustainable civil infrastructures. Editors J. Pombo, and G. Jing (Springer), 133–141. doi:10.1007/978-3-319-77682-8_11

CrossRef Full Text | Google Scholar

Montabert, A., Mercerat, E. D., Lyon-Caen, H., and Lancieri, M. (2024). Highlighting the impact of the construction history of a cultural heritage building through a vibration-based finite element model updated by particle swarm algorithm. Int. J. Archit. Herit. 18 (8), 1263–1288. doi:10.1080/15583058.2023.2219237

CrossRef Full Text | Google Scholar

Page, A. W. (1978). Finite element model for masonry. J. Struct. Div. 104 (8), 1267–1285. doi:10.1061/jsdeag.0004969

CrossRef Full Text | Google Scholar

Pan, C., Zeng, J., Tang, Z., Zhang, Y., and Wang, L. (2013). A study of sediment characteristics and riverbed erosion/deposition in Qiantang estuary [In Chinese]. Hydro-Science Eng. (1), 1–7.

Google Scholar

Poovarodom, N., Choopthong, W., Bhadrakom, B., Chaiyasarn, K., Limsamphancharoen, N., and Hussain, Q. (2024). Assessment of traffic-induced ground vibrations and effects on masonry monuments in Ayutthaya Historical Park, Thailand. Stud. Conservation 69 (4), 230–242. doi:10.1080/00393630.2023.2213922

CrossRef Full Text | Google Scholar

Sadeghi, J., and Esmaeili, M. H. (2017). Safe distance of cultural and historical buildings from subway lines. Soil Dyn. Earthq. Eng. 96, 89–103. doi:10.1016/j.soildyn.2017.02.008

CrossRef Full Text | Google Scholar

Xie, Y. G. (2013). Mechanical behavior of glutinous rice mortar and damage mechanism of ancient sea ponds [Master’s thesis, Hangzhou, China: Zhejiang University]. (In Chinese).

Google Scholar

Xin, Y., Li, X., and Wang, J. (2019). “Risk analysis of the impact of metro construction activities on cultural relics,” in Proceedings of the sixth symposium of risk analysis and risk management in western China (WRARM 2019) (Paris, France: Atlantis Press). doi:10.2991/wrarm-19.2019.39

CrossRef Full Text | Google Scholar

Yang, Y., and Wu, Y. (2001). A versatile element for analyzing vehicle–bridge interaction response. Eng. Struct. 23 (5), 452–469. doi:10.1016/s0141-0296(00)00065-1

CrossRef Full Text | Google Scholar

Yu, X., Li, L., and Wu, X. (2010). Numerical simulation and analysis on tidal inundation of northern plain in Qiantang River estuary under ultra-violent typhoon [In Chinese]. Yangtze River, 41(8), 14–17, 50.

Google Scholar

Zhao, T. F., Meng, Z. B., Jin, J., and Li, X. F. (2013). Dynamic response analysis of Xi’an Bell Tower timber structure under the metro-vibration load of Line 6. Appl. Mech. Mater. 353–356, 1718–1723. doi:10.4028/www.scientific.net/AMM.353-356.1718

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, Y., Chen, Z., Zhang, K., Zhang, D., and Liu, J. (2014). Field test on earth pressure of ancient seawall with different backfills for Qiantang River [In Chinese]. Rock Soil Mech. 35 (6), 1623–1628.

Google Scholar

Zhu, S., Tu, X., Hu, M., Wang, T., and Zhou, L. (2023). Field investigation on the impact of vehicle traffic on the vibration of ancient seawalls in Qiantang River. Front. Mar. Sci. 10, 1212413. doi:10.3389/fmars.2023.1212413

CrossRef Full Text | Google Scholar

Zou, Z., and Shen, Y. (2017). Influence of the reclamation project at Qiantang estuary on the hydrodynamics and water environment in Hangzhou Bay [In Chinese]. Port & Waterw. Eng. (1), 26–33.

Google Scholar