Fault surface construction method based on point cloud surface reconstruction

Fault surface construction plays an important role in seismic structural interpretation and building structural models. Significant research studies have been carried out regarding fault surface extraction in the past few years. In these studies, the main challenges include the following: some fault samples are locally missing, the noise and the geological discontinuity features, some fault surfaces may form complicated intersections with each other, and some adjacent faults with similar directions are difficult to classify. In this paper, we propose a point cloud surface reconstruction method to automatically construct and classify the fault surfaces from a 3D seismic image so that the fault surfaces are constructed completely and accurately. In this method, we first use the fault-scanning method to smooth the fault attribute image and thin the smoothed fault attribute image. We then pick the seed points from the thinned attribute image as control points and use the random sample consensus method to compute the optimal surface that passes through these seed points. Finally, we construct the complete fault surfaces by merging all these optimal surface patches and use moving least square (MLS) to reconstruct the fault surfaces to smooth them and interpolate possible holes. With fitting the fault surfaces by MLS, we can also accurately estimate fault orientations. We demonstrate the efficiency and effectiveness of the method by using model seismic data and open access seismic data that are complicated by intersecting faults and noise.

Introduction

Faults are important discontinuous geological structures in analysis of underground oil reservoirs. Therefore, fault interpretation is an important part of seismic interpretation. To construct fault surfaces from seismic data, we often compute a fault attribute volume, in which the faults are the most prominent. Various approaches have been proposed to calculate fault attribute images to detect faults, such as semblance (Marfurt et al., 1998; Lou et al., 2019a), coherency (Marfurt et al., 1999 Qi et al., 2017a), variance (Van Bemmel and Pepper, 2000; Randen et al., 2001), curvature (Roberts, 2001; Al-Dossary and Marfurt, 2006), and gradient magnitude (Aqrawi and Boe, 2011). However, these attributes are sensitive to the discontinuous features unrelated to faults, such as stratigraphic features or noise. With the rise of artificial intelligence, researchers have shown research interest in using artificial intelligence techniques for automatic identification of faults, such as convolutional neural networks (Huang et al., 2017; Di et al., 2018; Wu et al., 2019b) and transfer learning (Zhou et al., 2021).

Constructing fault surfaces from fault attribute images often requires additional processing. Lees (1999) built triangulated surfaces from the point cloud obtained by voxel tracking from semblance volumes. Pedersen et al. (2002) proposed an ant-tracking method to extract fault surfaces, which significantly improves the visual appearances of fault surfaces and reveals details hidden by noise. Gibson et al. (2005) proposed the highest confidence first merging strategy combined with parametric models and residual fields, which merges small fault surfaces into a set of complete fault surfaces. Cohen et al. (2006) used skeletonization to operate fault extraction. Kadlec et al. (2008) used level sets to construct fault surfaces from fault attribute images and proposed a hierarchical clustering algorithm constrained by orientations to automatically classify faults. Wang and AlRegib (2014) used 3D Hough transform and the weighted plane fitting method to detect fault planes and extract smooth fault surfaces. Because the Hough transform is suitable for straight-line detection, it may work well in the case of approximately planar faults, but not for curved faults. Hale (2013) applied a crease-surface-based method to construct surfaces from fault likelihood attributes. Wu and Zhu (2017) used a tensor-voting method to construct fault surfaces that reasonably fit locations and orientations of fault samples and fill holes due to the missing samples. Zhou et al. (2022) developed a novel fault extraction workflow from a global perspective and used topological metrics to automatically generate fault surfaces from seismic attribute data. Bi and Wu (2021) adopted the Poisson equation surface method and the point-set surface method to automatically construct complete faults from the fault attribute image without any holes. Zhou et al. (2022) proposed a novel fault extraction workflow from a global perspective, which can extract fault surfaces on the premise of obtaining the fault distribution of the entire data set.

We first discuss the method of optimal surface picking by using the random sample consensus (RANSAC) algorithm (Li et al., 2023). As it solves for the optimal surface in a small box window, the RANSAC method is robust for computing the optimal surfaces passing through the control point from the thinned fault attribute image in the small box window that has noise and multiple faults.

To construct fault surfaces from 3D seismic attribute images by using the point cloud surface reconstruction method, we first apply the fault-scanning method (Hale, 2013; Wu and Hale, 2016) to smooth the fault attribute image and thin the smoothed attribute image. Then, we pick seed points from the thinned attribute image. For each seed point, we efficiently pick an optimal surface patch that passes through the seed point. Finally, we merge all these picked optimal surfaces into a set of complete fault surfaces and automatically classify the fault surfaces according to their orientations at the same time. We reconstruct the merged fault surfaces by using the moving least square (MLS) method (Zeng and Lu, 2004) to smooth the fault surfaces and interpolate possible holes on the fault surfaces. We demonstrate the efficiency and effectiveness of the method by using multiple examples that are complicated by intersecting faults and heavy noise.

Optimal surface picking

Faults are approximately planar surfaces in small 3D seismic image cubes (Figure 1a). Therefore, fault surface picking from the seismic attribute image is a problem of searching for an optimal surface in a small box window. We use the RANSAC algorithm to efficiently pick such optimal surface patches.

Figure 1

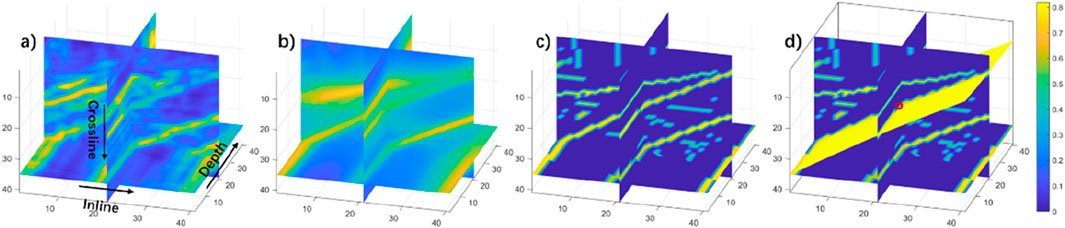
Figure 1. Process of optimal fault surface picking. (a) Seismic attribute image; (b) enhanced fault attribute image, and (c) thinned fault attribute image; (d) the optimal fault surface is picked from the thinned attribute image that passes through the control point (red circle).

To explain how to pick the optimal surface at the specified point from the attribute image in a small box window (Figure 1a), we first smooth the image, as shown in Figure 1b. The fault features become more continuous after smoothing. Then, we apply a non-maximum suppression to thin the fault attributes (Figure 1c) so that the faults are more easily recognized. By choosing the points in the thinned attribute image, whose values are larger than the set threshold, the fault points can be selected by setting the threshold of 0.2. By doing this, the fault points can be regarded as a three-dimensional point cloud, and we are able to pick the optimal surface passing through the control point (the red point in Figure 1d) by the RANSAC method.

The RANSAC algorithm can be summarized into two parts: hypothesis and validation. The assumption part of the work requires the assumption of the parameters in the algorithm validation, which include the distance deviation threshold T to satisfy the plane model, the threshold M for the number of point clouds to satisfy the plane model, and the number of validation iterations N. The algorithm will verify whether the model parameters calculated from the minimum sample subset selected during the iterative calculation process can meet the optimal model parameters. In our paper, the RANSAC algorithm process is implemented as follows:

1) Select three points to form the plane model S (one point is the control point, and the other two points are randomly selected from the fault points; these three points are not collinear), and calculate the plane equation. If the three points P1, P2, and P3 are $\left(x_1,y_1,z_1\right)$, $\left(x_2,y_2,z_2\right)$, and $\left(x_3,y_3,z_3\right)$, the plane equation is $\text{Ax}+\text{By}+\text{Cz}+\mathrm{D}=0$, and we can calculate the coefficient of the plane equation as follows Equations 1–4:

$\mathrm{A}=\frac{\left(x_3\left(y_2-z_2\right)-y_3\left(x_2-z_2\right)-z_3\left(y_2-z_2\right)+z_3\left(x_2-z_2\right)\right)}{\left(\left(x_1-z_1\right)\left(y_2-z_2\right)-\left(y_1-z_1\right)\left(x_2-z_2\right)\right)}.(1)$

$\mathrm{B}=\frac{\left(x_3-\mathrm{a}\left(x_1-z_1\right)-z_3\right)}{\left(x_2-z_2\right)}.(2)$

$\mathrm{C}=-1.(3)$

$\mathrm{D}=z_3-a*z_1-b*z_2.(4)$

2) Assuming that the k-neighborhoods of these three points have k1, k2, and k3 points, m points need to meet the condition of conforming to the interior point before continuing with the next step of the algorithm, otherwise reselecting the initial three points. The m points can be calculated as follows Equation 5:

$\mathrm{m}>\mathrm{t}\times \left(k_1+k_2+k_3\right).(5)$

In this paper, t is taken as 0.5.

3) Calculate the distance from all the fault points to the plane S. The distance can be calculated as follows Equation 6:

$d_k=\mathrm{A}{\mathrm{x}}_k+\mathrm{B}{\mathrm{y}}_k+\mathrm{C}{\mathrm{z}}_k+\mathrm{D}.(6)$

Here, $d_k$ is the distance from point $\left(x_k,y_k,z_k\right)$ to the plane S.

4) Checking the fitting plane. The point whose distance from the plane is less than the distance threshold T is called the inner point, and the point that does not meet is called the outer point, and the number of points of the current inner point is saved. If the proportion of points in the current plane to the fault points is greater than the set threshold M, or the number of random sampling reaches the maximum number N of iterations of the algorithm, the algorithm ends; otherwise, it continues.

The yellow surface in Figure 1d shows the selected optimal surface, which passes through the control point and correctly follows the high fault attribute values and the most inner points in the fault points. We display the picked surface with the thinned fault attribute images (Figure 1d), where we observe that the surface correctly follows the picked fault.

3D fault surface construction

We have discussed automatically picking the optimal fault surface passing through the control point from a fault attribute image with noisy and discontinuous fault features in small box windows by using the RANSAC method. In picking a single fault surface, we have assumed that there is only one fault corresponding to the control point and that the fault is an approximately planar plane surface in a small seismic attribute image cube. However, a 3D seismic fault attribute image often contains multiple faults with different orientations and spatial extensions. In this section, we use the point cloud surface reconstruction method to robustly construct complete fault surfaces in 3D seismic fault attribute images. The surface construction procedure consists of three steps. We first use the fault-scanning method (Hale, 2013; Wu and Hale, 2016) to smooth the fault attribute image and thin the smoothed attribute image. Then, we pick seed points from the thinned attribute image and pick the optimal surface patches that pass through these seed points. Finally, we merge all these picked optimal surfaces into a set of complete fault surfaces and reconstruct the merged fault surfaces by using the MLS method to smooth the fault surfaces and interpolate possible holes on fault surfaces.

Step 1: 3D fault attribute image smoothing and thinning

To highlight faults in a seismic attribute image (such as Figure 2b), we use the fault scanning method to smooth the fault attribute image (Hale, 2013; Wu and Zhu, 2017). This is a simple and efficient method to smooth a 3D fault image by applying a smoothing filter defined by all possible directions of the strike angle and dip angle. The whole process can be expressed as follows Equation 7:

$\mathrm{m}\left(\mathrm{x}\right)=\underset{\phi ϵ{\phi }_s,\theta ϵ{\theta }_s}{\arg \max }f\left(x\right)*g\left(\phi ,\theta \right),(7)$

where ${\phi }_s=\left\{0°,d_{\phi },{2d}_{\phi },\cdots 360°\right\}$, ${\theta }_s=\left\{{\theta }_{\mathit{min}},{\theta }_{\mathit{min}}+d_{\theta },{\theta }_{\mathit{min}}+{2d}_{\theta },\cdots {\theta }_{\mathit{max}}\right.$$\left.\cdots |{\theta }_{\mathit{max}}\right\}$, and $g\left(\phi ,\theta \right)$ denotes the filters defined by the fault dip and strike. $f\left(x\right)$ denotes the 3D fault attribute image. $\mathrm{m}\left(\mathrm{x}\right)$ denotes the maximum smoothing response. We choose a model data set to display the smoothing result (Figure 2c). We find that the smoothed fault image highlights most of the fault features. However, it is still challenging to construct fault surfaces because many spurious fault features are enhanced with high values, which significantly blurs the surface construction. In addition, a basic assumption of the scanning method is that one seismic image point exactly corresponds to one fault. However, that is no longer valid for a complicated intersected fault system because the fault attribute values in other crossed directions can also be high enough to be interpreted as faults. The fault samples near the fault intersections and noise cannot be completely obtained, and thus, the constructed fault surfaces suffer from holes.

Figure 2

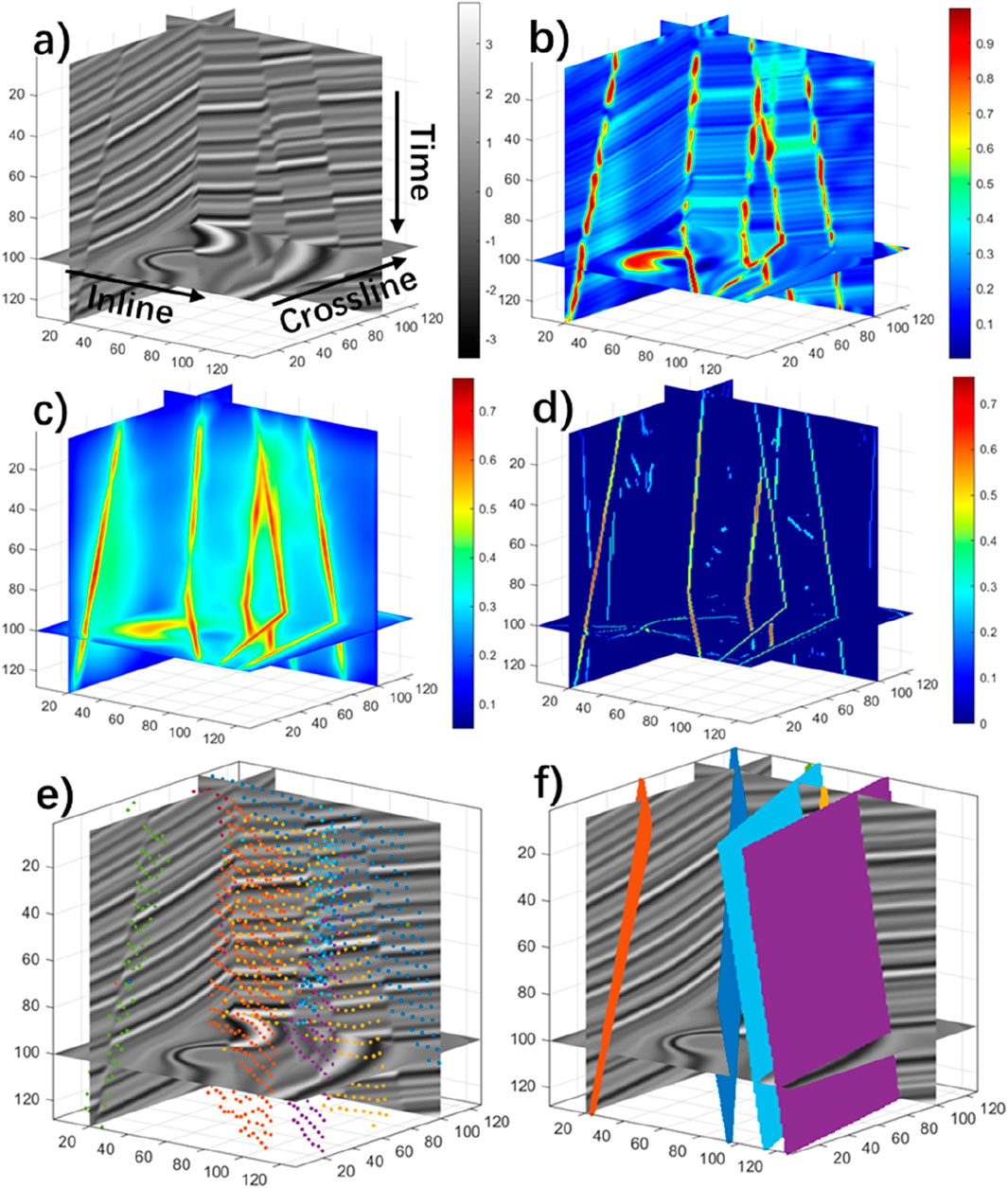
Figure 2. Process of fault surface construction in synthetic seismic data. (a) synthetic seismic image; (b) fault attribute image computed from the seismicimage; (c) smoothed fault attribute image computed from the fault attribute image; (d) thinned fault attribute image; (e) seed points picked from the thinned attribute image; (f) surface constructed by the point cloud method.

Step 2: seed point picking and optimal surface patch picking

With the smoothed fault attribute image, our next step is to automatically compute seed points and pick the optimal fault surface patches at seed points.

In computing the seed points, we first compute a thinned fault attribute image by applying non-maximum suppression to the smoothed fault attribute image. In this non-maximum suppression, we keep only the attribute values on the ridges of the fault attribute image and set zeros elsewhere to obtain the thinned attribute image (Figure 2d). Then, we select seed candidates from the thinned attribute image by collecting all the image samples with attribute values that are larger than some thresholds. Finally, we check in the true seeds from all the candidate points in order from the one with the highest attribute value to the one with the lowest value. In checking in the seeds, we compute the distances between the current candidate to all the previously checked-in seeds and check the current candidate as a true seed only if the minimum distance is larger than some predefined radius ($\mathrm{r}=6$ for the example in Figure 2e). By doing this, we can greatly reduce the number of seed points and, therefore, save computational time for the followed optimal surface picking at the seed points. A smaller radius will yield more seed points, which would be better for the next step of constructing the surface, but this requires more computational time for computing the optimal surface. Based on our experience, the radius r depends on the fault curvature. When the fault curvature is high, a smaller r should be selected to ensure the accuracy of fault surface calculation. When the fault curvature is low, a larger r should be selected to ensure the accuracy of fault surface calculation.

For each seed point, we define a 3D box window that is centered at the seed and is aligned in the x–y–z space (x denotes the inline direction, y denotes the crossline direction, and z denotes the time direction). We use the seed as a control point in the RANSAC algorithm to pick the optimal surface from the thinned fault attribute patch located within the box window (as shown in Figure 1). In this way, we pick all the optimal surface patches at these seed points.

Step 3: fault surface construction

In this paper, there are two main steps to construct the fault surfaces: (1) linking the nearby optimal surface patches to construct fault surfaces (Figure 3b) and (2) using MLS to reconstruct fault surfaces without any holes.

Figure 3

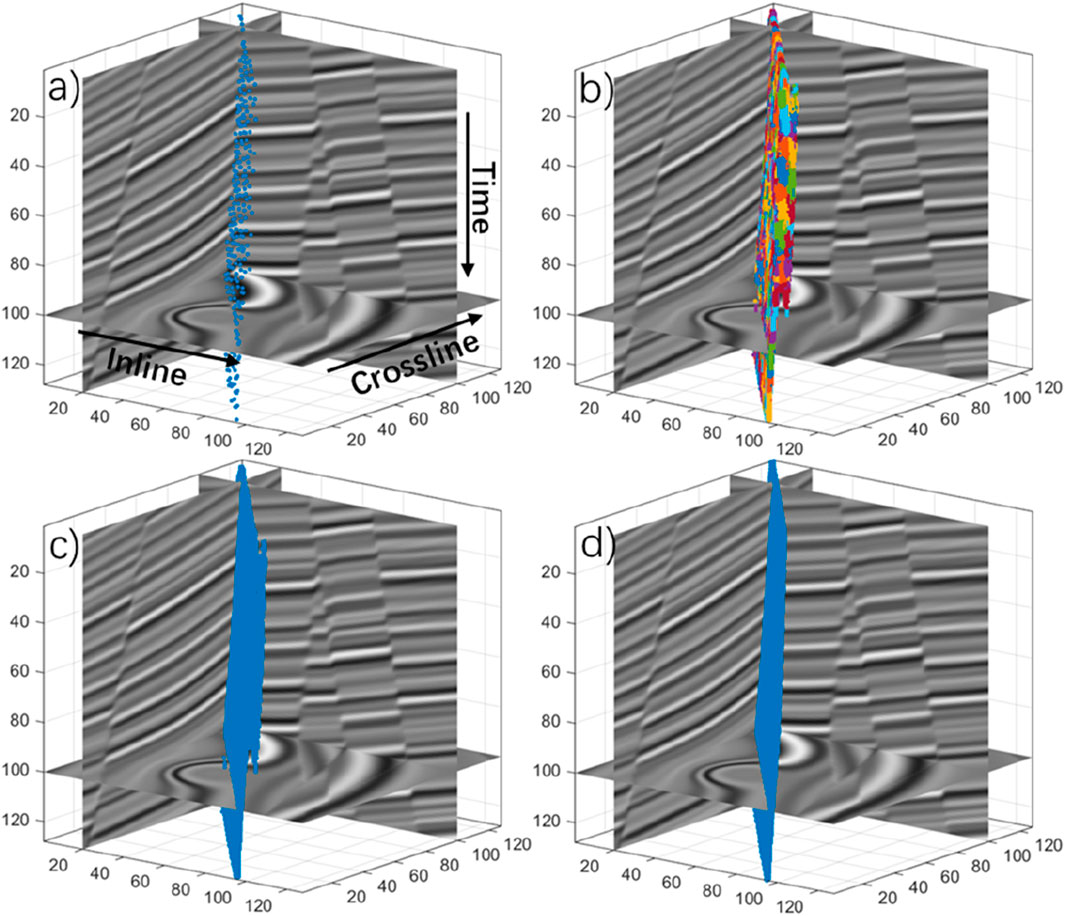
Figure 3. Process of a fault surface construction. (a) the seed points picked from the thinned attribute of this fault surface; (b) the optimal surface patches from the seed point; (c) the merged fault surface of the optimal surface patches; (d) fault surface reconstructed by using the MLS method.

Constructing fault surfaces from the optimal surface patches is more straightforward and accurate than the thinned fault attribute image. The plane equations of optimal surfaces are also helpful for tracking fault surfaces. However, by directly linking the nearby optimal surfaces, the constructed fault surfaces usually suffer from holes (Figure 3c). The noise level in the seismic image is significantly responsible for the holes appearing on the surfaces. In addition, the RANSAC method assumes that the faults are locally planar, implying by linking nearby optimal surfaces, only the nearby fault samples are connected to a fault skin and approximate a fault surface (Figure 3c). Therefore, after linking nearby optimal surface-constructed fault surfaces, we use MLS to construct fault surfaces without any holes apparent on surfaces even with some missing fault samples (Figure 3d).

Merging fault surface patches

We define three criteria for merging the fault surface patches.

The first criterion is that the analyzed fault surface patch can only merge with its neighboring fault surface patches if the angle between their normal vectors is less than the angle threshold A ($5°$ for the example in Figure 3b). The normal vectors are given by the plane equation. If the plane equation is $\text{Ax}+\text{By}+\text{Cz}+\mathrm{D}=0$, the normal vector u is Equation 8:

$\mathrm{u}=\left[\mathrm{A},\mathrm{B},\mathrm{C}\right].(8)$

The second criterion is that the analyzed fault surface patch and its neighboring fault surface patches should be inclined in the same direction. The normal vector of the analyzed fault surface patch is $u_1=\left(x_1,y_1,z_1\right)$, and the normal vector of a nearby surface patch is $u_2=\left(x_2,y_2,z_2\right)$. If $y_1/y_2$ and $z_1/z_2$ are both positive or both negative, the two patches are inclined in the same direction.

The third criterion is that the overlap rate of planar projections of the analyzed fault surface patch and its neighboring fault surface patches should be less than the threshold S (0.1, for example, in Figure 3). The normal vector of the analyzed fault surface patch is $u_1=\left(x_1,y_1,z_1\right)$. If $\left|x_1/y_1\right|>1$, these surface patches are projected to the YOZ plane; if $\left|x_1/y_1\right|<1$, these surface patches are projected to the XOZ plane. If $n_1$ is the number of the fault samples projected by the analyzed fault surface patch, $n_2$ is the number of the fault samples projected by a nearby surface patch, $n_3$ is the number of fault samples where the projections of these patches overlap, the projection overlap rate $\text{Pj}$ is given by Equation 9:

$\text{Pj}=\left\{\begin{array}{c}\frac{n_3}{n_1},if{n}_1<n_2\\ \frac{n_3}{n_2},if{n}_1>n_2\end{array}\right..(9)$

The analyzed fault surface patch only merges with the neighboring fault surface patches that satisfy these three criteria, and the merged fault surface patch functions as the new analyzed fault surface patch in the following merging process. The merging process continues until the algorithm cannot merge any fault surface patches.

Reconstructing fault surfaces by using MLS

The MLS method is mainly applied to curve and surface fitting. The method is based on compact-supported weighting functions (the function values are defined to be greater than 0 only in a closed domain of finite size and 0 outside the domain) and polynomial basis functions. The fitting function suitable for the scattered points model is established by the weighted least square method.

Reconstruction of fault surfaces from the merged fault surface patches is similar to the problem of surface reconstruction from the 3D point cloud, which is well-studied in computer graphics and computer version. Therefore, we choose the MLS method to reconstruct fault surfaces from the merged optimal fault surfaces because it makes the fault surfaces smoother while maintaining the space configuration of the faults.

In the MLS method, we first choose a merged surface and divide it into $\mathrm{N}\times \mathrm{N}$ rule section grid of points and count the node value at the grid point. The node value at the grid point is calculated as follows Equation 10:

$\mathrm{f}\left(\mathrm{x}\right)=O^k\left(x\right)y.(10)$

Here, $\mathrm{y}=\left[y_1,y_2,\cdots y_n\right]$, and $y_i$ is the node value at the grid point $x_i$. $O^k\left(x\right)$ is called the shape function, and k denotes the order of the basis function. $O^k\left(x\right)$ is counted as follows Equation 11:

$O^k\left(x\right)=p^T\left(x\right)A^{-1}\left(x\right)B\left(x\right).(11)$

Here, Equations 12, 13:

$\mathrm{A}\left(\mathrm{x}\right)={\displaystyle \sum _{i=1}^n}w\left(x-x_1\right)p\left(x_1\right)P^T\left(x_1\right).(12)$

$\mathrm{B}\left(\mathrm{x}\right)=\left[w\left(x-x_1\right)p\left(x_1\right),w\left(x-x_2\right)p\left(x_2\right),\cdots ,w\left(x-x_n\right)p\left(x_n\right)\right].(13)$

Here, $p\left(x\right)={\left[p\left(x_1\right),p\left(x_2\right),\cdots p\left(x_3\right)\right]}^T$, and $p\left(x\right)$ is the basis function. We use quadratic polynomial basis functions in the fitting process. $w\left(x-x_i\right)$ is a smooth continuous weight function at node $x_i$ with the compact support property. The weight function w is given by Equation 14:

$\mathrm{w}\left(\mathrm{x}\right)=\left\{\begin{array}{l}\frac{1}{2}{\left|x\right|}^3-{\left|x\right|}^2+\frac{2}{3}\left|x\right|<1\\ \frac{1}{6}{\left(2-\left|x\right|\right)}^{3}1\le \left|x\right|<2\\ 0else\end{array}\right..(14)$

We use Equation 10 to calculate the node values for all grid nodes and connect the mesh nodes to form the fitting surface. By fitting the merged surface, we can calculate the values of all the points on the fault surface. As shown in Figure 2a, most fault samples are aligned approximately coplanar and are linked to form fault surfaces, as shown in Figure 2d. Some misaligned fault samples (often with low fault likelihoods) are also apparent; however, they cannot be linked together to form significant locally planar fault surfaces. We filter out small surfaces and keep only those with significant numbers of fault samples. For example, in Figure 2f, we have discarded small fault surfaces and kept only the five largest surfaces to demonstrate the effectiveness of our methods.

Applications to seismic images

To further demonstrate the effectiveness of our methods, we apply the point cloud surface method reconstruction to the real 3D seismic image (287 [inline] ×735 [crossline] ×425 [time] samples) shown in Figure 4a. Figure 4b shows the fault attribute image computed from Kerry 3D seismic data. The fault attribute image provides a good detection of the fault discontinuities from the seismic image. However, some noisy features are also detected in the fault attribute image. From the thinned fault attribute image (Figure 4d), most of the large fault surfaces can be successfully extracted by linking nearby fault samples. However, many noisy fault surfaces are also generated, which are difficult to separate, and some faults also have local discontinuities. These problems will make fault surface construction difficult. Figure 4b shows the fault surfaces constructed by the point cloud surface reconstruction method from Kerry 3D seismic data. We display the fault surfaces with inline, crossline, and time section and compare them with the fault attribute data. It can be seen in Figure 4e that the extracted fault surfaces are consistent with the locations of faults in the seismic data, which shows the effectiveness of our proposed method. In addition, compared with the fault attribute data in the inline (or crossline) section, the results of our method have more continuity and are cleaner. Therefore, our method can effectively construct complete and continuous fault surfaces.

Figure 4

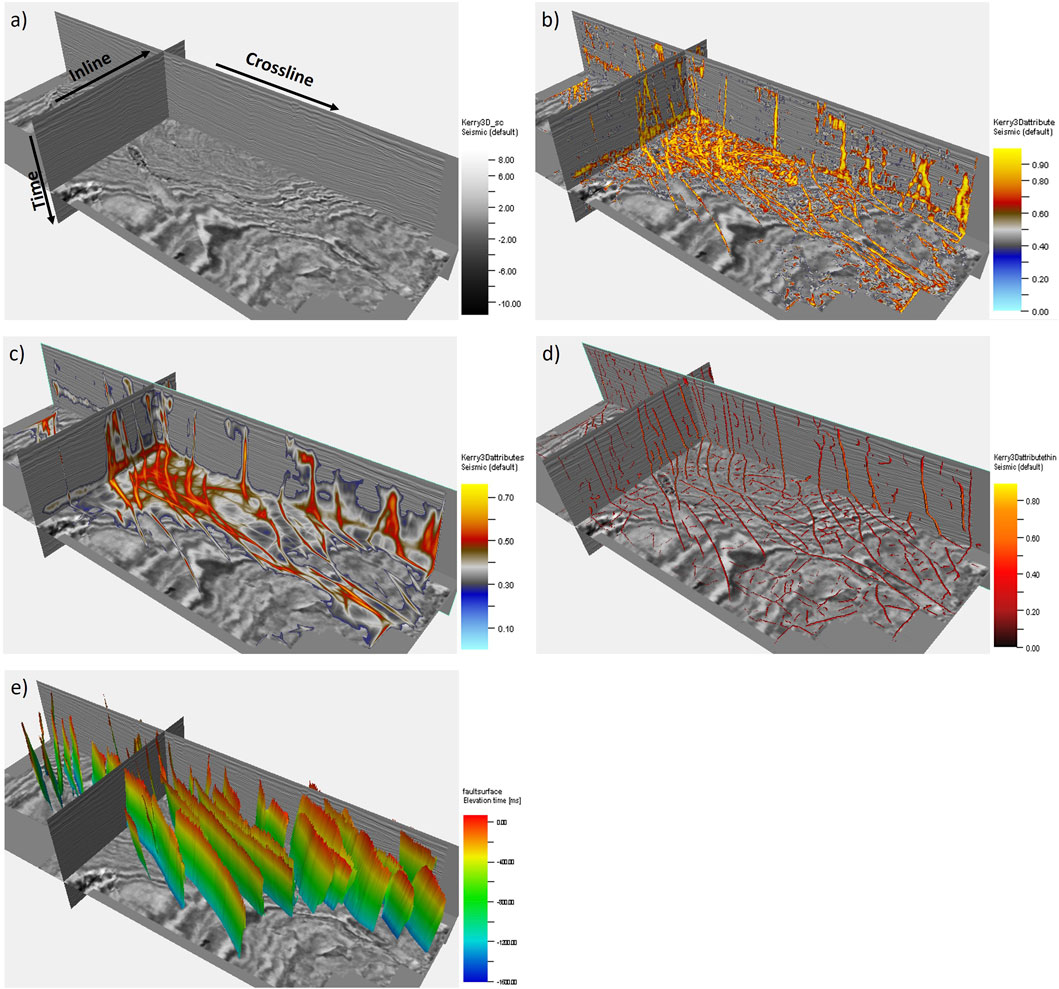
Figure 4. Process of real 3D seismic image. (a) Kerry 3D seismic data; (b) fault attribute computed from Kerry 3D seismic data; (c) smoothed fault attribute image; (d) thinned fault attribute section; (e) fault surface reconstructed by the point cloud surface reconstruction method.

Discussion

We apply our proposed methods to synthetic seismic data and Kerry 3D seismic data to illustrate the effectiveness of our method. Figure 2 shows the results of our method on synthetic seismic data with intersecting faults, which means that our method can effectively address the intersected faults. Figure 4 shows the results of our method on Kerry 3D seismic data with complicated faults, which indicates that our method can extract fault surfaces accurately and completely.

However, our method also has several limitations. The fault surface patches are directly picked by the RANSAC method with the assumption that the fault should be approximately planar within a small box window. This assumption is true for most cases, but it may fail for some special faults, such as conical faults (Hale and Groshong, 2014), with the full range of fault strike angles. In that case, using RANSAC to find spherical or cylindrical planes instead of finding planar planes may also lead to the selection of the optimal fault surface.

Because the fault surface is nearly planar within the local box window when the moving least squares method (MLS) is used to reconstruct the merged complete fault plane, a quadratic polynomial basis function is sufficient to handle the majority of cases during the fitting process.

In addition, our method relies heavily on the quality of the fault detection attribute. For some regions with relatively strong noise and complicated faults, the insufficient ability to delineate the fault detection attribute anomalies limits the performance of our method.

Therefore, we use the fault scanning method to highlight faults in a seismic attribute image. The deep-learning-based fault attribute algorithms can produce high-quality seismic fault attributes without staircase artifacts and undesired stratigraphic anomalies. Thus, using fault attributes generated by the deep learning algorithm as the input for our algorithm can yield better results.

The Kerry seismic data were processed on a computer with a CPU (Intel(R) Core(TM) i7-7700, 3.6 GHz). The entire code was run via the MATLAB Parallel Computing Toolbox. The computation times of the fault scanning method are approximately 3 and 4 h. The computation times of fault surface construction are approximately 3 and 4 h. Note that our algorithm does not extract the fault surface if the fault surface on the vertical slice is smaller than approximately 60 ms. Thus, we conclude that our method is effective for medium to large faults, but the effect is not obvious for small faults.

Conclusion

In this study, we proposed a new workflow for extracting fault surfaces via the 3D point cloud surface reconstruction method. We regarded the fault points in the fault attribute volume as 3D point clouds and use the 3D point cloud surface reconstruction algorithm to construct complete fault surfaces. First, we performed fault scanning method processing on the fault attribute volume and obtained 3D fault samples from the enhanced and thinned fault attribute volumes. These fault samples were the initial 3D point clouds of the faults. Then, we uniformly selected seed points from these 3D fault samples and used the random sample consensus (RANSAC) algorithm to calculate the local optimal surface patches at the seed points. Based on the relationship of adjacent local optimal surface patches, we connected the local fault surface patches belonging to the same fault to form a complete fault surface. Finally, we used the MLS (moving least squares) method to reconstruct the merged complete fault surface to fill in the possible holes on the merged fault surface and make the fault surface smoother. Since the construction of the fault surface via the point cloud surface reconstruction method involves classifying and merging local optimal surface patches and then reconstructing, our method performs well in complex situations, such as those with multiple intersecting faults.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

LD: writing – original draft and writing – review and editing. WS: writing – original draft. JH: writing – review and editing. CZ: writing – review and editing. WT: writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

CZ was employed by CNOOC China Limited, Hainan Branch.

WT was employed by Changqing Petroleum Exploration Bureau.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Dossary, S., and Marfurt, K. J. (2006). 3D volumetric multispectral estimates of reflector curvature and rotation. Geophysics 71 (5), P41–P51. doi:10.1190/1.2242449

CrossRef Full Text | Google Scholar

Aqrawi, A. A., and Boe, T. H. (2011). Improved fault segmentation using a dip guided and modified 3D sobel filter: 81St annual international meeting. Seg. Expand. Abstr., 999–1003. doi:10.1190/1.3628241

CrossRef Full Text | Google Scholar

Bi, Z., and Wu, X. (2021). Improving fault surface construction with inversion-based methods. Geophysics 86 (1), IM1–IM14. doi:10.1190/geo2019-0832.1

CrossRef Full Text | Google Scholar

Cohen, I., Coult, N., and Vassiliou, A. A. (2006). Detection and extraction of fault surfaces in 3D seismic data. Geophysics 71 (4), P21–P27. doi:10.1190/1.2215357

CrossRef Full Text | Google Scholar

Di, H., Shafiq, M., and AlRegib, G. (2018). Patch-level MLP classification for improved fault detection: 88Th annual international meeting. Seg. Expand. Abstr., 2211–2215. doi:10.1190/segam2018-2996921.1

CrossRef Full Text | Google Scholar

Gibson, D., Spann, M., Turner, J., and Wright, T. (2005). Fault surface detection in 3-D seismic data. IEEE Trans. Geoscience Remote Sens. 43, 2094–2102. doi:10.1109/TGRS.2005.852769

CrossRef Full Text | Google Scholar

Hale, D. (2013). Methods to compute fault images, extract fault surfaces, and estimate fault throws from 3D seismic images. Geophysics 78 (2), O33–O43. doi:10.1190/geo2012-0331.1

CrossRef Full Text | Google Scholar

Hale, D., and Groshong, R. H. (2014). Conical faults apparent in a 3D seismic image. Interpretation 2 (1), T1–T11. doi:10.1190/INT-2013-0121.1

CrossRef Full Text | Google Scholar

Huang, L., Dong, X., and Clee, T. E. (2017). A scalable deep learning platform for identifying geologic features from seismic attributes. Lead. Edge 36, 249–256. doi:10.1190/tle36030249.1

CrossRef Full Text | Google Scholar

Kadlec, B. J., Dorn, G. A., Tufo, H. M., and Yuen, D. A. (2008). Interactive 3-D computation of fault surfaces using level sets. Vis. Geosci. 13, 133–138. doi:10.1007/s10069-008-0016-9

CrossRef Full Text | Google Scholar

Lees, J. A. (1999). Constructing faults from seed picks by voxel tracking. Lead. Edge 18, 338–340. doi:10.1190/1.1438287

CrossRef Full Text | Google Scholar

Li, P., Wang, M., Fu, J., and Wang, Y. (2023). “Plane detection based on an improved RANSAC algorithm,” in 2023 IEEE 3rd international conference on computer communication and artificial intelligence (CCAI), 211–215. doi:10.1109/CCAI57533.2023.10201261

CrossRef Full Text | Google Scholar

Lou, Y., Zhang, B., Wang, R., Lin, T., and Cao, D. (2019a). Seismic fault attribute estimation using a local fault model. Geophysics 84 (4). doi:10.1190/geo2018-0678.1

CrossRef Full Text | Google Scholar

Marfurt, K. J., Kirlin, R. L., Farmer, S. L., and Bahorich, M. S. (1998). 3-D seismic attributes using a semblance-based coherency algorithm. Geophysics 63 (4), 1150–1165. doi:10.1190/1.1444415

CrossRef Full Text | Google Scholar

Marfurt, K. J., Sudhaker, V., Gersztenkorn, A., Crawford, K. D., and Nissen, S. E. (1999). Coherency calculations in the presence of structural dip. Coherency Calc. presence Struct. dip Geophys. 64, 104–111. doi:10.1190/1.1444508

CrossRef Full Text | Google Scholar

Pedersen, S. I., Randen, T., Sonneland, L., and Steen, Ø. (2002). Automatic fault extraction using artificial ants: 72Nd annual international meeting. Seg. Expand. Abstr., 512–515. doi:10.1190/1.1817297

CrossRef Full Text | Google Scholar

Qi, J., Li, F., and Marfurt, K. (2017a). Multiazimuth coherence. Geophysics 82 (6), O83–O89. doi:10.1190/geo2017-0196.1

CrossRef Full Text | Google Scholar

Randen, T., Pedersen, S. I., and Sønneland, L. (2001). Automatic extraction of fault surfaces from three-dimensional. Seg. Expand. Abstr., 551–554. doi:10.1190/1.1816675

CrossRef Full Text | Google Scholar

Roberts, A. (2001). Curvature attributes and their application to 3D interpreted Horizons. First break 19, 85–100. doi:10.1046/j.0263-5046.2001.00142.x

CrossRef Full Text | Google Scholar

Van Bemmel, P. P., and Pepper, R. E. (2000). Seismic signal processing method and apparatus for generating a cube of variance values. U. S. Pat. 6 (151)–555.

Google Scholar

Wang, Z., and AlRegib, G. (2014). Automatic fault surface detection by using 3D hough transform: 84Th annual international meeting. Seg. Expand. Abstr., 1439–1444. doi:10.1190/segam2014-1590.1

CrossRef Full Text | Google Scholar

Wu, X., and Hale, D. (2016). 3D seismic image processing for faults. Geophysics 81 (2), IM1–IM11. doi:10.1190/geo2015-0380.1

CrossRef Full Text | Google Scholar

Wu, X., Shi, Y., Fomel, S., Liang, L., Zhang, Q., and Yusifov, A. Z. (2019b). FaultNet3D: predicting fault probabilities, strikes, and dips with a single convolutional neural network. IEEE Trans. Geoscience Remote Sens. 57, 9138–9155. doi:10.1109/TGRS.2019.2925003

CrossRef Full Text | Google Scholar

Wu, X., and Zhu, Z. (2017). Methods to enhance seismic faults and construct fault surfaces. Comput. and Geosciences 107, 37–48. doi:10.1016/j.cageo.2017.06.015

CrossRef Full Text | Google Scholar

Zeng, Q. H., and Lu, D. T. (2004). Curve and surface fitting based on moving least-squares methods. J. Eng. Graph. 25 (1), 84–89. doi:10.1007/BF02973453

CrossRef Full Text | Google Scholar

Zhou, C., Zhou, R., Zhan, X., Cai, H., Yao, X., and Hu, G. (2022). Fault surface extraction from a global perspective. Geophysics 87, 189–206. doi:10.1190/GEO2022-0030.1

CrossRef Full Text | Google Scholar

Zhou, R., Yao, X., Hu, G., and Yu, F. (2021). Learning from unlabelled real seismic data: fault detection based on transfer learning. Geophys. Prospect. 69, 1218–1234. doi:10.1111/1365-2478.13097

CrossRef Full Text | Google Scholar