Stability influence of weak interlayer rock slope under rainfall

In this study, we investigate the stability of soft rock slopes with weak interlayers under rainfall through indoor model tests and numerical simulations, focusing on a slope in northeast China. Weak interlayers, characterized by low thickness and mechanical strength compared to adjacent rock masses, are prone to water-induced softening, threatening slope stability. Key findings reveal the following: 1) rainfall triggers sliding along weak interlayers, accumulating debris at slope toes. Prolonged infiltration reduces rock–soil friction, potentially extending failure zones through slightly weathered tuff; 2) Non-rainfall scenarios induce slope failures primarily at crests and shoulders, whereas rainfall shifts the maximum displacement to the slope feet; 3) Expanding plastic zones under intensified rainfall indicate progressive instability development toward deeper slope surfaces. The results demonstrate rainfall’s critical role in altering failure mechanisms and depth, providing insights for risk mitigation in geotechnical projects involving weak interlayers.

1 Introduction

Slope refers to an engineered slope with a certain degree of inclination formed by excavation or other human activities. Landslide refers to the soil or rock mass sliding on the slope. Under the influence of factors such as river erosion, groundwater activity, rainwater immersion, earthquake, and artificial slope cutting, the natural phenomenon of soil or rock mass sliding down the slope along a certain weak surface or weak zone is one of the common geological disasters and a form of slope deformation and failure (Shao et al., 2023a). The inducing factors of landslide mainly include rainfall, ground motion, and human engineering activities (Oh and Vanapalli, 2010). Rainfall is one of the most common inducing factors of slope instability and failure. When there is a weak interlayer in the slope, rainfall will lead to a decrease in the shear strength of the weak interlayer in the slope and a decrease in the overall anti-sliding force of the slope (Jacques, 2007). When rainwater infiltrates into the slope, it will lead to an increase of the weight of the slope rock mass, an increase of the sliding force of the slope, and a decrease of the stability. Therefore, the slope will likely slide along the weak interlayer.

A weak interlayer is a kind of layered or banded weak structural layer with smaller thickness and mechanical properties than the adjacent rock mass. Its mechanical properties are easily affected by water. When rainfall infiltrates or groundwater level rises, the weak interlayer absorbs water and causes its own water content to rise rapidly. Its shear strength will decrease rapidly, and the slope is easy to slide along the weak interlayer (Hsuan, 2015). It can be seen that the weak interlayer exists in the slope as a special structure because of its thickness and mechanical properties. The stability of the slope is greatly reduced due to the existence of the weak interlayer. At the same time, the existence of the weak interlayer also affects the sliding mode of the slope. Therefore, in the analysis of slope stability, the important influence of weak interlayers on slopes cannot be ignored.

Sun et al. (2022a) proposed a method to evaluate the stability of slopes with multiple regular interlayers. The energy coefficient obtained by the mobile displacement method is used as the evaluation index of slope stability, and the feasibility of the standard is verified. Wang et al. (2020) studied the law of suction and deformation of slopes under rainfall conditions by the centrifugal model test of cohesive soil slope with weak interlayers and analyzed the influence of the existence of weak interlayers on the overall stability of slope. Based on the orthogonal design method, Zhou et al. (2022) analyzed the stability of rock slopes with weak interlayers and concluded that the dip angle and internal friction of the weak interlayer in the rock slope are the most sensitive influencing factors. Shuai et al. (2025) believed that the anti-dip of the weak interlayer has a certain influence on the stability of the slope, and through the real-time deformation monitoring of an anti-dip slope with a weak interlayer, it was proposed that the anti-dip weak interlayer poses a certain threat to the overall deformation of the slope. Zhong and Miao (2021) used similar tests to carry out large-scale shaking table tests on slopes with horizontal weak interlayers of different thicknesses. It was concluded that the thin interlayer slope is destroyed before the thick interlayer slope, and the scale and degree of damage are greater.

Xie et al. (2023) calculated the stability coefficient of basalt slopes with weak interlayers (tuff) under rainfall conditions using the Mohr–Prince method in the Geo-Slope software application. Qu et al. (2024) established a numerical model using the GeoStudio software and combined the fluid–solid coupling principle to study the variation law of the safety factor of the slope under different rainfall intensities with and without considering the fluid–solid coupling effect. The results showed that the safety factor of the slope was positively correlated with the rainfall intensity within a certain rainfall duration; when the fluid–solid coupling effect was considered, the safety factor first decreased and then tended to be stable, whereas when it was not considered, the safety factor first decreased and then increased, but it was always greater than the former. Based on a large number of actual engineering projects, Zhang et al. (2012) discussed the variation law of the safety factor and the location of the failure surface of layered rock slopes under different rock layer dip angles, slope angles, and structural plane spacing conditions, based on the Sarma limit equilibrium method and the finite element strength reduction method, revealing the failure mechanism and stability characteristics of complex multilayered weak interlayer rock slopes. Liu and Zhou (2002) focused on the problem of rainfall infiltration and used the updated Abaqus software application combined with field tests to simulate the situation where the infiltration rate can change during rainfall infiltration. Zeng et al. (2017) established a finite element numerical model using GeoStudio software and used the SEEP/W and SLOPE/W modules to study the variation law of the transient seepage field and the safety factor of the slope under different rainfall intensities. Based on the Green-Ampt model, Sun Yiqing et al. (2022b) established the LSGA model that simultaneously considered the seepage in the saturated layer and the water content distribution characteristics in the wetting layer and established the calculation expression of the safety factor of the slope under this model. Based on the existing relevant theories, Zeng et al. (2017) sorted and analyzed to master the solution method of the safety factor of multilayered soil slopes under the influence of rainfall, and applied it to the calculation of the safety factor of the slope under different rainfall conditions. The results showed that the safety factor of the slope was negatively correlated with the rainfall infiltration depth under the same rainfall conditions: when the infiltration depth reached the contact surface between the saturated zone and the unsaturated zone, the stability of the slope suddenly decreased. Gengqian et al. (2024) self-programmed a MATLAB program to analyze the influence of four different rainfall patterns on slope stability. The results revealed that different rainfall characteristics had different time-related effects on slope stability. Shao et al. (2023b) modified the Green-Ampt infiltration model and analyzed the evolution characteristics of the depth of the wetting front and the volumetric water content of the slope under different rainfall durations. At the same time, they considered the combined influence of soil matrix suction, permeability coefficient, and initial surface tension on the stability of the slope. Rakshanda et al. (2022) considered that the strength of soft rock would gradually decrease due to the softening effect during the process of rainfall infiltration and conducted numerical research on slope stability using the idea of indirect coupling. Based on the generalized limit equilibrium method, Young-Suk and Hyo-Sung (2023) studied the stability of three-layer nonuniform slopes under different rainfall conditions and evaluated the influence of different rainfall periods and rainfall intensities on the pore water pressure, safety factor, and volumetric water content of the slope.

In summary, although the above scholars have studied the influence of slope deformation and the occurrence characteristics of weak interlayers on slope stability under rainfall infiltration conditions from field tests, physical model tests, and numerical simulation methods, the material composition and mechanical properties of inclusions in the weak interlayer and the thickness of the interlayer still need to be studied further and a physical model should be constructed for detailed analysis. Some scholars use various numerical simulation software or programs, such as FLAC3D, self-made MATLAB program, and GeoStudio and Abaqus software applications, to analyze and comprehensively study the stability of the slope with weak interlayers under rainfall. However, how to reveal the failure process of a weak interlayer rock slope under rainfall conditions according to different internal failure positions, stress fields, and displacement fields needs to be further explored. Therefore, according to the general situation of the example slope engineering, in this paper, we use the indoor model test device of rainfall landslide, combine the GeoStudio numerical simulation to carry out the numerical test of landslide with different factors, and reveal the influence of various factors on the stability of rock slopes with weak interlayers.

2 Calculation principle

The weak interlayer will be softened when it encounters water, and softening mainly refers to the decrease of shear strength of the weak interlayer (Hou et al., 2021). According to non-saturation,

${\mathit{\tau }}_{\mathit{f}}={\mathit{c}}^{\prime }+\left(\mathit{\sigma }-{\mathit{u}}_{\mathit{a}}\right)+\mathit{t}\mathit{a}\mathit{n}{\mathit{\varphi }}^{\prime }+\left({\mathit{u}}_{\mathit{a}}-{\mathit{u}}_{\mathit{w}}\right)\mathit{t}\mathit{a}\mathit{n}{\mathit{\varphi }}^{\mathit{b}}.$

In the formula, τ_f is the shear strength, c' is the effective cohesion, σ is the normal stress, u_a is the atmospheric pressure, u_w is the pore water pressure, u_a-u_w is the matrix suction, ϕ′ is the saturated friction angle, and ϕ^b is the internal friction angle of strength changing with suction.

The seepage field, saturated zone, and unsaturated zone of soft rock slope under rainfall condition are correlated to dynamic flow. The seepage problem of soft rock slope under rainfall condition is related to the saturated–unsaturated seepage problem, and the permeability coefficient of rock and soil mass can be obtained based on the curve of soil water characteristic curve and matrix suction (Shao et al., 2024). According to Darcy’s law, the calculation formula of unsteady seepage is as follows:

$\frac{\mathit{\vartheta }}{\mathit{\vartheta }\mathit{x}}\left(\mathit{k}\mathit{x}\frac{\mathit{\vartheta }\mathit{h}}{\mathit{\vartheta }\mathit{x}}\right)+\frac{\mathit{\vartheta }}{\mathit{\vartheta }\mathit{y}}\left(\mathit{k}\mathit{y}\frac{\mathit{\vartheta }\mathit{h}}{\mathit{\vartheta }\mathit{y}}\right)+\mathit{w}={\mathit{m}}_{\mathit{w}}{\mathit{\rho }}_{\mathit{w}}\mathit{g}\frac{\mathit{\vartheta }\mathit{h}}{\mathit{\vartheta }\mathit{t}}.$

In the formula, h is the total head, k_x is the permeability coefficient in the x direction, k_y is the permeability coefficient in the y direction, m_w is the water bulk density, ρ_w is the water density, g is the gravity acceleration, and t is the time.

The finite element equation of unsteady flow (Santha and Thote, 2011) is

$\left[\mathit{K}\right]\left\{\mathit{H}\right\}+\left[\mathit{M}\right]\left\{\mathit{H}\right\}=\left\{\mathit{Q}\right\}.$

In the formula, {Q} is the node traffic, [K] is the element characteristic matrix, and [M] is the element mass matrix.

The initial condition of unsteady seepage analysis is

$\mathit{h}\left(\mathit{x},\mathit{y},0\right)={\mathit{h}}_0,\left(\mathit{x},\mathit{y}\right)\in \mathrm{\Omega }.$

3 Laboratory test on the stability of rock slopes with weak interlayers

3.1 Project overview

The research area is located in an open-pit mine. The geological zoning of the mine is mainly divided into the following six areas: the western end slope area, the western north slope area, the western south slope area, the eastern north slope area, the eastern south slope area, and the eastern end slope area.

The Quaternary loose layer soil engineering geological unit (upper) and the bedrock rock mass engineering geological unit (underlying) are the main engineering geological units in the mining area. The former is mainly distributed in the southern slope of the Qiantai Mountain and the western end of the west open-pit mine on the south side of the study area. The latter is mainly distributed in the south and north sides of the west open-pit mine. From top to bottom, it is described as follows:

(1) Quaternary loose layer engineering geological unit

The upper part is miscellaneous fill and plain fill soil layer, and the lower part is the quaternary loose layer composed of fine sand, silty clay, and gravel.

(2) Engineering geological unit of bedrock rock mass

1) Tuff: mainly a strong weathered structure, mainly exposed in the south, north, and east slope positions.

2) Fracture zone: mainly exposed in the tuff, including the middle of the tuff with coal seam and the lower part of the tuff. There are mudded interlayers in the unconformity contact area between tuff and gneiss.

3) Granitic diorite: distributed in the east and south of the Qiantai boiler room. Weathering crust is generally grayish white, with local mud filling; moderately weathered rocks are generally yellowish brown, with medium-coarse grained crystal structure and block structure.

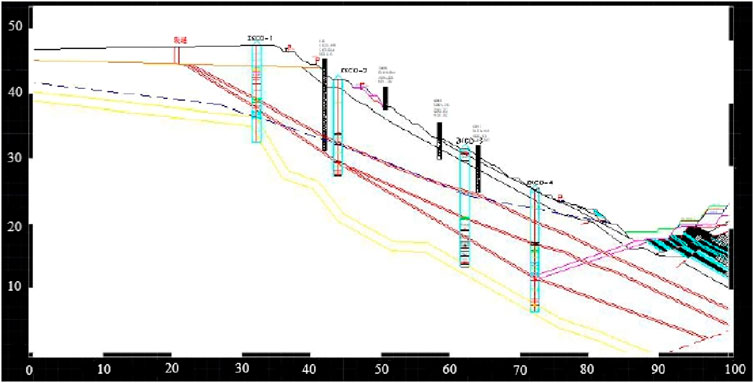
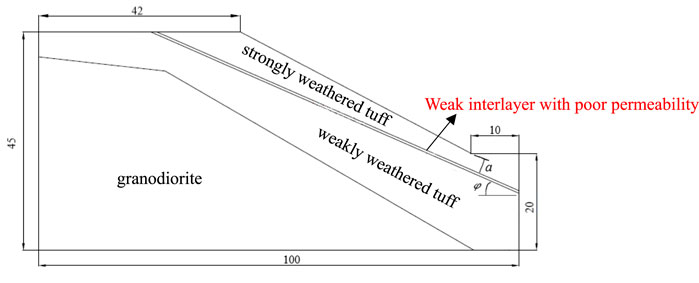
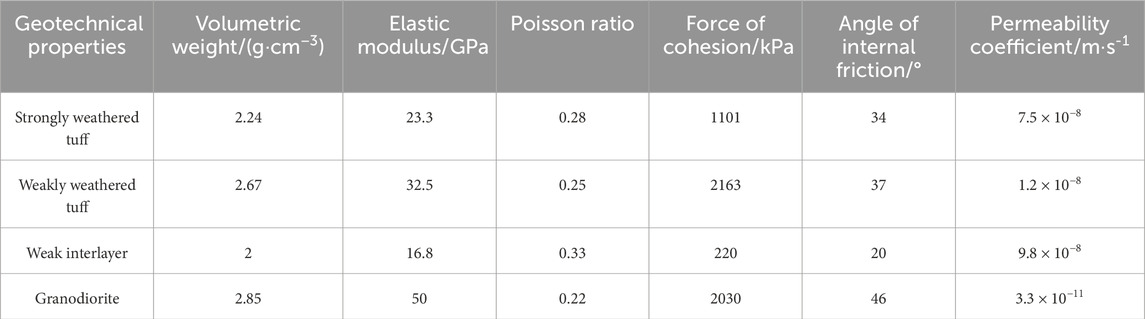
According to the data of engineering geological mapping and drilling (geophysical) exploration, the stratum composition of the south slope of the western open-pit mine mainly includes Archean granodiorite, strongly weathered tuff, and weakly weathered tuff. There are three proven weak interlayers, but in this paper, we select one of the more typical interlayers as the main research object. According to the drilling results, the geological data of the D1 section are the most detailed. The final slope angle of the D1 profile slope is 28°. Compared with other geological profiles, it is found that the slope height difference at the D1 profile is the largest, and the final slope angle is the steepest, which is the most unstable profile in the south. Therefore, based on the D1 section, in this paper, we construct the typical geological model map of this study. The geological profile of D1 is shown in Figure 1. The simplified model size according to the D1 geological profile is shown in Figure 2, and the geotechnical parameters of each rock stratum at the slope are shown in Table 1.

Figure 1

Figure 1. D1 geological profile (unit: m).

Figure 2

Figure 2. Section model size (unit: m).

Table 1

Table 1. Rock and soil mechanics parameters of each layer.

3.2 Indoor model test design

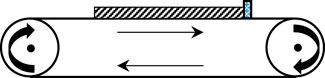
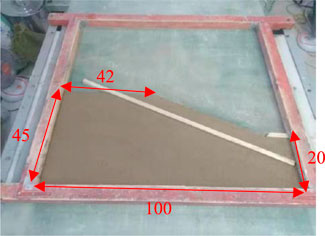
The bottom friction test mainly uses the friction force on the bottom of the physical model to simulate the gravity of the prototype natural slope. The principle is as follows: the test model is placed in the framework of the bottom friction test machine model, and the bottom of the model is in contact with the rubber belt. This test uses a fully automated bottom friction tester, where the template size is 1 × 1m, the speed range is 0∼100r/min, and the friction force is 0∼1000N; the test machine diagram is shown in Figure 3. When the rubber belt rotates, the relative motion between the model and the rubber belt is generated due to the blocking of the model frame to the test model. When the test model is destroyed, the test is terminated, and friction force F is generated on the bottom surface of the test model during the movement.

$F=\left(p+{\mathrm{{\rm Y}}}_{M}t\right)\mu .$

In addition, p is the pressure acting on the normal unit area of the model, and the normal stress is not applied in this study, so p = 0; Υ_M is the bulk density of the model material, t is the thickness of the model, and μ is the sliding friction coefficient of the contact surface between the model and the rubber belt.

Figure 3

Figure 3. Schematic diagram of the bottom friction testing machine.

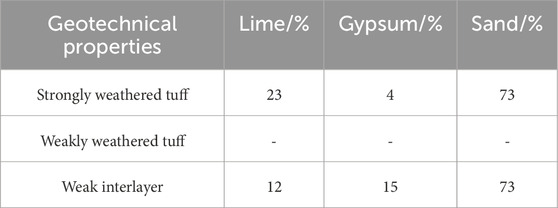
Combining the geological model in Figure 2 with the actual situation of the size of the bottom friction testing machine, the geometric similarity ratio of the simulation test is determined to be 100:1. The simulation range includes the main strata of the prototype slope and the corresponding boundary conditions, so it can meet the requirements of this test. In this experiment, mixed materials were used to simulate the prototype. Granodiorite and upper strongly weathered tuff were simulated by a mixture of different proportions of sand, lime, and gypsum. After repeated tests, the mass percentage of each material is determined as shown in Table 2. The actual model is shown in Figure 4.

Table 2

Table 2. Mass ratio of each material.

Figure 4

Figure 4. Completed indoor model (unit: cm).

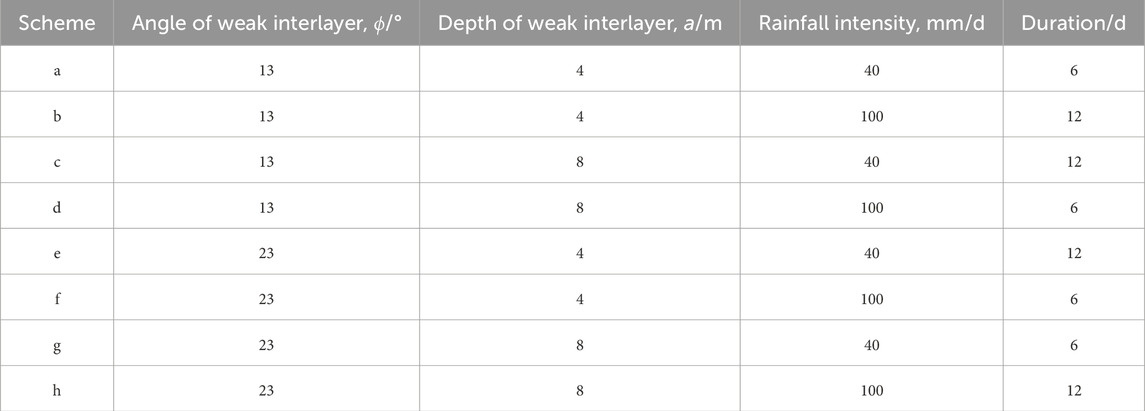
In order to study the influence of the inclination angle φ and the buried depth a of the weak interlayer on the sliding mode of the rock slope stability machine in more detail, a total of four sets of tests were designed, as shown in Table 3.

Table 3

Table 3. Indoor test scheme.

3.3 Analysis of indoor test results

During the test, the camera was used to record the real-time video at a fixed position to analyze the failure process of the slope. From the analysis of the overall instability process of the test model, the slope has different failure phenomena under the four different test schemes, as shown in Figure 5. The comparative analysis of the specific failure process is as follows: (1) when only changing the inclination angle of the weak interlayer φ, compared with T1 and T2, with the gradual increase of the inclination angle of the weak interlayer, the failure process changes from slope foot→breaking surface→slope top→overall instability to slope top→breaking surface→slope foot→overall instability. The failure mode of the strongly weathered tuff layer changes from local failure to overall failure, and the phenomenon of sliding along the weak interlayer occurs. The vertical sinking amount of T1 compared to T2 is 6.3 cm, and the horizontal sliding amount is 11.2 cm. (2) When only changing the buried depth of weak interlayer a, comparing T1 and T3, it can be seen that with the gradual increase of the buried depth of the weak interlayer, the strong weathered tuff in the slope is transformed from the overall (large-scale) failure to the local (small-scale) stability failure. This phenomenon shows that the increase of the buried depth of the weak interlayer significantly improves the overall stability of the slope. (3) When inclination angle φ and buried depth a of the weak interlayer increase at the same time, compared with T1, T2, T3, and T4, it can be observed that cracks appear on the slope surface and the slope foot at the same time. However, due to the increase of inclination angle φ, the slope foot is first broken, which makes the slope lose stability. It can be seen that the dip angle of the weak interlayer is more unfavorable to the overall stability of the slope than the buried depth. The above is the whole process simulation experiment analysis of slope stability under the condition of no rainfall, but in order to better study the stability characteristics of weak interlayer rock slopes under rainfall, the next part makes an in-depth study on the slope stability under different rainfall modes.

Figure 5

Figure 5. Failure process of indoor model tests: (a) T1, (b) T2, (c) T3, and (d) T4.

4 Numerical simulation test of rock slope stability with a weak interlayer

4.1 Numerical simulation scheme

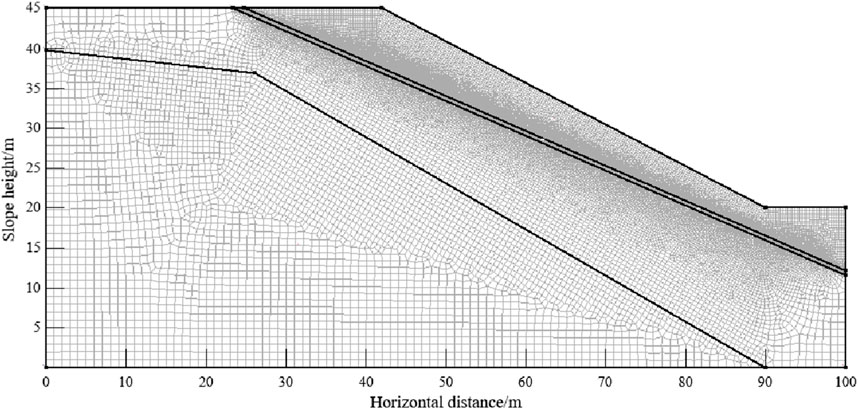
According to the engineering geological situation of the study area, the finite element software (GeoStudio) is used to establish the numerical model, and the SEEP/W module is used to analyze the influence of rainfall intensity and rainfall duration on the seepage field of the slope. Finally, SLOPE/W is used to calculate the change of slope stability under the influence of rainfall. The numerical model is established with the section of Figure 2 to monitor the change of slope displacement field, the distribution of plastic zone, and the influence of safety factor under the influence of rainfall. The slope is divided into 1 m as a unit. Because the seepage field of the slope near the slope surface is greatly affected by rainfall, the weakly weathered basalt, the strongly weathered basalt, and the weak layer are encrypted and divided. The unit size is 0.3 m. A total of 72,756 nodes and 37,199 grids are divided globally, as shown in Figure 6.

Figure 6

Figure 6. Slope numerical model and grid division.

In the natural state, the volumetric water content of the slope soil is the saturated volumetric water content (groundwater level and below) in the saturated zone, and it is basically not affected by the infiltration of rainwater during the rainfall process. In the unsaturated zone, the volumetric water content of the soil is less than the saturated volumetric water content and decays with height. In the study, the V-G model is used to fit the volumetric water content of the soil in the unsaturated zone, and the distribution of the volumetric water content of the slope under the initial state is obtained. When setting the boundary conditions, the boundary conditions of the model set the above groundwater level line as the zero flow boundary, the slope top and slope surface as the rainfall boundary, the slope toe as the overflow boundary, and the slope bottom as the zero flow boundary. The basic mechanical parameters of the model are shown in Table 1.

According to the hydrogeological data of the study area, the annual average rainfall in the study area is 802.5 mm, and it is mostly concentrated in July and August. The maximum daily rainfall is 191.8 mm/d, and the maximum continuous rainfall is 967.2 mm. As the 24-h rainfall that is equal to and greater than 100 mm rainfall is a rainstorm, the maximum daily rainfall can cover heavy rainstorm, rainstorm, heavy rain, moderate rain, and light rain. In order to better study the influence of rainfall on the seepage field of slopes in practical engineering, according to different angles and distances of weak interlayers, as well as the four factors of rainfall intensity and rainfall duration, the orthogonal experimental design scheme is shown in Table 4.

Table 4

Table 4. Numerical simulation test scheme.

4.2 Simulation test results and analysis

4.2.1 Analysis of slope displacement field under different types

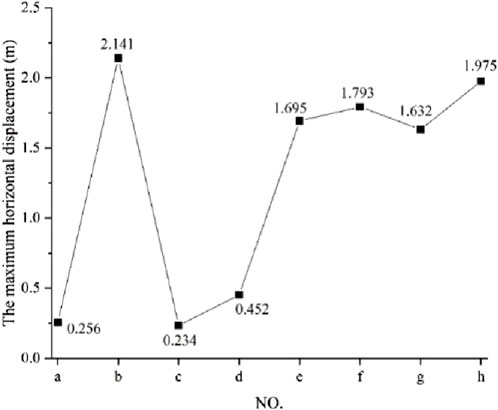
According to Figures 7, 8, the numerical simulation results under different types are analyzed. The angle of the weak interlayer, the distance of the weak interlayer, the rainfall intensity, and the duration have no direct linear influence on the maximum displacement in the horizontal direction of the slope. However, according to the phenomenon shown in the horizontal displacement distribution of the slope under different types, the following results can be obtained: (1) the maximum horizontal displacement value of scheme b (weak interlayer angle 13°, weak interlayer distance 4m, rainfall 100 mm/d, and duration 12d) is the largest, which is 2.141 m, and the maximum horizontal displacement occurs at the slope foot, which proves that this scheme causes serious landslide and accumulates at the slope foot. (2) Compared with scheme c and scheme d, the angle and distance of the weak interlayer are unchanged, and the total rainfall increases from 480 mm to 600 mm. The maximum horizontal displacement caused by it increases from 0.234 m to 0.452 m, and the location of the maximum displacement also changes from the top of the slope to the slope surface. (3) Compared with scheme e and scheme g, the maximum horizontal displacement changes little, and both occur at the upper position of the slope foot, indicating that when the angle of the weak interlayer is 23°, the depth of the weak interlayer and the rainfall intensity have little effect on the horizontal displacement field. (4) Comparing scheme a and scheme c, when the angle of the weak interlayer is consistent with the rainfall intensity, the distance of the weak interlayer and the duration of rainfall have little effect on the maximum horizontal displacement, but the location of the maximum displacement is obviously different. The maximum displacement position of scheme a occurs at the slope angle, whereas the maximum displacement of scheme c occurs at the top of the slope.

Figure 7

Figure 7. Maximum horizontal displacement in X direction under each type.

Figure 8

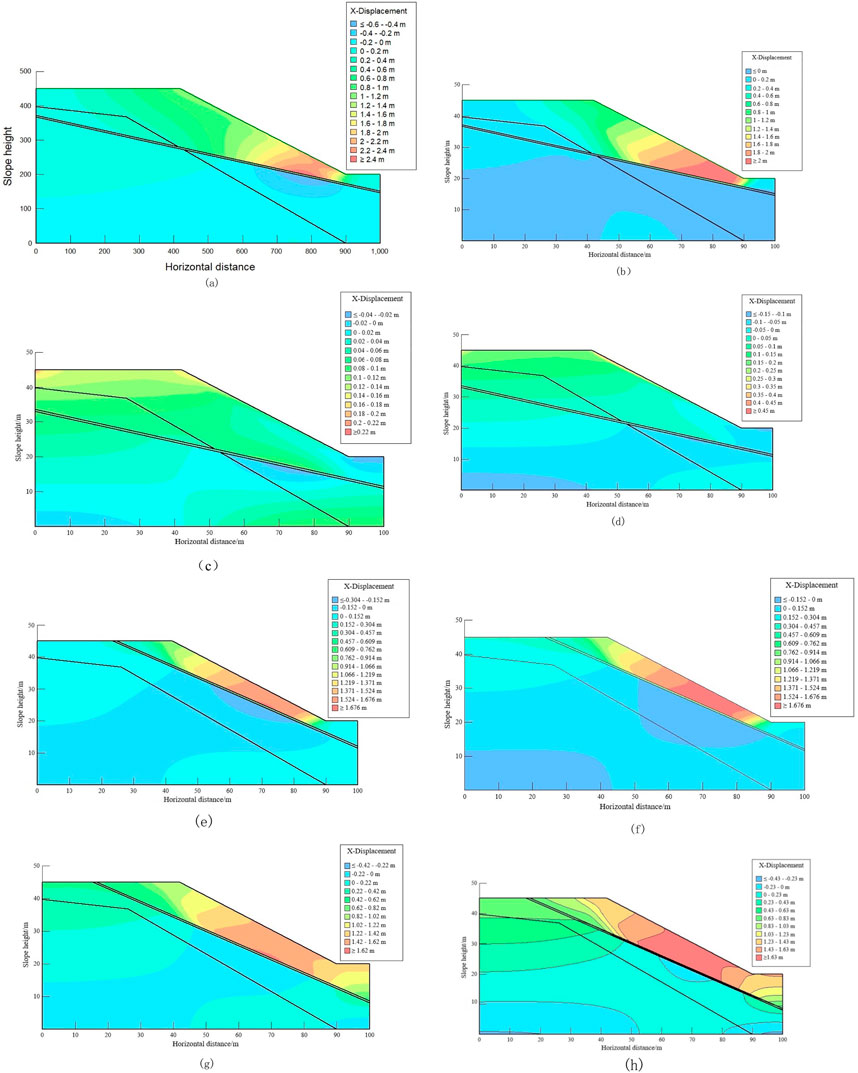
Figure 8. Horizontal displacement distribution of a slope under different types. (a–h) The x-direction displacement cloud diagram of specimen.

4.2.2 The change of the plastic zone of a slope under analysis types

According to the distribution of the slope, the plastic zone changes under different schemes, as shown in Figure 9. It can be concluded that (1) the plastic zone is only distributed in the slope angle, slope surface, and weak interlayer, and it does not penetrate the whole slope surface; (2) The plastic zone of scheme b is distributed above the slope angle and the weak interlayer; in particular, the plastic zone area at the weak interlayer is larger, and combined with the displacement distribution in Figures 9e, f, it can be judged that the slope under this scheme has a sliding condition and accumulates at the plastic zone area of the slope angle; (3) The plastic zone of scheme c and scheme d is only distributed in the weak interlayer, and the distribution area is small. Combined with the maximum displacement value in Figure 7 and the displacement field distribution in Figure 8, the slope under the two schemes has no risk of sliding; and (4) The slope plastic zone of schemes e–h is distributed at the top of the slope and the slope surface. Only schemes f and g have a small area distribution at the weak interlayer. Combined with Figures 7, 8, the slope under these four schemes is only damaged at the slope surface, but the overall stability of the slope is still possible.

Figure 9

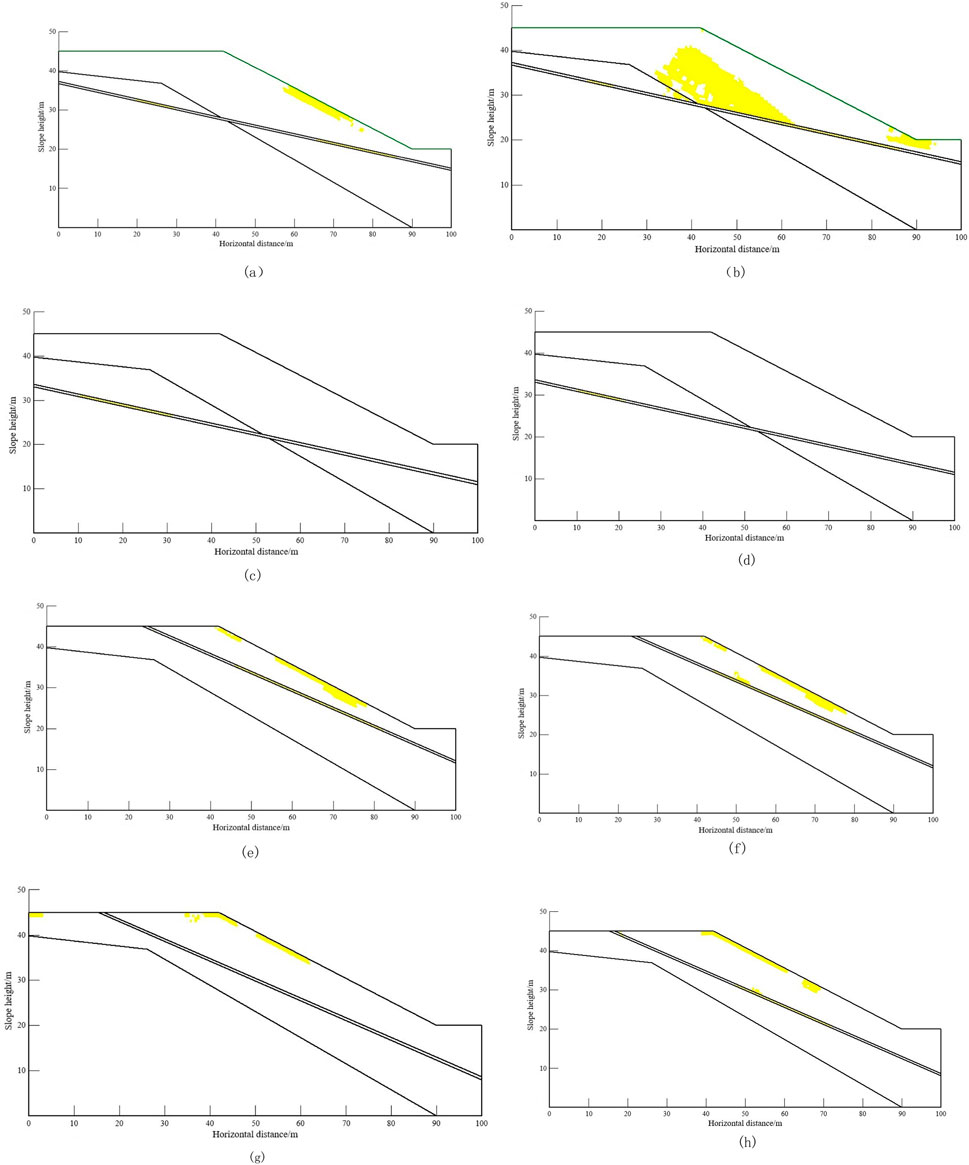
Figure 9. Variation of the plastic zone of a slope under different schemes. (a–h) Plastic zone distribution of specimen.

4.2.3 Analysis of the change of slope safety factor under different types

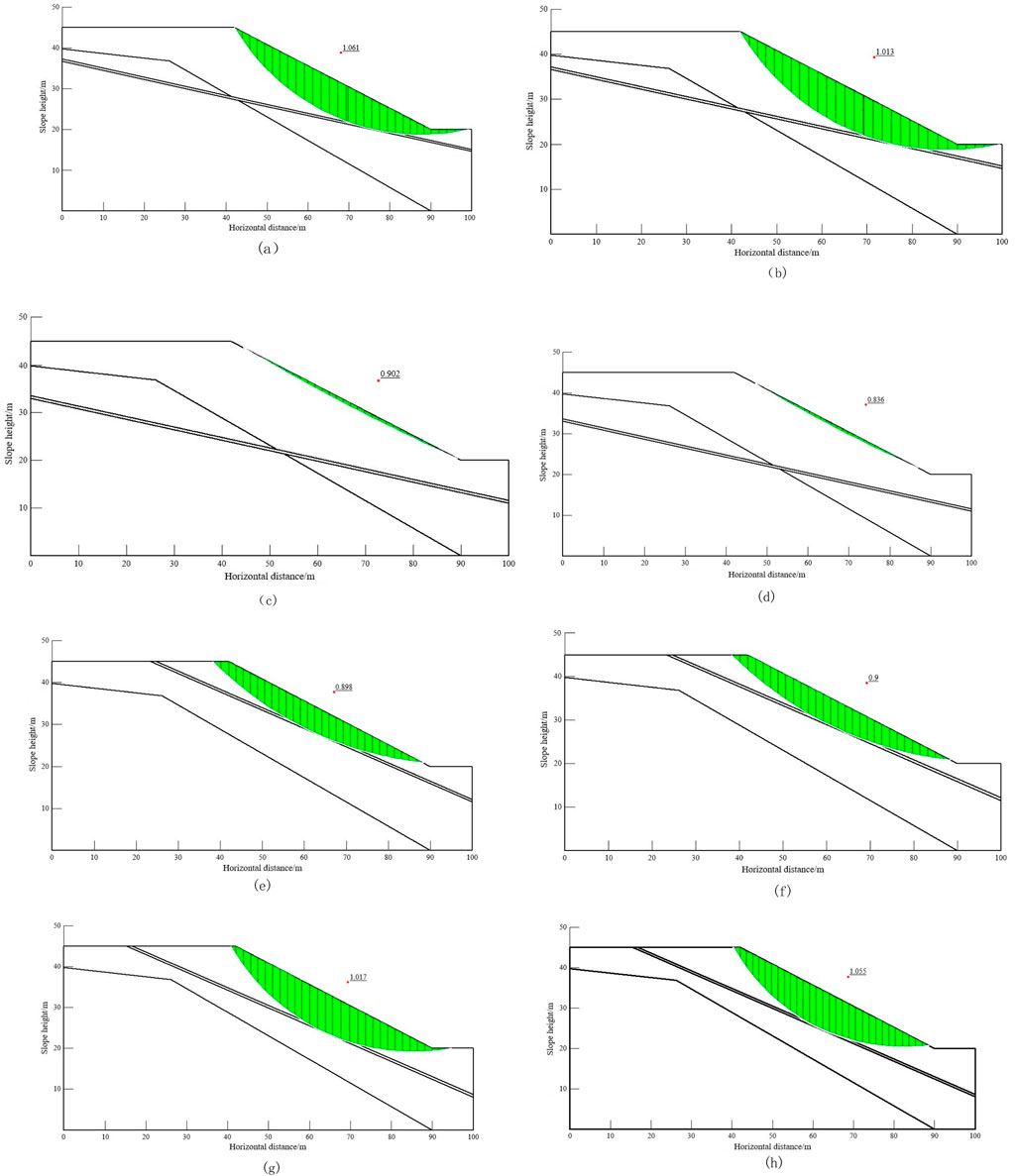
According to the relevant provisions in the 《Specification for Investigation of Landslide Prevention and Control Engineering》 (Table 5), the factor of safety (FoS) of the slope in Figures 10, 11 is summarized and studied. The following specific conclusions can be drawn: (1) the slope stability under the eight simulation schemes is in an unstable, unstable, and basically stable state, and the FoS value in the basic stable state is basically at the critical value of the unstable and basically stable state values, indicating that the slope stability under the eight simulation schemes is relatively poor. (2) The safety factor of scheme d (the angle of weak interlayer is 13°, the distance of interlayer is 8m, the rainfall intensity is 100 mm/d, and the duration is 6d) is the smallest, which is 0.836, indicating that landslide has occurred at this time, but it can be seen from Figure 11d that only the slope surface has the risk of landslide. (3) Comparing the FoS values of schemes c, e, and f in Figure 10, the FoS values are almost the same, but according to the range of the unstable region in Figure 11, the unstable regions of schemes e and f are almost the same, but it is very different from the unstable region of scheme c. (4) During distribution comparison of schemes a and h and schemes b and g, although the FoS values are very similar, the unstable area shows a large difference at the slope angle.

Table 5

Table 5. Slope grade gradient division table.

Figure 10

Figure 10. Safety factors under different types.

Figure 11

Figure 11. Safety factor of each type. (a–h) Safety factor of specimen.

5 Conclusion and discussions

5.1 Discussions

5.1.1 Comparison of the indoor test and numerical simulation results

Indoor scheme T1 is consistent with simulation schemes e and f in terms of the angle and buried depth of the weak interlayer. Due to rainfall, the slope slides along the weak interlayer and accumulates at the slope angle (Xiaohua and Shuangxiang, 2014; Huang and Wang, 2011; Zhou et al., 2014). Continuous rainwater infiltration reduces the friction coefficient of rock and soil at the slope surface, possibly causing the slope sliding zone to pass through the weak interlayer and destroy slightly weathered tuff. However, when the weak interlayer angle is 23° and the buried depth is 4m, two different rainfall types (e: rainfall intensity 40 mm/d and duration 12d; f: rainfall intensity 100 mm/d and duration 6d) have almost the same impact on the safety of the slope.

When there is no rainfall, the slope failure position in indoor scheme T2 is at the top and shoulder of the slope. Considering the influence of rainfall, schemes a and b show that the maximum displacement occurs at the slope angle, but the damage location is at the slope surface, the weak interlayer, and the slope angle due to the influence of rainfall. This is because rainfall reduces the internal friction angle of the rock and soil on the slope surface, and as rainfall increases, rainwater penetrates into the slope, causing damage to the internal rock and soil.

According to T3 and schemes g and h, the location of slope failure in the laboratory test and the location of maximum displacement in the simulation scheme are consistent with the phenomenon of research results (2), and their principles are also consistent. With the increase of rainfall, the unstable area appears in the depth of the slope surface, mainly due to the decrease of the internal friction angle caused by the infiltration of rainwater.

5.1.2 Limitations of the study

Although the indoor model test and numerical simulation test have qualitatively and quantitatively analyzed the stability of the slope under different conditions (Xiao and Li, 2020; Niu et al., 2009; Ming-liang et al., 2022; Li et al., 2018), the previous indoor model test scheme was poorly considered, and a comprehensive and detailed analysis has not been carried out.

The parameters selected in the numerical simulation test are relatively few, which cannot truly reflect the slope site conditions. However, it can provide the necessary reference value for the later maintenance of the slope.

5.2 Conclusion

Because the indoor test cannot simulate real rainfall, GeoStudio numerical simulation software is used to quantitatively and qualitatively analyze the slope stability problems under eight different types of schemes. However, because the numerical simulation scheme is completely designed by orthogonal experiment, indoor test scheme T4 cannot be completely included in the simulation scheme. The following are the key conclusions:

(1) Indoor scheme T1 and simulation schemes e and f are similar in the weak interlayer angle and buried depth. Rainfall causes slope sliding along the weak interlayer and affects the safety factor and slip zone size similarly for different rainfall types when the weak interlayer angle is 23° and the buried depth is 4 m.

(2) Without rainfall, slope failure occurs at the top and shoulder; with rainfall, damage is at the slope surface, weak interlayer, and slope angle due to reduced internal friction angle and rainwater penetration.

(3) Laboratory test T3 and simulation schemes g and h show consistent failure locations and principles. Increased rainfall leads to unstable areas in the slope surface depth due to decreased internal friction angle from rainwater infiltration.

Through the comprehensive analysis of indoor test and numerical simulation results, the influence of weak interlayers on the slope stability mechanism can be discussed in depth. Studies have shown that the angle and depth of the weak interlayer are the key factors affecting the slope instability mode. When the weak interlayer angle is 23° and the buried depth is 4 m, rainfall will significantly change the mechanical properties of the slope, resulting in the expansion of the sliding surface along the weak interlayer and affecting the safety factor and the size of the sliding area. In addition, rainfall causes the slope surface, weak interlayer, and slope angle to become the main instability areas by reducing the internal friction angle and permeability. The consistency of laboratory test and numerical simulation results shows that the existence of weak interlayers not only controls the local stress state but also significantly increases the risk of slope instability. Further analysis shows that with the increase of rainfall intensity, the unstable area of slope surface depth gradually expands, which is closely related to the change of mechanical properties of weak interlayers. Therefore, the angle, buried depth, and rainfall conditions of the weak interlayer jointly determine the instability mode and the stability of the slope, which provides an important reference for the stability evaluation of the weak interlayer slope in engineering practice.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SZ: Writing – original draft, Writing – review and editing. GZ: Conceptualization, Data curation, Formal Analysis, Methodology, Writing – review and editing. CX: Funding acquisition, Resources, Writing – review and editing. JM: Methodology, Supervision, Writing – review and editing. ZS: Investigation, Software, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The Ordos City Iconic Innovation Team Program (TD20232305); The Innovation Capability Support Plan in Shaanxi Province of China (2024RS-CXTD-54); The National Institute of Natural Hazards, Ministry of Emergency Management of China (2023-JBKY-57); The National Key Research and Development Program of China (2021YFB3901205); National Natural Science Foundation of China Youth Science Fund Project (52304109); R&D Program of Beijing Municipal Education Commission (No. KM202311417004); Academic Research Projects of Beijing Union University (No. ZK20202214).

Acknowledgments

The authors would like to thank the National Institute of Natural Hazards, Ministry of Emergency Management of China, for helpful discussions on topics related to this work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor WT declared a shared affiliation with the author GZ at the time of review.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Gengqian, N., Chen, Z., Zhu, T., Zhang, L., and Zhou, Z. (2024). Experimental study on the failure of fractured rock slopes with anti-dip and strong weathering characteristics under rainfall conditions. Landslides 21 (1), 165–182. doi:10.1007/s10346-023-02142-3

CrossRef Full Text | Google Scholar

Hou, T.-S., Duan, X., and Liu, H. Y (2021). Study on stability of exit slope of Chenjiapo tunnel under condition of long-term rainfall. Environ. Earth Sci. 80 (17), 590. doi:10.1007/s12665-021-09895-x

CrossRef Full Text | Google Scholar

Hsuan, Ho I. (2015). Numerical study of slope-stabilizing piles in undrained clayey slopes with a weak thin layer. Int. J. Geomechanics 15 (5). doi:10.1061/(asce)gm.1943-5622.0000445

CrossRef Full Text | Google Scholar

Huang, Q., and Wang, J. (2011). Study of the deformation characteristics of an anti-dip slope with soft internal layers. China Civ. Eng. J. 05, 109–114. doi:10.1111/j.1759-6831.2010.00113.x

CrossRef Full Text | Google Scholar

Jacques, M. (2007). Numerical validation of an elastoplastic formulation of the conventional limit pressure measured with the pressuremeter test in cohesive soil. J. Geotechnical Geoenvironmental Eng. 133 (9), 1119–1127. doi:10.1061/(asce)1090-0241(2007)133:9(1119)

CrossRef Full Text | Google Scholar

Li, S., Zhu, J., Wang, S., and Wu, L. (2018). Stability analysis method for bedrock-type shallow slopes considering rainfall types. Hydrogeology Eng. Geol. 45 (2), 131–135+149. doi:10.16030/j.cnki.issn.1000-3665.2018.02.20

CrossRef Full Text | Google Scholar

Liu, X. L., and Zhou, D. P. (2002). Stability evaluation of rock mass slope with weak intercalated layers. J. Southwest Jiaotong Uni. 04, 382–386. doi:10.1007/s11769-002-0042-8

CrossRef Full Text | Google Scholar

Ming-liang, W., Li-Yue, H. U., Jin, L., Chang-Liang, S., and Hong-yu, B. A. I. (2022). Changes of rainy season in Northeast China in recent 21 years. J. Anhui Agric. Sci. 50 (20), 197–200. doi:10.3969/j.Issn.0517-6611.2022.20.051

CrossRef Full Text | Google Scholar

Niu, W., Ye, W., Liu, S., et al. (2009). Limit analysis of a soil slope considering saturated-unsaturated seepage. Rock Soil Mech. 30 (08), 2477–2482. doi:10.1016/S1874-8651(10)60073-7

CrossRef Full Text | Google Scholar

Oh, W. T., and Vanapalli, S. K. (2010). Influence of rain infiltration on the stability of compacted soil slopes. Comput. Geotechnics 37 (5), 649–657. doi:10.1016/j.compgeo.2010.04.003

CrossRef Full Text | Google Scholar

Qu, H., Song, Z., Zhang, Z., et al. (2024). Dynamic characteristics of deposit slope under coupled action of earthquake and rainfall. Soil Dyn. Earthq. Eng., 176.

Google Scholar

Rakshanda, S., Mohammadi, H., and Babu G. L., S. (2022). Effect of rainfall infiltration on the stability of compacted embankments. Int. J. Geomechanics 22 (7). doi:10.1061/(asce)gm.1943-5622.0002425

CrossRef Full Text | Google Scholar

Santha, R. A., and Thote, N. R. (2011). Empirical slope design for friable ore bodies with weak wall rocks. Int. J. Earth Sci. Eng. 4 (6), 1067–1074.

Google Scholar

Shao, X., Ma, S., Chong, X., Cheng, J., and Xu, X. (2023a). Seismically-induced landslide probabilistic hazard mapping of Aba Prefecture and Chengdu Plain region, Sichuan Province, China for future seismic scenarios. Geosci. Lett. 10 (1), 55. doi:10.1186/s40562-023-00307-5

CrossRef Full Text | Google Scholar

Shao, X., Ma, S., Chong, X, and Xu, Y. (2023b). Insight into the characteristics and triggers of loess landslides during the 2013 heavy rainfall event in the tianshui area, China. Remote Sens. 15 (17), 4304. doi:10.3390/rs15174304

CrossRef Full Text | Google Scholar

Shao, X., Xu, C., Lei, L., Yang, Z., Yao, X., Shao, B., et al. (2024). Spatial analysis and hazard assessment of large-scale ancient landslides around the reservoir area of Wudongde hydropower station, China. Nat. Hazards 120 (1), 87–105. doi:10.1007/s11069-023-06201-9

CrossRef Full Text | Google Scholar

Shuai, Xu, Wang, A., Jiang, H., and Xu, Y. (2025). Failure mechanism of deep weak interlayer of expansive soil slope based on fractal theory. Comput. Geotechnics 179, 107051. doi:10.1016/j.compgeo.2024.107051

CrossRef Full Text | Google Scholar

Sun, S.-W., Liu, L., Jia-Bing, H., and Ding, H. (2022a). Failure characteristics and mechanism of a rain-triggered landslide in the northern longwall of Fushun west open pit, China. Landslides 19 (10), 2439–2458. doi:10.1007/s10346-022-01926-3

CrossRef Full Text | Google Scholar

Sun, Y., Deying, L., Miao, F., She, X., Yang, S., and Xie, X. (2022b). Effects of weak bedding plane, fault, and extreme rainfall on the landslide event of a high cut-slope. Sensors 22 (18), 6790. doi:10.3390/s22186790

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Chai, J., Cao, J., Qin, Y., Xu, Z., and Zhang, X. (2020). Effects of seepage on a three-layered slope and its stability analysis under rainfall conditions. Nat. Hazards 102 (3), 1269–1278. doi:10.1007/s11069-020-03966-1

CrossRef Full Text | Google Scholar

Xiao, Y. Y., and Li, A. R. (2020). Change of soft rock slope stability with weak interlayer under rainfall conditions. J. Yibin Univ. 20 (12), 16–19. doi:10.19504/j.cnki.issn1671-5365.2020.12.003

CrossRef Full Text | Google Scholar

Xiaohua, M., and Shuangxiang, Z. (2014). Influencing factors of rock slope with weak interlayer based on orthogonal design method. North. Commun. 10, 66–68. doi:10.15996/j.cnki.bfjt.2014.10.055

CrossRef Full Text | Google Scholar

Xie, C., Huang, Y., Lei, L., and Xu, C. (2023). Detailed inventory and spatial distribution analysis of rainfall-induced landslides in jiexi county, guangdong province, China in august 2018. Sustainability 15 (18), 13930. doi:10.3390/su151813930

CrossRef Full Text | Google Scholar

Young-Suk, S., and Hyo-Sung, S. (2023). Experimental study to estimate the criteria for shallow landslides under various geological conditions in South Korea. Environ. Earth Sci. 82 (23), 582. doi:10.1007/s12665-023-11269-4

CrossRef Full Text | Google Scholar

Zeng, L., Han-Bing, B., Shi, Z.-N., et al. (2017). Forming condition of transient saturated zone and its distribution in residual slope under rainfall conditions. J. Central South Univ. 24 (8), 1866–1880. doi:10.1007/s11771-017-3594-6

CrossRef Full Text | Google Scholar

Zhang, Ga, Wang, R., Qian, J., and Zhang, J. M. (2012). Effect study of cracks on behavior of soil slope under rainfall conditions. Soils Found. 52 (4), 634–643. doi:10.1016/j.sandf.2012.07.005

CrossRef Full Text | Google Scholar

Zhong, S., and Miao, Y. (2021). Research on the influence of weak interlayer in open-pit slope on stability. Adv. Civ. Eng. 2021, 2021. doi:10.1155/2021/4256740

CrossRef Full Text | Google Scholar

Zhou, F., Qiang, X, and Liu, H. (2014). Shaking table model test on deformation and failure characteristics of slope with horizontal weak interlayer. Mt. Res. 05, 587–594. doi:10.16089/j.cnki.1008-2786.2014.05.010

CrossRef Full Text | Google Scholar

Zhou, T., Zhang, L., Cheng, J., Wang, J., Zhang, X., and Li, M. (2022). Assessing the rainfall infiltration on FOS via a new NSRM for a case study at high rock slope stability. Sci. Rep. 12 (1), 11917. doi:10.1038/s41598-022-15350-z

PubMed Abstract | CrossRef Full Text | Google Scholar