Investigation on indentation test of green sandstone under coupled effect of axial and confining stress

To study the effect of confining stress on the indentation test of rock under different axial stress and the corresponding mechanism of penetrating rock fragmentation, physical and numerical experiments of single spherical button penetration into green sandstone under triaxial stress conditions were conducted. The results indicate that the indices of crushing load, yield, brittleness feature, and energy consumption first decrease and then increase with increasing confining pressure, under high axial pressure conditions (30 MPa) and the thickness of rock chips increases by 37%, from 1.11 mm to 1.52 mm. The opposite pattern is observed under low axial pressure conditions (15 MPa). The thickness decreases from 1.475 mm to 0.915 mm, with a reduction of about 50%. In general, under all confining stress conditions, specific energy under high axial pressure conditions is lower than that under low axial pressure conditions. The maximum difference reaches 285%. The numerical experiments suggest that the total number, direction and distribution of cracks show great consistency with experimental results of indentation tests. The smaller total number of cracks under high axial pressure conditions may be the main reason for the lower specific energy. This present study may provide some primary knowledge about the rock cracking character and breaking efficiency under different stress conditions. The analysis of micro-cracks provides an explanation for the patterns of rock fragmentation.

1 Introduction

Mechanized excavation has been widely used in underground engineering because of its advantages of safety, high efficiency, and low disturbance while common problems such as low crushing efficiency and large tool loss have been encountered when crushing deep underground rock mass (Ergin and Acaroglu, 2007; Yang et al., 2015). The reasons for these problems are considered to be the exacerbated cuttability of hard rock under harsh deep underground conditions. It proves that in-situ stress and high rock hardness play a significant role in the application of mechanized excavation at depth (Balci and Bilgin, 2007). Despite the adverse effect of deep underground conditions, field observations have indicated that rock cuttability can be improved probably by high geostress during the process of excavation unloading, inducing pre-existed fractures within rock mass (Innaurato et al., 2011). Therefore, the controversy makes it necessary to investigate the performance and mechanism of hard rock mechanized fragmentation under high in-situ stress conditions.

Research on deep-underground mechanical rock fragmentation has been developed in applications such as TBM tunneling, road headers, and petroleum drilling (Copur et al., 2024; Thyagarajan and Rostami, 2024; Kim et al., 2023). Estimating stability and fragmentation performance of rock mass at depth, which plays a key role in mechanical excavation, are diversified in the fields mentioned above. In practical engineering projects, for instance, the field penetration index, defined as the ratio of the applied thrust per cutter to the penetration per revolution, is adopted to describe rock boreability in TBM tunneling projects (Yin et al., 2014a; Yin et al., 2014b; Gou and Zhang, 2022). As a result of the difficulties in obtaining applicable information from field measurements, laboratory tests have raised attention (Li et al., 2022a; Li et al., 2018). It has been pointed out that the behavior of the indenter penetrating rock is the basic process concerning the mechanical fragmentation of rock. This certain simplification of mechanical rock fragmentation contributes greatly to solving rock-fragmentation-related problems in various fields (Yin et al., 2014a; Yin et al., 2014b). Firstly, in the application of road headers, drag picks were pressed into the specimen to study the influence of confining stress and loading patterns. Wang et al. (2018) found that rock cuttability decreased first but improved after the confining stress exceeded 40 MPa. Secondly, investigations of indentation tests by TBM disc cutters are abundant. Liu et al. (2016b) exerted two disc cutters into the rock under biaxial unequal pressure and found that with the minimal stress fixed, rock fragment efficiency improved because of the enlarged crushing zone as the maximum stress increased. Thirdly, in the field of petroleum drilling, diversified shaped indenters were widely used in indentation tests under pressure as a result of the large depth in drilling. Fang et al. (2019) conducted a cone penetration experiment and found that minimum stress played a leading role in the indentation process, in which the ultimate force increased and cracks grow shallower as confining stress increased. To sum up, researchers concerned with drag tools take into consideration the cutting or dragging behavior and corresponding splitting pattern of the specimen, while investigations of TBM roller cutter largely focus on restoring the squeezing-and-stripping behavior of fragmentation, and impacting under pressure is the key element in drilling-related investigations.

Although the significance of triaxial stress conditions in terms of rock fragmentation has been acknowledged, the influence and mechanism of triaxial stress on fragmentation remain implicit (Liu et al., 2016a; Wang et al., 2019). Numerical methods, especially the discrete element method (DEM) have made a great contribution in uncovering the mechanism of rock fragmentation by cutters under stress conditions, which prevails in showing the pattern of cracks (Zhang Kui, 2010; Xie et al., 2024a; Wu et al., 2024; Huang et al., 2025; Wu et al., 2021; Wu et al., 2020). Liu et al. (2015) made use of PFC2D in exhibiting the crack patterns and explained the mechanism of the influence of confining stress on the indentation test. Confining pressure decreased fragment width by increasing the deflection angle of the crack initiation. Kaitkay and Lei (2005) concluded from their simulation that external hydrostatic pressure is found to assist in chip formation and transform the mode of cutting from a dominantly brittle mode to a ductile-brittle mode. Despite the great effort in simulating the cutting behavior under stress conditions, triaxial stress conditions have received little attention (Xiong et al., 2021; Saksala, 2016). It is necessary that a systematic investigation on the indentation test of hard rock under triaxial stress conditions be conducted and the corresponding mechanism is uncovered.

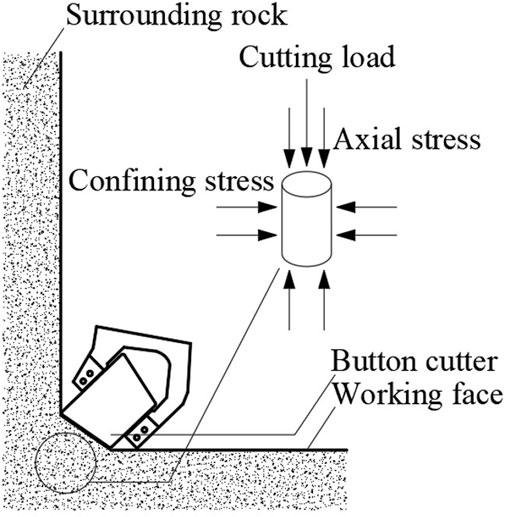
Research has confirmed that due to stress concentration on the edge of the working face in deep underground excavation projects, the rock mass to be excavated is confined with both the horizontal and vertical in situ stress (Yang et al., 2024a). Due to the limitation of experiment equipment, current experimental investigations on the stress conditions in penetration tests are largely restricted to the effect of horizontal confining stress and mud column pressure (Saksala, 2016; Li Y. et al., 2022; Shaterpour-Mamaghani et al., 2022). Additionally, the stress state of the rock is influenced by its position on the working face. When the drilling fluid pressure is too high or the rock is close to the excavation side boundary, the rock material is often under triaxial stress conditions, as shown in Figure 1. This study simplifies the stress parallel to the drilling direction to axial stress and the stress perpendicular to the drilling direction to confining pressure (Zou et al., 2022).

In this paper, the coupled effect of axial (vertical) and confining (horizontal) stress on the indentation test of green sandstone was investigated by means of physical and numerical experiments. It was for the first time to make a comparison between the effect of small and large axial stress conditions on penetrating fragmentation of rock under confinement employing physical experiments and to establish appropriate explanations for the certain effect from the point of meso scale. For this purpose, this investigation adopted a piece of equipment providing a triaxial stress condition for penetration. To estimate the performance of rock fragmentation, three types of indices concerning cuttability are used, namely load-penetration-related indices such as applied force and corresponding penetration depth, debris-related, brittleness-related and energy-related indices. Apart from physical experiments, numerical simulation was conducted and focused on the feature of cracks, in an attempt to find out the mechanism of rock fragmentation by indentation under the coupled effect of axial and confining stress conditions.

2 Test methodology

2.1 Rock samples

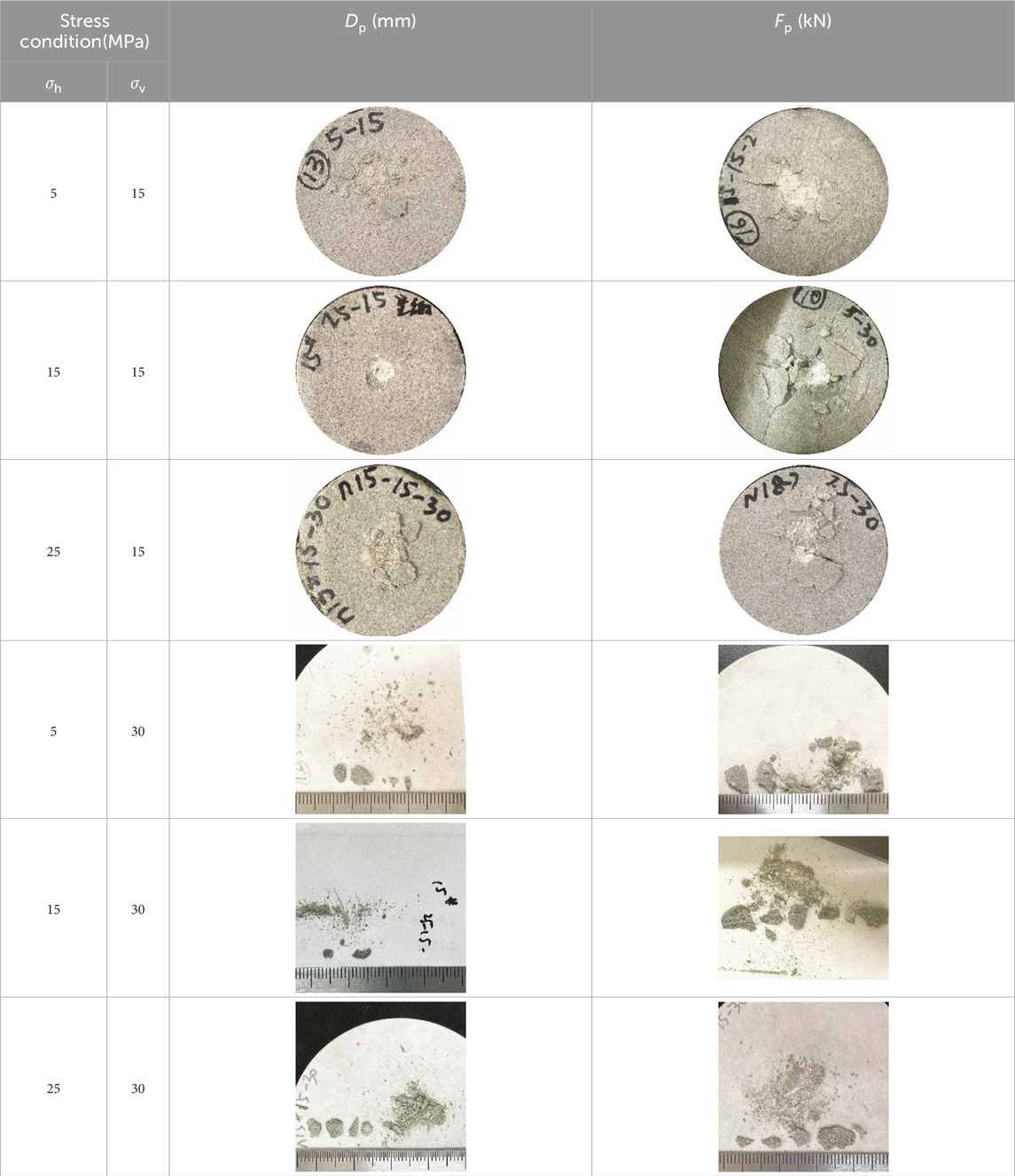
To investigate the fragmentation of rock in penetration test under triaxial pressure conditions, polished cylindrical green sandstone samples with a diameter of 36 mm and height of 50 mm were adopted and thus the stress condition was axial symmetric. The sandstone was taken from a relatively homogeneous rock block, with the axis of the core oriented perpendicular to the bedding plane, thus minimizing the impact of the stratification characteristics of the sandstone on fragmentation to the greatest extent. According to the analysis based on the cavity expansion model theory, the size of the rock sample was reasonable (Yin et al., 2014a; Yin et al., 2014b; Alehossein et al., 2000; Chen and Labuz, 2006). Mechanical properties including uniaxial and triaxial compressive strength and Brazilian tensile strength listed in Table 1, were tested according to International Society for Rock Mechanics (ISRM) recommendations.

Table 1

Table 1. Mechanical parameters of the green sandstone.

2.2 Penetration testing apparatus

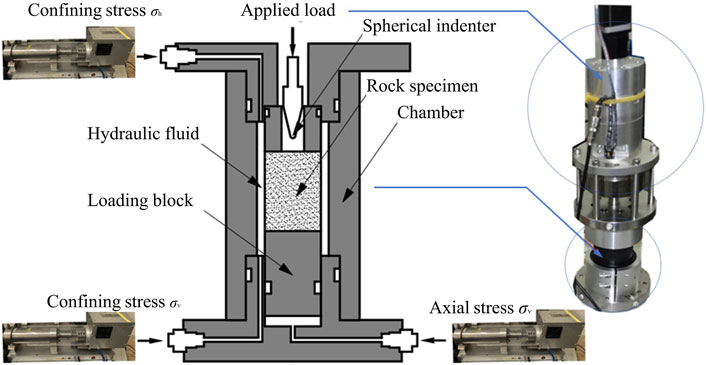
Penetration was conducted on the system of single indenter penetration equipment, shown in Figure 2, which included the part of penetration and that of the pressure chamber (Zou et al., 2022). A stepping motor whose loading ability is up to 20 kN and the indenter made the penetration part. Sphere-shaped cutter is widely applied in the fragmentation of hard rock for its feature of long duration and thus spherical indenter with a radius of 2.5 mm was adopted in this experiment. The indenter was made up of hard alloy whose deformation was neglected during penetrating. The pressure chamber is different from a traditional cell in that it provides vertical pressure condition ${\sigma }_{\mathrm{v}}$ or namely axial stress except for horizontal confining pressure ${\sigma }_{\mathrm{h}}$, which simulated the complex triaxial stress state in the vicinity of the edge of the working face. In detail, horizontal stress was held by hydraulic fluid, which is advantageous because it largely reduces the abrasive effect on the edge of the specimen compared with the traditional rigid loading method.

Figure 1

Figure 1. Schematic of the in situ stress condition at the edge of the working face.

Figure 2

Figure 2. Testing apparatus and schematic diagram.

2.3 Laboratary design

As mentioned, rock in an excavation project at depth can be held in complex stress conditions. Estimated with a lithostatic slope of 27 MPa/km, in situ stress reaches 27 MPa when the excavation project exceeds 1,000 m (Saksala, 2016). In actual engineering, in situ stress varies a lot influenced by many factors. For instance, according to the statistics in a tunnel project buried in as deep as 1800 m, horizontal in situ stress varies around 25 MPa, and vertical stress reaches 33 MPa (Cheng et al., 2020). Based on the information above, concerning the ability of the current equipment, the stress level was set as listed in Table 2. The test procedure was as follows:

(1) Sample packed in the membrane was set into the cell and hydraulic fluid was injected. It was guaranteed that the pressure chamber was firmly sealed.

(2) The height of the indenter was adjusted so that the bottom of the indenter was close to the surface of the example.

(3) Both the vertical and horizontal stress was exerted at the same rate until the target pressure was reached. The target pressure was maintained by pressure-volume controllers (PVC) during the course of the experimentation.

(4) The indenter was driven vertically downwards at the speed of 0.4 mm/min until the sample was broken or the target penetration (2.5 mm) was reached. Load-penetration curve was recorded using a linear variable differential transformer and a load cell.

(5) The sample was taken out from the cell and the debris was weighed and its size measured.

Table 2

Table 2. Confining stress σ_v and vertical stress σ_h exerted in green sandstone indentation test.

2.4 Numerical simulation model

DEM prevails among numerical methods with respect to the investigation of discontinuous behavior, especially to the patterns of fracture. PFC2D discretizes objects into rigid circular or cylindrical particles, and interactions between elements only happen at contact points, and thus the feature of the material is controlled by the characteristics of contact models and their parameters. Despite the advantage of PFC2D, the difficulty in simulating a high ratio of uniaxial compressive strength (UCS) to tensile strength (TS) has been encountered in PFC2D simulations using traditional contact models (Shi et al., 2023; Shi et al., 2024). To solve this problem, Potyondy proposed a flat-joint model, or FJM, which operates well in simulating the behavior of rock with a high UCS/TS ratio (Wu and Xu, 2016). Therefore, in this paper, FJM is used to simulate the mechanical behavior of green sandstone.

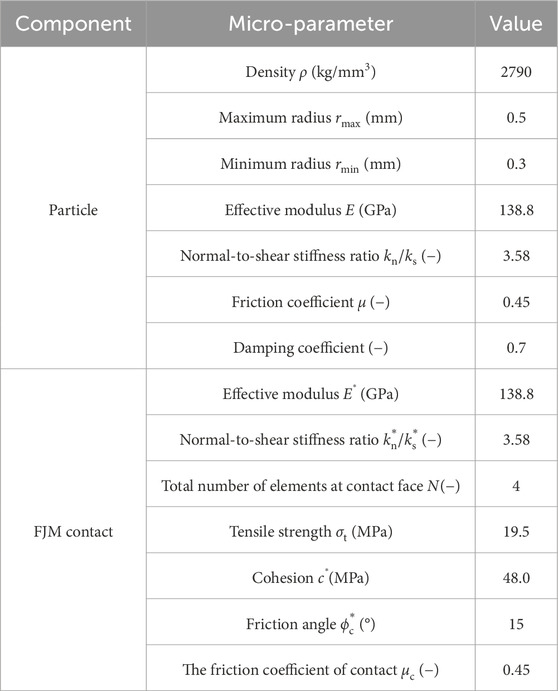
Uniaxial compressive strength and Brazilian tensile strength are fundamental indices for calibration in PFC2D. The calibration results of micro-parameters are summarized in Table 3. The macro-properties between experimental and numerical studies are compared in Table 4. As can be seen, the numerically obtained parameters (UCS, Young’s modulus, Poisson’s ratio, and BTS) show a good agreement with those measured in the laboratory. It is concluded that the micro-parameters calibrated for the sandstone model are valid and reliable.

Table 3

Table 3. Micro-parameters calibrated for green sandstone.

Table 4

Table 4. Comparison of macro-properties between laboratory experiment and numerical simulation for sandstone.

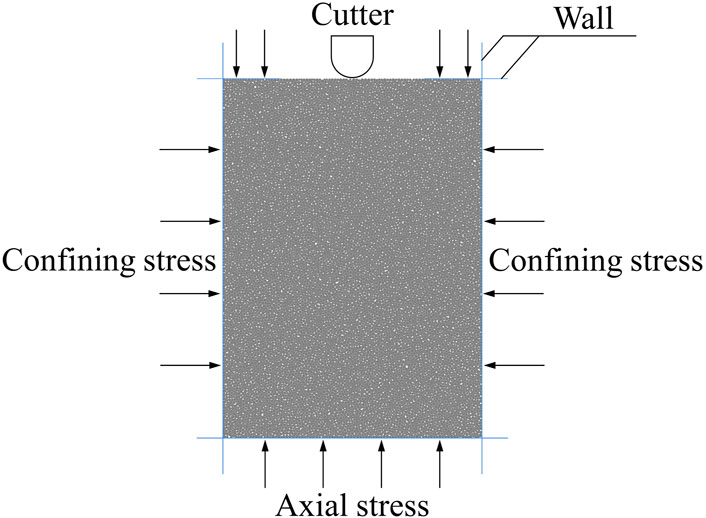
The confining and axial stress is exerted by rigid and frictionless walls in PFC2D, which is a traditional loading method. Considering that the modulus of the indenter is large compared with rock, the indenter is also simulated using a rigid spherical wall. It is necessary to point out here that friction has been established between the rigid wall that constitutes the cutter tooth and the particles, in order to simulate the friction between the cutter tooth and the rock during the intrusion process, and that friction has a significant impact on the intrusion process. The simulated model is shown in Figure 3.

Figure 3

Figure 3. Simulated indentation test model under confining stress and axial stress.

3 Results and discussion

3.1 Analysis of load-penetration-related indices

The first rupture of the rock during the course of penetration acts as an important basis to evaluate the intrusion process. When the applied load increases to a critical value during the intrusion into the rock, a sudden leap or the first rupture occurs. At this point, the rock in the vicinity of the dense core breaks up and the load suddenly falls. The critical penetration depth and the load threshold can be directly related to the stability or the crushing difficulty of the rock. Typical curves of applied load concerning penetration depth under different stress conditions are shown in Figure 4. Based on this feature of leaping, the ratio of critical force to the corresponding depth represents the force required for per unit penetration, also reflecting the elastic feature of rock under indentation (Fang et al., 2019). In this paper, this certain feature and the corresponding statistics called load-penetration-related indices were adopted to assess the difficulty of breaking the rock. About the load-penetration curve, the critical force is equivalent to the first peak force, denoted by F_p, and the corresponding penetration (critical depth) is denoted by d_p. Hither the load penetration ratio F_p/d_p was examined to study the elastic feature under indentation. Figure 5 records the critical load F_p, the corresponding critical depth d_p, and the ratio F_p/d_p during penetration of rock samples by spherical indenter under different pressure conditions. F_p is a direct indicator in assessing cutting difficulty among these indices.The effect of stress conditions is divided into two cases as below.

Figure 4

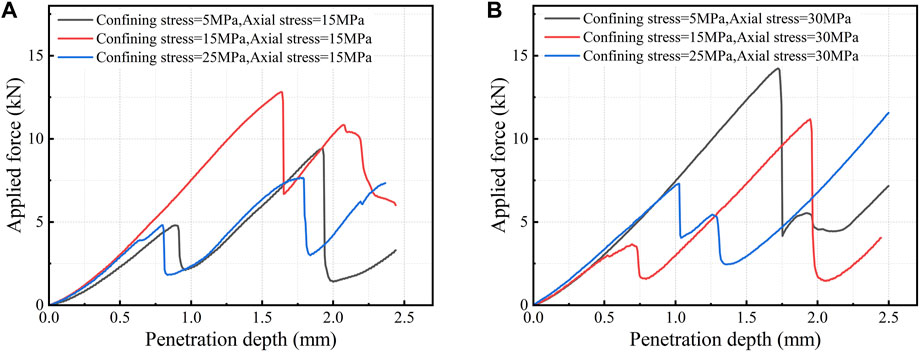
Figure 4. Typical curves of applied load concerning penetration depth under the condition of (A) axial stress = 15 MPa and (B) axial stress = 30 MPa.

Figure 5

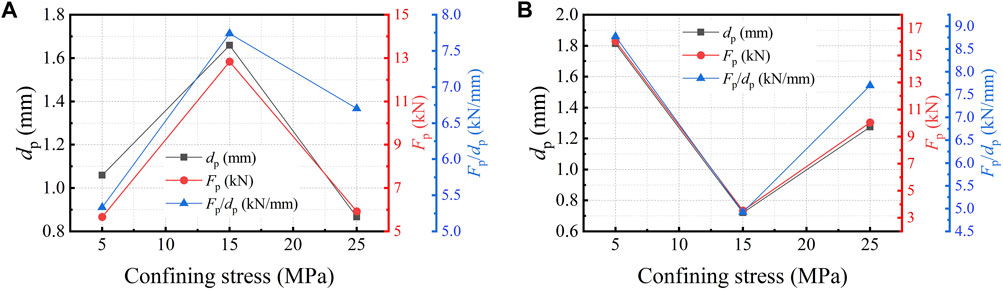
Figure 5. The first peak load F_p, the corresponding penetration depth d_p and F_p/d_p under the axial stress of (A) 15 MPa and (B) 30 MPa.

The first is the case for the ${\sigma }_{\mathrm{v}}=15\text{\hspace{0.17em}MPa}$ pressure environment. F_p is small when confining stress is low, and so are d_p and the ratio F_p/d_p. As the confining stress increases, these three indices show a trend of first increasing and then decreasing, and reach the maximum when ${\sigma }_{\mathrm{h}}=15\text{\hspace{0.17em}MPa}$. This certain rise-and-fall trend corresponds to that in previous studies where no axial stress was exerted. For instance, Yin et al. (Yin et al., 2014a) penetrated marble with a disc-cutter-shaped indenter under equivalent confining stress, and the peak value of load happens when confining stress equals 25 MPa.

In terms of the extent of the effect of stress conditions, with detailed statistics depicted in Table 5, the maximum F_p under the condition of 15 MPa axial pressure is 2.69 times the minimum value, and the corresponding ratio of d_p is 2.05, indicating that confining pressure at the same axial pressure level has a significant effect on the excavability of the rock. In detail, it is easy to rupture the rock when confining pressure is small under this axial pressure condition, but it is significantly hard to break the rock when confining pressure increases to a certain value.

Table 5

Table 5. Statistics in penetration under different stress conditions.

As depicted in Figure 5, F_p/d_p shows the same trend as that of intrusion depth d_p. As mentioned above, a larger F_p/d_p means that the rock is stable and hard to break. The pressure environment with axial pressure ${\sigma }_{\mathrm{v}}=15\text{MPa}$ and circumferential pressure ${\sigma }_{\mathrm{h}}=15\text{MPa}$ constitutes a harsh condition for penetrating. In other words, it is necessary to increase the feed force into the deeper part of the rock to break the rock.

The other is the case under the condition of σ_v = 30 MPa. As depicted in Figure 5B, the first peak load F_p and corresponding penetration depth d_p first falls and then rises with the increasing confining pressure, and so does F_p/d_p. The minimum value of all of the three indices is obtained when ${\sigma }_{\mathrm{h}}=15\text{\hspace{0.17em}MPa}$. This trend is quite the opposite of that under the confining pressure ${\sigma }_{\mathrm{v}}=15\text{\hspace{0.17em}MPa}$, indicating that large axial stress may change the mechanism of rock fragmentation pressed by the indenter. Specifically, comparatively large horizontal confining stress which is unfavorable under small axial stress, contributes to the rupture of rock under large axial stress. Researchers have pointed out that large axial stress would direct cracks in a vertical direction extending to a deeper part of the rock, under which circumstance damage in the inner part of the rock is promoted, while the first rupture is not easy to happen under pressure (Bingxiang et al., 2017). As confining stress increases, horizontal stress leads to cracks deviating from the vertical direction and extending to the surface of the rock, facilitating the formation of chips or the first rupture (Innaurato et al., 2011; Wang et al., 2021). It is speculated that whether a large amount of cracks extending to the inner part or not determines the accessing of the first rupture.

3.2 Analysis of debris under different stress conditions

From the above analysis, the larger the value of F_p/d_p is, the harder and less economical it is for the indenter to enter the rock. However, the purpose of mechanical rock breaking is to break the rock both economically and effectively. That is, it is the ideal mechanical rock-breaking process that a smaller intrusion force required for pressing into the rock produces a larger amount of rock chips. Thus the amount and appearance of chips are examined to evaluate the effectiveness of penetration.

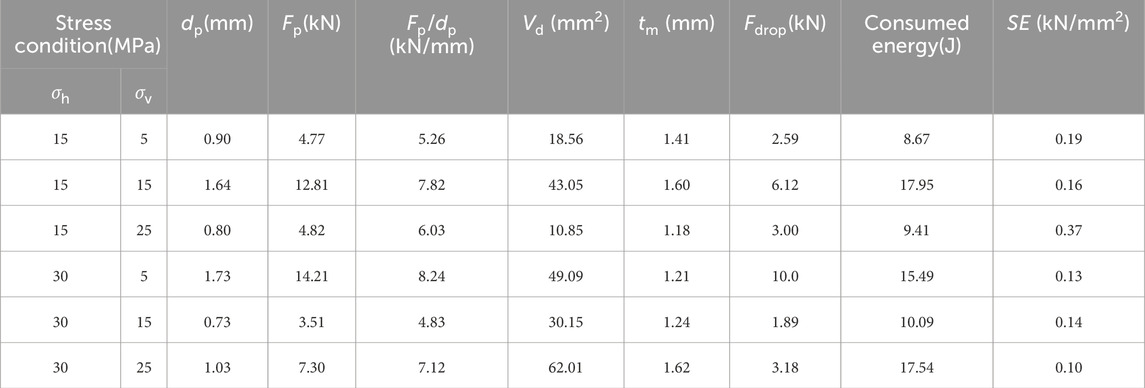
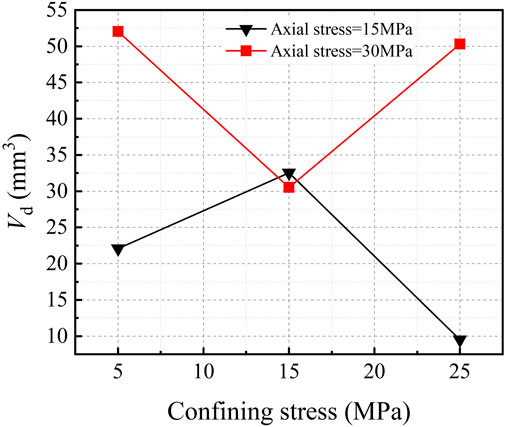
In the present paper, V_d is defined to evaluate the chip production efficiency and is calculated by V_d = V/d, in which V is the volume of debris and d is the penetration depth. Figure 6 depicts the curves of V_d concerning different pressure environments, and the patterns are generally consistent with that of the load-penetration-related indices. The variation of the maximum thickness of rock chips, denoted by t_m, is shown in Figure 7.

Figure 6

Figure 6. V_d as the confining stress increases under different axial stress.

Figure 7

Figure 7. $t_m$ as the confining stress increases under different axial stress.

Under the condition ${\sigma }_{\mathrm{v}}=15\text{\hspace{0.17em}MPa}$, V_p increases first and then decreases with the increase of the confining pressure, which corresponds to the curve of Figure 5, while the maximum thickness of rock chips gradually decreases in general. Previous research recorded the law of thickness of chips concerning confining stress, and generally shows similar trends (Fang et al., 2019; Liu et al., 2016c). It can be found that the rock chips under the conditions of ${\sigma }_{\mathrm{v}}=15\text{MPa}$ and ${\sigma }_{\mathrm{h}}=15\text{MPa}$ are larger in size and the amount of large chips is more, as shown in Table 6. The boreability analysis above also shows that the critical force F_p and the corresponding depth of penetration dp are larger under this stress condition, indicating that the larger force produces a considerable amount of rock chips. Under the condition of ${\sigma }_{\mathrm{v}}=15\text{MPa}$ and ${\sigma }_{\mathrm{h}}=25\text{MPa}$ rock chips are thinner by up to 26% compared to the optimal condition, and V_d is reduced by up to 75%. Meanwhile, the chip size decreases. It is clear that under this pressure environment, rock crushing occurs at smaller loads, but the effectiveness of fragmentation is not satisfactory.

Under the condition of axial pressure 30 MPa, V_d decreases and then increases with the increase of circumferential pressure, and the maximum thickness of rock chips gradually increases, both of which are opposite to the trend under the condition of axial pressure 15 MPa. From the appearance of the rock chips, the changing pattern of rock chip bulk and V_d are the same. Consistent with the axial pressure of 15 MPa, the larger crushing load can produce a larger amount of rock chips, and the rock chip size is also larger. When ${\sigma }_{\mathrm{v}}=30\text{MPa}$, the maximum thickness increased by 34% compared with the minimum, and the maximum chip volume increased by 106% compared with the minimum value when the circumferential pressure increased to 25 MPa. From the curve of Fp and dp, the specific pressure environment of ${\sigma }_{\mathrm{v}}=30\text{\hspace{0.17em}MPa}$ and ${\sigma }_{\mathrm{h}}=25\text{MPa}$ is not favorable for the first crushing to happen, but the volume, thickness, and bulk of the rock chips are larger, showing better breaking effectiveness. As indicated above, the influence of confining stress upon the effectiveness of indentation is different, depending on the axial stress exerted on the rock.

Comparing the effects of different axial pressures on the yield under the same confining pressure conditions, it can be found that the amount of rock chips produced under the condition of axial pressure ${\sigma }_{\mathrm{v}}=30\text{\hspace{0.17em}MPa}$ is significantly larger than that under the condition of axial pressure ${\sigma }_{\mathrm{v}}=15\text{\hspace{0.17em}MPa}$ when ${\sigma }_{\mathrm{h}}=25\text{\hspace{0.17em}MPa}$ and ${\sigma }_{\mathrm{h}}=5\text{\hspace{0.17em}MPa}$. Only at the confining pressure of 15 MPa, the amount of rock chips under different axial pressure conditions is close. Given the effectiveness of fragmentation, although large axial stress demands a larger load, more debris would be produced.

3.3 Analysis of the feature of brittleness

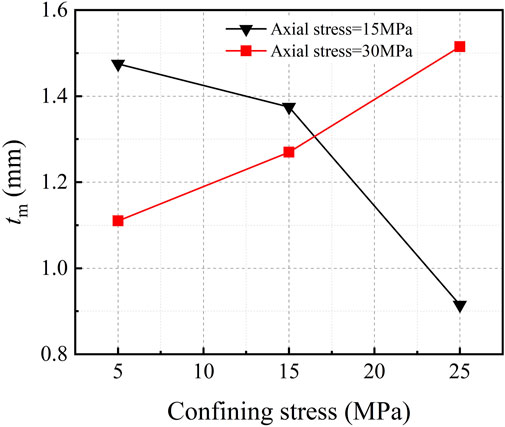
When the applied force reaches a critical value, a sudden drop in the load is typical for the penetration process. The jump point could represent the point of crack initiation or chip formation. When the stiffness of the loading mechanism is fixed, the feature of the brittleness of the rock fragmentation determines the magnitude of the drop. A large drop reflects significant brittle damage to the rock. Research has shown that brittle damage facilitates the formation of stripped rock chips and improves the efficiency of mechanical rock breaking (Gong and Zhao, 2007; Kahraman, 2002). Figure 8 records the load drops F_drop, calculated by F_drop = F_p- F_b. F_p is the first peak of indentation force as mentioned, and F_b is defined as the applied force after the drop. On one hand, as depicted, it can be seen that F_drop shows a trend of decreasing and then increasing with the increase of the confining pressure under the condition of larger axial pressure. The value of F_drop is the largest when confining pressure is at the lowest level, and rock fragmentation shows the feature of brittleness. The F_drop decreases significantly and so does the volume of rock chips when the confining pressure increases to 15 MPa. The brittle characteristics of rock fragmentation are restrained and plasticity is increased under this certain pressure environment, which is companied by the comparatively small yield shown in Table 6. The corresponding decrease of V_d to that of F_drop is consistent with the accepted conclusion that the feature of brittleness largely contributes to the strip of debris (Liu Quansheng, 2016). Following this, further increase of the confining pressure conditions results in significant increases of F_drop, and the corresponding increase in chip yield is remarkable.

Figure 8

Figure 8. F_drop as the confining stress increases under different axial stress.

Table 6

Table 6. Typical surface of the samples after indentation and appearance of debris.

It can be seen that certain confining pressure environments enhance the brittle fragmentation of penetration, and significantly improve the breaking effectiveness from the perspective of the amount of rock chips. Meanwhile, the adverse effect should not be neglected, for frequent and aggressive drops of load would aggravate the fatigue failure of the cutting tools. On the other hand, when the axial stress is set to a lower level, the curve of F_drop and the corresponding phenomenon show the opposite trend.

3.4 Analysis of energy consumption

The consumed energy W during indentation behavior is calculated by the Equation 1:

$W={\int }_0^d{F}_i\mathrm{d}x(1)$

where F_i is the recorded applied force, and d is the penetration depth of the indenter. The variation of energy consumption of penetration with confining pressure, shown in Figure 9, is similar to that of the applied load. The energy consumption increases first and then decreases under ${\sigma }_{\mathrm{v}}$ = 15 MPa while first decreases and then increases under ${\sigma }_{\mathrm{v}}$ = 30 MPa. When confining stress equals 15 MPa, the consumed energy under the axial stress condition of 15 MPa is more than that under the axial stress condition of 30 MPa. In other cases, the consumption is smaller when axial pressure is small.

Figure 9

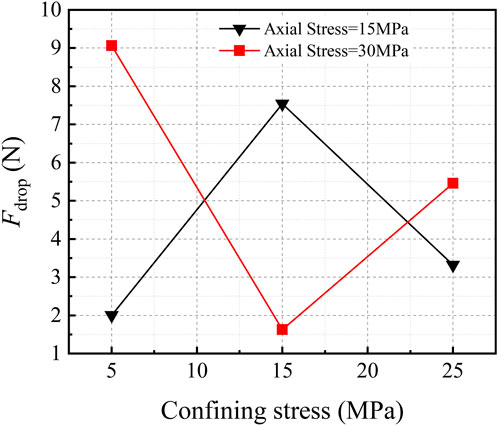
Figure 9. Consumed energy in the indentation process as the confining stress increases under different axial stress.

The specific energy for the estimation of rock crushing efficiency is calculated by the Equation 2:

$SE=W/V={\int }_0^d{F}_i\mathrm{d}x/V(2)$

where W is the consumed energy and V is the volume of rock debris (Liu et al., 2016b).

As shown in Figure 10, under the condition of axial pressure 15 MPa, the specific energy consumption increases with the increase of the surrounding pressure in general, which agrees with previous investigations (Wang et al., 2021). However, under the condition of axial pressure 30 MPa, the specific energy is not sensitive to the increase of the confining pressure. SE is generally lower under high axial pressure conditions than under low axial pressure conditions. In other words, relatively large axial stress may promote the indenter to produce effective fractures, and thus the energy is utilized more efficiently. In addition, the difference is more pronounced under higher confining pressures.

Figure 10

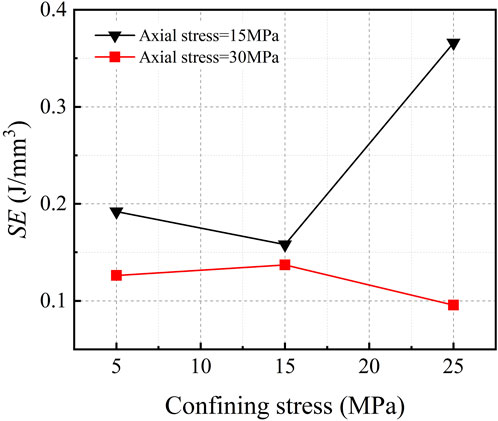
Figure 10. SE in the indentation process as confining stress increases under different axial stress.

3.5 Numerical analysis and discussion

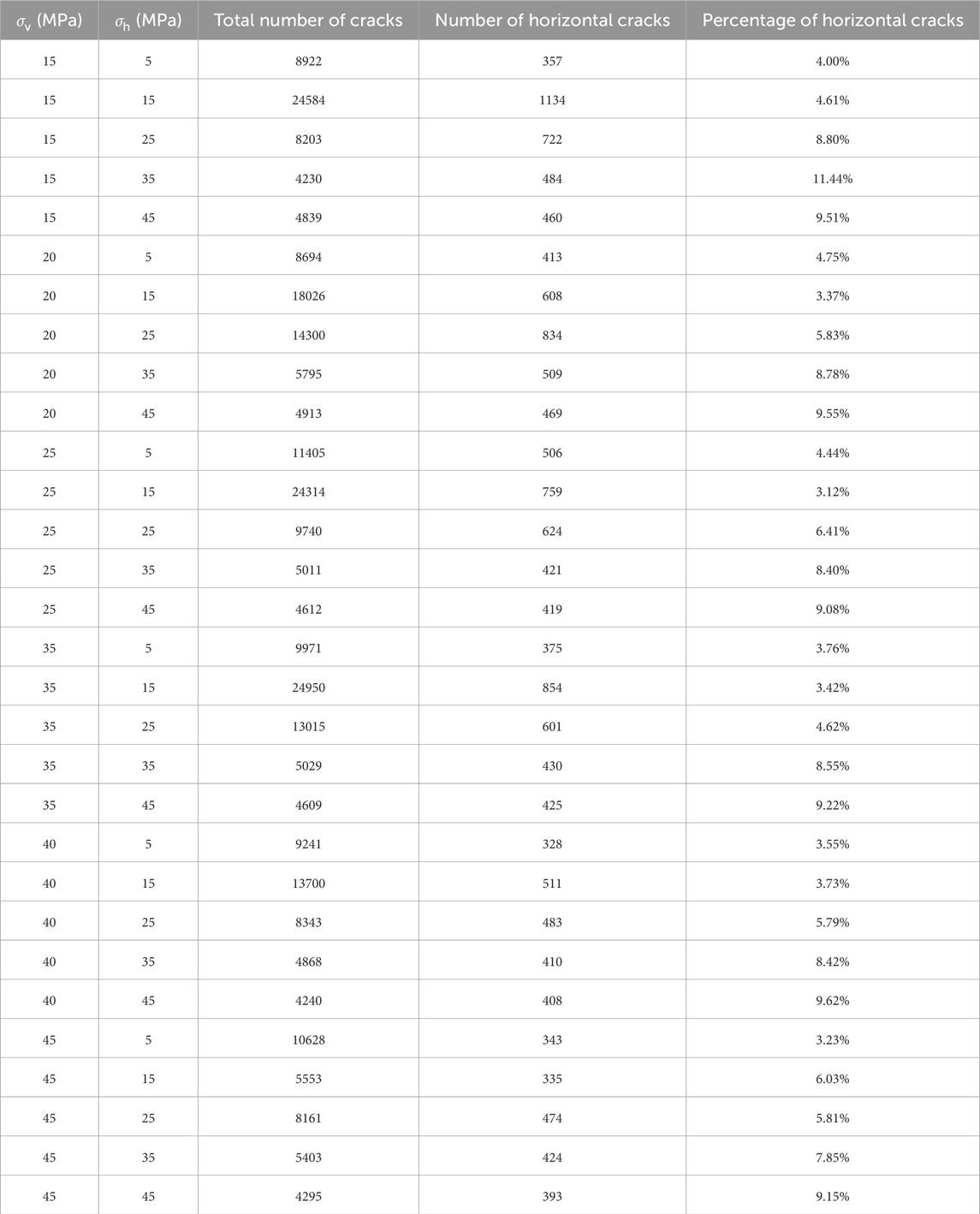
The statistics of fracture in numerical experiments are shown in Table 7. Figures 11, 12 record the number of cracks generated by the indenter and the typical crack distribution concerning the surrounding pressure under different axial pressure conditions, respectively. Blue and red bars represent shear cracks and tensile cracks respectively and obviously, the cracks are mainly tensile (Li et al., 2016). Lateral cracks with a comparatively small angle to the horizontal play a major role in rock chip production (Wu and Xu, 2016). Thus Figures 13, 14 count the number of cracks with an angle less than 15° to the horizontal direction and the percentage of the total number of cracks, and this paper calls this part of cracks horizontal cracks. The trend of the total number of cracks with surrounding pressure in the range of 5–25 MPa is the same as the trend of load-penetration-related indicators, rock chip volume, brittle damage indicators, and energy dissipation in the physical experiments, which are similarly divided into two distinct trends depending on the axial pressure. Therefore, it may be reasonable to interpret the two results in the physical experiments according to the number and distribution of cracks. Corresponding to the physical experiments, the pattern of changes in the number and distribution of cracks is also divided into two categories depending on the axial pressure conditions.

Table 7

Table 7. Statistics of cracks in simulation under different stress conditions.

Figure 11

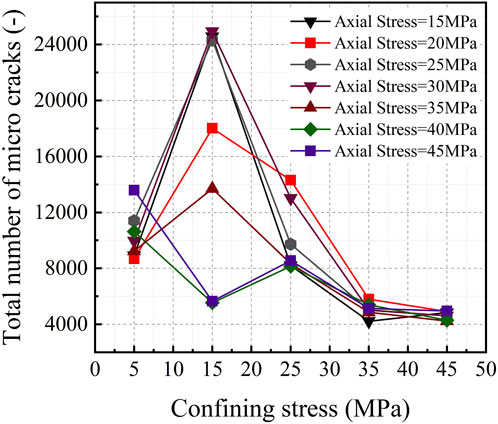
Figure 11. Effect of confining stress on the total number of cracks produced by penetration under different axial stress.

Figure 12

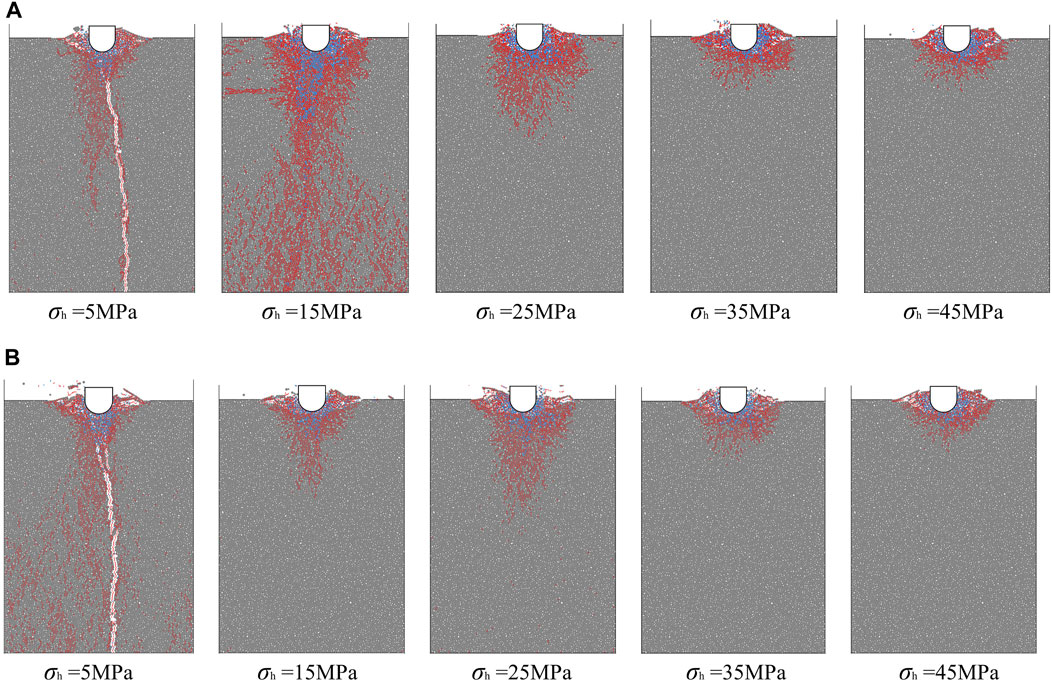
Figure 12. Typical patterns of cracks as confining stress increases, under the condition of (A) small axial stress (15 MPa) and (B) large axial stress (45 MPa).

Figure 13

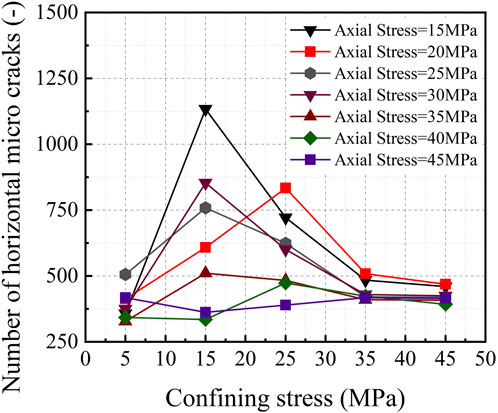
Figure 13. Effect of confining stress on the number of horizontal cracks produced by penetration under different axial stress.

Figure 14

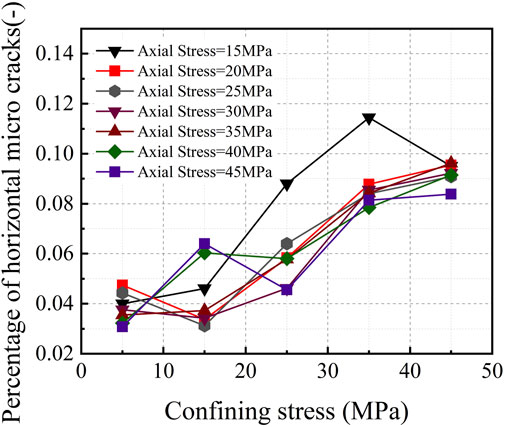
Figure 14. Effect of confining stress on the percentage of horizontal cracks produced by penetration under different axial stress.

In the first case, the number of cracks increases and then decreases with the increase of the circumferential pressure at a smaller axial pressure. Figure 12A shows the variation of crack expansion with the circumferential pressure at an axial pressure of 15 MPa. As depicted, the crack distribution range was mainly concentrated near the specimen axis, while the total number of cracks, the number, and the percentage of horizontal cracks were small. When the circumferential pressure was increased to 15 MPa, the number of cracks and horizontal cracks increased significantly, both reflected by the increase of debris volume in physical experiments as shown in Figure 6, but the growth of the percentage of horizontal cracks was not obvious. The crack distribution also shows that the intermediate cracks are very developed and extend in the middle and lower parts of the specimen. The physical experimental results above show a consistent increase in chip yield and energy consumption. From the simulation results, it can be seen that a large area of damage occurred in the rock, which consumed a large amount of energy; at the same time, the total number of cracks increased, which was conducive to increasing the rock chip output, which provided a mesoscale explanation for the physical experimental results. With further increase of the surrounding pressure, the total number of cracks decreases, and accordingly, the consumed energy and yield in physical experiment decreases; the percentage of horizontal cracks increases because the intermediate cracks are suppressed. However, the number of horizontal cracks still decreases, which is not conducive to the rock chip output, which provides a mesoscale explanation for the decrease of rock chip volume and increase of specific energy in the physical experiment. As the surrounding pressure increases further, the total number of cracks decreases, and the number of horizontal cracks also tends to decrease in general, while the percentage increases in general.

In the second case, under the large axial pressure condition, the number of cracks decreases and then increases with the increase of the circumferential pressure and gradually converges with the small axial pressure condition, and the number of horizontal cracks does not fluctuate much with the circumferential pressure. Figure 12B shows the variation of crack expansion with the circumferential pressure under the 45 MPa axial pressure condition. At a surrounding pressure of 5 MPa, unlike the small axial pressure condition, the cracks are already widely distributed in the middle and lower parts of the specimen, and the number of cracks is the maximum within the range of the surrounding pressure. When the confining pressure was increased to 15 MPa, the crack distribution range was significantly reduced, and the number of horizontal cracks under the large axial pressure condition was not as large as that under the small axial pressure condition, but its number accounted for a larger proportion of the total number of cracks. It can be considered that the energy of intrusion is effectively utilized, which is a relatively favorable stress environment for rock breaking from the perspective of energy utilization. Compared with the physical experiments, the total energy consumption is significantly lower at this point. When the surrounding pressure is increased to 25 MPa, the crack extension range increases and the total number of cracks increases, which explains the increase in total energy consumption in the physical experiments. The distribution and number of cracks in the high axial pressure condition converge with those in the low axial pressure condition with a further increase in the confining pressure. On the whole, it is of great interest that the total number of cracks under the small axial stress conditions is larger compared to that under large axial stress conditions, which may be the key reason for the comparatively higher SE under the small axial stress conditions in physical experiments.

It should be noted that the two-dimensional numerical simulation of lateral cracks does not fully reflect the cutting effect of surface cracks on rock chips, and previous studies have demonstrated that the cutting effect of surface cracks is an important factor in the generation of rock chips (Liu et al., 2002; Liu and Jiang, 2021). So to deeply study the influence mechanism of related factors on the rock chip output, further studies should be conducted using improved contact models in three-dimensional numerical simulation methods (Wu et al., 2024; Jing et al., 2021; Wu et al., 2025; Xie et al., 2024b; Yang et al., 2024b; Zhang et al., 2024).

4 Conclusion

In this paper, the fundamental relationship between the performance of green sandstone fragmentation in penetration test and the state of triaxial stress of the rock was investigated, accompanied by numerical simulation, which established corresponding explanations for the physical experimental phenomenon. The performance of indentation under triaxial stress provides the basis for further investigations and the optimization of deep underground excavation by cutters inserted with buttons. The main conclusions are as follows:

(1) Under the high axial pressure condition, the load-penetration-related indices, brittle damage index, and total energy consumption first decrease and then increase with the surrounding pressure. Correspondingly, in numerical experiments, both the distribution range and the number of micro cracks in numerical results climb up and then decline, which uncovers the influencing mechanism of confining stress on the penetrating performance of rock. Contrarily, the indices above show the opposite trend under a low axial pressure condition, which is consistent with previous investigations. The critical value to distinguish high axial pressure from the low is 35 MPa.

(2) The pressure 35 MPa is also the critical value to distinguish high axial pressure from the low when assessing crushing effect and energy. Rock chip yield and SE are more satisfactory under high axial pressure conditions compared with that under low axial pressure conditions. The smaller amount of micro-cracks under high axial pressure in numerical results account for the phenomenon in that less energy is consumed, making the penetrating fragmentation performance more energy-saving.

(3) Rock fragmentation by indenter should be evaluated from various aspects such as load-penetration analysis, rock chip morphology, and energy indices. Under certain pressure environments (σ_h = σ_v = 15 MPa, σ_h = 5 MPa & σ_v = 30 MPa and σ_h = 25 MPa & σ_v = 30 MPa) the load and the corresponding depth of the first crushing occurs is larger, i.e., the rock breaking is more difficult, but the rock chip and specific energy performance is satisfactory. Conversely, rock breaking is less difficult under certain conditions (σ_h = 5 MPa & σ_v = 15 MPa, σ_h = 25 MPa & σ_v = 15 MPa and σ_h = 15 MPa & σ_v = 30 MPa), but the rock chip yield and specific energy are inefficient.

Overall, this study approximates the performance of spherical cutter in breaking rock by simulating single-tooth indentation, and addressing challenges of laboratory simulations. Future work should focus on increasing the scale of the experiment to better reduce the size effect.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

RF: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Resources, Software, Writing – original draft, Writing – review and editing. WY: Conceptualization, Funding acquisition, Resources, Supervision, Validation, Visualization, Writing – review and editing. JZ: Project administration, Visualization, Writing – review and editing. XH: Data curation, Software, Visualization, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This study was supported by National Key Research and Development Program (No. 2022YFC3005902), National Natural Science Foundation of China (No. 42302273), Natural Science Foundation of Jiangsu Province (No. BK20231080), China Postdoctoral Science Foundation (No. 2022M713367).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alehossein, H., Detournay, E., and Huang, H. (2000). An analytical model for the indentation of rocks by blunt tools. Rock Mech. Rock Eng. 33, 267–284. doi:10.1007/s006030070003

CrossRef Full Text | Google Scholar

Balci, C., and Bilgin, N. (2007). Correlative study of linear small and full-scale rock cutting tests to select mechanized excavation machines. Int. J. Rock Mech. Min. Sci. 44, 468–476. doi:10.1016/j.ijrmms.2006.09.001

CrossRef Full Text | Google Scholar

Bingxiang, H., Xinglong, Z., Shuliang, C., and Jiangwei, L. (2017). Theory and technology of controlling hard roof with hydraulic fracturing in underground mining. Chin. J. Rock Mech. Eng. 36, 2954–2970. doi:10.13722/j.cnki.jrme.2017.0078

CrossRef Full Text | Google Scholar

Chen, L. H., and Labuz, J. F. (2006). Indentation of rock by wedge-shaped tools. Int. J. Rock Mech. Min. Sci. 43, 1023–1033. doi:10.1016/j.ijrmms.2006.03.005

CrossRef Full Text | Google Scholar

Cheng, J., Jiang, Z., Han, W., Li, M., and Wang, Y. (2020). Breakage mechanism of hard-rock penetration by TBM disc cutter after high pressure water jet precutting. Eng. Fract. Mech. 240, 107320. doi:10.1016/j.engfracmech.2020.107320

CrossRef Full Text | Google Scholar

Copur, H., Shaterpour-Mamaghani, A., Tumac, D., and Balci, C. (2024). Relationships between performances of a button cutter and a disc cutter based on full-scale linear cutting tests. Acta Geotech. 19, 2731–2752. doi:10.1007/s11440-023-02146-2

CrossRef Full Text | Google Scholar

Ergin, H., and Acaroglu, O. (2007). The effect of machine design parameters on the stability of a roadheader. Tunn. Undergr. Space Technol. 22, 80–89. doi:10.1016/j.tust.2006.04.003

CrossRef Full Text | Google Scholar

Fang, K., Zhao, T., Zhang, Y., Qiu, Y., and Zhou, J. (2019). Rock cone penetration test under lateral confining pressure. Int. J. Rock Mech. Min. Sci. 119, 149–155. doi:10.1016/j.ijrmms.2019.04.018

CrossRef Full Text | Google Scholar

Gong, Q. M., and Zhao, J. (2007). Influence of rock brittleness on TBM penetration rate in Singapore granite. Tunn. Undergr. Space Technol. 22, 317–324. doi:10.1016/j.tust.2006.07.004

CrossRef Full Text | Google Scholar

Gou, B., and Zhang, M. (2022). Effects of surface grooves on rock cutting performance and contact behavior of a TBM disc cutter. Eng. Fract. Mech. 267, 108466. doi:10.1016/j.engfracmech.2022.108466

CrossRef Full Text | Google Scholar

Huang, X., Chang, J., Li, C., Yang, W., Pang, J., Zou, J., et al. (2025). Experimental study on the rock breaking effect of different tooth shapes of inserted teeth in a hobbing-cone hybrid PDC bit under complex stress environment. Geoenergy Sci. Eng. 246, 213390. doi:10.1016/j.geoen.2024.213390

CrossRef Full Text | Google Scholar

Innaurato, N., Oggeri, C., Oreste, P., and Vinai, R. (2011). Laboratory tests to study the influence of rock stress confinement on the performances of TBM discs in tunnels. Int. J. Minerals, Metallurgy, Mater. 18, 253–259. doi:10.1007/s12613-011-0431-z

CrossRef Full Text | Google Scholar

Jing, H., Yin, Q., Yang, S., and Chen, W. (2021). Micro-mesoscopic creep damage evolution and failure mechanism of sandy mudstone. Int. J. Geomech. 21, 45667. doi:10.1061/(ASCE)GM.1943-5622.0001940

CrossRef Full Text | Google Scholar

Kahraman, S. (2002). Correlation of TBM and drilling machine performances with rock brittleness. Eng. Geol. 65, 269–283. doi:10.1016/S0013-7952(01)00137-5

CrossRef Full Text | Google Scholar

Kaitkay, P., and Lei, S. (2005). Experimental study of rock cutting under external hydrostatic pressure. J. Mater. Process. Technol. 159, 206–213. doi:10.1016/j.jmatprotec.2004.04.418

CrossRef Full Text | Google Scholar

Kim, H., Ha, S., Rehman, H., and Yoo, H. (2023). Analysis of mechanical excavation characteristics by pre-cutting machine based on linear cutting tests. Appl. Sci. 13, 1205. doi:10.3390/app13021205

CrossRef Full Text | Google Scholar

Li, Q., Cheng, B., Li, X., Yin, T., and Huang, L. (2022a). Fracture behaviour of microwave-heated granite under indentation: experimental and numerical investigation. Eng. Fract. Mech. 269, 108535. doi:10.1016/j.engfracmech.2022.108535

CrossRef Full Text | Google Scholar

Li, S. W. S. W. X., Wang, S., and Wang, S. (2018). Experimental investigation of the influence of confining stress on hard rock fragmentation using a conical pick. Rock Mech. Rock Eng. 51, 255–277. doi:10.1007/s00603-0171309-9

CrossRef Full Text | Google Scholar

Li, X. F., Li, H. B., Liu, Y. Q., Zhou, Q. C., and Xia, X. (2016). Numerical simulation of rock fragmentation mechanisms subject to wedge penetration for TBMs. Tunn. Undergr. Space Technol. 53, 96–108. doi:10.1016/j.tust.2015.12.010

CrossRef Full Text | Google Scholar

Li, Y., Peng, J., Li, J., and Ge, D. (2022b). Theoretical and experimental study on single spherical button penetration into granite rock under dynamic impact loading. Rock Mech. Rock Eng. 55, 213–233. doi:10.1007/s00603-021-02688-5

CrossRef Full Text | Google Scholar

Liu, J., Cao, P., and Han, D. (2016a). The influence of confining stress on optimum spacing of TBM cutters for cutting granite. Int. J. Rock Mech. Min. Sci. 88, 165–174. doi:10.1016/j.ijrmms.2016.07.017

CrossRef Full Text | Google Scholar

Liu, J., Cao, P., and Han, D. (2016b). The influence of confining stress on optimum spacing of TBM cutters for cutting granite. Int. J. Rock Mech. Min. Sci. 88, 165–174. doi:10.1016/j.ijrmms.2016.07.017

CrossRef Full Text | Google Scholar

Liu, J., Cao, P., and Han, D. (2016c). Sequential indentation tests to investigate the influence of confining stress on rock breakage by tunnel boring machine cutter in a biaxial state. Rock Mech. Rock Eng. 49, 1479–1495. doi:10.1007/s00603-015-0843-6

CrossRef Full Text | Google Scholar

Liu, J., Cao, P., and Li, K. (2015). A study on isotropic rock breaking with TBM cutters under different confining stresses. Geotech. Geol. Eng. 33, 1379–1394. doi:10.1007/s10706-015-9907-3

CrossRef Full Text | Google Scholar

Liu, J., and Jiang, G. (2021). Use of laboratory indentation tests to study the surface crack propagation caused by various indenters. Eng. Fract. Mech. 241, 107421. doi:10.1016/j.engfracmech.2020.107421

CrossRef Full Text | Google Scholar

Liu, S. Q. K. P. H. Y., Kou, S., Lindqvist, P. A., and Tang, C. (2002). Numerical simulation of the rock fragmentation process induced by indenters. Int. J. Rock Mech. Min. 39, 491–505. doi:10.1016/S13651609(02)00043-6

CrossRef Full Text | Google Scholar

Liu Quansheng, L. J. S. K. (2016). Evaluation of rock brittleness indexes on rock fragmentation efficiency by disc cutter. Chin. J. Rock Mech. Eng. 35, 498–510.

Google Scholar

Saksala, T. (2016). Numerical study of the influence of hydrostatic and confining pressure on percussive drilling of hard rock. Comput. Geotech. 76, 120–128. doi:10.1016/j.compgeo.2016.02.021

CrossRef Full Text | Google Scholar

Shaterpour-Mamaghani, A., Copur, H., Gumus, A., Tumac, D., Balci, C., Erdogan, T., et al. (2022). Full-Scale linear cutting tests using a button cutter and deterministic performance prediction modeling for raise boring machines. Tunn. Undergr. Space Technol. 127, 104609. doi:10.1016/j.tust.2022.104609

CrossRef Full Text | Google Scholar

Shi, H., Chen, W., Zhang, H., Song, L., Li, M., Wang, M., et al. (2023). Dynamic strength characteristics of fractured rock mass. Eng. Fract. Mech. 292, 109678. doi:10.1016/j.engfracmech.2023.109678

CrossRef Full Text | Google Scholar

Shi, H., Zhang, H., Chen, W., Song, L., and Li, M. (2024). Pull-out debonding characteristics of rockbolt with prefabricated cracks in rock: a numerical study based on particle flow code. Comput. Part. Mech. 11, 29–53. doi:10.1007/s40571-023-00607-9

CrossRef Full Text | Google Scholar

Thyagarajan, M. V., and Rostami, J. (2024). Study of cutting forces acting on a disc cutter and impact of variable penetration measured by full scale linear cutting tests. Int. J. Rock Mech. Min. Sci. 175, 105675. doi:10.1016/j.ijrmms.2024.105675

CrossRef Full Text | Google Scholar

Wang, S., Li, X., Du, K., and Wang, S. (2018). Experimental investigation of hard rock fragmentation using a conical pick on true triaxial test apparatus. Tunn. Undergr. Space Technol. 79, 210–223. doi:10.1016/j.tust.2018.05.006

CrossRef Full Text | Google Scholar

Wang, S., Li, X., Yao, J., Gong, F., Li, X., Du, K., et al. (2019). Experimental investigation of rock breakage by a conical pick and its application to non-explosive mechanized mining in deep hard rock. Int. J. Rock Mech. Min. Sci. 122, 104063. doi:10.1016/j.ijrmms.2019.104063

CrossRef Full Text | Google Scholar

Wang, S., Tang, Y., Li, X., and DU, K. (2021). Analyses and predictions of rock cuttabilities under different confining stresses and rock properties based on rock indentation tests by conical pick. Trans. Nonferrous Met. Soc. China. 31, 1766–1783. doi:10.1016/S1003-6326(21)65615-7

CrossRef Full Text | Google Scholar

Wu, G., Liu, K., Hu, W. R., Li, J. C., Dehkhoda, S., and Zhang, Q. B. (2021). Quantification of dynamic damage and breakage in granite under confined indentation. Int. J. Rock Mech. Min. Sci. 144, 104763. doi:10.1016/j.ijrmms.2021.104763

CrossRef Full Text | Google Scholar

Wu, H. J. Q. Y. J., Jing, H., Yin, Q., Yu, L., Meng, B., and Li, S. (2020). Strength prediction model considering material, ultrasonic and stress of cemented waste rock backfill for recycling gangue. J. Clean. Prod. 276, 123189. doi:10.1016/j.jclepro.2020.123189

CrossRef Full Text | Google Scholar

Wu, J., Wong, H. S., Zhang, H., Yin, Q., Jing, H., and Ma, D. (2024). Improvement of cemented rockfill by premixing low-alkalinity activator and fly ash for recycling gangue and partially replacing cement. Cem. Concr. Compos. 145, 105345. doi:10.1016/j.cemconcomp.2023.105345

CrossRef Full Text | Google Scholar

Wu, J., Yang, S., Williamson, M., Wong, H. S., Bhudia, T., Pu, H., et al. (2025). Microscopic mechanism of cellulose nanofibers modified cemented gangue backfill materials. Adv. Compos. Hybrid. Mater. 8, 177. doi:10.1007/s42114-025-01270-9

CrossRef Full Text | Google Scholar

Wu, S., and Xu, X. (2016). A study of three intrinsic problems of the classic discrete element method using flat-joint model. Rock Mech. Rock Eng. 49, 1813–1830. doi:10.1007/s00603-015-0890-z

CrossRef Full Text | Google Scholar

Xie, W., Liu, X., Zhang, X., Yang, X., and Zhou, X. (2024a). A review of rock macro-indentation: theories, experiments, simulations, and applications. J. Rock Mech. Geotech. Eng. 16, 2351–2374. doi:10.1016/j.jrmge.2023.07.022

CrossRef Full Text | Google Scholar

Xie, W., Liu, X., Zhang, X., Yang, X., and Zhou, X. (2024b). A review of rock macro-indentation: theories, experiments, simulations, and applications. J. Rock Mech. Geotech. Eng. 16, 2351–2374. doi:10.1016/j.jrmge.2023.07.022

CrossRef Full Text | Google Scholar

Xiong, Z. H. H. S. C., Huang, Z., Shi, H., Yang, R., Dai, X., and He, W. (2021). 3D cutting force model of a stinger PDC cutter: considering confining pressure and the thermal stress. Rock Mech. Rock Eng. 54, 5001–5022. doi:10.1007/s00603-021-02494z

CrossRef Full Text | Google Scholar

Yang, D., Li, J., Wang, L., Gao, K., Tang, Y., and Wang, Y. (2015). Experimental and theoretical design for decreasing wear in conical picks in rotation-drilling cutting process. Int. J. Adv. Manuf. Technol. 77, 1571–1579. doi:10.1007/s00170-014-6472-5

CrossRef Full Text | Google Scholar

Yang, H., Dahlhaus, N., and Renner, J. (2024a). On the effect of lateral confinement on rock-cutting tool interactions. Rock Mech. Rock Eng. 57, 6063–6083. doi:10.1007/s00603-024-03837-2

CrossRef Full Text | Google Scholar

Yang, H., Dahlhaus, N., and Renner, J. (2024b). On the effect of lateral confinement on rock-cutting tool interactions. Rock Mech. Rock Eng. 57, 6063–6083. doi:10.1007/s00603-024-03837-2

CrossRef Full Text | Google Scholar

Yin, L. J., Gong, Q. M., Ma, H. S., Zhao, J., and Zhao, X. B. (2014a). Use of indentation tests to study the influence of confining stress on rock fragmentation by a TBM cutter. Int. J. Rock Mech. Min. Sci. 72, 261–276. doi:10.1016/j.ijrmms.2014.07.022

CrossRef Full Text | Google Scholar

Yin, L. J., Gong, Q. M., and Zhao, J. (2014b). Study on rock mass boreability by TBM penetration test under different in situ stress conditions. Tunn. Undergr. Space Technol. 43, 413–425. doi:10.1016/j.tust.2014.06.002

CrossRef Full Text | Google Scholar

Zhang, T., Gao, Y., Liu, S., Yu, J., and Zhang, C. (2024). Experimental and numerical studies of breakage and fractal characteristics of silica sands in high-pressure triaxial tests. Adv. Powder Technol. 35, 104548. doi:10.1016/j.apt.2024.104548

CrossRef Full Text | Google Scholar

Zhang Kui, X. Y. T. Q. (2010). Numerical study on modes of breaking rock by TBM cutter under different confining pressures. Chin. J. GEOTECHNICAL Eng. 32, 1780–1787.

Google Scholar

Zou, J., Yang, W., Zhang, T., Wang, X., and Gao, M. (2022). Experimental investigation on hard rock fragmentation of inserted tooth cutter using a newly designed indentation testing apparatus. Int. J. Min. Sci. Technol. 32, 459–470. doi:10.1016/j.ijmst.2022.02.002

CrossRef Full Text | Google Scholar

Nomenclature

d Penetration depth [mm]

d_p Penetration depth at the first peak force [mm]

F_drop Drop of force at the first peak [kN]

F_p The first peak force [kN]

t_m Maximum thickness of debris [mm]

V Volume of debris [mm³]

V_d Volume of debris per penetration depth [mm²]

σ_h Horizontal confining stress [MPa]

σ_v Vertical or axial stress [MPa]

Subscripts

d depth

h horizontal

m maximum

p first peak

v vertical

Abbreviations

SE Specific energy [kN·mm⁻²]

UCS Uniaxial compressive strength [MPa]

TS Tensile strength [MPa]