Mechanical and deformation behaviors of sandy mudstone under triaxial unloading creep testing

The deformation caused by excavation unloading has a temporal effect, and its transient mechanical and rheological responses will change to some extent. Currently, most research findings on rheological behaviors are based on loading mechanics. However, the rheological behaviors under the unloading stress path are not considered, so the current findings are often inconsistent with the results of actual mechanical processes. In this study, we conducted preliminary unloading rheological tests of argillaceous sandstone in the Tingzikou Irrigation District under constant axial pressure and gradual unloading confining stress paths to evaluate the triaxial unloading rheological characteristics of the rocks. The test results show that the instantaneous and creep deformations of sandy mudstone increase with the deviational stress under step-by-step unloading of the stress levels; further, under gradual unloading of the confining pressure and greater unloading history, the creep rate as well as creep deformation are larger and the unloading effect and rheological characteristics are more obvious. Based on the experimental results, the unloading rheological behavior of sandy mudstone under this stress path is described well by the Hooke–Kelvin three-element model, and the parameters of the unloading rheological constitutive equation for sandy mudstone can be obtained through regression fitting.

1 Introduction

The basic conditions for extrusion deformation include deep underground projects through soft ground, high in situ stress of the surrounding rock, and structure of the surrounding rock. Of these, soft rock has a significant temporal effect while excavation and unloading of the deformation impose serious constraints on the safety of the project, leading to tunnel boring machine (TBM)-based tunneling surrounded by extrusion of large deformations of the machine; this causes the peripheral rocks in the tunnel to prevent deformation or even destabilization of the damage, thereby affecting the engineering, construction, and stability later (Barla, 1995). Additionally, reconstruction of geological reservoirs can lead to stress reduction, which could induce rock mass creep behavior and affect the reservoir stability (Ma et al., 2025; Ma et al., 2024).

Rock creep testing is important for studying the time-dependent deformation of the compressibility of soft rocks (ISRM, 1995). The earliest research on rock creep tests were reported in the 1930s; for example, Griggs (1939) conducted creep testing on sandstone, mudstone, and other rocks and reported that when the stress level reached a certain proportion of the destructive load value, the rock underwent creep. Furthermore, Danesh et al. (2016) showed that a logarithmic empirical function can be used to describe the intrinsic structure of such creep. Since the 1950s, there has been extensive research attention on the rheological properties of rocks (Tang et al., 2018; Yang and Hu, 2018; Yu et al., 2019; Zhou et al., 2019). Zhao et al. (2018) were the first group of researchers to introduce creep theory to rock mechanics and proposed the idea of rock creep. Soft rocks are the main objects of studies involving the rheological mechanical properties of rocks. Yongsheng (1995) conducted uniaxial compression creep and relaxation tests on rocks with different lithologies, such as siltstone, marble, red sandstone, and mudstone, and noted that the rocks generally experience three stages of decreasing, stable, and increasing creep rates under a certain constant stress. Other authors have conducted systematic studies on the stress relaxation, uniaxial, and triaxial creep laws of salt rocks and established a corresponding intrinsic model (Yang and Shiwei, 1999; Yang et al., 1998).

The indoor rheological test methods for rocks mainly include uniaxial compression creep, triaxial compression creep, and direct shear rheological tests. Based on the results of such rheological tests, the rheological mechanical properties and intrinsic models of rocks are investigated. The confining pressure of the surrounding rock after underground engineering excavation is in a state of continuous unloading. At present, there are more research findings on the effects of unloading on the transient deformations and damage characteristics of rocks than those on the effects of unloading on the rheological mechanical behaviors of rock; further, there are relatively fewer research results on the rheological characteristics of rock under the unloading stress path. For example, Zhu (2009) carried out unloading rheological tests on shale and sandstone using a constant axial pressure and stepwise unloading of the confining pressure to investigate the preliminary triaxial unloading rheological properties of rocks. Therefore, high-stress unloading creep tests are necessary to study the mechanical behaviors of deep surrounding rocks after excavation unloading.

In this study, we used triaxial unloading creep to conduct experimental research on sandy mudstone. The triaxial unloading creep tests were intended to reflect the deformation characteristics of soft rocks that change over time after excavation. The experiments yielded the creep deformation and damage patterns of sandy mudstone under various confining pressures. These findings provide insights into the deformation mechanisms of surrounding rocks and help establish an intrinsic model for large deformations under squeezing conditions.

2 Experimental materials and methods

Considering the convenience of testing and the stress state of the excavated surrounding rock, we adopted the triaxial unloading creep test with constant axial pressure and stepwise unloading of the confining pressure. In the first deviatoric stress level of deformation stabilization, we drew upon the hierarchical approach of Chen’s loading method with graded unloading of the confining pressure; to maintain the axial stress unchanged while unloading stepwise, we unloaded the confining pressure at the rate of 2 MPa per level at each unloading level to maintain a consistent stress level. The creep stability after a given duration was considered before proceeding to the next level of unloading; here, the unloading time was set to more than 12,500 s or until the deformation rate reached 0.0002 mm s⁻¹ after unloading of the confining pressure or specimen destruction (Table 1). The stopping point for the test was when the target pressure unloading was achieved or when the specimen was damaged.

Table 1

Table 1. Variation of the experimental conditions.

The rock specimens used in the test were of the sandy mudstone type retrieved from a mudstone tunnel at the project site of the Tingzikou Irrigation District in China. For testing purposes, standard specimens of size 50 mm × 100 mm were prepared. The specimens were then processed using the recommended methods for rock mechanical tests and prepared with flat end faces; the flatness of each side face was controlled to be within ±0.03 mm. The perpendicularity error between the center line of the specimen and its end face was less than 0.25°. Before performing the triaxial unloading creep test, we carried out uniaxial and triaxial compression tests, and the confining pressure of 20 MPa was determined as per the geological requirements as well as maximum and minimum ground stresses in the tunnel surrounding rocks. The relevant test results are shown in Figure 1. The basic mechanical properties of the sandy mudstone were obtained, and the uniaxial compressive strength was 38.26 MPa. The stress applied during the rheological test at each level of the confining pressure was determined from the triaxial compressive strength and deformation parameters obtained. In this work, two groups of tests were conducted on a total of two specimens; graded unloading was performed under different initial axial pressures and common confining pressure. The initial axial pressures were 50 and 70 MPa for the two groups of tests, and the confining pressure was unloaded in several stages from 20 MPa at the rate of 2 MPa per stage; the next stage of unloading was carried out after creep stabilization at the current stage.

Figure 1

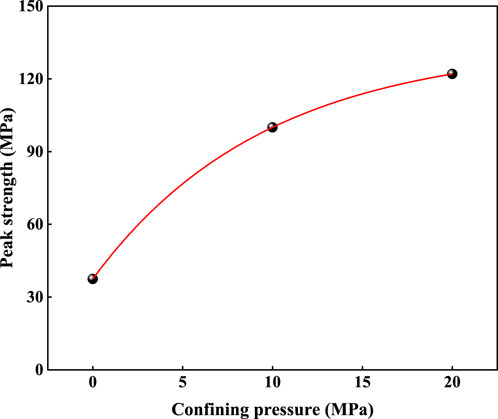
Figure 1. Evolution of the triaxial compression strength of sandy mudstone with increasing confining pressure.

The stresses for the unloading tests were chosen to be 50% and 70% based on the typical mechanical behaviors of rock materials. The 50% stress level is close to the end of the linear elastic deformation of the material, while the 70% stress level is close to the yield strength; these levels were used to investigate the effects on the material when entering a microplastic phase or producing irreversible damage from unloading deformation. This testing scheme is a multifield coupled rock mechanics test system developed at the State Key Laboratory of Deep Geotechnics and Underground Engineering of the China University of Mining and Technology, and the experimental apparatus is as shown in Figure 2. The equipment has the advantages of high precision of loading control; automatic real-time collection of the test results; availability of three sets of independent closed-loop servo control systems for the axial, confining, and pore water pressures; and option for four basic test functions, namely, uniaxial compression, conventional triaxial compression, pore water pressure, and water penetration tests. The test system fully meets the testing requirements of this project, and the basic performance of the equipment is as follows: axial pressure <2,000 kN; confining pressure ≤50 MPa; pore water pressure ≤80 MPa; frame rigidity of 10.5 × 10 N/m; hydraulic power source of 18 kW; hydraulic source flow of 31.8 L/min; data acquisition frequency of 5 kHz; output waveforms selectable from straight line, sine wave, half sine wave, triangle wave, square wave, any regular curved waveform, and random waveforms.

Figure 2

Figure 2. Experimental apparatus used in the present study.

3 Results and analyses

In this section, we analyze the unloading creep test results of sandy mudstone obtained via triaxial unloading creep measurements to study its rheological deformation damage law under different stress level conditions.

3.1 Creep deformation behaviors at different stress levels

The creep law of sandy mudstone was obtained through creep testing via stepwise unloading of the confining pressure at two different axial pressures of 50 and 70 MPa, as shown in Figures 3, 4. The graded loading or unloading creep conditions are obtained as increasing deviatoric stress of the creep curve; these are integrated with the principle of superposition and rock test specifications for graded incremental loading of the creep test data as well as the entire curve for all levels of loading of the creep curve. The stress level conditions under creep deformation were analyzed further according to the data in Figures 3, 4, and it can be seen that sandy mudstone shows significant rheological deformations at all stress levels, while the axial deformation is composed of transient and creep deformations generated by unloading. All creep curves are characterized by decay creep and steady-state creep. At each loading level, the initial creep rate grows rapidly with time but is quickly attenuated to a steady-state value; the greater the deviatoric stress, the greater is the slope of the attenuation creep, longer is the attenuation creep time, and longer is the time required to achieve steady-state creep when the creep rate is high. The measured attenuation creep time was 12,500 s, and the deformation amount accounted for up to 60% of the total proportion of creep deformation. Thus, for TBM-based excavation of a weak perimeter rock section, special attention should be devoted to the perimeter rocks after instantaneous deformation because this period is usually the attenuation creep stage of the rocks; here, the deformation rate is high, deformation amount is large, and extrusion deformation shells can be easily caused.

Figure 3

Figure 3. Unloading creep curves of sandy mudstone under an axial pressure of 50 MPa showing (a) instantaneous deformation under increasing deviatoric stress and (b) creep deformations under different unloading confining pressures.

Figure 4

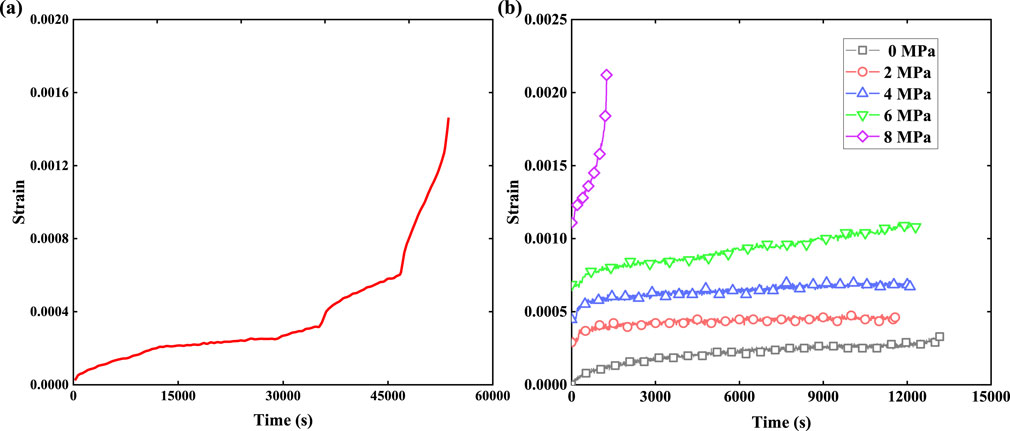
Figure 4. Unloading creep curve of sandy mudstone under an axial pressure of 70 MPa showing (a) instantaneous deformation under increasing deviatoric stress and (b) creep deformations under different unloading confining pressures.

The instantaneous deformation at each level of the unloading pressure comprises not only elastic deformation but also plastic deformation, and the creep strain calculated according to the viscoelastic model will be less than the measured creep strain; this indicates that the creep strain in the test results includes viscoplastic deformation, such that the creep curve as a whole is in line with the elastoplastic deformation law. The 50% specimen at the fourth level of stress (axial pressure: 50 MPa, confining pressure: 12 MPa) is in the late stage of accelerated creep and is ultimately destroyed; the 70% specimen under the third level of confining pressure (14 MPa) is damaged when unloaded to the fourth level (confining pressure: 10 MPa). The triaxial unloading creep test results of the 50% samples, where each stress level is unloaded at the rate of 2 MPa, generates increasing instantaneous deformation with increase in the deviatoric stress (Figure 3a); the loading level under creep deformation also increases with increase in deviatoric stress, along with an increase in the deformation magnitude. The percentage of creep deformation is relative to the instantaneous deformation under a load at a given level, and the ratio of creep to total deformation increases with increase in deviatoric stress.

This is because the specimen integrity is better under high confining pressure and lower deviatoric stress level conditions, whereby the damage accumulated inside the rock specimen, transient deformation, creep deformation, and ratio of creep to transient deformations are all low. For the first loading level, the stress did not reach the yield strength of the specimen, the transient deformation was mainly elastic, and some damage was produced during creep. For each subsequent level of unloading, the transient deformation generated was both elastic and plastic, the creep damage increased compared to the transient deformation at the previous level, and both the transient deformation and unloading of the initial damage increased, thereby exacerbating the level of creep. When the confining pressure was decreased stepwise, the deviatoric stress correspondingly increased stepwise, and the specimen developed internal vertical tensile cracks that gradually evolved and expanded; as the creep time increased, the microcrack expansion accelerated and deviatoric stress increased, resulting in a gradual decrease of the load-bearing capacity of the specimen owing to internal damage as well as constant accumulation of the unloading confining pressure. As the confining pressure unloading continued, for low confining pressure and high deviatoric stress values, the internal damage of the specimen deteriorated and accumulated with time; this caused the accelerated creep phenomenon and increased the creep deformation of the specimen significantly. When the final accumulated damage reaches or exceeds the damage limit, macroscopic main cracks are produced and accompanied by significant expansion of the volumetric strain (Figure 5). In summary, for soft rocks like sandy mudstone, the intrinsic mechanism of long-term deformation after excavation is attributable to creep damage and temporal expansion of the microcracks, which are collectively referred to as “time-damage rupture.”

Figure 5

Figure 5. Fracture morphology of unloading creep for 50 and 70 MPa of axial stress, where (a,b) represent 50% and 70% axial stresses, respectively.

Rock properties are readily affected by factors such as the stress state and stress path, and many scholars have studied the rheological properties of rocks under conventional triaxial loading conditions; the creep properties of soft rocks under triaxial unloading of the peripheral compressive stress paths under different stress states are explored next. It is noted that for a given confining pressure, the higher the axial pressure (i.e., higher the deviatoric stress), the greater is the extent of creep deformation (Figure 6) and greater is the proportion of creep deformation in the total deformation. In particular, when the confining pressure is low, the rock bearing capacity is lower, axial stress is more visible, more damage is accumulated internally, microscopic cracks are developed to a greater extent, creep rate is higher, and rheological deformation is more obvious. When the deviatoric stress is maintained constant, the circumferential pressure of the specimen with low axial pressure is also low, and the initial circumferential pressures are equal such that the specimen accumulates more damage and plastic deformation internally; a specimen with low axial pressure under these loading conditions has a greater creep rate, larger creep deformation, and more obvious unloading effects and creep characteristics. This shows that the damage and plastic deformation produced by unloading and creep have very significant effects on the subsequent mechanical behaviors. Therefore, when establishing the constitutive equation for creep, we cannot ignore the unloading instantaneous and creep plastic deformations as well as damage.

Figure 6

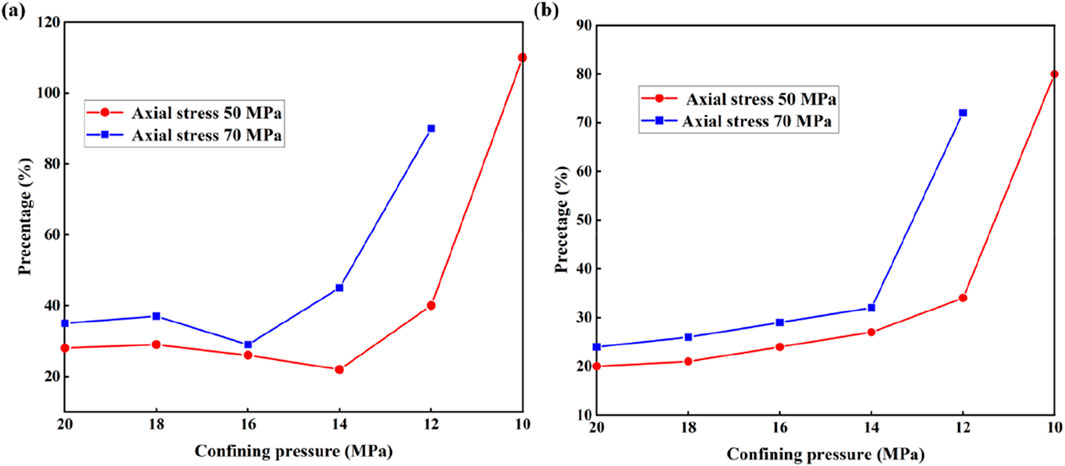
Figure 6. Percentage of creep strain to (a) instantaneous deformation and (b) total deformation under 50% and 70% axial stresses.

3.2 Stress–strain relationship during unloading creep

To analyze the deviatoric stress–strain relationship of the specimen and further investigate the deformation characteristics of the rock during the unloading creep test, we obtained the stress–strain curve of sandy mudstone for triaxial unloading creep, as shown in Figure 7. The straight lines parallel to the horizontal axis are the creep strain values of the rock sample, while the diagonal lines are the instantaneous strain values of the unloading pressure. From the unloading creep deviatoric stress–strain curves, it is observed that the deformations of the rock samples change significantly during unloading of the confining pressure transient. The slope of the axial strain curve of the 50% specimen decreases from 5.303 GPa at the first level to 3.819 GPa for the fifth level, while that of the 70% specimen decreases from 6.078 GPa at the first level to 3.042 GPa for the fourth level (Table 2).

Figure 7

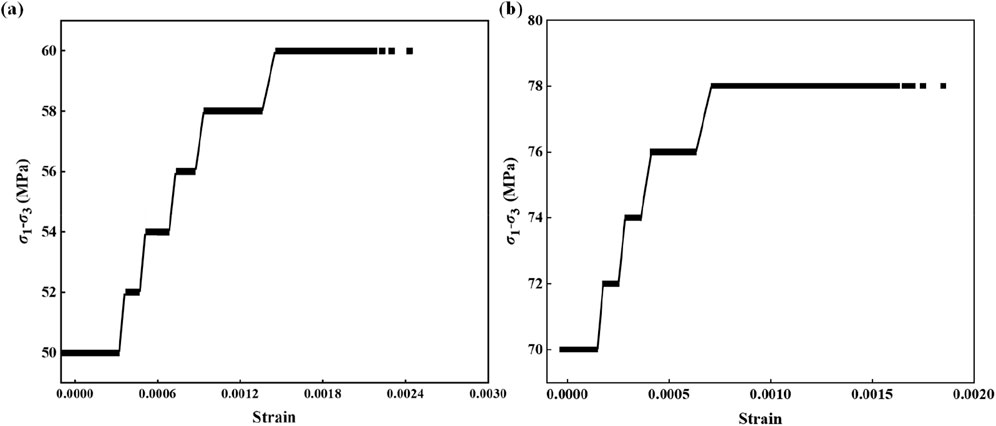
Figure 7. Deviatoric stress–strain curves of sandy mudstone during the process of unloading creep for (a) 50% and (b) 70% axial stresses.

Table 2

Table 2. Mechanical characteristics under each stress level.

As the confining pressure and creep reduce, the slopes of the axial deformation curves gradually decrease; this is due to the gradual lifting of the constraints and continuous accumulation of damage in the creep process. At the end of the test, crack patterns are observed on the surface and inside the specimen, which constitute a part of a vertical tensile crack; at the same time, the cracks evolved during development of the internal damage, resulting in obvious expansion of the specimen. Based on the plastic strain at each stage of creep, the unloading creep test is used to produce the deviatoric stress and irrecoverable strain curve. This curve shows that in the process of unloading confining pressure creep, as the creep time and continuous unloading of the confining pressure increase, the cracks inside the rock expand gradually, the damage accumulates, and the specimen experiences a large internal plastic deformation; as this plastic deformation increases more violently in the axial direction, and the expansion effect becomes more significant.

4 Rheological model and parameter identification

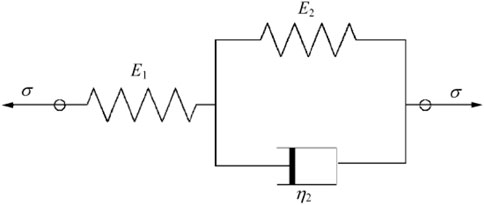
From the triaxial unloading creep curves, it is seen that there is a transient deformation at each level of unloading confining pressure that increases with the bias stress level, such that an elastic element can be used to mimic this phenomenon. Over time, the creep deformation of the rock increases rapidly during the initial stage and then decreases progressively until it remains unchanged, indicating convergence to a certain asymptote in the form of an approximate negative exponent. Therefore, the three-element Hooke–Kelvin (H-K) rheological model (Figure 8) can be used to simulate its deformation behavior, and the constitutive equation is given as

$\frac{{\eta }_2}{E_1+E_2}\dot{\sigma }+\sigma =\frac{E_1{E}_2}{E_1+E_2}\epsilon +\frac{E_1{\eta }_2}{E_1+E_2}\dot{\epsilon },(1)$

where E₁ and E₂ are elastic moduli, ${\eta }_2$ is the viscous component, $\sigma$ and $\epsilon$ are the respective stress and strain of the model, respectively, and $\dot{\sigma }$ and $\dot{\epsilon }$ are the derivations of the corresponding stress and strain of the model, respectively. Differential decomposition of Equation 1 gives

$\frac{\epsilon }{{\sigma }_c}=-\frac{1}{E_2}{e}^{-\frac{E_2}{{\eta }_2}t}+\frac{E_1+E_2}{E_1{E}_2}.(2)$

Figure 8

Figure 8. Schematic of the three-element Hooke–Kelvin rheological model.

Here, when the stress conditions are $\sigma ={\sigma }_c=constant$ and $t=0$, we obtain the solution $\epsilon =\epsilon ={\sigma }_c/E_1$. Additionally, to identify the parameters of the rheological constitutive model, the Boltzmann superposition principle can be used to process the original data under the assumption of a linear viscoelastic body; then, the axial curves under various deviatoric stresses can be obtained as shown in Figure 9, and the non-linear degradation algorithm can be used to fit these curves.

Figure 9

Figure 9. Testing and fitting curves of axial creep under various deviatoric stresses.

Since the constitutive equation for fitting the H-K model is Equation 2, by letting P₁ = (E₁+ E₂)/E₁*E₂, P₂ = E₂, and P₃ = η₂, we get Equation 3:

$\frac{\epsilon }{{\sigma }_c}=-\frac{1}{P_2}{e}^{-\frac{P_2}{P_3}t}+P_2(3)$

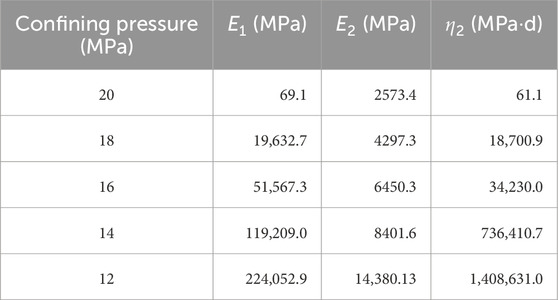
The regression calculation results of the creep parameters of the H-K three-element model are shown in Table 3.

Table 3

Table 3. Identification results of the creep parameters for the H-K three-element model.

5 Conclusion

Triaxial unloading creep test of sandy mudstone as a typical soft rock was conducted under a confining pressure of 20 MPa, and the rheological deformation damage law was obtained. From the experiments and results, the following conclusions are drawn:

1. The larger the deviatoric stress, the longer is the decay creep time and larger is the creep rate after reaching the steady state. The instantaneous and creep deformations produced at each level of stress unloading increase with increase in deviatoric stress, and lower confining pressures result in larger deformations.

2. Starting from a confining pressure of 20 MPa, the stress was unloaded at the rate of 2 MPa per level. At the 50% axial stress level with an axial pressure of 50 MPa and confining pressure of 10 MPa, creep acceleration was observed at the seventh unloading level, which ultimately resulted in destruction of the specimen; at the 70% axial stress level with an axial pressure of 70 MPa and confining pressure of 12 MPa, creep acceleration was observed at the fifth unloading level, which was also the point of destruction.

3. Based on the experimental results, the creep behaviors can be simulated using the H-K three-element model. The parameters of this model were obtained by non-linear regression, and the model was shown to reflect the rheological behaviors of the soft rock sample during unloading.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors without undue reservation.

Author contributions

XL: Methodology, Resources, Validation, Writing – original draft. ZY: Data curation, Investigation, Methodology, Writing – review and editing. FZ: Formal analysis, Supervision, Validation, Writing – review and editing. CD: Resources, Supervision, Investigation, Writing – review and editing. HW: Writing – review and editing, Methodology. YH: Investigation, Methodology, Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

Authors XL, ZY, FZ, CD, and HW were employed by CCCC Fourth Harbor Engineering Institute Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer JZ declared a shared affiliation with the author HY to the handling editor at the time of review.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Barla, G. (1995). Squeezing rocks in tunnels. Int. Soc. Rock Mech. News J. 2 (3/4), 44–49.

Google Scholar

Danesh, N. N., Chen, Z. W., Aminossadati, S. M., Kizil, M. S., Pan, Z. J., and Connell, L. D. (2016). Impact of creep on the evolution of coal permeability and gas drainage performance. J. Nat. Gas. Sci. Eng. 33, 469–482. doi:10.1016/j.jngse.2016.05.033

CrossRef Full Text | Google Scholar

Griggs, D. T. (1939). Creep of rocks. J. Geol. 47 (3), 225–251. doi:10.1086/624775

CrossRef Full Text | Google Scholar

ISRM. Commissions on squeezing rocks in tunnels (1995). Tunnelling in difficult ground. Proc. Workshop 8th ISRM. Tokyo.

Google Scholar

Ma, D., Wu, Y., Geng, H., Ma, X., Zhang, Y., Pu, H., et al. (2024). Mechanical behavior of multi-fracturing under confining pressure: effects of borehole diameter and rock type. Rock Mech. Rock Eng. 57, 11333–11350. doi:10.1007/s00603-024-04145-5

CrossRef Full Text | Google Scholar

Ma, D., Wu, Y., Ma, X., Hu, X., Dong, W., Li, D., et al. (2025). Fracture behavior of sandstone with partial filling flaw under mixed-mode loading: three-point bending tests and discrete element method. J. Rock Mech. Geotech. Eng. 17, 291–308. doi:10.1016/j.jrmge.2023.12.034

CrossRef Full Text | Google Scholar

Tang, S. B., Yu, C. Y., Heap, M. J., Chen, P. Z., and Ren, Y. G. (2018). The influence of water saturation on the short- and long-term mechanical behavior of red sandstone. Rock Mech. Rock Eng. 51, 2669–2687. doi:10.1007/s00603-018-1492-3

CrossRef Full Text | Google Scholar

Yang, C., and Shiwei, B. A. I. (1999). “Analysis of stress relaxiation behaviour of salt rock,” in Proceedings of the 37th U.S. Rock mechanics symposium. New York: John Wiley and Sons, 935–938.

Google Scholar

Yang, C. H., Daemen, J. J. K., and Yn, J. H. (1998). Experimental investigation of creep behavior of salt rock. Int. J. Rock Mech. Min. Sci. 36 (2), 233–242. doi:10.1016/s0148-9062(98)00187-9

CrossRef Full Text | Google Scholar

Yang, S. Q., and Hu, B. (2018). Creep and long-term permeability of a red sandstone subjected to cyclic loading after thermal treatments. Rock Mech. Rock Eng. 51, 2981–3004. doi:10.1007/s00603-018-1528-8

CrossRef Full Text | Google Scholar

Yongsheng, L. (1995). Creep and relaxation of 4 kinds of rock under uniaxial compression tests. Chin. J. Rock Mech. Eng. 14 (1), 39–47.

Google Scholar

Yu, C. Y., Tang, S. B., Tang, C. A., Duan, D., Zhang, Y. J., Liang, Z. Z., et al. (2019). The effect of water on the creep behavior of red sandstone. Eng. Geol. 253, 64–74. doi:10.1016/j.enggeo.2019.03.016

CrossRef Full Text | Google Scholar

Zhao, J., Feng, X. T., Zhang, X. W., Yang, C. X., and Zhou, Y. Y. (2018). Time-dependent behaviour and modeling of Jinping marble under true triaxial compression. Int. J. Rock Mech. Min. Sci. 110, 218–230. doi:10.1016/j.ijrmms.2018.08.009

CrossRef Full Text | Google Scholar

Zhou, H. W., Wang, L. J., Rong, T. L., Zhang, L., Ren, W. G., and Su, T. (2019). Creep-based permeability evolution in deep coal under unloading confining pressure. J. Nat. Gas. Sci. Eng. 65, 185–196. doi:10.1016/j.jngse.2019.03.010

CrossRef Full Text | Google Scholar

Zhu, J. (2009). Study on unloading mechanics and its rheological properties of rock under high stress. Beijing: Graduate School of the Chinese Academy of Sciences.

Google Scholar