Investigating the tensile cracking mechanisms of rock masses containing random fissures from the perspective of meshless numerical method

This paper focuses on the tensile cracking mechanisms of rock masses containing random fissures and conducts research based on the meshless numerical method. In view of the shortcomings in traditional research on rock crack propagation, such as the difficulty of experiments in reflecting stress changes, the inapplicability of theoretical research to complex geometric conditions, and the limitations of existing numerical simulation methods, this paper proposes an improved Smooth Particle Hydrodynamics (SPH) method. The traditional SPH smooth kernel function is re-written, a parameter к that can represent particle failure is introduced, the Mohr-Coulomb criterion is combined to judge particle failure, and the control equations are updated to simulate the progressive failure processes of particles. Under the SPH framework, the Monte Carlo method and the linear congruence method are used to develop a random fissure generation algorithm, which can effectively simulate the real distribution of random fissures inside rock masses. By simulating the crack propagation process under uniaxial tensile stress with different fissure lengths, numbers, and dip angles, the mechanical behaviors of random fissure rocks during the tensile process are analyzed in depth. The results show that an increase in fissure length makes cracks more likely to occur and changes the failure mode; Variations in fissure angles affect the crack propagation paths and the dominant final failure morphologies; An increase in the number of fissures changes the failure mode from simple crack penetration to complex fragmentation. At the same time, the stress-strain curves under different schemes are analyzed, and the influence laws of fissure characteristics on the elastic modulus and peak strength of rocks are clarified. The research results provide a new perspective for understanding the mechanical behavior of rocks under tensile loads and offer theoretical and numerical references for the analysis and design of tensile failure problems in geotechnical engineering. In addition, the application prospects and limitations of the SPH method in rock fracture simulation are discussed, and it is pointed out that future research should focus on developing 3D parallel programs to more accurately simulate the real rock fracture process and contribute to the development of geotechnical engineering theory and practice.

1 Introduction

In a wide range of geotechnical engineering domains, including slope stability analysis, tunnel excavation, and mining operations, the mechanical behavior of rocks is of utmost significance for ensuring the safety and stability of engineering structures (Nallala et al., 2025). The crack propagation behavior of rocks represents a crucial aspect of rock mechanics research. It encompasses the initiation, propagation, and interaction of internal cracks within rocks under stress, which directly influence the strength, deformation characteristics, and ultimate failure mode of rocks. A profound understanding of the crack propagation mechanism in rocks is instrumental in accurately predicting the stability of rock engineering projects, optimizing engineering designs, and preventing potential geological disasters such as landslides and collapses. This not only guarantees the smooth progress of engineering construction but also safeguards the safety of personnel and property, thereby holding substantial theoretical and practical value for the sustainable development of the geotechnical engineering field.

Previous research on rock crack propagation can be broadly categorized into three main areas: experimental studies, theoretical investigations, and numerical simulations. In the realm of experimental research on rock crack propagation, numerous scholars have dedicated efforts. For instance, Kytýř et al. (2024) utilized acoustic emission (AE) and 4D X-ray computed tomography (4D XCT) to study crack initiation and propagation in two different types of quartz-rich sandstones; Khalili et al. (2023) conducted laboratory studies on rock-like material specimens to investigate the effect of bedding planes on the failure and crack propagation mechanisms; Erarslan (2016) performed laboratory diametrical compression tests on Brisbane tuff disc specimens to develop much-needed understanding of the micro-mechanical and micro-structural dynamics of sub-critical crack propagation. Lawankar et al. (2025) investigated the effect of different parameters on the dynamic response of Kishangarh marble; Abi et al. (2025) conducted CO₂ rock fracturing experiments to measure acoustic wave velocity, rock damage, and energy distribution; Mei et al. (Mei et al., 2023) explored the propagation characteristics of adjacent cracks under hydro - mechanical coupling. Li Z. et al. (2024) conducted macroscopic and microscopic experiments to study the crack healing mechanism of salt rocks. Wang et al. (2024a) utilized digital image correlation technology to analyze the crack propagation characteristics of unconventional reservoir rocks. Jia et al. (2024) examined the influence of strength ratios and soft layer thicknesses on the micro - crack evolution mechanism of stratified composite rocks. Nevertheless, experimental studies are often limited to obtaining the morphological features of rock crack propagation and struggle to reflect the stress changes during the crack propagation process. Consequently, it is challenging to directly acquire the fracture mechanics mechanism underlying rock degradation.

Theoretical research, on the other hand, is grounded in the outcomes of experimental studies. It aims to summarize and formulate crack propagation criteria or sets of equations that describe the constitutive relationships of fractured rock masses. For example, Justo et al. (2022) developed a theoretical model for the analysis of the fracture behavior of different rocks containing circular holes subjected to uniaxial compressive uniform loads; Aligholi et al. (2022) explored the ability of the Theory of Critical Distances (TCD) to determine accurately both the tensile strength and fracture toughness; Bahrami et al. (2022) presented a set of correction factors as functions of specimen size to determine the value of K_IIc; Zhao X. et al. (2024) studied the fatigue crack propagation at the rock - concrete interface and proposed an adjusted Paris law. Cui et al. (2024) developed a micro - scale crack propagation criterion applicable to red - bed soft rocks. Li S. et al. (2024) established an impact rock - breaking mechanical theory model and simulated the rock - breaking process of an impact hammer. However, theoretical research is typically applicable only to simplified boundary conditions and geometric shapes. When dealing with complex geometric conditions, it becomes difficult for theoretical research to provide accurate solutions.

Numerical simulation, regarded as the “third method” of scientific research, offers the ability to analyze a variety of complex rock mechanics problems. By assigning appropriate parameters and boundary conditions, numerical simulations can yield relatively accurate results. Scholars have conducted extensive numerical simulation studies on rock crack propagation. For example, Wang et al. (2024b) developed an improved particle - based model to simulate the direct shear test of granite. De Silva et al. (2024a) used the 3DEC software to simulate the expansion process of soundless cracking demolition agents (SCDA) in boreholes and joints. Su et al. (2024) proposed a three - dimensional numerical manifold method based on a local tracking algorithm to simulate rock crack propagation. Wang L. et al. (2024) employed the phase - field method to explore the influence of specimen geometric configurations and loading modes on the mixed - mode I/II fracture characteristics of rocks. Li G. et al. (2024) proposed a non - fracture modeling strategy to simulate the failure process of non - intact rocks. De Silva et al. (2024b) developed a numerical method to evaluate the effects of mineral heterogeneity and rock mass defects on the fracturing performance of SCDA. Zhao C. et al. (2024) investigated the excavation - induced damage and failure phenomena of Opalinus Clay shale through field experiments and three - dimensional numerical simulations. Wang et al. (2023) studied the damage mechanism of cracked rocks under the impact of steel - particle water jets based on the SPH - FEM coupling algorithm. Liang et al. (2024) proposed a thermo - mechanical coupling model based on the numerical manifold method to simulate the crack initiation and propagation in fractured rock masses. Ouyang et al. (2024) conducted experimental and numerical studies to explore the shear properties and failure mechanisms of the bonded rock - cement interface. Li J. et al. (2024) constructed an impact rock - breaking mechanical model and simulated the secondary rock - breaking process of an impact hammer. Xia et al. (2024) used self - developed programs and neural network models to study the crack propagation and uniaxial compressive strength of randomly multi - fractured rocks. Xu et al. (2024) developed a 3D adaptive crack - growth model integrated with the phase - field method to study internal cracks in rocks. However, traditional numerical methods face certain limitations. The finite element method, for example, FEM simulates rock crack propagation through mesh re - meshing, which may lead to severe mesh distortion and computational failure when dealing with complex crack networks (Zhu et al., 2025). The discrete element method has a large number of meso - scale parameters that require complex calibration prior to numerical simulation (Han et al., 2025). In the numerical manifold method, cracks need to be aligned with the grid, and the phase - field method has limitations in simulating the interaction of multiple cracks (Su et al., 2024). The smooth particle hydrodynamics (SPH) method, a meshless approach, has shown great potential in simulating large - deformation and discontinuous problems and has thus been widely applied in rock fracture mechanics simulations (Yu et al., 2023a; Yu et al., 2023b; Yu et al., 2025a; Yu et al., 2025b; Hu et al., 2024; Yu et al., 2024a; Yu et al., 2024b; Yu et al., 2023c; Yu et al., 2023d) based on the SPH method. Nevertheless, due to the prevalence of random cracks in natural rocks, the application of SPH in simulating the propagation of these random cracks remains relatively scarce.

In light of the aforementioned limitations of previous studies, this paper undertakes two key tasks. First, it modifies the traditional SPH smooth kernel function to enable the simulation of the progressive failure process of particles. Second, it develops a random crack generation algorithm within the SPH framework, facilitating the creation of randomly distributed cracks. By simulating the crack propagation processes under different crack lengths, numbers, and inclinations subjected to uniaxial tensile stress, this study analyzes the initiation, propagation paths, interaction patterns, and final failure modes of cracks in randomly cracked rocks during the tensile process. The research findings are expected to offer novel insights into understanding the mechanical behavior of rocks under tensile loads and provide theoretical and numerical references for the analysis and design of tensile - related failure problems in geotechnical engineering.

2 Treatment of particle failure in the SPH framework

2.1 Basic theory of SPH

In SPH calculations, kernel function approximation and particle approximation are the first steps. Kernel function approximation is to approximate the values and derivatives of continuous field variables through discrete sampling points (particles). Its expression is as follows:

$f\left(\mathit{x}\right)\approx {\displaystyle \underset{\mathrm{\Omega }}{\int }}f\left({\mathit{x}}^{\prime }\right)W\left(\mathit{x}-{\mathit{x}}^{\prime },h\right)\mathrm{d}{\mathit{x}}^{\prime }(1)$

where x represents the coordinate vector of the particle, f is the field variable function, which can represent variables such as density and velocity, Ω is the calculation domain of SPH, and W is the smoothing kernel function in the SPH framework.

The particle approximation method further approximates the kernel approximation equation by using discrete particles in SPH. It replaces the integral of the field function and its derivative with the superposition of the corresponding values of adjacent particles in the local area. The expression can be rewritten based on Equation 1 as:

$f\left({\mathit{x}}_i\right)={\displaystyle \sum _{j=1}^N}\frac{m_j}{{\rho }_j}f\left({\mathit{x}}_j\right)·W_{ij}(2)$

In Equation 2, m is the mass of the particle, and ρ is the density of the particle.

2.2 SPH governing equations

During the SPH calculation process, the governing equations are used to transfer parameters between particles and update the particle parameters. The key governing equations in SPH include the continuity equation and the momentum equation, and their expressions are as follows:

$\frac{d{\rho }_i}{dt}={\displaystyle \sum _{j=1}^N}{m}_j{v}_{ij}^{\beta }\mathrm{\partial }{W}_{ij,\beta }(3)$

$\frac{d{v}_i^{\alpha }}{dt}={\displaystyle \sum _{j=1}^N}{m}_j\left(\frac{{\sigma }_{ij}^{\alpha \beta }}{{\rho }_i^2}+\frac{{\sigma }_{ij}^{\alpha \beta }}{{\rho }_j^2}+T_{ij}\right)\mathrm{\partial }{W}_{ij,\beta }(4)$

where and v、σ are the velocity and stress of the particle respectively. The subscripts i and j represent the particle numbers, t is the time parameter, N is the total number of SPH particles, and α and β are Einstein notations.

2.3 SPH fracture treatment method

In this section, the Mohr - Coulomb criterion is adopted to determine whether a particle fails, which has been widely applied in previous simulations. First, it is judged whether the maximum principal stress of the particle reaches its tensile strength. If it does, the particle fails; if not, it is then judged whether the particle undergoes shear failure. The expressions of the Mohr - Coulomb criterion are as follows:

${\sigma }_1={\sigma }_t(5)$

${\tau }_f=c+{\sigma }_f\tan \phi (6)$

where c is the cohesion of the SPH particle, and σ_f and τ_f are the normal stress and shear stress on the material failure surface respectively.

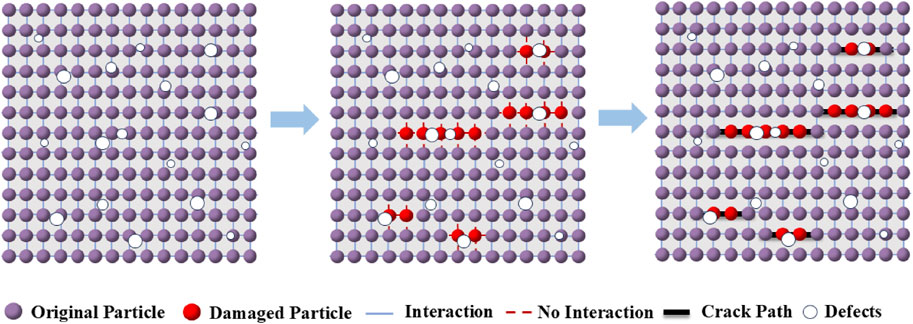
It can be seen from the SPH governing Equations 3, 4 that the derivative of the kernel function controls the parameter transfer between SPH particles. Therefore, in this section, a parameter к that can represent whether a particle fails is introduced. When the particle is not damaged, к = 1 is set; when the particle meets the failure criteria Equations 5, 6, к = 0 is set, indicating that the particle fails. The numerical processing flow of the particle failure process in the SPH framework is shown in Figure 1. By multiplying the fracture marker к before the traditional smoothing kernel function W, the expression of the improved kernel function I considering particle failure can be obtained, as shown in Equation 7:

$I\left(\mathit{x}-{\mathit{x}}^{\prime },h\right)=\kappa ·W\left(\mathit{x}-{\mathit{x}}^{\prime },h\right)(7)$

Figure 1

Figure 1. Particle failure process in the SPH framework.

By replacing the traditional smoothing kernel function W with the improved kernel function I, the SPH governing equations considering particle failure can be obtained, as shown in Equations 8, 9:

$\frac{d{\rho }_i}{dt}={\displaystyle \sum _{j=1}^N}{m}_j{v}_{ij}^{\beta }\mathrm{\partial }{I}_{ij,\beta }(8)$

$\frac{d{v}_i^{\alpha }}{dt}={\displaystyle \sum _{j=1}^N}{m}_j\left(\frac{{\sigma }_{ij}^{\alpha \beta }}{{\rho }_i^2}+\frac{{\sigma }_{ij}^{\alpha \beta }}{{\rho }_j^2}+T_{ij}\right)\mathrm{\partial }{I}_{ij,\beta }(9)$

3 Generation method of random fractures in the SPH framework

The formation of random fractures within rock masses is attributed to a multitude of complex factors. Geological tectonic movements play a pivotal role. Plate - scale processes such as compression, tension, shear, folding, and seismic activities are key contributing factors. The compressive forces in plate collision zones, tensile stresses in extensional regions, uneven stress distribution during folding, and the powerful dynamic stresses generated by seismic wave propagation all contribute to the formation of fractures. Additionally, the physical property disparities within rocks cannot be overlooked. Rocks composed of different mineral components, due to variations in thermal expansion coefficients and hardness, tend to develop fractures at the contact interfaces when subjected to temperature and pressure changes. Similarly, regions with distinct rock structures, such as those with varying particle sizes, shapes, or porosities, are prone to fracture formation under external forces. Moreover, weathering processes are also significant. In physical weathering, the thermal expansion and contraction of rocks due to temperature fluctuations, and the expansion of pore - water during freezing in freeze - thaw cycles, gradually initiate and propagate fractures.

The fractures within rock masses are numerous, and their geometric structures are often difficult to precisely determine. However, their spatial distribution follows macroscopic statistical laws. That is, their geometric parameters, including fracture occurrences, densities, and trace lengths, can be described by probability - statistical density functions. In this section, the Monte Carlo method is introduced into the SPH framework, and the linear congruential method is employed to generate uniformly distributed random numbers. The recurrence formula is expressed as follows:

$\left\{\begin{array}{l}{x}_n=\left(a{x}_{n-1}+c\right)\left(\mathrm{mod}M\right)\\ r_n=x_n/M\\ Initialvalue{x}_0\end{array}\right.(10)$

where M is the modulus, mod M represents taking the remainder with respect to the modulus, a is the multiplier, c is the increment, x₀ is the initial value, and r_n is the generated random number within the range [0-1]. Thus, the formula for generating random numbers following a normal distribution can be expressed as:

$x_n^{\prime }={\mu }_x+{\sigma }_x\times \sqrt{-2\ln \left(r_n\right)}\times \cos \left(2\times \pi \times r_n\right)(11)$

where μ_x is the mean value and σ_x is the standard deviation.

Two - dimensional fractures can be parametrically characterized. Specifically, a two - dimensional fracture can be described by its center - point coordinates (fx₀,fy₀), fracture trace length fl, and fracture orientation angle θ. Therefore, the endpoint coordinates of the fracture can be expressed, as shown in Equation 12:

$\left\{\begin{array}{l}fx=f{x}_0\pm \left(fl/2\right)\cos \theta \\ fy=f{y}_0\pm \left(fl/2\right)\cos \theta \end{array}\right.(12)$

where fx is the abscissa of the fracture endpoint and fy is the ordinate of the fracture endpoint. The fracture density Q is defined as the ratio of the number of fractures N to the generation domain S. Consequently, the geometric generation process of random fractures is outlined as follows:

First, determine the size of the generation domain. It is important to note that when the analysis domain has an irregular shape, the size of the generation domain is generally larger than that of the analysis domain. Then, calculate the number of fractures N = Q × S.

Determine the random parameter properties of each fracture. According to Equation 10, generate N groups of random numbers that follow a normal distribution and are within the range [0-1], thereby generating N groups of fracture center - point coordinates (fx₀, fy₀), fracture trace lengths fl, and fracture orientation angles θ that follow a normal distribution.

Determine the endpoint coordinates of each fracture. Based on the fracture parameters generated in Step 2, use Equation 11 to generate N groups of fracture endpoint coordinates (fx, fy).

4 Analysis of numerical simulation results

4.1 Numerical model and calculation scheme

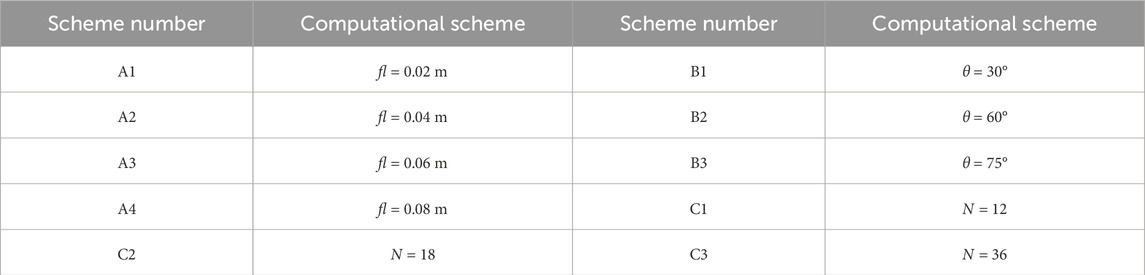
To explore the influence of the characteristics of random fractures within rock masses on the mechanical properties of rocks under tensile stress, random fractures were first generated according to the method described in Section 3 of this paper. The improved SPH method is validated in previous studies (Ren et al., 2021). The following calculation schemes were set: Scheme A: Different fracture lengths; Scheme B: Different fracture numbers; Scheme C: Different fracture angles. The specific schemes are shown in Table 1. The size of the rock mass model is 0.6 m × 0.6 m, and the entire model is divided into 200 × 200 = 40,000 particles. The upper and lower ends of the model are subjected to tensile stress with a loading rate of 0.005 m/s. Randomly distributed fractures are generated inside the model using the method introduced in Section 3. The model size and particle discretization are shown in Figure 2. The model parameters are as follows: Elastic modulus E = 17 GPa, Poisson’s ratio μ = 0.2, and tensile strength σ_t = 1 Mpa.

Table 1

Table 1. Numerical simulation calculation schemes.

Figure 2

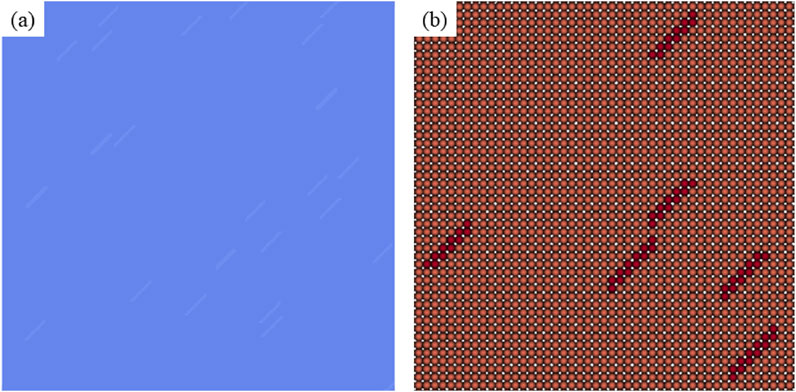
Figure 2. Numerical model and particle discretization. (a) SPH numerical calculation model; (b) local particle discretization.

4.2 Crack propagation process

4.2.1 Influence of different fracture lengths on the failure morphology of rock masses

Figure 3 shows the propagation process of random fractures inside rock masses with different fracture lengths fl. Here, blue represents the rock matrix, light blue represents random fractures, and red represents crack propagation. As can be seen from the figure: When fl = 0.02 m, the short pre - fabricated fractures act as stress - concentration areas. Under tensile stress, cracks initiate from these fractures and expand horizontally. As the cracks grow, their tips approach, and the overlapping stress fields lead to model failure. The short fractures have little impact on the crack propagation path, which is mainly perpendicular to the principal tensile stress.

Figure 3

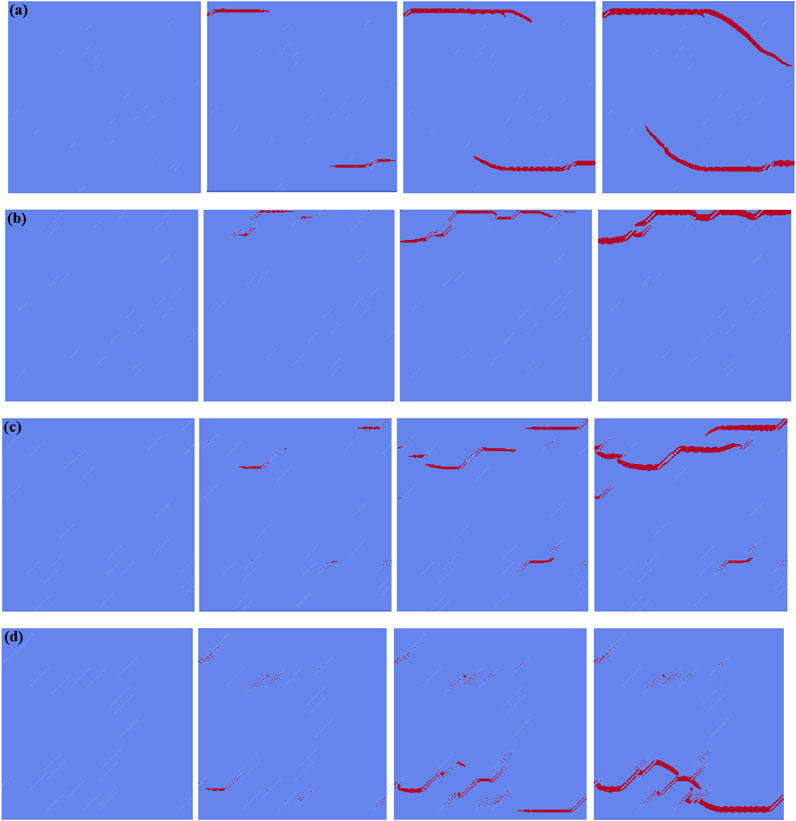
Figure 3. Propagation Process of Random Fractures Inside Rock Masses with Different Fracture Lengths. (a) fl = 0.02 m; (b) fl = 0.04 m; (c) fl = 0.06 m; (d) fl = 0.08 m.

When fl = 0.04 m, cracks occur in the upper part of the model due to local stress concentration. The pre - fabricated fractures significantly affect the crack propagation path, causing cracks to interact and form a complex network. Although the final fracture path is still horizontal, the presence of fractures makes the microscopic process more complex.

When fl = 0.06 m, multiple crack propagation paths form inside the model. A crack from a middle pre - fabricated fracture becomes dominant and extends to the model edge, resulting in failure.

When fl = 0.08 m, the long pre - fabricated fractures store a large amount of strain energy. After loading, numerous cracks expand at these fractures, intersect with each other, and the cracks from the lower - part fractures overlap, changing the failure mode from scattered crack expansion to failure mainly caused by long - fracture - related crack overlap.

4.2.2 Influence of different fracture angles on the failure morphology of rock masses

Figure 4 shows the propagation process of random fractures inside rock masses with different pre - fabricated fracture inclination angles θ. As can be seen from the figure: When θ = 30°, the pre - fabricated fractures make the stress distribution non - uniform. Micro - cracks appear near the tips of some fractures close to the loading end, expand at an angle to the principal tensile stress, and interact with the fractures to form a complex network. The model fails along multiple intersecting crack surfaces.

Figure 4

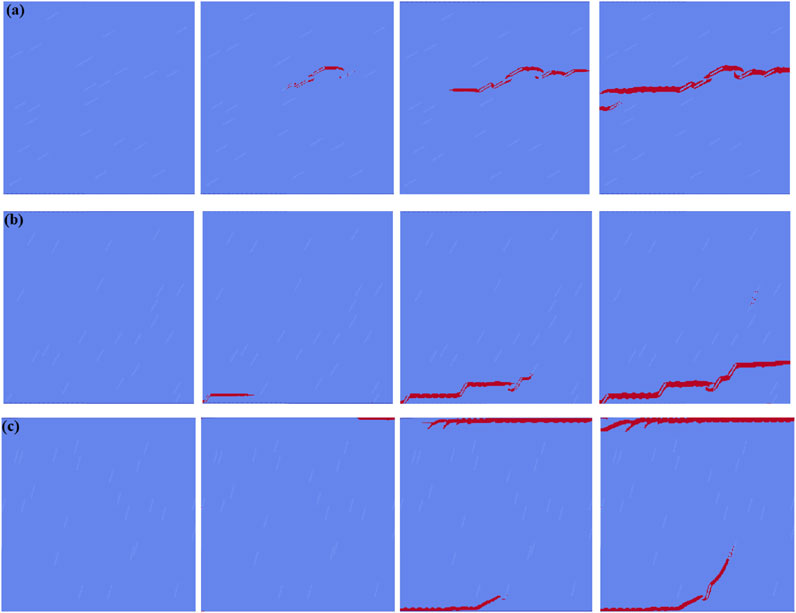
Figure 4. Propagation Process of Random Fractures Inside Rock Masses with Different Fracture Inclination Angles. (a) θ = 30°; (b) θ = 60°; (c) θ = 75°.

When θ = 60°, cracks initiate at stress - concentration areas, mainly near the fractures and the model boundary. They preferentially expand along the fractures, are disturbed by the surrounding rock mass, and generate branch cracks. Some branch cracks deflect towards the direction perpendicular to the principal tensile stress. The model fails as multiple cracks connect.

When θ = 75°, cracks first occur along the upper boundary of the model due to stress concentration. They expand horizontally first, then overlap with the lower pre - fabricated fractures and turn to expand along the 75° direction. The pre - fabricated fractures play a guiding role in the crack expansion direction, and the model fails when these cracks form a macroscopic fracture surface.

4.2.3 Influence of different fracture numbers on the failure morphology of rock masses

Figure 5 shows the propagation process of random fractures inside rock masses with different numbers of pre - fabricated fractures N. As can be seen from the figure: When N = 12, the stress - concentration areas are dispersed. Cracks initiate at the ends of some pre - fabricated fractures, expand independently, and have a simple path along the principal tensile stress. The model fails mainly due to the penetration of several long cracks.

Figure 5

Figure 5. Propagation process of random fractures inside rock masses with different numbers of fractures. (a) N = 12; (b) N = 18; (c) N = 36.

When N = 18, more pre - fabricated fractures increase the probability of crack initiation at multiple positions. The cracks interact during expansion, form local crack clusters, and finally connect to form a macroscopic fracture zone, causing the rock mass to lose its bearing capacity.

When N = 36, a large number of cracks initiate simultaneously around the numerous pre - fabricated fractures. The high fracture density leads to a complex crack network. The rock mass is divided into small pieces, and the model undergoes fragmented failure.

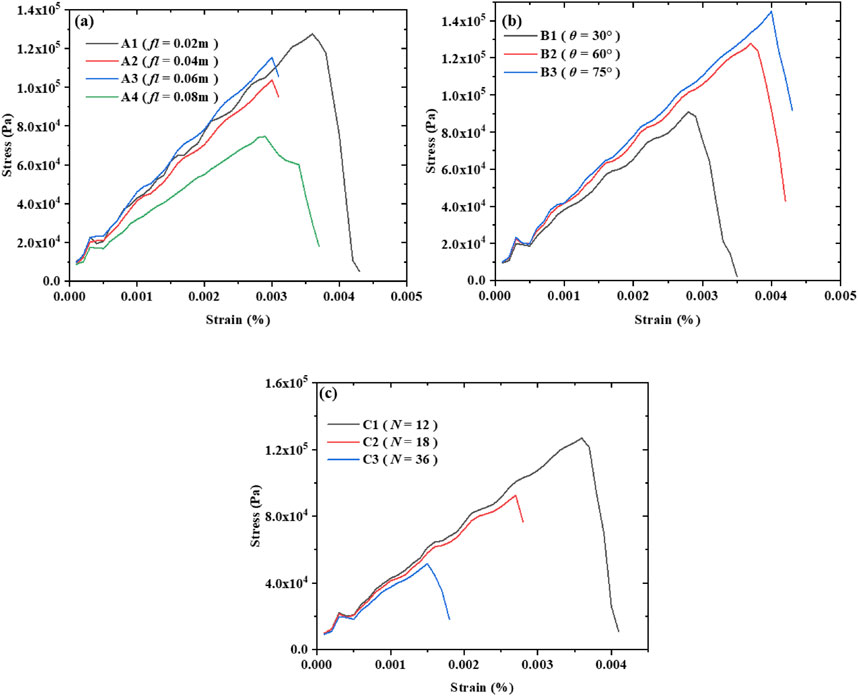
4.3 Stress - strain curves

Figure 6 shows the stress - strain curve patterns under different schemes. Looking at the stress - strain curves of Scheme A (different fracture lengths) in Figure 6a, in the elastic stage, the curves approximately show a linear change. However, as the fracture length increases from 0.02 m to 0.08 m, the slope of the elastic segment gradually decreases. This means that as the fracture length increases, under the same stress increment, the strain increment of the rock becomes larger, that is, the ability of the rock to resist elastic deformation gradually weakens, and the elastic modulus gradually decreases. In terms of peak strength, when fl = 0.02 m, the peak strength is relatively high. This is because although the short pre - fabricated fractures are the initiation points of cracks at the initial stage of tension, they generally have a relatively small weakening effect on the internal structure of the rock. The crack expansion is relatively orderly, and the rock can withstand a large tensile stress before reaching the peak strength. When fl = 0.08 m, due to the long pre - fabricated fractures, a large amount of strain energy is stored inside. At the initial stage of loading, it will trigger the initiation and expansion of many cracks. These numerous cracks intersect with each other, causing the rock structure to deteriorate rapidly, and the peak strength is reached at a lower stress, that is, the peak strength is significantly reduced. From the numerical simulation results, it can be seen that when the fractures are short, the cracks mainly initiate from the pre - fabricated fractures and then expand horizontally, and the process is relatively simple. When the fractures are long, a large number of cracks are generated and overlap at the pre - fabricated fractures in the lower part of the model, leading to failure. The change in the failure mode also reflects the significant influence of the fracture length on the peak strength.

Figure 6

Figure 6. Stress-strain curves under different schemes. (a) Scheme A; (b) B; (c) C.

For the stress - strain curves of Scheme B (different fracture angles) in Figure 6b, the curves in the elastic stage are also approximately linear. However, as the fracture angle increases from 30° to 75°, the slope of the elastic segment also shows a decreasing trend, indicating that the elastic modulus gradually decreases. This is because a larger fracture angle makes the stress transfer path more complex, and it is easier for stress concentration and local deformation to occur inside the rock, thereby reducing the overall elastic performance of the rock. In terms of peak strength, the peak strength is relatively low when θ = 30°. At the initial stage of applying tensile stress, the stress inside the model is unevenly distributed due to the pre - fabricated fractures. Micro - cracks are generated near the tips of the fractures in the area close to the loading end. The crack expansion path is tortuous, and they intersect with each other to form a complex network, causing the bearing capacity of the rock mass to decrease and reach the peak strength at a lower stress. The peak strengths when θ = 60° and θ = 75° are relatively high, but the difference between them is not very significant. Taking θ = 60° as an example, at the initial stage of loading, cracks initiate at the stress - concentration areas, preferentially expand along the direction of the pre - fabricated fractures, and are disturbed by the stress field of the surrounding rock mass and generate branch cracks. Some branch cracks deflect towards the direction perpendicular to the principal tensile stress. When θ = 75°, cracks are first generated on the upper boundary of the model. After horizontal expansion, they overlap with the lower prefabricated fractures and then expand along the 75° direction, eventually leading to failure. Numerical simulation shows that although a larger fracture angle changes the crack propagation direction, to a certain extent, the crack propagation is more orderly, enabling the rock to withstand a higher stress before reaching the peak strength.

For the stress-strain curves of Scheme C (different numbers of fractures) in Figure 6c, the curves in the elastic stage basically coincide at first. However, as the number of fractures increases from 12 to 36, the slope of the elastic segment gradually decreases, reflecting a gradual decrease in the elastic modulus. This is because as the number of fractures increases, the number of internal defects in the rock increases, the connection force between particles weakens, and relative displacement is more likely to occur under stress, resulting in a decrease in the ability to resist elastic deformation. In terms of peak strength, the peak strength is the highest when N = 12. Because the number of fractures is small, the stress concentration areas are dispersed. After cracks initiate at the ends of some prefabricated fractures, they expand relatively independently with weak interaction, and the rock can maintain its structural integrity well, thus being able to withstand a large tensile stress. The peak strength is the lowest when N = 36. A large number of cracks initiate simultaneously at the moment of loading. The high fracture density leads to frequent encounters and interference between cracks, forming a complex crack network. The rock structure is rapidly damaged and reaches the peak strength at a lower stress. From the results of numerical simulation, when N = 12, the failure of the model is mainly caused by the penetration of several long cracks, and the failure mode is single. When N = 36, the model shows a fragmented failure, and the rock mass is divided into many small pieces, fully reflecting the influence of the number of fractures on the peak strength and failure mode.

5 Discussion

5.1 Influence of random fracture morphology on rock failure modes

The morphological characteristics of random fractures, including fracture length, angle, and number, have a significant impact on the failure modes of rocks. From the results of numerical simulations, different fracture morphologies cause rocks to exhibit various failure processes and final failure forms under tensile stress.

In terms of fracture length, when the fracture is short, such as 0.02 m, during the initial stage of rock tension, cracks mainly initiate from the prefabricated fractures. Subsequently, they approximately propagate perpendicular to the direction of the principal tensile stress. This is because although the short fractures are stress concentration points, they have little restriction on the crack propagation direction. The stress distribution within the rock is relatively simple, and the crack propagation path is relatively single. The final failure mode is caused by the gradual extension of cracks, their approaching each other, and the intensification of stress concentration, leading to the failure of the model. As the fracture length increases, for example, when it reaches 0.08 m, the strain energy stored in the prefabricated fractures increases. After loading, numerous cracks will initiate and propagate, and these cracks intersect with each other. Eventually, the model mainly fails due to the connection of cracks generated at the longer prefabricated fractures at the bottom. The failure mode changes from relatively scattered crack propagation to failure concentrated at the longer fractures. The integrity of the rock is severely weakened, and its bearing capacity is greatly reduced.

The influence of fracture angles on the failure mode is also quite evident. When the fracture dip angle is 30°, the stress inside the model is unevenly distributed due to the presence of fractures. Microcracks appear near the tips of fractures close to the loading end. Their propagation paths are tortuous and interact with the prefabricated fractures to form a complex network. Before the model fails, the connection of the crack network leads to a sharp drop in the bearing capacity of the rock mass, and it fails along multiple intersecting crack surfaces. Under the fracture dip angles of 60° and 75°, although the crack propagation is significantly affected by the direction of the prefabricated fractures, to a certain extent, it is more orderly. Taking the 75° fracture as an example, cracks first appear at the upper boundary of the model. After horizontal propagation, they connect with the lower prefabricated fractures and then propagate along the 75° direction, ultimately forming a macroscopic fracture surface and causing failure. This indicates that although a larger fracture angle changes the crack propagation direction, under specific stress conditions, the cracks can propagate relatively orderly. Overall, the change in fracture angles makes the rock failure mode transform from complex and disorderly to relatively orderly, while also altering the crack propagation path and the dominant factor of the final failure.

The change in the number of fractures also profoundly affects the failure mode of rocks. When the number of fractures is small, such as N = 12, the stress concentration areas are dispersed. Cracks initiate independently at the ends of some prefabricated fractures and have weak interactions. The propagation path is simple, mainly extending along the direction of the principal tensile stress. Ultimately, the model failure is mainly caused by the penetration of several relatively long cracks, and the failure mode is single. As the number of fractures increases to N = 36, a large number of cracks initiate simultaneously at the moment of loading. The high fracture density causes the cracks to meet and interfere with each other frequently, forming a highly complex intersecting network. During the loading process, the crack network continues to develop, and the rock mass is divided into small pieces. Finally, it shows a fragmented failure, which is significantly different from the case with a small number of fractures. This fully demonstrates that an increase in the number of fractures can change the rock failure mode from simple crack penetration to complex fragmentation.

The change in the morphology of random fractures can significantly alter the stress distribution state inside the rock, affect the initiation position, propagation path, and interaction mode of cracks, and thus lead to diverse failure modes of rocks. These research results are of great theoretical significance for deeply understanding the mechanical behavior of rocks in complex stress environments and for accurately evaluating rock stability and optimizing engineering designs in geotechnical engineering.

5.2 Application prospects of the SPH method in rock fracture process simulation

The SPH method exhibits many unique advantages in the simulation of rock fracture processes, giving it broad application prospects in this field. From the perspective of calculation principles, as a meshless method, it effectively circumvents some of the drawbacks of traditional grid - based methods. When simulating rock crack propagation, the finite element method faces the problem that complex fracture networks can cause extreme grid distortion, making calculations impossible. The numerical manifold method requires cracks to be located on the grid. These limitations do not exist in the SPH method. The SPH method uses kernel function approximation and particle approximation to describe the rock medium with discrete particles. It can flexibly handle large - deformation and discontinuous problems and can simulate the complex crack propagation and rock fragmentation phenomena that occur during the rock fracture process more realistically. In dealing with multi - physical - field coupling problems, the SPH method also has significant advantages. The fracture process of rocks often involves the interaction of multiple physical processes, such as stress, seepage, and temperature. The SPH method can conveniently couple and solve the control equations of these physical fields. By adjusting the interactions and parameter transfers between particles, it can simulate the crack propagation characteristics of rocks under different physical field conditions. For example, when studying the impact of groundwater seepage on rock fractures, the SPH method can consider both the flow of the fluid and the deformation and failure of the rock, providing a powerful tool for in - depth understanding of the mechanical behavior of rocks under multi - field coupling. In addition, the SPH method performs well in simulating rock engineering problems with complex geometric shapes and boundary conditions. The structures of natural rock masses are complex and diverse. Traditional theoretical research often has difficulty providing accurate solutions when dealing with complex geometric conditions. The SPH method can easily adapt to various complex rock geometric shapes by setting the distribution and parameters of particles. It is also more flexible in dealing with irregular boundaries and can more accurately simulate the mechanical response of rocks in actual projects.

However, when using the SPH method to simulate two - dimensional problems in this study, there are still certain limitations. Although two - dimensional simulations can reveal some basic laws and characteristics of rock crack propagation, they cannot fully reflect the complexity of the real rock fracture process. The real rock fracture process has a complex three - dimensional morphology. Two - dimensional simulations ignore factors such as the differences in stress distribution in the three - dimensional space of rocks, the diversity of crack propagation directions, and the interactions between different parts. For example, in actual rocks, cracks may propagate along different planes in three - dimensional space and will be constrained and affected by the surrounding rock mass in three directions. Two - dimensional simulations are difficult to accurately describe these phenomena. Given the three - dimensional characteristics of the real rock fracture process, future research should focus on the development of three - dimensional parallel programs. Developing three - dimensional parallel programs can fully utilize the multi - core computing power of modern computers and significantly improve simulation efficiency. When dealing with large - scale rock models and complex crack propagation problems, the computational amount will increase sharply, and traditional serial computing methods are difficult to meet the requirements of computing time. Through parallelization technology, the computational tasks can be distributed to multiple processor cores for simultaneous calculation, greatly shortening the calculation time and making it possible to simulate more complex and realistic rock fracture processes. During the development of three - dimensional parallel programs, a series of technical problems need to be solved. First is the problem of data communication and synchronization. In a parallel computing environment, different processor cores need to exchange data frequently. How to perform data communication efficiently and ensure data consistency is the key. Second, the algorithm needs to be optimized to meet the requirements of three - dimensional simulations. For example, the particle search algorithm can be improved to increase the efficiency of finding adjacent particles in three - dimensional space, thereby accelerating the calculation speed. In addition, the program needs to be effectively verified and tested to ensure the accuracy and reliability of the three - dimensional simulation results. With the continuous improvement and development of three - dimensional parallel programs, the application of the SPH method in rock fracture process simulation will become more in - depth and extensive. It will provide more accurate analysis methods for many practical problems in the geotechnical engineering field, such as the prediction of surrounding rock fractures during underground tunnel excavation, slope stability analysis, and the study of rock fragmentation laws in mine exploitation, providing a more reliable theoretical basis and technical support for engineering design and disaster prevention.

5.3 Comparison with previous literature

This study on the tensile cracking mechanisms of rock masses containing random fissures contributes to the existing literature in several ways. When compared with previous research on the same topic, it offers new perspectives and improvements.

5.3.1 Contributions to the existing literature

(1) Improved Numerical Methodology: Many previous studies used traditional numerical methods like the finite element method (FEM) (Pletz et al., 2024; Giannella et al., 2018), discrete element method (DEM) (Nallala et al., 2025; Ferguen et al., 2019), or numerical manifold method (Kamalodini et al., 2022; Hasibi et al., 2023) to study rock crack propagation. As mentioned in the Introduction, FEM often faces issues with mesh distortion for complex crack networks (Gibert et al., 2019), DEM requires complex calibration of numerous meso - scale parameters (Nitka and Rucka, 2025), and the numerical manifold method needs cracks to align with the grid (Tal et al., 2014). In contrast, this paper improves the SPH method. By modifying the smooth kernel function and introducing the parameter κ, we can better simulate the progressive failure process of particles. This provides a more reliable numerical approach for studying rock crack propagation, especially for problems involving large - deformation and discontinuous media, which is a significant contribution to the numerical methods in rock mechanics research.

(2) Realistic Random Fissure Simulation: The development of a random fracture generation algorithm within the SPH framework is another key contribution. While previous studies have attempted to simulate rock fractures, accurately representing the real - world distribution of random fissures in rock masses has been a challenge. Our algorithm, which uses the Monte Carlo method and the linear congruence method, can effectively generate randomly distributed fractures. This allows for a more in - depth analysis of the influence of different fracture characteristics (length, angle, and number) on rock mechanical properties, filling a gap in the existing literature on simulating the complex fracture conditions in natural rock masses.

5.3.2 Comparison with other literature: pros and cons

The advantages of the method are as follows:

(1) Adaptability to Complexity: As a meshless method, SPH used in this study has an edge over grid - based methods in handling complex geometric shapes and large - deformation problems. For example, when simulating rock masses with irregularly shaped fractures and large - scale deformation during the fracture process, grid - based methods may encounter difficulties in mesh generation and distortion. The SPH method can overcome these problems by using discrete particles to represent the rock medium, providing a more accurate simulation of the actual situation.

(2) Multiphysics Coupling Capability: In real - world rock engineering, the fracture process often involves multiple physical fields, such as stress, seepage, and temperature. The SPH method can conveniently couple and solve the control equations of these physical fields. In comparison, some previous studies using other methods may have limitations in handling such multi - physical - field coupling problems. Our approach can better simulate the complex physical processes during rock fracture, providing more realistic results for engineering applications.

The limitations of the method are as follows:

(1) Two - Dimensional Simulation: Although two - dimensional simulations in this study can reveal some basic laws of rock crack propagation, they have limitations compared to three - dimensional simulations in previous literature. The real rock fracture process is three - dimensional, and two - dimensional simulations cannot fully reflect the complexity of stress distribution, crack propagation directions, and interactions in three - dimensional space. For instance, in actual rocks, cracks can propagate along different planes in three - dimensional space and be affected by the surrounding rock mass in all three directions. This is an area where our current study is less comprehensive compared to some three - dimensional research.

(2) Computational Intensity: The SPH method, especially when dealing with large - scale models and complex crack propagation problems, can be computationally intensive. Compared to some simplified numerical models in previous literature, our method may require more computing resources and longer calculation times. This could limit its application in some scenarios where quick results are needed, although with the development of parallel computing technology, this limitation can be gradually overcome.

6 Conclusion

(1) The traditional SPH smooth kernel function was modified. By introducing the parameter κ and applying the Mohr - Coulomb criterion, a new SPH algorithm was developed. This algorithm can accurately simulate the progressive failure process of particles, providing a more reliable way to study rock crack propagation.

(2) A random fracture generation algorithm was created within the SPH framework. It uses the Monte Carlo method and the linear congruential method to generate randomly distributed fractures, effectively simulating the real - world distribution of fissures in rock masses. This helps analyze the influence of different fracture characteristics on rock mechanical properties.

(3) The length, angle, and number of random fractures significantly affect rock fracture morphology. Longer fractures make cracks more likely to occur and change the failure mode; fracture angles influence the crack propagation path and final failure morphology; an increased number of fractures transforms the failure mode from simple crack penetration to complex fragmentation.

(4) The SPH method has advantages in rock fracture simulation, such as handling large - deformation, discontinuous, and multi - physical - field coupling problems, as well as adapting to complex geometric shapes. However, two - dimensional simulations are limited. Future research should focus on developing 3D parallel programs to improve simulation accuracy and efficiency, which will benefit geotechnical engineering applications.

(6) In addition to developing 3D parallel programs, integrating emerging technologies into the SPH method offers great potential. Artificial intelligence - assisted optimization algorithms can analyze the massive data from simulations to optimize SPH parameters. This will refine the simulation accuracy, better predicting the mechanical behavior of rock masses. For example, machine learning can identify complex patterns in crack propagation data. Meanwhile, new - type sensors can measure in - situ rock mass parameters with higher precision. Incorporating these accurate data into SPH models will enhance their realism, providing more reliable support for geotechnical engineering design and disaster prevention efforts.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

JC: Investigation, Methodology, Validation, Writing – original draft, Writing – review and editing. YS: Investigation, Writing – original draft, Resources, Supervision, Validation, Writing – review and editing. WL: Investigation, Writing – original draft. BZ: Investigation, Writing – original draft. SY: Investigation, Writing – original draft.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abi, E., Zeng, Q., Liu, M., Zheng, Y., Han, Y., Jiang, M., et al. (2025). Study on the computational model and distribution characteristics of rock fracture energy induced by supercritical CO2 phase transition. Geoenergy Sci. Eng. 251, 213862. doi:10.1016/j.geoen.2025.213862

CrossRef Full Text | Google Scholar

Aligholi, S., Ponson, L., Torabi, A., and Zhang, Q. (2022). A new methodology inspired from the Theory of Critical Distances for determination of inherent tensile strength and fracture toughness of rock materials. Int. J. Rock Mech. Min. Sci. 152, 105073. doi:10.1016/j.ijrmms.2022.105073

CrossRef Full Text | Google Scholar

Bahrami, B., Ghouli, S., Nejati, M., Ayatollahi, M. R., and Driesner, T. (2022). Size effect in true mode II fracturing of rocks: theory and experiment. Eur. J. Mech. - A/Solids 94, 104593. doi:10.1016/j.euromechsol.2022.104593

CrossRef Full Text | Google Scholar

Cui, G., Lan, C., Zhou, C., Liu, Z., and Xia, C. (2024). Wmic - GMTS and Wmic - GMERR criteria for micron - scale crack propagation in red - bed soft rocks under hydraulic action. J. Rock Mech. Geotechnical Eng. 16 (12), 3641–3660. doi:10.1016/j.jrmge.2023.12.031

CrossRef Full Text | Google Scholar

De Silva, V. R. S., Konietzky, H., Märten, H., Ranjith, P. G., Lei, Z., and Xu, T. (2024b). Grain-scale numerical simulation of crystalline rock fracturing using Soundless Cracking Demolition Agents for in-situ preconditioning. Comput. Geotechnics 155, 105187. doi:10.1016/j.compgeo.2022.105187

CrossRef Full Text | Google Scholar

De Silva, V. R. S., Konietzky, H., Ranjith, P. G., and Manatunga, U. I. (2024a). Strain energy dependent numerical simulation of rock fracture initiation and propagation using soundless cracking demolition agents (SCDA): effects of SCDA-filled rock joints. Int. J. Rock Mech. and Min. Sci. 177, 105740. doi:10.1016/j.ijrmms.2024.105740

CrossRef Full Text | Google Scholar

Erarslan, N. (2016). Microstructural investigation of subcritical crack propagation and Fracture Process Zone (FPZ) by the reduction of rock fracture toughness under cyclic loading. Eng. Geol. 208, 181–190. doi:10.1016/j.enggeo.2016.04.035

CrossRef Full Text | Google Scholar

Ferguen, N., Mebdoua-Lahmar, Y., Lahmar, H., Leclerc, W., and Guessasma, M. (2019). DEM model for simulation of crack propagation in plasma-sprayed alumina coatings. Surf. Coatings Technol. 371, 287–297. doi:10.1016/j.surfcoat.2018.07.065

CrossRef Full Text | Google Scholar

Giannella, V., Vivo, E., Mazzeo, M., and Citarella, R. (2018). FEM-DBEM approach to simulate crack propagation in a turbine vane segment undergoing a fatigue load spectrum. Procedia Struct. Integr. 12, 479–491. doi:10.1016/j.prostr.2018.11.070

CrossRef Full Text | Google Scholar

Gibert, G., Prabel, B., Gravouil, A., and Jacquemoud, C. (2019). A 3D automatic mesh refinement X-FEM approach for fatigue crack propagation. Finite Elem. Analysis Des. 157, 21–37. doi:10.1016/j.finel.2019.01.008

CrossRef Full Text | Google Scholar

Han, G., Wang, S., Zhou, Y., Li, B., Lv, W., Chen, W., et al. (2025). An improved local coarsening method for discrete element simulation on cracking propagation in rock and rock-like materials. Comput. Geotechnics 179, 107002. doi:10.1016/j.compgeo.2024.107002

CrossRef Full Text | Google Scholar

Hasibi, H., Kamalodini, M., Hamzehei-Javaran, S., and Shojaee, S. (2023). The LSPIM-based numerical manifold method (NMM) for modeling transition elements. Eng. Analysis Bound. Elem. 149, 177–189. doi:10.1016/j.enganabound.2023.01.023

CrossRef Full Text | Google Scholar

Hu, X., Yu, S., Ying, P., and Dong, J. (2024). Effects of fissure locations on the crack propagation morphologies of 3D printing tunnel models: experiments and numerical simulations. Theor. Appl. Fract. Mech. 133, 104631. doi:10.1016/j.tafmec.2024.104631

CrossRef Full Text | Google Scholar

Jia, Q., Liu, X., and Tan, X. (2024). Crack evolution mechanism of stratified rock mass under different strength ratios and soft layer thickness: insights from DEM modeling. Soils Found. 64, 101534. doi:10.1016/j.sandf.2024.101534

CrossRef Full Text | Google Scholar

Justo, J., Castro, J., Miranda, M., Gatica, D., and Cicero, S. (2022). The theory of critical distances applied to fracture of rocks with circular cavities. Theor. Appl. Fract. Mech. 121, 103530. doi:10.1016/j.tafmec.2022.103530

CrossRef Full Text | Google Scholar

Kamalodini, M., Hamzehei-Javaran, S., and Shojaee, S. (2022). Static and dynamic analysis of plane elasticity using complex Fourier manifold method based on numerical improvement of Gauss–Legendre quadrature techniques. Eng. Analysis Bound. Elem. 143, 353–382. doi:10.1016/j.enganabound.2022.06.022

CrossRef Full Text | Google Scholar

Khalili, M., Fahimifar, A., and Shobeiri, H. (2023). The effect of bedding planes on the bending strength of rock-like material and evaluation of the crack propagation mechanism. Theor. Appl. Fract. Mech. 127, 104061. doi:10.1016/j.tafmec.2023.104061

CrossRef Full Text | Google Scholar

Kytýř, D., Koudelka, P., Drozdenko, D., Vavro, M., Fíla, T., Rada, V., et al. (2024). Acoustic emission and 4D X-ray micro-tomography for monitoring crack propagation in rocks. Int. J. Rock Mech. Min. Sci. 183, 105917. doi:10.1016/j.ijrmms.2024.105917

CrossRef Full Text | Google Scholar

Lawankar, S., Kumar, S., Pandit, B., Tiwari, G., and Deshpande, V. (2025). Dynamic behaviour of un-grouted and grouted jointed samples of a brittle rock in Split Hopkinson Pressure Bar tests: insights from experiments and DEM modelling. Eng. Geol. 351, 108033. doi:10.1016/j.enggeo.2025.108033

CrossRef Full Text | Google Scholar

Li, G., Wang, K., Tang, C., and Ye, J. (2024c). Non-break modeling and numerical simulation for non-intact rock failure process. Int. J. Rock Mech. Min. Sci. 176, 105725. doi:10.1016/j.ijrmms.2024.105725

CrossRef Full Text | Google Scholar

Li, J., Dai, L., Wang, S., Liu, Y., Sun, Y., Wang, J., et al. (2024d). Theoretical and numerical analysis of the rock breaking process by impact hammer. Powder Technol. 448, 120254. doi:10.1016/j.powtec.2024.120254

CrossRef Full Text | Google Scholar

Li, S., Huang, Z., Huang, K., Li, Y., Peng, H., Liang, Q., et al. (2024b). Study on the evolution law and quantitative characterization of micro-crack propagation in the compressive failure process of rocks. Eng. Fail. Anal. 155, 107743. doi:10.1016/j.engfailanal.2023.107743

CrossRef Full Text | Google Scholar

Li, Z., Kang, Y., Fan, J., Fourmeau, M., Jiang, D., Nelias, D., et al. (2024a). Macroscopic experimental study and microscopic phenomenon analysis of damage self-healing in salt rock. Eng. Geol. 338, 107634. doi:10.1016/j.enggeo.2024.107634

CrossRef Full Text | Google Scholar

Liang, J., Tong, D., Tan, F., Yi, X., Zou, J., and Lv, J. (2024). Numerical manifold method for thermo-mechanical coupling simulation of fractured rock mass. J. Rock Mech. Geotechnical Eng. 16, 1977–1992. doi:10.1016/j.jrmge.2023.07.020

CrossRef Full Text | Google Scholar

Mei, J., Yang, L., Zhang, W., Rong, Y., and Zhang, X. (2023). Stress corrosion and interaction behaviour of adjacent cracks in rock - like material under hydro - mechanical coupling: an experimental and numerical study. Mater. and Des. 236, 112522. doi:10.1016/j.matdes.2023.112522

CrossRef Full Text | Google Scholar

Nallala, S., He, H., and Senetakis, K. (2025). DEM multi-scale insights on the stress, energy and crack propagation in proppant-fractured rock collisions. Comput. Geotechnics 183, 107234. doi:10.1016/j.compgeo.2025.107234

CrossRef Full Text | Google Scholar

Nitka, M., and Rucka, M. (2025). 3D DEM modelling of acoustic emission in concrete: insights into elastic waves initiated by microcracks. Ultrasonics 150, 107599. doi:10.1016/j.ultras.2025.107599

PubMed Abstract | CrossRef Full Text | Google Scholar

Ouyang, S., Zhang, X., Yao, C., Ma, Y., Yang, J., Ye, Z., et al. (2024). Shear property and failure mechanism of bonded rock-cement interface: experimental and numerical approaches. J. Rock Mech. Geotechnical Eng. 17, 1018–1036. doi:10.1016/j.jrmge.2024.02.045

CrossRef Full Text | Google Scholar

Pletz, M., Frankl, S., and Schuecker, C. (2024). Evaluation of existing and introduction of new incremental crack propagation approaches in FEM. Theor. Appl. Fract. Mech. 131, 104452. doi:10.1016/j.tafmec.2024.104452

CrossRef Full Text | Google Scholar

Ren, X., Yu, S., Wang, H., Zhang, J. X., and Sun, Z. H. (2021). An improved form of SPH method and its numerical simulation study on the rock crack propagation containing fissures and holes. Arabian J. Sci. Eng. 46 (11), 11303–11317. doi:10.1007/s13369-021-05784-4

CrossRef Full Text | Google Scholar

Su, B., Xu, T., Shi, G., Heap, M. J., Yu, X., and Zhou, G. (2024). 3D numerical manifold method for crack propagation in rock materials using a local tracking algorithm. J. Rock Mech. Geotechnical Eng. 31, 177–182. doi:10.1016/j.jrmge.2024.04.038

CrossRef Full Text | Google Scholar

Tal, Y., Hatzor, Y., and Feng, X. (2014). An improved numerical manifold method for simulation of sequential excavation in fractured rocks. Int. J. Rock Mech. Min. Sci. 65, 116–128. doi:10.1016/j.ijrmms.2013.10.005

CrossRef Full Text | Google Scholar

Wang, L., Liu, H., and Zhou, X. (2024c). Investigating the influence of geometric configurations and loading modes on mixed mode I/II fracture characteristics of rocks: Part I-Numerical simulation. Eng. Fract. Mech. 311, 110575. doi:10.1016/j.engfracmech.2024.110575

CrossRef Full Text | Google Scholar

Wang, Z., Lei, X., Zhou, W., Wang, Y., Cao, J., Li, L., et al. (2023). Numerical simulation of the damage process of rock containing cracks by impacts of steel-particle water jet. Powder Technol. 422, 118465. doi:10.1016/j.powtec.2023.118465

CrossRef Full Text | Google Scholar

Wang, Z., Lian, H., Liang, W., Wu, P., Li, W., Yu, Y., et al. (2024a). Experimental study on crack propagation characteristics of unconventional reservoir rocks. Theor. Appl. Fract. Mech. 131, 104335. doi:10.1016/j.tafmec.2024.104335

CrossRef Full Text | Google Scholar

Wang, Z., Peng, J., Kwok, F. C. Y., Xu, C., Wang, L., and Dai, B. (2024b). Numerical simulation of failure and micro-cracking behavior of non-persistent rock joint under direct shear. Eng. Geol. 342, 107760. doi:10.1016/j.enggeo.2024.107760

CrossRef Full Text | Google Scholar

Xia, J., Li, D., Su, X., Zhao, J., Liu, Z., and Lyu, X. (2024). Image-based learning and experimental verification of crack propagation in random multi-fractures rock. Theor. Appl. Fract. Mech. 133, 104640. doi:10.1016/j.tafmec.2024.104640

CrossRef Full Text | Google Scholar

Xu, B., Xu, T., Heap, M. J., Kushnir, A. R. L., Su, B., and Lan, X. (2024). An adaptive phase field approach to 3D internal crack growth in rocks. Comput. Geotechnics 173, 106551. doi:10.1016/j.compgeo.2024.106551

CrossRef Full Text | Google Scholar

Yu, S., Hu, X., and Liang, Z. (2025a). Exploring the elliptic fissure cracking mechanisms from the perspective of sand 3D printing technology and Meshfree numerical strategy. Int. J. Solids Struct. 310, 113216. doi:10.1016/j.ijsolstr.2025.113216

CrossRef Full Text | Google Scholar

Yu, S., Huang, S., Li, Y., and Liang, Z. (2025b). Insights into the frost cracking mechanisms of concrete by using the coupled thermo-hydro-mechanical-damage meshless method. Theor. Appl. Fract. Mech. 136, 104814. doi:10.1016/j.tafmec.2024.104814

CrossRef Full Text | Google Scholar

Yu, S., Ren, X., and Zhang, J. (2024b). Modeling the rock frost cracking processes using an improved ice - stress -Damage coupling method. Theor. Appl. Fract. Mech. 131, 104421. doi:10.1016/j.tafmec.2024.104421

CrossRef Full Text | Google Scholar

Yu, S., Ren, X., Zhang, J., and Sun, Z. (2023a). Numerical simulation on the excavation damage of Jinping deep tunnels based on the SPH method. Geomechanics Geophys. Geo-Energy Geo-Resources 9, 1. doi:10.1007/s40948-023-00545-z

CrossRef Full Text | Google Scholar

Yu, S., Sun, Z., Qian, W., Yu, J., and Yang, J. (2023d). A meshless method for modeling the microscopic drying shrinkage cracking processes of concrete and its applications. Eng. Fract. Mech. 277, 109014. doi:10.1016/j.engfracmech.2022.109014

CrossRef Full Text | Google Scholar

Yu, S., Sun, Z., Yu, J., Yang, J., and Zhu, C. (2023b). An improved meshless method for modeling the mesoscale cracking processes of concrete containing random aggregates and initial defects. Constr. Build. Mater. 363, 129770. doi:10.1016/j.conbuildmat.2022.129770

CrossRef Full Text | Google Scholar

Yu, S., Wang, J., Gao, Y., Sun, W., Lu, J., Liu, R., et al. (2024a). Effects of fissure properties on the tunnel damage evolutions: insights from DIC-based 3D printing experiments and meshless numerical simulations. Tunn. Undergr. Space Technol. 149, 105817. doi:10.1016/j.tust.2024.105817

CrossRef Full Text | Google Scholar

Yu, S., Yang, X., Ren, X., Zhang, J., Gao, Y., and Zhang, T. (2023c). Shear damage simulations of rock masses containing fissure-holes using an improved SPH method. Materials 16, 2640. doi:10.3390/ma16072640

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, C., Lei, Q., Ziegler, M., and Loew, S. (2024b). Structurally-controlled failure and damage around an opening in faulted Opalinus Clay shale at the Mont Terri Rock Laboratory: in-situ experimental observation and 3D numerical simulation. Int. J. Rock Mech. Min. Sci. 180, 105812. doi:10.1016/j.ijrmms.2024.105812

CrossRef Full Text | Google Scholar

Zhao, X., Dong, W., and Li, S. (2024a). Investigation on the fatigue crack propagation of rock - concrete interface under fatigue loading below the initial cracking load. Eng. Struct. 315, 118407. doi:10.1016/j.engstruct.2024.118407

CrossRef Full Text | Google Scholar

Zhu, X., Lin, X., and Liu, W. (2025). Microscopic crack propagation and rock-breaking mechanism of heterogeneous granite under impact by special-shaped PDC cutters. Geoenergy Sci. Eng. 247, 213716. doi:10.1016/j.geoen.2025.213716

CrossRef Full Text | Google Scholar