Wide-field electromagnetic method for deep hot dry rock fracturing monitoring: penetrating thick low-resistivity overburden

Introduction: Hot dry rock (HDR) geothermal reservoirs are a vital renewable energy source, but their exploitation requires hydraulic fracturing (HF) to enhance permeability. However, traditional electromagnetic (EM) methods face significant limitations in monitoring deep HDR fracturing due to the shielding effect of thick low-resistivity overburden layers (>4,000 m, ρ < 80 Ωm). Overcoming this challenge is critical for optimizing HF operations and ensuring reservoir efficiency.

Methods: We propose the wide-field electromagnetic method (WFEM) as a novel solution for real-time HF monitoring in shielded environments. Through 3D numerical simulations and field applications in an Ordovician-Cambrian HDR reservoir (4,200–5,600 m depth), we evaluated WFEM’s sensitivity to resistivity changes induced by fracturing fluids. Key acquisition parameters were optimized via forward modeling, including transmitter-receiver distance (*r* = 15 km), current (I = 130 A), and electrode spacing (AB = 3,000 m, MN = 100 m).

Results: Field data revealed distinct resistivity reduction zones (1,000→25 Ωm) spatially correlated with active fracturing wells, demonstrating WFEM’s ability to detect fluid-induced anomalies (Δρ up to 30%). The method successfully mapped fluid distribution patterns, validating its resolution in deep, shielded geological settings.

Discussion: This study provides the first evidence of WFEM’s efficacy in monitoring deep HDR fracturing, offering a cost-effective alternative to microseismic methods. The results highlight WFEM’s potential for real-time HF monitoring in environments where conventional EM techniques fail. Future work should focus on integrating WFEM with multi-physical data to further improve fracture network characterization.

1 Introduction

Geothermal energy extraction from hot dry rock (HDR) reservoirs has emerged as a cornerstone for achieving carbon neutrality, with global HDR resources estimated at 3 × 10²¹ J (Tan et al., 2021; Wang et al., 2023; Wang et al., 2018). However, HDR systems typically exhibit ultra-low permeability (<0.1 mD) and require engineered hydraulic fracturing to create sustainable fracture networks for heat exchange (Breede et al., 2013; Olasolo et al., 2016). While microseismic monitoring remains the industry standard for fracture characterization, its limitations in resolving fluid migration and pre-existing fracture connectivity are well-documented (Cladouhos et al., 2013; Patel et al., 2017; Palisch et al., 2018).

Electromagnetic methods (EM) offer complementary advantages by directly probing resistivity changes induced by conductive fracturing fluids (Heagy et al., 2014; He et al., 2012). Magnetotelluric data from Australia’s Paralana project revealed 5% electromagnetic variations during fluid injection (Balfour et al., 2015; Macfarlane et al., 2014; Moore and Glaser, 2007). Domestic studies show comparable results: CSEM monitoring in Yichang shale wells detected 7% anomalies (Luo et al., 2022), while WFEM applications achieved effective monitoring at 1.8 km depth (Hu et al., 2023; Yan et al., 2018). Previous attempts, including magnetotellurics (Heinson et al., 2015; Macfarlane et al., 2014) and controlled-source EM (Zhang et al., 2023; Wang et al., 2017), achieved partial success but faced signal attenuation in thick conductive overburden (>4,000 m, ρ < 80 Ωm). The wide-field electromagnetic method (WFEM), originally developed for hydrocarbon exploration (He, 2015), utilizes a grounded dipole source and multi-frequency signals to penetrate high-resistivity contrast layers—a capability yet untested for HDR applications.

The significant attenuation of electromagnetic signals caused by the shielding effect of low-resistivity layers under thick overburden and deep geological conditions remains a major technical challenge. Current research primarily focuses on shallow shale gas fracturing monitoring (typically <3 km depth), while systematic studies on electromagnetic monitoring technologies for deep resource development (commonly >4 km) such as hot dry rock (HDR) systems remain scarce. The wide-field electromagnetic method (WFEM) presents a novel technical solution to these challenges, owing to its distinctive anti-interference capability, deep detection advantages, and high resolution.

This study addresses two critical gaps: (1) the absence of WFEM-based protocols for deep HDR fracturing monitoring, and (2) quantitative evaluation of parameter sensitivity (e.g., transmitter-receiver geometry, current intensity) in overburden-dominated systems. We integrate 3D forward modeling with field data from the Jiangsu EGS project to establish WFEM as a viable monitoring tool for reservoirs below 4,000 m.

2 Methodology

2.1 Principles of WFEM and design of observation system

The wide-field electromagnetic method (WFEM) is a frequency-domain EM method first introduced by He (2015). It involves the use of electromagnetic (EM) fields to detect and monitor subsurface structures and properties. Unlike traditional seismic methods, which primarily focus on the mechanical waves in the subsurface, WFEM uses electromagnetic waves to capture variations in the electrical resistivity of the earth’s materials. These variations can provide valuable information about subsurface fluid distribution, fracture networks, and other reservoir characteristics.

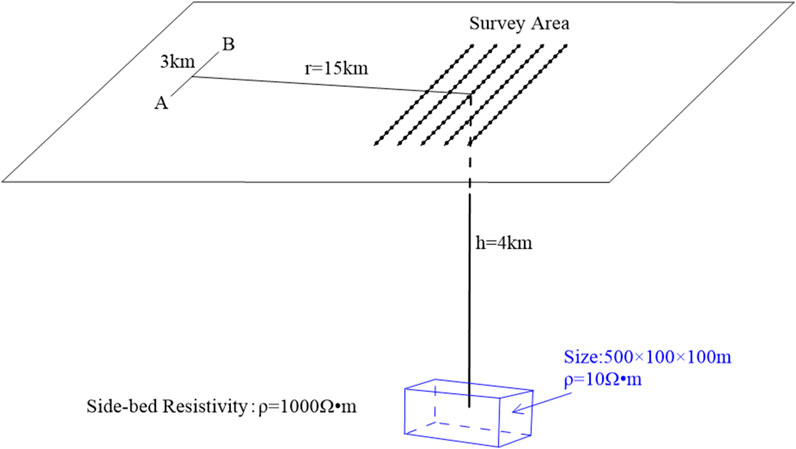
The WFEM method uses a grounded dipole AB as the source. It measures the perturbations in the electromagnetic fields by using the receiver electrodes MN, providing wide-field apparent resistivity data across a range of frequencies (Figure 1). This broad frequency range allows the WFEM method to detect subsurface targets at varying depths. The principle of WFEM for hydraulic fracturing monitoring involves utilizing electromagnetic signals to observe and analyze changes in the subsurface induced by the fracturing process.

Figure 1

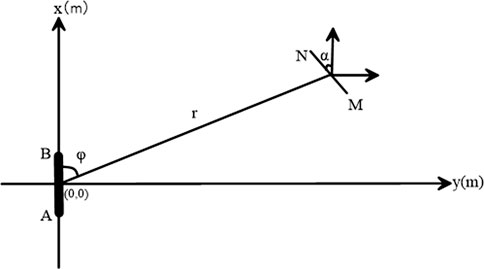
Figure 1. The schematic diagram for $E_{MN}$. AB denotes the source electrodes and MN denotes the receiver electrodes.

The magnetotelluric method (MT) has the characteristics of utilizing natural field sources, large detection depth, adopting plane wave theory, concise impedance form, and simple explanation. However, fracturing monitoring requires attention to timeliness, which is precisely the weakness of MT, with weak and random signals. In order to improve accuracy, it is necessary to stack the data multiple times during measurement, and the measurement speed is very slow. Therefore, it is necessary to use measurement points and frequency points with sparse intervals, resulting in low vertical and horizontal resolutions.

Compared with the MT method, the CSAMT method uses an artificial field source to overcome the randomness of the field source in the MT method, and the signal strength is greatly improved compared to the MT method. However, its detection depth is limited, and this study is based on the monitoring of deep fracturing in thick cover layers, which is obviously somewhat difficult for the CSAMT method.

The WFEM has established an electromagnetic exploration theory centered on surface waves, constructed a holographic electromagnetic exploration technology system, and achieved a theoretical leap from plane waves to surface waves in the frequency domain electromagnetic method. The method neither employs the Cagniard formula nor applies near-field-to-far-field corrections. Instead, it utilizes unsimplified full-domain formulations suitable for global-scale modeling, which are implemented through computer-programmed iterative inversion. This approach significantly expands the observable range of controlled-source electromagnetic methods while enhancing measurement speed, accuracy, and field operation efficiency. At the same time, the WFEM only measures one electric field component, reducing electromagnetic interference. The integration of wide-field resistivity method with 2n -sequence pseudo-random signals leads to the development of the 2n -sequence pseudo-random signal wide-field electromagnetic method, which effectively combines the advantages of both approaches.

Pseudo random signal is an artificially designed deterministic signal with approximate random statistical properties. Its characteristics include: broadband coverage, which means that a single transmission contains multiple frequency components, achieving multi frequency synchronous measurement. And with strong autocorrelation characteristics, that is, low cross-correlation with noise, effective signals can be extracted through correlation operations.

The WFEM method employs pseudo-random signal encoding to achieve three fundamental advantages over conventional electromagnetic techniques. First, multi-frequency synchronous excitation capability that acquires broadband data in a single transmission, significantly enhancing acquisition efficiency compared to the sequential frequency scanning of CSAMT. Secend, superior noise immunity through encoded signal correlation techniques that effectively suppress random noise and power-line interference, thereby improving signal-to-noise ratios. Again, concentrated energy distribution within designed frequency bands, overcoming the spectral dispersion limitations inherent in natural-field MT methods (He, 2019). These characteristics collectively enable more efficient, accurate, and high-resolution deep subsurface investigations.

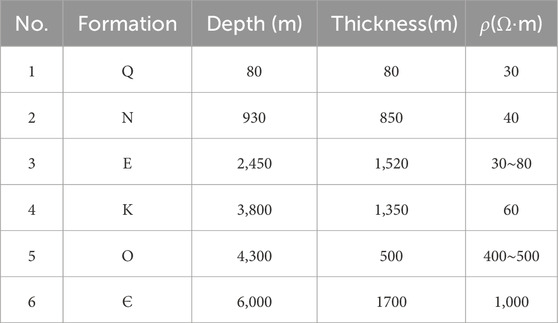
To monitor the HF for HDR, we first need to perform forward modeling to understand how the electromagnetic field may respond to the subsurface changes during HF. Therefore, a layered model (Figure 2) is created from a well log near the target area, with the electrical properties listed in Table 1. Layer 0 in Figure 2 is the air layer, and the electric dipole source is placed within the air layer at a height h₀ above the ground surface. Set the origin of the coordinate system at the ground surface directly below the center point of the electric dipole source, with the positive direction pointing vertically downward and the negative direction pointing upward. The bottom layer, i.e., the Nth layer, is usually taken as infinitely thick.

Figure 2

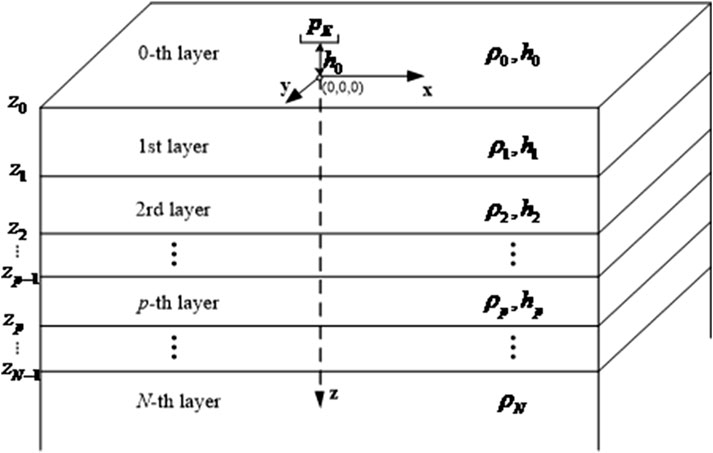
Figure 2. Schematic diagram of the isotropic layered electric model from a resistivity well log. The resistivity is denoted by ρ and the corresponding thickness is denoted by h.

Table 1

Table 1. Model parameters.

Let’s assume the relative permittivity ε and relative magnetic permeability μ of each layer are equal to 1. Then, we have the following descriptions of the EM field of the model shown in Figure 2:

$\left\{\begin{array}{l}{E}_x=i\omega \mu \frac{P_E}{2\pi }{\int }_0^{\infty }\left\{\begin{array}{l}\left(A\left(\lambda \right)+{\cos }^2\phi ·B\left(\lambda \right)\right)·\lambda ·J_0\left(\lambda r\right)+\\ \frac{1}{r}\left(1-2{\cos }^2\phi \right)·B\left(\lambda \right)·J_1\left(\lambda r\right)\end{array}\right\}d\lambda \\ E_y=i\omega \mu \frac{P_E}{2\pi }\frac{k_1^2}{k^2}\frac{xy}{r^2}{\int }_0^{\infty }B\left(\lambda \right)·\left(\lambda ·J_0\left(\lambda r\right)-\frac{2}{r}·J_1\left(\lambda r\right)\right)·d\lambda \\ E_{\mathrm{z}}=0\end{array}\right.(1)$

and

$\left\{\begin{array}{l}{H}_x=\frac{P_E}{4\pi }\sin 2\phi {\int }_0^{\infty }\lambda A\left(\lambda \right)\left(-\frac{2}{r}{J}_1\left(\lambda r\right)+\lambda J_0\left(\lambda r\right)\right)d\lambda \\ H_y=-\frac{P_E}{2\mathrm{\pi }}{\int }_0^{\infty }\left\{\left(\frac{u_1\lambda }{\lambda R_1\left(0\right)+u_1}+{\cos }^2\phi {\lambda }^{2}A\left(\lambda \right)\right)·J_0\left(\lambda r\right)-\frac{1}{r}\cos 2\phi A\left(\lambda \right)\lambda ·J_1\left(\lambda r\right)\right\}d\lambda \\ H_z=\frac{P_E}{4\pi }\frac{y}{r}{\int }_0^{\infty }2{\lambda }^{2}A\left(\lambda \right)J_1\left(\lambda r\right)d\lambda \end{array}\right..(2)$

The parameters E_x, E_y, E_z are the x, y, z components of the electric field E(V/m), while H_x、H_y、H_z are x, y, z components of the magnetic field H(A/m). The imaginary number is denoted by $i=\sqrt{-1}$ and f is the frequency in Hz and ω is the angular frequency. The parameter P_E (A·m) is the strength of the electric field and can be related to the current I (A) by $P_E=Idl$ with dl (m) be the length of the dipole, and the wavenumber is defined as $k^2=-i\omega \mu /\rho -{\omega }^2\epsilon \mu$. The parameters A(λ) and B(λ) are defined as

$\left\{\begin{array}{l}A\left(\lambda \right)\equiv \frac{1}{\lambda +u_1/R_1\left(0\right)}\\ B\left(\lambda \right)\equiv \frac{u_1}{R_1^{*}\left(0\right)k_1^2}-A\left(\lambda \right)\end{array}\right.,(3)$

with

$\left\{\begin{array}{l}{R}_1\left(0\right)=\text{cth}\left[a_1{z}_1+\text{arcth}\frac{a_1{b}_1}{a_2{b}_2}\text{cth}\left(a_2{z}_2+\cdots +\text{arcth}\frac{a_{N-1}{b}_{N-1}}{a_N{b}_N}\right)\right]\\ R_1^{*}\left(0\right)=\text{cth}\left[u_1{z}_1+\text{arcth}\frac{u_1{\rho }_1}{u_2{\rho }_2}\text{cth}\left(u_2{z}_2+\cdots +\text{arcth}\frac{u_{N-1}{\rho }_{N-1}}{u_N{\rho }_N}\right)\right]\end{array}\right.(4)$

As shown in Figure 1, if the angle between MN and E_x is α, then we have arbitrary horizontal electric field components E_MN as:

$E_{MN}=i\omega \mu \frac{P_E}{2\pi }\left[E_x\cos \alpha +E_y\sin \alpha \right].(5)$

During the hydraulic processing, the same acquisition system is maintained on the ground to ensure the parameters for the observation system are unchanged. Thus the measurement error is greatly reduced and the abnormality due to formation fracturing can stand out. A parameter η_MN is defined to describe the variation of the electrical field before and after hydraulic fracturing:

${\eta }_{MN}\equiv \frac{E_{MN2}-E_{MN1}}{E_{MN1}}=\frac{E_{MN2}}{E_{MN1}}-1(6)$

Here, the subscripts ₁ and ₂ indicate the electric field before and after hydraulic fracturing, respectively, determined by using Equations 1, 5.

2.2 Experimental design for parameter optimization

A layered model shown in Table 1 is created from the well log data from the thick coverage area. Then, Equations 1–6 are applied to this layered model for forward modeling analysis. The shallow overburden layers Q and N have much lower resistivity and a total thickness of about 930 m. The formation E also with low resistivity and a thickness of over 1,000 m. The target zone for a hot dry rock reservoir is within the formation Є and is at about 5,000 m,which is assumed as a uniform medium with infinite extension. The resistivity of formation Є is about 1,000 Ωm, which is about 15 times higher than the overburden layers. This noticeable contrast in electrical resistivity leads to the low-resistivity shielding effect, which prevents the electromagnetic waves from effectively penetrating deeper areas.

Around the target zone, a 100 m long section is assembled with equipment for hydraulic fracturing to create an enhanced geothermal system. For the numerical simulation, we assume that the resistivity of the target area is reduced from 1,000 to 25 Ωm (Didana et al., 2017). In the following, a detailed analysis of the transmitter-receiver distance r, current I, power electrode spacing AB, and receiver electrode spacings MN is conducted to evaluate how these parameters may influence the received signal, and thus an optimal acquisition system can be designed for hydraulic fracturing monitoring.

2.2.1 Transmitter-receiver distance r

We first assume the power electrode spacing is a constant AB = 3000 m, the current is I = 130 A, and the receiver electrode spacing is MN = 100 m. Then, the test is done with transmitter-receiver distance r to be 9, 12, 15, and 18 km, respectively. With varying r, the WFEM forward modeling is implemented for the reservoir before and after hydraulic fracturing, with the corresponding result shown by Figures 3a,b, respectively. It clearly shows that as the transmitter-receiver distance r increases, the horizontal component E_MN of the electric field for both before and after hydraulic fracturing decreases with increasing r. However, the difference η_MN defined by Equation 6 is increasing with increased r, the maximum value of which is about 16%. Thus, a transmitter-receiver distance of r = 15 km is chosen as this selection can assure a relatively high SNR for η_MN, and achieve reliable monitoring.

Figure 3

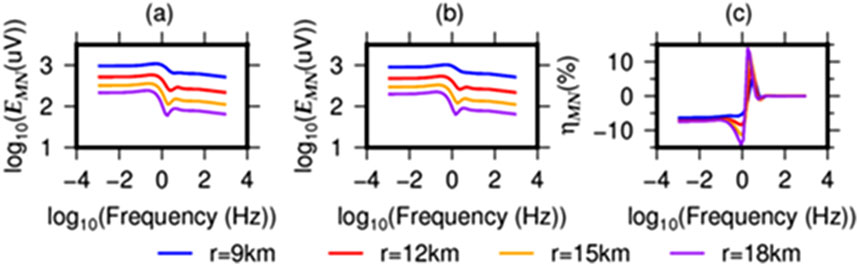
Figure 3. Change in the strength E_MN of the electric field with varying transmitter-receiver distance r (a) before and (b) after hydraulic fracturing, and (c) the difference η_MN. The resistivity of the target area is assumed to be reduced from 1,000 Ωm to 25 Ωm after hydraulic fracturing.

2.2.2 Current intensity (I)

For this modeling, we maintain power electrode spacing AB = 3000 m, receiver electrode spacing MN = 100 m, and a transmitter-receiver distance r = 15 km as constant, but test how varying current I may influence the abnormal η_MN. This time, I = 50, 100, and 150 A are considered. A similar forward modeling is done as in Section 2.1, which gives us the results shown in Figure 4. Results in Figures 4a,b show that E_MN is proportional to the intensity of current I, but interestingly, the abnormal η_MN due to hydraulic fracturing is independent of varying current I. Thus, to ensure the signal SNR, a higher current is preferable within the permissible range of the WFE equipment (with a 180 KW transmitter, the actual working current can reach a maximum of 130–150 A).

Figure 4

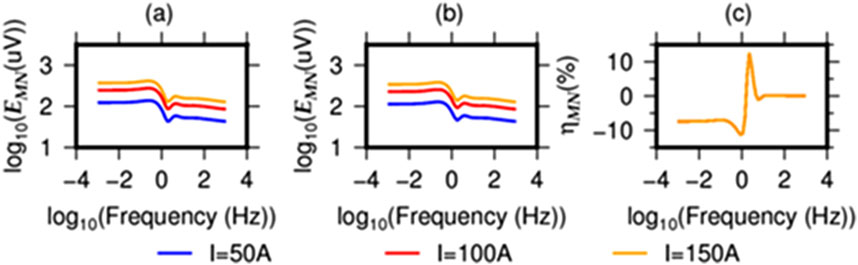
Figure 4. The E_MN (a) before and (b) after hydraulic fracturing as the current I varies. (c) Indicates the percentage difference.

2.2.3 Dipole length (AB)

In this investigation, we change the spacing AB of the power electrode (AB = 1000, 2000, 3000 m), but with I = 130 A, MN = 100 m, r = 15 km remain unchanged. The corresponding results in Figures 5a,b indicate that with increasing AB, the E_MN increases. However, similar to the analysis on the current I, the η_MN is independent of changing AB (Figure 5C). This test shows that a larger AB should be recommended as it gives higher E_MN.

Figure 5

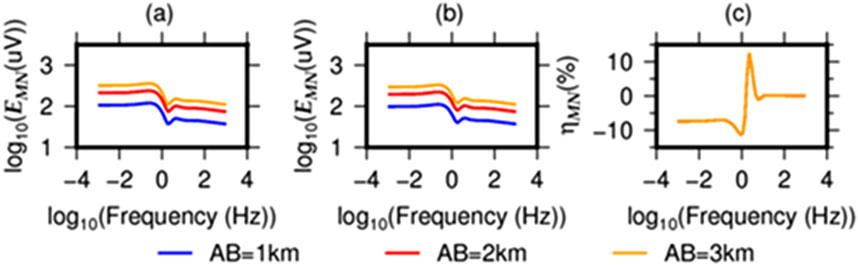
Figure 5. The E_MN (a) before and (b) after hydraulic fracturing with varying power supply electrode distance AB. Similar to Figure 4, the difference in percentage is shown by (c).

2.2.4 Receiver spacing (MN)

Similar to the other tests, only the receiver electrode spacing MN will be changed (MN = 50, 100, 200 m), while the I = 130 A, AB = 3000 m, and r = 15 km are kept constant. Again, the abnormal η_MN is not influenced by the changing MN (Figure 6c). Although, a larger MN means a stronger E_MN (Figures 6a,b), this time MN = 100 m is recommended as a smaller MN indicates a higher resolution.

Figure 6

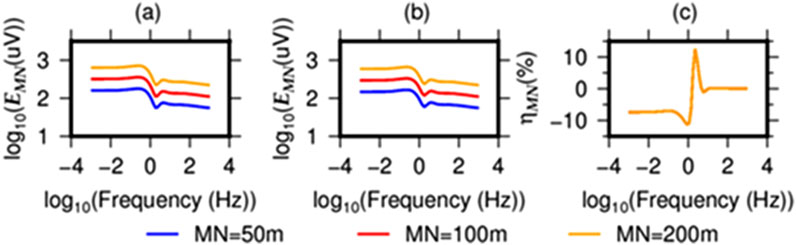
Figure 6. The E_MN (a) before and (b) after hydraulic fracturing with varying receiver spacing MN. Similar to Figure 4, the difference in percentage is shown by (c).

In summary, it can be concluded that for better hydraulic fracturing monitoring, stronger current I, larger transmitter electrode distance (AB), larger receiver electrode distance (MN), and a smaller transmitter-receiver distance (r) should be selected. However, as r increases, the intensity of the observed monitoring signals decreases which may result in noisy E_MN. In such cases, it is necessary to increase both the current I and the transmitter electrode distance AB to ensure the SNR is high enough. Considering the monitoring depth and post-fracturing anomaly magnitude, the observation system parameters for deep fracturing monitoring with a thick coverage area of 5000 m are chosen as follows: I = 130A, r = 15 km, AB = 3000 m, MN = 100 m. Furthermore, from the analysis above, it is found that noticeable anomaly η_MN mainly occurs within the frequency range of 10–0.1 Hz, with the largest anomaly response close to 1 Hz, meeting the acquisition requirements for WFEM.

2.3 Analysis of the effectiveness of deep fracturing monitoring in thick coverage areas

Based on the aforementioned thick-overburden stratigraphic model, we assume a fracturing interval thickness of 100 m located at a depth of approximately 5,000 m, into which fracturing fluid (resistivity = 0.3 Ωm) is injected. The pre-fracturing resistivity of the target interval is 1,000 Ωm. We calculate the monitoring signals before and after fracturing, as well as the post-fracturing anomaly response, for scenarios where the resistivity of the fractured zone is altered to 100, 50, 25, and 10 Ωm, respectively. The simulation parameters are set as follows: current I = 130 A, transmitter-receiver distance r = 15 km, transmitter dipole length AB = 3,000 m, and receiver dipole length MN = 100 m.

The results (Figure 7) demonstrate that a lower post-fracturing resistivity correlates with a stronger electric field variation in the low-frequency band and a higher anomaly amplitude. Specifically, at a post-fracturing resistivity of 25 Ωm, the relative anomaly amplitude is approximately ±12%; and at a post-fracturing resistivity of 10 Ωm, the relative anomaly amplitude increases to ±25%.

Figure 7

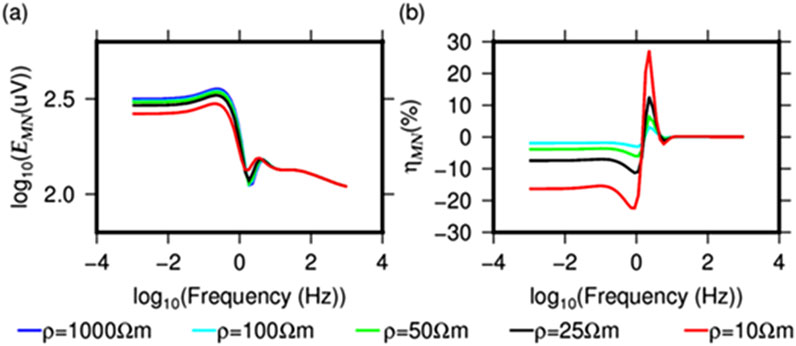
Figure 7. (a) The E_MN by assuming different resistivities of the target formation and (b) the percentage difference compared to ρ = 1,000 Ωm.

Given the low resistivity of the fracturing fluid (0.3 Ωm) and the fact that reservoir stimulation typically involves multi-stage fracturing, a post-fracturing resistivity of 25 Ωm is a realistic assumption. Under this condition, the anomaly amplitude of ±12% is detectable using the Wide-Field Electromagnetic Method (WFEM), enabling effective monitoring of resistivity changes and extraction of fracturing-induced anomalies.

3 Results and discussion

In this section, a numerical simulation is first conducted to predict if the designed acquisition system can effectively detect the changes in the E_MN. Then, during hydraulic fracturing monitoring, a three-dimensional array measurement network is set up: the emission source is grounded with a dipole AB of 3,000 m, arranged along the x-axis direction, and the center point is located at the coordinate origin; Receiving array: centered on the fracturing well, the measuring points are distributed in a grid pattern, with MN = 100 m parallel to AB, and finally all measuring points are subjected to 3D inversion. Real data are shown to prove the effectiveness of the WFEM approach.

3.1 Numerical simulation

Based on the geological parameters in Table 1, we developed a three-dimensional geoelectric model (Figure 8). The three-dimensional numerical simulation method adopts the integral equation method. Firstly, the conjugate Green’s function is introduced to transform the Maxwell equation system into the second type of Fredholm type integral equation. The second type of Fredholm type integral equation is transformed into a matrix equation using numerical methods, and the electric field distribution inside the anomalous body is obtained by solving the matrix equation. Then, numerical integration of the electric field inside the anomalous body is performed using the corresponding conjugate Green’s function to obtain the electric field at any point outside the anomalous body.

Figure 8

Figure 8. Schematic diagram of three-dimensional geoelectric model.

Numerical simulations were performed to evaluate the electromagnetic responses of both the background formation model (representing pre-fracturing conditions) and the three-dimensional geoelectric model (characterizing post-fracturing conditions). The relative amplitude variations between these states were quantitatively assessed using Equation 6, enabling systematic analysis of the fracturing-induced electromagnetic signature alterations.

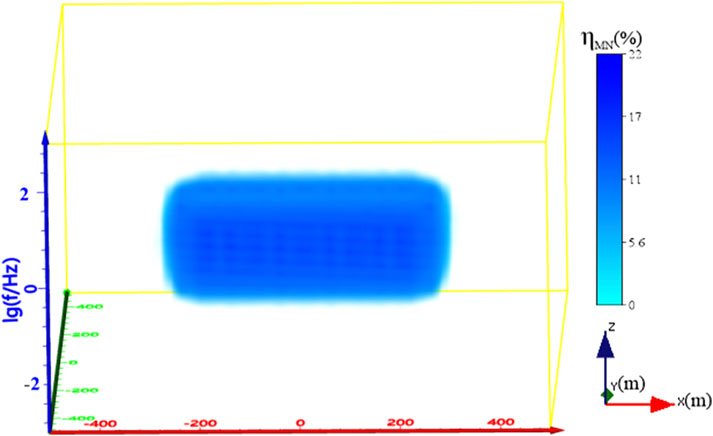
For a fracture zone measuring 500 m × 100 m × 100 m with a post-fracturing resistivity of 10 Ωm, Figure 9 presents the corresponding three-dimensional electromagnetic simulation results. The simulated anomaly exhibits a spatial extent approximately 15%–20% larger than the actual fracture dimensions, a phenomenon attributable to volumetric effects in electromagnetic induction. Nevertheless, the results demonstrate clear resolution of the fracture geometry, with observed anomalous amplitudes exceeding 20% which is significant.

Figure 9

Figure 9. Three dimensional simulation diagram of fracture abnormal amplitude.

Previous studies were based on horizontally layered models. To better align with actual geological conditions, the current model integrates the following field-specific characteristics from Well 1 and Well 2, including variations in fracturing well trajectories. Wireline perforation technology (creating 8–12 mm diameter perforations) was employed to establish initial fluid pathways for hydraulic fracturing, directly influencing fracture initiation points and propagation patterns. A total fracturing fluid volume of 10,000 m³ was injected in five staged segments, with fluid migration radiating outward from the wellbore along perforation channels.

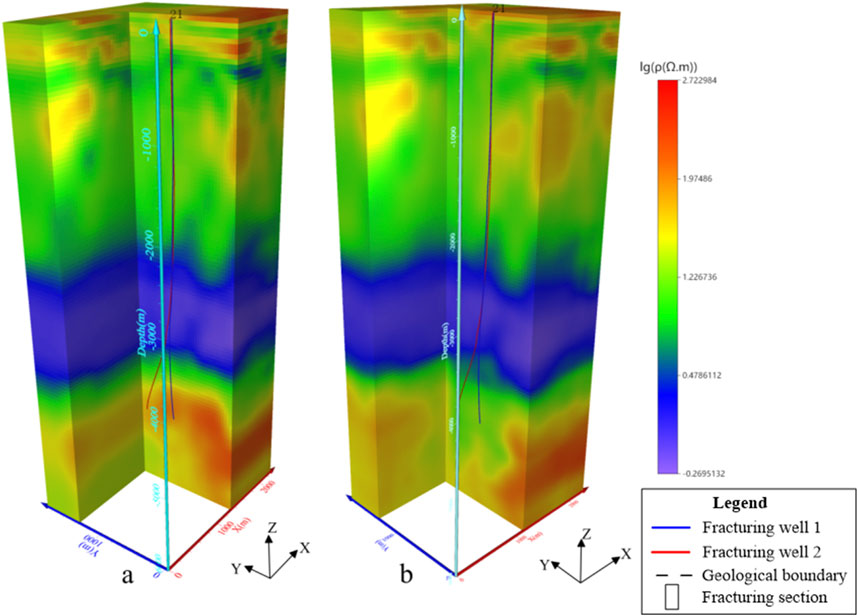
The left of Figure 10 shows the resistivity anomaly amplitude contour map within 4,500–5,500 m after fracturing, and the right of Figure 10 is the depth slice at 5000 m displaying the resistivity anomaly amplitude contour map. Figure 10 clearly illustrates the extent and spatial distribution characteristics of the fracturing fluid after fracturing: the resistivity is lowest at the center of the fracturing and gradually increases towards the periphery, indicating that the low-resistivity range is the extent of the fracturing fluid’s influence. The maximum resistivity anomaly can be as high as 25%, indicating that the WEFM technique is feasible for monitoring hot dry rock fracturing in thick overburden areas.

Figure 10

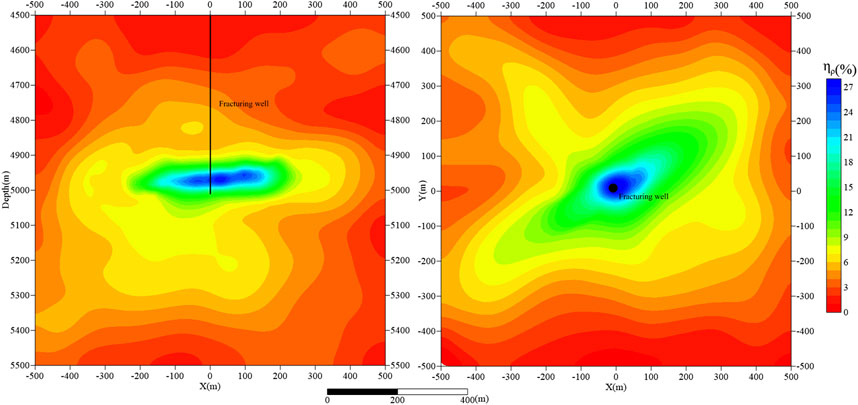
Figure 10. Contour maps of the perturbation η_MN after fracturing: vertical (left) and horizontal (right) sections. This result is obtained by forward modeling.

3.2 Field application

This monitoring work is a three-dimensional survey network. The integral equation method is used to carry out data inversion with three-dimensional CSEM inversion software. Before inversion, the two-dimensional stratigraphic model is structured and set as the inversion background. The inversion space depth is 6,000 m. Because the two-dimensional inversion results are used as the background model in the inversion, the inversion can increase the continuity of the vertical direction of the survey line on the basis of the two-dimensional inversion results, making the inversion results more authentic and reliable.

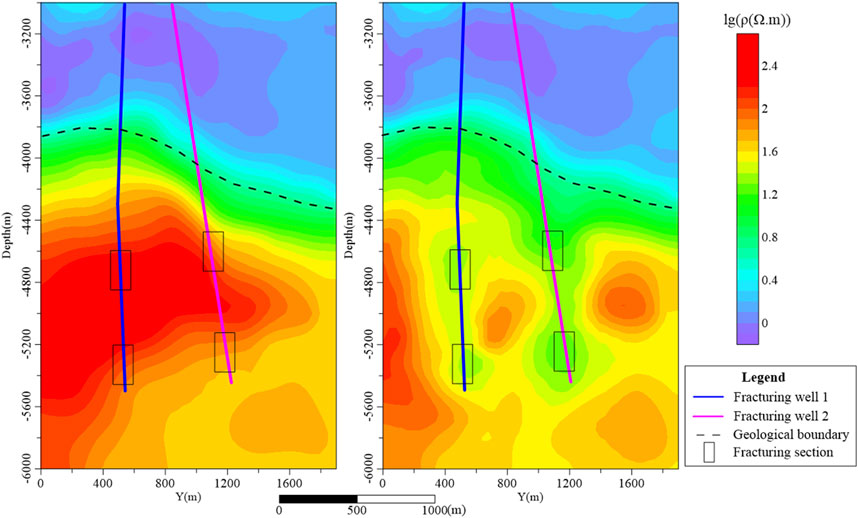
In this field example, the thickness of the overburden layer of the hot dry rock reservoir is nearly 4,000 m, with an overall much lower resistivity. Two fracturing wells are arranged in the study area, and the reconstruction target areas are located in the deep section of 4,400 m, which are fractured in multiple sections. Measurement nets are set up with Fracturing Well 1 and Fracturing Well 2 as the centers, and WFEM is carried out before and after the hydraulic fracturing. The corresponding results are shown in Figures 11, 12: the left plot indicates the resistivity map before the hydraulic fracturing, and in the right plot the resistivity map after fracturing is shown. The resistivity changes in non-fractured sections (above the dashed line in Figures 11, 12) are minimal. However, there is a significant change in the resistivity of the fractured zones: the resistivity has been remarkably reduced. Some high-resistivity bodies have been disrupted and transformed into medium-low resistivity anomalies. These medium-low resistivity anomalies are near the wellbore, suggesting where fracturing fluid has been accumulated. The comparison between the well-log measurements and the predicted results indicates that the WFEM is highly reliable (Figure 13). These results demonstrate that the application of WFEM for monitoring hot dry rock fracturing beneath thick overburden layers is highly effective.

Figure 11

Figure 11. Resistivity map before (left) and after (right) fracturing predicted by WFEM.

Figure 12

Figure 12. Resistivity map of 3D before (a) and after (b) fracturing predicted by WFEM.

Figure 13

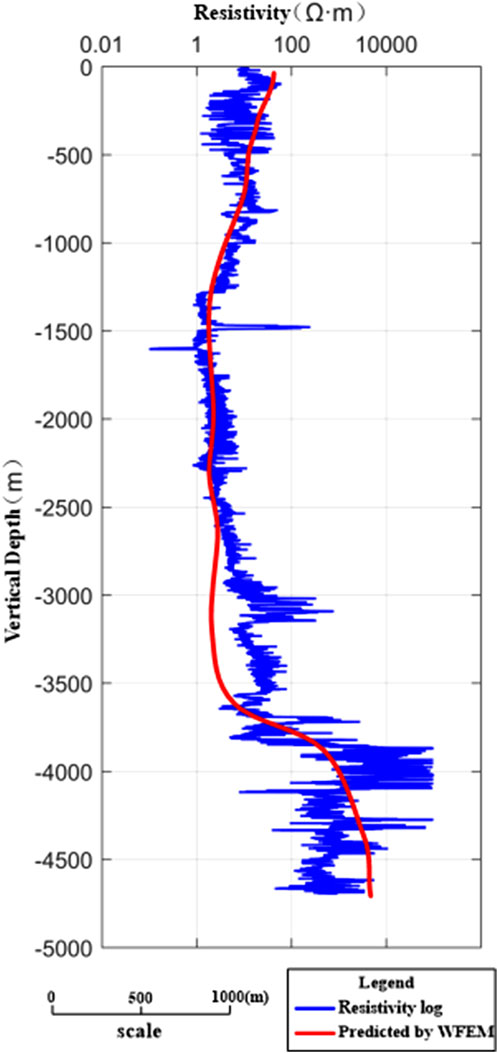
Figure 13. Resistivity log (blue) along the blue well log in Figure 9a before hydraulic fracturing and the predicted resistivity by using WFEM (red).

3.3 Compared to traditional methods

Compared with other electromagnetic methods, the exploration depth is large, the signal-to-noise ratio is strong, and the advantages are very obvious. Compared to microseismic monitoring in parallel wells, WFEM achieved 25% higher spatial resolution in mapping fluid boundaries, albeit with lower temporal resolution. This trade-off positions WFEM as ideal for post-fracturing reservoir assessment.

4 Conclusion

Based on the Wide-Field Electromagnetic method, this study explores the feasibility of monitoring hydraulic fracturing at great depth overlaid by thick layers. The results show that the electrical characteristics of the fractured formation undergo significant changes before and after fracturing. With a fixed ground observation system and constant system parameters, the changes in electrical properties caused by fracturing fluid can be accurately measured. The amplitude of anomaly is only related to the transmitter-receiver distance r, while the signal strength during monitoring is associated with current I, transmitter electrode distance AB, receiver electrode distance MN, and also transmitter-receiver distance r.

This study establishes WFEM as the first EM-based method capable of monitoring hydraulic fracturing in HDR reservoirs beneath >4,000 m conductive overburden. Key advances include:

(1) Parameter optimization: 15 km transmitter-receiver distance with 130 A current maximizes anomaly detection (η_MN = 16–30%) while maintaining SNR.

(2) Field validation: Resistivity reduction from 1,000 to 25 Ωm in target zones aligns with independent well logs, confirming WFEM’s accuracy in fluid distribution mapping.

(3) Economic impact: WFEM reduces monitoring costs by 40% compared to microseismic arrays, critical for large-scale EGS deployment.

Future work should integrate WFEM with distributed acoustic sensing (DAS) to achieve spatiotemporal synergy in fracture characterization.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SG: Writing – original draft, Writing – review and editing. WD: Methodology, Writing – review and editing. JW: Methodology, Writing – review and editing. MX: Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Balfour, N. J., Cummins, P. R., Pilia, S., and Love, D. (2015). Localization of intraplate deformation through fluid-assisted faulting in the lower-crust: the Flinders Ranges, South Australia. Tectonophysics 655, 97–106. doi:10.1016/j.tecto.2015.05.014

CrossRef Full Text | Google Scholar

Breede, K., Dzebisashvili, K., Liu, X., and Falcone, G. (2013). A systematic review of enhanced (or engineered) geothermal systems: past, present and future. Geotherm. Energy 1 (1), 4–27. doi:10.1186/2195-9706-1-4

CrossRef Full Text | Google Scholar

Cladouhos, T. T., Petty, S., Nordin, Y., Moore, M., Grasso, K., Uddenberg, M., et al. (2013). “Microseismic monitoring of newberry volcano EGS demonstration,” in Proceedings of the 38th Workshop on Geothermal Reservoir Engineering (Stanford, CA), 11–13.

Google Scholar

Didana, Y. L., Heinson, G., Thiel, S., and Krieger, L. (2017). Magnetotelluric monitoring of permeability enhancement at enhanced geothermal system project. Geothermics 66, 23–38. doi:10.1016/j.geothermics.2016.11.005

CrossRef Full Text | Google Scholar

He, J. (2015). Wide field electromagnetic methods. SEG Technical Program Expanded Abstracts 2015, 34 (1), 1006–1011. doi:10.1190/segam2015-5835894.1

CrossRef Full Text | Google Scholar

He, J. (2019). Theory and technology of wide field electromagnetic method. Chin. J. Nonferrous Metals 29 (9), 1809–1816. in Chinese. doi:10.19476/j.ysxb.1004.0609.2019.09.02

CrossRef Full Text | Google Scholar

He, L., Hu, X., Xu, L., He, Z., and Li, W. (2012). Feasibility of monitoring hydraulic fracturing using time-lapse audio-magnetotellurics. Geophysics 77 (4), WB119–WB126. doi:10.1190/geo2011-0378.1

CrossRef Full Text | Google Scholar

Heagy, L. J., Oldenburg, D. W., and Chen, J. (2014). Where does the proppant go? examining the application of electromagnetic methods for hydraulic fracture characterization. GeoConvention 2014.

Google Scholar

Heinson, G., Carter, S., Krieger, L., Boren, G., and Matthews, C. (2015). “Magnetotelluric monitoring of a hydraulic fracturing in Moomba, South Australia,” in International Conference and Exhibition, Melbourne, Australia, 13-16 September 2015, 506. doi:10.1190/ice2015-2209947

CrossRef Full Text | Google Scholar

Hu, Z. F., Luo, W. F., and Wang, S. J. (2023). Application of wide field electromagnetic method in the fracturing monitoring of well Anye-2. Geophys. Geochem. Explor. 47 (3), 718–725. in Chinese. doi:10.11720/wtyht.2023.1089

CrossRef Full Text | Google Scholar

Luo, W. F., Hu, Z. F., and Wang, S. J. (2022). Monitoring test of shale fracturing based on controlled source electromagnetic technology: taking well Eyangye 2HF in Yichang area as an example. J. Jilin Univ. Sci. Ed. 52 (4), 1338–1347. in Chinese. doi:10.13278/j.cnki.jjuese.20210274

CrossRef Full Text | Google Scholar

Macfarlane, J., Thiel, S., Pek, J., Peacock, J., and Heinson, G. (2014). Characterisation of induced fracture networks within an enhanced geothermal system using anisotropic electromagnetic modelling. J. Volcanol. Geotherm. Res. 288, 1–7. doi:10.1016/j.jvolgeores.2014.10.002

CrossRef Full Text | Google Scholar

Moore, J. R., and Glaser, S. D. (2007). Self-potential observations during hydraulic fracturing. J. Geophys. Res. 112, B02204. doi:10.1029/2006jb004373

CrossRef Full Text | Google Scholar

Olasolo, P., Juárez, M. C., Morales, M. P., and Liarte, I. A. (2016). Enhanced geothermal systems (EGS): a review. Renew. Sustain. Energy Rev. 56, 133–144. doi:10.1016/j.rser.2015.11.031

CrossRef Full Text | Google Scholar

Palisch, T., Al-Tailji, W., Bartel, L., Cannan, C., Zhang, J., Czapski, M., et al. (2018). Far-field proppant detection using electromagnetic methods: latest field results. SPE Prod. and Operations 33 (03), 557–568. doi:10.2118/184880-pa

CrossRef Full Text | Google Scholar

Patel, S., Sondergeld, C., and Rai, C. (2017). Laboratory studies of hydraulic fracturing by cyclic injection. Int. J. Rock Mech. Min. Sci. 95, 8–15. doi:10.1016/j.ijrmms.2017.03.008

CrossRef Full Text | Google Scholar

Tan, H., Ling, F., Guo, Z., Li, J., and Liu, J. (2021). Application of a wide-field electromagnetic method for hot dry rock exploration: a case study in the Gonghe basin, Qinghai, China. Minerals 11, 1105. doi:10.3390/min11101105

CrossRef Full Text | Google Scholar

Wang, G., Zhang, W., Ma, F., Lin, W., Liang, J., and Zhu, X. (2018). Overview on hydrothermal and hot dry rock researches in China. China Geol. 1 (2), 273–285. doi:10.31035/cg2018021

CrossRef Full Text | Google Scholar

Wang, J., Zhao, Z., Gao, S., Luo, C., Li, L., Xu, M., et al. (2023). Application of a comprehensive geophysical exploration methods in the exploration of geothermal resources in Yueliangwan, Binhai County. Geophys. Geochem. Explor. 47 (2), 321–330. in Chinese. doi:10.11720/wtyht.2023.1205

CrossRef Full Text | Google Scholar

Wang, Z., Gang, Y., Zhang, L., Wang, C., Zhang, J., and Liu, Z. (2017). The use of time-frequency domain electromagnetic technique to monitor hydraulic fracturing: SEG Technical Program, Expanded Abstracts, 1268–1273.

Google Scholar

Yan, L., Chen, X., Tang, H., Xie, X., Zhou, L., Hu, W., et al. (2018). Continuous TDEM for monitoring shale hydraulic fracturing. Appl. Geophys. 15, 26–34. doi:10.1007/s11770-018-0661-1

CrossRef Full Text | Google Scholar

Zhang, Z., Liu, J., Guo, R., Kouadio, K., Zhan, S., Li, A., et al. (2023). Electromagnetic monitoring with local mesh for time-lapse monitoring of hydraulic fracturing. J. Appl. Geophys. 212, 104995. doi:10.1016/j.jappgeo.2023.104995

CrossRef Full Text | Google Scholar